Machine Learning-Based Partition Method for Cyclic Development Mode of Submarine Soil Martials from Offshore Wind Farms
Abstract
1. Introduction
2. Tests and Samples
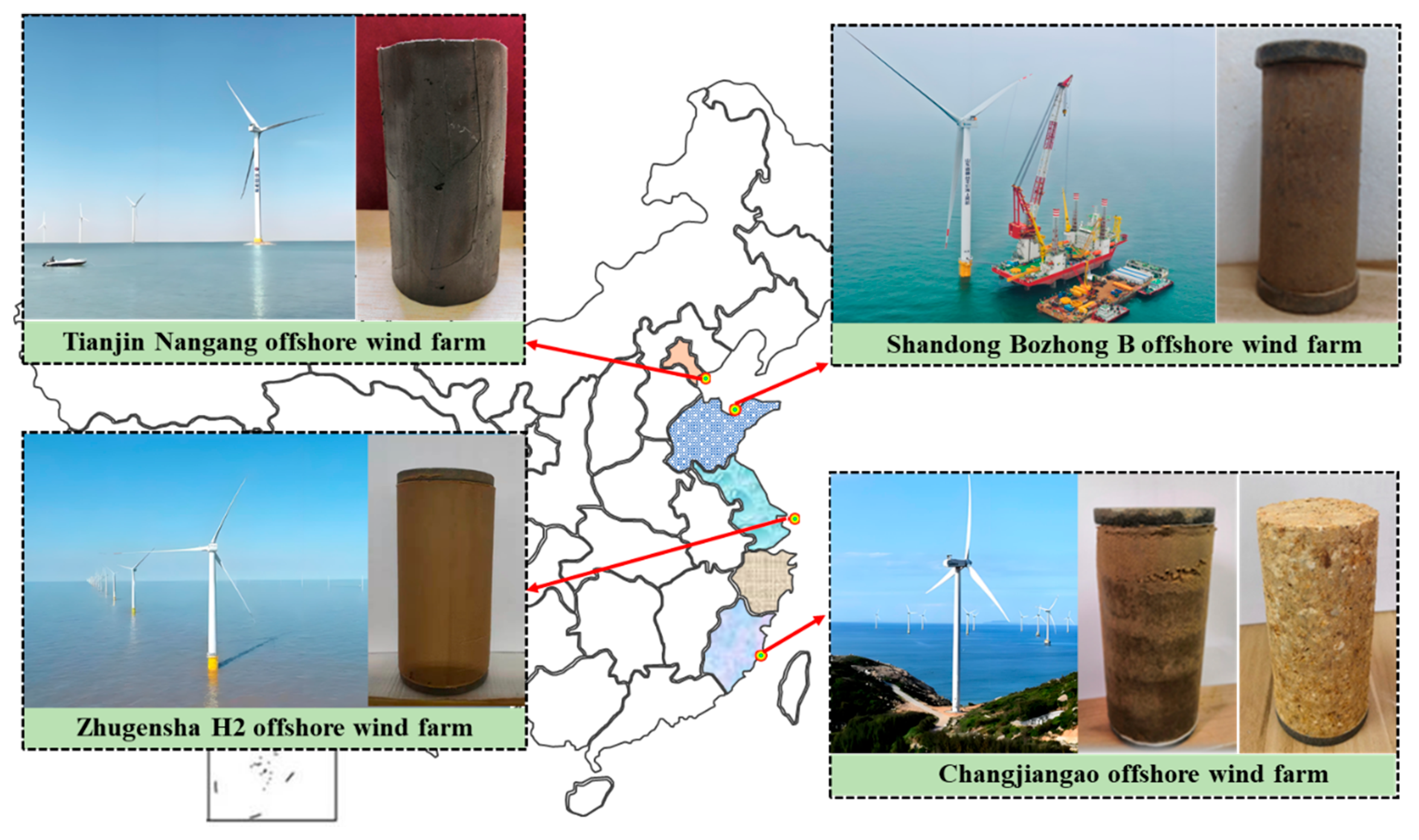
2.1. Submarine Soils from Offshore Wind Farms
2.2. Testing Instrument and Experimental Processes
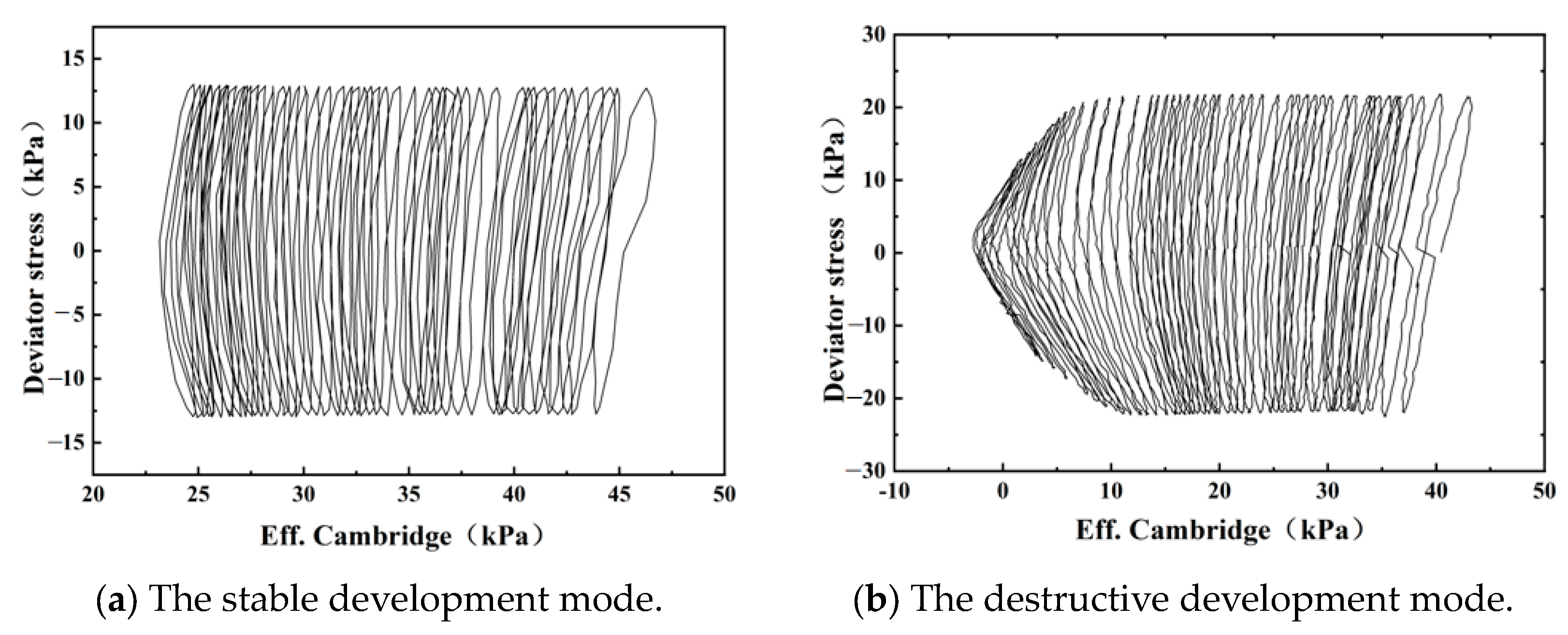
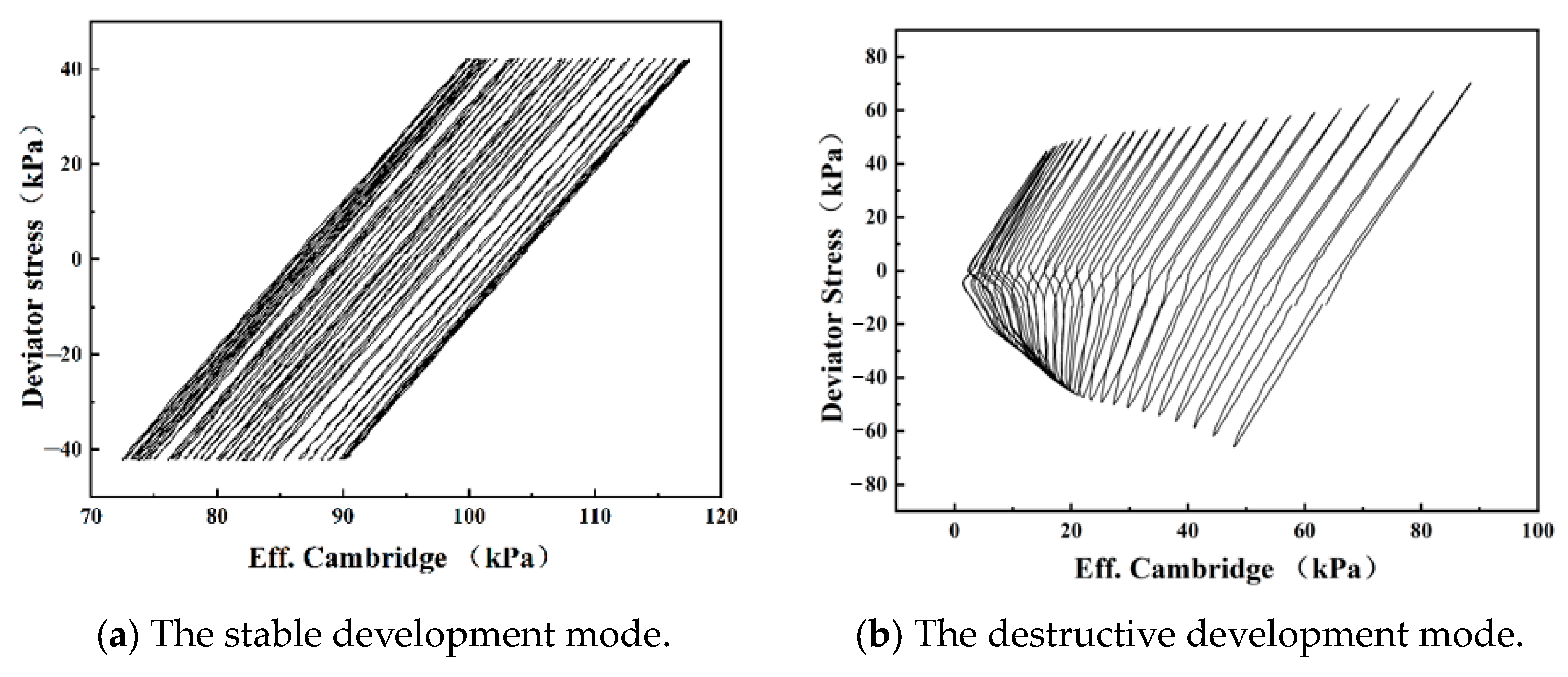
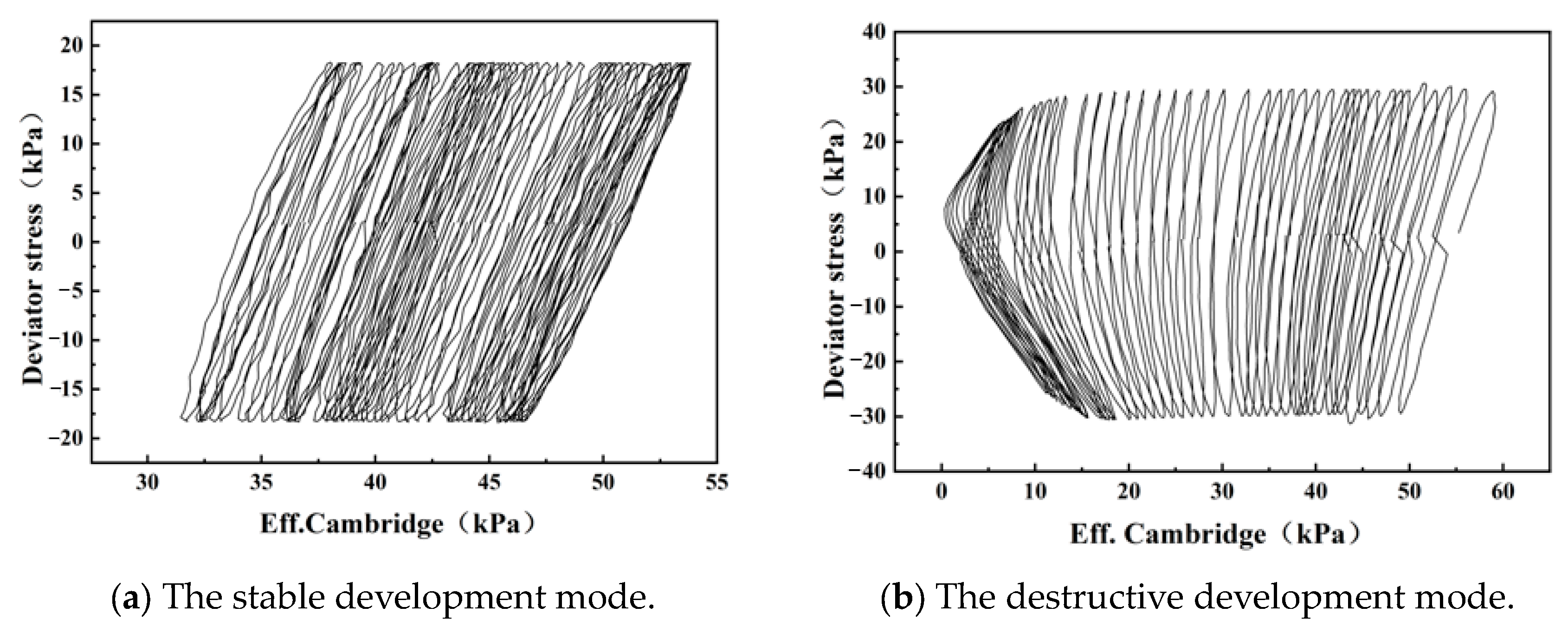
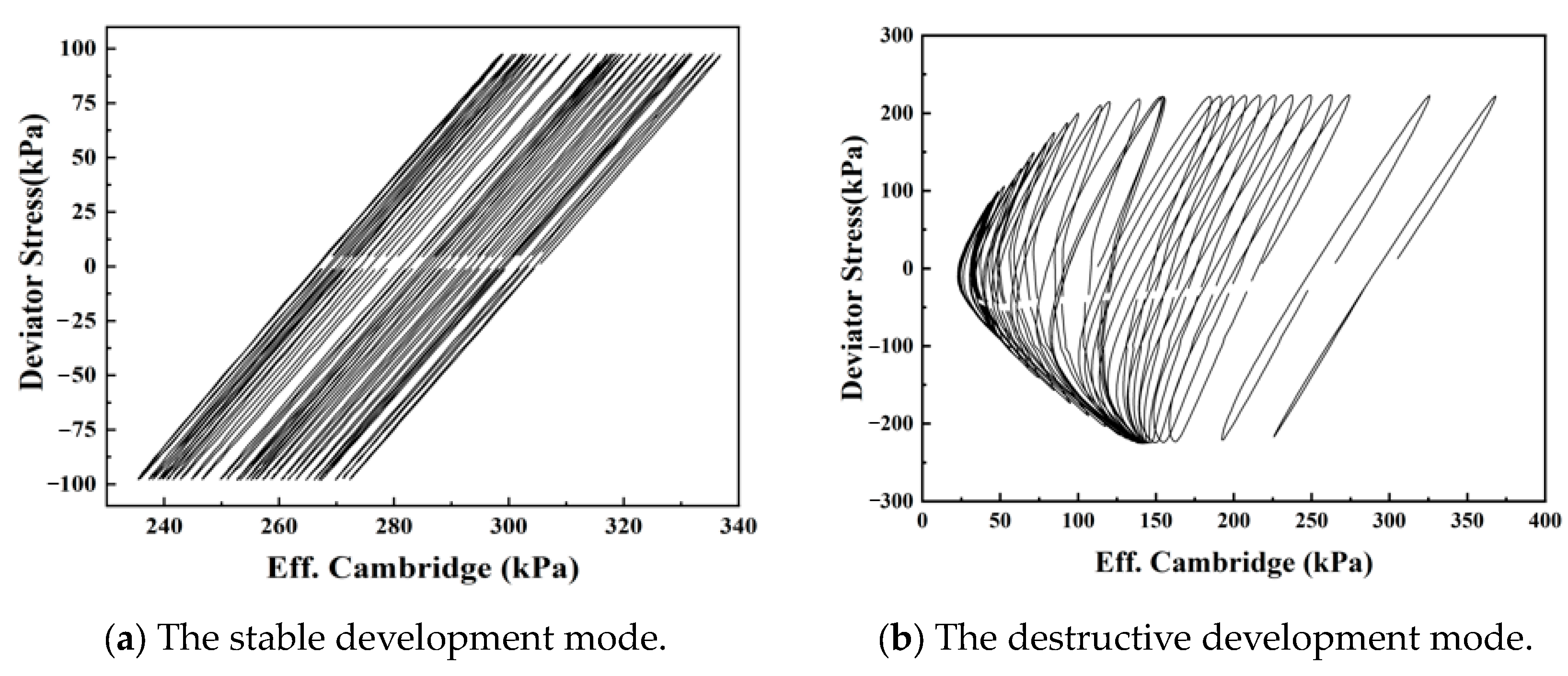
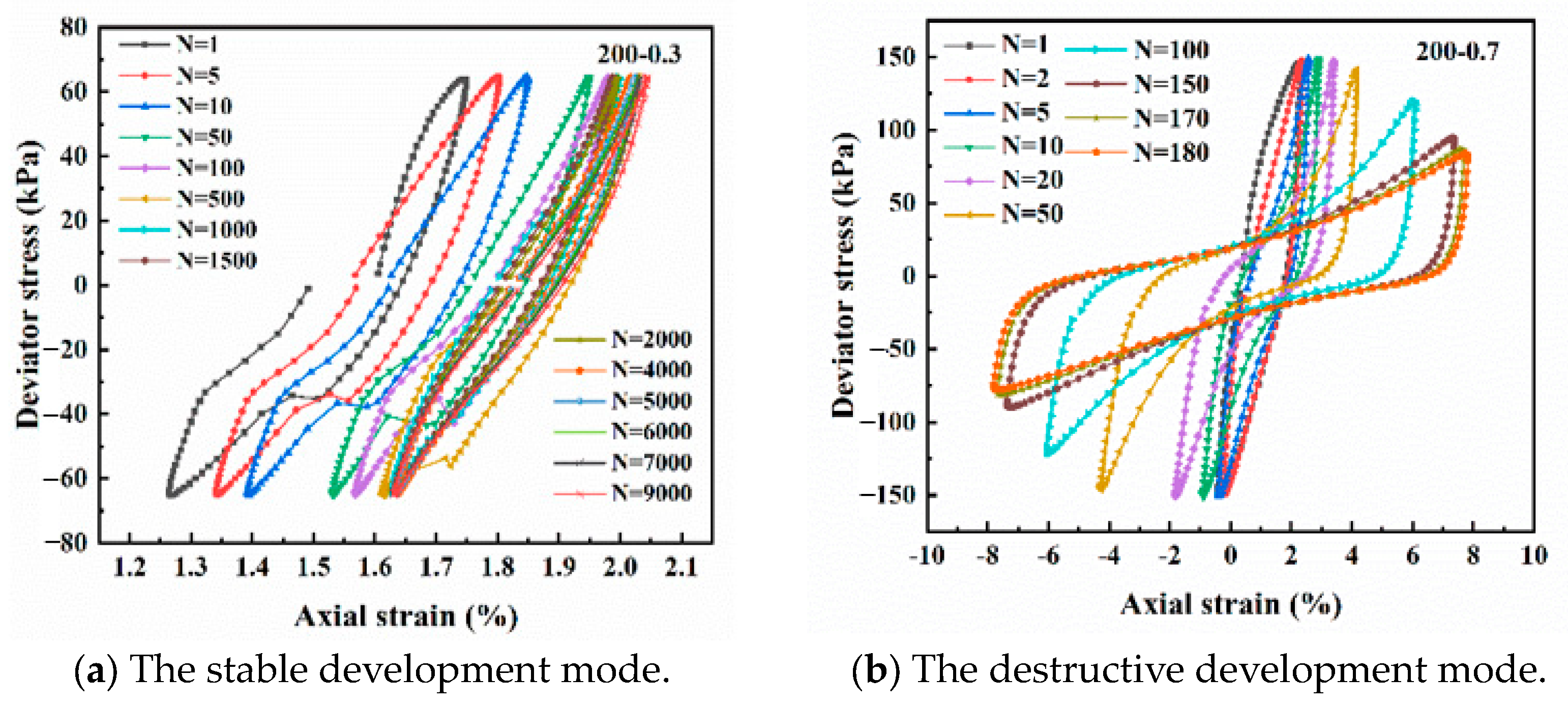
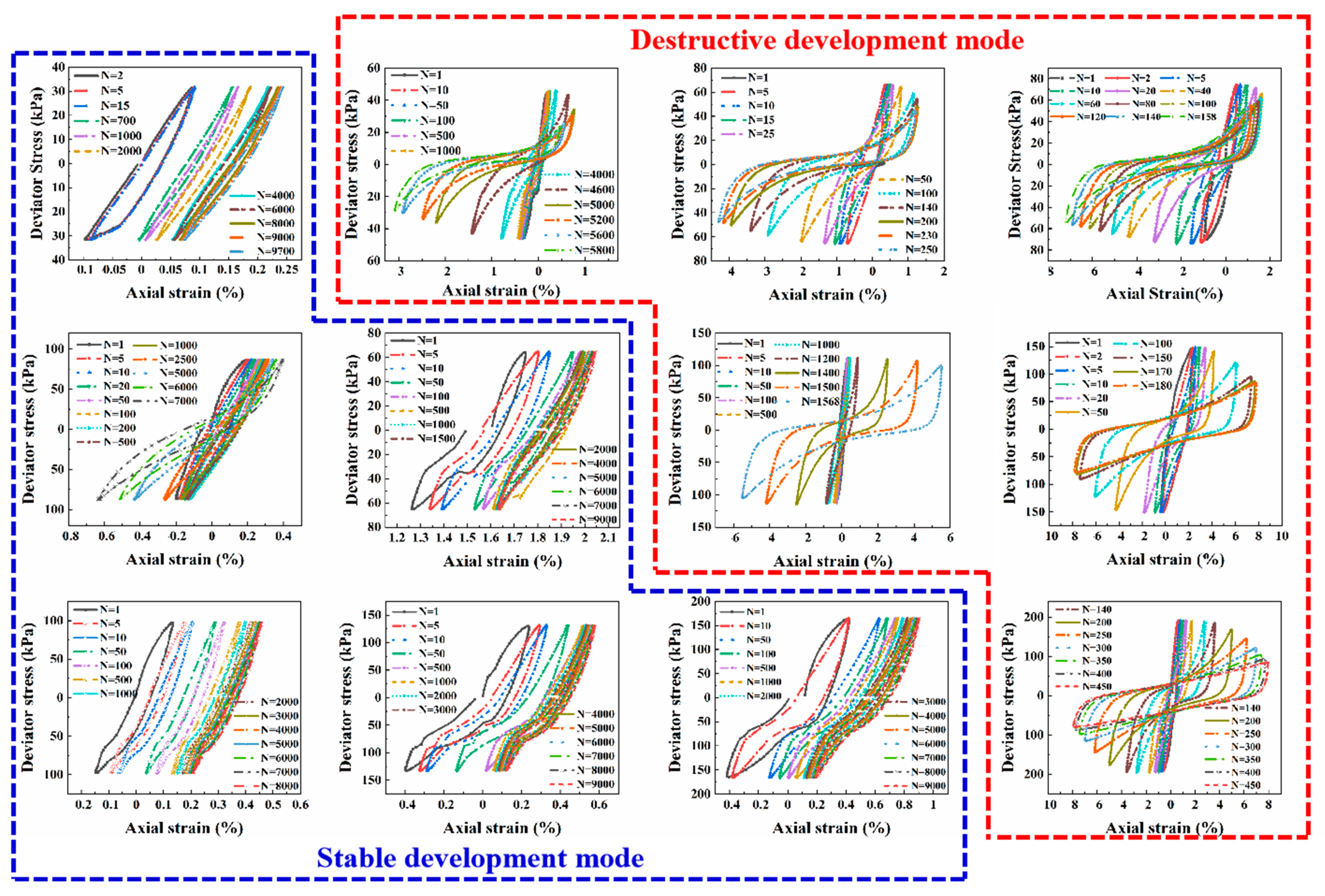
3. Cyclic Failure Mode of Submarine Soil
3.1. Cyclic Behavior of Submarine Soil
3.2. Critical CSR of Submarine Soil
4. Methodology
4.1. Random Forest
4.2. Gradient Boosting Decision Tree
4.3. Modeling Development
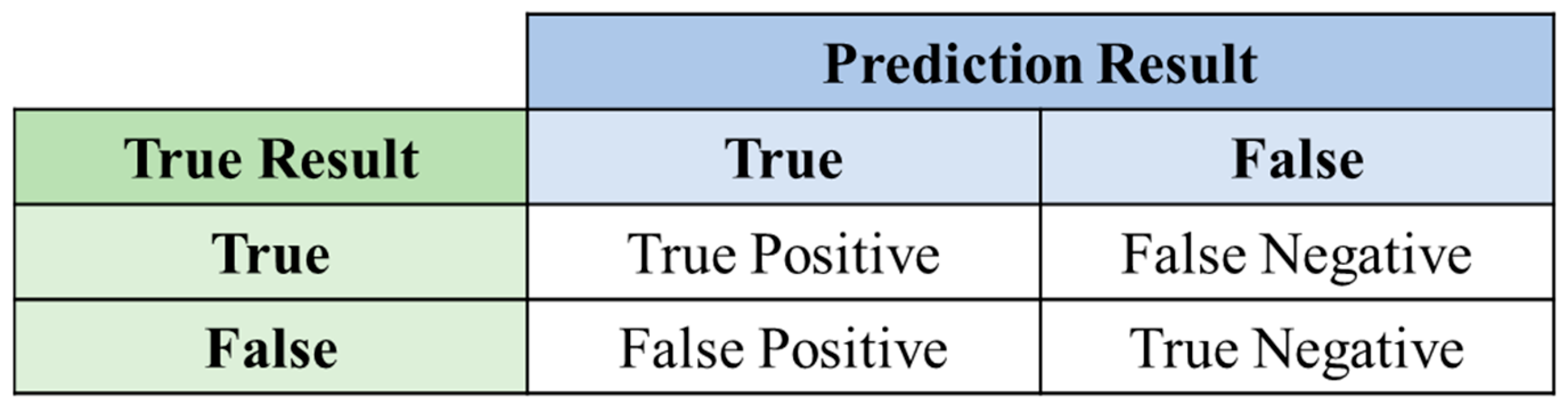
4.4. Model Evaluation Indexes
5. Results and Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Liu, D.; Liu, M.; Xu, X.; Wang, J.; Fan, C.; Li, X.; Han, J. Future prospects research on offshore wind power scale in China based on signal decomposition and extreme learning machine optimized by principal component analysis. Energy Sci. Eng. 2020, 8, 3514–3530. [Google Scholar] [CrossRef]
- Jansen, M.; Staffell, I.; Kitzing, L.; Quoilin, S.; Wiggelinkhuizen, E.; Bulder, B.; Riepin, I.; Müsgens, F. Offshore wind competitiveness in mature markets without subsidy. Nat. Energy 2020, 5, 614–622. [Google Scholar] [CrossRef]
- GWEC.NET. Associate Sponsors Podcast Sponsor Leading Sponsor Supporting Sponsor Co-Leading Sponsor (n.d.). Available online: www.gwec.net (accessed on 1 January 2025).
- Wang, Y.; Zhang, S.; Yin, S.; Liu, X.; Zhang, X. Accumulated Plastic Strain Behavior of Granite Residual Soil under Cycle Loading. Int. J. Geomech. 2020, 20, 04020205. [Google Scholar] [CrossRef]
- Yan, X.; Zhang, N.; Ma, K.; Wei, C.; Yang, S.; Pan, B. Overview of Current Situation and Trend of Offshore Wind Power Development in China. Power Gener. Technol. 2024, 45, 1. [Google Scholar] [CrossRef]
- Ma, H.; Deng, Y.; Chang, X. Effect of long-term lateral cyclic loading on the dynamic response and fatigue life of monopile-supported offshore wind turbines. Mar. Struct. 2024, 93, 103521. [Google Scholar] [CrossRef]
- Zhang, X.; Zhou, R.; Han, Y. Study on p-y curve of large diameter pile under long-term cyclic loading. Appl. Ocean Res. 2023, 140, 103736. [Google Scholar] [CrossRef]
- Xiao, W.; Wu, K.; Xu, W.; Liu, Y.; Lu, H.; Chen, R. Experiment and analysis on dynamic characteristics of marine soft clay. Mar. Georesources Geotechnol. 2024, 12, 1549. [Google Scholar] [CrossRef]
- Yang, J.; Cui, Z.D.; Xi, B.; Song, W. Experimental study on cyclic triaxial behaviors of saturated soft soil considering time intermittent and variable confining pressure. Soil Dyn. Earthq. Eng. 2024, 179, 108508. [Google Scholar] [CrossRef]
- Dai, S.; Yu, X.; Han, B.; He, B. Cyclic behavior of seabed building material of offshore wind farm in rock-based sea area: Submarine completely weathered granite. Ocean Eng. 2024, 296, 117024. [Google Scholar] [CrossRef]
- Jiang, L.; Sun, J.; Liu, X. Pore-space microstructure and clay content effect on the elastic properties of sandstones. Pet. Sci. Technol. 2012, 30, 830–840. [Google Scholar] [CrossRef]
- Liu, F.; Cai, Y.; Xu, C.; Wang, J. Research on the attenuation law of dynamic elastic modulus of soft soil under cyclic loading. J. Zhejiang Univ. Eng. Ed. 2008, 9, 1479–1483. [Google Scholar]
- Samir El-Kady, M.; ElMesmary, M.A. Cyclic strengths for high density soils related to pore water pressure. Innov. Infrastruct. Solut. 2018, 3, 46. [Google Scholar] [CrossRef]
- Kim, J.; Yoo, M. Development of Excess Pore Water Pressure in Sand during K0-Controlled Cyclic Loading. KSCE J. Civ. Eng. 2024, 28, 1790–1796. [Google Scholar] [CrossRef]
- Dai, S.; Yu, X.; Han, B.; Zhang, Z.; He, B.; Lin, M. Failure criterion of submarine completely weathered granite under cyclic loads in rock-based sea area. Ocean Eng. 2024, 313, 119422. [Google Scholar] [CrossRef]
- Gao, H.; Sun, J.; Stuedlein, A.W.; Li, S.; Wang, Z.; Liu, L.; Zhang, X. Flowability of Saturated Sands under Cyclic Loading and the Viscous Fluid Flow Failure Criterion for Liquefaction Triggering. J. Geotech. Geoenviron. Eng. 2024, 150, 04023130. [Google Scholar] [CrossRef]
- Jiao, G.; Zhao, S.; Ma, W.; Luo, F.; Kong, X. The evolution law of hysteresis loop of frozen soil under cyclic loading. J. Geotech. Eng. 2013, 7, 1343–1349. [Google Scholar]
- Bocheńska, M.; Srokosz, P.E. Artificial Neural Network-aided Mathematical Model for Predicting Soil Stress-strain Hysteresis Loop Evolution. Civ. Environ. Eng. Rep. 2024, 34, 120–135. [Google Scholar] [CrossRef]
- Dai, S.; Han, B.; Li, N.; Wang, B.; He, B.; Liu, J. Morphologic analysis of hysteretic behavior of China Laizhou Bay submarine mucky clay and its cyclic failure criteria. Bull. Eng. Geol. Environ. 2022, 81, 52. [Google Scholar] [CrossRef]
- Doygun, O.; Brandes, H.G. High strain damping for sands from load-controlled cyclic tests: Correlation between stored strain energy and pore water pressure. Soil Dyn. Earthq. Eng. 2020, 134, 106134. [Google Scholar] [CrossRef]
- Alyami, M.; Onyelowe, K.; AlAteah, A.H.; Alahmari, T.S.; Alsubeai, A.; Ullah, I.; Javed, M.F. Innovative hybrid machine learning models for estimating the compressive strength of copper mine tailings concrete. Case Stud. Constr. Mater. 2024, 21, e03869. [Google Scholar] [CrossRef]
- Inqiad, W.B.; Dumitrascu, E.V.; Dobre, R.A.; Khan, N.M.; Hammood, A.H.; Henedy, S.N.; Khan, R.M.A. Predicting compressive strength of hollow concrete prisms using machine learning techniques and explainable artificial intelligence (XAI). Heliyon 2024, 10, e36841. [Google Scholar] [CrossRef] [PubMed]
- Ozkaynak, M.I.; Yilmaz, Y. Prediction of resilient modulus with pre-post experimental data of undisturbed subgrade soils using machine learning algorithms. Transp. Geotech. 2024, 49, 101396. [Google Scholar] [CrossRef]
- Wang, X.; Dong, X.; Zhang, Z.; Zhang, J.; Ma, G.; Yang, X. Compaction quality evaluation of subgrade based on soil characteristics assessment using machine learning. Transp. Geotech. 2022, 32, 100703. [Google Scholar] [CrossRef]
- Sun, J.; Zhang, R.; Zhang, A.; Wang, X.; Wang, J.; Ren, L.; Zhang, Z.; Zhang, Z. Rock strength prediction based on machine learning: A study from prediction model to mechanism explanation. Measurement 2024, 238, 115373. [Google Scholar] [CrossRef]
- Hansen, T.F.; Erharter, G.H.; Liu, Z.; Torresen, J. A comparative study on machine learning approaches for rock mass classification using drilling data. Appl. Comput. Geosci. 2024, 24, 100199. [Google Scholar] [CrossRef]
- Arif, M.; Jan, F.; Rezzoug, A.; Afridi, M.A.; Luqman, M.; Khan, W.A.; Kujawa, M.; Alabduljabbar, H.; Khan, M. Data-driven models for predicting compressive strength of 3D-printed fiber-reinforced concrete using interpretable machine learning algorithms. Case Stud. Constr. Mater. 2024, 21, e03935. [Google Scholar] [CrossRef]
- Zhang, Z.; Yu, X.; Han, B.; Dai, S. Cumulative strain intelligent evaluation of marine soil from offshore wind farms based on enhanced machine learning. Appl. Ocean Res. 2024, 153, 104265. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, Z.; Song, Z.; Li, J. Engineering properties of marine soft clay stabilized by alkali residue and steel slag: An experimental study and ANN model. Acta Geotech. 2022, 17, 5089–5112. [Google Scholar] [CrossRef]
- Zhao, Y.; Teng, C. Classification of soil layers in Deep Cement Mixing using optimized random forest integrated with AB-SMOTE for imbalance data. Comput. Geotech. 2025, 179, 106976. [Google Scholar] [CrossRef]
- Huang, C.; Du, H.; Li, L.; Ni, J.; Sun, Y. Application of tree-based methods in predicting the surface settlement arising from the tunnel excavation with large mix-shield. Soils Found. 2023, 63, 101379. [Google Scholar] [CrossRef]



| Soil Type | Natural Density (g/cm3) | Water Content (%) | Liquid Limit (%) | Plastic Limit (%) | Plasticity Index | Uniformity Coefficient Cu | Curvature Coefficient Cc |
|---|---|---|---|---|---|---|---|
| MC | 1.68 | 21.2 | 50.28 | 24.53 | 25.75 | 2.40 | 0.82 |
| SC | 2.01 | 15.28 | 21.72 | 13.21 | 8.51 | 8.30 | 0.75 |
| SS | 1.89 | 26.53 | 46.82 | 25.17 | 21.65 | 29.20 | 3.10 |
| WRS | 1.90 | 31.36 | 37.05 | 22.98 | 14.07 | 100.20 | 0.18 |
| CWG | 1.51 | 19.36 | 40.20 | 25.20 | 15.00 | 202.00 | 0.65 |
| Soil Type | Confining Pressure (kPa) | CSR |
|---|---|---|
| MC | 40, 55, 70 | 0.3, 0.35, 0.4, 0.5 |
| SC | 100, 200, 300 | 0.3, 0.35, 0.4, 0.6, 0.7 |
| SS | 100, 160, 220 | 0.09, 0.12, 0.14, 0.16, 0.19, 0.21 |
| WRS | 40, 55, 70 | 0.4, 0.45, 0.5, 0.6, 0.7 |
| CWG | 100, 200, 300 | 0.3, 0.4, 0.5, 0.6, 0.7 |
| Soil Type | Confining Pressure (kPa) | Critical CSR |
|---|---|---|
| MC | 40, 55, 70 | 0.3875, 0.3625, 0.3375 |
| SC | 100, 200, 300 | 0.65, 0.55, 0.45 |
| SS | 100, 160, 220 | 0.095, 0.105, 0.110 |
| WRS | 40, 55, 70 | 0.525, 0.425, 0.425 |
| CWG | 100, 200, 300 | 0.35, 0.45, 0.55 |
| Model | Hyperparameter Type | Corresponding Parameter Range |
|---|---|---|
| RF | max_features max_depth | (0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9) (1,2,3,4,5,6,7,8,9,10) |
| n_estimators | (10,20,30,40,50,60,70,80,90,100) | |
| GBDT | learning_rate max_depth | (0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9) (1,2,3,4,5,6,7,8,9,10) |
| n_estimators | (10,20,30,40,50,60,70,80,90,100) |
| Model | Hyperparameter Type | Corresponding Parameter Range |
|---|---|---|
| RF | max_features max_depth | 0.6 8 |
| n_estimators | 90 | |
| GBDT | learning_rate max_depth | 0.8 3 |
| n_estimators | 50 |
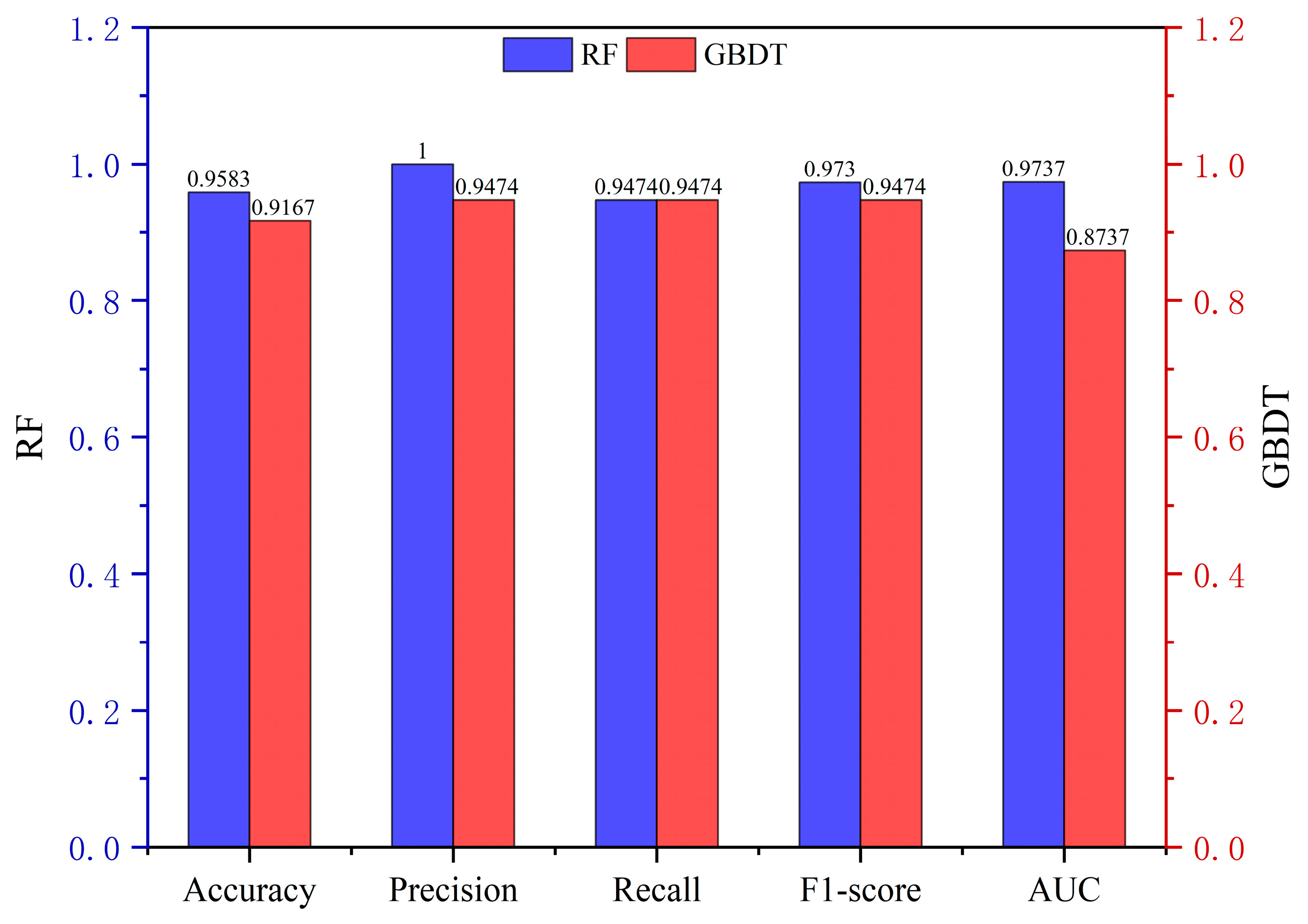
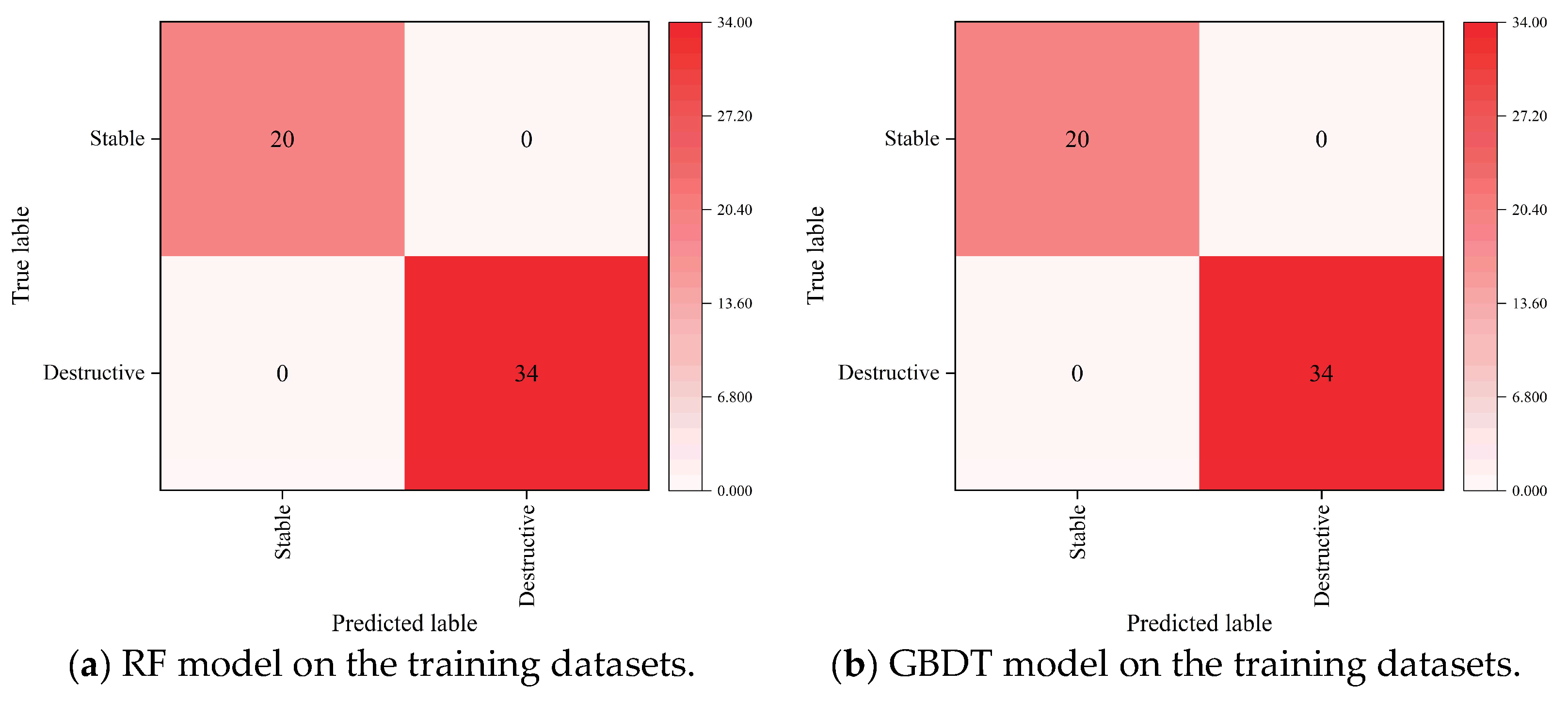
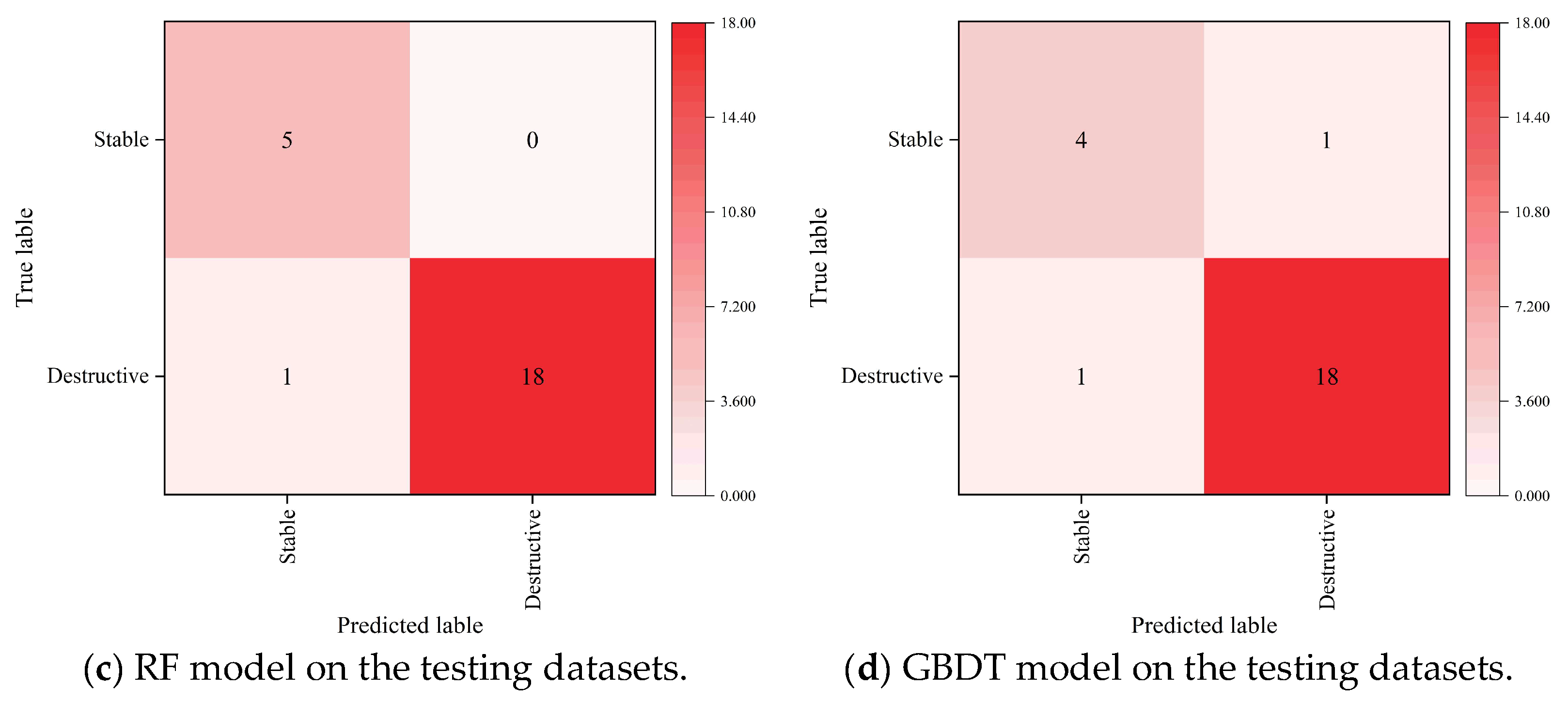
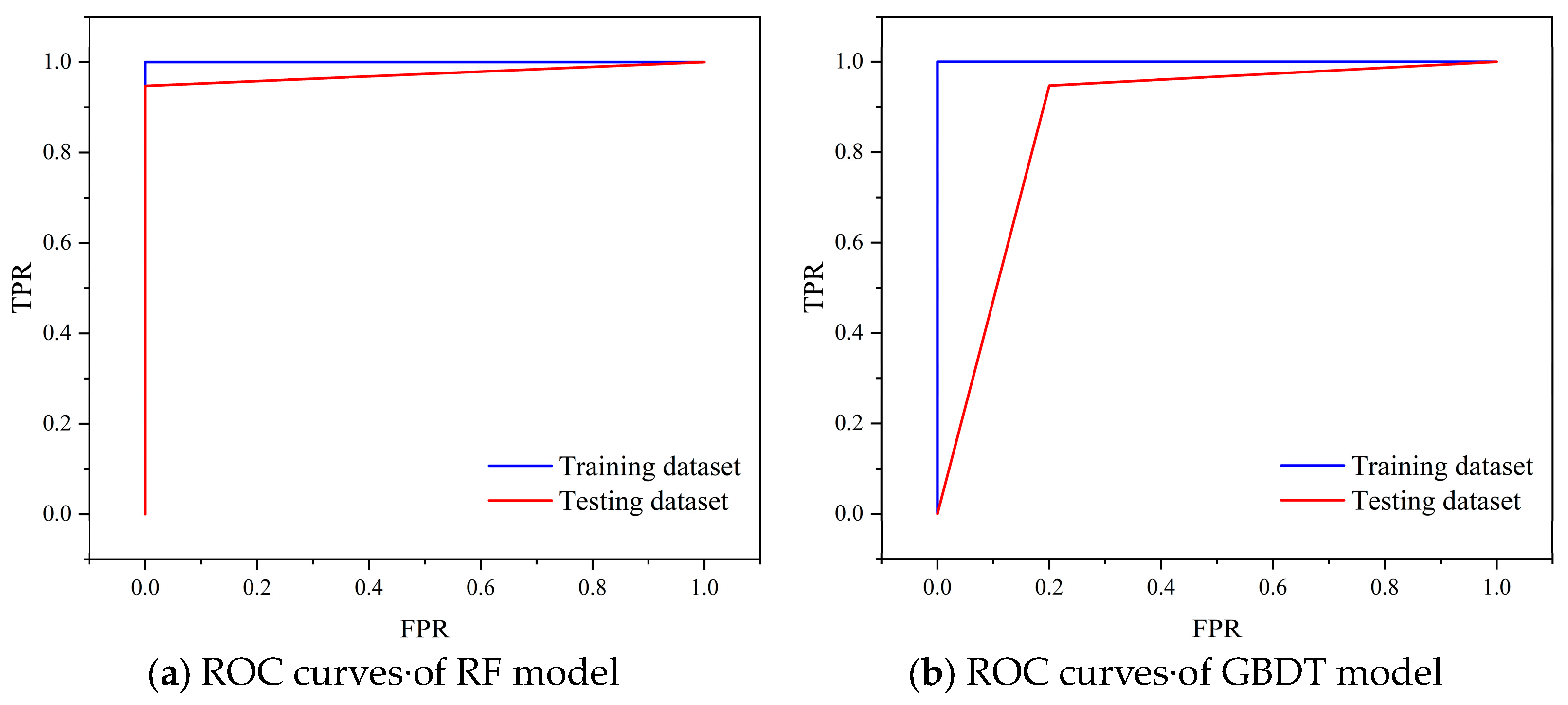
| Model | Dataset | Accuracy | Precision | Recall | F1-Score | AUC |
|---|---|---|---|---|---|---|
| RF | Training dataset | 1 | 1 | 1 | 1 | 1 |
| Testing dataset | 0.9583 | 1 | 0.9474 | 0.9730 | 0.9737 | |
| GBDT | Training dataset | 1 | 1 | 1 | 1 | 1 |
| Testing dataset | 0.9167 | 0.9474 | 0.9474 | 0.9474 | 0.8737 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, B.; Lin, M.; Zhang, Z.; Han, B.; Yu, X. Machine Learning-Based Partition Method for Cyclic Development Mode of Submarine Soil Martials from Offshore Wind Farms. J. Mar. Sci. Eng. 2025, 13, 533. https://doi.org/10.3390/jmse13030533
He B, Lin M, Zhang Z, Han B, Yu X. Machine Learning-Based Partition Method for Cyclic Development Mode of Submarine Soil Martials from Offshore Wind Farms. Journal of Marine Science and Engineering. 2025; 13(3):533. https://doi.org/10.3390/jmse13030533
Chicago/Turabian StyleHe, Ben, Mingbao Lin, Zhishuai Zhang, Bo Han, and Xinran Yu. 2025. "Machine Learning-Based Partition Method for Cyclic Development Mode of Submarine Soil Martials from Offshore Wind Farms" Journal of Marine Science and Engineering 13, no. 3: 533. https://doi.org/10.3390/jmse13030533
APA StyleHe, B., Lin, M., Zhang, Z., Han, B., & Yu, X. (2025). Machine Learning-Based Partition Method for Cyclic Development Mode of Submarine Soil Martials from Offshore Wind Farms. Journal of Marine Science and Engineering, 13(3), 533. https://doi.org/10.3390/jmse13030533





