An Adaptive Local Time-Stepping Method Applied to Storm Surge Inundation Simulation

Abstract

This study proposes an adaptive local time stepping (LTS) method based on a two-dimensional shallow water model for simulating multi-scale storm surge inundation in coastal regions. By dynamically monitoring the variation in the proportion of dry/wet cells during the simulation, the method adaptively adjusts the maximum local time step level, improving computational efficiency and minimizing human intervention in traditional LTS schemes. Through a series of idealized cases, this paper derives an empirical criterion for selecting the maximum LTS level and performs detailed analysis for two typical scenarios: in the absence of dry cells, the optimal LTS level is based on the maximum local time step under quiescent conditions; in complex hydrodynamic models with dry cells, the adaptive adjustment strategy based on the dry cell proportion is required to handle the increased computational complexity. The results show that when the proportion of dry cells was between 40% and 70%, the maximum LTS level increased by one level, and when it exceeded 70%, the maximum LTS level increased by two levels, with a recommended maximum limit of 7 levels. In ideal cases, the adaptive LTS method improves efficiency, with speedups of up to 5.83 times compared to traditional methods. Furthermore, the adaptive LTS method is successfully applied to storm surge and seawater inundation simulations, with validation through comparison with observational data. In particular, the simulation of the seawater backflow event in Erjiegou demonstrated the method’s ability to capture both the occurrence time and extent of seawater backflow, confirming its efficiency and reliability in complex hydrodynamic processes. The proposed method holds significant promise for applications in storm surge forecasting, disaster assessment, and emergency management.

1. Introduction

With the intensification of global climate change, the occurrence and severity of extreme weather events have markedly risen, with storm surges posing an increasingly severe threat to coastal regions [1,2,3]. The coastal regions, being the primary area impacted by storm surges, demonstrates pronounced spatial heterogeneity and dynamic variability due to its unique topography and complex hydrodynamic conditions [4]. These low-lying regions are highly vulnerable to storm surge impacts, and seawater overflow or backflow not only causes severe urban flooding in coastal cities, but also exerts profound effects on the ecological environment and socio-economic systems [5,6]. For instance, between October and November 2024, several coastal regions in China experienced seawater backflow due to the combined effects of storm surges and astronomical tides, leading to widespread urban flooding and significant disruptions to residents’ daily lives. This series of extreme events highlights the urgent need for more accurate and high-resolution forecasting models, particularly in areas prone to storm surge inundation. Current forecasting methods often struggle to account for the rapid changes in water levels and the complex dynamics of these events, which can lead to significant prediction errors and delayed warnings. Therefore, high-resolution and adaptive prediction tools are essential for improving the accuracy of storm surge forecasts in such critical regions [7].

And with the widespread availability of high-resolution observational data, significant progress has been achieved in the study of multi-scale hydrodynamic simulation techniques [8,9]. These techniques dynamically allocate computational resources according to geographical features and event complexity, employing finer grid cells in high-resolution regions to enhance simulation accuracy while using coarser grid cells in low-resolution regions to alleviate computational load. However, the time step in traditional multi-scale hydrodynamic models is typically constrained by the global CFL (Courant–Friedrichs–Lewy) condition. Although this method is straightforward to implement, it is inefficient for handling complex systems with pronounced multi-scale and dynamic characteristics, often resulting in substantial computational resource waste. This inefficiency is particularly evident when large regions of the computational domain transition from wet to partially wet or dry states during storm surge events, leading to frequent time step adjustments. To enhance the efficiency of multi-scale simulations, parallel computing methods [10,11,12] have been extensively adopted in hydrodynamic models. Nevertheless, parallel computing primarily improves the overall runtime through task distribution but cannot fundamentally improve the computational efficiency of models. As a result, the local time stepping (LTS) scheme has emerged as an effective solution, allowing for adaptive time stepping in different grid regions based on local CFL conditions, significantly reducing computational costs while maintaining accuracy in high-resolution areas.

The LTS method was initially introduced by Osher and Sanders [13] for solving one-dimensional scalar conservation equations, demonstrating first-order accuracy in both spatial and temporal dimensions. Later, Dawson et al. [14,15] proposed a high-resolution finite element method for the advection–diffusion equation, and further investigated a second-order temporal scheme for one-dimensional scalar conservation laws. This research confirmed the LTS scheme’s potential for enhancing temporal accuracy and successfully applied it to tidal and storm surge simulations [16,17]. Crossley et al. [18,19] developed two time-accurate LTS algorithms for Saint–Venant equations, establishing a theoretical foundation for shallow water models. Krámer and Józsa [20] introduced a simple yet robust LTS algorithm based on the finite volume method, which was further refined by Tan et al. [21]’s correction method for interface flux calculations. Sanders [22] implemented the LTS method in an explicit Godunov-type shallow water model and provided a comprehensive explanation of its algorithmic design. In recent years, research on the LTS method has further advanced. Yang et al. [23] explored the implementation of the LTS algorithm in two-dimensional (2D) shallow water dynamic models and examined its key influencing factors and applicability. Hu et al. [24,25] enhanced the LTS handling of dry/wet and moving/static fronts, successfully applying the improved algorithm to tidal and sediment morphodynamic simulations. They also developed a GPU-accelerated [26,27] LTS-based finite-volume shallow water model, which was further extended to rainfall–runoff and hydro-sediment-morphodynamic simulations. To improve temporal accuracy, Hoang et al. [28] proposed an explicit LTS scheme based on the predictor–corrector algorithm for shallow water equations (MPAS-O), achieving a discrete conservation of mass, potential vorticity, and energy. Building upon Hoang’s LTS scheme, Capodaglio and Petersen [29] assessed the performance of the local time stepping approach in the cross-scale prediction model (MPAS). Liliy et al. [30] further extended the fourth-order Runge–Kutta (RK4) LTS scheme and, for the first time, applied it to storm surge simulations in the cross-scale ocean prediction model (MPAS-O), demonstrating the practical viability of the LTS scheme. Liu et al. [31,32] optimized the LTS scheme in the 2D shallow water model based on the Hoang’s LTS framework and combined it with Hu’s improved algorithm for dry/wet cells, successfully applying it to storm surge simulations.

However, the performance of the LTS method is highly dependent on the optimal configuration of the maximum time step level ($m_{\max }$). Existing level-setting approaches typically rely on simple formulas or manual adjustments through numerical experiments. However, these methods lack the flexibility to adapt to significant variations in the wet/dry cell ratio, often resulting in increased computational costs. Moreover, artificially constraining $m_{\max }$ or applying coarse-level partitioning methods, while straightforward to implement, may fail to achieve optimal computational efficiency. For instance, in the case presented in Figure 1, the computation time exhibits a “first decrease and then increase” trend as the LTS level rises, suggesting that excessively coarse LTS level settings can introduce unnecessary memory overhead. This inefficiency arises from the over-allocation of computational resources to regions with low computational demands, ultimately degrading the model’s overall computational performance. To address this issue, this study introduces an adaptive LTS level control algorithm that dynamically adjusts the maximum time step level based on the varying wet/dry cell ratio and local time step changes across the computational domain. To address this issue, this study introduces an adaptive LTS level control algorithm based on dynamic variations in cell time steps, aimed at optimizing the selection of the maximum time step level. Specifically, the algorithm determines the appropriate level for each grid cell by monitoring dynamic changes in local time steps and adaptively adjusts the $m_{\max }$ according to the wet/dry cell ratio across the computational domain. This approach mitigates the overly conservative or coarse-level selection inherent in traditional LTS algorithms, thereby enhancing computational resource utilization. Additionally, this study employs the finite volume method [33,34] to discretize the 2D shallow water governing equations implemented on an unstructured grid. This choice is motivated by the fact that, compared to one-dimensional and three-dimensional models, 2D shallow water models offer greater practicality and computational efficiency in critical hydrological scenarios such as lakes, rivers, and coastal regions.

The structure of this paper is arranged as follows: Section 1 is the introduction, which elaborates on the research background, the development status of the LTS method, and its limitations. Section 2 presents the theoretical methods, introducing the basic equations of the 2D shallow water model and the LTS scheme. Section 3 focuses on numerical tests and result analysis, including ideal test cases and empirical formulas for the adaptive LTS algorithm. Section 4 discusses practical engineering applications, using the storm surge simulations in the Yellow Sea and Bohai Sea regions, and the seawater backflow event in Erjiegou as examples to verify the model’s practicality. Section 5 and Section 6 provide the conclusion and discussion, summarizing the research findings and exploring future improvement directions.

2. Model Formulations

2.1. Governing Equations

The theoretical framework for the study is based on the 2D shallow water equations, which describe the conservation of mass and momentum in fluid dynamics. These equations are represented as

$${\displaystyle \frac{\partial U}{\partial t}}+{\displaystyle \frac{\partial F}{\partial x}}+{\displaystyle \frac{\partial G}{\partial y}}=S$$

(1)

$$U=\left[\begin{array}{c}h\\ hu\\ hv\end{array}\right],F=\left[\begin{array}{c}hu\\ h{u}^2+g{h}^2/2\\ huv\end{array}\right],G=\left[\begin{array}{c}hv\\ huv\\ h{u}^2+g{h}^2/2\end{array}\right],S=\left[\begin{array}{c}0\\ -gh\left(S_{ox}+S_{fx}+S_{px}\right)+F_{bx}+{\tau }_{fwx}\\ -gh\left(S_{oy}+S_{fy}+S_{py}\right)+F_{by}+{\tau }_{fwy}\end{array}\right]$$

(2)

where U represents the conserved physical vector; F and G denote the convective fluxes in the x and y directions, respectively; and S stands for the source term. $\eta =h+z_b$ is the water surface elevation, with h representing the water depth and $z_b$ representing the riverbed elevation. The variables u and v correspond to the depth-integrated velocities in the x and y directions, respectively; g is the gravitational acceleration; and $S_{ox}$ and $S_{o\mathrm{y}}$ indicate the bottom slope terms in the x and y directions, respectively,

$$S_{ox}={\displaystyle \frac{\partial z_b}{\partial x}},S_{oy}={\displaystyle \frac{\partial z_b}{\partial y}}$$

(3)

$S_{fx}$ and $S_{fy}$ are the bottom friction terms in the x and y directions, respectively:

$$S_{fx}={\displaystyle \frac{n^{2}u\sqrt{u^2+v^2}}{h^{4/3}}},S_{fy}={\displaystyle \frac{n^{2}v\sqrt{u^2+v^2}}{h^{4/3}}}$$

(4)

where n represents the Manning coefficient; and $S_{px}$ and $S_{py}$ represent the atmospheric pressure gradients in the x and y directions, respectively.

$$S_{px}={\displaystyle \frac{1}{{\rho }_w}}{\displaystyle \frac{\partial P}{\partial x}},S_{py}={\displaystyle \frac{1}{{\rho }_w}}{\displaystyle \frac{\partial P}{\partial y}}$$

(5)

where P is the atmospheric pressure and ${\rho }_w$ is the density of water $(\mathrm{kg}/{\mathrm{m}}^3)$. $F_{bx}$ and $F_{by}$ denote the Coriolis force for the northern hemisphere:

$$F_{bx}=2\omega \sin \varphi ·v,F_{by}=-2\omega \sin \varphi ·u$$

(6)

where $\omega =7.29\times {10}^{-5} \mathrm{rad}/\mathrm{s}$, $\varphi$ is the latitude; and ${\tau }_{fwx}$ and ${\tau }_{fwy}$ represent the drag forces of the wind in the x and y directions, respectively:

$${\tau }_{fwx}={\displaystyle \frac{{\rho }_a}{{\rho }_w}}{C}_w{W}_x\sqrt{W_x^2+W_y^2},{\tau }_{fwy}={\displaystyle \frac{{\rho }_a}{{\rho }_w}}{C}_w{W}_y\sqrt{W_x^2+W_y^2}$$

(7)

where ${\rho }_a$ is the air density:

$${\rho }_a=0.3485{\displaystyle \frac{P}{273.15+T_{emp}}}\left(\mathrm{kg}/{\mathrm{m}}^3\right)$$

(8)

and $T_{emp}$ is the air temperature ${(}^{°}\mathrm{C})$, which can be taken as a constant at a normal temperature $({\rho }_a=1.293 \mathrm{kg}/{\mathrm{m}}^3)$, and $C_w$ is the drag coefficient of wind [35].

$$C_w=C_w^0{\left(1+{\displaystyle \frac{\eta \sqrt{C_w^0}}{4}}\right)}^2$$

(9)

where $C_w^0$ is the wind drag coefficient, traditionally taken as 0.0026, and $W_x$ and $W_y$ are the velocities of the wind in the x and y directions, respectively.

Equation (1) written in compact form is as follows:

$${\displaystyle \frac{\partial U}{\partial t}}+(\nabla •E)=S$$

(10)

where $E=\left(F(U),G(U)\right)$ is the convective flux.

2.2. Equation Discretization and Flux Solving

The computational domain is divided using unstructured triangles and the variables are arranged in the center of the grid. Using the finite volume method, Equation (10) is integrated over the control volume:

$${\iint }_{\mathsf{\Omega }}{\displaystyle \frac{\partial U}{\partial t}} \mathrm{d}\mathsf{\Omega }+{\iint }_{\mathsf{\Omega }}(\nabla \cdot E)\mathrm{d}\mathsf{\Omega }={\iint }_{\mathsf{\Omega }}S \mathrm{d}\mathsf{\Omega }$$

(11)

Using the rotational invariance of Euler equations, the discretization of cell i can be derived as follows:

$$U_i^{n+1}=U_i^n-{\displaystyle \frac{\Delta t^n}{A_i}}{\displaystyle \sum }_{j=1}^{M_f}{T}^{-1}{E}_{nj}({\overline{U}}_i^n)L_j+\Delta t^n{S}_i(U_i^n)$$

(12)

where $U_i^{n+1},U_i^n$ represent two consecutive time steps; i is the cell number, $i=1,2,3,\cdots \cdots ,N_c$, $N_c$ is the total number of cells; j is the cell interface number, $j=1,2,3,\cdots \cdots ,M_f$, and $M_f$ is the total number of cell interfaces; $A_i$ is the area of the i-th control volume; T is the rotation matrix; $E_{nj}$ is the normal flux of the j-th edge; and $L_j$ is the edge length of the j-th edge. The fluxes at the cell interfaces are calculated using Roe’s approximate Riemann solver, adapted for non-linear systems with entropy corrections to stabilize the solution near discontinuities.

$$E(\overline{U})={\displaystyle \frac{1}{2}}\left(E(U_L)+E(U_R)\right)-{\displaystyle \frac{1}{2}}{\displaystyle \sum }_{j=1}^3{\alpha }_j^{\prime }\left|{\tilde{\lambda }}_j\right|{\gamma }_j$$

(13)

where $E(U_L)$ and $E(U_R)$ are the fluxes at the left and right sides of the interface, and ${\tilde{\lambda }}_j$ and ${\gamma }_j$ are the eigenvalues and eigenvectors of the modified Jacobian matrix, respectively.

2.3. Local Time Stepping Scheme

The LTS method enables numerical models to advance computational cells with varying time steps according to local CFL conditions. This approach is especially beneficial for multi-scale hydrodynamic models, as it reduces redundant computations in low-resolution regions while preserving accuracy in high-resolution areas, thus enhancing computational efficiency. The core components of the LTS scheme include the calculation of local time steps, hierarchical classification of time step levels, and a predictor–corrector algorithm to ensure both stability and conservation. This study employs the improved LTS scheme proposed by Liu. The subsequent sections will elaborate on the theoretical framework of the LTS method, the rationale behind each step, and its numerical implementation.

2.3.1. Local Time Step Calculation

The LTS scheme calculates the time step for each cell based on local hydrodynamic conditions, ensuring stability according to the CFL condition. The key idea is to adapt the time step to the local flow velocity, grid resolution, and physical parameters, thus balancing accuracy and computational cost. For a computational cell, the local time step is determined as

$$\Delta t_i=Cr\underset{j=1,3}{\min }\left({\displaystyle \frac{r_{ij}}{\sqrt{u_{ij}^2+v_{ij}^2}+\sqrt{g{h}_i}}}\right) \left(i=1,2,3,\cdots \cdots ,N_c\right) \mathrm{for} h_i\ge h_{cwd}$$

(14)

$$\Delta t_i=\underset{h_i\ge h_{cwd},i=1,N_c}{\max \left(\Delta t_i\right)} \mathrm{for} 0<h_i<h_{cwd}$$

(15)

where $Cr$ is the Courant number, typically set to 0.9; $r_{ij}$ is the distance from the i-th cell center to its j-th edge; $u_{ij},v_{ij}$ are flow velocities in the normal local coordinate system to j-th edge of i-th cell; $h_i$ is water depth of the i-th cell; and $h_{cwd}$ is the critical water depth, which is determined based on the actual situation or numerical experiment results. In the case study presented in this paper, the critical water depth is set to 0.01 m. For dry cells, since their local time step can theoretically be infinitely large, it is assigned the maximum time step of the wet cells within the domain.

The minimum global time step can be obtained from the maximum time step of each cell:

$$\Delta t_{\min }=\underset{i=1,2\dots N_c}{\min (\Delta t_i)}$$

(16)

2.3.2. Time Step Classification and Adjustment

To synchronize the computations across cells, the LTS scheme classifies local time steps into discrete hierarchical levels. This ensures that cells with different time step sizes can interact seamlessly while preserving stability. A wet cell’s time step level is calculated as follows:

$$m_i=\underset{i=1,2\dots N_c}{\min \left[\mathrm{int}\left({\displaystyle \frac{\lg \left(\Delta t_i/\Delta t_{\min }\right)}{\lg 2}}\right),m_{\max }\right]}\mathrm{for} h_i\ge h_{cwd}$$

(17)

$$m_i=m_{\max } \mathrm{for} h_i<h_{cwd}$$

(18)

$$m_{\max }=\underset{i=1,2,\dots N_c}{\max (m_i)}$$

(19)

where $m_{\max }$ is the maximum allowable time step level, set to limit computational complexity and prevent excessively large time steps. When $m_{\max }=0$, the model is equivalent to a GTS model. $m_{\max }$ is typically manually set as $m_{\mathrm{user}}$, through numerical experiments to ensure an optimal time step level that balances accuracy and efficiency. This choice helps prevent time step levels from increasing indefinitely and ensures the model runs efficiently. However, manually setting $m_{\max }$ (or $m_{\mathrm{user}}$) can be cumbersome and may not always lead to the most efficient performance. As mentioned earlier, it may not always guarantee the optimal trade-off between computational cost and accuracy. Therefore, having an adaptive mechanism that adjusts $m_{\max }$ based on the evolving conditions during the computation would allow the model to consistently operate within the optimal efficiency range. The specific details of this configuration will be presented in Section 3.

After we have classified the time step levels for each cell, two types of adjustments are needed: adjustment based on wet/dry and dynamic/static fronts and adjustment based on large time step level differences. Following Hu’s method [24], we adjusted the time step levels of cells based on the wet/dry and dynamic/static fronts, i.e., when the flow velocity of one side is 0 or $h_i<h_{cwd}$ and of the other side $h_i\ge h_{cwd}$, or the flow velocity is greater than 0. Of note, the adjustment process depends not only on the cell state (wet or dry), but also on the difference in time step levels of the cells on either side of the boundary. For example, if a wet cell has an LTS level of 0, and an adjacent dry cell has an LTS level of 4, it may require significant adjustments to maintain consistency. This is because dry cells could require additional layers (e.g., 16 layers of LTS level 4 cells) to match wet cells’ behavior. This increases the computational burden, making it an important factor for limiting $m_{\max }$, as excessive adjustments would hinder computational efficiency. Moreover, Sanders suggested adjusting the time step levels when there is a significant discrepancy between the levels of adjacent cells. Specifically, when the difference in time step levels exceeds 1 (i.e., $\left|m_i-m_{\mathrm{neighbor}}\right|>1$), adjustments are made to ensure that the solution remains stable. This adjustment method ensures that neighboring cells, which are directly interacting, have compatible time step levels, thereby avoiding errors due to mismatched time scales.

After the modification is completed, the LTS level $m_{ij}$ of the cell edges is calculated. Depending on the obtained LTS level, the local time step $\Delta t_{L-i}$ and time interval $\Delta T$ of a coarse cycle can also be calculated.

$$m_{ij}=\min (m_{ij},m_i) i=1,2,3,\cdots \cdots ,N_c j=1,2,3,\cdots \cdots ,M_f$$

(20)

$$\Delta t_{L-i}=2^{m_i}\Delta t_{\min }$$

(21)

$$\Delta T=2^{m_{\max }}\Delta t_{\min }$$

(22)

2.3.3. Time Step Update and Predictor–Corrector Algorithm

Once all the LTS parameters are calculated, the numerical fluxes and physical variables can be updated through the intermediate time steps $s_n$, $s_n=1,2,3,\cdots \cdots ,2^{m_{\max }}$. When $(s_n-1)/2^{m_{ij}}$ is an integer, i.e.,

$$\mathrm{mod}\left({\displaystyle \frac{s_n-1}{2^{m_{ij}}}}\right)=0$$

(23)

edges numerical fluxes are updated. After the physical variables of interface cells are updated to the next time cycle with a “coarse” time step, the physical variables of fine cells are synchronized to the first cycle. We used the Taylor series expansion to predict the values of intermediate time levels in interface cells.

$$U^{n,k}=(1-{\alpha }_k)U^{n,k}+{\alpha }_k{U}^{n+1}$$

(24)

where ${\alpha }_k={\displaystyle \frac{k}{M_t}}$, $k=0,\cdots \cdots ,M_t-1$.

After obtaining the values of the intermediate time levels, the numerical fluxes of the fine cells on the subcycles can be further calculated. Then, when $(s_n-1)/2^{m_{ij}}$ is an integer, i.e.,

$$\mathrm{mod}\left({\displaystyle \frac{s_n-1}{2^{m_i}}}\right)=0$$

(25)

cells’ physical variables are updated.

When a coarse time cycle is completed, the interface needs to be corrected in order to guarantee flux conservation between all cells. When

$$m_i-l_0(s_n)<0$$

(26)

$$\mathrm{where} l_0(s_n)={\displaystyle \sum _{k=0,m_{user}}\left[(k+1)•temp\right]},\mathrm{where} temp=\left\{\begin{array}{c}1, \mathrm{mod}(s_n,2^k)=0\\ 0, \mathrm{mod}(s_n,2^k)\ne 0\end{array}\right.$$

(27)

the physical variables of interface cells are corrected using the interface flux. The specific correction algorithm is

$$U_i^{n+1}=U_i^n+{\displaystyle \frac{\Delta t^n}{M_t}}{\displaystyle \sum _{k=0}^{M_t-1}\overline{F}(U_i^{n,k})},\forall i\in C_{\mathrm{int}}^P$$

(28)

where the fluxes of shared edges of fine cells and interface cells need to be recalculated. The complete solution flowchart, encompassing equation discretization, solution procedures, and the LTS scheme, is illustrated in Figure 2.

3. Numerical Tests

3.1. Test Setup

To validate the effectiveness of the LTS method in storm surge inundation simulations and derive an empirical formula for the calculation of $m_{\max }$, an idealized test case is designed in this section. By simulating the tidal fluctuation process in an idealized tidal flat and varying the proportion of dry cells during computation, the optimal $m_{\max }$ for the LTS model under different inundation conditions is investigated. The core concept of this design is to adjust the dry cell proportion and manually control its values, analyze the experimental results, and thus identify the optimal range for time step constraints applicable to different grid and computational conditions. Unlike the ideal test case with analytical solutions, we opted for a simplified numerical model for simulation, as its accuracy has been validated through prior experiments and real data, and this case more effectively demonstrates the application of the LTS method in coastal terrain conditions. To facilitate a more comprehensive efficiency comparison, all models were run on a PC with an Intel^® Xeon^® CPU E5-2640 v3 (Santa Clara, CA, USA) (2.60 GHz) and 64.0 GB RAM, without parallel processing.

The simulation domain (Figure 3) in this study is a rectangular area with a length of 2000 m and a width of 1000 m. The topographic slope distribution is as follows: at x = 2000 m, the slope is 1°, extending to x = 4000 m; at x = 1000 m, the slope is 2°, extending from x = 2000 m to x = 1000 m; and from x = 0 m to x = 1000 m, the topographic depth remained constant. In terms of grid configuration, eight different grid setups were employed in this study. Specifically, in the region from x = 0 m to x = 2000 m, the grid resolution gradually decreased from 100 m to 5 m; in the region from x = 2000 m to x = 4000 m, the grid resolution started at 5 m and gradually changed, with the resolution decreasing from 180 m to 10 m at x = 4000 m based on the specific conditions. To comprehensively assess the performance of the LTS method, each grid configuration was associated with 8 different LTS conditions, with muser values ranging from 0 to 7, resulting in a total of 64 simulation conditions.

In terms of model parameters and boundary conditions, the hydrodynamic processes within the simulation domain are governed solely by a tidal model. The initial water level was set to 0, and external forcing terms were applied to simulate the effects of wind speed and pressure fields, representing the storm surge. For the boundary conditions, the water level boundary was specified on the left side of the simulation domain (x = 0 m), with a water level amplitude of 10 m and a period of 4 h, meaning the water level fluctuated sinusoidally over time. On the right side of the domain (x = 4000 m), an open boundary condition was applied, allowing for free flow of water in and out. Additionally, the Manning coefficient was set to 0.01.

3.2. Results

Table 1. Configuration and efficiency enhancement of different grid models. The proportion of dry cells is the average value throughout the computational process.

Model	1	2	3	4	5	6	7	8
Number of nodes	6425	8278	9381	14,934	16,606	18,799	26,532	50,221
Number of cells	12,624	16,282	18,463	29,467	32,785	37,139	52,506	99,648
Proportion of dry cells	35%	42%	46%	58%	60%	64%	71%	82%
Maximum level ($m_{\mathrm{user}}$)	7	7	7	7	7	7	7	7
Optimal efficiency level	4	4	5	5	5	5	6	6
Speedup	1.71	1.79	2.12	3.00	3.34	3.58	5.02	5.69

presents the changes in the number of cells, number of nodes, proportion of dry cells, $m_{\mathrm{user}}$, optimal efficiency level, and the speedup across eight different grid models. The results show that as the complexity of the grid models increased (with the increase in the number of grid cells and nodes), the LTS method exhibited significant improvements in computational efficiency. Specifically, the proportion of dry cells increased progressively with grid refinement, from 35% in Model 1 to 82% in Model 8. In models with a higher proportion of dry cells, adopting a higher optimal efficiency level (e.g., level 6 in Models 7 and 8) further enhanced computational efficiency. The speedup was calculated as the ratio of computation time for the optimal fixed LTS level to the computation time for the adaptive scheme, with computation time being recorded based on the CPU time spent only on the computation loop. Compared to the GTS model, the efficiency enhancement factor increased from 1.71 in Model 1 to 5.69 in Model 8, suggesting that under more complex terrain conditions and higher proportions of dry cells, the LTS method can more effectively allocate computational resources, thereby significantly reducing the overall computation time.

Furthermore, the optimal efficiency level did not simply increase; instead, it was adjusted within a reasonable range as the model complexity and proportion of dry cells increased. The optimal efficiency levels for Models 1 to 3 were 4 or 5, while for Models 7 and 8, they needed to be raised to level 6 to achieve optimal computational efficiency. According to the results in Figure 4, it can be observed that under different $m_{\mathrm{user}}$, the total computation time (Total Time) initially decreased and then increased as the LTS level increased, displaying a clear optimal point. Further analysis of the LTS module ratio and time loop ratio shows that although the proportion of the LTS module increased slightly with the LTS level, the time loop portion remained the primary computational bottleneck. Specifically, the LTS module ratio refers to the proportion of time spent on the LTS module within the total computation loop, while the time loop ratio represents the proportion of time spent on computations within the overall time loop. These ratios help identify the relative contribution of the LTS module and computational time in the total simulation process. This suggests that a reasonable increase in the LTS level can effectively reduce the computational burden of the time loop portion, thereby optimizing the overall computational efficiency. However, an excessively high $m_{\mathrm{user}}$ can lead to increased memory overhead and synchronization costs, potentially reducing computational efficiency.

Figure 5 presents the variations in the cell ratio, which represents the proportion of each level’s grid cells, and the runtime ratio, which represents the proportion of computation time spent on each level relative to the total computation time, at different $m_{\mathrm{user}}$. The results show that at a lower $m_{\mathrm{user}}$ (0–3), most of the cells are concentrated, and the computational time is predominantly consumed at these levels. 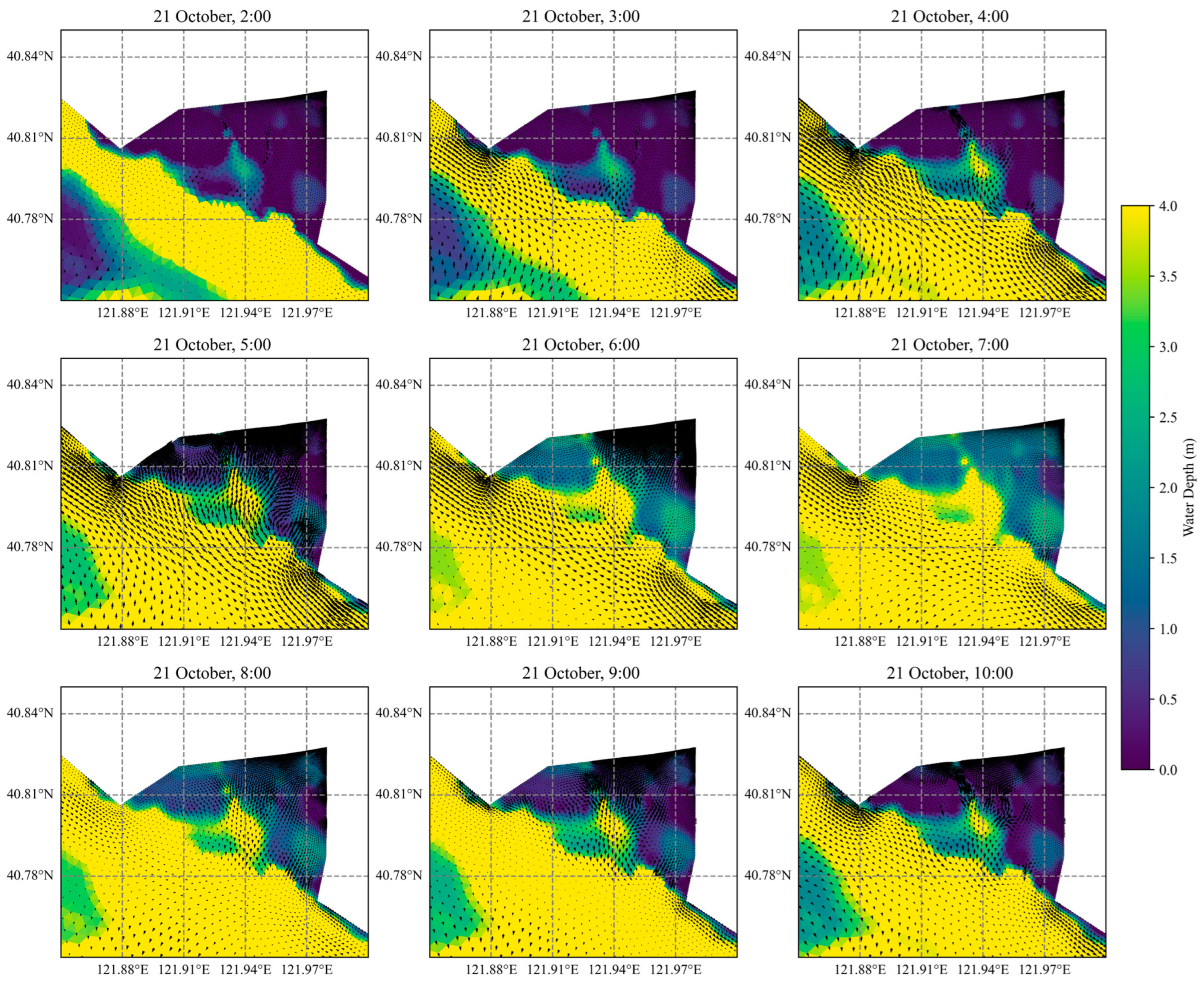As the LTS level increases, the number of high-level LTS cells gradually rises, and the distribution of runtime across the levels becomes more balanced, particularly in models with higher proportions of dry cells.

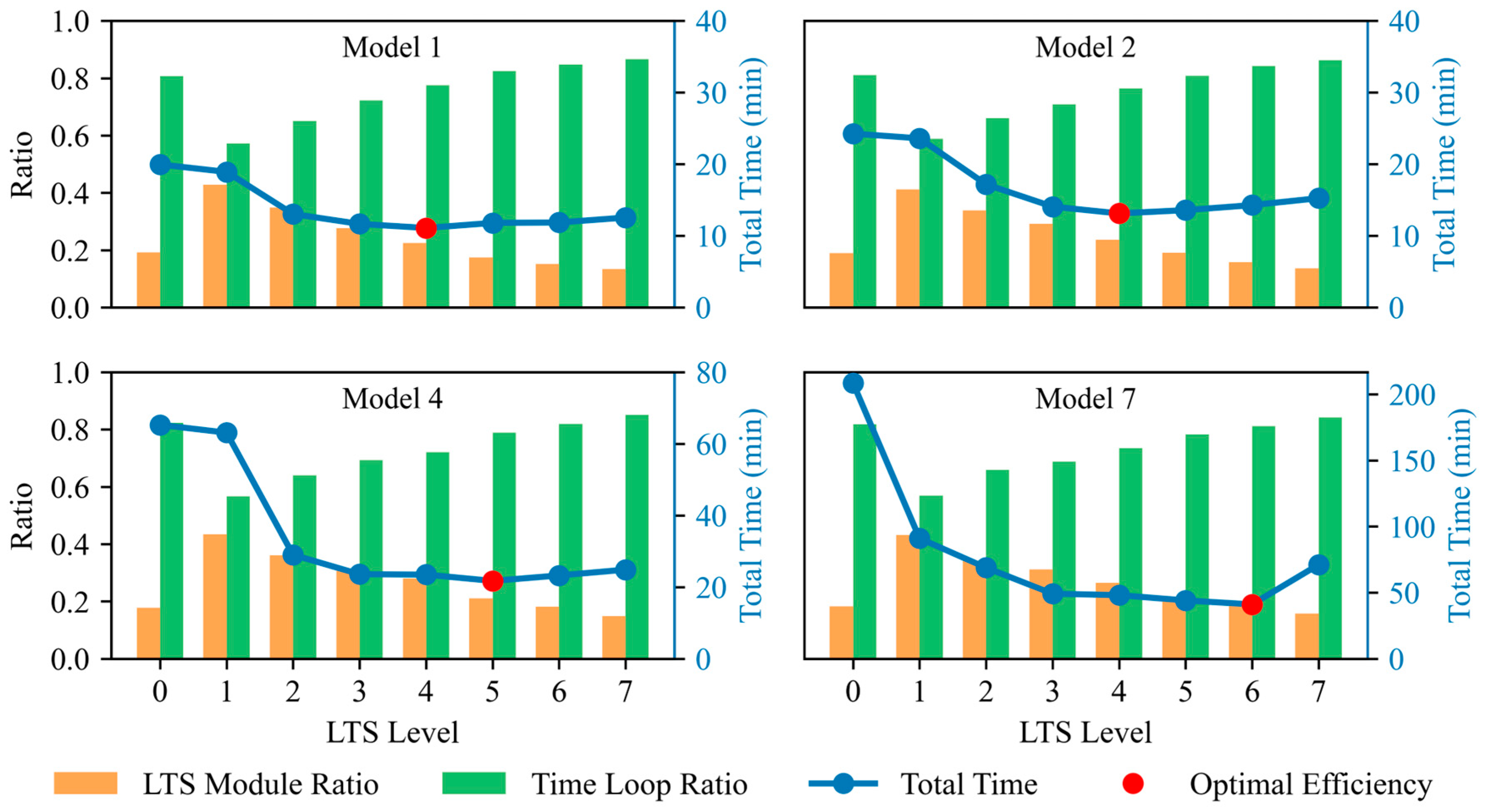
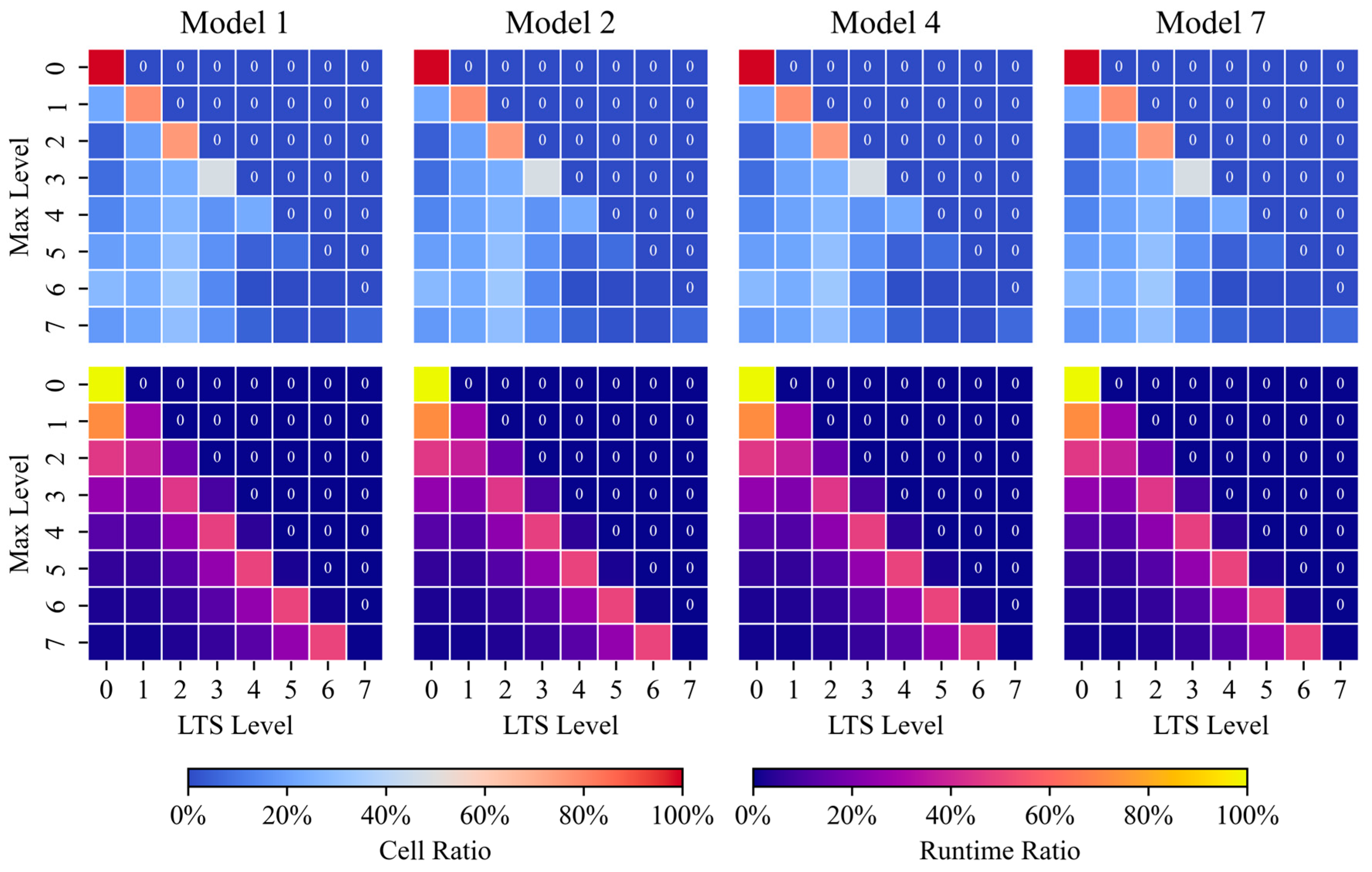
3.3. Adaptive LTS Method

Based on the numerical results, we found that the selection of the optimal $m_{\max }$ in the computational process cannot be entirely free from manual intervention. This is because the impact of the number of dry cells on the LTS level is uncertain and cannot be described precisely through mathematical relationships. To minimize the impact of manual settings on computational efficiency, we propose an empirical formula based on the dry cell ratio to dynamically adjust the $m_{\max }$, ensuring that it remains within the optimal efficiency range at the given level.

The presence or absence of dry cells in the model was analyzed by dividing the situation into two categories:

(1)

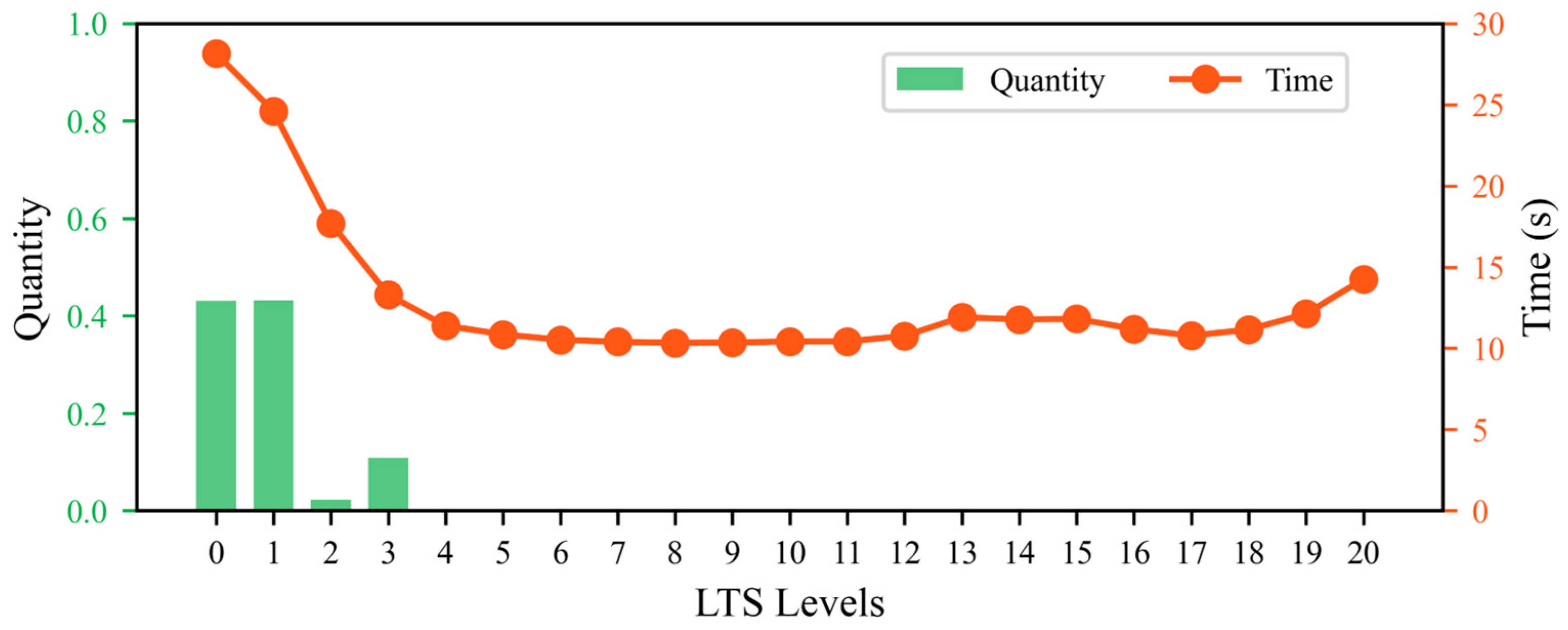
Model without dry cells: In this case, the model contained no dry cells, and the computational process was stable with an even distribution of computational load across cells. Experimental results indicate that, in this case, the optimal LTS level can directly adopt the $m_{\max }$, meaning the optimal level is identical to the $m_{\max }$ under quiescent water conditions.

(2)

Model with dry cells: In the presence of dry cells, frequent changes at the dry–wet interface significantly increase computational complexity and instability. Therefore, we dynamically adjusted $m_{\max }$ based on the dry cell ratio ($R_{\mathrm{dry}}$). Through extensive experimental data analysis, we modeled this adjustment as a piecewise function (Equation (29)), with breakpoints set at $r_1$ and $r_2$, with the following rules: when the $R_{\mathrm{dry}}$ is between 30 and 50%, $m_{\max }$ increases by one level from $m_{\mathrm{sta}}$, i.e., $m_{\max }=m_{\mathrm{sta}}+1$; when $R_{\mathrm{dry}}$ is between 60 and 80%, $m_{\max }$ increases by two levels from $m_{\mathrm{sta}}$, i.e., $m_{\max }=m_{\mathrm{sta}}+2$. To maintain consistency across different models, we adopted conservative critical values of $r_1=0.40$ and $r_2=0.70$ in all experiments in this study. Finally, considering the impact of frequent changes at the dry–wet interface on computational stability and efficiency, the experiments revealed that when $m_{\max }$ exceeds 7, the improvement in computational efficiency diminishes and may even introduce additional computational overhead. Therefore, it is not recommended to set $m_{\max }$ above 7.

$$m_{\max }=\left\{\begin{array}{l}{m}_{\mathrm{sta}}\\ m_{\mathrm{sta}}+1\\ m_{\mathrm{sta}}+2\end{array}\right.\begin{array}{c}{R}_{\mathrm{dry}}\le 40\%\\ 40\%<R_{\mathrm{dry}}\le 70\%\\ R_{\mathrm{dry}}>70\%\end{array}$$

(29)

Table 2. The level selection of the adaptive LTS scheme and its efficiency comparison with the GTS scheme and the optimal limiting level scheme.

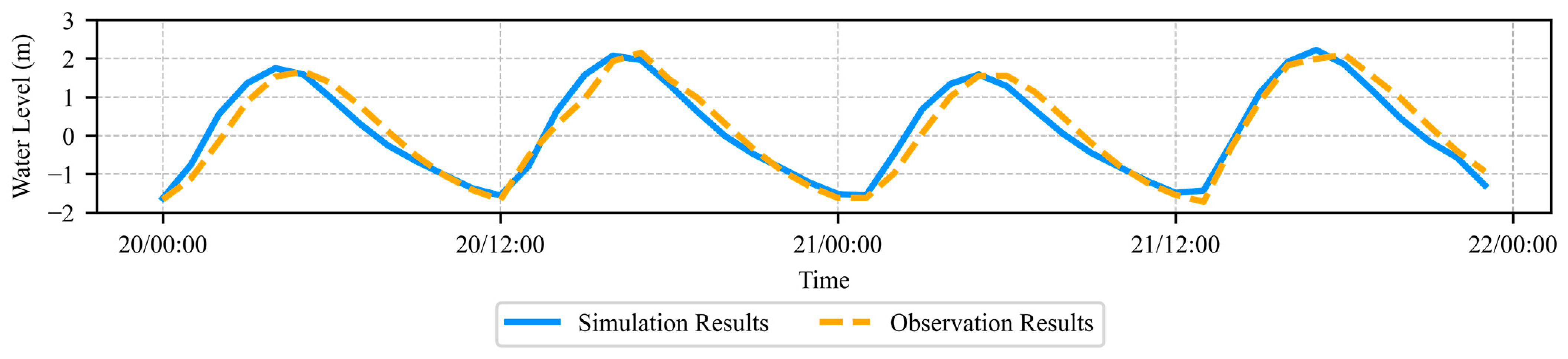
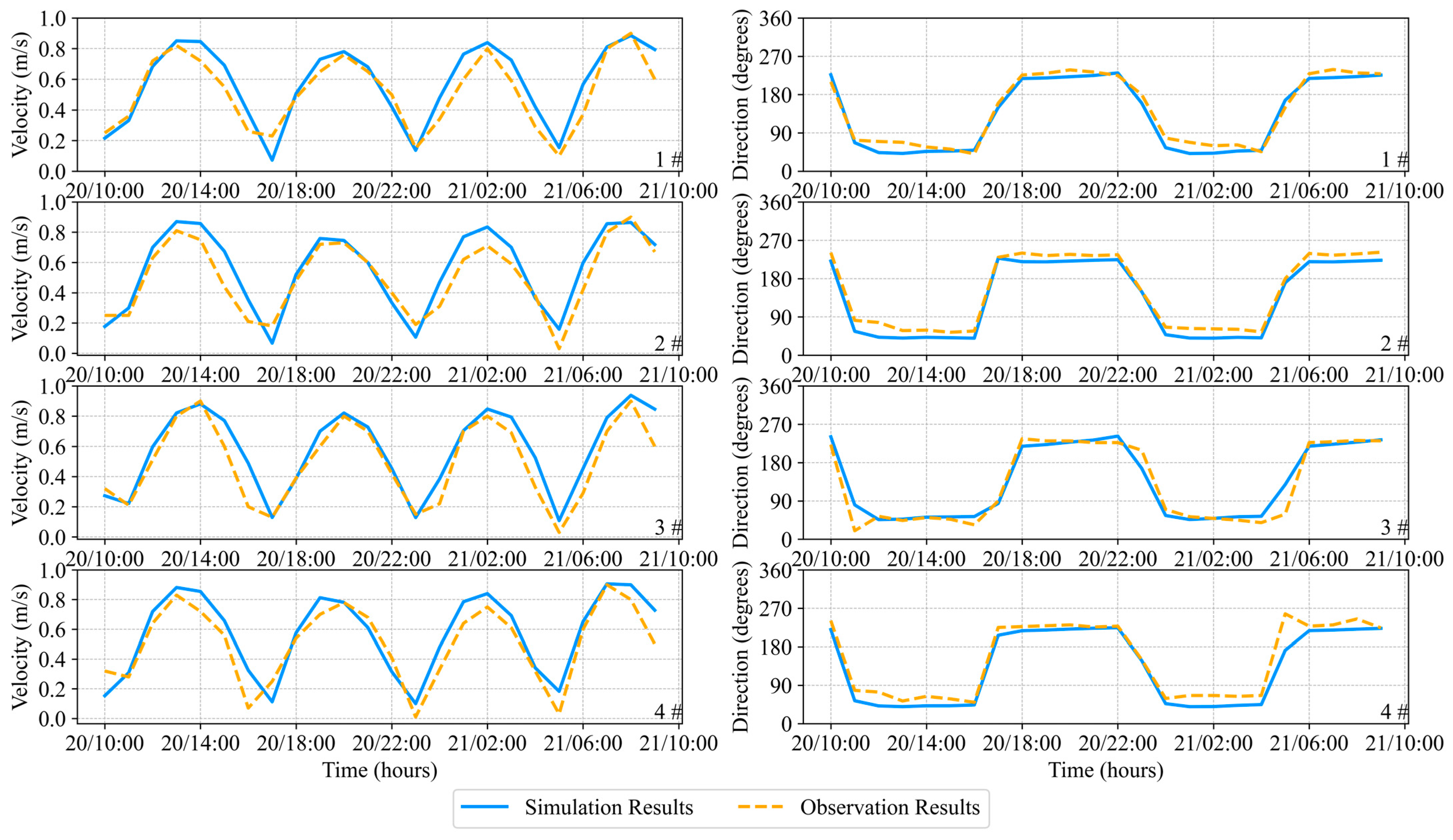
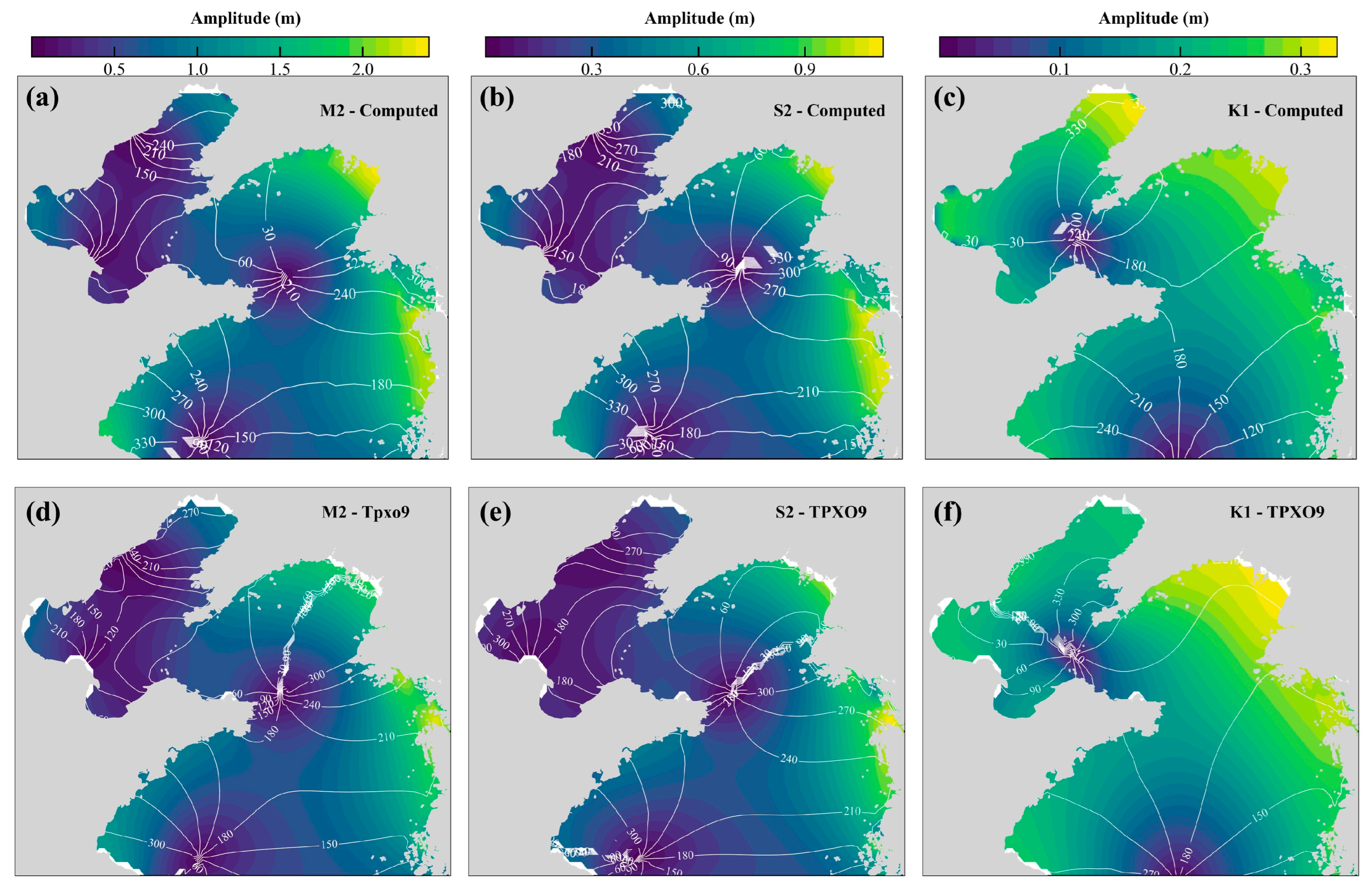
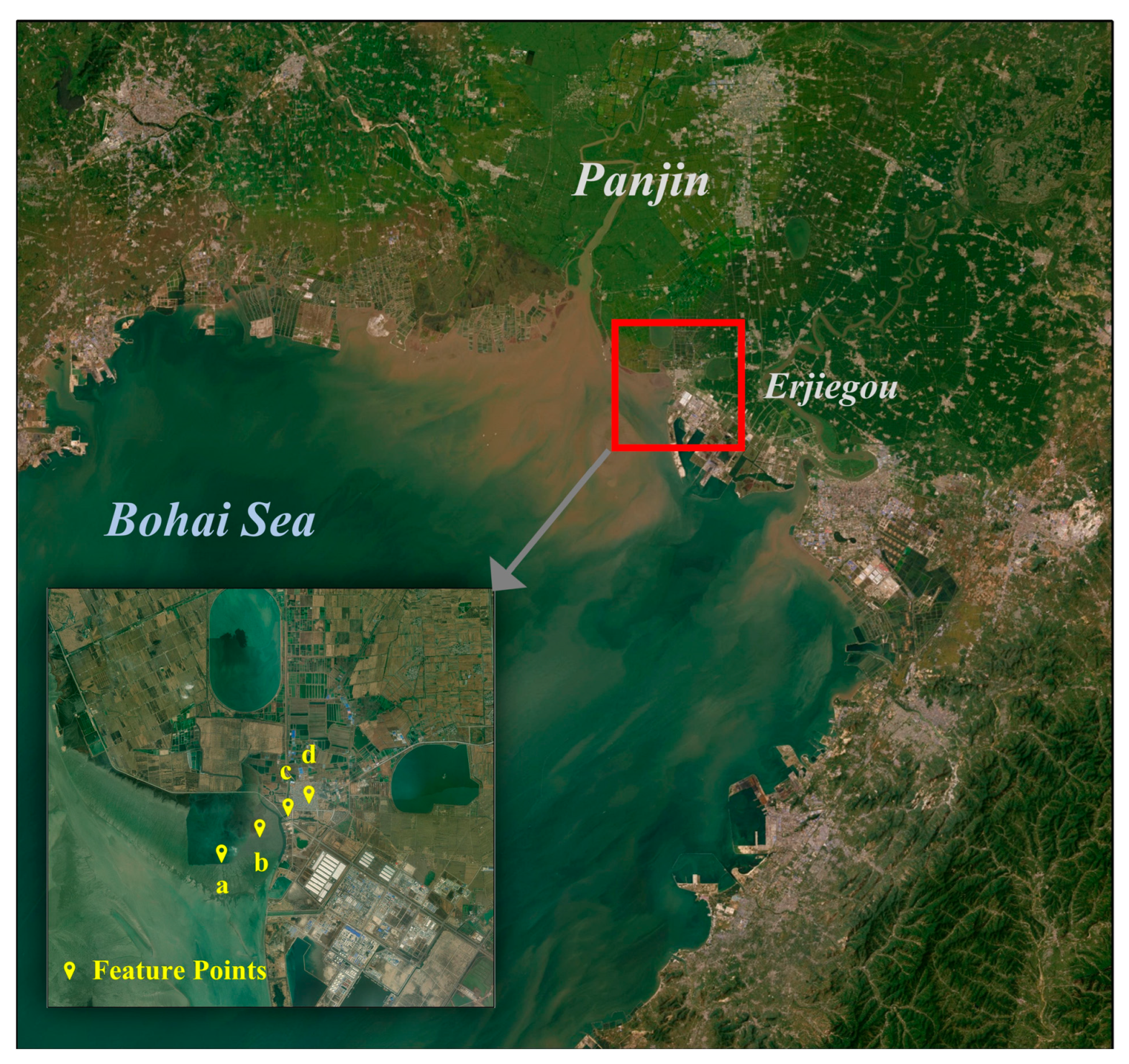
Model	1	2	3	4	5	6	7	8
Minimum Level	4	4	4	4	4	4	4	4
Maximum Level	5	6	6	6	6	6	6	6
Vs. GTS	1.83	1.87	2.71	3.16	3.66	3.51	5.30	5.83
Vs. $m_{\mathrm{user}}$	+0.12	+0.08	+0.59	+0.16	+0.32	−0.07	+0.28	+0.12

presents a comparison of the computational efficiency of the designed adaptive LTS scheme with the GTS scheme and the optimal limiting level scheme. Compared to the GTS method, the adaptive LTS scheme achieved significant improvements in computational efficiency across all models. The efficiency enhancement factor increased from 1.83 (Model 1) to 5.83 (Model 8). A comparison with the optimal limiting level method further validated the effectiveness of the new scheme. In most models, the new scheme outperformed the optimal limiting level method, with efficiencies in Model 3 and Model 5 increasing by 0.59 and 0.32, respectively, indicating that the new method exceled in dynamically adjusting the LTS levels. However, in Model 6, the new method’s efficiency was slightly lower than that of the optimal limiting level method (a decrease of 0.07), though this still fell within a high-efficiency range.

4. Application to Simulating Storm Surge Inundation in a Complex Coastal Area

To further assess the applicability of the adaptive LTS method proposed in this study for practical engineering applications, this section uses a wide-area hydrodynamic model, covering the Yellow Sea and Bohai Sea, to simulate storm surge propagation and the combined effects of astronomical tides in complex topographies. The focus is on the Erjiegou area in Panjin City, Liaoning Province, where a severe disaster occurred on 21 October 2024 due to seawater inundation, leading to widespread flooding, submerging houses in low-lying areas, and severely impacting local infrastructure and residents’ daily lives. Through the refined modeling and simulation of this area, the applicability of the proposed method in large-scale simulations and localized disaster analysis was evaluated.

The simulation model covered the Yellow Sea to the entire Bohai Sea, with a focus on detailed modeling in the key area of the Erjiegou region (Figure 6a). The model used unstructured grids, coupling different resolutions for large-scale and localized areas based on the regional topography. Grids with a resolution of 20,000 m were used for the ocean open-boundary region to capture large-scale tidal fluctuations, while the Erjiegou region was progressively refined to 10 m to reflect the complex topography and variations in the dry–wet interface. The model generated an unstructured grid with 62,114 cells and 31,959 nodes, effectively controlling computational resource consumption while meeting accuracy requirements. The tidal boundary conditions of the model were generated using the TPXO9 [36] global tidal model, which accurately simulated the tidal dynamics of the study area, including 10 primary tidal constituents (e.g., M2, S2, K1, O1). The wind field data were obtained from ERA5 [37] meteorological reanalysis data, characterized by high temporal and spatial resolution, global coverage, and multi-source data assimilation, providing reliable wind speed and direction driving conditions for the storm surge simulation. In addition, based on the seabed characteristics of the study area, the roughness coefficient was calibrated through numerical experiments, with values set between 0.010 and 0.020.

In order to comprehensively validate the model’s performance, typical scenarios were designed for simulation in this study. First, the astronomical tides from 1 April to 30 April 2019 were selected as the validation case. The model’s ability to simulate tidal wave propagation was assessed based on the phase and amplitude matching of the tidal levels. Next, a severe cold front storm surge event on 3 October 2022 was simulated, with a simulation period from 28 September to 6 October 2022. This simulation aimed to validate the model’s ability and accuracy in simulating storm surge inundation driven by wind fields. Critically, the model was used to simulate the seawater backflow event in Erjiegou on 21 October 2024, with a simulation period from 16 October to 23 October. The impact of the combined scenario of an astronomical spring tide and storm surge on the regional hydrodynamic response was analyzed, and the disaster process and its trend were evaluated.

Our primary focus was on the performance of the adaptive LTS method proposed in this paper for real-world hydrodynamic processes, with the results shown in

Table 3. Efficiency comparison between the adaptive LTS scheme, GTS scheme, and optimal limit level scheme.

Model	Tidal Flow Process	Storm Surge Process1	Storm Surge Process2
GTS Time (h)	58.36	18.65	18.13
Optimal Limit Level ($m_{\mathrm{user}}$)	7	7	7
Limit Level Time (h)	9.58	3.32	3.27
Speedup	6.09	5.62	5.54
Adaptive Method Time (h)	9.03	3.29	3.18
Speedup	6.46	5.67	5.70
Speedup Difference	+0.37	+0.05	+0.16

. In the tidal flow simulation, the GTS method took 58.36 h, while the non-adaptive LTS method with the optimal limit level (level 7) reduced the simulation time to 9.58 h, achieving a speedup of 6.09 times. In comparison, the adaptive LTS method further reduced the simulation time to 9.03 h, with a speedup of 6.46 times, improving efficiency by +0.37 times over the non-adaptive method. In the storm surge process 1, the GTS method took 18.65 h, while the optimal limit level method reduced the simulation time to 3.32 h, achieving a speedup of 5.62 times. The adaptive LTS method further reduced the simulation time to 3.29 h, with a speedup of 5.67 times, improving efficiency by +0.05 times compared to the non-adaptive method. In storm surge process 2, the GTS method took 18.13 h, while the optimal limit level method reduced the simulation time to 3.27 h, with a speedup of 5.54 times. The adaptive LTS method further reduced the simulation time to 3.18 h, with a speedup of 5.70 times, improving efficiency +0.16 times compared to the optimal limit level method. Although the speedup effect of the adaptive LTS method varied slightly across all scenarios—due to the dry unit ratio being only 10–20% in the grid design and the maximum static water level already reaching level 7—the adaptive scheme still effectively enhanced computational efficiency in each scenario while ensuring that the limit level selection remained within the optimal range.

The accuracy and applicability of the model in tidal current simulation are validated below. This study selected data from a tidal level observation station and four tidal current observation stations located near Yingkou Port for comparison analysis (Figure 6b). By comparing with the observed data, it was found that the simulation results were in good agreement with the observed data (Figure 7 and Figure 8).

To further quantify the simulation accuracy, the root mean square error (RMSE), mean absolute error (MAE), and skill score (SS) for tidal level, flow velocity, and flow direction were calculated.

$$\mathrm{RMSE}=\sqrt{{\displaystyle \frac{1}{N}}{\displaystyle \sum _{i=1}^N{\left[X^{\mathrm{obs}}-X_i^{\mathrm{mod}}\right]}^2}}$$

(30)

$$\mathrm{MAE}={\displaystyle \frac{1}{N}}{\displaystyle \sum _{i=1}^N\left|X^{\mathrm{obs}}-X_i^{\mathrm{mod}}\right|}$$

(31)

$$\mathrm{Skill} \mathrm{score}=1-{\displaystyle \frac{{{\displaystyle \sum _{i=1}^N\left(X_i^{\mathrm{mod}}-X^{obs}\right)}}^2}{{\displaystyle \sum _{i=1}^N{\left(\left|X_i^{\mathrm{mod}}-\overline{X^{obs}}\right|+\left|X^{obs}-\overline{X^{obs}}\right|\right)}^2}}}$$

(32)

where $X_i^{\mathrm{mod}}$ and $X^{\mathrm{obs}}$ represent simulated and observed values, respectively, and $\overline{X^{obs}}$ represents the mean value of the observed data. Skill score = 1 indicates perfect agreement between the model and observed results.

The results are shown in the

Table 4. Errors between simulated data and observed data at each station.

	Water Level	1# Velocity	1# Direction	2# Velocity	2# Direction	3# Velocity	3# Direction	4# Velocity	4# Direction
RMSE	0.31	0.10	15.15	0.10	17.83	0.11	22.83	0.11	24.32
MAE	0.25	0.08	13.36	0.09	16.48	0.08	14.55	0.10	18.00
Skill Score	0.93	0.79	0.96	0.80	0.95	0.81	0.93	0.78	0.91

. The RMSE of the tidal level simulation was 0.31 m, the MAE was 0.25 m, and the SS reached 0.93, indicating a high accuracy of the model in simulating tidal levels. At tidal current observation station 1, the RMSE of flow velocity was 0.10 m/s, the MAE was 0.08 m/s, and the SS was 0.79; the RMSE of flow direction was 15.15°, the MAE was 13.36°, and the BSS was 0.96. The simulation results at the other stations (2#, 3#, and 4#) also showed high consistency with the observed data, with the RMSE for flow velocity and flow direction being less than 0.12 m/s and 25°, and the BSS reaching 0.95. In addition, to further validate the model from a regional perspective, a comparison analysis of the co-tidal charts (Figure 9) within the computational domain was conducted. By calculating the amplitudes and phases of the M2, S2, and K1 principal tidal constituents, and comparing them with the results from the TPXO9 tidal model, it was found that the model’s amplitude and phase distributions are in good agreement with the TPXO9 results, and the locations of the amphidromic points are also accurately reproduced.

To further verify the applicability and accuracy of the model in storm surge simulations, this study compares the model results with data from six observation stations around the Bohai Sea, namely Bayuquan, Huludao, Tanggu, Huanghua, Weifang, and Longkou (Figure 10). The results show that the simulated data generally matched the observed data well in terms of the dynamic processes of storm surge rising and receding. Specifically, at Bayuquan, Huludao, Tanggu, and Weifang stations, the model accurately reproduced the storm surge variation trend, including the time of maximum surge, and the error in the maximum surge height did not exceed 0.2 m. At Tanggu station, although there was some deviation in the receding surge at certain times, the overall trend remained consistent. However, at Huanghua and Longkou stations, although the overall trend of the simulation matched the observed data, certain details exhibited discrepancies. These discrepancies may be attributed to uncertainties in coastal terrain data or wind field inputs. Specifically, the discrepancies in extreme water levels at Huanghua and Longkou stations reached 0.4–0.6 m, which emphasizes the impact of data uncertainties on model accuracy.

For the storm surge inundation event in the Erjiegou area caused by the combination of the astronomical tide and storm surge on 21 October 2024, we selected four feature points (denoted as a, b, c, and d) for analysis (Figure 11), focusing on the formation process and development trend of the saltwater inundation. From the simulation results, it was evident that two significant water increase processes occurred on 21 October.

At points a and b, directly impacted by the storm surge, the water increase was more pronounced. The first surge, driven by the storm, reached a height of up to 0.9 m. However, at points c and d, located farther from the center of the storm surge, only the effects of the typhoon were felt, and no significant water rise was observed. But after incorporating the astronomical tide boundary conditions, the water level at points c and d began to rise rapidly, reaching 2.5 m. This indicates that the combined effect of the astronomical tide significantly expanded the influence range of the storm surge, especially in areas farther from the center of the storm surge.

From the flow field changes (Figure 12), it can be observed that the water level began to rise around 4 a.m. By 5 a.m., the rate of rise accelerated, and the flow speed noticeably increased, exhibiting a significant saltwater inundation trend. Hydrodynamic conditions in the region fluctuated sharply. By 7 a.m., the water level peaked, with a maximum surge of approximately 2.8 m. At this point, the water flow direction changed from the sea into the Erjiegou area, creating a clear inundation phenomenon. As the combined effect of the storm surge and astronomical tide began to diminish, the water level started to decline from 8 a.m., and the flow intensity gradually weakened. The simulation results of this saltwater inundation event suggest that the combined effect of the storm surge and astronomical tide was the main cause of the large-scale saltwater inundation.

It is important to note that due to the lack of observational data and measured wind field terrain data, we were unable to conduct a more precise quantitative verification of the saltwater inundation process. However, based on the simulation results, the proposed model demonstrated significant applicability and reliability in simulating the complex dynamics of the combined effects of storm surge and astronomical tides.

5. Conclusions

This study presents an adaptive local time stepping (LTS) method that dynamically adjusted the maximum local time step ($m_{\max }$) to accommodate changes in the proportion of dry cells, thereby reducing manual intervention and ensuring that LTS computational efficiency remained within the optimal range. Traditional methods typically rely on manually setting $m_{\max }$, a setting that fails to adapt to the variations in complex terrain and hydrodynamic processes. In contrast, the proposed adaptive LTS method monitors changes in the proportion of dry cells in real time, allowing for the flexible adjustment of $m_{\max }$ and automatically optimizing computational performance.

Through a series of idealized numerical experiments, we developed an empirically-based formula for selecting $m_{\max }$ and analyzed two different scenarios. The first scenario was when the model contained no dry cells, in which case the optimal LTS level could directly be set as the maximum local time step under quiescent water conditions ($m_{\mathrm{sta}}$) as the initial value. The second scenario involved the presence of dry cells, where the frequent changes in the wet–dry interface increased computational complexity. In this case, we proposed a dynamic adjustment strategy based on the proportion of dry cells. The analysis of experimental data revealed that when the dry cell proportion was between 30% and 50%, $m_{\max }$ was increased by 1 level; when the dry cell proportion exceeded 60% to 80%, $m_{\max }$ was increased by 2 levels, with the maximum recommended level not exceeding 7. The results show that the adaptive LTS scheme can adaptively select $m_{\max }$ and ensure that the computational efficiency stays in the optimal interval, which further improved the efficiency by up to 0.59 times.

Additionally, we successfully applied the adaptive LTS method to storm surge and the associated seawater inundation simulations. By comparing the simulation results with the observed data, we validated the model’s applicability. In the simulation of the tidal process, the adaptive LTS method improved the efficiency by a factor of 6.46 compared to the GTS method. In the storm water augmentation process, the adaptive LTS method improved 0.05 times compared to the optimal limiting level method, while in the second storm water augmentation process, the efficiency improved 0.16 times compared to the GTS method. Notably, for the simulation of the seawater inundation event in the Erjiegou region on 21 October 2024, the model successfully captured the occurrence time and surge magnitude of the seawater inundation, particularly in the Erjiegou area. Through trend analysis, we further confirmed the advantages of the adaptive LTS method in capturing storm surge, receding surge, and seawater inundation processes, demonstrating its efficiency and reliability in simulating complex hydrodynamic processes. The adaptive LTS method proposed in this study holds great potential for application in storm surge forecasting, disaster assessment, and emergency management.

6. Discussion

The adaptive LTS method proposed in this study can dynamically adjust the selection of LTS levels based on the proportion of dry cells, significantly enhancing the computational efficiency of storm surge and seawater inundation simulations. However, the current study also has some limitations. We found that when the model had a relatively small grid size, the advantages of the adaptive LTS method were not very apparent. As the grid size increased, the benefits of this method became more pronounced, making it particularly suitable for large-scale simulation scenarios. Additionally, when the initial LTS level of the model was already set to 7 or higher, the advantages of the LTS method were diminished. Nevertheless, we still recommend setting the maximum LTS level to 7 to avoid excessive computational overhead and resource waste due to higher levels.

Future research can further improve the accuracy of the adaptive LTS method in complex hydrodynamic processes, especially in dynamic environments such as storm surge and seawater inundation. The adaptive LTS method is an algorithmic improvement for computing LTS parameters, and it does not affect the parallelism of explicit LTS schemes. Therefore, future studies could integrate this method with more efficient parallel computing architectures to further enhance computational efficiency and real-time performance. Additionally, Hu et al. [26,27] have combined LTS schemes with GPU acceleration, ecology, and sedimentary processes. Building upon this, future research could extend the adaptive LTS method to multi-physics-coupled models to tackle more complex hydrological and climate issues.