Abstract
Visualization of marine environmental field elements is one of the core technologies in marine science research. Particularly in the context of “digital twin of the ocean” (DTO) construction and application, accurately reproducing the dynamic evolution of marine environmental elements remains a critical challenge. Existing visualization methods are primarily limited to static displays and fail to achieve deep integration and dynamic expression of marine environmental elements and sea conditions. To address this, this paper proposes a new visualization method for marine environmental element fields in a twin-space framework. This method first constructs dynamic wave twin objects based on wave data, then develops a marine environmental element field model based on environmental element data, and finally generates a coupled marine environmental element twin object through integration. This approach facilitates the dynamic and collaborative visualization of multiple marine elements. The collaborative visualization results of wave information, ocean surface temperature, and salinity data indicate that this method effectively enhances the dynamic expression capability and information fusion level of the ocean environment feature field. It provides new ideas and approaches for the development of ocean environment visualization technology in twin spaces, with promising application potential.
1. Introduction
The ocean is an extremely complex system that encompasses a wide range of geophysical processes and has a significant impact on global climate [1]. With the continuous expansion of marine environmental data, effectively visualizing these complex spatiotemporal datasets has become a critical issue that urgently needs to be addressed. However, existing visualization methods for marine environmental element fields are mostly limited to static 2D images or simplified 3D representations, lacking in-depth expression of multi-element dynamic coupling. Moreover, these methods often disconnect marine environmental elements from real-world scenarios, creating an “information silo” phenomenon. This not only limits researchers’ intuitive understanding of the relationship between marine environmental elements and actual scenes but also hinders in-depth data analysis and decision support.
A digital twin (DT) is a virtual representation of real-world entities and processes, with synchronized interaction at a specified frequency. In recent years, digital twin technology has rapidly advanced and has gradually found applications in marine environmental research, giving rise to the emerging concept of “digital twin of the ocean (DTO)” [2]. While digital twin of the ocean technology holds tremendous potential, it is important to note that its application in marine research is still in the early stages. Most oceanographers use classical conservative methods for the analysis of oceanographic fields. The community of scientists who apply digital twin methods almost does not intersect with field oceanographers, theoreticians, satellite oceanographers, and those who work with numerical models and laboratory experiments. The digital twin of the ocean utilizes modeling and twin technologies to dynamically reflect changes in the marine environment in real time, allowing researchers to observe, analyze, and predict oceanic changes within the twin environment. This has injected new vitality into the development of marine science. The digital twin of the ocean not only provides a powerful tool for marine scientific research but also offers precise and efficient solutions for marine environmental monitoring, resource management, and early natural disaster warnings [3].
Digital twin visualization achieves three-dimensional twin modeling of real-world scenarios through data visualization techniques, presenting the multidimensional value of data in a richer, more intuitive, and realistic manner [4]. The application of digital twin technology in the marine domain compensates for the shortcomings of traditional marine visualization methods [5]. However, despite its great potential, the practical application of digital twin of the ocean technology still faces numerous challenges. According to existing literature and publicly available information, a systematic theoretical framework, technical support, and specific application scenarios have not been established for the use of digital twins in the marine domain [6]. Therefore, exploring deep integration methods for visualizing marine environmental element fields within twin ocean spaces has become a crucial research direction in digital twin of the ocean visualization.
To address these issues, this paper proposes a visualization method for marine environmental element fields in twin spaces. The proposed method constructs dynamic wave twin objects and marine environmental element field object models, achieving deep coupling and dynamic representation of sea state information and environmental element data. This significantly enhances visualization expressiveness and interactivity, providing a new technical pathway for the construction of digital twin of the oceans. The remainder of this paper is organized as follows: Section 2 introduces related work. Section 3 presents the proposed method. Experiments and results are discussed in Section 4. Finally, Section 5 provides conclusions and future research directions.
2. Related Work
2.1. Wave Twin
With the gradual application of digital twin (DT) technology in the marine field, 3D modeling and dynamic visualization of ocean waves have become a research hotspot. Despite significant progress in the 3D modeling and visualization of ocean waves, there are still many challenges in dynamically displaying waves due to their diversity and complexity [7]. Common wave simulation methods include physical modeling, geometric modeling, and wave spectrum modeling [8]. Geometric modeling methods [9,10,11,12] are relatively simple, with controllable wave shapes, but they often result in regular waveforms with obvious human traces. Physical [13,14,15] and wave spectrum-based methods [16,17,18] are more complex, computationally expensive, and less efficient, but they generally yield more realistic results. Current research mostly focuses on wave simulation modeling, with little attention to wave twin objects based on actual sea condition data. This lack of integration between real-world measurements and wave models prevents an accurate reflection of real sea conditions. Therefore, while wave simulation modeling has achieved many breakthroughs in research, there is still insufficient research on wave twins. Constructing wave twin objects based on actual measurement data requires not only ensuring authenticity and accurate reproduction but also considering the efficiency of real-time wave field rendering. Effectively integrating actual sea condition data with wave models to create wave twin objects that reflect real conditions in geometric form remains a significant challenge in the visualization of marine environments in digital twin spaces.
2.2. Visualization of Marine Environmental Element Fields
Marine environmental element fields are characterized by multisource origins, polymorphism, and diversity [19]. Based on spatial characteristics, they can be categorized into scalar fields and vector fields. Common vector field data include ocean currents and wind fields, while scalar field data include temperature and salinity. The visualization of marine environmental element fields has been widely applied in oceanography. For scalar fields, many researchers use color mapping and volume-rendering methods [20,21,22,23] to visually present the spatial distribution of marine scalar data. For vector fields, methods such as arrow plots and particle systems [24,25,26,27] are commonly used to visualize the spatial distribution characteristics of marine vector data. These methods have made significant advances in data visualization and analysis. However, with the development of digital twin of the ocean technology, higher demands are being placed on marine environmental element field visualization techniques, including more realistic scene presentation, multidimensional comprehensive representation, dynamism, and interactivity. Traditional 2D or simple 3D visualization methods often fail to reproduce the spatial distribution of marine environmental elements in dynamic scenes, and they are also insufficient for demonstrating the complex coupling relationships between different elements. Therefore, in the context of digital twins, innovative visualization methods for marine environmental element fields are urgently needed to meet these emerging requirements.
2.3. Marine Environmental Element Field Twin
Although some research on digital twin technology has been conducted in the marine field, the visualization methods for “digital twin of the oceans” have not been fully explored. Some existing studies have simply overlaid the visualization of marine environmental element fields with wave data, but most of them remain at the 2D display level and fail to effectively achieve the deep integration of wave data with marine environmental element field data. This makes it difficult to meet the high realism and multidimensional requirements of digital twin of the oceans. Therefore, exploring visualization methods that deeply integrate marine environmental element fields with the marine twin space has become an important direction in the research of digital twin of the ocean visualization.
3. Method
3.1. Research Framework
The framework of this paper is shown in Figure 1. First, wave twin objects were constructed based on wave information combined with lighting-rendering techniques. Then, a representation model for marine environmental element data was designed, and marine environmental element field objects were constructed using color mapping methods. Finally, the wave twin objects were overlaid and coupled with the marine environmental element field objects to create marine environmental element field twin objects. This process achieves the overlay and coupling visualization of sea state information and marine environmental element data, providing new insights for the development of digital twin of the ocean environmental element field visualization methods.
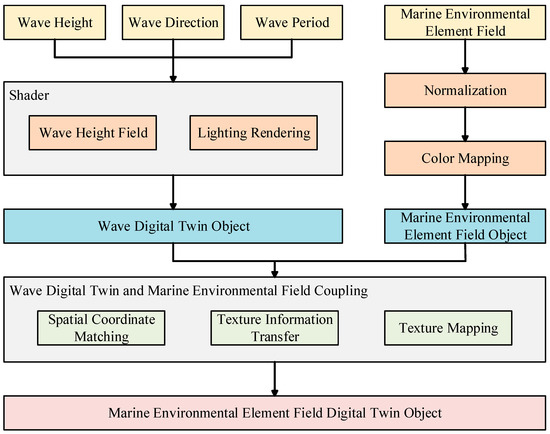
Figure 1.
Marine environmental element field twin visualization technical roadmap.
3.2. Wave Twin Object Modeling
Based on wave height, direction, and period data, wave height field modeling and surface lighting rendering were performed to create a dynamic wave twin object, accurately reflecting the wave data in its geometric form and achieving a realistic ocean visual effect. The process is shown in Figure 2.
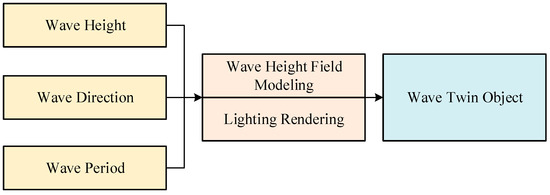
Figure 2.
Wave twin modeling technical roadmap.
3.2.1. Wave Height Field Modeling
In digital twin modeling of the ocean environment, simulating the wave height field is crucial. Using wave height, wave direction, and wave period data, a dynamic sea surface was created through a sine wave model to simulate real wave characteristics. The wave height on a 2D plane can be expressed as:
where represents the amplitude (the maximum height of the wave). and represent the wave numbers in the and directions, respectively, defined as , where is the wavelength. represents the angular frequency, defined as , where is the wave frequency. represents the phase, which controls the initial position of the wave. represents time, indicating the wave’s variation over time.
Since real ocean waves are the result of multiple sine waves of different frequencies, directions, and amplitudes, the height of the sea surface can be modeled by summing multiple sine waves. The superposed wave height can be expressed as:
where represents the number of waves. represents the amplitude of the -th wave. and represent the wave numbers of the -th wave, which determine the wave’s direction. represents the angular frequency of the -th wave. represents the initial phase of the -th wave.
Ocean waves exhibit significant periodicity, and since sine waves themselves possess inherent periodic characteristics, they can effectively simulate the oscillation and regular variations of ocean waves. The mathematical expression of sine waves is simple, and both computation and analysis are relatively easy. Their relationships in terms of frequency, wavelength, and amplitude are clear and well defined, thus improving computational efficiency. Furthermore, sine waves possess the property of superposition, allowing multiple sine waves with different frequencies, directions, and amplitudes to be combined, forming more complex wave surfaces. Since actual ocean waves are composed of the superposition of waves with various frequencies and directions, the superposition property of sine waves makes them particularly suitable for simulating the complex structure of ocean waves, thereby enhancing the efficiency of digital twins and visualization. This method creates a dynamic sea surface with multiple wave features. However, real ocean waves are not perfectly regular; they contain random noise and disturbances. To improve the natural feel of the simulation, Gaussian noise is introduced to simulate irregular waves. The noise expression is:
where represents the noise intensity, controlling the amplitude of the noise. is a Gaussian noise function, and its value changes with variations in time and spatial position and is typically modeled with a normal distribution:
where represents a standard normal distribution with a mean of 0 and a variance of 1. By introducing Gaussian noise, small amplitude fluctuations and irregular disturbances on the wave surface can be effectively simulated, enhancing the dynamic variation and natural appearance of the waves.
Gaussian noise introduces randomness and irregularity to the wave surface, simulating the natural fluctuations of waves in the real ocean. Gaussian noise is both random and smooth, enhancing the natural appearance of the waves and preventing the simulation from appearing overly regular or artificial. Additionally, Gaussian noise follows the random distribution characteristics found in many natural phenomena, effectively replicating the complexity and dynamic changes of ocean waves, thus improving the realism and expressiveness of the simulation. By incorporating noise, the wave model becomes more representative of the actual ocean environment, enhancing both visualization and dynamic performance.
3.2.2. Surface Lighting Rendering
Dynamic reflection, specular highlights, and shadow simulations on the water surface are crucial for enhancing the realism and immersion of virtual environments. The surface lighting-rendering section integrates refined normal calculations with a lighting model, allowing the simulation results to more closely match the actual performance of a complex ocean environment.
The normal vector of the water surface is perpendicular to the surface, determining how the surface reflects and refracts light, thus affecting the final lighting effect. In traditional lighting models, normal calculation is often simplified, but to enhance the realism of the water surface simulation, we adopted a normal estimation method based on the height difference between adjacent points on the water surface. By estimating the normal vector of each point, we can more accurately calculate the dynamic lighting effects on the water surface, thereby improving the detail of the lighting representation. To calculate the normal vector at each point on the water surface, the height differences between neighboring points were used to estimate the local normal vector. With , , , and as the height values of four neighboring points on the water surface, the normal vector in the -direction component is , while in the y-direction, the component is , and the z-direction component is a constant , as follows:
To ensure that the normal vector was a unit vector, the normalization process was applied:
Through this normalization process, the normal information at each point on the water surface was obtained. This information was then used for subsequent lighting calculations to ensure the water surface effect’s realism.
In lighting calculations, the Blinn–Phong lighting model [28] was employed. The Blinn–Phong model is widely used in real-time rendering, game engines, and graphics due to its low computational complexity and good visual effects. Normal calculation can accurately describe the details and shape of the water surface, and the Blinn–Phong model can then compute the correct lighting effects based on these details, enhancing the visual representation. This model combines diffuse reflection and specular reflection to create a more realistic lighting effect on the water surface.
Diffuse reflection describes the reflection phenomenon when light strikes a rough surface, and the reflection intensity is closely related to the angle between the light and the normal vector. The diffuse reflection intensity is calculated as:
where is the normal vector at the water surface point, is the direction vector of the light source, and is the dot product representing the angle between the normal vector and light direction. When the angle is less than 90°, the dot product is positive, meaning that the light is reflected onto the water surface, generating diffuse reflection. The formula ensures the physical correctness of the lighting intensity, preventing negative values and ensuring that diffuse reflection only produces lighting intensity when the light strikes the surface of the object.
Specular reflection describes the reflection phenomenon when light strikes a smooth surface. The intensity of specular reflection primarily depends on the angle between the reflected light and the observation direction. It is calculated as:
where is the specular reflection coefficient, is the shininess exponent, is the reflected light direction, and is the observation direction vector.
The reflected light is calculated as:
The intensity is controlled by the angle between the reflected light and the observation direction. The smaller the reflection angle, the stronger the specular reflection, resulting in more noticeable highlights.
The final water surface lighting intensity is a weighted sum of the diffuse and specular reflections:
where and are the weights for diffuse and specular reflection. By adjusting these coefficients, the contributions of diffuse and specular reflections can be controlled to achieve the desired lighting effect on the water surface.
3.3. Ocean Environmental Element Field Object Modeling
Ocean environmental element data were organized into a raster model, and normalization techniques were used to unify the value range of the elements to the interval [0, 1], ensuring that the data were processed on the same scale, thus improving the model’s consistency and applicability. Next, color mapping technology was applied to convert the normalized values into intuitive color gradients, allowing the spatial distribution characteristics of the ocean environmental elements to be clearly presented. To further enhance the visualization effect, interpolation methods were introduced to smooth the raster data, improving the continuity of the data. The process is shown in Figure 3.

Figure 3.
Ocean environmental element field object modeling technical roadmap.
3.3.1. Ocean Environmental Element Field Representation Model
The ocean environmental element field describes the spatial distribution of various elements in the ocean environment, such as sea surface temperature fields, sea surface salinity fields, etc. Therefore, the expression model of the ocean environmental element field can be represented as a spatial function, as follows:
where represents the ocean environmental element field; represents the function value of the ocean environmental element at spatial positions and ; and represents the spatial range of the ocean environmental element field.
Considering that ocean remote sensing data and numerical model data have become important data sources for ocean environment studies and that such data mainly exist in raster data format, this study adopted the raster field model to construct the ocean environmental element field model.
The raster field model presented the ocean environmental element field as a two-dimensional matrix (raster), with each raster cell storing the value of an ocean environmental element. The advantage of the raster model is that it can flexibly express the spatial distribution of ocean environmental elements and can be easily integrated with remote sensing data and numerical model data for further analysis and applications. In the raster model, the ocean environmental element field can be expressed as the following spatial function:
where represents the ocean environmental element field; represents the function value of the ocean environmental element field at the -th row and -th column of the raster; and and represent the maximum number of rows and columns in the ocean environmental element field.
Raster modeling of the ocean environmental element field provides a flexible and efficient way to represent the spatial distribution of ocean environmental elements. By using a raster data format, ocean environment data can be easily analyzed, simulated, and visualized while being highly compatible with remote sensing and numerical model data, thus providing technical support for accurate representation of ocean environmental elements.
3.3.2. Normalization and Color Mapping
The ocean environmental element field exhibits spatial distribution characteristics, which need to be expressed using color mapping to highlight differences in their values. Color mapping is an important visualization technique, and it was applied to map the values of ocean environmental elements to the color space, thereby intuitively displaying the spatial distribution of these elements. Gradient changes in color allowed a clear view of variations in the ocean environmental elements within the study area.
Before performing color mapping, the data of ocean environmental elements needed to undergo normalization to transform their values to the range of [0, 1]. Assuming that the range of a specific ocean environmental element is and that the actual value of the element at a particular point is “value”, the normalization formula is as follows:
where is the normalized value in the range of [0, 1], and and represent the minimum and maximum values of the ocean environmental element field, respectively. The normalized value indicates the relative position of an element within its value range, ensuring that all environmental elements were processed on a unified scale.
Once the normalized value is obtained, it can be mapped to the color space. The choice of color space is typically based on the variation characteristics of the environmental elements and the visual effects to be expressed. A common color mapping method is to use linear interpolation to transition between two colors. Supposing that the ocean environmental element values are mapped to two colors, the linear interpolation formula is:
where represents the color corresponding to the minimum value (for example, the color for the lowest temperature), and colorHigh represents the color corresponding to the maximum value (for example, the color for the highest temperature). The value is the normalized ocean environmental element value. This interpolation formula generated a smooth color gradient between and colorHigh based on the value of .
In a raster model, bilinear interpolation [29] is often used to calculate the color value for each grid cell. Bilinear interpolation is a method used for interpolation on a two-dimensional grid and is commonly applied in image processing and texture mapping. The basic idea is to first perform linear interpolation along the row direction and then perform another linear interpolation along the column direction. The principle is shown in Figure 4. The specific process is as follows:
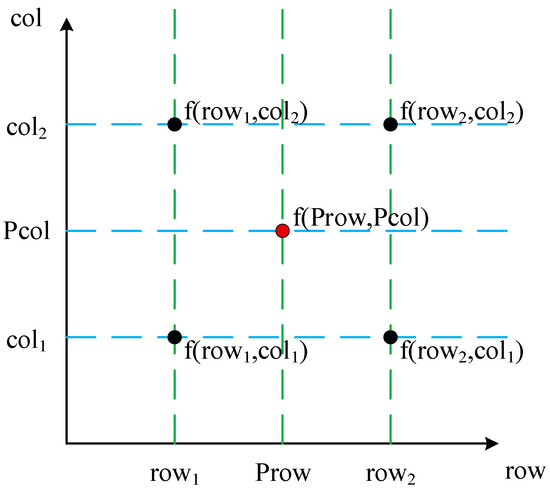
Figure 4.
Raster bilinear interpolation.
In the row direction, interpolate the lower row to obtain :
Similarly, interpolate the upper row to obtain :
After obtaining the interpolation results for the upper and lower rows, perform linear interpolation along the column direction to obtain :
where represents the value to be interpolated at the target point, and , , , and represent the known values of adjacent grid cells. , , and , and represent the coordinates of adjacent rows and columns.
When representing multiple environmental elements, it is often necessary to overlay multiple colors to comprehensively display the spatial distribution of different elements. This can be achieved by linear interpolation, transparency adjustment, or texture composition. When there are two colors (for example, temperature and salinity colors), they can be combined using a weighted average:
where is the adjustment parameter that controls the weight of the two colors, and and represent the color mappings for temperature and salinity, respectively. By adjusting the value of , the blending effect of the two colors can be flexibly controlled.
3.4. Overlay Coupling
3.4.1. Spatial Coordinate Matching
The data of ocean environmental element fields are typically represented in a two-dimensional grid format, where each data point is described by spatial coordinates . The surface of the wave twin object was described by two-dimensional texture coordinates , which represent the mapping of the texture image on the surface. The mapping relationship between spatial coordinates and texture coordinates is as follows:
where represents the spatial coordinates of the ocean environmental element field; represents the texture coordinates of the wave twin object; and , , , and represent the coordinate ranges of the ocean environmental element field.
Using the above formula, the spatial coordinates of each data point in the ocean environmental element field could be mapped to texture coordinates in the range of [0, 1], representing the corresponding sampling location on the texture image. This ensured an accurate match between the two. Moreover, the linear mapping method ensured that the proportionality and positional relationship between the ocean environmental element field and the wave twin object were maintained, avoiding distortion or offset issues caused by inconsistent coordinate systems.
3.4.2. Texture Information Transfer and Texture Mapping
The data of ocean environmental element fields are typically stored in the form of color information, where the color values represent the spatial distribution characteristics of the environmental elements. After spatial coordinate matching, the color texture information needed to be accurately mapped to the surface of the wave twin object. The mapping relationship is as follows:
where represents the spatial coordinates of the ocean environmental element field, represents the texture coordinates of the wave twin object, and is the color information corresponding to the ocean environmental element field. The color values in the equation needed to remain consistent on both sides to ensure the consistency between the spatial distribution of the ocean environment feature field and the wave twin object.
Through texture mapping, the data of the environmental element field was coupled with the dynamic representation of the waves, allowing the geometric form of the waves to exhibit realistic wave characteristics, while the color of the waves reflected the spatial variation of the ocean environmental elements. This mapping method provided a new dimension for visualizing ocean environmental elements, effectively revealing their spatial distribution while facilitating better integration with the physical representation of the waves.
4. Experiments and Results
The experimental procedure is illustrated in Figure 5. It mainly included the acquisition and preprocessing of wave data and ocean environmental element data, modeling of wave twin objects and ocean environmental element fields, and the final overlay coupling visualization based on the Web. Table 1 lists the detailed information about the development and operating environment.
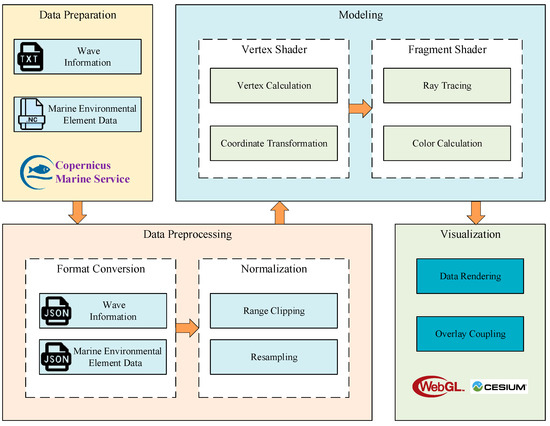
Figure 5.
Experimental flowchart.

Table 1.
Development environment.
4.1. Study Area and Dataset
To validate the feasibility of the ocean environmental element field visualization method oriented toward twin spaces proposed in this paper, a region in the South China Sea was selected as the study area. The specific geographic range is from 111°50′ E to 112°00′ E in longitude and from 16°50′ N to 17°00′ N in latitude. The ocean environmental factors in the South China Sea are complex and variable, exhibiting significant local variations, making it an ideal region for studying ocean environmental changes and verifying the effectiveness of the proposed method. By studying this region, the applicability and advantages of the proposed method in handling complex ocean environments could be fully demonstrated.
The wave data used in this study were obtained from the China Ocean Forecasting Network. The data are stored in text file format and include information such as wave height, wave direction, and wave period within the study area. The sea surface temperature and sea surface salinity datasets were sourced from the Copernicus Marine Environment Monitoring Service (CMEMS), which provides global ocean physical analysis and forecasting data. These datasets are part of marine environment monitoring and forecasting efforts and cover key oceanographic parameters, such as sea surface temperature, sea surface height, ocean currents, and salinity, on a global scale. CMEMS data are widely used in scientific research, environmental monitoring, shipping, fisheries, and climate studies [30,31]. Table 2 lists the attribute information of the datasets.

Table 2.
Summary of the experimental dataset.
The wave data, stored in text file format, and the ocean environmental element data, stored in NetCDF4 format, were extracted and converted into JSON files containing both metadata and numerical data. By calculating the latitude–longitude range, resolution, and other necessary parameters, JSON files with a specific structure were generated. These files also supported the handling of missing values to ensure data integrity and universality, providing support for subsequent data analysis and visualization.
4.2. Modeling
The modeling process was carried out within shaders, which are core components in modern computer graphics. A shader is a small program written by programmers to execute specific tasks in different stages of the graphics-rendering pipeline. Shaders run on the GPU, efficiently handling large-scale parallel computing tasks. Through flexible shader programming, dynamic geometric transformations, complex lighting effects, and realistic material rendering can be achieved, significantly enhancing the rendering quality of 3D graphics. The main types of shaders are vertex shaders and fragment shaders. Vertex shaders are responsible for processing the vertex data in graphics and allow vertex transformations, normal vector calculations, and the transfer of vertex data to subsequent fragment shaders. Fragment shaders, also known as pixel shaders, process each pixel (fragment) of a graphic, generating the final color used for rendering on the screen. Fragment shaders calculate attributes such as color, lighting, and transparency based on vertex data and texture information.
First, based on the acquired wave data, including wave height, direction, and period, a vertex shader dynamically constructed the wave height field. The vertex shader transformed the input vertex coordinates and adjusted the heights of the vertices according to the wave data, simulating the real geometric shapes of the waves. Specifically, wave height was used to adjust the vertical displacement of the vertices, and wave direction and period modulated the waveform. This allowed the generated wave height field to reflect real-world sea conditions in terms of geometry, as shown in Figure 6. The wave twin object constructed used a wave height of 1.6 m, a wave period of 5.5 s, and a wave direction of 189.6°. In the constructed wave height field, each grid corresponded to 2 m in the real world.

Figure 6.
Wave height field.
Next, in a fragment shader, the constructed wave height field underwent lighting rendering to enhance its realism and visual effect. The fragment shader calculated the interaction between the light source direction, the view direction, and the normal vector of the wave surface to generate realistic lighting and shadow effects. Specifically, the surface normal vector was passed from the vertex shader to the fragment shader to capture the local inclination and curvature of the waves. Then, based on the Blinn–Phong lighting model, the color value for each fragment was determined. The relative angles between the light source direction and the view direction dictated the distribution of highlights and shadows, simulating the light and shadow changes on the waves under sunlight, as well as their reflection effects. An example of the wave twin object is shown in Figure 7.


Figure 7.
Wave twin object.
4.3. Visualization
Based on the constructed wave twin object, color mapping of the sea surface temperature data was applied to build a marine temperature field twin object. This allowed the object to not only dynamically reflect real sea conditions in terms of geometry but also represent sea surface temperature information in terms of color. Temperature is a critical factor influencing marine environmental changes. By visually displaying the temperature distribution across different regions, it becomes easier to quickly identify the spatial distribution of and local variations in sea temperature. Higher-temperature areas were mapped to red, while lower-temperature areas were mapped to blue. The rendered result is shown in Figure 8. The spatial resolution of the ocean surface temperature data used was 6 × 6 grids, with each grid point corresponding to a temperature value. This method served as an effective approach for the visual analysis of marine environmental data, allowing a clearer presentation of the temperature field’s variations and potential influencing factors.

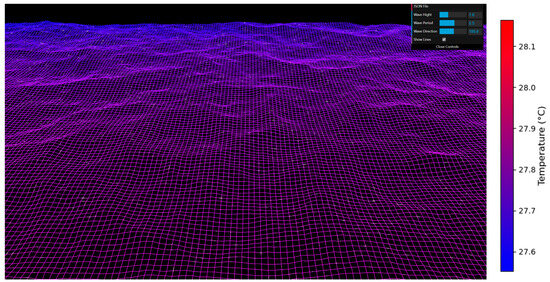
Figure 8.
Twin visualization of the sea surface temperature field.
To validate the versatility of the proposed method, a similar process was applied to the sea surface salinity data. By constructing a marine salinity field twin object, the salinity distribution could be visualized through color mapping. Salinity is an important parameter in the marine environment, influencing water quality, marine life distribution, and ocean circulation. The geometric shape of the wave twin object provided the basis for spatial variation, while color mapping offered an intuitive representation of salinity changes. As the waves moved dynamically, the salinity field’s color variations exhibited corresponding fluctuations, making the changes in the entire marine environment more three-dimensional and vivid. This further validates the method’s generalizability and effectiveness in visualizing different marine environmental fields. Higher-salinity areas were mapped to cyan, and lower-salinity areas were mapped to yellow. The rendered result is shown in Figure 9. The spatial resolution of the ocean surface salinity data used was 6 × 6 grids, with each grid point corresponding to a salinity value.

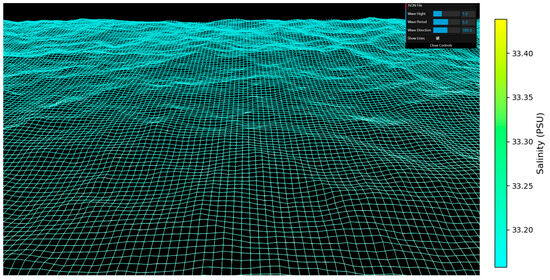
Figure 9.
Twin visualization of the sea surface salinity field.
5. Conclusions
With the continuous development of digital twin technology, digital twin of the oceans (DTOs) have emerged as a new research direction, offering fresh perspectives and powerful tools for marine science research and environmental monitoring. This paper proposes a visualization method for ocean environmental element fields oriented toward twin spaces, addressing the visualization needs of digital twin of the ocean environments. The method constructs digital twin objects for ocean waves and ocean environmental element fields and implements the superposition and coupling visualization of both, thereby providing new ideas and technical solutions for the visualization of digital twin of the ocean environmental elements. The visualization results of wave information, ocean temperature data, and ocean salinity data indicate that this method effectively enhances the dynamic expression capability and information integration of ocean environmental element fields. It offers new insights and approaches for the development of ocean environment visualization technologies in twin spaces and holds potential for future applications.
Author Contributions
Conceptualization, C.X.; Methodology, L.L.; Visualization, S.W.; Color rendering, Y.M.; Data processing, Q.Q.; Funding acquisition, L.L. and C.X.; Writing—original draft, L.L. and S.W.; Writing—review and editing, C.X. and S.W. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by National Key Research and Development Program of China [2022YFC3103102] and the National Natural Science Foundation of China [42376193].
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The datasets generated and analyzed during the current study are available from the corresponding author upon reasonable request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Tian, F.; Mao, Q.; Zhang, Y.; Chen, G. i4Ocean: Transfer function-based interactive visualization of ocean temperature and salinity volume data. Int. J. Digit. Earth 2021, 14, 766–788. [Google Scholar] [CrossRef]
- Chen, G.; Yang, J.; Huang, B.; Ma, C.; Tian, F.; Ge, L.; Xia, L.; Li, J. Toward digital twin of the ocean: From digitalization to cloning. Intell. Mar. Technol. Syst. 2023, 1, 3. [Google Scholar] [CrossRef]
- Xu, J.; Zhao, B.; Wei, S.; Li, G.; Xu, J.; Xiao, X. Discussion and practice on visualization technology of digital twin watershed. Express Water Resour. Hydropower Inf. 2023, 44, 127–130. [Google Scholar] [CrossRef]
- Vasilijevic, A.; Brönner, U.; Dunn, M.; Valle, G.G.; Fabrini, J.; Jones, R.S.; Bye, B.L.; Mayer, I.; Berre, A.; Ludvigsen, M.; et al. A Digital Twin of the Trondheim Fjord for Environmental Monitoring—A Pilot Case. J. Mar. Sci. Eng. 2024, 12, 1530. [Google Scholar] [CrossRef]
- Qiao, Y.; Shan, H.; Wang, H.; Zhu, C.; Sun, Z.; Jia, Y. Implementation and application of digital twin-based visualization technology for spatial and temporal variation of seafloor suspensions. Haiyang Xuebao 2023, 45, 166–177. [Google Scholar]
- Zhao, L.; Jiang, X.; Hong, Y.; Sun, M.; Wang, Y.; Kang, L.; Cao, L. Smart ocean digital twin technology and its application. Sci. Technol. Rev. 2024, 42, 91–101. [Google Scholar]
- Han, Y.; Huang, J.; Ma, C.; Yang, J.; Chen, G. Research on Key Technologies and Implementation on Virtual Marine Environment Simulation. Period. Ocean. Univ. China 2023, 53, 111–117. [Google Scholar] [CrossRef]
- Fu, J.; Huang, F.X.; Gao, W.; Yin, B.G.; Li, L.H. A Research Review on Wave Modeling and Simulation Methods in Marine Environment. In Proceedings of the 2019 IEEE International Conference on Mechatronics and Automation (ICMA), Tianjin, China, 4–7 August 2019; pp. 303–307. [Google Scholar] [CrossRef]
- Duan, X.; Liu, J.; Wang, X. Real-Time Wave Simulation of Large-Scale Open Sea Based on Self-Adaptive Filtering and Screen Space Level of Detail. J. Mar. Sci. Eng. 2024, 12, 572. [Google Scholar] [CrossRef]
- Kellomäki, T. Fast Water Simulation Methods for Games. Comput. Entertain. (CIE) 2017, 16, 1–14. [Google Scholar] [CrossRef]
- Jeschke, S.; Hafner, C.; Chentanez, N.; Macklin, M.; Müller-Fischer, M.; Wojtan, C. Making Procedural Water Waves Boundary-aware. Comput. Graph. Forum 2020, 39, 47–54. [Google Scholar] [CrossRef]
- Stomakhin, A.; Selle, A. Fluxed animated boundary method. ACM Trans. Graph. (TOG) 2017, 36, 1–8. [Google Scholar] [CrossRef]
- Kryachko, Y.A. Sea surface visualization in world of warships. In Proceedings of the International Conference on Computer Graphics and Interactive Techniques, ACM, Anaheim, CA, USA, 24–28 July 2016. [Google Scholar]
- Hu, X.; Yang, H.; Wan, Y. Research and implementation of screen space based ocean simulation. Comput. Eng. Des. 2015, 36, 452–457. [Google Scholar] [CrossRef]
- Chang, Z.; Han, F.; Sun, Z.; Gao, Z.; Wang, L. Three-dimensional dynamic sea surface modeling based on ocean wave spectrum. Acta Oceanol. Sin. 2021, 40, 38–48. [Google Scholar] [CrossRef]
- Li, T.; Ji, M.; Jin, F.; Zhang, J.; Sun, Y. Research on ocean wave simulation based on the method of combining smoothed particle hydrodynamics with marching cubes algorithm. J. Geo-Inf. Sci. 2017, 19, 161–166. [Google Scholar]
- English, R.E.; Qiu, L.; Yu, Y.; Fedkiw, R. Chimera grids for water simulation. In Proceedings of the Computer Animation, Anaheim, CA, USA, 19–21 July 2013. [Google Scholar]
- Nielsen, M.B.; Söderström, A.; Bridson, R. Synthesizing waves from animated height fields. ACM Trans. Graph. (TOG) 2013, 32, 1–9. [Google Scholar] [CrossRef]
- Han, X.; Liu, J.; Tan, B.; Duan, L. Design and Implementation of Smart Ocean Visualization System Based on Extended Reality Technology. J. Web Eng. 2021, 20, 557–574. [Google Scholar] [CrossRef]
- Guo, X.; Zhu, J.; Wan, J.; Wang, X. 3D visualization of marine environmental elements based on Cesium. Mar. Sci. 2021, 45, 130–136. [Google Scholar]
- Li, W.; Liang, C.; Yang, F.; Ai, B.; Shi, Q.; Lv, G. A Spherical Volume-Rendering Method of Ocean Scalar Data Based on Adaptive Ray Casting. ISPRS Int. J. Geo-Inf. 2023, 12, 153. [Google Scholar] [CrossRef]
- Qin, R.; Feng, B.; Xu, Z.; Zhou, Y.; Liu, L.; Li, Y. Web-based 3D visualization framework for time-varying and large-volume oceanic forecasting data using open-source technologies. Environ. Model. Softw. 2021, 135, 104908. [Google Scholar] [CrossRef]
- Lv, T.; Fu, J.; Li, B. Design and Application of Multi-Dimensional Visualization System for Large-Scale Ocean Data. ISPRS Int. J. Geo-Inf. 2022, 11, 491. [Google Scholar] [CrossRef]
- Fan, Y.; Lv, X.; Zhang, J.; Wang, Y.; Zhang, X. Research and realization of flow field dynamic visualization based on geometric shader. Comput. Eng. Appl. 2019, 55, 157–161. [Google Scholar]
- Fan, D.; Liang, T.; He, H.; Guo, M.; Wang, M. Large-Scale Oceanic Dynamic Field Visualization Based on WebGL. IEEE Access 2023, 11, 82816–82829. [Google Scholar] [CrossRef]
- Li, R. Dynamic 3-D Visualization System of Sea Flow Field Based on Virtual Reality Technology in the Environment of Internet of Things. J. Test. Eval. 2024, 52, 1542–1552. [Google Scholar] [CrossRef]
- Shi, Q.; Ai, B.; Wen, Y.; Feng, W.; Yang, C.; Zhu, H. Particle System-Based Multi-Hierarchy Dynamic Visualization of Ocean Current Data. ISPRS Int. J. Geo-Inf. 2021, 10, 667. [Google Scholar] [CrossRef]
- Wang, P.; Wang, F.; Zhang, Y.; Zhang, B.; Poon, T.C. Improved rapid algorithm for continuous shading based on the fully analytical polygon-based method. Opt. Express 2024, 32, 37418–37433. [Google Scholar] [CrossRef] [PubMed]
- Zheng, H.; Chen, J.; Qin, X.; Ma, J.; Zhang, M. Visualization Method of Vertical Profile for Meteorological Multi-element Data. J. Chin. Comput. Syst. 2021, 42, 2350–2355. [Google Scholar]
- Le Traon, P.Y.; Reppucci, A.; Alvarez Fanjul, E.; Aouf, L.; Behrens, A.; Belmonte, M.; Bentamy, A.; Bertino, L.; Brando, V.E.; Kreiner, M.B.; et al. From Observation to Information and Users: The Copernicus Marine Service Perspective. Front. Mar. Sci. 2019, 6, 234. [Google Scholar] [CrossRef]
- Xi, H.; Losa, S.N.; Mangin, A.; Soppa, M.A.; Garnesson, P.; Demaria, J.; Liu, Y.; d’Andon, O.H.F.; Bracher, A. Global retrieval of phytoplankton functional types based on empirical orthogonal functions using CMEMS GlobColour merged products and further extension to OLCI data. Remote Sens. Environ. 2020, 240, 111704. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).