A Hybrid-Surrogate-Calibration-Assisted Multi-Fidelity Modeling Approach and Its Application in Strength Prediction for Underwater Gliders
Abstract
1. Introduction
2. Short Reviews of the Basic Theories
2.1. Polynomial Response Surface Model
2.2. Kriging Model
2.3. Radial Basis Function Model
3. Description of Proposed HSC-MFM Approach
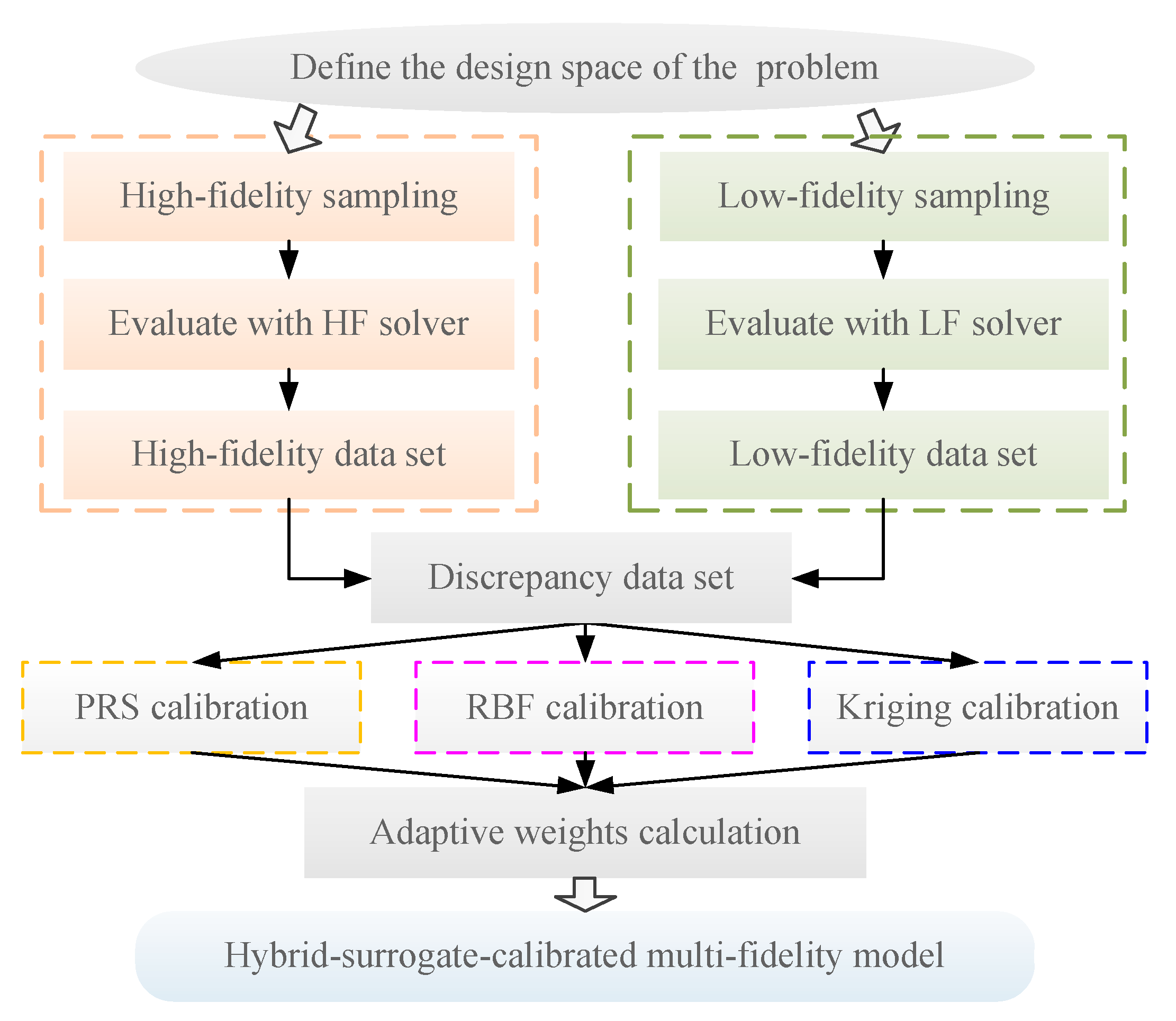
3.1. Main Procedures of HSC-MFM
| Main steps of HSC-MFM: |
|
3.2. Calculation of Weight Coefficient
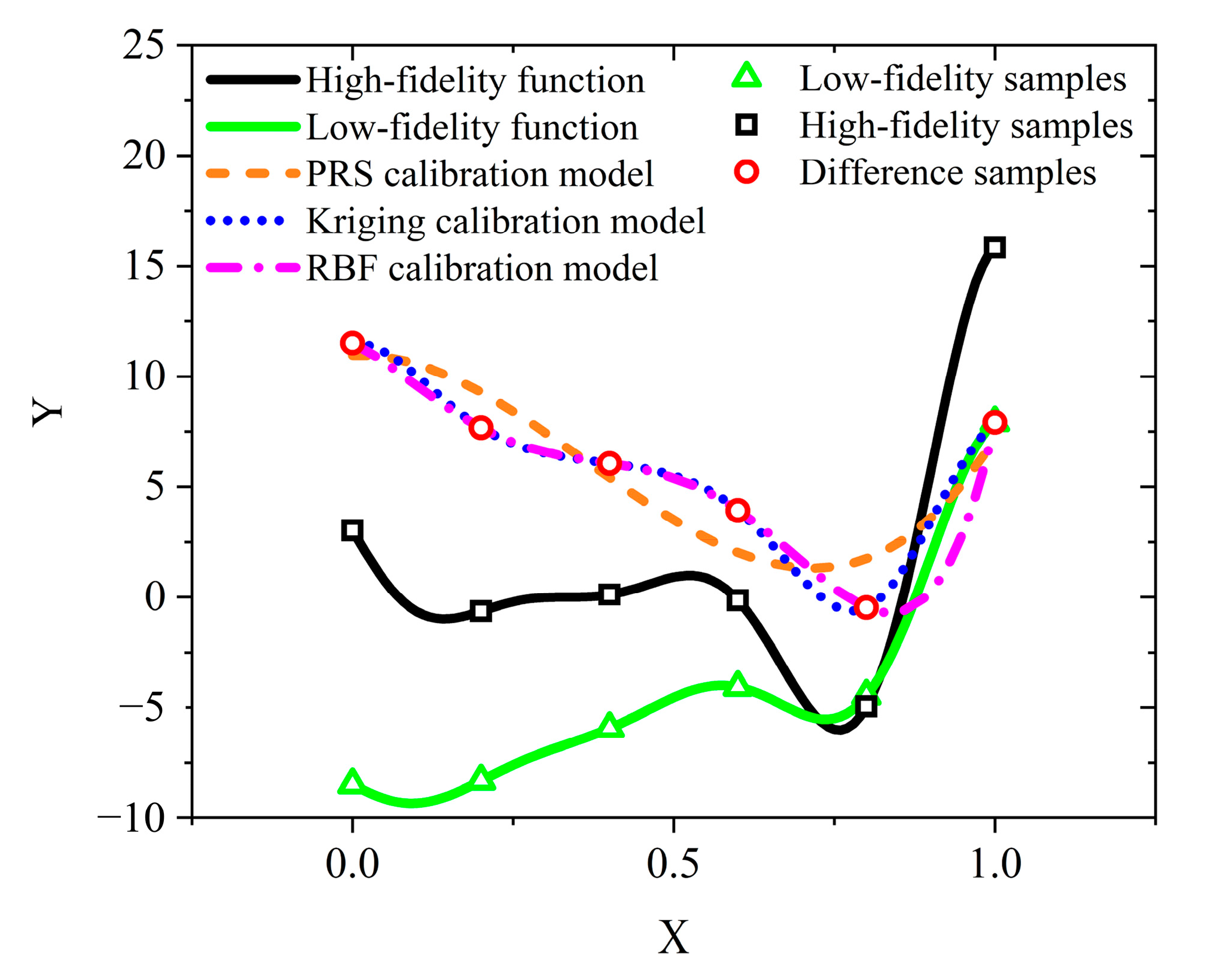
3.3. Demonstration of HSC-MFM
4. Mathematical Problem Testing
4.1. Test Problem Suite
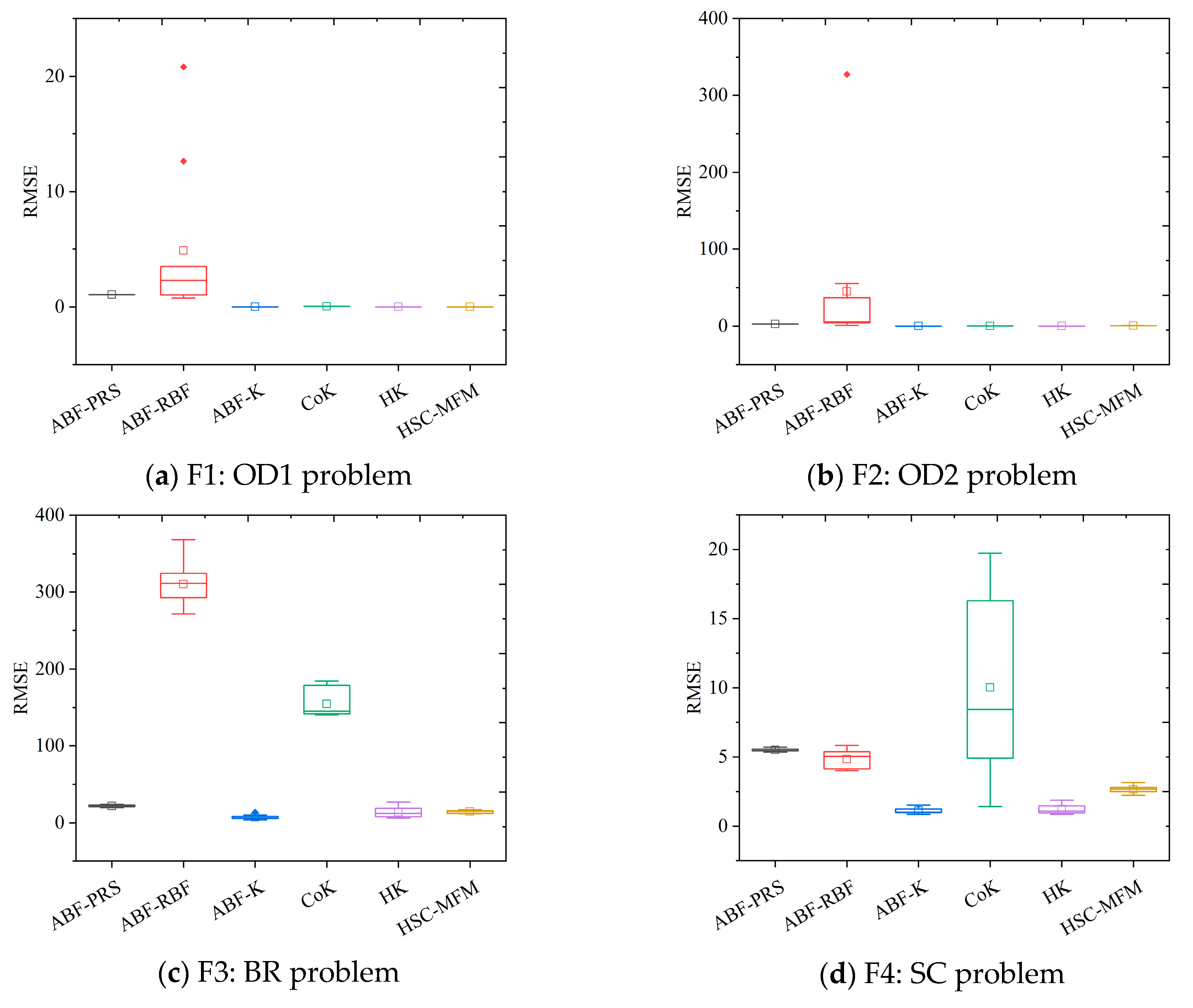
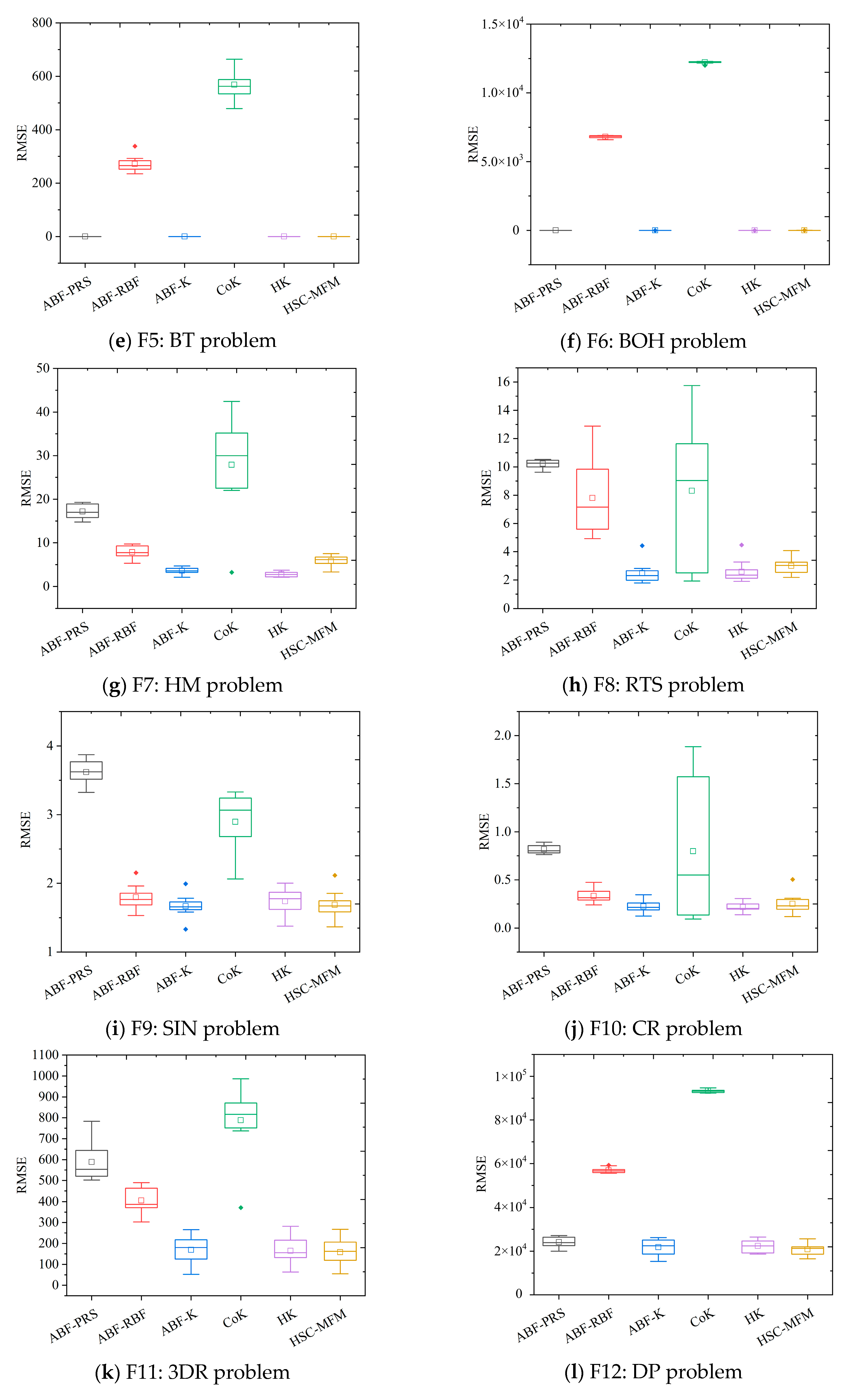
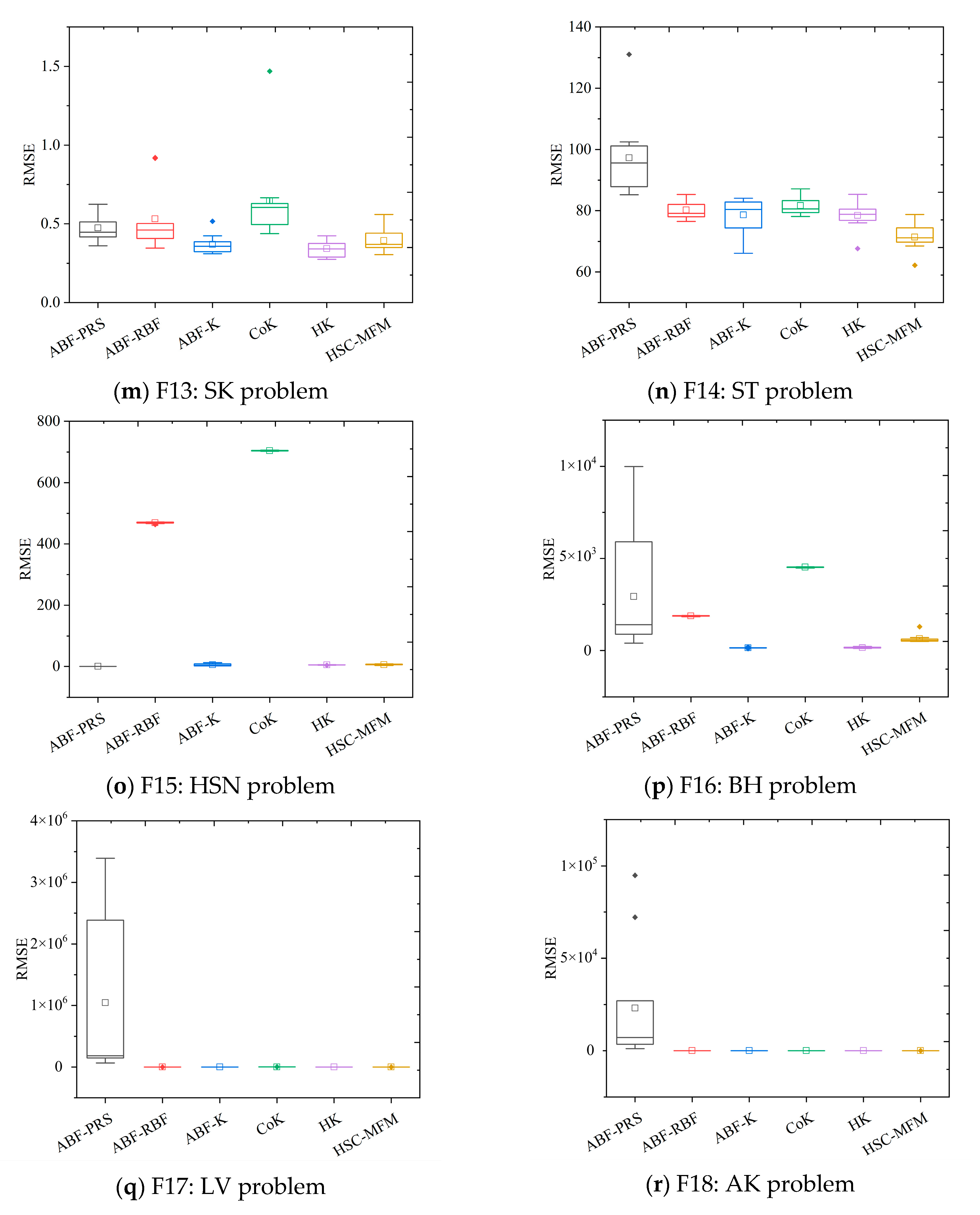
4.2. Comparison and Results Discussion
5. Frame Strength Prediction for a Blended-Wing-Body Underwater Glider
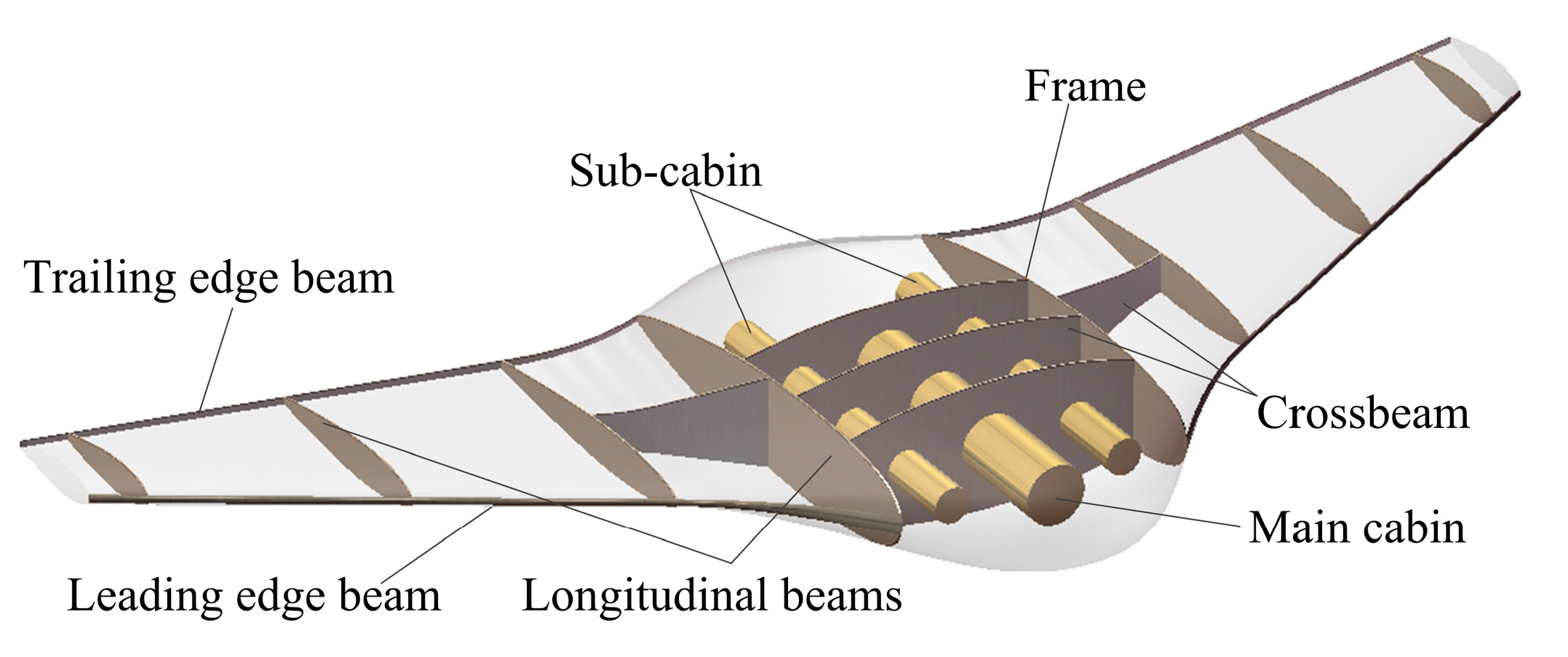
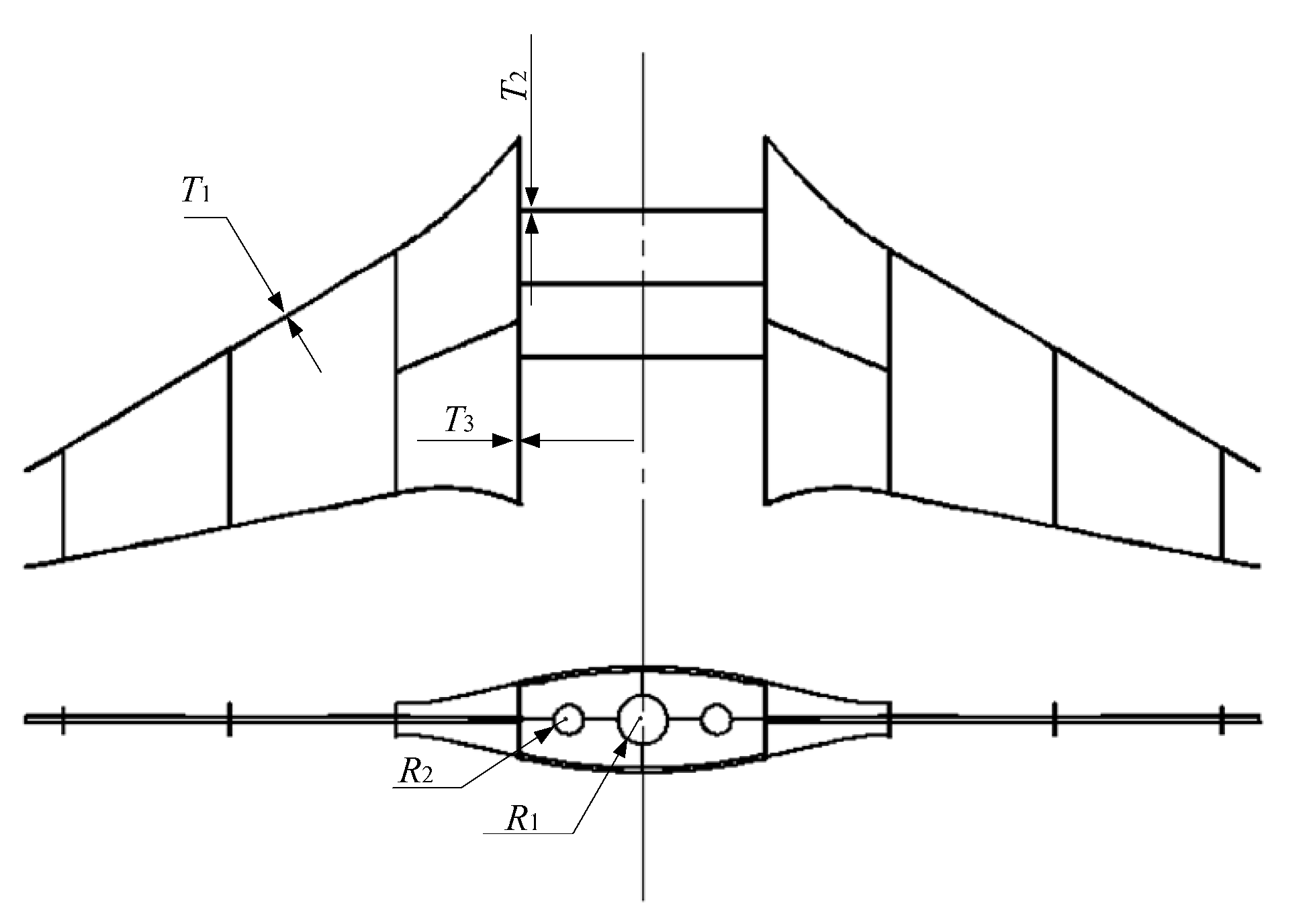
5.1. Problem Description
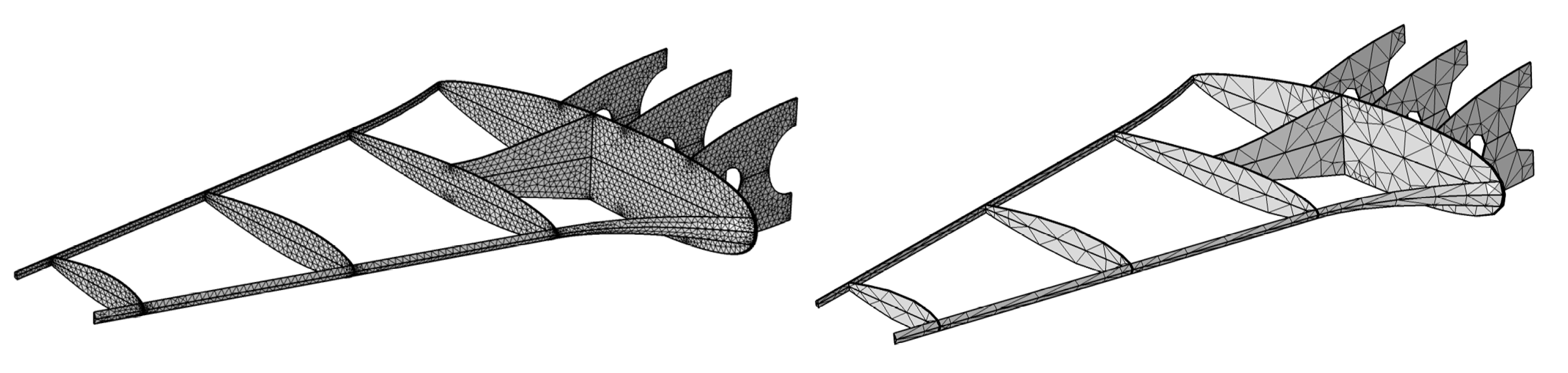
5.2. Multi-Fidelity Simulations for Structure Analysis
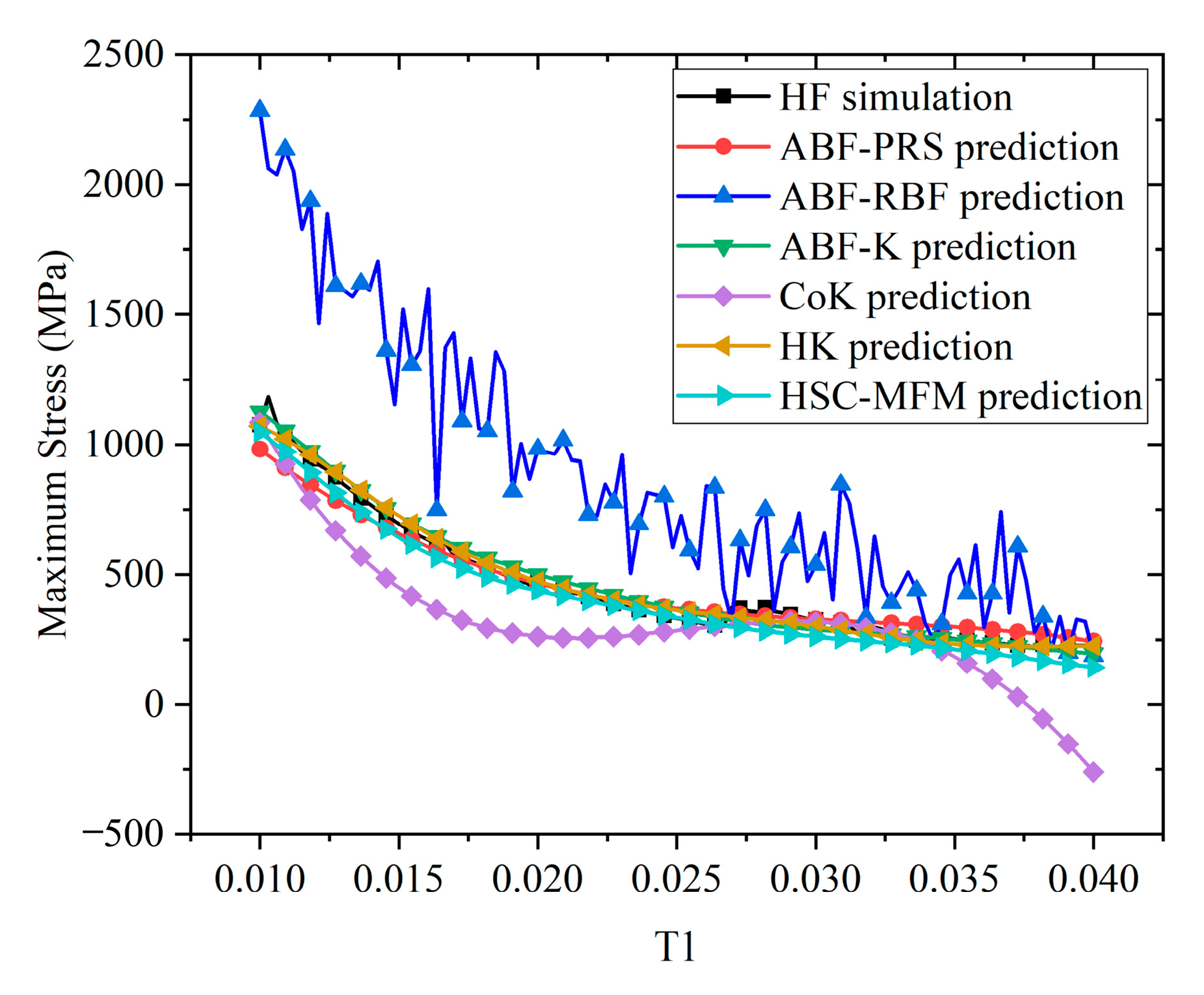
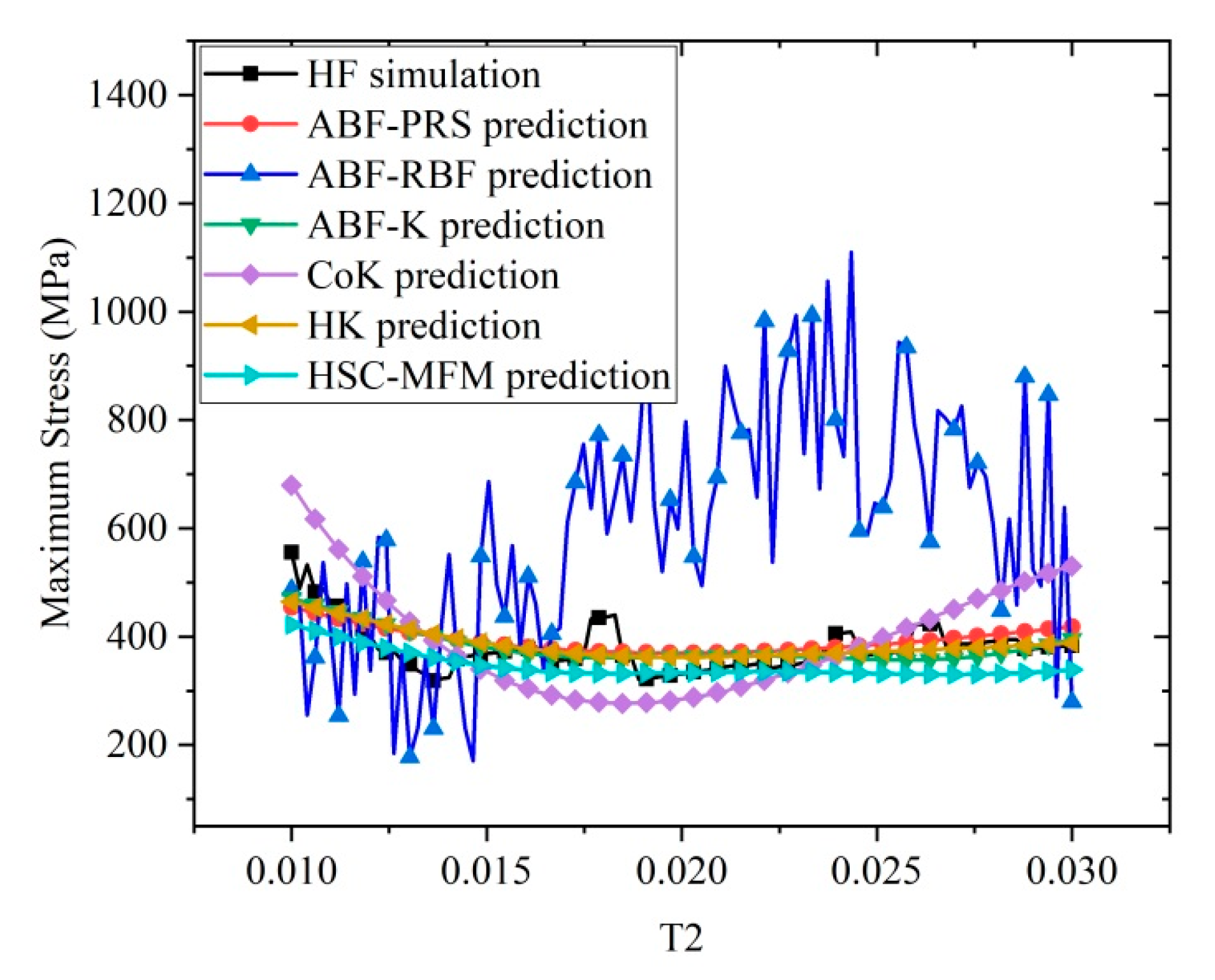
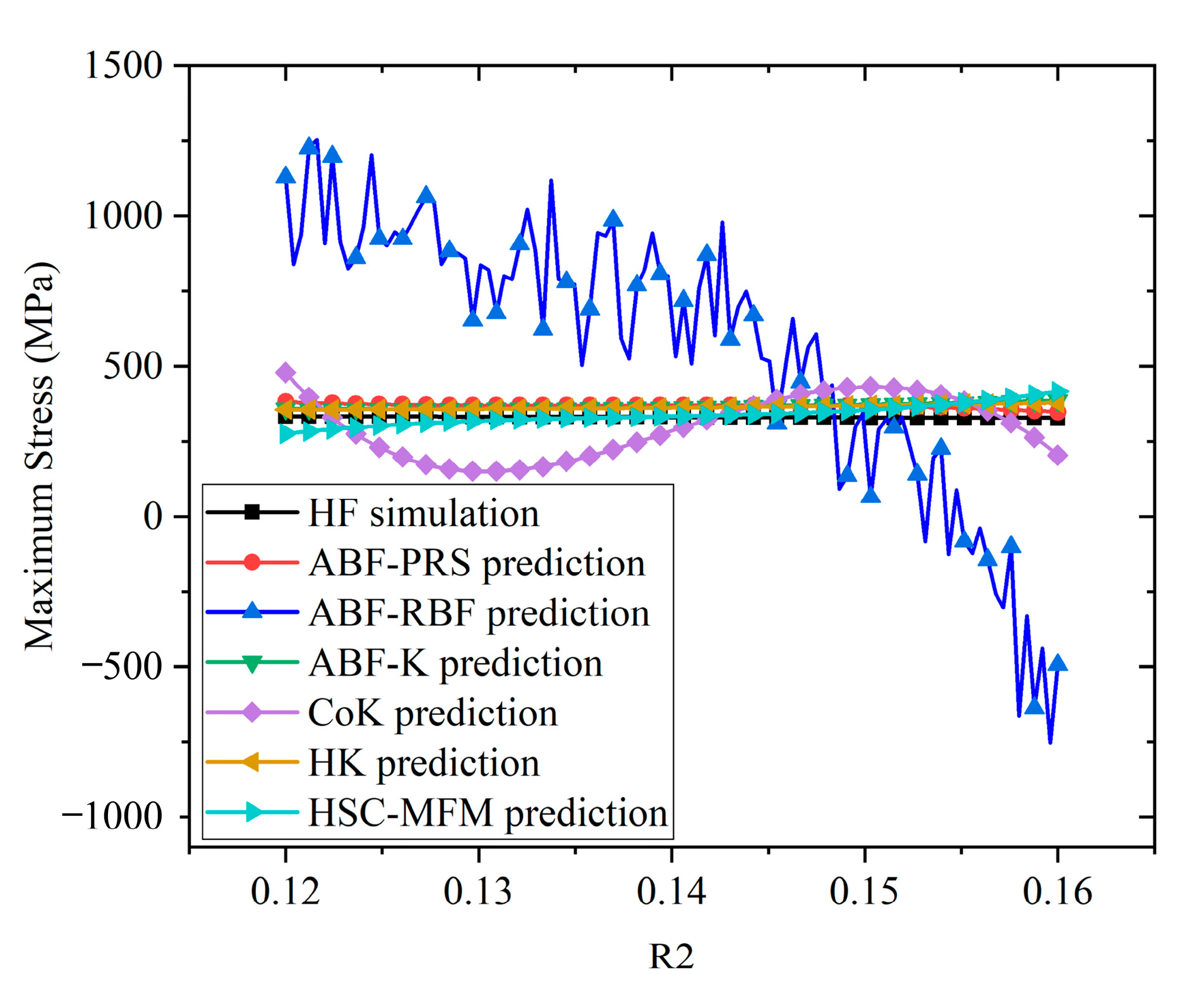
5.3. Strength Prediction and Result Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| LF | Low-fidelity |
| HF | High-fidelity |
| MF | Multi-fidelity |
| SM | Surrogate model |
| LFM | Low-fidelity model |
| HFM | High-fidelity model |
| MFSM | Multi-fidelity surrogate model |
| RSM | Response surface model |
| CoK | Cooperative Kriging |
| KM | Kriging model |
| RBF | Radial basis function |
| HSC-MFM | Hybrid-surrogate-calibration-assisted multi-fidelity modeling |
| HK | Hierarchical Kriging |
| Co-RBF | Cooperative radial basis function model |
| LOOCV | Leave-one-out cross-validation |
| ABF | Additive bridge function |
| ABF-PRS | Polynomial response surface-based additive bridge function |
| ABF-K | Kriging-based additive bridge function |
| ABF-RBF | Radial basis function-based additive bridge function |
| OLHS | Optimal Latin Hypercube sampling |
| BWBUG | Blended-wing-body underwater glider |
| FEA | Finite element analysis |
Appendix A
References
- Zheng, H.; Wang, Z.; Zhang, W.; Yu, H.; Wu, C. Surrogate-based pneumatic and aerodynamic allocation design optimization for flapping-wing micro air vehicles. Aerosp. Sci. Technol. 2024, 148, 109108. [Google Scholar] [CrossRef]
- Xiaozhe, X.; Guangli, L.; Kaikai, Z.; Yao, X.; Siyuan, C.; Kai, C. Surrogate-based shape optimization and sensitivity analysis on the aerodynamic performance of HCW configuration. Aerosp. Sci. Technol. 2025, 152, 109347. [Google Scholar] [CrossRef]
- Han, Z.H.; Görtz, S. Hierarchical kriging model for variable-fidelity surrogate modeling. Aiaa J. 2012, 50, 1885–1896. [Google Scholar] [CrossRef]
- Zheng, J.; Shao, X.; Gao, L.; Jiang, P.; Qiu, H. Difference mapping method using least square support vector regression for variable-fidelity metamodelling. Eng. Optim. 2015, 47, 719–736. [Google Scholar] [CrossRef]
- Jiang, P.; Xie, T.; Zhou, Q.; Shao, X.; Cao, L. A space mapping method based on gaussian process model for variable fidelity metamodeling. Simul. Model. Pract. Theory 2018, 81, 64–84. [Google Scholar] [CrossRef]
- Li, X.; Gao, W.; Gu, L.; Gong, C.; Jing, Z.; Su, H. A cooperative radial basis function method for variable-fidelity surrogate modeling. Struct. Multidiscip. Optim. 2017, 56, 1077–1092. [Google Scholar] [CrossRef]
- Bertram, A.; Zimmermann, R. Theoretical investigations of the new Cokriging method for variable-fidelity surrogate modeling: Well-posedness and maximum likelihood training. Adv. Comput. Math. 2018, 44, 1693–1716. [Google Scholar] [CrossRef]
- Balabanov, V.; Grossman, B.; Watson, L.; Mason, W.; Haftka, R. Multifidelity response surface model for HSCT wing bending material weight. In Proceedings of the 7th AIAA/USAF/NASA/ISSMO Symposium on Multidisciplinary Analysis and Optimization, St. Louis, MO, USA, 2–4 September 1998. [Google Scholar] [CrossRef]
- Alexandrov, N.M.; Lewis, R.M.; Gumbert, C.R.; Green, L.L.; Newman, P.A. Approximation and model management in aerodynamic optimization with variable fidelity models. J. Aircr. 2001, 38, 1093–1101. [Google Scholar] [CrossRef]
- Alexandrov, N.M.; Lewis, R.M.; Gumbert, C.R.; Green, L.L.; Newman, P.A. Optimization with variable-fidelity models applied to wing design. In Proceedings of the 38th Aerospace Sciences Meeting and Exhibit, 2000, Reno, NV, USA, 10–13 January 2000. [Google Scholar] [CrossRef]
- Eldred, M.; Giunta, A.; Collis, S. Second-order corrections for surrogate-based optimization with model hierarchies. In Proceedings of the 10th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference, Albany, NY, USA, 30 August–1 September 2004; American Institute of Aeronautics and Astronautics Inc.: Albany, NY, USA, 2004; pp. 1754–1768. [Google Scholar]
- Gano, S.; Renaud, J.; Sanders, B. Hybrid variable fidelity optimization by using a Kriging-based scaling function. AIAA J. 2005, 43, 2422–2430. [Google Scholar] [CrossRef]
- Sun, G.; Li, G.; Zhou, S.; Xu, W.; Yang, X.; Li, Q. Multifidelity optimization for sheet metal forming process. Struct. Multidiscip. Optim. 2011, 44, 111–124. [Google Scholar] [CrossRef]
- Han, Z.H.; Görtz, S.; Zimmermann, R. Improving variable-fidelity surrogate modeling via gradient-enhanced Kriging and a generalized hybrid bridge function. Aerosp. Sci. Technol. 2013, 25, 177–189. [Google Scholar] [CrossRef]
- Zheng, J.; Shao, X.; Gao, L.; Jiang, P.; Li, Z. A hybrid variable-fidelity global approximation modelling method combining tuned radial basis function base and kriging correction. J. Eng. Des. 2013, 24, 604–622. [Google Scholar] [CrossRef]
- Tyan, M.; Nguyen, N.V.; Lee, J.W. Improving variable-fidelity modelling by exploring global design space and radial basis function networks for aerofoil design. Eng. Optim. 2015, 47, 885–908. [Google Scholar] [CrossRef]
- Wang, P.; Li, Y.; Li, C. An Optimization Framework Based on Kriging Method with Additive Bridge Function for Variable-Fidelity Problem. In Proceedings of the 14th International Symposium on Distributed Computing and Applications for Business Engineering and Science (DCABES), Guiyang, China, 18–24 August 2015. [Google Scholar]
- Palar, P.S.; Tsuchiya, T.; Parks, G.T. Multi-fidelity non-intrusive polynomial chaos based on regression. Comput. Methods Appl. Mech. Eng. 2016, 305, 579–606. [Google Scholar] [CrossRef]
- Zheng, J. An output mapping variable fidelity metamodeling approach based on nested latin hypercube design for complex engineering design optimization. Appl. Intell. 2018, 48, 3591–3611. [Google Scholar] [CrossRef]
- Kou, J.; Zhang, W. Multi-fidelity modeling framework for nonlinear unsteady aerodynamics of airfoils. Appl. Math. Model. 2019, 76, 832–855. [Google Scholar] [CrossRef]
- Zhang, S.; Liang, P.; Pang, Y.; Li, J.; Song, X. Multi-fidelity surrogate model ensemble based on feasible intervals. Struct. Multidiscip. Optim. 2022, 65, 212. [Google Scholar] [CrossRef]
- Hai, C.; Qian, W.; Wang, W.; Mei, L. Active learning-assisted multi-fidelity surrogate modeling based on geometric transformation. Comput. Methods Appl. Mech. Eng. 2024, 426, 116990. [Google Scholar] [CrossRef]
- Kennedy, M.; O’Hagan, A. Predicting the output from a complex computer code when fast approximations are available. Biometrika 2000, 87, 1–13. [Google Scholar] [CrossRef]
- Forrester, A.I.J.; Sóbester, A.; Keane, A.J. Multi-fidelity optimization via surrogate modelling. Proc. R. Soc. A Math. Phys. Eng. Sci. 2007, 463, 3251–3269. [Google Scholar] [CrossRef]
- Ulaganathan, S.; Deschrijver, D.; Pakparvar, M.; Couckuyt, I.; Liu, W.; Plets, D.; Joseph, W.; Dhaene, T.; Martens, L.; Moerman, I. Building accurate radio environment maps from multi-fidelity spectrum sensing data. Wirel. Netw. 2016, 22, 2551–2562. [Google Scholar] [CrossRef]
- Xiao, M.; Zhang, G.; Breitkopf, P.; Villon, P.; Zhang, W. Extended Co-Kriging interpolation method based on multi-fidelity data. Appl. Math. Comput. 2018, 323, 120–131. [Google Scholar] [CrossRef]
- Dong, H.; Song, B.; Wang, P.; Huang, S. Multi-fidelity information fusion based on prediction of kriging. Struct. Multidiscip. Optim. 2015, 51, 1267–1280. [Google Scholar] [CrossRef]
- Zhou, Q.; Wang, Y.; Choi, S.K.; Jiang, P.; Shao, X.; Hu, J. A sequential multi-fidelity metamodeling approach for data regression. Knowl.-Based Syst. 2017, 134, 199–212. [Google Scholar] [CrossRef]
- Liu, H.; Ong, Y.S.; Cai, J.; Wang, Y. Cope with diverse data structures in multi-fidelity modeling: A gaussian process method. Eng. Appl. Artif. Intell. 2018, 67, 211–225. [Google Scholar] [CrossRef]
- Hu, J.; Peng, Y.; Lin, Q.; Liu, H.; Zhou, Q. An ensemble weighted average conservative multi-fidelity surrogate modeling method for engineering optimization. Eng. Comput. 2020, 38, 2221–2244. [Google Scholar] [CrossRef]
- Xu, Y.; Song, X.; Zhang, C. Hierarchical regression framework for multi-fidelity modeling. Knowl.-Based Syst. 2021, 212, 106587. [Google Scholar] [CrossRef]
- Li, K.; Li, Q.; Lv, L.; Song, X.; Ma, Y.; Lee, I. A nonlinearity integrated bi-fidelity surrogate model based on nonlinear mapping. Struct. Multidiscip. Optim. 2023, 66, 196. [Google Scholar] [CrossRef]
- Tang, L.; Liu, F.; Wu, A.; Li, Y.; Jiang, W.; Wang, Q.; Huang, J. A combined modeling method for complex multi-fidelity data fusion. Mach. Learn. Sci. Technol. 2024, 5, 035071. [Google Scholar] [CrossRef]
- He, Y.; Luo, J. Efficient hierarchical kriging modeling method for high-dimension multi-fidelity problems. Chin. J. Mech. Eng. 2024, 37, 151. [Google Scholar] [CrossRef]
- Wang, Y.; Pang, Y.; Xue, T.; Zhang, S.; Song, X. Ensemble learning based hierarchical surrogate model for multi-fidelity information fusion. Adv. Eng. Inform. 2024, 60, 102535. [Google Scholar] [CrossRef]
- Forrester, A.J.; Keane, A. Recent advances in surrogate-based optimization. Prog. Aerosp. Sci. 2009, 45, 50–79. [Google Scholar] [CrossRef]
- Fan, C.; Huang, Y.; Wang, Q. Sparsity-promoting polynomial response surface: A new surrogate model for response prediction. Adv. Eng. Softw. 2014, 77, 48–65. [Google Scholar] [CrossRef]
- Krige, D.G. A statistical approach to some basic mine valuation problems on the Witwatersrand. OR 1951, 4, 18. [Google Scholar]
- Sacks, J.; Welch, W.J.; Mitchell, T.J.; Wynn, H.P. Design and analysis of computer experiments. Stat. Sci. 1989, 4, 409–423. [Google Scholar] [CrossRef]
- Yi, J.; Li, X.; Xiao, M.; Xu, J.; Zhang, L. Construction of nested maximin designs based on successive local enumeration and modified novel global harmony search algorithm. Eng. Optim. 2017, 49, 161–180. [Google Scholar] [CrossRef]
- Durantin, C.; Rouxel, J.; Désidéri, J.A.; Glière, A. Multifidelity surrogate modeling based on radial basis functions. Struct. Multidiscip. Optim. 2017, 56, 1061–1075. [Google Scholar] [CrossRef]
- Zhou, Q.; Shao, X.; Jiang, P.; Zhou, H.; Shu, L. An adaptive global variable fidelity metamodeling strategy using a support vector regression based scaling function. Simul. Model. Pract. Theory 2015, 59, 18–35. [Google Scholar] [CrossRef]
- Liu, B.; Koziel, S.; Zhang, Q. A multi-fidelity surrogate-model-assisted evolutionary algorithm for computationally expensive optimization problems. J. Comput. Sci. 2016, 12, 28–37. [Google Scholar] [CrossRef]
- Lophaven, S.N. DACE—A MATLAB Kriging Toolbox—Version 2.0 2002. Available online: https://github.com/psbiomech/dace-toolbox-source (accessed on 13 April 2020).
- Mueller, J. Matsumoto: The matlab surrogate model toolbox for computationally expensive black-box global optimization problems. arXiv 2014, arXiv:1404.4261. Available online: https://github.com/Piiloblondie/MATSuMoTo (accessed on 25 December 2018).
- Jekabsons, G. Radial Basis Function Interpolation for Matlab. 2009. Available online: http://www.cs.rtu.lv/jekabsons/ (accessed on 17 March 2022).
- Kitson, R.C.; Cesnik, C.E.S. High speed vehicle fluid-structure-jet interaction analysis and modeling. In Proceedings of the 58th AIAA/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, AIAA 2017-0405, Grapevine, TX, USA, 9–13 January 2017; AIAA Structural Dynamics Best Student Paper. Available online: https://github.com/rckitson/cokriging (accessed on 24 January 2019).
- Li, C.; Wang, P.; Qiu, Z.; Dong, H. A double-stage surrogate-based shape optimization strategy for blended-wing-body underwater gliders. China Ocean. Eng. 2020, 34, 400–410. [Google Scholar] [CrossRef]




| Fixed Basis Functions | Parametric Basis Functions | ||
|---|---|---|---|
| Linear | Gaussian | ||
| Cubic | Multiquadric | ||
| Thin plate spline | Inverse multiquadric | ||
| Models | High-Fidelity Kriging | PRS-Calibrated | Kriging-Calibrated | RBF-Calibrated | HSC-MFM |
|---|---|---|---|---|---|
| RMSE | 1.6630 | 1.4404 | 0.6490 | 1.2368 | 0.8143 |
| MAX | 4.5493 | 2.4297 | 1.8403 | 3.7015 | 1.8103 |
| R2 | 0.8674 | 0.9006 | 0.9798 | 0.9267 | 0.9682 |
| Problems | Dimensions | Properties | Relations Between LFM and HFM |
|---|---|---|---|
| F1 | 1 | Multimodal | Additional nonlinear terms |
| F2 | 1 | Multimodal | Scaling transformation, additional linear terms |
| F3 | 2 | Multimodal | Translation, scaling transformation, and additional nonlinear terms |
| F4 | 2 | Valley-Shaped, Multiple Optima | Translation, scaling transformation, and additional nonlinear terms |
| F5 | 2 | Plate-Shaped | Scaling transformation and additional nonlinear terms |
| F6 | 2 | Bowl-shaped | Translation, scaling transformation, and additional nonlinear terms |
| F7 | 2 | Multimodal | Scaling transformation and additional nonlinear terms |
| F8 | 2 | Multimodal | Piecewise transformation |
| F9 | 2 | Multimodal | Scaling transformation and additional nonlinear terms |
| F10 | 2 | Unimodal | Translation |
| F11 | 3 | Valley-Shaped, Multimodal | Additional nonlinear terms |
| F12 | 4 | Valley-Shaped, Multimodal | Additional nonlinear terms |
| F13 | 4 | Multimodal | Additional nonlinear terms |
| F14 | 5 | Multimodal | Translation |
| F15 | 6 | Unimodal | Scaling transformation and additional nonlinear terms |
| F16 | 8 | Flat Region | Scaling transformation and additional nonlinear terms |
| F17 | 10 | Multimodal | Periodic transformation and additional nonlinear terms |
| F18 | 10 | Multimodal | Periodic transformation and phase conversion |
| Problems | ABF-PRS | ABF-RBF | ABF-K | CoK | HK | HSC-MFM |
|---|---|---|---|---|---|---|
| F1 | 1.0518 × 100 | 4.8729 × 100 | 1.4144 × 10−5 | 4.1824 × 10−2 | 1.2552 × 10−5 | 3.8716 × 10−5 |
| F2 | 2.6872 × 100 | 4.5001 × 101 | 9.0088 × 10−2 | 1.4882 × 10−1 | 1.9961 × 10−4 | 5.9185 × 10−1 |
| F3 | 2.1874 × 101 | 3.1004 × 102 | 7.2702 × 100 | 1.5465 × 102 | 1.3541 × 101 | 1.4570 × 101 |
| F4 | 5.5044 × 100 | 4.8413 × 100 | 1.1230 × 100 | 1.0015 × 101 | 1.2229 × 100 | 2.6400 × 100 |
| F5 | 1.4431 × 10−13 | 2.7098 × 102 | 1.1361 × 10−3 | 5.6859 × 102 | 1.1398 × 10−3 | 6.8552 × 10−2 |
| F6 | 4.2279 × 10−1 | 6.8027 × 103 | 6.8418 × 10−1 | 1.2221 × 104 | 6.8599 × 10−1 | 2.8430 × 100 |
| F7 | 1.7173 × 101 | 7.8404 × 100 | 3.6187 × 100 | 2.7896 × 101 | 2.8063 × 100 | 5.8137 × 100 |
| F8 | 1.0220 × 101 | 7.8034 × 100 | 2.4921 × 100 | 8.3069 × 100 | 2.5841 × 100 | 3.0034 × 100 |
| F9 | 3.6173 × 100 | 1.7958 × 100 | 1.6677 × 100 | 2.8952 × 100 | 1.7382 × 100 | 1.6871 × 100 |
| F10 | 8.1771 × 10−1 | 3.3198 × 10−1 | 2.2361 × 10−1 | 7.9763 × 10−1 | 2.1671 × 10−1 | 2.5109 × 10−1 |
| F11 | 5.8859 × 102 | 4.0519 × 102 | 1.6888 × 102 | 7.8797 × 102 | 1.6447 × 102 | 1.5822 × 102 |
| F12 | 2.4108 × 104 | 5.6950 × 104 | 2.1833 × 104 | 9.3315 × 104 | 2.2406 × 104 | 2.0859 × 104 |
| F13 | 4.7439 × 10−1 | 5.3121 × 10−1 | 3.6882 × 10−1 | 6.4735 × 10−1 | 3.4227 × 10−1 | 3.9371 × 10−1 |
| F14 | 9.7275 × 101 | 8.0240 × 101 | 7.8636 × 101 | 8.1655 × 101 | 7.8442 × 101 | 7.1389 × 101 |
| F15 | 5.2541 × 10−10 | 4.6921 × 102 | 5.2030 × 100 | 7.0416 × 102 | 4.6751 × 100 | 5.4962 × 100 |
| F16 | 2.9307 × 103 | 1.8813 × 103 | 1.4469 × 102 | 4.5232 × 103 | 1.5647 × 102 | 6.3707 × 102 |
| F17 | 1.0461 × 106 | 3.7876 × 102 | 3.5627 × 102 | 1.1195 × 103 | 3.5038 × 102 | 4.3075 × 102 |
| F18 | 2.3104 × 104 | 4.1653 × 10−1 | 3.3220 × 10−1 | 2.0996 × 101 | 3.3484 × 10−1 | 3.7858 × 10−1 |
| Problems | ABF-PRS | ABF-RBF | ABF-K | CoK | HK | HSC-MFM |
|---|---|---|---|---|---|---|
| F1 | 5 | 6 | 2 | 4 | 1 | 3 |
| F2 | 5 | 6 | 2 | 3 | 1 | 4 |
| F3 | 4 | 6 | 1 | 5 | 2 | 3 |
| F4 | 5 | 4 | 1 | 6 | 2 | 3 |
| F5 | 1 | 5 | 2 | 6 | 3 | 4 |
| F6 | 1 | 5 | 2 | 6 | 3 | 4 |
| F7 | 5 | 4 | 2 | 6 | 1 | 3 |
| F8 | 6 | 4 | 1 | 5 | 2 | 3 |
| F9 | 6 | 4 | 1 | 5 | 3 | 2 |
| F10 | 6 | 4 | 2 | 5 | 1 | 3 |
| F11 | 5 | 4 | 3 | 6 | 2 | 1 |
| F12 | 4 | 5 | 2 | 6 | 3 | 1 |
| F13 | 4 | 5 | 2 | 6 | 1 | 3 |
| F14 | 6 | 4 | 3 | 5 | 2 | 1 |
| F15 | 1 | 5 | 3 | 6 | 2 | 4 |
| F16 | 5 | 4 | 1 | 6 | 2 | 3 |
| F17 | 6 | 3 | 2 | 5 | 1 | 4 |
| F18 | 6 | 4 | 1 | 5 | 2 | 3 |
| Average ranking | 4.5 | 4.6 | 1.8 | 5.3 | 1.9 | 2.9 |
| Synthetic ranking | 4 | 5 | 1 | 6 | 2 | 3 |
| Problems | ABF−PRS | ABF−RBF | ABF−K | CoK | HK | HSC−MFM |
|---|---|---|---|---|---|---|
| F1 | [1.0518 × 100, 1.0518 × 100] | [7.5658 × 10−1, 2.0816 × 101] | [1.4125 × 10−5, 1.4165 × 10−5] | [4.1820 × 10−2, 4.1828 × 10−2] | [1.2532 × 10−5, 1.2575 × 10−5] | [3.7965 × 10−5, 4.0373 × 10−5] |
| F2 | [2.6872 × 100, 2.6872 × 100] | [1.0522 × 100, 3.2749 × 102] | [9.0088 × 10−2, 9.0088 × 10−2] | [1.4881 × 10−1, 1.4883 × 10−1] | [1.9932 × 10−4, 1.9992 × 10−4] | [5.5891 × 10−1, 6.2633 × 10−1] |
| F3 | [1.9846 × 101, 2.3923 × 101] | [2.7138 × 102, 3.6815 × 102] | [3.8191 × 100, 1.3711 × 101] | [1.4003 × 102, 1.8446 × 102] | [5.9702 × 100, 2.7032 × 101] | [1.2037 × 101, 1.7066 × 101] |
| F4 | [5.3492 × 100, 5.7161 × 100] | [4.0177 × 100, 5.8328 × 100] | [8.5869 × 10−1, 1.5177 × 100] | [1.4184 × 100, 1.9733 × 101] | [8.6214 × 10−1, 1.8685 × 100] | [2.2283 × 100, 3.1551 × 100] |
| F5 | [9.4312 × 10−14, 2.362310−13] | [2.3499 × 102, 3.3763 × 102] | [6.4820 × 10−4, 1.7686 × 10−3] | [4.7896 × 102, 6.6342 × 102] | [6.3921 × 10−4, 1.7430 × 10−3] | [3.0798 × 10−2, 1.3450 × 10−1] |
| F6 | [3.8649 × 10−1, 4.5133 × 10−1] | [6.5972 × 103, 6.8997 × 103] | [4.7392 × 10−1, 1.4890 × 100] | [1.2001 × 104, 1.2290 × 104] | [4.7437 × 10−1, 1.5115 × 100] | [1.5547 × 100, 7.0302 × 100] |
| F7 | [1.4767 × 101, 1.9298 × 101] | [5.3147 × 100, 9.7227 × 100] | [2.1127 × 100, 4.6744 × 100] | [3.2360 × 100, 4.2446 × 101] | [2.1047 × 100, 3.7336 × 100] | [3.3077 × 100, 7.5260 × 100] |
| F8 | [9.6199 × 100, 1.0528 × 101] | [4.9300 × 100, 1.2885 × 101] | [1.7886 × 100, 4.4250 × 100] | [1.9226 × 100, 1.5752 × 101] | [1.9067 × 100, 4.4760 × 100] | [2.1831 × 100, 4.0809 × 100] |
| F9 | [3.3239 × 100, 3.8729 × 100] | [1.5309 × 100, 2.1523 × 100] | [1.3315 × 100, 1.9935 × 100] | [2.0635 × 100, 3.3301 × 100] | [1.3770 × 100, 2.0023 × 100] | [1.3663 × 100, 2.1148 × 100] |
| F10 | [7.6293 × 10−1, 8.9196 × 10−1] | [2.4046 × 10−1, 4.7536 × 10−1] | [1.2354 × 10−1, 3.4622 × 10−1] | [9.2184 × 10−2, 1.8856 × 100] | [1.3738 × 10−1, 3.0593 × 10−1] | [1.1831 × 10−1, 5.0501 × 10−1] |
| F11 | [5.0181 × 102, 7.8323 × 102] | [3.0272 × 102, 4.8962 × 102] | [5.2400 × 101, 2.6588 × 102] | [3.7116 × 102, 9.8608 × 102] | [6.3355 × 101, 2.8188 × 102] | [5.5181 × 101, 2.6792 × 102] |
| F12 | [1.9972 × 104, 2.7167 × 104] | [5.5590 × 104, 5.9249 × 104] | [1.5328 × 104, 2.6200 × 104] | [9.2322 × 104, 9.4701 × 104] | [1.8681 × 104, 2.6466 × 104] | [1.6487 × 104, 2.5678 × 104] |
| F13 | [3.6052 × 10−1, 6.2468 × 10−1] | [3.4562 × 10−1, 9.2010 × 10−1] | [3.0980 × 10−1, 5.1600 × 10−1] | [4.3802 × 10−1, 1.4692 × 100] | [2.7476 × 10−1, 4.2387 × 10−1] | [3.0451 × 10−1, 5.6002 × 10−1] |
| F14 | [8.5232 × 101, 1.3104 × 102] | [7.6501 × 101, 8.5319 × 101] | [6.6111 × 101, 8.4078 × 101] | [7.8151 × 101, 8.7131 × 101] | [6.7639 × 101, 8.5380 × 101] | [6.2201 × 101, 7.8781 × 101] |
| F15 | [1.0849 × 10−10, 1.1268 × 10−9] | [4.6382 × 102, 4.7232 × 102] | [1.3250 × 100, 1.2217 × 101] | [7.0215 × 102, 7.0569 × 102] | [3.6108 × 100, 5.7333 × 100] | [3.1018 × 100, 7.9125 × 100] |
| F16 | [4.0403 × 102, 9.9898 × 103] | [1.8323 × 103, 1.9039 × 103] | [1.0089 × 102, 1.9075 × 102] | [4.4827 × 103, 4.5441 × 103] | [1.0891 × 102, 2.1442 × 102] | [5.0223 × 102, 1.2954 × 103] |
| F17 | [6.7254 × 104, 3.3907 × 106] | [3.5343 × 102, 3.8872 × 102] | [3.3086 × 102, 3.7779 × 102] | [1.1111 × 103, 1.1229 × 103] | [3.2570 × 102, 3.6815 × 102] | [3.1860 × 102, 9.3009 × 102] |
| F18 | [1.0807 × 103, 9.4839 × 104] | [3.9137 × 10−1, 4.3746 × 10−1] | [2.9929 × 10−1, 3.8168 × 10−1] | [2.0989 × 101, 2.1000 × 101] | [3.0348 × 10−1, 3.8163 × 10−1] | [2.8465 × 10−1, 6.4916 × 10−1] |
| Parameters | Description (Unit: m) | Lower Boundary | Upper Boundary |
|---|---|---|---|
| T1 | Thickness of leading and trailing edge beams | 0.01 | 0.04 |
| T2 | Thickness of crossbeams | 0.01 | 0.03 |
| T3 | Thickness of longitudinal beams | 0.01 | 0.03 |
| R1 | Radius of main cabin mounting hole | 0.20 | 0.24 |
| R2 | Radius of sub-cabin mounting hole | 0.12 | 0.16 |
| Metrics | ABF-PRS | ABF-RBF | ABF-K | CoK | HK | HSC-MFM |
|---|---|---|---|---|---|---|
| RMSE | 6.6701 × 101 | 1.0209 × 103 | 5.9820 × 101 | 5.9332 × 102 | 5.1296 × 101 | 8.1235 × 101 |
| MAX | 2.2910 × 102 | 5.3806 × 103 | 2.8485 × 102 | 4.1669 × 103 | 2.4714 × 102 | 2.9398 × 102 |
| R2 | 9.0760 × 10−1 | −2.0645 × 101 | 9.2568 × 10−1 | −6.3113 × 100 | 9.4535 × 10−1 | 8.6294 × 10−1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, C.; Cao, Y.; An, X.; Lyu, D.; Liu, J. A Hybrid-Surrogate-Calibration-Assisted Multi-Fidelity Modeling Approach and Its Application in Strength Prediction for Underwater Gliders. J. Mar. Sci. Eng. 2025, 13, 416. https://doi.org/10.3390/jmse13030416
Li C, Cao Y, An X, Lyu D, Liu J. A Hybrid-Surrogate-Calibration-Assisted Multi-Fidelity Modeling Approach and Its Application in Strength Prediction for Underwater Gliders. Journal of Marine Science and Engineering. 2025; 13(3):416. https://doi.org/10.3390/jmse13030416
Chicago/Turabian StyleLi, Chengshan, Yufan Cao, Xiaoyi An, Da Lyu, and Junxiao Liu. 2025. "A Hybrid-Surrogate-Calibration-Assisted Multi-Fidelity Modeling Approach and Its Application in Strength Prediction for Underwater Gliders" Journal of Marine Science and Engineering 13, no. 3: 416. https://doi.org/10.3390/jmse13030416
APA StyleLi, C., Cao, Y., An, X., Lyu, D., & Liu, J. (2025). A Hybrid-Surrogate-Calibration-Assisted Multi-Fidelity Modeling Approach and Its Application in Strength Prediction for Underwater Gliders. Journal of Marine Science and Engineering, 13(3), 416. https://doi.org/10.3390/jmse13030416






