Optimization of Inbound and Outbound Vessel Scheduling in One-Way Channel Based on Reinforcement Learning
Abstract
1. Introduction
- (1)
- Method Improvement: By combining reinforcement learning with unidirectional channel ship scheduling problem, we comprehensively consider channel capacity, ship size, sailing speed, and other factors, and we strive to be close to the real port environment and build a more efficient scheduling model.
- (2)
- Algorithm Optimization: A strategy of gradually approaching Q value in reinforcement learning algorithm is adopted to reduce the resource consumption and shorten the running time of the intelligent scheduling algorithm for ships entering and leaving ports in one-way channel.
2. Literature Review
2.1. Current Research on Ship Scheduling
2.2. Reinforcement Learning in Combinatorial Optimization
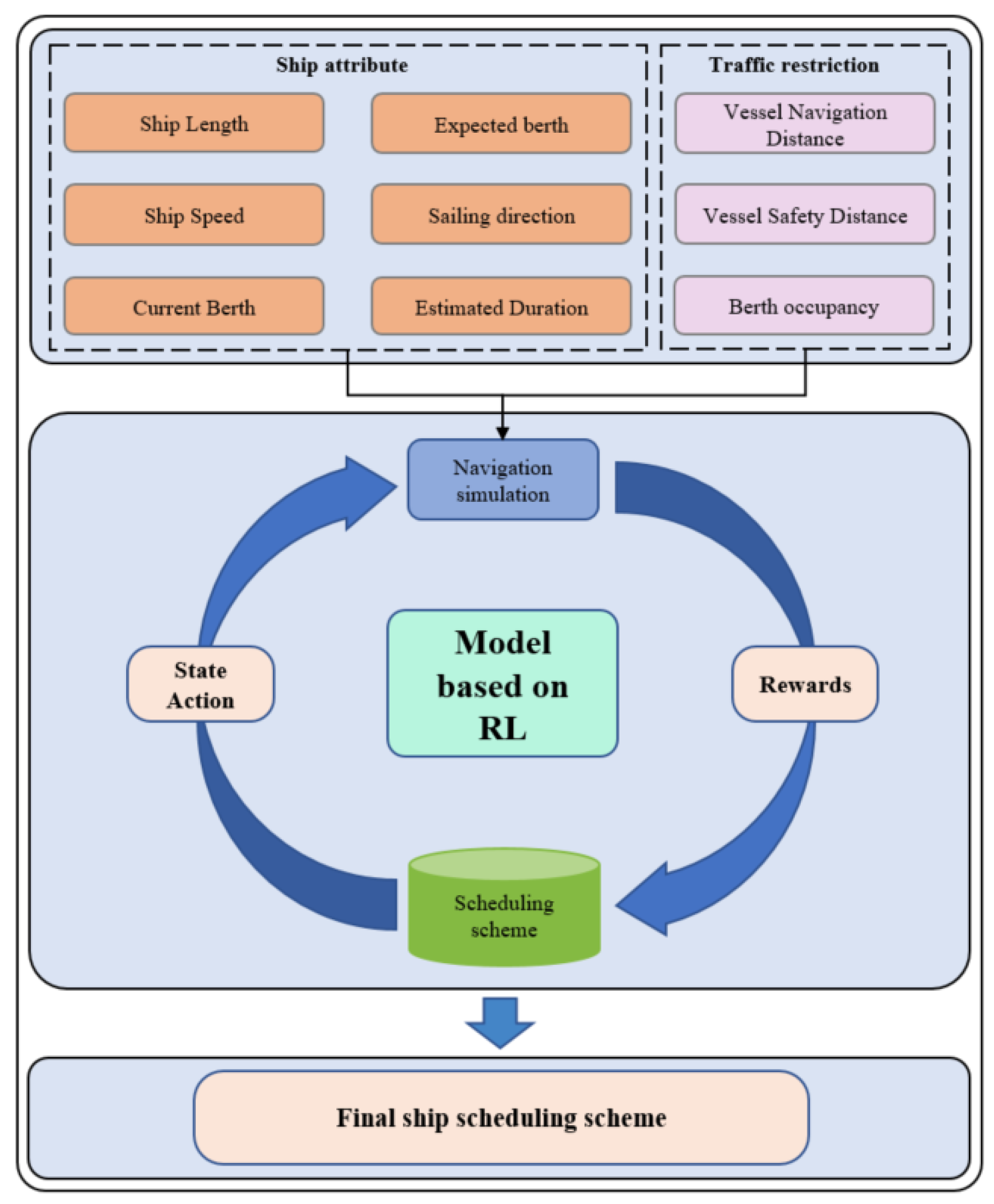
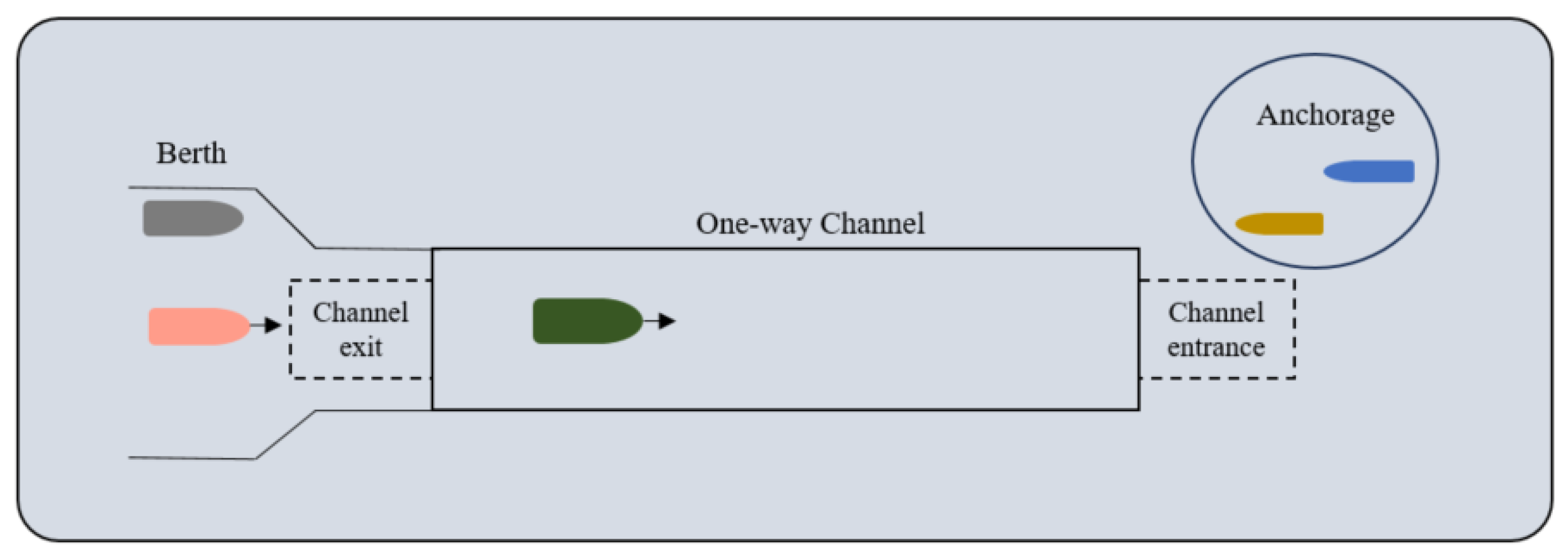
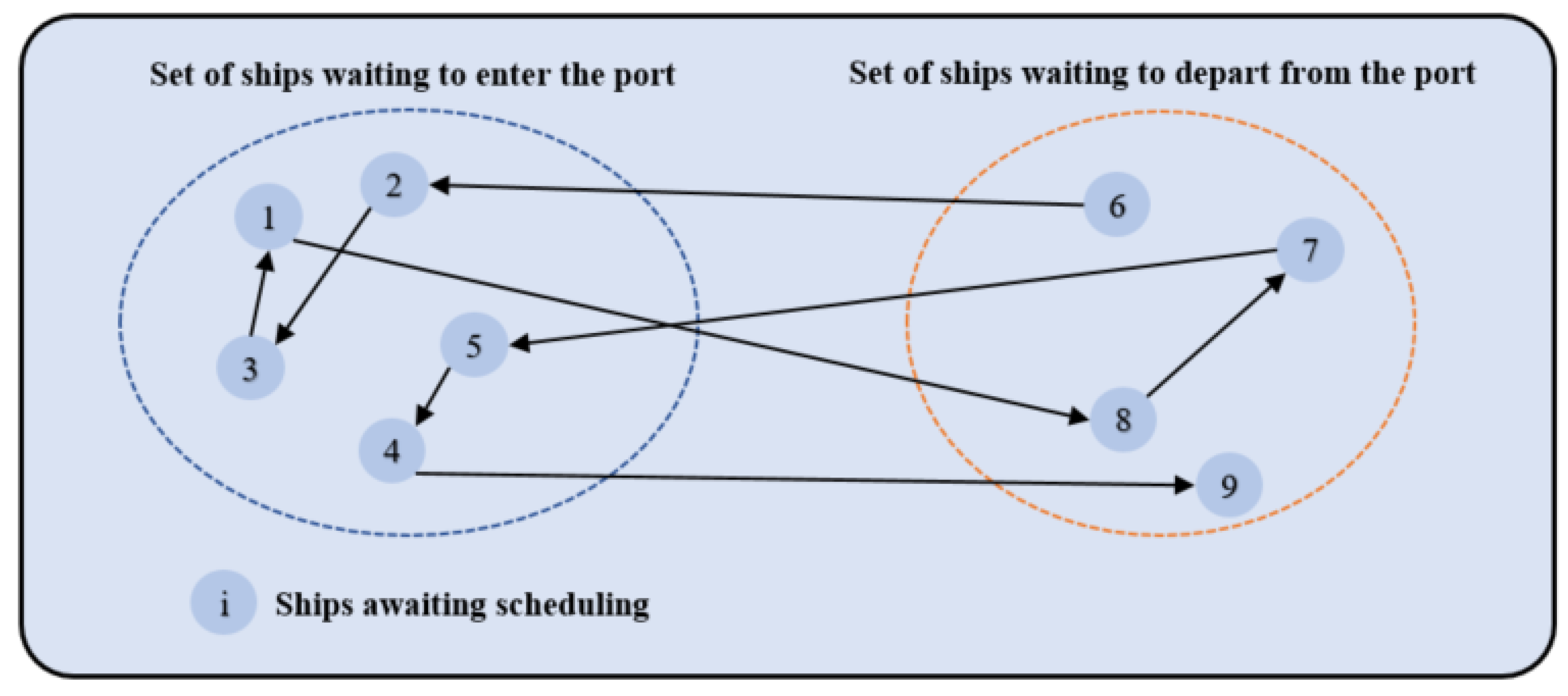
3. Model of Ship Scheduling Problem in One-Way Channels
3.1. Construction of One-Way Channel Ship Scheduling Model
- (1)
- For incoming ships, the application time is considered to be from the moment they apply for entry, and for outgoing ships, the application time is the time when they apply to leave the berth.
- (2)
- The berths for incoming ships have already been pre-assigned.
- (3)
- There are sufficient pilots available.
- (4)
- During the ship scheduling process, factors such as weather, accidents, and other disturbances are not considered.
- (5)
- All ships entering and leaving the port are in the same position near and far from the waterway, that is, the sailing distance of the ship in the waterway is the same.
- (6)
- When applying for entry or exit, pilots and tugboats have already been assigned and are ready.
- (1)
- Scheduling time constraint
- (2)
- Same-direction ship constraint
- (3)
- Switching constraints for in-and-out channel process
- (4)
- Constraints for Vessels in Opposite Directions
- (5)
- Constraints for the ship following process
- (6)
- Constraints to avoid berth conflicts
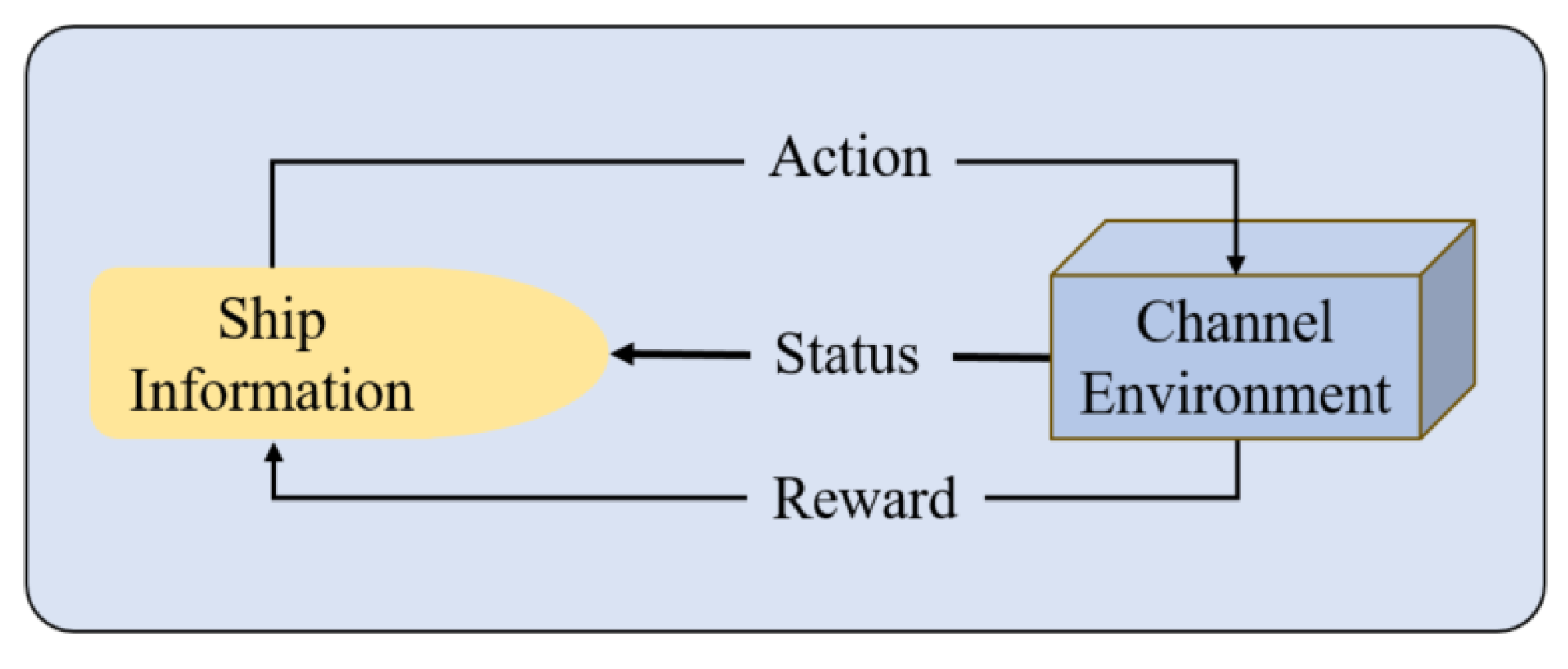
3.2. Solving Ship Scheduling Problems Using Reinforcement Learning Algorithms
3.2.1. Algorithm Framework
3.2.2. Q-Learning-Based Ship Scheduling Optimization Model Design
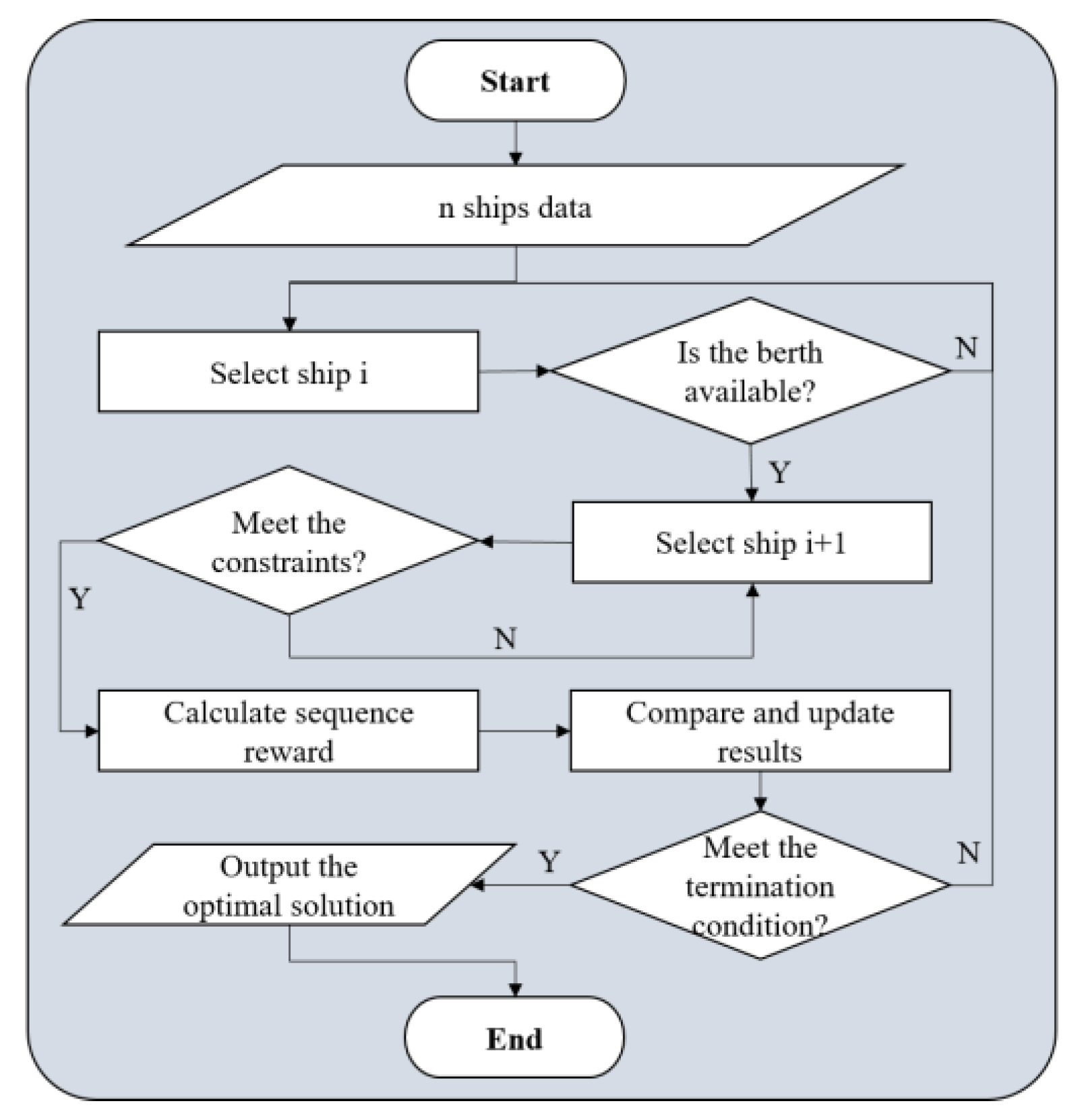
3.2.3. Algorithm Process
4. Experimental Case Analysis
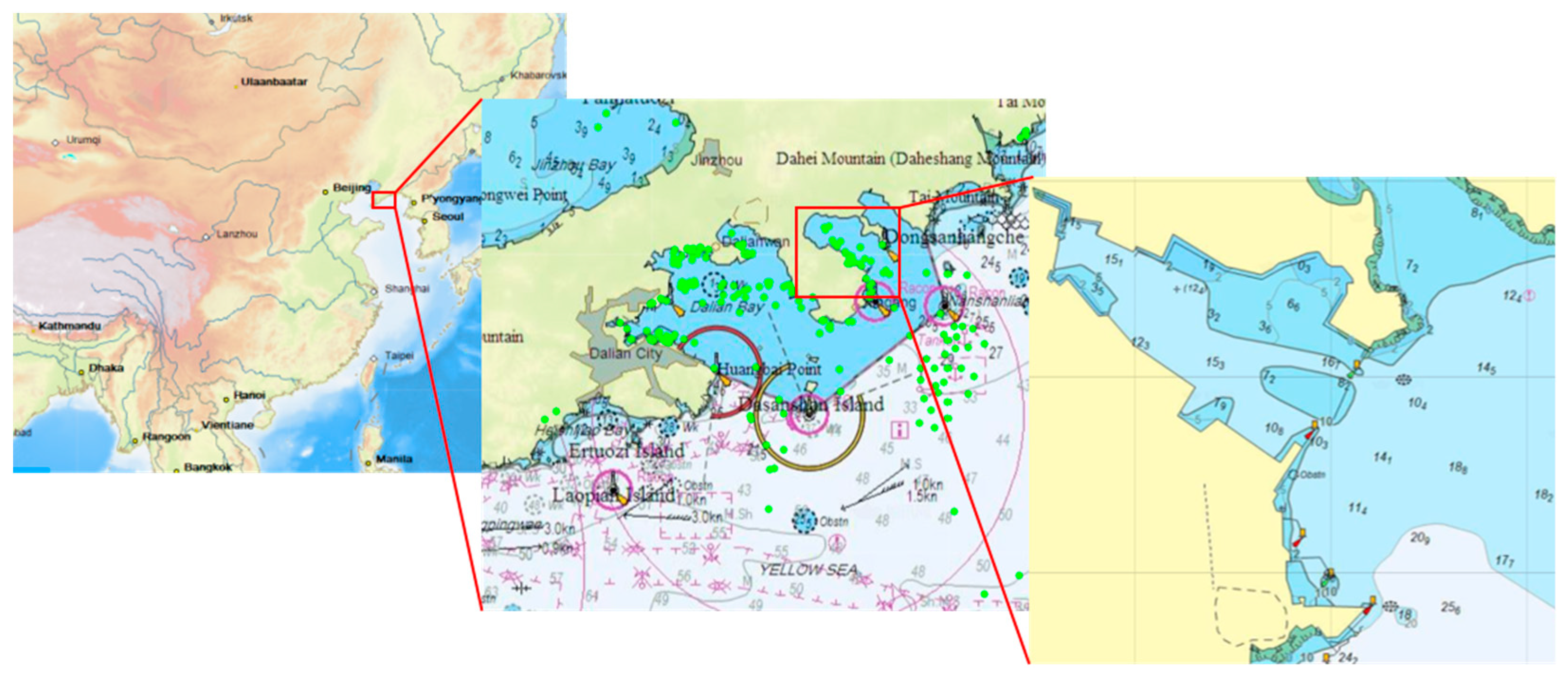
4.1. Parameter Input
4.2. Results Analysis
- (1)
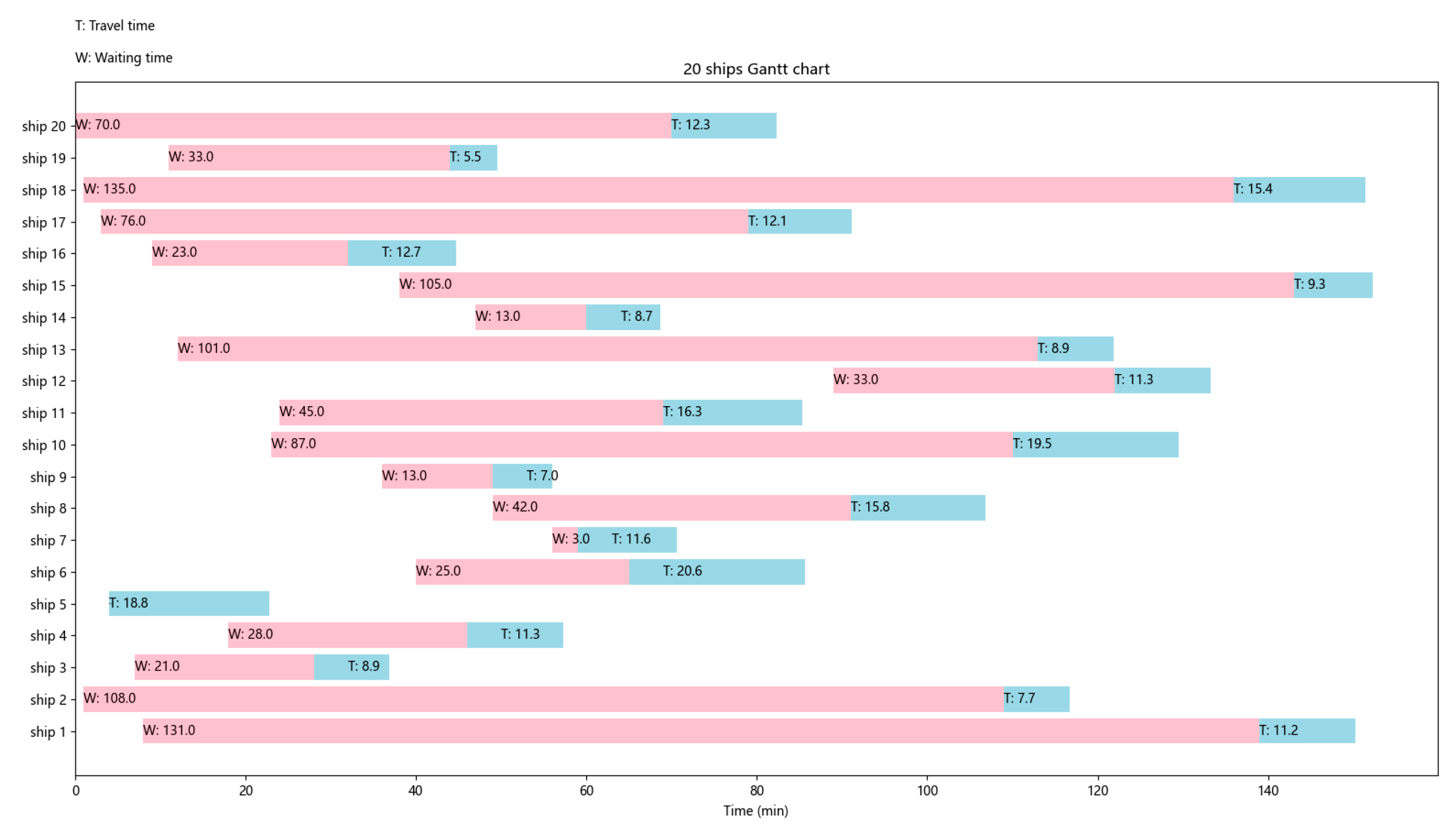
- Reasonableness verification
- (2)
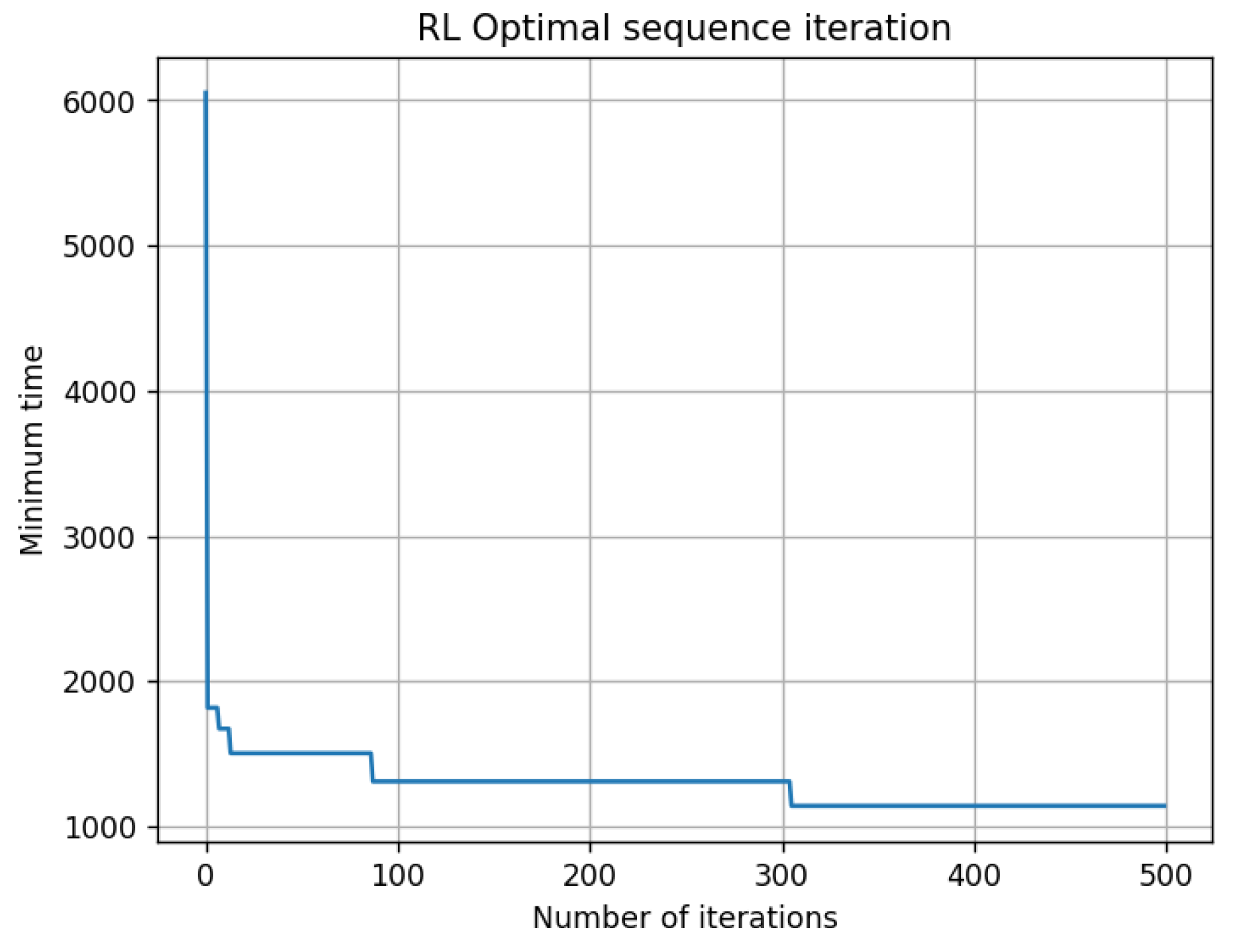
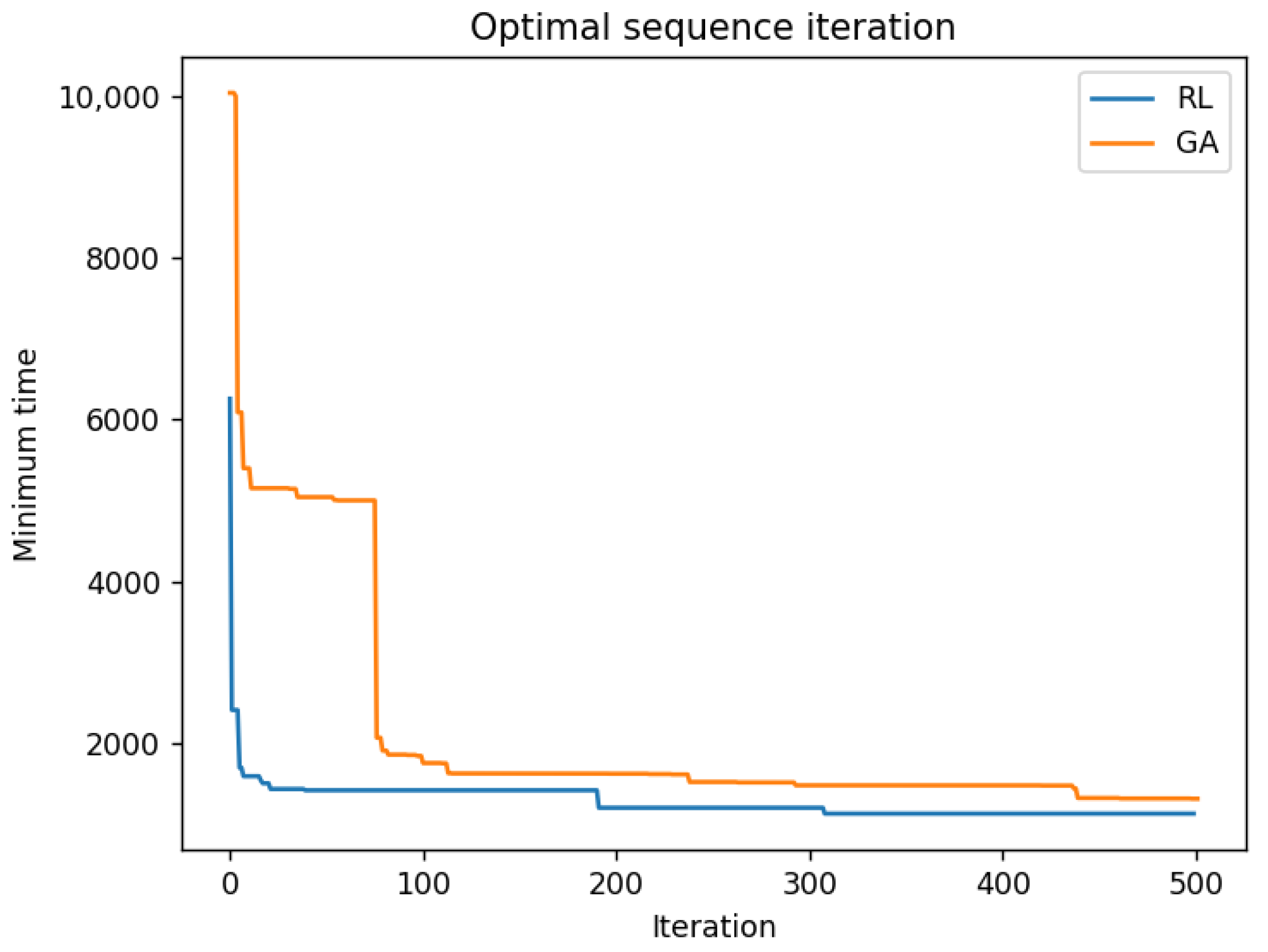
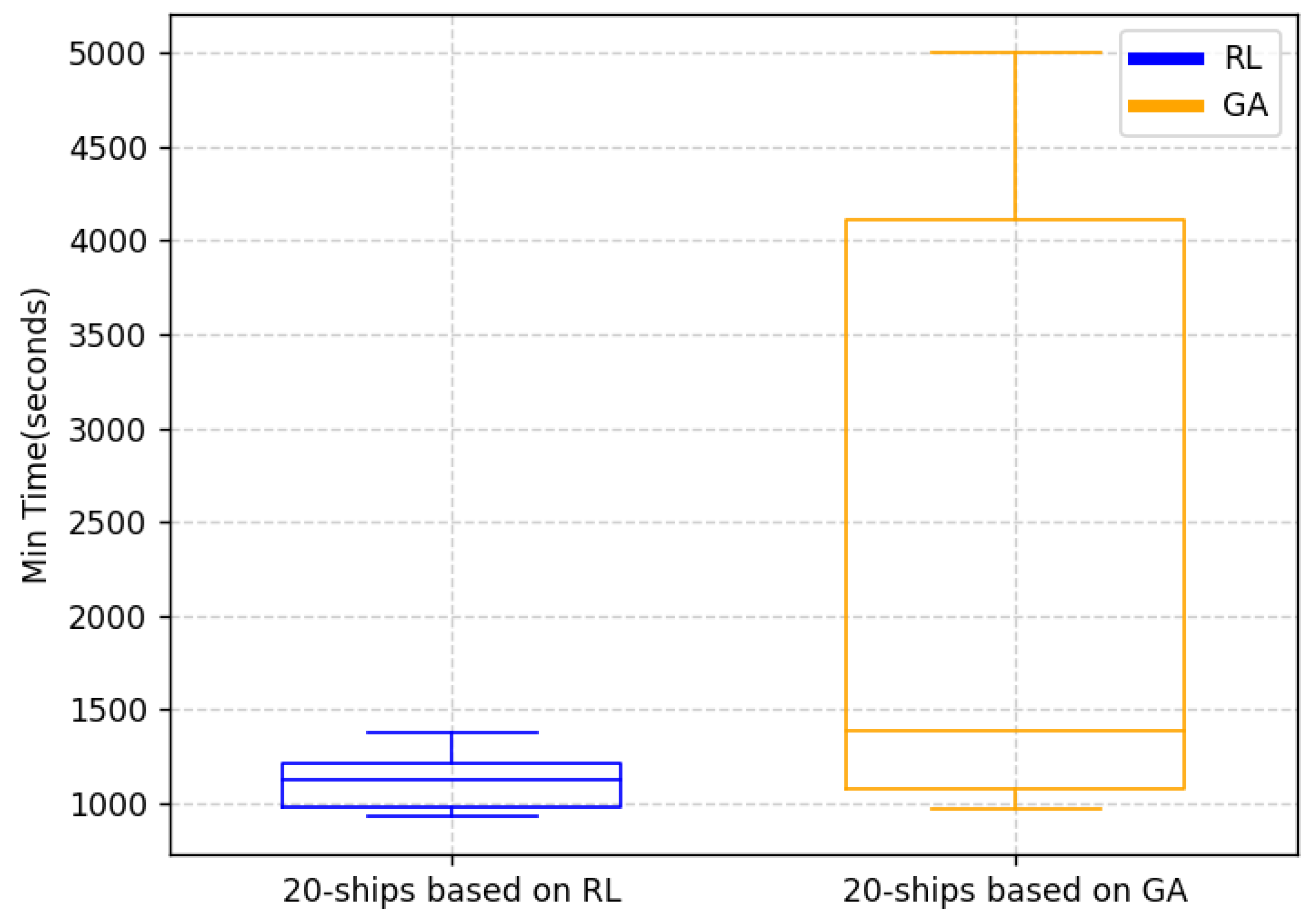
- Algorithm Superiority
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lalla-Ruiz, E.; Shi, X.; Voss, S. The Waterway Ship Scheduling Problem. Transport. Res. Part D-Transport. Environ. 2018, 60, 191–209. [Google Scholar] [CrossRef]
- Zhen, R.; Shi, Z.; Gu, Q.; Yang, S. A Novel Deterministic Search-Based Algorithm for Multi-Ship Collaborative Collision Avoidance Decision-Making. Ocean Eng. 2024, 292, 116524. [Google Scholar] [CrossRef]
- Tong, Y.; Zhen, R.; Dong, H.; Liu, J. Identifying Influential Ships in Multi-Ship Encounter Situation Complex Network Based on Improved WVoteRank Approach. Ocean Eng. 2023, 284, 115192. [Google Scholar] [CrossRef]
- Jiang, X.; Zhong, M.; Shi, G.; Li, W.; Sui, Y. Vessel Scheduling Model with Resource Restriction Considerations for Restricted Channel in Ports. Comput. Ind. Eng. 2023, 177, 109034. [Google Scholar] [CrossRef]
- Liu, B.; Li, Z.-C.; Wang, Y. A Two-Stage Stochastic Programming Model for Seaport Berth and Channel Planning with Uncertainties in Ship Arrival and Handling Times. Transp. Res. Part E Logist. Transp. Rev. 2022, 167, 102919. [Google Scholar] [CrossRef]
- Zhang, P. Optimization Study of Ship Scheduling in Unidirectional Channel Considering Ship Extension. Master’s Thesis, Dalian Maritime University, Dalian, China, 2023. [Google Scholar]
- Lei, K. Integrated Scheduling Optimization of One-Way Channel Vessel Entry and Exit and Tugboat Distribution. Master’s Thesis, Dalian Maritime University, Dalian, China, 2022. [Google Scholar]
- Shang, W.-L.; Zhang, J.; Wang, K.; Yang, H.; Ochieng, W. Can Financial Subsidy Increase Electric Vehicle (EV) Penetration---Evidence from a Quasi-Natural Experiment. Renewable and Sustainable Energy Reviews 2024, 190, 114021. [Google Scholar] [CrossRef]
- Shang, W.-L.; Chen, Y.; Yu, Q.; Song, X.; Chen, Y.; Ma, X.; Chen, X.; Tan, Z.; Huang, J.; Ochieng, W. Spatio-Temporal Analysis of Carbon Footprints for Urban Public Transport Systems Based on Smart Card Data. Appl. Energy 2023, 352, 121859. [Google Scholar] [CrossRef]
- Zhen, R.; Lv, P.; Shi, Z.; Chen, G. A Novel Fuzzy Multi-Factor Navigational Risk Assessment Method for Ship Route Optimization in Costal Offshore Wind Farm Waters. Ocean Coast. Manag. 2023, 232, 106428. [Google Scholar] [CrossRef]
- Dong, H.; Zhen, R.; Gu, Q.; Lin, Z.; Chen, J.; Yan, K.; Chen, B. A Novel Collaborative Collision Avoidance Decision Method for Multi-Ship Encounters in Complex Waterways. Ocean Eng. 2024, 313, 119512. [Google Scholar] [CrossRef]
- Huang, L.; Wan, C.; Wen, Y.; Song, R.; van Gelder, P. Generation and Application of Maritime Route Networks: Overview and Future Research Directions. IEEE Trans. Intell. Transp. Syst. 2025, 26, 620–637. [Google Scholar] [CrossRef]
- Wang, D.; Liao, F. Analysis of First-Come-First-Served Mechanisms in One-Way Car-Sharing Services. Transp. Res. Part B Methodol. 2021, 147, 22–41. [Google Scholar] [CrossRef]
- Xia, Z.; Guo, Z.; Wang, W.; Jiang, Y. Joint Optimization of Ship Scheduling and Speed Reduction: A New Strategy Considering High Transport Efficiency and Low Carbon of Ships in Port. Ocean Eng. 2021, 233, 109224. [Google Scholar] [CrossRef]
- Xu, G.; Guo, T.; Wu, Z. Optimum Scheduling Model for Ship in/Outbound Harbor in One-Way Traffic Fairway. J. Shanghai Marit. Univ. 2008, 34, 50–153, 157. [Google Scholar]
- Zheng, H.; Liu, B.; Deng, C.; Feng, P. Ship Scheduling Optimization in One-Way Channel Bulk Harbor. Oper. Res. Manag. Sci. 2018, 27, 28–37. [Google Scholar]
- Xu, D.; Li, C.-L.; Leung, J.Y.-T. Berth Allocation with Time-Dependent Physical Limitations on Vessels. Eur. J. Oper. Res. 2012, 216, 47–56. [Google Scholar] [CrossRef]
- Ting, C.-J.; Wu, K.-C.; Chou, H. Particle Swarm Optimization Algorithm for the Berth Allocation Problem. Expert Syst. Appl. 2014, 41, 1543–1550. [Google Scholar] [CrossRef]
- Mauri, G.R.; Ribeiro, G.M.; Lorena, L.A.N.; Laporte, G. An Adaptive Large Neighborhood Search for the Discrete and Continuous Berth Allocation Problem. Comput. Oper. Res. 2016, 70, 140–154. [Google Scholar] [CrossRef]
- Bai, X.; Li, B.; Xu, X. Sequencing of Ships Entering a Port Based on an Improved Artificial Fish Swarm Algorithm. J. Shanghai Marit. Univ. 2021, 42, 85–90. [Google Scholar]
- Li, R.; Zhang, X.; Li, J.; Jiang, L. Application of Self-Learning Genetic Algorithm Based on Reinforcement Learning in Ship Scheduling. J. Dalian Marit. Univ. 2022, 48, 20–30. [Google Scholar] [CrossRef]
- Zhang, X.; Lin, J.; Guo, Z.; Chen, X. Vessel Scheduling Optimization Based on Simulated Annealing and Multiple Population Genetic Algorithm. Navig. China 2016, 39, 26–30. [Google Scholar]
- Zhang, B.; Zheng, Z.; Wang, D. A Model and Algorithm for Vessel Scheduling through a Two-Way Tidal Channel. Marit. Policy Manag. 2020, 47, 188–202. [Google Scholar] [CrossRef]
- Zhang, X.; Li, R.; Lin, J. Vessel Scheduling Optimization in Two-Way Traffic Ports. Navig. China 2018, 41, 36–40. [Google Scholar]
- Wang, H.; Tian, W.; Zhang, J.; Li, Y. A Hybrid Self-Organizing Scheduling Method for Ships in Restricted Two-Way Waterways. Brodogradnja 2020, 71, 15–30. [Google Scholar] [CrossRef]
- Meisel, F.; Fagerholt, K. Scheduling Two-Way Ship Traffic for the Kiel Canal: Model, Extensions and a Matheuristic. Comput. Oper. Res. 2019, 106, 119–132. [Google Scholar] [CrossRef]
- Gong, H. Research on Integrated Dispatching Optimization of Compound Channel and Tugboat. Master’s Thesis, Dalian Maritime University, Dalian, China, 2022. [Google Scholar]
- Zhang, B.; Zheng, Z. Model and Algorithm for Vessel Scheduling Optimisation through the Compound Channel with the Consideration of Tide Height. Int. J. Shipp. Transp. Logist. 2021, 13, 445–461. [Google Scholar] [CrossRef]
- Wang, W.; Ding, A.; Cao, Z.; Peng, Y.; Liu, H.; Xu, X. Deep Reinforcement Learning for Channel Traffic Scheduling in Dry Bulk Export Terminals. IEEE Trans. Intell. Transp. Syst. 2024, 25, 17547–17561. [Google Scholar] [CrossRef]
- Chen, X.; Wu, H.; Han, B.; Liu, W.; Montewka, J.; Liu, R.W. Orientation-Aware Ship Detection via a Rotation Feature Decoupling Supported Deep Learning Approach. Engineering Applications of Artificial Intelligence 2023, 125, 106686. [Google Scholar] [CrossRef]
- Lin, C.; Zhen, R.; Tong, Y.; Yang, S.; Chen, S. Regional ship collision risk prediction: An approach based on encoder-decoder LSTM neural network model. Ocean Eng. 2024, 296, 117019. [Google Scholar] [CrossRef]
- Jonathan, H. Connell and Sridhar Mahadevan. In Robotica; Cambridge University Press: Cambridge, UK, 1999; Volume 17, pp. 229–235. [Google Scholar] [CrossRef]
- Lopes Silva, M.A.; de Souza, S.R.; Freitas Souza, M.J.; Bazzan, A.L.C. A Reinforcement Learning-Based Multi-Agent Framework Applied for Solving Routing and Scheduling Problems. Expert Syst. Appl. 2019, 131, 148–171. [Google Scholar] [CrossRef]
- Hottung, A.; Kwon, Y.-D.; Tierney, K. Efficient Active Search for Combinatorial Optimization Problems. Available online: https://arxiv.org/abs/2106.05126v3 (accessed on 16 September 2024).
- Ottoni, A.L.C.; Nepomuceno, E.G.; de Oliveira, M.S.; de Oliveira, D.C.R. Reinforcement Learning for the Traveling Salesman Problem with Refueling. Complex Intell. Syst. 2022, 8, 2001–2015. [Google Scholar] [CrossRef]
- Gambardella, L.M.; Dorigo, M. Ant-Q: A Reinforcement Learning Approach to the Traveling Salesman Problem. In Machine Learning Proceedings 1995; Prieditis, A., Russell, S., Eds.; Morgan Kaufmann: San Francisco, CA, USA, 1995; pp. 252–260. ISBN 978-1-55860-377-6. [Google Scholar]
- Duan, H.; Liu, P.; Li, Z.; Tang, D. Variable Speed Limit Control at Freeway Merge Bottlenecks Based on Reinforcement Learning. J. Transp. Syst. Eng. Inf. Technol. 2015, 15, 55–61. [Google Scholar]
- Fotuhi, F.; Huynh, N.; Vidal, J.M.; Xie, Y. Modeling Yard Crane Operators as Reinforcement Learning Agents. Res. Transp. Econ. 2013, 42, 3–12. [Google Scholar] [CrossRef]
- Huang, H.; Fang, Z.; Wang, Y.; Tang, J.; Fu, X. Analysing Taxi Customer-Search Behaviour Using Copula-Based Joint Model. Transp. Saf. Environ. 2022, 4, tdab033. [Google Scholar] [CrossRef]
- Meng, X.; Tang, J.; Yang, F.; Wang, Z. Lane-Changing Trajectory Prediction Based on Multi-Task Learning. Transp. Saf. Environ. 2023, 5, tdac073. [Google Scholar] [CrossRef]
- Xiang, Z.; Zhou, D.; Sun, H.; Chu, T. Research on Departure Sequencing in Multi- airport Terminal Area Based on Reinforcement Learning. Aeronaut. Comput. Tech. 2023, 53, 30–34. [Google Scholar]
- Zhu, C.; Zhang, Z. Application of Q-Learning Agent in Aircraft Sequencing at En-Route Intersection. Aeronaut. Comput. Tech. 2015, 45, 68–70. [Google Scholar]
- Wang, Y. Ship Traffic Organization in Intersection Waters Based on Reinforcement Learning. Master’s Thesis, Dalian University of Technology, Dalian, China, 2022. [Google Scholar]
- Du, J.; Zhao, X.; Guo, L.; Wang, J. Machine Learning-Based Approach to Liner Shipping Schedule Design. J. Shanghai Jiaotong Univ. (Sci.) 2022, 27, 411–423. [Google Scholar] [CrossRef]
- Xin, X.; Liu, K.; Zhang, J.; Chen, S.; Wang, H.; Cheng, Z. A Self-Organizing Grouping Approach for Ship Traffic Scheduling in Restricted One-Way Waterway. Mar. Technol. Soc. J. 2019, 53, 83–96. [Google Scholar] [CrossRef]
- Jiang, J. Analysis of Domestic Intelligent Ship Traffic Management System. Mar. Equip./Mater. Mark. 2023, 31, 26–28. [Google Scholar] [CrossRef]
- Liu, C.; Liu, J.; Zhou, X.; Zhao, Z.; Wan, C.; Liu, Z. AIS Data-Driven Approach to Estimate Navigable Capacity of Busy Waterways Focusing on Ships Entering and Leaving Port. Ocean Eng. 2020, 218, 108215. [Google Scholar] [CrossRef]
- Liu, X.; Tang, J.; Yuan, C.; Gao, F.; Ding, X. Examining the Characteristics between Time and Distance Gaps of Secondary Crashes. Transp. Saf. Environ. 2024, 6, tdad014. [Google Scholar] [CrossRef]
- Zheng, H.; Xu, H.; Liu, B.; Cao, H. One-Way Channel Ship Inbound Order and Berth Allocation Collaborative Optimization. Oper. Res. Manag. Sci. 2017, 26, 37–45. [Google Scholar]
- Naderi, E.; Pourakbari-Kasmaei, M.; Cerna, F.V.; Lehtonen, M. A Novel Hybrid Self-Adaptive Heuristic Algorithm to Handle Single- and Multi-Objective Optimal Power Flow Problems. Int. J. Electr. Power Energy Syst. 2021, 125, 106492. [Google Scholar] [CrossRef]
- Naeem, M.; Rizvi, S.T.H.; Coronato, A. A Gentle Introduction to Reinforcement Learning and Its Application in Different Fields. IEEE Access 2020, 8, 209320–209344. [Google Scholar] [CrossRef]
- Clifton, J.; Laber, E. Q-Learning: Theory and Applications. Annu. Rev. Stat. Its Appl. 2020, 7, 279–301. [Google Scholar] [CrossRef]
- Wang, T.; Zhang, Y.; Hu, X. A Q-Learning Based Hyper-Heuristic Scheduling Algorithm with Multi-Rule Selection for Sub-Assembly in Shipbuilding. Comput. Ind. Eng. 2024, 197, 110567. [Google Scholar] [CrossRef]
- Bianchi, R.A.; Ribeiro, C.H.; Costa, A.H. On the Relation between Ant Colony Optimization and Heuristically Accelerated Reinforcement Learning. In Proceedings of the 1st International Workshop on Hybrid Control of Autonomous System, Pasadena, CA, USA, 13 July 2009; AAAI: Palo Alto, CA, USA, 2009; pp. 49–55. [Google Scholar]
- Ottoni, A.L.C.; Nepomuceno, E.G.; de Oliveira, M.S. A Response Surface Model Approach to Parameter Estimation of Reinforcement Learning for the Travelling Salesman Problem. J. Control Autom. Electr. Syst. 2018, 29, 350–359. [Google Scholar] [CrossRef]
- Júnior, F.C.D.L.; Neto, A.D.D.; De Melo, J.D. Hybrid Metaheuristics Using Reinforcement Learning Applied to Salesman Traveling Problem. In Traveling Salesman Problem, Theory and Applications; IntechOpen: Rijeka, Croatia, 2010; ISBN 953-307-426-4. [Google Scholar]
- Zhang, X.; Chen, X.; Ji, M.; Yao, S. Vessel Scheduling Model of a One-Way Port Channel. J. Waterw. Port Coast. Ocean Eng. 2017, 143, 04017009. [Google Scholar] [CrossRef]



| Ship Number | Direction | Length (m) | Berth Number | Speed (kn) | Sailing Distance (n mile) | Setup Time (hh:mm) |
|---|---|---|---|---|---|---|
| 1 | In | 148 | 3 | 8.0 | 1.5 | 7:08 |
| 2 | In | 142.7 | 6 | 14.0 | 1.8 | 7:01 |
| 3 | In | 84.4 | 1 | 8.8 | 1.3 | 7:07 |
| 4 | Out | 144.8 | 5 | 9.0 | 1.7 | 7:18 |
| 5 | Out | 278.7 | 14 | 8.3 | 2.6 | 7:04 |
| 6 | In | 241.3 | 12 | 7.1 | 2.4 | 7:40 |
| 7 | In | 115.8 | 9 | 11.2 | 2.1 | 7:56 |
| 8 | Out | 97.2 | 13 | 9.5 | 2.5 | 7:49 |
| 9 | Out | 150.4 | 6 | 15.5 | 1.8 | 7:36 |
| 10 | In | 88.8 | 13 | 7.7 | 2.5 | 7:23 |
| 11 | In | 130 | 17 | 10.7 | 2.9 | 7:24 |
| 12 | Out | 108.4 | 10 | 11.7 | 2.2 | 8:29 |
| 13 | In | 142.7 | 5 | 11.5 | 1.7 | 7:12 |
| 14 | In | 72 | 2 | 9.6 | 1.4 | 7:47 |
| 15 | In | 166.2 | 7 | 12.3 | 1.9 | 7:38 |
| 16 | In | 147.5 | 11 | 10.9 | 2.3 | 7:09 |
| 17 | In | 334.1 | 14 | 12.9 | 2.6 | 7:03 |
| 18 | In | 85.5 | 10 | 8.6 | 2.2 | 7:01 |
| 19 | Out | 145.1 | 3 | 16.5 | 1.5 | 7:11 |
| 20 | In | 95.2 | 4 | 7.8 | 1.6 | 7:00 |
| Ship Number | Direction | Setup Time (hh/mm) | Start Time (hh/mm) | Delay Time (min) |
|---|---|---|---|---|
| 5 | Out | 7:04 | 7:04 | 0 |
| 3 | In | 7:07 | 7:28 | 21 |
| 16 | In | 7:09 | 7:32 | 21 |
| 19 | Out | 7:11 | 7:44 | 28 |
| 4 | Out | 7:18 | 7:46 | 0 |
| 9 | Out | 7:36 | 7:49 | 25 |
| 7 | In | 7:56 | 7:59 | 3 |
| 14 | In | 7:47 | 8:00 | 42 |
| 6 | In | 7:40 | 8:05 | 13 |
| 11 | In | 7:24 | 8:09 | 87 |
| 20 | In | 7:00 | 8:10 | 45 |
| 17 | In | 7:03 | 8:19 | 33 |
| 8 | Out | 7:49 | 8:31 | 101 |
| 2 | In | 7:01 | 8:49 | 13 |
| 10 | In | 7:23 | 8:50 | 105 |
| 13 | In | 7:12 | 8:53 | 23 |
| 12 | Out | 8:29 | 9:02 | 76 |
| 18 | In | 7:01 | 9:16 | 135 |
| 1 | In | 7:08 | 9:19 | 33 |
| 15 | In | 7:38 | 9:23 | 105 |
| FCFS | RL | GA | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Ship Number | Direction | Setup Time (hh:mm) | Start Time (hh:mm) | Ship Number | Direction | Setup Time (hh:mm) | Start Time (hh:mm) | Ship Number | Direction | Setup Time (hh:mm) | Start Time (hh:mm) |
| 20 | In | 7:00 | 7:00 | 5 | Out | 7:04 | 7:04 | 19 | Out | 7:11 | 7:11 |
| 18 | In | 7:01 | 7:12 | 3 | In | 7:07 | 7:28 | 16 | In | 7:09 | 7:19 |
| 5 | Out | 7:04 | 7:27 | 16 | In | 7:09 | 7:32 | 20 | In | 7:00 | 7:21 |
| 17 | In | 7:03 | 7:46 | 19 | Out | 7:11 | 7:44 | 1 | In | 7:08 | 7:24 |
| 3 | In | 7:07 | 7:58 | 4 | Out | 7:18 | 7:46 | 9 | Out | 7:36 | 7:36 |
| 16 | In | 7:09 | 8:07 | 9 | Out | 7:36 | 7:49 | 4 | Out | 7:18 | 7:37 |
| 19 | Out | 7:11 | 8:20 | 7 | In | 7:56 | 7:59 | 2 | In | 7:01 | 7:51 |
| 1 | In | 7:08 | 8:25 | 14 | In | 7:47 | 8:00 | 3 | In | 7:07 | 7:52 |
| 4 | Out | 7:18 | 8:36 | 6 | In | 7:40 | 8:05 | 14 | In | 7:47 | 7:53 |
| 13 | In | 7:12 | 8:48 | 11 | In | 7:24 | 8:09 | 12 | Out | 7:23 | 8:29 |
| 11 | In | 7:24 | 8:56 | 20 | In | 7:00 | 8:10 | 15 | In | 7:38 | 8:42 |
| 9 | Out | 7:36 | 9:13 | 17 | In | 7:03 | 8:19 | 7 | In | 7:56 | 8:44 |
| 2 | In | 7:01 | 9:20 | 8 | Out | 7:49 | 8:31 | 6 | In | 7:40 | 8:48 |
| 15 | In | 7:38 | 9:27 | 2 | In | 7:01 | 8:49 | 8 | Out | 7:49 | 9:09 |
| 6 | In | 7:40 | 9:37 | 10 | In | 7:23 | 8:50 | 5 | Out | 7:04 | 9:14 |
| 14 | In | 7:47 | 9:57 | 13 | In | 7:12 | 8:53 | 17 | In | 7:03 | 9:38 |
| 8 | Out | 7:49 | 10:06 | 12 | Out | 8:29 | 9:02 | 13 | In | 7:01 | 9:40 |
| 10 | In | 7:23 | 10:22 | 18 | In | 7:01 | 9:16 | 11 | In | 7:24 | 9:43 |
| 7 | In | 7:56 | 10:41 | 1 | In | 7:08 | 9:19 | 18 | In | 7:01 | 9:44 |
| 12 | Out | 8:29 | 10:52 | 15 | In | 7:38 | 9:23 | 10 | In | 7:23 | 9:46 |
| Total delay (h) | 30.37 | 18.20 | 21.90 | ||||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhen, R.; Sun, M.; Fang, Q. Optimization of Inbound and Outbound Vessel Scheduling in One-Way Channel Based on Reinforcement Learning. J. Mar. Sci. Eng. 2025, 13, 237. https://doi.org/10.3390/jmse13020237
Zhen R, Sun M, Fang Q. Optimization of Inbound and Outbound Vessel Scheduling in One-Way Channel Based on Reinforcement Learning. Journal of Marine Science and Engineering. 2025; 13(2):237. https://doi.org/10.3390/jmse13020237
Chicago/Turabian StyleZhen, Rong, Meng Sun, and Qionglin Fang. 2025. "Optimization of Inbound and Outbound Vessel Scheduling in One-Way Channel Based on Reinforcement Learning" Journal of Marine Science and Engineering 13, no. 2: 237. https://doi.org/10.3390/jmse13020237
APA StyleZhen, R., Sun, M., & Fang, Q. (2025). Optimization of Inbound and Outbound Vessel Scheduling in One-Way Channel Based on Reinforcement Learning. Journal of Marine Science and Engineering, 13(2), 237. https://doi.org/10.3390/jmse13020237






