Low-Complexity 2D DOA Estimation via L-Shaped Array for Underwater Hexapod Robot

Abstract

This paper takes underwater hexapod robot target grasping in an extremely shallow water environment as the research goal and carries out the research on a high-precision and low-complexity method of target positioning. We address the above problem of estimating the two-dimensional (2D) directions of arrival (DOAs) of targets, using an L-shaped ultrasonic array. Based on the above considerations, low-complexity 2D multiple signal classification (MUSIC) based on sparse signal recovery (SSR) is proposed to enhance the super-resolution capability and DOA estimation accuracy. In the first step, subspace dimension is determined based on space distance. Then, a mixed-norm method is exploited to construct the projection subspace and new noise subspace. Finally, the orthogonality between the noise and signal subspaces is used to estimate DOAs. Via a numerical simulations analysis, we illustrate that the proposed technique can enhance the accuracy of DOA estimation while also being robust against coherent sources and limited snapshots.

1. Introduction

Currently, traditional underwater robots can achieve deep-sea and shallow water exploration and operations. The extremely shallow water area (water depth 0–5 m) is a key exclusion zone for entering land from the ocean, with complex flow fields, variable sediment, and amphibious switching, greatly increasing the difficulty of robot operations [1,2]. Traditional floating or tracked robots are unable to carry out underwater operations in this area. Underwater hexapod robots (UHRs), due to their unique structural advantages, can operate stably in various underwater terrains and have good adaptability to complex underwater environments, making them an ideal platform for exploration and operations in extremely shallow water areas. Based on the application background of target disposal operation in an extremely shallow water environment, this paper focuses on the research of high-precision target positioning, i.e., the direction of arrival (DOA) estimation for environment awareness and operations.

Ultrasound array is employed to estimate the DOAs of the detection targets, suppress the effect of a sidelobe-interfering signal via reducing the energy leaks, enhance signal amplitude, and improve the detection probability of weak signals [3,4]. To achieve DOA estimation, different antenna array shapes are proposed, including circular array [5], L-shaped arrays [6], linear arrays [7], and rectangular arrays [8]. In this context, an L-shaped array, which consists of two orthogonal uniform linear arrays, offers the advantage of a more straightforward geometric structure and reduced coverage area when compared to rectangular and circular arrays [9]. Research has shown that the L-shaped array outperforms the rectangular array, as it offers a 37% reduction in the Carmer–Rao bound (CRB) for DOA estimation [10]. Consequently, it is commonly applied in 2D DOA estimation, which involves jointly estimating the elevation and azimuth angles of targets. In pursuit of this goal, several 2D DOA estimation algorithms have been formulated using the L-shaped array [11,12,13].

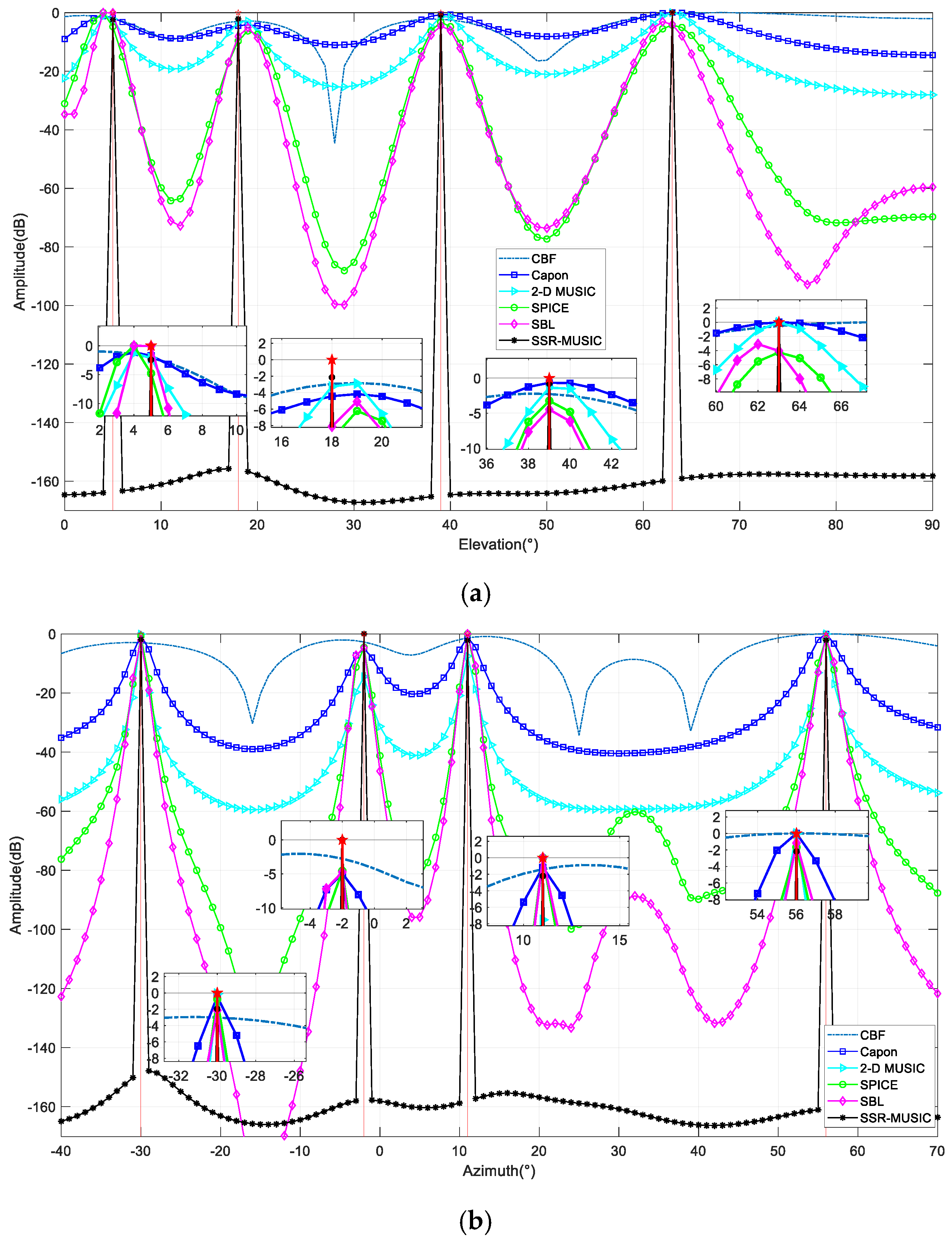
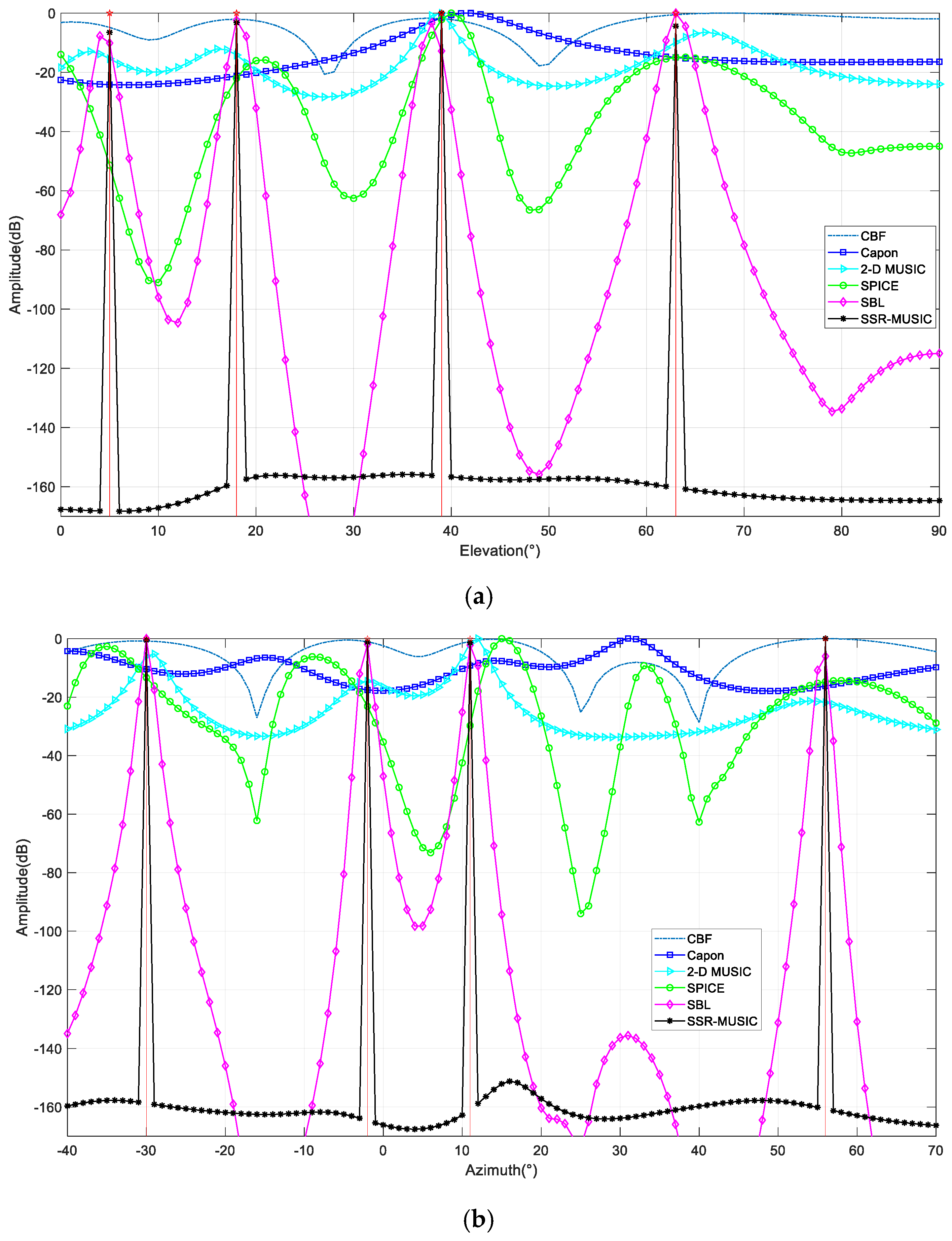
Traditionally, according to an L-shaped array, the conventional beamforming (CBF) technology is the most well-known 2D DOA estimation method to obtain a 2D image of azimuth and elevation angles. It is well established that CBF is robust versus the nonideal array and underwater scenes like the steering vector errors and echo distortion. Nonetheless, the CBF has to face the great challenges of low resolution and a high sidelobe. Intuitively, a larger array aperture will lead to a higher resolution ability of 2D DOAs. However, due to the realistic constraints in UHRs, such as platform size and power consumption, the available array aperture is very limited. Therefore, novel array processing methods with super-directivity capabilities will be discussed in the following. Super-directivity implies that through a novel processing method, a small array using a super-resolution algorithm can match the DOA performance of a large array using CBF.

The conventional super-resolution methods for DOA estimation are typically classified into three groups, i.e., Capon-based minimum variance method (MMV) [14], subspace-based multiple signal classification (MUSIC) [15] and estimation signal parameter via rotational invariance technique (ESPRIT) [16], and the maximum likelihood method. Among them, the MUSIC algorithm is the most widely used, which decomposes the covariance matrix of array echo signals to obtain two orthogonal subspaces of signal and noise, constructing spectral peaks. In the case that the SNR is satisfied, as snapshots increase, the estimation accuracy comes closer to the Cramer–Rao bound. However, when there are correlated sources in space or fewer snapshots, the signal cannot be distinguished. Although the problem of correlated sources can be solved by spatial smoothing, it will result in the loss of array aperture and reduce the resolution performance.

In recent years, some new methods have also emerged for the uniqueness of the DOA estimation problem. The DOA estimation can be equivalent to dividing the space of interest into grids. The incoming signals only occupy a few cells in the partition space, and the number of sources is small compared with the whole discrete space; thus, a spatial sparse signal is formed. Utilizing the sparse signal recovery (SSR) theory and spatial domain sparsity, compressed sensing (CS) can capitalize on the sparse nature of signal distributions [17,18,19,20]. Consequently, CS can use a small number of array elements to reach a resolution similar to that of a larger-aperture array. For the 2D DOA estimation mentioned above, the CS method can not only enhance the resolution but also suppress background noise levels significantly. There are four main categories for SSR-based DOA estimation methods, one of which is the matching pursuit methods [17], the atomic norm-based methods [18], the covariance-based methods [19], and the sparse Bayesian learning (SBL) methods [20]. However, the computation complexity in atomic norm-based methods, covariance-based methods, and SBL methods is too high to be suitable for UHRs.

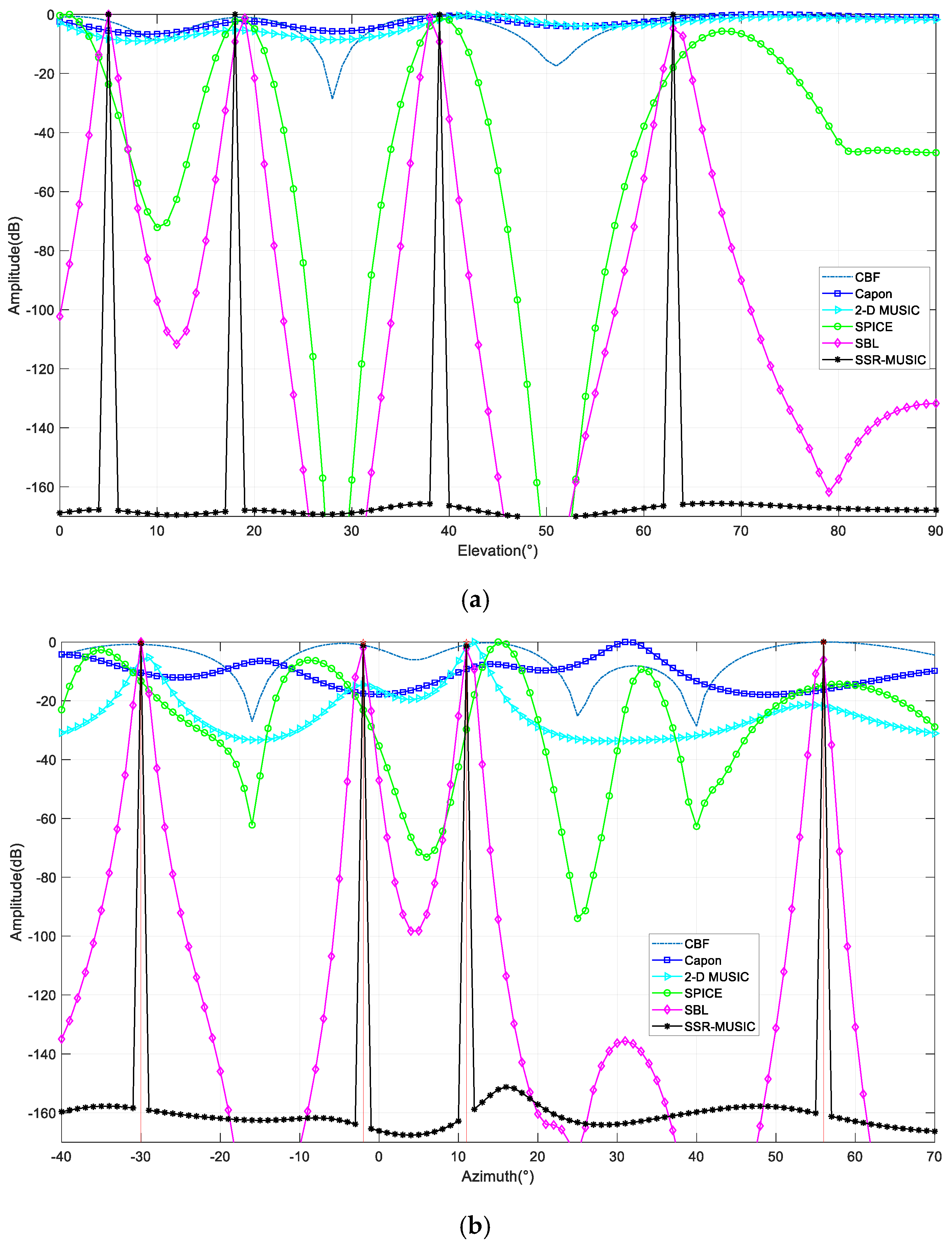
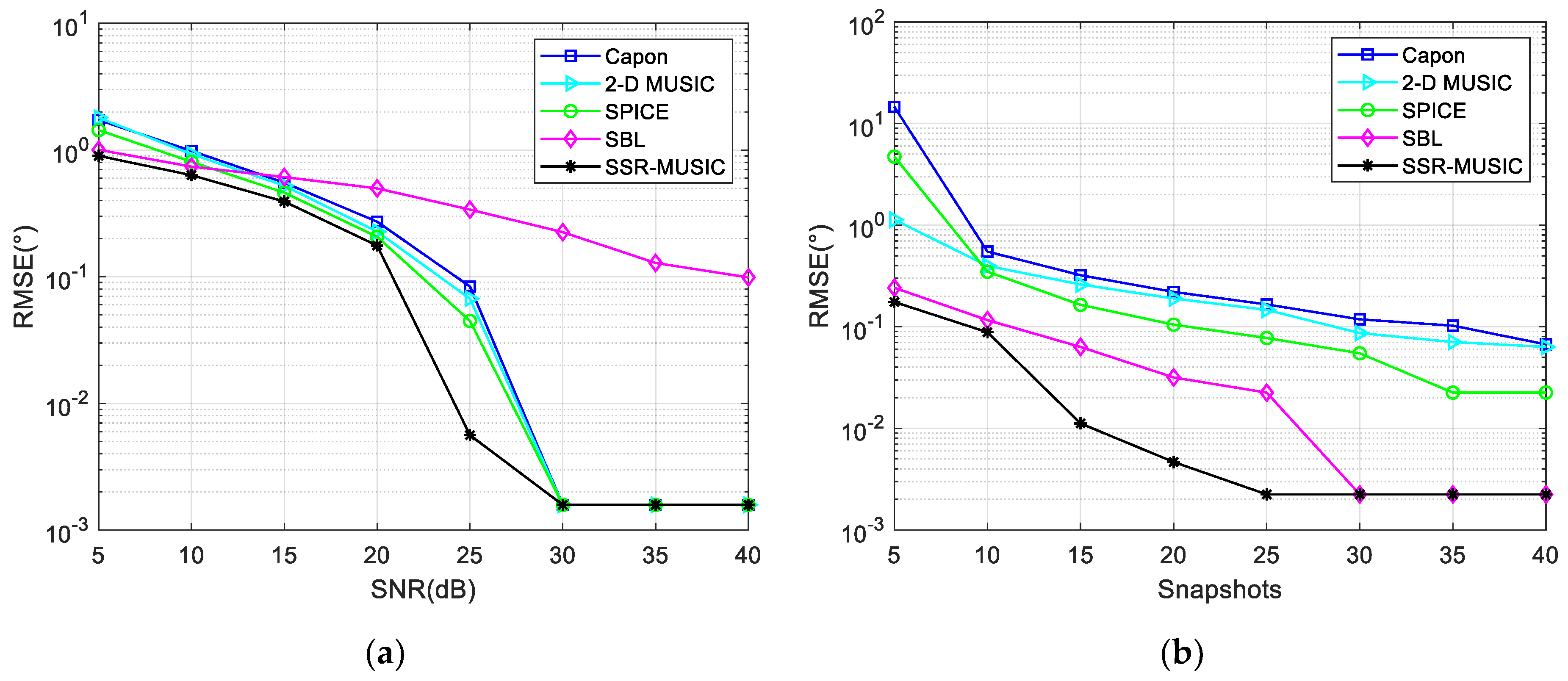
The prominent advantage of CS is its high resolution with a small number of snapshots, and its special reconstruction way makes the method itself coherence resistant. However, when more snapshots are taken, the CS method cannot offer clear spectral peak estimates. Based on the above analysis, CS theory and MUSIC have their own advantages and disadvantages under specific conditions, and this separation between the two is the fundamental reason for the difficulties encountered in specific applications.

Considering the points discussed above, we propose a novel signal processing method, i.e., low-complexity 2D MUSIC of an L-shaped array based on SSR, to enhance the super-resolution capability. Lee [21] believed that CS reconstructed the signal in a probabilistic way, while MUSIC constructed spatial spectrum in a deterministic way, and the study gave the relationship between the CS and MUSIC methods when the number of snapshots changed from less to more. In this paper, based on CS and MUSIC theory, we propose an SSR-MUSIC theory for 2D DOA estimation applications. The algorithm makes full use of the advantages of the two methods. Compared with the traditional methods, it has high resolution, can deal with coherent sources, and gives good results for different numbers of snapshots.

2. Array Signal Model

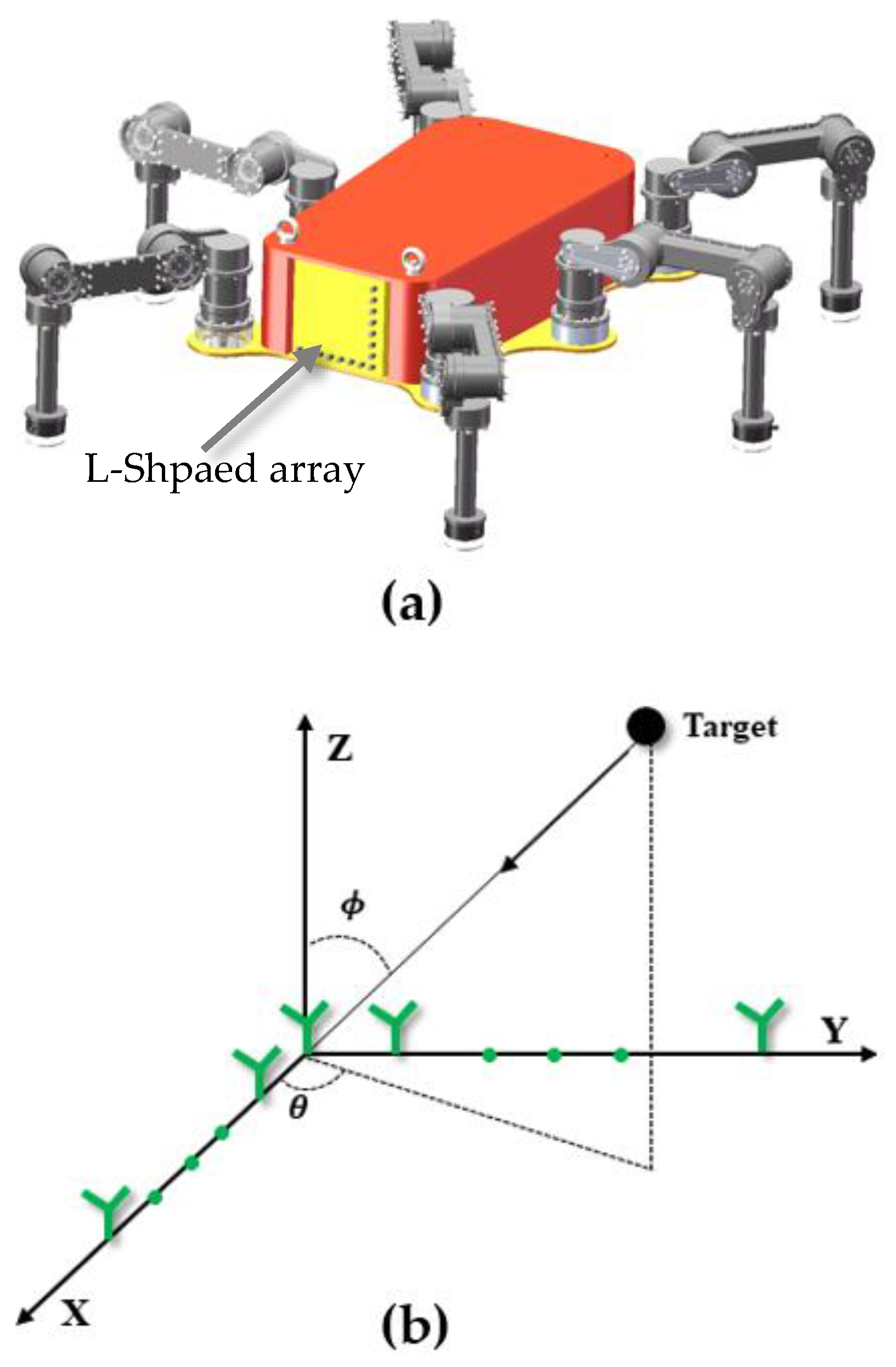
As depicted in Figure 1, an L-shaped array with $P+Q-1$ omnidirectional antennas was considered, which was mounted on the front of an underwater hexapod robot. Two identical linear subarrays were positioned along the x-axis and y-axis with equal spacing, where $P$ and $Q$ denoted the number of array elements along with the x-axis and y-axis, respectively. The sensor positioned at the origin was considered the reference point. The distance between sensors in each subarray was $d=\lambda /2$, where $\lambda$ is defined as the wavelength. It was assumed that $K$ narrowband signals from the far field hit this L-shaped array. The azimuth and elevation angles of the $k$th signal can be expressed as ${\phi }_k\in \left(-{90}^{°},{90}^{°}\right)$ and ${\theta }_k\in \left(0^{°},{90}^{°}\right)$, respectively. The azimuth angle is measured from the x-axis, while the elevation angle is measured from the y-axis. Thus, the array output at time $l$ along the x-axis and y-axis can be expressed as

$${\mathit{y}}_x\left(l\right)={\mathbf{A}}_x{\mathbf{s}}_x\left(l\right)+{\mathbf{n}}_x\left(l\right)$$

(1)

$${\mathit{y}}_y\left(l\right)={\mathbf{A}}_y{\mathbf{s}}_y\left(l\right)+{\mathbf{n}}_y\left(l\right)$$

(2)

where $l=1,2,\cdots ,L$, $L$ is the number of snapshots, and $\mathbf{s}\left(t\right)={\left[s_1\left(l\right),s_2\left(l\right),\cdots ,s_K\left(l\right)\right]}^T$ denotes the signal waveform vector. The variables ${\mathbf{n}}_x$ and ${\mathbf{n}}_y$ are the additive white Gaussian noise along the x-axis and y-axis, respectively. The variables ${\mathbf{A}}_x$ and ${\mathbf{A}}_y$ denote the manifold matrices of the x-axis and y-axis subarrays, respectively, which are defined as

$${\mathbf{A}}_x=\left[{\mathit{a}}_x\left({\phi }_1,{\theta }_1\right),\cdots ,{\mathit{a}}_x\left({\phi }_K,{\theta }_K\right)\right],{\mathit{a}}_x\left({\phi }_k,{\theta }_k\right)={\left[1,\cdots ,\exp \left(j2\pi r_{P-1}/\lambda \sin {\theta }_k\cos {\phi }_k\right)\right]}^T$$

(3)

$${\mathbf{A}}_y=\left[{\mathit{a}}_y\left({\phi }_1,{\theta }_1\right),\cdots ,{\mathit{a}}_y\left({\phi }_K,{\theta }_K\right)\right],{\mathit{a}}_y\left({\phi }_k,{\theta }_k\right)={\left[1,\cdots ,\exp \left(j2\pi r_{Q-1}/\lambda \sin {\theta }_k\sin {\phi }_k\right)\right]}^T$$

(4)

where $r_p=p\times d, p=0,1\cdots P-1$ and $r_q=q\times d, q=0,1\cdots Q-1$. Then, we sample the azimuth angle and elevation angle with uniform interval $\eta$ to construct two finite grid sets ${\left\{{\overline{\phi }}_m\right\}}_{m=1}^{2M}$ and ${\left\{{\overline{\theta }}_m\right\}}_{m=1}^M$. Thus, the manifold matrices can be rewritten as

$${\mathcal{A}}_x=\left[{\mathit{a}}_x\left({\overline{\phi }}_1,{\overline{\theta }}_1\right),\cdots ,{\mathit{a}}_x\left({\overline{\phi }}_1,{\overline{\theta }}_{2M}\right),{\mathit{a}}_x\left({\overline{\phi }}_2,{\overline{\theta }}_1\right),\cdots ,{\mathit{a}}_x\left({\overline{\phi }}_{2M},{\overline{\theta }}_1\right),\cdots ,{\mathit{a}}_x\left({\overline{\phi }}_{2M},{\overline{\theta }}_{2M}\right)\right]$$

(5)

$${\mathcal{A}}_y=\left[{\mathit{a}}_y\left({\overline{\phi }}_1,{\overline{\theta }}_1\right),\cdots ,{\mathit{a}}_y\left({\overline{\phi }}_1,{\overline{\theta }}_M\right),{\mathit{a}}_y\left({\overline{\phi }}_2,{\overline{\theta }}_1\right),\cdots ,{\mathit{a}}_y\left({\overline{\phi }}_M,{\overline{\theta }}_1\right),\cdots ,{\mathit{a}}_y\left({\overline{\phi }}_M,{\overline{\theta }}_M\right)\right]$$

(6)

In general, the grid set contains far more elements than the numbers of array elements and signals, i.e., $2M\times M\gg P+Q-1>K$, and the set is overcomplete. According to model (5) and model (6), the sparse representation form of the L-shaped array can be given by

$$\mathbf{Y}=\mathcal{A}\mathbf{S}+\mathbf{N}$$

(7)

where $\mathcal{A}=\left[{\mathcal{A}}_x,{\mathcal{A}}_y\right]\in {ℂ}^{\left(P+Q-1\right)\times \left(2M\times M\right)}$, $\mathbf{S}=\left[\overline{s}\left(1\right),\overline{s}\left(2\right),\cdots ,\overline{s}\left(L\right)\right]\in {ℂ}^{\left(2M\times M\right)\times L}$ is the expanded signal amplitude matrix, and $\overline{s}\left(l\right)={\left[s_1\left(l\right),s_2\left(l\right),\cdots ,s_{2M\times M}\left(l\right)\right]}^T$ indicates sparse signal vector corresponding to the grid sets. The non-zero entries of $\overline{s}\left(l\right)$ indicate the true DOAs. $\mathbf{N}=\left[{\mathbf{n}}_1\left(1\right),{\mathbf{n}}_2\left(2\right),\cdots ,{\mathbf{n}}_{P+Q-1}\left(L\right)\right]\in {ℂ}^{\left(P+Q-1\right)\times L}$ is white noise matrix.

3. Two-Dimensional DOA Estimation Algorithm Based on SSR

From the perspective of matrix theory, it is impossible to solve under-determined Equation (7) because the number of snapshots $L$ is significantly less than the grid set length $2M\times M$. In this section, the SSR theory is introduced. The primary goal of the compressed sensing model focuses on reconstructing an unknown sparse signal amplitude matrix via a multiple measurement vector (MMV) method. With the assumption that $\mathbf{S}$ is $K$-sparse in common rows, minimizing $l_1$ norm optimization can be used to address the problem of under-determined equations. The expression can be written as

$$\left\{\begin{array}{c}\min {‖\tilde{\mathbf{S}}‖}_{2,1}\\ s.t. ‖\mathbf{Y}-\mathcal{A}\tilde{\mathbf{S}}‖\le \epsilon \end{array}\right.$$

(8)

where $\tilde{\mathbf{S}}$ denotes the estimated sparse solution, $\epsilon$ is a small parameter (i.e., noise disturbance), and ${‖·‖}_{2,1}$ indicates the $l_{2,1}$ mixed norm. Thus, the estimated DOAs of the spatial signals can be decided by the non-zero position of the sparse solution.

According to the signal reconstruction theory of CS, four category methods based on SSR theory can be utilized to solve model (8). Considering both computational complexity and estimation accuracy, the greedy-type algorithm was used in this paper. However, as the number of snapshots increases, the CS method cannot give sharp spectral peak estimates, and the reconstruction algorithm of CS is very sensitive to the rank of the matrix in the noisy case. In order to solve the above problems, considering the characteristics of subspace decomposition algorithm that uses the space orthogonality instead of solving the rank of covariance matrix, we can also use this way to transform. Therefore, from the perspective of subspace construction, we proposed a joint 2D DOA estimation algorithm based on MUSIC and SSR methods named SSR-MUSIC algorithm, which can realize the super-resolution algorithm under any number of snapshots and coherent source.

$R\left(·\right)$ is defined to denote the feature subspace, ${‖\tilde{\mathbf{S}}‖}_0=\left|\mathrm{supp} \tilde{\mathbf{S}}\right|=K$, ${‖·‖}_0$ denotes the number of non-zero element, region $\mathrm{supp} \tilde{\mathbf{S}}=\left\{1\le m\le 2M\times M,{\tilde{\mathbf{S}}}_{m·}\ne 0\right\}$ is supported, and ${\tilde{\mathbf{S}}}_{m·}$ is the $m$th row of $\tilde{\mathbf{S}}$. When the observed signal is limited by the number of snapshots or coherent signals, the dimension of the estimated signal subspace is $r<K$, which will lead to a part of the lost signal subspace where $R\left({\mathcal{A}}_{I_{\mathrm{K}-\mathrm{r}}}\right)$ is no longer orthogonal to the noise space $R\left(Q\right)$, $I_{K-r}\subset \mathrm{supp} \tilde{\mathbf{S}}$, and $\left|I_{K-r}\right|=K-r$. ${\mathcal{A}}_{I_{\mathrm{K}-\mathrm{r}}}\in {ℂ}^{\left(P+Q-1\right)\times \left(K-r\right)}$ denotes the matrix consisting of the columns of $\mathcal{A}$ whose indices of the corresponding columns belong to the set $I_{K-r}$.

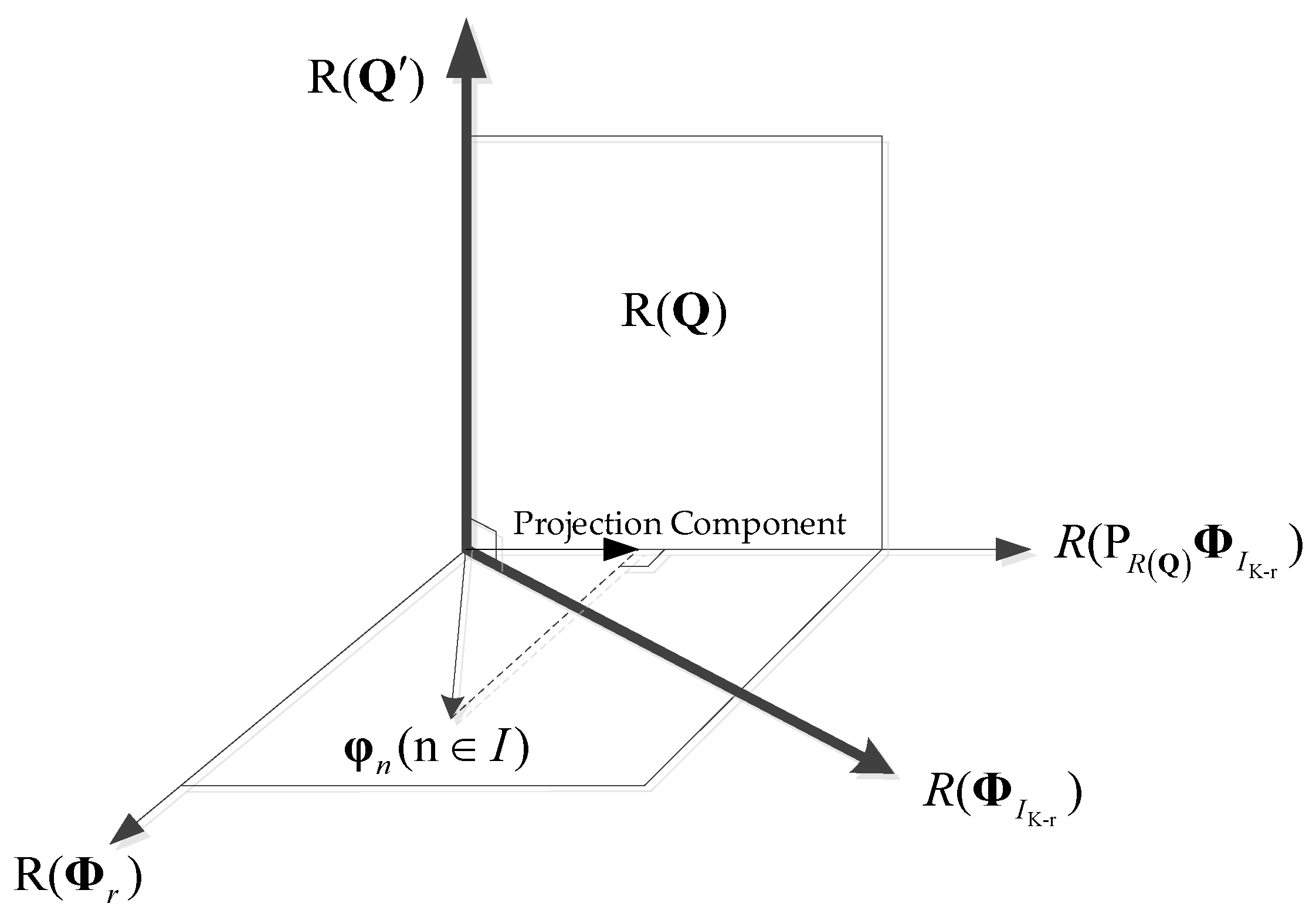
The basic principle and geometric representation of SSR-MUSIC are shown in Figure 2. The principle of SSR-MUSIC algorithm is to use the SSR algorithm to estimate $K-L$ column vector space subscripts, derive the projection of column vector space $R\left({\mathcal{A}}_{I_{\mathrm{K}-\mathrm{r}}}\right)$ in noise space $R\left(Q\right)=Q{Q}^{\mathrm{H}}$, and then construct a new noise subspace $R(Q^{\prime })$. It makes the newly constructed space satisfy the orthogonality relation, i.e., $R(Q^{\prime })\perp R\left({\mathcal{A}}_{I_{\mathrm{K}-\mathrm{r}}}\right)$. Thus, the non-orthogonal space caused by the lack of a snapshot number is converted to the two newly constructed orthogonal spaces $R\left({\mathcal{A}}_{I_{\mathrm{K}-\mathrm{r}}}\right)$ and $R(Q^{\prime })$. The constructed form is shown as a thick solid line in Figure 2 and then scanned through space to form sharp spectral peaks.

To estimate the subspace dimension $r$, a small threshold $\epsilon$ is set as the judgment, and the search problem can be established as follows:

$$\underset{r=1,\cdots ,P+Q}{\min r}\hspace{1em}\mathrm{s}.\mathrm{t}.\hspace{1em}{D}_r\left(\tilde{\mathbf{R}}\right)>\epsilon$$

(9)

where $D_r\left(·\right)$ denotes the subspace distance and $\tilde{\mathbf{R}}$ is the constructed eigen matrix by eliminating noise perturbations, that is,

$$D_r\left(\tilde{\mathbf{R}}\right)=\left|{\mathcal{l}}_r(\tilde{R})-{\mathcal{l}}_{r+1}(\tilde{R})\right|/\left|{\mathcal{l}}_{\max }(\tilde{R})\right|$$

(10)

$$\tilde{R}=R-{\mathcal{l}}_{\min }(R)I_{P+Q-1},\mathbf{R}=\mathbf{Y}{\mathbf{Y}}^H/L$$

(11)

where ${\mathcal{l}}_{\max }$, ${\mathcal{l}}_{\min }$, and ${\mathcal{l}}_r$ indicate the maximum, minimum, and $r$th eigenvalues of the matrix. The following implementation process of the algorithm is closely related to the $r$, and it can be divided into the following two cases for $r$:

(1) When $r<K$, the mixed-norm strategy is exploited to improve the subspace estimation accuracy. Now, the $K-r$ support region can be estimated by rewriting the model (8) as

$$f\left(\tilde{\mathbf{S}}\right)=\arg \min {‖\tilde{\mathbf{S}}‖}_{p,q}+\lambda \hspace{0.33em}{‖\mathbf{Y}-\mathcal{A}\tilde{\mathbf{S}}‖}_F^2$$

(12)

where ${‖\tilde{\mathbf{S}}‖}_{p,q}={\displaystyle \sum _{m=1}^{M\times M}{\left({‖x\left[m\right]‖}_q\right)}^p},\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}0\le p\le 1,\hspace{0.33em}\hspace{0.33em}q\ge 1$, $\tilde{s}\left[m\right]=\left[{\tilde{s}}^{\left(1\right)}\left[m\right],{\tilde{s}}^{\left(2\right)}\left[m\right],\cdots ,{\tilde{s}}^{\left(L\right)}\left[m\right]\right]$, and $m$ denotes the row index of sparse matrix $\tilde{\mathbf{S}}$. Then, the problem (12) can be solved using gradient descent. Taking the partial derivatives of $f\left(\tilde{\mathbf{S}}\right)$ with respect to $\tilde{\mathbf{S}}$ and $\lambda$, we can obtain the following:

$${\tilde{\mathbf{S}}}_{\mathrm{idx}+1}=W_{\mathrm{idx}+1}{\mathcal{A}}_{\mathrm{idx}+1}^H{\left({\mathcal{A}}_{\mathrm{idx}+1}{\mathcal{A}}_{\mathrm{idx}+1}^H+\lambda I\right)}^{-1}Y$$

(13)

where $\mathrm{idx}$ indicates number of iterations, ${\mathcal{A}}_{k+1}={\mathcal{A}}_k{W}_{k+1}$, $\lambda \ge 0$ is the regularization parameter, and

$$W_{\mathrm{idx}+1}=\mathrm{diag}\left(c_{\mathrm{idx}}{\left[n\right]}^{1-p/2}\right),c_{\mathrm{idx}}\left[m\right]={\left({\displaystyle \sum _{l=1}^L{\left(x_{\mathrm{idx}}^{\left(l\right)}\left[m\right]\right)}^2}\right)}^{1/2},p\in \left[0,1\right]$$

(14)

The iteration stops if ${‖{\tilde{\mathbf{S}}}_{\mathrm{idx}+1}-{\tilde{\mathbf{S}}}_{\mathrm{idx}}‖}_F/{‖{\tilde{\mathbf{S}}}_{\mathrm{idx}+1}‖}_F\le \gamma$. The set $I_{K-r}$ of subscripts corresponding to the largest $K-r$ components in ${‖\tilde{\mathbf{S}}‖}_{p,q}$ is chosen as the support region.

Then, the extended signal subspace is constructed and decomposed by singular value decomposition, that is

$$\dot{\mathbf{U}}S\dot{\mathbf{V}}=\mathrm{SVD}\left\{\left[Y,{\mathcal{A}}_{I_{\mathrm{K}-\mathrm{r}}}\right]\right\}$$

(15)

The new noise subspace $R(Q^{\prime })$ with the orthogonality relation can be written as follows:

$$R(Q^{\prime })={\mathbf{I}}_{P+Q-1}-\dot{\mathbf{U}}\left[:,1:K\right]{\dot{\mathbf{U}}}^H\left[:,1:K\right]$$

(16)

To determine the remaining support region, the orthogonality of the noise subspace and the signal subspace is utilized, i.e.,

$$I_r=\min {‖R(Q^{\prime }){\mathcal{A}}_{·m}‖}_2^2,\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}m=1,2,\cdots ,M\times M\hspace{0.33em}\hspace{0.33em}\mathrm{and}\hspace{0.33em}\hspace{0.33em}m\notin I_{K-r}$$

(17)

By now all the support region $I_K=I_{K-r}\cup I_r$ have been obtained, that is, the DOA information corresponding to all targets.

(2) When $r\ge K$, the signal subspace ${\mathcal{A}}_{I_{\mathrm{K}-\mathrm{r}}}$ in model (15) is empty, that is, $R(Q)\perp R\left({\mathcal{A}}_{I_{\mathrm{K}-\mathrm{r}}}\right)$. Thus, the models (15)–(17) can be redefined as

$$\dot{\mathbf{U}}S\dot{\mathbf{V}}=\mathrm{SVD}\left\{\left[Y,\varnothing \right]\right\}$$

(18)

$$R(Q)={\mathbf{I}}_{P+Q-1}-\dot{\mathbf{U}}\left[:,1:K\right]{\dot{\mathbf{U}}}^H\left[:,1:K\right]$$

(19)

$$I_r=\min {‖R(Q){\mathcal{A}}_{·m}‖}_2^2,\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}m=1,2,\cdots ,M\times M$$

(20)

Essentially, $r\ge K$ is a special case of $r<K$. At this time, the algorithm is consistent with the orthogonal space condition of the MUSIC method.

4. Results

Simulations are presented in this section to assess the performance of the proposed method in estimating the 2D DOA via comparing it with existing methods, such as the CBF, 2D MUSIC [15], SPICE [22], and SBL [20], respectively. In the following simulations, the number of the sensors along with the x-axis and y-axes is 8, i.e., $P=Q=8$. The elevation-azimuth DOAs of the four incoming signals are $\left\{5^{°},-{30}^{°}\right\}$, $\left\{{18}^{°},-2^{°}\right\}$, $\left\{{39}^{°},{11}^{°}\right\}$, and $\left\{{63}^{°},{56}^{°}\right\}$, respectively. A uniform sampling grid is applied over the elevation space $\left[0^{°},{90}^{°}\right]$ and azimuth space $\left[-{90}^{°},{90}^{°}\right]$ with grid intervals of $1^{°}$. In each simulation, the number of Monte Carlo trials is set to 500. The experiments are carried out in MATLAB R2020a on a PC with an Intel (R) Core (TM) i7-13700H CPU, 2.1 GHz.

4.1. Performance Comparison of Amplitude Spectrum with Enough Snapshots

In the first experiment, the SNR of four uncorrelated signals is set at 10 dB, and the snapshot number is $L=25$. Figure 3 compares the amplitude spectrum estimation results of all methods, and Figure 3a indicates that our method achieves higher DOA estimation accuracy than the others. In addition, in the estimation results of the proposed method, there are nearly no false peaks, indicating that it is more resilient to measurement noise. In Figure 3b, all methods can estimate the azimuth DOAs of four signals accurately. This is because the azimuth space and DOA spacing of the signals are larger compared to the elevation angle.

4.2. Performance Comparison of Amplitude Spectrum with Finite Snapshots

In the second experiment, the SNR of four uncorrelated signals is set at 10 dB, and the snapshot number is $L=K=4$. We examine the DOA estimation performance in the case of finite snapshot, where the simulation results are shown in Figure 4. It can be seen that the CBF, 2D MUSIC, and Capon miss part of the signals, the resolution performance of SBL is not good enough, and SPICE forms some false peaks. Therefore, as depicted in Figure 4, SSR-MUSIC demonstrates superior performance compared to other methods when dealing with a limited number of snapshots.

4.3. Performance Comparison of Amplitude Spectrum with Coherent Signals

In this part, we consider four coherent signals arriving at the L-shaped array. The SNR and number of snapshots are set at 10 dB and 25, respectively. Figure 5 demonstrates that the Capon and 2D MUSIC methods produce entirely ineffective DOA estimation results, the CBF and SPICE present a fairly large deviation, and the SBL present a slight deviation with the DOAs in the coherent case. Conversely, our proposed method can achieve a significantly more precise DOA estimation and is robust for both uncorrelated and coherent signals.

4.4. Performance Comparison of RMSE

For statistical comparison in this section, the root mean square error (RMSE) is employed as the criterion of judgment defined as

$$\mathrm{RMSE}={\mathrm{RMSE}}_{\theta }+{\mathrm{RMSE}}_{\varphi }$$

(21)

where ${\mathrm{RMSE}}_{\theta }$ and ${\mathrm{RMSE}}_{\varphi }$ indicate the RMSE of the azimuth angle $\theta$ and the elevation angle $\varphi$, respectively, defined as

$${\mathrm{RMSE}}_{\theta }=\sqrt{{\displaystyle \frac{1}{CK}}{\displaystyle \sum _{c=1}^C{\displaystyle \sum _{k=1}^K{\left({\tilde{\theta }}_{c,k}-{\theta }_{c,k}\right)}^2}}}$$

(22)

$${\mathrm{RMSE}}_{\varphi }=\sqrt{{\displaystyle \frac{1}{CK}}{\displaystyle \sum _{c=1}^C{\displaystyle \sum _{k=1}^K{\left({\tilde{\varphi }}_{c,k}-{\varphi }_{c,k}\right)}^2}}}$$

(23)

where $C$ denotes the number of Monte Carlo trials and $\left\{{\tilde{\theta }}_{c,k},{\tilde{\varphi }}_{c,k}\right\}$ and $\left\{{\theta }_{c,k},{\varphi }_{c,k}\right\}$ represent the estimated and true 2D DOAs of the $k$th signal in the $c$th trial, respectively. The methods are evaluated at different SNR values, and Figure 6a depicts the average RMSE versus SNR curves with a snapshot number of 25. Figure 6b shows the simulation results of RMSE versus snapshots with a fixed SNR of 20 dB. The other simulation conditions are the same as in Section 4.1. From Figure 6a, it is evident that the SSR-MUSIC outperforms the other four methods in DOA estimation performance across all SNRs. According to Figure 6b, our method not only achieves higher DOA estimation accuracy than the other four methods but also converges faster across all snapshot numbers.

4.5. Performance Comparison of CPU Time

In the final experiment, we compare the CPU time of these algorithms. Then, the SNR and the snapshot number change from 0 dB and 5 to 40 dB and 40, respectively. Other parameters remain unchanged. From Figure 7, it can be observed that the CPU time of the proposed algorithm is significantly shorter than the SPICE and SBL method and slightly longer than Capon and 2D MUSIC methods. However, the performance of Capon and 2D MUSIC methods is severely degraded for the situations of coherent signals and fewer snapshots. The CPU time fluctuation of the SBL method is mainly caused by the number of iteration variations.

According to the above results, we can see that our proposed algorithm can obtain better estimation accuracy and resolution than traditional super-resolution algorithms. On the other hand, our hexapod robot works in the extremely shallow water area, where it is a complex scenario, including complex flow fields and variable sediment. The above reason will result in an echo signal with strong space-varying and time-varying characteristics. This limits the number of homogeneous samples, i.e., few snapshots. It is well known that deep learning methods require a large number of training samples with similar characteristics, such as hundreds or even tens of thousands. Therefore, the performance of super-resolution algorithms based on deep learning will be significantly degraded by few effective training samples. Taking into account the above considerations, we believe that the proposed algorithm currently has more application potential in the hexapod robot.

5. Conclusions

In this paper, we present a novel 2D DOA estimation algorithm named SSR-MUSIC tailored for an L-shaped array, which can operate on coherent signals and fewer snapshots. By taking advantage of azimuth angle-elevation sparsity in two dimensions and of SSR theory, SSR-MUSIC can improve DOA estimation accuracy according to both theoretical analysis and simulations. Our proposed method not only has the advantages of CS in array signal processing but also has the stability characteristics of the MUSIC method, such as fewer sensors and the number of snapshots, robustness to noise, and the ability to deal with any coherent source problems. Our approach achieves high accuracy and low computational complexity. The simulation experiments demonstrate the superiority of our algorithm over comparison methods. Specifically, our approach significantly improving estimation accuracy and enhancing resolution, which will significantly improve the underwater autonomous operation ability of the hexapod robot. In the future, we will focus on the experimental validation of our proposed algorithm using the hexapod robot at a river and lake.