Research on Fault Diagnosis of Ship Propulsion System Based on Improved Residual Network

Abstract

In ship propulsion, accurately diagnosing faults in permanent magnet synchronous motor is essential but challenging due to limitations in the intuitive characterization and feature extraction of fault signals. This study presents an innovative approach to motor fault detection by integrating phase-contrastive current dot patterns with an enhanced residual network, enhancing the diagnostic effect. Initially, the research involves creating a dataset that simulates stator currents. It is achieved through mathematical modeling of two common faults in permanent magnet synchronous motors: inter-turn short circuits and demagnetization. Subsequently, the parameters of the phase-contrastive current dot pattern are optimized using the Hunter-Prey Optimization technique to convert the three-phase stator currents of the motor into grayscale images. Lastly, a residual network, which includes a Squeeze-and-Excitation module, is engineered to boost the identification of crucial fault characteristics. The experimental results show that the proposed method achieves a high accuracy rate of 98.5% in the fault diagnosis task of motors, which can accurately identify the fault information and is significant in enhancing the reliability and safety of ship propulsion systems.

1. Introduction

With the rapid development of the global shipping industry, electric propulsion systems have become the mainstream choice of ship propulsion system due to its environmental friendliness, cost-effectiveness and technical advantages. In this context, the safety and reliability of ship electric propulsion systems have become the core considerations for design and operation. In recent years, permanent magnet synchronous motor (PMSM) has gradually become the core component of ship electric propulsion system due to its high efficiency, high power density and low maintenance cost. However, PMSMs are susceptible to a range of malfunctions over pro-longed periods of operation, including inter-turn short circuits and demagnetization, which can degrade performance and lead to failures in the propulsion system, thereby affecting its operational reliability and navigational safety. Consequently, accurate and timely fault diagnosis of PMSM is crucial to avoid accidents, minimize downtime, and decrease maintenance expenditures, ultimately improving the safety and reliability of ship propulsion systems and promoting the development of intelligent shipping technologies.

Fault diagnosis of PMSM typically involves time-domain and frequency-domain feature analysis, which identifies potential faults by examining variations in the amplitude and frequency of three-phase current signals. Commonly utilized techniques include the short-time Fourier transform [1], wavelet transform [2], and variational mode decomposition [3] are commonly used. While these methods are theoretically advantageous, they encounter practical limitations, particularly under variable speed and load conditions, where signal noise greatly complicates fault detection.

In response to these challenges, researchers have delved into employing image processing methodologies for the smart fault diagnosis of PMSM. They have done this by converting the characteristic signals of the motor’s state into visual image data. This process includes techniques like rotation, scaling, blurring, and shifting, making it possible to visually clarify previously obscured signals [4]. Pietrzak et al. [5] suggested a method that leverages stator phase current bispectrum analysis in conjunction with a Convolutional Neural Network (CNN) to assess the health of PMSM stator windings. Similarly, Li et al. [6] developed a grayscale image algorithm that improves the feature representation of stator currents through an autocorrelation matrix, using a deep CNN for diagnosing eccentricity and demagnetization faults. Additionally, Ping et al. [7] introduced a customized phase space reconstruction method that improves diagnostic accuracy by transforming leakage magnetic signals into customized phase space reconstruction images for deep feature extraction and encoding. These methods significantly improve feature extraction capabilities over traditional techniques, though the complexity of converting signals to images may limit practical application.

To further enhance diagnostic techniques, researchers have introduced the symmetric dot pattern technique, which projects one-dimensional time-series signals onto a polar coordinate plane [8,9,10]. This method enables intuitive comparisons of signal amplitude and frequency within specific regions, offering an effective and efficient visualization technique with low time complexity. Currently, its primary application is in analyzing vibration signals, with its use on current signals being comparatively limited. This is largely attributed to the three-dimensional nature of time-series information and strong periodicity in current signals, which introduces significant redundancy. To overcome this limitation, Xia et al. [11] introduced the phase-contrastive current dot pattern (PCCDP), a specialized visualization technique that enhances the representation and processing efficiency of three-phase current signals.

Moreover, comprehensive diagnostic analyses require optimal feature extraction from signal images, for which deep learning, especially CNN, has shown significant potential. CNN are favored due to their sparse connections, weight sharing, and local feature recognition capabilities, making them highly effective for feature extraction. Skowron et al. [12] have indeed utilized CNN to extract features from the raw stator current data of PMSM for fault diagnosis. Similarly, Wang et al. [13] applied a one-dimensional CNN to diagnose faults in PMSM by analyzing torque and current signals. However, in complex real-world scenarios, these CNN-based diagnostic models often fail to meet expected results due to challenges in network structure and performance. Addressing these limitations, He et al. [14] introduced the Residual Network (ResNet), which utilizes residual connections to ease parameter optimization and enhance network depth, thereby improving feature extraction capabilities. Additionally, Ma et al. [3] combined the robust fault feature extraction capabilities of ResNet with bidirectional long short-term memory networks to accurately classify faults in propulsion motor drive inverters. Mahmoud et al. [15] utilized ResNet-18 to enhance the network’s learning capabilities during training, effectively diagnosing various faults in PMSM. Despite these developments, the traditional residual unit modules have exhibited certain limitations. Progressing further, He et al. [16] observed that the original residual unit’s structure impeded the model’s learning capacity during training, leading to the development of the pre-activated residual unit, which consistently outperforms the original.

Inspired by the existing literature, this paper introduces an innovative method for fault diagnosis in PMSM by leveraging an improved residual network (IResNet) coupled with PCCDP images. Initially, the Hunter-Prey Optimization (HPO) algorithm optimizes the PCCDP parameters to accentuate fault distinctions. Following this optimization, the current signals are converted into detailed PCCDP images, enhancing the visualization of various PMSM states. The methodology further integrates a pre-activated Residual module equipped with an attention mechanism that prioritizes significant channels based on data features. This adaptation enables the model to concentrate on critical feature channels, which significantly enhances performance across various conditions and ensures accurate fault diagnosis in PMSM.

A primary strength of this study lies in the proposed method, which not only visually displays changes in PMSM current fault signals but also automatically extracts fault characteristics, which significantly enhances the effectiveness of fault diagnosis. The key contributions encapsulated in this paper are outlined below:

(1)

Utilizing PCCDP technology, this method transforms current signals into images that depict the state of the signals. Furthermore, it employs a combined measure of Euclidean distance and cosine similarity to optimize PCCDP parameters.

(2)

By integrating PCCDP with an IResNet, the method automates the extraction of deep features from the current signal states, streamlining the diagnostic process.

(3)

Integrating the squeeze-and-excitation (SE) module into the ResNet architecture enhances the model’s capacity to learn the relationships between channels, which in turn improves its feature recognition capabilities. This integration significantly amplifies both the accuracy and robustness of the fault diagnosis process.

The structure of this paper is outlined as follows: Section 2 delves into the mathematical description of the PMSM drive system. Section 3 provides a detailed description of the proposed fault diagnosis framework for PMSM. Section 4 provides a comprehensive description of the experimental process undertaken and offers a thorough analysis of the obtained results. Finally, Section 5 concludes the work and outlines future research directions.

2. Description of the PMSM-Drives System

The most common faults in the PMSM of ship propulsion systems are inter-turn short circuits in the stator windings and demagnetization faults [17]. This paper constructs three mathematical models of the PMSM: normal condition, inter-turn short circuit fault, and demagnetization fault.

2.1. Mathematical Model of PMSM Drives

The PMSM, which consists of a combination of stator windings and permanent magnets, is a complex nonlinear system with strong coupling characteristics. To simplify the analysis, assuming that the three-phase PMSM is an ideal motor, with magnetic saturation neglected, eddy currents and hysteresis losses disregarded and the air gap magnetic field sinusoidally distributed [18], the voltage equation of the PMSM in the d-q coordinate system is given by:

$$\begin{array}{c}\hfill \begin{array}{c}\hfill \left\{\begin{array}{c}{u}_d=R_s{i}_d+L_d{\displaystyle \frac{d}{dt}}{i}_d-{\omega }_e{L}_q{i}_q\hfill \\ u_q=R_s{i}_q+L_q{\displaystyle \frac{d}{dt}}{i}_q+{\omega }_e(L_d{i}_d+{\psi }_f)\hfill \end{array}\right.\end{array}\end{array}$$

(1)

where $i_d$ and $i_q$ are the d-q-axis stator currents, $u_d$ and $u_q$ are the d-q-axis voltages, $R_s$ are the stator winding resistances, $L_d$ and $L_q$ are the d-q-axis stator inductances, ${\omega }_e$ are the electrical angular velocities, and ${\psi }_f$ are the permanent magnet chains.

The electromagnetic torque equation of the PMSM is:

$$\begin{array}{c}\hfill \begin{array}{c}\hfill T_e=1.5p_n{i}_q\left(\left(L_d-L_q\right)i_d+{\psi }_f\right)\end{array}\end{array}$$

(2)

where, $p_n$ denotes the number of pole pairs, $T_e$ denotes the electromagnetic torque.

The mechanical equation of motion of the PMSM is:

$$\begin{array}{c}\hfill \begin{array}{c}\hfill J{\displaystyle \frac{d{\omega }_m}{dt}}=T_e-B{\omega }_m-T_L\end{array}\end{array}$$

(3)

where ${\omega }_m$ is the mechanical angular velocity, $T_L$ is the load torque, B is the damping factor, J is the moment of inertia.

In addition to the above equations, the following equations are needed:

$$\begin{array}{c}\hfill \begin{array}{c}\hfill {\omega }_e=p_n{\omega }_m\end{array}\end{array}$$

(4)

$$\begin{array}{c}\hfill \begin{array}{c}\hfill N_r={\displaystyle \frac{30}{\pi }}{\omega }_m\end{array}\end{array}$$

(5)

$$\begin{array}{c}\hfill \begin{array}{c}\hfill {\theta }_e=\int {\omega }_{e}dt\end{array}\end{array}$$

(6)

where, $N_r$ is the rotational speed of the PMSM, ${\theta }_e$ is the electrical angle.

2.2. Fault Analysis of Inter-Turn Short Circuit

The paper presents the equivalent circuit diagram for a PMSM experiencing an inter-turn short circuit fault in Figure 1. It is assumed that such a fault manifests in the B-phase stator winding. In Figure 1, the B-phase winding is divided into two parts: the healthy part and the faulty part, and a short-circuit resistor $R_f$ is connected in parallel to the faulty winding of the B-phase.

The PMSM inter-turn short circuit model can be obtained by solving using Kirchhoff’s law based on the equivalent circuit [19] in Figure 1, denoted as:

$$\begin{array}{c}\hfill \begin{array}{c}\hfill U_{abc,f}=R_{abc,f}{i}_{abc,f}+{\displaystyle \frac{d}{dt}}\left(L_{abc,f}{i}_{abc,f}\right)+e_{abc,f}\end{array}\end{array}$$

(7)

where

$$\begin{array}{c}\hfill \begin{array}{c}\hfill U_{abc,f}={\left[\begin{array}{cccc}{u}_a& u_b& u_c& 0\end{array}\right]}^T\end{array}\end{array}$$

(8)

$$\begin{array}{c}\hfill \begin{array}{c}\hfill R_{abc,f}=\left[\begin{array}{cccc}{R}_a& 0& 0& 0\\ 0& R_b& 0& \sigma R_b\\ 0& 0& R_c& 0\\ 0& \sigma R_b& 0& \sigma R_b+R_f\end{array}\right]\end{array}\end{array}$$

(9)

$$\begin{array}{c}\hfill \begin{array}{c}\hfill i_{abc,f}={\left[\begin{array}{cccc}{i}_a& i_b& i_c& i_f\end{array}\right]}^T\end{array}\end{array}$$

(10)

$$\begin{array}{c}\hfill \begin{array}{c}\hfill e_{abc,f}={\left[\begin{array}{cccc}{e}_a& e_b& e_c& \sigma e_b\end{array}\right]}^T={\psi }_f{\displaystyle \frac{d}{dt}}\left[\begin{array}{c}cos\theta \\ \\ cos(\theta -{\displaystyle \frac{2}{3}}\pi )\\ \\ cos(\theta +{\displaystyle \frac{2}{3}}\pi )\\ \\ \sigma cos(\theta -{\displaystyle \frac{2}{3}}\pi )\end{array}\right]\end{array}\end{array}$$

(11)

where, $R_f$ denotes the fault resistance, $R_a$, $R_b$ and $R_c$ denotes the stator resistance for phase A, phase B and phase C, respectively. $U_{abc,f}$ denotes the stator winding voltage, $u_a$, $u_b$ and $u_c$ denotes the winding voltage for phase A, phase B and phase C, respectively, $i_{abc,f}$ denotes the current matrix, $i_a$, $i_b$ and $i_c$ denotes the current in the three phase stator winding, $i_f$ denotes the fault current, $L_{abc,f}$ denotes the inductance matrix, $e_a$, $e_b$ and $e_c$ denotes the back electromotive force of phase A, phase B and phase C, respectively. $\sigma$ denotes the inter-turn short circuit ratio, which is defined as:

$$\begin{array}{c}\hfill \begin{array}{c}\hfill \sigma ={\displaystyle \frac{n}{N}}\end{array}\end{array}$$

(12)

where n denotes the number of turns of the stator winding being short-circuited and N denotes the total number of turns of the stator winding.

However, the calculation of the inductance matrix $L_{abc,f}$ is more complicated because the phase B winding is divided into two parts, and it is necessary to consider the mutual inductance of the windings of these two parts for the other phase winding and the self-inductance of the faulty winding, respectively. Therefore, the inductance matrix $L_{abc}$ is changed from the original 3 × 3 to 4 × 4 inductance matrix $L_{abc,f}$.

$$\begin{array}{c}\hfill \begin{array}{c}\hfill L_{abc}=\left[\begin{array}{ccc}{L}_{aa}& L_{ab}& L_{ac}\\ L_{ba}& L_{bb}& L_{bc}\\ L_{ca}& L_{cb}& L_{cc}\end{array}\right]=\left[\begin{array}{ccc}{L}_{sl}+L_m& -{\displaystyle \frac{1}{2}}{L}_m& -{\displaystyle \frac{1}{2}}{L}_m\\ \\ -{\displaystyle \frac{1}{2}}{L}_m& L_{sl}+L_m& -{\displaystyle \frac{1}{2}}{L}_m\\ \\ -{\displaystyle \frac{1}{2}}{L}_m& -{\displaystyle \frac{1}{2}}{L}_m& L_{sl}+L_m\end{array}\right]\end{array}\end{array}$$

(13)

where, $L_{aa}$, $L_{bb}$, $L_{cc}$ represents the self-inductance of the winding, $L_{ab}$, $L_{ac}$, $L_{ba}$, $L_{bc}$, $L_{ca}$, $L_{cb}$ represents the mutual inductance between the two phases of the winding, which is the phase self-inductance and the mutual inductance. $L_{sl}$ is the phase self-inductance and $L_m$ is the mutual inductance, during normal operation of the motor, the self-inductance of each phase is the same, and the mutual inductance is also the same.

$$\begin{array}{c}\hfill \begin{array}{c}\hfill L_{abc,f}=\left[\begin{array}{cccc}{L}_{aa}& L_{ab}^{\prime }& L_{ac}& L_{af}\\ L_{ba}^{\prime }& L_{bb}^{\prime }& L_{bc}^{\prime }& L_{bf}\\ L_{ca}& L_{cb}^{\prime }& L_{cc}& L_{cf}\\ L_{fa}& L_{fb}& L_{fc}& L_{ff}\end{array}\right]\end{array}\end{array}$$

(14)

where, $L_{ab}^{\prime }$, $L_{ba}^{\prime }$, $L_{cb}^{\prime }$, $L_{bc}^{\prime }$ denotes the mutual inductance between the non-faulted winding part of the faulted phase and the other two phases, $L_{bb}^{\prime }$ denotes the self-inductance of the non-faulted winding part of the faulted phase, and $L_{ff}$ denotes the self-inductance of the faulted winding part, $L_{af}$, $L_{bf}$, $L_{cf}$, $L_{fc}$, $L_{fb}$, $L_{fa}$ denotes the mutual inductance between the faulted winding part and the normal winding parts of the other three phases.

For the calculation of the above parameters, the inductance parameters can be processed using the consistency principle, the leakage principle and the proportionality principle [20]. Considering firstly the calculation of the inductance parameters related to the faulty phase winding, the above mentioned three principles can be used to solve for $L_{bb}^{\prime }$, $L_{bf}$, $L_{fb}$ and $L_{ff}$:

The formula for the consistency principle is as follows:

$$\begin{array}{c}\hfill \begin{array}{c}\hfill L_{bb}^{\prime }+2L_{bf}+L_{ff}=L_{bb}\end{array}\end{array}$$

(15)

where $L_{bb}^{\prime }$ indicates the need to solve for the self-inductance under inter-turn short circuit, and $L_{bb}$ indicates the self-inductance under normal conditions.

The formula for the leakage principle is as follows:

$$\begin{array}{c}\hfill \begin{array}{c}\hfill {\delta }_{bf}=1-{\displaystyle \frac{L_{bf}^2}{L_{bb}^{\prime }{L}_{ff}}}\end{array}\end{array}$$

(16)

where ${\delta }_{bf}$ denotes the leakage factor, which is usually a small positive constant and is related to the current in the short-circuit branch.

The formula for the proportionality principle is as follows:

$$\begin{array}{c}\hfill \begin{array}{c}\hfill {\displaystyle \frac{L_{bb}^{\prime }}{L_{bf}}}={\left({\displaystyle \frac{1-\sigma }{\sigma }}\right)}^2\end{array}\end{array}$$

(17)

The four parameters of the faulty phase are finally solved for:

$$\begin{array}{c}\hfill \begin{array}{c}\hfill L_{bb}^{\prime }=(L_{sl}+L_m){\displaystyle \frac{1}{{\left(\frac{\sigma }{1-\sigma }\right)}^2+2\frac{\sigma }{1-\sigma }\sqrt{1-{\delta }_{bf}}+1}}\end{array}\end{array}$$

(18)

$$\begin{array}{c}\hfill \begin{array}{c}\hfill L_{fb}=L_{bf}=(L_{sl}+L_m){\displaystyle \frac{\sqrt{1-{\delta }_{bf}}}{\frac{1-\sigma }{\sigma }+\frac{\sigma }{1-\sigma }+2\sqrt{1-{\delta }_{bf}}}}\end{array}\end{array}$$

(19)

$$\begin{array}{c}\hfill \begin{array}{c}\hfill L_{ff}=(L_{sl}+L_m){\displaystyle \frac{1}{{\left(\frac{\sigma }{1-\sigma }\right)}^2+2\frac{\sigma }{1-\sigma }\sqrt{1-{\delta }_{bf}}+1}}\end{array}\end{array}$$

(20)

Secondly, for the calculation of the mutual inductance parameters between the faulty phase and the other two phases, the principle of consistency and the principle of proportionality [20] can be used for the calculation, the expression as follows:

$$\begin{array}{c}\hfill \begin{array}{c}\hfill \left\{\begin{array}{c}{L}_{bx}^{\prime }+L_{fx}=L_{bx}\hfill \\ {\displaystyle \frac{L_{bx}^{\prime }}{L_{fx}}}={\displaystyle \frac{1-\sigma }{\sigma }}\hfill \end{array}\right. \mathrm{where}x=a,c\end{array}\end{array}$$

(21)

$L_{ba}^{\prime }$, $L_{bc}^{\prime }$, $L_{fa}$, $L_{fc}$ and can be calculated as follows:

$$\begin{array}{c}\hfill \begin{array}{c}\hfill L_{ba}^{\prime }=L_{ba}(1-\sigma ); L_{bc}^{\prime }=L_{bc}(1-\sigma )\end{array}\end{array}$$

(22)

$$\begin{array}{c}\hfill \begin{array}{c}\hfill L_{fa}=L_{ba}\sigma ; L_{fc}=L_{bc}\sigma \end{array}\end{array}$$

(23)

Finally, the inductance matrix for an inter-turn short circuit fault is obtained as:

$$\begin{array}{c}\hfill \begin{array}{c}\hfill \begin{array}{cc}\hfill L_{abc,f}& =\left[\begin{array}{cccc}{L}_{sl}+L_m& -{\displaystyle \frac{1}{2}}(1-\sigma )L_m& -{\displaystyle \frac{1}{2}}(1-\sigma )L_m& -{\displaystyle \frac{1}{2}}\sigma L_m\\ \\ -{\displaystyle \frac{1}{2}}(1-\sigma )L_m& L_{bb}^{\prime }& -{\displaystyle \frac{1}{2}}(1-\sigma )L_m& L_{bf}\\ \\ -{\displaystyle \frac{1}{2}}(1-\sigma )L_m& -{\displaystyle \frac{1}{2}}(1-\sigma )L_m& L_{sl}+L_m& -{\displaystyle \frac{1}{2}}\sigma L_m\\ \\ -{\displaystyle \frac{1}{2}}\sigma L_m& L_{fb}& -{\displaystyle \frac{1}{2}}\sigma L_m& L_{ff}\end{array}\right]\hfill \end{array}\end{array}\end{array}$$

(24)

Given that the inter-turn short circuit fault equation is formulated within the ABC three-phase coordinate system, it follows that the torque equation for the PMSM is similarly developed within this three-phase framework. The torque equation, in this context, can be articulated as:

$$\begin{array}{c}\hfill \begin{array}{c}\hfill T_e=p_n\left({\displaystyle \frac{1}{2}}{i}_{abc,f}^T{\displaystyle \frac{\partial L_{abc,f}}{\partial \theta }}{i}_{abc,f}+i_{abc,f}^T{\displaystyle \frac{e_{abc,f}}{{\omega }_e}}\right)\end{array}\end{array}$$

(25)

The model for inter-turn short circuit faults in PMSMs is achieved by combining the above equations with Equations (3)–(6).

2.3. Fault Analysis of Demagnetization

In Figure 2, the demagnetization faults’ impact on the magnetic flux linkage of the permanent magnets is depicted.

Under the assumption that the motor operates under normal conditions, the original q axis and d axis become $q^{\prime }$ axis and $d^{\prime }$ axis after the $\gamma$ angle change [21]. However, the occurrence of a demagnetization fault alters the magnetic circuit of the permanent magnet. The original chain value ${\psi }_f$ becomes ${\psi }_r$, and ${\psi }_r$ is re-decomposed to the original d-q axis. ${\psi }_{rd}$ and ${\psi }_{rq}$ are the new components generated by the demagnetized permanent magnet in the d-q axis.

$$\begin{array}{c}\hfill \begin{array}{c}\hfill \left\{\begin{array}{c}{\psi }_{rd}={\psi }_{r}cos\left(\gamma \right)\hfill \\ {\psi }_{rq}={\psi }_{r}sin\left(\gamma \right)\hfill \end{array}\right.\end{array}\end{array}$$

(26)

Substituting Equation (26) into Equation (1) is:

$$\begin{array}{c}\hfill \begin{array}{c}\hfill \left\{\begin{array}{c}{u}_d=R_s{i}_d+L_d{\displaystyle \frac{d}{dt}}{i}_d+{\displaystyle \frac{d}{dt}}{\psi }_d-{\omega }_e{L}_q{i}_q-{\omega }_e{\psi }_{rq}\hfill \\ u_q=R_s{i}_q+L_q{\displaystyle \frac{d}{dt}}{i}_q+{\displaystyle \frac{d}{dt}}{\psi }_q+{\omega }_e(L_d{i}_d+{\psi }_{rd})\hfill \end{array}\right.\end{array}\end{array}$$

(27)

Considering that in practical engineering systems, the rate of change of the magnetic flux linkage of permanent magnets is negligible compared to state variables such as current, ${\displaystyle \frac{d}{dt}}{\psi }_d\approx 0$ and ${\displaystyle \frac{d}{dt}}{\psi }_q\approx 0$ can be assumed. Eventually, the voltage equation under the demagnetization fault is expressed as:

$$\begin{array}{c}\hfill \begin{array}{c}\hfill \left\{\begin{array}{c}{u}_d=R_s{i}_d+L_d{\displaystyle \frac{d}{dt}}{i}_d-{\omega }_e{L}_q{i}_q-{\omega }_e{\psi }_{rq}\hfill \\ u_q=R_s{i}_q+L_q{\displaystyle \frac{d}{dt}}{i}_q+{\omega }_e(L_d{i}_d+{\psi }_{rd})\hfill \end{array}\right.\end{array}\end{array}$$

(28)

The corresponding electromagnetic torque equation for a PMSM is:

$$\begin{array}{c}\hfill \begin{array}{c}\hfill T_e={\displaystyle \frac{3}{2}}{p}_n\left({\psi }_{rd}{i}_q-{\psi }_{rq}{i}_d+(L_d-L_q)i_d{i}_q\right)\end{array}\end{array}$$

(29)

The model for demagnetization faults in PMSMs is achieved by combining the above equations with Equations (3)–(6).

3. Proposed PMSM Fault Diagnosis Framework

The framework for the proposed PMSM fault diagnosis method based on IResNet, is first introduced in this section and then provides a detailed explanation of this fault diagnosis method.

3.1. Overview of the Proposed Framework

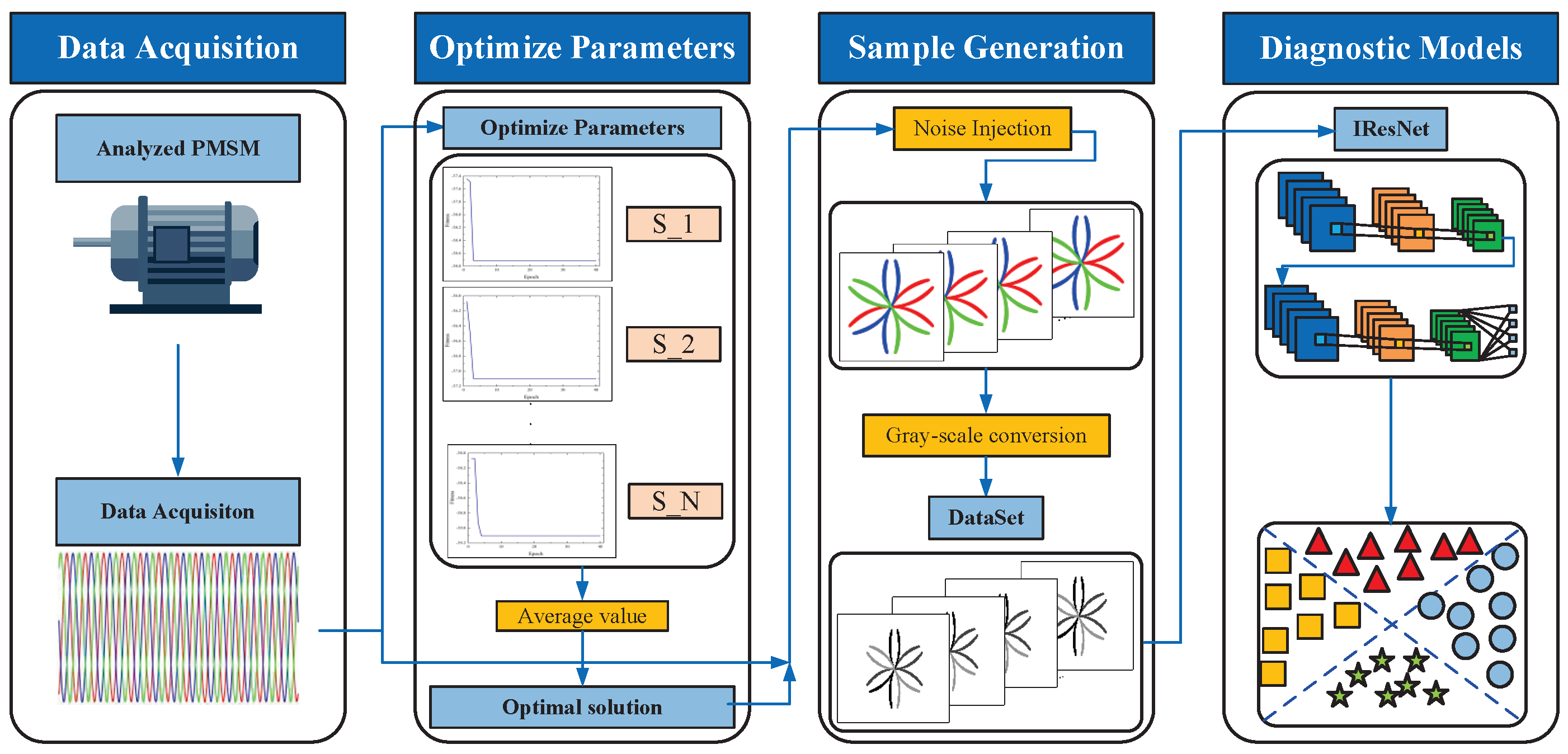
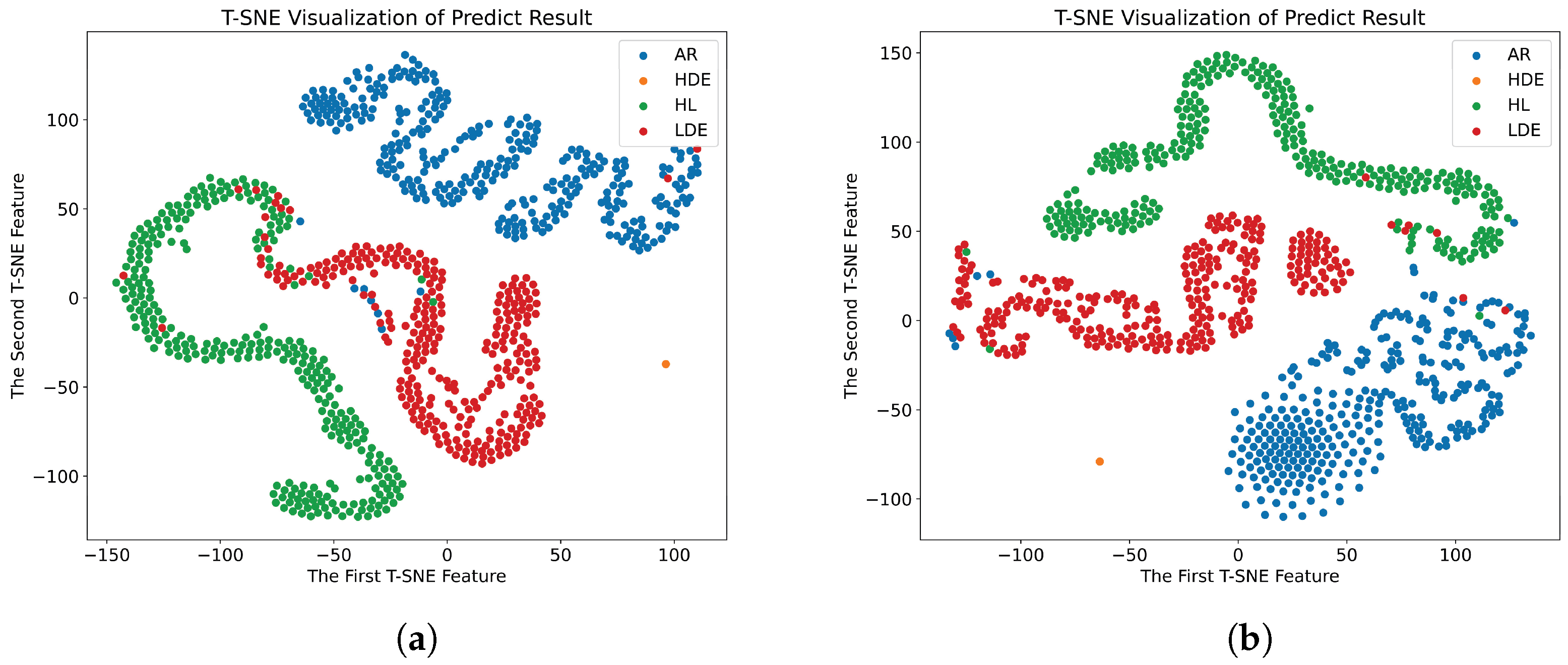
Figure 3 depicts the structure of the proposed method detailed in this paper, which is primarily composed of four key sections: Data acquisition, parameter optimization, sample generation, and fault diagnosis. Firstly, the current signals of PMSM in different fault states are collected by the simulation model; secondly, the key parameters in the transformation process are optimized using the HPO algorithm in order to generate PCCDP images with high variability; then these image samples are input into a well-trained fault diagnosis model; finally, the model learns the image features to realize the accurate identification of PMSM faults. The detailed diagnosis steps are shown below:

(1)

Data Acquisition. The data were acquired via model simulation. Firstly, the corresponding fault simulation model is constructed in Simulink according to the PMSM fault mathematical model. Secondly, the PMSM parameters are input to simulate the PMSM operation state under various faults and different operating conditions. Finally, stable current signals are extracted from the simulation results for acquisition.

(2)

Image discrepancy optimization. To further improve diagnostic effectiveness, we need to make the correlation between the images corresponding to each fault state as small as possible before image transformation. Therefore, we need to optimize the PCCDP image parameters. First, the acquired three-phase current signals are divided into a sequence of samples with a fixed size. Subsequently, the HPO algorithm is used to optimize the parameters of the images, and the image discrimination function is used as the metric for evaluating the algorithm’s performance to ultimately obtain the optimal parameters of the images.

(3)

Sample generation. To ensure the data acquired from the simulation realistically reflects the actual performance of PMSM, Gaussian white noise is injected into the segmented current samples to simulate noise in real applications [11]. Then, based on the optimized parameters, the noise-injected samples are converted into corresponding PCCDP grayscale images.

(4)

Based on IResNet diagnostic models. Enhancing the network’s feature extraction capacity involves improving the conventional ResNet by incorporating the SE attention mechanism into the pre-activated residual units, which bolsters the model’s fault feature extraction efficacy. Subsequently, this enhanced model is implemented in the fault diagnostic procedure for PMSM, facilitating the accurate identification of motor malfunctions.

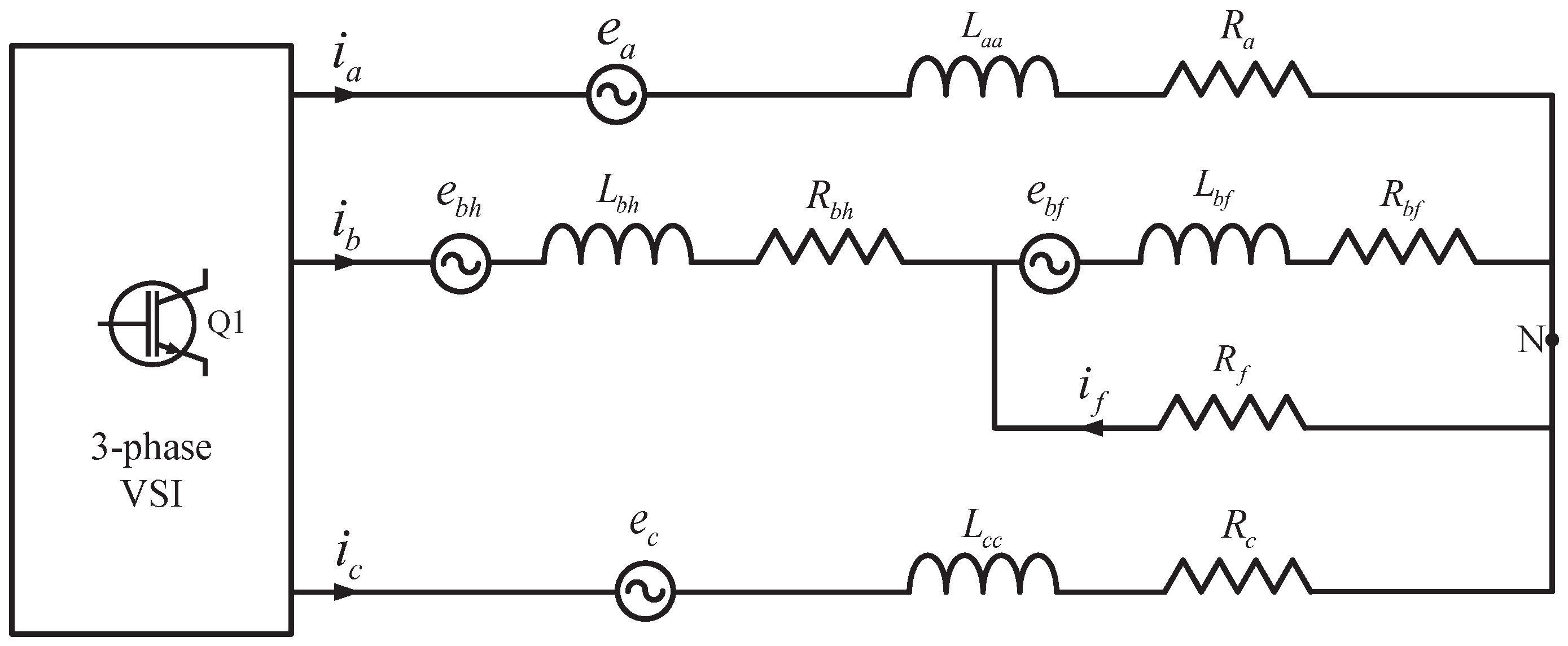
3.2. Data Acquisition

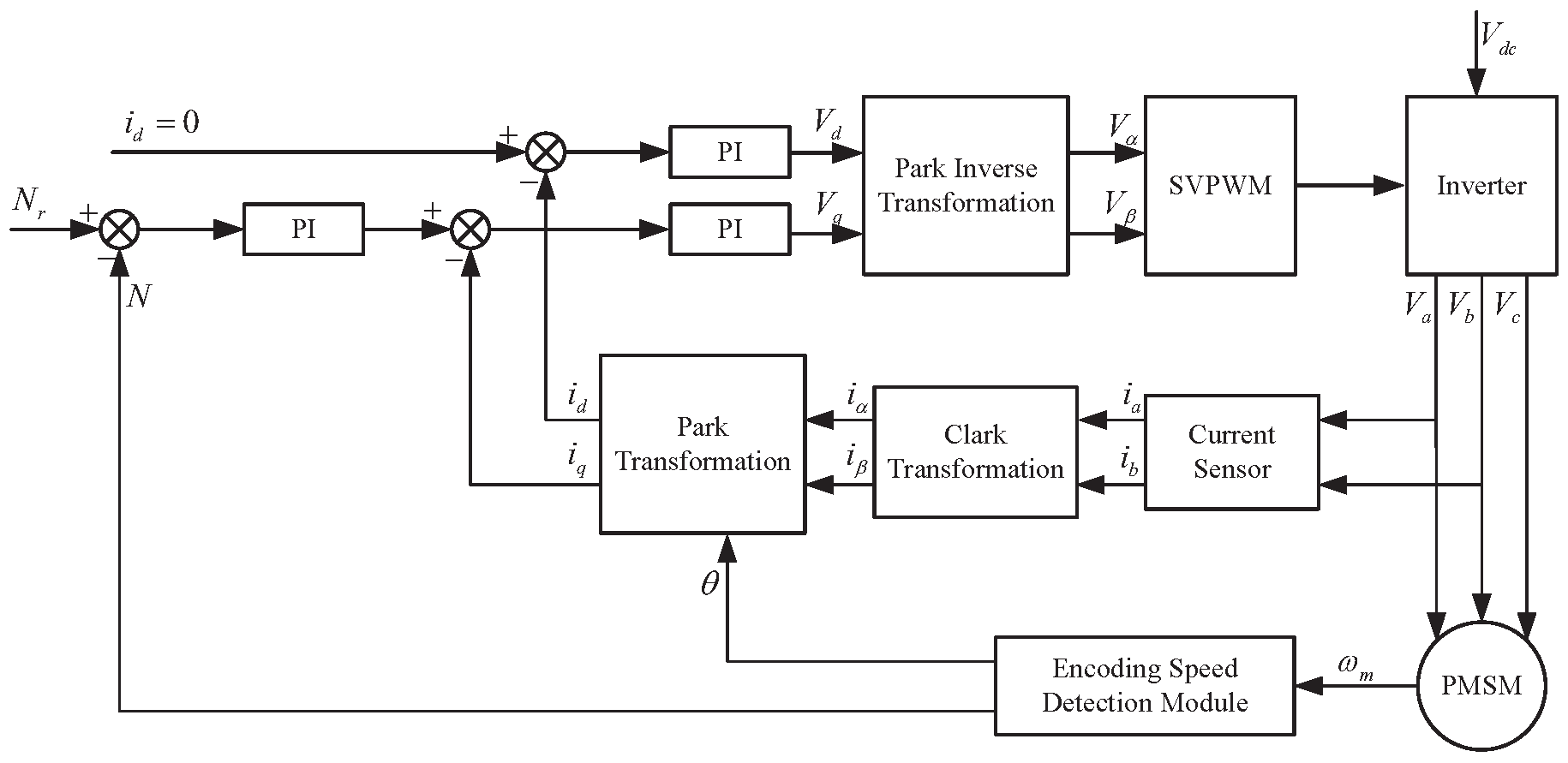
First, the mathematical model was established based on the operational characteristics of PMSM under different fault states. Subsequently, the PMSM control system model based on Field-Oriented Control algorithm was constructed on the Simulink simulation platform, with the control system as shown in Figure 4. Finally, motor-related parameters were input into the model for simulation, thereby obtaining the three-phase current signals of the motor, with the simulation parameters related to the motor shown in

Table 1. PMSM simulation parameter settings.

Parameter	Value	Parameter	Value
Stator resistance ($\Omega$)	0.958	Rated speed (rpm/min)	1000
Self-inductance (H)	$11.76\times {10}^{-3}$	Inertia (kg.m2)	0.003
Mutual inductance (H)	$0.24\times {10}^{-3}$	Friction coefficient (N.m/rad/s)	0.0008
Pole pairs	4	Magnetic flux of PM (Wb-turn)	0.1827
Bus voltage (V)	311	Leakage factor	0.2
Rated torque (N × m)	20	Rated power (KW)	3.14
Winding connection type	Y type	Sampling frequency(KHz)	1000

.

To ensure comprehensive data collection, the PMSM operating conditions are categorized prior to fault simulations. Consequently, torque and speed serve as the parameters for defining these conditions. Specifically, two speed levels, 750 rpm and 1000 rpm, and four torque levels, 25%, 50%, 75%, and 100% of the rated torque, are selected. This categorization results in eight distinct operating conditions. To enrich the data obtained from the fault simulation model, fault parameters are also categorized. In the inter-turn short circuit fault simulation, fault severity and short circuit resistance are used as parameters for division, with fault severity divided into 5% and 10%, and short circuit resistance divided into 0.01, 0.1, 0.5, and 0.8. Similarly, in the demagnetization fault simulation, amplitude demagnetization and angle demagnetization are used as parameters for division, with amplitude demagnetization divided into 25% and 50% of the magnetic flux linkage, and angle demagnetization divided into 30° and 20°. By categorizing the parameters of the PMSM simulation model according to the above methods, we successfully acquired different current signals of PMSMs under various health states and operating conditions, providing rich data support for subsequent fault diagnosis.

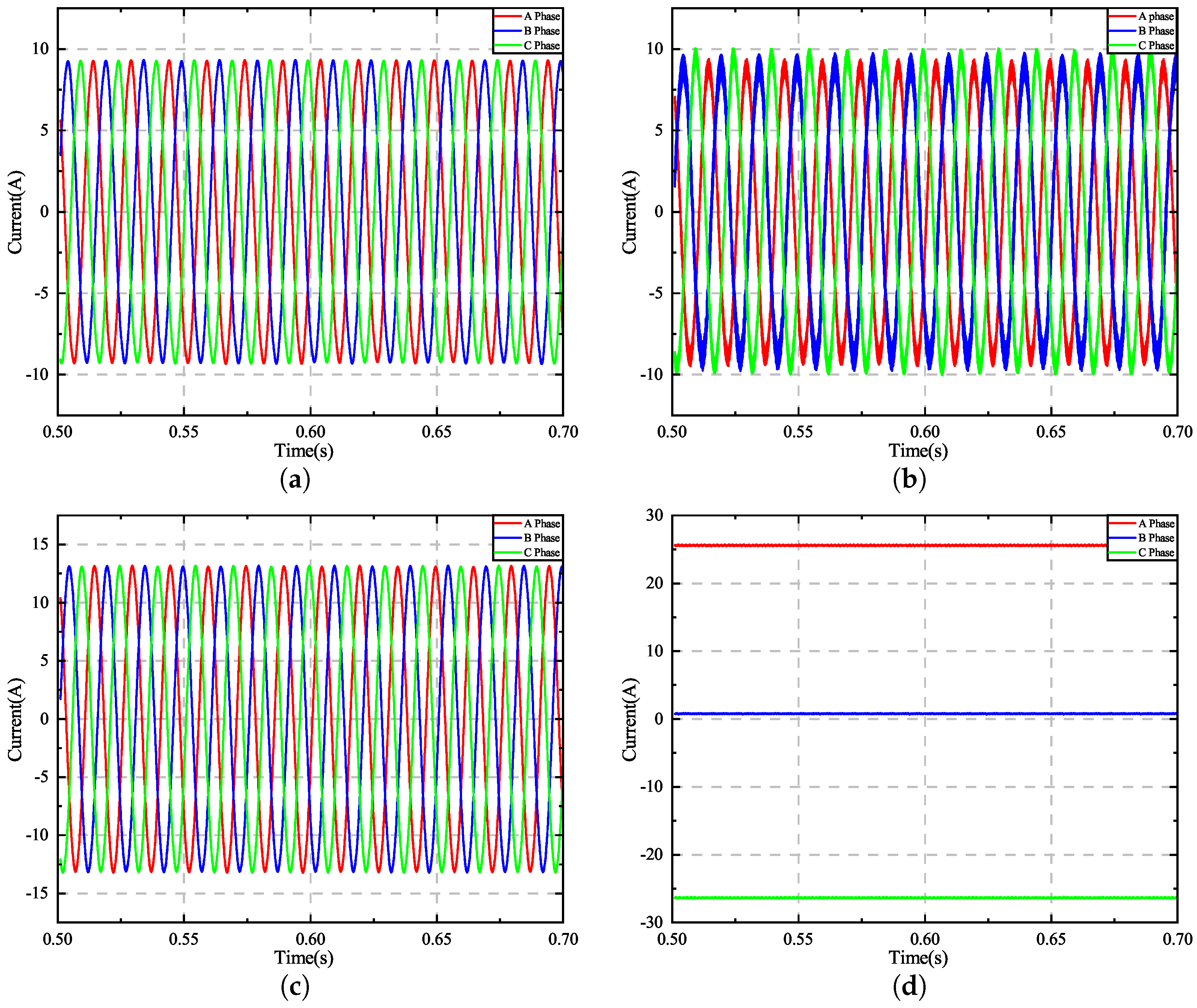
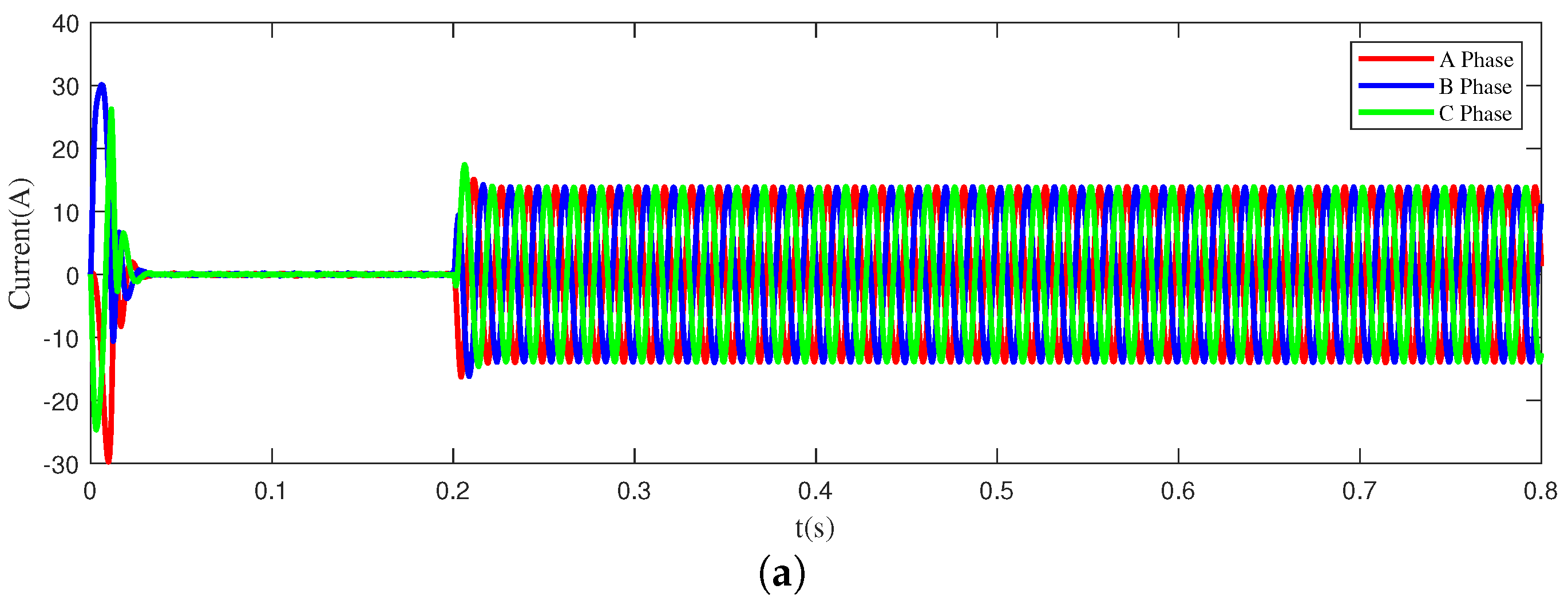
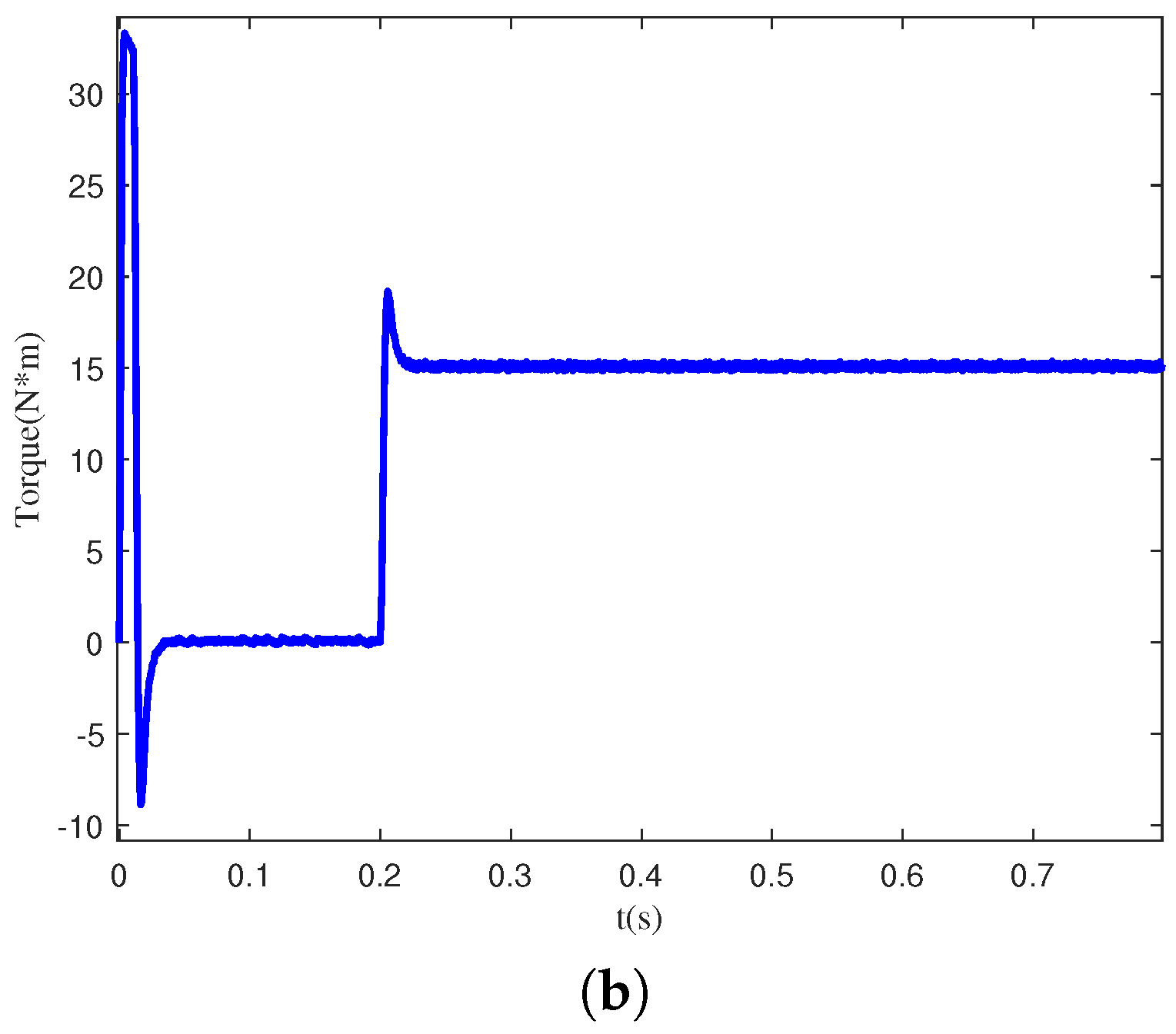
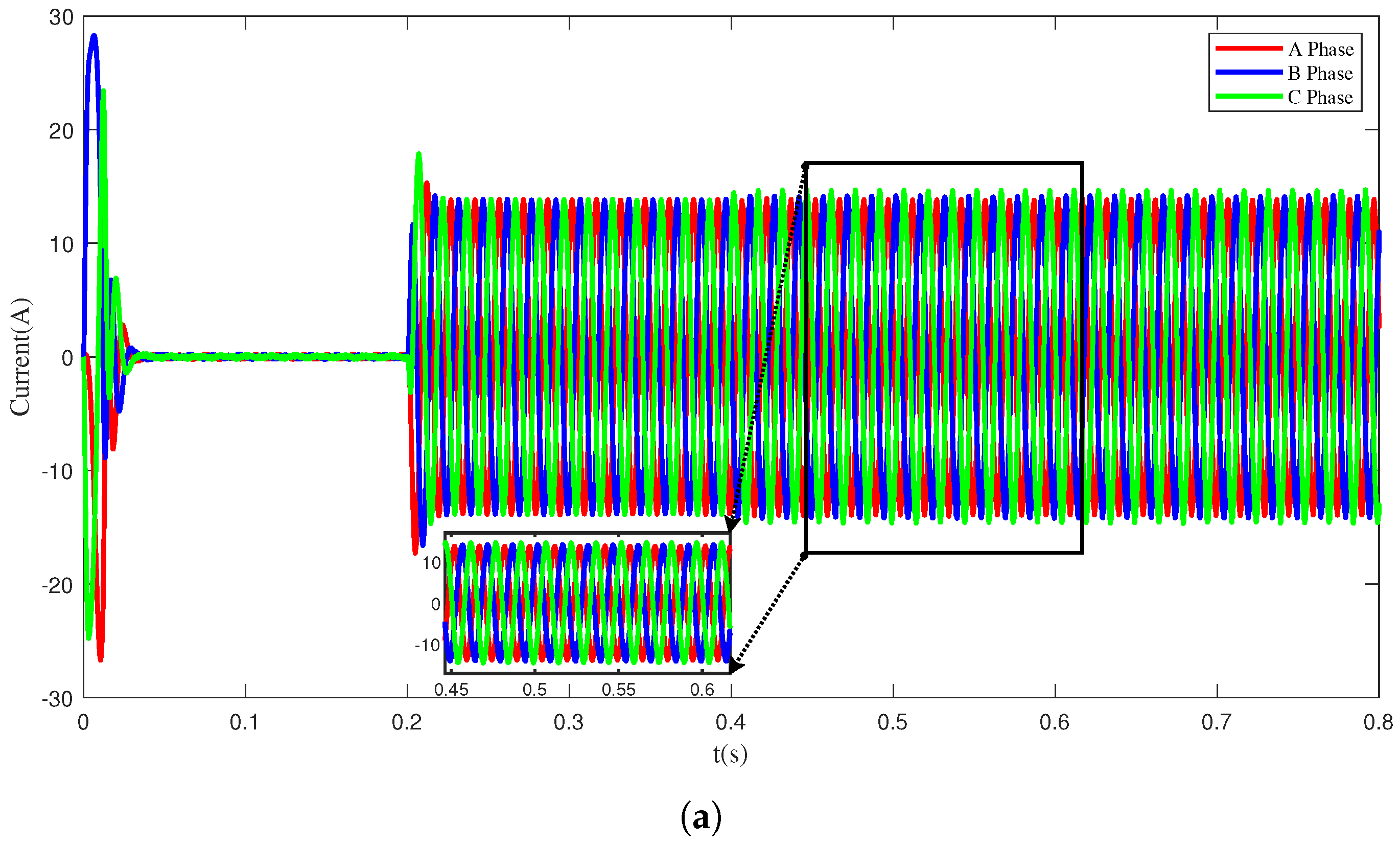
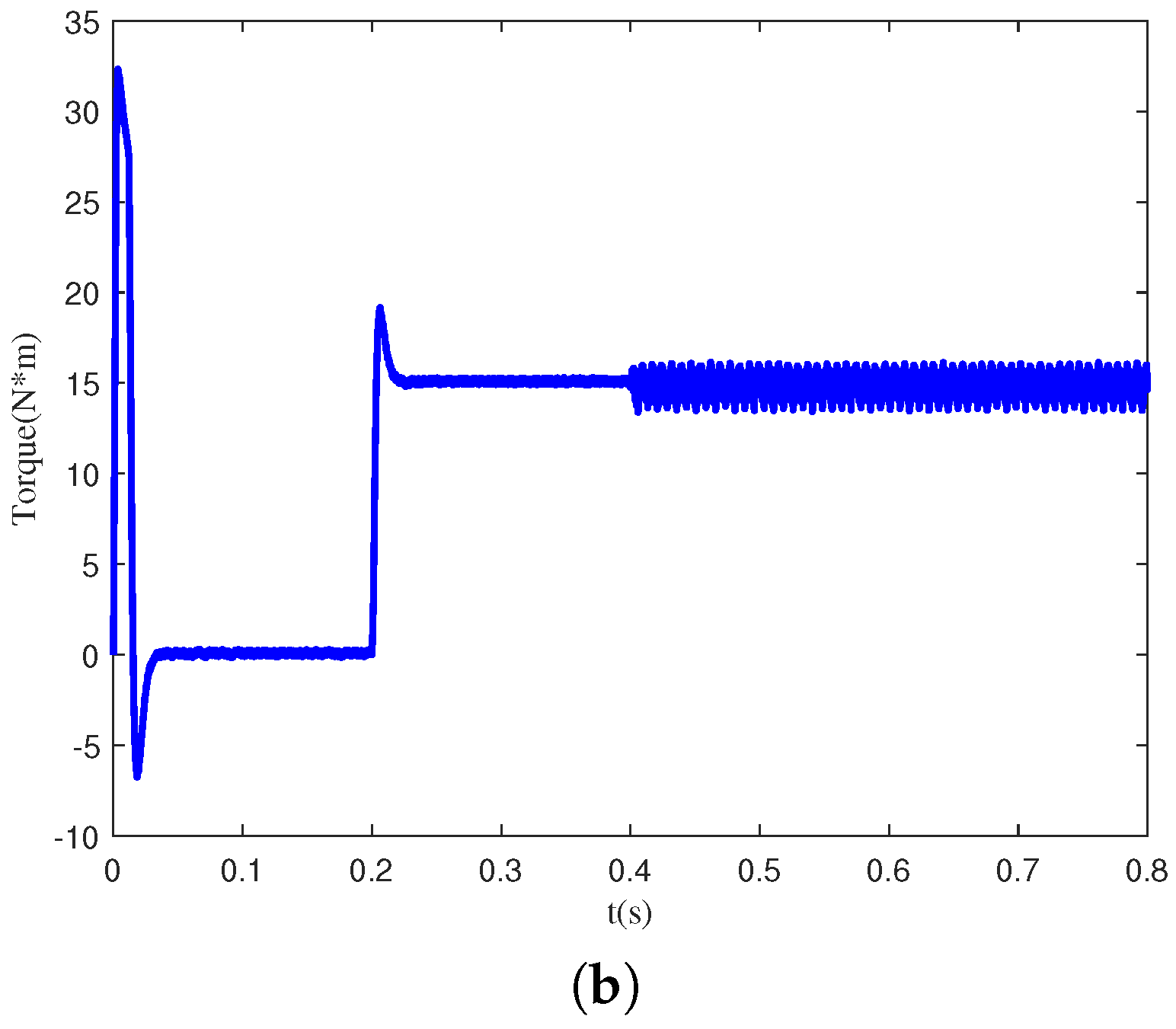
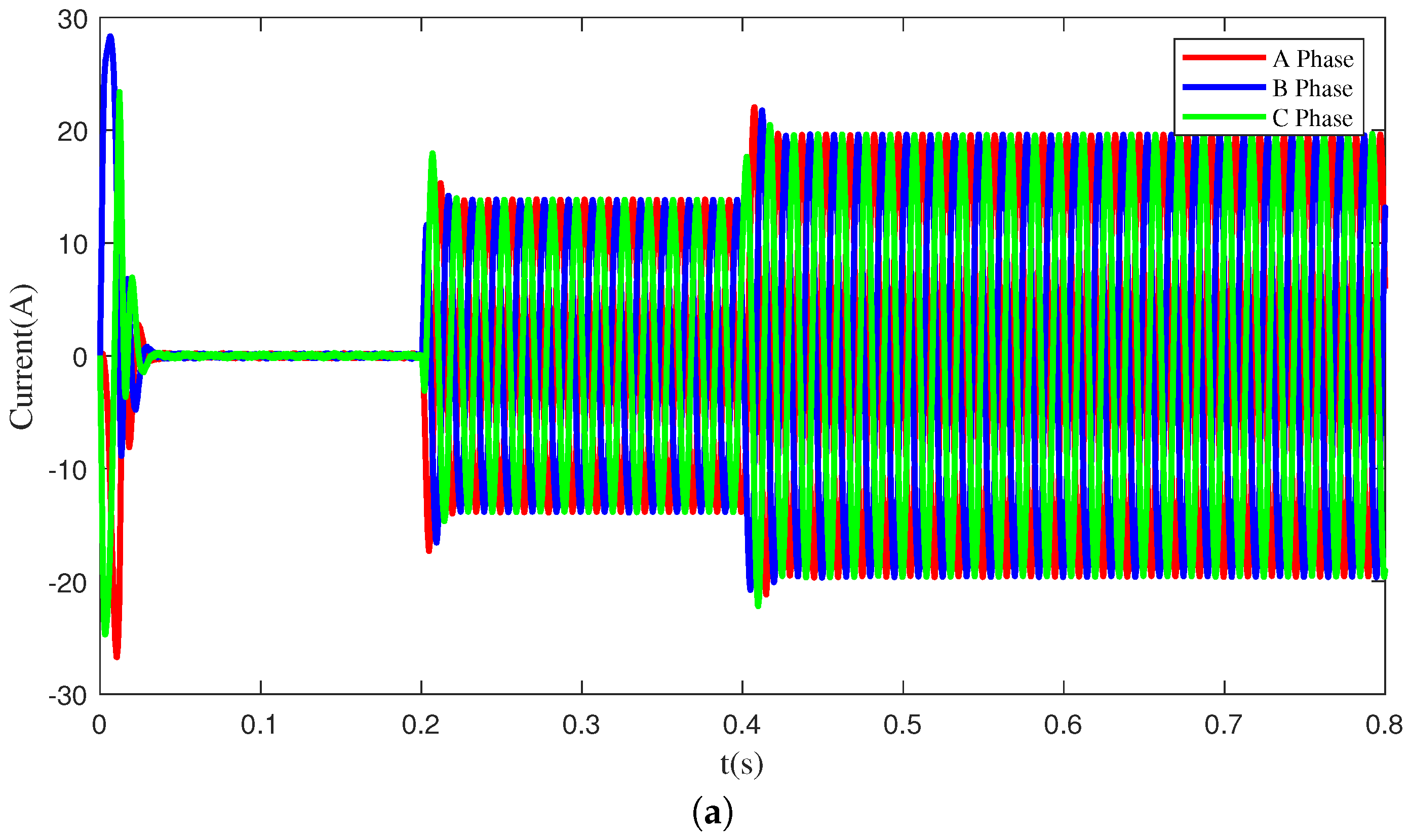
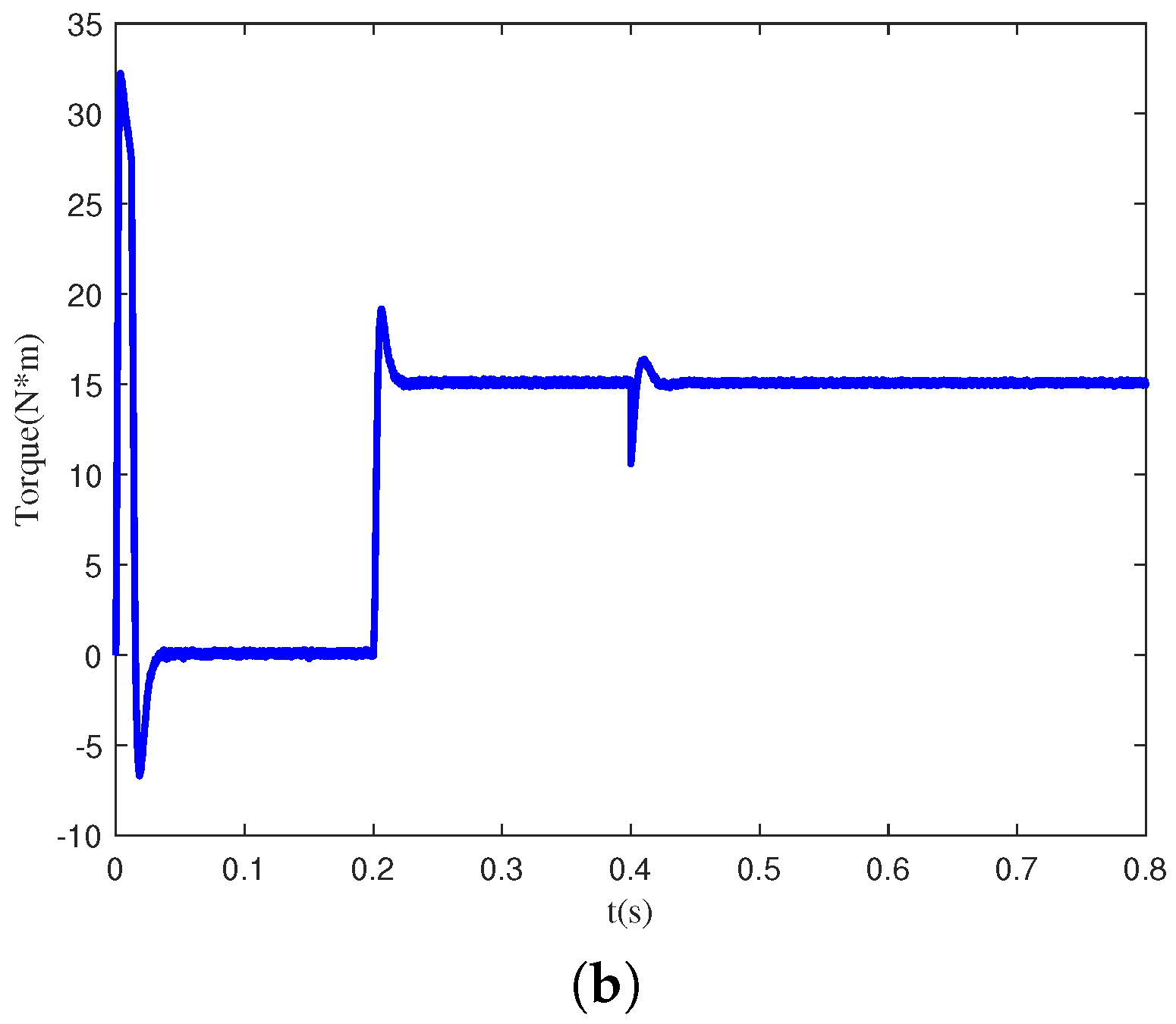
Figure 5 shows the current signals of PMSM in four different states: normal, inter-turn short circuit, light demagnetization, and heavy demagnetization. From Figure 5, it is evident that the current signals in the normal state are sinusoidal waves with balanced three-phase output. However, the inter-turn short circuit fault signal exhibits a significant imbalance among the three phases, and the amplitude of this signal varies over time. Additionally, the difference between the light demagnetization fault signal and the normal state signal of the motor is not readily apparent to the naked eye, involving only changes in amplitude. For the heavy demagnetization fault signal, due to heavy demagnetization faults in the motor affecting normal operation, the current waveform no longer changes.

3.3. Image Discrepancy Optimization

This paper employs the HPO algorithm to refine the parameters of PCCDP images, utilizing the image degree of difference function as the evaluation criterion for the optimization process. This section explains the fundamental principles of PCCDP images, the HPO algorithm, and the image degree of difference function.

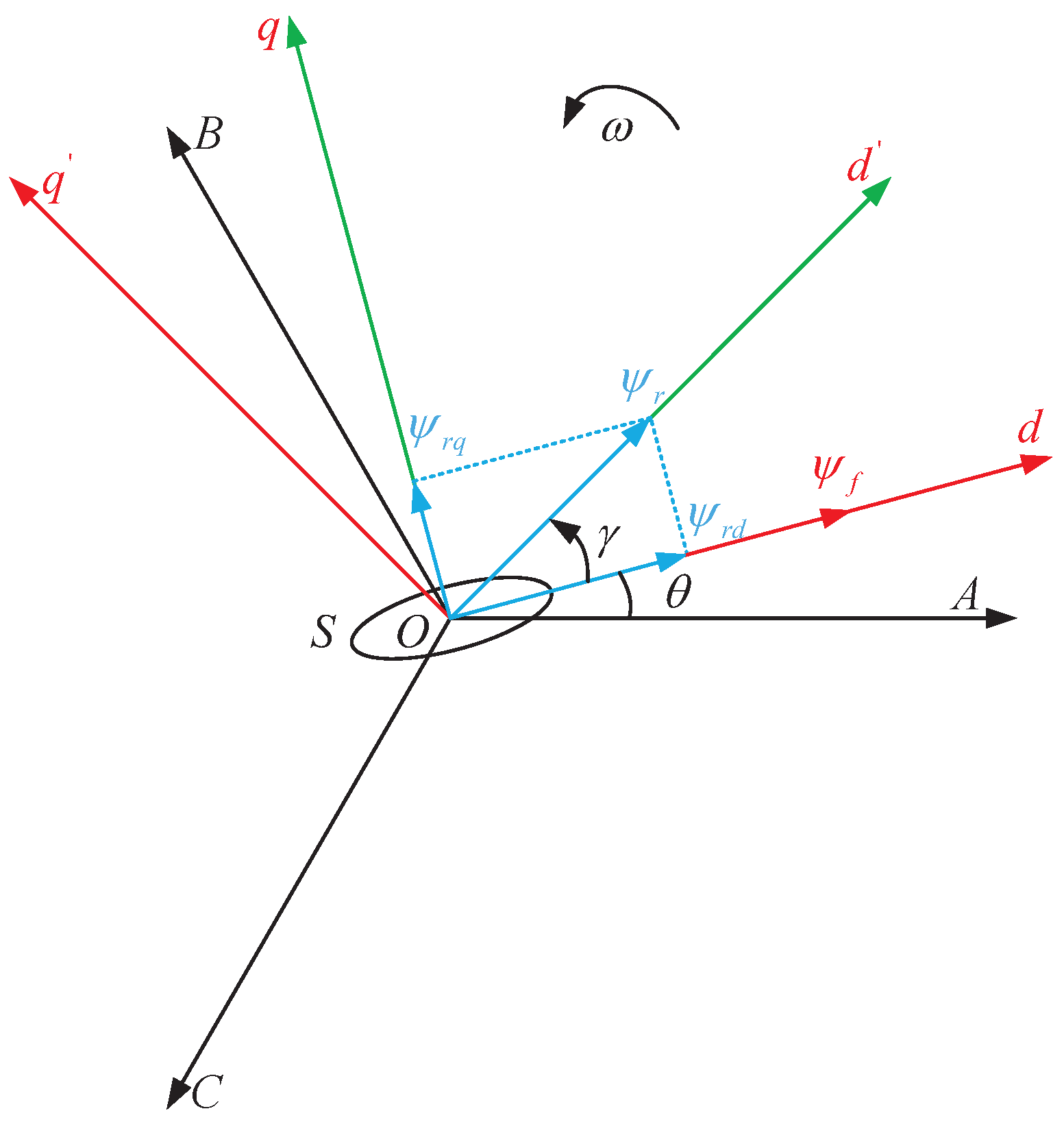
3.3.1. PCCDP

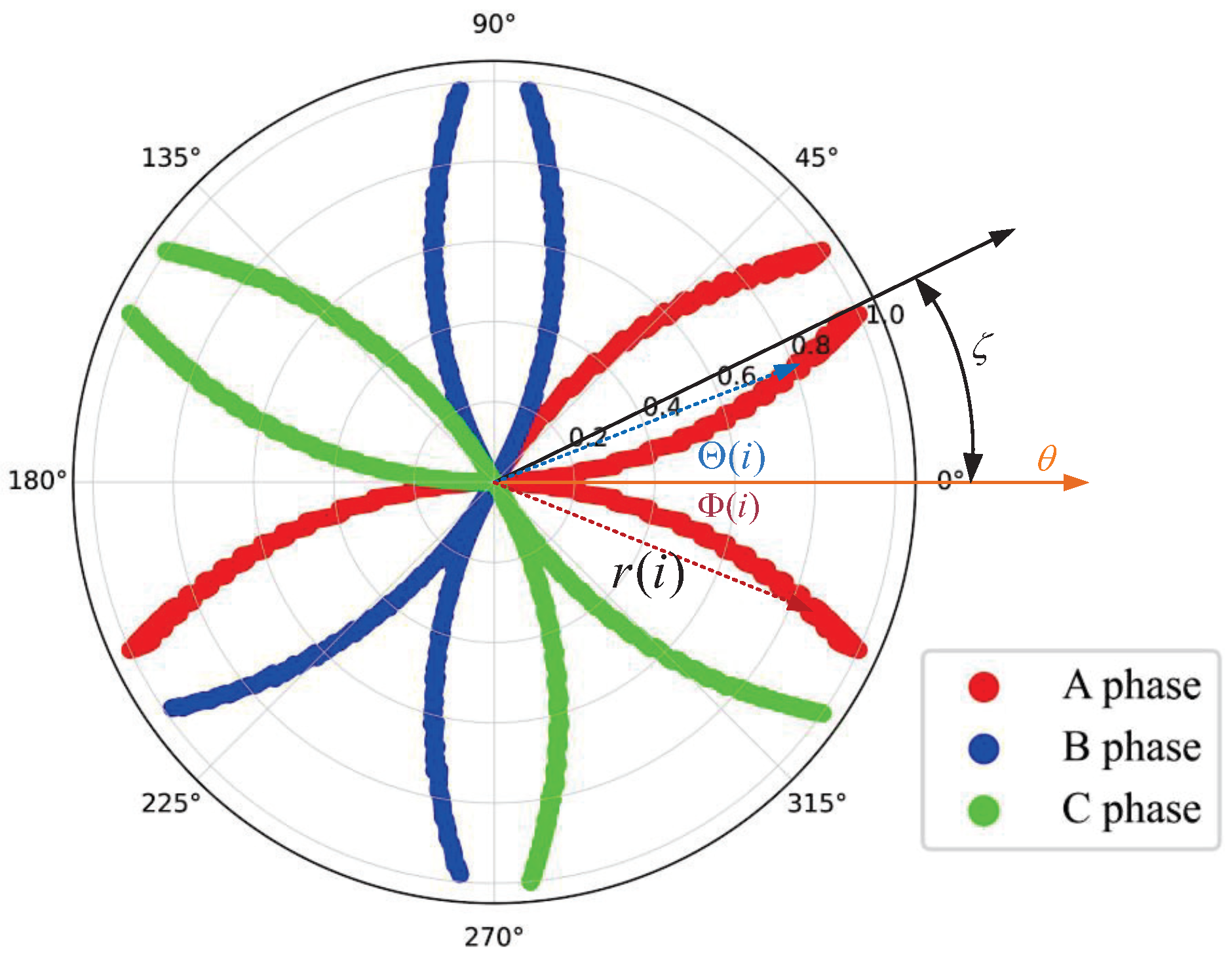
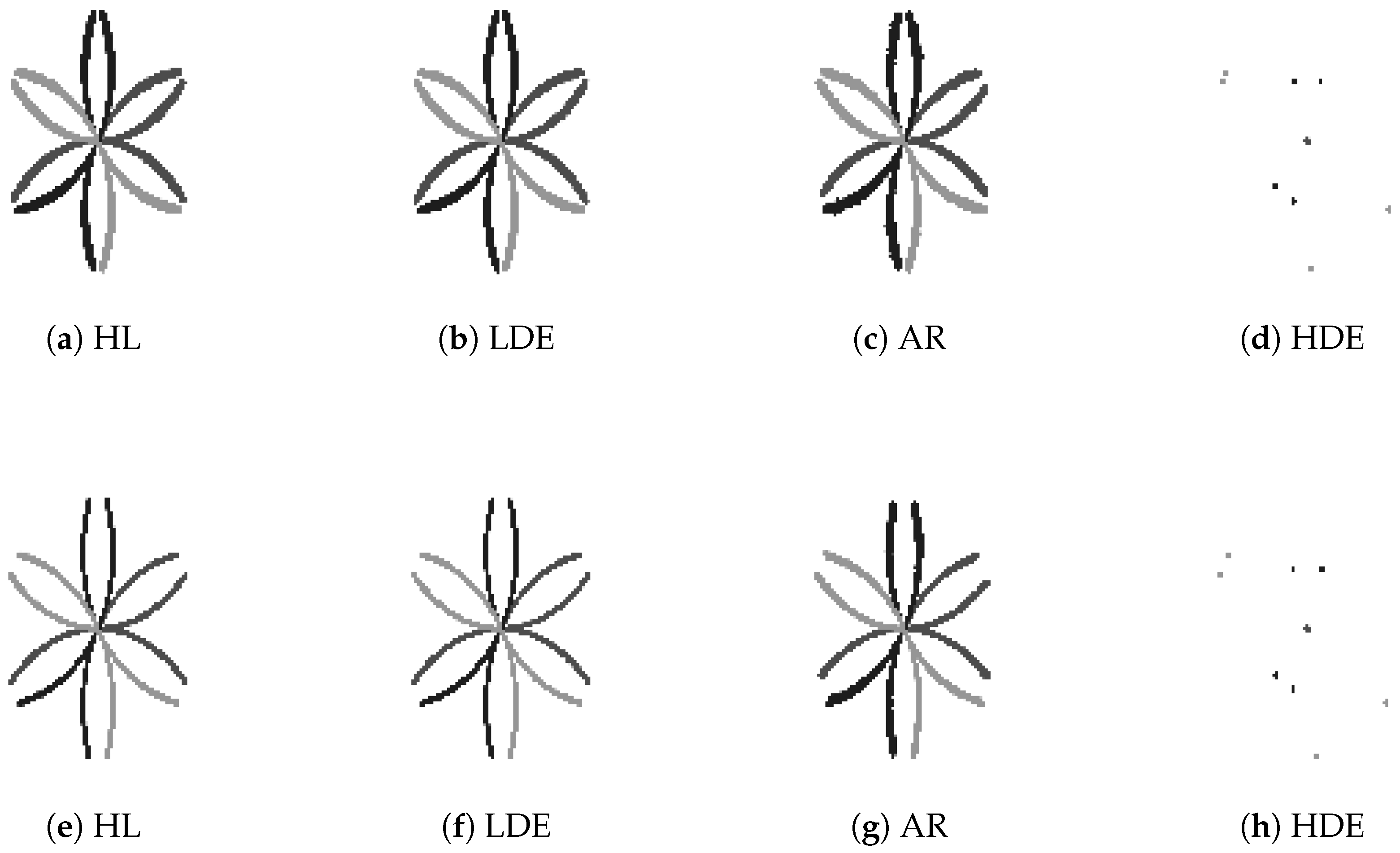
The PCCDP image method is a visualization technique for three-phase current signals, with its implementation process shown in Figure 6. It divides the entire polar coordinate plane into six 60° sectors, mapping two-phase current signals in each sector [11]. Three-phase current information is mapped onto two convex and two concave lobes. Each phase’s current data point corresponds to each point on the lobes. Thus, in the polar coordinate system, each point maps to four points with the same radius but different angles. For each sampling point in each phase of the current, its radius is expressed as:

$$\begin{array}{c}\hfill \begin{array}{c}\hfill r\left(i\right)={\displaystyle \frac{x_i-x_{min}}{x_{max}-x_{min}}}\end{array}\end{array}$$

(30)

where $x_i$ denotes the ith sampling point of each phase current signal, $x_{min}$ and $x_{max}$ denote the minimum and maximum values of the current, respectively.

The angles of the convex and concave lobes have been calculated as variables. The angle of the convex pleated lobe is expressed as:

$$\begin{array}{c}\hfill \begin{array}{c}\hfill \Theta \left(i\right)=\theta +{\displaystyle \frac{x_{i+\tau }-x_{\min }}{x_{\max }-x_{\min }}}\zeta ,\theta =\left\{\begin{array}{cc}{0}^{\circ },{180}^{\circ }\hfill & \mathrm{Phase}\mathrm{A}\hfill \\ {60}^{\circ },{240}^{\circ }\hfill & \mathrm{Phase}\mathrm{B}\hfill \\ {120}^{\circ },{300}^{\circ }\hfill & \mathrm{Phase}\mathrm{C}\hfill \end{array}\right.\end{array}\end{array}$$

(31)

where $\zeta$ denotes the angular amplification factor and $\tau$ denotes the predefined time interval factor.

The angle of the concave pleated leaf is denoted as:

$$\begin{array}{c}\hfill \begin{array}{c}\hfill \Phi \left(i\right)=\theta -{\displaystyle \frac{x_{i+\tau }-x_{\min }}{x_{\max }-x_{\min }}}\zeta ,\theta =\left\{\begin{array}{cc}{0}^{\circ },{60}^{\circ }\hfill & \mathrm{Phase}\mathrm{A}\hfill \\ {120}^{\circ },{240}^{\circ }\hfill & \mathrm{Phase}\mathrm{B}\hfill \\ {180}^{\circ },{300}^{\circ }\hfill & \mathrm{Phase}\mathrm{C}\hfill \end{array}\right.\end{array}\end{array}$$

(32)

The visualization of three-phase current signals can be achieved by using the above method, which can intuitively reflect the frequency and amplitude changes of the signals.

When creating PCCDP images, to minimize the overlap of the three-phase current signals, appropriate upper and lower bound parameters can be set. $\zeta$ is used as the angular amplification coefficient, and the upper boundaries should not exceed 30°. Beyond this range, part of the signal will overlap, considering the drawing process will produce errors, the range can be set at [5, 28], $\tau$ is generally set to [1, 10] [8].

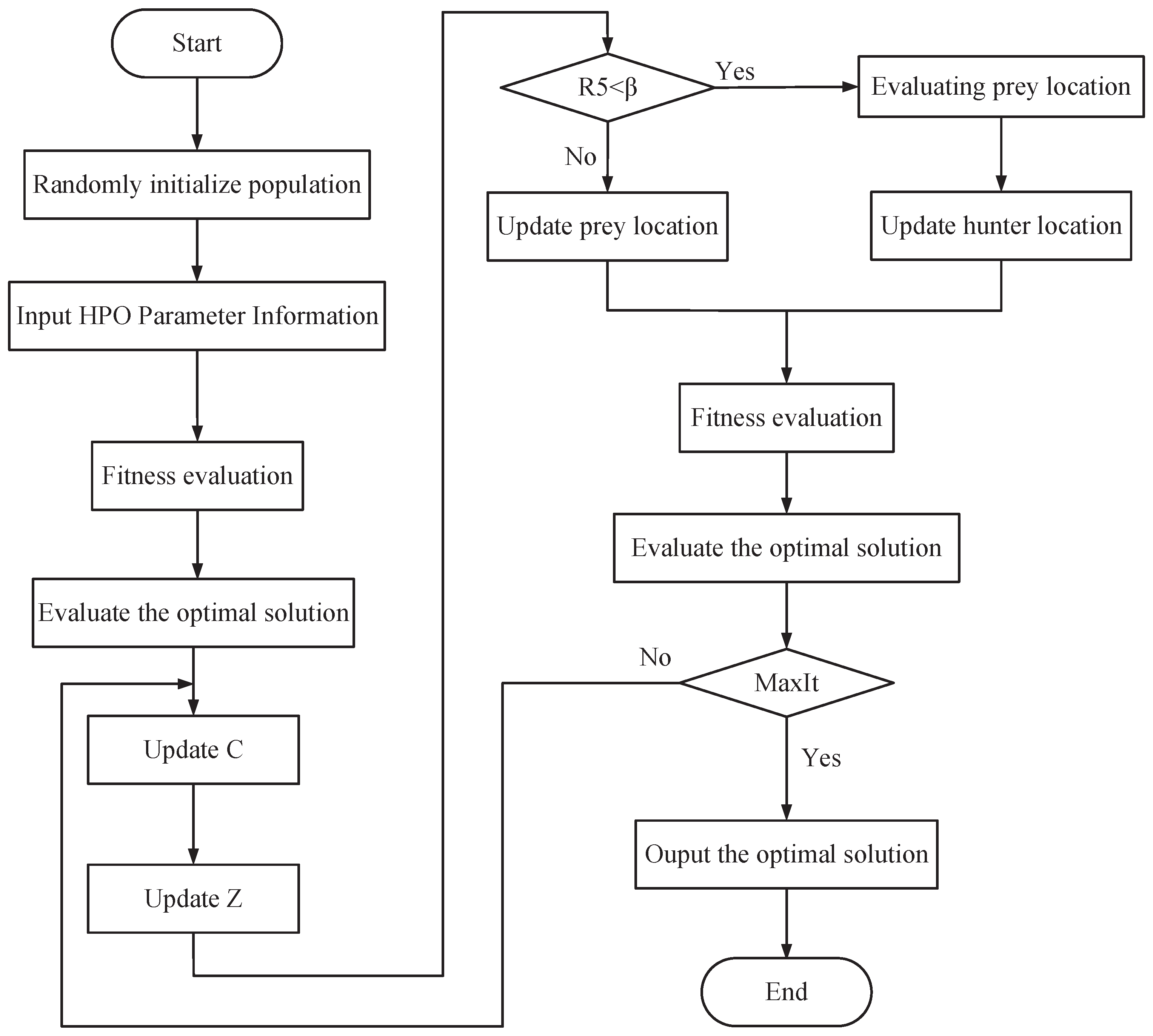
3.3.2. HPO

Drawing inspiration from the interactions between predators and their prey, the HPO algorithm is used to optimize two parameters [22]. In this algorithm, the prey represents solutions within the problem space, while the predators act as search agents. To ensure its safety, the prey continually seeks the global optimum to evade predators. Predators target prey that strays from the group and strive to find the optimal solution through continuous iterations and strategy updates, as shown in Figure 7. The specific optimization process of the HPO algorithm involves the following three parts:

(1)

Initialization of population positions. The random positions of the initialized populations are distributed as shown below:

$$\begin{array}{c}\hfill \begin{array}{c}\hfill x_i=rand(1,d)·(ub-lb)+lb\end{array}\end{array}$$

(33)

where $x_i$ denotes the initial position of the hunter or prey, d denotes the dimension, $ub$ denotes the upper limit of the solution space vector, and $lb$ denotes the lower limit of the solution space.

(2)

Hunter position update. Utilizing the distance to the prey’s position from the mean position, the hunter can dynamically modify their own location. The mechanism for the hunter’s search strategy is detailed as follows:

$$x_{i,j}(t+1)=x_{i,j}\left(t\right)+0.5\left[\left(2CZ{P}_{pos\left(j\right)}-x_{i,j}\left(t\right)\right)+\right.\left.\left(2(1-C)Z{\mu }_{\left(j\right)}-x_{i,j}\left(t\right)\right)\right]$$

(34)

where $x\left(t\right)$ is the current position of the hunter, $x(t+1)$ is the position of the hunter in the next iteration, and $P_{pos}$ is the position of the prey; $\mu$ is the average of the positions of all populations; and Z is the fitness parameter computed from Equation (35):

$$\begin{array}{c}\hfill \begin{array}{c}\hfill \begin{array}{c}\hfill P={\overrightarrow{R}}_1<C;IDX=(P==0);\\ \hfill Z=R_2\otimes IDX+{\overrightarrow{R}}_3\otimes (\sim IDX)\end{array}\end{array}\end{array}$$

(35)

where ${\overrightarrow{R}}_1$ and ${\overrightarrow{R}}_3$ are random vectors between $[0,1]$ and $R_2$ is a random value of $[0,1]$. $IDX$ is the index at which ${\overrightarrow{R}}_1$ satisfies condition $P==0$. C is the balance parameter between exploration and exploitation, and its value decreases from 1 to 0.02 during the iteration process. The formula is as follows:

$$\begin{array}{c}\hfill \begin{array}{c}\hfill C=1-it\left({\displaystyle \frac{0.98}{MaxIt}}\right)\end{array}\end{array}$$

(36)

where $it$ is the current iteration value and $Maxlt$ denotes the maximum number of iterations. The prey’s position is determined based on the individual’s distance from the mean position within the population, with the individual farthest from the mean being designated as the prey. Firstly, the mean value of each all positions should be calculated as:

$$\begin{array}{c}\hfill \begin{array}{c}\hfill \mu ={\displaystyle \frac{1}{n}}\sum _{i=1}^n{\overrightarrow{x}}_i\end{array}\end{array}$$

(37)

Next, the distance from the prey to that average position is calculated as:

$$\begin{array}{c}\hfill \begin{array}{c}\hfill D_{euc\left(i\right)}={\left(\sum _{j=1}^d{\left(x_{i,j}-{\mu }_j\right)}^2\right)}^{{\displaystyle \frac{1}{2}}}\end{array}\end{array}$$

(38)

Finally, the one with the largest distance is captured as the prey with the formula:

$$\begin{array}{c}\hfill \begin{array}{c}\hfill {\overrightarrow{P}}_{pos}={\overrightarrow{x}}_i\mid iisindexofMax\left(end\right)sort\left(D_{euc}\right)\end{array}\end{array}$$

(39)

When a hunter captures a prey, the prey dies and next time, the hunter moves to a new prey. To address the issue, we implement a diminishing mechanism, namely:

$$\begin{array}{c}\hfill \begin{array}{c}\hfill kbest=round(C\times N)\end{array}\end{array}$$

(40)

where N is the number of hunters. Substituting Equation (40) into Equation (39) yields the recalculated hunter position as:

$$\begin{array}{c}\hfill \begin{array}{c}\hfill {\overrightarrow{P}}_{pos}={\overrightarrow{x}}_i\mid iissorted{D}_{euc}\left(kbest\right)\end{array}\end{array}$$

(41)

(3)

Prey position update. When the prey is discovered by the hunter and started to be caught, the prey will move to the safe position, which is called the global optimal position. its position update formula is as follows:

$$\begin{array}{c}\hfill \begin{array}{c}\hfill x_{i,j}(t+1)=T_{pos\left(j\right)}+CZcos\left(2\pi R_4\right)\times (T_{pos\left(j\right)}-x_{i,j}\left(t\right))\end{array}\end{array}$$

(42)

where $x_i$, j, and $t+1$ denote the current and next prey positions, respectively, $T_{pos\left(j\right)}$ is the currently obtained best position, and $R_4$ is a random value in between $[-1,1]$.

3.3.3. Image Degree of Difference Function

In this study, we utilize a fusion of Euclidean distance and cosine similarity as the degree of difference function, which fully considers the distance and angle differences between the data. The detailed process is as follows:

First, assume that the pixel matrix of a grayscale image can be represented as:

$$\begin{array}{c}\hfill \begin{array}{c}\hfill G=\left[\begin{array}{cccc}G(1,1)& G(1,2)& \cdots & G(1,n)\\ G(2,1)& G(2,2)& \cdots & G(2,n)\\ ⋮& ⋮& \ddots & ⋮\\ G(m,1)& G(m,2)& \cdots & G(m,n)\end{array}\right]\end{array}\end{array}$$

(43)

where m denotes the number of rows and n denotes the number of columns of the pixel matrix. For a certain fault state information, it can be represented by the average value $\overline{G}$ of the pixel matrix of all sample information contained in that state.

Secondly, a fusion of Euclidean distance [23] and cosine similarity [24] is used as the degree of difference function. The representation difference between state k and state u can be defined based on the cosine similarity as:

$$\begin{array}{c}\hfill \begin{array}{c}\hfill CS={\displaystyle \frac{{\sum }_{i=1}^m{\sum }_{j=1}^n({\overline{G}}_k(i,j)·{\overline{G}}_u(i,j))}{\sqrt{{\sum }_{i=1}^m{\sum }_{j=1}^n{\overline{G}}_k{\left(i,j\right)}^2}·\sqrt{{\sum }_{i=1}^m{\sum }_{j=1}^n{\overline{G}}_u{\left(i,j\right)}^2}}}\end{array}\end{array}$$

(44)

where $CS$ is the cosine similarity between the data, with smaller values indicating less similarity.

The difference in representation between state k and state u can be defined based on the Euclidean distance as:

$$\begin{array}{c}\hfill \begin{array}{c}\hfill ED={\displaystyle \frac{{\sum }_{i=1}^m{\sum }_{j=1}^n\sqrt{{({\overline{G}}_k(i,j)-{\overline{G}}_u(i,j))}^2}}{255·m·n}}\end{array}\end{array}$$

(45)

where $ED$ is the Euclidean distance between the data, with larger values indicating less similarity.

From the above analysis and fully considering the distance and angle differences between the data. From this, the degree of difference function between state k and state u is obtained as:

$$\begin{array}{c}\hfill \begin{array}{c}\hfill Dif{f}_{k,u}=-\lambda E{D}_{k,u}-(1-\lambda )(1-C{S}_{k,u})\end{array}\end{array}$$

(46)

where $\lambda$ is the moderating factor, the smaller $Diff$ is, the smaller the similarity is. Then the degree of difference function of the N-class PCCDP image is:

$$\begin{array}{c}\hfill \begin{array}{c}\hfill Diff\left(N\right)=\sum _{k=1}^N\sum _{u=1}^{N}Dif{f}_{k,u}\end{array}\end{array}$$

(47)

3.4. Based on IResNet Diagnostic Models

In this section, we introduce an IResNet as a model for fault diagnosis in PMSM. This model enhances the pre-activated residual module and integrates the SE channel attention module, thereby improving the performance and generalization capabilities of the diagnostic model.

3.4.1. Basic Components

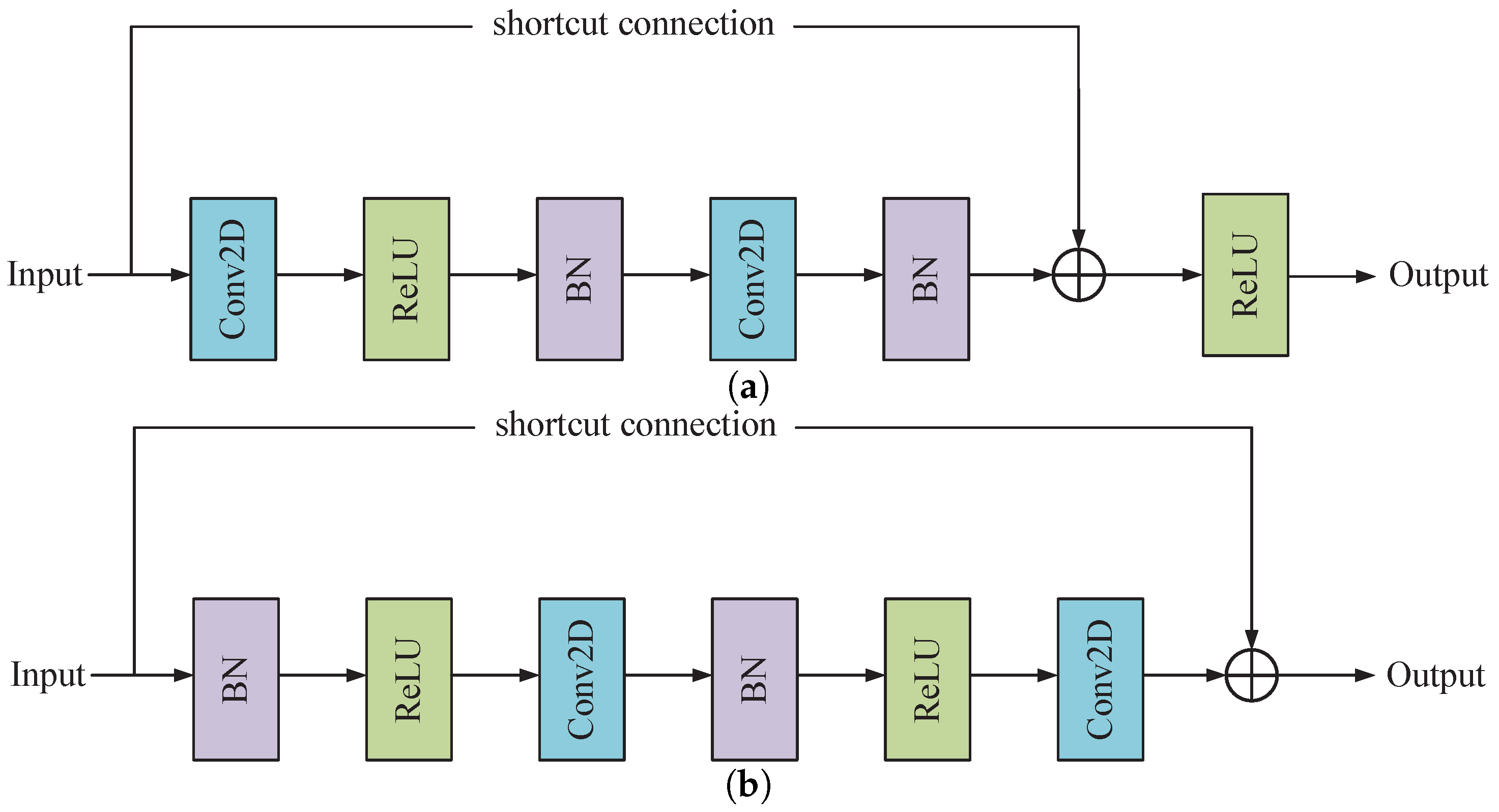
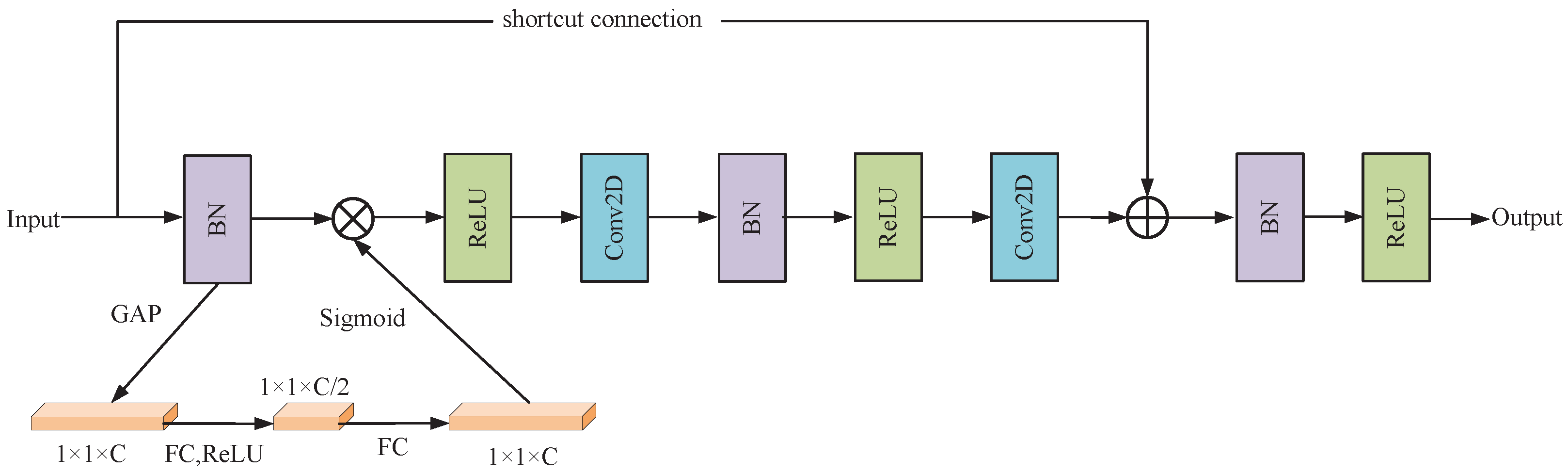
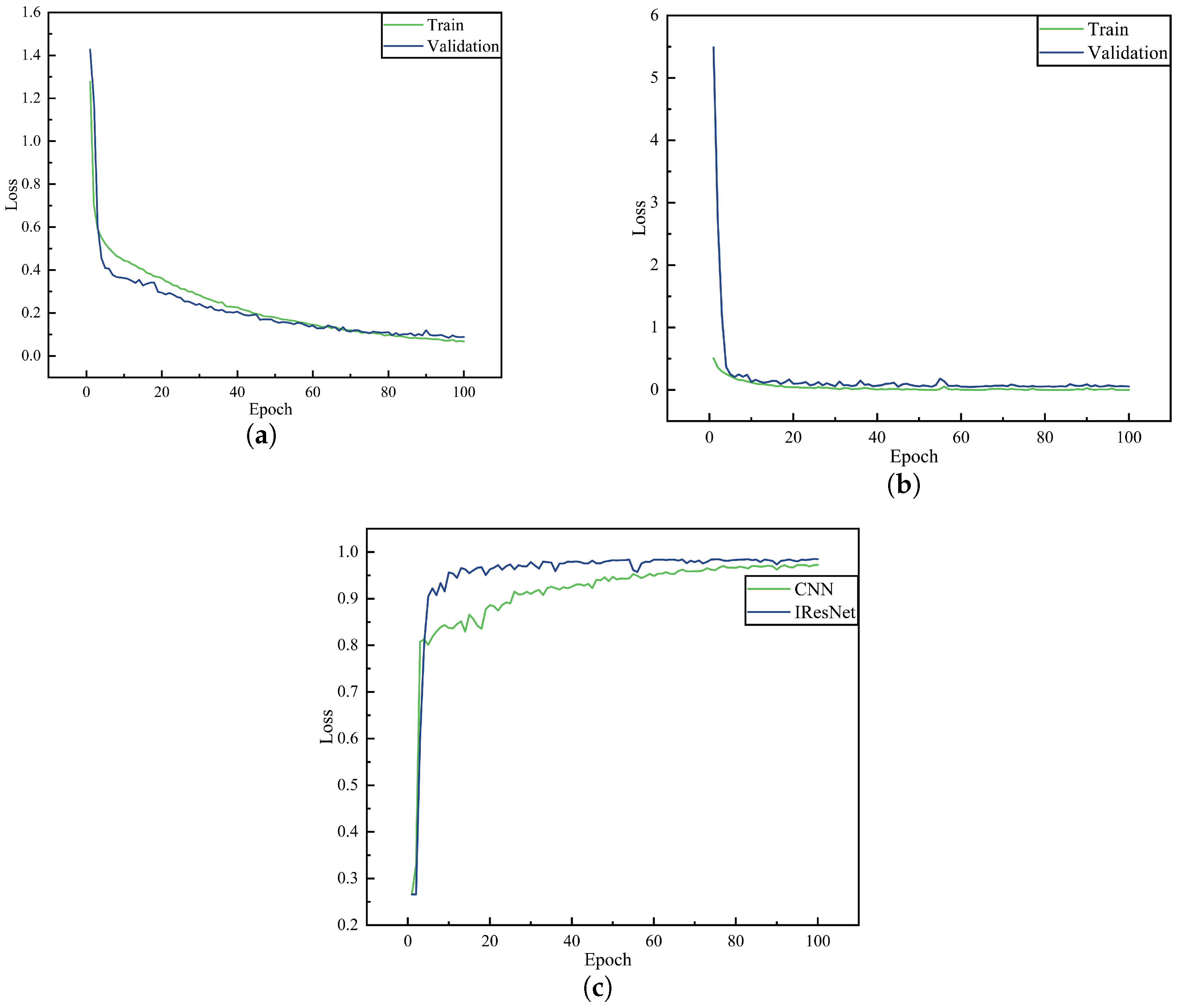
The fault diagnosis model will use the pre-activated residual unit as the basic building block, and the common residual module structure is shown in Figure 8. Figure 8a represents the original residual module and Figure 8b represents the pre-activated residual module. As depicted in the figure, each residual module comprises two Batch Normalization (BN) layers, two Rectified Linear Unit (ReLU) activation functions, two convolutional layers, and a shortcut connection. In the original network structure of the basic residual block, the signals are not normalized before entering the branches, and the distribution of each layer gradually shifts or changes as the network is superimposed, which causes difficulties in network learning. However, the pre-activated ResNet highlights more advantages, structurally simplifying the ResNet structure compared to the original basic residual block. Moreover, the pre-activation unit improves the model is regularization, which makes the model easy to optimize by stabilizing the distribution of input values.

3.4.2. SE Networks

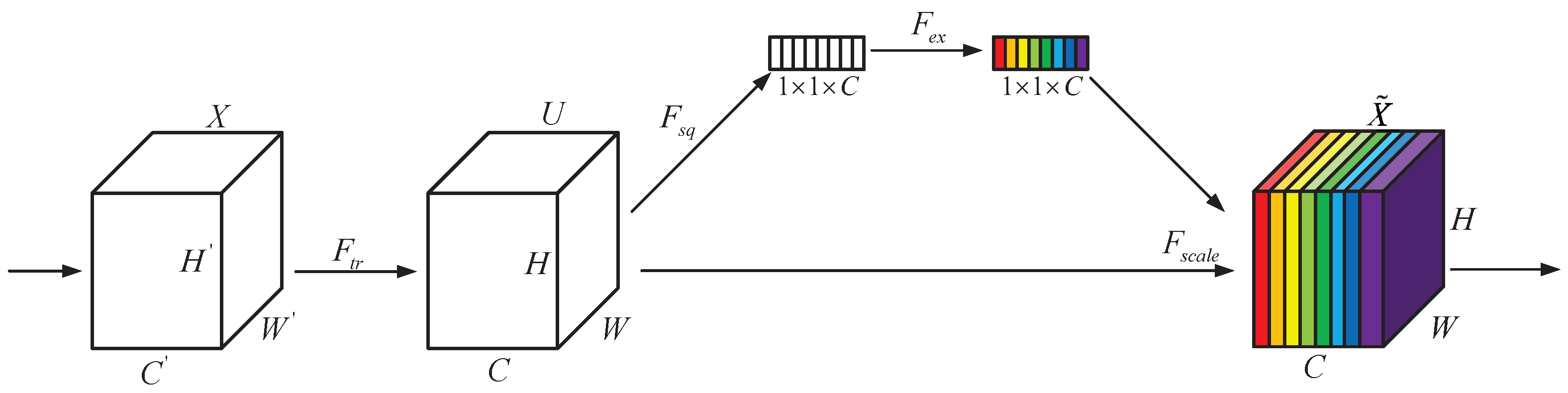
Singular residual connections fail to learn channel importance, diminishing attention to crucial features and degrading feature extraction performance. The SE channel attention mechanism adaptively learns the significance of each channel, enabling the network to concentrate more on pivotal features. The core idea is to compress and excite input features; specifically, it includes two primary steps: squeezing and excitation, as illustrated in Figure 9. In the process of feature compression, the input feature map undergoes reduction through global average pooling to form a vector, which is subsequently downsized into a more compact vector by a dense layer. In the subsequent excitation phase, a sigmoid function is applied to scale each component of the vector between 0 and 1. The scaling vector is utilized to weight and modulate the original input feature map, thereby creating a feature map that emphasizes the most significant features.

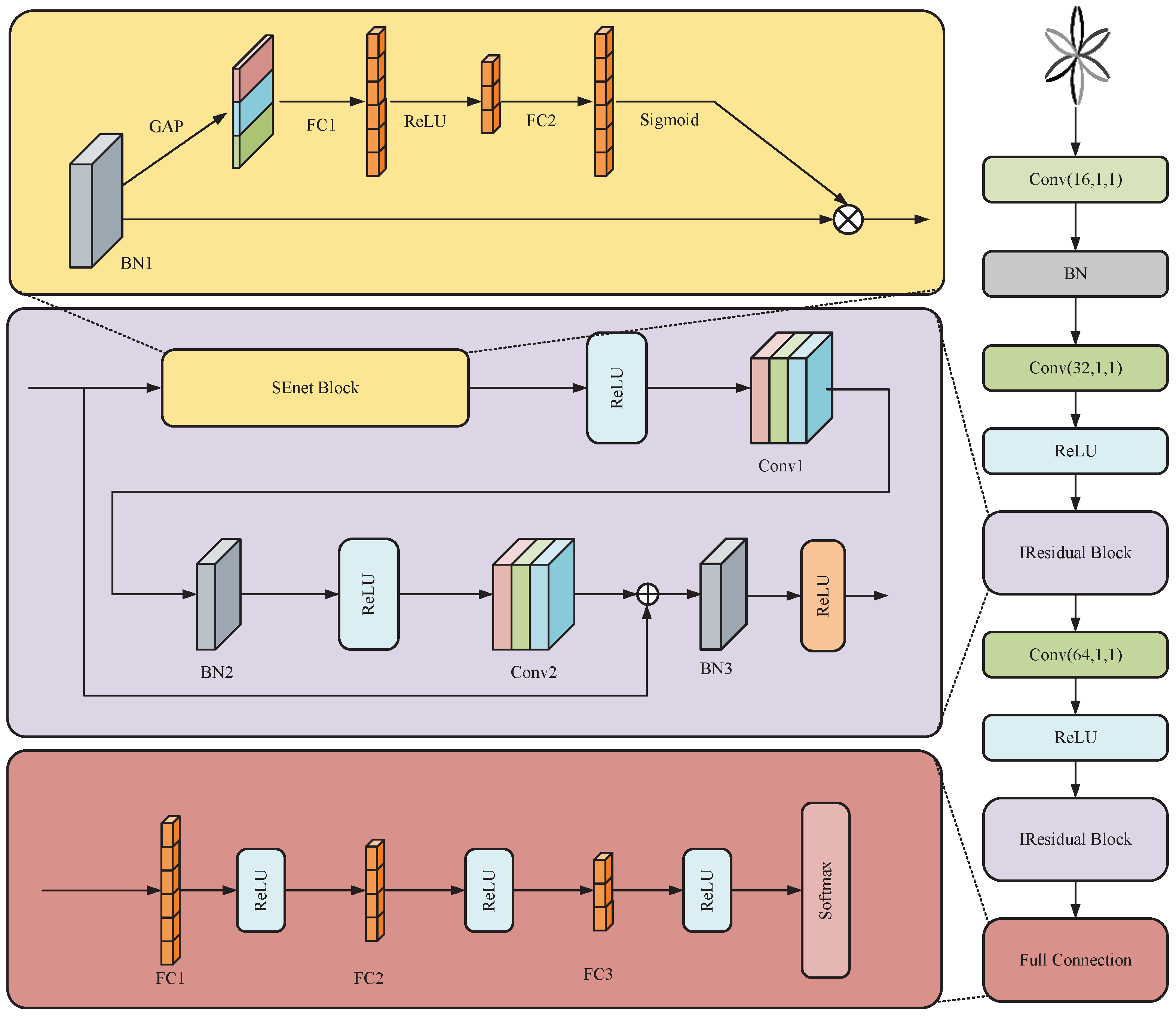
3.4.3. IResNet Architecture Design

The architectural design of the ResNet model developed in this research is depicted in Figure 10. This model structure has two main differences compared with the original pre-activated residual block: first, the original pre-activated block information propagation is also not applied regularization on the path of the most direct unit constant mapping, which is prone to over-fitting phenomenon. In this regard, a BN layer needs to be added after the addition operation to regularize the signal output. Then activation is performed through the ReLU layer to avoid over-fitting phenomenon and improve the feature learning ability of the model. Secondly, to enhance the ability of the network to recognize important fault features, the SE module is integrated into the residual unit, and this integration suppresses less relevant fault features, thus improving the sensitivity and robustness of fault diagnosis.

In the Figure 10, Conv is mainly responsible for the convolution operation [25], equation:

$$\begin{array}{c}\hfill \begin{array}{c}\hfill X_i^k=\sum X^{k-1}\ast w_i^k+b_i^k\end{array}\end{array}$$

(48)

where * denotes the convolution operation, k denotes the index of the layer, i denotes the index of the convolution kernel, and $b_i^k$ and $w_i^k$ denote the bias and weight of the first layer, respectively.

$BN$ denotes batch normalization, which makes the input values become standard normal distribution [26]. It can effectively avoid the disappearance of low-level gradients during back-propagation and prevent over-fitting. The calculation process is as follows:

$$\begin{array}{c}\hfill \begin{array}{c}\hfill {\mu }_B={\displaystyle \frac{1}{m}}\sum _{i=1}^m{x}_i\end{array}\end{array}$$

(49)

$$\begin{array}{c}\hfill \begin{array}{c}\hfill {\sigma }_B^2={\displaystyle \frac{1}{m}}\sum _{i=1}^m{\left(x_i-{\mu }_B\right)}^2\end{array}\end{array}$$

(50)

$$\begin{array}{c}\hfill \begin{array}{c}\hfill {\widehat{x}}_i={\displaystyle \frac{x_i+{\mu }_B}{\sqrt{{\sigma }_B^2}+\epsilon }}\end{array}\end{array}$$

(51)

$$\begin{array}{c}\hfill \begin{array}{c}\hfill y_i=\gamma {\widehat{x}}_i+\beta \end{array}\end{array}$$

(52)

where m denotes the training batch size, $x_i$ denotes the input sample, ${\mu }_B$ denotes the sample mean, ${\sigma }_B^2$ denotes the sample standard deviation, and ${\widehat{x}}_i$ denotes the normalized sample. $\epsilon$ denotes very small constant, $\gamma$ and $\beta$ denote learnable parameters.

ReLU is a prevalent nonlinear activation function that efficiently mitigates the issue of vanishing gradients, making it a staple in deep learning applications. The ReLU activation function is mathematically defined as:

$$\begin{array}{c}\hfill \begin{array}{c}\hfill ReLU\left(x\right)=max(x,0)\end{array}\end{array}$$

(53)

GAP is a common pooling operation that computes the average of each feature map, providing a holistic representation of that feature. Utilizing the GAP technique can streamline the model’s architecture, decrease the parameter count, enhance the network’s generalization capabilities, and to a certain extent, curb the over-fitting phenomenon.

Within the SE channel attention mechanism, the input tensor undergoes global average pooling to condense the spatial dimensions of the feature map into a 1 × 1 × C tensor, with C representing the channel count. Subsequently, the channel dimension is reduced to C/2 by a dense layer. This intermediate representation is then subjected to a ReLU activation function to introduce nonlinearity. Following this, the channel dimension is expanded back to C channels via another dense layer. Ultimately, a sigmoid activation function is applied to produce attention weights ranging between 0 and 1. These weights are used to scale the elements of the original input tensor, yielding a feature representation that reflects the learned importance of each feature.

The overall structure is shown in Figure 11. The input to the network is a grayscale PCCDP image with dimensions of 64 × 64 × 1 pixels. The core structure of the network is composed of a preprocessing layer, an SE module, and a cascade of residual blocks that are stacked together.

4. Experiments and Results

In this section, firstly, the four fault state simulated current signals are verified to illustrate the reliability of the simulated signals. Secondly. PCCDP image datasets with two different parameters are used to verify the superiority of the optimization algorithm. Finally, the IResNet model is analyzed in comparison with other state-of-the-art methods to evaluate the fault diagnosis performance of the proposed method.

4.1. Experiment Setup

We use Simulink in Matlab to simulate the motor in two faulty and one normal state of the PMSM system, and the data from the simulation is used to validate the proposed method. The simulation process time of the signals for each state is set to 1.5 s. The signals for the first 0.5 s when in the startup process are not collected, and the signals after the collection are used to create the dataset. Since the output frequency of the motor fault simulation is 1000 KHz, it results in a substantial volume of redundant data within the collected samples, complicating the data processing task. Therefore, firstly, we need to downsample the acquired signal to get a 10 KHz signal. Second, the signal is then sliced and segmented to form samples with a fixed length of 1024, and 1000 samples are collected for each state, finally generating a dataset containing 4000 samples. Then, the HPO algorithm is used to optimize the dataset to obtain the parameter information of the optimal PCCDP image, and the optimization parameters are shown in

Table 2. HPO parameter settings.

Parameter	Value	Parameter	Value
Max_iter	40	upper bound	$[10,28]$
Population size	30	lower bound	$[1,5]$
Beta	0.1	$\lambda$	0.5

.

Then, Gaussian white noise with a standard deviation of 0.1 is integrated into each sample to simulate the ambient noise present in practical operating conditions, and all the current signals are converted into samples of 64 × 64 PCCDP grayscale images according to the optimally obtained parameter information, and the sample information is shown in

Table 3. Sample labeling information.

Category	Description	Label
0	inter-turn short-circuit fault	AR
1	Heavy demagnetization fault	HDE
2	Normal	HL
3	Light demagnetization fault	LDE

.

Ultimately, the 4000 image samples were partitioned in the ratio of 7:1:2 to get the samples of training set, validation set and test set. And the training set data were input to IResNet for training, and the parameters in the model were adjusted using the validation set, and the parameters of the network structure are shown in

Table 4. IResNet structure parameter settings.

Number of Components	Input Size	Operation	Output Size
1	64, 64, 1	Input	64, 64, 1
1	64, 64, 1	Conv (16, 1, 1, ‘same’)	64, 64, 16
1	64, 64, 16	BN	64, 64, 16
1	64, 64, 16	Conv (32, 1, 1, relu, ‘same’)	64, 64, 32
1	64, 64, 32	RBU (32, 5)	64, 64, 32
1	64, 64, 32	Conv (64, 1, 1, relu, ‘same’)	64, 64, 64
1	64, 64, 64	RBU (64, 5)	64, 64, 64
1	64, 64, 64	Flatten	262,144
1	262,144	FC1 (1024, relu)	1024
1	1024	FC2 (512, relu)	512
1	512	FC3 (256, relu)	256
1	256	SoftMax	4

. Once training was completed, the trained network parameters were applied to the test dataset to validate the model’s performance, thereby demonstrating the model’s effectiveness.

The entire experimental training process was executed on a computer with Intel(R) Core(TM) i7-9700 CPU and NVIDIA GeForce GTX 2060 SUPER GPU. The network architecture was coded within the TensorFlow framework, and the model’s parameters were optimized and tuned using the Adam optimization algorithm in conjunction with the cross-entropy loss function. The specific settings for the training parameters are outlined in

Table 5. Training parameter settings.

Parameter	Value	Parameter	Value
Batch size	16	Beta_1	0.9
Epoch	100	Beta_2	0.999
Learning rate	0.00001	Epsilon	$1\times {10}^{-8}$

.

To ascertain the efficacy of each component of the proposed method, a three-part experiment is designed for comparison, and the experiments are described as follows:

(1)

Verify the reliability of the simulated analog current signals: the current signals under each fault state will be analyzed to show the effect of the simulated analog experiment.

(2)

Verify the effect of parameter optimization: the dataset corresponding to the optimized parameters and the dataset corresponding to the parameters in the literature [11] are trained to compare the diagnostic accuracy corresponding to the two datasets.

(3)

Validating the fault diagnosis effect of the proposed residual network: the diagnostic model network proposed in this paper is compared with the CNN in the literature [27], and the diagnostic accuracies of the two methods, IResNet and CNN, are compared.

4.2. Experiment Results

4.2.1. Effectiveness of the Simulation Model

We simulated the state of normal operation of PMSM by Simulink in MATLAB. The simulation time is set to 0.8 s, and when the simulation runs to 0.2 s, the 15 $N\times m$ load is suddenly added to the simulated PMSM system, so as to verify the effect of the simulation model constructed in the paper by analyzing the changes of the three-phase stator currents, torque and other signals.

Figure 12 is the simulation diagram of the normal operation of the PMSM, Figure 12a represents the three-phase stator current signal under the normal state of the PMSM, and Figure 12b represents the torque signal under the normal state of the PMSM. From the figure, it can be seen that the starting current is large when the motor is started with no load in 0.1 s time, but since the torque is set to 0 at this time, the current is rapidly adjusted to about 0 again after being regulated by the double-closed-loop control system; when the 15 $N\times m$ load is added at 0.2 s, the torque becomes 15 $N\times m$, and at this time, the current increases instantaneously and rapidly tends to a sinusoidal curve.

We assume that the inter-turn short circuit fault occurs in phase B at 0.4 s. The simulation results are shown in Figure 13. Figure 13a shows the three-phase stator current signal under the PMSM inter-turn short circuit fault, and Figure 13b indicates the torque signal under the PMSM inter-turn short circuit fault. From Figure 13, it can be seen that under normal conditions, the three-phase currents of the PMSM are periodic waveforms, and after an inter-turn short circuit fault occurs after 0.4 s, the amplitude and other phases of the B phase current change, and the change of the B-phase current will be transmitted to the A phase and C phase, and thus, the A phase and C phase currents also change under the closed-loop control. Among them, the current amplitude of phase C will be significantly higher than that of phase B, and the amplitude of phase A is the smallest, which is consistent with the simulation results of literature [3]. In addition, when the inter-turn short circuit fault occurs, the torque of the motor is also significantly perturbed [15].

We set a light demagnetization fault to occur at 0.4 s. The simulation results are shown in Figure 14. Figure 14a represents the three phase stator current signal of the PMSM under light demagnetization fault, and Figure 14b represents the torque signal of the PMSM under light demagnetization fault. From Figure 14, it can be seen that after the light demagnetization fault occurs after 0.4 s, its three phase current changes are very obvious, and the amplitude of the three phase current becomes larger, and the torque fluctuates, but it quickly recovers to 15 $N\times m$. This is consistent with the simulation results in literature [28].

Finally, we change the parameter information and set the heavy demagnetization fault to occur at 0.4 s. The simulation results are shown in Figure 15. Figure 15a shows the three phase stator current signal of the PMSM under a severe demagnetization fault, and Figure 15b indicates the torque signal of the PMSM under a severe demagnetization fault. From Figure 15, it can be seen that when a severe demagnetization fault occurs, it will lead to an increase in the stator current and a significant decrease in the motor torque, which finally leads to the three-phase current also ceasing to change until the motor stops.

From the above study, it can be seen that the stator current signal simulated using Matlab successfully simulates a variety of fault types and meets the needs of fault diagnosis. The current waveform is consistent with the response during the actual fault, which verifies the reasonableness of the simulation data and provides a reliable basis for fault diagnosis.

4.2.2. Effectiveness of Based on HPO Optimization Algorithm

In this paper, the HPO algorithm is used to find the optimal information of the two parameters of the 64 × 64 PCCDP grayscale image, which is trained for a total of 10 times, and the average of the results is taken.To assess the impact of optimization on diagnostic accuracy, the optimized results are contrasted with the parameters referenced in literature [11], which are then used to generate corresponding PCCDP images. The PCCDP images generated by these two parameter structures corresponding to the four fault states are shown in Figure 16. Figure 16a–d corresponds to the PCCDP image under the optimization-seeking parameter $\tau =8$, $\zeta =28$, and Figure 16e–h corresponds to the PCCDP image under the parameter $\tau =2$, $\zeta =25$ in literature [11].

As can be seen from the figure, for PCCDP images with the same parameters, the samples with HDE fault state have the greatest variability in image shape with the other three fault types, the samples with AR fault state have significant differences in flap shapes and lengths in different phases, and the samples with LDE fault state have slight differences in curvature with the samples with HL state. These differences will be captured by the network model for effective differentiation. For the samples of PCCDP images with different parameters for the same fault state, the PCCDP image in Figure 16a–d is overall fuller and the petals are more centered compared to Figure 16e–h.

Figure 17 presents the outcomes of training on datasets derived from PCCDP images created under varying parameters. Figure 17a shows the confusion matrix trained on the dataset corresponding to the parameters $\tau =2$, $\zeta =25$ from literature [11], and Figure 17b shows the confusion matrix after training on the dataset corresponding to the parameters $\tau =8$, $\zeta =28$ from the optimization search results. From Figure 17, both HDE faults are both able to be diagnosed. For the AR fault state, the diagnosis of Figure 17a is better than that of Figure 17b, being able to accurately diagnose six more samples compared to Figure 17b. However, for the two fault states of HL and LDE, the diagnosis of Figure 17b is better than that of Figure 17a. The final fault identification accuracies for the two different parameters are 88.5% and 98.5%, respectively.

To visualize the classification performance between the two methods, we employ the t-SNE algorithm to project the output from the final layer of the diagnostic model onto a 2D scatter plot. The resulting experimental visualization is depicted in Figure 18. Figure 18a represents the t-SNE visualization of the test dataset prediction results corresponding to the parameters $\tau =2$, $\zeta =25$ in the literature [11], and Figure 18b is the t-SNE visualization of the test dataset prediction results corresponding to the parameters $\tau =8$, $\zeta =28$ of the optimization search results. In Figure 18, the fault states of four different motors are shown in different colors. The results show that both models have a lot of feature overlap in one region, compared to Figure 18b where the overlap region is much less, implying better clustering of the extracted features. Figure 18a has a large overlapping area and the features are difficult to extract accurately. The selection of the two parameters of the PCCDP image will have a great impact on the troubleshooting results.

4.2.3. Effectiveness of the IResNet-Based Fault Diagnosis Model

In order to verify the superiority of the method proposed in this paper, we compare and analyze the IResNet model with the common CNN model [27].

Table 6. CNN structure parameter settings.

Number of Components	Input Size	Operation	Output Size
1	64, 64, 1	Input	64, 64, 1
1	64, 64, 1	Conv (32, 5, 1, relu, ‘same’)	64, 64, 32
1	64, 64, 32	BN	64, 64, 32
1	64, 64, 32	MP (2, 2, ‘same’)	32, 32, 32
1	32, 32, 32	Conv (64, 5, 1, relu, ‘same’)	32, 32, 64
1	32, 32, 64	BN	32, 32, 64
1	32, 32, 64	MP (2, 2, ‘same’)	16, 16, 64
1	16, 16, 64	Flatten	16,384
1	16,348	FC1 (1024, relu)	1024
1	1024	dropout (0.5)	1024
1	1024	FC3 (256, relu)	256
1	256	dropout (0.5)	256
1	256	SoftMax	4

represents the structural parameters of the CNN model. in terms of network structure, the CNN model performs feature extraction through the traditional structure of convolutional, batch normalization and pooling layers, but this method is relatively simple and fails to take full advantage of the importance differences between channels. the IResNet model significantly enhances the depth of feature extraction and focuses on the importance of the channels through the introduction of an improved RBU module. The model preprocesses before inputting the RBU module and adds additional layers after the fully connected layer to further integrate the features. In addition, the risk of overfitting is effectively controlled due to the extensive use of the BN module in the feature extraction layer, which reduces the dependence on the dropout layer without sacrificing the generalization capability of the model.

Table 7. Network training parameters.

Method	Accuracy (%)	Trainable Parameter	Train Time (s)
CNN	96.5	170, 939, 56	171.12378
IResNet	98.5	269, 194, 548	11,413.1854

shows the parameters related to the training process of CNN models and IResNet models, from which it can be seen that IResNet outperforms CNN in terms of accuracy, but due to the large number of improvements made to the feature extraction layer, IResNet corresponds to a larger number of training parameters and a significant increase in training time as compared to the CNN model network. the CNN model is more efficient in terms of training time and the number of parameters, but has a slightly lower accuracy rate.

The curves of the experimental training results are shown in Figure 19. Figure 19a represents the loss curves of CNN on the training and validation sets, Figure 19b represents the loss curves of IResNet on the training and validation sets, and Figure 19c represents the accuracy curves of CNN and IResNet models on the test set. From the figure, it can be seen that both the training loss and the validation loss of the conventional CNN model decrease with training and remain relatively close during most of the training. In contrast, both the training loss and validation loss of the IResNet model decline rapidly as training progresses and level off after about the 10th epoch. Both curves fluctuate very little during and after the descent and are close to each other without significant separation. Since the training loss and validation loss curves of these two models are very close to each other, this indicates that the models perform similarly on the training and validation sets, and there is no overfitting phenomenon during the training process, and the trained models can be used for subsequent diagnostic studies. From Figure 19c, it can be seen that the training accuracy of IResNet is significantly higher than that of CNN, and it has begun to converge after the 20th iteration, which is much faster, and stabilizes after the 50th iteration, while the CNN model has not converged after 100 iterations.

Subsequently, we plotted the subject operating characteristic (ROC) curves and calculated the area under the curve (AUC) for four different faults to demonstrate the performance of each fault. Figure 20 shows the corresponding ROC curves and AUC for the two models, Figure 20a represents the ROC curves and AUC for the CNN model, and Figure 20b represents the ROC curves and AUC for the IResNet model.As can be seen from the figure, for the HDE fault state, the corresponding ROC curves and AUC for the two models are all 1. However, for the other three fault states, the IResNet models have better ROC curves and AUC than the CNN model.

Figure 21 presents the confusion matrix for the fault classification models when applied to the test dataset. Specifically, Figure 21a depicts the confusion matrix for the CNN model, while Figure 21b represents that of the IResNet model. Figure 22 shows the t-SNE visualization of the prediction results of the fault classification model on the test dataset. Figure 22a corresponds to the CNN model’s t-SNE visualization, and Figure 22b corresponds to that of the IResNet model. For HDE faults, both the CNN and IResNet models exhibit accurate diagnostic capabilities.For AR fault states, the IResNet model has the same diagnosis results compared to the conventional CNN model. For HL states, the IResNet model diagnoses one more number of errors compared to the traditional CNN model. However, for LDE fault states, the IResNet model shows fewer diagnostic errors than the CNN model. And combined with Figure 22, it indicates that the features extracted by the IResNet model are more effectively discriminated than those by the CNN model. Ultimately, the average accuracy of fault recognition of the two methods is 96.5% and 98.5%, respectively.

After comparing the two fault diagnosis models, we found that compared to the traditional CNN-based model, although the IResNet model network requires higher number of parameters and computational resources, and takes longer training time, the model performs well in feature extraction, and has significant advantages in fault diagnosis accuracy and robustness, which can effectively classify common electrical faults of PMSMs. Therefore, despite requiring more computational investment, the IResNet model proves to be worth adopting due to its excellent performance in fault diagnosis.

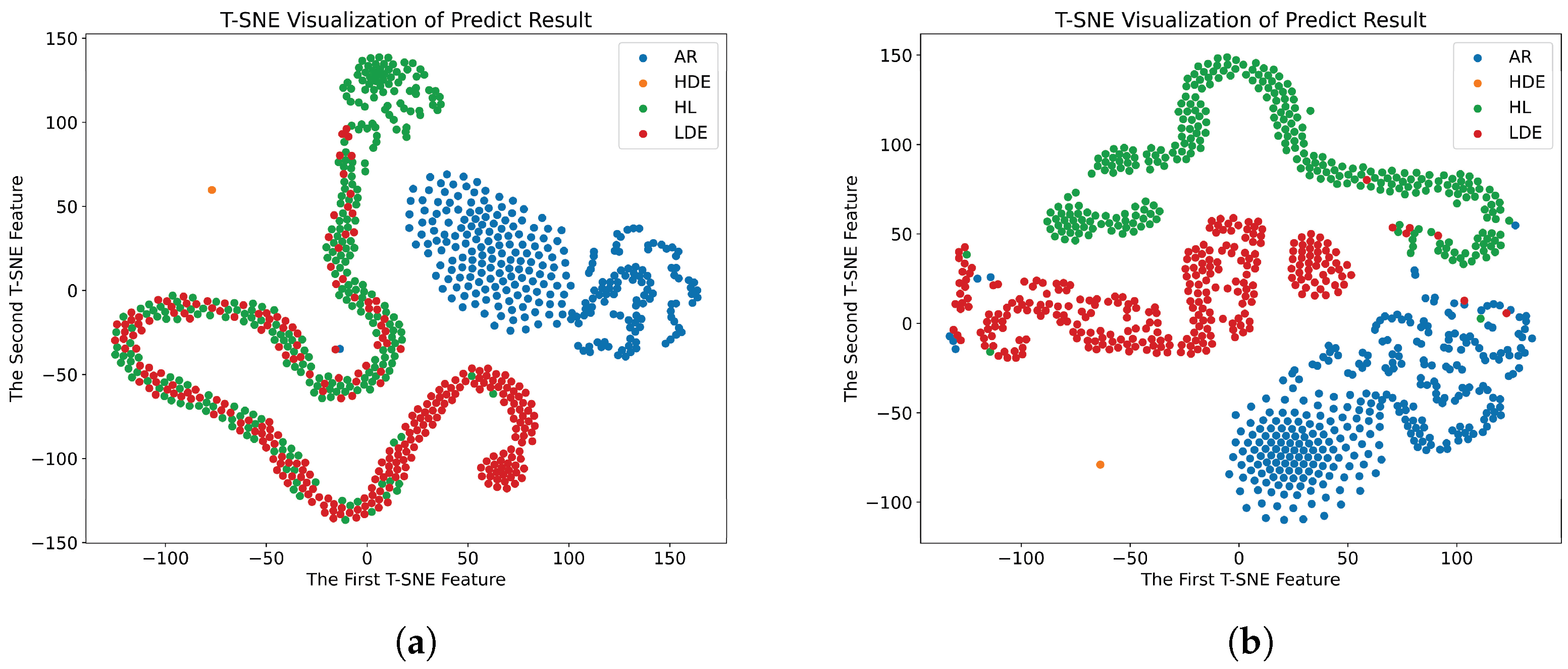
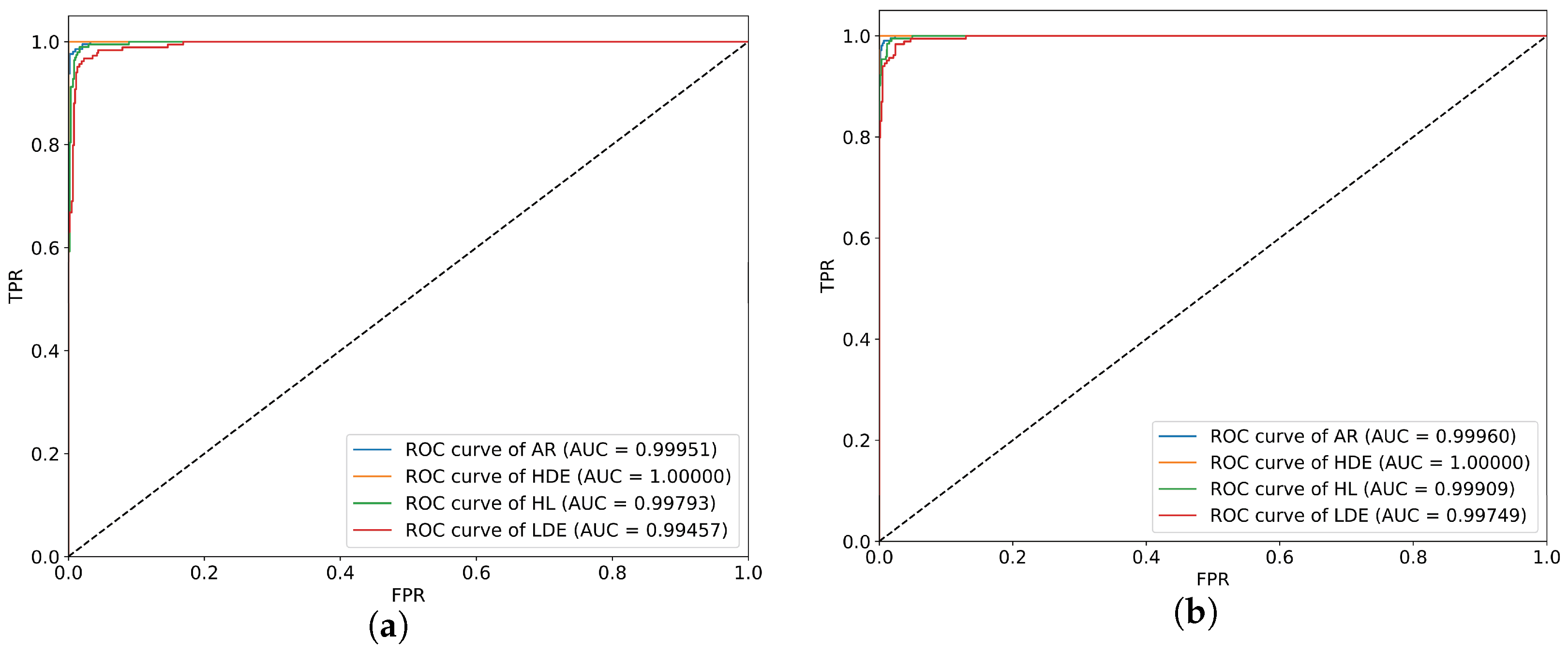
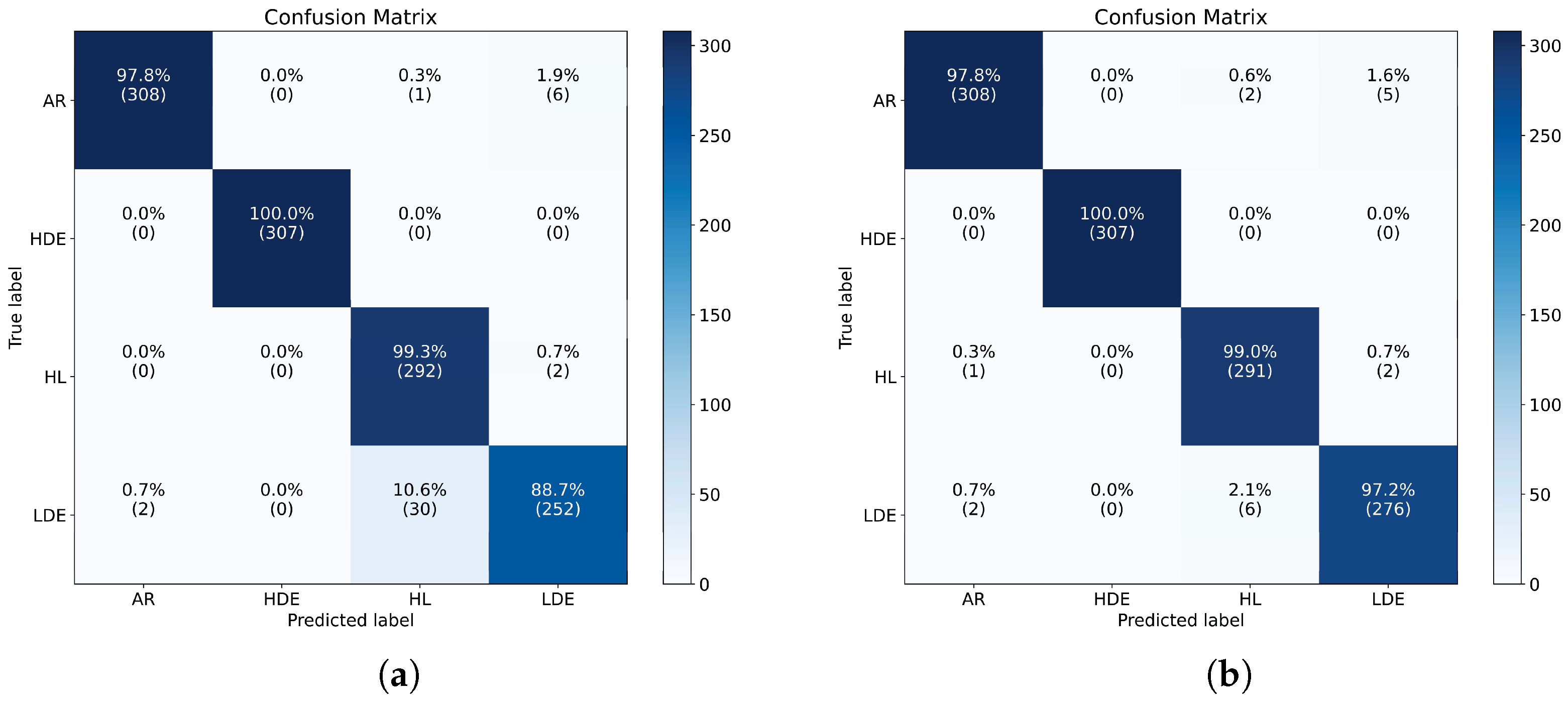
5. Conclusions and Future Works

In this study, a novel method for motor fault diagnosis is introduced. Initially, the fundamental principles behind inter-turn short circuit and demagnetization faults in PMSM are examined, and stator current data are gathered through a Simulink simulation. Subsequently, the HPO algorithm is deployed to optimize the PCCDP parameters, aiming to enhance the distinguish ability of different fault states. Ultimately, an advanced diagnostic model based on a residual network is proposed, enhancing the diagnostic accuracy and enabling the identification of four distinct fault states in PMSM. The experimental outcomes demonstrate that this method not only offers superior diagnostic performance across various PMSM fault states but also boasts rapid convergence and effective fault detection capabilities. The conclusions drawn from this paper are as follows:

(1)

The HPO algorithm is used to determine the optimal parameters within the PCCDP technique. The maximization of the combined metrics of Euclidean distance and cosine similarity serves as the objective function, aiming to enhance the differentiation between varying degrees of faults.

(2)

The pre-activated ResNet module has been enhanced by incorporating the SE attention mechanism, which significantly boosts the model’s capacity to extract fault-related features.

(3)

For practical engineering applications, this paper introduces an innovative fault diagnosis method, steering towards more intelligent fault diagnostics.

The fault diagnosis method proposed in this paper only investigates two types of faults, inter-turn short circuit and demagnetization, in the PMSM stator winding, which can provide high diagnostic accuracy but still has some limitations, mainly in the fact that there are fewer types of faults, and further adjustment and optimization may be required to adapt to different types of faults or under different conditions. This may affect its generalizability to different propulsion systems. Secondly, the long experimental period for the whole diagnosis of our method may require a relatively long time for data processing and model training. In the future, we will conduct more extensive experimental studies on other fault types of PMSM to expand the dataset, and at the same time, we need to consider how to simplify the model in order to reduce the computational complexity while maintaining sufficient accuracy, and finally apply the fault diagnosis method in reality.