Numerical Analysis Comparison Between ANSYS AQWA and OrcaFlex for a Hollow Box-Shaped Floating Structure

Abstract

This study presents a numerical comparison between ANSYS AQWA (2023 R2) and the OrcaFlex package (OrcaWave + OrcaFlex) for a 10 × 10 × 2 m rectangular floating structure. The hydrodynamic coefficients and displacement/load RAOs obtained from the two solvers exhibit nearly identical behavior, with deviations below 1% across all six motion modes. Under irregular wave conditions (Hs = 7 m, Tp = 8 s, 0° heading) and three mooring line lengths (145, 150, and 155 m), both solvers produced comparable mean surge motions and mean mooring tensions. However, OrcaFlex predicted 40–50% higher peak tensions due to its fully dynamic representation of slack–taut transitions and snap loading effects, whereas AQWA’s quasi-static catenary formulation filtered out these short-duration peaks. These findings confirm that although the two solvers are highly consistent in frequency-domain hydrodynamics, their time-domain predictions diverge when nonlinear mooring behavior becomes dominant. The study provides a transparent and reproducible benchmarking framework for cross-validation of potential-flow-based tools used in floating offshore structure design.

1. Introduction

With the global efforts to reduce carbon emissions, CCS (carbon capture systems) and offshore renewable energy have gained attention as promising alternatives [1]. In particular, the installation and operation of offshore structures under actual field conditions have been steadily increasing [2,3]. As the application areas expand, such as the operation of large floating structures based on wet docks and the spread of floating wind farms, the ability to precisely predict dynamic responses under environmental loads combined with waves, wind, and ocean currents has become a key prerequisite for design optimization and safety assurance [4]. In floating structures, the hydrodynamic coefficients calculated in the frequency domain, namely added mass, radiation damping, and response amplitude operators (RAOs), determine the motion characteristics and are directly linked to mooring line design, fatigue life prediction, and ultimate limit state review. The reliability, consistency, and reproducibility of these coefficients determine both the economic feasibility and reliability of offshore structures [5,6]. To address these needs, various commercial tools are being utilized, and ANSYS AQWA and OrcaWave are widely used commercial software as representative solvers based on the boundary element method [7,8]. The validity of ANSYS AQWA for frequency-domain analysis has been confirmed in various experimental/numerical comparison studies [9,10]. Although OrcaWave is more recent, studies have benchmarked its results against reference codes such as WAMIT [7]. Moreover, its tight integration with OrcaFlex facilitates the direct use of computed hydrodynamic coefficients in time-domain simulations, streamlining reproducible workflows.

Even when applying identical geometries and conditions, the results of the various programs can differ. These differences stem from a variety of factors, including mesh density, water depth, boundary conditions representing the free surface and seabed, unit wave definitions and normalization rules based on half-amplitude, coordinate systems and sign conventions, fine-grained modeling such as frequency sampling and numerical attenuation, and inconsistencies in postprocessing choices [11]. These deviations can propagate into the time domain and significantly affect the peak magnitude and frequency content of mooring tension, the distribution of low-frequency drift components, and the behavior of slack and snap loading [12]. Therefore, a reproducible comparison procedure is needed that presupposes unification of wave definitions, normalization, coordinates, signs, and degrees of freedom notation.

However, despite the widespread use of ANSYS AQWA and OrcaWave/OrcaFlex, no study has performed a fully standardized and reproducible comparison between the two solvers under identical hydrodynamic and mooring conditions. This gap is critical because even small solver-dependent differences can influence design conservatism, reliability of fatigue assessments, and cost-sensitive decisions such as mooring sizing or anchor count. Therefore, the objective of this study is to provide the first comprehensive and reproducible comparison of hydrodynamic coefficients, RAOs, and time-domain mooring responses between AQWA and OrcaFlex. Establishing such consistency is practically important for ensuring transparent modeling workflows and reducing uncertainty in offshore engineering design.

Recently, as integrated designs at the array level, including shared moorings and power cables, have become more common beyond single platforms, subtle differences in frequency-domain coefficients can cumulatively affect the global response, narrowing mooring and power cable design margins and potentially amplifying cost, reliability, and schedule risks [13,14]. Furthermore, the demand for data model reproducibility and transparent comparison procedures is growing across both practice and academia, and the need for systematic cross-verification of results across analysis software has become clear.

For example, a study comparing WAMIT, NEMOH, and HAMS (2022) found that the excitation force, hydrodynamic coefficients, and RAO were generally consistent, while noting that irregular-frequency treatment and panel splitting choices could introduce differences [15]. Another study reported that CFD aided linearization and improved predictions of angular motions and structural loads for a floater with damping plates, highlighting damping modeling as a key sensitivity [5]. In addition, catenary and semi-taut moorings were optimized in the frequency domain to quantify sensitivities of low-frequency surge and line tension [6]. The effects of submersible buoy (SB) geometry and modeling fidelity on mooring dynamics and tension ranges were also analyzed, confirming that consistent drag and added-mass parameterization is a prerequisite for comparative studies [16]. Finally, cross-validation of scaled semi-submersible FOWT model tests against numerical analyses systematically organized how radiation and diffraction modeling choices propagate to global loads and fatigue responses [17].

In addition to these studies, several works have investigated the hydrodynamic responses of floating docks and pontoon-type structures with various geometries such as semicircular, circular, and rectangular forms using potential-flow-based numerical methods. For example, the attenuation of wave forces on a floating dock surrounded by multiple porous breakwaters has been analyzed [18], while wave attenuation on a floating rigid dock equipped with multiple perforated barriers has also been examined [19]. These studies mainly focused on the wave structure interaction mechanisms and damping effects for specific structural configurations. However, direct quantitative comparisons between commercial hydrodynamic solvers under identical modeling and boundary conditions have not yet been reported. The present study fills this gap by performing a comprehensive numerical comparison between ANSYS AQWA and OrcaWave/OrcaFlex for a rectangular box-type floating body, thereby providing new insight into the consistency and reliability of potential-flow-based solvers widely used in offshore engineering. This comparison is practically significant because even small discrepancies in hydrodynamic predictions can influence design conservatism, fatigue safety margins, and workflow efficiency in offshore engineering.

As far as the authors know, there are no reported direct numerical analysis comparison results between ANSYS AQWA and the OrcaFlex package (OrcaWave and OrcaFlex). Thus, to compare numerical results, this study adopts a 10 × 10 × 2 m hollow rectangular floating body as a common target structure. The hydrodynamic coefficients calculated by ANSYS AQWA and the OrcaFlex package are quantitatively compared using identical and transparent settings, and the impact of these differences on time-domain mooring response is also assessed. Specifically, wave definitions and normalization, coordinate, and sign conventions are unified, and geometry, material properties, water depth and mesh, boundary conditions, and numerical parameters are standardized. Next, the magnitude and phase of added mass, radiation damping, displacement/load RAOs, and as peak frequency differences are indexed. Time-domain analysis is performed using identical irregular wave input conditions to analyze changes in tension peaks, tension range distribution, and low-frequency components. Through this process, the causes of discrepancies between commercial boundary element tools are decomposed in terms of definition, normalization, and numerical settings. The study concludes by presenting a reproducible comparative-verification procedure and setup guidelines for floating structure design. The study assumes the linear potential flow and focuses on first-order wave forces. Aerodynamic effects and second-order wave forces are outside the present scope. These effects were excluded to isolate the differences arising solely from first-order hydrodynamics and mooring line modeling between the two solvers. Including aerodynamic loading or second-order wave forces would introduce additional nonlinear components such as mean drift forces and slow drift motions, whose implementation differs between AQWA and OrcaFlex. Although these effects could increase low-frequency surge motion and mean mooring tension, they would influence both solvers in a similar physical manner and therefore would not change the comparative conclusions drawn in this study.

2. Numerical Analysis Method

Generally, the coordinate system is $\left[\mathrm{x},\mathrm{y},\mathrm{z}\right]= \left[\mathrm{S}\mathrm{u}\mathrm{r}\mathrm{g}\mathrm{e},\mathrm{S}\mathrm{w}\mathrm{a}\mathrm{y},\mathrm{H}\mathrm{e}\mathrm{a}\mathrm{v}\mathrm{e}\right]$, and the rotation is $\left[\mathsf{\varphi },\mathsf{\theta },\mathsf{\psi }\right]=\left[\mathrm{R}\mathrm{o}\mathrm{l}\mathrm{l},\mathrm{P}\mathrm{i}\mathrm{t}\mathrm{c}\mathrm{h},\mathrm{Y}\mathrm{a}\mathrm{w}\right]$, and it follows the right-hand rule, with $+\mathrm{z}$ pointing upward. The wave normalization is unified based on the half-amplitude $\mathsf{\alpha }(=\mathrm{H}/2)$, and the phase reference is COG (Center of Gravity). In addition, to avoid symbol conflict, the wave angular frequency is expressed as $\mathsf{\Omega }$, and the line weight (unit length diving weight) is expressed as $\omega$. The hydrodynamic analysis in this study is based on the three-dimensional linear potential-flow theory, assuming an inviscid, incompressible, and irrotational fluid. The velocity field is therefore represented by a scalar potential satisfying the Laplace equation. The linearized free surface boundary conditions are applied under the assumption of small wave amplitude and linear body motion response. These assumptions are appropriate for the present study because the motions of the box-shaped floating body remain small relative to its characteristic length, and viscous or nonlinear effects are negligible within the investigated frequency range.

2.1. Hydrodynamic Coefficients Equation

Both programs calculate the added mass $A\left(\mathsf{\Omega }\right)$, radiation damping $B\left(\mathsf{\Omega }\right)$, and wave excitation ${\mathrm{F}}_{\mathrm{e}\mathrm{x}\mathrm{c}}\left(\mathsf{\Omega }\right)$ based on linear potential theory. The frequency-domain equilibrium equation is given in Equation (1) [20,21].

$$\left[-{\mathsf{\Omega }}^2\left(M_{RB}+A\left(\mathsf{\Omega }\right)\right)+i\mathsf{\Omega }B\left(\mathsf{\Omega }\right)+C_{HS}+K_{moor}\right]\xi \left(\mathsf{\Omega }\right)=F_{exc}\left(\mathsf{\Omega }\right)$$

(1)

Here, $\xi = {\left[x,y,z,\varphi ,\theta ,\psi \right]}^T$ represents the six-degree-of-freedom displacements, ${\mathrm{M}}_{\mathrm{R}\mathrm{B}}$ is the rigid body mass/inertia, and ${\mathrm{C}}_{\mathrm{H}\mathrm{S}}$ is the hydrostatic restoring matrix. ${\mathrm{K}}_{\mathrm{m}\mathrm{o}\mathrm{o}\mathrm{r}}$ is the externally applied linear stiffness. When using time-domain nonlinear mooring, ${\mathrm{K}}_{\mathrm{m}\mathrm{o}\mathrm{o}\mathrm{r}}$ is excluded from Equation (1) and compared with the free-floating RAO.

The displacement/load RAO is defined by Equations (2) and (3), where

$$R_{\mathsf{\xi }}\left(\mathsf{\Omega }\right)={\displaystyle \frac{\mathsf{\xi }\left(\mathsf{\Omega }\right)}{\mathsf{\alpha }}}$$

(2)

$${\mathrm{R}}_{\mathrm{F}}\left(\mathsf{\Omega }\right)={\displaystyle \frac{{\mathrm{F}}_{\mathrm{e}\mathrm{x}\mathrm{c}}\left(\mathsf{\Omega }\right)}{\mathsf{\alpha }}}$$

(3)

The normalized wave amplitude is the half-amplitude α, the units of $R_{\mathsf{\xi }}$ are m/m (rotation is rad/m), and ${\mathrm{R}}_{\mathrm{F}}$ is N/m (moment is N$·$m/m). ANSYS AQWA, OrcaWave, and OrcaFlex are all directly compared based on $\mathsf{\alpha }$ [22,23].

2.2. Time-Domain Dynamics Methods

In this study, the time-domain motion is described by two systems: the linear Cummins equation (ANSYS AQWA) and the six-degree-of-freedom Newton–Euler equation (OrcaFlex). Frequency-dependent radiation attenuation is reflected in the time domain through a memory function (convolution kernel) [24]. The linear Cummins equation is shown in Equations (4) and (5).

$$\left({\mathrm{M}}_{\mathrm{R}\mathrm{B}}+{\mathrm{A}}_{\mathrm{\infty }}\right)\ddot{\mathsf{\xi }}\left(\mathrm{t}\right)+{\int }_0^{\mathrm{t}}\mathrm{K}\left(\mathrm{t}-\mathsf{\tau }\right)\dot{\mathsf{\xi }}\left(\mathsf{\tau }\right)\mathrm{d}\mathsf{\tau }+{\mathrm{C}}_{\mathrm{H}\mathrm{S}}\mathsf{\xi }\left(\mathrm{t}\right)={\mathrm{F}}_{\mathrm{e}\mathrm{x}\mathrm{t}}\left(\mathrm{t}\right)+{\mathrm{F}}_{\mathrm{m}\mathrm{o}\mathrm{o}\mathrm{r}}\left(\mathrm{t}\right)$$

(4)

$$K\left(t\right)={\displaystyle \frac{2}{\pi }}{\int }_0^{\infty }\mathrm{B}\left(\mathsf{\Omega }\right)\cos \left(\mathsf{\Omega }t\right)d\mathsf{\Omega }, {\mathrm{A}}_{\mathrm{\infty }}=\underset{\mathsf{\Omega }\to \infty }{\lim }\mathrm{A}\left(\mathsf{\Omega }\right)$$

(5)

${\mathrm{A}}_{\mathrm{\infty }}$ and $\mathrm{K}\left(t\right)$ are constructed from $\mathrm{A}\left(\mathsf{\Omega }\right)$ and $\mathrm{B}\left(\mathsf{\Omega }\right)$ calculated in the frequency domain, and the linear six-degree-of-freedom motion is integrated.

Next, the complete six-degree-of-freedom Newton–Euler is expressed in Equation (6) [22].

$$M\left(q\right)\ddot{q}+C\left(q,\dot{q}\right)\dot{q}+K_{HS}\left(q\right)=F_{ext}\left(t\right)+F_{moor}\left(t\right)+F_{visc}\left(t\right)$$

(6)

Time-integrate the six-degree-of-freedom nonlinear equations for the generalized coordinate system $q$, including rotations. Directly integrate the large rotational/geometric nonlinearities, the geometric dependence of the gravity buoyancy moments, and the Morison-based viscous forces as $F_{visc}$.

2.3. Mooring Line Tension Analysis Method

OrcaFlex discretizes mooring lines into a number of line segments, and time-integrates Newton’s second law of motion, $F=ma$, for each node. The axial force–deformation relationship is expressed using a linear (or user-defined nonlinear) material model, and the line element fluid force uses the Morison formula.

$$m_i{\ddot{r}}_i=T_{i-1,i}+T_{i,i+1}+m_{i}g+F_i^{hyd}+F_i^{seabed}$$

(7)

$$T=EA\epsilon +c_{a}EA\dot{\epsilon }, \epsilon ={\displaystyle \frac{l-l_0}{l_0}}$$

(8)

$$F_i^{hyd}={\displaystyle \frac{1}{2}}\rho C_{D}D∆s\left|u_r\right|u_r+\rho C_M\left({\displaystyle \frac{\pi D^2}{4}}\right)∆s{\dot{u}}_r$$

(9)

Equation (7) is the translational dynamics at node $i$, Equation (8) is the axial force–strain relationship of the line segment [25], and Equation (9) is the Morison fluid force [26]. $T_{i-1,i}$ and $T_{i,i+1}$ are the axial force vectors acting in the direction of the line segment tangent, and $F_i^{seabed}$ is the seabed reaction force and friction.

In the quasi-static mode of ANSYS AQWA, the tension displacement according to the position change is calculated using the catenary solution, which can be expressed as Equation (10) [24].

$$a\equiv {\displaystyle \frac{H}{\omega }}$$

(10)

Here, $H$ is the horizontal tension and $\omega$ is the submerged weight. The horizontal/vertical coordinates for the length $s$ of the arc are given in Equation (11).

$$x\left(s\right)=a\sinh \left({\displaystyle \frac{s}{a}}\right), z\left(s\right)=a\left[\mathrm{c}\mathrm{o}\mathrm{s}h\left({\displaystyle \frac{s}{a}}\right)-1\right]$$

(11)

The total tension magnitude $T_f$ and components in the fairlead are shown in Equation (12).

$$T_f=\sqrt{H^2+{\left(\omega s_f\right)}^2}, \left(T_h,T_v\right)=\left(H, \omega s_f\right)$$

(12)

If necessary, the pre-existing axial stiffness effect is compensated for by adding elongation correction using Equation (13).

$$\mathsf{\Delta }l={\displaystyle \frac{Tl}{EA}}$$

(13)

3. Structural Design and Analysis Conditions

The subject of this study is a hollow box-shaped floating body. Its external dimensions are a length ($L_{out}$) of 10 m, width ($B_{out}$) of 10 m, and height ($H_{out}$) of 2 m. The material used is concrete, and the structure is modeled as a hollow box with a thickness of 0.1 m on all sides. The internal dimensions (empty space) are a length ($L_{in}$) of 9.8 m, width (${ B}_{in}$) of 9.8 m, and height ($H_{in}$) of 1.8 m. The equation for calculating the volume obtained by the difference between the external and internal volumes is shown in (14).

$$V_{shell}=L_{out}{B}_{out}{H}_{out}-L_{in}{B}_{in}{H}_{in}$$

(14)

The volume obtained through the formula is 27.128${\mathrm{m}}^3$, and the mass of the structure is set to 65,107$\mathrm{k}\mathrm{g}$ by multiplying the concrete density ${\rho }_c\approx 2400 \mathrm{k}\mathrm{g}/{\mathrm{m}}^3$.

In the center of mass and moments of inertia, the coordinate system was set at the center of the shape, X-Y-Z are the length–width–height directions, and the center of mass was set as $\left(X_G,Y_G,Z_G\right)=(\mathrm{0,0},0)$. The moments of inertia were used as $I_{xx}=1.1\times {10}^6, { I}_{yy}=1.1\times {10}^6, I_{zz}=2.7\times {10}^6 (\mathrm{k}\mathrm{g}·{\mathrm{m}}^2)$. When checking the static buoyancy, the equilibrium displacement volume is 63.52 ${\mathrm{m}}^3$ at the seawater density ${\rho }_w\approx 1025 \mathrm{k}\mathrm{g}/{\mathrm{m}}^3$, and is obtained through the following Equation (15).

$$V_{disp}={\displaystyle \frac{m}{{\rho }_w}}$$

(15)

Since the waterline area is $A_{wp}=L\times B=100 {\mathrm{m}}^2$, the static draft is expressed using the following Equation (16).

$$d={\displaystyle \frac{V_{disp}}{A_{wp}}}$$

(16)

The static draft obtained through Equation (16) is 0.635 m, and the structure used in this study floats with only about 31.8% of its total height submerged. A panel mesh was constructed by dividing the panels into equal sections at intervals of approximately 0.2 m on all sides. To ensure strict reproducibility, the identical panel mesh generated in AQWA was directly exported and imported into OrcaWave without any modification, guaranteeing that both solvers operate on an exactly matched hydrodynamic discretization. The total number of nodes was 7002, and the total number of elements was 7000 for the analysis. The panel mesh was generated with a uniform distribution over all surfaces to maintain geometric consistency. The body boundary was discretized using flat quadrilateral elements. The adequacy of the panel resolution was verified by checking that further mesh refinement did not cause noticeable changes in the calculated hydrodynamic coefficients or motion RAOs. Therefore, the adopted panel configuration was considered sufficient to ensure numerical stability and convergence of the analysis. To verify the adequacy of this mesh resolution, a mesh refinement study was performed using three different panel sizes: 0.4 m, 0.3 m, and 0.2 m. As shown in Appendix D, the surge, heave, and pitch displacement RAOs obtained from these three meshes exhibit less than 1% variation across the entire period range, including the resonance frequencies. Furthermore, a comparison by mesh size is shown in Appendix G.

The geometric configuration and coordinate definition of the box-shaped floating body are illustrated in Figure 1, while Figure 2 presents the environmental load directions (wave, wind, and current at 0 deg heading) and mooring line arrangement. These schematics clearly show the coordinate axes (X, Y, Z) and principal dimensions of the floating structure, which enhance the reproducibility of the model setup.

In this study, the calculation results of two different commercial analysis tools (ANSYS AQWA and the OrcaFlex package (OrcaWave and OrcaFlex)) were compared by matching the geometry, mass properties, draft, panel division, and boundary conditions, and by unifying the external force definition and output normalization. The frequency-domain analysis was conducted for wave periods ranging from T = 0.95 s to 16 s (ω = 0.39~6.63 rad/s), covering short-to-long wave conditions. The incident wave angle was fixed at 0 deg head sea with respect to the global x-axis of the hull, and all hydrodynamic coefficients including added mass, radiation damping, and exciting force were evaluated under the same heading. The same 0 deg incidence condition and identical numerical parameters were applied to the subsequent time-domain simulations for both regular and irregular waves. In addition, the mooring lines were modeled such that Line 1 acted in the direction of the environmental load and Line 2 in the opposite direction, as shown in Figure 2. This mooring layout was intentionally selected so that the windward line (Line 1) directly experiences the incident wave loading, enabling a direct comparison of slack–taut behavior and snap–load sensitivity between the solvers. Lines 2–4 provide symmetric lateral restoring in sway and yaw, forming a standard cross-line configuration used for rectangular pontoons. The corresponding surface panel mesh used for the frequency-domain analysis is presented in Figure 3, and the mooring line connection points are summarized in

Table 1. Mooring line connection coordinates of hollow box-shaped floating body (fairlead and anchor locations).

Variable (Mooring Line)	Coordinate Point (x, y, z)
	Fairlead	Anchor
Line 1	(−5, −5, −1)	(−100, −100, −50)
Line 2	(5, −5, −1)	(100, −100, −50)
Line 3	(−5, 5, −1)	(−100, 100, −50)
Line 4	(5, 5, −1)	(100, 100, −50)

.

4. Analysis Results

4.1. Hydrodynamic Coefficients

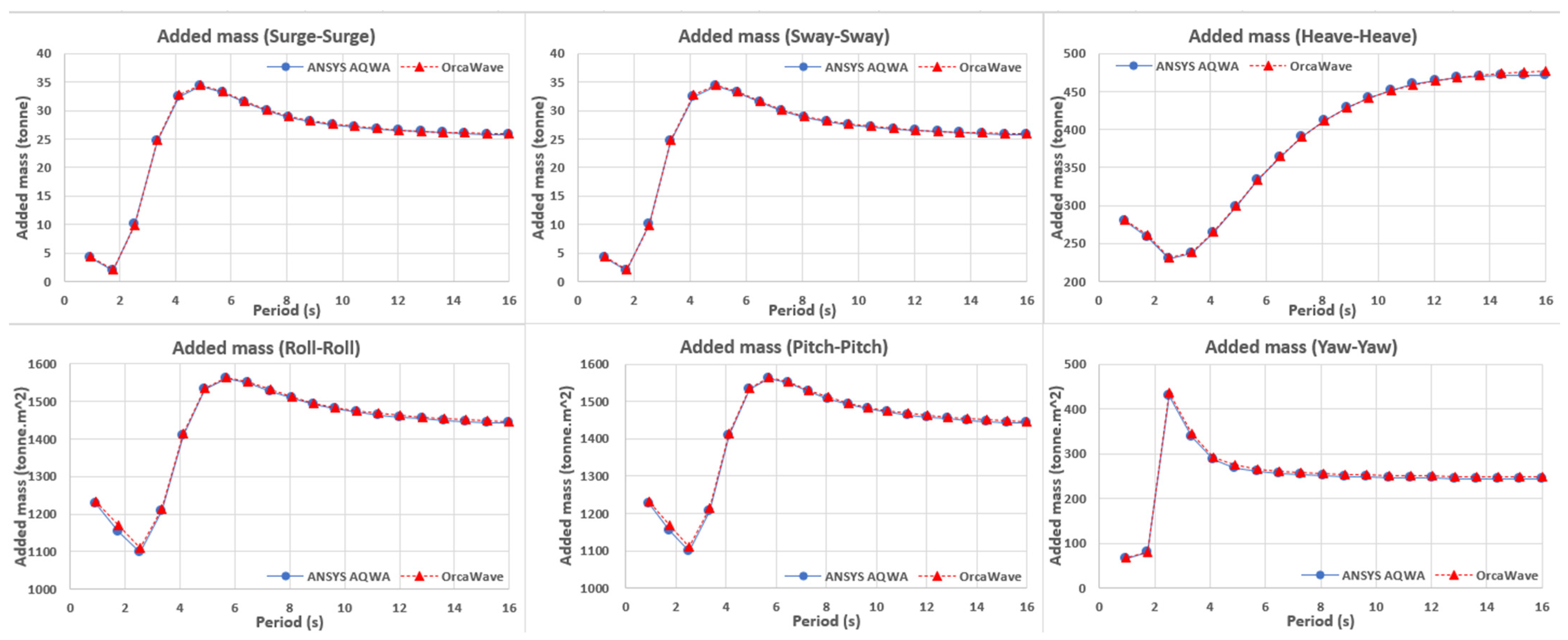
To compare the hydrodynamic coefficients, the structure designed by ANSYS AQWA was input directly into OrcaWave and analyzed. The analysis results are shown in Figure 4 and Figure 5. The six-degree-of-freedom added mass/moment of inertia calculated under 0 deg incidence conditions were nearly identical in shape and magnitude across the entire periodic range between the two solvers (AQWA and OrcaWave). Surge and sway exhibited typical behavior, with equivalent short-period values, a gentle plateau around 4~5 (s), and then a very gradual decrease in the longer-period range. Heave increased monotonically with increasing period and tended to converge at the long-period limit. Roll and pitch peaked at $T\approx 5~6 \left(\mathrm{s}\right)$ after a low point in the short-period range and then converged thereafter. Yaw exhibited a rapid decrease in damping after a rapid change in short-period values, and overall, no significant differences were observed in any case.

Continuously, radiation damping also showed high similarity across all cases, with the peak period, long-period limit, and curve shape consistently reproduced in both software, ensuring interoperability in this study. Therefore, the differences that appear in the subsequent comparison of regular and irregular waves in the time domain are unlikely to stem from the frequency-domain hydrodynamic coefficients within the tested range, and are more plausibly attributed to mooring nonlinearity and time-integration settings.

Quantitative comparisons of the hydrodynamic coefficients are summarized in Appendix H, where the corresponding numerical indicators have been explicitly included for clarity. The relative deviations between AQWA and OrcaWave are very small across all degrees of freedom, with added-mass errors below 1.0%, radiation-damping errors below 0.5%, and displacement and load RAO deviations generally within 0.1–1.0%. These very small differences confirm that the two solvers produce numerically consistent frequency-domain hydrodynamic coefficients.

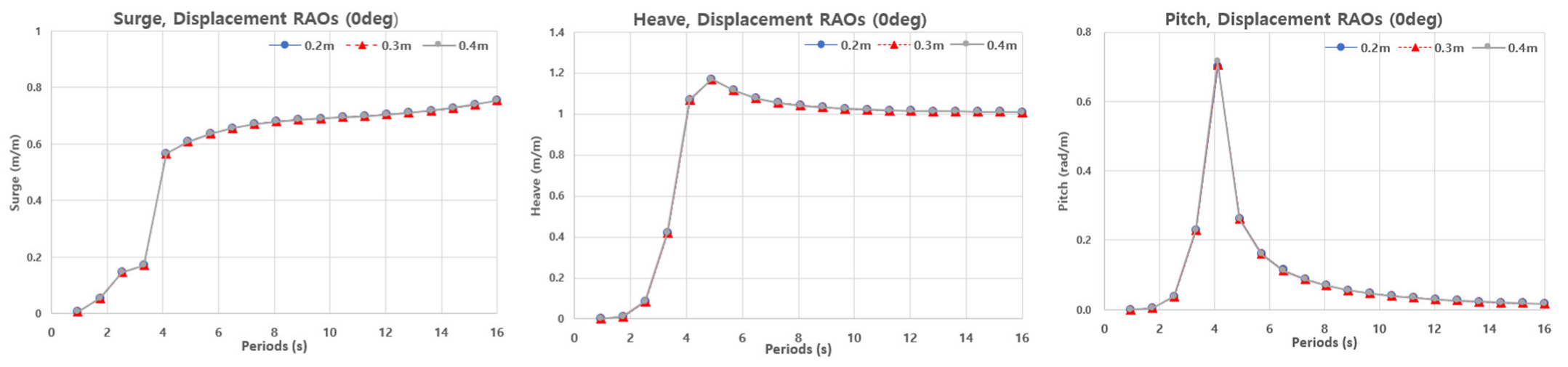
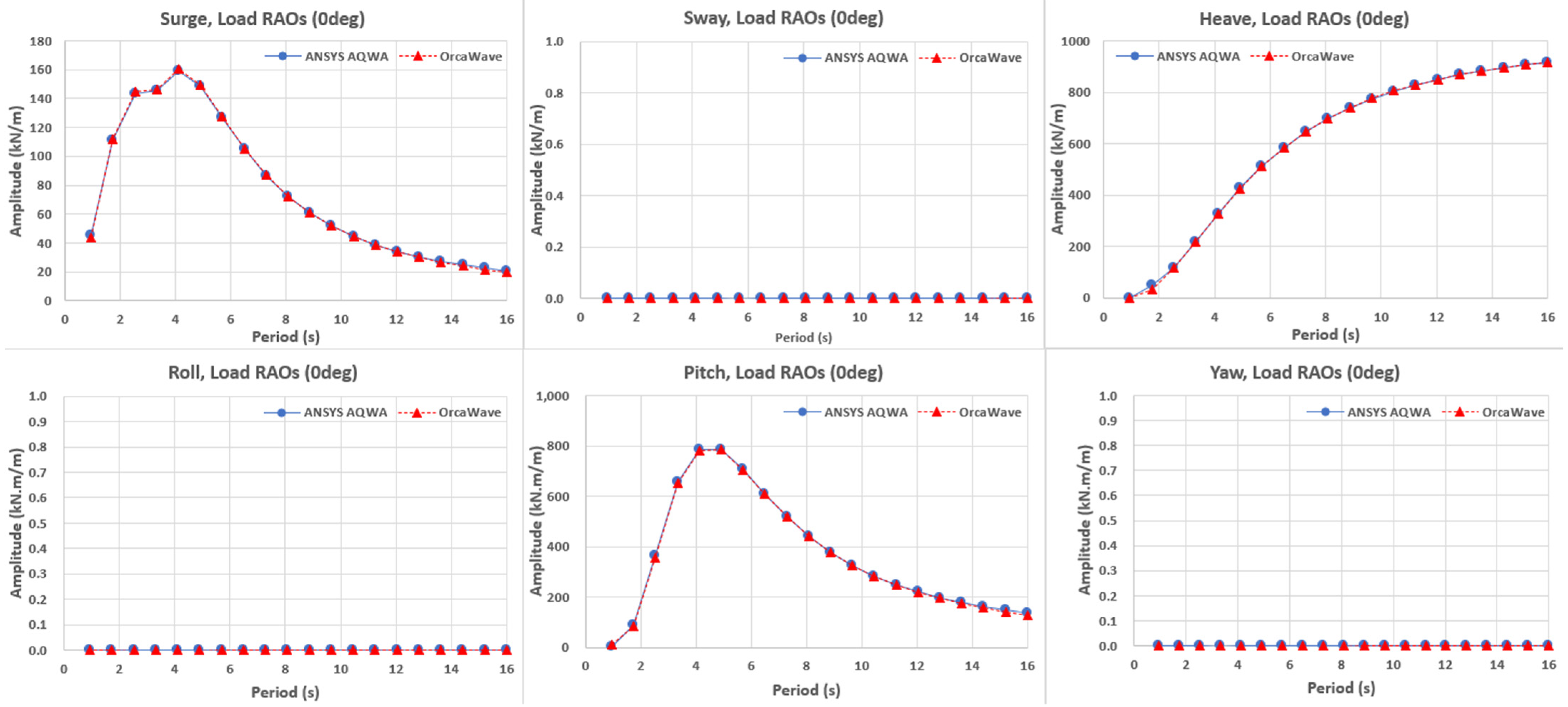
The corresponding RAO curves including displacements and loads under 0 deg heading are presented in Figure 6 and Figure 7. Displacement RAOs calculated at 0 deg frontal incidence showed virtually identical results across the entire period between the two programs, which is expected given the identical conditions. Surge increased progressively in short periods, reaching a gentle plateau after $T\approx 5 \left(\mathrm{s}\right)$, while AQWA showed only a slight additional increase in long periods. Sway, roll, and yaw remained near zero due to the symmetry of frontal incidence. Heave peaked around $T\approx 5 \left(\mathrm{s}\right)$ and then steadily converged, decreasing slightly over long periods. Pitch peaked around $T\approx 4 \left(\mathrm{s}\right)$ and then rapidly decreased. This trend indicates that only surge, heave, and pitch significantly reflect physical characteristics at frontal incidence. Consequently, the RAO results between the two software programs are nearly identical. Quantitatively, the deviation in RAO magnitude between AQWA and OrcaWave remained below 1% for all principal motion modes (surge, heave, and pitch) across the entire frequency range. These very small differences indicate that the frequency-domain hydrodynamic responses of both solvers are effectively identical under the unified modeling conditions. This demonstrates the compatibility of frequency-domain hydrodynamic coefficients computation, as wave normalization (half-amplitude), phase, COG (Center of Gravity), coordinate/sign, and heading definitions are identical. In addition to these definitions, further measures were taken to minimize numerical discrepancies arising from modeling choices. First, the hydrodynamic coefficients were evaluated at identical discrete wave frequencies in both AQWA and OrcaWave, ensuring that the added mass, radiation damping, and RAOs were compared without interpolation errors or sampling mismatches. Second, a mesh refinement study using panel sizes of 0.4 m, 0.3 m, and 0.2 m confirmed that the hydrodynamic results were mesh-independent, with RAO variations below 1%. These steps collectively minimized frequency sampling, mesh resolution, and postprocessing errors, enabling a fair and direct comparison of the hydrodynamic responses.

Before comparing the results between ANSYS AQWA and OrcaWave/OrcaFlex, the reliability of the present hydrodynamic model was examined using previously published experimental data. In the study [27], the heave motion and excitation forces of a rectangular box were measured under regular and irregular waves and compared with linear potential-flow predictions. Their results showed that the heave RAO agreed well with linear theory across most frequencies, whereas noticeable deviations occurred near resonance due to additional viscous damping effects. Furthermore, the first-harmonic vertical excitation forces were reported to be approximately 10–15% lower than theoretical predictions, representing the typical level of discrepancy between experiments and potential-flow models. Since both ANSYS AQWA and OrcaWave employ the same linear potential-flow formulation, the small RAO differences observed in this study are consistent with this experimentally established accuracy range and reflect numerical differences rather than theoretical inconsistency.

4.2. Regular and Irregular Wave Effect

In this section, we aim to compare the dynamic behavior and mooring line tension for regular and irregular waves. All environmental heading conditions were set to 0 deg, the simulation time was 120 s, and the time step was set to 0.1 s, except for the 10 s transient response. Since the purpose was to compare the differences between the two programs, the simulation lengths were set to the same even in irregular wave conditions. To ensure the same wave settings for both programs, wave surface elevations were extracted from ANSYS AQWA at first and input into OrcaFlex again for both regular and irregular waves. This procedure was adopted because the default wave conventions of AQWA and OrcaFlex are not identical: AQWA defines wave height as crest-to-trough and uses a global phase origin, whereas OrcaFlex employs half-amplitude normalization and a COG-based phase reference [22,28]. Directly re-using the AQWA generated η(t) time history therefore ensures that both solvers are driven by an identical wave signal, eliminating inconsistencies in amplitude definition, phase, and heading. Through this process, absolute consistency in the environmental loading was achieved, which is essential for fair comparison of time-domain responses. All wind and current conditions were set identically for comparison for both programs. The JONSWAP spectrum properties were used to reflect the design of the substructure in the OrcaFlex example structure, and a peak enhancement factor of 3.3 was applied [29,30]. The JONSWAP spectrum with γ = 3.3 was adopted because it corresponds to the default irregular wave condition used in the OrcaFlex example model and represents a typical North Sea state commonly used for validation purposes. Since the objective of the irregular wave analysis is to provide a consistent input for comparing the numerical behavior of the two solvers, the results are primarily influenced by mooring line nonlinearity rather than small variations in the spectral peak enhancement factor. Thus, using γ = 3.3 does not materially affect the comparative conclusions of this study. All environmental conditions are summarized in

Table 2. Environmental conditions used in the analysis of regular waves (Airy) and irregular waves (JONSWAP).

Environment	Airy		JONSWAP
Wave	Amplitude (m)	2	Significant wave height (m)	7
	Period (s)	8	Peak enhancement factor	3.3
	Frequency (Hz)	0.125	Peak frequency (Hz)	0.0972
Wind	Spectrum	Constant	Spectrum	Constant
	Speed (m/s)	11	Speed (m/s)	11
Current	Type	Constant	Type	Constant
	Speed (m/s)	0.5	Speed (m/s)	0.5

. The mooring lines were modeled as 145 m studlink R4 chains, and their mechanical and hydrodynamic properties are listed in

Table 3. Mooring line properties.

Type	Chain (R4)
Line type	Studlink (steel chain)
Bar diameter (m)	0.05
Diameter (m)	0.0945
Mass per unit length (kg/m)	54.75
Axial stiffness (kN)	2.53 × 105
Min breaking load (kN)	2740
Drag coefficients (x, y)	2.6
Drag coefficients (z)	1.4
Seabed condition	Contact allowed (no friction)

. Each line had an equivalent diameter of 0.05 m, an axial stiffness (EA) of $2.525 \times {10}^5$ kN, a unit submerged mass of 54.75 kg/m, and was attached to a seabed anchor located at a 50 m water depth. The R4 studlink chain type was selected because it represents an industry-standard chain class widely used for barge-type and rectangular floating structures. Its mechanical stiffness, mass properties, and hydrodynamic drag characteristics provide a realistic and practically relevant baseline for catenary mooring behavior, ensuring that the comparison between the two solvers is conducted under representative offshore design conditions.

During both the static and dynamic analyses, the lines exhibited intermittent seabed contact. In OrcaFlex, seabed interaction is modeled using a linear elastic foundation, with only normal reaction forces applied when a segment touches the seabed (with friction set to zero). In contrast, ANSYS AQWA accounts for touchdown analytically through its quasi-static catenary formulation. A frictionless seabed was applied in both solvers to avoid introducing solver-dependent variability, ensuring that any differences observed originate solely from the hydrodynamic and mooring line dynamic formulations rather than from seabed-interaction effects. Furthermore, the static equilibrium configuration and pretension levels are summarized in Appendix E. Identical material properties and boundary definitions were applied in both solvers to ensure consistent initial conditions for the subsequent dynamic simulation.

To compare the dynamic behaviors under regular and irregular waves, statistical analysis results were presented as mean, maximum, minimum, and standard deviation. To ensure fairness in comparison, the absolute difference $\left|∆X\right|=\left|X_{Orca}-X_{AQWA}\right|$ was reported first for the mean, maximum, minimum, and standard deviation. The absolute relative error for each was defined as $\left|(OrcaFlex-AQWA)\right|/\left|AQWA\right|\times 100\%$. Furthermore, the dynamic behavior of the floater was compared only for surge, which is most significantly affected by environmental conditions. As previously explained, the mooring line tensions were compared for Lines 1 and 2. Because the environmental heading is 0 deg, surge is the dominant degree of freedom excited by incident waves and horizontal-mooring-restoring forces. For completeness, the corresponding heave and pitch responses are presented in Appendix C, where only minor differences were observed due to their hydrostatic-dominated behavior.

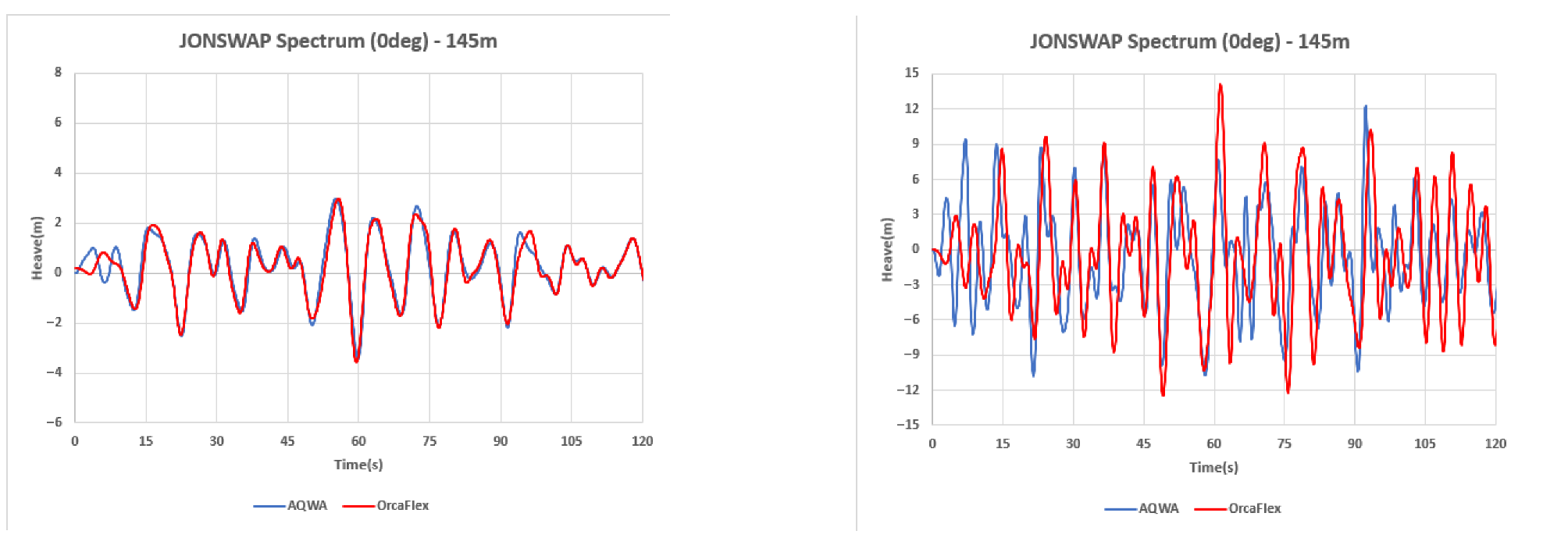
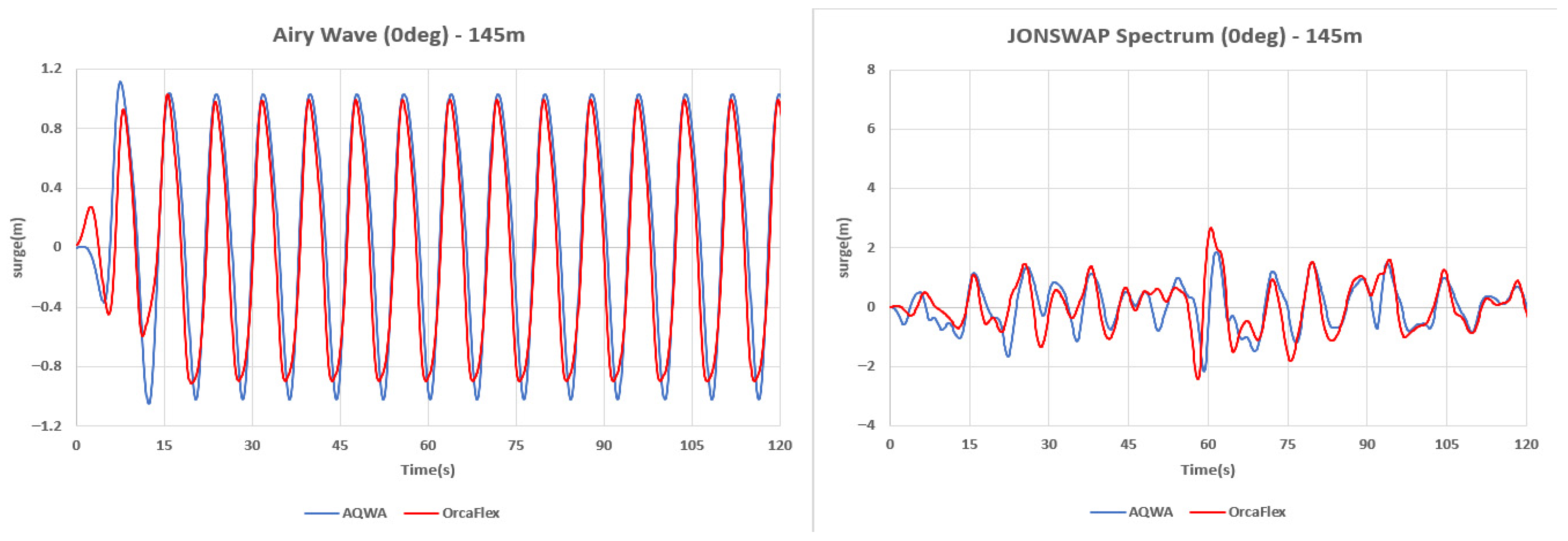
In the regular wave case, the two time series nearly overlapped as shown in Figure 8. However, there was a slight error with respect to the mean value. In reality, the mean differed by approximately 0.12 m, indicating good agreement. The absolute errors of maximum, minimum, and standard deviation, which reflect the dynamic characteristics, were 7.6%, 13.2%, and 6.0%, respectively, showing good agreement. On the other hand, in irregular waves, although the overall trend was maintained, differences can be observed at some local peaks. The relative error of the mean was large, and the difference was amplified in the variance and peak point, showing a large difference in the absolute errors of maximum, minimum, and standard deviation, at 43.8%, 12.5%, and 11.5%, respectively. This is interpreted as being because, although the frequency-domain coefficients and RAO were almost identical, differences occurred in the time domain, such as mooring nonlinearity and differences in the integration process, causing the peak to be sensitively amplified. The corresponding numerical comparison results are presented in Figure 8 and

Table 4. Comparison table of platform surge response statistics for AQWA and OrcaFlex (mooring line length 145 m, 0 deg).

145 m	Average	Max.	Min.	Std.	145 m	Average	Max.	Min.	Std.
Airy surge (m) (AQWA)	0.109	1.114	−1.051	0.703	JONSWAP surge (m) (AQWA)	0.041	1.855	−2.162	0.744
Airy surge (m) (ORCA)	−0.011	1.029	−0.913	0.660	JONSWAP surge (m) (ORCA)	0.047	2.668	−2.432	0.829
Relative error, %	110	7.6	13.2	6.0	Relative error, %	13.6	43.8	12.5	11.5
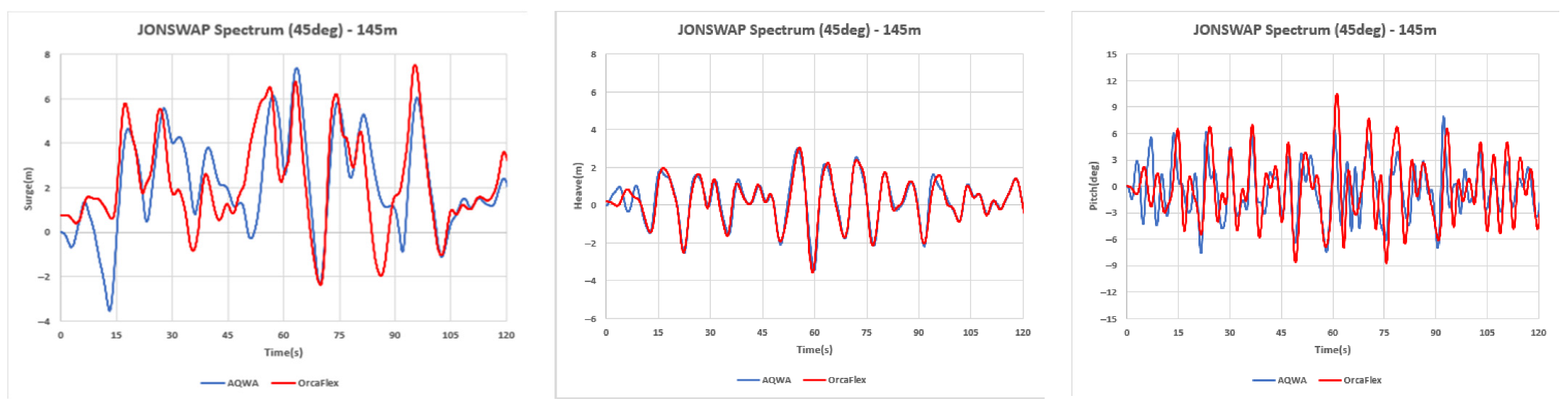
Difference value (m)	0.12	0.09	0.14	0.04	Difference value (m)	0.006	0.813	0.27	0.085

. To further assess the directional sensitivity of the platform motion, an additional case with 45 deg wave incidence was evaluated for the 145 m mooring configuration. Compared with the 0 deg condition, the heave response remains almost unchanged, whereas the low-frequency surge motion becomes slightly larger under oblique incidence. In contrast, the pitch response exhibits greater amplitudes under 0 deg frontal waves, where symmetric head sea loading generates a stronger overturning moment, while 45 deg incidence redistributes a portion of this excitation into sway, roll, and yaw. The full RAO and time series comparisons for the 45 deg heading are provided in Appendix A and Appendix B, and the reference 0 deg heave and pitch responses are shown in Appendix C.

Continuously, in this section, mooring line tension at the fairlead point is compared for both regular and irregular waves. As previously explained, Line 1 is positioned in the direction of the environmental load (upwind), while Line 2 is positioned in the opposite direction (downwind).

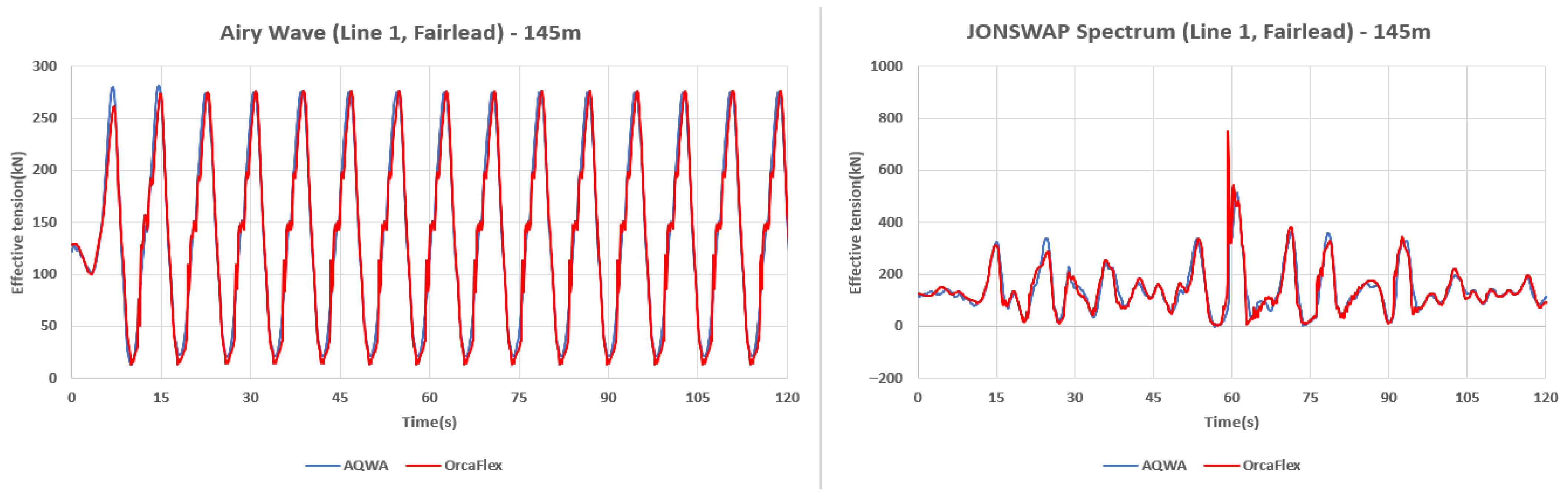
Comparing the relative error (%) of Line 1, the average value remains largely unchanged at 2.5% for regular waves and 0.8% for irregular waves. However, the absolute errors of the maximum, minimum, and standard deviation are 1.7%, 3.6%, and 1.2%, respectively, for regular waves, and 45.8%, 41.3%, and 5.0% for irregular waves, showing a significant increase in error for irregular waves. As shown in Figure 9, under irregular wave conditions, OrcaFlex exhibits a larger peak. This is interpreted as being due to OrcaFlex’s greater sensitivity to snap loading, which occurs when entering slack and then rapidly re-tensioning.

Line 2 also showed a similar relative error in average tension, at 3.0% for regular waves and 1.1% for irregular waves. However, the differences in maximum, minimum, and standard deviation were 3.3%, 4.4%, and 0.6% for regular waves, and 3.9%, 52.1%, and 7.0% for irregular waves, significantly increasing in irregular waves. This also stems from the difference in sensitivity to snap loading. The standard deviation of Line 2, in particular, is significantly larger than that of Line 1, as it is located on the opposite side (downwind) of the environmental load, making it more sensitive to slack generation. Quantitatively, the mean fairlead tensions from both solvers agreed within ≤3% for both Lines 1 and 2 under regular and irregular waves. Under irregular waves, the extremes diverged asymmetrically for Line 1—the maximum and minimum tensions differed by 45.8% and 41.3%, respectively; for Line 2 the maximum differed by only 3.9%, whereas the minimum differed by 52.1%. This pattern indicates that the windward line experiences much larger re-tension peaks, while the leeward line exhibits more pronounced slack-induced minima. The average loads remain nearly identical, but the extremes diverge due to differences in line dynamics and slack-to-taut re-tension modeling.

In summary, OrcaFlex models the line as a multi-degree-of-freedom lumped-mass system, directly integrating axial wave propagation, Morison nonlinear resistance, and the stick–slip and slack–taut transitions of seabed contact and friction in the time domain. This better preserves the high-frequency components and peaks of snap loading that occur during re-tension after slack, resulting in a relatively larger estimate compared to ANSYS AQWA under the same conditions [31,32]. These differences stem from the fundamentally different numerical formulations employed by the two solvers. OrcaFlex uses a multi-degree-of-freedom lumped-mass approach that explicitly integrates inertia, axial-wave propagation, and dynamic strain energy release in time, allowing the short-duration force spikes generated during slack–taut re-tension to be fully resolved. In contrast, ANSYS AQWA computes mooring loads using a quasi-static catenary equilibrium solution, which assumes instantaneous force balance and therefore filters out the transient elastic and inertial components responsible for peak amplification. Consequently, the two solvers show good agreement in mean tensions but diverge in short-duration extremes under irregular waves. These snap loading discrepancies can be mitigated by increasing the mooring pretension or avoiding excessively soft mooring configurations, which reduce slack–taut cycles. Additional damping or drag on the mooring lines can also limit the severity of transient peaks. Conversely, ANSYS AQWA may exhibit lower conservativeness due to partial mitigation of high-frequency peaks due to differences in the line model, numerical attenuation, and output smoothing. The corresponding comparison results are presented in Figure 9 and Figure 10 and

Table 5. Tension statistics comparison table for Mooring Line 1 (fairlead) of AQWA and OrcaFlex (mooring line length 145 m, 0 deg).

145 m	Average	Max.	Min.	Std.	145 m	Average	Max.	Min.	Std.
Airy Line 1 (kN) (AQWA)	138.49	280.94	13.33	85.66	JONSWAP Line 1 (kN) (AQWA)	141.42	515.65	−0.63	87.18
Airy Line 1 (kN) (ORCA)	135.06	276.17	12.85	84.66	JONSWAP Line 1 (kN) (ORCA)	142.52	751.99	−0.89	91.58
Relative error, %	2.5	1.7	3.6	1.2	Relative error, %	0.8	45.8	41.3	5.0
Difference value (kN)	3.43	4.77	0.48	1.00	Difference value (kN)	1.10	236.34	0.26	4.40

and

Table 6. Tension statistics comparison table for Mooring Line 2 (fairlead) of AQWA and OrcaFlex (mooring line length 145 m, 0 deg).

145 m	Average	Max.	Min.	Std.	145 m	Average	Max.	Min.	Std.
Airy Line 2 (kN) (AQWA)	118.51	147.59	86.00	14.74	JONSWAP Line 2 (kN) (AQWA)	121.28	268.32	41.01	25.29
Airy Line 2 (kN) (ORCA)	122.02	152.41	82.21	14.65	JONSWAP Line 2 (kN) (ORCA)	122.64	257.72	19.66	27.06
Relative error, %	3.0	3.3	4.4	0.6	Relative error, %	1.1	3.9	52.1	7.0
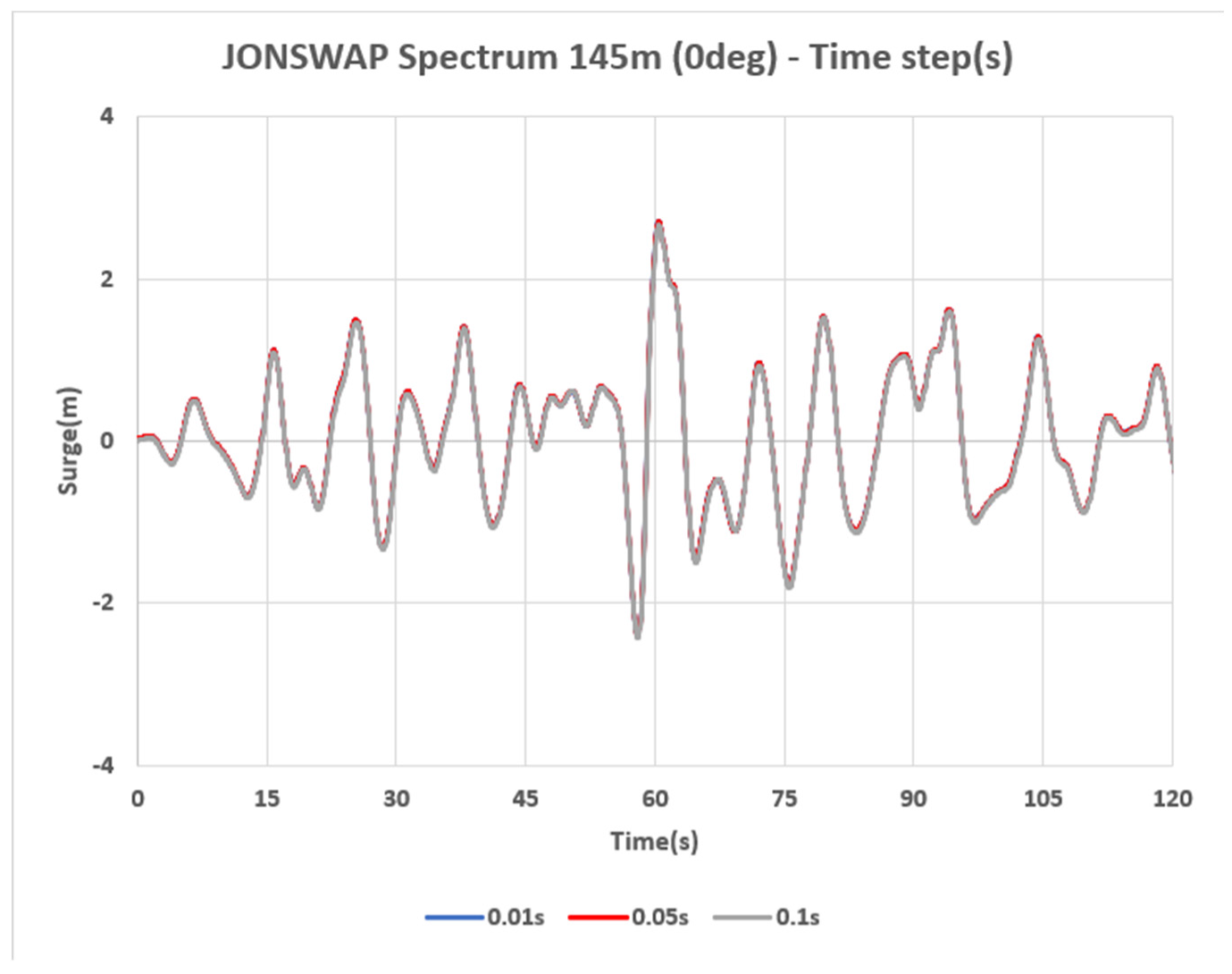
Difference value (kN)	3.51	4.82	3.79	0.09	Difference value (kN)	1.36	10.60	21.35	1.77

. To assess numerical stability, a time-step sensitivity study was conducted for the 145 m mooring line case, which represents the baseline configuration. Three different integration time steps, 0.1 s, 0.05 s, and 0.01 s, were tested under identical JONSWAP irregular wave conditions. As shown in Appendix F, the resulting surge motions from all three time steps are nearly indistinguishable, and no noticeable differences were observed in the corresponding mooring line tensions. This confirms that the dynamic responses are fully converged with respect to time-step refinement, and that the default time step of 0.1 s provides numerically stable and accurate results. It should be emphasized that the present comparison is limited to operational regular and irregular wave conditions. Scenarios involving combined wave–wind–current loading or extreme storm seas were not included, as they introduce additional nonlinear interactions that may mask the isolated influence of the mooring line modeling approaches. These aspects will be explored in future work to assess whether solver-dependent differences become more pronounced under ultimate limit state conditions.

4.3. Mooring Line Length Effect

This section compares the effects of various mooring line lengths (145, 150, and 155 m) on the platform surge response (mean, maximum, minimum, and standard deviation) using ANSYS AQWA and OrcaFlex results. Only the mooring length was changed, while all other inputs remained constant as shown in Figure 11. Only irregular wave conditions were considered. Mooring line length was selected as the primary variable because it directly governs the global restoring stiffness of the system and, more importantly, controls the occurrence of slack–taut transitions. These transitions are the dominant mechanism responsible for the differences observed between ANSYS AQWA and OrcaFlex, especially in peak tension responses. In contrast, other mooring parameters such as axial stiffness, line diameter, and anchor layout modify the system response more gradually within the operational range considered here and do not fundamentally alter the onset of re-tension or snap loading events. For this reason, these parameters were held constant to isolate the primary mechanism driving solver-to-solver discrepancies. A broader parametric study including stiffness, diameter, and anchor position will be pursued as part of our future work.

At 145 m, the mooring is relatively tight, resulting in small overall displacement. The mean absolute difference between the two codes is only 0.12 m, and the standard deviation difference is 0.04 m. The maximum value is 0.09 m, and the minimum value is 0.14 m, indicating virtually no difference.

Increasing the mooring line length to 150 m softens the restoring force, amplifying low-frequency components and reducing the minimum difference to 0.08 m. At this time, the maximum difference increases to 0.67 m, the standard deviation difference increases to 0.07 m, and the mean increases to 0.47 m. However, this difference is difficult to consider significant.

Even when the mooring line is extended to 155 m, the difference is not significant. The standard deviation difference is 0.49 m, the mean difference is 0.34 m, the maximum value is 0.06 m, and the minimum value is 0.76 m. In summary, even when the mooring line length is longer, all results show differences of less than 1 m, and it is judged that no significant difference was observed with respect to the surge motion. 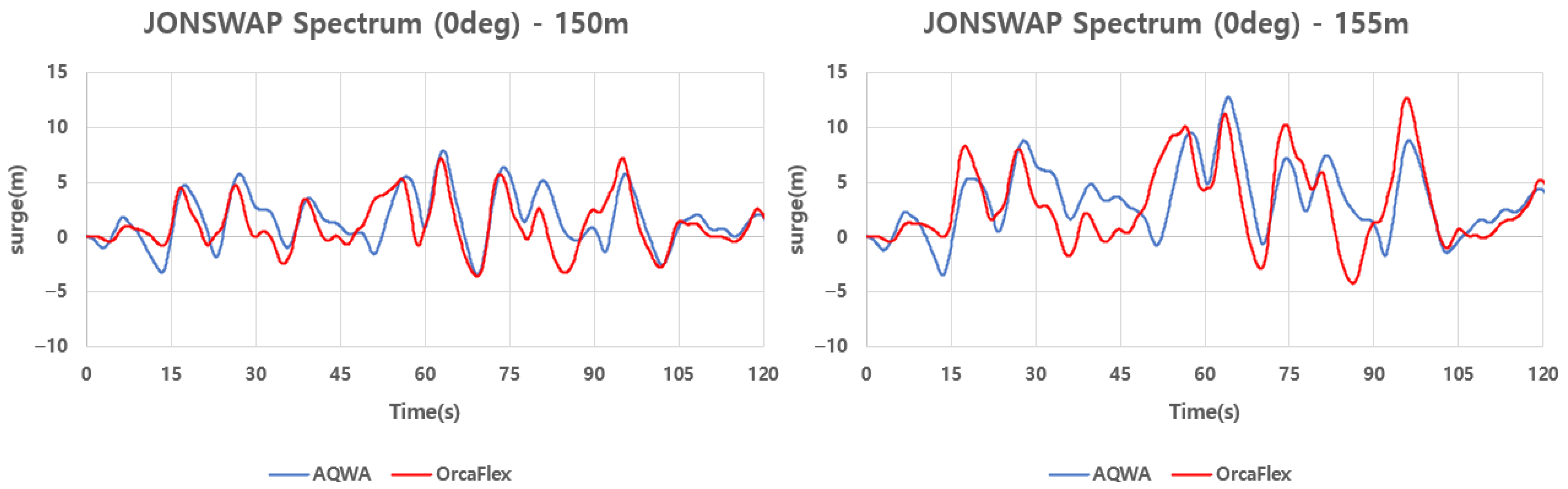The corresponding comparison results are presented in Figure 12 and

Table 7. Table comparing platform surge response statistics according to changes in mooring line length (150 m-155 m) (JONSWAP, 0 deg).

150 m	Average	Max.	Min.	Std.	155 m	Average.	Max.	Min.	Std.
JONSWAP surge (m) (AQWA)	1.57	7.87	−3.51	2.36	JONSWAP surge (m) (AQWA)	3.42	12.77	−3.50	3.22
JONSWAP surge (m) (ORCA)	1.10	7.20	−3.59	2.29	JONSWAP surge (m) (ORCA)	3.08	12.71	−4.26	3.71
Relative error, %	29.7	8.6	2.5	2.9	Relative error, %	9.8	0.5	21.4	15.4
Difference value (m)	0.47	0.67	0.08	0.07	Difference value (m)	0.34	0.06	0.76	0.49

.

To clarify the physical origin of the solver-dependent differences, the absolute surge responses independent of solver mismatch were also examined. In AQWA, the standard deviation of surge increased from 0.744 m at a 145 m line length to 3.22 m at 155 m, representing a 2.48 m amplification. To support this interpretation, static analyses were performed to compute the pretension for each mooring line length, and the results are summarized in Appendix E. The shorter lines exhibit higher pretension and consequently stronger stiffness, whereas longer lines develop lower pretension and allow larger surge excursions. This static behavior is fully consistent with the dynamic trend observed in the time-domain simulations.

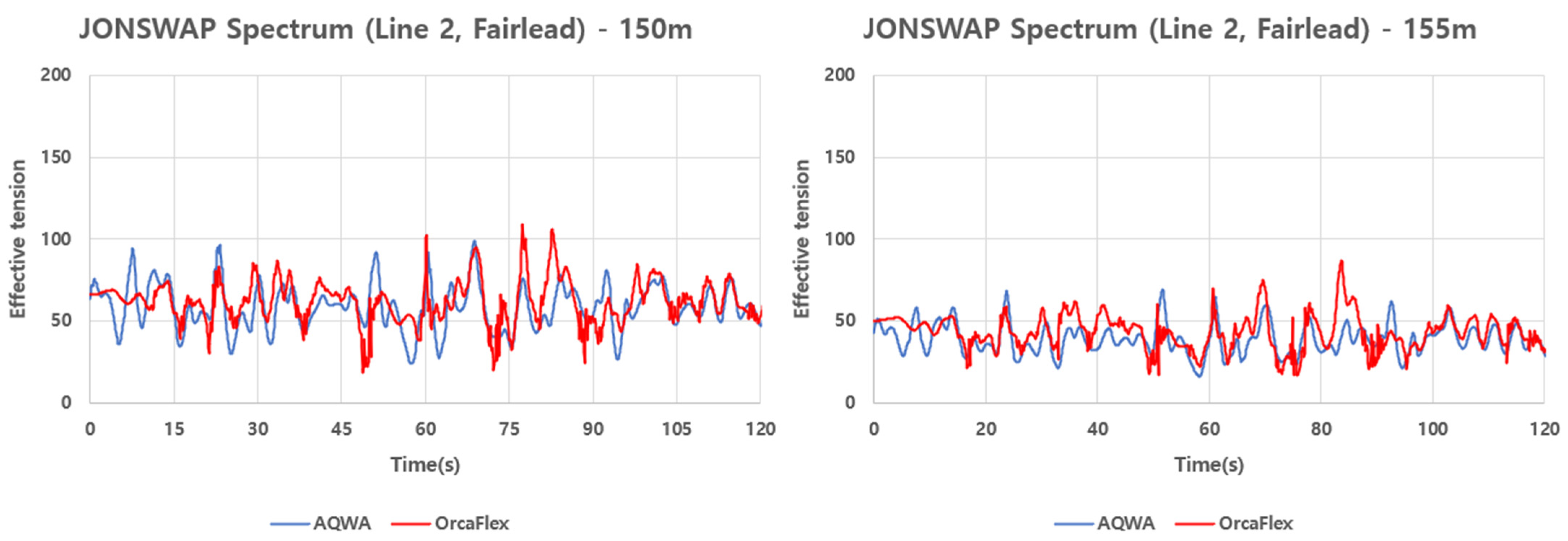
Furthermore, fairlead mooring tensions of Line 1 and 2 time series under JONSWAP conditions are shown in Figure 13 and Figure 14, while a numerical results comparison is tabulated in

Table 8. Mooring Line 1 (fairlead) tension statistics comparison table (JONSWAP, 0 deg) according to mooring line length (150 m–155 m).

150 m	Average	Max.	Min.	Std.	155 m	Average	Max.	Min.	Std.
JONSWAP Line 1 (kN) (AQWA)	80.03	297.45	2.63	48.69	JONSWAP Line 1 (kN) (AQWA)	57.19	207.53	5.56	30.52
JONSWAP Line 1 (kN) (ORCA)	80.23	468.63	3.74	52.28	JONSWAP Line 1 (kN) (ORCA)	62.73	357.21	3.08	42.54
Relative error, %	0.02	57.6	42.1	7.4	Relative error, %	9.8	72.1	44.6	39.4
Difference value (kN)	0.2	171.18	1.11	3.59	Difference value (kN)	5.54	149.68	2.48	12.02

and

Table 9. Mooring Line 2 (fairlead) tension statistics comparison table (JONSWAP, 0 deg) according to mooring line length (150 m–155 m).

150 m	Average	Max.	Min.	Std.	155 m	Average	Max.	Min.	Std.
JONSWAP Line 2 (kN) (AQWA)	58.46	98.96	23.83	13.92	JONSWAP Line 2 (kN) (AQWA)	38.84	69.29	16.11	9.37
JONSWAP Line 2 (kN) (ORCA)	61.93	109.05	18.28	13.17	JONSWAP Line 2 (kN) (ORCA)	43.20	87.28	16.56	10.80
Relative error, %	5.9	10.3	23.3	5.4	Relative error, %	11.2	26.0	2.8	15.3
Difference value (kN)	3.47	10.09	5.55	0.75	Difference value (kN)	4.36	17.99	0.45	1.43

. The comparison was conducted using the previously defined indices (absolute difference, relative error). For Line 1 (windward), the average error was non-monotonic at 0.8%, 0.02%, and 9.8%, respectively, depending on the mooring line length (145, 150, and 155 m), while the standard deviation error increased to 5.0%, 7.4%, and 39.4%, respectively. In other words, the average error was smallest at 150 m and then increased significantly at 155 m. However, the decrease in average error was small when extending the length from 145 to 150 m, so the practical difference was considered limited. Line 2 (downwind) showed mean/standard deviation errors of 1.1/7.0% (145 m), 5.9/5.4% (150 m), and 11.2/15.3% (155 m), respectively. The mean error increased with increasing length, while the standard deviation error briefly decreased at 150 m before increasing significantly at 155 m. Therefore, the statement that both indices are at maximum at 155 m (catenary) is consistent with the numerical results. As the mooring line length increases, the effective horizontal restoring stiffness decreases, resulting in larger low-frequency surge excursions and an increase in standard deviation. At 155 m, the catenary becomes sufficiently soft that small variations in environmental loading generate larger fairlead displacements and more frequent slack–taut transitions. In OrcaFlex, these transitions are captured dynamically through inertia, axial elasticity, and transient snap loads, which amplify the variance and peak values. In contrast, AQWA’s quasi-static catenary formulation smooths out the transient elastic and inertial components, so the relative discrepancy becomes more pronounced at 155 m even though the absolute surge and tension differences remain small.

From a practical design perspective, the high snap load sensitivity predicted by OrcaFlex suggests the need for a dynamic mooring solver when relaxation–expansion transitions are expected. In contrast, the quasi-static formulation in ANSYS AQWA provides reliable estimates of global motions and mean- or fatigue-related loads but may underpredict short-duration snap events. Therefore, the selection of a solver should reflect the expected mooring line behavior: AQWA is suitable for global and fatigue assessments, whereas OrcaFlex is recommended when accurate snap load prediction is required.

Moreover, although the present study does not consider extreme sea states, the magnitude of the AQWA–OrcaFlex peak-tension deviation is consistent with previously reported differences between quasi-static and dynamic mooring formulations. Previous experimental work showed that quasi-static models significantly underpredict mooring loads, with extreme tensions underestimated by 10–25% and fatigue-related amplitudes by 65–75%, whereas dynamic lumped-mass models reproduce measured peak loads within approximately 10% [25]. Similar trends were also identified in comparative analyses demonstrating that quasi-static prescreening approaches consistently underestimate maximum mooring tensions relative to fully coupled dynamic simulations under identical environmental conditions [33].

Together, these findings explain why the quasi-static AQWA model produces substantially lower peak tensions than the fully dynamic OrcaFlex model in the present comparison. No dedicated basin or field measurements exist for the specific rectangular floater and mooring configuration considered here; therefore, a direct experimental validation of the numerical peak-tension differences is not possible. Nonetheless, the observed discrepancy aligns with the established behavior of catenary systems when quasi-static and dynamic mooring models are compared.

In addition, although the amplified low-frequency surge motion at 155 m could potentially affect fatigue accumulation or ultimate limit state (ULS) peak tensions in practical design, these consequences were not explicitly evaluated in this study. The present work focuses on quantifying the numerical differences between the solvers under operational irregular wave conditions rather than performing detailed fatigue or ULS assessments. A comprehensive investigation of these design implications is therefore recommended for future work. Overall, the results highlight that longer and more compliant mooring configurations lead to larger platform excursions, increased dynamic-tension variability, and a higher likelihood of slack–taut events. Such behavior directly affects station-keeping performance, fatigue life, and ULS safety margins. Therefore, mooring line length and pretension should be carefully selected to avoid excessive compliance that may reduce design robustness.

5. Conclusions

This study compared the hydrodynamic coefficients, displacement/load RAOs, and mooring line responses of a hollow rectangular floating body using ANSYS AQWA, OrcaWave, and OrcaFlex under unified modeling conditions. The frequency-domain results showed that AQWA and OrcaWave provided almost identical added mass, radiation damping, and RAOs, with deviations remaining below 1% across all modes. This confirms the strong consistency of the two solvers in linear hydrodynamic analysis.

In the time domain, however, notable differences were observed in mooring line tensions under irregular waves. These discrepancies, typically showing 40–50% differences in peak tension, arose from nonlinear damping, slack–taut transitions, snap loading, and low-frequency surge amplification, which are captured by OrcaFlex’s fully dynamic line model but not by AQWA’s quasi-static formulation. Increasing the mooring line length from 145 to 155 m further reduced restoring stiffness, enhanced low-frequency surge motions, and widened solver-to-solver differences, although the absolute surge mismatch remained within 1 m for all cases.

From a design perspective, these findings indicate that AQWA is suitable for predicting global motions and mean or fatigue-level mooring loads, whereas OrcaFlex provides more conservative and physically realistic peak-tension estimates essential for ultimate limit state evaluation. In practice, AQWA is most appropriate for assessments dominated by global motions or fatigue loading, while OrcaFlex should be used when accurate prediction of transient peak tensions is required, particularly in scenarios involving slack–taut transitions, snap loading, or significant low-frequency surge amplification. Accordingly, practical engineering workflows should incorporate cross-validation between solvers, using a quasi-static solver for global response and a dynamic line solver for peak-tension enveloping. The dynamic line solver leads to a higher required safety margin and more robust components, while the quasi-static solver enables more efficient designs. Ensuring consistent hydrodynamic inputs and reviewing both mean and peak tensions offers a more robust basis for offshore mooring design and reduces the risk of underpredicting extreme loads. These numerical differences directly influence engineering decisions regarding safety margins, fatigue design, and the choice of appropriate mooring-solver formulations in offshore practice.