Effects of Mesoscale Eddies on Acoustic Propagation with Preliminary Analysis of Topographic Influences

Abstract

This study investigates underwater acoustic propagation patterns under mesoscale eddy conditions through numerical modeling and parametric analysis. A mathematical model of mesoscale eddies was developed, and acoustic transmission loss was computed using the BELLHOP ray-tracing model. Systematic simulations were conducted to examine the effects of source depth, eddy polarity (cold/warm), eddy intensity, and seabed topography. The results reveal distinct acoustic behaviors: cold-core eddies shift convergence zones forward, reduce their width, elevate their depth, and enhance convergence gain within certain ranges. In contrast, warm-core eddies displace convergence zones backward, broaden their width, and can induce surface duct formation. Furthermore, seabed topography exerts minimal influence on acoustic propagation under cold-core eddies but significantly modulates propagation under warm-core eddies, with different topographies producing markedly distinct effects. These findings provide valuable insights for marine scientific research and engineering applications leveraging mesoscale eddy phenomena.

1. Introduction

Mesoscale eddies are coherent rotating water bodies in the ocean, analogous to atmospheric cyclones or storms. They commonly form alongside ocean currents and represent a ubiquitous marine phenomenon [1]. They are typically categorized into two types: cyclonic eddies (cold-core eddies), wherein central seawater ascends from depths, transporting cold subsurface water into warm upper layers, resulting in lower internal temperatures relative to the temperatures of surrounding waters, and anticyclonic eddies (warm-core eddies), wherein central seawater descends from the surface, carrying warm upper water into cold deep layers, leading to high internal temperatures. Numerous eddies exist in various regions, such as the Kuroshio Current and Gulf Stream systems. Typical mesoscale eddies exhibit horizontal scales of 50–500 km, temporal scales of days to hundreds of days, and surface rotational speeds exceeding 3 knots. They have slow core movements, with lifespans lasting up to one year. Given their importance for sonar detection and submarine stealth navigation, coupled with their large spatial scales, studying the effect of mesoscale eddies on acoustic propagation is of critical importance [2,3].

Research on the influence of mesoscale eddies on acoustic propagation has expanded in recent years. For example, BEAR et al. [4] employed a 3D parabolic equation model to study horizontal and vertical refractions induced by cold-core eddies when sound sources are positioned outside eddies. ZHANG et al. (2011) [5] analyzed acoustic propagation effects in cold-core eddy environments by employing measured data and found the maximum convergence zone (CZ) distances corresponding to the eddy center’s sound speed structure. By using observational data, BAO Senliang et al. (2016) [6] demonstrated that cyclonic eddies in the Kuroshio Extension region shift CZ positions forward and reduce CZ widths. ZHU Fengqin et al. (2021a) [7] utilized field observations to analyze warm-core eddy effects in shallow water. They reported that transmission loss differences exceed 30 dB between eddy and non-eddy conditions. CHEN et al. (2022) [8] investigated the combined effects of warm-core eddies and topography on CZs through synchronous hydrographic–acoustic observations. Through deep-water experiments and hydrographic data, WU et al. (2023) [9] revealed that anticyclonic eddies redistribute acoustic energy, altering the positions of CZs and shadow zones. M. A. Sorokin et al. (2023) [10,11] investigated the effect of horizontal refraction caused by an anticyclonic eddy on long-range sound propagation in the Sea of Japan and its influence on acoustic ranging.

Currently, obtaining comprehensive and real-time characteristic data of mesoscale eddies through measurement methods remains challenging, while environmental data can only provide deterministic parameters for specific eddies, which is insufficient for analyzing how variations in eddy parameters affect acoustic propagation patterns. Therefore, this study employs a mesoscale eddy model combined with an ocean acoustic propagation model to analyze acoustic characteristics under different eddy conditions. Through comprehensive investigation of how mesoscale eddies influence sound propagation, along with analysis of acoustic field characteristics under different seabed topographies in mesoscale eddy environments, this research aims to provide valuable physical insights for improving target detection and acoustic source localization technologies in complex marine environments [12,13].

2. Ocean Mesoscale Eddy and Acoustic Field Calculation Models

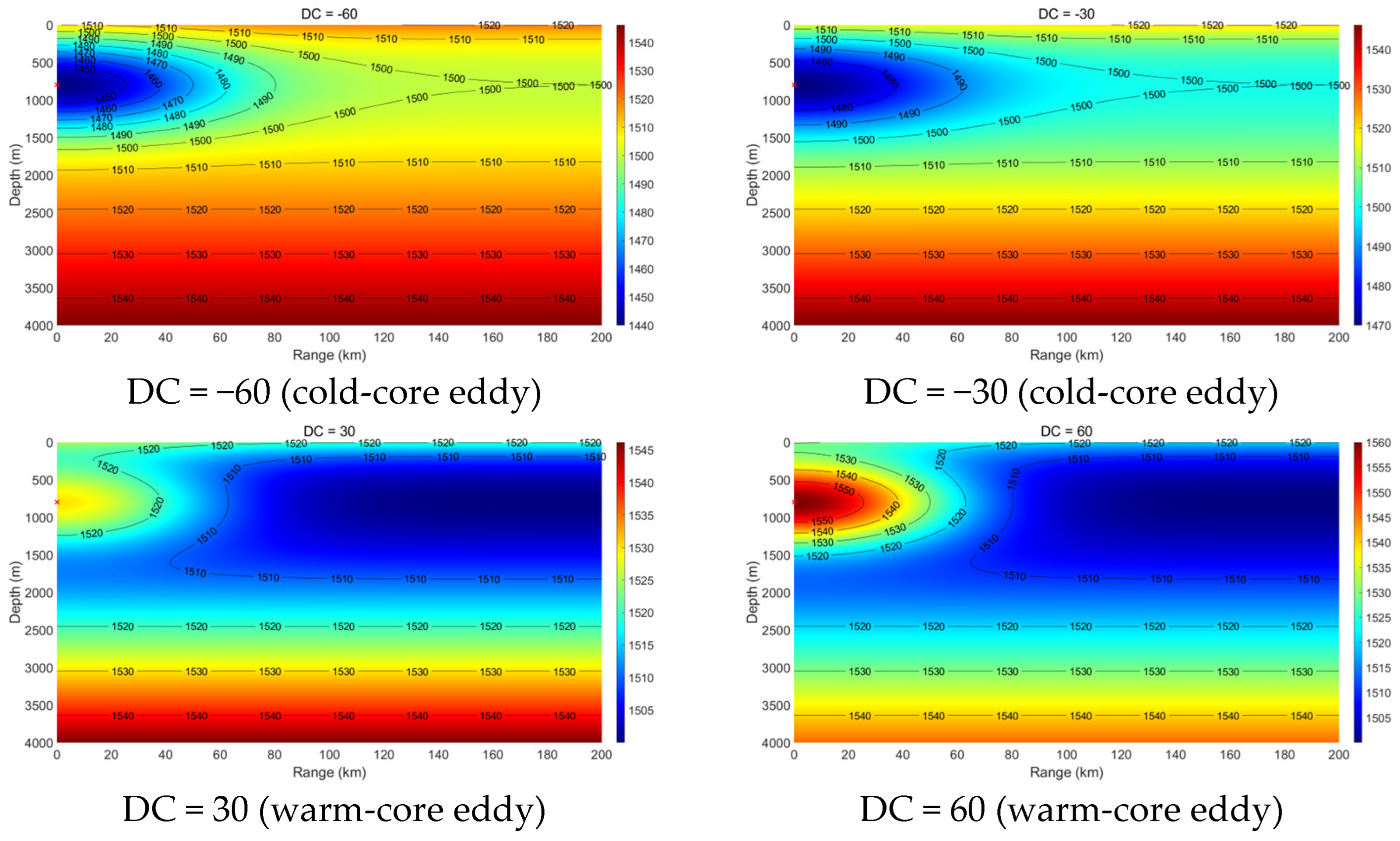
2.1. Ocean Mesoscale Eddy Model

Given the spatial configurations of cold/warm-core eddies and their associated temperature field distributions, a Gaussian eddy model [14,15] is adopted to characterize mesoscale ocean eddies. The sound speed expression is defined as [16]

$$c(r,z)=c_0(z)+\Delta c(r,z),$$

(1)

$$c_0(z)=1500\{1+0.0057[{\mathrm{e}}^{-\eta }-(1-\eta )]\},$$

(2)

$$\Delta c(r,z)=\mathrm{DC}\ast \exp [-{({\displaystyle \frac{r-r_c}{\mathrm{DR}}})}^2-{({\displaystyle \frac{z-z_c}{\mathrm{DZ}}})}^2],$$

(3)

where $c_0(z)$ is the background sound speed profile (Munk profile), $\eta =2\ast (z-1000)/1000$, and $\Delta c(r,z)$ is the Gaussian eddy term. DC represents the eddy intensity, defined as the maximum sound speed difference between the eddy center and periphery induced by an eddy. DC takes negative values for cold-core eddies and positive values for warm-core eddies. DR and DZ denote the horizontal and vertical scales of an eddy, respectively. $r_c$ denotes the horizontal position of the eddy center, whereas $z_c$ represents its vertical position.

The computational domain is configured with a horizontal range of 200 km and water depth of 4000 m by using the parameter values DR = 60 km, DZ = 600 m, $r_c=100 \mathrm{km}$, and $z_c=800 \mathrm{m}$. Sound speed distributions for cold-core eddies, warm-core eddies, and different eddy intensities are obtained by varying DC values.

As shown in Figure 1, sound speed contour maps are generated for DC values of −60, −30, 30, and 60. The results demonstrate the following: Warm-core eddy centers exhibit local sound speed maxima, and cold-core eddy centers exhibit local sound speed minima. Within a specific eddy type (cold core/warm core), increased eddy intensity (|DC|) yields progressively densifying sound speed contours. This finding confirms the Gaussian eddy model’s capability to represent mesoscale ocean eddy phenomena accurately. By adjusting model parameters, acoustic propagation characteristics under varying eddy conditions can be systematically analyzed.

2.2. Acoustic Field Calculation Model

The BELLHOP ray model [17] is selected for acoustic field computation. This model, which was developed by Porter through the Gaussian beam approximation method from geoacoustics, effectively addresses the influence of caustics on sound field calculations. Compared with conventional ray models, it demonstrates remarkable improvements in handling acoustic energy focusing and shadow zones while maintaining capability for 3D sound field simulations [18,19].

BELLHOP integrates two differential equations governing sound beam width and curvature alongside standard ray equations to compute the acoustic field near beam centers. Gaussian beam ray tracing initializes beam width and curvature at the source, permitting curvature variations during outward propagation. Beam evolution is determined by the beam width parameter $p$ and curvature parameter $q$ [20].

$${\displaystyle \frac{\mathrm{d}p}{\mathrm{d}s}}=c(s)p(s),$$

(4)

$${\displaystyle \frac{\mathrm{d}q}{\mathrm{d}s}}=-{\displaystyle \frac{c_m}{c^2(s)}}q(s),$$

(5)

where $c_m$ denotes the second derivative of the sound speed normal to the ray path.

The Gaussian beam, given the initial width and curvature of the sound source, allows its curvature to increase or decrease as it propagates outward from the source. The solution in the vicinity of the central ray that can ultimately be derived is

$$p(s,n)=A{\sqrt{{\displaystyle \frac{c(s)}{rq(s)}}}}^{\{-j\omega [\tau (s)+{\displaystyle \frac{p(s)}{2q(s)}}{n}^2]\}}$$

(6)

In this expression, $A$ is an arbitrary constant, $n$ is the perpendicular distance from the central ray, and ${\tau }_s$ is the phase delay along the ray path. $p$ and $q$ are chosen as complex numbers. Therefore, the real and imaginary parts of $p/q$ can be associated with the beam width $W$ and curvature $K$:

$$W(s)=\sqrt{{\displaystyle \frac{-2}{\omega I_m[p(s)/q(s)]}}}$$

(7)

$$K(s)=-c(s)\mathrm{Re}[p(s)/q(s)]$$

(8)

Dynamic ray equations can thus be solved simply by using complex initial conditions representing the initial beam width and curvature. Finally, by summing all the beams, the complex sound pressure is obtained, where the weighting coefficients for the individual beams are determined by the standard point source problem in a homogeneous medium. For a point source, the corresponding weighting for the beams is:

$$A({\theta }_0)=\delta {\theta }_0{\displaystyle \frac{1}{c_0}}\sqrt{{\displaystyle \frac{q(0)\omega \cos {\theta }_0}{2\pi }}}{\mathrm{e}}^{{\displaystyle \frac{j\pi }{4}}}.$$

(9)

In this expression, $\delta {\theta }_0$ is the angle between the beams, and ${\theta }_0$ is the emission angle.

3. Study on the Influence of Mesoscale Eddies on Sound Propagation in the Ocean

Disturbances in the sound speed field induced by mesoscale eddies can markedly affect sound propagation, thereby altering the acoustic characteristics of the sea area. According to the fundamental principles of sound propagation, acoustic rays always bend toward regions of low sound speed. The presence of mesoscale eddies modifies the sound speed distribution, affecting propagation in surface ducts and deep sound channels.

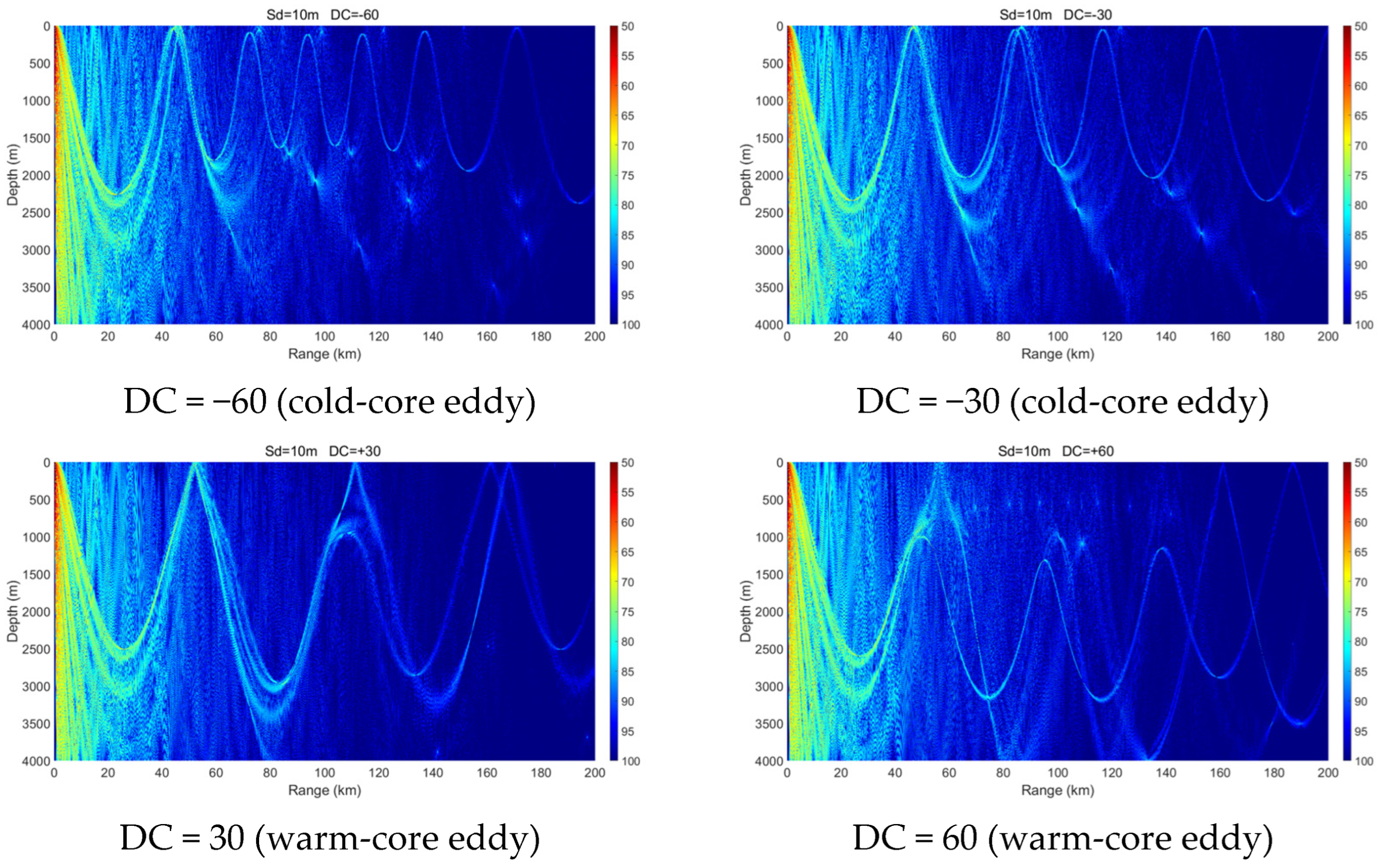
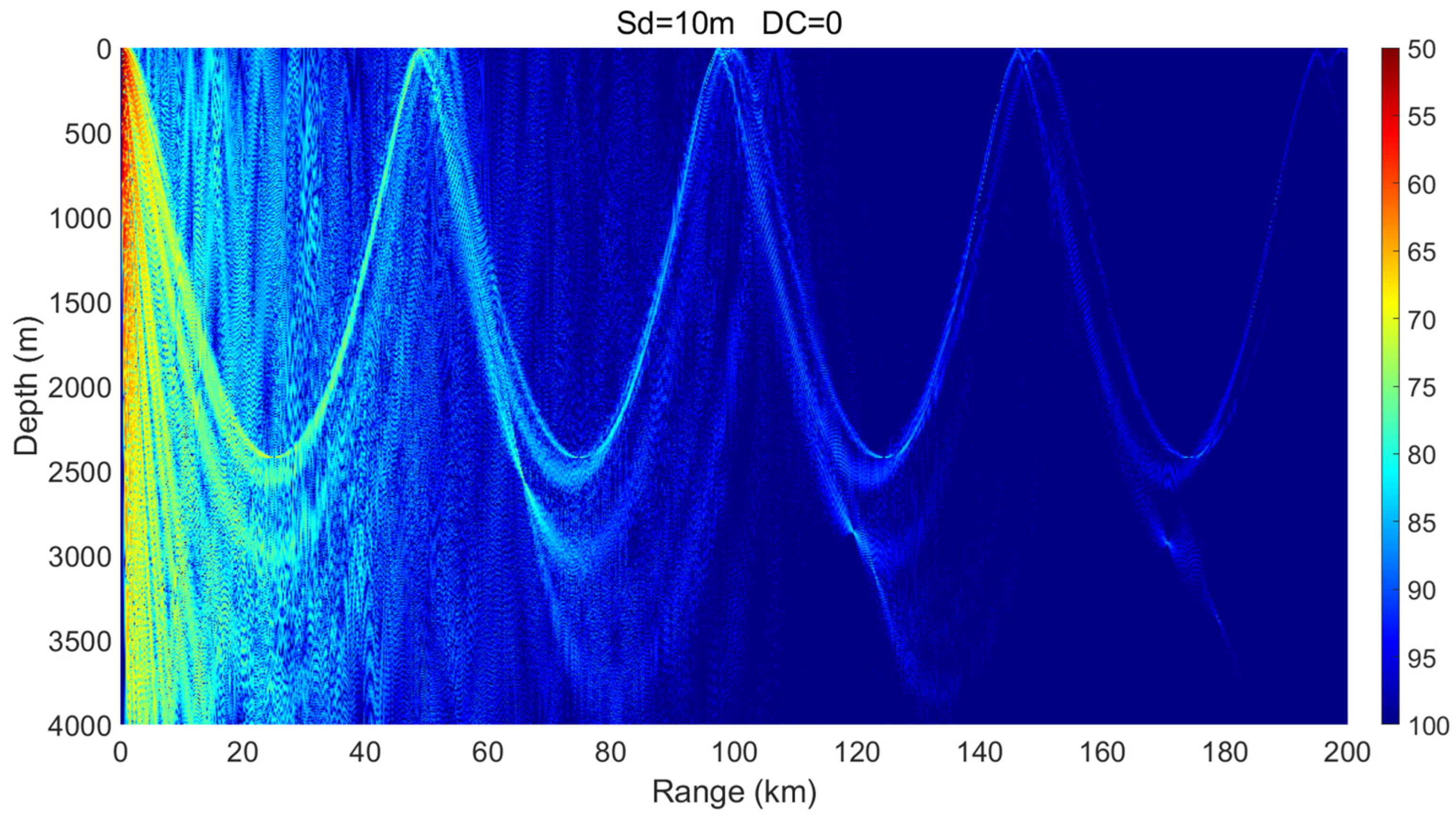
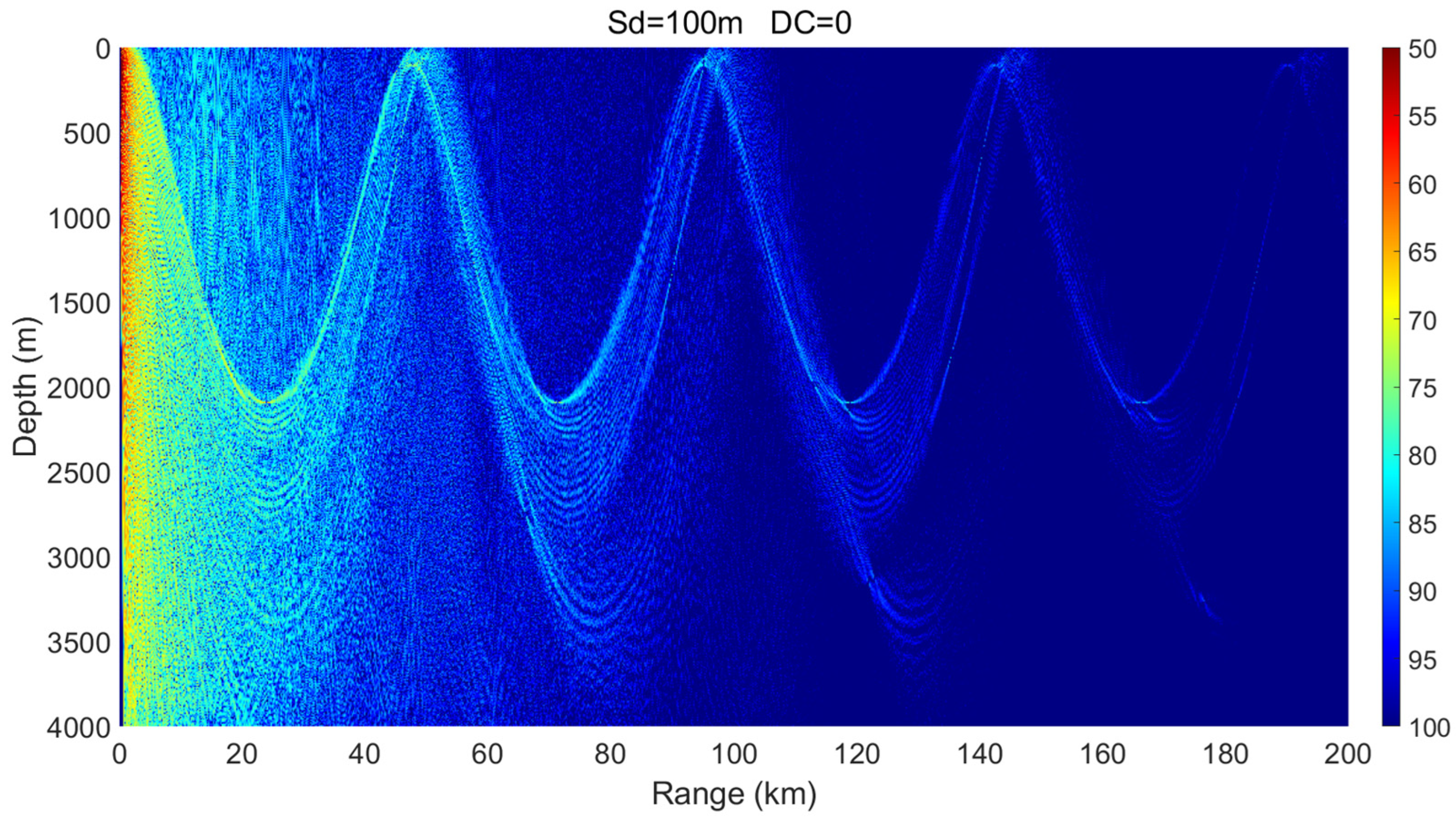
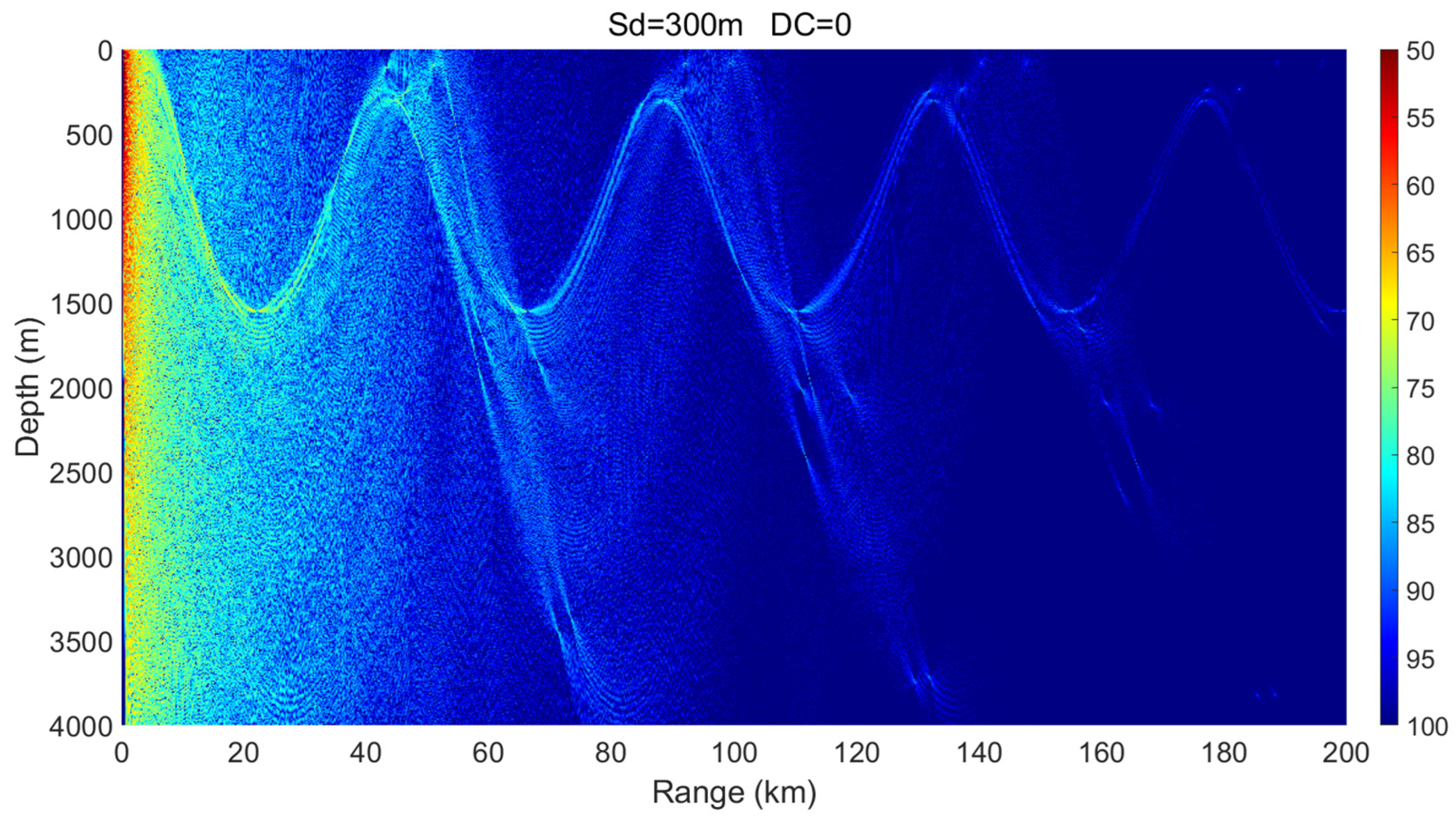
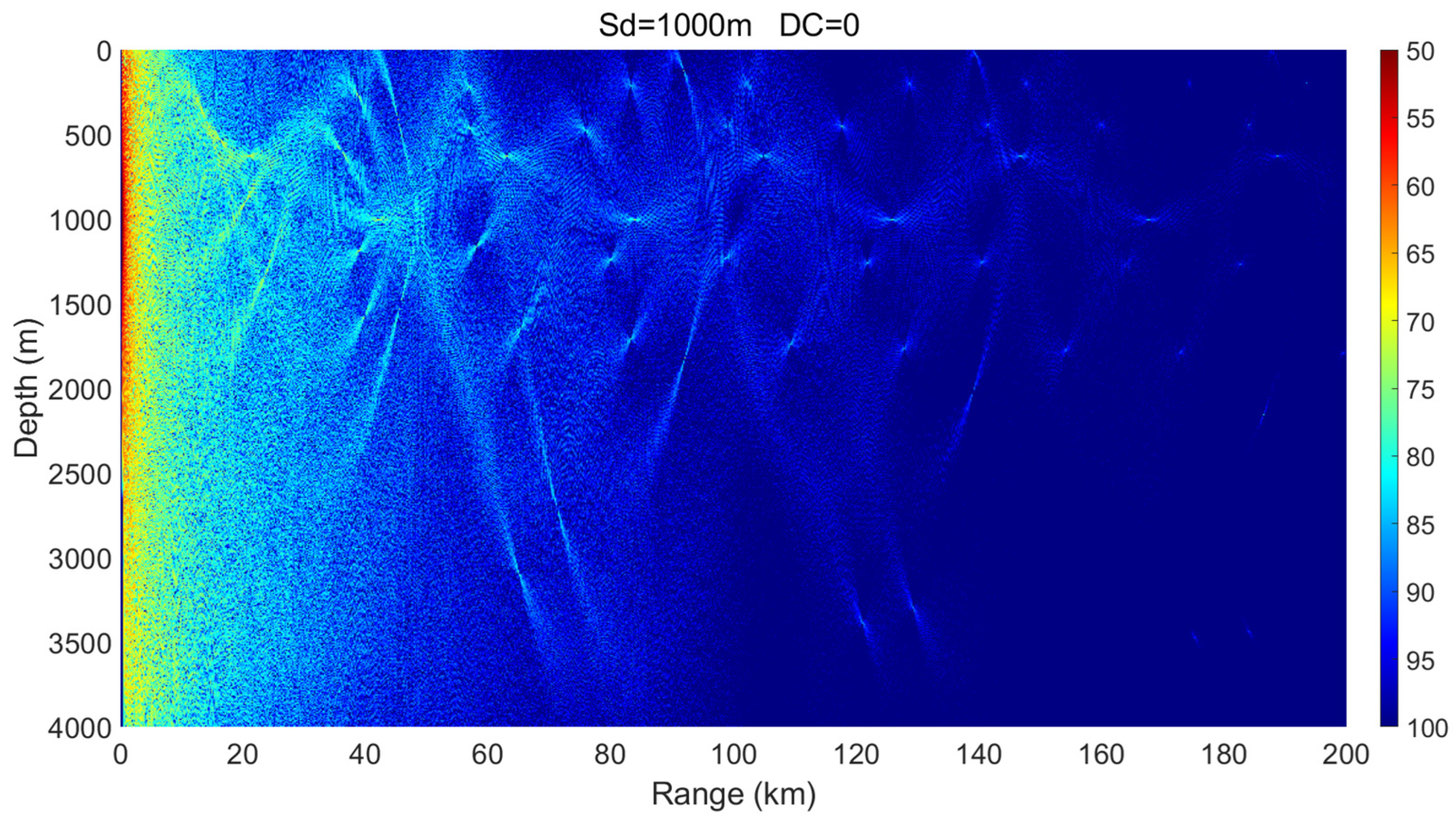
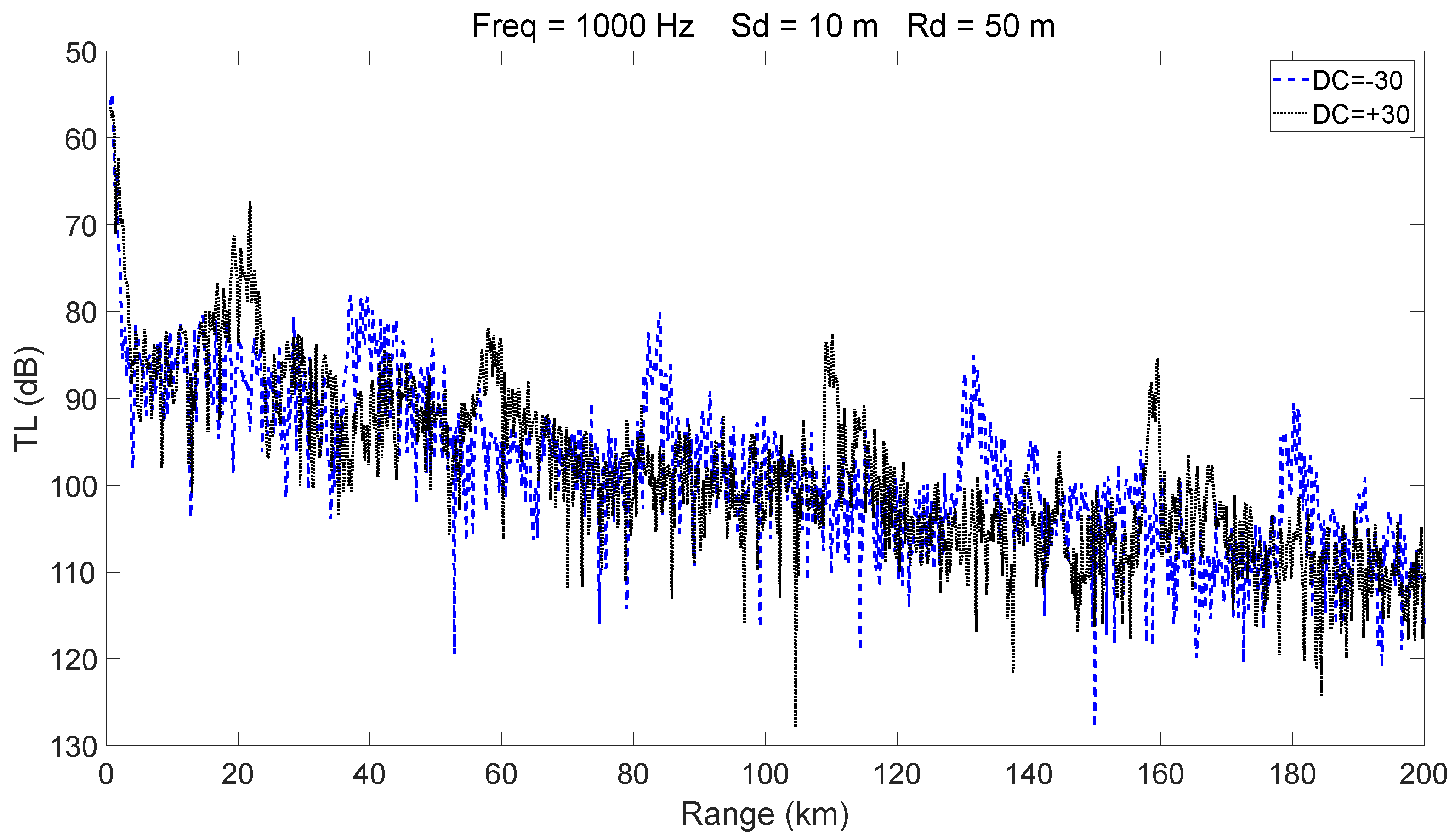
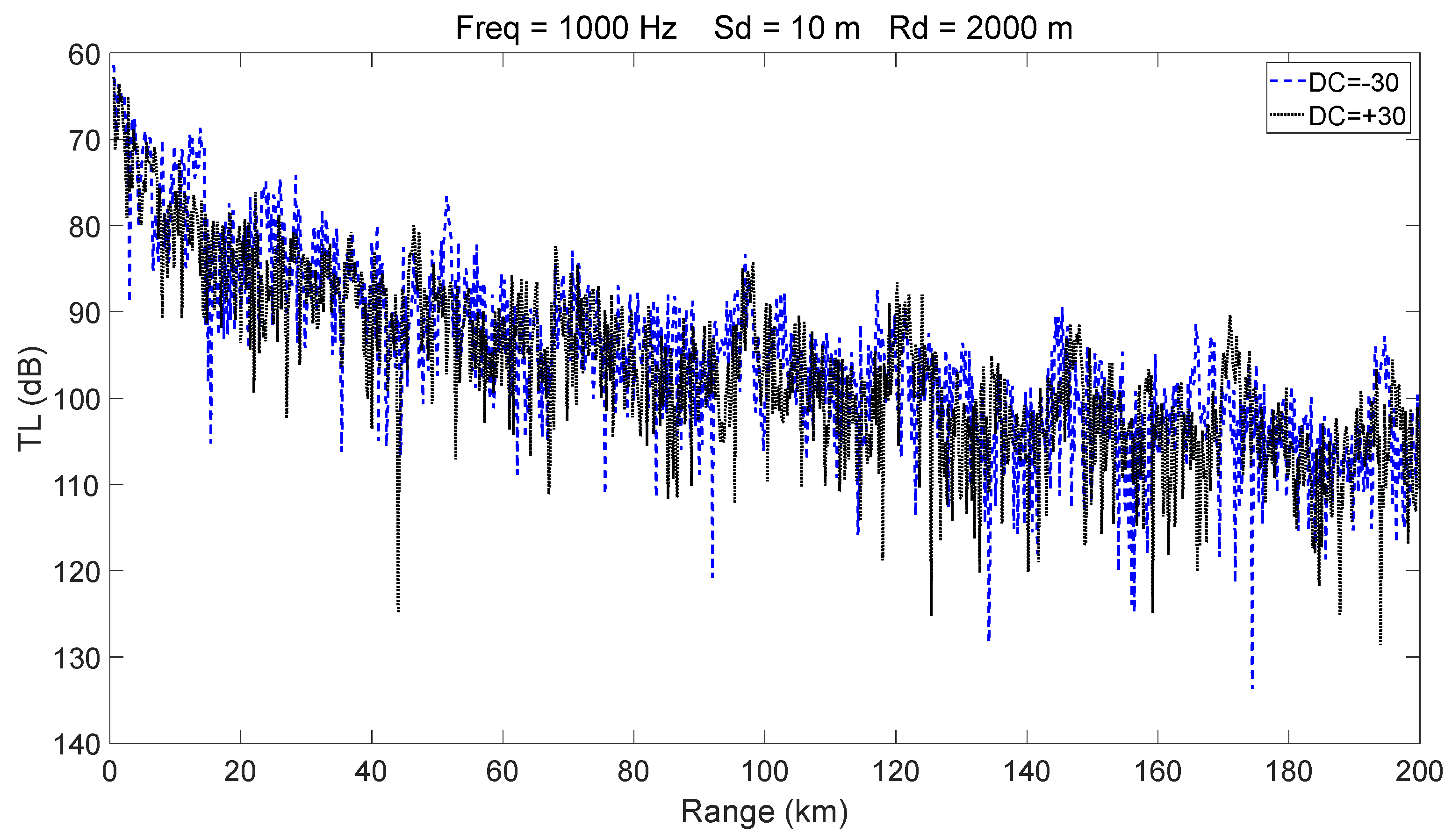
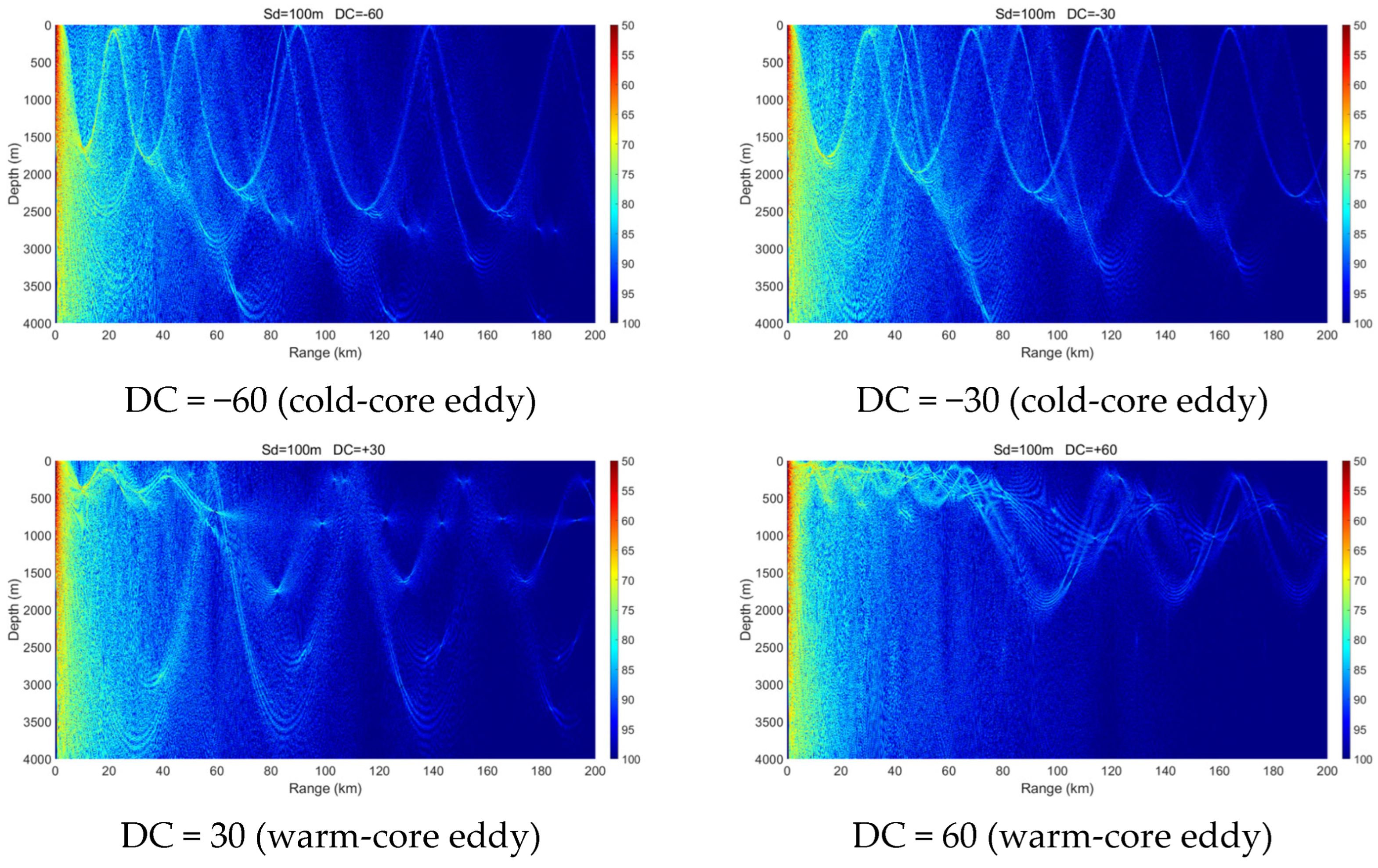
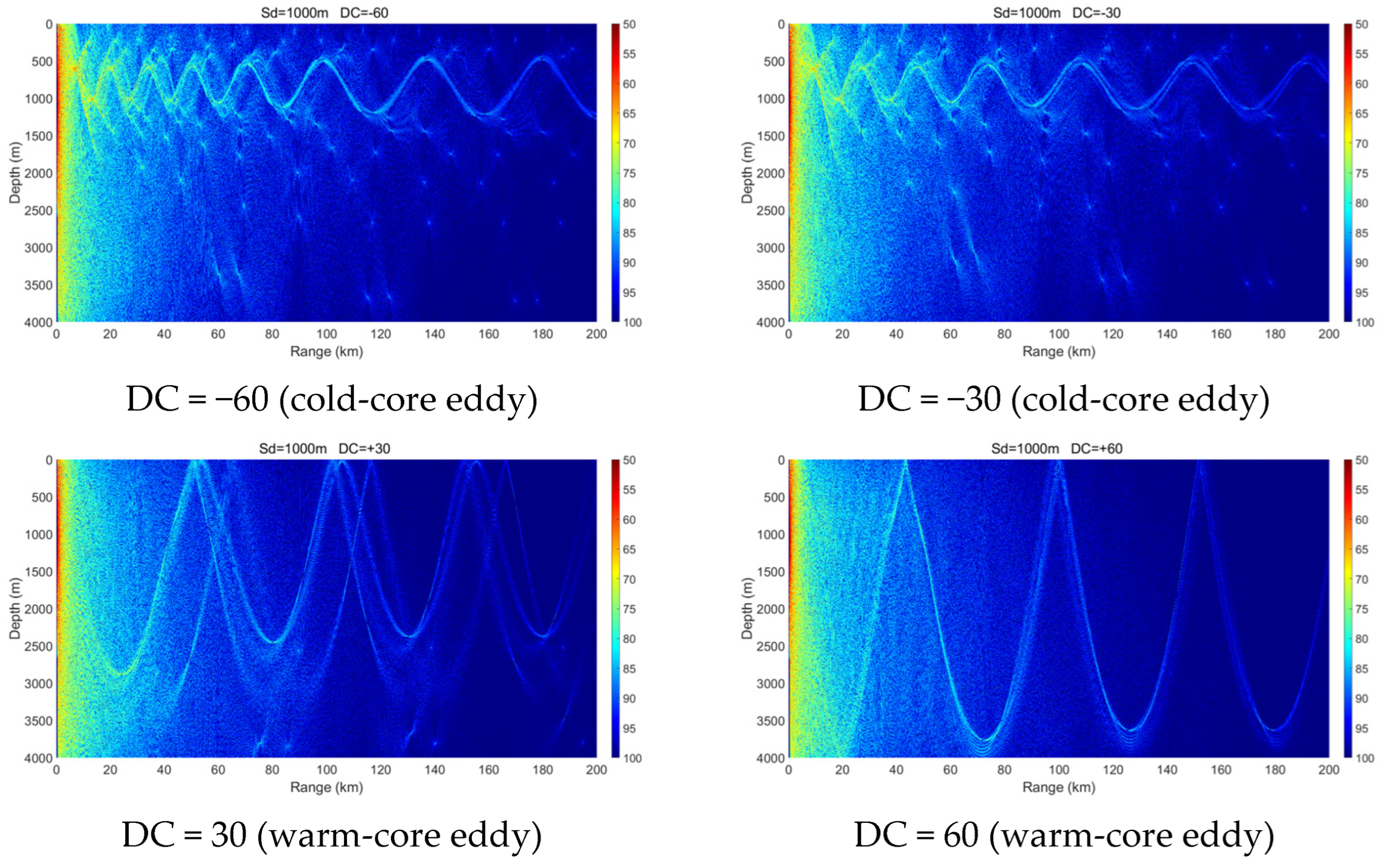
3.1. Sound Source Located Outside an Eddy

This section presents the examination of sound propagation through an eddy when the source is positioned at different depths (10, 100, 300, and 1000 m) outside the eddy. This analysis is conducted with a source frequency of 1000 Hz, calculation depth of 4000 m, horizontal range of 200 km, and a flat seafloor. DC values of −60, −30, 30, and 60 are considered. Seawater acoustic absorption coefficient is expressed as [21,22]: $\alpha =3.3\times {10}^{-3}+{\displaystyle \frac{0.11f^2}{1+f^2}}+{\displaystyle \frac{44f^2}{4100+f^2}}+3\times {10}^{-4}{f}^2$; When the source frequency is 1000 Hz, the seawater acoustic absorption coefficient is 0.069 dB/km. The seafloor absorption coefficient is set as [22]: ${\alpha }_p=0.8\mathrm{dB}/\lambda$.

The results obtained under the conditions described above are compared with those acquired under eddy-free conditions to analyze the eddy’s influence on sound propagation.

Source Depth: 10 m

Figure 2 presents the calculated sound fields for a source depth of 10 m under different eddy intensities. For comparison, Figure 3 shows the sound field under eddy-free conditions at the same source depth (10 m).

Comparing Figure 2 and Figure 3 reveals that when sound waves pass through a cold eddy, the position of the CZ shifts forward, the entire CZ experiences an uplifting effect, and the CZ width decreases. Strong cold eddy intensities are associated with narrow CZ widths. When sound waves pass through a warm eddy, the position of the CZ shifts backward, the CZ width increases, and the CZ depth exhibits a depressing effect. For example, when DC = 60, the first CZ depth is depressed to approximately 1000 m, and the second CZ is depressed to approximately 1500 m. After traversing the warm eddy, the CZ depth returns to normal.

As shown in the sound speed profiles in Figure 1, after entering the cold eddy region, as a result of the decrease in temperature, the sound speed near the channel axis decreases overall, and the number of times that sound waves refract toward the center increases. This change in the vertical distribution structure of sound speed leads to the entire CZ experiencing an uplifting effect and shrinking when sound waves pass through the cold eddy. When entering the warm eddy region, the original sound speed near the channel axis increases overall because of the increase in temperature, causing the point of minimum sound speed to appear at a deep region, and the number of sound wave refractions decreases. Taking DC = 60 as an example, within the warm eddy region, the depth of the minimum sound speed point is approximately 2000 m.

Therefore, when sound waves pass through a warm eddy, the depth of the CZ exhibits a remarkable depressing effect.

To quantitatively analyze the effects of different mesoscale eddies on acoustic propagation loss within a 200 km range, Figure 4 and Figure 5 present the distribution of propagation loss for DC values of −30 and +30 at reception depths of 50 m and 2000 m, respectively. It can be observed that at shallower receiver depths, the convergence zone width under cold-eddy conditions is narrower than that under warm-eddy conditions, with more convergence zones appearing within a 200 km range in the cold-eddy scenario. At greater receiver depths, however, the results for cold and warm eddies show little difference.

Source Depth: 100 m

The sound field results calculated under different eddy intensities when the source depth is 100 m are shown in Figure 6. The sound field result calculated under eddy-free conditions at a source depth of 100 m is presented in Figure 7. When the source depth further increases, the CZ width under cold eddy conditions further shrinks. By contrast, under warm eddy conditions, the CZ depth is further depressed, and the CZ width increases further. Additionally, when DC = 60, a propagation path similar to a channel axis forms near the surface because at this eddy intensity, a sound speed minimum point exists near the depth of 150 m, indicating that a negative sound speed gradient from 0 m to 150 m and a positive sound speed gradient from 150 m to 800 m exist, forming a structure analogous to a deep-sea sound channel axis in the surface layer.

Source Depth: 300 m

The sound field results calculated under different eddy intensities when the source depth is 300 m are shown in Figure 8. The sound field result calculated under eddy-free conditions at a source depth of 300 m is given in Figure 9. As the source depth increases further, the CZ width under cold eddy conditions shrinks further, the shoreward shift in the CZ becomes increasingly pronounced, and the turning depth of the CZ remarkably increases. For warm eddies, the CZ depth is notably depressed. Additionally, when DC = 30, a propagation path similar to a channel axis forms near the surface because at this eddy intensity, a sound speed minimum exists near the depth of 280 m, allowing the acoustic energy entering this layer to be effectively confined within the channel without leakage.

Figure 10 and Figure 11 show the sound propagation loss results for a source depth of 300 m at receiver depths of 50 m and 2000 m, respectively. It can be observed that at the shallower receiver depth (50 m), warm-eddy conditions provide relatively better propagation performance. At the deeper receiver depth (2000 m), the overall difference in acoustic propagation effects between cold and warm eddies is minimal. Notably, at a reception distance of approximately 150 km, a local minimum in propagation loss occurs under warm-eddy conditions, suggesting a potential opportunity for long-range detection in warm-eddy environments.

Source Depth: 1000 m

The sound field results calculated under different eddy intensities when the source depth is 1000 m are provided in Figure 12. The sound field result calculated under eddy-free conditions at a source depth of 1000 m is shown in Figure 13. The presence of cold eddies induces the intense refraction of acoustic rays near the sound channel axis, thereby enhancing the propagation effect of the deep-sea sound channel. Conversely, the appearance of warm eddies weakens the convergence gain effect, leading to the fragmentation of the CZ beyond certain distances.

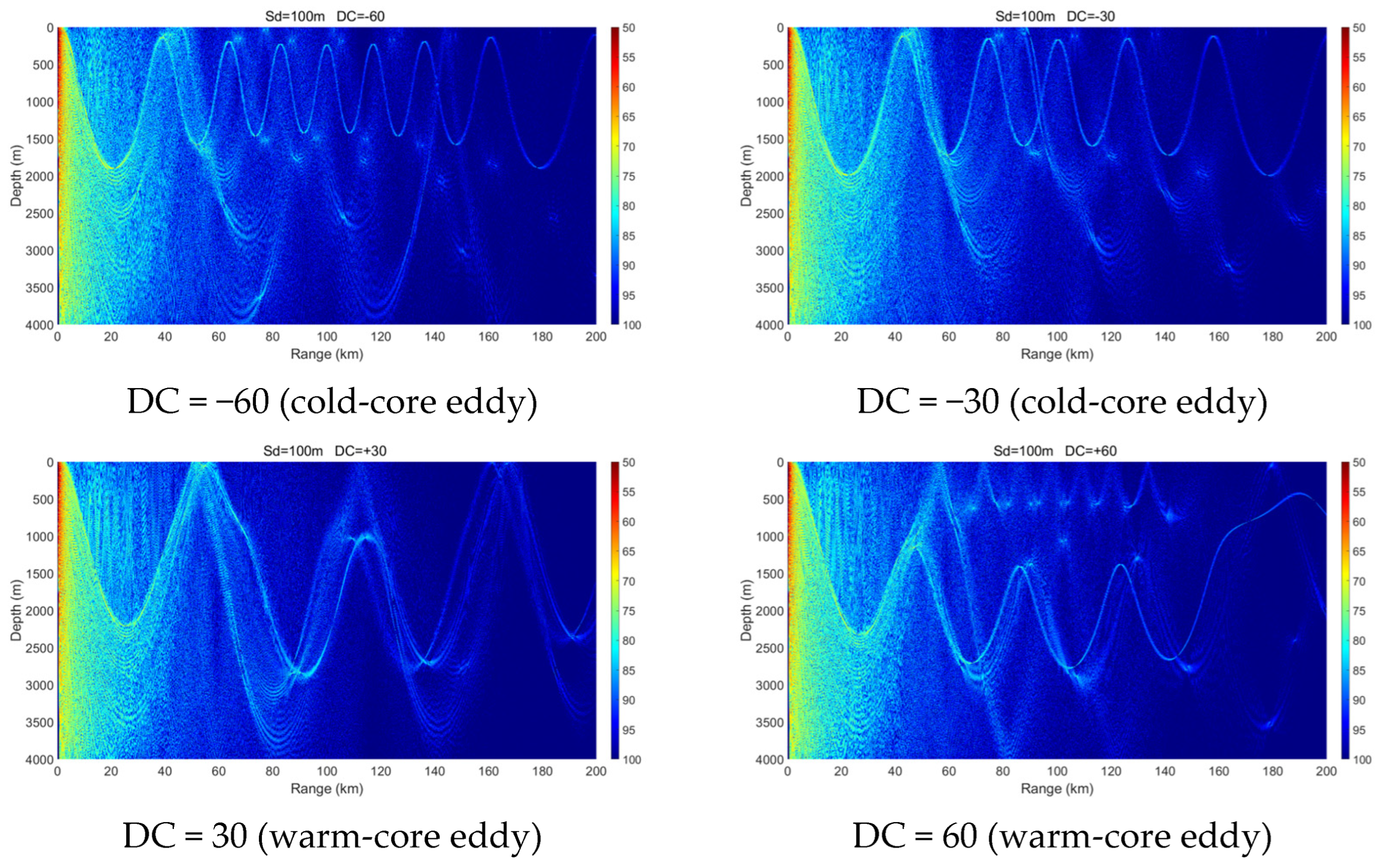
3.2. Sound Source Located at the Eddy Center

Previous analyses addressed sound propagation when the source is outside the eddy and waves traverse the eddy. The acoustic characteristics when the source is positioned at the eddy center are now examined. The source frequency is maintained at 1000 Hz, with a calculation depth of 4000 m, horizontal range of 200 km, and flat seafloor. Simulations are conducted at source depths of 10, 100, 300, and 1000 m, with DC = −60, −30, 30, and 60.

The sound speed distributions reflecting eddy intensity variations at different distances are given in Figure 14.

The calculated sound field results under different eddy intensities when the source depth is 10 m and positioned at the eddy center are given in Figure 15. Comparison with Figure 3 reveals that when the source is at the center of a cold eddy, the first and second CZs shift shoreward toward the source under the influence of the eddy. When the source is at the center of a warm eddy, a positive sound speed gradient forms in the surface layer under the effect of the warm eddy, creating surface duct propagation within the 0–60 km range.

Figure 16 and Figure 17 present the sound propagation loss results for a source depth of 10 m propagating outward from the eddy center, at receiver depths of 50 m and 2000 m, respectively. The analysis shows that at the shallow receiver depth (50 m), a convergence structure emerges at relatively close range under warm-eddy conditions, whereas the first convergence zone under cold-eddy conditions occurs farther away. This suggests that deployment strategies for acoustic detection should differ between cold and warm eddies. At the deeper receiver depth (2000 m), the overall difference in acoustic propagation effects between cold and warm eddies is relatively small.

The calculated sound field when the source depth is 100 m and positioned at the eddy center under different eddy intensities is shown in Figure 18. Comparison with Figure 5 demonstrates that when the source is at the center of a cold eddy, the presence of the cold eddy causes the CZ position to shift shoreward, the CZ width to decrease, and the CZ depth to rise. When the source is at the center of a warm eddy, a propagation pattern of a sound channel axis forms in the surface layer under the influence of the warm eddy.

The sound field results calculated under different eddy intensities when the source depth is 300 m and positioned at the eddy center are illustrated in Figure 19. Comparison with Figure 9 shows that when the source is at the center of a cold eddy, the presence of the cold eddy causes the CZ position to shift shoreward, with the increased eddy intensity resulting in a pronounced shift effect. When the source is at the center of a warm eddy, a propagation pattern of a sound channel axis forms in the surface layer under the influence of the warm eddy.

The sound field results calculated under different eddy intensities when the source depth is 1000 m and positioned at the eddy center are given in Figure 20. Comparison with Figure 13 demonstrates that when the source is at the center of a cold eddy, the presence of the cold eddy similarly causes the CZ position to shift shoreward, the CZ width to decrease, and the CZ depth to rise, with the increased eddy intensity resulting in a pronounced shoreward shift effect and a small CZ width. When the source is at the center of a warm eddy, the CZ width increases, and as a result of the increased source depth combined with the influence of the sound speed gradient, acoustic rays exhibit a remarkable downward depression.

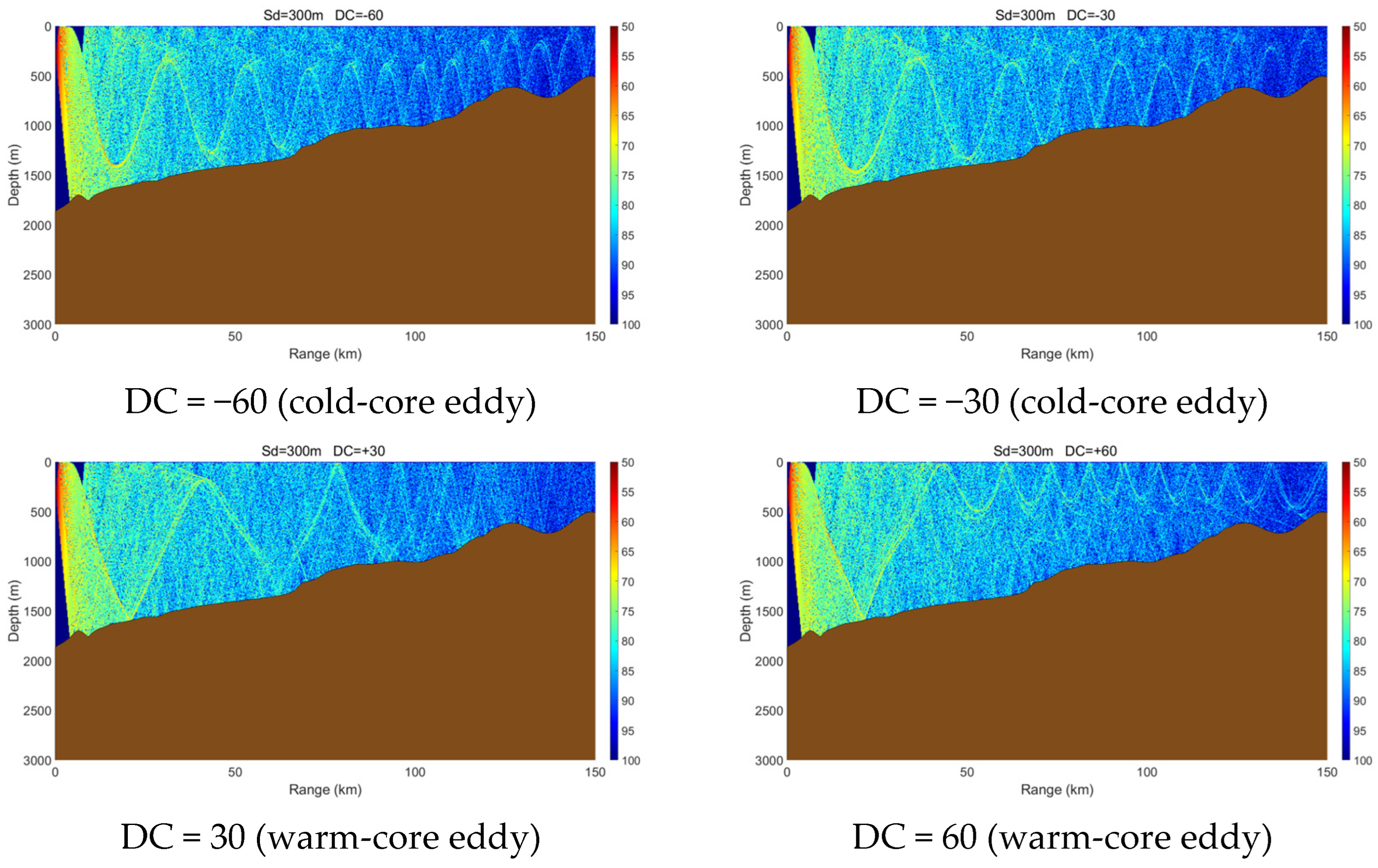
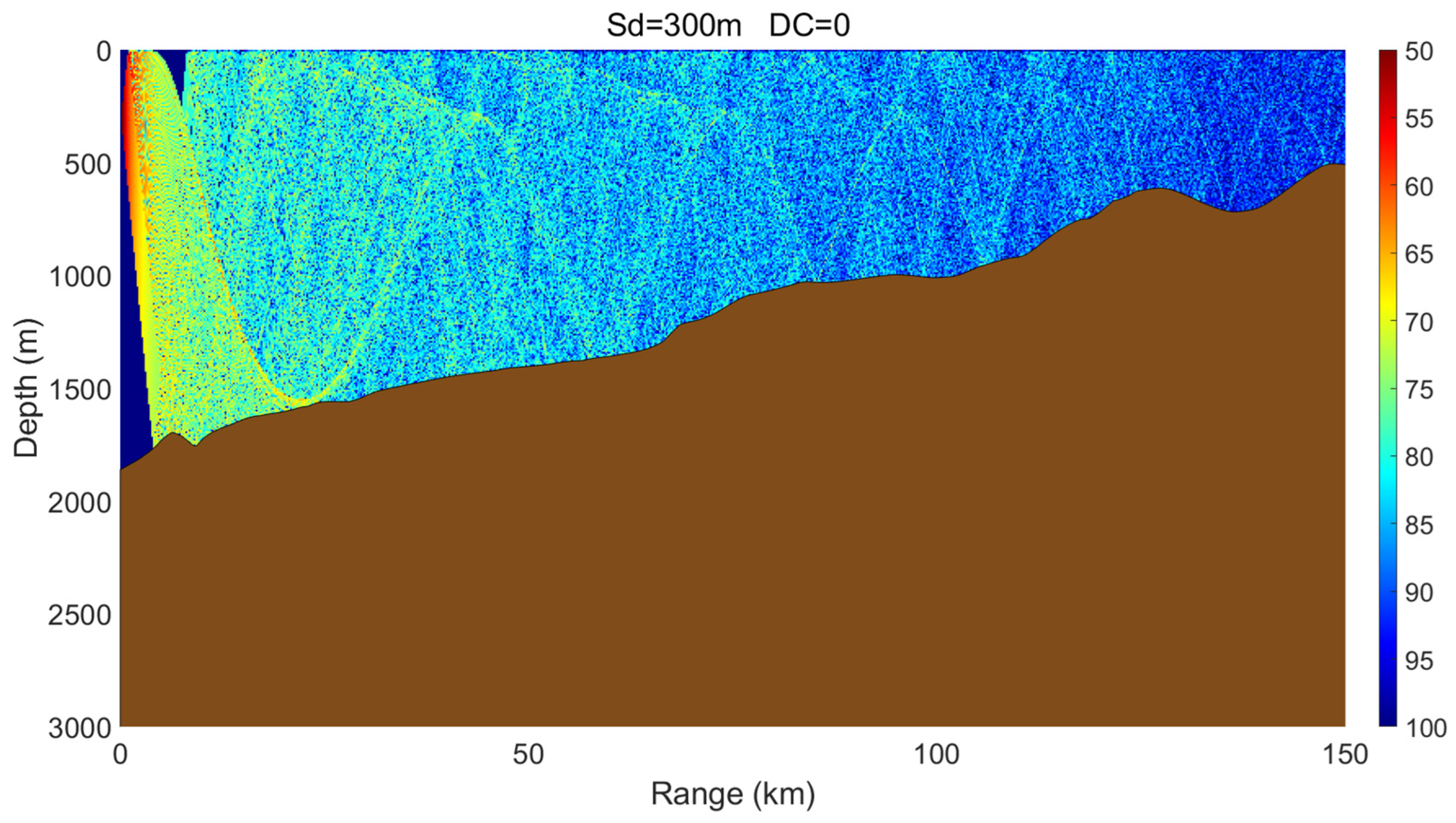
3.3. Effects of Variable Seabed Topography

The preceding analysis assumed a flat seabed. In reality, the seafloor exhibits complex and variable topography [23]. Such bathymetric variations can significantly modulate acoustic propagation within mesoscale eddy environments—a coupled interaction that has received limited attention in existing literature. To address this gap, the present study employs the actual bathymetry of the South China Sea, a region renowned for its high mesoscale eddy activity as a basis for investigation [24,25]. The topographic data were sourced from the GEBCO_2020 global grid [26]. We systematically examine the characteristics of acoustic propagation under three distinct topographic scenarios: up-slope, down-slope, and seamount-affected. For all simulations, a sound source at a depth of 300 m with a frequency of 1000 Hz was configured.

3.3.1. Up-Slope Propagation

Figure 21 and Figure 22 depict the acoustic field characteristics for up-slope propagation. Under this condition, the presence of a cold-core eddy narrows the convergence zone, a result consistent with simulations assuming a flat seabed. In contrast, a warm-core eddy induces a pronounced uplift of the acoustic propagation paths. The magnitude of this uplift is positively correlated with the eddy’s intensity, a phenomenon that diverges markedly from the acoustic behavior predicted in flat-bottomed environments.

For example, in the scenario with an eddy intensity (DC) of 60, acoustic rays are initially refracted downward, interacting with the seabed at relatively short ranges. The sloping topography then facilitates efficient reflection of this energy toward the sea surface. Subsequently, influenced by the warm-core eddy, the acoustic signal becomes trapped in a surface duct, enabling sustained propagation along the surface layer.

3.3.2. Down-Slope Propagation

Figure 23 and Figure 24 illustrate the down-slope propagation results. Under this condition, the presence of a cold-core eddy narrows the convergence zone, a finding consistent with the acoustic patterns observed over a flat seabed. In contrast, the propagation characteristics under a strong warm-core eddy differ markedly from the flat-seabed case. Specifically, while the deep sound channel weakens, a distinct surface duct forms, giving rise to a dual-channel propagation phenomenon. This unique mechanism offers practical potential for enhancing target detection performance in operational scenarios.

3.3.3. Seamount-Affected Propagation

Figure 25 and Figure 26 illustrate the acoustic propagation results in the presence of a seamount. It can be observed that when a seamount obstructs the propagation path, the acoustic field is less affected under the cold-core eddy condition. This is attributed to the upward refraction of the convergence zone induced by the cold-core eddy, which lifts acoustic energy away from the seamount, reducing interaction with the topography. In contrast, under the warm-core eddy condition, the downward refraction of the CZ enhances acoustic interaction with the seamount, leading to more significant propagation distortion.

For example, in the case of DC = 30, the transmission loss in the first CZ, located upstream of the seamount, remains largely unaffected. However, the second and third CZs, situated downstream of the seamount, exhibit markedly increased transmission loss, and their distinct spatial patterns become less pronounced.

4. Conclusions

Based on the Gaussian eddy model, this study established a theoretical framework for oceanic mesoscale eddies and employed the BELLHOP underwater acoustic model to analyze sound propagation characteristics with sources located both outside and at the center of eddies. The influence of variable seabed topography on acoustic propagation under different eddy conditions was also investigated. The main conclusions are as follows:

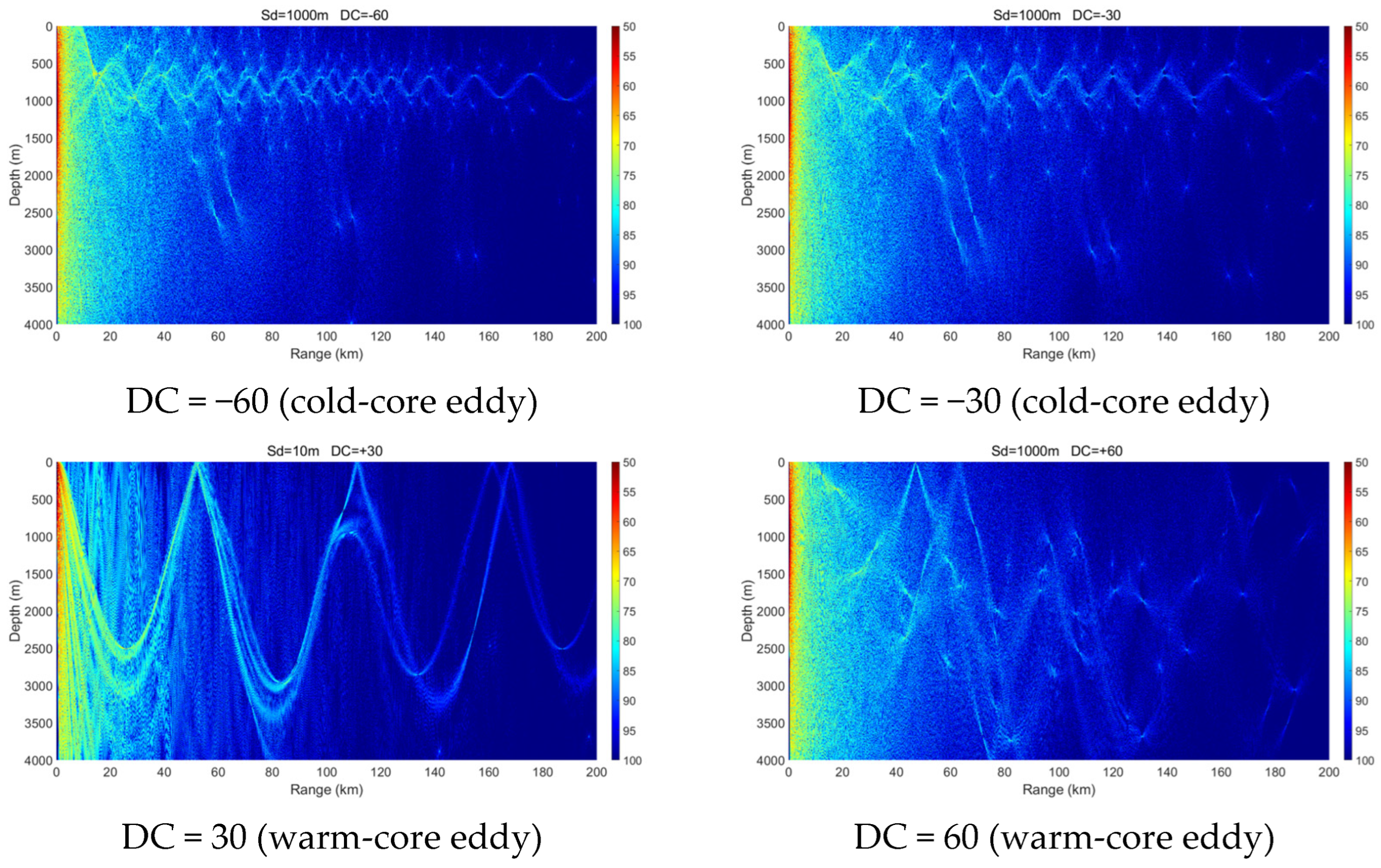
• Mesoscale eddies alter the vertical sound speed distribution, and such alterations—particularly when modifying sound channel properties such as the surface channel or the deep sound channel—can lead to significant changes in acoustic propagation behavior. Warm-core and cold-core eddies exhibit distinctly different propagation mechanisms.
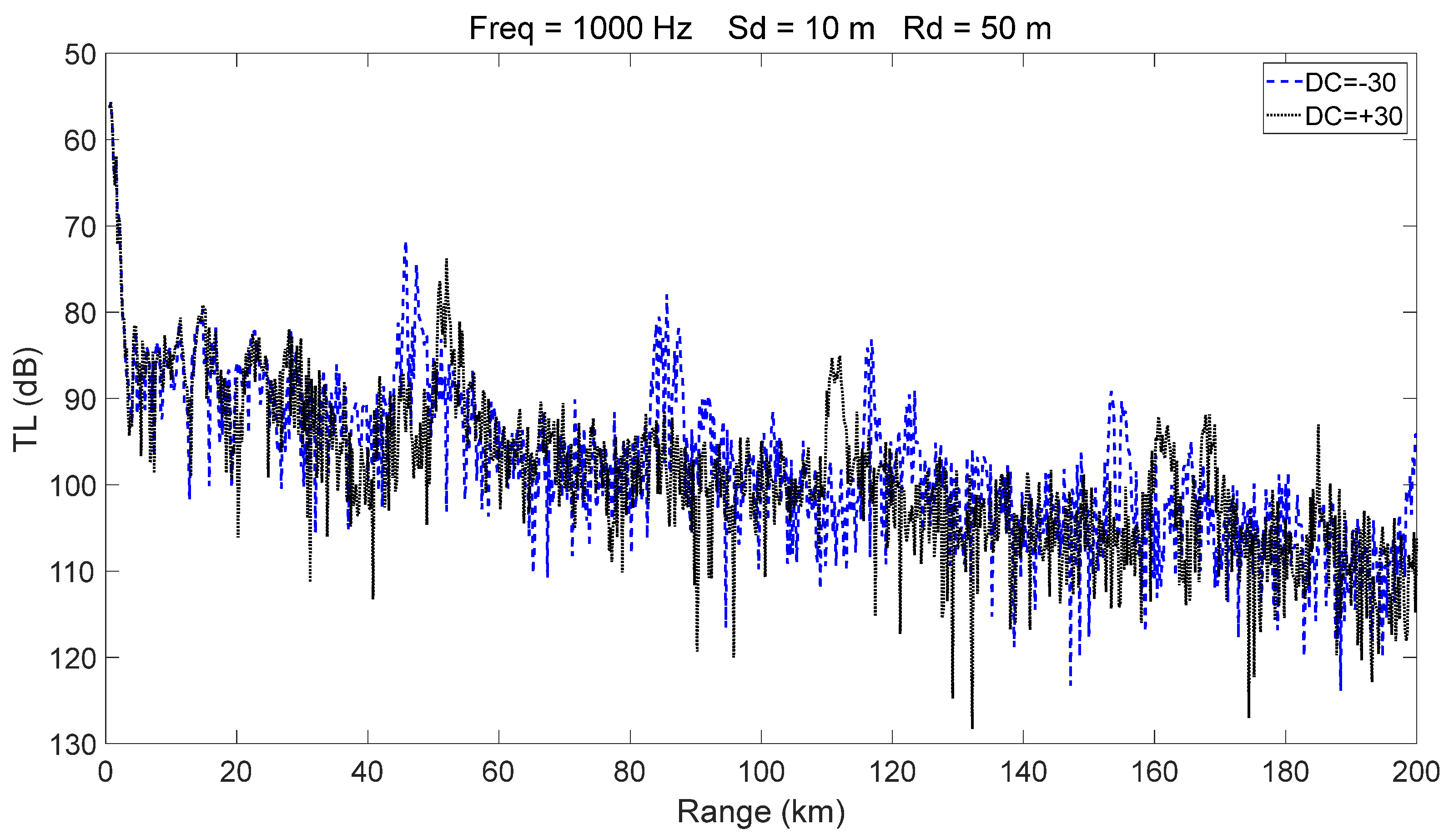
• Within a certain depth range, cold-core eddies shift the convergence zone forward, reduce its width, and elevate its depth, whereas warm-core eddies displace it backward and broaden its width. The magnitude of these effects is positively correlated with eddy intensity.
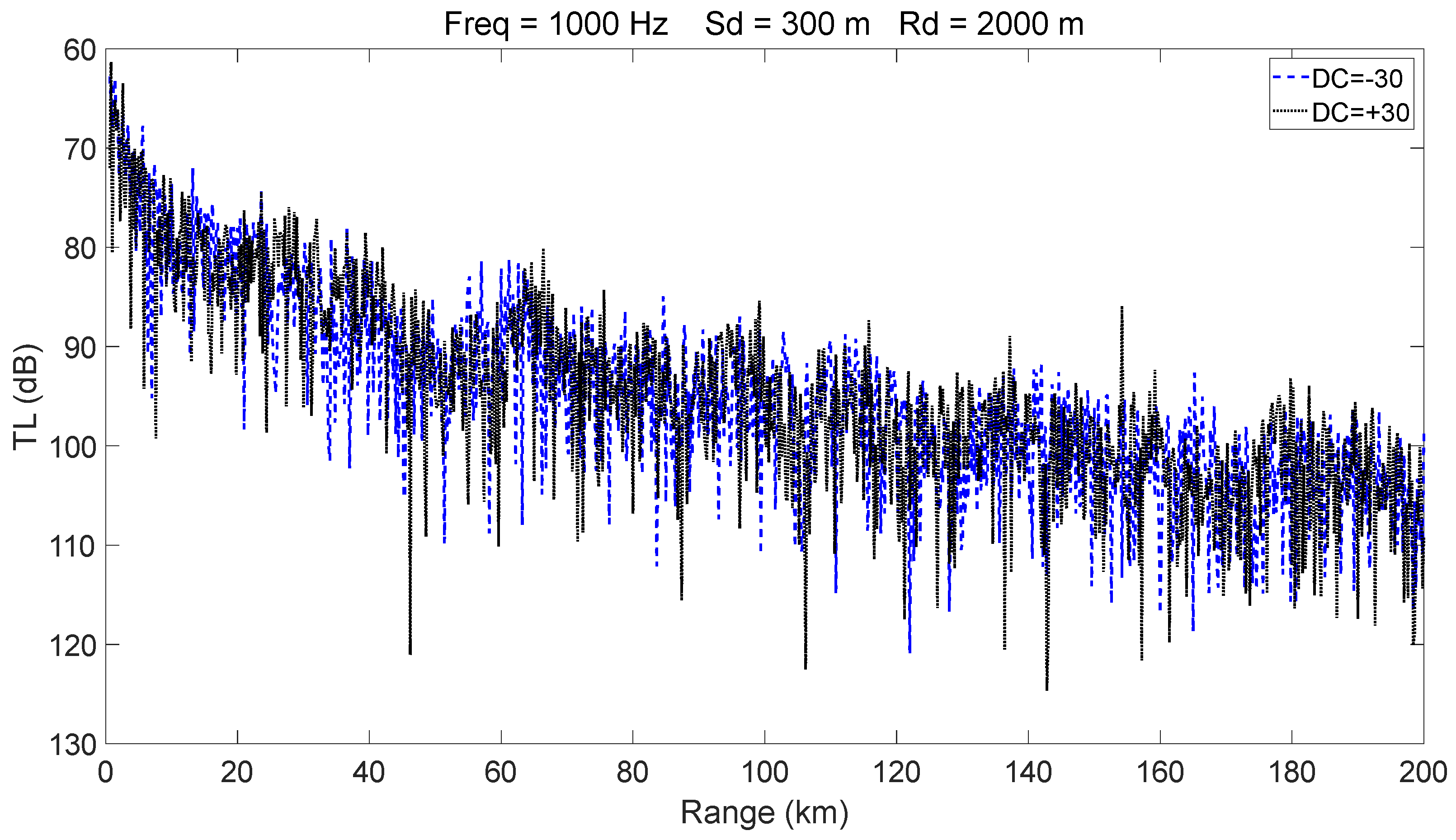
• The presence of a warm-core eddy in the convergence region weakens the convergence gain and leads to noticeable convergence zone splitting beyond a certain range. In contrast, a cold-core eddy enhances the convergence gain under the same conditions.
• Under warm-core eddy conditions, influenced by variations in both source depth and seawater depth, a surface duct structure analogous to the deep-water sound channel axis may form. This structure can effectively trap and guide acoustic energy with minimal leakage.
• A cold-core eddy behaves as an upward-focusing acoustic lens, refracting sound rays upward and concentrating acoustic energy in the upper ocean, which makes propagation relatively insensitive to seabed topography. In contrast, a warm-core eddy acts as a downward-focusing acoustic lens, enhancing downward refraction and increasing acoustic interaction with the seabed. As a result, its propagation characteristics are strongly modulated by seabed variations, exciting complex phenomena such as surface ducts, dual-channel propagation, or significant acoustic loss in different topographic settings.