Effects of Anchor Chain Arrangements on the Motion Response of Three-Anchor Buoy Systems

Abstract

As a new kind of large observation platform, the three-anchor buoy system can effectively realize multifunctional ocean observation, e.g., ocean profiling and autonomous underwater vehicle docking. In order to understand effects of different anchor chain arrangements on the motion response of the three-anchor buoy system under the coupling effect of wind, wave, and current loads, a hydrodynamic model of the buoy system was developed. Wave-period-dependent characteristics of added mass, radiation damping, and the motion response amplitude operator (RAO) were analyzed to derive their response curves; the effects of adding additional viscous damping on RAO performance were investigated. Subsequently, frequency domain and time domain analyses were conducted on five three-anchor buoy systems with distinct anchor chain arrangements to investigate the variation patterns of 6-DOF motion response amplitudes, top-chain tension characteristics, and submarine anchor chain length alterations under combined wind, wave, and current loading conditions. The results show that under the same environmental load, when the three anchor chains are evenly distributed at 120°, the 6-DOF motion response amplitude of the buoy system is the smallest, the top-chain tension and the submarine anchor chain length are more in line with the design requirements, and the comprehensive performance is better.

1. Introduction

Ocean observation is the basis of and an important support for the development of marine science. At present, ocean observation is showing a three-dimensional development trend: the observation range is constantly expanding, extending from the sea surface and the seabed to the water profile in the vertical direction, and achieving multi-dimensional integration. At the same time, the correlation, real-time and continuity of observation data have also received increasing attention. The technical difficulty of water profile observation in shallow seas (water depth ≤ 200 m) is often higher than that in deep seas [1]. This is mainly due to the particularities of shallow sea environments: low water depth and strong hydrodynamic forces. In this environment, observation equipment is more significantly affected by environmental loads such as wind, waves, and currents, and the risk of human interference or damage to passing ships is higher. Therefore, the development of offshore water profile observation technology is lagging behind. Even if continuous profile observation technology that has been successfully applied in the deep sea is transplanted to offshore environments, it is often difficult to achieve the desired results.

The buoy system is an indispensable platform for marine monitoring applications. It can obtain marine environmental data continuously and in real time through fixed-point, long-term observation. It is an important part of the integrated marine monitoring infrastructure. According to different anchoring methods, buoy systems can be divided into single-anchor buoy systems and multi-anchor buoy systems [2]. The observational function of traditional single anchor chain buoys is simple, which has gradually become unsuitable for the development trend of ocean observation. Therefore, expanding the observation function of buoys has become a new direction in buoy technology development and an urgent technical problem to be solved. As a novel large-scale comprehensive observation platform, the three-anchor buoy system changes the single-anchor mooring mode located in the center of the buoy bottom to the three-anchor mooring mode fixed on the side of the buoy body, which expands the space under the buoy and makes it possible for the lifting winch on the deck to observe the water profile, thus greatly enhancing the ability to observe the water profile. The schematic diagram of its structural composition is shown in Figure 1. In addition, an autonomous underwater vehicle dock can be installed at the bottom of the three-anchor buoy system.

When the three-anchor buoy system is subjected to wind, waves, and currents at sea, it will inevitably sway, which will affect the measurement effect of the measuring instruments and equipment such as the observation device on the buoy‘s upper profile. At the same time, the buoy will have a large range of displacement under various loads. Therefore, higher requirements are needed for the design of its mooring system. Compared with other marine engineering equipment, the mooring system of the three-anchor buoy system accounts for a large proportion of it. The mooring system has a great influence on the motion and force of the three-anchor buoy system, and the coupling effect is obvious. Different forms of mooring systems have a significant impact on the hydrodynamic performance of the buoy. It is necessary to analyze relevant mooring methods and hydrodynamic characteristics. Therefore, it has always been the core goal of the design and development of the three-anchor buoy system to study the mooring mode and hydrodynamic characteristics of the three-anchor buoy system and its mooring system, verify whether they can work in complex sea conditions, improve the measurement effect of the observation elements, and ensure the normal operation of the observation equipment.

At present, many scholars have carried out static calculations and dynamic response analyses of single-anchor and multi-anchor buoy systems, which have very important significance as references in research on three-anchor buoy systems. The buoy system is primarily subjected to wind, current, and wave loads during operation; however, the methods for calculating wave loads vary for different structures (for example, Morison equation can be applied to small-sized structures). The three-dimensional potential flow theory and the Morison formula, such as the common wave load calculation theory, have been adopted by many scholars in the analysis of ocean structure and dynamics. Wave loads acting on marine structures are fundamentally classified into three components: drag force, inertia force, and diffraction force, and the calculation of wave loads for different structural scales is not the same. Specifically, for large-scale structures with the characteristic size of the member-to-wave-wavelength ratio exceeding 0.2 (D/L > 0.2), the dominant load components are inertia and diffraction forces; the wave load on the offshore structure can be solved for by applying the wrap-around theory based on the three-dimensional potential flow theory [3,4,5,6]. For small-scale structures (D/L < 0.2), which mainly bear drag force and inertia force, the wave load can be solved by the Morison formula, which ignores the diffraction effect [7,8,9,10,11]. In recent years, many scholars have simplified or improved and expanded the existing Morison formula to meet the needs of different types of marine engineering calculations [12,13]. In engineering, the potential flow theory and Morison formula are often combined to add the influence of viscous effects through the coefficient of the Morison formula to make up for the deficiency of the full potential flow theory [14,15]. With the rapid development of computer technology, a numerical simulation method based on the combination of mathematics, fluid mechanics, and computer technology, computational fluid dynamics (CFD), has been formed. This methodology integrates wave-induced hydrodynamic effects comprehensively, and fluid flow is numerically simulated based on fundamental physical principles and fluid dynamics equations. It has progressively emerged as a principal approach for calculating the response of floating structures in waves and currents, while accounting for the viscous effects of fluids [16,17,18,19]. However, it is also worth noting that the CFD method still has important difficulties in dealing with complex motion and free surface problems, and for complex coupling problems of floating systems, a large number of grids are required and the calculation time is too long.

The dynamic behavior of buoy systems under combined wind–wave–current loading conditions demonstrates significant coupling effects, which necessitates systematic integration of interaction mechanisms in analytical modeling. Existing analytical methods for assessing these coupled dynamics are predominantly divided into frequency domain and time domain analysis. Despite its computational efficiency advantages for preliminary evaluations, frequency domain analysis exhibits fundamental constraints in adequately addressing nonlinear phenomena and interaction coupling, potentially yielding unreliable predictions under complex multi-directional environmental loads. However, due to the fast calculations, the calculation results can lay a foundation for subsequent time domain analysis, so some scholars still adopt the frequency domain analysis method to analyze mooring systems [20]. The time domain analysis method, while inherently more complex and computationally intensive due to its simultaneous resolution of floating body wave-frequency motion and low-frequency motion within a temporal framework, provides enhanced accuracy and reliability in hydrodynamic solutions. This approach remains the predominant analytical methodology for comprehensive assessment of integrated system motion performance, maintaining its status as the current mainstream technique in offshore engineering applications [21,22,23]. In time domain analysis, the quasi-static analysis, decoupling dynamic analysis, and fully coupled analysis methods are usually used to consider the different coupling mechanisms between structures and mooring systems [24]. Based on the catenary theory, the quasi-static analysis method employs the mooring tension at the structure’s offset position from the previous time step as the input parameter. Through iterative computations, this methodology determines the current structural position, thereby enabling the determination of 6-DOF motion responses and corresponding horizontal mooring tensions [25]. The decoupling dynamic analysis methodology involves modeling the mooring system as an elastic continuum that undergoes spatial discretization. This approach employs the quasi-statically derived structural motion response as prescribed kinematic boundary conditions at the upper termination of the mooring assembly. Subsequent dynamic time domain simulations are then conducted through numerical integration of the discretized system, incorporating environmental loads and other relevant hydrodynamic factors [26]. The fully coupled dynamic analysis method considers the structure and mooring system as an integrated system, for which the fully coupled governing equations are formulated and solved simultaneously [27,28,29]. At the same time, there are still many scholars using frequency domain analysis and time domain analysis to compare mooring systems [30,31,32,33]. Many scholars also use ocean engineering analysis software for frequency domain analysis and time domain analysis of mooring systems. ANSYS AQWA 25.1 is widely used in complex ocean engineering design and calculation due to its advantages of high efficiency, accuracy, strong nonlinear processing ability, and multi-physical field coupling in solving the motion response problem of offshore structures [34,35,36].

At present, in the field of dynamic response analysis of buoy systems, relevant studies mainly focus on the single-anchor buoy system, and there are few studies on the three-anchor buoy system, and relevant studies mainly focus on the three-anchor buoy system with a uniform distribution of three anchors at 120°. In the relevant studies, there is a lack of comparative analysis of the motion response of the three-anchor buoy system with different anchor chain arrangements. It is not possible to show that the layout configuration with uniform distribution of three chains is the optimal design. This study investigates the influence of anchor chain arrangements on the dynamic behavior of a three-anchor buoy system through frequency and time domain analyses using ANSYS AQWA software under combined wind, wave, and current loading conditions. The results elucidate the correlations between the system’s response amplitudes in 6-DOF, mooring tensions and submarine anchor chain lengths with respect to variations in chain arrangements, wave periods and combined incident angle of environmental loads. The method used in this paper can be used to predict the motion of the three-anchor buoy system and the force analysis and estimation of the mooring system, which can provide an important reference for the selection and optimization of the anchor chain arrangement of the three-anchor buoy system.

2. Theoretical Methodology

2.1. Wind Load

The wind load is constant wind, with the wind coefficient matrix being derived from the wind speed–thrust relationship and projected wind area through systematic computational integration. In general, the wind load on the buoy above the waterline surface can be calculated according to the following formula:

$$F_w={\displaystyle \frac{1}{2}}{\rho }_a{C}_s{C}_{h}A{V}^2$$

(1)

where ${\rho }_a$ denotes the air density (typically taken as $1.226\mathrm{k}\mathrm{g}/{\mathrm{m}}^3$), $C_s$ represents the shape coefficient, $C_h$ is the height coefficient, $A$ corresponds to the windward area above the buoy waterline surface, and $V$ signifies the wind speed.

2.2. Wave Load

2.2.1. Three-Dimensional Potential Flow Theory

The three-dimensional potential flow theory incorporates diffraction and radiation theories, operating under the following fundamental assumptions: (1) seawater is modeled as an inviscid, incompressible, irrotational fluid with uniform density; (2) gravitational forces dominate over surface tension effects; and (3) wave amplitudes remain infinitesimal relative to wavelength (small-amplitude wave approximation). Considering the buoy’s interaction with incident waves, the total velocity potential $\Phi$ in the fluid domain can be decomposed into three distinct components:

$$\Phi (x,y,z,t)={\varphi }_i(x,y,z,t)+{\varphi }_d(x,y,z,t)+{\varphi }_r(x,y,z,t)$$

(2)

where ${\varphi }_i$ represents the incident wave potential in the absence of structural interference, ${\varphi }_d$ denotes the diffraction potential arising from wave–buoy interactions under fixed body conditions, and ${\varphi }_r$ corresponds to the radiation potential generated by buoy motion in otherwise calm water.

The incident potential ${\varphi }_i$ needs to satisfy the following boundary conditions:

$$\begin{array}{c}\left\{\begin{array}{c}{\nabla }^2{\varphi }_i=0\\ \left({\displaystyle \frac{\partial {\varphi }_i}{\partial z}}-{\displaystyle \frac{{\omega }^2}{g}}{\varphi }_i\right){|}_{z=0}=0\\ {\displaystyle \frac{\partial {\varphi }_i}{\partial z}}{|}_{z=-d}=0\\ {\displaystyle \frac{\partial {\varphi }_i}{\partial t}}+{\displaystyle \frac{p-p_0}{\rho }}+gz=0\end{array}\right.\end{array}$$

(3)

The incident potential ${\varphi }_i$ can be obtained according to the linear wave theory of equal water depth:

$${\varphi }_i\left(x,y,z\right)=-i{\displaystyle \frac{ga}{\omega }}{\displaystyle \frac{coshk(z+d)}{coshkd}}{e}^{ik(xcos\beta +ysin\beta )}$$

(4)

where a is the wave amplitude; k, the wave number; ω, the angular frequency; and $\beta$, the angle between the wave propagation direction and the $x$ axis.

The corresponding time domain velocity potential is

$$\begin{array}{c}{\varphi }_i\left(x,y,z,t\right)=\mathrm{Re}\left\{{\varphi }_i\left(x,y,z\right)e^{-i\omega t}\right\}={\displaystyle \frac{ga}{\omega }}{\displaystyle \frac{\mathrm{c}\mathrm{o}\mathrm{s}\mathrm{h}\left(k\left(z+d\right)\right)}{\mathrm{c}\mathrm{o}\mathrm{s}\mathrm{h}\left(kd\right)}}\sin \left[k\left(x\mathrm{c}\mathrm{o}\mathrm{s}\beta +y\mathrm{s}\mathrm{i}\mathrm{n}\beta \right)-\omega t\right]\end{array}$$

(5)

The diffraction potential ${\varphi }_d$ is solved with the following conditions:

$$\left\{\begin{array}{c}{\nabla }^2{\varphi }_d=0\\ ({\displaystyle \frac{\partial {\varphi }_d}{\partial z}}-{\displaystyle \frac{{\omega }^2}{g}}{\varphi }_d){|}_{z=0}=0\\ {\displaystyle \frac{\partial {\varphi }_d}{\partial z}}{|}_{z=-d}=0\\ {\displaystyle \frac{\partial {\varphi }_d}{\partial \overrightarrow{n}}}=-{\displaystyle \frac{\partial {\varphi }_i}{\partial \overrightarrow{n}}}\end{array}\right.$$

(6)

The radiation potential ${\varphi }_r$ is solved using the following conditions:

$$\left\{\begin{array}{c}{\nabla }^2{\varphi }_r=0\\ ({\displaystyle \frac{\partial {\varphi }_r}{\partial z}}-{\displaystyle \frac{{\omega }^2}{g}}{\varphi }_r){|}_{z=0}=0\\ {\displaystyle \frac{\partial {\varphi }_r}{\partial z}}{|}_{z=-d}=0\\ {\displaystyle \frac{\partial {\varphi }_r}{\partial \overrightarrow{n}}}=-{\displaystyle \frac{\partial {\varphi }_i}{\partial \overrightarrow{n}}}\end{array}\right.$$

(7)

After obtaining diffraction potential ${\varphi }_d$ and radiative potential ${\varphi }_r$ by the Green function method, the first-order wave load $F_b$ can be solved by the Bernoulli equation, which consists of first-order wave disturbance force $F_{di}$ and first-order wave radiation force $F_{ri}$. The formula is as follows:

$$F_b=F_{di}+F_{ri}$$

(8)

$$F_{di}=-{\rho }_c{\iint }_S\left({\displaystyle \frac{\partial {\varphi }_i}{\partial t}}\right)n_{i}dS-{\rho }_c{\iint }_S\left({\displaystyle \frac{\partial {\varphi }_d}{\partial t}}\right)n_{i}dS$$

(9)

$$F_{ri}=-\rho {\iint }_S\left({\displaystyle \frac{\partial {\varphi }_r}{\partial t}}\right)n_{i}dS$$

(10)

In this formulation, ${\rho }_c$ denotes the seawater density (typically assigned a value of $1025\mathrm{k}\mathrm{g}/{\mathrm{m}}^3$), S represents the wet surface area of the floating body, and $n_i$ corresponds to the normal vector directed towards the surrounding flow field.

2.2.2. Morison Formula

The Morison formula demonstrates that the hydrodynamic load on a structure consists of two components: an inertia force induced by accelerating fluid motion and a drag force arising from viscous fluid effects. The mathematical formulation can be expressed as follows:

$$dF={\displaystyle \frac{1}{4}}\pi D^2{\rho }_c(C_M\dot{u}-C_A\ddot{x})dz+{\displaystyle \frac{1}{2}}{\rho }_c{C}_{D}D|u-\dot{x}|(u-\dot{x})dz$$

(11)

The parameters are defined as follows: $D$ denotes the diameter of the structural member; $C_M$ represents the inertia force coefficient; $C_A$ corresponds to the additional mass coefficient; and $C_D$ indicates the drag coefficient. The values adopted in the calculation are $C_M=2.0$, $C_A=1.0$, and $C_D=1.2$. The velocity and acceleration components of the structural member relative to the fluid are expressed as $\dot{x}$ and $\ddot{x}$, respectively, while $u$ and $\dot{u}$ describe the velocity and acceleration components of fluid particles relative to the structural member.

2.3. Current Load

The hydrodynamic load acting below the waterline surface of the buoy can be determined using the following governing equation:

$$F_c={\displaystyle \frac{1}{2}}{\rho }_c{C}_{d}S{V}_c^2$$

(12)

where $S$ is the wet surface area of the floating body; $V_c$ is the current velocity.

2.4. Dynamic Response Analysis Theory of Mooring System

The load and motion between the buoy and the mooring system under the influence of wind, wave, and current loads are interactive, coupled and influenced by each other, which should be fully considered in the calculation of the system. At present, the commonly used analysis methods can be divided into three categories: non-coupling analysis, semi-coupling analysis, and full coupling analysis. Non-coupling analysis is mainly based on the frequency domain analysis method, and semi-coupling analysis and full coupling analysis are mainly based on the time domain analysis method. The frequency domain analysis method has a fast calculation speed and can initially reflect the motion of the structure to a certain extent. However, due to a lack of consideration of the coupling effect, the calculation results have deviations and are suitable for preliminary analysis. Although the time domain analysis method is more complicated and takes a longer time, it solves the wave-frequency motion and low-frequency motion of the floating body in the time domain together. The solution is more accurate and the calculation result is reliable. It is suitable for the analysis of the overall motion performance of the system and is still the current mainstream analysis method.

2.4.1. Frequency Domain Analysis Theory

The dynamic response of the buoy subjected to regular wave excitation is determined through frequency domain analysis by solving the 6-DOF governing equations of buoy motion. The control equation is

$$(\mathit{M}+{\mathit{M}}_{\mathit{a}})\ddot{\mathit{X}}+(\mathit{C}+\mathsf{\Delta }\mathit{C})\dot{\mathit{X}}+\mathit{K}\mathit{X}=\mathit{F}$$

(13)

where $\mathit{M}$ denotes the buoy mass matrix, ${\mathit{M}}_{\mathit{a}}$ represents the additional mass matrix, $\mathit{C}$ corresponds to the radiation damping matrix, $\mathsf{\Delta }\mathit{C}$ indicates the additional viscous damping matrix, and $\mathit{K}$ signifies the hydrostatic recovery stiffness matrix; $\ddot{\mathit{X}}$, $\dot{\dot{\mathit{X}}}$ and $\mathit{X}$ describe the acceleration, velocity and displacement vectors of the buoy’s 6-DOF motion, respectively; $\mathit{F}$ denotes the wave excitation force.

As the fundamental component of the decoupled computational framework, the frequency domain analysis methodology incorporates three critical considerations: mooring system stiffness, hydrodynamic loading effects, and environmental forces acting on anchor chains. The overall dynamic response is decomposed into three distinct components, mean, low-frequency, and wave-frequency responses, which are subsequently solved independently through numerical segregation. Extreme value estimation for each degree-of-freedom response of the buoy system under mean, wave-frequency, and low-frequency loading conditions is performed utilizing Rayleigh distribution theory, so the minimum and maximum values of the system under wave frequency and low-frequency motion are obtained. These parameters undergo systematic processing through standardized computational procedures to determine motion amplitudes under specified sea states [37].

$$\left\{\begin{array}{c}{\sigma }_1={\sigma }_{Wfmax}+{\sigma }_{Dfsig}\\ {\sigma }_2={\sigma }_{Wfsig}+{\sigma }_{Dfmax}\\ {{\sigma }_{max}=\sigma }_{mean}+\mathit{max}\left({\sigma }_1,{\sigma }_2\right)\\ {{\sigma }_{min}=\sigma }_{mean}-\mathit{max}\left({\sigma }_1,{\sigma }_2\right)\\ {\sigma }_{MAX}=\mathit{max}\left(\left|{\sigma }_{max}\right|,\left|{\sigma }_{min}\right|\right)\end{array}\right.$$

(14)

where ${\sigma }_{MAX}$ and ${\sigma }_{mean}$ denote the maximum and average values of a mooring system’s specific degrees of freedom; ${\sigma }_{Wfmax}$ and ${\sigma }_{Wfsig}$ are, respectively, the maximum value and mean value of the wave-frequency motion, while ${\sigma }_{Dfmax}$ and ${\sigma }_{Dfsig}$ are, respectively, the maximum value and mean value of low-frequency motion.

2.4.2. Time Domain Analysis Theory

The time domain analysis method is mainly used to couple the average response, low-frequency response, and wave-frequency response, and integrate various loads (including wind, wave, and current loads and system restoring forces) into the same time domain equations. Through numerical simulations and analytical methods, the temporal profiles of floating body displacement, cable tension, and submarine anchor chain length can be derived. Subsequent statistical post-processing of these time-dependent variations enables determination of extreme values for each parameter. The time domain analysis employs a unit impulse function that elicits a system response, mathematically represented as the impulse response function. The response of the buoy system is the response generated after receiving the pulse effect, which expresses the response characteristics of the buoy system during the process of the buoy system being affected and moving until a calm state is restored.

The time domain motion equations governing the buoy system under coupled wind–wave–current loading conditions are formulated as follows:

$$(\mathit{M}+{\mathit{M}}_{\mathit{a}})\ddot{\mathit{X}}(t)+{\int }_0^t\mathit{H}(t-\tau )\dot{\mathit{X}}(t)d\tau +\mathit{K}\mathit{X}(t)=\mathit{F}(t)$$

(15)

where $\mathit{H}(t-\tau )$ denotes the time-delay function matrix of the system; $\mathit{F}\left(t\right)$ represents the resultant external force vector comprising both environmental loads and restorative forces inherent to the system.

3. Numerical Simulation Model

3.1. Buoy Geometric Parameters

Referring to the existing buoy design literature in combination with the geometric modeling estimation method, the geometric parameters of the surface buoy were systematically determined. The structural schematic diagram and main dimensional parameters of the surface buoy are shown in Figure 2, and the relevant geometric parameters are shown in

Table 1. Main design parameters of the buoy.

Parameters	Value	Parameters	Value
Mass/t	45.0	Heave natural period/s	3.26
Displacement/m3	43.9	Roll natural period/s	2.76
Draft/m	0.862	Transverse metacentric height/m	8.20
Base cylindrical height/m	2.2	Longitudinal metacentric height/m	8.20
Bottom round table high/m	1.0	Rolling inertia radius/m	2.59
Center of buoyancy/m	(0, 0, −0.378)	Pitching inertia radius/m	2.59
Center of gravity/m	(0, 0, 0.533)	Yawing inertia radius/m	3.28

. The geometric parameters of the buoy, such as the barycenter coordinate, the buoy center coordinate, and the inertia radius, are calculated based on the simplified model with the waterline surface as the benchmark. The diameter of the buoy deck is 10 m, the diameter of the bottom surface is 6.5 m, and the operating water depth is 150 m.

3.2. Geometric Parameters

The hydrodynamic analysis in this study was performed using the commercial software ANSYS AQWA (Version 25.1) [38]. The waterline plane is defined by the $xoy$ coordinate system, with the $z$-axis oriented vertically along the buoy’s central axis to ensure computational accuracy and efficiency while maintaining grid quality, particularly considering the structural complexity of submerged hydrodynamic loads. After many calculations and optimizations, the grid size below the water line is finally set to 0.1 m, and the grid size above the water line surface is 0.15 m. The grid type is quadrilateral, and the grid type at the local curvature change is triangular. The hydrodynamic calculation model and grid diagram of the buoy are shown in Figure 3.

3.3. Anchor Chain Arrangement

In this paper, the influence of different anchor chain arrangements on the buoy system under the same environmental conditions and anchor chain pre-tension was studied. The three-anchor buoy system with five different anchor chain arrangements is calculated in frequency domain and time domain, respectively, and the relevant results are compared and analyzed. The buoy system was secured using a three-point mooring configuration, with all mooring attachment points positioned 0.138 m above the waterline. A horizontal separation distance of 570 m was maintained between the seabed anchorage locations and the buoy’s geometric center. The mooring assembly employed Hall anchors interconnected to the buoy through anchor chains, implementing a catenary mooring arrangement characterized by its natural chain curvature under static loading conditions. The main design parameters of the anchor chain are shown in

Table 2. Main design parameters of anchor chain.

Parameters	Value
Diameter/mm	48.0
Mass per unit length (in the air)/(kg/m)	50.46
Length/m	600
Breaking strength/kN	1270

. For buoy systems with multiple anchor chains, the anchor chains are usually symmetrically arranged in the design. This arrangement can resist wind, wave, and current loads to a certain extent, and provide restoring forces for the buoy system from all directions to ensure the stability of its motion. Therefore, in this paper, five kinds of anchor chain arrangements with certain symmetries are mainly studied, as shown in Figure 4. The schematic representation of the three-anchor buoy system (with configuration 4 as the representative configuration) and associated coordinate system definitions are presented in Figure 5.

4. Frequency Domain Analysis

4.1. Hydrodynamic Analysis of the Buoy

4.1.1. Added Mass

Due to the viscosity of the fluid, when the buoy moves in the fluid, it will drive the fluid around it to move together, which is equivalent to increasing the mass of the buoy, termed as the added mass. It depends on three primary factors: fluid density, submerged geometry of the buoy, and wave period. However, analysis of the added mass of the buoy in the surge, sway, and yaw directions is not helpful for follow-up research, and the added mass of the buoy in the roll and pitch directions is basically the same. Consequently, Figure 6 exclusively presents added mass variations with wave periods for heave and roll motions.

According to the above figure, it can be seen that the added mass in the heave and roll motions of the buoy increases first, then decreases and then tends to be stable with the increase in the wave period. Among them, the added mass in the roll motion peaked at a wave period of about 5 s, and the value was $1.00\times 10^4 \mathrm{k}\mathrm{g}\cdot {\mathrm{m}}^2{/1}^{\circ }$. The added mass in the heave motion peaked at about 15 s into the wave period, and the corresponding value was $2.75\times {10}^5 \mathrm{k}\mathrm{g}$. As demonstrated in Figure 6, the added mass in the heave motion exceeded that observed in the roll motion under identical wave periods. This is because the projection area of the buoy during the heave is greater than that in other directions.

4.1.2. Radiation Damping

The hydrodynamic motion of a floating body on the water surface induces wave propagation through the surrounding fluid medium. This motion-induced radiation phenomenon generates wave energy dissipation known as radiation damping, which is proportional to the velocity of the floating body. Referring to the analytical content of the additional mass, here, only the variation in radiative damping in the heave and roll directions with the fluctuation period is considered, as illustrated in Figure 7.

According to the above figures, it can be seen that radiation damping in the heave and roll of the buoy exhibits an initial increase followed by a decrease with increasing wave period. Among them, radiation damping in the heave and roll peaked at about 3 s and 2.5 s and the corresponding values were $1.65\times 10^5 \mathrm{N}/(\mathrm{m}/\mathrm{s})$ and $9.32\times 10^3 \mathrm{N}\cdot \mathrm{m}/{(}^{\circ }/\mathrm{s})$. According to the above figure, it can be inferred that when the wave period tends to infinity (wave frequency tends to 0), the radiation damping tends to 0, because when the wave frequency is extremely low, the buoy’s own movement is not enough to drive the surrounding fluid’s movement, hence there will be no radiation damping.

4.1.3. Motion Response Amplitude Operator (RAO)

The response amplitude operator (RAO) is defined as the ratio between the motion amplitude of a floating structure and the incident wave amplitude across each degree of freedom, characterizing the motion response features under linear wave excitation. The wave propagation direction is specified as initially aligned with the positive $x$-axis (0°), then progressively rotated counterclockwise to 90°. Considering the buoy’s geometric symmetry, computational analysis was confined to wave incidence angles spanning 0° to 90° with 15° increments. Figure 8 illustrates the angular-dependent variations in RAO magnitudes for surge, heave, roll, and yaw motions.

According to the above figures, we can see the following:

• The RAO curves exhibit analogous trends in both surge and yaw motions. Under surge conditions, the RAO amplitude approaches zero at a wave incident angle of 90°; however, the RAO demonstrates a proportional relationship with increasing wave period at non-orthogonal wave directions. For fixed wave periods, the RAO exhibits an inverse correlation with wave incident angle. During yaw motion, minimal RAO amplitudes occur at 0° wave incidence, and the RAO demonstrates a proportional relationship with increasing wave period while non-orthogonal wave angles. Notably, under constant wave periodicity, the yaw RAO displays a direct proportionality to the wave incidence angle magnitude.
• The heave motion displays angular independence, with all RAO curves following identical growth trajectories. The response increases monotonically with wave period before asymptotically approaching a 1 m/m amplitude ratio.
• The roll RAO curves exhibited consistent variation patterns across different wave incident angles as a function of wave period. Initially, all curves demonstrated an ascending trend with increasing wave period, reaching peak magnitudes at approximately 3 s, followed by a gradual decline until asymptotic convergence toward zero. Notably, under equivalent wave period conditions, the roll RAO magnitude showed proportional enhancement with increasing wave incident angle. As illustrated in Figure 8c, the maximum roll RAO peak value of 24.65°/m was recorded at a 90° wave incidence. This critical value, indicative of potential buoy capsizing, deviates from practical operational conditions, thereby necessitating implementation of damping correction measures to ensure system stability.

Because AQWA software uses three-dimensional potential flow theory to perform calculations, ignoring the viscosity of water, the hydrodynamic calculation results are too large, so additional viscous damping matrix needs to be added in the simulation. Referring to the specification [39], the calculation formula of the critical viscous damping is

$$D_{critical}=2\sqrt{(M+M_a)\cdot K}$$

(16)

where $M$ represents the mass of the buoy; $M_a$ and $K$, respectively, represent the additional mass and hydrostatic stiffness in each degree of freedom direction.

Simulation results indicate that the buoy exhibits negligible hydrostatic restoring stiffness in surge, sway, and yaw, thus precluding the calculation of critical damping for these modes. Due to identical calculation outcomes for roll and pitch motions, only the critical damping values for heave and roll were computed. The additional viscous damping coefficient equivalent to 5% of the critical damping was applied, with detailed numerical findings summarized in

Table 3. Additional viscous damping calculation table of heave and roll.

Parameters	Mass /kg	Added Mass /kg	Stiffness /N·m−1	Critical Damping /N·m·s·deg−1	Viscous Damping /N·m·s·deg−1
Heave	45,000	$2.66\times {10}^5$	$7.85\times {10}^5$	$9.88\times {10}^5$	$4.94\times {10}^4$
Roll		$4.92\times {10}^5$	$4.38\times {10}^6$	$3.07\times {10}^6$	$1.53\times {10}^5$

.

After adding additional viscous damping, the RAO curves of the buoy roll and pitch are redrawn. The results are shown in Figure 9:

Comparative analyses of heave and roll RAO curves, presented in Figure 8 and Figure 9, reveal that supplementary viscous damping exerts a negligible influence on the heave RAO response, while demonstrating a significant impact on roll motion characteristics. The RAO curves for heave remained consistent before and after the addition of viscous damping. In roll, the modified RAO curve attained a peak response at approximately 5 s wave period. Under a 90° wave incidence, the maximum roll RAO amplitude decreased substantially to 1.93°/m, representing a 92% reduction from pre-damping values. Surface-applied viscous damping demonstrates critical importance in hydrodynamic analysis of the buoy structure, effectively enhancing simulation fidelity to real-world operational conditions.

4.2. Frequency Domain Analysis of the Three-Anchor Buoy System

4.2.1. Environmental Conditions

According to conventional observation parameters and meteorological data in the East China Sea’s waters, and taking into account the designed life of the buoy system and the designed water depth, regular waves were used for analysis and the wave height was set to 1 m and the wave period was 30 s in the hydrodynamic analysis stage. The calculation conditions of the designed limit sea state were as follows: the wind spectrum adopts the NPD spectrum [40], taking the wind speed at 10 m from the sea level, and the wind speed is 10 m/s; the wave spectrum is the JONSWAP spectrum [41], with the significant wave height of 2.5 m, the spectral period of the peaks of the spectrum is 4 s, the spectral crest factor is 3.3; the surface current velocity of the sea current is 1.5 m/s, the velocity varies uniformly with depth, and the current velocity at the depth of $x\mathrm{m}$ (negative value) from the sea surface can be calculated according to the following formula:

$$v_c=0.1x+1.5$$

(17)

We calculated the working conditions by selecting wind, waves, and currents acting in the same direction. Considering the symmetry of the three-anchor buoy system, we only calculated the interval of $0^{°}~{180}^{°}$, with calculations performed every 15°. The directions of the combined loads for the five configurations is illustrated in Figure 10.

4.2.2. Maximum Offset of Buoy System

When the buoy system is working, it will be subjected to the combined action of wind, wave, and current loads. In order to ensure the stable operation of the buoy system, there are usually certain requirements for its maximum offset value. Referring to the horizontal displacement allowed by the drilling platform and the requirements of relevant specifications and the literature, the horizontal displacement of the three-anchor buoy system is set in this paper to not exceed 10% of the water depth, and the rotational degree of freedom is not more than 10°.

4.2.3. Calculation of Wind/Current Force Coefficient Matrix

In ANSYS AQWA software, the wind load and current load of the structure cannot be directly calculated according to the buoy hydrodynamic model, wind speed, and flow velocity but instead need to be added to the software by calculating the wind/current coefficient matrix. In AQWA, the wind/current coefficient is defined without wind speed and flow velocity. The solution methods of the two are similar. Combined with the calculation formulas of wind load and current load, the calculation formula of the wind/current coefficient is as follows:

$$F_{X-wind/current}={\displaystyle \frac{1}{2}}\rho C_{D}Acos{\beta }_{w/c}$$

(18)

$$F_{Y-wind/current}={\displaystyle \frac{1}{2}}\rho C_{D}Asin{\beta }_{w/c}$$

(19)

where $F_{X-wind/current}$ and $F_{Y-wind/current}$ are the wind/flow force coefficients in the X direction and the Y direction, respectively. When calculating the wind coefficient, $\rho$ is the air density; $C_D$ is the wind coefficient, and $C_D=0.5$; $A$ is the windward area; and ${\beta }_{w/c}$ is the angle between the wind and the windward area. When calculating the flow coefficient, $\rho$ is the density of seawater; $C_D$ is the flow force coefficient, and $C_D=1.2$; $A$ is the inflow area; and ${\beta }_{w/c}$ is the angle between the current and the current area.

Taking the calculation of wind coefficient in the positive direction of Y axis as an example, the calculation steps are as follows:

• We calculated the area and centroid coordinates of each part of the windward area;
• The centroid coordinates of the whole windward area are obtained by weighted average after multiplying the wind coefficient of each part of the above area and combining the centroid coordinates;
• According to Formulas (18) and (19), the wind coefficients of the X and Y directions at any angle are obtained;
• Because the wind load is acting on the centroid of the wind area, and the centroid and the center of gravity do not coincide, it will also produce the relevant torque $M_{X-wind}$ and $M_{Y-wind}$;
• Because, in the Z direction, the center of gravity and the centroid overlap, there is no $F_{Z-wind}$ or $M_{Z-wind}$ along the positive direction of the wind when the wind coefficient is solved;
• The whole wind coefficient matrix can be obtained by calculating the wind coefficient at other angles.

4.2.4. Results and Discussions

The 6-DOF dynamic responses of a three-anchor buoy configuration under five distinct anchor chain arrangements and specified environments were numerically simulated using ANSYS AQWA software through the frequency domain analysis methodology detailed in Section 2.4. The frequency domain response amplitude for each degree of freedom was determined by selecting the maximum absolute value between the peak positive and negative responses. The results are shown in Figure 11:

According to the above figures, the following can be seen:

• The motions of the buoy system with five anchor chain arrangements in the sway, roll, and yaw directions all show a symmetry of about 90°, and all increase from 0 to the minimum. In the sway direction, the amplitude of configuration 1 is the largest and reaches 46.715°, which will obviously lead to capsizing. The motion amplitude of the buoy system of configuration 5 is the smallest. In the roll direction, the motion amplitude of each medium configuration is small. On the whole, configuration 1 is the smallest and configuration 3 is the largest. In the yaw direction, except for configuration 1, the motion amplitude of the buoy shows fluctuating changes.
• The response amplitudes in surge, heave, and pitch for each configuration exhibit a close alignment with the variation curve of the load angle. But with the increase in the load angle, the motion amplitude of configuration 5 in the surge and pitch decrease, while for the heave, it increases. Moreover, the maximum value of configuration 5 in the surge reaches 24.756 m, which exceeds our set value, so configuration 5 also has shortcomings. In the heave and pitch directions, the motion amplitude of configuration 4 is basically smaller than that of other configurations, and the motion response of configuration 4 also shows a symmetry of about 90° in the pitch but not in the heave.
• Through the above analysis, the variation curve and the maximum value of the motion amplitude with the change in wave angle of each configuration can be obtained. Through comparison, it can be found that configuration 1 and configuration 5 have the maximum offset values, exceeding the set value in the roll and pitch, respectively, so they have obvious defects. Except for in roll, the motion response of configuration 4 is basically smaller than that of configuration 2 and configuration 3, so configuration 4 is the optimal design as a whole.

5. Time Domain Analysis of Three-Anchor Buoy System

The hydrodynamic parameters of the three-anchor mooring system and its each degree-of-freedom dynamic responses were determined through frequency domain analysis. However, due to the exclusion of coupling effects in frequency domain simulations, computational discrepancies persist, necessitating subsequent time domain coupled analysis incorporating wind, wave, and current loads and mooring system interactions. Through time domain analysis, the time domain response, anchor chain tension, and submarine anchor chain length of the buoy system with six degrees of freedom can be solved, and the influence of different anchor chain arrangement on the motion response of three-anchor mooring system under the same ocean environment can be more accurately reflected.

In this section, AQWA software is used to consider the wind, wave, and current loads and mooring system coupling, and the computational conditions are the same as in the combined load direction and frequency domain analyses (shown in Figure 10), but for the same combined load directions, different random wave seeds were chosen to carry out five instances of 3 h time domain simulation analyses of the buoy system, and the average of the results of the calculations of the five times was taken for comparative analyses. The safety factor was defined as the ratio of the anchor chain breaking load to the maximum tension. In accordance with specifications, the safety factor of dynamic analysis for intact mooring systems had to satisfy a minimum threshold of 1.67 [42]. Time domain dynamic analysis quantified 6-DOF motion extremes, peak anchor chain tensions, and the minimum submarine anchor chain length across different load combination angles under extreme environmental conditions, as presented in the following figures.

The following conclusions can be drawn from Figure 12, Figure 13, Figure 14 and Figure 15:

• For anchor chain 1^#, the maximum tension in all configurations exhibited a positive correlation with the load combination angle, while the minimum submarine anchor chain length demonstrated an inverse relationship. Under identical load angles, configurations 1 to 5 sequentially displayed decreasing tension magnitudes and correspondingly increasing minimum submarine anchor chain lengths.
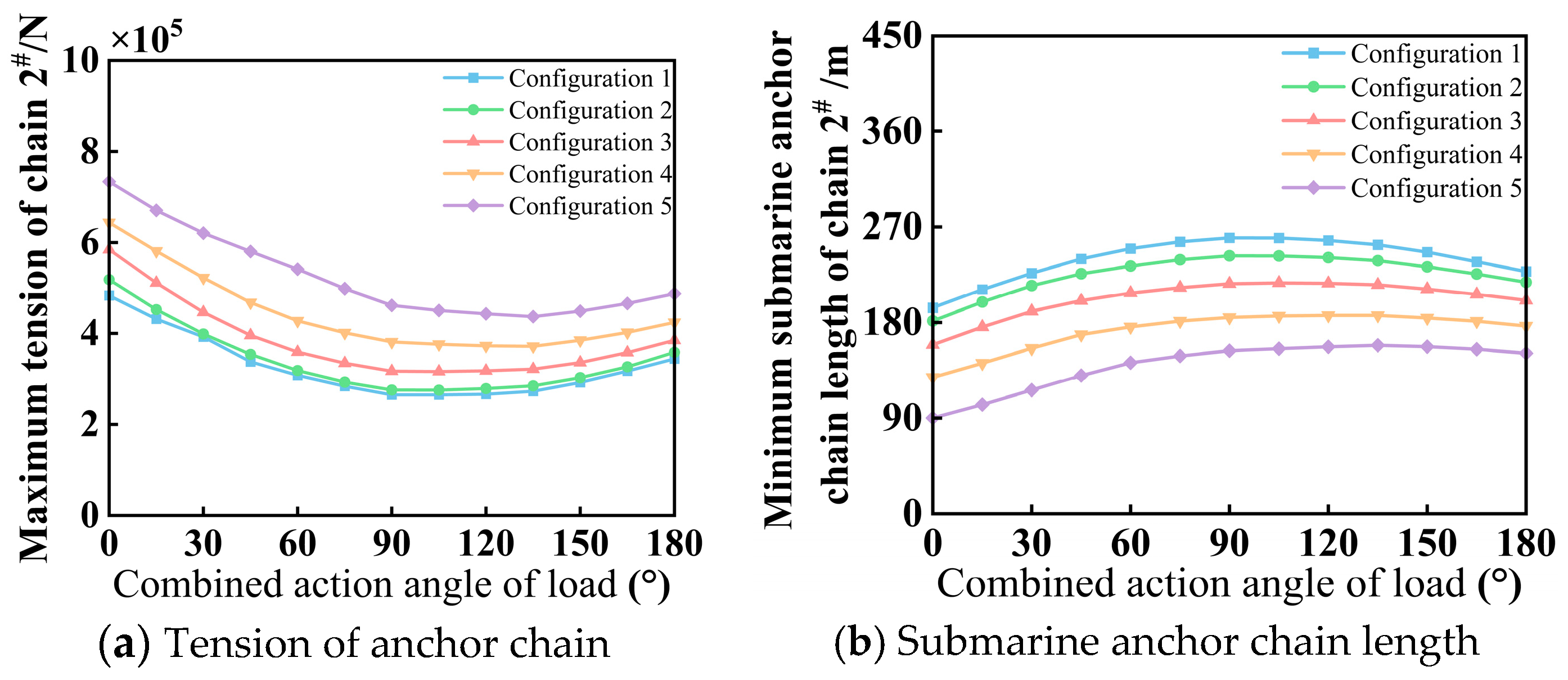
• For anchor chain 2^#, the maximum tension in anchor chains in all configurations demonstrated a non-monotonic response to increasing load angles, exhibiting an initial decrease followed by a subsequent increase. The minimum submarine anchor chain length displayed the following behavior: initially increasing then decreasing with angular progression. Comparative analysis revealed that, at equivalent load angles, configurations 1 through 5 exhibited sequential reductions in the minimum submarine anchor chain length and increases in chain tension.
• For anchor chain 3^#: As the load angle increased, the maximum tension of the anchor chain in each configuration increased and then decreased, while the minimum submarine anchor chain length decreased and then increased; when the load angle was the same, the tension in configuration 1 to configuration 5 increased in turn, while the minimum submarine anchor chain length decreased in turn.

By comparing the results of frequency domain analysis and time domain analysis, the following can be found:

• The variation curves of buoy motion amplitude with load angle obtained by frequency domain analysis and time domain analysis are basically the same in each degree of freedom.
• The numerical values of frequency domain analysis are basically larger than those of time domain analysis to a certain extent, and some of the analysis values are far beyond the maximum value of motion set by us. This is because frequency domain analysis does not consider the coupling effect, and the calculation results can only be used as a preliminary analysis.
• It can be seen that frequency domain analysis can quickly determine the response of the motion response of the buoy system with the change in the load angle. However, because the coupling effect is not considered in the calculations, time domain analysis should be carried out in order to reflect the motion response of the buoy system more comprehensively.

In order to make the time domain analysis results more intuitive, three-anchor mooring systems with five anchor chain arrangements were compared and analyzed under extreme working conditions based on their maximum six-degree of freedom response, maximum cable tension, and minimum submarine anchor chain length, as shown in

Table 4. The maximum time domain response value of 6-DOF for five kinds of arrangements of anchor chains.

Parameters	Configuration 1		Configuration 2		Configuration 3		Configuration 4		Configuration 5
	Angle	Value	Angle	Value	Angle	Value	Angle	Value	Angle	Value
Surge/m	180°	8.212	180°	7.707	180°	6.612	0°	5.551	0°	20.277
Sway/m	90°	34.803	90°	16.547	90°	8.659	90°	4.971	90°	3.301
Heave/m	75°	1.294	60°	1.243	165°	1.225	15°	1.197	75°	1.261
Roll/°	90°	18.601	90°	12.379	90°	7.322	90°	4.389	90°	3.191
Pitch/°	135°	6.479	180°	5.925	180°	5.202	0°	5.024	0°	11.847
Yaw/°	75°	1.172	90°	0.638	150°	0.331	90°	0.231	60°	0.459

,

Table 5. The maximum time domain response value of tension for five kinds of arrangements of anchor chains.

Parameters	Configuration 1	Configuration 2	Configuration 3	Configuration 4	Configuration 5
Angle	180°	180°	180°	180°	45°
Anchor chain	1#	1#	1#	1#	3#
Maximum tension/kN	952.23	927.55	878.03	778.72	838.81
Safety factor	1.33	1.37	1.45	1.63	1.51

and

Table 6. The minimum time domain response value of submarine anchor chain length for five kinds of arrangements of anchor chains.

Parameters	Configuration 1	Configuration 2	Configuration 3	Configuration 4	Configuration 5
Angle	180°	180°	180°	180°	180°
Anchor chain	1#	1#	1#	1#	3#
Submarine anchor chain length/m	45.30	52.96	70.31	103.93	78.27

:

According to the above data, analysis results can be obtained:

• Under the designed sea conditions, the maximum 6-DOF time domain responses of the buoy system with five anchor chain arrangements were analyzed. In the surge, configuration 4 exhibited the minimum response amplitude of 5.551 m when subjected to a combined action angle of 0°. Configuration 5 had the largest response amplitude, which was 20.277 m when the combined load action angle was 0°. In the sway, configuration 5 had the smallest response amplitude, which was 3.301 m when the combined load action angle was 90°; configuration 1 had the largest response amplitude, which was 34.803 m when the combined loading angle was 90°. In the heave, configuration 4 had the smallest response amplitude, which was 1.197 m when the combined load action angle was 15°; configuration 1 had the largest response amplitude, which was 1.294 m when the combined load action angle was 75°. In the roll, configuration 5 had the smallest response amplitude, which was 3.191° when the combined action angle of load was 90°; configuration 1 had the largest response amplitude, which was 18.601° when the combined load action angle was 90°. In the pitch, configuration 4 had the smallest response amplitude, which was 5.024° when the combined load action angle was 0°; configuration 5 had the largest response amplitude, which was 11.847° when the combined load action angle was 0°. In the yaw, configuration 4 had the smallest response amplitude, which was 0.231° when the combined action angle of load was 90°; configuration 1 had the largest response amplitude, which was 1.172° when the combined load action angle was 75°.
• In the time domain analysis of cable tension responses, configuration 1 exhibited the maximum tension value of 952.23 kN, occurring at anchor chain 1^# under a combined load angle of 180°, with a corresponding safety factor of 1.33. Configuration 4 demonstrated the minimum tension response of 778.72 kN under identical load conditions, achieving a safety factor of 1.63. Notably, while all five configurations failed to meet the specified safety factor requirement (>1.67) for anchor chain tension standards, configuration 4 showed the closest compliance with this criterion, suggesting better alignment with design specifications. Ways to the improve safety factor include an increase in anchor chain length or anchor chain diameter or higher-strength types of anchor chains.
• For the time domain analysis of horizontal chain length responses, configuration 4 exhibited the maximum displacement of 103.93 m at anchor chain 1^# under the combined loading angle of 180°, whereas configuration 1 demonstrated the minimum response amplitude of 45.30 m at the same chain location under identical angular loading conditions.

In summary, under the extreme sea conditions designed in this paper, under the combined action of wind, wave, and current loads, configuration 4 had relatively smaller motion amplitude responses at 6-DOF compared with other configurations, except for configuration 5, and the mooring system had better restrictions on the movement of buoys. Although configuration 5 had slightly lower motion amplitudes than configuration 4 in the sway and roll directions, its maximum response amplitude in the surge direction was 20.277 m and its maximum response amplitude in the pitch direction was 11.847°. It is obvious that the design still has defects. Configuration 4 has more advantages than the other configurations in terms of maximum tension of each anchor chain and the minimum submarine anchor chain length. Therefore, it can be concluded that in the above five kinds of three-anchor buoy systems, the design with 120° uniform distribution of three anchor chains could effectively limit the movement of the buoy, and the anchor chain tension and submarine anchor chain length were the best, so this design can better adapt to a marine environment.

6. Conclusions

This study conducts hydrodynamic analysis on a 10 m buoy to investigate the influence of wave period variations on both the added mass characteristics and radiation damping coefficients of the buoy. The investigation further evaluates the effects of viscous damping implementation (presence vs. absence) and wave incidence angles on the RAO of the buoy. Subsequent frequency domain and time domain analyses of five different three-anchor buoy systems with varying mooring arrangements systematically examine the interdependent effects of 6-DOF response amplitudes, anchor chain tensions, and minimum submarine anchor chain length on the resultant load angles characterizing each buoy system’s combined environmental interactions. The main conclusions are as follows:

• The hydrodynamic analysis revealed distinct trends in the 6-DOF responses of the buoy under varying wave periods. For surge, sway, heave, roll, and pitch, both added mass and radiation damping led to a trend characterized by an initial increase, followed by a decrease and subsequent stabilization as wave period increased. The yaw demonstrated an initial decrease and then stabilization with increasing wave period. Under constant wave incidence angles, the RAO displayed period-dependent characteristics: the RAO of pitch and roll showed progressive enhancement with increasing wave period; the RAO of heave initially increased before stabilizing at higher periods; and roll response exhibited a unique pattern of initial amplification followed by reduction. Under constant wave periods: the RAO of pitch decreased with increasing wave incidence angle; the RAO of heave remained essentially constant regardless of incidence angle variations; roll and yaw responses demonstrated positive correlation with wave incidence angles. Notably, the addition of additional viscous damping demonstrated significant effects on the RAO value of roll response mitigation.
• With an increase in the angle of the combined action of loads, the maximum tension of anchor chain 1^# increased and the minimum submarine anchor chain length decreased; the maximum tension of anchor chain 2^# firstly decreased and then increased and the minimum submarine anchor chain length firstly increased and then decreased; the maximum tension of anchor chain 3^# firstly increased and then decreased, and the minimum submarine anchor chain length firstly decreased and then increased.
• Compared with the other four anchor chain arrangement configurations, the response amplitude of the three-anchor buoy system with a uniform distribution of three anchors at 120° was basically the minimum value for six degrees of freedom, and the maximum tension of the anchor chain and the minimum submarine anchor chain length were also at a relatively optimal state. Therefore, the design with a uniform distribution of three anchor chains can effectively limit the movement of the buoy and better adapt to a marine environment.