Semidiurnal Internal Tide North and South of the Critical Latitude in the Kara Sea

Abstract

Temperature measurements data are analyzed from two moorings in the Kara Sea, north of the critical latitude for semidiurnal internal tides (74°30′ N) at a point at 74°54.3′ N, 69°43.6′ E, and south of the critical latitude at a point at 71°14.2′ N, 65°36.3′ E. The moorings operated over one year from 15 October 2021 to 15 September 2022. However, only the data from ice-free months were analyzed. Temperature fluctuations measured on the moorings reflect vertical motions associated with internal waves. The estimated temperature fluctuation spectra were either characterized by a reliable peak related to semidiurnal internal tide (period 12.4 h) or this peak was absent. The semidiurnal spectral peak appeared when the spectrum was calculated from the temperature measurements on the moorings when mean vorticity in the mooring region, derived from satellite altimetry data, was anticyclonic (negative). Those without peaks were related to the periods of cyclonic vorticity. High-resolution SAR data showed numerous packets of short-period internal solitary waves in the vicinity of moorings when peaks at the M₂ frequency were present. At such periods, anticyclonic vorticity permitted free propagation of internal tidal waves from the slope regions, and generation of high-frequency waves could have resulted from internal tide evolution.

1. Introduction

Tides play a major role in the generation of internal waves and especially tidal internal waves. Tidal forcing is responsible for approximately 50% of the internal wave energy [1,2]. Generation occurs over sloping bottom topography, which characterizes coastal regions [3,4]. A review in [5] that appeared half a century ago describes many aspects of tides, especially in coastal regions. The author developed a tidal model using the tidal components of different frequencies of sea level fluctuations from direct or remote observations. Baines [3] presented a model of generation of internal tides over sloping continental slopes and indicated the regions of most intense generation of internal tides. The model involved generation of internal tides on the shallow thermocline and on the continuous stratification below this thermocline. Morozov [6] extended this model to generation over submarine ridges. Garrett and Kunze [4] presented a model of internal tides generated when tidal currents overflow bottom topography. They introduced key dimensionless parameters governing this generation.

Tides occur not only in seawater but also in solid Earth. A review of Earth tides was conducted by Agnew [7]. Ray [8] reported that the amplitude of the M₂ tide increased over the 20th century. This was recorded with the tide gauges in the Gulf of Maine. Many papers report on tides in various coastal regions. Erkoç and Doğan [9] performed tidal modeling on the basis of data from pressure gauges and altimetry on the southwestern coast of Turkey. Soltanpour, with coauthors [10], analyzed data and introduced an empirical model of tides in the Persian Gulf and northern part of the Indian Ocean. Ansari et al. [11] presented a regional model of tides on the European coast over a period of 60 years (1961–2020) based on data from tide gauges and satellite altimetry. Marone and coauthors [12] compared tides in two regions of the Adriatic Sea and Brazil; they also compared methods of recording.

The most intense internal tides are generated when the currents of the barotropic tide in a stratified ocean overflow underwater slopes of continental margins and submarine ridges, thus obtaining a vertical velocity component. Vertical currents periodically displace isopycnals, thus generating internal waves. The generated waves propagate from the slope [3,4]. The most intense internal tides appear when the tidal currents are normal to the slope and the topographic slope is the same as the inclination of the characteristic surfaces of internal waves, which are governed by the following equation:

$${\displaystyle \frac{dz}{dx}}=\sqrt{{\displaystyle \frac{{\mathsf{\sigma }}^2 -{ f}^2}{{N\left(z\right)}^2 -{\mathsf{\sigma }}^2}}},$$

(1)

where N is the buoyancy frequency, σ is the wave frequency, and f is the Coriolis frequency. The tangent of the inclination of the ellipse to the horizontal plane depends on the ratio of the vertical and horizontal wavenumbers. Since ${\mathsf{\sigma }}^2-f^2$ is very small at latitudes close to 71–74° N, the slope needed to generate intense internal tides is of the order of 1/100, which is usual in the Kara Sea.

In the high-latitude basins, north of 74°30′ N, the rotation of the Earth prevents the free propagation of internal tides if the sea floor is flat. This latitude has been considered critical for the M₂ tide in many previous publications because at this latitude the M₂ frequency becomes equal to the Coriolis frequency. This can be easily seen from the solution of the following differential equation for vertical velocities w induced by internal waves [13,14]:

$${\displaystyle \frac{d^{2}w}{d{z}^2}}+{\displaystyle \frac{N^2\left(z\right)}{g}}{\displaystyle \frac{dw}{dz}}+{\displaystyle \frac{N^2\left(z\right)-{\mathsf{\sigma }}^2}{{\mathsf{\sigma }}^2-f^2}}{k}^{2}w=0.$$

(2)

Here, σ is the wave frequency. The boundary conditions for vertical velocity w are zero at the bottom and surface. Thus, the spatially oscillating solutions for this eigen function problem in the linear case do not exist north of 74°30′ N.

However, currents of the barotropic tide flow over sloping topography and periodically displace isopycnals. Internal tides that appear as oscillations of isopycnals over the slopes are forced internal tides. The internal tide wave rapidly decays during propagation from the slope. This phenomenon has been described in the literature [15,16,17,18,19,20,21].

Propagating semidiurnal internal tides can be recorded even over flat bottoms due to a decrease in the effective Coriolis frequency (absolute vorticity) caused by anticyclonic (negative) vorticity. Effective inertial frequency is the sum of the planetary vorticity and the vorticity of the velocity field. Mesoscale eddies form a variating vorticity field. Thus, we can write the effective Coriolis frequency as

$$f_{eff}=f_{local}+vorticity=f_{local}+\left({\displaystyle \frac{dv}{dx}}-{\displaystyle \frac{du}{dy}}\right).$$

(3)

Here, f_local = 2Ωsinφ at latitude φ; Ω is the angular velocity of the Earth’s rotation. When vorticity is negative (anticyclonic), the effective Coriolis frequency decreases and the difference (ω − f) is positive. If the vorticity is positive (cyclonic), f_eff becomes larger and the difference (ω − f) can become below zero, which excludes oscillatory solutions. This happens at latitude 74°30′ N and north of it; therefore, this latitude is critical for the existence of internal tide M₂. In was shown in [22] that anticyclonic vorticity up to 5.0 × 10⁻⁶ s⁻¹, which is observed in the Arctic, can displace the critical latitude to Spitsbergen (78° N).

Generation of diurnal internal tides over topography in the Kuril Straits north of the critical latitude was reported by Nakamura and coauthors [23]. They observed the generation of internal tides over bottom slopes north of the critical latitude for the diurnal tide K₁ at 47° N; the critical latitude for this wave is 30° N. Vlasenko et al. [24] report that if nonlinearity of internal tides is high, they may exist north of the critical latitude. This was shown based on modeling and data from the Barents Sea. If nonlinearity is strong the energy transfer from the barotropic tide to the baroclinic modes at high latitudes can cause generation of semidiurnal internal tides with multiple harmonics.

D’Asaro and Morison [25] report on variable internal tides north of Spitsbergen. Internal wave measurements in the Arctic generally show that the internal wave spectrum is characterized by lower energy levels compared to the mid-latitudes.

Urbancic et al. [26] report on spreading of semidiurnal internal waves M₂ over the Yermak Plateau. The M₂ internal tide is sub-inertial (the M₂ frequency is lower than the Coriolis frequency); however, propagating beams of internal waves with frequency just over the Coriolis frequency were recorded. The authors associate these with variable background vorticity. He and Lamb [27] consider the influence of an along-shelf current near the critical latitude on the generation of internal tides. The horizontal shear of the background current causes varying effective Coriolis frequency over space.

Wang et al. [28] studied diurnal and semidiurnal internal waves on the southern slope of the Yermak Plateau based on three moorings. Tidal generation induces internal tides up to 100 m high (double amplitude). Rippeth et al. [29] showed that nonlinear waves were responsible for about 70% of the total tidal conversion over the Spitsbergen Bank (at 75.6° N); hence, internal waves are the main source of energy for mixing.

Cao et al. [30] reported that mesoscale eddies can enhance turbulent mixing. Intense turbulent mixing was found at the southern flank of the anticyclonic eddy below 300 m, which showed little correlation with topographic roughness and local winds. Enhanced mixing was caused by a sub-thermocline anticyclonic eddy that could change vorticity and cause generation of internal waves. Fer et al. [31] found that energetic internal tides cause strong spatial variability over the Yermak Plateau north of the critical latitude.

MacKinnon et al. [32] reported on the evidence of energy transfer from the internal tide to near-inertial motions near 29°N (critical latitude for the diurnal tide) in the Pacific Ocean. The transfer is accomplished by means of parametric sub-harmonic instability during interaction between the internal tide and two smaller-scale waves of nearly half the frequency.

In this research we analyze the periodical appearance of a semidiurnal peak on the temperature spectra from moored sensors in the Kara Sea north and south of the critical latitude, and associate the appearance of this peak with variable vorticity in the region of moorings.

The general circulation of the Kara Sea is cyclonic. It is more pronounced in the southern part. This was shown in our previous publication [33]. The southern gyre is formed by the western branch of the Ob–Yenisei Current and the inflow of Barents Sea waters into the Kara Sea through the Kara Gates. The Ob–Yenisei Current, as it moves north, divides into three branches: western, northern, and eastern. At the Kara Gate Strait, the Litke Current separates from the Novaya Zemlya Current, flowing into the Barents Sea, and the main flow turns east and, merging with the flow of water from the Barents Sea, heads to the coast of the Yamal Peninsula, along which it goes north under the name of the Yamal Current until it meets the western branch of the Ob–Yenisei Current, thereby closing the circulation of surface waters in the southwestern part of the sea.

2. Materials and Methods

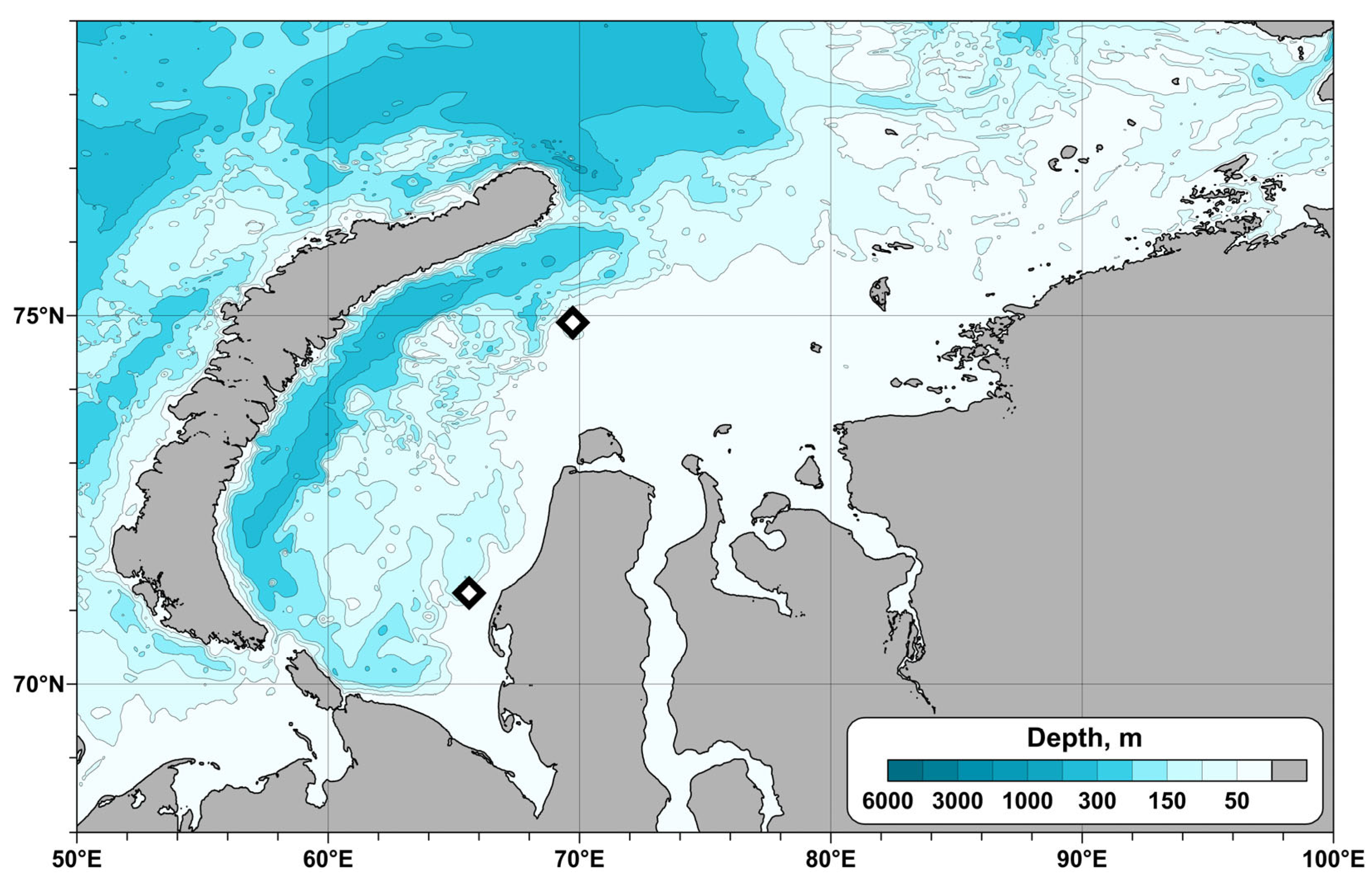
We analyzed temperature measurements from two moorings in the Kara Sea north of the critical latitude for semidiurnal internal tides (74°30′ N): a northern one at 74°54.3′ N, 69°43.6′ (instrument ADCP Argonaut-MD Sontek at 32 m) and one south of the critical latitude at 71°14.2′ N, 65°36.3′ E (the same instrument at 32 m). Both moorings were deployed at a depth of 42 m. The moorings operated over one year from 15 October 2021 to 15 September 2022. A bathymetric map of the Kara Sea with positions of moorings is shown in Figure 1. The study relies on only two moorings north and south of the critical latitude. Only the ice-free period was analyzed. We do not extend our analysis over the entire Kara Sea. The resolution of the Argonaut MD instruments is 0.01 °C, and the accuracy is 0.05 °C. The sampling rate was set to 1 h. Data was filtered to exclude unreasonable measurements, which were extremely rare.

We used altimetry data to determine the position of the eddies and estimate the vorticity in the basin. Vorticity in the surface layer was determined based on the estimates of the currents from satellite data of sea surface height at horizontal scales of 36 km (zonal) and 41 km (meridional). The positions of the moorings on a topographical map of the area and mean currents are shown in Figure 2.

Our analysis of vorticity was based on the ideas reported in [34]. Satellite altimetry provides sea surface height data that can be used to estimate variations in sea level and surface circulation. We used altimetry data from the internet site https://data.marine.copernicus.eu/product/SEALEVEL_GLO_PHY_L4_MY_008_047/download?dataset=cmems_obs-sl_glo_phy-ssh_my_allsat-l4-duacs-0.125deg_P1D_202411 (accessed on 1 November 2025). We analyzed quasi-geostrophic currents based on surface elevation satellite data with a step of 1/8 of a degree (geographical coordinates). In the study region, 1/8 of a degree is approximately equal to 4.3 km in the zonal direction and 13.8 km in the meridional direction.

We calculated the altimetry-derived vorticity maps using the geostrophic altimetry-derived meridional and zonal velocity components. The errors of the currents are presented based on the same satellite altimetry product.

In the summer period the formal error of altimetry mapping in the Kara Sea is 3–4 cm, and the corresponding errors of the vector components of surface current u and v are up to 3 cm/s at our northern point and up to 2 cm/s at the southern point. In this paper we are interested not in the absolute units but in the sign of vorticity to check whether a cyclone or anticyclone is present in the region of the moorings. Figure 3 shows the mean errors in the summer season (June–August, 2022) at the study sites in the Kara Sea.

Of course, the errors of altimetry-derived velocities are higher in the high-latitude region and they are even greater in the shallow waters. However, they do not exceed 3–4 cm/s. In this section, we specifically estimate the errors of altimetry-derived velocities provided by the developers, showing that they are not very high, meaning we are able to conclude that either an anticyclone or a cyclone was present at the location of the moorings.

We selected steps of 36 km and 41 km, respectively, so that the steps were close to the Rossby radius. Then vorticity was estimated from the following formula based on the satellite data of surface currents: $\left({\displaystyle \frac{dv}{dx}}-{\displaystyle \frac{du}{dy}}\right).$Although vorticity based on altimetry data is shown over the entire period of mooring operation, we think that vorticity data from the period when the sea was covered with ice are not very reliable.

We also used Sentinel-1A satellite synthetic aperture radar (SAR) images to detect surface manifestations of high-frequency internal solitary waves (ISWs) and ocean eddies. Altogether, 21 Sentinel-1 SAR images covering various dates in June–September 2022 were used in the analysis. The SAR images were selected according to the specific dates when there were distinct anomalies in vorticity at the locations of the moorings.

Signatures of ISWs and eddies can be easily detected in SAR images due to their effect on short wind waves responsible for radar backscatter from the sea surface. Very clear SAR signatures of ISWs in the form of alternating bright and dark bands are formed [34,35,36], while eddies are most often seen as ubiquitous spiraling features [34]. Detection of signatures of ISWs and eddies in SAR data is based on visual analysis, described in detail by Kozlov et al. [35,37]. However, the SAR data were used only to check whether these signatures were present in the images, not for any quantitative derivation of their properties.

3. Results and Discussion

Variations in vorticity estimated over the entire period of measurement are shown in Figure 4 at the point of the southern mooring, and in Figure 5 for the northern point.

We selected the time periods for temperature spectrum calculation from sensors on both moorings during the ice-free period only. In general, the sea is covered with ice from the end of October to mid-June. More detailed data about the ice cover in 2021 are given in [38,39]. The regions around our moorings were free of ice until 20 October 2022.

The Coriolis parameter at the latitudes of our moorings is 0.000022 s⁻¹. One can see from the graphs in Figure 4 and Figure 5 that the absolute value of negative (anticyclonic) vorticity is smaller than this value. However, based on our calculations, the peaks on the temperature spectra at the semidiurnal frequency begin to appear even at lower (by the absolute value) anticyclonic vorticity.

In the analysis presented below, we presume that horizontal advection of a propagating anticyclonic eddy and the negative vorticity that occurs during its passage over the mooring location facilitate the occurrence of internal tide M₂, which can be generated over sloping bottom topography by tidal currents. When a strong cyclone appears, positive vorticity can prevent the free internal tidal wave from spreading outward from the generation region. We estimate the vorticity of waters based on the currents calculated from the sea surface height averaged over a day based on satellite altimetry data. We analyze temperature spectra from moored measurement sensors. We judge the existence of internal tides using temperature measurements when a spectral peak at the semidiurnal frequency M₂ appears.

We analyzed charts of vectors over the period of summer observations and found that the pattern of currents does not change strongly over a period of 20 days. In addition, a 20-day of time series is sufficient for spectral statistics of semidiurnal tides. This determined our choice to use a 20-day interval when calculating temperature spectra. We selected periods of cyclone passage (positive vorticity) near the southern mooring and calculated temperature spectra at a depth of 32 m based on 20-day measurement series. This period fell on the interval centered on 29 June 2022. There are no spectral peaks at the M₂ frequency. The period of anticyclone passage (negative vorticity) fell on 15 August 2022 (central date) (Figure 6).

Let us analyze the maps of vectors of the surface current near the southern mooring when peaks were recorded at the M₂ and when they were not. Figure 7a,b show the maps of the surface velocity vectors constructed on 29 June 2022 (cyclone), when there was no peak in the spectrum, and 15 August 2022 (anticyclone), when such a spectral peak was found. Vorticity maps are also shown in this figure in the bottom panels (Figure 7c,d). The maps were constructed based on altimetry-derived velocity data. On 29 June 2022, the mooring was located on the boundary of the cyclone and anticyclone, closer to the anticyclonic part with low anticyclonic vorticity.

At the northern mooring point, we selected the intervals of cyclones (positive vorticity) and estimated the spectra of temperature oscillations at a depth of 32 m using 20-day time series measurements. This period fell on the interval centered on 6 September 2022. There is no peak on the spectrum at the M₂ frequency. The period of anticyclone (negative vorticity) activity fell centered on 20 June 2022. A peak on the spectrum is noted (Figure 8).

The maps of surface current vectors near the northern mooring were plotted for the days when peaks were recorded at the M₂ frequency and on the days when they were not. Figure 9 shows the maps of surface velocity vectors plotted on the dates of 6 September 2022 (cyclone), when there was no peak in the spectrum, and 20 June 2022 (anticyclone), when such a peak in the spectrum was present. Vorticity maps are also shown in this figure in the bottom panels. The maps are plotted based on altimetry-derived data on currents.

Generation and propagation of internal tides is generally accompanied by waves breaking into trains or packets of high-frequency internal waves that can be detected at the sea surface by remote sensing. Appearance of high-frequency wave packets in a high-latitude region is different from that at mid- and low latitudes. Usually, packets of internal waves appear after the tidal wave propagates some distance from the source of generation. This is can easily be seen on the satellite images of the Strait of Gibraltar. Waves are generated over the Camarinal Sill at 5.75° W; they propagate to the east, and wave packets are seen at the surface on the aerial and space images at 5.25° W in the Alboran Sea. At high latitudes the process is different. Tidal internal waves of the M₂ frequency do not propagate from the slope, but become standing forced waves, and the energy is transferred to high-frequency waves immediately over the sill if this happens [24].

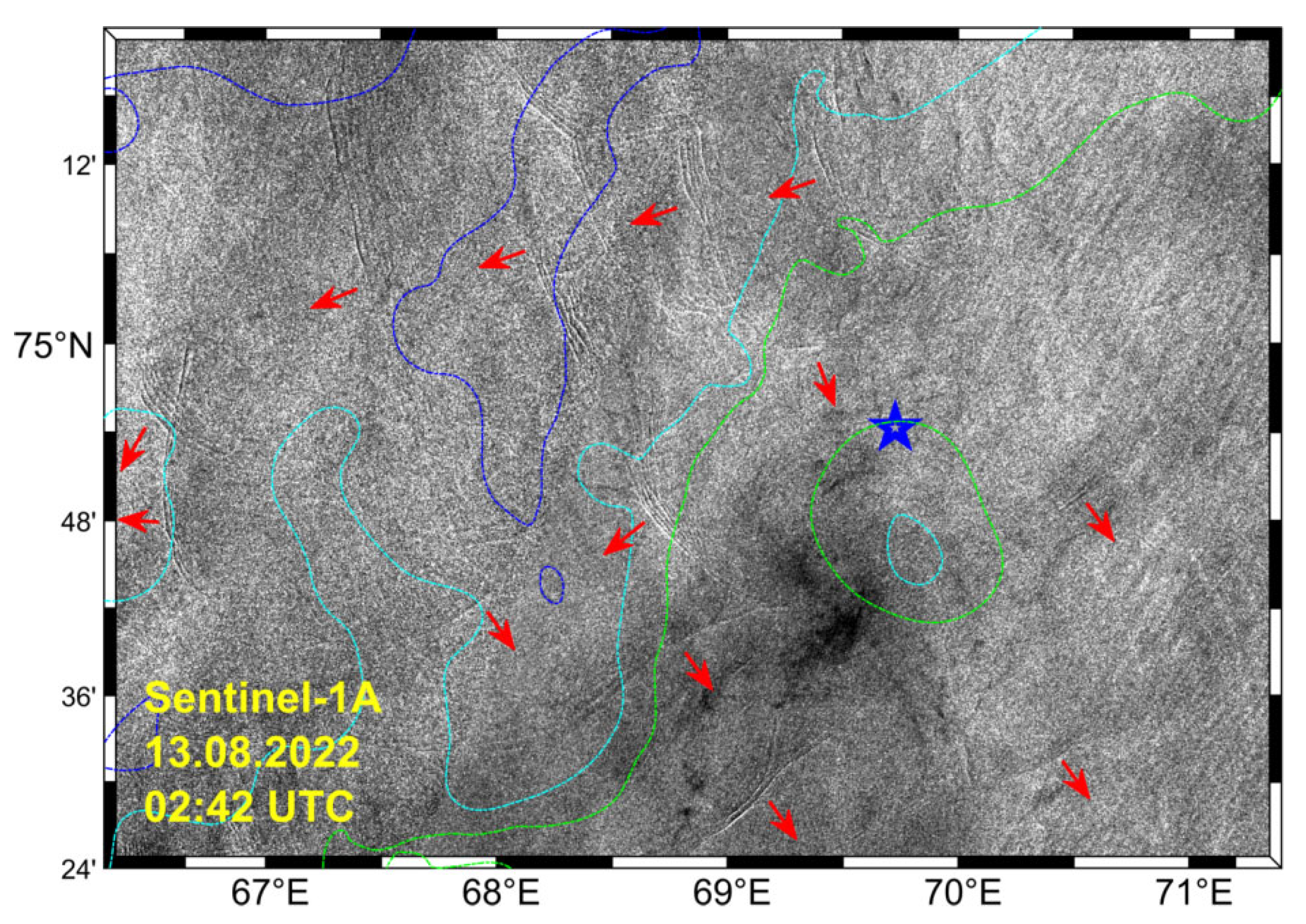
We analyzed several satellite images of internal wave manifestation at the surface. The processing method is described in [35,39,40]. Figure 10 shows a zoomed region of a Sentinel-1A image depicting the presence of an oceanic cyclonic eddy (highlighted by red arrows in Figure 10) near the northern mooring. No surface manifestation of high-frequency internal waves is seen in the image.

An image taken on 13 August 2022 (Figure 11) shows many wave packets propagating from the slope and near the slope shown by the isobaths of 50, 100, and 200 m, indicated by green to blue colors.

Figure 5 and Figure 6 show that anticyclonic vorticity was observed at this date in this region and that the spectrum has a peak at the M2 frequency. The time series for spectrum calculation was from 5 to 25 August 2022.

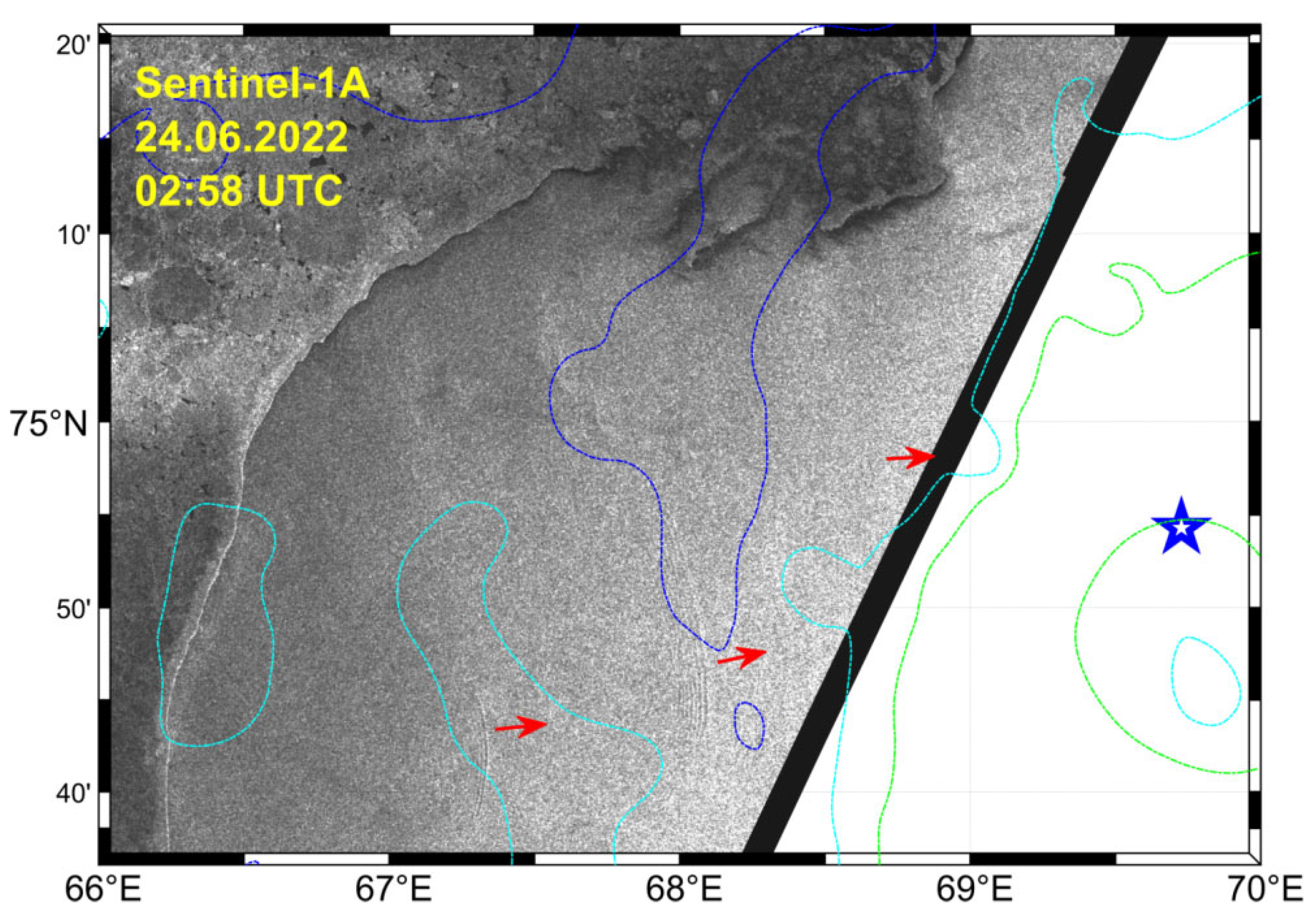
Figure 12 shows a satellite image of the surface near the northern mooring on 29 June 2022, which is a day when anticyclonic vorticity was observed in the region of the northern mooring. The maximum negative vorticity was on 26 June. High-frequency internal waves propagate from the slope, shown by isobaths of 50 and100 m (green and cyan blue), towards the mooring location.

4. Conclusions

In this paper we focus on the physical problem of M₂ internal tide existence near the critical latitude (74°30′ N). This paper is not intended to characterize internal tides in the Kara Sea as a whole in a geographical aspect. We use two moorings, north and south of the critical latitude for M₂ internal tides, to show that this latitude is not a fixed boundary north of which internal tides of the M₂ critical frequency do not exist.

The novelty of this research is the experimental confirmation of the dependence of existence of the M₂ internal tide near the critical latitude on the presence or absence of an anticyclonic eddy in the region. We show that, depending on the effective vorticity in the region, which is the sum of the planetary vorticity and vorticity induced by mesoscale eddies, internal tides of the M₂ frequency can either exist north of the formal critical latitude or not exist south of this line. This problem has also been partly investigated in [22].

Another factor that facilitates the appearance of the M₂ internal tide in the region of critical latitudes is sloping bottoms. In the linear approach, the M₂ internal tide cannot exist north of the critical latitude, but it is possible for it to do so if the sea floor is sloping. Forced internal tides can exist over a sloping bottom because currents of the barotropic tide transport water particles over the slope. Strong nonlinearity, or in other words the high amplitudes of internal oscillations induced by the barotropic tide over slopes, can facilitate internal tides north of the critical latitude, which is shown in [24].

We associate appearance of a reliable peak on the temperature spectra at the M₂ frequency with the propagation of internal tides. The duration of the time series to estimate the spectra was taken as 20 days, which is slightly longer than the period of spring–neap variation. Thus, we filter out the variations in tides and internal tides associated with spring–neap variation. At the same time, the duration of the time series is almost 40 times longer than the studied period (12.4 h), which makes our estimates reliable.

The peaks on the spectra appear even when the absolute value of the sum of the planetary vorticity and vorticity associated with the anticyclonic eddies is lower than the absolute value of the negative vorticity—in other words, when the sum of the wave frequency and effective Coriolis frequency is not positive and seemingly the M₂ internal tide should not be generated. At the same time, both moorings were deployed in areas with gentle slopes of bottom topography. This may facilitate appearance of internal tides with less assistance from negative vorticity.

Theoretically, the southern mooring, located south of the critical latitude, should have always recorded an internal tide. However, this is not true, especially when cyclonic activity is strong in the region and prevents generation of internal tides.

The records of the M₂ internal tide on the northern mooring (north of the critical latitude) reveal internal tides only when vorticity in the region is negative, but not necessarily negative enough to make the denominator in the third term of Equation (2) positive.

Of course, these two moorings in the Kara Sea do not represent the whole state of internal tides in the entire sea. The region is poorly studied, and deployment of even these two moorings gives much information on the processes at play in this remote region. We tried to show the physical aspect of how vorticity influences internal tides near the critical latitude. Vorticity was estimated from satellite altimetry measurements, from which altimetry-derived surface currents were estimated. The accuracy of these estimates in the shelf shallow regions is worse than in the deep open sea. The error estimates given by the developers of the site are within 3–4 cm/s. However, the maps of currents based on these estimates are smooth, and the eddies are distinguishable. No other measurements for estimating vorticity are available. We only analyzed time periods during the ice-free season.

Spectral peaks in the temperature spectra from measurements on moorings at the frequency of the semidiurnal tide M₂ (period 12.4 h) appear in the presence of anticyclonic vorticity in the velocity field of surface currents. Two moorings were located near the critical latitude 74°30′ N, one north of this latitude and the other to the south. Regardless of whether the mooring was located south or north of the critical latitude (but near this latitude), the peaks on the semidiurnal period appear during periods of anticyclonic vorticity and disappear when a cyclonic eddy appears at the mooring location, which leads to positive cyclonic vorticity. The vorticity was determined from the altimetry-derived currents.

Altimetry data at northern latitudes are not very reliable. Satellites visit the region once every few days. The everyday satellite altimetry data we used are produced by interpolation. The eddies can move during the day without direct satellite measurement, and errors can increase. The authors of [41] analyzed large river plumes of low salinity from the Ob and Yenisei rivers based on satellite altimetry. They concluded that plumes are clearly seen on the satellite images averaged over long time periods (three months in summer). However, everyday images contain unexpected regions of low sea level. This may be associated with the tidal forcing over uneven topography in shallow regions.

Spaceborne SAR images show the appearance of high-frequency internal wave packets in the presence of an anticyclonic eddy in the area of the moorings and the underwater slope.

We presume there were no sampling biases in the SAR analysis because there were no quantitative aspects related to the interpretation of the SAR data. We only checked whether surface signatures of ISWs and eddies very clearly present or absent in the data.

Our analysis shows correlation between the appearance of an anticyclonic eddy and the presence of the M₂ spectral peak (which indicated the presence of semidiurnal internal tide). This analysis was performed only for the summer period when water was stratified and ice-free so that we could estimate the vorticity based on altimetry-derived velocities. We did not have measurements of stratification during the period of the operation of the moorings. Winds generally do not influence tides. The influence of the spring–neap variability of the tides on our opinion was excluded by selecting 20-day time series to make our spectral estimates.