Simulation and Optimization of Collaborative Scheduling of AGV and Yard Crane in U-Shaped Automated Terminal Based on Deep Reinforcement Learning

Abstract

In U-shaped automated container terminals (U-shaped ACTs), automated guided vehicles (AGVs) need to frequently interact with yard cranes (YCs), and separate scheduling of the two devices will affect terminal efficiency. Therefore, this study explores the coordinated scheduling problem between the two devices. To solve this problem, a high-precision simulation model of the U-shaped ACTs is established, which incorporates real operational logic. Second, an Improved Non-dominated Sorting Genetic Algorithm II based on Proximal Policy Optimization (INSGAII-PPO) is proposed. The algorithm uses PPO to realize dynamic genetic operator selection and makes related improvements, which improve the multi-objective optimization ability of NSGAII, and solve the collaborative scheduling problem by combining simulation. Finally, a hybrid weighted Technique for Order Preference by Similarity to Ideal Solution with preferences is proposed to select the final solution. The experimental results show that the scheme obtained by INSGAII-PPO exhibits better convergence and diversity, and offers significant advantages compared with the comparison algorithms. Moreover, the energy consumption and waiting time of the final solution selected by the proposed method are reduced by 3.42% and 4.87% on average. The proposed method has the capability of providing a theoretical reference for the AGVs and YCs collaborative scheduling of U-shaped ACTs.

1. Introduction

In 2024, global container port throughput experienced a significant increase, presenting new challenges to various ports. Studies have shown that Automated Container Terminals (ACTs) can effectively improve terminal efficiency, reduce labor requirements, and thereby lower operational costs [1]. However, the growth in container throughput demands that ACTs achieve higher efficiency and larger container yard capacity. Traditional automated container terminals typically adopt either a parallel or vertical layout, where loading and unloading operations are conducted at the end and sides of the container yard, respectively [2]. To further enhance space utilization and operational efficiency, a yard layout scheme for U-shaped ACTs has emerged.

The U-shaped layout of ACTs differs from traditional layouts in the following respects: In terminals with the traditional vertical layout, the movement range of Automated Guided Vehicles (AGVs) is limited to the end of the container yard, and AGVs do not enter the yard to interact directly with Yard Cranes (YCs); thus, their operational processes are relatively independent. In contrast, in U-shaped ACTs, AGVs need to move deep into the container yard for direct and frequent interactions with YCs. Additionally, there are multiple loading/unloading points within the yard, which render the scheduling and collaborative coordination between AGVs and YCs more complex than ever before. The layout of the U-shaped ACTs system is mainly divided into three parts: the seaside area, the horizontal transportation area, and the landside area. The layout of the U-shaped automated terminal is illustrated in Figure 1. The seaside area is used for container loading/unloading operations, including berths and Quay Cranes (QCs). The horizontal transportation area is designed for AGVs to transfer containers between the seaside and landside areas, consisting of horizontal transportation lanes and AGVs. The landside area is utilized for container storage, transfer, and other related operations, primarily including YCs and yard blocks.

Studies have indicated that the energy consumption of YCs accounts for 25–35% of the total energy consumption in container terminals. In contrast, although the energy consumption of AGVs merely constitutes 1.04% of the total operational energy consumption of terminals, their scheduling exerts a substantial impact on the operational efficiency of terminals [3]. Consequently, in U-shaped ACTs, inadequate coordination between AGVs and YCs not only leads to a significant reduction in terminal operational efficiency but also results in increased equipment energy consumption and inter-equipment waiting time, which severely constrains the overall operational efficiency and service quality of the terminal.

Furthermore, in the current research on the collaborative scheduling of AGVs and YCs in U-shaped ACTs, the majority of proposed solutions rely on mathematical modeling approaches and tend to focus on the optimization of a single objective (e.g., maximum makespan). Nevertheless, in U-shaped ACTs, there exists a complex coupling relationship between AGVs and YCs, coupled with intensive operations at loading and unloading points. Conducting multi-objective optimization research on this system necessitates that the established model not only accurately characterizes the dynamically interactive relationships among equipment but also enables the solution of multi-dimensional objectives. However, traditional mathematical modeling methods are limited by fixed assumptions (such as simplified equipment interaction rules, a large number of conditional constraints) and a single-objective optimization framework, which are difficult to adapt to the dynamic coupling characteristics of U-shaped terminals. By comparison, the simulation-based optimization approach can truly reproduce the overall system operation of automated terminals. Through dynamic simulation of full-process operations under different scheduling schemes, it allows for the direct observation of real-time trade-off results among multiple objectives (e.g., efficiency improvement and energy consumption control). This approach can assist decision-makers in formulating optimization strategies that balance multi-dimensional requirements, including efficiency and energy consumption, thereby rendering it more suitable for addressing the multi-objective optimization problem of AGVs and YCs collaborative scheduling in U-shaped ACTs.

Therefore, the multi-objective optimization problem of AGVs and YCs collaborative scheduling, which comprehensively considers efficiency, energy consumption, and equipment waiting time, is an urgent scheduling issue to be addressed in U-shaped ACTs. Based on the operational characteristics of U-shaped ACTs, multi-equipment collaborative scheduling exhibits high coupling and complexity, leading to significant limitations in research utilizing mathematical modeling approaches. Furthermore, many studies lack sufficient granularity in optimizing objectives such as computational efficiency and energy consumption, resulting in deviations between the final solutions obtained and real-world scenarios. In addition, traditional heuristic methods have limited search capabilities when solving high-dimensional and complex scheduling problems and are prone to falling into local optima, which leads to insufficient diversity of solutions. In summary, this study focuses on the collaborative scheduling problem of AGVs and YCs in U-shaped ACTs, and proposes a multi-objective optimization algorithm based on Deep Reinforcement Learning (DRL) with the triple objectives of reduce the task completion time, reducing equipment energy consumption and shortening AGVs waiting time. Moreover, a high-precision simulation platform is built to combine with the algorithm, and the collaborative improvement of multi-objectives is realized through the iterative optimization mechanism, which provides a new solution for the equipment collaborative scheduling in complex terminal scenarios.

The main contributions of this paper are as follows:

(1)

Based on a simulation platform, a U-shaped ACTs simulation model with a standardized layout and complete operational logic is constructed. In the simulation model, the accuracy of the operation process of AGVs and YCs is mainly considered. For this reason, a refined road network structure for the horizontal transportation area is built, real operational logics such as AGVs charging and parking waiting in buffer zones are implemented, and a refined control logic for YCs single-step actions is designed—all to ensure high-precision reproduction of equipment operations by the simulation model. The high-precision nature of this simulation model provides a reliable data foundation for the subsequent iterative optimization of the multi-objective simulation optimization algorithm.

(2)

Aiming at the multi-objective optimization problem of AGVs and YCs collaborative scheduling in U-shaped ACTs, this paper utilizes the powerful learning ability of the Proximal Policy Optimization (PPO) algorithm and the multi-objective optimization ability of the Non-dominated Sorting Genetic Algorithm II (NSGA-II), combined with a high-precision simulation model, and for the first time proposes an improved NSGAII multi-objective simulation optimization method based on PPO (INSGAII-PPO). This method uses the simulation model to perform real-time full-process simulation of the scheduling schemes generated by the multi-objective optimization algorithm, and feeds back high-fidelity data to the algorithm for iterative optimization. This ensures that the final solutions obtained are more in line with practical requirements and provide a guiding basis for real-world decision-making.

(3)

Considering the complexity of the multi-objective optimization for AGVs and YCs collaborative scheduling, a hybrid initialization strategy integrating Logistic chaotic mapping and Latin Hypercube Sampling (LHS) is proposed. To enhance the search capability and efficiency of the algorithm, a dynamic genetic operator selection strategy is proposed using the learning mechanism of PPO, which is used to select appropriate genetic operators from different candidate operators; a prioritized experience replay mechanism and an ε-greedy (Epsilon-greedy) strategy are also introduced. Finally, in accordance with the characteristics of multi-objective problems, a preference-based hybrid weighted Technique for Order Preference by Similarity to Ideal Solution (TOPSIS) is designed to select the optimal solution from the Pareto solution set, thereby enabling more accurate and preference-oriented multi-objective decision-making.

The remaining structure of this paper is organized as follows: Section 2 provides a review of the relevant literature. Section 3 elaborates on the constructed simulation model. Section 4 introduces the PPO-based improved NSGA-II algorithm. Section 5 conducts comparative experiments and analyzes the results. Section 6 provides the conclusions.

2. Literature Review

This section primarily reviews existing studies relevant to the present research in recent years. It may be split into the following three components: scheduling research based on mathematical models, scheduling research based on simulation methods, and scheduling research based on deep reinforcement learning.

2.1. Scheduling Research Based on Mathematical Models

Both in the intelligent manufacturing industry and automated terminal AGVs are gradually becoming the main means of transportation, the reasonable scheduling and associated equipment can significantly improve the working efficiency. Li et al. [4] proposed a DQN algorithm for solving the dynamic job-shop scheduling problem with AGVs and random job arrivals to ensure that the makespan is minimized. Fan et al. [5] and Cheng et al. [6] proposed different algorithms to solve the model for the collaborative scheduling problem of AGV and other equipment in manufacturing workshops, and optimized the total processing time or total power consumption. Yang et al. [7] and Zhang et al. [8] have investigated scheduling issues related to AGVs in automated container terminals under traditional layouts. As large-scale equipment for container handling, YCs have been the subject of scheduling studies by Li et al. [9] and Zhou et al. [10], focusing on conflict-free operations and optimal sequencing to minimize YCs’ makespan. As key equipment for landside operations, AGVs and YCs interact during operations. Their efficiency and energy consumption levels profoundly impact the entire terminal. Consequently, numerous studies focus on optimizing the coordinated scheduling of AGVs and YCs. Chen et al. [1] developed an AGV-CRANE synchronization model based on an extended spatiotemporal network to better coordinate AGVs and cranes in both spatial and temporal dimensions. They treated the integrated scheduling of gantry cranes and AGVs as a multi-robot coordination problem, providing precise spatiotemporal paths for AGVs and crane robots within terminal systems. Addressing scenarios with multiple cranes in a yard, Zhang et al. [11] investigated the integrated scheduling of AGVs and YCs within a yard block while accounting for crane conflicts. Furthermore, leveraging the charging functionality of AGVs’ companion integration, Yang et al. [12] studied the collaborative scheduling of AGVs and YCs under charging/swapping modes, simultaneously optimizing equipment energy consumption and operational delay costs. The above studies reveal that most current research on AGVs and YCs coordination remains focused on traditional vertical or parallel automated terminal layouts. In U-shaped automated terminals, collaborative scheduling research between AGVs and YCs is still in its exploratory phase. Liu et al. [13] designed a two-layer genetic algorithm to optimize yard crane scheduling, AGVs task allocation, and path planning. Yang et al. [14] proposed a multi-device collaborative scheduling method based on precise AGVs path planning for U-shaped automated terminal equipment scheduling, aiming to optimize total equipment energy consumption.

Based on the aforementioned findings, extensive exploration has been conducted on scheduling issues related to individual pieces of equipment. However, insufficient research has been carried out on the collaborative scheduling problem between AGVs and YCs under the U-shaped layout. Furthermore, most scheduling research focuses on improving operational efficiency, with limited studies simultaneously considering multi-objective optimization such as energy consumption.

2.2. Scheduling Research Based on Simulation Methods

Simulation not only enables experimentation with various schemes and extraction of targeted metrics as needed, but also provides extensive data for analysis through simple modifications, meeting the dynamic requirements of automated terminals. Zhang et al. [15] employed systems thinking to propose an integrated scheduling optimization solution and implemented a web-based simulation framework, offering a novel approach for network-centric simulation and monitoring of actual processes. Hsu et al. [16] proposed a simulation-based optimization framework employing four heuristic algorithms to concurrently address YCs scheduling for export containers, yard truck scheduling, and QCs scheduling. Furthermore, (Xiang and Liu [17]; Zhang et al. [18]; Zhong et al. [19]) first solved scheduling problems using algorithms and then validated the results through simulation, demonstrating that simulation can also serve as a means to compare and verify models and algorithms. Liang et al. [20] further demonstrated the validity of simulation verification by inputting algorithm-generated path scheduling plans and AGVs scheduling plans into a simulation model, successfully comparing the maximum completion times obtained from simulation and algorithms.

In order to further improve the real effectiveness of the algorithm, some scholars try to add simulation to the iterative optimization process of the algorithm. Junqueira et al. [21], Li et al. [22], and Qin et al. [23] employed simulation modules as performance metrics for algorithmic solutions, using them to evaluate scheduling schemes and provide feedback to the algorithms to facilitate iterative optimization. Yu et al. [24] embedded a simulation module within a genetic algorithm framework, utilizing the module’s output of reprocessing counts alongside AGVs’ waiting times and retrieval times as objective functions to update the population. Additionally, Yang et al. [25] designed a multi-agent simulation optimization method based on DRL to address the joint scheduling problem of bidirectional task assignment and charging for an intelligent guided vehicle. By integrating simulation with DRL, network training for specific scenarios was achieved.

Simulation-based optimization methods not only validate the effectiveness of obtained scheduling schemes but also leverage simulation to assist algorithmic iterative optimization, further enhancing the realism of the solutions. However, existing research indicates that simulation optimization methods have seen limited application in multi-objective optimization studies for U-shaped ACTs, necessitating further exploration.

2.3. Scheduling Research Based on Deep Reinforcement Learning

DRL demonstrates exceptional adaptability in complex environments, with its decision models capable of dynamically adjusting strategies in real-time based on environmental feedback. Zhou et al. [26] proposed a method that combines hyperparameter optimization based on a genetic algorithm with PPO to address the dynamic flexible job-shop scheduling problem, significantly enhancing the learning efficiency and scheduling performance of the algorithm. DRL also brings new opportunities to address complex scheduling challenges in port operations. Gong et al. [27] proposed a hybrid multi-AGV scheduling algorithm based on the multi-agent Deep Deterministic Policy Gradient (DDPG) method, optimizing both AGVs’ energy consumption and makespan. Che et al. [28] developed a novel scheduling approach based on an actor-critic multi-agent deep reinforcement learning framework to enhance collaboration between vehicles and charging stations, considering battery energy capacity and charging station constraints. Hau et al. [29] and Hu et al. [30] investigated path planning for AGVs within horizontal transport zones of ACTs. They solved the proposed mathematical model using methods like multi-agent reinforcement learning to obtain optimal paths. Zhou et al. [31] proposed an AGVs scheduling method integrating simulation environments with the PPO algorithm to balance vehicle charging and task completion. Additionally, Wang et al. [32] pioneered the inclusion of QCs and YCs scheduling operations within terminal scheduling workflows, proposing a reinforcement learning-based algorithm for handling real-world-scale instances. For U-shaped automated terminals, Yang et al. [33] proposed an improved PPO-based simulation optimization method for AGVs’ charging strategies. Tang et al. [34] introduced a real-time scheduling optimization framework based on deep reinforcement learning to address the scheduling of automated twin-boom rail cranes in real-time digital twins within U-shaped automated terminals. Xu et al. [35] investigated the integrated scheduling of dual-gantry cranes, conflict-free AGVs, and rail cranes during loading/unloading modes using a reinforcement learning-based hyper-heuristic genetic algorithm. In general, deep reinforcement learning is still in the preliminary stage of exploration in the field of port scheduling, and there are still a large number of research gaps in the field of AGVs and YCs collaborative scheduling.

In summary, the current research is still mainly focused on the single-objective scheduling problem of terminals with traditional layouts, such as operational efficiency and energy consumption. Few scholars have studied the multi-objective optimization problem of equipment co-scheduling under U-shaped layout. In terms of methods, most of the research adopts mathematical modeling, and the simulation optimization method is rarely applied to the collaborative scheduling problem. DRL possesses powerful adaptive and complex decision-making capabilities, but its application in terminal scheduling remains in the early stages of exploration. This paper aims to remedy the shortcomings of existing studies. Therefore, a high-precision simulation model of U-shaped ACTs was established, and it was combined with the optimization algorithm combined with DRL to carry out multi-objective simulation optimization research on the collaborative scheduling problem of AGVs and YCs in U-shaped ACTs.

3. Simulation Modeling of U-Shaped Automated Container Terminal

This section focuses on presenting the constructed refined U-shaped ACTs simulation model and clarifying the functions of each of its simulation modules, thereby offering a basis for subsequent research work.

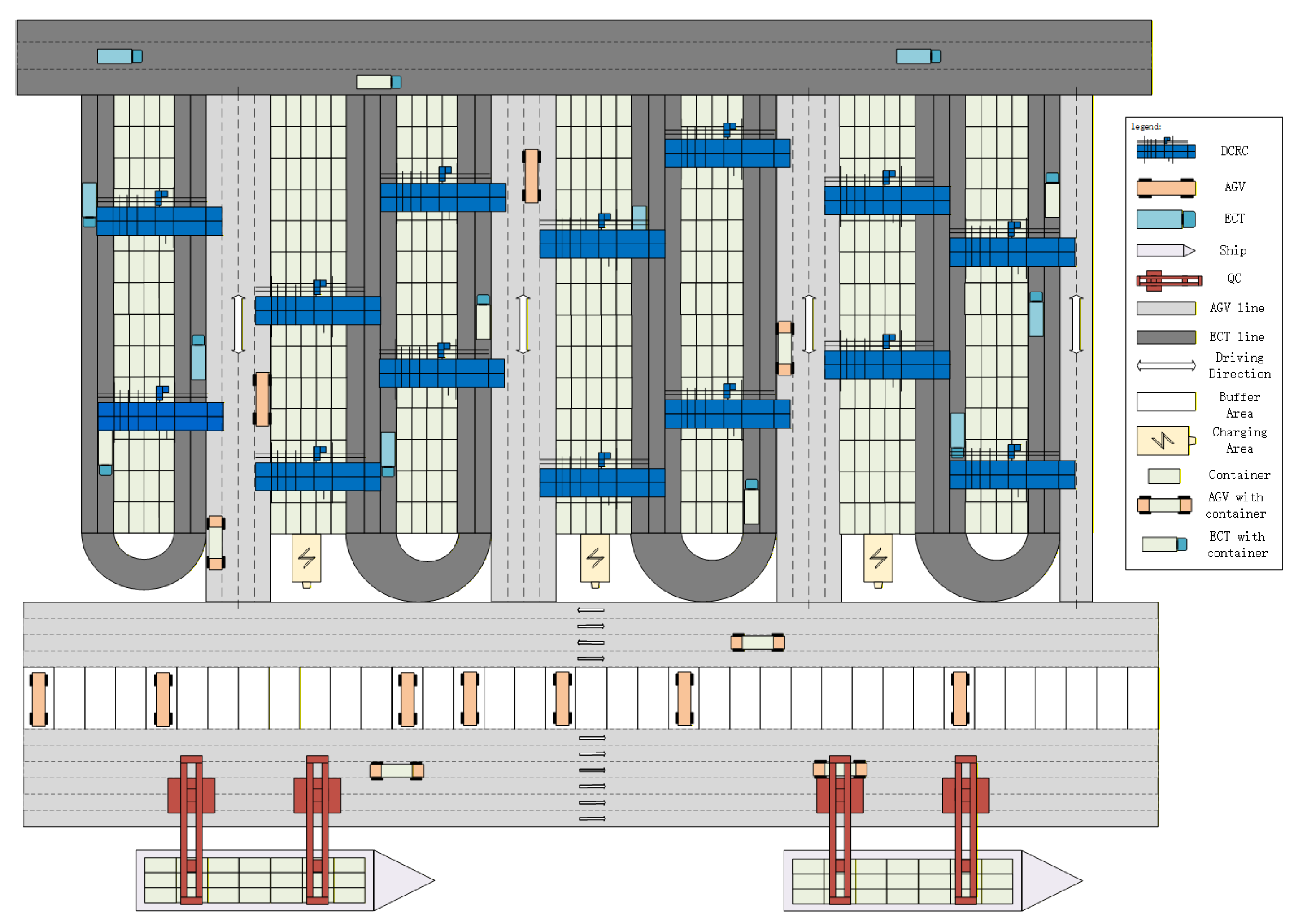
3.1. U-Shaped ACTs Simulation Model

The U-shaped ACTs simulation model was developed using Siemens Digital Industries Software’s (Plano, TX, USA) Plant Simulation 15.0 platform. It incorporates the SimTalk programming language to simulate the terminal’s unique operational workflows, as illustrated in Figure 2. The simulation model primarily comprises the quay loading/unloading area, horizontal transport zone, and landside loading/unloading area. The quay loading/unloading area is equipped with three QCs, each serving three loading/unloading points. These points adhere to a “6-in, 2-out” rule, meaning AGVs can enter via six lanes and exit via two lanes. To ensure realistic AGVs operation, the horizontal transport zone features a detailed road network structure and buffer zones. The road network strictly follows actual terminal traffic rules, while buffer zones accommodate AGVs’ parking. The landside handling area comprises 6 yards, each containing 32 bays and 2 YCs. Single-step motion control is designed for each yard crane to enhance operational precision. There are two passing lanes and two loading/unloading lanes between the two stockyards. The model simplifies loading/unloading lanes by using Buffer controls to simulate AGVs’ loading/unloading points. Additionally, the charging station is located at the end of the yard. When an AGVs requires charging, it travels to the nearest charging station via the horizontal transport zone. This configuration more closely aligns with actual terminal operations.

Functionally, the developed control module ensures the simulation model can execute the entire container handling process: After the simulation starts, the task generation module creates a task table based on the input scheduling plan, containing information such as task start positions, assigned AGVs and YCs. Containers are then generated at corresponding locations in the quay loading/unloading area. The scheduling module dispatches the assigned AGVs to transport them. Upon arrival at the loading/unloading point, the container is loaded onto the AGVs by the QCs. The loaded AGVs follow the shortest path through the horizontal transport zone to deliver the container to the designated yard area in the land-side loading/unloading zone. Finally, YCs unload the container from the AGVs onto the designated location. Furthermore, as this research emphasizes the coordinated scheduling of AGVs and YCs, the yard area does not consider external trucks, making the model more targeted in its functionality.

3.2. Simulation Assumptions

In order to enhance the consistency between simulation and actual U-shaped ACTs operations, the following assumptions are made:

• Containers are standardized 20-foot equivalent units (TEUs).
• Container flipping issues are not considered.
• Storage locations for each container are randomly generated.
• All containers are imported.
• Only one container is allowed on each AGV.
• External trucks and their corresponding lanes are not considered.
• All lanes in the horizontal transport zone are one-way.
• A fixed number of QCs and YCs are used in the simulation.
• The yard internal loading/unloading lanes are simulated using multiple loading/unloading points.
• Upon reaching the specified bay position, the AGVs move to a buffer zone. It can only leave the buffer zone and exit the yard after the YC has retrieved the container.
• The parameters and speed of each part of the YC are set in the simulation, which is used to simulate the movement time of each part.
• If the AGV does not need to be charged after completing its task, it will return to the buffer to wait for the next job.
• The AGV travels according to the shortest path principle.
• AGVs operate in either loaded or empty states, with varying power consumption between states; AGVs consume no energy while in a waiting state.

3.3. AGV and YC Control Module

To achieve more refined operations, control modules for AGVs and YCs were developed using the SimTalk language within the simulation software to support the workflow within the simulation model.

For AGVs, an initialization module and a scheduling module were implemented. The initialization module controls AGVs generation and initializes status information such as battery levels. This module ensures AGVs are uniformly distributed across the buffer zone at startup. The scheduling module handles AGVs’ dispatch. When a container is generated, it calls the corresponding AGVs to proceed to the container location for loading. After the AGV has finished its current task, the dispatching module determines the current status of the AGV and gives the next instruction: (1) If a task exists and battery level exceeds the charging threshold, proceed to the next task’s initial position; (2) If it has a task but its battery level is below the charging threshold, it is assigned to a charging station and resumes operations after charging; (3) If it has no task and its battery level is above the charging threshold, it proceeds to the nearest buffer zone to wait; (4) If it has no task and its battery level is below the charging threshold, it goes to a charging station to charge. After charging, if no new task is available, it returns to the buffer zone to wait.

For YCs, a single-step motion control module was designed to enable precise operations, comprising three main functions: (1) The large vehicle controlling the YC moves from the current position to the loading and unloading position of the task; (2) Control the crossbeam trolley to move from the storage position of the previous task to the current loading and unloading point or from the loading and unloading point to the storage position of the current task; (3) Controlling the lifting or lowering of the lifting device, as well as the grabbing and releasing of containers (all lifting device actions can only be performed after the crossbeam trolley reaches the designated position). Through the single-step motion control module, YCs operations more closely match real port scenarios, thereby improving the accuracy of optimization target calculations.

3.4. Charge Module

The charging module comprises charging stations and a charging strategy module. In the simulation model, charging stations are simulated using Buffer components, and AGVs can travel from the horizontal transport zone to charge at these stations. In the current study, the charging strategy employs fixed-threshold charging, where the threshold can be set as required. When an AGV requires charging, the dispatching module assigns a charging station. Upon arrival, the charging strategy module calculates the required charging time based on the current battery level. The AGV then remains at the buffer for the corresponding duration to simulate the charging event. The charging capacity and time will be recorded by the statistics module.

3.5. Statistics Module

The simulation incorporates an information statistics module, encompassing task information statistics and AGVs status information, which were summarized in the corresponding Excel tables. During simulation, real-time access to task information or AGVs’ status data is available, as shown in Figure 3. Additionally, upon simulation completion, the statistics module’s data is utilized for metric calculations and returned to external algorithms.

4. Improved NSGAII-PPO Simulation Optimization Method

To effectively address the multi-objective collaborative scheduling problem between AGVs and YCs, a dynamic genetic operator selection strategy based on PPO is proposed and embedded into the improved NSGA-II algorithm. The resulting multi-objective collaborative scheduling algorithm is termed the INSGAII-PPO algorithm. Through iterative optimization via simulation interactions with the INSGAII-PPO algorithm, the multi-objective collaborative scheduling problem for AGVs and YCs is solved. The algorithm flowchart is shown in Figure 4. This section details the INSGAII-PPO simulation optimization algorithm, including the calculation of optimization objectives, population initialization, state space, action space, and the definition of the reward function.

4.1. Optimization Objective Calculation

In this study, the optimization objectives are the task completion time, total equipment energy consumption, and total load waiting time for AGVs. As the simulation model built in this study incorporates the full-process operation logic of the wharf, the coupling effect between AGVs and YCs operations will naturally manifest through the discrete event simulation framework. Therefore, the data obtained based on simulation can ensure that the interrelationships among various optimization objectives are truly reflected in the calculation of the final objective values. Each objective value is calculated as follows. The task completion time is calculated based on the simulated time controller, where the completion time of the last task serves as the final completion time. The total equipment energy consumption of the U-shaped ACTs primarily consists of the energy consumption of AGVs and YCs, as Equation (1). AGVs energy consumption is calculated based on battery usage, as Equation (2). AGVs battery consumption is derived from data collected by the simulation model’s statistical module. YCs energy consumption is calculated based on the operating durations of the main and auxiliary cranes during empty/loaded operations, as well as the working duration of the lifting equipment, as Equation (3). The parameters in the formula are defined in

Table 1. Definition of parameters.

Parameter	Description	Parameter	Description
$E_{agv}$	Total energy consumption of AGV operation (kwh)	${\alpha }_{yc\_wl}$	Energy consumption rate of empty movement (kwh/h)
$C_{charge}$	Total power consumption of AGV (Ah)	${\beta }_{yc\_l}$	Energy consumption rate of load lifting (kwh/h)
$V_{agv}$	AGV rated operating voltage (V)	${\beta }_{yc\_wl}$	Energy consumption rate of empty lifting (kwh/h)
$E_{yc}$	Total energy consumption of YC operation (kwh)	$t_{m\_l}$	Load movement time (h)
$E_m$	Total energy consumption of the YC movement (kwh)	$t_{m\_wl}$	Empty movement time (h)
$E_h$	Total energy consumption of YC lifting (kwh)	$t_{h\_l}$	Load lifting time (h)
${\alpha }_{yc\_l}$	Energy consumption rate of load movement (kwh/h)	$t_{h\_wl}$	Empty lifting time (h)

. The energy consumption rates for crane movement and lifting vary with load conditions, as listed in

Table 2. Relevant parameters for energy consumption calculation of YC.

Parameter	Value
Lifting energy consumption rate of the YC under heavy load	115 kwh/h
Mobile energy consumption rate of the YC under heavy load	55 kwh/h
Lifting energy consumption rate of the YC under without load	55 kwh/h
Mobile energy consumption rate of the YC under without load	55 kwh/h

Note: The relevant values in the table are quoted from reference [36].

[36]. The total load waiting time for AGVs is the sum of waiting times when all AGVs complete all tasks. Waiting time is calculated based on the time difference between each AGV arriving at the yard loading/unloading point and the YCs completing container retrieval during each task.

$$E_{all}=E_{agv}+E_{yc}$$

(1)

$$E_{agv}={\displaystyle \frac{C_{charge}·V_{agv}}{1000}}$$

(2)

$$E_{yc}=E_m+E_h={\alpha }_{yc\_l}·t_l+{\alpha }_{yc\_wl}·t_{wl}+{\beta }_{y{c\_}_l}·t_{h_l}+{\beta }_{yc\_wl}·t_{h\_wl}$$

(3)

4.2. Chromosome Encoding and Population Initialization

In the study of collaborative scheduling between AGVs and YCs, three subproblems are primarily addressed: task sequence decision planning, AGVs allocation planning, and YCs allocation planning. For these problems, each chromosome encodes three components. The first component represents the sequence of container tasks, where each number denotes a container ID arranged in operational order. The second part indicates the AGV number assigned to the corresponding task. The third part indicates the YC number assigned to the corresponding task. Figure 5 illustrates an example involving 10 container tasks, 3 AGVs, and 2 YCs, interpreted as follows:

(1)

Taking AGV1 as an example, it will first transport Container No. 4, then Container No. 2 and No. 7, and finally Container No. 3.

(2)

For YCs, taking YC1 as an example, it first unloads Container No. 8 from AGV3, then sequentially unloads Container No. 4 from AGV1, Container No. 5 from AGV2, Container No. 10 from AGV2, and Container No. 9 from AGV3.

(3)

Interpretations for other AGVs and YCs follow the same steps.

Figure 5. Chromosome coding.

Figure 5. Chromosome coding.

The initial population is a fundamental condition for optimization algorithms, directly impacting the convergence speed and performance of the algorithm. Randomly generated individuals may sometimes be unevenly distributed across the search space, potentially leading to individuals being far from the optimal solution. Addressing the characteristics of the AGV and YC collaborative scheduling problem, this study employs a hybrid approach combining the Logistic chaotic map and LHS with heuristic methods to generate the initial population. This ensures the initial population exhibits maximum diversity while maintaining a degree of guidance.

The initial population consists of subpopulations generated by three distinct methods. The first subpopulation, comprising 30% of the total population, first generates a chaotic sequence with good ergodicity and distribution within the (0, 1) interval using the Logistic chaotic sequence. The coding segment order of individuals—specifically the task sequence, AGVs, and YCs allocation—is then determined by the sorting order of this sequence. Individuals generated by this method exhibit strong dynamic perturbations and high structural discontinuity. The second subpopulation, comprising 50% of the population, first constructs multidimensional samples based on problem characteristics. Multiple solutions are then generated using LHS sampling and mapped into a three-layer encoding structure. Individuals generated by this method exhibit more uniform spatial distribution and broader coverage. The third subpopulation comprises 20% of the population. It randomly generates task sequences, computes task information, and assigns tasks to the nearest AGV and the YC with the shortest processing time. This aims to produce partially directional individuals. These three strategies collectively ensure structural diversity and spatial uniformity within the population. Furthermore, the heuristically generated individuals provide guidance to accelerate convergence.

4.3. Dynamic Operator Selection Strategy

For this study, the designed genetic operators include three crossover techniques: single-point crossover, double-point crossover, and uniform ordered crossover, along with two mutation techniques: random mutation and exchange mutation. In crossover operations, the distinction between single-point and double-point crossover lies in the former using single-point segmentation to exchange parental genes, while the latter employs double-point segmentation to exchange genes from the middle segment of parental genes. Uniform crossover employs a random approach, selecting genes from the parent generation at corresponding positions for exchange. For mutation operations, random mutation randomly selects any position within one of the three parental coding segments for mutation; exchange mutation randomly selects two positions within one parental coding segment to swap their codes. To prevent the generation of infeasible solutions, after each crossover or mutation operation, the validity of chromosome coding must be verified, conflicting genes removed, and missing genes replaced. Furthermore, since YCs typically handle loading/unloading tasks within fixed zones in port environments, the coding segments for YCs require adjustments based on task endpoint information to correct YCs’ assignments. Non-compliant codes necessitate YCs’ reassignment.

Throughout the evolutionary algorithm’s iterative process, employing different operators at distinct stages helps balance exploration and exploitation [37]. Therefore, this study utilizes the PPO algorithm for dynamic operator selection within the NSGA-II algorithm. The objective is to enable the agent to select optimal behavioral strategies based on its state through continuous interaction and learning with the environment, thereby maximizing cumulative reward. Within the algorithmic framework, sample information requires feedback from simulations. To reduce computational resources and enhance sample utilization efficiency, a priority experience replay mechanism is designed. Rewards obtained are used to assign priorities to each sample, thereby increasing the sampling probability of those that are more critical to the learning process. Additionally, an ε-greedy-based action selection mechanism is established to enhance PPO’s exploration capability in discrete spaces and prevent premature algorithmic convergence. By dynamically selecting operators through PPO, the INSGAII-PPO algorithm not only improves the search capability of multi-objective optimization but also further prevents the algorithm from becoming stuck in local optima, ultimately yielding a higher-quality solution set.

The core of designing multi-objective optimization algorithms using deep reinforcement learning lies in establishing robust state and reward mechanisms. This enables the agent to effectively learn the relationship between states and rewards through neural networks, thereby making rational action selections. The state space, action space, and reward mechanism design in this paper are outlined as follows.

(1)

State Space: During the algorithm’s iterative process, the agent’s state space design incorporates several key factors to comprehensively reflect the search state. These factors include diversity within the current population across both the objective space and decision space, indicating whether the population is in an exploration or exploitation phase. The distribution characteristics of the Pareto frontier serve as the core metric for evaluating the quality of non-dominated solution distributions and form the foundational component of the state space. The algorithm’s convergence progress quantifies its approximation to the optimal solution. The state space constructed from these factors provides a comprehensive basis for the agent to assess the population’s state and select appropriate operation operators. Therefore, the agent’s state can be represented as shown in Equation (4):

$$S=[D(X),D(f(X)),D(p(X)),C(p(X)),R(c(X))]$$

(4)

Here, D(X) denotes the diversity of population X within the decision space, represented as the normalized mean Euclidean distance. D(f(X)) indicates the diversity of the population within the objective space, which is the standard deviation of the current solution. D(p(X)) and C(p(X)), respectively, denote the normalized mean Euclidean distance and the standard deviation of crowding on the Pareto frontier. R(c(X)) represents the convergence ratio between the current optimal solution and the initial optimal solution.

(2)

Action Space: In the dynamic operator selection strategy, agents must choose a combination of operators from 3 crossover operators and 2 mutation operators. The combination of these two types of genetic operators yields a total of 6 possibilities. Thus, the number of actions is equivalent to the product of the number of candidate operators. An agent’s action can be represented as shown in Equation (5):

$$A=\{a_1,a_2,\cdots ,a_{n_c\times n_m}\}, a_{\mathrm{i}}=\{a_j^c,a_k^m\}$$

(5)

Here, n_c denotes the number of crossover operators, and n_m denotes the number of mutation operators. Within this action space, if an agent selects the i_th genetic operator, it corresponds to the [i/n_m] crossover operator and the [(i − 1) mod n_m] + 1 mutation operator.

(3)

Reward Mechanism: The design of the reward mechanism is crucial for DRL. For selecting genetic operators in evolutionary algorithms, existing research typically modifies the actual optimization objective value into a fitness value as the reward for the selected operator. However, fitness values gradually decrease or exhibit significant fluctuations as the algorithm iterates, and using them directly as rewards may compromise the stability of agent learning. To mitigate this issue, this paper proposes a novel hybrid reward mechanism. First, if an action improves a specific optimization objective, the reward is set to 1; otherwise, it is 0. Second, the population’s state change reflects the selected genetic operator’s optimization capability. The calculation of rewards relies on the state change pre-action and post-action: a reward of 1 is provided when the state is improved, and 0 if it is not. The reward calculation is shown in Equation (6).

$${\mathrm{r}}_{score\_obj}=r_{score\_state}=\left\{\begin{array}{l}1\hspace{1em}\hspace{1em}\hspace{1em}{f}^o<f^p or s^{new}>s^{old}\\ 0\hspace{1em}\hspace{1em}\hspace{1em}otherwise\end{array}\right.$$

(6)

Here, $f^o$ and $f^p$ denote the objective values of offspring and parents, respectively, while ${\mathrm{s}}^{new}$ and ${\mathrm{s}}^{old}$ represent the new and old population states. Additionally, the ratio r_process between the current optimal solution and the initial optimal solution is incorporated as part of the reward to reflect the contribution of genetic operators to the global optimization of the population. The final reward is calculated as a weighted sum of these three components, as shown in Equation (7).

$$\tilde{\mathrm{r}}(a_i)=\alpha \times r_{score\_obj}+\beta \times r_{score\_state}+\gamma \times r_{process}$$

(7)

To ensure more stable rewards, a sliding reward window W_r has been designed to store the instant rewards from each operation. The tuples within the sliding reward window can be represented as $W_{\mathrm{r}}^i=[a_i,\tilde{r}(a_i)]$. The sliding window stores rewards from a past period and possesses memory capabilities. Therefore, the actual reward can be calculated by combining the currently received instantaneous reward with the historical rewards for that action stored in the sliding window, as shown in Equation (8). $\left|{\mathrm{a}}_i\right|$ denotes the quantity of a_i in W_r.

$$\tilde{\mathrm{r}}(s,a_i)={\displaystyle \frac{1}{\left|a_i\right|}}{\displaystyle \sum _{\left[a_i,\tilde{r}(a_i)\right]\in W_r}\tilde{r}(a_i)}$$

(8)

Overall, this study employs PPO for dynamic operator selection in the NSGA-II algorithm. It designs comprehensive state and action spaces alongside a reward mechanism, thereby enhancing the NSGA-II algorithm’s inherent search capability and reducing the risk of becoming stuck in local optima. Furthermore, during simulation optimization, the constructed U-shaped automated terminal simulation model serves as the iterative optimization environment for the algorithm: When a new scheduling plan is generated, it triggers the external interaction module. Data exchange between the simulation and the algorithm is achieved via Socket communication. Upon receiving the scheduling plan, the simulation module executes the tasks according to the plan using relevant functions and feeds back the final optimization objective value to the algorithm module. After iterative optimization, the algorithm outputs a new scheduling plan to the simulation model. This process continues until the simulation optimization of the algorithm concludes.

4.4. Selection of the Final Solution

Through iterative optimization using INSGAII-PPO, a set of Pareto optimal solutions is obtained. Ultimately, one individual must still be selected from this set as the final solution to the problem. Different problems require tailored solutions. The TOPSIS is a method for determining the optimal solution within a Pareto set by calculating the distance between an individual objective value and both the best and worst objective values. This method typically employs equal weights or subjectively assigned weights, which can easily introduce bias when objective scales vary significantly or objectives are unevenly distributed. Another subjective weighting approach involves assigning weights based on the priority relationships among objectives, followed by calculating the weighted sum of multiple objectives; however, due to its heavy reliance on human experience, this method struggles to adapt to complex data structures. Both methods are used to select optimal solutions from the Pareto optimal set, yet they exhibit limitations when handling complex objective relationships [38,39]. Particularly in this study, the three optimization objective values not only exhibit mutual constraints but also display significant differences in data scales, making it difficult for existing methods to balance objectivity and decision-making practicality. Therefore, this study proposes a preference-based hybrid weighted TOPSIS method. This approach integrates the decision preferences of subjective weighting methods and the scientific objective weighting capability of the Criteria Importance Through Intercriteria Correlation (CRITIC) method while preserving the core principles of TOPSIS. This ensures the final solution meets practical decision-making requirements while maintaining objective justification.

In this study, the optimization objectives are task completion time, equipment energy consumption, and AGVs’ load waiting time, with their importance decreasing in that order. The rationale is as follows: based on actual terminal operations, the rapid and efficient handling of large volumes of containers is the most critical factor. Therefore, the primary goal is to minimize task completion time to ensure high terminal efficiency. When completion times are comparable, efforts should focus on reducing equipment energy consumption and AGVs waiting time, so as to reduce the terminal operation cost and improve the utilization rate of equipment.

Within the Pareto solution set, complex relationships exist between individuals. Often, when one objective exhibits relatively outstanding performance, it typically comes at the expense of poorer performance on at least one other objective. In order to follow the relative importance between the three goals, the selected individuals should try to ensure that the condition is that the 2 goals are relatively excellent and 1 goal is relatively slightly worse. Therefore, a method is needed to select the final solution from the solution set that can consider conflicts and trade-offs between objectives, integrate subjective and objective factors, and respect decision preferences. The proposed method generates hybrid weights by integrating subjective weights with objective weights derived from data relationships. It then employs the TOPSIS method to score all individuals based on these hybrid weights, followed by preference decision-making to select the final solution. Numerical experiments in Section 5 demonstrate that, under identical weight settings, the proposed algorithm more effectively selects the final solution that best meets the requirements compared to the other two algorithms. The detailed content of the proposed algorithm is as follows.

$${\mathrm{c}}_j={\sigma }_j{\displaystyle \sum _{k=1}^m(1-r_{jk})}$$

(9)

$${\omega }_j=\alpha \cdot {\omega }_j^s+(1-\alpha ){\omega }_j^o$$

(10)

$${\omega }_j^{final}={\displaystyle \frac{{\omega }_j}{{\displaystyle \sum {\omega }_j}}}$$

(11)

$${\mathrm{x}}_{ij}^{\prime }={\displaystyle \frac{\max (x_j)-x_{ij}}{\max (x_j)-\min (x_j)}}$$

(12)

$${\nu }_{ij}={\omega }_j^{final}\cdot x_{ij}^{\prime }$$

(13)

$${\nu }_{\mathrm{j}}^{+}=\underset{i}{\max }({\nu }_{ij}),{\nu }_j^{-}=\underset{i}{\min }({\nu }_{ij})$$

(14)

$$D_{\mathrm{i}}^{+}=\sqrt{{\displaystyle \sum _{j=1}^m{(v_{ij}-v_j^{+})}^2}},D_{\mathrm{i}}^{-}=\sqrt{{\displaystyle \sum _{j=1}^m{(v_{ij}-v_j^{-})}^2}}$$

(15)

$$C_{\mathrm{i}}={\displaystyle \frac{D_i^{+}}{D_i^{-}+D_i^{+}}}$$

(16)

$$scor{e}_e=(X[j,1]-X[i,1])\times \eta$$

(17)

The hybrid-weighted TOPSIS method incorporates three key techniques: the CRITIC method, which calculates objective weights by measuring target conflict and discrimination based on variance and correlation coefficients; the subjective weighting method, which determines relative importance of objectives through expert or experiential judgment (subjective weights); The TOPSIS method, based on the principle of distance from the ideal point, evaluates the superiority of non-dominated solutions. The hybrid weighted TOPSIS method combines subjective preferences with objective data characteristics. This approach first involves decision-makers setting the importance of each optimization objective as subjective weights. Simultaneously, the CRITIC method is employed to calculate the discrimination and conflict levels of objectives within the solution set, thereby generating objective weights. The objective weight calculation is shown in Equation (9), where σ_j denotes the standard deviation of each column, r_jk represents the correlation coefficient between each column and others, and c_j is the objective weight of each column. The final weighted coefficient ${\omega }_{\mathrm{j}}^{final}$ is obtained through the fusion of subjective and objective weights, where ${\omega }_{\mathrm{j}}^{\mathrm{s}}$ is the subjective weight, ${\omega }_{\mathrm{j}}^o$ is the normalized objective weight, and $\alpha$ is the fusion coefficient, as shown in Equations (10) and (11). Subsequently, the TOPSIS technique is employed to evaluate each solution’s proximity to both the ideal solution and the worst solution. Higher scores indicate superior solutions, as demonstrated in Equations (12)–(16). Finally, the top five solutions by score are selected using hybrid TOPSIS. A secondary screening is then conducted based on local preferences, as shown in Equation (17), where $X\left[j,1\right]$ represents the energy consumption value of the jth individual in the Pareto solution set, and $\eta$ denotes the bonus coefficient. During local screening, completion times across all solutions are compared. Solutions with similar completion times but lower energy consumption receive additional bonus points. After screening, the solution with the highest score is selected as the final recommendation. This method ensures the selected solution balances subjective preferences and data characteristics, making it particularly suitable for multi-objective problems like port scheduling.

In summary, this study addresses the multi-objective optimization problem of coordinating AGVs and YCs in U-shaped ACTs by proposing an improved multi-objective optimization algorithm based on PPO. First, a hybrid initialization strategy combining the Logistic chaotic map and LHS is designed to enhance the quality of initial solutions. Second, a dynamic operator selection strategy based on PPO is introduced, incorporating a priority experience replay mechanism and an ε-greedy-based action selection mechanism to enhance thorough exploration of the solution space. Finally, a hybrid weighted TOPSIS method is proposed to ensure the selected final solution aligns with practical decision preferences while maintaining objective justification.

5. Experiments and Results

This section introduces the experimental setup and evaluates the performance of the proposed algorithm using two widely adopted metrics. Subsequently, multiple experiments of varying scales were conducted to compare the INSGAII-PPO algorithm against the NSGAII algorithm, the NSGAII-PPO algorithm, and the MOPSO algorithm [40]. An explicit definition of the different algorithms is given in

Table 3. A clear definition of the different algorithms.

Algorithm	Definition
INSGAII-PPO	NSGAII-PPO combines hybrid initialization and other improvements
NSGAII-PPO	NSGAII combines the dynamic operator selection of PPO
NSGAII	Baseline NSGA-II
MOPSO	Baseline MOPSO

.

5.1. Experimental Parameter Settings

A U-shaped ACTs was simulated in the simulation software, comprising 3 QCs, 6 container yards each equipped with 2 YCs, and 4 charging stations. According to the actual operation situation, AGVs enter the yard via the left-hand road between yard blocks, proceed to designated loading/unloading points, and exit the yard via the right-hand road. Specific equipment parameters in the simulation are detailed in

Table 4. Parameters of Simulation Equipment.

Parameter	Value
Movement speed of the YC	1 m/s
Mobile speed of the YC trolley	1 m/s
Speed of YC lifting device	1 m/s
AGV operating Speed	4 m/s
AGV battery consumption when load	1.2%/km
AGV battery consumption when empty	0.6%/km

. When performing simulation optimization, the entities and data in the simulation are generated in the following way: Each AGV’s initial battery charge is generated based on a uniform distribution within the range (85, 95). The starting position of each container is generated according to the data table. The operation sequence and corresponding handling equipment are allocated and invoked by the simulation based on the algorithm’s output data, sequentially performing container transportation and stacking operations. The time for QCs and YCs to load or unload containers from AGVs is set to 30 s.

For each comparative algorithm in the experiment, the corresponding parameter settings are as follows: Iteration count: 200, Population size: 30, Maximum simulation evaluations: 24,000, Sliding reward window size: 50, Experience replay pool size: 500, Policy network learning rate: 5 × 10⁻⁵, Value network learning rate: 1 × 10⁻⁴, Clipping factor: 0.1, Training sample batch size: 128. All experiments were conducted on a computer equipped with an Intel Corei7-13700 CPU @2.10 GHz processor and 32 GB RAM. The algorithms were implemented in Python 3.11. The reward curves for model training across different task scales are shown in Figure 6.

5.2. Performance Metrics

To evaluate the performance of solutions obtained by different algorithms, relevant performance metrics are introduced, defined as follows:

(1)

Hypervolume (HV) is a comprehensive metric that calculates the cumulative normalized volume covered by a solution set relative to a given reference point. A larger hypervolume value indicates better convergence and diversity of the solution set. Hypervolume is defined as follows:

$$HV(A,q)=volume(U_{x\in A}[f_1(X),q_1]\times \cdots \times [f_M(X),q_M])$$

Here, A is the solution set obtained through an algorithm, and $q=(q_1,q_2,\cdots ,q_M)$ represents the HV reference points. M denotes the number of targets. In this work, each reference point is set to 1.1 times the maximum target value obtained by all comparison algorithms [41].

(2)

Inverted Generational Distance (IGD) is a widely used metric for evaluating multi-objective optimization algorithms. It comprehensively assesses the performance of solution sets by measuring aspects such as diversity and proximity. A smaller value indicates better diversity and distribution. Its definition is as follows:

$$IGD(A,B^{*})={\displaystyle \frac{1}{\left|B^{*}\right|}}{\displaystyle \sum _{x\in B^{*}}\underset{y\in A}{\min }} d(x,y)$$

Here, B* denotes the true Pareto frontier, A is the obtained solution set, and d(x, y) is the Euclidean distance between points x and y. In this work, B* consists of all non-dominated solutions obtained by all comparison algorithms [42]. The smaller the value of IGD(A, B*), the closer A is to B*.

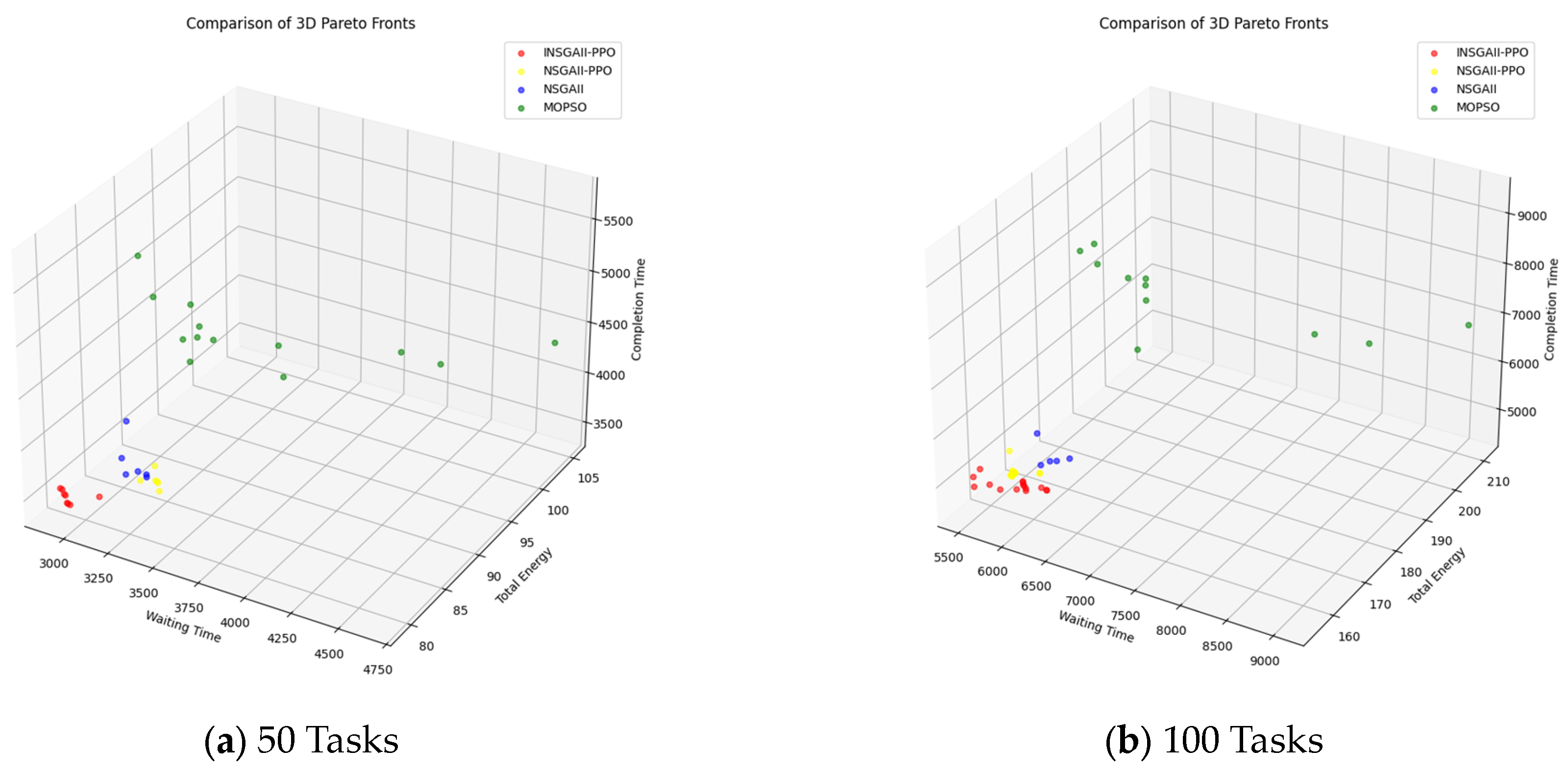
5.3. Comparison and Analysis of Optimization Algorithms

Figure 7 illustrates the convergence curves of the minimum completion times obtained by the four algorithms across different task scales. Among the four algorithms, MOPSO tends to become stuck in local optima and fails to thoroughly explore the solution space, particularly in larger-scale tasks. Compared to other algorithms, the INSGAII-PPO algorithm exhibits a relatively smooth downward trend throughout the entire iteration process, both for large-scale and small-scale tasks. It is less prone to becoming stuck in local optima and performs a more thorough search of the solution space.

Figure 8 illustrates the comparison of the minimum objective values within the Pareto solution sets obtained by the four algorithms across different task scales. The comparison clearly reveals that for small-scale tasks, the minimum objective values obtained by all four algorithms are relatively close. However, as the task scale increases, the INSGAII-PPO algorithm consistently achieves smaller objective values than the other algorithms in most cases, followed by the NSGAII-PPO algorithm. This demonstrates that the proposed improved algorithm exhibits significant advantages in solving the multi-objective optimization problem for the coordinated scheduling of AGVs and YCs.

To visualize the Pareto frontiers obtained by different algorithms, the distribution of Pareto frontier solutions in three-dimensional space was selected from four instances of varying task scales, as shown in Figure 9. It can be observed that the MOPSO algorithm generally yields a larger number of Pareto frontier solutions, but these solutions exhibit the highest objective values and an uneven distribution. In contrast, the INSGAII-PPO algorithm typically produces Pareto frontier solutions with the lowest objective values and a more uniform distribution compared with the comparison algorithms. This indicates that this method demonstrates superior performance in solving the multi-objective cooperative scheduling problem for AGVs and YCs.

In order to conduct a deeper evaluation of the algorithms’ performance,

Table 5. Algorithm performance metrics at different task scales.

Index	Number of Tasks	Number of AGV	INSGAII-PPO		NSGAII-PPO		NSGAII		MOPSO
			HV	IGD	HV	IGD	HV	IGD	HV	IGD
1	20	3	0.0018	0.0021	0.0016	0.0051	0.0017	0.0018	0.0016	0.0149
2	20	4	0.0015	0.0083	0.0017	0.0070	0.0012	0.0194	0.0017	0.0065
3	30	4	0.0036	0.0104	0.0054	0.0053	0.0022	0.0406	0.0022	0.0651
4	30	5	0.0046	0.0006	0.0017	0.0406	0.0025	0.0264	0.0029	0.0353
5	50	5	0.0239	0.0022	0.0189	0.0258	0.0190	0.0257	0.0108	0.1215
6	50	6	0.0094	0.0087	0.0087	0.0207	0.0118	0.0026	0.0045	0.0971
7	80	6	0.0769	0.0122	0.0927	0.0010	0.0531	0.0913	0.0294	0.2554
8	80	8	0.0670	0.0173	0.0637	0.0232	0.0502	0.0498	0.0333	0.1585
9	100	8	0.1215	0.1143	0.1292	0.1106	0.0517	0.2525	0.0284	0.3720
10	100	10	0.2772	0.0002	0.2389	0.0199	0.2117	0.0535	0.1119	0.2606
11	120	8	0.1756	0.0015	0.1555	0.0172	0.1342	0.0568	0.0734	0.2708
12	120	10	0.1177	0.0018	0.0981	0.0180	0.0184	0.2430	0.0262	0.2774
13	140	8	0.1934	0.0047	0.1918	0.0119	0.0455	0.2209	0.0635	0.3321
14	140	10	0.4085	0.0023	0.3593	0.0235	0.2709	0.0971	0.0997	0.3421
15	160	10	0.8446	0.0304	0.9386	0.0003	0.3872	0.3136	0.2261	0.5016
16	160	12	1.0668	0.0072	0.7897	0.1064	0.2339	0.4747	0.2826	0.5110
17	180	10	0.9322	0.0044	0.6860	0.0587	0.6588	0.1211	0.1654	0.5422
18	180	12	1.0309	0.0124	0.7739	0.0892	0.2699	0.4249	0.1602	0.5963
19	200	10	1.0097	0.0023	0.9452	0.0250	0.4419	0.2628	0.1904	0.5930
20	200	12	0.5604	0.0098	0.5433	0.0159	0.2243	0.2219	0.1488	0.4285
21	200	14	1.4289	0.0078	1.2342	0.0402	1.0743	0.1082	0.2555	0.6481
22	250	12	2.0329	0.0176	1.3172	0.1952	0.3801	0.6753	0.4843	0.6405
23	250	14	1.4679	0.0222	1.3331	0.0468	0.9020	0.2025	0.4679	0.4177
24	250	16	1.8666	0.0074	1.6394	0.0306	0.9282	0.3443	0.5922	0.5202
25	300	14	2.6819	0.0178	2.6538	0.0243	1.0903	0.4138	0.6514	0.6976
26	300	16	2.0792	0.0054	1.4998	0.1202	0.9093	0.3389	0.4153	0.6381
27	300	18	4.1298	0.0169	2.9772	0.1730	1.0055	0.7175	0.6736	0.9410
28	400	20	2.9982	0.0137	1.5503	0.2518	1.0811	0.5172	0.9517	0.5927
29	400	22	4.9691	0.0066	3.9364	0.1044	2.3033	0.3785	1.7905	0.5916
30	400	24	5.5949	0.0253	3.8896	0.2136	1.9027	0.5303	1.1764	0.8565
31	500	20	11.2545	0.0994	5.5249	0.4835	5.8899	0.6513	4.9769	0.6621
32	500	22	8.1808	0.0772	4.2320	0.3694	2.2938	0.7760	2.5739	0.8429
33	500	24	7.8940	0.1045	7.4504	0.1192	2.2318	0.8396	2.9733	0.7800
34	500	26	5.6274	0.0796	3.4978	0.2525	2.1434	0.5481	1.6391	0.6477
MIN			0.0015	0.0002	0.0016	0.0003	0.0012	0.0018	0.0016	0.0065
MAX			11.2545	0.1143	7.4504	0.4835	5.8899	0.8396	4.9769	0.9410
Average			2.0371	0.0220	1.4511	0.0879	0.8039	0.2957	0.6257	0.4520
Std. Dev			2.7143	0.0311	1.7685	0.1105	1.1331	0.2405	1.0322	0.2525

presents the HV values, IGD values, and their standard deviations for the Pareto solution sets obtained by each algorithm across different task scales (the optimal HV and IGD values for each group are highlighted in bold).

Table 6. Statistical Data of HV Values for Different Task Scales.

HV	Number of Best	Number of Suboptimal	Number of Worst
INSGAII-PPO	28	5	0
NSGAII-PPO	5	24	2
NSGAII	1	3	8
MOPSO	0	2	24

and

Table 7. Statistical Data of IGD Values for Different Task Scales.

IGD	Number of Best	Number of Suboptimal	Number of Worst
INSGAII-PPO	27	6	0
NSGAII-PPO	4	26	1
NSGAII	2	2	3
MOPSO	1	0	30

provide statistical data on the performance metrics. It can be observed that the INSGAII-PPO algorithm achieves an average HV of 2.0371, maintaining optimality in most cases but exhibiting the highest standard deviation. The average IGD value for INSGAII-PPO is 0.022, compared to 0.0879, 0.2957, and 0.4520 for NSGAII-PPO, NSGAII, and MOPSO, respectively. Furthermore, the standard deviation of INSGAII-PPO is significantly lower than that of the three comparison algorithms. Therefore, the Pareto solution set obtained by the INSGAII-PPO algorithm demonstrates superior convergence and diversity compared to other comparative algorithms. In summary, the dynamic operator selection strategy and improvements proposed by the algorithm in this paper are effective.

5.4. Comparison of Final Solution Selection Methods

To demonstrate the practicality of the proposed method in selecting the final solution from the Pareto solution set for this problem, comparative experiments were conducted against the weighted sum method and the widely used TOPSIS method, employing consistent subjective weights. Four case groups were selected, with the results presented in Figure 10 and

Table 8. Results of Final Solutions Selected by Different Methods.

	Case1			Case2
	Completion Time	Energy Consumption	Waiting Time	Completion Time	Energy Consumption	Waiting Time
Max	2925	60	2550	9350	224	9887
Min	2260	55	2253	6640	170	6202
Proposed	2300	57	2388	7345	170	6459
TOPSIS	2300	57	2388	7205	174	6671
Weighted	2260	58	2407	7205	174	6671
Gap1	0	0	0	−1.94%	2.3%	3.18%
Gap2	−1.77%	1.72%	0.79%	−1.94%	2.3%	3.18%
	Case3			Case4
	Completion Time	Energy Consumption	Waiting Time	Completion Time	Energy Consumption	Waiting Time
Max	5725	106	4646	4940	97	4285
Min	4345	83	3208	3730	84	3325
Proposed	4705	85	3396	4135	86	3475
TOPSIS	4500	89	3747	3900	91	3736
Weighted	4480	90	3709	3900	91	3736
Gap1	−4.56%	4.49%	9.37%	−6.03%	5.5%	6.99%
Gap2	−5.02%	5.56%	8.44%	−6.03%	5.5%	6.99%

Note: Gap1 = (TOPSIS − Proposed)/TOPSIS, Gap2 = (Weighted − Proposed)/Weighted.

and

Table 9. Statistical Data of GAP under Different Cases.

	Completion Time	Energy Consumption	Waiting Time
Average1	−3.13%	3.07%	4.89%
Average2	−3.69%	3.77%	4.85%
Average	−3.41%	3.42%	4.87%

Note: Average1 represents the average value of Gap1, and Average2 represents the average value of Gap2.

.

In Case 1, the final solutions selected by the three methods are similar, indicating that all three methods can be applied simultaneously to the same Pareto solution set. When the Pareto solution set exhibits different distribution states, the three methods will select different solutions. It can be seen that in Case 2, the solution selected by the method proposed in this paper is more advantageous. The reasons are as follows: The final solutions selected by the three methods are very close in completion time, with the difference being negligible. However, in terms of energy consumption and waiting time, the solution selected by the method proposed in this paper is significantly superior to those selected by the other two methods. Currently, terminals are promoting cost reduction and efficiency improvement, and the energy consumption indicator plays an indispensable role. When the completion time difference is not significant, individuals with lower energy consumption are definitely superior to others. Furthermore, the individuals selected by this method exhibit significantly lower waiting times compared to those chosen by the other two methods. Therefore, although the completion time of the individuals selected by this method is slightly longer, it achieves substantial improvements in energy consumption and waiting time, better aligning with the scheduling requirements of U-shaped ACTs. In Cases 3 and 4, the method proposed in this paper also selects the optimal solution. The statistical data in Table 9 further demonstrates that while the final solution selected by this method exhibits slightly longer completion times, it achieves superior performance across the other two objectives. This outcome aligns with the practical requirements of high efficiency and low energy consumption in actual terminal operations.

6. Conclusions

This paper investigates the coordinated scheduling problem between AGVs and YCs in U-shaped ACTs, simultaneously optimizing task completion time, equipment energy consumption, and AGV load waiting time. Addressing the limitations of traditional mathematical modeling approaches, this paper proposes an improved NSGA-II multi-objective simulation optimization method based on PPO. First, a simulation model of a U-shaped ACT is established. In order to improve the simulation accuracy, the model incorporates the refined road network structure, AGVs’ charging mechanism, and single-step YCs control, which reflects the real terminal operation. Subsequently, an improved NSGA-II multi-objective optimization algorithm based on PPO is proposed to efficiently address the multi-objective optimization problem. This algorithm is integrated with the simulation model to solve the coordinated scheduling issue between AGVs and YCs. Furthermore, a novel final solution selection method is proposed to address the interdependent characteristics of the multiple objectives being solved. Finally, multiple experiments compared the proposed algorithm with other multi-objective optimization methods. The results demonstrated that the INSGAII-PPO approach consistently achieved smaller objective values, with average HV and IGD values of 2.0371 and 0.022, respectively. In contrast, the best results from comparison algorithms were only 1.4511 and 0.0879. Thus, this method delivers solutions with superior convergence and diversity. In addition, the energy consumption and waiting time of the final solution selected by the proposed method are reduced by 3.42% and 4.87% on average, with a small efficiency gap.

However, the coordinated scheduling of equipment in U-shaped ACTs is a highly complex problem. This study has certain limitations that warrant further investigation in future research. For instance, the impact of external container trucks on the yard area was not incorporated into the constructed simulation model, and random disturbances in the terminal are not considered, despite being a critical factor affecting the U-shaped ACT’s efficiency, energy consumption, and AGVs’ waiting times. By jointly considering the complex coupling relationships among AGVs, YCs, and external container trucks, the scheduling problem of U-shaped ACTs can be explored in greater depth. In addition, this study uses a hybrid strategy combining an evolutionary algorithm and deep reinforcement learning. Deep reinforcement learning is only used for dynamic adaptation at the operation policy level, and does not directly output scheduling results; so, it has strong potential for online deployment. In view of the fact that most equipment scheduling in the actual port scenario is triggered by rolling, the optimization framework proposed in this study can also be combined with the periodic simulation platform in the future to improve the real-time performance and practicability of decision-making in complex environments.