Spatial Analysis of Extreme Coastal Water Levels and Dominant Forcing Factors Along the Senegalese Coast

Abstract

Coastal flooding risk is intensifying under climate change, especially along the low sandy Senegalese coastline. This study explores the spatiotemporal variability of extreme coastal water levels (ECWL) from 1993 to 2023 by combining ERA5 reanalysis (waves, wind, pressure), tide gauge and meteorological data, and applying a generalized Pareto distribution (GPD) to estimate the 99th percentile and return levels for 50 and 100 year events. The analysis of the upper 1% of ECWLs reveals significant spatial heterogeneity: 99th percentile values exceed 1.2 m in the Dakar region (Yoff, Ouakam, Ngor) and around Saint-Louis/Langue de Barbarie, with 95% confidence intervals ranging from approximately 1.15 m to 1.30 m, while Casamance and the Saloum Delta exhibit much lower extremes (0.8–1.0 m). For return periods, ECWLs vary between 1.6 m and 2.3 m, with the 100 year return level (T100) exceeding 2.25 m in Dakar, above 2.0 m in Saint-Louis, and intermediate values (1.5–1.9 m) along the Petite Côte (Mbour–Toubab Dialaw) and in the Saloum Delta. The 50 year return level (T50) follows a similar spatial pattern but is 5–10 cm lower than T100 in the most exposed areas. Sensitivity analysis shows that ECWLs are primarily controlled by astronomical tide along much of the coast, whereas wave runup dominates in the southern estuarine zones (Saloum, Casamance, Mbour). Trend analysis using the Mann–Kendall test reveals a latitudinal gradient: stronger positive slopes in the south, weaker trends in central and northern sections, but all p values lie between 0.1 and 0.4, meaning none of the trends reach conventional significance. These findings point to a potential intensification of extreme water levels in socio-economically critical areas (Dakar, Saint-Louis, Mbour) but should be interpreted with caution given the lack of robust statistical significance. The results provide a quantitative basis for coastal risk management in light of projected sea level rise.

1. Introduction

Nowadays, coastal zones are among the ecosystems most threatened by the effects of climate change. Beyond coastal erosion, they are exposed to flooding caused by extreme coastal water levels (ECWL). Because of the considerable impacts of these events on coastal communities, scientific studies focusing on ECWLs have been increasing. Examining the evolution of ECWLs along the South American Pacific coast, the authors [1] show that these extreme levels are strongly influenced by variations in sea level anomalies (SLA), with a trend reaching 2.26 mm/yr. Moreover, wave runup is identified as the main factor contributing to ECWLs. In the same perspective, the author of [2] analyzed the spatial distribution of coastal total water levels (TWL) and their components during this period, evaluating the relative contribution of each TWL component along the coastline. Today, the vulnerability faced by coastal zones does not spare those of West Africa.

With an extensive coastline, the West African coastal countries are increasingly affected by coastal issues such as erosion and marine flooding. Numerous studies conducted along the West African coasts have shown that they face a wide range of coastal hazards, primarily erosion and coastal flooding [3,4]. Composed mainly of low sandy shores, the West African coasts are extremely vulnerable to these hazards. Erosion and coastal flooding are among the most visible consequences of the degradation of West African coastal zones. Both anthropogenic and natural processes, intensified by the effects of climate change, drive coastal erosion and flooding [4,5]. These coastal risks severely affect human lives and socio-economic well-being [5,6]. Moreover, this state of vulnerability is exacerbated by the lack of adaptation measures [7], as well as by the precarious economic conditions of populations living along the West African coasts [3,8,9]. Prospective studies on future coastal flooding at the global scale indicate this trend. A significant proportion of coastal communities will be severely impacted [10,11,12,13,14]. Located at the extreme western tip of the African continent and open to the Atlantic Ocean, the Senegalese coasts mostly low and sandy, are affected by a range of challenges including rapid urbanization, intense coastal concentration, coastal erosion, marine flooding, and the lack of protective and adaptive measures [15,16,17,18]. Although highly vulnerable, this vulnerability varies spatially along the Senegalese coastline. The most affected sections, in order of vulnerability, are Saint-Louis, Cap Skirring, and the sandy spits of the Saloum islands River Delta [17]. Furthermore, these hazards have significant impacts on the local economies of these coastal sectors [19]. Despite this situation of high vulnerability, most existing research along the Senegalese coast has focused on shoreline change dynamics, sedimentary morphodynamics, and socio-economic impacts [20,21,22,23,24]. However, studies addressing flooding risks associated with Extreme Coastal Water Levels (ECWLs) remain rare or insufficient. Yet, in the context of climate change, the risk of coastal flooding is becoming increasingly imminent. According to [25], coastal storm intensity is expected to increase in tropical coastal regions. The few studies focusing on coastal flooding have been conducted mainly in the Saint-Louis coastal area and on small sections of the Dakar coastline [18,26,27].

Considering these limitations, the present study aims to highlight the spatial variability of Extreme Coastal Water Levels (ECWLs) along the entire Senegalese coastline. Using Extreme Value Theory (EVT), particularly the Peaks Over Threshold (POT) approach based on the Generalized Pareto Distribution (GPD), the 99th percentile of ECWLs was quantified. These ECWLs comprise storm surge (DAC), tide, sea level anomaly (SLA), and wave runup (R), as estimated from Equations (1) and (2). The analysis focused on the spatial distribution of these values along the coast. In addition, 50- and 100-year return periods associated with the 99th percentile were estimated. Finally, the main variables contributing to ECWL generation and their temporal evolution from 1993 to 2023 along the Senegalese coast were analyzed. A detailed understanding of the coastal sections most vulnerable to marine flooding is essential for effective coastal risk management. Moreover, knowledge of the spatial variability of extreme sea levels is crucial for understanding extreme oceanographic conditions, for designing coastal protection infrastructure, and for safeguarding coastal communities [28,29,30,31].

2. Materials and Methods

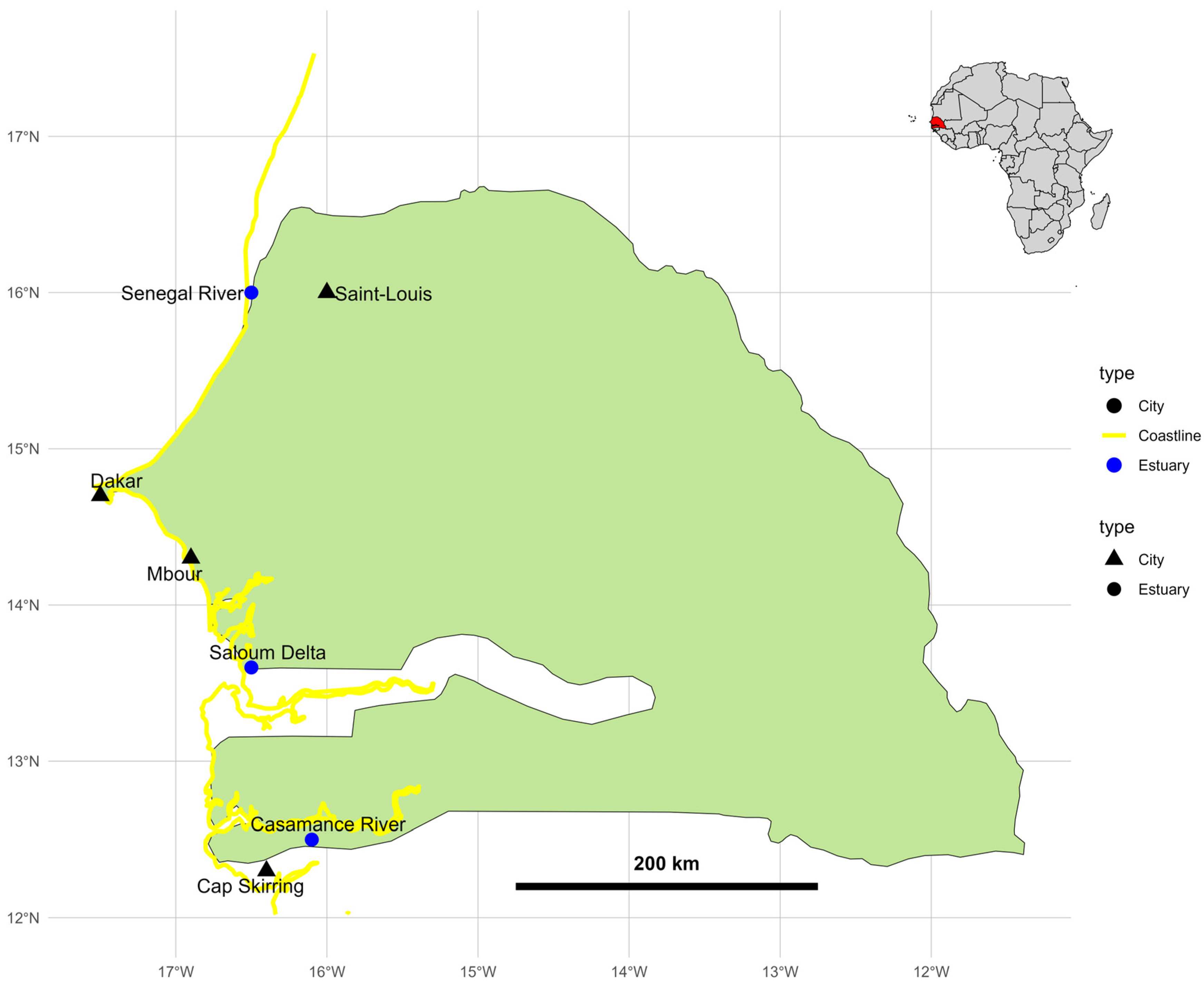
2.1. Study Area

The coastal stretch under study extends over approximately 700 km, from Saint-Louis in the north to Casamance in the south (Figure 1). This coastline is composed of coastal segments with diverse geomorphological characteristics.

The northern section of the coast is predominantly sandy, characterized by the presence of dunes. In contrast, the southern section, extending from Dakar to the Saloum Delta estuary, is marked by an alternation of rocky and sandy coasts. At the Saloum Delta, the geometric configuration of the coastline changes noticeably with the emergence of sandy spits. Finally, the extreme southern part of the coast is characterized by the presence of mangroves, tidal channels (bolongs), and the Atlantic Ocean opening into the Casamance River. From a demographic perspective, a significant portion of the Senegalese population lives in coastal regions. Among them, Dakar is the most urbanized area [15], with an urban growth rate of about 6% according to [16]. Today, the Senegalese coastline is both highly urbanized and densely populated. This rapid coastal urbanization, combined with the progressive rise in sea level, amplifies the exposure to coastal hazards. As in many other coastal regions, a wide range of socio-economic activities are concentrated along the Senegalese coast, including trade, tourism, fishing, and related activities. However, under the growing influence of coastal risks such as erosion and marine flooding, most of these activities are in decline. The beaches, which once served as active spaces for economic activities and as landing sites for fishing boats (pirogues), are experiencing increasing erosion. From a hydrodynamic standpoint, three main wave regimes affect the Senegalese coasts [32,33,34,35]. The most frequent is the northwesterly swell originating from the North Atlantic Ocean, which undergoes refraction around the Cape Verde Peninsula [32]. This explains its limited influence on the morphodynamics of the beaches located south of the peninsula. Furthermore, the Kayar Canyon, located near the peninsula, alters wave propagation and significantly reduces the energy of swells coming from the North Atlantic. Conversely, the southerly swell is highly energetic and is responsible for most of the flooding and flooding events along the coast [33]. In addition, the Senegalese coasts exhibit the characteristics of a microtidal environment, as the tidal range does not exceed 2 m, even during spring tides (new and full moon periods) [31].

2.2. Hydrodynamic Data

The quantification of extreme water levels involves the combination of several variables, including hydrodynamic, tidal, and meteorological parameters. Specifically, the ECWL time series was constructed at predefined “virtual coastal stations” located every 0.27° (~27 km) along the coastline, even if the resolution increase locally at rugged coast and decrease at straight open stretches of coasts. At each station, the total ECWL was computed hourly as the linear superposition of its physical components (Equation (3)). Reanalysis data from ERA5 with a spatial resolution of 0.25° × 0.25° [36], developed by the European Centre for Medium-Range Weather Forecasts (ECMWF), were used. These data have an hourly temporal resolution, meaning they were downloaded at hourly time steps covering the period 1993–2023, along the Senegalese coast, from Saint-Louis to Casamance. It is worth noting that this time frame corresponds to the launch of the first altimetric satellites [37], which made it possible to quantify sea level anomalies (SLA) using satellite altimetry data referenced to the WGS84 datum [38]. In other words, Sea Level Anomaly (SLA): For the 1993–2023 period, SLA was obtained directly from the multi-mission altimetry product SSALTO/DUACS (Copernicus Marine Service), which combines sterodynamic and manometric components relative to WGS84. Data were extracted at the grid points nearest to the coast, typically within 25–50 km offshore. Data gaps near the coast were minimized, but not eliminated, using the multi-mission merging technique and temporal interpolation, ensuring a continuous daily record. For earlier years (1958–1992), SLA was taken from the ORA-S5 ocean reanalysis, and the two products were merged to ensure long-term continuity.

In addition, tidal data were extracted using the global tidal model FES2014 (Finite Element Solution) [39], which provides hourly resolution outputs produced by LEGOS (Laboratory for Studies in Geophysics and Space Oceanography). Dynamic atmospheric corrections (DAC) were obtained from the MOG2D barotropic model, developed by LEGOS and distributed by AVISO (Archiving, Validation, and Interpretation of Satellite Oceanographic Data) with the support of the French Space Agency (CNES). The storm surge component (DAC) was derived from the MOG2D-G barotropic model, which is driven by surface wind forcing. The wave runup (R) was calculated according to the dissipative beach form proposed in [40] (Equation (1)). Explicitly, the MOG2D-G barotropic model (also Copernicus/AVISO) was used to add the high-frequency wind and pressure-driven component not included in SSALTO/DUACS. Also, outputs were interpolated in time to hourly resolution and spatially matched with the SLA field before summation. The ERA5 wave parameters (Hs and Tp) were extracted offshore at the grid points closest to each virtual station (typically < 50 km). Runup was computed following (Equations (2) and (3)), using coastal slopes derived from AW3D30 within 1 km of the shoreline. All ECWL components (SLA, storm surge, tide, and runup) are referenced to the WGS84 ellipsoid, consistent with the SSALTO/DUACS altimetry product. Therefore, ECWL values represent heights above the local mean sea level (MSL) implied by the altimetric baseline.

All components were interpolated to a common hourly time base and co-located spatial grid. The final ECWL field was thus built as a temporally and spatially consistent product over the entire Senegalese coast. This approach ensures reproducibility and internal consistency, while the interpolation and merging strategy minimizes spatial discontinuities along irregular coastlines such as deltas or estuaries. We have added a detailed description of this procedure and clarified the treatment of altimetry-based SLA, data merging, and virtual station definition in the revised Methods section.

Wave Runup (R)

In this study, wave runup was estimated using the Stockdon et al. [40] parameterization, which includes both dissipative and intermediate–reflective formulations depending on the Iribarren number (ξ₀). The foreshore coastal slope (β) required for this computation was not assumed constant but obtained from the global coastal slope dataset of [41], which provides consistent slope information at a quasi-global scale. This dataset captures regional variations in the nearshore beach slope and thus allows the model to distinguish between gentler (dissipative) and steeper (intermediate/reflective) sectors along the Senegalese coast.

Nevertheless, we recognize that this global product cannot resolve small-scale topographic variability, roughness, or local structures (e.g., rocky headlands, berms, or seawalls) that may significantly modify runup locally. We have therefore added a discussion of this limitation in the revised manuscript, noting that runup heights represent regionally coherent but approximate estimates, and that deviations may occur in complex morphodynamic zones such as the Dakar Peninsula or estuarine areas.

Wave runup, (R) [m], was computed using the classical [40] parameterization, which depends on the Iribarren number $(\epsilon$) (ratio between coastal slope and incident wave steepness):

Equation (1) at coasts $\epsilon <0.3$

$$R=0.043\sqrt{Hs\times Lo}$$

(1)

Equation (2) at coasts $\epsilon >0.3$

$$R=1.1\left(0.35\mathsf{\beta }\sqrt{HsLp+0.5\left[HsLp\left(0.5625{\mathsf{\beta }}^2+0.004\right)\right]}\mathrm{½}\right)$$

(2)

where (R) is expressed as a function of deep-water significant wave height (Hs), wavelength (Lo), foreshore coastal slope (beta) from [41], and peak wave period (Tp). See [42] for further details.

Automated procedures ensure that Equation (1) is applied to natural beaches with gentle slopes, while Equation (2) is used for steep profiles such as engineered or defended coasts. All components contributing to Equation (1) were ultimately interpolated to an hourly resolution for consistency across datasets.

Where R is the wave runup; Hs is the significant offshore wave height, and Lo is the wavelength of the waves.

Considering that extreme coastal water levels (ECWL) result from the combination of several variables, in this study, the ECWL is estimated using the following equation.

$$ECWL=SLA+DAC+Tide+R$$

(3)

where ECWL is the extreme coastal water level; SLA refers to sea level anomalies; DAC represents the storm surge; Tide is the astronomical tide; and R is the wave runup.

2.3. Application of the Generalized Pareto Distribution (GPD) Model for the Analysis of ECWL Extreme Values

The determination of extreme water levels requires the application of extreme value theory, and the most used method is the GPD through a Peak Over Threshold (POT) approach. In this study, the 99th percentile was estimated based on hourly ECWL data. Here, to identify extreme water levels at the coast, the Generalized Pareto Distribution was adjusted using a Peak Over Threshold, specifically the 99th percentile. The GPD involves the selection of a threshold (μ) [43]. In this study, the empirical quantile method, specifically the 99th percentile, was chosen as the threshold value for ECWLs.

It is important to note that the threshold selection is critical in extreme value analysis. The choice of threshold represents a compromise between bias and variance, since a low threshold may violate the model’s asymptotic assumptions, resulting in bias [31,44,45]. Conversely, a high threshold will generate fewer exceedances for precise parameter estimation, which increases variance [44]. Therefore, an appropriate threshold allows a balance between bias and variance.

The POT approach uses a probability function to model the intensity of exceedances above a properly defined threshold [46,47,48,49]. Although a high threshold can increase variance, the authors of [31] state that it must be sufficiently high for exceedances to converge to the GPD model, and the POT dataset must also contain multiple extreme events for reliable and precise parameter estimation. In this study, the mean residual lifetime function was examined, as well as the stability of the GPD parameters (shape and scale parameters). First, a threshold sensitivity analysis was performed by adjusting thresholds between the 90th and 99th percentiles. The results show that approximate linearity is observed beyond the 97.5th percentile. In addition, verification of the stability of the shape and scale parameters indicates that the 99th percentile is a relevant threshold insofar as the GPD parameters, particularly the shape and scale parameters, are stable. For this reason, the 99th percentile was selected for the detection of extreme events.

To ensure statistical independence of events, an inter-event period of 48 h was chosen. In other words, two successive extreme events are statistically independent when the extreme coastal water level (ECWL) is below the selected threshold (99th percentile) for at least 48 h. This inter-event period was chosen because two successive extreme events can be generated by different synoptic or meteorological systems. This approach first highlights the sections of the coastal zone with the highest ECWL values, which are indicators of vulnerability to coastal flooding. Numerous studies on coastal extremes have used the GPD [46,50,51,52,53,54,55,56]. Moreover, studies have shown that GPD is preferable for capturing more extremes compared to the Generalized Extreme Value (GEV) distribution, which focuses on block maxima (hourly, daily, monthly, annual). Coastal flooding can occur multiple times within the same year, so the selection of block maxima may lead to the loss of information on extreme events. In fact, ref. [31] reported that the GPD is the most efficient estimator for return periods.

Accordingly, the GPD is fitted to the data to estimate the 50 and 100-year return periods associated with the 99th percentile of ECWLs. To ensure the validity of the results, a confidence interval was defined. Defining confidence intervals (IC 95) makes it possible to show the certainty of the values obtained for the T50 and T100-year return periods.

The mathematical expression for the GPD fit in this study was performed using Equation (4).

$$G_{\gamma ,\sigma }\left(\gamma \right)=\left\{\begin{array}{c}1-({1+y{\displaystyle \frac{\gamma }{\sigma }})}^{-{\displaystyle \frac{1}{\gamma }}},si \gamma ⧧0\\ 1-\exp \left(-{\displaystyle \frac{\gamma }{\sigma }}\right),si \gamma =0\end{array}\right.$$

(4)

where γ is the shape parameter and σ is the scale parameter. When the shape parameter γ equals 0, the Generalized Pareto Distribution (GPD) reduces to an exponential distribution. Furthermore, when γ < 0, the GPD becomes a Pareto distribution. Finally, when the shape parameter γ > 0, the GPD follows a beta distribution [46]. The RStudio (version 4.3.3) programming environment allowed the Generalized Pareto Distribution to be adjusted to the data. Maximum likelihood estimation was applied to estimate the parameters of the GPD.

2.4. Analysis of Trends in Extreme Water Levels

To determine the evolutionary trend of ECWLs, two combinatorial and complementary approaches were applied at each station in the coastal region studied. First, the non-parametric Mann–Kendall test was applied to determine the nature of the trend, i.e., whether it was upward or downward (positive or negative Mann–Kendall tau). This test is often used to track trends in hydrological, meteorological, oceanographic, and other variables. Using the Kendall package from RStudio, the replication that was performed returned a p-value for each station, indicating whether the trend was significant (p < 0.05 or 5%) or not. When the trend is significant, the directional slope is estimated by estimating Pearson’s correlation coefficient between time (years) and the upper 1% value of the ECWLs. It should be noted that this correlation is interpreted as a measure of the intensity and direction of the trend (positive or negative) over the period considered.

2.5. Sensitivity Analysis of Factors Controlling Extreme Water Levels

To identify the main factor controlling extreme coastal water level (ECWL) variation along the coast under study, a correlation analysis was performed between the variables or main components likely to influence ECWLs. For each station, the relative contribution of each factor to the variability of extremes was quantified using the correlation coefficients between ECWL values and each of these components. The factor with the highest correlation is considered the dominant factor. The results are then integrated into a spatial database containing the coordinates of the stations to produce a map using R software (version 4.3.3). This approach makes it possible to visualize the factors controlling ECWLs along the coast under study. In other words, this approach highlights the regional contrasts between the sections of the Senegalese coast mainly subject to tidal action and those where other factors exert a significant influence.

3. Results

The Senegalese coastline presents a complex and dynamic maritime environment with a wide range of different oceanographic and climatological conditions. Consequently, knowledge of the spatial distribution of extreme water levels (Figure 2) is of paramount importance for understanding coastal risks.

The analysis of the top 1% of ECWLs from 1993 to 2023 along the Senegalese coastline indicates spatial heterogeneity. First, the northern section of the coast, particularly Saint-Louis and the Langue de Barbarie, is extremely exposed. Similarly, certain areas around the Dakar region, especially Yoff, Ouakam, and Ngor, show high values. Similarly, certain areas around the Dakar region, especially Yoff, Ouakam, and Ngor, show high values. In these sectors, the 99th percentile of ECWLs exceeds 1.2 m. The lower and upper bounds of the 95% confidence intervals range approximately from 1.15 m to 1.3 m, reflecting the uncertainty in the estimates and highlighting spatial variability in Extreme Coastal Water Levels. In fact, it is in this part of the country that the lowest ECWL values are recorded, notably in Casamance, particularly near the Casamance River estuary and near Cap Skirring. This pattern is also observed in the Saloum River delta, as well as in the extreme south of the Senegalese coast, where the Saloum River delta is characterized by very low ECWLs. It should be noted that areas with estuaries, except Saint-Louis, are characterized by low ECWL values. Furthermore, regions experiencing intense urban growth, such as Saint-Louis, Dakar, and Mbour, register very high ECWL values. Unlike the Grande Côte of Senegal, much of the Petite Côte (Mbour-Toubab Dialaw) shows intermediate levels ranging from 0.8 to 1 m. Although these water levels are intermediate, they can still cause damage, especially in areas with high urban activity. Knowledge of the probability of extreme water levels occurring is important for effective coastal risk management. To this end, extreme water levels associated with 50- and 100-year return periods are estimated in this study (Figure 3).

The analysis of the top 1% of ECWLs for the 50-year (T50) and 100-year (T100) return periods highlights a spatial contrast along the Senegalese coast (Figure 3). Indeed, ECWL values range between 1.6 and 2.3 m, with significant differences between the two return periods as well as among the different sections of the Senegalese coastline. Figure 3 shows that the maximum ECWL values exceed 2.25 m for the 100-year return period (T100). ECWLs associated with the centennial return period vary spatially, with the Dakar region, particularly the capital, being especially exposed. This is followed by the northern section of the coast, namely the Saint-Louis region, particularly the Langue de Barbarie. In this area, ECWLs exceed 2.0 m, while in Dakar, the ECWL value associated with the 100-year return period is over 2.2 m. Additionally, the coastal sections at Mbour and Toubab Dialaw record intermediate values, ranging from 1.5 to 1.9 m. Similarly, ECWL values for the centennial return period are observed in the extreme south of the coastline, as is the case in the Saloum delta.

For the 50-year return period (T50), a spatial distribution of ECWLs like T100 is observed along the entire coast. Maximum levels are still recorded in the same coastal regions, Dakar and Saint-Louis, but they reach approximately 2 and 2.2 m, which is 5 to 10 cm lower than for the 100-year return period. Figure 3 shows that the difference between T50 and T100 is more pronounced in the most exposed areas (Dakar and Saint-Louis). Coastal sections in the extreme south (Saloum delta and Casamance) show minor variations between T50 and T100. ECWLs are generated by the combination of several variables (see Equation (2)). Therefore, it is important to highlight the factors that contribute most significantly to ECWLs along the Senegalese coast (Figure 4).

Considering that ECWLs are generated by the combination of oceanic, meteorological, and tidal parameters, it seems important to carry out a sensitivity analysis to identify the parameter or parameters that have the greatest influence on extreme coastal water levels (Figure 4). Figure 4 shows the spatial distribution of the factors controlling ECWLs at the different observation points along the Senegalese coast.

In this study, ECWL is considered as the sum of the following parameters: SLA + DAC + Tide + Runup (Equation (1)). The results of the sensitivity analysis reveal that only two parameters, tide and runup, have a significant impact on ECWLs. Moreover, the results indicate that tide has a strong predominance along the entire coastline (Figure 4). Examining the figure, in Dakar and Saint-Louis (14.7° N and 16° N–17° N, respectively), most points are dominated by the astronomical tide. These two sections of the Senegalese coast are characterized by a semi-diurnal tide with a microtidal regime, where the tidal range does not exceed 2 m even during spring tides. Although the points representing runup (in red) few in number (Figure 4), it should be noted that the influence of runup on extreme coastal water levels is more pronounced in the extreme south, particularly in the Saloum delta and Casamance. More specifically, points representing the effect of runup on ECWLs appear mainly south of Dakar, in coastal areas near Mbour, Joal Fadiouth, the Saloum delta, and Cap Skirring (between 12.5° N and 13.5° N). It should be noted that the influence of tide is reduced in areas where runup has a stronger impact on ECWLs.

Figure 5 illustrates the spatial distribution of trends in the upper 1% of ECWLs along the Senegalese coastline, based on the analysis of slope values and associated p-values calculated using the Mann–Kendall test. The results reveal a pronounced latitudinal gradient: stations located in the southern part of the coastline show more pronounced positive trends, while the central and northern areas display weaker variations. However, all p-values fall between 0.1 and 0.4, indicating that none of the observed trends reach conventional thresholds for statistical significance. Therefore, although some regions appear to evolve more rapidly, these variations should be interpreted with caution, as they may reflect natural variability rather than a statistically robust signal.

In more detail, the Dakar region exhibits a moderate to strong slope, suggesting a relative increase in the studied variable, whereas the Casamance and the Saloum Delta, despite showing high slopes, do not reach statistical significance. Along the Petite Côte, particularly around Mbour, positive trends display greater spatial variability, with some stations showing weaker slopes. This spatial heterogeneity suggests that local dynamics, linked to coastal processes and environmental conditions, strongly influence the evolution of the studied variable along the Senegalese shoreline.

4. Discussion

Extreme water levels play a determining role in coastal evolution. Numerous studies have shown the impact of ECWLs on coastal communities and ecosystems [55,56]. These levels of water can cause flooding with significant impacts [57]. The analysis of the results shows that the 99th percentile values of ECWLs are unevenly distributed along the Senegalese coastline. The highest values are recorded in the north (Saint-Louis, Langue de Barbarie) and at the Cape Verde Peninsula. Intermediate values are located along the Petite Côte (Mbour-Toubab Dialaw), while ECWLs are very low in the Saloum delta and the Casamance river estuary. This spatial variability is comparable to that observed in other coastal regions, such as the west coast of the United States [58] and other areas studied by [59].

The variability observed along the Senegalese coast could result from local topographic and bathymetric characteristics that modulate extreme water levels. The ECWL peaks observed in Dakar and Saint-Louis are explained by a strong semi-diurnal tidal influence. Regional variability of coastal water levels can be attributed to a combination of differences in tidal amplitude, storm patterns, and seasonal cycles [58]. Conversely, the low ECWLs in Casamance and the Saloum Delta may result from the influence of mangroves and bolongs, which help modulate extreme water levels. The interaction between marine waters and estuaries also contributes to this modulation. From a risk management and anticipation perspective, it is relevant to focus on Saint-Louis and Dakar. These areas not only have the highest ECWLs but also experience strong urban growth, around 6% per year according to [18], which increases their vulnerability to flooding. Morphologically, the Langue de Barbarie, a low-lying sandy spit [60], is particularly exposed to flooding, and the recently observed subsidence [61] will further exacerbate this risk. Although the Cape Verde Peninsula shows a high 99th percentile, its vulnerability is limited due to rocky coasts and steep cliffs [62], reducing the risk of overtopping or flooding.

Estimating the return periods of extreme water levels is essential for effective flood risk management [63]. Water levels associated with the T50 and T100 return periods also show spatial heterogeneity, with values exceeding 2 m in the northern and western tip of the coastline. These areas, combining high water levels and strong urbanization, require particular attention. Return periods T50 and T100 can be critical for low-lying areas, such as the Langue de Barbarie, a situation like that observed in El Djamila Bay, Algeria [46].

ECWL results from the combination of several parameters, whose contributions vary spatially and temporally. Sensitivity analysis shows that only tide and wave runup have a significant impact on ECWLs along the Senegalese coast. Tide dominates, followed by wave runup, while SLA and DAC have negligible impact. This situation may be explained by the influence of east winds transporting storm waves from afar [35]. It should be noted that the relatively low contribution of DAC in our analysis may partly reflect an underestimation of local storm surges by global barotropic models or ERA 5. However, it would be interesting in future studies to carry out comparisons between regional storm surge models or validations using tide gauges to assess the representativeness of DAC in the Senegalese context. Although storm waves are responsible for flooding in many regions worldwide [63,64,65,66,67], they do not significantly affect ECWLs in Senegal, as also observed in Ghana and Côte d’Ivoire [68,69].

The predominance of tide in the north and center of the coast reflects the amplitudes of semi-diurnal tides, in agreement with observations by [70]. In Saint-Louis, tidal amplitude increased after the breach opening in 2003 [71]. Other studies have highlighted the leading role of tide in flooding and in increasing the annual frequency of tidal floods [72,73]. The low contribution of wave runup in Dakar and Saint-Louis could be explained by the gentle slope of the continental shelf, whereas its contribution is more important where slopes are steeper [66]. In the far south (Casamance, Petite Côte, and Saloum delta), wave runup plays a significant role. This dynamic is like that observed in other tropical areas with low tidal range, where swell can strongly influence extreme water levels [74]. The combined tide-runup effect in estuaries could result from the presence of mangroves and bolongs modulating the tide [75]. Estimating ECWLs in these areas is complex due to the estuarine dynamics [38]. Cross-shore winds explain the significant contribution of runup to extreme water levels in the extreme south of the coastline. As highlighted by [69], such winds can generate strong swells in estuarine and shallow areas. The linear relationship observed between ECWL and years in estuaries indicates an increase in extreme water levels, which is concerning in the context of climate change and sea-level rise. However, the associated p-values range between 0.1 and 0.4, meaning that these trends are not statistically significant according to conventional thresholds. Therefore, although the upward tendencies suggest a possible increase in extreme coastal water levels, they should be interpreted with caution, as the observed variations may reflect natural variability rather than a robust long-term signal. These areas are exposed to flooding and the risk of saltwater intrusion into agricultural lands [76]. The author [77] identified two distinct wet periods (1994-2007 and 2008-2023) using the Standardized Precipitation Index (SPI), the Standardized Streamflow Index (SSI), and the non-parametric Mann-Kendall test. These results suggest a gradual return of rainfall in the study region. Consequently, these wet periods could lead to increased river discharge, which may, in turn, contribute to higher estuarine water levels (ECWLs) and influence local hydrological dynamics. Finally, the contribution of ECWL components varies over time [28]. Between 1993 and 2023, a moderate to strong positive trend is observed in Dakar, which is concerning given the urbanization, socio economic, and heritage stakes; however, the associated p values range between 0.1 and 0.4, indicating that the trend is not statistically significant. The Petite Côte shows more variable positive trends, with p values also between 0.1 and 0.4, suggesting caution in interpretation. Saint-Louis displays relative stability, with higher p values (0.2–0.4), but continued monitoring is recommended. In the estuaries (Saloum Delta and Casamance), the trends exhibit large slopes, but the p values remain above 0.1, indicating that these trends are not statistically significant, although they highlight a potential vulnerability to flooding driven by tides, storm surges, and wave action [78]. The upward trend in extreme water levels along the coast in the extreme south of the coastline seems logical. Indeed, the work of [38] on monitoring sea level rise using space altimetry along the West African coast shows that on the Senegalese coast, sea level rise is around 4 mm/year in the southern part of the coast (Saloum Delta and Casamance), while in Saint-Louis and Dakar, the gradual rise in sea level fluctuates between 3 and 3.5 mm/year. In addition, the work of [79,80] has shown that large plumes of fresh water from rivers can alter the density of seawater, thereby affecting sea level.

These results provide essential insight into the spatial variability of coastal extremes in Senegal and identify priority sectors for flood risk management related to sea-level rise and extreme weather events.

Like any research work, this one has some limitations. First, the spatial resolution of ERA 5 data appears to be coarse. Indeed, this global product cannot resolve issues related to small-scale topographic variability, roughness, or local structures (e.g., rocky headlands, berms, or dikes) that can significantly alter wave height at the local level. As a result, breaking wave heights are consistent at the regional level but approximate, and discrepancies may occur in complex morphodynamic areas such as the Dakar peninsula or estuarine areas. When estimating runup, it is useful to consider all factors that may influence wave breaking. Moreover, the work of [81] has shown that on the Portuguese coast, the presence of reefs significantly modifies wave height due to diffraction and refraction. In future work, it would be interesting to incorporate these elements into the estimation of wave runup. Furthermore, ERA 5 tends to underestimate coastal wave energy in grids partially covered by land, but our interpolation approach mitigates this limitation without eliminating it. In addition, it should be noted that the ERA5 wave data, with a spatial resolution of 0.5° (~55 km), do not resolve nearshore wave transformation processes such as refraction, shoaling, or breaking. Therefore, the authors of [33] parameterization applied here provides a first-order approximation of runup suitable for large-scale analyses but may not capture local-scale variability, particularly in complex coastal settings such as estuaries and deltas. The resulting ECWL estimates should thus be interpreted as spatially consistent indicators of relative variability rather than precise local predictions. Future efforts coupling regional wave models or high-resolution remote-sensing data would improve local ECWL representation.

To make this work more scientifically interesting, it would be useful to validate the results relating to ECWL values associated with T50 and T100 year return periods, but this validation is made difficult by the lack of data. In fact, the only site with a tide gauge along the coast under study is Dakar. Although this site has a tide gauge, it should be noted that the time spectrum of data is not wide. For this reason, the results have not been validated. Nevertheless, we believe that validation should be carried out. Following the trend of sea level rise, the authors of [69] state that the West African coastline lacks tide gauges. In addition, the few records available are short and suffer from numerous gaps (many holes in the tide gauge data series). This validation work could be helpful from a coastal risk management perspective.

5. Conclusions

This study highlights the spatial variability and potential intensification of extreme coastal water levels (ECWL) along the Senegalese coastline from 1993 to 2023. The 99th percentile of ECWLs exceeds 1.2 m in Dakar and Saint-Louis, with 95% confidence intervals of 1.15–1.30 m, while Casamance and the Saloum Delta exhibit lower extremes (0.8–1.0 m). For return periods, the 50-year (T50) and 100-year (T100) levels range from 1.5–1.9 m and 1.6–2.3 m, respectively, with T100 exceeding 2.25 m in Dakar and 2.0 m in Saint-Louis. Sensitivity analysis indicates that astronomical tides primarily drive ECWLs along most of the coast, whereas wave runup dominates in southern estuarine areas. Trend analysis shows a latitudinal gradient of increasing ECWLs southward, though trends are not statistically significant (p = 0.1–0.4).

These results provide a quantitative basis for coastal risk management. Urgent implementation of site-specific protection strategies is needed, particularly in socio-economically critical areas such as Dakar, Saint-Louis, and Mbour. Enhanced data collection and detailed morphodynamic studies will be crucial to design sustainable and effective coastal management plans in the context of rising sea levels.