The Influence of Sampling Hole Size and Layout on Sediment Porewater Sampling Strategies

Abstract

The dynamics of chemical components in sediment porewater are crucial for marine ecological research, resource assessment, and environmental monitoring. A scientific sampling strategy is key to obtaining high-quality porewater. This study aims to explore the effects of circular sampling hole size and layout on sampling effectiveness to optimize the sampling strategy. First, this study analyzed the flow field from time and spatial flow. Then, a simulation model was built using COMSOL Multiphysics 6.2 to simulate changes in the flow field, Darcy velocity, and effective sampling depth under different conditions. The results showed that the sampling holes finished sampling earlier due to being close to the open boundary; small sample hole sizes could suppress this time lag but reduce efficiency, and the effective sampling range increased exponentially with volume. When R = 5 mm, D = 150 mm, and V = 10 mL, interference between adjacent layers was effectively avoided, balancing timeliness and sample representativeness. Laboratory experiments and sea trials validated the effectiveness of the sampling strategy. This study provides theoretical and practical guidance for deep-sea porewater sampling technology, supporting marine scientific research.

1. Introduction

The interactions among sediments, overlying water, and pore water in marine environments constitute a complex dynamic system in which pore water actively participates in numerous biogeochemical reactions [1,2,3]. Monitoring spatial and temporal variations in the chemical composition of pore water across different stratigraphic layers is essential for a comprehensive understanding of sedimentary geochemical processes [4,5]. However, if the sampling interval between adjacent sampling holes is too wide, detailed tracking may become impossible, potentially missing critical information; while overly narrow intervals may result in excessive sample volume, blurring chemical distinctions between adjacent holes, and complicating the identification of reaction boundaries [6]. Therefore, researching the impact of sampling hole size and layout on sediment pore water sampling strategies is crucial for enhancing the scientific rigor and practicality of pore water sampling techniques. By optimizing sampling intervals, mutual interference between adjacent sampling holes can be avoided [7,8].

The Plymouth Marine Laboratory has developed a multi-layer in situ pore water sampler for intertidal sediments [9]. Each sample chamber is equipped with a filter plate (3.5 cm long, 1.0 cm high, 0.5 cm thick). These filter plates are arranged in a spiral pattern along the outer surface of the cylinder, spaced 1 cm apart, enabling pore water to be drawn into the sample chambers from different depths. The University of Florida has developed the Multisampler [10], featuring eight sampling ports to enable the extraction of pore water from different depths. The University of Oldenburg has developed an in situ pore water sampler [11]. Its sampling holes incorporate filter membranes with pore sizes of 100 and 50 μm. Adjacent sampling holes are spaced 5 cm apart and arranged along the sampling tube with a 90° rotation. The aforementioned samplers all utilize filter membranes to achieve multi-depth pore water sampling. However, the inherent dimensional constraints of filter membranes limit the flexibility of sampling intervals, and the precision of sampling intervals also faces limitations [12,13,14].

The core objective of this study is to design sampling strategies tailored to filter membrane size constraints to enhance the resolution of sediment porewater sampling. First, the theoretical mechanism of porewater flow in sediments is analyzed, laying a framework for understanding flow behavior during sampling. Second, a numerical simulation model for porewater sampling is constructed using COMSOL Multiphysics software, enabling analysis of sediment porewater flow characteristics under varying sampling hole parameters. Third, by comparing the simulation results with experimental data, a sampling strategy tailored to filter membrane size constraints is developed. Finally, a sampler is designed based on this strategy, and the effectiveness of the proposed approach is verified through sea trial results. This study provides technical support for advancing the practical application of high-precision sediment porewater sampling technology.

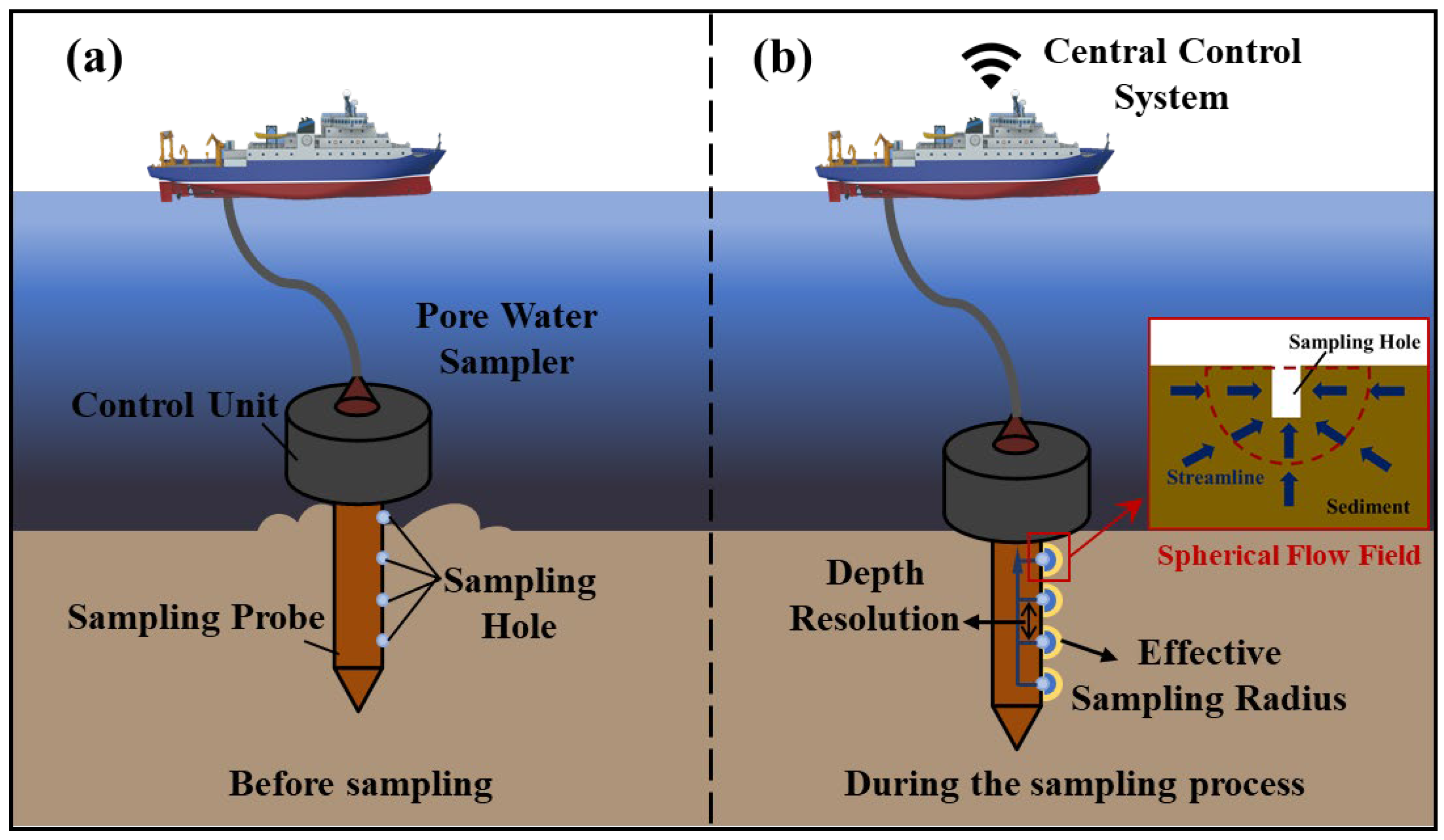
2. Multi-Level Sampling Technology for Pore Water

Figure 1 illustrates the workflow of depth-resolved in situ porewater sampling in deep-sea sediments, a critical technique for capturing vertical geochemical gradients. The sampling process commences with the deployment of a multi-channel sampling probe, which penetrates the sediment column to the target depth range under controlled pressure. Following probe insertion, a stabilization period (typically 30–60 min, depending on sediment permeability) is implemented to allow the porewater flow field to recover from mechanical disturbance, ensuring that subsequent sampling reflects natural in situ conditions. Once stabilized, the central control system synchronously transmits sampling commands to prefabricated sampling holes distributed at discrete depths along the probe. These sampling holes are equipped with filter membranes to prevent sediment particle intrusion while enabling selective passage of porewater, which then flows through the channels under the driving force of capillary action and slight pressure differentials, ultimately being collected in hermetically sealed sample chambers for subsequent geochemical analysis [15,16,17].

Figure 1. Schematic Diagram of Multi-Level Sampling Process for Pore Water: (a) Before sampling; (b) During the sampling process.

However, the rational design of depth resolution between adjacent sampling holes is a key technical challenge that directly determines the quality and interpretability of the resulting data. As depicted in Figure 1b, an excessively large depth resolution may fail to capture fine-scale variations in porewater chemical compositions that are indicative of localized biogeochemical reactions, resulting in the loss of critical information. Conversely, an overly small depth resolution can induce inter-layer interference. Porewater from adjacent sampling zones mixes due to overlapping flow fields during sampling. This mixing effect blurs the true chemical profiles, distorts concentration gradients, and compromises the accurate identification of key reaction interfaces. Therefore, it is critical to optimize the depth resolution between adjacent sampling holes to capture fine-scale geochemical gradients with the imperative of avoiding inter-layer interference induced by overlapping flow fields. This optimization ensures the comprehensive capture of key in situ porewater geochemical information, thereby enabling precise characterization of depth-dependent geological and geochemical variations in deep-sea sediments and facilitating robust interpretations of subsurface biogeochemical processes.

3. Methods

3.1. Theory of Pore Water Flow in Sediment

The pressure gradient serves as the primary driving force for pore water flow within sediments. As sampling progresses, the pressure around the sampling hole decreases and exhibits an increasing gradient distribution. Under the influence of this pressure gradient, pore water moves from high-pressure zones toward low-pressure zones [18,19].

3.1.1. Time Flow

Pore water sampling is influenced by various factors such as ambient temperature and pressure. Therefore, it is necessary to calculate variables, including pore water velocity, pressure, and concentration at any point within the flow field over time.

3.1.2. Spatial Flow

As sampling progresses, the pore water pressure near the sampling hole decreases. Based on the spatial characteristics, the pore water flow field can be classified into three states: (1) Unidirectional flow field (Figure 2a): A flow field where the velocity is nonzero in one of the three directions, while the other two directions have zero velocity. The flow direction at any point within a unidirectional flow field remains parallel, conforming to laminar motion; (2) Radial flow field (Figure 2b): Any two directions within the flow field possess velocity components, while the velocity component in the remaining direction is zero. Pore water pressure isosurfaces increase from the center, forming a flow pattern resembling concentric circles; (3) Spherical flow field (Figure 2c): Component velocities exist in all three directions within the flow field. During sampling, pore water flows toward the sampling hole from all directions.

Figure 2. Three States of Pore Water Flow Field.

In actual sampling, the pore water flow field within sediment is complex and variable, often comprising several distinct flow fields. This paper primarily analyzes the unidirectional flow field. With the X-axis as the flow direction, the linear unstable flow of pore water in a unidirectional flow field per unit area can be expressed as follows:

$${\displaystyle \frac{\partial X}{\partial t}}=\nabla \left[{\displaystyle \frac{K}{\mu }}\left({\displaystyle \frac{\partial p}{\partial x}}i+{\displaystyle \frac{\partial p}{\partial y}}j+{\displaystyle \frac{\partial p}{\partial z}}k\right)\right]=0$$

(1)

In example 1, $X$ is the pore water content in the sediment; $K$ is sediment permeability; $\mu$ is the dynamic viscosity of pore water, and $p$ is pore water pressure. Since the flow velocity of pore water along the x and y axes is zero, example 1 can be expressed as follows:

$${\displaystyle \frac{\partial X}{\partial t}}+{\displaystyle \frac{\partial }{\partial x}}\left({\displaystyle \frac{K}{\mu }}{\displaystyle \frac{dp}{dx}}\right)=0$$

(2)

$$X=\lambda \sqrt{p}$$

(3)

In example 3, $\lambda$ is the content coefficient of pore water in the sediment. Substituting example 3 into 2:

$${\displaystyle \frac{\partial p^2}{\partial t}}=a_p{\displaystyle \frac{{\partial }^2{p}^2}{\partial x^2}}$$

(4)

$$a_p={\displaystyle \frac{4\lambda p^{1.5}}{\alpha }}$$

(5)

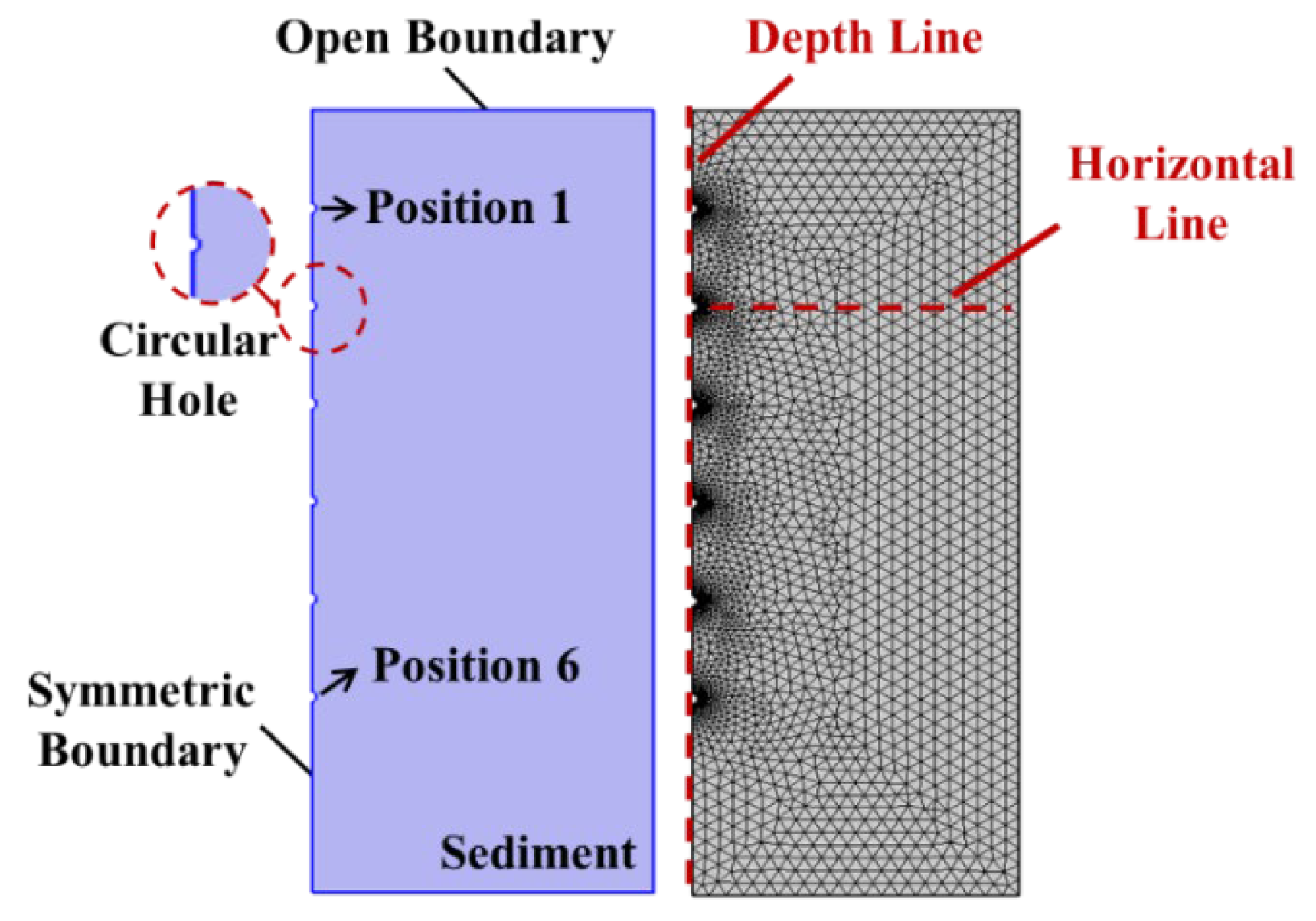
3.2. Numerical Calculation of Multi-Level Pore Water Sampling

This study employs the Porous Media Flow Module in COMSOL Multiphysics for computational analysis, with the simulation process based on the following assumptions: (1) The sediment is a homogeneous, continuous porous medium; (2) The sampling temperature is maintained at 4 °C, disregarding the influence of temperature variations on pore water transport; (3) The seepage process of pore water follows Darcy’s Law. Since the sampling process follows the Law of Conservation of Mass [20,21,22]:

$${\displaystyle \frac{\partial m_{pw}}{\partial t}}+\nabla \left({\rho }_{pw}·q_{pw}\right)=0$$

(6)

In example 6, $q_{pw}$ is the Darcy velocity vector of pore water. The expression for the mass of pore water per unit volume is:

$$m_{pw}={\rho }_{pw}·V_{pw}={\rho }_{pw}·V_s·\phi$$

(7)

In example 7, $\phi$ is the porosity of the sediment. If gravity is neglected, $q_{pw}$ can be expressed as follows:

$$q_{pw}=-{\displaystyle \frac{k}{\mu }}\nabla p$$

(8)

This study employs Darcy’s Law to simulate pore water flow within sediments. A sediment model with a width of 350 mm and a height of 800 mm was established for simulation. Based on sampling conditions, the initial pressure of the sediment was set at 30 MPa (working depth of 3000 m). As shown in Figure 3, circular sampling holes of varying sizes are fixed at different depth resolutions along the left side of the sediment model, labeled from top to bottom as Position 1 to Position n. The sampling hole pressure is set to 10 kPa to simulate pore water flow under negative pressure conditions (Other simulation parameters are shown in Table 1).

Figure 3. Simulation Model of Pore Water Sampling within Sediment.

Table 1. COMSOL Simulation Parameters [23,24,25,26].

Parameter	Value	Description
rho_s	1440 (kg/m3)	Density of Sediment
mu_l	1.32 × 10−3 (Pa·s)	Pore-water Viscosity
phi	0.6	Porosity
k0	1 × 10−16 (m2)	Penetration Rate
T_ref	277.15 (K)	Ambient Temperature

3.3. Experiment of Sampling Depth Resolution

To validate the accuracy of the simulation, this study designed a sampling depth resolution experiment to analyze the relationship between the effective sampling radius and sampling volume. The sediment was collected using a gravity sampler near Zhejiang, China (with a porosity of approximately 0.5). As shown in Figure 4a, the side walls of the sediment containers are provided with circular holes at regular intervals. To track pore water flow, before the experiment, a tracer (sodium fluorescein, maximum absorption wavelength 490 nm) of 5 mg/L was added above the sediment. Samples were collected in 1 mL units for the fluorescent tracer test. The sodium fluorescein in the samples was detected using a Hybrid microplate detector (Synergy H1, Figure 4b).

Figure 4. Depth Resolution Experiment: (a) Experimental setup; (b) Synergy H1.

3.4. Sea Trial

Based on the results, this paper designed a sampling strategy and a multi-level pore water sampler. As shown in Figure 5, the sampler was deployed in the coastal waters near Zhoushan, China, during sea trials. The pore water samples were tested further to validate changes in depth resolution during practical application.

Figure 5. Multi-level Pore Water Sampler Sea Trial.

4. Results

4.1. Effect of Sampling Hole Size on the Flow Field of Sediment

During the initial sampling stage (Figure 6), sediment internal pressure exhibits a gradient increase centered around the sampling hole. In the stable sampling stage (Figure 7), the internal pressure gradually decreases from top to bottom, which is related to the collection of pore water and the permeation of overlying water.

Figure 6. Initial Sampling Stage: The Pressure Field and Streamlines within the Sediment.

Figure 7. Stable Sampling Stage: The Pressure Field and Streamlines within the Sediment.

As shown in Figure 8a, during the initial sampling stage, the Darcy velocity varies with sampling location as follows: $v_{P1}>v_{P6}>v_{P2}>v_{P3}=v_{P4}=v_{P5}$. This relates to permeation: P1 is closer to the sediment surface and experiences greater boundary flux, while a larger fluid space is beneath P6. Consequently, P1 and P6 exhibit higher initial Darcy velocities. The relationship between position and sample volume is (Figure 8b): $V_{P1}>V_{P2}>V_{P3}>V_{P4}>V_{P5}=V_{P6}$. P1 is closest to the open boundary and completes sampling first; P6 is farthest from the open boundary and completes sampling last. This position effect causes sampling end times for lower-level sampling holes to lag. However, a smaller sampling radius can mitigate the position effect. Therefore, the sampling hole size must be determined based on specific conditions in practical applications.

Figure 8. (a) Darcy Velocity Curve over Time during Sampling; (b) Sampling Volume Curve over Time during Sampling (with R = 2.5 mm).

4.2. Analysis of Effective Sampling Range

4.2.1. Consider Sampling Depth and Sampling Interval

Considering the time sensitivity of sampling, this section utilizes sampling holes with a radius of 5 mm to investigate sampling depth and sampling intervals at different center-to-center distances (D = 50 mm, 100 mm, 150 mm, and 200 mm). As shown in Figure 9, during the initial sampling stage, when D = 50 mm, a distinct mixing phenomenon occurs at the boundary of the Darcy velocity distribution. As the sampling interval increases, this mixing gradually diminishes, owing to reduced interaction between adjacent sampling holes. At smaller intervals, enhanced hydraulic interference leads to greater fluid mixing. When D = 150 mm, the mixing phenomenon disappears, and the interaction between neighboring sampling holes can be neglected.

Figure 9. Cloud Map of Darcy Velocity Isoclines During the Initial Sampling Stage.

As shown in Figure 10, during the stable sampling stage, the Darcy velocity in shallow sediments (depth: 0–400 mm) remains nearly constant across different sampling intervals. This suggests that, in shallow sediments, the sampling mode gradually transitions from collecting pore water around the sampling hole to collecting overlying water. However, in deep sediments (depth > 400 mm), the sampling hole primarily collects pore water around the hole. Due to increased flow resistance in deep sediments, a significant time lag occurs during sampling. Furthermore, as sampling intervals decrease, mixing phenomena between Darcy velocity isosurfaces become more pronounced in shallow sediments. This leads to mutual interference of pore water between adjacent sampling holes. Therefore, when R = 5 mm and D = 150 mm, the flow field within the model reaches a stabilized pattern.

Figure 10. Cloud Map of Darcy Velocity Isoclines During the Stable Sampling Stage.

4.2.2. Calculation of Effective Sampling Range (ESR)

Based on the results from the preceding section, this section continues to calculate the variation patterns of the effective sampling range. To realistically simulate the sampling process and reduce the impact of time lag, we introduce a new boundary condition (as shown in Figure 11): once a sampling hole collects a certain volume of sample, it transitions to a no-flow boundary and ceases sampling. As shown in Figure 12, the magnification of P1 and P5 reveals that the ESR is not centrally symmetric. As shown in Figure 13, nonlinear fitting of the data shows the ESR as a function of sampling volume ($R^2=0.99$). As the sampling volume increases, the ESR grows exponentially. When collecting a 10 mL sample, the ESR for P1 is approximately 130 mm, while that for P5 is 90 mm. This finding provides important guidance for the design of quantitative sampling systems.

Figure 11. Cloud Map of Sampling Range Variation with Sampling Volume.

Figure 12. Cloud Map of Effective Sampling Range (Sample Volume: 10 mL): (a) P1; (b) P5.

Figure 13. The Variation in ESR with the Sampling Volume at Different Positions.

4.3. Results of Sampling Depth Resolution

As shown in Figure 14, the concentration of the fluorescent reagent in the sample at P1 ranged between 4.5–5.5 mg/L during the first 7 mL. At 8 mL, the concentration decreased to 4.35 mg/L, and further decreased to 3.90 mg/L at 11 mL. In contrast, the reagent concentration at P2 remained near 0 mg/L for the first 9 mL. At 13 mL, it was approximately 0.58 mg/L. This indicates that the fluorescent reagent at P1 had already influenced the sample at P2.

Figure 14. Fluorescent Sodium Concentration Variation with Sampling Volume.

The comparison of simulation and experimental results reveals that when R = 5 mm and V = 10 mL, the ESR is approximately 150 mm. Therefore, the center-to-center spacing between sampling holes should not be less than 150 mm. This sampling strategy not only enhances the timeliness of sampling but also reduces interference between adjacent sampling holes. As a result, it improves both the representativeness and reliability of the samples.

4.4. Results of Sea Trial

Based on the preceding research, we designed a porewater sampler with the following sampling strategy: R = 5 mm, D = 150 mm, V = 10 mL. As shown in Figure 15 [17], the ion concentrations in pore water samples vary with sampling depth. Ion concentrations at P1 are lower than at other positions, indicating no cross-contamination between sampling holes. This confirms the validity of the proposed sampling strategy.

Figure 15. Variation in Ion Concentrations in Pore Water Samples with Sampling Depth.

5. Discussion and Conclusions

This study investigates sampling strategies for multi-level sampling of pore water using circular sampling holes. It analyzes the effects of sampling hole size, sampling interval, and sampling depth on the flow field within sediments, enabling the design of corresponding sampling strategies based on application requirements.

5.1. The Applicability of the Sampling Strategy

In in situ porewater sampling, sampling interval design and sample accuracy remain widely discussed challenges in the field. Most multi-level in situ porewater samplers developed by researchers can achieve centimeter-scale sampling intervals [7,8,9,10], few studies have addressed whether inter-sample interference occurs between adjacent sampling intervals. The University of Oldenburg attempted to mitigate such interference by arranging adjacent sampling tubes at a 90° rotational offset [11]. However, this work failed to propose a systematic computational method to quantify the interference mitigation effect. Additionally, a German research institute was the first to identify the correlation between sampling volume and sampling radius, but it did not further investigate the dynamic characteristics of porewater flow field evolution within sediments during the sampling process [15]. Building on these research gaps, the present study analyzes how the size and layout of circular sampling holes influence the internal flow field of sediments, with the aim of developing a practically applicable technical scheme for in situ porewater sampling. Firstly, this paper describes the flow state of pore water within sediments, analyzing flow models based on temporal and spatial flow within sediments. Secondly, a simulation model for pore water sampling was constructed using COMSOL Multiphysics software to analyze flow characteristics under various operating conditions. This study reveals a time lag in sampling completion across different depths during the sampling. When collecting the same sample volumes, P1 is closest to the open boundary, completes sampling first, while P6 is farthest from the open boundary, completes last. Although smaller sampling hole sizes suppress time lag, small holes further reduce sampling efficiency. Furthermore, as the sampling volume increases, the effective sampling range between adjacent layers grows exponentially. By comparing simulation and laboratory experimental data, this paper establishes a sampling strategy: R = 5 mm, D = 150 mm, V = 10 mL, with a sampling depth of 0.6 m. Ultimately, a sampler was designed based on this strategy and underwent sea trials. Porewater sample test results from the sea trial further validated the effectiveness of the sampling strategy.

5.2. Study Limitations

Despite the validity of the proposed strategy, the current study has several limitations: (1) The simulation and experiments were conducted based on uniform sediment properties (constant porosity and permeability), while natural sediments exhibit significant spatial heterogeneity (e.g., layered structure, mineral composition variations), which may affect flow field distribution and sampling accuracy. (2) This study focused on circular sampling holes with R = 3–7 mm, sampling intervals of 100–200 mm, and volumes of 5–15 mL. Parameters beyond this range (e.g., rectangle, ultra-small intervals) were not investigated, restricting the strategy’s generalizability. (3) Neglect of dynamic environmental factors: In situ marine environments involve dynamic factors such as seabed currents and temperature variations, which were not incorporated into the simulation model, potentially influencing the practical application of the strategy.

5.3. Future Research Perspectives

To address the aforementioned limitations, our future work will focus on the following directions:

(1) Consider sediment heterogeneity: By characterizing the spatial variations in porosity, permeability, and particle size of sediments, the simulation model is further modified to adapt to heterogeneous conditions, enhancing the adaptability of the sampling strategy to complex geological environments.

(2) Expanding sampling hole parameter: Investigate the effects of irregular sampling hole (e.g., rectangular, oval) and broader parameter ranges (e.g., hole radius < 3 mm, interval < 100 mm) on flow fields, exploring more flexible and efficient sampling schemes.

(3) Integrating dynamic environmental factors: Introduce seabed current velocity, temperature, and pressure parameters into the simulation model, and conduct sea trials under different marine conditions to validate the strategy.

(4) Combining with advanced detection technologies: Integrate the sampling strategy with in situ porewater chemical sensors to achieve real-time monitoring of sampling quality and further enhance sampling accuracy.

In summary, this study establishes an effective design method for multi-level porewater sampling strategies, with the optimized parameters validated through laboratory experiments and sea trials. The findings provide technical support for porewater sampling and hold significant implications for deep-sea scientific research, such as marine biogeochemical cycle studies and environmental pollution monitoring. Addressing the current limitations through future research will further improve the strategy’s comprehensiveness and practicality, promoting its broader application in marine and terrestrial sediment porewater sampling fields.