Lagrangian Coherent Structures for Mapping Mesoscale Circulation in the Western Equatorial Atlantic
Abstract
1. Introduction
2. Methods
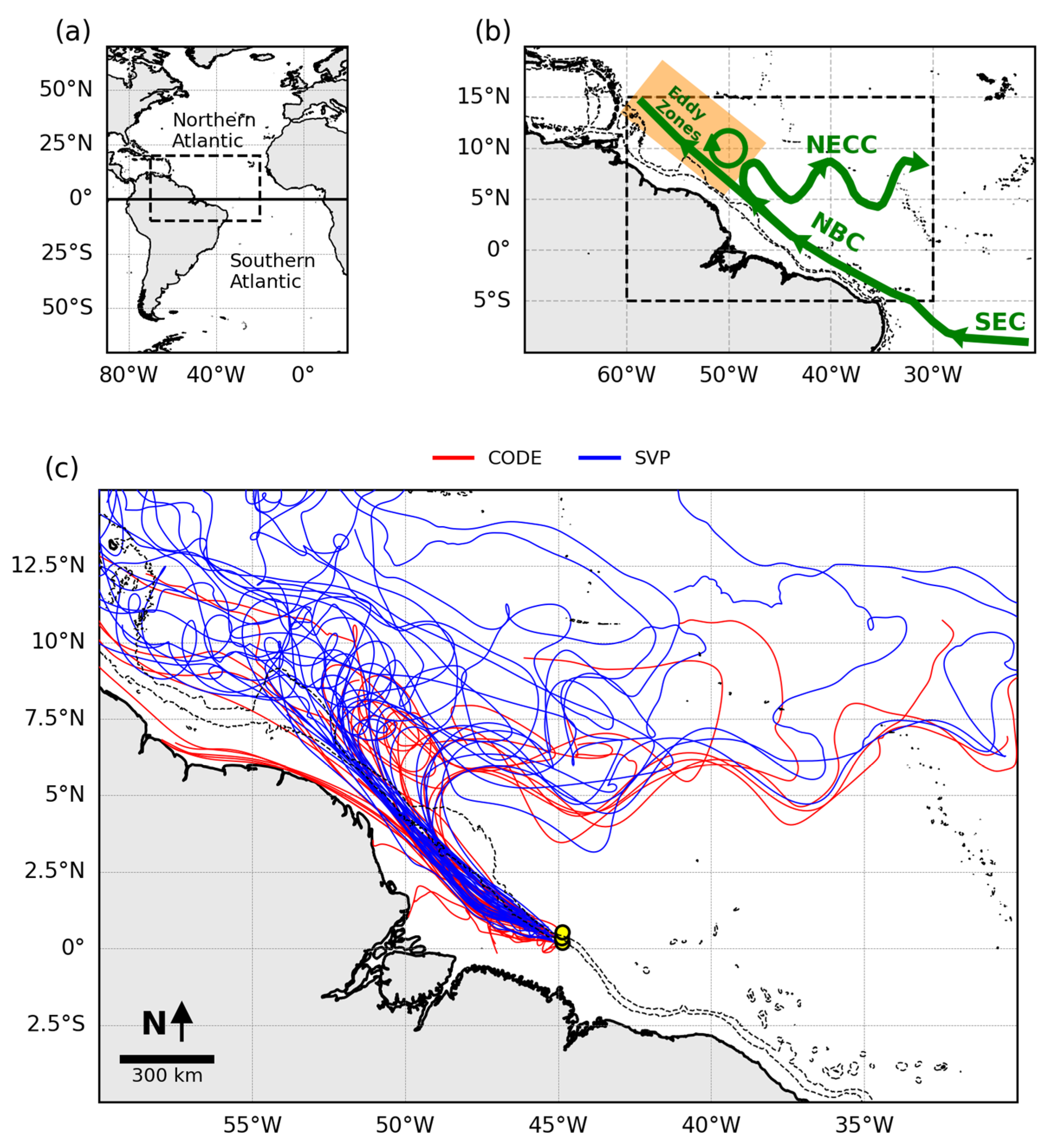
2.1. The Western Equatorial Atlantic Ocean
2.2. Surface Drifters
2.3. Global Analysis and Forecast
2.4. Finite-Time Lyapunov Exponent
2.5. Physical Parameters
3. Results
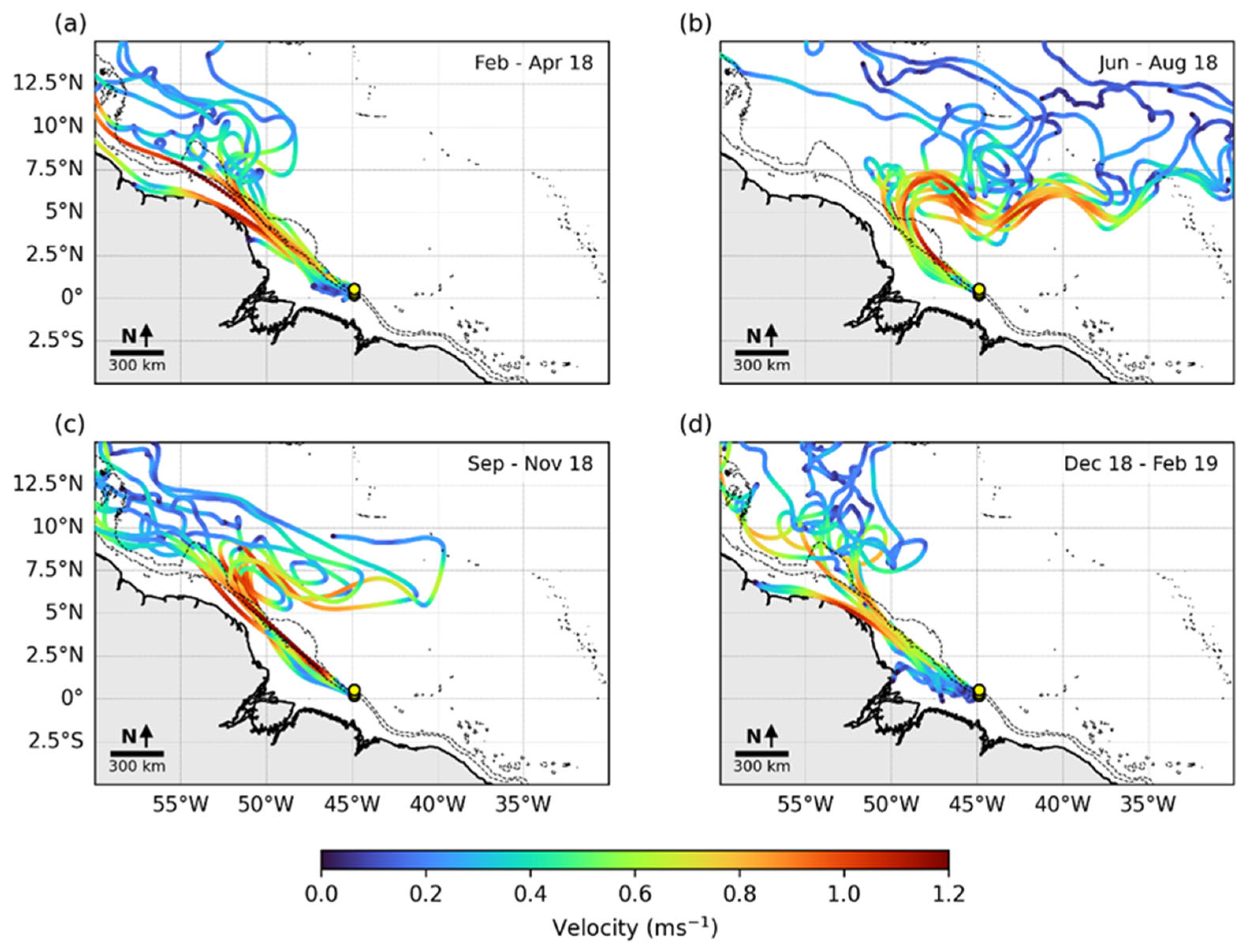
3.1. Drifter Dispersion
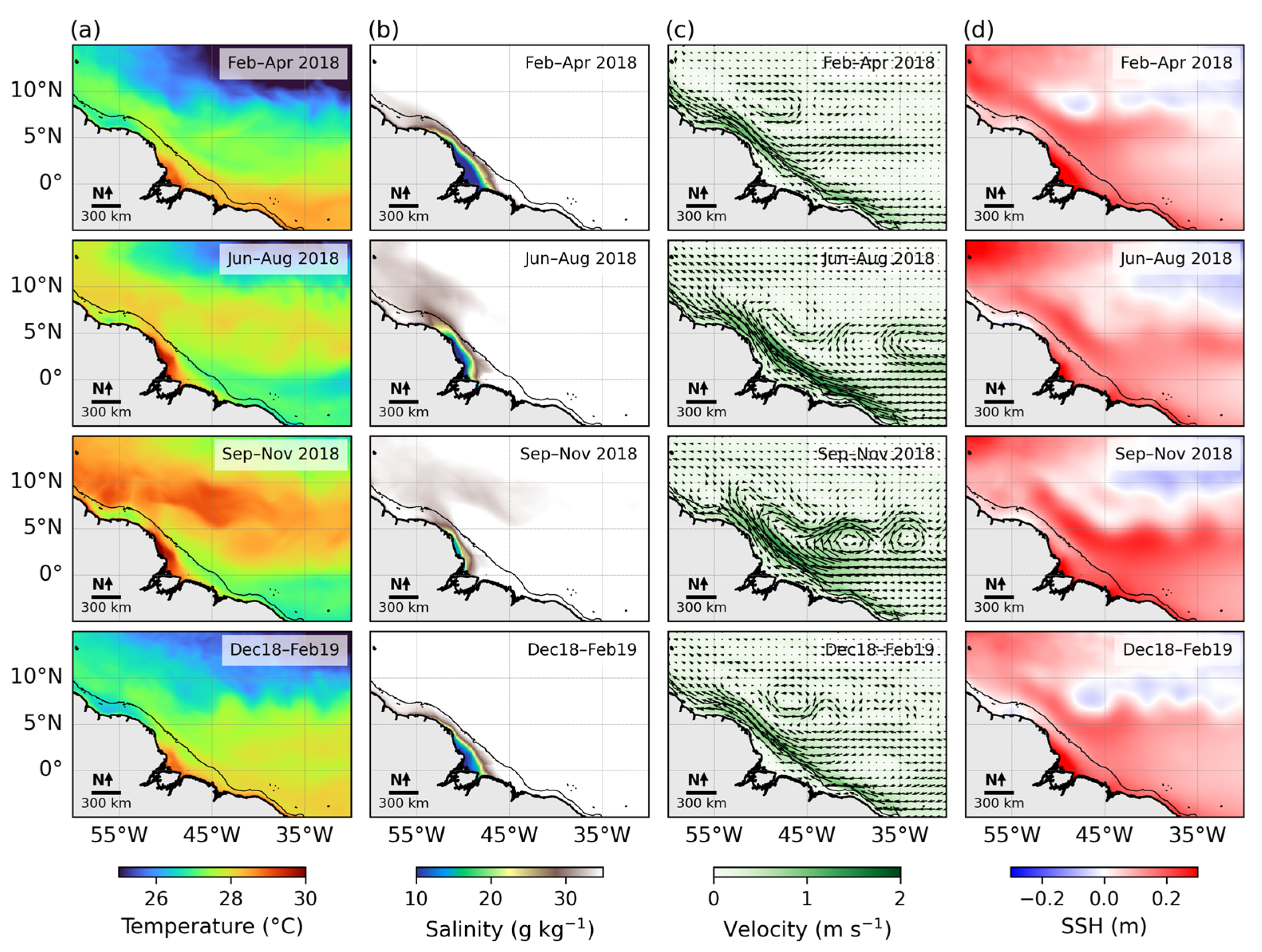
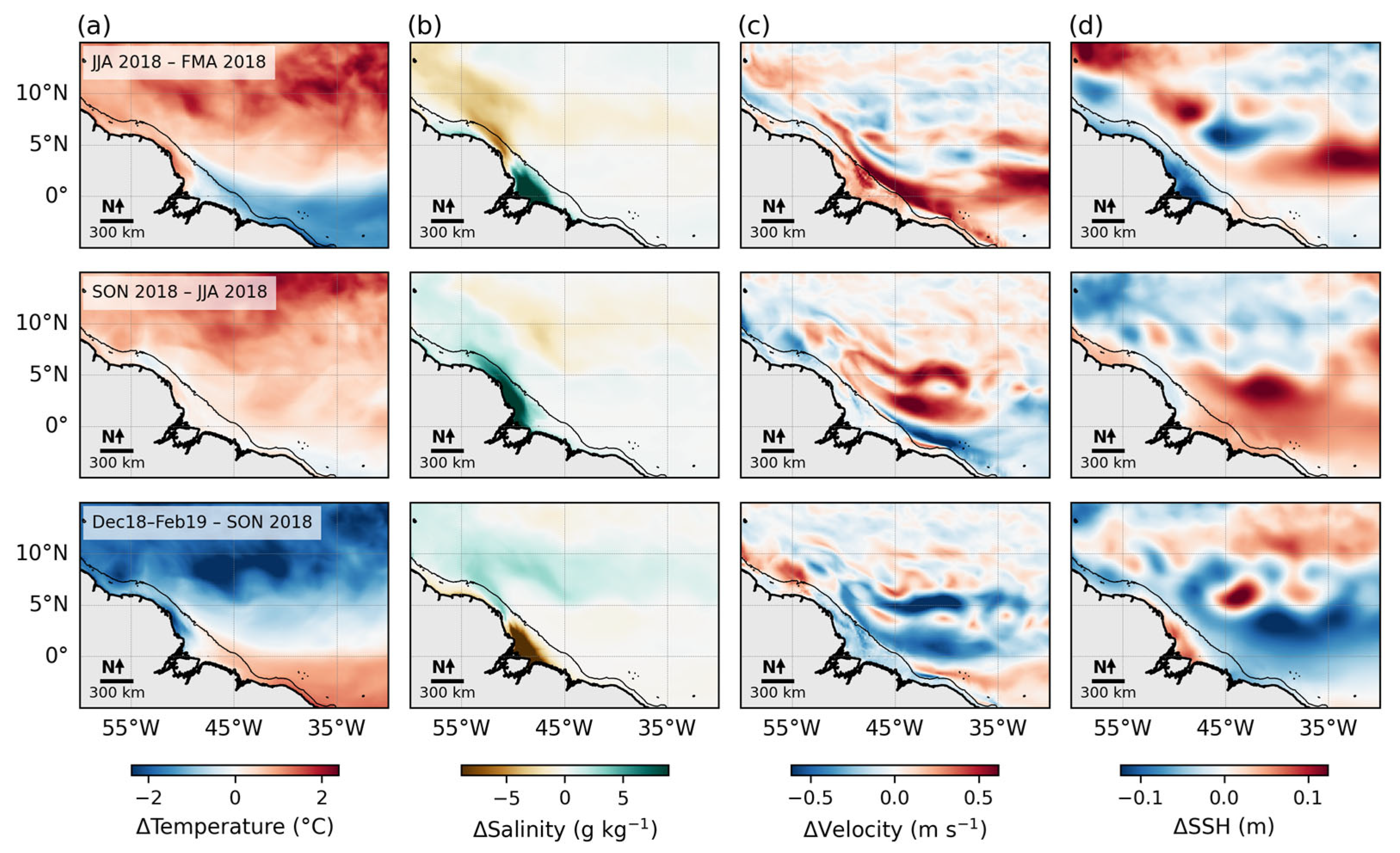
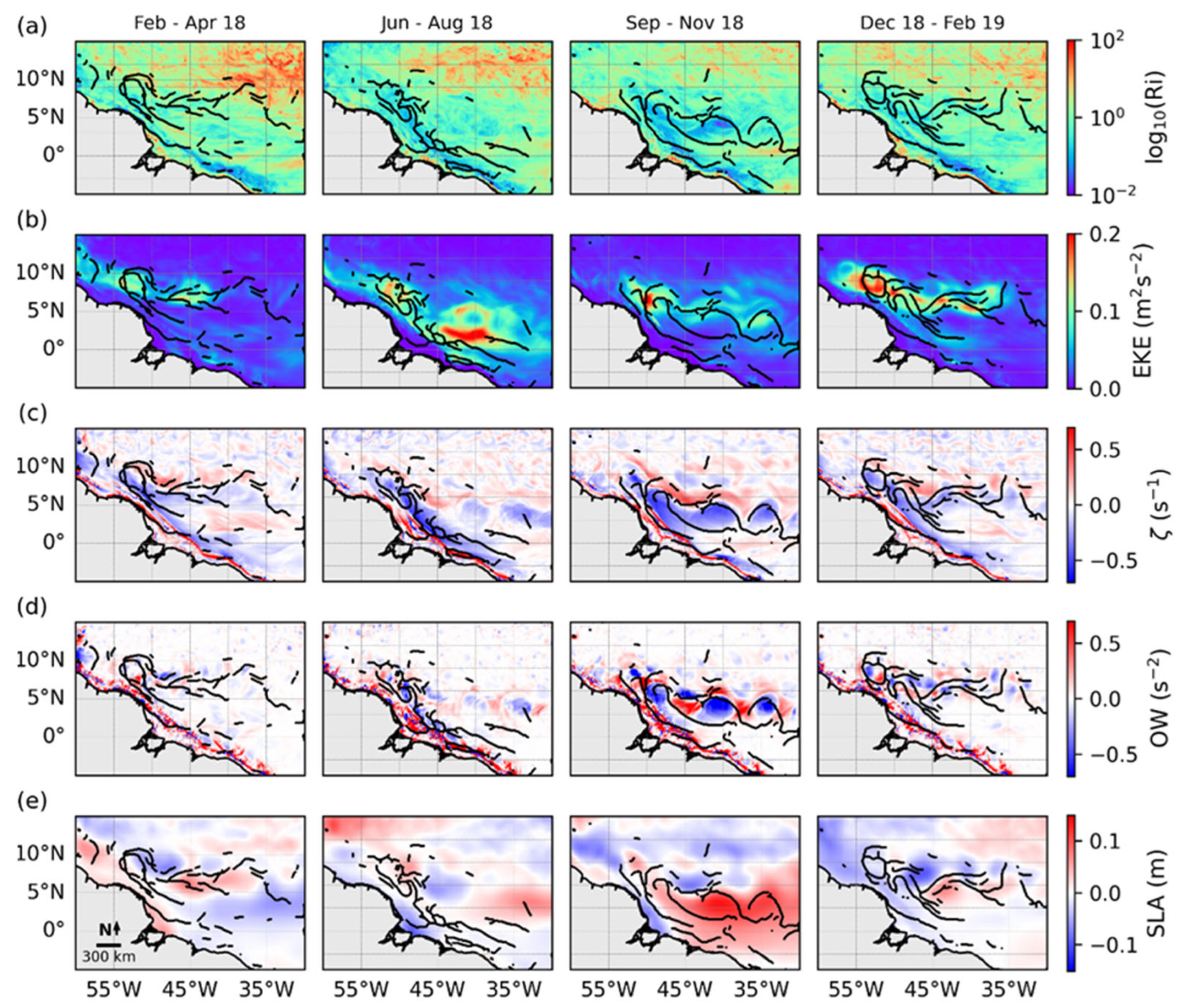
3.2. Seasonality of the Analysis/Forecast Parameters
3.3. Validation of the FTLE with Surface Drifters
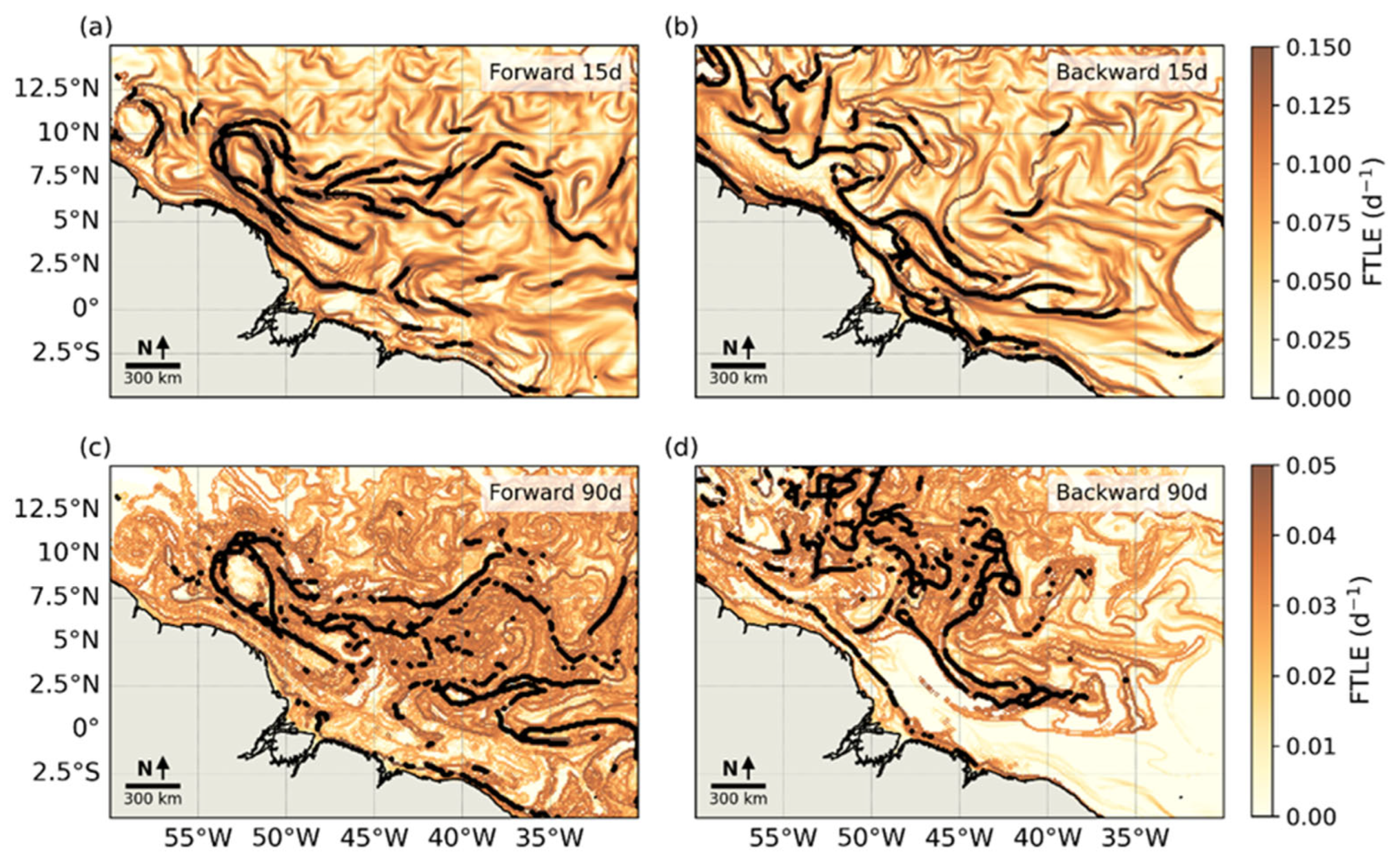
3.4. The FTLE Field
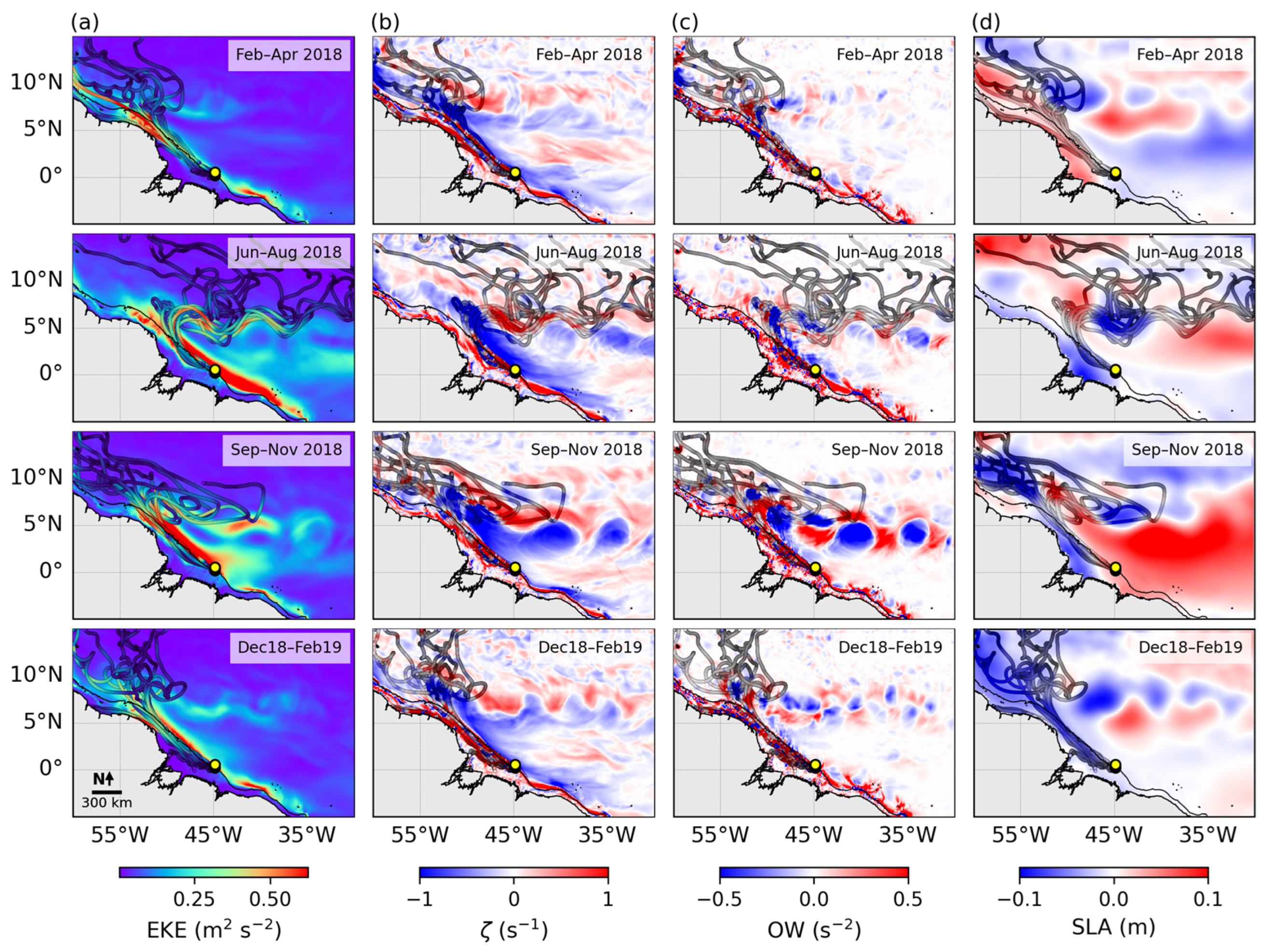
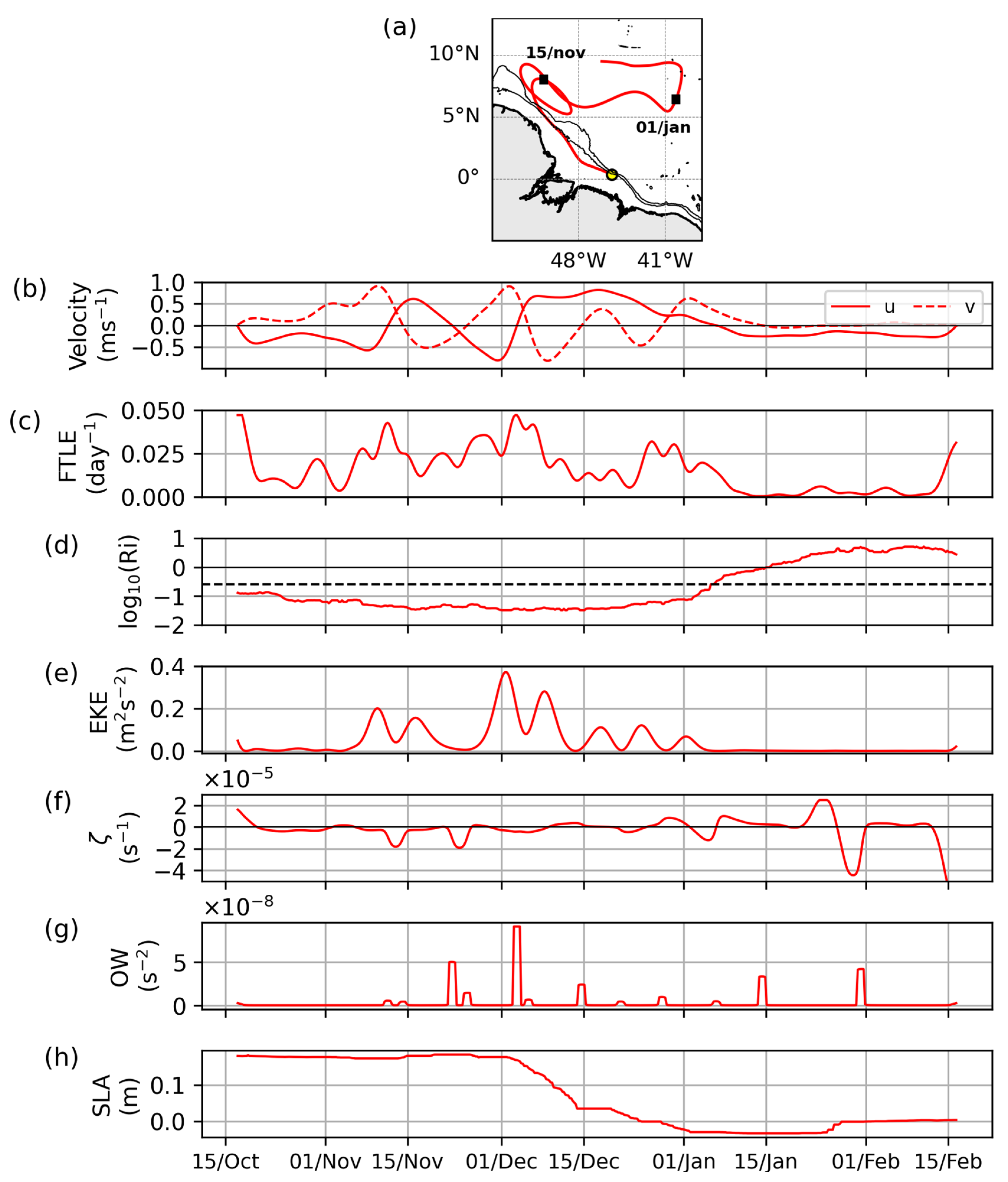
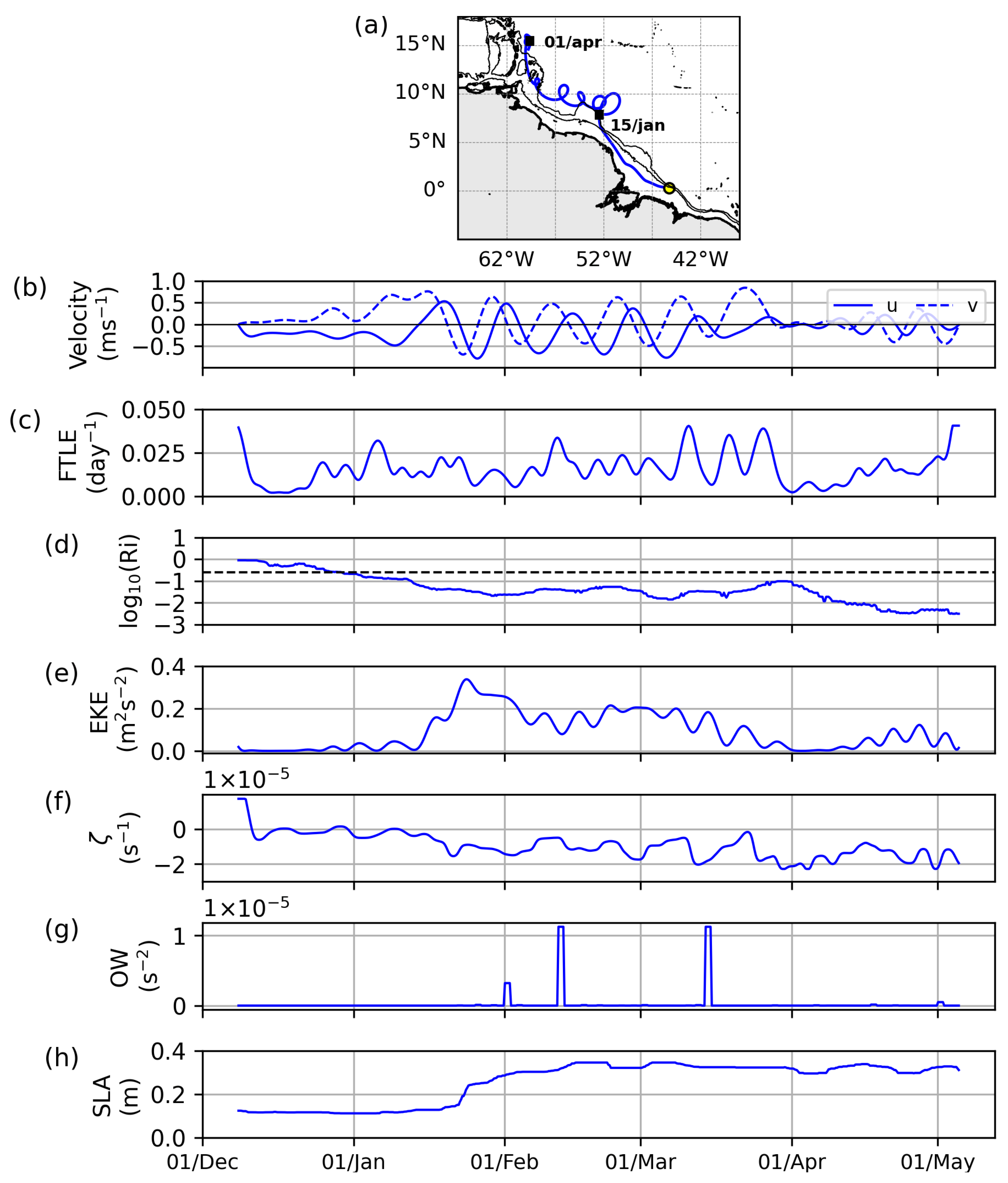
3.5. Case Studies: Time Series
4. Discussion
4.1. Mesoscale Circulation
4.2. LCSs in the WEA
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Flagg, C.N.; Gordon, R.L.; McDowell, S. Hydrographic and Current Observations on the Continental Slope and Shelf of the Western Equatorial Atlantic. J. Phys. Oceanogr. 1986, 16, 1412–1429. [Google Scholar] [CrossRef]
- Johns, W.E.; Lee, T.N.; Schott, F.A.; Zantopp, R.J.; Evans, R.H. The North Brazil Current Retroflection: Seasonal Structure and Eddy Variability. J. Geophys. Res. 1990, 95, 22103–22120. [Google Scholar] [CrossRef]
- Johns, W.E.; Lee, T.N.; Beardsley, R.C.; Candela, J.; Limeburner, R.; Castro, B. Annual Cycle and Variability of the North Brazil Current. J. Phys. Oceanogr. 1998, 28, 103–128. [Google Scholar] [CrossRef]
- Richardson, P.L.; Hufford, G.E.; Limeburner, R.; Brown, W.S. North Brazil Current Retroflection Eddies. J. Geophys. Res. Oceans 1994, 99, 5081–5093. [Google Scholar] [CrossRef]
- Prestes, Y.O.; Borba, T.A.D.C.; Silva, A.C.D.; Rollnic, M. A Discharge Stationary Model for the Pará-Amazon Estuarine System. J. Hydrol. Reg. Stud. 2020, 28, 100668. [Google Scholar] [CrossRef]
- Fratantoni, D.M.; Johns, W.E.; Townsend, T.L.; Hurlburt, H.E. Low-Latitude Circulation and Mass Transport Pathways in a Model of the Tropical Atlantic Ocean. J. Phys. Oceanogr. 2000, 30, 1944–1966. [Google Scholar] [CrossRef]
- Silva, A.C.; Bourles, B.; Araujo, M. Circulation of the Thermocline Salinity Maximum Waters off the Northern Brazil as Inferred from in Situ Measurements and Numerical Results. Ann. Geophys. 2009, 27, 1861–1873. [Google Scholar] [CrossRef]
- Bueno, L.F.; Costa, V.S.; Mill, G.N.; Paiva, A.M. Volume and Heat Transports by North Brazil Current Rings. Front. Mar. Sci. 2022, 9, 831098. [Google Scholar] [CrossRef]
- Van Sebille, E.; Griffies, S.M.; Abernathey, R.; Adams, T.P.; Berloff, P.; Biastoch, A.; Blanke, B.; Chassignet, E.P.; Cheng, Y.; Cotter, C.J.; et al. Lagrangian Ocean Analysis: Fundamentals and Practices. Ocean Model. 2018, 121, 49–75. [Google Scholar] [CrossRef]
- Peng, Y.; Xu, X.; Shao, Q.; Weng, H.; Niu, H.; Li, Z.; Zhang, C.; Li, P.; Zhong, X.; Yang, J. Applications of Finite-Time Lyapunov Exponent in Detecting Lagrangian Coherent Structures for Coastal Ocean Processes: A Review. Front. Mar. Sci. 2024, 11, 1345260. [Google Scholar] [CrossRef]
- Haller, G. Distinguished Material Surfaces and Coherent Structures in Three-Dimensional Fluid Flows. Phys. D Nonlinear Phenom. 2001, 149, 248–277. [Google Scholar] [CrossRef]
- Haller, G. Lagrangian Coherent Structures from Approximate Velocity Data. Phys. Fluids 2002, 14, 1851–1861. [Google Scholar] [CrossRef]
- Shadden, S.C.; Lekien, F.; Paduan, J.D.; Chavez, F.P.; Marsden, J.E. The Correlation between Surface Drifters and Coherent Structures Based on High-Frequency Radar Data in Monterey Bay. Deep Sea Res. Part II Top. Stud. Oceanogr. 2009, 56, 161–172. [Google Scholar] [CrossRef]
- Veatch, J.M.; Kohut, J.T.; Oliver, M.J.; Statscewich, H.; Fredj, E. Quantifying the Role of Submesoscale Lagrangian Transport Features in the Concentration of Phytoplankton in a Coastal System. ICES J. Mar. Sci. 2024, 81, 760–773. [Google Scholar] [CrossRef]
- Kumar, A.; Dwivedi, S.; Pandey, A.C. Quantifying Predictability of Sea Ice around the Indian Antarctic Stations Using Coupled Ocean Sea Ice Model with Shelf Ice. Polar Sci. 2018, 18, 83–93. [Google Scholar] [CrossRef]
- Beron-Vera, F.J.; Olascoaga, M.J.; Goni, G.J. Oceanic Mesoscale Eddies as Revealed by Lagrangian Coherent Structures. Geophys. Res. Lett. 2008, 35, 2008GL033957. [Google Scholar] [CrossRef]
- Xia, Q.; Li, G.; Dong, C. Global Oceanic Mass Transport by Coherent Eddies. J. Phys. Oceanogr. 2022, 52, 1111–1132. [Google Scholar] [CrossRef]
- Bruera, R.; Curbelo, J.; García-Sánchez, G.; Mancho, A.M. Mixing and Geometry in the North Atlantic Meridional Overturning Circulation. Geophys. Res. Lett. 2023, 50, e2022GL102244. [Google Scholar] [CrossRef]
- Allende-Arandía, M.E.; Duran, R.; Sanvicente-Añorve, L.; Appendini, C.M. Lagrangian Characterization of Surface Transport From the Equatorial Atlantic to the Caribbean Sea Using Climatological Lagrangian Coherent Structures and Self-Organizing Maps. J. Geophys. Res. Ocean. 2023, 128, e2023JC019894. [Google Scholar] [CrossRef]
- Rousselet, L.; d’Ovidio, F.; Izard, L.; Penna, A.D.; Petrenko, A.; Barrillon, S.; Nencioli, F.; Doglioli, A. A Software Package for an Adaptive Satellite-Based Sampling for Oceanographic Cruises (SPASSOv2.0): Tracking Fine-Scale Features for Physical and Biogeochemical Studies. J. Atmos. Ocean. Technol. 2025, 42, 979–990. [Google Scholar] [CrossRef]
- Veatch, J.M.; Roarty, H.; Oliver, M.J.; Fredj, E.; Kohut, J.T. Attractive Lagrangian Features in the Mid-Atlantic Bight: Using Lagrangian Coherent Structures to Describe Seasonal and Interannual Changes in Circulation. J. Geophys. Res. Ocean. 2025, 130, e2025JC022447. [Google Scholar] [CrossRef]
- Schott, F.A.; Fischer, J.; Stramma, L. Transports and Pathways of the Upper-Layer Circulation in the Western Tropical Atlantic. J. Phys. Oceanogr. 1998, 28, 1904–1928. [Google Scholar] [CrossRef]
- Schott, F.A.; Brandt, P.; Hamann, M.; Fischer, J.; Stramma, L. On the Boundary Flow off Brazil at 5–10°S and Its Connection to the Interior Tropical Atlantic. Geophys. Res. Lett. 2002, 29, 21-1-21-4. [Google Scholar] [CrossRef]
- Bourles, B.; Molinari, R.L.; Johns, E.; Wilson, W.D.; Leaman, K.D. Upper Layer Currents in the Western Tropical North Atlantic (1989–1991). J. Geophys. Res. 1999, 104, 1361–1375. [Google Scholar] [CrossRef]
- Barnier, B.; Reynaud, T.; Beckmann, A.; Böning, C.; Molines, J.-M.; Barnard, S.; Jia, Y. On the Seasonal Variability and Eddies in the North Brazil Current: Insights from Model Intercomparison Experiments. Prog. Oceanogr. 2001, 48, 195–230. [Google Scholar] [CrossRef]
- Fratantoni, D.M.; Johns, W.E.; Townsend, T.L. Rings of the North Brazil Current: Their Structure and Behavior Inferred from Observations and a Numerical Simulation. J. Geophys. Res. 1995, 100, 10633–10654. [Google Scholar] [CrossRef]
- Fratantoni, D.M.; Glickson, D.A. North Brazil Current Ring Generation and Evolution Observed with SeaWiFS. J. Phys. Oceanogr. 2002, 32, 1058–1074. [Google Scholar] [CrossRef]
- Fratantoni, D.M.; Richardson, P.L. The Evolution and Demise of North Brazil Current Rings. J. Phys. Oceanogr. 2006, 36, 1241–1264. [Google Scholar] [CrossRef]
- Jochum, M.; Malanotte-Rizzoli, P. On the Generation of North Brazil Current Rings. J. Mar. Res. 2003, 61, 147–173. [Google Scholar] [CrossRef]
- Garzoli, S.L.; Ffield, A.; Yao, Q. North Brazil Current Rings and the Variability in the Latitude of Retroflection. In Elsevier Oceanography Series; Elsevier: Amsterdam, The Netherlands, 2003; Volume 68, pp. 357–373. [Google Scholar]
- Fonseca, C.A.; Goni, G.J.; Johns, W.E.; Campos, E.J.D. Investigation of the North Brazil Current Retroflection and North Equatorial Countercurrent Variability. Geophys. Res. Lett. 2004, 31, 2004GL020054. [Google Scholar] [CrossRef]
- Sharma, N.; Anderson, S.P.; Brickley, P.; Nobre, C.; Cadwallader, M.L. Quantifying the Seasonal and Interannual Variability of the Formation and Migration Pattern of North Brazil Current Rings. In Proceedings of the OCEANS 2009, Bremen, Germany, 11–14 May 2009; IEEE: Biloxi, MS, USA, 2009; pp. 1–7. [Google Scholar]
- Aroucha, L.C.; Veleda, D.; Lopes, F.S.; Tyaquiçã, P.; Lefèvre, N.; Araujo, M. Intra- and Inter-Annual Variability of North Brazil Current Rings Using Angular Momentum Eddy Detection and Tracking Algorithm: Observations From 1993 to 2016. JGR Oceans 2020, 125, e2019JC015921. [Google Scholar] [CrossRef]
- Boussidi, B.; Le Goff, C.; Galard, C.; Carton, X.; Speich, S. The Analysis of North Brazil Current Rings from Automatic Identification System Data and Altimetric Currents. Remote Sens. 2024, 16, 2828. [Google Scholar] [CrossRef]
- Davis, R.E. Drifter Observations of Coastal Surface Currents during CODE: The Method and Descriptive View. J. Geophys. Res. 1985, 90, 4741–4755. [Google Scholar] [CrossRef]
- Lumpkin, R.; Pazos, M. Measuring Surface Currents with Surface Velocity Program Drifters: The Instrument, Its Data, and Some Recent Results. In Lagrangian Analysis and Prediction of Coastal and Ocean Dynamics; Griffa, A., Kirwan, A.D., Jr., Mariano, A.J., Özgökmen, T., Rossby, H.T., Eds.; Cambridge University Press: Cambridge, UK, 2007; pp. 39–67. ISBN 978-0-521-87018-4. [Google Scholar]
- Sybrandy, A.L.; Niiler, P.P. The WOCE/TOGA SVP Lagrangian Drifter Construction Manual; SIO reference; University of California: San Diego, CA, USA, 1991. [Google Scholar]
- Lumpkin, R.; Özgökmen, T.; Centurioni, L. Advances in the Application of Surface Drifters. Annu. Rev. Mar. Sci. 2017, 9, 59–81. [Google Scholar] [CrossRef]
- Hansen, D.V.; Poulain, P.-M. Quality Control and Interpolations of WOCE-TOGA Drifter Data. J. Atmos. Ocean. Technol. 1996, 13, 900–909. [Google Scholar] [CrossRef]
- Shadden, S.C.; Lekien, F.; Marsden, J.E. Definition and Properties of Lagrangian Coherent Structures from Finite-Time Lyapunov Exponents in Two-Dimensional Aperiodic Flows. Phys. D Nonlinear Phenom. 2005, 212, 271–304. [Google Scholar] [CrossRef]
- Haller, G. Lagrangian Coherent Structures. Annu. Rev. Fluid Mech. 2015, 47, 137–162. [Google Scholar] [CrossRef]
- Boffetta, G.; Lacorata, G.; Redaelli, G.; Vulpiani, A. Detecting Barriers to Transport: A Review of Different Techniques. Phys. D Nonlinear Phenom. 2001, 159, 58–70. [Google Scholar] [CrossRef]
- Otsu, N. A Threshold Selection Method from Gray-Level Histograms. IEEE Trans. Syst. Man Cybern. 1979, 9, 62–66. [Google Scholar] [CrossRef]
- Gill, A.E. Atmosphere-Ocean Dynamics; Academic Press: Cambridge, MA, USA, 1982; ISBN 978-0-12-283522-3. [Google Scholar]
- Zaron, E.D.; Moum, J.N. A New Look at Richardson Number Mixing Schemes for Equatorial Ocean Modeling. J. Phys. Oceanogr. 2009, 39, 2652–2664. [Google Scholar] [CrossRef]
- Aguedjou, H.M.A.; Dadou, I.; Chaigneau, A.; Morel, Y.; Alory, G. Eddies in the Tropical Atlantic Ocean and Their Seasonal Variability. Geophys. Res. Lett. 2019, 46, 12156–12164. [Google Scholar] [CrossRef]
- Matsuoka, D.; Araki, F.; Inoue, Y.; Sasaki, H. A New Approach to Ocean Eddy Detection, Tracking, and Event Visualization –Application to the Northwest Pacific Ocean. Procedia Comput. Sci. 2016, 80, 1601–1611. [Google Scholar] [CrossRef]
- Bunge, L.; Clarke, A.J. Seasonal Propagation of Sea Level along the Equator in the Atlantic. J. Phys. Oceanogr. 2009, 39, 1069–1074. [Google Scholar] [CrossRef]
- Prestes, Y.O.; Silva, A.C.D.; Jeandel, C. Amazon Water Lenses and the Influence of the North Brazil Current on the Continental Shelf. Cont. Shelf Res. 2018, 160, 36–48. [Google Scholar] [CrossRef]
- Wilson, W.D.; Johns, W.E.; Garzoli, S.L. Velocity Structure of North Brazil Current Rings. Geophys. Res. Lett. 2002, 29, 114-1–114-4. [Google Scholar] [CrossRef]
- Garraffo, Z.D.; Johns, W.E.; Chassignet, P.E.; Goni, G.J. North Brazil Current Rings and Transport of Southern Waters in a High Resolution Numerical Simulation of the North Atlantic. In Elsevier Oceanography Series; Elsevier: Amsterdam, The Netherlands, 2003; Volume 68, pp. 375–409. [Google Scholar]
- Johns, W.E.; Zantopp, R.J.; Gustavo, G.J. Cross-Gyre Transport by North Brazil Current Rings. In Elsevier Oceanography Series; Elsevier: Amsterdam, The Netherlands, 2003; Volume 68, pp. 411–441. [Google Scholar]
- Jochumsen, K.; Rhein, M.; Hüttl-Kabus, S.; Böning, C.W. On the Propagation and Decay of North Brazil Current Rings. J. Geophys. Res. 2010, 115, 2009JC006042. [Google Scholar] [CrossRef]
- Assad, L.P.d.F.; Toste, R.; Böck, C.S.; Nehme, D.M.; Sancho, L.; Soares, A.E.; Landau, L. Ocean Climatology at Brazilian Equatorial Margin: A Numerical Approach. J. Comput. Sci. 2020, 44, 101159. [Google Scholar] [CrossRef]
- Zharkov, V.; Nof, D. Why Does the North Brazil Current Regularly Shed Rings but the Brazil Current Does Not? J. Phys. Oceanogr. 2010, 40, 354–367. [Google Scholar] [CrossRef]
- Biello, J.A.; Majda, A.J. A Multiscale Model for the Modulation and Rectification of the ITCZ. J. Atmos. Sci. 2013, 70, 1053–1070. [Google Scholar] [CrossRef]
- Tomaziello, A.C.N.; Carvalho, L.M.V.; Gandu, A.W. Intraseasonal Variability of the Atlantic Intertropical Convergence Zone during Austral Summer and Winter. Clim. Dyn. 2016, 47, 1717–1733. [Google Scholar] [CrossRef]
- Prestes, Y.O.; Da Silva, A.C.; Marquez, A.L.; Gomes Junior, G.D.; Hernandez, F. Climate Variability and Atlantic Surface Gravity Wave Variability Based on Reanalysis Data. JMSE 2025, 13, 1536. [Google Scholar] [CrossRef]
- Ramotubei, T.S.; Landman, W.A.; Mateyisi, M.J.; Nangombe, S.S.; Beraki, A.F. Response of the Global ITCZ to ENSO and How the ITCZ Determined from Maximum Precipitation Compares with the Surface Tropical Wind Convergence. Environ. Dev. 2025, 55, 101210. [Google Scholar] [CrossRef]
- Dutrieux, P.; Menkes, C.E.; Vialard, J.; Flament, P.; Blanke, B. Lagrangian Study of Tropical Instability Vortices in the Atlantic. J. Phys. Oceanogr. 2008, 38, 400–417. [Google Scholar] [CrossRef]
- Song, Q.; Aiki, H. Equatorial Wave Diagnosis for the Atlantic Niño in 2019 with an Ocean Reanalysis. Ocean Sci. 2023, 19, 1705–1717. [Google Scholar] [CrossRef]
- Metcalf, W.G. Shallow currents along the northeastern coast of South America. J. Mar. Res. 1968, 26, 3. [Google Scholar]
- Gibbs, R.J. Currents on the Shelf of North-Eastern South America. Estuar. Coast. Shelf Sci. 1982, 14, 283–299. [Google Scholar] [CrossRef]
- Molinari, R.L. Observations of Near-surface Currents and Temperature in the Central and Western Tropical Atlantic Ocean. J. Geophys. Res. 1983, 88, 4433–4438. [Google Scholar] [CrossRef]
- Bruce, J.G.; Kerling, J.L.; Beatty, W.H. On the North Brazilian Eddy Field. Prog. Oceanogr. 1985, 14, 57–63. [Google Scholar] [CrossRef]
- Didden, N.; Schott, F. Eddies in the North Brazil Current Retroflection Region Observed by Geosat Altimetry. J. Geophys. Res. 1993, 98, 20121–20131. [Google Scholar] [CrossRef]
- Allshouse, M.R.; Ivey, G.N.; Lowe, R.J.; Jones, N.L.; Beegle-Krause, C.J.; Xu, J.; Peacock, T. Impact of Windage on Ocean Surface Lagrangian Coherent Structures. Environ. Fluid Mech. 2017, 17, 473–483. [Google Scholar] [CrossRef]
- Liu, Y.; Wilson, C.; Green, M.A.; Hughes, C.W. Gulf Stream Transport and Mixing Processes via Coherent Structure Dynamics. JGR Ocean. 2018, 123, 3014–3037. [Google Scholar] [CrossRef]
- Zhan, P.; Guo, D.; Krokos, G.; Dong, J.; Duran, R.; Hoteit, I. Submesoscale Processes in the Upper Red Sea. JGR Ocean. 2022, 127, e2021JC018015. [Google Scholar] [CrossRef]
- Trinadha Rao, V.; Suneel, V.; Gulakaram, V.S.; Sravani, C.L. Extraction of Persistent Lagrangian Coherent Structures for the Pollutant Transport Prediction in the Bay of Bengal. Sci. Rep. 2024, 14, 8761. [Google Scholar] [CrossRef]
- Matuszak, M.; Röhrs, J.; Isachsen, P.E.; Idžanović, M. Uncertainties in the Finite-Time Lyapunov Exponent in an Ocean Ensemble Prediction Model. Ocean Sci. 2025, 21, 401–418. [Google Scholar] [CrossRef]
- Sulman, M.H.M.; Huntley, H.S.; Lipphardt, B.L.; Kirwan, A.D. Leaving Flatland: Diagnostics for Lagrangian Coherent Structures in Three-Dimensional Flows. Phys. D Nonlinear Phenom. 2013, 258, 77–92. [Google Scholar] [CrossRef]
| Deployment Site | ||
| Site ID | Longitude | Latitude |
| DF1 | 44° 51.82′ W | 0° 11.49′ N |
| DF2 | 44° 52.84′ W | 0° 20.40′ N |
| DF3 | 44° 51.99′ W | 0° 32.29′ N |
| Instruments Count | ||
| Total Deployed = 72 | CODE | SVP |
| Used in Analysis = 63 | 30 | 33 |
| Sample interval (h) | 0.5 | 1 |
| Mean lifetime (days) | 54 | 253.4 |
| Minimum lifetime (days) | 15.2 | 16.3 |
| Maximum lifetime (days) | 122.6 | 515.4 |
| Drifters/Parameter | February–April 18 | June–August 18 | September–November 18 | December 18–February 19 |
|---|---|---|---|---|
| CODE mean (ms−1) | −0.32 ± 0.27 | 0.1 ± 0.47 | −0.04 ± 0.35 | −0.2 ± 0.29 |
| CODE mean (ms−1) | 0.19 ± 0.23 | 0.15 ± 0.35 | 0.17 ± 0.3 | 0.1 ± 0.21 |
| SVP mean (ms−1) | −0.21 ± 0.29 | −0.04 ± 0.25 | −0.03 ± 0.27 | −0.12 ± 0.16 |
| SVP mean (ms−1) | 0.23 ± 0.3 | 0.11 ± 0.2 | 0.1 ± 0.23 | 0.07 ± 0.16 |
| CMEMS Analysis/Forecast | ||||
| 1.0 m mean (ms−1) | −0.15 ± 0.25 | −0.17 ± 0.35 | −0.13 ± 0.34 | −0.17 ± 0.27 |
| 15 m mean (ms−1) | −0.1 ± 0.24 | −0.1 ± 0.34 | −0.07 ± 0.34 | −0.12 ± 0.26 |
| 1.0 m mean (ms−1) | 0.04 ± 0.18 | 0.1 ± 0.26 | 0.1 ± 0.24 | 0.04 ± 0.21 |
| 15 m mean (ms−1) | 0.06 ± 0.17 | 0.08 ± 0.24 | 0.08 ± 0.24 | 0.06 ± 0.21 |
| Temperature 1.0 m mean (°C) | 26.71 ± 1.2 | 27.28 ± 0.92 | 28.03 ± 0.71 | 26.98 ± 0.98 |
| Temperature 15 m mean (°C) | 26.68 ± 1.2 | 27.22 ± 0.92 | 27.96 ± 0.72 | 26.94 ± 0.97 |
| Salinity 1.0 m mean (gkg−1) | 35.15 ± 4.1 | 34.88 ± 3.5 | 35.13 ± 2.2 | 35.33 ± 3.2 |
| Salinity 15 m mean (gkg−1) | 35.81 ± 1.4 | 35.53 ± 1.5 | 35.45 ± 1.1 | 35.76 ± 1.2 |
| Sea Surface Height mean (m) | 0.081 ± 0.08 | 0.087 ± 0.09 | 0.097 ± 0.09 | 0.077 ± 0.08 |
| Spearman Correlation Coefficient | ||||
| CODE x Analysis/Forecast (1.0 m) | 0.511 | 0.807 | 0.851 | 0.575 |
| CODE x Analysis/Forecast (1.0 m) | 0.664 | 0.692 | 0.665 | 0.526 |
| SVP x Analysis/Forecast (15 m) | 0.749 | 0.645 | 0.714 | 0.536 |
| SVP x Analysis/Forecast (15 m) | 0.717 | 0.365 | 0.538 | 0.462 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Prestes, Y.O.; Rosário, R.P.; Rollnic, M. Lagrangian Coherent Structures for Mapping Mesoscale Circulation in the Western Equatorial Atlantic. J. Mar. Sci. Eng. 2025, 13, 2310. https://doi.org/10.3390/jmse13122310
Prestes YO, Rosário RP, Rollnic M. Lagrangian Coherent Structures for Mapping Mesoscale Circulation in the Western Equatorial Atlantic. Journal of Marine Science and Engineering. 2025; 13(12):2310. https://doi.org/10.3390/jmse13122310
Chicago/Turabian StylePrestes, Yuri Onça, Renan Peixoto Rosário, and Marcelo Rollnic. 2025. "Lagrangian Coherent Structures for Mapping Mesoscale Circulation in the Western Equatorial Atlantic" Journal of Marine Science and Engineering 13, no. 12: 2310. https://doi.org/10.3390/jmse13122310
APA StylePrestes, Y. O., Rosário, R. P., & Rollnic, M. (2025). Lagrangian Coherent Structures for Mapping Mesoscale Circulation in the Western Equatorial Atlantic. Journal of Marine Science and Engineering, 13(12), 2310. https://doi.org/10.3390/jmse13122310






