Navigation Risk Assessment of Arctic Shipping Routes Based on Bayesian Networks

Abstract

In recent years, the Arctic region, with its abundant oil and gas resources, has become a new focus of global resource development. However, the complex natural environment, especially the effect of sea ice, poses a serious threat and challenge to the navigation safety. Accordingly, this paper focuses on the navigation risks of drilling ships in five sea areas of the Northeast Passage of the Arctic under the influence of environmental factors. A dynamic Bayesian network structure was established using the Interpretative Structural Model–Bayesian network method. Since some risk elements cannot be directly measured, the combined weight method is adopted to fill the sample data. The navigation risk situations of the five sea areas is analyzed by forward causal reasoning. Through reverse diagnostic reasoning, the main risk factors affecting navigation are obtained, and relevant suggestions are given. This has important implications for improving the ability of accident prevention and emergency handling in practical applications. The model was verified through instance verification based on scenario analysis and model verification based on sample data. The average accuracy rate of the obtained model is 83.4%. The results show that the model has certain validity and practicability in the analysis of navigation risks in Arctic shipping routes.

1. Introduction

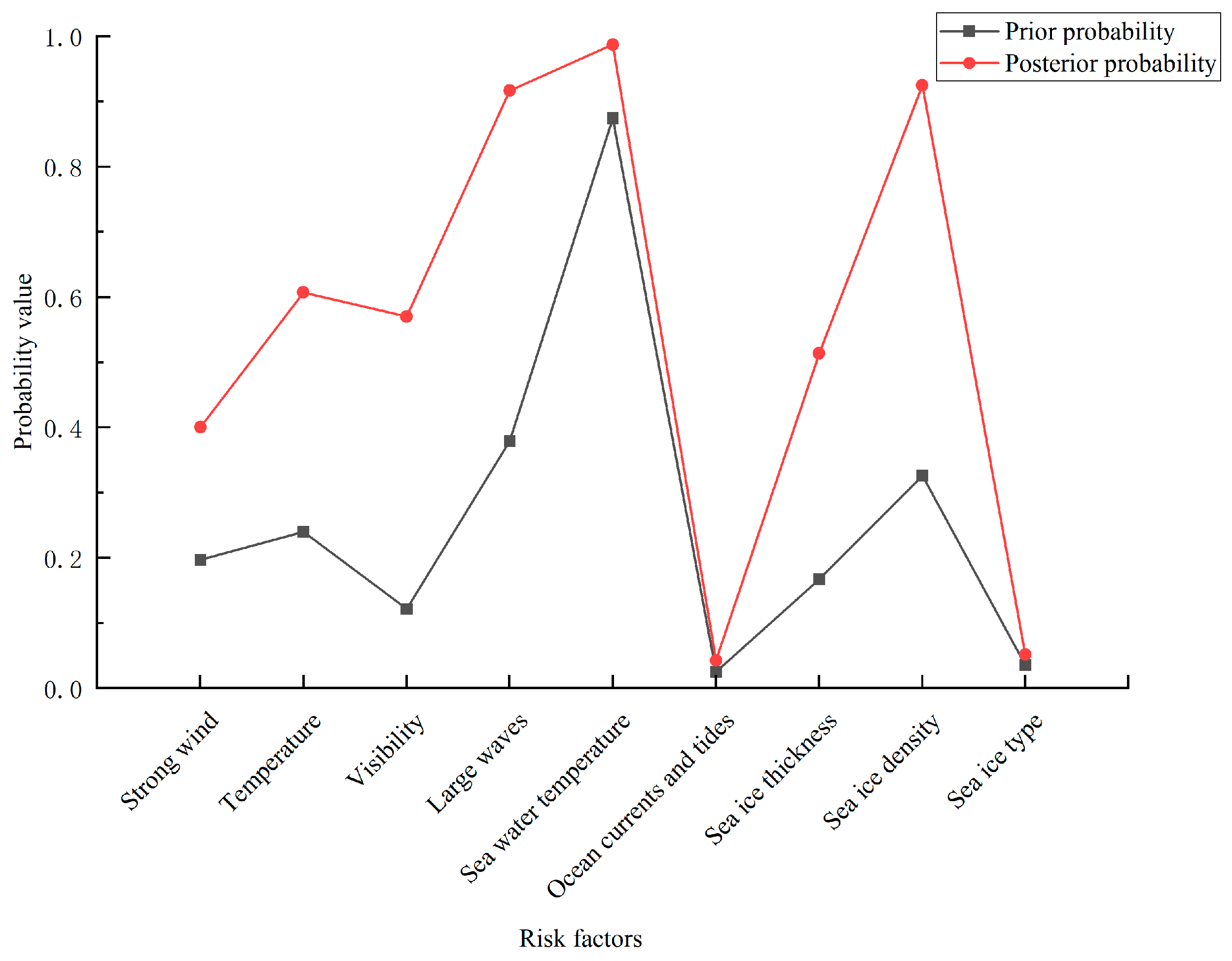
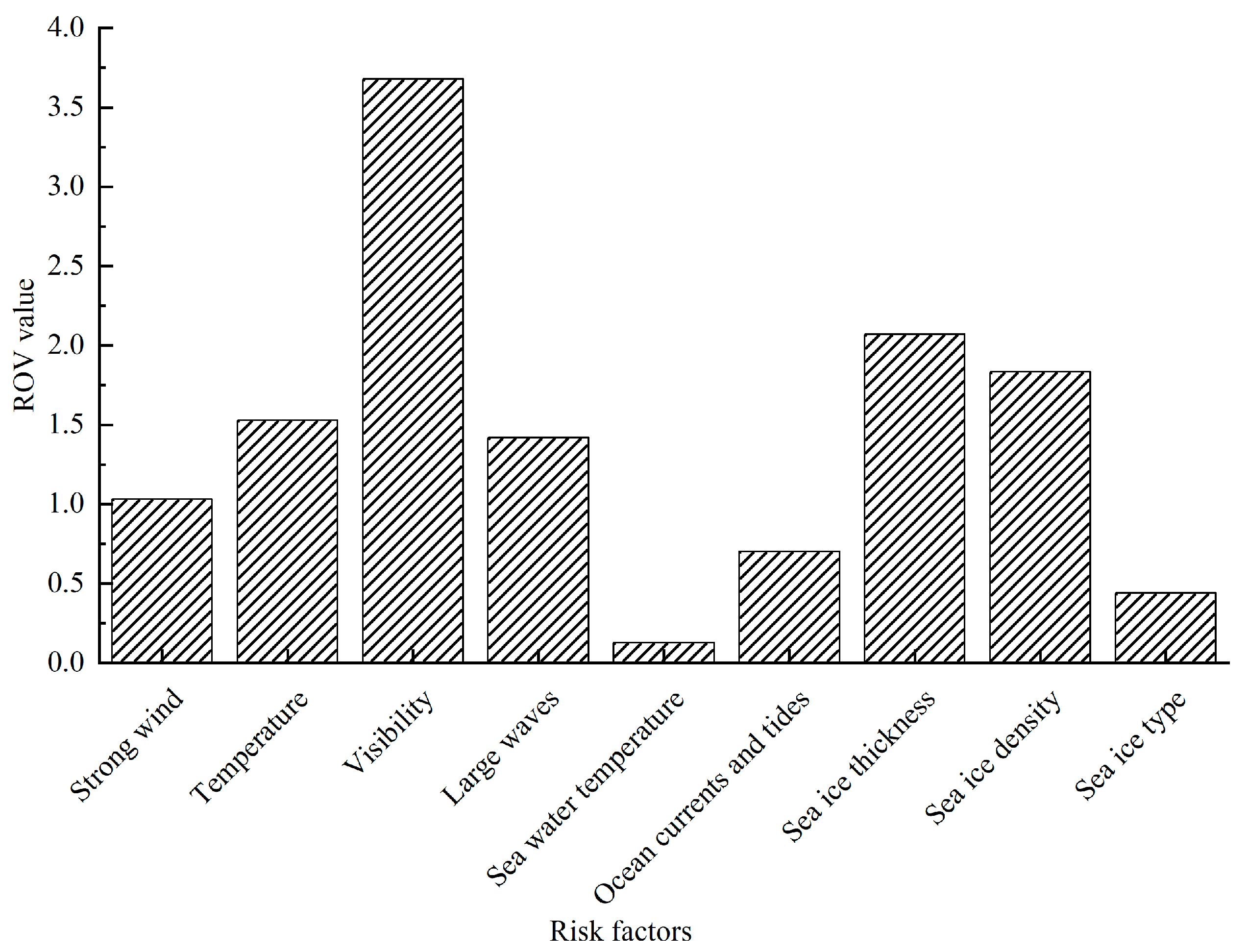
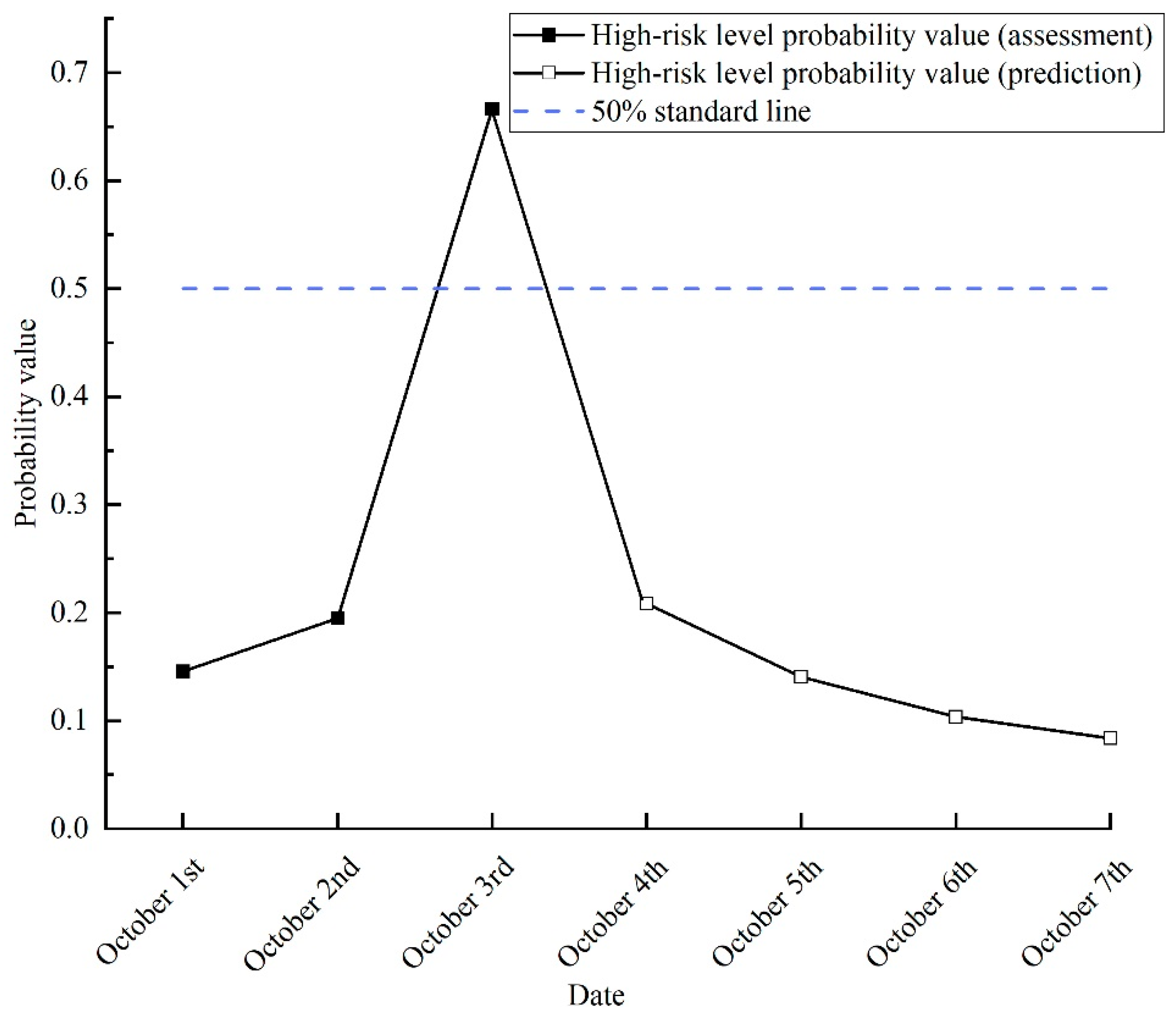
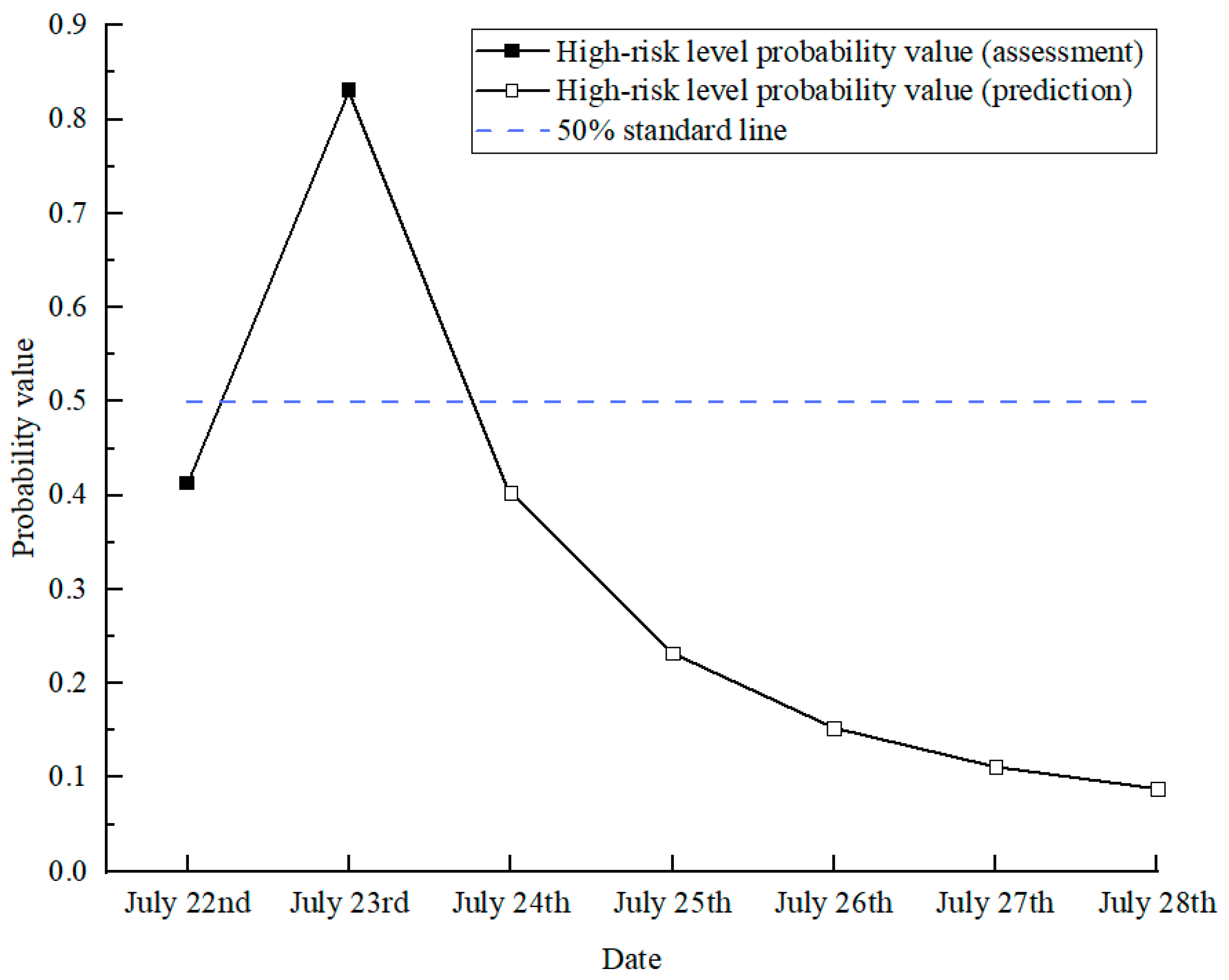
In the navigational environment of the Arctic Passage, potential accidents involving oil and gas drilling vessels not only endanger human lives and result in significant lost workdays, but also severely disrupt operational productivity [1]. Furthermore, the downtime resulting from such incidents leads to substantial operating profit losses and unexpected cost increases [2]. With the increase in Arctic shipping activities, research on ship navigation safety risk assessment technology is becoming increasingly in-depth [3]. Considering the complexity of ship accidents in Arctic waters, in order to effectively prevent the occurrence of accidents, it is necessary to establish an efficient risk analysis and management system to provide timely and accurate early safety warnings and emergency support for ships. Navigation risk in this context is defined as the likelihood of a vessel encountering hazardous situations (such as entrapment in ice or collision with floating ice) driven by dynamic meteorological and hydrological factors. 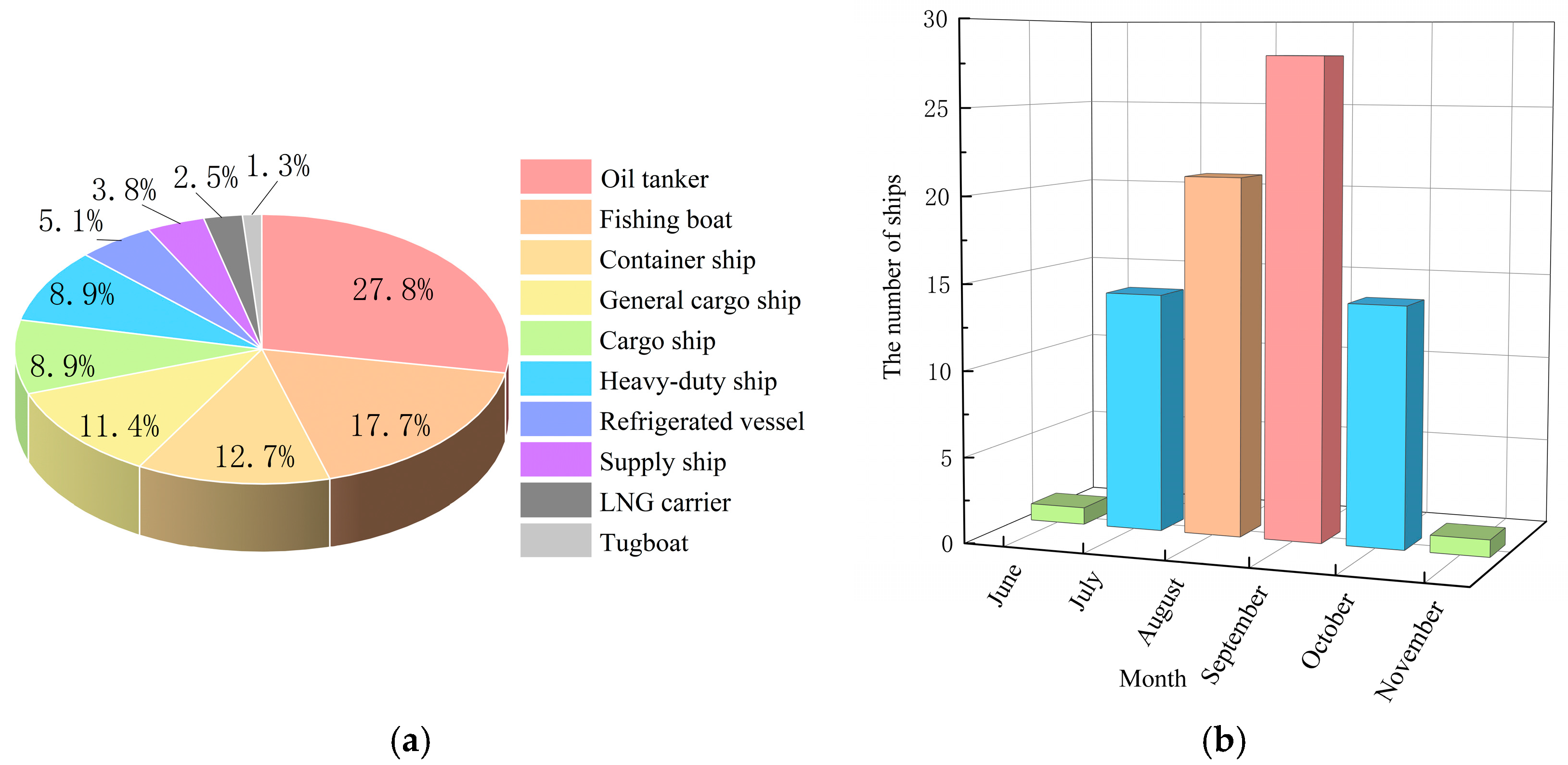Figure 1 shows the navigation situation of ships in the Northeast Passage of the Arctic. Figure 1a tallies the types of ships crossing the Northeast Passage of the Arctic. Oil tankers and fishing boats dominate with proportions of 27.8% and 17.7%, respectively. 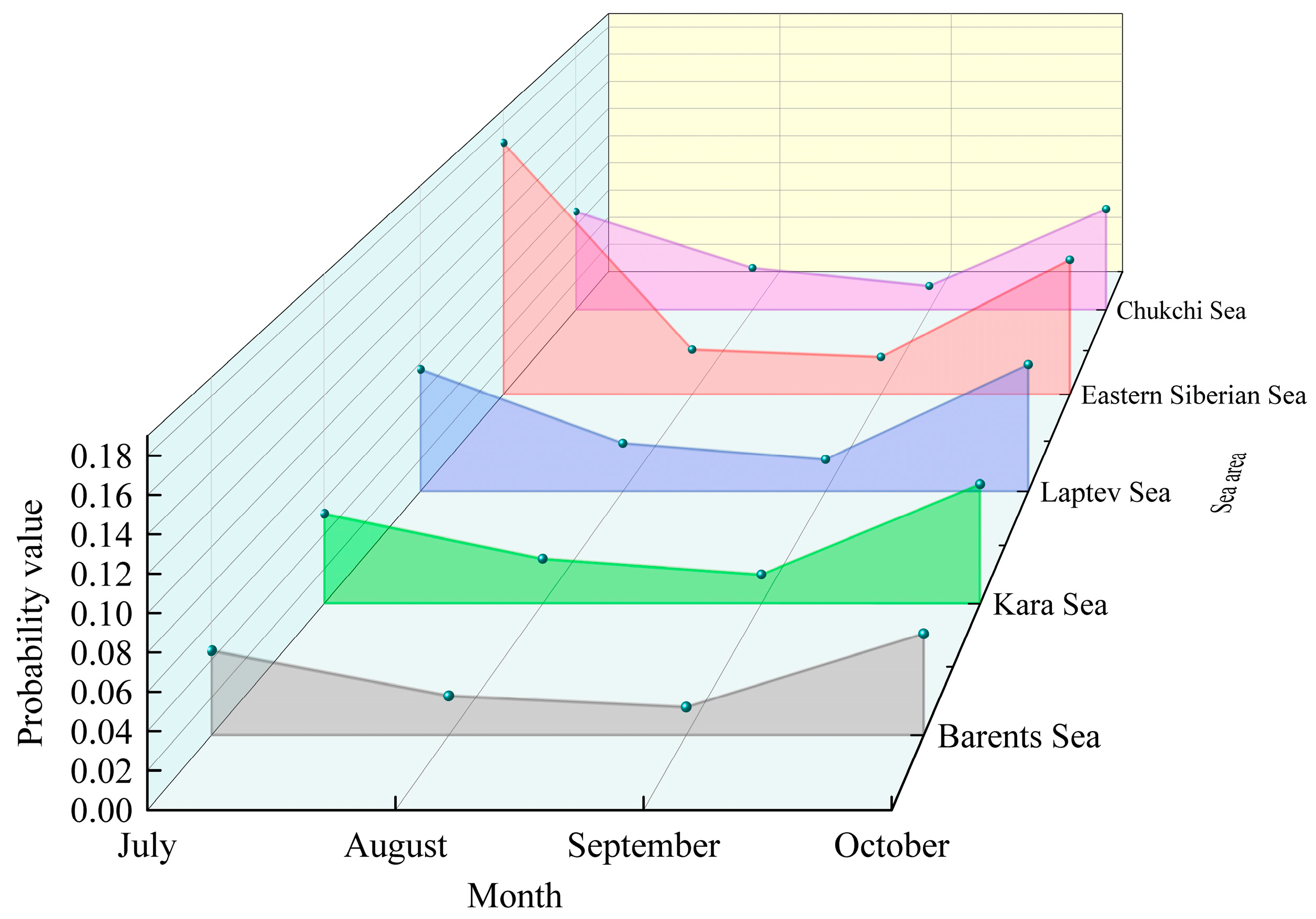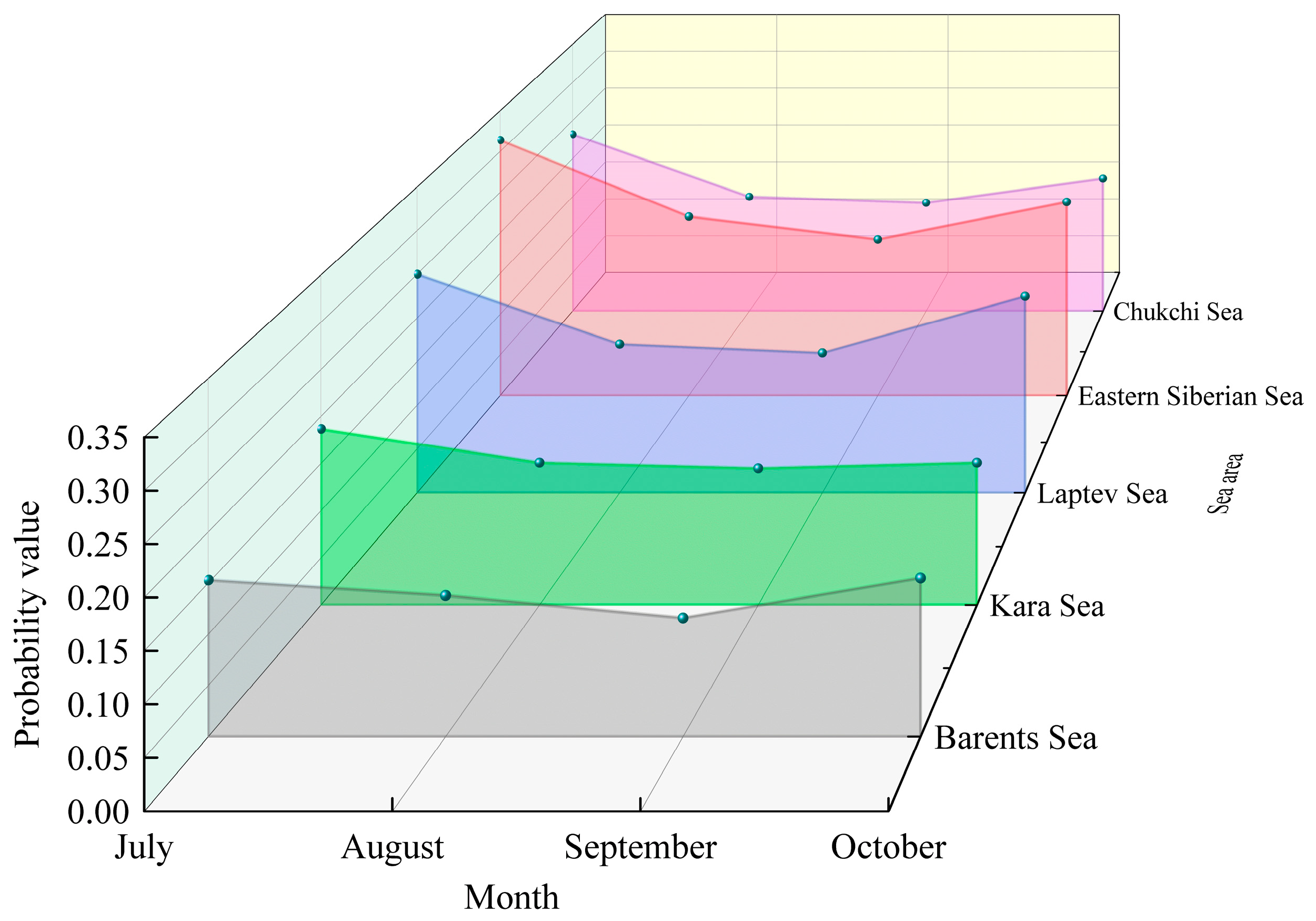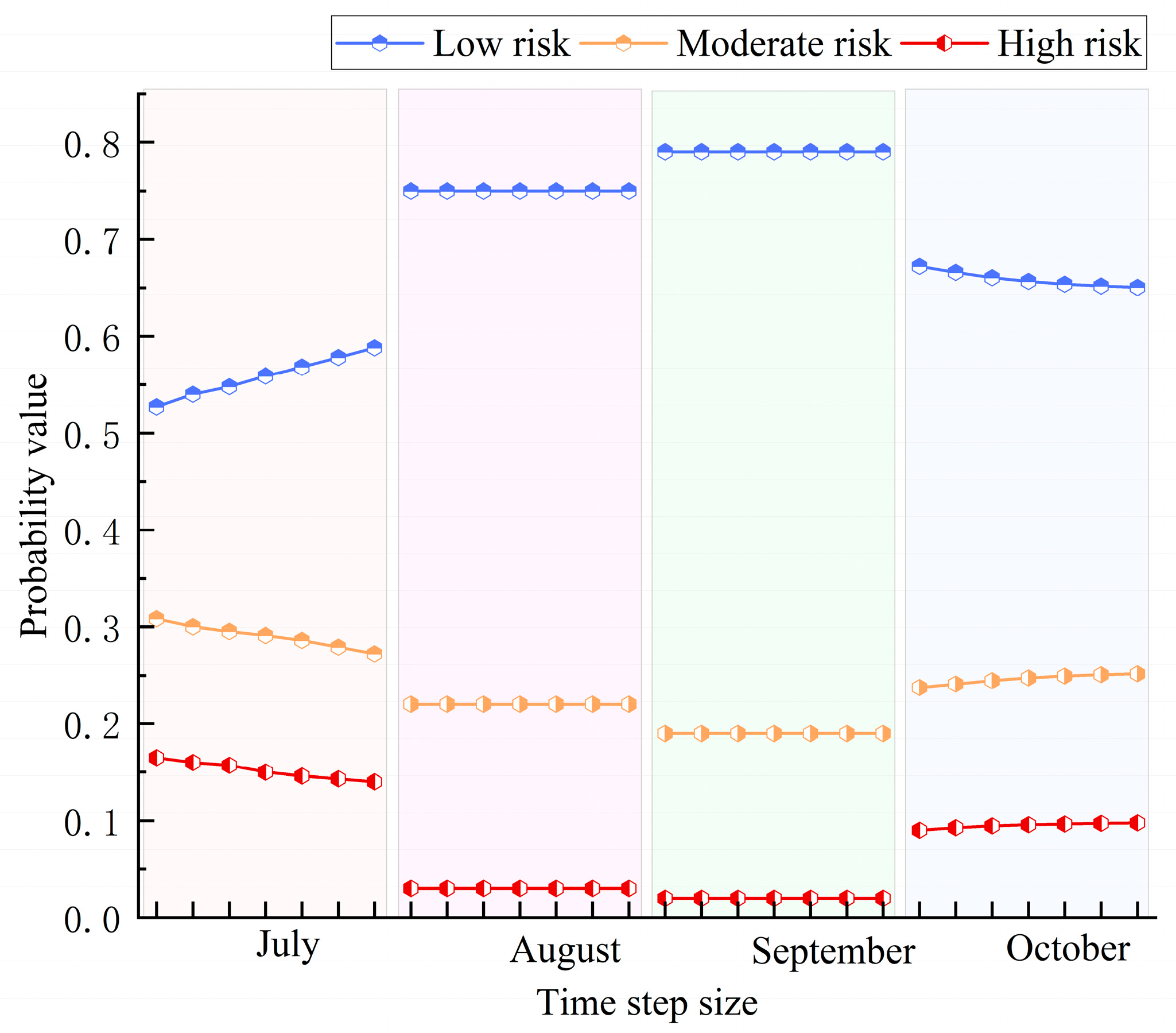Figure 1b statistically analyzes the ship navigation situation from June to November. It is obvious that sea ice gradually melts in summer. Therefore, July to October is the peak period for navigation, especially in September. Thus, this paper mainly studies the navigation risks of five sea areas in the Northeast Passage of the Arctic from July to October.

In the field of polar shipping safety research, researchers have carried out a large number of studies. Zhenfu Li et al. [4] and B Sahin [5] utilized fuzzy analytic hierarchy process and grey fuzzy comprehensive evaluation methods to establish a channel risk identification and quantification model based on the expert knowledge system, achieving a systematic assessment of Arctic navigation risks. Bergstrom et al. [6] established a complete risk assessment system for the Arctic ship navigation system. By decomposing the shipping system into multiple subsystems for individual design, the applicability of the assessment model was effectively enhanced. Shanshan Fu et al. [7] constructed a causal probability model based on the Bayesian belief network. This model took the meteorological and hydrological factors around the channel as input variables and achieved the assessment of the ice distress risk of ships in the Arctic sea area by establishing a causal relationship network. Bushra Khan et al. [8] proposed a ship ice collision risk assessment system based on object-oriented Bayesian networks in the field of polar shipping safety, achieving dynamic prediction of risk probabilities. Moreover, they further simplified complex accident scenarios through a hierarchical decomposition strategy, thereby supporting the dynamic adjustment of navigation decisions. Al-Amin Baksh et al. [9] analyzed the possibility of accidents such as ship collisions, sinks, and stranding using static Bayesian networks and verified it through case studies of oil tanker navigation. They found that the probability of accidents in the East Siberian Sea was the highest, and through sensitivity analysis, they found that sea ice was the key factor affecting the occurrence of accidents. Heng Qian et al. [10] conducted a dynamic assessment of the natural environmental risk factors at key nodes of the Northwest Passage of the Arctic using dynamic Bayesian networks. By constructing a risk assessment index system, they identified key navigation nodes and verified the validity of the model based on evidence-based reasoning. This study proves that the dynamic Bayesian network model can effectively handle information uncertainty and provides a certain scientific basis for the research in this paper at the same time. Chi Zhang et al. [11] proposed a comprehensive risk assessment model based on static Bayesian networks, obtaining the overall risk of ship navigation. Meanwhile, they estimated the probability of accidents and the severity of possible consequences of ship ice trapping and ship ice collision. The validity of the model was verified through case studies, ultimately providing safe speed suggestions for Arctic navigation. Weiliang Qiao et al. [12] proposed a risk assessment model based on fuzzy Bayesian networks for the security issues of the Northern Sea Route. Among them, emergency response capacity, ice-breaking capacity and rescue, and anti-pollution facilities were the critical factors that contribute to the resilience, and the significant influence of these factors was further verified through sensitivity analysis. Sheng Xu et al. [13] established a Bayesian network model based on expert opinions to predict the ice-trapped probability of the first assisted vessel in the escort of icebreaker vessels in the Arctic shipping route and verified the validity of the model through actual cases. It was found that ice density, distance between ships and navigation experience are the key factors causing ice entrapment. Shanshan Fu et al. [14] proposed a quantitative risk assessment model based on object-oriented Bayesian network, selecting four typical accident cases of ship collision, grounding, ice entrapment, and ship–ice collision. The identification of risk factors, risk analysis, and assessment of navigation in the Arctic ice area were systematically analyzed. Based on Arctic wind and ice data in the past decade, Xiaoting Yu et al. [15] constructed dual indicators of “ice-free/light ice days” and “strong wind disasters”, revealing the risk distribution pattern of the northeast shipping route being higher in the west and lower in the east, and the northwest shipping route being higher on both sides and lower in the middle. The results show that July to October is the best navigation period. The Kara Sea and Barents Sea of the Northeast Passage and the Davis Strait of the Northwest Passage are low-risk areas. Q Wang et al. [16] focused on the safety risks faced by drilling ships and related equipment in the extremely remote marine environment of the polar regions. Through an accident data-driven sample library and sensitivity analysis, they provided corresponding decision-making suggestions, confirming that this model can effectively predict and identify potential dangers and ensure the continuous and stable development of polar economic activities. Jiacai Pan et al. [17] systematically reviewed the research progress and deficiencies in the field of navigation safety in the Northwest Passage of the Arctic in recent years and proposed that future research should combine real-time and high-dimensional ice conditions, meteorological and hydrological data to construct more accurate models of navigability, navigation risk and route planning to support scientific decision-making on navigation safety in the Northwest Passage.

Most of the above-mentioned studies adopt traditional methods (such as analytic hierarchy process, fuzzy comprehensive evaluation, etc.) to assess the navigation risks of the Northeast Passage of the Arctic. 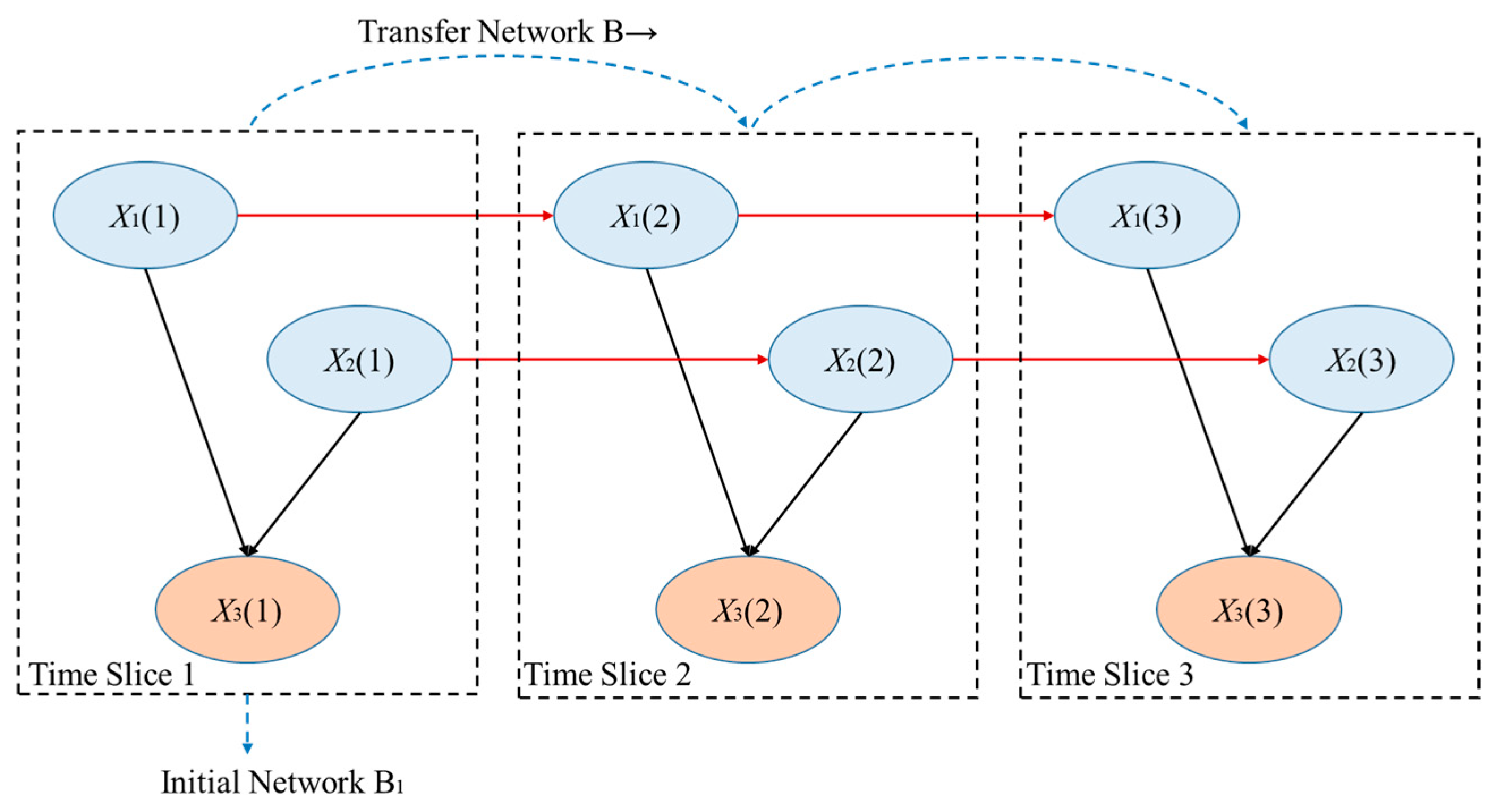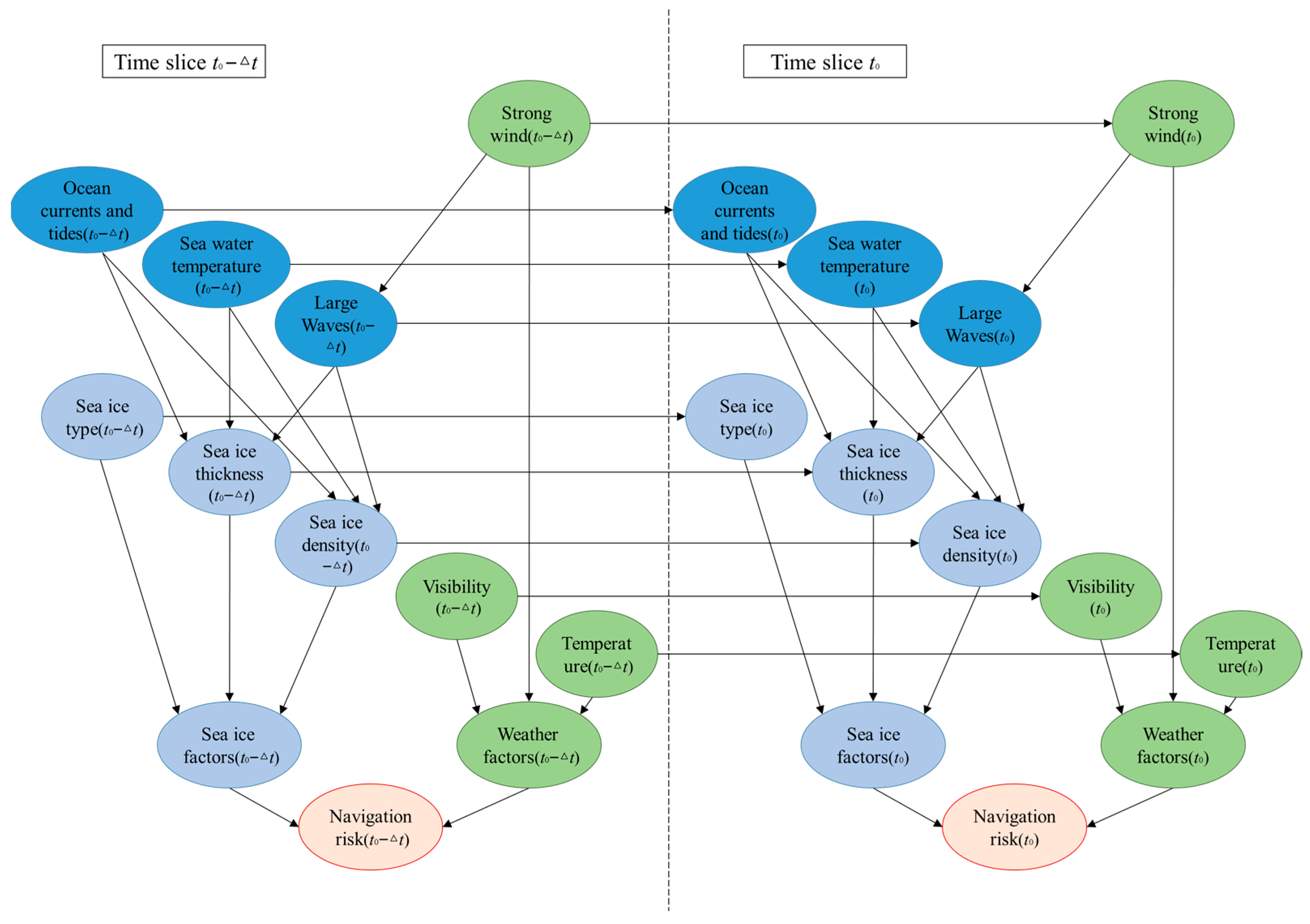Although key risk factors can be identified, they fail to fully consider that ship navigation is a continuous process and its navigation risks will show obvious dynamic evolution characteristics with environmental changes [18]. The dynamic Bayesian network has strong advantages in dealing with the time-varying laws of risk factors and the related reasoning problems of complex structures. Therefore, based on the natural environment risk factors, this paper selects the dynamic Bayesian network to dynamically evaluate and predict the navigation risks of five important sea areas in the Northeast Passage of the Arctic. Thus, it provides more scientific theoretical support for the dynamic risk assessment, short-term emergency decision-making, and long-term planning of the Arctic shipping routes.

The structure of this paper is arranged as follows:

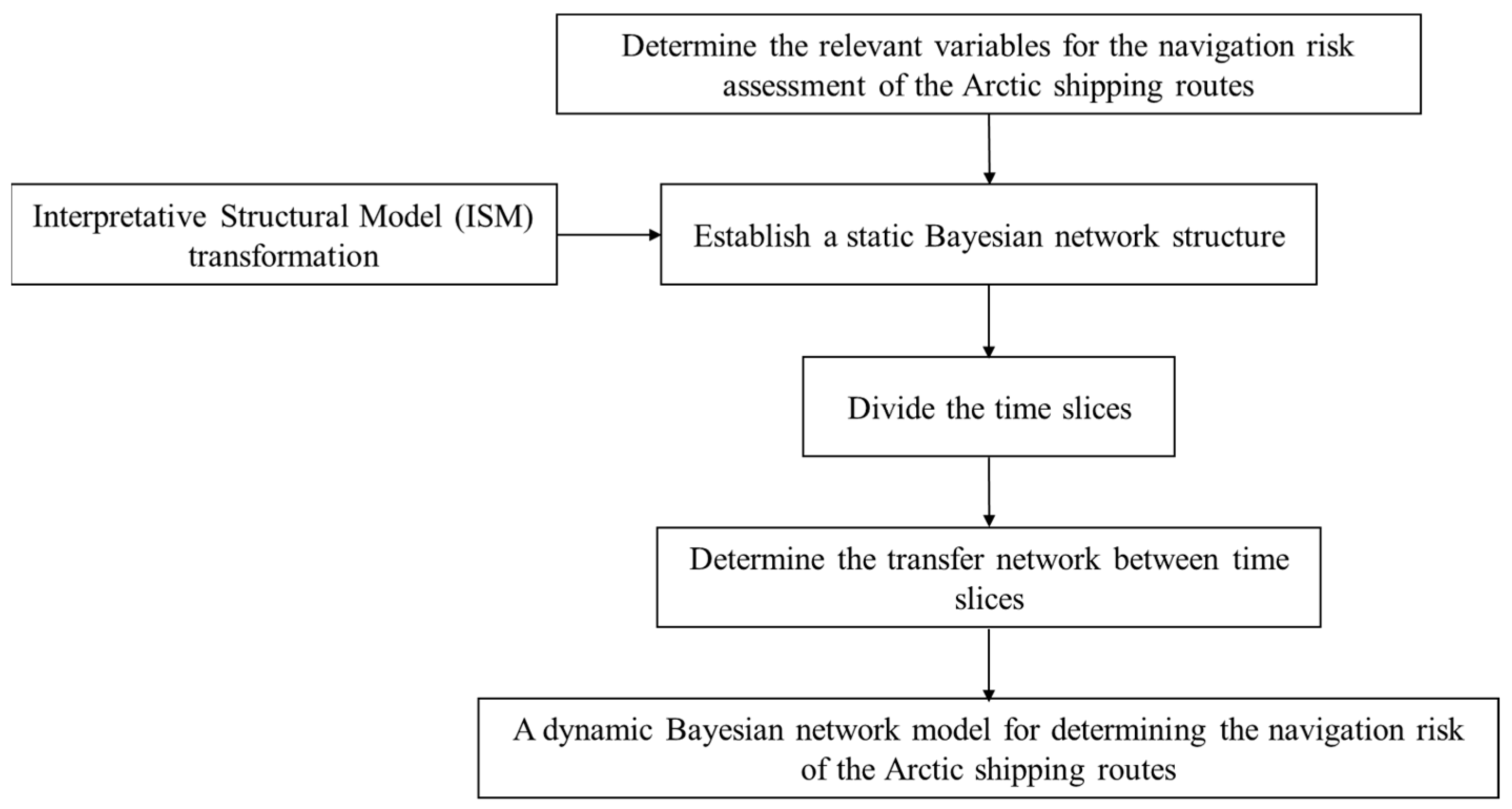
The first part introduces the relevant research methods, mainly including the Interpretative Structural Model and the dynamic Bayesian network. The second part introduces the main risk factors affecting the navigation of the Northeast Passage of the Arctic, mainly including meteorological factors, sea conditions, and ice conditions. The third part introduces the construction of the risk model, mainly including the establishment of the dynamic Bayesian network structure, the discretization processing of risk nodes, data preprocessing, and the calculation of the conditional overview table. The fourth part introduces risk analysis based on dynamic Bayesian networks, mainly including model-based bidirectional reasoning, model validation, and risk prediction applications. The fifth part introduces the conclusion and future work.

2. Basic Principle

2.1. Interpretative Structural Modeling Method

The Interpretative Structural Model (ISM) was proposed by American professor J. Warfield in 1973 [19]. It is an analytical tool that transforms vague subjective cognition into clear structured expression. The core idea is to decompose the complex system into multiple subsystems. With the help of experts’ experience and knowledge, reachable sequences are generated through multiple topological operations assisted by computers. Eventually, a multi-level hierarchical structural model is constructed, and the analysis results are presented in the form of a hierarchical directed graph.

The main components of the ISM model are divided into three parts: directed graph, adjacency matrix, and reachability matrix. The first step in model construction is to draw a directed graph based on the interaction relationships among system elements, where the causal relationships between elements are represented by directed edges with arrows. For example, when element S1 has an effect on S2, it is denoted as S1→S2. Subsequently, the directed graph is transformed into the mathematical expression form of the adjacency matrix. This matrix uses binary variables (0 or 1) to precisely describe the correlation between elements. When the element Si has an influence on Sj, the value of the matrix element Sij is 1; otherwise, it is 0. The transition matrix (A + I) is obtained by performing matrix addition operations on the adjacency matrix A and the identity matrix I. Then, the Boolean operation of the transition matrix is carried out using the principle of Boolean algebra until the convergence condition of (A + I) i = (A + I) i + 1 = M, where i ≤ n − 1 is satisfied. Finally, the reachable matrix M of the system is obtained. Further analysis based on the reachability matrix can reveal the hierarchical structure and internal action mechanism among system elements, providing a quantitative basis for the structural analysis of complex systems.

2.2. Dynamic Bayesian Network

A dynamic Bayesian network (DBN) can effectively represent the temporal evolution characteristics of some or all node states by introducing the time dimension [20]. This type of network is mainly applied to engineering problems that require consideration of time-varying utility, including long-term prediction scenarios such as dynamic risk assessment and system life prediction. The specific introduction is as follows.

DBN is based on BN and introduces time-dimension variables and state transition mechanisms to characterize the evolution law of the system over time [21]. A DBN is mathematically represented by a tuplet (B₁, B_→), where B₁ represents the initial network, which completely characterizes each random variable Ω₁ of the system within the initial time as {X₁(1), X₂(1) … The prior probability distribution Pr{Ω₁} of Xn(1)}; B_→ represents the transition network, which describes the transition probability Pr{Ω_t|Ω_t−1} of the system state variables between adjacent time slices. Its expression is as follows:

$$Pr\left\{{\mathsf{\Omega }}_t|{\mathsf{\Omega }}_{t-1}\right\}={\displaystyle \prod _{i=1}^{n}Pr\left\{X_i\left(t\right)|Pa\left(X_i\left(t\right)\right)\right\}}$$

(1)

In the formula, n represents the total number of nodes in a single time slice; X_i(t) represents the i-th node within the t-th time slice. The composition of the parent node Pa(X_i(t)) is mainly in two cases: when t = 1, Pa(X_i(1)) ⊆ Ω₁; When t > 1, P_a(X_i(t)) ⊆ Ω_t−1∪Ω_t. In DBN, the directed edges within time slices represent causal relationships among variables, while the directed edges across time slices represent time dependencies. By extending the B_→ delay interval axis to T segments, the expression of DBN can be obtained:

$$Pr\left\{{\mathsf{\Omega }}_{1:t}\right\}=Pr\left\{{\mathsf{\Omega }}_1\right\}\cdot {\displaystyle \prod _{t=2}^{T}Pr\left\{{\mathsf{\Omega }}_t|{\mathsf{\Omega }}_{t-1}\right\}}={\displaystyle \prod _{t=1}^T{\displaystyle \prod _{i=1}^{n}Pr\left\{X_i\left(t\right)|Pa\left(X_i\left(t\right)\right)\right\}}}$$

(2)

It should be noted that the “dynamic” in DBN does not refer to the changes in the structure and parameters of DBN over time, but specifically refers to the temporal evolution behavior of its modeling object: the dynamic system. Figure 2 shows a DBN containing three time slices. The red arrows between different time slices represent transition probabilities, and the black arrows within the same time slice represent conditional probabilities.

3. Analysis of Influencing Factors of the Navigation Environment in the Northeast Passage of the Arctic

Screening and analyzing the factors that affect the navigation safety of ships in the Northeast Passage of the Arctic is the prerequisite and foundation for establishing a Bayesian network model for the research of navigation risks in the Arctic. Based on a thorough review of the relevant data on the environmental risks of vessel navigation in Arctic waters, combined with the unique environmental characteristics of the Northeast Passage of the Arctic, and through expert consultation, after summarization and screening, three major types of key factors affecting navigation safety were finally determined. The experts’ information is shown in

Table 1. Expert information.

Expert	Professionalism	Work Experience (Years)	Education Level	Age
E1	Professor	40	Doctor	67
E2	Professor	18	Doctor	47
E3	Associate Professor	12	Doctor	41
E4	Assistant Professor	9	Doctor	36

.

3.1. Meteorological Factors

3.1.1. Temperature

Temperature has a significant impact on the navigation safety of ships, mainly reflected in three aspects. Firstly, low-temperature environments are prone to causing seawater to freeze, which not only affects the navigation of ships but may also lead to the icing of deck equipment, thereby resulting in the insufficient stability of ships and damage to mechanical equipment. Secondly, the hull is prone to ice accumulation in low-temperature environments. A large amount of ice piled up in pipes and superstructures will further affect the stability of the ship. Finally, low-temperature environments also have adverse effects on the living and working conditions of crew members, which may lead to physical and psychological changes, reduce the ability to control ships, and thus affect navigation safety.

3.1.2. Visibility

Visibility, as a key parameter of the ship’s navigation environment, has a significant impact on safe navigation. When visibility is low, the driver’s field of vision shortens, which can easily lead to lookout failure and decision-making mistakes, thereby increasing the risk of maritime safety accidents.

3.1.3. Wind

Wind is also an important factor affecting the navigation safety of ships, especially in the Northeast Passage of the Arctic. Changes in wind speed and direction directly affect the maneuverability of ships. Strong winds can easily cause ships to deviate, run aground, or lose anchor, especially for large ships, where the area affected by the wind is larger and the impact is more significant. Therefore, wind is an important factor affecting the navigation safety of the Northeast Passage of the Arctic.

3.2. Sea Conditions

3.2.1. Ocean Currents and Tides

Ocean currents have a significant impact on navigation safety. As an important marine dynamic factor, their force will directly affect the performance of navigation operations. In areas with restricted waterways, the relative movement of ocean currents and ships can complicate the hydrodynamic environment. When navigating against the current, the increase in relative velocity will intensify the shore wall effect of ships and simultaneously increase the navigable risks of ships. In addition, when the counter-current flow velocity is relatively large, small-tonnage vessels are more significantly affected by ocean currents. When the downstream flow velocity is relatively high, the acceleration of water flow may lead to a decrease in maneuverability, thereby increasing the navigation risk. In addition, there is often a large amount of floating ice in the Arctic waters. Ocean currents can drive the movement of floating ice, thereby affecting navigation safety.

3.2.2. Seawater Temperature

Low-temperature seawater is one of the main factors for the formation of sea ice. The existence of sea ice not only affects the navigation speed of ships, but may also lead to accidents such as collisions or stranding of ships. When the seawater temperature is too low, it may cause ice to form on the upper layer and deck of the hull. Ice formation on the hull will affect the stability of the ship. Meanwhile, a large amount of ice accumulation not only makes the operation of ships more difficult, but may also damage their mechanical equipment and increase their maintenance costs and accident risks.

3.2.3. Large Waves

Large waves have a strong seasonality. Under large-wave weather conditions, the stability and maneuverability of ships will be severely affected. Huge waves can cause ships to sway violently, increase the angle of their tilt, and thereby affect the direction and speed of their navigation.

3.3. Ice Condition

Based on the differences in the morphological characteristics of sea ice and its development process, sea ice can be classified as: resilient ice, ice skin, Nero ice, lotus leaf ice, gray ice, and grayish-white ice. Taking into account the characteristics and development stages of Arctic sea ice comprehensively, it can be classified into new ice, initial ice, one-year ice, and multi-year ice. Different types of sea ice have different features and have different impacts on ship navigation, as shown in

Table 2. Characteristics of sea ice at different stages and its influence on navigation.

Sea Ice Type	Characteristics	Navigation Influence
New ice	Its initial development stages mainly include mud ice, ice chips, ice needles, and oily ice. In the later stage, it develops into Nero ice, with a thickness ranging from 10 to 30 cm.	It has basically no impact on the navigation of ships. It is necessary to pay attention to avoiding the blockage of seawater pipes.
Initial ice	It can be further classified into gray ice and grayish-white ice, with a thickness ranging from 10 to 30 cm.	Ice-class ships have basically no impact.
One year of ice	Its occurrence and disappearance both occur within one year, and its thickness is generally between 30 and 200 cm.	Has a certain impact.
Years of ice	After a melting season, it remains and can be further classified into 2-year ice, 3-year ice, and so on, with no thickness limit.	Sailing is difficult and icebreakers need to be used when necessary.

[22].

In addition, the navigation safety of ships in the Arctic is closely related to the density of sea ice. Different levels of sea ice density have different degrees of impact on navigation safety [23].

4. Construction of a Navigation Risk Model for Arctic Shipping Routes

4.1. Establishment of Dynamic Bayesian Network Structure

The objects and purposes of the assessment are determined by taking the navigation risk assessment of the Arctic shipping routes as the lead, and then the relevant influencing factors are analyzed. The risk elements are abstracted and their correlations are mapped into a Bayesian network structure. The construction of the dynamic Bayesian network model structure in this study mainly includes the following steps, as shown in Figure 3.

Based on the analysis in the previous text and the statistics of predecessors on the main risk factors affecting Arctic vessel navigation, among the sea ice factors, the ones with a relatively high influence are sea ice density, sea ice thickness, and sea ice type; the weather factors mainly include strong wind, visibility, and temperature; and the hydrological factors mainly include ocean currents and tides, seawater temperature, and large waves. In order to simplify the model structure and avoid too many nodes pointing to the target node, two intermediate variables, “weather factor” and “sea ice factor”, are introduced. To facilitate subsequent operations, the screened influencing factors are re-encoded and uniformly represented by Si, as shown in

Table 3. List of factors influencing the risk assessment model of Arctic shipping routes.

Coding	Risk Factors
S1	Sea ice thickness
S2	Sea ice density
S3	Sea ice type
S4	Strong wind
S5	Temperature
S6	Visibility
S7	Large Waves
S8	Seawater temperature
S9	Ocean currents and tides
S10	Sea ice factors
S11	Weather factors
S12	Navigation risk

. This study adopted expert interviews to conduct an in-depth analysis and evaluation of the relationship among the navigable risk factors of the Arctic shipping routes. According to the steps in Section 2.1, a systematic analysis is conducted on the logical relationships among the key influencing factors of navigation risks in the Arctic shipping routes. Based on this, the ISM of the Arctic shipping route navigation risk assessment model obtained is shown in Figure 4. All of the Si are listed in Table 3.

After determining the initial static structure of the Bayesian network, it is necessary to determine the dynamic nodes. Each dynamic node has an arc pointing to itself, indicating that the risk index of this node on a certain time slice will have an impact on the next time slice, and this impact conforms to the Markov process. Considering that the Arctic environment is rather complex, in order to better reflect the temporal variations and mutual influences among the node factors, the intermediate nodes “weather factors” and “sea ice factors” as well as the target node are set as static nodes, and all other nodes are set as dynamic nodes. According to the navigation characteristics, in this study, the time step of the dynamic Bayesian network was set to 7. Based on logical analysis, the navigation risk assessment model of the Arctic shipping route obtained is shown in Figure 5.

4.2. Discretization of Risk Factors

Based on the 12 meteorological, hydrological, and sea ice risk factors identified in the previous text, as well as the analysis of each risk factor node in the previous text, and in accordance with expert experience and the relevant literature [7,11], the discretized division status of each node is shown in

Table 4. Discrete state division of each risk factors.

Risk Factors	Risk Level
	State 1	State 2	State 3
Navigation risk	Low	Medium	High
Sea ice factors	Low	Medium	High
Weather factors	Low	Medium	High
Sea ice thickness (m)	<0.4	0.4–0.8	>0.8
Sea ice density (%/100)	<0.5	0.5–0.7	>0.7
Sea ice type (year)	New ice, Initial ice	One year of ice	Years of ice
Strong wind (m/s)	<5.5	5.5–7.9	>7.9
Temperature (°C)	>0	−5–0	<−5
Visibility (n mile)	>5	3–5	<3
Large Waves (m)	<0.5	0.5–1.25	>1.25
Seawater temperature (°C)	>2	0–2	<0
Ocean currents and tides (Kn)	<0.5	0.5–1	>1

. Among them, each node is divided into three risk-level states, namely “low risk”, “medium risk”, and “high risk”, denoted as State 1, State 2, and State 3, respectively.

For the discretization of the intermediate nodes “weather factors”, “sea ice factors”, and the target node “navigation risks”, the traditional discretization method, namely equal-width binning, is adopted. First, the data is normalized according to Formula (3), and then discretized according to the partitioning method in

Table 5. Index dispersion and grade division.

Risk Changes	Distribution Range	Discretized Risk Value
Low risk	[0, 0.333)	State 1
Moderate risk	[0.333, 0.667)	State 2
High risk	[0.667, 1]	State 3

.

$$d={\displaystyle \frac{x-x_{\min }}{x_{\max }-x_{\min }}}$$

(3)

In the formula, x is the original value of the risk factor, and x_min and x_max are the minimum and maximum values, respectively.

4.3. Data Preparation

The data sources adopted in this study mainly include two parts: One part is the objective environmental data obtained through remote-sensing monitoring such as satellites, such as the measured data of atmospheric environmental elements and marine hydrological parameters; Another part cannot be obtained through direct observation, such as the data of the intermediate nodes “weather factors”, “sea ice factors”, and the target node “navigation risks” in this study. Such nodes need to be obtained through further calculation and filling based on the existing data.

4.3.1. Objective Data

For environmental data, the daily average values of five sea areas, namely the Chukchi Sea, the East Siberian Sea, the Laptev Sea, the Kara Sea, and the Barents Sea, were extracted successively over a period of 24 years from 2000 to 2023 [10]. The data of the six key marine environmental parameter nodes involved in this study (including sea ice thickness, sea ice density, sea ice type, large waves, seawater temperature, ocean currents, and tides) are all derived from the dataset released by the European Centre for Medium-Range Weather Forecasts. The data of the three nodes, namely temperature, strong wind speed, and visibility, all come from the dataset published by the National Environmental Information Center (NCEI) under the National Oceanic and Atmospheric Administration (NOAA) of the United States.

4.3.2. Subjective Data

In this study, by integrating the order relation analysis method (G1 method) and the entropy weight method and using the combined weight method, the final weight was obtained. Based on the relevant experience of predecessors, the subjective and objective weights adopted in this study are 0.4 and 0.6, respectively [10]. Meanwhile, the data of the intermediate node and the target node are obtained through weighted fusion calculation based on the data of their parent node. Taking the “weather factors” of the East Siberian Sea as an example, the results of its subjective and objective and combined weights are shown in

Table 6. Index dispersion and grade division.

Indicator	G1 Method	Entropy Weight Method	Combined Weight Result
Visibility	35.5%	43.5%	40.3%
Strong wind	39.1%	21.8%	28.7%
Temperature	25.4%	34.7%	31.0%

.

The calculation results show that the weights of “weather factors” in the East Siberian Sea area are visibility 40.3%, strong wind 28.7%, and temperature 31.0%, respectively. It can be seen from this that visibility has the most significant impact on “weather factors”, and further affects the safe navigation of ships in the Arctic quite obviously. After comparative analysis, the final weight distribution result has a good consistency with the actual situation of the current sea area.

In the process of constructing the risk assessment model, indicator integration is one of the more important links. In this study, the weighted combination method was adopted to fuse and calculate the data of each index after standardized preprocessing and their corresponding weight coefficients. The specific expression is as follows.

$$R={\displaystyle \sum _{i=1}^n{w}_i{x}_i}$$

(4)

In the formula, R represents the comprehensive risk assessment value, w_i represents the weight coefficient of the i-th assessment index, x_i is the standardized value of the corresponding index, and n indicates the index number.

After filling the dataset by the above method, a complete dataset can be obtained. The training sample set is shown in

Table 7. Training sample set (using the East Siberian Sea “weather factor” data for July as an example).

Indicator	Days
	1	2	3	4	5	6	…	…	672
Weather factors	2	2	2	1	2	3	…	…	1
Visibility	2	2	3	1	3	3	…	…	1
Strong wind	3	2	1	1	2	3	…	…	1
Temperature	1	2	1	1	1	3	…	…	1

.

After data processing is completed, discretization is carried out according to the equal interval division method in Table 4. The next step is to learn the parameters of the Bayesian network model. Analysis was performed using GeNIe Academic 4.1. Due to the incomplete data of some sea areas, this study adopts the Expectation-Maximization Algorithm for parameter learning. Taking the “strong wind” node as an example, its transfer probability is shown in

Table 8. Transfer probability distribution table of node “strong wind” (taking the East Siberian Sea in July as an example).

P[R(t)]	P[R(t + 1)]
	Low Risk	Moderate Risk	High Risk
Low risk	0.609	0.564	0.312
Moderate risk	0.220	0.247	0.440
High risk	0.171	0.189	0.248

. Among them, P[R(t + 1)] represents the probability of the next time segment occurring in the t-th time slice of the dynamic Bayesian network model.

5. Navigation Risk Analysis of the Northeast Arctic Passage

5.1. Causal Reasoning of Navigation Risks in the Arctic Shipping Routes

Based on the dynamic Bayesian network model and parameter learning established in the previous text, through the automatic iterative update of the system, the occurrence probabilities of the target node at different time steps are obtained, thereby achieving the preliminary reasoning and analysis of the navigation risks in each sea area of the Northeast Arctic Passage without evidence input. When there is no evidence input, the monthly variation distribution of each sea area of the Chukchi Sea, the East Siberian Sea, the Laptev Sea, the Kara Sea, and the Barents Sea under high and medium navigation risks is shown in Figure 6 and Figure 7. During the period from July to October, the drilling vessels’ navigation in various sea areas was mainly low risk, indicating that the overall navigation conditions were relatively ideal. Among them, the risk levels in July and October were significantly higher than those in August and September, indicating that the navigation conditions in August and September were more ideal and consistent with the actual situation. Moreover, during the periods with higher risk levels, risk monitoring should be strengthened and key protection measures should be implemented during the periods with higher risks. Furthermore, from the comparison of navigation risks in the five sea areas, the navigation risk in the East Siberian Sea is the highest, especially in July when it is most significant. The probabilities of high and medium risks are 0.168 and 0.314, respectively. By contrast, the Barents Sea has the lowest navigation risk.

In this study, the dynamic Bayesian network model was divided into seven time steps with days as the time period, which can reflect the risk change trend within a week. From the above analysis, it can be known that compared with other sea areas, the navigation risk of the East Siberian Sea is the highest. Therefore, taking the East Siberian Sea as an example, Figure 8 shows the dynamic change characteristics of the navigation risk during the period from July to October. Specifically, the risk showed a downward trend in July and an upward trend in October. The risk levels in August and September are relatively stable and are the most suitable periods for navigation.

5.2. Reverse Diagnosis of Navigation Risks in the Arctic Shipping Routes

Assuming that all ships are in a “high-risk” state when navigating in the Arctic shipping route within all time slices, this is input as evidence into the model, and reverse reasoning is conducted on the dynamic Bayesian network model to obtain the posterior probabilities of each risk factor node, as shown in Figure 9. Then, based on Formula (5), the ROV values of each node were calculated, and the results are shown in Figure 10. The results in the figure show that the ROV values of visibility, sea ice thickness, sea ice density, temperature, large waves, and strong winds are relatively high, being 3.68, 2.07, 1.83, 1.42, 1.53, and 1.03, respectively. This indicates that the above factors are more likely to be the causes of danger for ships in the Arctic shipping routes, and these risk factors need to be focused on. In practical applications, implementing targeted risk management strategies at each stage before, during, and after an accident for these key risk factors is of great guiding significance for improving the ability of accident prevention and emergency response.

$$ROV\left(i\right)={\displaystyle \frac{\pi \left(i\right)-\theta \left(i\right)}{\theta \left(i\right)}}\times 100\%$$

(5)

In the formula, ROV(i) is the probabilistic fuzzy alienation ratio of the event corresponding to the i-th node; π(i) is the posterior probability; and θ(i) is the prior probability.

Meanwhile, based on the above analysis, several precautions for ships sailing in the Arctic shipping routes are given:

• Ensure the normal operation of the navigation system in polar environments, regularly inspect its accuracy, and prevent ships from mistakenly entering the density of floating ice due to equipment failure. Meanwhile, a multi-source positioning system is adopted as a backup to monitor the ship’s position in real time and prevent route deviation.
• Maintain all-weather regular lookout, identify floating ice or icebergs as early as possible, and leave sufficient distance to avoid them. When visibility is low, increase the dispatch of lookout personnel and reduce the speed to ensure the feasibility of emergency braking or turning.
• Regularly inspect the operating equipment to ensure its reliability at low temperatures. In waters with severe ice conditions, maintain a low speed of navigation to avoid the ship being squeezed by ice currents due to stagnation which may cause the ship to run aground or have its hull damaged.

5.3. Verification of the Navigation Risk Model of the Arctic Shipping Routes

5.3.1. Instance Verification Based on Scenario Analysis

This study adopts the method of forward reasoning to verify the reliability of the model, that is, to verify whether the nodes and their relationships in the Arctic shipping route navigation risk assessment model established earlier are consistent with those in the Arctic ship navigation accidents. If they are consistent, it indicates that the model is reliable. On the contrary, it is unreliable. In this study, nine accident samples were selected from the GISIS maritime database and previous recorded cases of Arctic ship navigation accidents to verify the reliability of the model. The causal elements of the nine accident cases, namely the risk nodes that affect the occurrence of the accidents, were extracted, respectively, and they were input as evidence successively into the established Arctic shipping route navigation risk assessment model for forward reasoning to verify the reliability of the model.

• The following takes the two accidents in the Kara Sea and the Laptev Sea, respectively, as examples to verify the model.
  • Barge “BCR-26-30”

The accident overview is as follows: On 3 October 2020, near the waters of the Kara Sea, during the loading operation, the barge BBR-26-30 was affected by wind and waves. The starboard side of the hull turned towards the coast. When the tugboat ADMIRAL KOLCHAK attempted to separate the barge from the shore, it ran aground, resulting in a crack in the ice in the engine room area of the underwater part on its starboard side. Ultimately, the tugboat ran aground on the beach, while the barge was pushed to the shore by the waves and partially sank. GISIS classifies accidents into three categories: very serious maritime accidents, general maritime accidents, and maritime incidents. It is recorded that the above-mentioned accident belongs to a very serious maritime accident category.

After analysis, the above-mentioned accident was found to have been mainly caused by wind and waves. Therefore, the high-risk level “State 3” of the relevant nodes such as “strong wind and large waves” in the above scenario was set to “State 3 = 1” and input into the model for reasoning and analysis of the navigation risk of the Arctic shipping route with evidence input. The dynamic probability changes in the navigation risk when there is evidence input are shown in Figure 11.

• • The “Vetlugales” ship

The accident overview is as follows: On July 23, 1986, the “Vetlugales” (ice Class L1, 22 years old) belonging to the Northern Sea Shipping Company encountered severe ice conditions during its voyage in the waters of the Laptev sea (ice density: 10/10; ice layer thickness: 1.5 m for current ice and 3.5 m for multi-year ice. Under the continuous ice pressure, the hull cracked in many places which resulted in multiple water ingress accidents in the cargo hold successively.

After analysis, the above-mentioned accident was found to be mainly caused by the severe ice conditions. Therefore, the high-risk level “State 3” of relevant nodes such as “ice density and ice thickness” in the above scenario was set to “State 3 = 1” and input into the model for reasoning and analysis of the navigation risks of the Arctic shipping route with evidence input. The dynamic probability changes in navigation risks when there is evidence input are shown in Figure 12.

According to the reasoning and analysis results of Figure 11 and Figure 12, the probability that the drilling vessel was at the high-risk level “State 3” during its voyage on October 3rd and July 23rd was much higher than that of the other risk levels. Therefore, when the above-mentioned causal factors occur, the “navigation risk” of the target node is most likely to be at a high-risk level, which is consistent with the facts. It also indicates that the established Bayesian network model is applicable to these two accidents.

2.

To further verify the validity of the model, the same method was adopted to verify each of the other seven accident samples one by one. The verification results are shown in Figure 13.

The criterion for judging whether a case is qualified is whether the output result of the model is consistent with the actual situation of the accident case. The test results show that for the nine accident case samples given, the dynamic Bayesian network model built in this study can predict all of them accurately, among which the excellent rate (posterior probability greater than 0.75) is 77.8%. From the overall model verification results, this model can describe the logical relationships between each node relatively accurately, proving that the Bayesian network model established in this study has high effectiveness in the analysis of navigation risks in the Arctic shipping routes.

5.3.2. Model Validation Based on Sample Data

To further illustrate the accuracy of the model, based on the established dynamic Bayesian network model, this study adopted the method based on sample data to verify the accuracy of the model. A temporal splitting strategy was employed for the time series data. The dataset covering the period from 2000 to 2022 was utilized for model training, while the data from the most recent year, 2023, was reserved as the testing set to verify the prediction accuracy. In this study, three groups of samples from five sea areas, namely 21-day sample data, were selected from the retained data, respectively. The evidence of time steps 1 to 7 was successively input into the model to observe the probabilities of occurrence of the low, medium, and high risk levels, namely “State 1”, “State 2”, and “State 3”. We compared the probabilities of occurrence of the three levels. The larger the value, the more likely it is to happen. The criterion for judging whether the model verification results are accurate is as follows: If the predicted results of the seven time steps are all correct, it is qualified and marked with “√”. Conversely, if one or more of the seven time step prediction results are incorrect, it is considered unqualified and marked with an “×”. The specific situation of model verification is shown in

Table 9. The validation of the risk assessment model for the navigation of Arctic shipping routes based on sample data.

Serial Number	Enter the Number of Time Steps
	1	2	3	4	5	6	7
1	√	√	√	√	√	√	√
2	×	×	√	√	√	√	√
3	√	√	√	√	√	√	√
4	√	√	√	√	√	√	√
5	√	√	√	√	√	√	√
6	×	×	×	×	×	×	√
7	√	√	√	√	√	√	√
8	√	√	√	√	√	√	√
9	×	√	×	√	√	√	√
10	√	√	√	√	√	√	√
11	√	√	√	√	√	√	√
12	×	×	×	×	×	√	√
13	×	√	√	√	√	√	√
14	√	√	√	√	√	√	√
15	×	×	√	√	√	√	√

.

The number of time steps input into the risk assessment model is increased successively to test the accuracy of the model under the condition of increased time steps. The specific verification situations of the five sea areas are shown in Figure 14. It is not difficult to see from the figure that when the evidence of the current time step is input, the accuracy rate of the navigation risk assessment of the current time step is 100%, indicating that the prediction of the current time step by this model is relatively accurate. At the same time, it also shows that this model has a certain degree of reliability. The overall accuracy rate result of this risk assessment model is shown in Figure 15. The average accuracy rate of the model is 83.4%. We compare the model proposed in this study with the model proposed by Brandt et al. with an average accuracy rate of 70.83% [24], indicating that this model has a relatively high accuracy rate in the navigation risk assessment of Arctic shipping routes and can be applied to the navigation risk assessment of ships in the Arctic. In addition, it can also be seen that as the number of input time steps increases, the model reasoning becomes more accurate.

Furthermore, for the incorrect prediction points in Figure 14, the following analysis is made: Taking the evidence of inputting six time steps in the East Siberian Sea as an example, according to the results, the prediction result of the seventh time step is incorrect. The prediction results of the key nodes are shown in

Table 10. The prediction results of key nodes after inputting evidence.

Node	Risk Level	Input Evidence						Prediction	Actual Situation
Sea ice type	I	1	1	1	1	1	1	0.724	I
	II	0	0	0	0	0	0	0.231
	III	0	0	0	0	0	0	0.044
Sea ice thickness	I	0	0	1	1	1	0	0.274	III
	II	0	0	0	0	0	0	0.043
	III	1	1	0	0	0	1	0.683
Sea ice density	I	0	0	0	0	0	0	0.118	III
	II	0	0	0	0	0	0	0.032
	III	1	1	1	1	1	1	0.850
Visibility	I	1	0	1	1	1	0	0.435	III
	II	0	0	0	0	0	0	0.073
	III	0	1	0	0	0	1	0.492
Strong wind	I	0	0	1	1	1	0	0.308	III
	II	1	0	0	0	0	0	0.308
	III	0	1	0	0	0	1	0.384
Temperature	I	0	0	0	0	0	0	0.374	III
	II	0	0	0	0	0	0	0.060
	III	1	1	1	1	1	1	0.566
Node	Risk level	Prediction
		Day 1	Day 2	Day 3	Day 4	Day 5	Day 6	Day 7
Navigation risk	I	0.027	0.012	0.970	0.970	0.970	0.012	0.311
	II	0.946	0.019	0.028	0.028	0.028	0.019	0.342
	III	0.027	0.969	0.002	0.002	0.002	0.969	0.347
	Actual situation	II	III	I	I	I	I	II

. According to the data in the table, it is not difficult to find that although the prediction result of the “strong wind” node is correct, the probability values of its three levels are too average, resulting in prediction errors that affect the result of the target node. Further analysis shows that this is due to the limited amount of data currently collected for learning that the accuracy of the transfer probability table of the “strong wind” node is not high. As a result, the predicted probability value of the high-risk level in the prediction result of the seventh time step has a relatively small gap compared with the other two nodes. After appropriately modifying the transition probability table of its nodes, it was found that the prediction of the target node had improved significantly, and the probabilities of its low, medium, and high risk levels were 0.241, 0.338, and 0.421, respectively. Therefore, in the following research, data from more years can be collected for learning to make the results more accurate.

5.4. Risk Prediction Application

The dynamic Bayesian network model built in this study can realize the risk prediction function by updating the state of nodes based on the changes in information in the past, present, or future. In practical applications, staff can update the dynamic nodes of the dynamic Bayesian network based on some data recorded in the past, the data observed on the current day, or the data obtained through the weather forecast system for the next few days, so as to better realize the navigation risks in the coming days. For example, suppose the staff obtain some information based on the data recorded a few days ago as follows: temperature: {State 2, State 3, State 2}; water temperature: {State 2, State 3, State 2}; sea ice density: {State 1, State 2, State 1}; strong wind: {State 1, State 2, State 1}, etc. The obtained information is input as new evidence into the model, and the result is shown in Figure 16. It can be seen from the results that the probabilities of medium and high risks increase significantly on the second day (with a time step of 1), which is due to the sudden adverse environment leading to an increase in navigation risks. The environmental conditions on the third day (with a time step of 2) eased somewhat, so the navigation risk began to decline, and it is predicted that it will continue to decline and gradually level off regionally in the following days.

6. Discussion

The findings of this study regarding the spatial distribution of risk align with historical accident data and previous academic research. Specifically, the East Siberian Sea has been found to have the highest risk for ship collision, foundering, and grounding, while the Barents Sea exhibits the lowest probability for these events. This spatial heterogeneity is consistent with the findings of Baksh et al. [9]. This elevated risk is primarily attributable to more severe ice conditions, characterized by the earlier and more rapid build-up of sea ice at the end of the summer season. The persistence of multi-year ice in the East Siberian Sea creates a complex navigational environment that challenges even ice-strengthened vessels.

A distinguishing feature of this study’s results is the identification of visibility (ROV = 3.68) as a critical risk factor. While often overshadowed by sea ice in polar research, visibility is receiving increasing attention as a determinant of safety. Advection fog occurs frequently in the Arctic Ocean during the summer months due to the interaction between warm air masses and cold sea surfaces. Consequently, Arctic shipping routes are often shrouded in sea fog, resulting in severely restricted visibility. Additionally, the high albedo of the Arctic environment, covered by sea ice and snow, makes crew members susceptible to snow blindness. This impairment of perception and judgment regarding the ship’s surroundings greatly increases the risk of major accidents. Statistical data supports this finding, indicating that 60–70% of maritime collisions are caused by insufficient visibility due to sea fog—a factor that becomes particularly acute during the ice-free or light-ice season.

Existing research predominantly identifies ice conditions as the dominant factor in accident causation. For instance, Sheng Xu et al. [13] and Shanshan Fu et al. [14] indicate that ice condition and concentration are the primary factors responsible for ship–ice collision accidents, followed by secondary factors such as ice strength, unsafe speed, and ice type. In these studies, the most important risk factor is consistently derived from the hard navigational environment (sea ice).

However, this study elevates visibility above these ice-related factors. This divergence does not contradict previous findings but rather reflects the specific seasonal window (July to October) analyzed in this paper. During this period, sea ice cover retreats and open water increases; thus, sea ice risks are relatively lower compared to winter. This suggests that while ice remains the primary structural threat, visibility is the primary operational threat during the summer navigation window—a distinction that is vital for the development of seasonal safety protocols in a changing Arctic climate.

7. Conclusions

This study constructs a DBN model to assess Arctic navigation risks, integrating ISM and combined weighting methods to capture the continuous evolution of environmental hazards. The model includes 12 risk factors in total and demonstrates high reliability, achieving an accuracy of 83.4% on sample data and the excellent rate (posterior probability greater than 0.75) is 77.8% for historical accident cases.

Research shows visibility, sea ice thickness, sea ice density, temperature, large waves, and strong winds as primary risk factors, with the East Siberian Sea exhibiting the highest regional risk, particularly in July. Based on these insights, the study recommends specific safety mandates, such as enhanced lookout protocols and speed reduction in severe ice zones, to facilitate proactive risk avoidance.

The proposed methodology provides a robust tool for government and corporate decision-making. The proposed method can also be transferred to non-Arctic maritime environments by replacing Arctic-specific nodes with locally relevant hazard factors.

This DBN framework does not explicitly include “ship structure” as a risk factor since the navigation risk assessment is only about the Arctic shipping routes. Future research may couple this environmental model with specific vessel structural parameters to quantify performance under identical risk conditions. Future practical application may integrate captains and engineers to calibrate risk levels with real situation feedback, thereby enhancing the model’s practical applicability.