Abstract
With the rapid advancement of battery technology, new energy hybrid tugboats have been progressively adopted. In order to align with the trend of electrifying tugboat fleets, a mixed-integer linear programming (MILP) model for the joint scheduling of new energy hybrid tugboats and berths has been established. The model incorporates the constraint imposed by the limited number of tugboat charging connectors. The objective is to minimize the total cost over the scheduling horizon, including ship waiting, delayed-departure costs, and the operating costs of both conventional diesel and hybrid tugboats. In light of the characteristics inherent to the problem, a hybrid solution approach combining CPLEX with a heuristic-enhanced whale optimization algorithm (WOA) is employed to solve the model. A case study was conducted using data on the energy consumption of tugboats at Xiamen Port. The effectiveness of the model and algorithm was then verified through a series of small-scale instance experiments. Finally, a comprehensive sensitivity analysis of key parameters is finally conducted, including the number of tugboat charging connectors, battery capacity, and charging rate. This analysis provides valuable guidance for port tugboat operations.
1. Introduction
In recent years, as the global shipping industry embarks on a transition towards more environmentally sustainable and technologically advanced practices, ports, as key nodes in the shipping logistics chain, have been facing revolutionary and significant transformations. In the field of port tugboats, the advancement of battery technology has precipitated the gradual substitution of traditional diesel tugboats with new energy hybrid tugboats, which are powered by a combination of battery and diesel engines [1]. Hybrid tugboats combine the advantages of traditional internal combustion engines and battery power systems, thereby achieving a reduction in energy consumption and emissions, while also adapting to the diverse operational conditions demanded by port environments.
Tugboat scheduling primarily involves the allocation of tugboat resources and the sequence of operations during ship berthing and unberthing. The optimization of tugboat scheduling has been demonstrated to be an effective strategy for reducing ship berthing and unberthing waiting times, mitigating berth congestion risks, and enhancing the overall utilization of port berths and tugboats. A number of scholars have conducted in-depth research on tugboat scheduling. However, in light of the social trend towards energy conservation and emission reduction, most studies focus on conventional diesel tugboats, with a lack of research on scheduling new energy tugboats. Moreover, the effective integration of berth allocation and tugboat scheduling is of considerable theoretical and practical importance for enhancing port operational efficiency. This work aims to improve operational efficiency on the port sea side by constructing a joint scheduling model for new energy hybrid tugboats and berths. This model employs optimization algorithms to ensure optimal utilization of resources, while also providing a theoretical foundation and practical guidelines for the operation of port new energy tugboats. The research endeavor addresses a significant gap in the existing literature by offering a comprehensive framework for the development of port tugboats that is focused on promoting environmentally sustainable practices.
In order to align with the process of electrifying tugboats, this paper proposes a mixed-integer linear programming model for the joint scheduling of hybrid tugboats and berths, while considering shore power constraint. The objective is to minimize the total cost, including ship waiting costs during port stay, delayed departure costs, operating costs of conventional diesel tugboats, and operating costs of hybrid tugboats. The model is solved using the CPLEX solver combined with a heuristic-enhanced whale optimization algorithm, and the effectiveness of the model and method is verified through case study experiments. The contributions of this paper are as follows:
- (1)
- A mixed-integer linear programming model for the joint scheduling of new energy hybrid tugboats and berths is established, breaking the traditional research boundaries that focus solely on conventional diesel tugboat.
- (2)
- A solution method combining the CPLEX solver with a heuristic-enhanced whale optimization algorithm is proposed for the established joint scheduling model of tugboats and berths. This method can obtain relatively accurate and feasible solutions in small-scale instances.
- (3)
- The impact of shore power facility constraint on hybrid tugboat scheduling is considered, specifically the limitations on tugboat charging periods due to a limited number of charging connectors. This analysis serves to enhance the practical applicability of the scheduling model.
The remainder of this paper is organized as follows. Section 2 reviews the literature on port tugboat scheduling, berth allocation, integrated tugboat–berth scheduling, and new energy hybrid tugboat, summarizing the deficiencies of the existing research. Section 3 constructs a mixed-integer linear programming model for the joint scheduling of hybrid tugboats and berths under shore power constraints. Section 4 designs the solution algorithm for the model. Section 5 presents a case study. Section 6 concludes with the research findings.
2. Literature Review
This section summarizes related research in four aspects: tugboat scheduling, berth allocation, integrated tugboat–berth scheduling, and new energy hybrid tugboat.
2.1. Research on Tugboat Scheduling
The tugboat scheduling problem is a classic port resource scheduling problem, and numerous studies have investigated it, with some focusing on tug operational efficiency as the optimization objective. Wang et al. [2] formulated a mixed-integer programming model for tugboat scheduling to minimize total task tardiness, proposed an enumeration-based solution method, and analyzed the effect of the number of tugboats on port operational efficiency. Subsequently, Wang et al. [3] studied tugboat scheduling under hybrid dispatching rules with the objective of minimizing ship turnaround time and solved it using a discrete particle swarm optimization algorithm. Kang et al. [4] considered uncertainties in ship arrival and tugging process times, developed a mixed-integer linear programming model to minimize the total weighted service time of tugboat operations, and designed a self-organizing map algorithm to solve the model. Hao et al. [5] examined the joint scheduling of barges and tugboats under tidal effects, aimed to minimize bulk cargo transshipment time, and developed a tailored variable neighborhood search algorithm to solve the problem.
Incorporating tugboat operating costs typically aligns better with practical production settings; accordingly, several studies explicitly consider the cost components of tugboat operations. Xu et al. [6] developed a three-stage model covering berthing, shifting, and unberthing to minimize the total operation time of all tugboats in a port, and devised a hybrid simulated annealing-based ant colony algorithm to solve it. Zhen et al. [7] examined a tugboat scheduling problem at a river mouth port, formulated a mixed-integer programming model to minimize tugboat sailing and delay costs, proposed a solution method based on a branch-and-price approach. Wei et al. [8] proposed a mixed-integer linear programming model for tugboat scheduling with multiple services from multiple waypoints to minimize sailing costs and developed a tailored branch-and-cut algorithm to solve the model. Jia et al. [9] developed a mixed-integer linear programming model for tugboat scheduling that incorporates ship berth plans and tug points, aiming to minimize the sum of tugboat operation and ship delay costs, and designed a heuristic method based on Lagrangian relaxation and Benders decomposition to solve the model. Zhu et al. [10] established a tugboat scheduling model considering the barge transshipment to minimize total carbon emissions cost and developed a variable neighborhood search algorithm to solve it. Zhong et al. [11] accounted for tidal time windows and formulated a multi-objective scheduling model that minimizes tugboat operation time and total fuel consumption, solved via the NSGA-II algorithm. Li et al. [12] proposed a fuzzy programming model for tugboat scheduling that minimizes the total cost of fuel and delays, developed a tailored gray wolf optimizer to solve it. Wang et al. [13] developed a model for tugboat scheduling by considering multiple ship entry path nodes, minimizing the sum of travel and fixed costs of tugboats, and designed an adaptive large neighborhood search algorithm to solve the model. Sun et al. [14] aimed to minimize tugboat sailing distance, developed a scheduling model that considers cross-regional constraints and operational uncertainties, and designed an improved genetic algorithm based on reversal operations to solve it.
2.2. Research on Berth Allocation
Berth allocation can be categorized into three types: discrete, hybrid, and continuous. In studies of the discrete berth allocation problem, Imai et al. [15] examined the discrete berth allocation problem and introduced a dynamic berth allocation model for container ports to minimize each ship’s waiting and service times, and devised a Lagrangian relaxation-based heuristic algorithm to solve it. Prencipe et al. [16] formulated a mixed-integer linear programming model to minimize the in-port time of ships and designed a bee colony optimization algorithm to solve it.
In hybrid berth allocation, Umang et al. [17] constructed a mixed-integer linear programming model to minimize the in-port time of ships and employed a squeaky wheel optimization algorithm to solve it. Kordić et al. [18] established a mixed-integer linear programming model to minimize the total port-entry costs of all ships and developed an exact algorithm based on the precipitation method to solve it.
Compared with discrete and hybrid berths, continuous berths offer higher space utilization and greater flexibility and have therefore been widely adopted in practice. Focusing on continuous berth allocation, Ernst et al. [19] studied berth allocation at dry bulk terminals under tidal constraints, developed two linear mixed-integer programming models, and proposed a two-phase method to solve the problem. Venturini et al. [20] integrated berth allocation with ship speed optimization and proposed a multi-port berth allocation optimization problem that accounts for environmental factors. Cheimanoff et al. [21] examined berth allocation at bulk terminals, emphasized the impact of tidal time windows, formulated a mixed-integer linear programming model and designed a variable neighborhood search algorithm to solve it. Martin-Iradi et al. [22] investigated the multi-port continuous berth allocation problem, developed a mixed-integer linear programming model for the problem, introduced an adaptive large neighborhood search algorithm enhanced with a local search procedure to solve it.
2.3. Integrated Tugboat–Berth Scheduling
The operational efficiency of a container terminal largely depends on the utilization efficiency of its seaside resources, including tugboats, berths, and quay cranes [23]. Research on integrated tugboat–berth scheduling is relatively limited, several studies have examined the joint scheduling of three resources—tugboats, berths, and quay cranes. Yang et al. [24] investigated the joint scheduling of tugboats, berths, and quay cranes; they formulated a mixed-integer nonlinear programming model that minimizes ships’ in-port time cost, truck-transportation costs, tugboat operating costs, and quay crane operating costs, constructs a new chaotic quantum adaptive satin bower bird optimizer algorithm. Chu et al. [25] established a mixed-integer linear programming model for the joint scheduling of tugboats, berths, and quay cranes to minimize the sum of ship in-port cost, tugboat operation cost, and quay crane operation cost, they proposed an adaptive large neighborhood search algorithm to solve it.
Furthermore, several studies have focused on the integrated scheduling of tugboats and berths. Wang et al. [26] considered the impact of shore-power cable connections on ship berthing and formulated a two-layer mixed-integer linear programming model to minimize environmental and economic costs; the first layer addresses berth allocation, and the second layer focuses on tugboat scheduling. They also devised a solution approach that combines the commercial solver CPLEX with an immune particle swarm optimization algorithm. Fan et al. [27] investigated tugboat–berth integrated scheduling under tidal constraints, established a two-layer mixed-integer linear programming model and solved it using enumeration and heuristic algorithms.
2.4. Research on New Energy Hybrid Tugboat
In recent years, with the rapid advancement of battery technology, new energy hybrid tugboats have been increasingly adopted and deployed. Kumar et al. [28] proposed a coordinated control system for diesel–electric hybrid tugboats that optimizes generator and battery usage based on load conditions to improve diesel-engine efficiency. Karaçay et al. [29] modeled propulsion systems for diesel, diesel–electric hybrid, LNG, and dual-fuel tugboats. They conducted a comparative long-term economic analysis, concluding that hybrid tugboats are preferable in terms of economic performance. Devarapali et al. [30] evaluated the economic benefits of electric, hybrid, and conventional diesel tugboats. They expected that for long-term planning, the electric and hybrid tugboat alternatives will become the preferential. Chen et al. [31] analyzed the factors that tugboat owners consider when making investment decisions regarding hybrid tugboats in the context of carbon-reduction policies.
Overall, hybrid tugboats have not been examined from a scheduling perspective in the literature. Table 1 compares this study with those of Wang et al. [26] and Fan et al. [27]. The distinguishing feature of this study is the explicit incorporation of new energy hybrid tugboats. In addition, although Wang et al. and Fan et al. also investigated the joint scheduling problem of tugboats and berths, their two-stage modeling approach, which separates berth allocation from tugboat scheduling, partly neglects the interdependence between the two. In contrast, our study develops a mixed-integer linear programming model for the joint scheduling of hybrid tugboats and berths, which can enhance the model’s practical applicability to a certain extent. The model is solved using CPLEX in combination with a heuristic-enhanced whale optimization algorithm.

Table 1.
Comparison of the study details.
Concurrently, the impact of shore power facilities on the scheduling of hybrid tugboats is also taken into consideration. In the contemporary context, a considerable number of ports are adopting electrified equipment. The integration of port resource scheduling with shore power energy management is of paramount importance in facilitating the green development of ports [32]. At present, only a limited number of studies have examined the impact of shore power facility availability on port resource scheduling, and these are primarily focused on berth allocation. Wang et al. [26] incorporated the limitation of available shore power facilities for ship connections into their berth allocation model. Zhang et al. [33] develops a multi-objective optimization model for the coordinated allocation of shore power and berth scheduling, integrating economic benefits, environmental benefits, and operational efficiency. The investigation examined the influence of the number of shore power connections on the objective function, and the sensitivity analysis indicated that when shore power capacity reaches 80% of the total number of berths, an optimal balance is achieved between cost, pollutant emissions, and ship waiting time. Overall, with the increasing adoption of new energy tugboats, shore power at ports must not only supply power to berthed ships but also accommodate the charging requirements of tugboats. Consequently, this study has the potential to further extend the existing body of research in this field to the domain of tugboat scheduling, thereby addressing a significant research gap.
3. Model
3.1. Problem Description
As shown in Figure 1, a hybrid tugboat is a new energy ship retrofitted from a conventional diesel tugboat with battery packs and an electric propulsion system. This design overcomes the limitation of relying solely on the diesel main engine, which leads to high pollution and emissions, thereby enabling flexible selection of propulsion modes according to operational load conditions. In conditions of low operational load, the decision may be taken for hybrid tugboats to opt for electric propulsion in order to reduce operating costs and emissions. Conversely, under conditions of high operational load, the diesel main engine is relied upon to ensure power performance. It is important to note that, under low-load conditions, hybrid tugboats prioritize battery propulsion. In the event that the state of charge becomes insufficient, they have the capacity to switch to diesel-engine propulsion rather than electric propulsion. This feature is a salient one that distinguishes hybrid tugboats from electric ones.
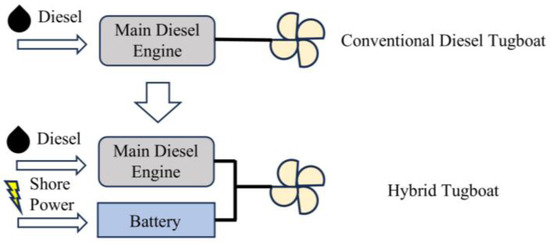
Figure 1.
Structure diagram of hybrid tugboat.
The joint scheduling problem of hybrid tugboats and berths is illustrated in Figure 2. Following the ship’s arrival at the designated anchorage, it is assisted by tugboats in berthing if the number of available berths meets the ship’s requirements. Once berthing operations are complete, the tugboats assists the ship back to the anchorage for departure. The following section will analyze the operating conditions of the tugboats during the scheduling horizon.
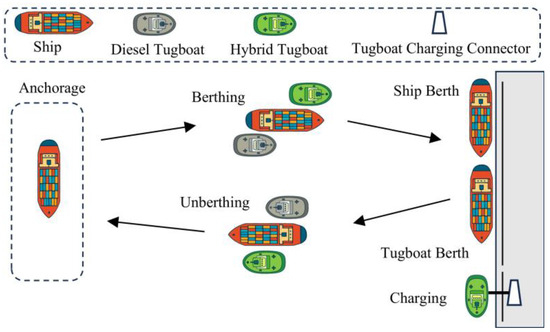
Figure 2.
Schematic diagram of joint scheduling of hybrid tugboats and berths.
- (1)
- The term “empty sailing” is used to describe the movement of a tugboat from berth to anchorage. In the context of hybrid tugboats, the operation of battery-electric mode within the port area is a viable option.
- (2)
- Layby is defined as the period during which a tugboat is berthed. For hybrid tugboats, shore power can be utilized during layby to facilitate the charging of the battery pack and ensure the maintenance of endurance.
- (3)
- The term “tugging” refers to the process in which a tugboat provides assistance to a ship in either its berthing or unberthing maneuvers. Specifically, this can be subdivided into low-load and high-load phases.
The impact of constraints in the infrastructure for shore power on the scheduling of hybrid tugboats is also considered in this study. For instance, Figure 2 illustrates three hybrid tugboats, yet only a single tugboat charging connector is available at the berth, thereby indicating that, at any given moment, only one tugboat can be charged. It is therefore vital that charging windows are allocated strategically among hybrid tugboats in order to enhance operational efficiency.
Furthermore, based on the information gathered, it can be concluded that both the hybrid tugboats currently in operation and those under construction are high-power tugboats. Consequently, the hybrid tugboats examined in this study are all of relatively high power.
3.2. Model Assumptions
(1) The safe distance between ships is included in the ship length. (2) The energy consumption incurred while tugboats wait for operations is considered negligible. (3) All tugboat charging facilities have identical specifications. (4) At the beginning of the scheduling horizon, all tugboats are located within the berth awaiting operations.
3.3. Model Parameters and Variables
The parameters and variables of the joint scheduling model for hybrid tugboats and berths under charging constraints constructed in this paper are shown in Table 2 and Table 3.

Table 2.
Model parameters.

Table 3.
Model variables.
3.4. Scheduling Model
3.4.1. Objective Function
In the objective function, F1 represents the ship waiting and delayed departure costs in port, and F2 represents the operational energy consumption costs of tugboats during the scheduling period.
3.4.2. General Constraints for Tugboats
Constraint (4) ensures that the number of tugboats allocated to each ship meets the required quantity; in this study, every ship is served by two tugboats [27]. Constraint (5) ensures that a tugboat serves only one ship at a time. Constraint (6) ensures that a tugboat does not serve the same task more than once. Constraint (7) ensures the continuity of tugboat tasks. Constraint (8) ensures that the tugboats assigned to a ship meet the required power level. Constraints (9) and (10) ensure that a tugboat must complete the previous task before starting the next; if empty sailing is required, the time allocated for this is taken into account.
3.4.3. Operational Constraints for Hybrid Tugboats
Constraints (11) to (16) represent the composition of tugboat operating energy consumption under low-load conditions. Constraints (17) to (19) govern the start time of charging for hybrid tugboats. Constraints (20) to (22) ensure that a hybrid tugboat may commence the current task only after charging has been completed. Constraints (23) to (24) specify the timing constraints for a hybrid tugboat to perform its first task.
3.4.4. Charging Constraints for Hybrid Tugboats
Constraints (25) to (28) are state of charge continuity constraints for hybrid tugboats. Constraint (29) ensures that a hybrid tugboat’s state of charge does not exceed battery capacity. Constraint (30) ensures that the hybrid tugboat’s electricity energy consumption does not exceed its current state of charge. Constraint (31) ensures that a hybrid tugboat’s electricity energy consumption does not exceed the energy required for the task. Constraints (32) to (34) ensure the continuity of the hybrid tugboats charging times. Constraint (35) ensures that, at any time, the number of hybrid tugboats being charged does not exceed the number of tugboat charging connectors in the port. Constraint (36) specifies the charging constraint for hybrid tugboats.
3.4.5. Ship-Related Constraints
Constraint (37) ensures that a ship berths upon arrival at the port. Constraint (38) ensures that a ship unberths after completing its operations. Constraint (39) defines the ship’s delayed departure time. Constraints (40) to (42) ensure that any two ships do not overlap simultaneously in time and space. Constraint (43) imposes a safety headway between berthing and unberthing at the same berth. Constraint (44) ensures that ships berth within the designated shoreline limits.
3.4.6. Variable Non-Negativity Constraints
4. Methodology
This paper establishes a mixed-integer linear programming model for tugboat–berth joint scheduling, which can be solved using the CPLEX solver. However, due to the complexity of the problem, the use of CPLEX is not a viable solution. The proposed methodology in this paper is a two-stage solution approach that integrates the CPLEX solver with a heuristic algorithm. In the first phase, the allocation of berths for incoming vessels is determined by utilizing the CPLEX optimization algorithm. In the subsequent phase, the tugboat scheduling problem is addressed through the implementation of a whale optimization algorithm enhanced with a heuristic strategy.
4.1. Berth Allocation Solution
The initial model is resolved through the utilization of the CPLEX solver, thereby yielding the designated berth and the scheduled berthing and unberthing times for each ship. Consequently, in the initial berth allocation solution, Constraints (37)–(45) are exclusively considered, with the objective function concentrating exclusively on the ship’s in-port costs. Despite the fact that this stage provides the precise solution for berth allocation, it does not mitigate the impact of the tugboat scheduling plan on the ship’s actual berthing and unberthing times. As demonstrated in Figure 3a, the berthing time of ship 2 directly follows that of ship 1; if ship 1 is delayed in berthing and unberthing, it may have an adverse effect on ship 2. However, as illustrated in Figure 3b, when the berth allocation plan is implemented, ship 2 is less likely to be impacted by ship 1.
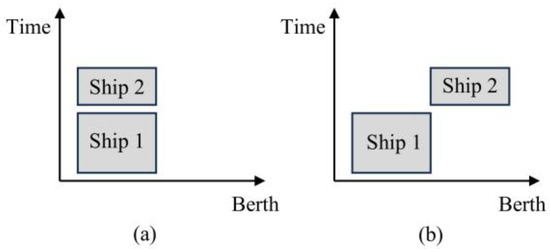
Figure 3.
Schematic diagram of berth allocation. (a) The first berth allocation scheme. (b) The second berth allocation scheme.
In order to mitigate the repercussions of the proposed tugboat scheduling plan on ship berthing and unberthing, this paper proposes a supplementary model to enhance the outcomes of the initial solution. The model reallocates berths for the ships without altering the optimal objective value that has already been obtained. Consequently, the scheduled berthing and unberthing times of ships in this model are the established parameters from the initial-stage solution, and a performance index, designated as FDi, is formulated for each ship. FDi represents the time distance between the berthing time of ship i and the unberthing time of the previously overlapping ship at the same berth. If ship i has no overlapping ships before berthing, it calculates the time distance from the time origin. Therefore, the objective function of this model is expressed by Equation (46), and the constraints are defined by Equations (37)–(45) and (47)–(49).
4.2. Solution Encoding
After solving the berth allocation in the first-stage model, a heuristic algorithm is used to solve the second-stage tugboat scheduling model. We adopt a multi-layer real number encoding as shown in Figure 4. As illustrated in Figure 4, a feasible encoding format for three ships is presented, with the meaning of each layer explained within the figure itself. Berth position and ship length are fixed information, either known or already solved. The ship numbers are fixed index values, since each ship requires both berthing and unberthing operations, the length of this encoding is twice the number of ships. The ship numbers in odd and even columns represent the berthing and unberthing tasks for the corresponding ships, respectively. The tugboat allocation encoding represents the tugboat numbers assigned to the tasks in each column. For instance, as illustrated in the figure, the tugboat numbers providing berthing service for ship 2 are 1 and 2, while the tugboat numbers providing unberthing service are 2 and 5. It is evident that the operation sequence encoding is indicative of the sequence of tugboat operations for tasks within the scheduling period. It is imperative to note that a tugboat is only able to undertake a subsequent task after successfully completing a task that is assigned a higher priority in the operation sequence. Furthermore, it is imperative that the berthing operation sequence of any vessel precedes its unberthing sequence; failure to do so will result in the generation of an unsustainable scheduling solution. The algorithm delineated in this paper performs transformation operations exclusively on the tugboat encoding, while the sequence encoding is determined using a heuristic strategy.
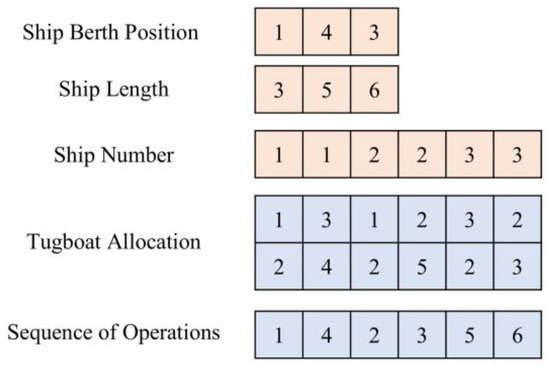
Figure 4.
Solution encoding format.
4.3. Tugboat Scheduling Solution
This paper employs a whale optimization algorithm (WOA) with a heuristic initial solution strategy to solve the second-stage tugboat scheduling problem [34]. The WOA simulates the hunting behavior of humpback whales in nature using the shrinkage encircling mechanism and bubble attack mechanism, with features such as a simple search mechanism and minimal parameter settings. The tugboat scheduling problem under consideration in this paper is a discrete optimization problem. The traditional WOA is only suitable for continuous optimization problems. This paper adapts crossover and mutation strategies from genetic algorithms to redefine the WOA’s search mechanism. This adaptation makes the algorithm suitable for solving the tugboat scheduling model, as shown in Equation (50).
4.3.1. First Type of Crossing Method
As shown in Figure 5, the first crossover method corresponds to the bubble attack phase of the whale individual. First, three random division points are generated for the task sequence from 1 to 2n, dividing the task sequence into four segments. The tugboat encoding corresponding to the task sequence values of the first and third segments in the optimal solution is extracted and used to replace the corresponding positions in the current whale individual, generating offspring whale individual 1. For offspring whale individual 2, the same operation is applied using the task sequences of the second and fourth segments.
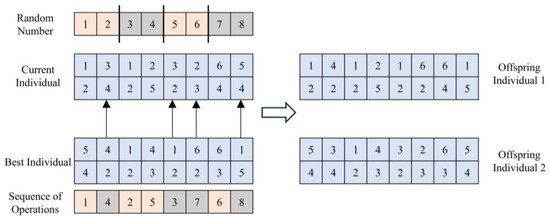
Figure 5.
First type of crossing method.
4.3.2. Second Type of Crossing Method
As shown in Figure 6, the second crossover method corresponds to the search and predation phase of the whale individual. For each task, a random number of 0 or 1 is generated with equal probability. The tugboat encoding of tasks with a random number of 1 in the current whale individual remains unchanged. For tasks with a random number of 0, the tugboat encoding is replaced with a randomly selected tugboat encoding of the same required tugboat class from another randomly selected whale individual, generating offspring whale individual 1. The generation of offspring whale individual 2 follows the reverse process.
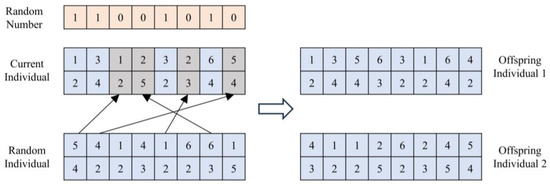
Figure 6.
Second type of crossing method.
4.3.3. Third Type of Crossing Method
The third crossover method corresponds to the shrinkage encircling phase of the whale individual. In this crossover method, three random division points are generated in the current whale individual’s tugboat encoding, dividing it into four segments. Then, the tugboat encodings of the optimal whale individual and the current whale individual are exchanged between segments to generate two offspring whale individuals.
The aforementioned position update strategies result in the generation of two offspring whale individuals. The individual with the higher fitness is then selected as the final whale individual following the position update.
4.3.4. Mutation Mechanism
A mutation operator that is frequently utilized in conventional genetic algorithms was employed to enhance global exploration and impede the convergence of solutions towards local optima. Following the modification of the position of the whale individual, the occurrence of mutation is subject to a certain probability. The mutation operator involves randomly reassigning tugboats to each task with a 20% probability.
4.3.5. Convergence Factor
The traditional linear convergence factor limits global search in the later stages of the algorithm’s iterations, increasing the likelihood of falling into local optima. In order to achieve equilibrium between global and local search, and to adapt the algorithm to the model under consideration, the conventional convergence factor’s linear decay was modified to the form given in Equation (51). In Equation (51), t denotes the current iteration number, and T signifies the maximum number of iterations permitted by the algorithm.
4.4. Objective Function Value
In this study, the objective function value (fitness) is determined by the tugboat encoding of each whale individual, as well as the tugboat operation sequence and the charging time windows for hybrid tugboats. Accordingly, the objective function value is computed from the tugboat encoding by applying the following heuristic rules.
- Step 1: Initialize I = 1. Proceed to Step 2.
- Step 2: If all ship berthing and unberthing tasks are completed (I > 2n), then end the process. Otherwise, find the task among all unsolved tasks that can start the earliest, designate this task as the current task, and mark its service sequence as I. (For ship requiring berthing, the earliest possible berthing time shall not be earlier than their arrival time and must maintain a safe time interval from the ship previously berthed at the same berth. If there is an unberthed ship occupying the planned berth, the incoming ship cannot commence berthing operations at that time. For ship scheduled to unberth, their earliest possible departure time corresponds to the completion time of berth operations.) Then proceed to Step 3.
- Step 3: The task’s start time is set to the earliest time at which the assigned tugboats can provide service. If a hybrid tugboat is included among the assigned tugboats, intermittent charging may be performed before the task’s start time. If the tugboat is waiting at the anchorage and the current task is a berthing task, the tugboat will not return to the berth for charging.
The charging strategy is illustrated with reference to Figure 7, where three priority rules are applied.
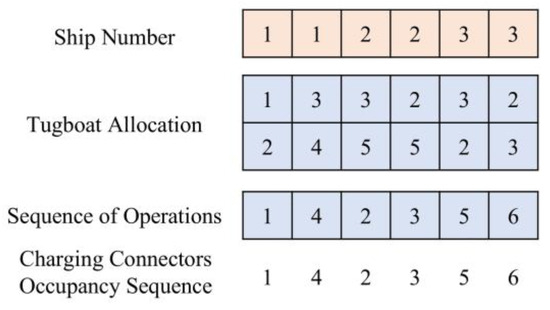
Figure 7.
Charging strategy.
- The first rule is that tugboats with earlier task sequences are given priority to use the earliest available charging connectors. Therefore, the operation sequence encoding also determines the priority of the tugboats using the charging connectors. For example, in Figure 7, tugboats 1 and 2, which perform berthing operations for ship 1, are scheduled to charge before tugboats 3 and 5, which perform berthing operations for ship 2.
- The second rule is that a tugboat in the first layer of the tugboat encoding is given higher charging priority than one in the second layer. For example, tugboat 1, which performs the berthing operation for ship 1, is scheduled to charge before tugboat 2.
- The third rule stipulates that a tugboat occupying a charging connector will continue charging until reaching the maximum feasible state of charge, or a level sufficient for use within the scheduling horizon, before disconnecting from the connector.
4.5. Initial Solution
This paper aims to generate feasible solutions using a heuristic strategy, which are incorporated into the population during the initialization process. Although the initial solution generated using a heuristic strategy may not be the optimal solution, it is usually closer to the optimal solution than randomly generated initial solutions, thereby enhancing the algorithm’s search efficiency. The rule is that after identifying the current task in the aforementioned steps, the operational costs and ship waiting costs for each tugboat to serve the task as quickly as possible are calculated sequentially. In the case of a hybrid tugboat, the operational cost is calculated on the basis of the use of the earliest charging connector that is available. Finally, the two tugboats that yield the minimum total cost and satisfy the power requirements are selected and assigned to the task.
5. Case Study Analysis
This paper conducts a study based on tugboat operation energy consumption data from a port in Xiamen. The specific information about the tugboats at this port is shown in Table 4, and the length of the port’s berth shoreline is 1400 m. The classification of ships entering the port is determined by their size, with the requirement for tugboat class being categorized as follows: 1 for small ships, 2 for medium ships, and 3 for large ships. The relevant parameters of the ships collected during a certain scheduling period are shown in Table 5. In this paper, both time and space are discretized, with the minimum space unit being 50 m and the minimum time unit being 0.25 h. Additionally, the energy consumption for tugboat operations is also discretized, with each unit of energy corresponding to 30 kWh of electricity consumption or 6 kg of diesel consumption. The fuel consumption per unit for tug tugging of the three types of ships is 8, 10, and 12, respectively. The selection of other relevant parameters is shown in Table 6. The experiment is implemented using the CPLEX solver version 12.10 and MATLAB R2020b software.

Table 4.
Tugboat information.

Table 5.
Ship information.

Table 6.
Parameter selection.
5.1. Model and Algorithm Validation
The maximum number of iterations for the algorithm is set to 100, the population size to 50, and the mutation probability to 0.2. To validate the effectiveness of the hybrid tugboats and berths joint scheduling model and solution method developed in this paper, the model is imported into the CPLEX solver and compared with the algorithm presented in this paper. The results of this comparison are shown in Table 7. Preliminary analysis indicates that, in instances where the sample size is minimal, CPLEX is capable of attaining the optimal solution within the stipulated timeframe. However, as the example size and complexity increase, the solving time for CPLEX increases significantly. Conversely, the algorithm presented in this paper can produce solutions close to those from CPLEX in a shorter time, with an error range controlled within 1.54%. The error level is within an acceptable range, validating the feasibility of the model and solution method proposed in this paper.

Table 7.
Experimental results of small-scale examples.
In order to verify the feasibility and effectiveness of the proposed model and solution method, a series of examples were constructed for computational experimentation. Each example involved 15 ships over the scheduling horizon. As illustrated in Table 8, the results of the solution for small-scale examples are reported. In these examples, the number of ships was set to five and six, respectively. The number of charging connectors is set to 1, for example, numbers 1–10 and to 2, for example, numbers 11–20. With respect to the main sources of error, when the number of ships was small, the available berths in the port were relatively sufficient; therefore, the berth allocation plan had little or no influence on the solution results. The primary sources of solution error were ascribed to the tugboat operation sequence and charging strategy. However, such errors did not accumulate as the number of ships increased in the test examples. As shown in Table 8, the solution error for the examples with six ships was generally not higher than that for the examples with five ships. The primary rationale for this phenomenon pertains to the escalating operational expenditures associated with tugboat operations, which exhibited an increasing trend with the augmentation of ships. Conversely, the repercussions of scheduling inaccuracies on the total cost remained within the bounds of acceptability.

Table 8.
Comparison of small-scale examples.
To further validate the advantages of the proposed algorithm, we compare it with the other algorithms designed in this study, as shown in Figure 8. Specifically, WOA1 is a whale optimization algorithm without the heuristic initial solution strategy; WOA2 is a whale optimization algorithm employing the conventional linear convergence factor; and GA is the classical genetic algorithm with crossover and mutation probability set to 0.8 and 0.2, respectively. Within the GA algorithm, the population size is set to 100, the encoding scheme adheres to the format depicted in Figure 4, and the crossover and mutation operators adopt the third crossover type and mutation mechanisms proposed in this study. It was observed that WOA1 was influenced by the initial population’s low quality, which constrained both the search efficiency and the optimization results of the algorithm. Conversely, the implementation of a heuristic initial-solution strategy facilitated the identification of a superior initial population at an early stage, thereby enhancing the algorithm’s search efficiency. WOA2 demonstrated inadequate global search capability during the middle and later stages of optimization due to the utilization of a conventional linear convergence factor. In contrast, the WOA incorporating an enhanced nonlinear convergence factor effectively balanced the global and local search capabilities, thereby preventing the algorithm from becoming trapped in local optima. As illustrated in Figure 9, the results of this study’s algorithm are compared with those of other algorithms for a range of large-scale examples. It can be observed that, in comparison with the other algorithms, the algorithm presented in this paper yields better objective values across different test examples. The proposed algorithm has been demonstrated to yield superior solution quality in addressing larger-scale integrated tugboat berth scheduling problems.
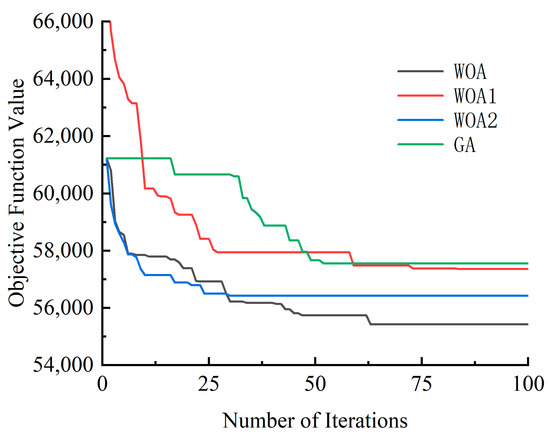
Figure 8.
Comparison of algorithms.
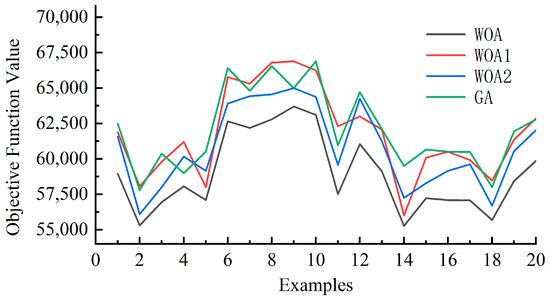
Figure 9.
Comparison of large-scale examples.
In order to further assess the impact of algorithm parameters on the solution results, Table 9 presents the optimal and average objective values obtained after 20 consecutive runs of the algorithm, considering different mutation probabilities and population sizes. From the perspective of mutation probability, a smaller mutation rate reduces population diversity, thereby making it more difficult for the algorithm to escape local optima. On the other hand, a larger mutation rate weakens the local exploitation ability and significantly increases the computation time. In terms of population size, increasing the population size enhances the search efficiency of the algorithm. Nonetheless, once the population size exceeds a certain threshold, the enhancement in search capability becomes negligible, whilst the computational time continues to increase.

Table 9.
Algorithm parameter analysis.
5.2. Solution Result Analysis
In order to validate the effectiveness of the jointly optimized tugboat–berth scheduling scheme derived in this study, the final berth allocation diagram and the integrated scheduling plan are presented in Figure 10 and Table 10. In Figure 10, the rectangular blocks represent the times when each ship berths and departs from the berth with the assistance of tugboats. Further details are provided in Table 10, including the berth assigned to each arriving ship and the tugboat numbers assigned to its berthing and unberthing tasks. It is evident that the berth allocation scheme and the tugboat assignment outlined in this study are both effective and feasible.
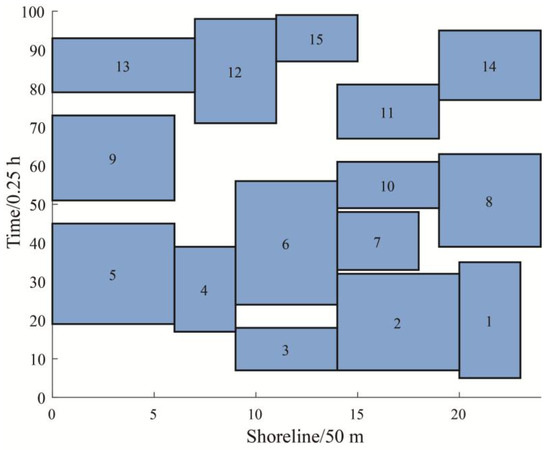
Figure 10.
Berth allocation diagram.

Table 10.
Joint scheduling scheme for tugboats and berths.
Figure 11 presents a Gantt chart outlining the scheduling of tugboats, providing a comprehensive representation of the assignments allocated to each tugboat and the charging strategy employed within the scheduling framework of the hybrid tugboat. Figure 11 clearly shows the time periods during which each tugboat performs various tasks within the scheduling period. Taking tugboat 4 as an example, the first task in its scheduling period is the berthing task for ship 3. However, because it initially departs from a port berth, a transit to the anchorage is required before ship 3 can be assisted to the berth. Subsequently, tugboat 4 is dispatched again to the anchorage to perform the berthing of ship 4. The third task for tugboat 4 during the scheduling horizon is the unberthing of ship 3. It is evident that, given the tugboat has already been berthed following the completion of the berthing process for ship 4, there is no requirement for empty sailing before the unberthing of ship 3 is carried out. Subsequent operations follow the same pattern.
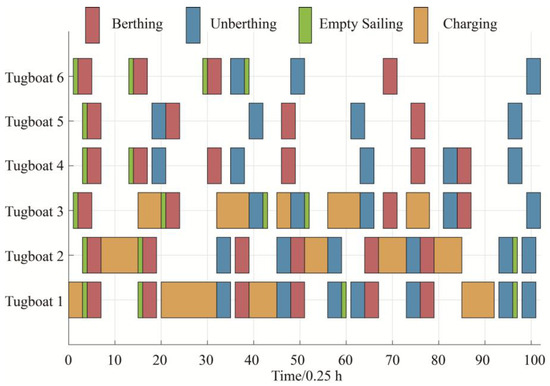
Figure 11.
Tugboat scheduling Gantt chart.
The example in this paper includes three new energy hybrid tugboats, and Figure 11 shows the charging time periods (yellow rectangular sections) for each hybrid tugboat during the scheduling period. In this example, only one charging connector is available at the port, so at any given time only one hybrid tugboat can be charged. As shown in Figure 11, the charging time periods for the hybrid tugboats do not overlap at any given time, indicating that no time point involves more than one yellow rectangular section simultaneously. Therefore, the hybrid tugboat charging strategy derived in this paper can be considered effective and feasible.
5.3. Sensitivity Analysis
In this particular instance, the number of hybrid tugboats and charging connectors is 3 and 1, respectively. This paper further explores the impact of charging connector quantity on the scheduling outcomes. As illustrated in Table 11, the total scheduling cost, total diesel consumption and total electricity consumption of tugboats are presented, contingent on the quantity of charging connectors utilized. The analysis indicates that an increase in the number of charging connectors has a beneficial effect on total scheduling costs and diesel consumption, while simultaneously increasing the total electricity consumption of hybrid tugboats. The rationale behind this phenomenon is that the augmentation of charging connectors facilitates the concurrent charging of multiple tugboats, thereby diminishing charging wait times and enhancing the utilization efficiency of hybrid tugboats.

Table 11.
Analysis of the impact of charging connector quantity.
However, once the number of charging connectors reaches a threshold, adding more connectors does not significantly reduce the total cost. This occurs because once the number of charging connectors is sufficient to meet the electricity demand of hybrid tugboats, the benefits of adding more connectors diminish, and at that point, the idle rate of the connectors increases. For instance, in Table 11, the total scheduling cost with two charging connectors is nearly identical to that with three charging connectors.
In order to further explore the combined impact of charging rate, battery capacity, and the number of tugboat charging connectors on scheduling, a comprehensive sensitivity analysis is conducted for different numbers of charging connectors, as shown in Figure 12, with the number of hybrid tugboats fixed at four.
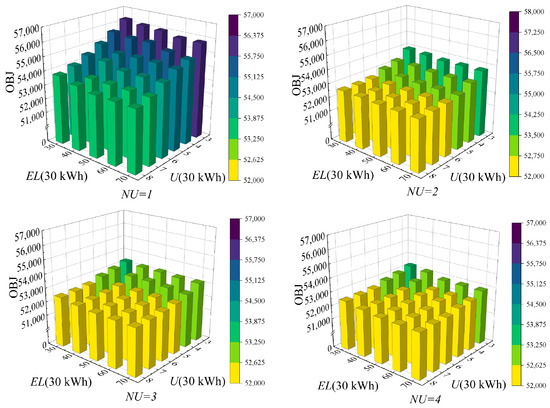
Figure 12.
Comprehensive sensitivity analysis.
From the perspective of battery capacity, increasing the battery capacity helps improve the energy endurance of hybrid tugboats, thereby reducing operational costs. However, when the number of charging connectors is limited, its impact on reducing total costs remains relatively marginal. The capacity of the battery is capable of being increased in order to extend the operating time of the hybrid tugboat; however, if the number of charging connectors is not increased accordingly, charging efficiency will still fall short of demand. Consequently, reliance on merely augmented battery capacity is inadequate to achieve a substantial enhancement in the operational efficiency of hybrid tugboats.
From the perspective of charging rate, an increase in the charging rate has been shown to reduce the charging time of hybrid tugboats, thereby lowering operational costs. Furthermore, it is worth noting that the aforementioned aspect serves to provide a certain degree of partial compensation for the restricted number of tugboat charging connectors. However, it is important to note that the charging rate of hybrid tugboats is subject to limitations in practice. It can thus be concluded that in circumstances where the number of charging connectors is restricted, an increase in the charging rate will only have a negligible effect on the reduction in total costs.
It is important to note that, when either battery capacity or charging rate is set to a relatively low value, the effect on reducing total costs remains limited, despite consideration of both parameters. However, it is evident that the establishment of appropriate values for both parameters has the capacity to result in a substantial reduction in operational costs.
It is evident that, by judiciously calibrating the battery capacity and charging rate parameters, it is possible to achieve a reduction in the overall operational costs of hybrid tugboats, even in the absence of an equivalent number of charging connectors. This can be accomplished through the implementation of efficient scheduling optimization and charging strategies. Furthermore, this approach has the potential to diminish the construction costs of charging facilities.
6. Conclusions
To improve the operational efficiency of the port’s seaward side and align with the development trend of green ports, this study develops a mixed-integer linear programming model for the joint scheduling of new energy hybrid tugboats and berths considering shore power constraints. A two-stage solution algorithm combining CPLEX with a heuristic whale optimization algorithm is designed based on the problem characteristics. The berth allocation plan obtained in the first stage by CPLEX is imported into the second stage to solve the tugboat scheduling problem, effectively enhancing the algorithm’s search efficiency and solution quality. The conclusions drawn from the experimental data are as follows:
- (1)
- The joint scheduling MILP model developed is effective. For small-scale examples, the algorithm in this paper can generate feasible scheduling solutions that are close to the exact solution in a short time. Furthermore, the utilization of a heuristic initial solution strategy has been demonstrated to have a substantial impact on the algorithm’s search efficiency.
- (2)
- The number of charging connectors for hybrid tugboats has a significant impact on the total scheduling cost. In scenarios where the number of charging connectors is limited, it becomes challenging to achieve a reduction in the overall scheduling cost. The required number of charging connectors should be determined according to the scheduling requirements of hybrid tugboats.
- (3)
- The appropriate values for the number of charging connectors, battery capacity, and charging rate for hybrid tugboats significantly affect the total scheduling cost. When battery capacity and charging rate values are appropriately selected, configuring a number of charging connectors different from the number of hybrid tugboats can still effectively reduce the tugboat operational costs. Consequently, the port authority can reduce the number of tugboat charging facilities to a certain extent.
Future research can be extended to the joint scheduling of other port resources, such as new energy tugboats, berths, and quay cranes, while considering additional factors such as time of use price and uncertainties in operation time. Moreover, extant research on the joint scheduling of tugboats and berths predominantly concentrates on a solitary terminal. Hence, subsequent research could delve deeper into the problem across multiple terminals. From an algorithmic perspective, the solution method adopted in this study still shows certain deviations from the exact solution in some cases. Future work should therefore explore more efficient and accurate algorithms for new energy tugboat scheduling.
Author Contributions
Conceptualization, L.C., J.L. and X.X.; methodology, L.C., J.L. and X.X.; software, J.L. and Z.Y.; validation, J.L. and Z.Y.; formal analysis, J.L.; investigation, L.C.; resources, L.C. and J.L.; data curation, L.C. and J.L.; writing—original draft preparation, L.C. and J.L.; writing—review and editing, L.C., J.L. and X.X.; visualization, J.L. and Z.Y.; supervision, L.C., Q.Y. and Z.Y.; project administration, L.C. and Q.Y.; funding acquisition, L.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Social Science Fund of China (grant number 24BGL282).
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding authors.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Iris, Ç.; Lam, J.S.L. A Review of Energy Efficiency in Ports: Operational Strategies, Technologies and Energy Management Systems. Renew. Sustain. Energy Rev. 2019, 112, 170–182. [Google Scholar] [CrossRef]
- Wang, S.; Kaku, I.; Chen, G.Y.; Zhu, M. Research on the Modeling of Tugboat Assignment Problem in Container Terminal. Adv. Mater. Res. 2012, 433–440, 1957–1961. [Google Scholar] [CrossRef]
- Wang, S.; Zhu, M.; Kaku, I.; Chen, G.; Wang, M. An Improved Discrete PSO for Tugboat Assignment Problem under a Hybrid Scheduling Rule in Container Terminal. Math. Probl. Eng. 2014, 2014, 714832. [Google Scholar] [CrossRef]
- Kang, L.; Meng, Q.; Tan, K.C. Tugboat Scheduling under Ship Arrival and Tugging Process Time Uncertainty. Transp. Res. Part E Logist. Transp. Rev. 2020, 144, 102125. [Google Scholar] [CrossRef]
- Hao, L.; Jin, J.G.; Zhao, K. Joint Scheduling of Barges and Tugboats for River–Sea Intermodal Transport. Transp. Res. Part E Logist. Transp. Rev. 2023, 173, 103097. [Google Scholar] [CrossRef]
- Xu, Q.; Mao, J.; Jin, Z. Simulated Annealing-Based Ant Colony Algorithm for Tugboat Scheduling Optimization. Math. Probl. Eng. 2012, 2012, 246978. [Google Scholar] [CrossRef]
- Zhen, L.; Wang, K.; Wang, S.; Qu, X. Tug Scheduling for Hinterland Barge Transport: A Branch-and-Price Approach. Eur. J. Oper. Res. 2018, 265, 119–132. [Google Scholar] [CrossRef]
- Wei, X.; Jia, S.; Meng, Q.; Tan, K.C. Tugboat Scheduling for Container Ports. Transp. Res. Part E Logist. Transp. Rev. 2020, 142, 102071. [Google Scholar] [CrossRef]
- Jia, S.; Li, S.; Lin, X.; Chen, X. Scheduling Tugboats in a Seaport. Transp. Sci. 2021, 55, 1370–1391. [Google Scholar] [CrossRef]
- Zhu, S.; Gao, J.; He, X.; Zhang, S.; Jin, Y.; Tan, Z. Green Logistics Oriented Tug Scheduling for Inland Waterway Logistics. Adv. Eng. Inform. 2021, 49, 101323. [Google Scholar] [CrossRef]
- Zhong, H.; Zhang, Y.; Gu, Y. A Bi-Objective Green Tugboat Scheduling Problem with the Tidal Port Time Windows. Transp. Res. Part Transp. Environ. 2022, 110, 103409. [Google Scholar] [CrossRef]
- Li, B.; Chen, Q.; Lau, Y.; Dulebenets, M.A. Tugboat Scheduling with Multiple Berthing Bases under Uncertainty. J. Mar. Sci. Eng. 2023, 11, 2180. [Google Scholar] [CrossRef]
- Wang, X.; Liang, Y.; Wei, X.; Chew, E.P. An Adaptive Large Neighborhood Search Algorithm for the Tugboat Scheduling Problem. Comput. Ind. Eng. 2023, 177, 109039. [Google Scholar] [CrossRef]
- Sun, C.; Li, M.; Chen, L.; Chen, P. Dynamic Tugboat Scheduling for Large Seaports with Multiple Terminals. J. Mar. Sci. Eng. 2024, 12, 170. [Google Scholar] [CrossRef]
- Imai, A.; Nishimura, E.; Papadimitriou, S. The Dynamic Berth Allocation Problem for a Container Port. Transp. Res. Part B Methodol. 2001, 35, 401–417. [Google Scholar] [CrossRef]
- Prencipe, L.P.; Marinelli, M. A Novel Mathematical Formulation for Solving the Dynamic and Discrete Berth Allocation Problem by Using the Bee Colony Optimisation Algorithm. Appl. Intell. 2021, 51, 4127–4142. [Google Scholar] [CrossRef]
- Umang, N.; Bierlaire, M.; Vacca, I. Exact and Heuristic Methods to Solve the Berth Allocation Problem in Bulk Ports. Transp. Res. Part E Logist. Transp. Rev. 2013, 54, 14–31. [Google Scholar] [CrossRef]
- Kordić, S.; Davidović, T.; Kovač, N.; Dragović, B. Combinatorial Approach to Exactly Solving Discrete and Hybrid Berth Allocation Problem. Appl. Math. Model. 2016, 40, 8952–8973. [Google Scholar] [CrossRef]
- Ernst, A.T.; Oğuz, C.; Singh, G.; Taherkhani, G. Mathematical Models for the Berth Allocation Problem in Dry Bulk Terminals. J. Sched. 2017, 20, 459–473. [Google Scholar] [CrossRef]
- Venturini, G.; Iris, Ç.; Kontovas, C.A.; Larsen, A. The Multi-Port Berth Allocation Problem with Speed Optimization and Emission Considerations. Transp. Res. Part Transp. Environ. 2017, 54, 142–159. [Google Scholar] [CrossRef]
- Cheimanoff, N.; Fontane, F.; Kitri, M.N.; Tchernev, N. A Reduced VNS Based Approach for the Dynamic Continuous Berth Allocation Problem in Bulk Terminals with Tidal Constraints. Expert Syst. Appl. 2021, 168, 114215. [Google Scholar] [CrossRef]
- Martin-Iradi, B.; Pacino, D.; Ropke, S. An Adaptive Large Neighborhood Search Heuristic for the Multi-Port Continuous Berth Allocation Problem. Eur. J. Oper. Res. 2024, 316, 152–167. [Google Scholar] [CrossRef]
- Iris, Ç.; Lam, J.S.L. Recoverable Robustness in Weekly Berth and Quay Crane Planning. Transp. Res. Part B Methodol. 2019, 122, 365–389. [Google Scholar] [CrossRef]
- Yang, Z.-Y.; Cao, X.; Xu, R.-Z.; Hong, W.-C.; Sun, S.-L. Applications of Chaotic Quantum Adaptive Satin Bower Bird Optimizer Algorithm in Berth-Tugboat-Quay Crane Allocation Optimization. Expert Syst. Appl. 2024, 237, 121471. [Google Scholar] [CrossRef]
- Chu, L.; Zhang, J.; Chen, X.; Yu, Q. Optimization of Integrated Tugboat–Berth–Quay Crane Scheduling in Container Ports Considering Uncertainty in Vessel Arrival Times and Berthing Preferences. J. Mar. Sci. Eng. 2024, 12, 1541. [Google Scholar] [CrossRef]
- Wang, Y.; Zou, T. Optimization of Berth-Tug Co-Scheduling in Container Terminals under Dual-Carbon Contexts. J. Mar. Sci. Eng. 2024, 12, 684. [Google Scholar] [CrossRef]
- Fan, H.; Zhang, T.-H.; Zhao, J.; Yue, L.-J. Berth Allocation and Tugboat Scheduling Problem for Tidal Ports with Compound Channels: The Case of Tianjin Port. Ocean Eng. 2025, 324, 120744. [Google Scholar] [CrossRef]
- Kumar, B.A.; Selvaraj, R.; Desingu, K.; Chelliah, T.R.; Upadhyayula, R.S. A Coordinated Control Strategy for a Diesel-Electric Tugboat System for Improved Fuel Economy. IEEE Trans. Ind. Appl. 2020, 56, 5439–5451. [Google Scholar] [CrossRef]
- Karaçay, Ö.E.; Özsoysal, O.A. Techno-Economic Investigation of Alternative Propulsion Systems for Tugboats. Energy Convers. Manag. X 2021, 12, 100140. [Google Scholar] [CrossRef]
- Devarapali, S.; Manske, A.; Khayamim, R.; Jacobs, E.; Li, B.; Elmi, Z.; Dulebenets, M.A. Electric Tugboat Deployment in Maritime Transportation: Detailed Analysis of Advantages and Disadvantages. Marit. Bus. Rev. 2024, 9, 263–291. [Google Scholar] [CrossRef]
- Chen, Y.-S.; Chang, T.-L.; Tsai, M.-C. Research on Adoption of Hybrid Electric Tugboats for Achieving Carbon Reduction Emissions in Taiwan. Mar. Pollut. Bull. 2025, 217, 118081. [Google Scholar] [CrossRef]
- Iris, Ç.; Lam, J.S.L. Optimal Energy Management and Operations Planning in Seaports with Smart Grid While Harnessing Renewable Energy under Uncertainty. Omega 2021, 103, 102445. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhu, Y.; Zhu, J.; Huang, D.; Yin, C.; Li, J. Collaborative Optimization of Shore Power and Berth Allocation Based on Economic, Environmental, and Operational Efficiency. J. Mar. Sci. Eng. 2025, 13, 776. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The Whale Optimization Algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).