A Lightweight Deep Learning Framework with Reduced Computational Overhead for Ship Detection in Satellite SAR Imagery

Abstract

Ship detection plays a pivotal role in safeguarding maritime security, regulating vessel traffic, and bolstering national maritime defense. While contemporary lightweight models predominantly emphasize parameter reduction, efforts to curtail computational demands remain underexplored. In this study, we propose a lightweight multi-feature channel convolution module (MFC-Conv) to create an efficient backbone network. This module adeptly propagates multi-scale feature information, yielding a holistic representation while approximating residual architectures in a computationally frugal manner, thereby promoting seamless gradient flow during optimization. Notably, MFC-Conv can be re-parameterized into a streamlined two-layer convolutional structure devoid of branching or partitioning, streamlining deployment on resource-constrained edge devices. Complementing this, a multi-feature attention module (MFA) is proposed to augment localization and classification efficacy with negligible overhead. Furthermore, leveraging the inherent resolution traits of satellite SAR imagery, the decoder is refined to minimize redundant computations. Empirical evaluations across diverse datasets reveal that our framework outperforms the baseline by slashing parameters by 57.8% and FLOPs by 42.7%. Relative to two leading lightweight state-of-the-art (SOTA) models, it achieves computational reductions of 51.4% and 25.0%, respectively, thereby enabling viable onboard satellite deployment for ship detection.

1. Introduction

Ship detection is a critical task in the field of marine affairs. As a key technological advancement, it supports the advancement of national marine economies, safeguards maritime rights and interests, and facilitates the intelligent transformation of the shipping industry. This technology has wide-ranging applications, including ensuring shipping safety, maintaining maritime traffic, supporting marine environmental protection, providing rescue services, and enhancing national maritime security control [1,2,3,4].

In the field of ship detection, high-frequency surface wave radars (HFSWRs) [5,6,7] have long served as a widely used ground-based sensing technology. It offers several advantages, including real-time monitoring capability, rich motion information, and relatively low operational costs. However, its limited spatial resolution prevents the extraction of detailed image features, its positioning accuracy is modest, and its detection range does not extend to deep-sea targets. These limitations significantly constrain its applicability across broader maritime scenarios. Traditional satellite-based ship detection methodologies have relied on optical, infrared, and microwave remote sensing modalities. Initially, optical-based approaches dominated, harnessing visible or infrared imagery to exploit color, morphology, and textural cues [8,9,10]. Despite their interpretability, these techniques are inherently vulnerable to atmospheric perturbations, with inclement weather precipitating marked declines in efficacy. Moreover, optical sensors preclude uninterrupted, all-weather surveillance. The continuous advancement of synthetic aperture radar (SAR) technology has propelled SAR as the modality of choice for ship detection [11,12]. Unlike optical data, SAR exhibits resilience to meteorological and illuminative variability, penetrating obfuscating phenomena like clouds and fog to enable persistent, round-the-clock monitoring. Moreover, maritime ships, especially those constructed from metallic materials, exhibit distinct radiometric characteristics in microwave remote sensing, often showing strong backscattering coefficients. These features effectively overcome the limitations of optical imaging systems.

Pioneering detection paradigms hinged on manually designed features, such as Histogram of Oriented Gradients (HOG) [13] and Deformable Part Model (DPM) [14], which suffered from limited generalization ability and poor adaptability to complex scenes. Subsequently, the task of object detection was advanced by models such as Region-based Convolutional Neural Networks (R-CNN) [15], Fast Region-based Convolutional Network (Fast R-CNN) [16], and Faster Region-based Convolutional Network (Faster R-CNN) [17], which adopted a two-stage detection framework. While these models provided significant advancements, they are relatively slow in computation and involve large numbers of parameters. Additionally, due to their reliance on fixed anchor boxes, their positioning accuracy is limited, and they struggle to detect small targets effectively. The introduction of the You Only Look Once (YOLO)v1-YOLOv3 series [18,19,20] marked a shift toward one-stage algorithms, significantly improving computational speed compared to earlier models. Subsequently, with the release of YOLOv5-YOLOv7 [21,22,23], dynamic anchor boxes were incorporated, enhancing the boundary accuracy of target detection. The latest iterations, YOLOv8-YOLOv12 [24,25,26,27,28], have adopted an anchor-free design, which further enhances the detection accuracy of small targets. Building upon these YOLO models, advanced methods for small target detection have emerged, including feature enhancement, fusion and context aware YOLO (FFCA-YOLO) [29] and faster and better for real-time YOLO (FBRT-YOLO) [30]. In recent years, alongside the YOLO series, transformer-based models [31] utilizing global attention mechanisms, such as real-time detection transformer (RT-DETR) [32], and models like efficient object detection V2 (EfficientDet-V2) [33], which offer self-supervised pre-training capabilities, have been developed. Some researchers have employed pruning techniques together with knowledge distillation to achieve both compact model size and low computational cost [34]. These models provide high accuracy and advanced features. However, despite their strengths, they are characterized by large model parameters and high computational demands. Additionally, their ability to capture small targets remains limited, making them less suitable for processing the vast amounts of data generated by maritime satellite monitoring.

Therefore, this study leverages SAR imagery to develop a lightweight, all-weather ship detection framework, prioritizing computational efficiency over mere parameter reduction, as 1M–3M parameters pose minimal burden on satellite-edge devices. We designed the Multi-Feature Channel Convolution (MFC-Conv) module to build an efficient backbone, enabling multi-scale feature propagation, lightweight residual approximation for improved gradient flow, and reparameterization into a branch-free dual-layer convolution for seamless edge deployment. The Multi-Feature Attention (MFA) module was incorporated to boost localization and classification with low overhead. Exploiting the limited scale variation in SAR vessel targets, the decoder was optimized by eliminating redundant heads, reducing computations and mitigating background noise. The main contributions are as follows:

• We unveiled MFC-Conv, a module that concurrently diminishes parameters and FLOPs, elevating operational efficiency, with reparameterization to dual convolutions for edge-device compatibility.
• An efficient emulation of residual blocks was introduced, balancing lightweight design with enhanced training dynamics.
• A novel multi-feature attention (MFA) module was proposed, which enhanced the model’s localization and recognition capabilities, improving overall detection accuracy.
• Exploiting SAR-specific traits, the decoder was rationalized, yielding reductions in parameters and computations while mitigating clutter and refining target acuity.

The remainder of this paper proceeds as follows: Section 2 presents the proposed method, elaborating on the structure of the key modules and the loss function used for training; Section 3 reports the experimental environment and parameter design of this paper, and conducts comparative tests on three datasets to evaluate the proposed method and other recent methods; Section 4 discusses the effectiveness of each module proposed in this paper, and also examines the impact of different parameter settings on the results; and finally, Section 5 summarizes the above results and presents the final conclusion.

2. Methodology

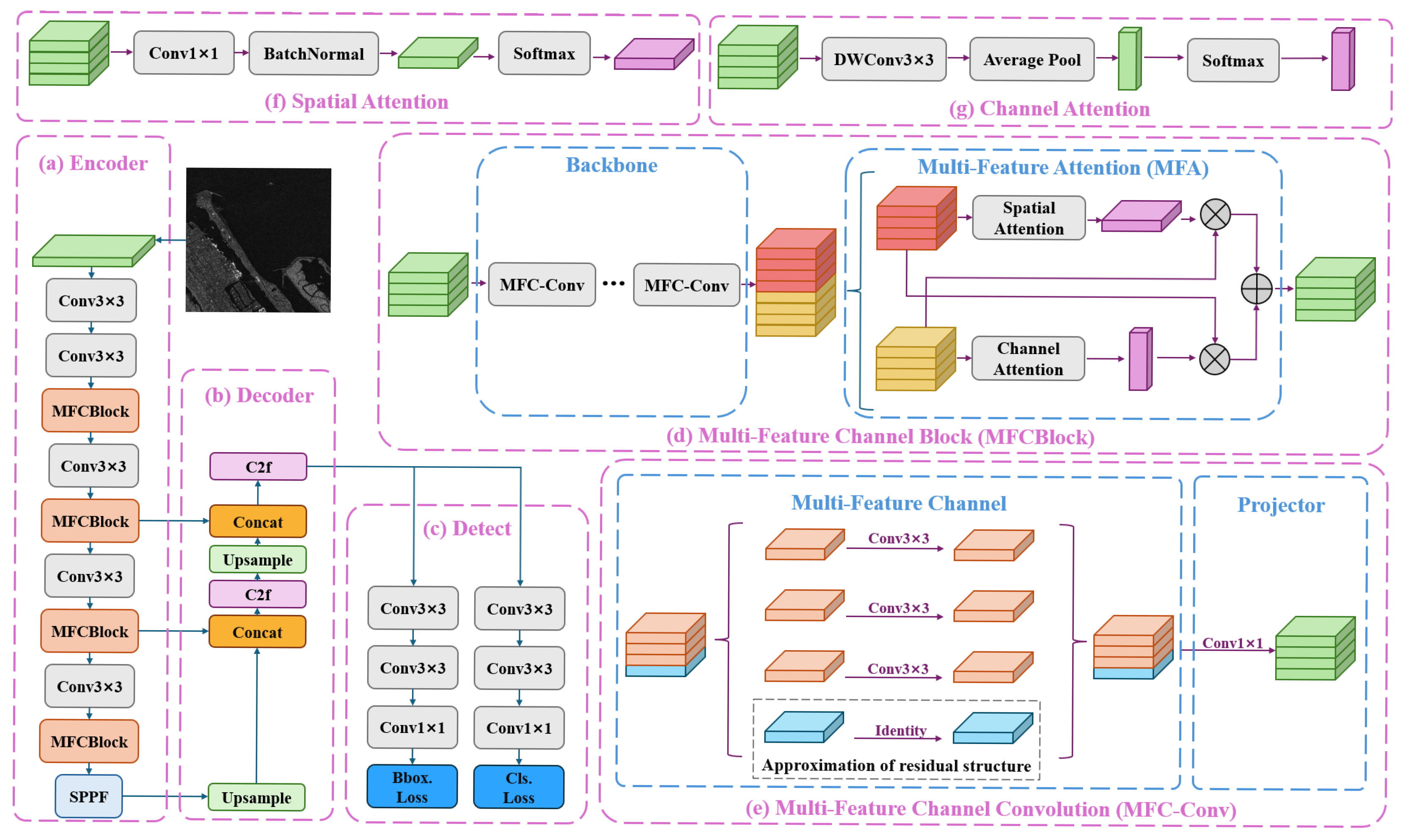
Our framework, MFCNet, as illustrated in Figure 1, builds upon the YOLOv8n model as the baseline through pivotal enhancements tailored to satellite SAR imagery. Firstly, we modified the decoder to better accommodate the characteristics of satellite SAR images, in which ship targets are typically small and may comprise only a few dozen pixels. In target detection tasks, such targets are classified as small objects. Consequently, the detect module responsible for identifying targets of other sizes can be pruned. By removing the unnecessary detect module, we reduce the model’s computational cost while allowing it to focus more effectively on learning the features of small ship targets. Second, we introduce the MFC-Conv to construct a new backbone. This modification further reduces the model’s computational cost, with only a slight trade-off in accuracy. Lastly, we integrate the MFA module on top of MFC-Conv. By leveraging the diverse feature information provided by MFC-Conv, MFA enhances both the spatial and channel aspects, significantly improving the model’s ability to recognize and localize targets. The overall architecture of the model is shown in the figure below:

In the Encoder section (as depicted in Figure 1a), all 3 × 3 convolutions within MFCNet are followed by a batch normalization layer and the SiLU activation function [35] to yield the resultant features. In this section, all independent 3 × 3 convolutions are configured with a stride of two, which serves to reduce the spatial resolution of the feature maps, thereby decreasing subsequent computational costs while simultaneously enlarging the receptive field of the deep model. In the decoder section (as depicted in Figure 1b), the upsampling module doubles the spatial resolution to align the feature maps with the subsequent concatenation layer in terms of spatial scale. In the detect section (as depicted in Figure 1c), the 3 × 3 convolutions across the dual branches emulate those in the primary pathway, with their outputs subsequently normalized via batch normalization and activated using SiLU. The terminal 1 × 1 convolution layer undergoes no additional post-processing.

2.1. Multi-Feature Channel Convolution

As shown in Figure 1e, the MFC-Conv module incorporates multiple feature channels, allowing for the simultaneous processing of several sets of feature information within a single layer. In each feature channel, a 3 × 3 convolution is employed to further extract features with high parameter and computational efficiency. This design ensures the overall computational efficiency of the model while maintaining compatibility with convolution acceleration algorithms. Furthermore, MFC-Conv includes an approximation of residual structure, enabling the model to retain essential shallow features while also facilitating the extraction of deeper features. Furthermore, just like the typical residual structure, it enables the gradient to be efficiently propagated during the training process, thereby enhancing the training performance of deep models. Finally, after completing feature extraction, a linear projection is applied along the channel direction to filter out the information requiring further extraction, as well as to preserve the necessary shallow features. The equation is expressed as follows:

$$(X^0, X^1, X^2, X^3)=Split\left(X^{input}\right),$$

(1)

$$Y^{\left(i\right)}=SiLu\left(BN(W_1^{\left(i\right)}\ast X^{\left(i\right)}+B_1^{\left(i\right)})\right)i\in [1, 2],$$

(2)

$$O=SiLu(BN(W_2\times Concat(Y^{\left(0\right)}, Y^{\left(1\right)}, Y^{\left(2\right)}, X^3)+B_2)),$$

(3)

where $X_{input}$ represents the model’s input. Through the split operation, the input is evenly divided into four parts, $X^0$ to $X^3$, along the channel dimension. The first three components are processed according to Equation (2), where the subscript (i) denotes the index corresponding to each input branch. $W_1^{\left(i\right)}$ and $B_1^{\left(i\right)}$ represent the weights and biases of the corresponding convolutional layers respectively. BN denotes the batch normalization layer, and SiLU is the activation function. Finally, in Equation (3), the outputs $Y^0$ to $Y^2$ obtained from Equation (2), together with $X^3$ from Equation (1), are concatenated along the channel dimension for fusion. The merged result is then processed through a convolutional layer, followed by batch normalization and the SiLU activation function, to produce the final output of the module.

The MFC-Conv module enhances parameter utilization efficiency by introducing multiple feature channels, thereby mitigating feature interference and reducing both the number of parameters and computational cost while maintaining model performance. MFC-Conv adopts an approximation of residual structure, which facilitates the downward transmission of shallow features and the upward propagation of error gradients during training. This design not only lowers computational costs during inference but also minimizes memory consumption by avoiding the overhead typically introduced by complex branching structures.

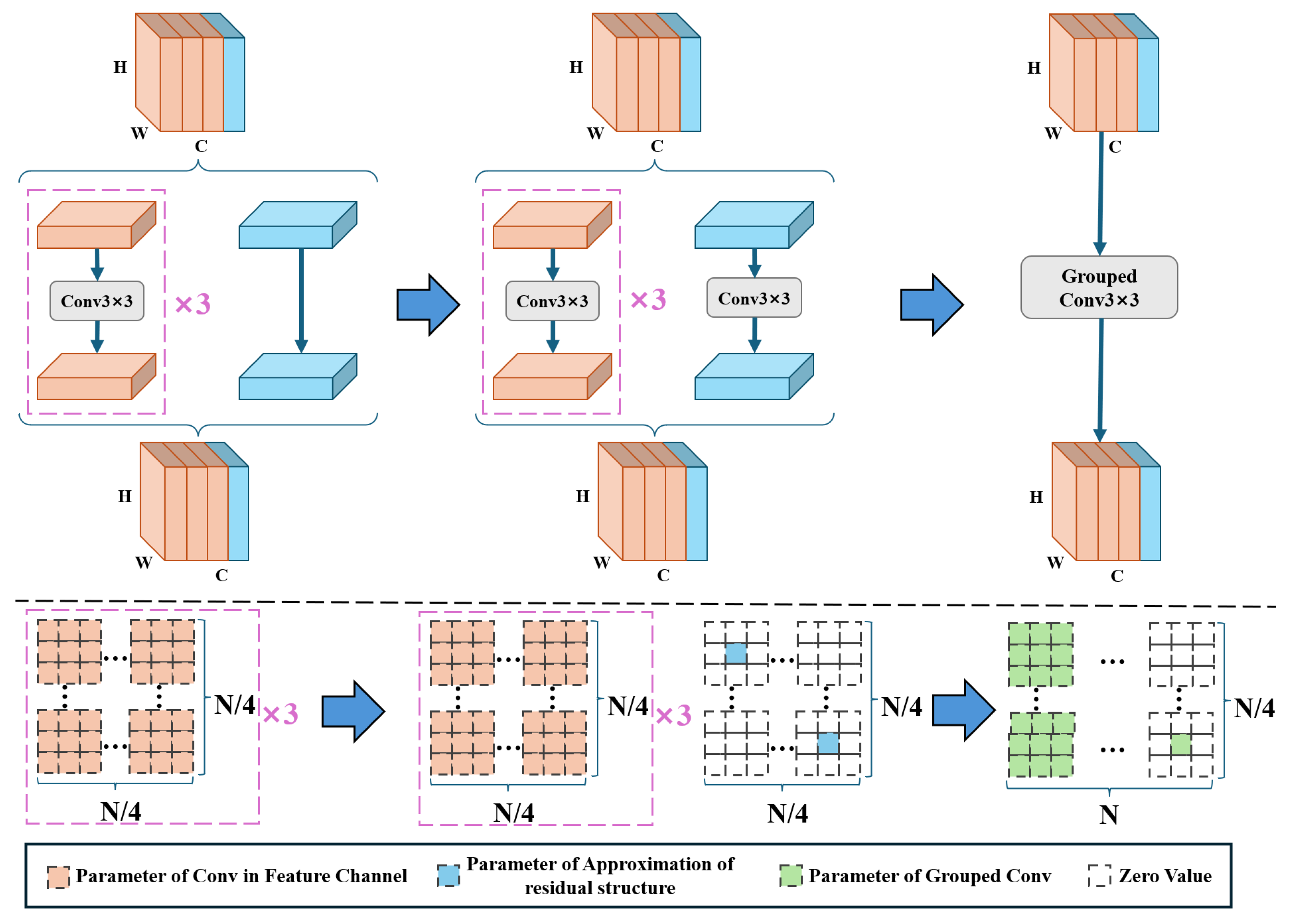
Furthermore, certain edge computing devices may provide only limited support for the split operation. To overcome this limitation, the first three convolutional branches in the MFC-Conv module can be seamlessly merged into a grouped convolution. The approximation of residual structure can also be equivalently transformed into a standard convolution by introducing a set of manually designed fixed parameters. As a result, the MFC-Conv module can be reconfigured, when necessary, into a simplified structure consisting of a 3 × 3 grouped convolution and a 1 × 1 standard convolution. This reconfiguration greatly enhances deployment efficiency on resource-constrained edge devices. The reconfiguration process is illustrated in the Figure 2.

The upper part of Figure 2 illustrates the structural evolution of the MFC-Conv module during the parameter reconstruction process, while the lower part shows the corresponding changes in the parameter structure. In this figure, the orange branch represents the multi-feature channel branch, and its parameters are depicted as orange squares. The blue branch denotes the approximation of residual structure, with the reconstructed parameters represented by blue squares, each assigned a value of one. The symbol N refers to the channel dimension of the input and output feature matrices. In the final step, the parameters from the four branches are integrated to form a grouped convolution with four groups. This design enables better adaptability to various types of deep learning edge computing devices.

2.2. Multi-Feature Attention

To enhance the model’s spatial localization and feature recognition capabilities, this study designs the MFA module based on the backbone constructed using the proposed MFC-Conv, leveraging its ability to transmit multi-level feature information. As illustrated in Figure 1d, the MFA module uses diverse feature channels propagated through the backbone network to generate both spatial and channel attention weights. These weights are then cross fused, complementing another set of features that lack corresponding information. The resulting features are subsequently aggregated and fused to produce an enhanced output that simultaneously strengthens both spatial and channel representations, thereby improving the overall performance of the model. The corresponding Equations are expressed as follows:

$$(X^{spatial}, X^{channel})=Split\left(X^{input}\right),$$

(4)

$$W_{attn}^{spatial}=Softmax\left(BN(W_s\times X^{spatial}+B_s)\right),$$

(5)

$$X_{dw}=W_{dw}\ast X^{channel}+B_{dw},$$

(6)

$$W_{attn}^{channel}=Softmax\left({\displaystyle \frac{1}{W\times H}}\sum _{i=0}^H\sum _{j=0}^W{X}_{dw}(i, j)\right),$$

(7)

$$O_{FCA}=W_{attn}^{channel}\times X^{spatial}+W_{attn}^{spatial}\times X^{channel}$$

(8)

The final 1 × 1 convolutional projection layer in the backbone’s MFC-Conv maps the output to twice the required number of channels. As shown in Equation (4), the input feature $X_{input}$ is divided into two independent data blocks, $X_{spatial}$ and $X_{channel}$, which are used to extract spatial and channel attention weights, respectively. This design prevents a single set of features from simultaneously containing spatial, channel, and object-level information, thereby providing dedicated and independent transmission pathways for spatial and channel features. As a result, the learning difficulty of the model is reduced. The computation of spatial weights is expressed in Equation (5), where $W_s$ and $B_s$ denote the weights and biases of a 1 × 1 convolution. The output is then processed by a batch normalization (BN) layer and a Softmax function to obtain the spatial attention weights. The calculation of channel weights is shown in Equations (6) and (7), where $W_{d}w$ and $B_{d}w$ represent the weights and biases of a 3 × 3 depth wise convolution. Each channel’s features are independently extracted through the depth wise convolution, followed by channel-wise average pooling and normalization using the Softmax activation function to produce the channel attention weights. Finally, the output of the MFA module is computed as shown in Equation (8). The channel weights are applied to the data block to refine spatial features, while the spatial weights are applied to enhance channel features. The two results are then combined through element-wise addition and fusion to generate the final output. This cross-attention mechanism compensates for the missing spatial or channel information in each feature subset, ultimately producing outputs with precise spatial localization and salient feature representation.

2.3. Loss Functions

In this paper, three loss functions [19] are employed to achieve accurate ship target detection. To determine the existence of a predicted bounding box, the binary cross-entropy loss, referred to as the classification loss (Cls loss), is utilized. Its equation is as follows:

$$L_{cls}=-{\displaystyle \frac{1}{N}}\sum _{n=1}^N[y_{n}log\left({\displaystyle \frac{1}{1+e^{-x_n}}}\right)+(1-y_n)log(1-{\displaystyle \frac{1}{1+e^{-x_n}}})],$$

(9)

where $y_n$ represents the true value in one-hot encoding, $x_n$ is the category logit output by the classification branch of the detect module of the model. N represents the number of candidate regions. The remaining two losses are box loss and DFL loss. These two are collectively referred to as bounding box loss (Bbox loss) and are calculated by the output of another branch of the detect module. Box loss is used to enhance the overlap between the predicted box and the real box. DFL loss optimizes the prediction of boundary positions and improves the robustness of the model. Their Equations are as follows:

$$IoU={\displaystyle \frac{Area(Bo{x}_{pre}\cap Bo{x}_{true})}{Area(Bo{x}_{pre}\cup Bo{x}_{true})}},$$

(10)

$$L_{box}=1-IoU,$$

(11)

$$L_{dfl}=-\sum [(\lceil y\rceil -y)log\left(S_1\right)+(y-\lfloor y\rfloor )log\left(S_2\right)]$$

(12)

The box loss is based on intersection over union (IoU), where $Bo{x}_{pre}$ represents the prediction box and $Bo{x}_{true}$ represents the ground truth box. For the DFL loss, y represents the value obtained by scaling the distance between one of the four boundaries and the center point of the true bounding box to the scale of the output feature. $S_1$ and $S_2$ are the predicted distribution probability values by the model for the two adjacent integer intervals where y lies. The overall loss is as follows:

$$L_{total}=w_{box}\times L_{box}+w_{dfl}\times L_{dfl}+w_{cls}\times L_{cls},$$

(13)

In this paper, the weighting parameters $w_{b}ox$, $w_{d}fl$, and $w_{c}ls$ are set to 7.5, 1.5, and 0.5, respectively.

3. Experiment Results

3.1. Dataset Description

This study leverages three benchmark datasets to assess the performance of the proposed model. The salient dataset attributes are tabulated in

Table 1. Basic parameters of the dataset.

Dataset Name	Sensors	Resolution	Image Count	Target Count	Train Count	Test Count
HRSID [36]	Sentinel-1BTerraSAR-XTanDEM-X	0.5 m 1 m 3 m	5604	16,951	3642	1962
SAR–Ship dataset [37]	GF-3 Sentinel-1	1–25 m	39,729	43,819	33,729	6000
SSDD [38]	RadarSat-2	1–15 m	1160	2456	928	232

:

The high-resolution SAR images for ship detection dataset (HRSID) and SAR–Ship dataset provide images with various imaging modes and resolutions, which can offer rich information on ship targets. The SAR ship detection dataset (SSDD) is a classic ship detection dataset. Due to its relatively small data scale and number of ship targets, it is used here as a supplementary dataset for comparison.

3.2. Experiment Setup

The software and hardware environments, along with the training parameter settings used in all experiments in this paper, are summarized in the

Table 2. Environment and training parameter configuration.

Hardware/Software	Value	Parameter Name	Value
CPU	i9-13900k	Input Size	800/256/544
GPU	RTX4090	Optimizer	SGD
Memory	128 G	Learning Rate	0.01
OS	Ubuntu22.04	Momentum	0.937
CUDA Version	12.1	Weight Decay	0.0005
Python Version	3.12	Batch Size	8/24/8
PyTorch Version	2.5.1	Epoch	300

. In addition, the training parameters are followed by YOLOv8 [24].

In this paper, three different evaluation metrics were used to assess the performance of the model. They were precision (P), recall (R), and mean average precision (mAP). Among them, mAP was divided into mAP50 and mAP50:95, which were used to evaluate the localization quality of the model’s predicted bounding boxes. Their equations are as follows:

$$P={\displaystyle \frac{TP}{TP+FP}},$$

(14)

$$R={\displaystyle \frac{TP}{TP+FN}},$$

(15)

$$AP={\int }_0^{1}P\left(R\right)dR,$$

(16)

$$mAP50={\displaystyle \frac{1}{C}}\sum _{c=1}^{C}A{P}_{c,50\%},$$

(17)

$$mAP50:95={\displaystyle \frac{1}{10\times C}}\sum _{t=50\%}^{95\%}\sum _{c=1}^{C}A{P}_{c,t},$$

(18)

where true positives (TP) encompass predicted bounding boxes exhibiting an Intersection over union (IoU) with their corresponding ground-truth counterparts at or exceeding the predefined threshold, without redundant matching. False positives (FP) include predictions with sub-threshold IoU or those exhibiting multiple matches, while false negatives (FN) denote unmatched ground-truth instances. The IoU metric is formalized in Equation (10). Herein, the confidence threshold for deriving precision (P) and recall (R) is established at 30%, with the IoU threshold fixed at 50%. Equation (16) delineates average precision (AP) as the integral under the precision–recall (PR) curve. In Equation (17), mAP50 quantifies the mean AP across all categories (C) at a fixed IoU threshold of 50%. Equation (18) computes mAP50:95 by averaging AP values over IoU thresholds spanning 50% to 95% in 5% increments. Precision (P) and recall (R) constitute foundational benchmarks, encapsulating the model’s discriminative accuracy and exhaustive coverage in target identification, respectively. Mean average precision (mAP) stands as the preeminent holistic metric in object detection, with mAP50 gauging coarse alignment proficiency and mAP50:95 appraising efficacy under rigorous localization exigencies.

3.3. Comparison

At present, the YOLO series continues to dominate the field of lightweight small object detection owing to its flexible and efficient architecture. Therefore, the comparative experiments in this study employ several representative YOLO models developed from 2023 onward, including YOLOv8, YOLOv10, YOLOv11, and YOLOv12. In addition, two SOTA lightweight models specifically designed for small object detection (FBRT-YOLO and FFCA-YOLO) are also included for comprehensive comparison.

3.3.1. Parameters and Computational Cost

The core objective of the proposed method is to develop an efficient and reliable lightweight deep learning model specifically tailored for satellite SAR image data. Existing lightweight models have already reduced their parameter counts to under 3M, which no longer imposes significant storage constraints on most edge devices used for ship detection tasks. Therefore, this work primarily focuses on optimizing the model’s computational cost, enabling direct deployment on edge computing platforms for efficient and real-time maritime data processing.

As shown in

Table 3. Comparison of parameters and computational cost.

Model	Parameters	FLOPs	FPS
YOLOv8n [24] (2023)	3.01 M	8.9 G	185.40
YOLOv10n [26] (2024)	2.70 M	8.4 G	186.38
YOLOv11n [27] (2024)	2.59 M	6.4 G	428.34
YOLOv12n [28] (2025)	2.57 M	6.5 G	261.60
FFCA-YOLO [29] (TGRS 2024)	0.93 M	10.5 G	278.73
FBRT-YOLO [30] (AAAI 2025)	0.85 M	6.8 G	524.40
MFCNet (Ours)	1.27 M	5.1 G	640.54

, the proposed model exhibits a clear advantage in computational cost, achieving a 42.70% reduction in computational cost compared with the baseline model (YOLOv8n), and reductions of 25.00% and 51.43% relative to the two latest SOTA models, FBRT-YOLO and FFCA-YOLO, respectively. In terms of real-time frame rate, the proposed method achieves 345.49% of the baseline’s frame rate. Compared with FBRT-YOLO and FFCA-YOLO, the frame rate of our method reaches 229.81% and 122.15%, respectively. Although the proposed method is not explicitly optimized for parameter minimization, it still outperforms the traditional YOLO series models and remains only slightly inferior to the two SOTA counterparts in terms of parameter count. The subsequent section presents the model’s performance evaluation across three benchmark datasets.

3.3.2. Comparison of Results on HRSID

Figure 3 presents an image from the HRSID test set along with the detection results produced by various models. Focusing first on the regions marked by blue circles, it can be observed that the ship targets in these areas are closely spaced, causing mutual interference in their backscattered signals. Additionally, since these targets are located near the image edges, their structural features appear incomplete. As a result of these adverse conditions, both the YOLO series models and the FFCA-YOLO model failed to accurately detect ships in this region. Although the FBRT-YOLO model successfully identified all ship targets within this complex area, as highlighted by the green circle in Figure 3g, it also produced false positives by misclassifying sea surface clutter and coastal structures as ships. Furthermore, as shown in the green circle in Figure 3f, YOLOv12n erroneously divided a single ship into multiple detections of varying sizes due to background noise interference. In contrast, MFCNet effectively enhances target feature representation and spatial localization through the MFA attention module while mitigating background noise via the decoder optimized for satellite SAR data. Consequently, it correctly detected all ship targets within this region. Only the target located in the lower-right corner of the blue circle exhibited slightly weaker bounding box localization, likely due to incomplete target information.

The quantitative evaluation results presented in

Table 4. Comparison of result on HRSID.

Model	P	R	mAP50	mAP50:95
YOLOv8n [24] (2023)	0.904	0.809	0.902	0.647
YOLOv10n [26] (2024)	0.894	0.829	0.903	0.677
YOLOv11n [27] (2024)	0.907	0.808	0.904	0.671
YOLOv12n [28] (2025)	0.901	0.823	0.904	0.670
FFCA-YOLO [29] (TGRS 2024)	0.910	0.837	0.919	0.692
FBRT-YOLO [30] (AAAI 2025)	0.902	0.837	0.918	0.668
MFCNet (Ours)	0.913	0.837	0.920	0.694

demonstrate that the proposed method achieves advantages on this dataset. In particular, the proposed model, along with the two SOTA counterparts, significantly outperforms the traditional YOLO series models on the HRSID dataset in terms of R and mAP50. Furthermore, regarding the precision-oriented metrics (P and mAP50:95), the proposed method attains an additional improvement of approximately 0.2% compared to the other SOTA models. These results indicate that, despite the substantial reduction in computational cost, the proposed model maintains strong recognition capabilities without compromising detection accuracy. Therefore, it can be regarded as an efficient and high-performance approach for ship target recognition in the SAR imagery.

3.3.3. Comparison of Results on SAR–Ship Dataset

For the SAR–Ship dataset, a total of 6000 images were randomly selected as the test set, accounting for approximately 15.1% of the entire dataset. Figure 4a presents one representative image from the test set. This image includes not only ship targets and land backgrounds but also multiple islands of varying sizes that act as interference factors. As indicated by the green and blue circles in the figure, all models were influenced by the presence of these small islands, leading to false detections where islands were mistakenly classified as ships. In addition, some models incorrectly identified the large island within the blue circle as a ship target. The model proposed in this paper effectively enhances target feature recognition by integrating the MFC-Conv-based backbone with the MFA attention module, thereby reducing the impact of small islands on detection. Moreover, the modified decoder helps mitigate the interference caused by large islands. As a result, the proposed model achieves accurate and efficient ship detection in this challenging scenario.

Table 5. Comparison of result on SAR–Ship dataset.

Model	P	R	mAP50	mAP50:95
YOLOv8n [24] (2023)	0.927	0.916	0.959	0.629
YOLOv10n [26] (2024)	0.921	0.911	0.956	0.626
YOLOv11n [27] (2024)	0.924	0.911	0.958	0.615
YOLOv12n [28] (2025)	0.919	0.916	0.956	0.611
FFCA-YOLO [29] (TGRS 2024)	0.923	0.911	0.958	0.613
FBRT-YOLO [30] (AAAI 2025)	0.927	0.917	0.958	0.622
MFCNet (Ours)	0.929	0.926	0.962	0.635

presents the performance of each model on the test subset of the SAR–Ship dataset, which aligns well with the analysis discussed above. On this dataset, the proposed model demonstrates improvements across all evaluation metrics. Compared with the baseline, the proposed model achieves gains of 0.2%, 1.0%, 0.3%, and 0.6% in P, R, mAP50, and mAP50:95, respectively. These results indicate that the proposed model effectively mitigates the impact of various types of noise, leading to more robust and reliable ship detection performance.

3.3.4. Comparison of Results on SSDD

Figure 5 presents the detection results of various models on an image from the SSDD dataset. Unlike the previous examples, the primary challenge in this image lies in accurately detecting densely distributed ship targets. As indicated by the blue circles in Figure 5e,f, YOLOv11n and YOLOv12n failed to correctly identify these dense ship targets, generating multiple incorrect bounding boxes. Similarly, in the regions marked by green circles, the traditional YOLO series models also produced a considerable number of false detections. In contrast, only the proposed MFCNet and the two SOTA models successfully identified all ship targets in this complex scene.

Table 6. Comparison of result on SSDD.

Model	P	R	mAP50	mAP50:95
YOLOv8n [24] (2023)	0.962	0.940	0.973	0.743
YOLOv10n [26] (2024)	0.943	0.902	0.957	0.715
YOLOv11n [27] (2024)	0.957	0.931	0.974	0.732
YOLOv12n [28] (2025)	0.950	0.921	0.965	0.725
FFCA-YOLO [29] (TGRS 2024)	0.954	0.949	0.984	0.738
FBRT-YOLO [30] (AAAI 2025)	0.973	0.932	0.976	0.735
MFCNet (Ours)	0.963	0.942	0.974	0.747

presents the accuracy metrics of each model on the SSDD test set. It can be observed that the proposed model and the two SOTA models outperform the traditional YOLO series models. The proposed model achieves the highest performance in precise localization, while FFCA-YOLO demonstrates stronger coarse localization capability, and FBRT-YOLO exhibits higher recognition accuracy. Overall, on the SSDD dataset, MFCNet achieves performance comparable to that of the two latest SOTA models.

4. Discussion

4.1. Ablation Experiment

To compare the effectiveness of each module of the model, we conducted ablation experiments on the decoder, the MFC-Conv backbone, and the MFA attention modules in each block, and verified them on the three datasets used in this paper. Firstly, the parameter quantities and computational cost under different configurations are as

Table 7. The parameters and computational cost of the ablation experiment.

Baseline	Decoder	MFC-Conv	MFA	Parameters	FLOPs
✓				3.01 M	8.9 G
✓	✓			1.61 M	6.1 G
✓	✓	✓		1.18 M	5.0 G
✓	✓	✓	✓	1.27 M	5.1 G

“✓” indicates the inclusion of the corresponding module.

.

It can be observed that by improving the decoder and introducing the MFC-Conv module proposed in this paper, the number of parameters and computational cost of the model have significantly decreased. The subsequently added MFA attention module only slightly increased the number of parameters and computational volume. The final model of this paper has reduced the parameter count by 57.8% and the computational cost by 42.7% compared to the baseline model. The

Table 8. Ablation experiment results.

Dataset	Baseline	Decoder	MFC-Conv	MFA	P	R	mAP50	mAP50:95
HRSID	✓				0.904	0.809	0.902	0.647
	✓	✓			0.913	0.836	0.917	0.682
	✓	✓	✓		0.912	0.829	0.914	0.673
	✓	✓	✓	✓	0.913	0.837	0.920	0.694
SAR–Ship dataset	✓				0.927	0.916	0.959	0.629
	✓	✓			0.929	0.919	0.961	0.627
	✓	✓	✓		0.924	0.920	0.958	0.623
	✓	✓	✓	✓	0.929	0.926	0.962	0.635
SSDD	✓				0.962	0.940	0.973	0.743
	✓	✓			0.960	0.936	0.976	0.744
	✓	✓	✓		0.944	0.921	0.967	0.735
	✓	✓	✓	✓	0.963	0.942	0.974	0.747

“✓” indicates the inclusion of the corresponding module.

presents the ablation experiment results for three datasets.

From the ablation experiment results on the above three datasets, it can be observed that the effects of each module are consistent with the expectations. The decoder simplified based on the resolution of the satellite SAR data reduces the computational load without causing any negative impact on the results. The backbone composed of MFC-Conv avoids the appearance of branch structures and further reduces the computational load, causing only a slight negative effect on the results. Finally, the added MFA module enhances the positioning and recognition capabilities, increasing a small amount of computational cost to improve the overall performance of the model.

4.2. Efficiency of MFA

To verify the effectiveness of the MFA attention module, we compared it with several other low-computation-volume attention mechanism modules, including channel attention, spatial attention, and CBAM [39]. The comparison results on the three datasets are shown in

Table 9. Comparison of the attention module.

Dataset	Attention	P	R	mAP50	mAP50:95
HRSID	Channel	0.903	0.837	0.917	0.694
	Spatial	0.909	0.834	0.917	0.676
	CBAM	0.913	0.834	0.918	0.690
	MFA	0.913	0.837	0.920	0.694
SAR–Ship dataset	Channel	0.931	0.924	0.960	0.630
	Spatial	0.927	0.916	0.957	0.620
	CBAM	0.923	0.926	0.958	0.619
	MFA	0.929	0.926	0.962	0.635
SSDD	Channel	0.974	0.923	0.982	0.740
	Spatial	0.962	0.929	0.980	0.729
	CBAM	0.972	0.912	0.979	0.746
	MFA	0.963	0.942	0.974	0.747

.

From the above results, it can be seen that the MFA module proposed in this paper can more effectively use the information transmitted by the main backbone composed of the MFC-Conv module, while improving the positioning accuracy of the target and the features of the target, thereby enhancing the overall accuracy of the model. Overall, the performance of MFA is superior to those of the other several low-computation-volume attention modules compared.

4.3. Feature Channels Experiment

The MFC-Conv module proposed in this study serves as the backbone of the model, and the selection of its internal feature channel number has a substantial influence on both the model’s overall performance and computational cost. Therefore, this subsection presents a comparative analysis of the model’s performance and computational cost under different channel configurations of the MFC-Conv module. The results across the three datasets are summarized in

Table 10. Compare the different numbers of feature channels.

Dataset	Channels	P	R	mAP50	mAP50:95
HRSID	2	0.916	0.839	0.920	0.676
	4	0.913	0.837	0.920	0.694
	8	0.917	0.829	0.918	0.693
SAR–Ship dataset	2	0.931	0.930	0.966	0.941
	4	0.929	0.926	0.962	0.935
	8	0.932	0.927	0.964	0.936
SSDD	2	0.969	0.940	0.983	0.952
	4	0.963	0.942	0.974	0.947
	8	0.960	0.930	0.970	0.938

.

From the data presented above, it can be observed that the model achieves higher overall performance when the number of feature channels is relatively small. However, as the number of channels increases, the limited amount of information contained within each channel becomes insufficient for effective feature transmission, which negatively impacts performance. For the backbone of a lightweight model, it is essential not only to consider the final performance but also to account for variations in computational cost.

Table 11. Compare the number of parameters with the computational cost.

Channels	Parameters	FLOPs
2	1.34 M	5.4 G
4	1.27 M	5.1 G
8	1.20 M	5.0 G

presents the number of parameters and computational load of the model under different feature channel configurations.

From the table above, it can be observed that when the number of feature channels is set to two, four, or eight, the differences in computational cost between adjacent configurations are approximately 5.9% and 2%, respectively. This indicates that as the number of feature channels increases, the computational efficiency gains gradually diminish. Moreover, when the number of feature channels is set to two or four, the variations in model accuracy across all evaluation metrics remain within 1%. Therefore, considering the trade-off between accuracy and computational efficiency, the configuration with four feature channels is ultimately selected as the standard setting for the MFC-Conv module.

4.4. The Current Shortcomings and Future Tasks

In the current implementation of the proposed model, all MFC-Conv modules use the same number of feature channels. However, the amount and complexity of feature information vary across different network depths. To optimize feature transmission and further reduce computational cost, it would be beneficial to assign different channel configurations to MFC-Conv modules at different depths. Future work will focus on a more comprehensive investigation of this aspect, analyzing the effects of various channel allocation strategies on ship target recognition performance in the SAR data. The goal is to achieve higher detection accuracy while maintaining an optimal balance between model efficiency and computational cost.

Regarding the influence of weather conditions on model accuracy, the special physical properties of the microwave signals used by satellite SAR ensure that fog and cloud cover cause virtually no interference, resulting in negligible impact on detection performance. However, heavy precipitation can induce scattering of the microwave signal, weakening the returned echoes and slightly reducing recognition accuracy. In addition, high wind speeds can generate a strong background on the sea surface, which may obscure the signatures of small vessels and make them difficult to detect.

5. Conclusions

The proposed MFCNet framework harnesses the MFC-Conv module as its cornerstone architecture, enabling efficient information transmission while significantly reducing model parameters and computational complexity. The MFA attention module fully leverages the multi-channel features propagated by the MFC-Conv backbone to enhance both spatial localization and feature recognition, all with a lightweight computational overhead. Compared with the baseline, the proposed model reduces the number of parameters by 57.8% and the computational cost by 42.7%, while maintaining a clear accuracy advantage over recent lightweight models on the HRSID and SAR–Ship dataset benchmarks. On the SSDD dataset, it achieves performance comparable to the latest state-of-the-art (SOTA) model. Therefore, for ship recognition tasks in the SAR imagery, the proposed approach represents an efficient and lightweight solution, offering strong potential for real-time, all-weather, on-orbit ship detection.