Interpretation Analysis of Influential Variables Dominating Impulse Waves Generated by Landslides
Abstract
1. Introduction
2. Physical Model Experiments
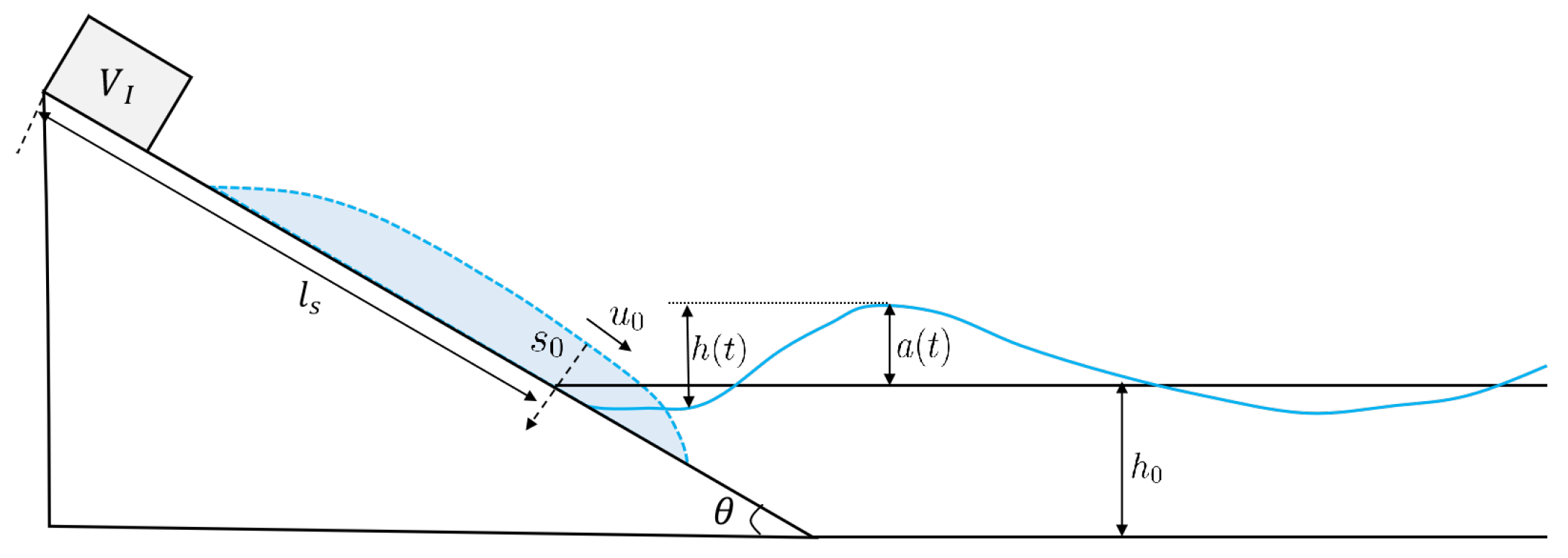
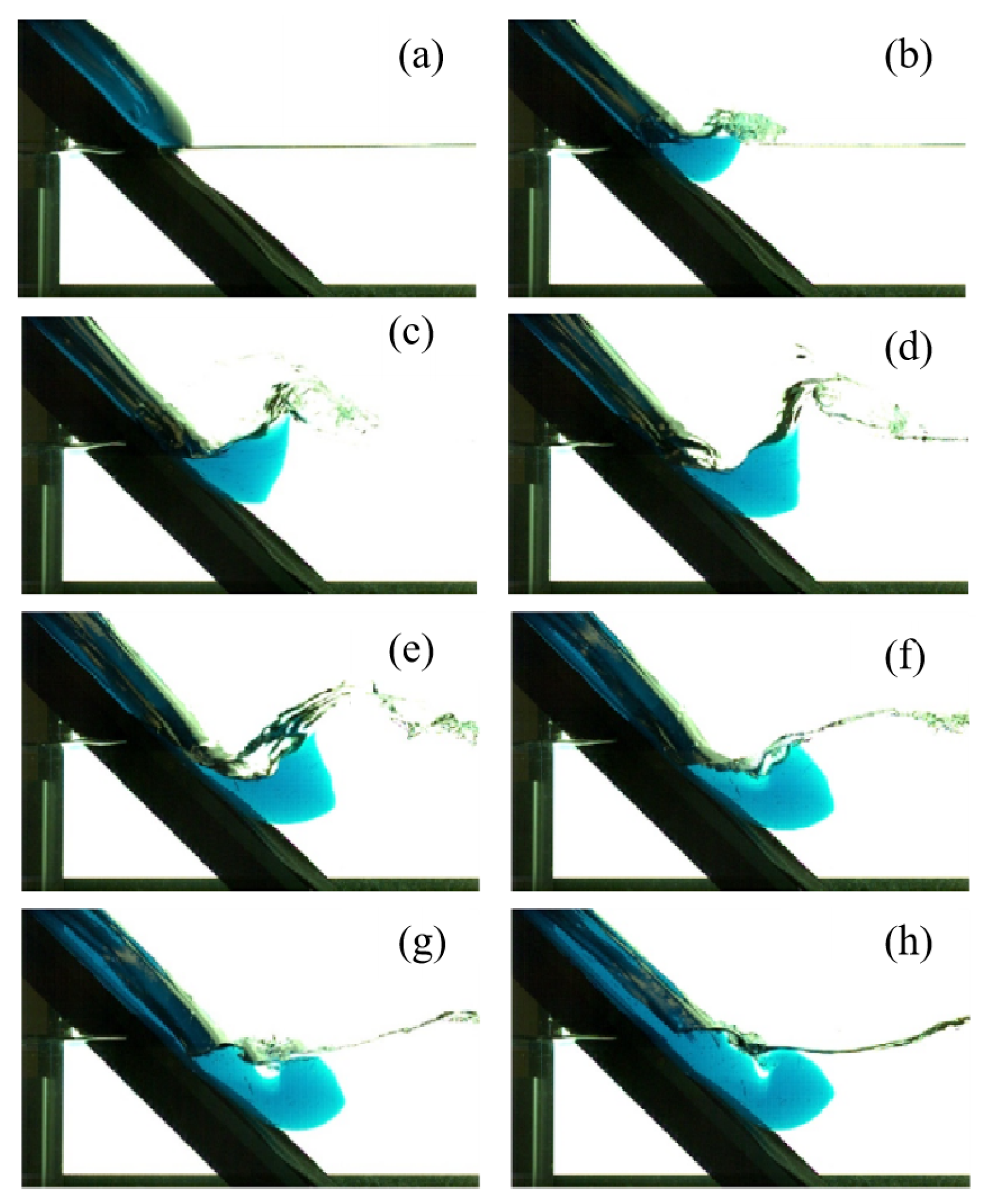
2.1. Experimental Facilities
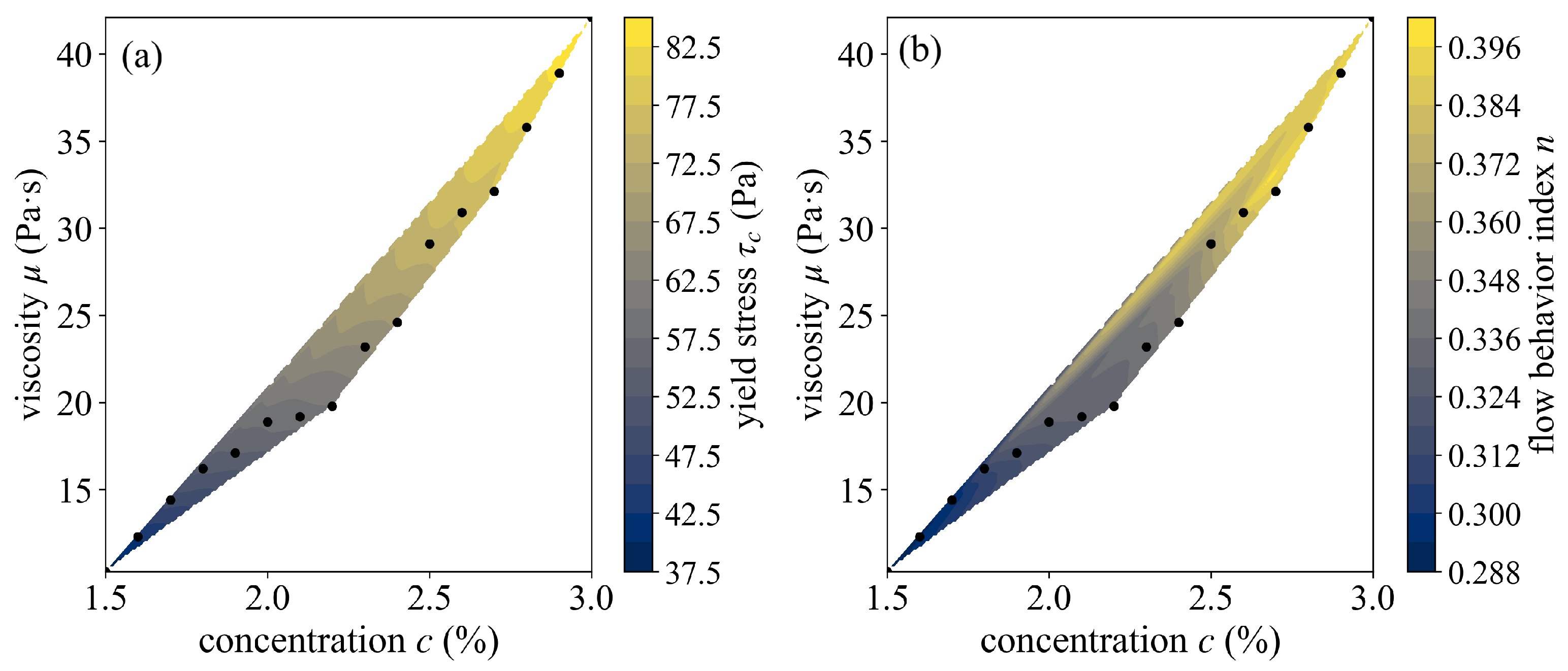
2.2. Slide Material
3. Dimensionless Analysis and Variables
3.1. Dimensionless Analysis
3.2. Data Distribution
4. Modeling Methods
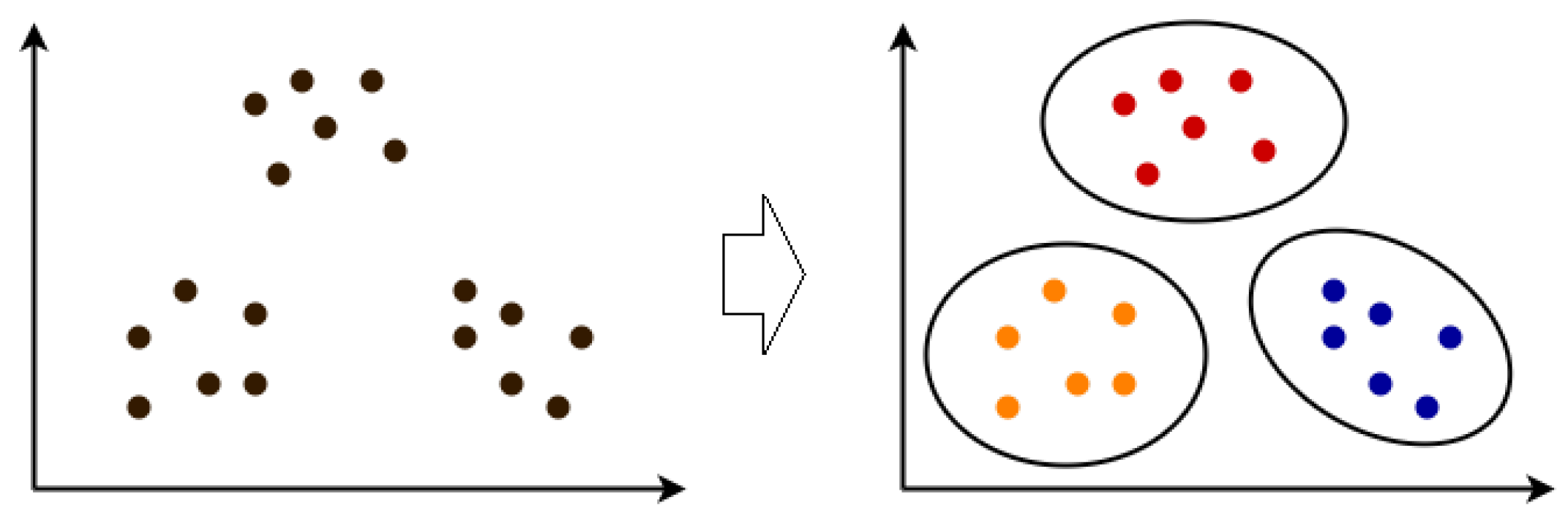
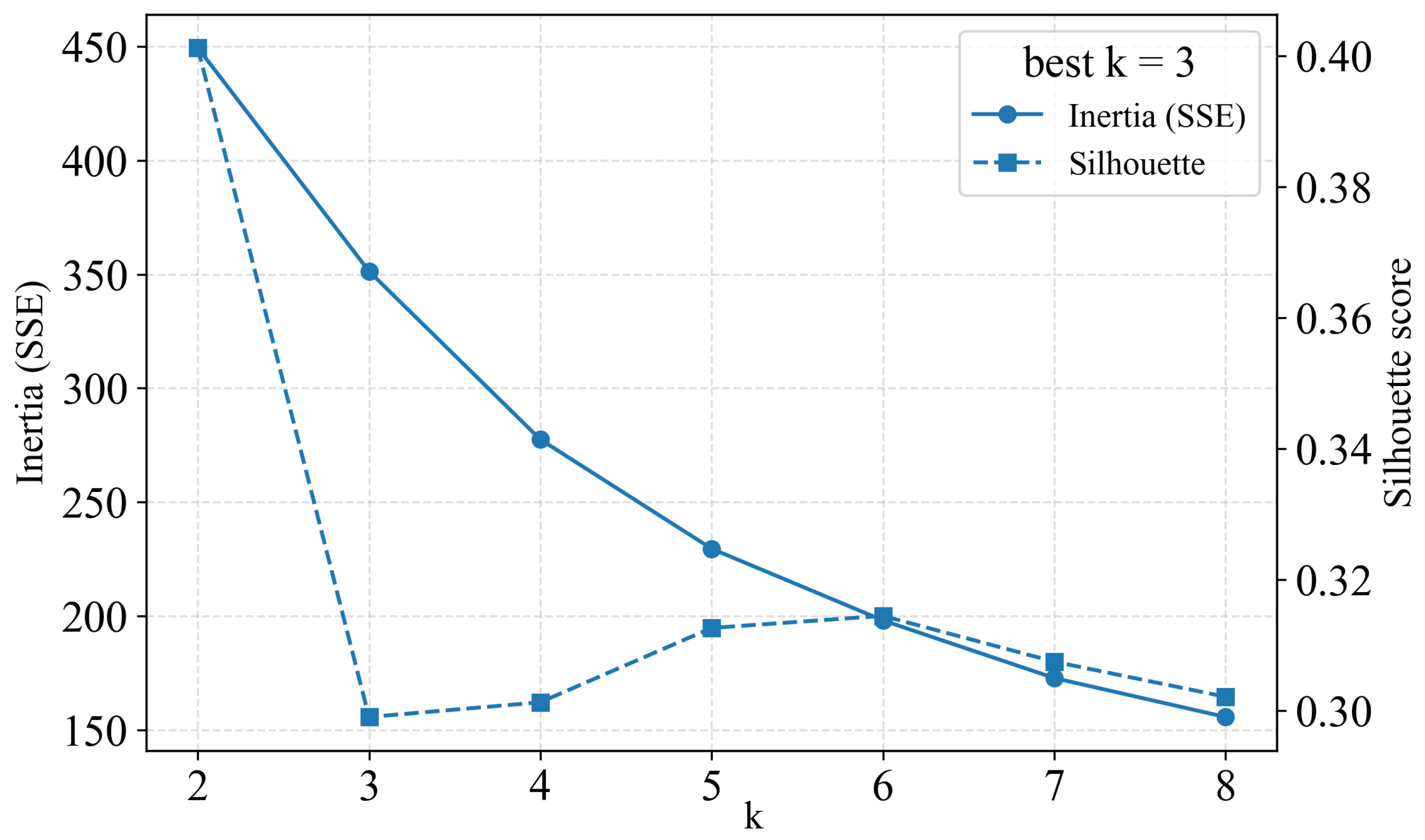
4.1. Pre-Clustering via k-Means on
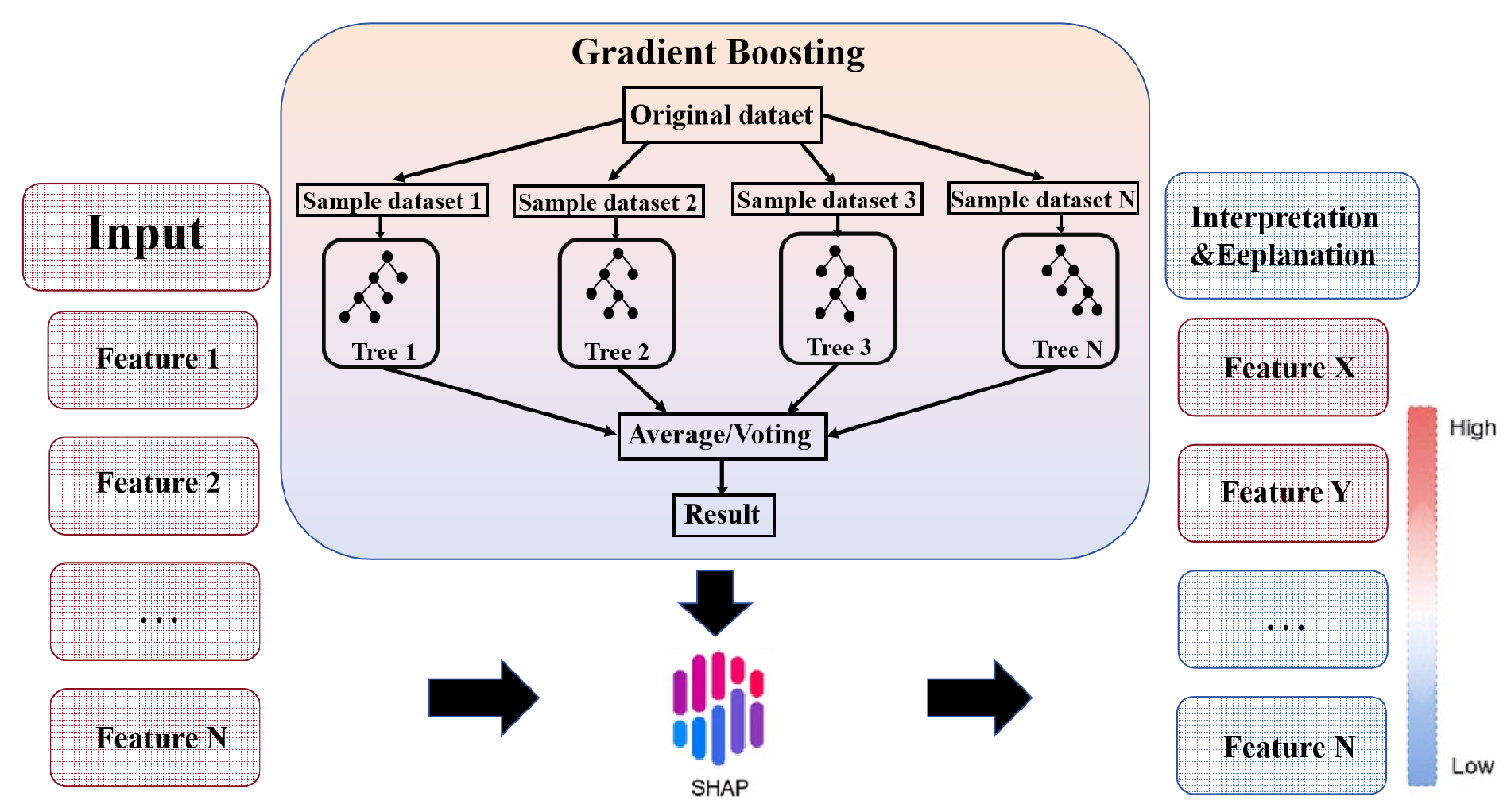
4.2. Gradient Boosting-Based SHAP Analysis for the Two Scenarios
5. Results
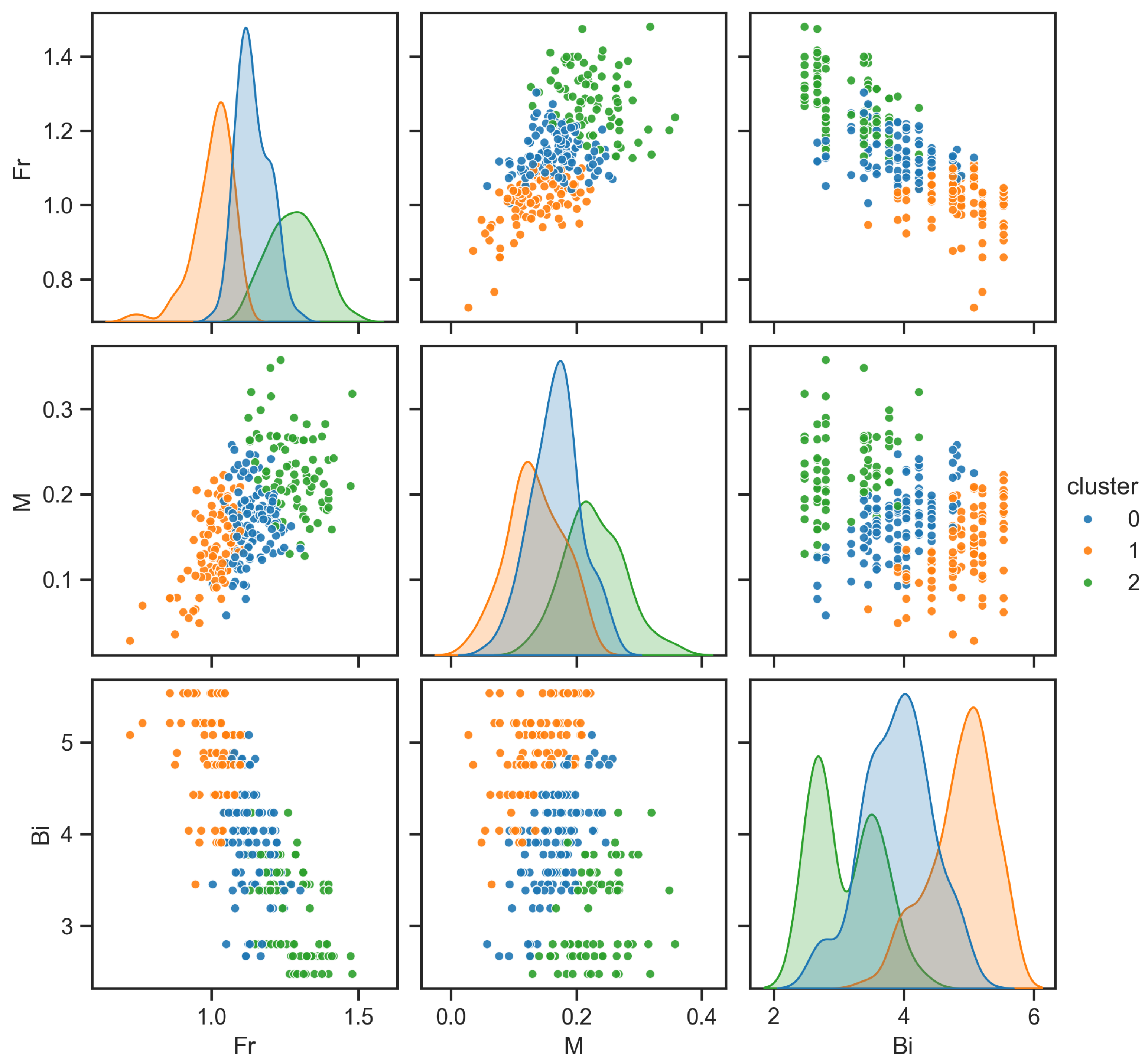
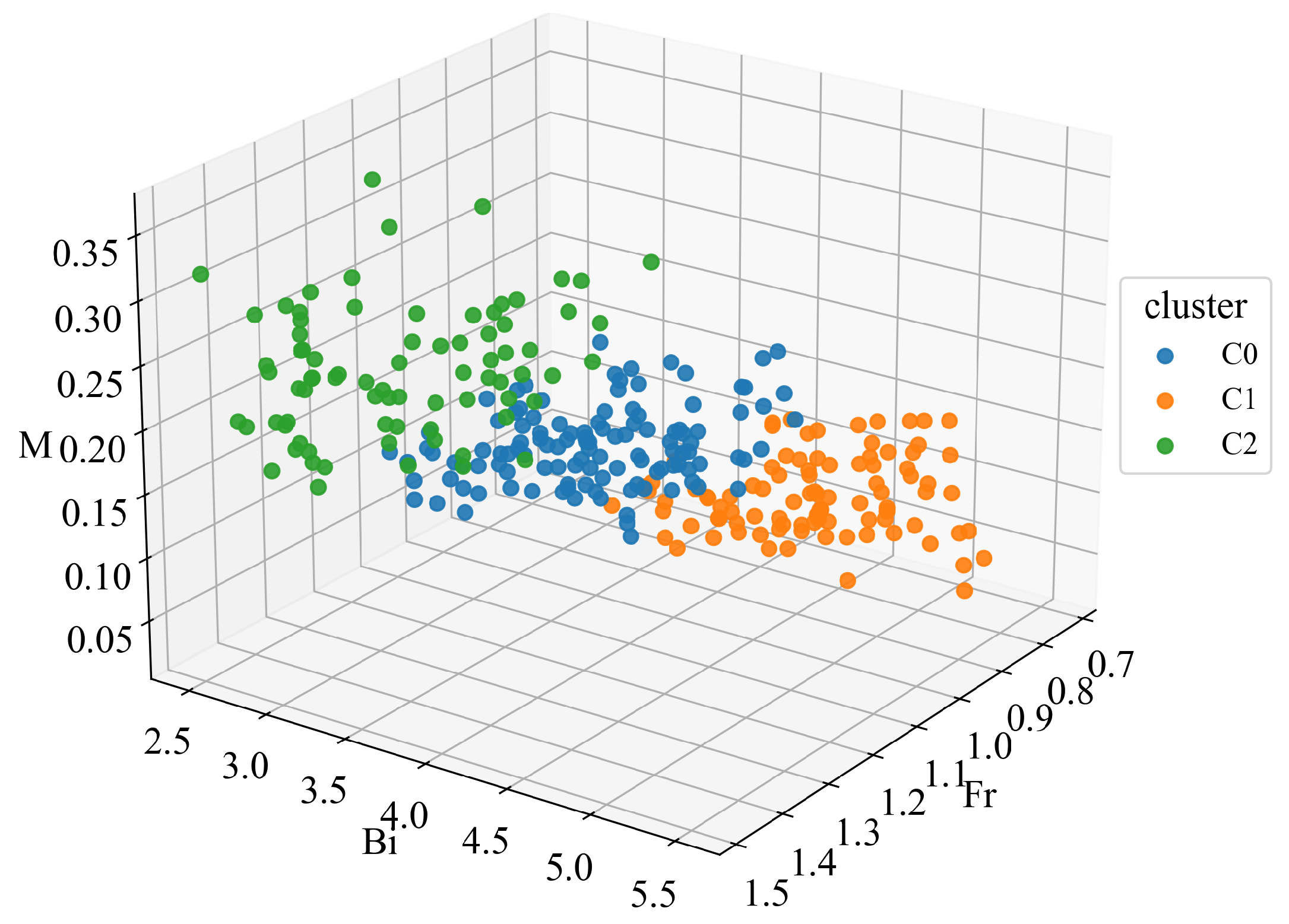
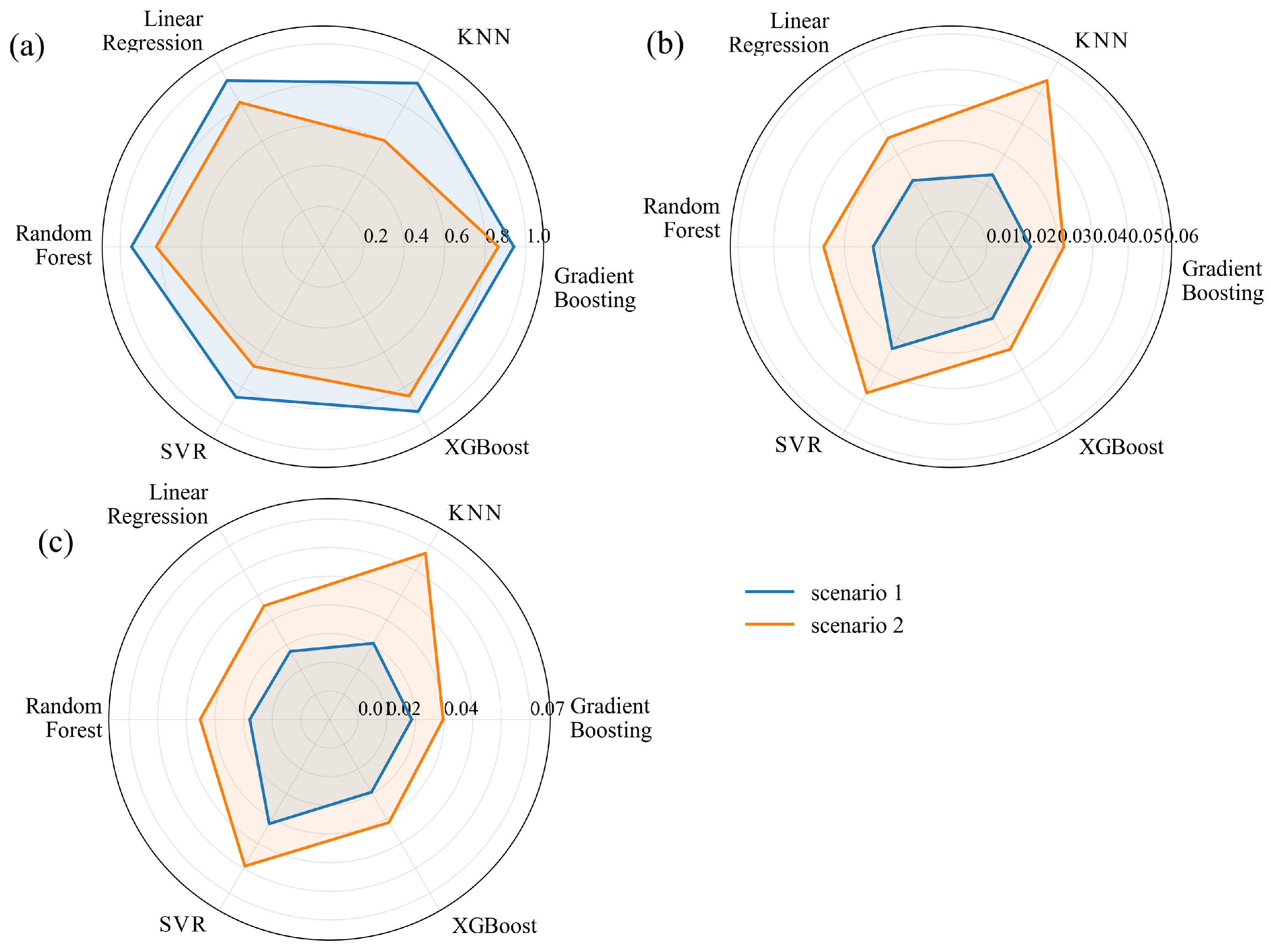
5.1. Data Clustering
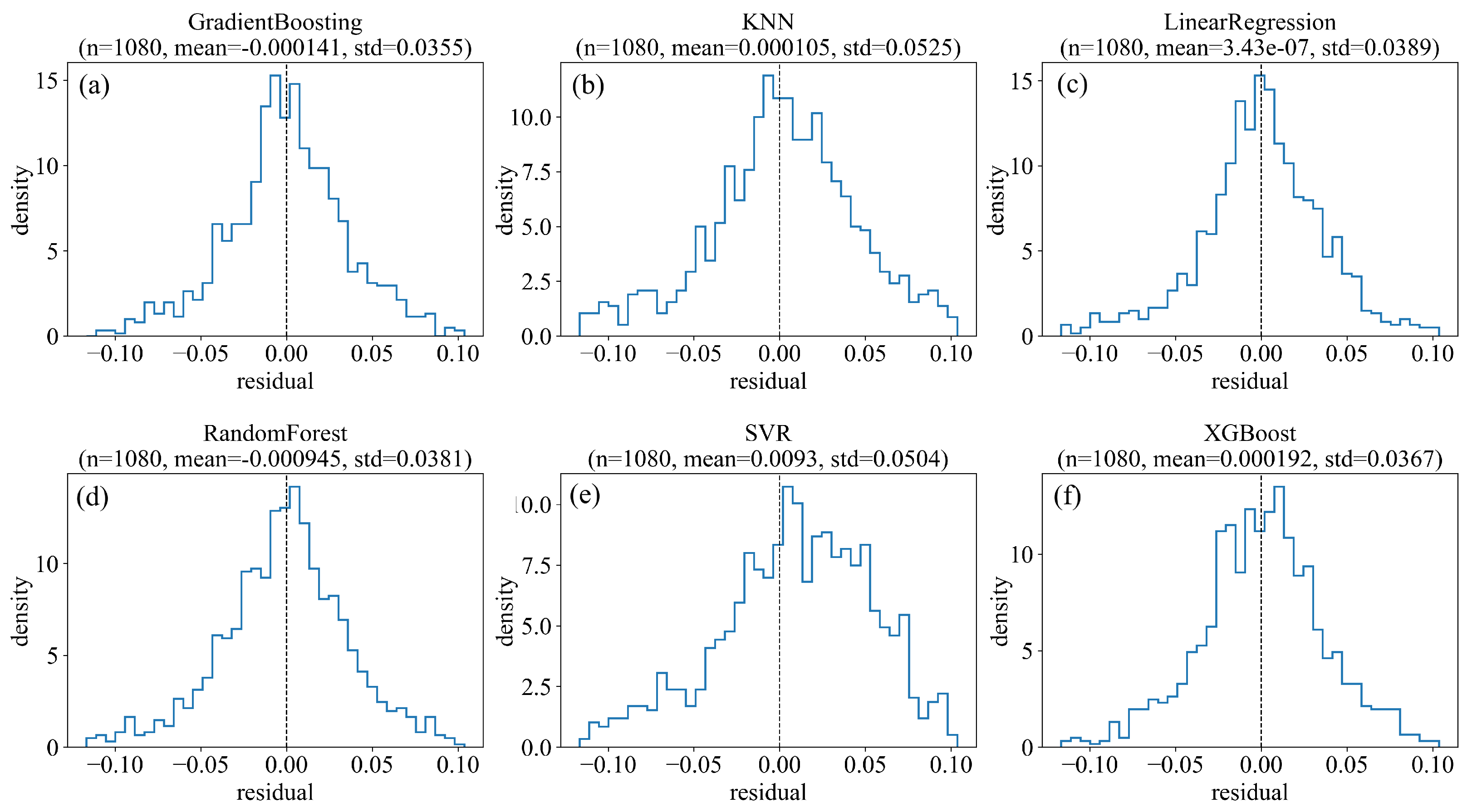
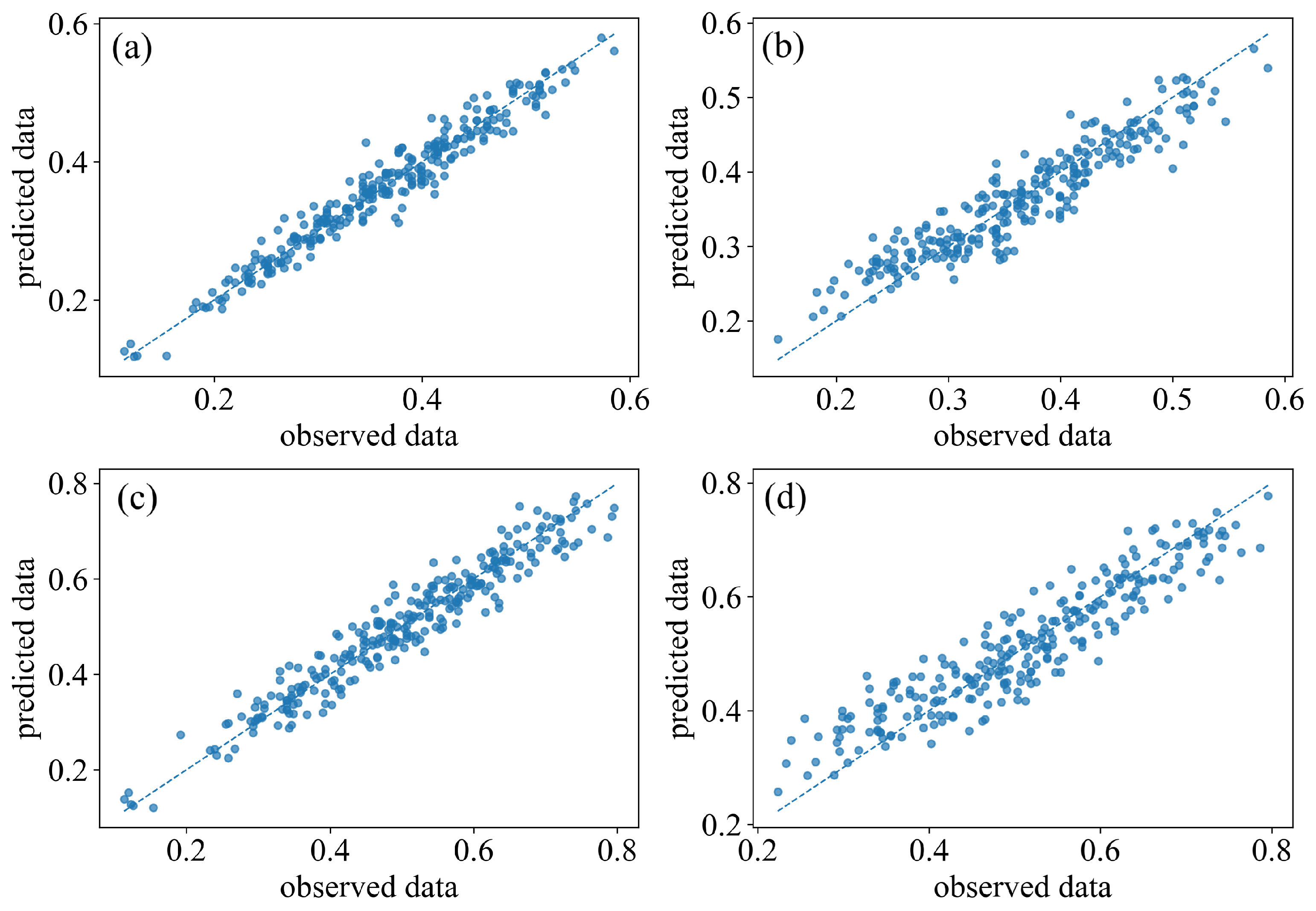
5.2. Prediction Results
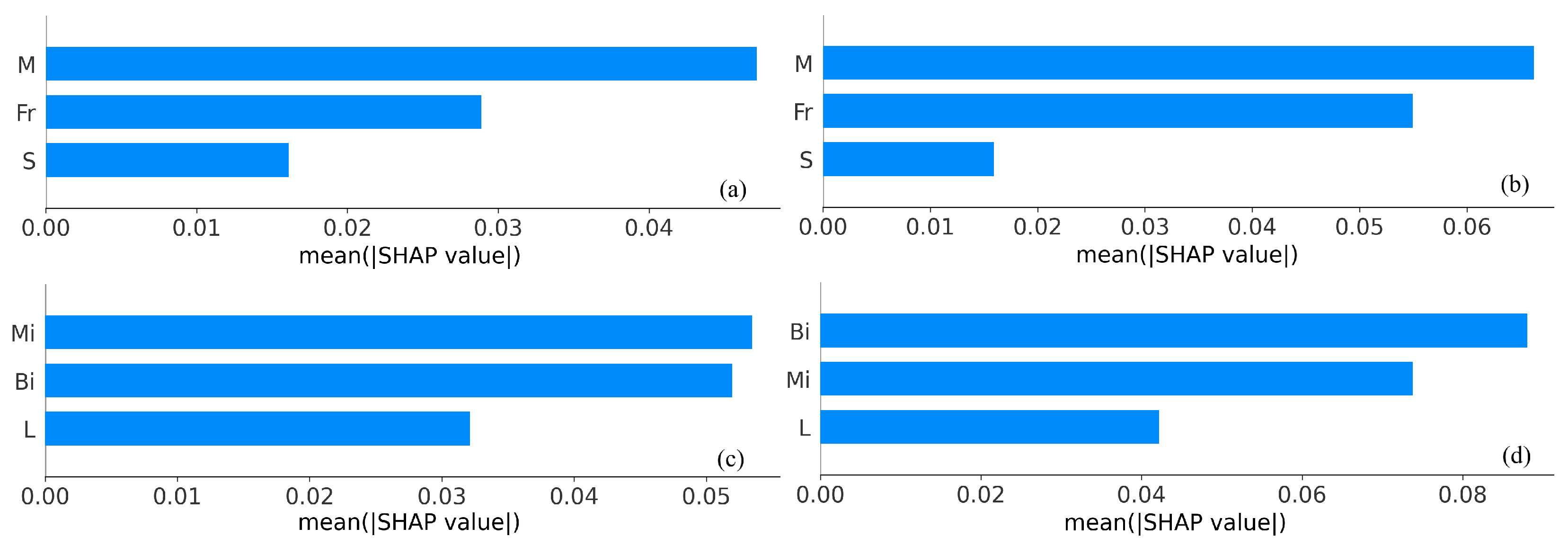
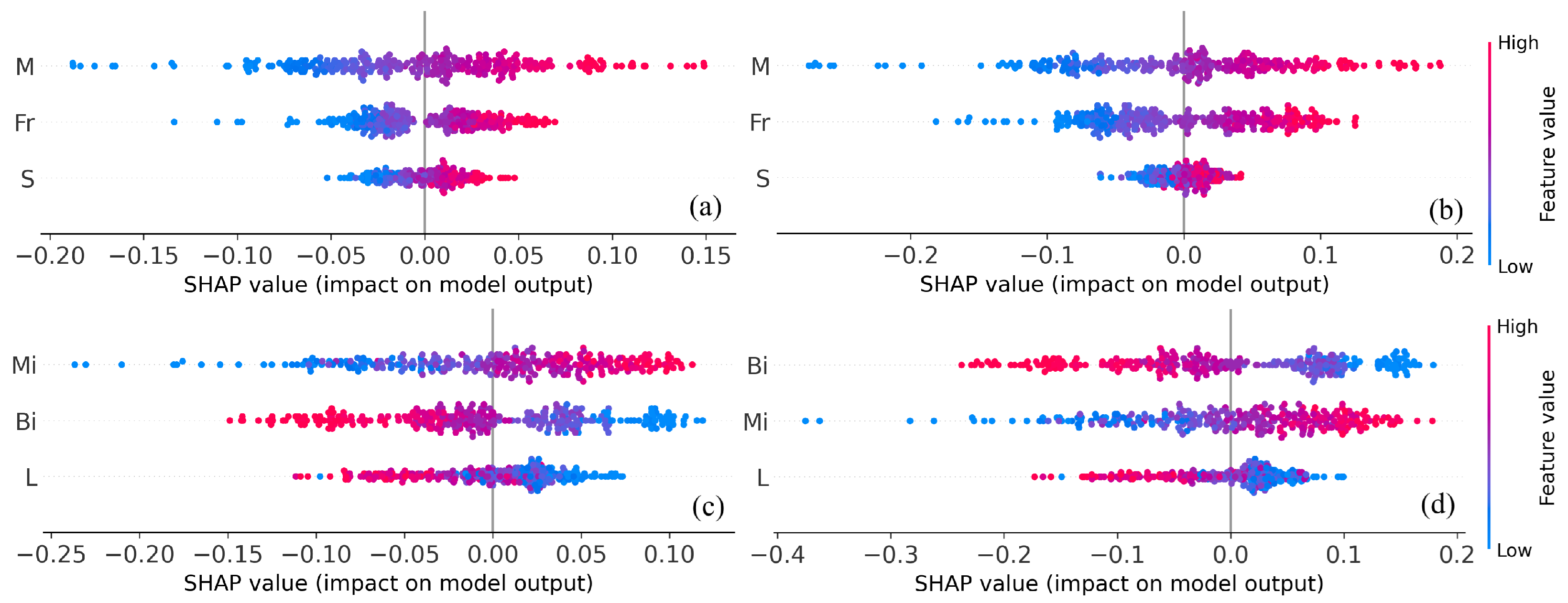
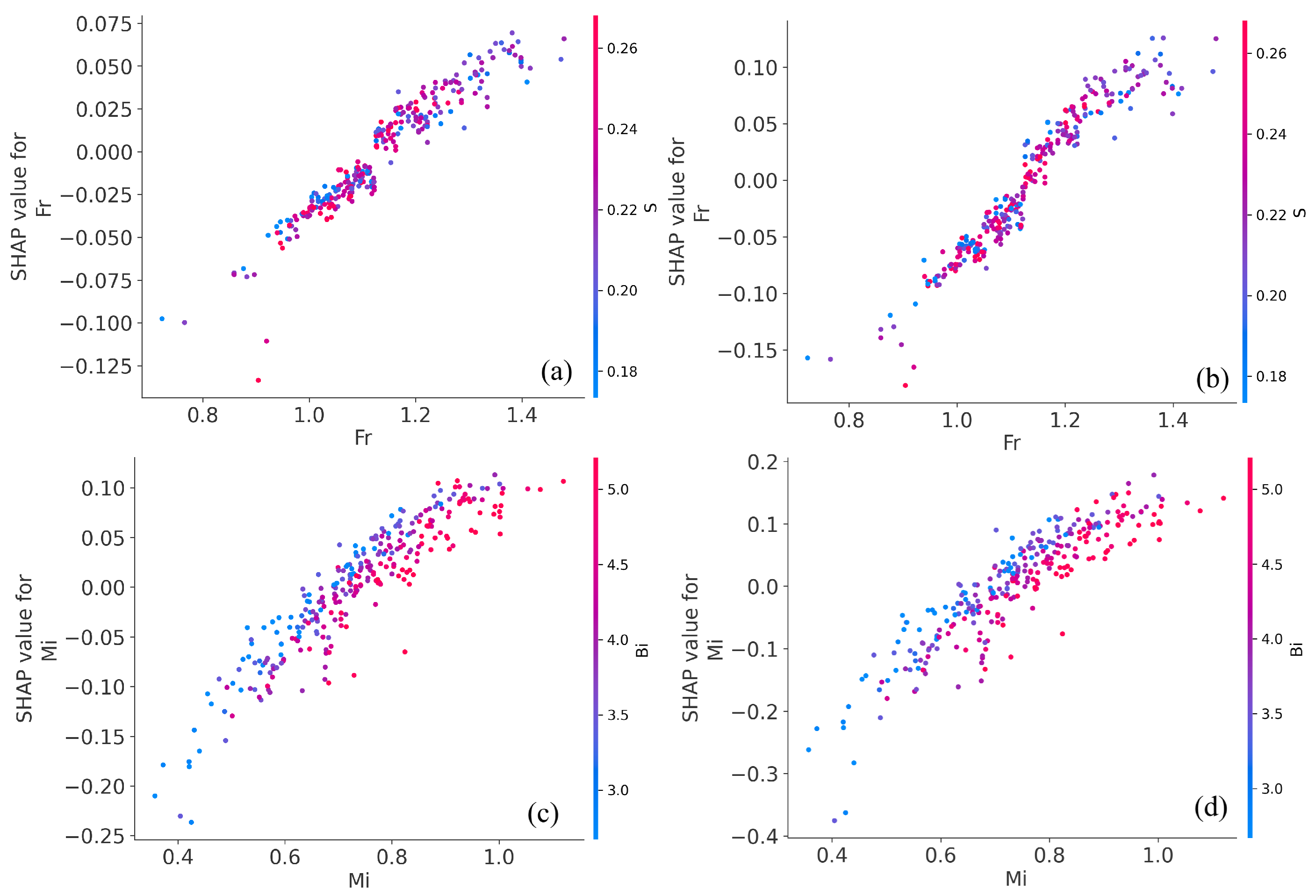
5.3. Interpretation Analysis Based on SHAP
6. Discussions
6.1. Key Findings and New Insights from Interpretability
6.2. Practical Significance and Geological Translation
6.3. Physics–Data Trade-Offs and Generalization Beyond Laboratory Settings
6.4. Field Validation and Limitations
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
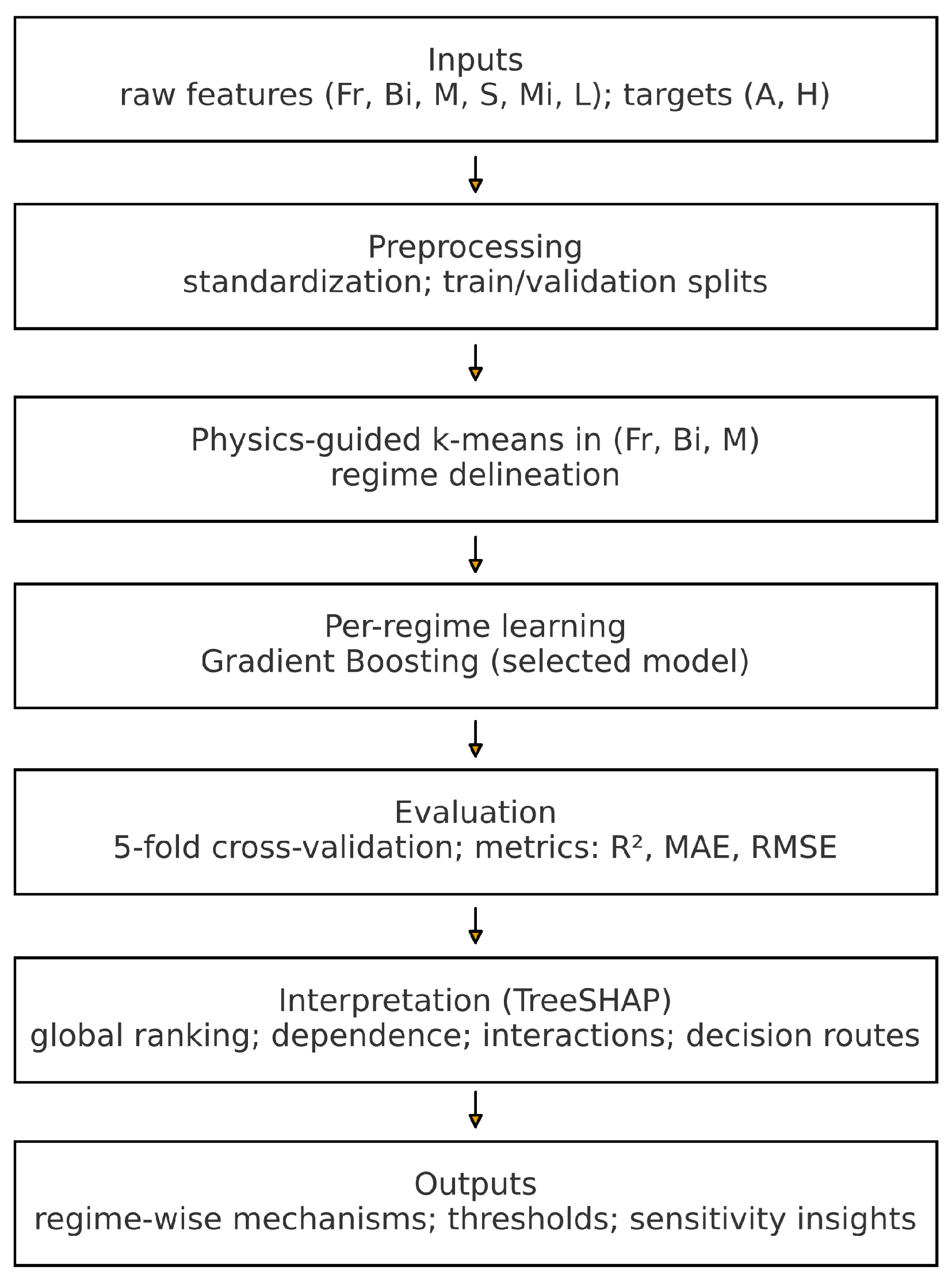
Appendix A. End-to-End Pipeline of the Modeling Procedure
| Algorithm 1: End-to-end pseudocode: k-means clustering → gradient boosting prediction per-cluster → SHAP interpretation. |
 |
Appendix B. Additional Model Comparisons
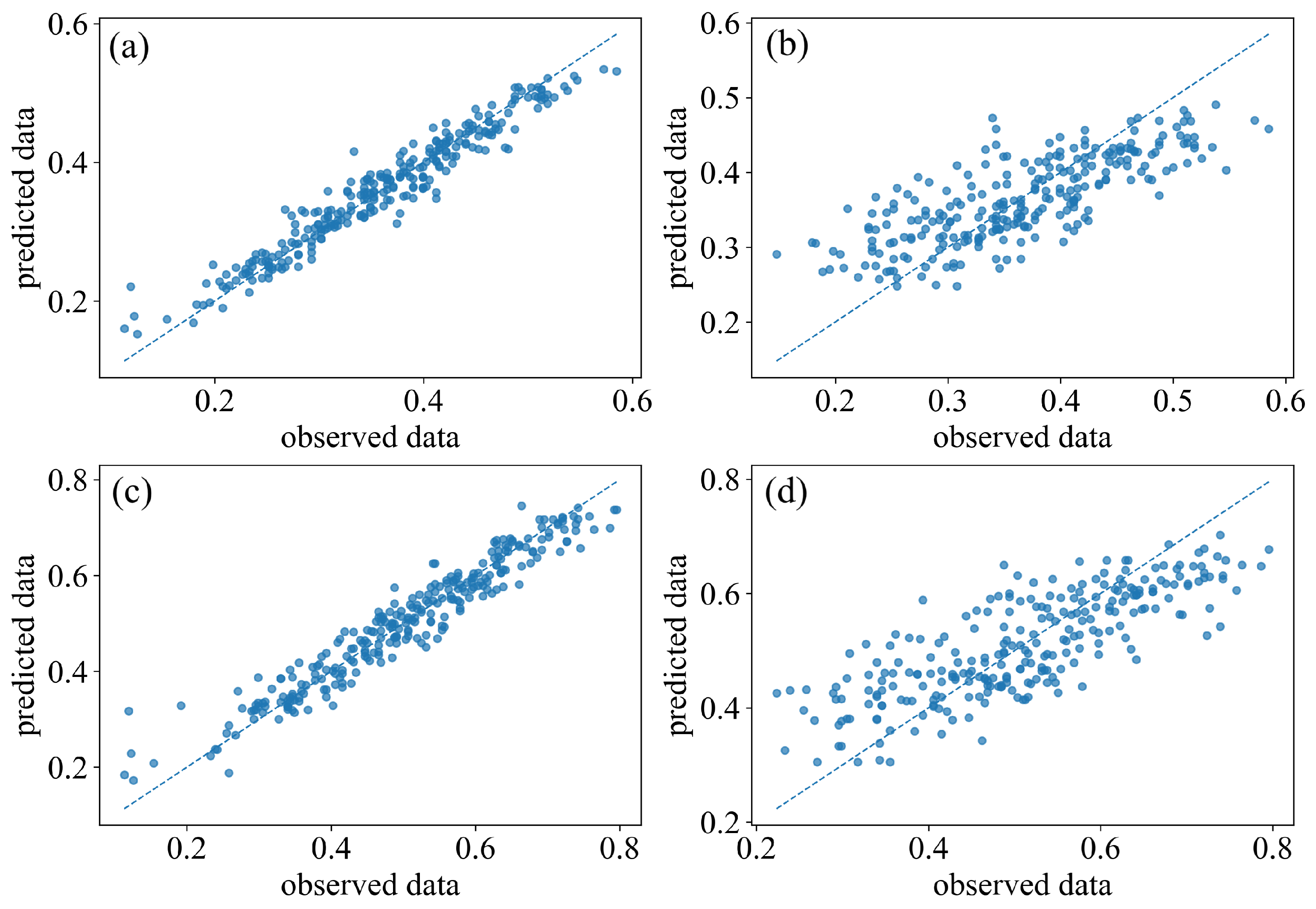
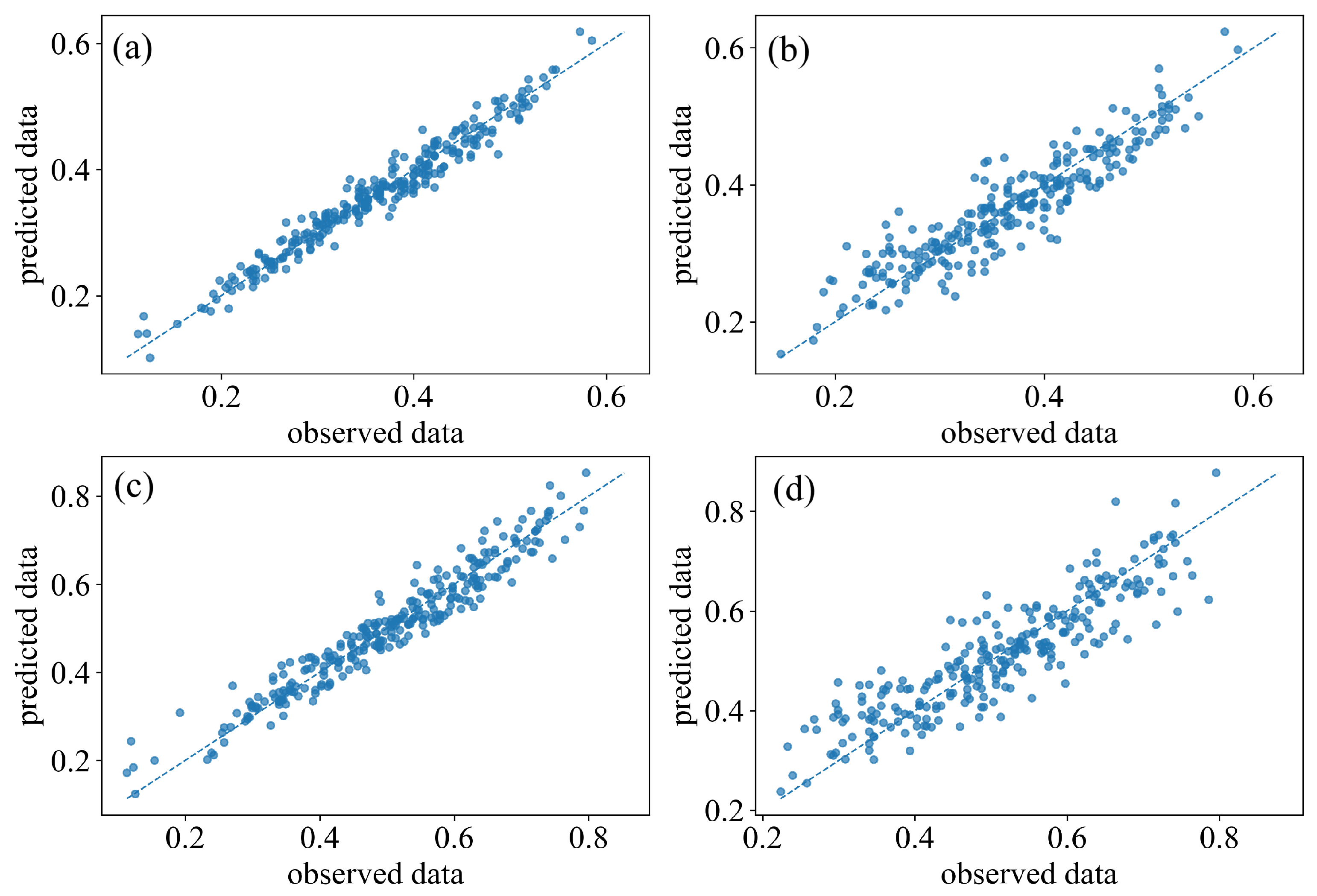
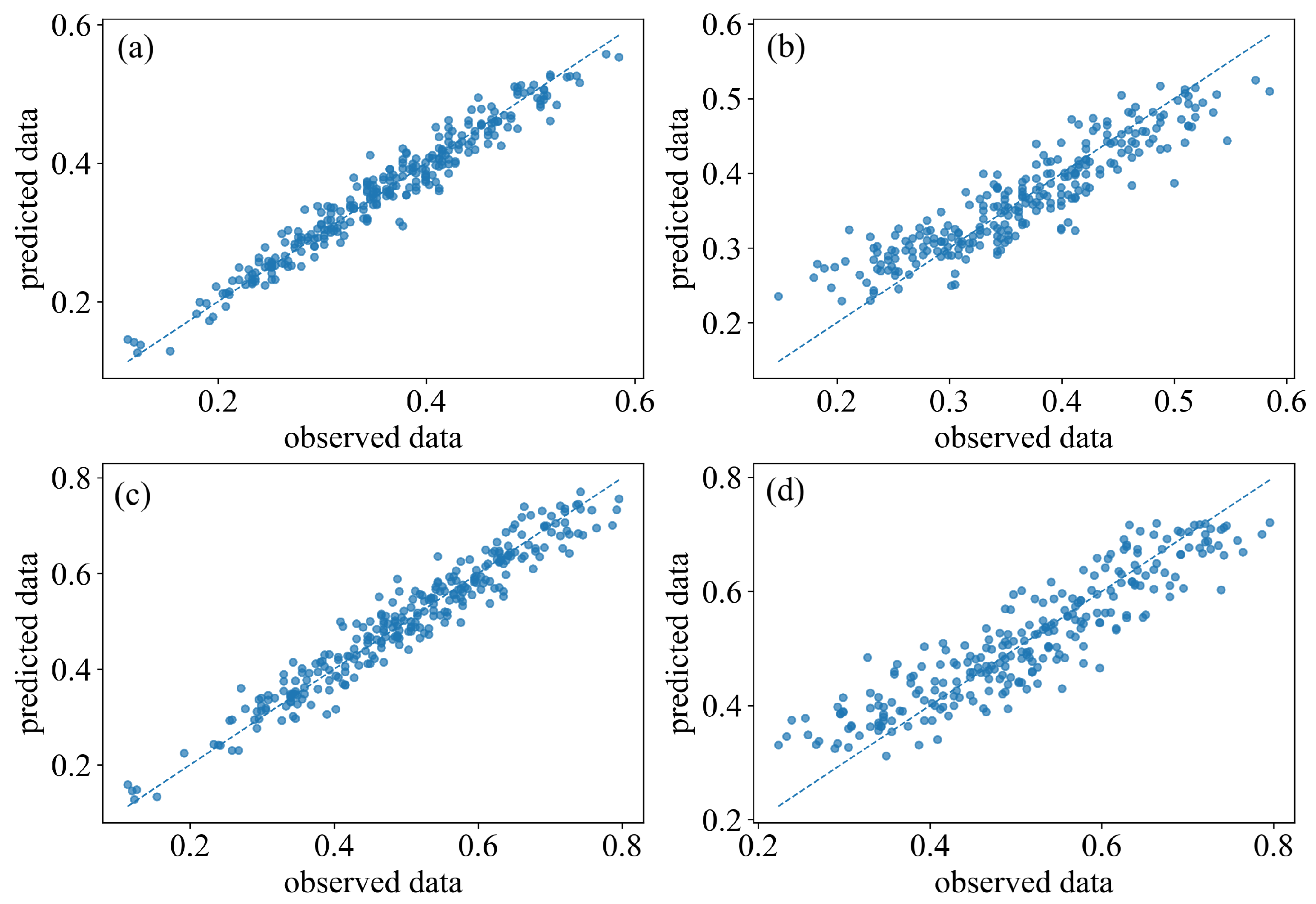
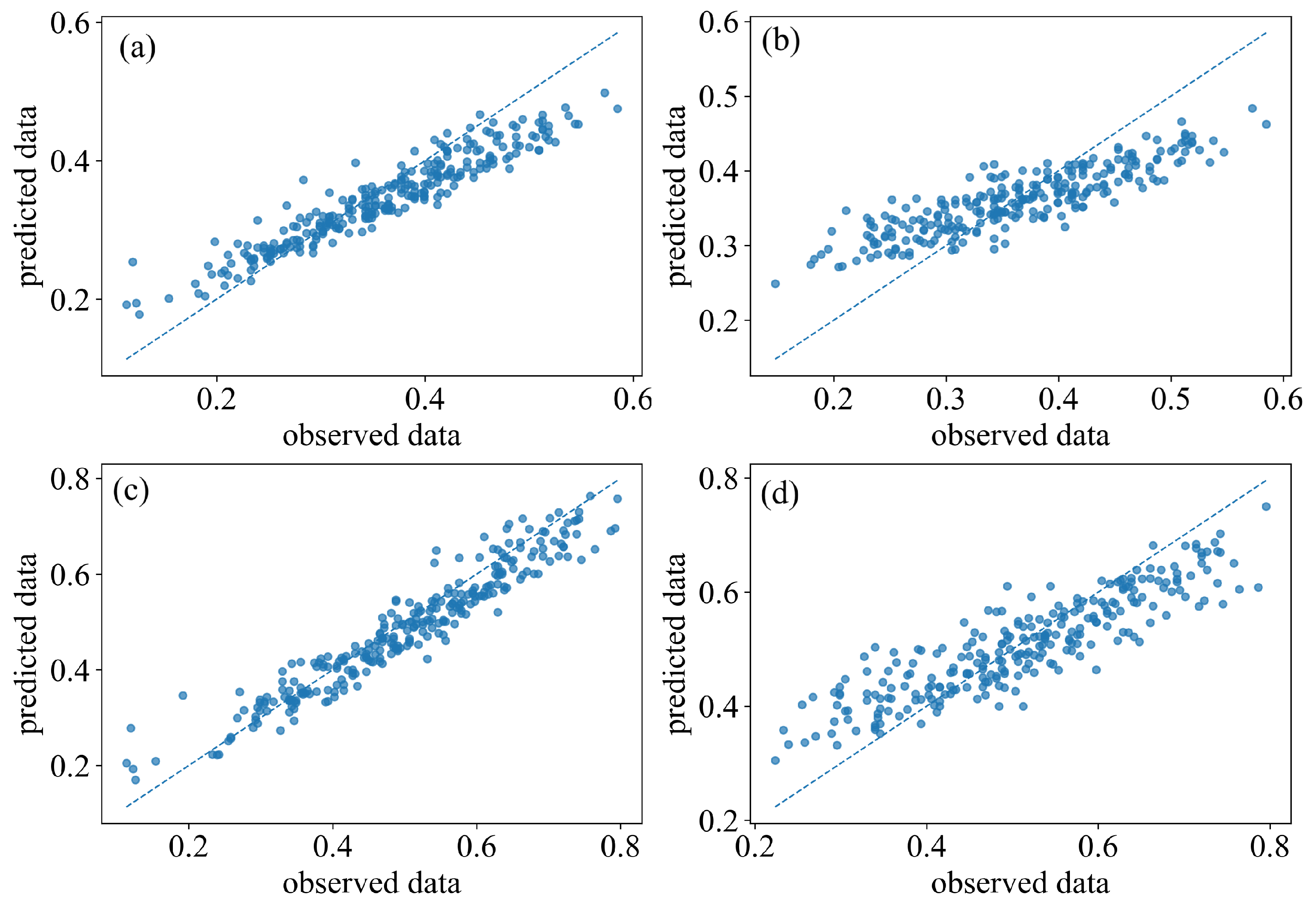
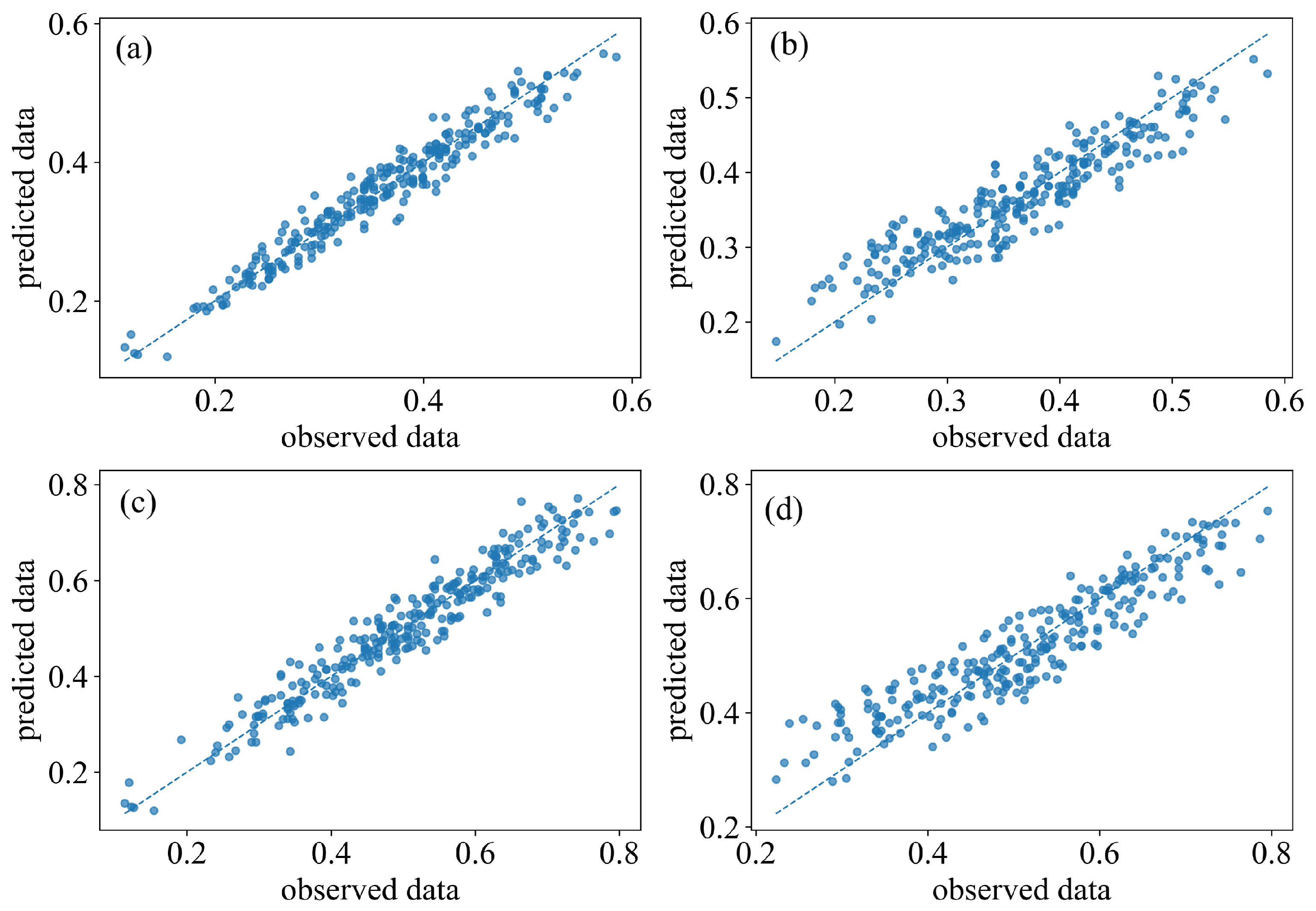
References
- Løvholt, F.; Pedersen, G.; Harbitz, C.B.; Glimsdal, S.; Kim, J. On the characteristics of landslide tsunamis. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2015, 373, 20140376. [Google Scholar] [CrossRef] [PubMed]
- Ward, S.N. Landslide tsunami. J. Geophys. Res. Solid Earth 2001, 106, 11201–11215. [Google Scholar] [CrossRef]
- Gao, J.; Ma, X.; Chen, H.; Zang, J.; Dong, G. On hydrodynamic characteristics of transient harbor resonance excited by double solitary waves. Ocean. Eng. 2021, 219, 108345. [Google Scholar] [CrossRef]
- Heller, V.; Hager, W.H.; Minor, H.E. Scale effects in subaerial landslide generated impulse waves. Exp. Fluids 2008, 44, 691–703. [Google Scholar] [CrossRef]
- Heller, V.; Hager, W.H. Impulse product parameter in landslide generated impulse waves. J. Waterw. Port Coast. Ocean. Eng. 2010, 136, 145–155. [Google Scholar] [CrossRef]
- Lynett, P.; Liu, P.L.F. A numerical study of submarine–landslide–generated waves and run–up. Proc. R. Soc. London Ser. A Math. Phys. Eng. Sci. 2002, 458, 2885–2910. [Google Scholar] [CrossRef]
- Panizzo, A.; De Girolamo, P.; Petaccia, A. Forecasting impulse waves generated by subaerial landslides. J. Geophys. Res. Ocean. 2005, 110, C12025. [Google Scholar] [CrossRef]
- Walder, J.S.; Watts, P.; Sorensen, O.E.; Janssen, K. Tsunamis generated by subaerial mass flows. J. Geophys. Res. Solid Earth 2003, 108, 2236. [Google Scholar] [CrossRef]
- Heller, V.; Spinneken, J. On the effect of the water body geometry on landslide–tsunamis: Physical insight from laboratory tests and 2D to 3D wave parameter transformation. Coast. Eng. 2015, 104, 113–134. [Google Scholar] [CrossRef]
- Fritz, H.M.; Hager, W.H.; Minor, H.E. Near field characteristics of landslide generated impulse waves. J. Waterw. Port Coastal Ocean. Eng. 2004, 130, 287–302. [Google Scholar] [CrossRef]
- Evers, F.M.; Hager, W.H. Spatial impulse waves: Wave height decay experiments at laboratory scale. Landslides 2016, 13, 1395–1403. [Google Scholar] [CrossRef]
- Mao, P.; Lei, J.; Tian, L. Research on the Spatiotemporal Evolution Patterns of Landslide-Induced Surge Waves Based on Physical Model Experiments. Water 2025, 17, 685. [Google Scholar] [CrossRef]
- Lindstrøm, E.K.; Pedersen, G.K.; Jensen, A.; Glimsdal, S. Experiments on slide generated waves in a 1: 500 scale fjord model. Coast. Eng. 2014, 92, 12–23. [Google Scholar] [CrossRef]
- Hu, Y.x.; Yu, Z.y.; Zhou, J.w. Numerical simulation of landslide-generated waves during the 11 October 2018 Baige landslide at the Jinsha River. Landslides 2020, 17, 2317–2328. [Google Scholar] [CrossRef]
- Wu, Y.; Shao, K.; Piccialli, F.; Mei, G. Numerical modeling of the propagation process of landslide surge using physics-informed deep learning. Adv. Model. Simul. Eng. Sci. 2022, 9, 14. [Google Scholar] [CrossRef]
- Feng, X.; Cheng, L.; Dong, Q.; Qi, X.; Xiong, C. Numerical study of hydraulic characteristics of impulse waves generated by subaerial landslides. AIP Adv. 2022, 12, 125118. [Google Scholar] [CrossRef]
- Ma, G.; Kirby, J.T.; Hsu, T.J.; Shi, F. A two-layer granular landslide model for tsunami wave generation: Theory and computation. Ocean. Model. 2015, 93, 40–55. [Google Scholar] [CrossRef]
- Zitti, G.; Ancey, C.; Postacchini, M.; Brocchini, M. Impulse waves generated by snow avalanches: Momentum and energy transfer to a water body. J. Geophys. Res. Earth Surf. 2016, 121, 2399–2423. [Google Scholar] [CrossRef]
- Meng, Z.; Hu, Y.; Ancey, C. Using a data driven approach to predict waves generated by gravity driven mass flows. Water 2020, 12, 600. [Google Scholar] [CrossRef]
- Lyu, C.; Xu, W.; Huang, Q.; Tian, L.; Shi, H.; Chen, H.; Liu, Y.; Lei, J. Predicting landslide surge waves from large-scale physical experimental using machine learning. Phys. Fluids 2025, 37, 036605. [Google Scholar] [CrossRef]
- Lyu, C.; Xu, W.; Huang, Q.; Tian, L.; Shi, H.; Chen, H.; Liu, Y.; Lei, J. Prediction of Landslide-Induced Surge Waves in Reservoir Areas Using Gated Recurrent Unit Networks Based on Physical Model Experiment Data. Available online: https://ssrn.com/abstract=5008900 (accessed on 1 November 2024).
- Chen, H.; Huang, S.; Qiu, H.; Xu, Y.P.; Teegavarapu, R.S.; Guo, Y.; Nie, H.; Xie, H.; Xie, J.; Shao, Y.; et al. Assessment of ecological flow in river basins at a global scale: Insights on baseflow dynamics and hydrological health. Ecol. Indic. 2025, 178, 113868. [Google Scholar] [CrossRef]
- Chen, H.; Xu, B.; Qiu, H.; Huang, S.; Teegavarapu, R.S.; Xu, Y.P.; Guo, Y.; Nie, H.; Xie, H. Adaptive assessment of reservoir scheduling to hydrometeorological comprehensive dry and wet condition evolution in a multi-reservoir region of southeastern China. J. Hydrol. 2025, 648, 132392. [Google Scholar] [CrossRef]
- Li, J.; Meng, Z.; Zhang, J.; Chen, Y.; Yao, J.; Li, X.; Qin, P.; Liu, X.; Cheng, C. Prediction of seawater intrusion run-up distance based on K-means clustering and ANN model. J. Mar. Sci. Eng. 2025, 13, 377. [Google Scholar] [CrossRef]
- Meng, Z.; Hu, Y.; Jiang, S.; Zheng, S.; Zhang, J.; Yuan, Z.; Yao, S. Slope Deformation Prediction Combining Particle Swarm Optimization-Based Fractional-Order Grey Model and K-Means Clustering. Fractal Fract. 2025, 9, 210. [Google Scholar] [CrossRef]
- Inan, M.S.K.; Rahman, I. Explainable AI integrated feature selection for landslide susceptibility mapping using TreeSHAP. SN Comput. Sci. 2023, 4, 482. [Google Scholar] [CrossRef]
- Zhou, X.; Wen, H.; Li, Z.; Zhang, H.; Zhang, W. An interpretable model for the susceptibility of rainfall-induced shallow landslides based on SHAP and XGBoost. Geocarto Int. 2022, 37, 13419–13450. [Google Scholar] [CrossRef]
- Zhang, J.; Ma, X.; Zhang, J.; Sun, D.; Zhou, X.; Mi, C.; Wen, H. Insights into geospatial heterogeneity of landslide susceptibility based on the SHAP-XGBoost model. J. Environ. Manag. 2023, 332, 117357. [Google Scholar] [CrossRef]
- Li, M.; Tian, H. Insights from optimized non-landslide sampling and SHAP explainability for landslide susceptibility prediction. Appl. Sci. 2025, 15, 1163. [Google Scholar] [CrossRef]
- Darvenne, A.; Viroulet, S.; Lacaze, L. Physical model of landslide-generated impulse waves: Experimental investigation of the wave-granular flow coupling. J. Geophys. Res. Ocean. 2024, 129, e2024JC021145. [Google Scholar] [CrossRef]
- Meng, Z.; Li, X.; Han, S.; Wang, X.; Meng, J.; Li, Z. The Motion and Deformation of Viscoplastic Slide while Entering a Body of Water. J. Mar. Sci. Eng. 2022, 10, 778. [Google Scholar] [CrossRef]
- Liu, X.; Jiang, S.H.; Xie, J.; Li, X. Bayesian inverse analysis with field observation for slope failure mechanism and reliability assessment under rainfall accounting for nonstationary characteristics of soil properties. Soils Found. 2025, 65, 101568. [Google Scholar] [CrossRef]
- Liu, X.; Li, X.; Ma, G.; Rezania, M. Characterization of spatially varying soil properties using an innovative constraint seed method. Comput. Geotech. 2025, 183, 107184. [Google Scholar] [CrossRef]
- Meng, Z.; Ancey, C. The effects of slide cohesion on impulse-wave formation. Exp. Fluids 2019, 60, 151. [Google Scholar] [CrossRef]
- Troncone, A. Numerical analysis of a landslide in soils with strain-softening behaviour. Geotechnique 2005, 55, 585–596. [Google Scholar] [CrossRef]
- Emami, N.; Ghazavi, M. Landslides and slope failures due to saturated soft soil: A case study. In Soft Soil Engineering; Routledge: London, UK, 2017; pp. 103–109. [Google Scholar]
- Meng, Z.; Zhang, J.; Hu, Y.; Ancey, C. Temporal Prediction of Landslide-Generated Waves Using a Theoretical–Statistical Combined Method. J. Mar. Sci. Eng. 2023, 11, 1151. [Google Scholar] [CrossRef]
- Heller, V.; Hager, W.H. Wave types of landslide generated impulse waves. Ocean. Eng. 2011, 38, 630–640. [Google Scholar] [CrossRef]
- Gao, J.; Ma, X.; Dong, G.; Zang, J.; Ma, Y.; Zhou, L. Effects of offshore fringing reefs on the transient harbor resonance excited by solitary waves. Ocean. Eng. 2019, 190, 106422. [Google Scholar] [CrossRef]
- Oyewole, G.J.; Thopil, G.A. Data clustering: Application and trends. Artif. Intell. Rev. 2023, 56, 6439–6475. [Google Scholar] [CrossRef]
- Gao, J.l.; Chen, H.z.; Ma, X.z.; Dong, G.h.; Zang, J.; Liu, Q. Study on influences of fringing reef on harbor oscillations triggered by N-waves. China Ocean. Eng. 2021, 35, 398–409. [Google Scholar] [CrossRef]
- Gao, J.; Ji, C.; Gaidai, O.; Liu, Y.; Ma, X. Numerical investigation of transient harbor oscillations induced by N-waves. Coast. Eng. 2017, 125, 119–131. [Google Scholar] [CrossRef]
- Morissette, L.; Chartier, S. The k-means clustering technique: General considerations and implementation in Mathematica. Tutor. Quant. Methods Psychol. 2013, 9, 15–24. [Google Scholar] [CrossRef]
- Chong, B. K-means clustering algorithm: A brief review. Acad. J. Comput. Inf. Sci. 2021, 4, 37–40. [Google Scholar] [CrossRef]
- Bentéjac, C.; Csörgő, A.; Martínez-Muñoz, G. A comparative analysis of gradient boosting algorithms. Artif. Intell. Rev. 2021, 54, 1937–1967. [Google Scholar] [CrossRef]
- Merabet, K.; Di Nunno, F.; Granata, F.; Kim, S.; Adnan, R.M.; Heddam, S.; Kisi, O.; Zounemat-Kermani, M. Predicting water quality variables using gradient boosting machine: Global versus local explainability using SHapley Additive Explanations (SHAP). Earth Sci. Inform. 2025, 18, 1–34. [Google Scholar] [CrossRef]
- Natekin, A.; Knoll, A. Gradient boosting machines, a tutorial. Front. Neurorobotics 2013, 7, 21. [Google Scholar] [CrossRef]
- Duan, T.; Anand, A.; Ding, D.Y.; Thai, K.K.; Basu, S.; Ng, A.; Schuler, A. Ngboost: Natural gradient boosting for probabilistic prediction. In Proceedings of the International Conference on Machine Learning, PMLR, Virtual, 13–18 July 2020; pp. 2690–2700. [Google Scholar]
- Das, P.; Kashem, A.; Hasan, I.; Islam, M. A comparative study of machine learning models for construction costs prediction with natural gradient boosting algorithm and SHAP analysis. Asian J. Civ. Eng. 2024, 25, 3301–3316. [Google Scholar] [CrossRef]
- Meng, Y.; Yang, N.; Qian, Z.; Zhang, G. What makes an online review more helpful: An interpretation framework using XGBoost and SHAP values. J. Theor. Appl. Electron. Commer. Res. 2020, 16, 466–490. [Google Scholar] [CrossRef]
- Van den Broeck, G.; Lykov, A.; Schleich, M.; Suciu, D. On the tractability of SHAP explanations. J. Artif. Intell. Res. 2022, 74, 851–886. [Google Scholar] [CrossRef]
- Meng, Z. Experimental study on impulse waves generated by a viscoplastic material at laboratory scale. Landslides 2018, 15, 1173–1182. [Google Scholar] [CrossRef]
- Zeebaree, D.Q.; Haron, H.; Abdulazeez, A.M.; Zeebaree, S. Combination of K-means clustering with Genetic Algorithm: A review. Int. J. Appl. Eng. Res. 2017, 12, 14238–14245. [Google Scholar]
- Kodinariya, T.M.; Makwana, P.R. Review on determining number of Cluster in K-Means Clustering. Int. J. 2013, 1, 90–95. [Google Scholar]
- Likas, A.; Vlassis, N.; Verbeek, J.J. The global k-means clustering algorithm. Pattern Recognit. 2003, 36, 451–461. [Google Scholar] [CrossRef]

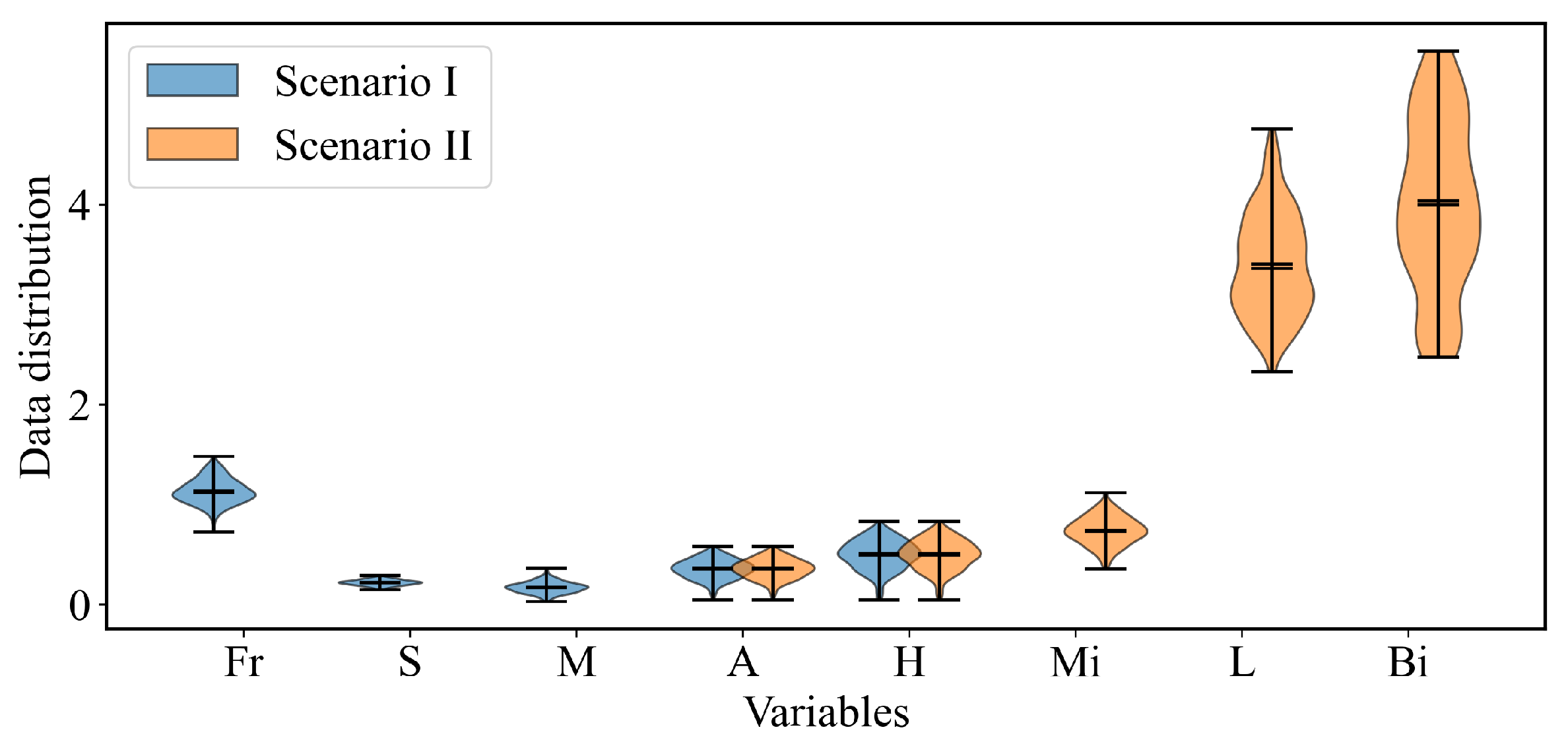
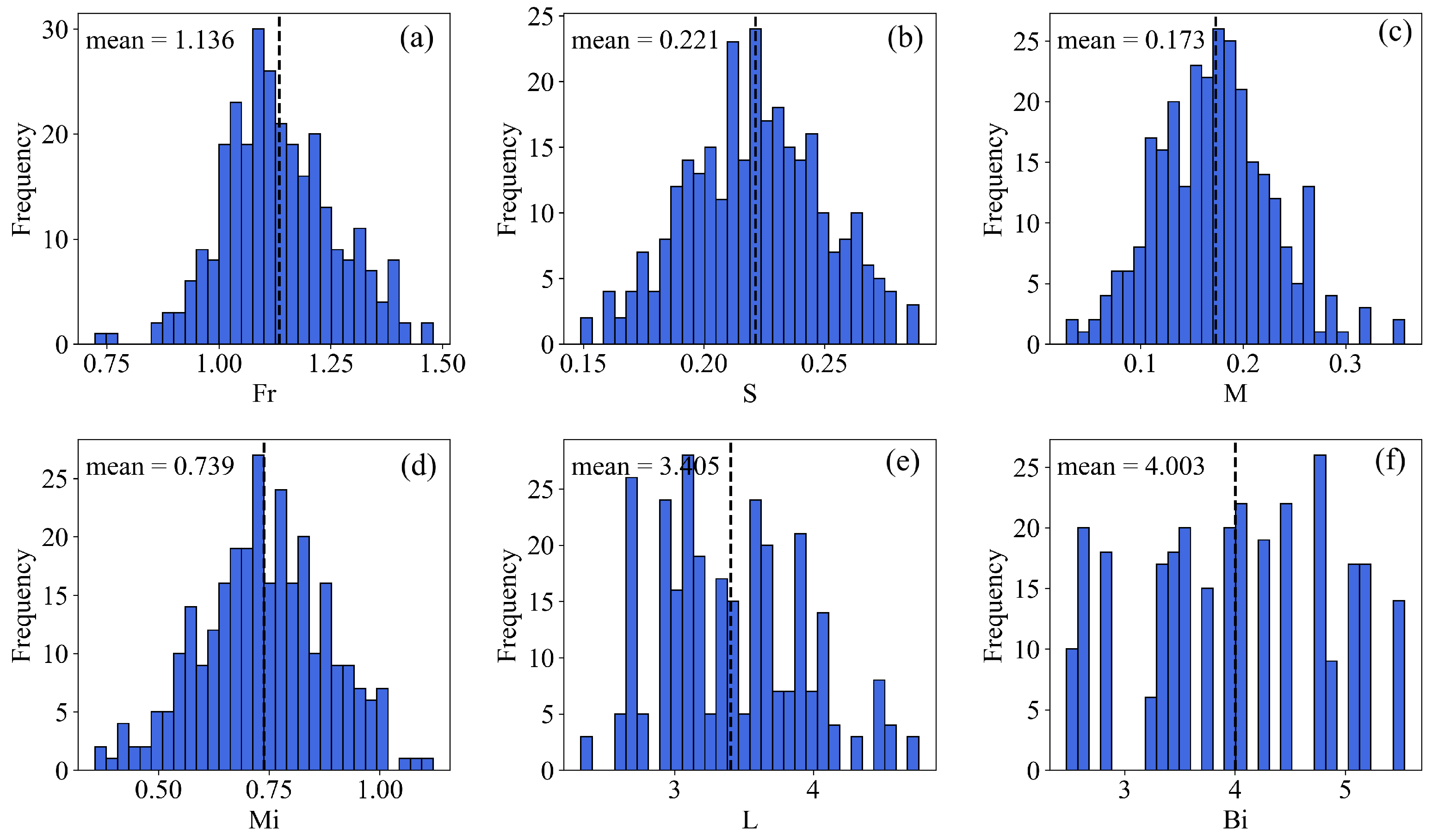


| Scenario I | Scenario II | |||||
|---|---|---|---|---|---|---|
| Fr | S | M | Mi | L | Bi | |
| Fr | 1.00 | −0.06 | 0.58 | |||
| S | −0.06 | 1.00 | 0.67 | |||
| M | 0.58 | 0.67 | 1.00 | |||
| Mi | 1.00 | 0.09 | 0.57 | |||
| L | 0.09 | 1.00 | −0.26 | |||
| Bi | 0.57 | −0.26 | 1.00 | |||
| Scenario | Target | Rank | Feature Pair | Mean|Interaction| |
|---|---|---|---|---|
| scenario I | A | 1 | 0.003003 | |
| 2 | 0.001905 | |||
| 3 | 0.001823 | |||
| H | 1 | 0.005306 | ||
| 2 | 0.004722 | |||
| 3 | 0.003846 | |||
| scenario II | A | 1 | 0.009974 | |
| 2 | 0.006596 | |||
| 3 | 0.005018 | |||
| H | 1 | 0.014730 | ||
| 2 | 0.009199 | |||
| 3 | 0.008363 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, X.; Qin, P.; Li, Z.; Wang, J.; Zhou, Y.; Zheng, S.; Meng, Z. Interpretation Analysis of Influential Variables Dominating Impulse Waves Generated by Landslides. J. Mar. Sci. Eng. 2025, 13, 2223. https://doi.org/10.3390/jmse13122223
Xu X, Qin P, Li Z, Wang J, Zhou Y, Zheng S, Meng Z. Interpretation Analysis of Influential Variables Dominating Impulse Waves Generated by Landslides. Journal of Marine Science and Engineering. 2025; 13(12):2223. https://doi.org/10.3390/jmse13122223
Chicago/Turabian StyleXu, Xiaohan, Peng Qin, Zhenyu Li, Jiangfei Wang, Yuyue Zhou, Sen Zheng, and Zhenzhu Meng. 2025. "Interpretation Analysis of Influential Variables Dominating Impulse Waves Generated by Landslides" Journal of Marine Science and Engineering 13, no. 12: 2223. https://doi.org/10.3390/jmse13122223
APA StyleXu, X., Qin, P., Li, Z., Wang, J., Zhou, Y., Zheng, S., & Meng, Z. (2025). Interpretation Analysis of Influential Variables Dominating Impulse Waves Generated by Landslides. Journal of Marine Science and Engineering, 13(12), 2223. https://doi.org/10.3390/jmse13122223






