Learning to Equalize for Single-Carrier Underwater Acoustic Communications

Abstract

Learning-based equalizers for multicarrier communication systems have been widely studied over underwater acoustic (UWA) channels. In this article, a learning-based equalizer is utilized for single-carrier (SC) underwater acoustic communications. A comprehensive comparison is made between existing deep learning (DL)-based approaches and a classical equalizer designed with adaptive filtering principles. It motivates the design of equalization for SC communications over underwater acoustic channels. To overcome distortion over the UWA channel, we propose a sliding deep learning-based equalizer that uses a sliding nonlinear network for equalization rather than a single-layer linear method. Moreover, to accelerate convergence during training, we proposed a preprocessing-based training phase. To mitigate the impact of time-varying channels, we additionally propose a meta-learning-enhanced adaptive filter algorithm for online adaptive equalization, named Meta-DNN. Based on the proposed DL equalizer, we leverage the pilot and data relationship to perform online transfer to achieve better BER performance. Moreover, to make this work more convincing, we test bit-error-rate (BER) performance across reproducible, realistic multi-scenario channels.

1. Introduction

Underwater communications are well needed for underwater information transmission, such as subsea facilities, test areas for autonomous vessels, underwater Internet of Things, and marine observatories [1,2]. In recent decades, numerous approaches using various media have been introduced to facilitate information interaction [3]. So far, light, magnidle, radio, and acoustic all aim to achieve high-rate, stable, and long-distance underwater communications [4,5]. Due to the nature of water, only the underwater acoustic (UWA) method can effectively achieve medium- and long-distance communication. Unfortunately, UWA communications face many challenges caused by physical factors, such as Doppler shifts, multi-path effects, and propagation loss [6].

In the literature, many methods have been proposed to reduce the distortion caused by UWA channels. Single-carrier (SC) and multi-carrier (MC) communication are two classical communication approaches [7]. In particular, orthogonal frequency division multiplexing (OFDM) is a typical multi-carrier modulation technique that is already widely applied to UWA communications [8]. OFDM can easily achieve frequency-domain equalization to combat multi-path interference and inter-symbol interference (ISI). However, UWA communications is a wideband system, and the small ratio of the carrier frequency to the signal bandwidth makes UWA OFDM more sensitive to Doppler shift. Meanwhile, the high peak-to-average ratio (PAPR) also poses problems for OFDM in long-distance transmission [9]. From this perspective, SC communications receive more attention because of their higher tolerance to Doppler shift than MC modulation over UWA channels and their lower PAPR. Generally, the equalization of SC modulation can be achieved in the time domain and/or frequency domain [10]. The recovery procedure can be performed in the time domain, especially under non-stationary conditions caused by platform and boundary movement. Meanwhile, the recovery procedure can also be performed in the frequency domain, and the complexity of frequency-domain equalization is relatively low. It is a pity that the classical adaptation-based equalizer usually uses a simple structure for reducing ISI, such as least mean square (LMS) [11] or least symbol error rate [12]. In addition, communication over the time-varying channel is a quite a prominent topic. In [13], a multi-scale time-varying multi-path amplitude model is proposed by using singular spectrum analysis, and a time-varying impulse response simulation framework is developed. In [14], an adaptive channel prediction scheme that extrapolates the channel knowledge estimated from a block of training symbols is proposed, and the predicted channel is used to decode consecutive data blocks. In [15], the received data are divided into subblocks, and the channel estimation of each subblock is regarded as a task. Meanwhile, a factor graph is proposed for multi-task channel estimation of subblocks to overcome the UWA time-varying channel.

Recently, deep learning has emerged as a novel approach for equalization, especially in challenging communication environments, e.g., molecular and UWA communications, whose communication channels are difficult to model accurately [16]. Many DL-based methods have been applied to UWA communications [7,17]. In [18], a hybrid architecture combining a convolutional neural network with a multi-layer perceptron was adopted, and a skip connection mechanism was introduced, leading to an effective reduction in the bit error rate (BER). To address data mismatch issues, the meta-learning algorithm was introduced in [19], which effectively improved the generalization of the DL-based receiver. In [20], an OFDM integrated receiver based on multi-task learning was proposed, improving the generalization of DL receivers through shared subtask parameters and a designed multi-task regularization loss function. In [21], inter-carrier interference was effectively suppressed through the use of autoencoder-based feature extraction and a sliding convolutional kernel structure, thereby reducing computational complexity while maintaining performance. In [22], downlink UWA communication using a deep neural network (DNN) utilizing a one-dimensional convolution neural network (CNN) is proposed, and the DNN-based DL NOMA UWA receiver outperformed the classical successive interference cancellation receiver. In [23], a DL-based receiver for single-carrier communication is proposed to mitigate time-varying UWA channels. In [24], a receiver system that explores the machine learning technique of a deep belief network is designed to combat distortion caused by the Doppler effect and multi-path propagation. There is little research on deep learning-based time-domain equalization methods for UWA single-carrier communication. The changing conditions of the UWA channel require retraining data-driven models from scratch for each new dataset, which poses a key limitation. Based on an online training mechanism, meta-learning, also known as learning to learn [25], is increasingly applied to UWA domains such as UWA OFDM, including channel estimation and detection, and it has become an effective solution [19,26]. In addition, some underwater communications systems are furnished for in-situ applications that operate in relatively stable locations. The parameters of in-situ equipment communication scenarios, including depth, distance, temperature, salinity, and even working hours, are either fixed or change periodically. Meanwhile, many direct and stochastic channel-replay tools have been found effective for validating the performance of UWA communications. Therefore, how to achieve better communication through known channels also becomes an interesting subject.

Motivated by the above reasons, we aim to apply deep learning methods to improve BER performance in underwater SC communications. The main contribution can be concluded as follows:

• To overcome the distortion of the UWA channel, we proposed a sliding deep learning-based framework for SC communications that uses a multi-layer neural network with ReLU nonlinearity to eliminate channel distortion rather than a single-layer linear method. The sliding framework accounts for the time-varying characteristics of the UWA channel, and multi-layer, non-linear neural networks can improve equalization performance. Additionally, to accelerate training convergence, we used a pre-processing-based training phase.
• Considering the impact of time-varying channels, we leverage the pilot and data symbol relationship to perform online transfer learning. A meta-learning-based SC equalizer is proposed in the time domain. In this process, the pilot is treated as labeled data, and the data symbol is regarded as the unlabeled data. A few-step learning procedure is performed, and the DL network is updated using the pilot. Then, the data symbol is equalized by the updated network. To make this article more convincing, the real-world UWA channels collected in different experiments are used to corroborate the effectiveness of the proposed algorithm.

The rest of this paper is divided into the following sections: Section 2 presents the structure of the single-carrier communication system. In Section 3, the learning-to-equalize approach is explained. Then, we present experimental settings and results in Section 4 and provide the conclusion in Section 5.

Notation: Column vectors and matrices are in the form of lowercase and capital bold letters, respectively. $\mathbb{R}$ indicates the set of real numbers. $|·|$ represents the cardinality of a set. $∥·∥$ stands for the Frobenius norm. $\mathcal{R}[·]$ means the real part operator. ∇ denotes the gradient operator.

2. System Model

The structure of the single-carrier communication system with N symbols is shown in Figure 1. At the transmitter, the transmitted bitstream, binary bit sequence $\{b_1,\dots ,b_i,\dots ,b_{MK},$ $b_i\in 0,1\}$, is split into K groups with $i=1,\dots ,MK$, and each group is mapped to one of the symbols of the $2^M$-QAM alphabet $\mathcal{A}$. The K generated symbols $x_1,x_2,\dots ,x_K$ are framed with pilots, then fed to a pulse-shaping filter to give the time-domain signal. Then, after the addition of pilots, the signal is transmitted over a time-varying channel.

At the receiver, the received signal can be expressed as

$$\mathit{y}=\mathit{H}\mathit{x}+\mathit{w},$$

(1)

where $\mathit{y}$ is a vector which contains ${[y_1,y_t,\dots ,y_K]}^T$, $\mathit{x}$ is a vevtor which represents ${[x_1,x_1,\dots ,x_K]}^T$, and $\mathit{w}$ denotes the additive white Guassian noise. $\mathit{H}$ is a channel response matrix, which can be expressed as

$$\mathit{H}=\left[\begin{array}{ccccccc}{h}_{[1,1]}& \dots & h_{[1,L-1]}& & & & \\ & \ddots & \ddots & \ddots & & & \\ & & h_{[3,1]}& \dots & h_{[3,L-1]}& & \\ & & & \ddots & \ddots & \ddots & \\ & & & & h_{[t,1]}& \dots & h_{[t,L-1]}\end{array}\right].$$

(2)

For UWA channels, we have two specific conditions. One is the time-varying (TV) channel, which is a tough case. TV channels will change within a data block. Each row in the channel matrix $\mathit{H}$ has a different value, meaning the channel ${\mathit{h}}_{\left[\mathit{t}\right]}=[h_{[t,1]},\dots ,h_{[t,l]}]$ is different at each time step. That is, each row in the matrix is distinct yet shares related properties. Another is the quasi-static (QS) channel, which is a mild status. QS channels are relatively fixed within a frame, i.e., time-invariant within a data block. In this condition, we assume that the CIR ${\mathit{h}}_{\left[\mathit{t}\right]}$ of each time slot t is the same. That is, each row in the matrix is the same.

3. Learning to Equalize

For UWA channels, channel parameters vary with the communication situation and are difficult to estimate due to their time-varying characteristics. The relationship between the transmitted symbols and the observed symbols can be described by

$$P_{ch}\{y_1,\dots ,y_k,\dots ,y_K|x_1,\dots ,x_k,\dots ,x_K;\mathit{H}\},$$

(3)

where $x_k$ means the transmitted symbol and $y_k$ represents the received symbol.

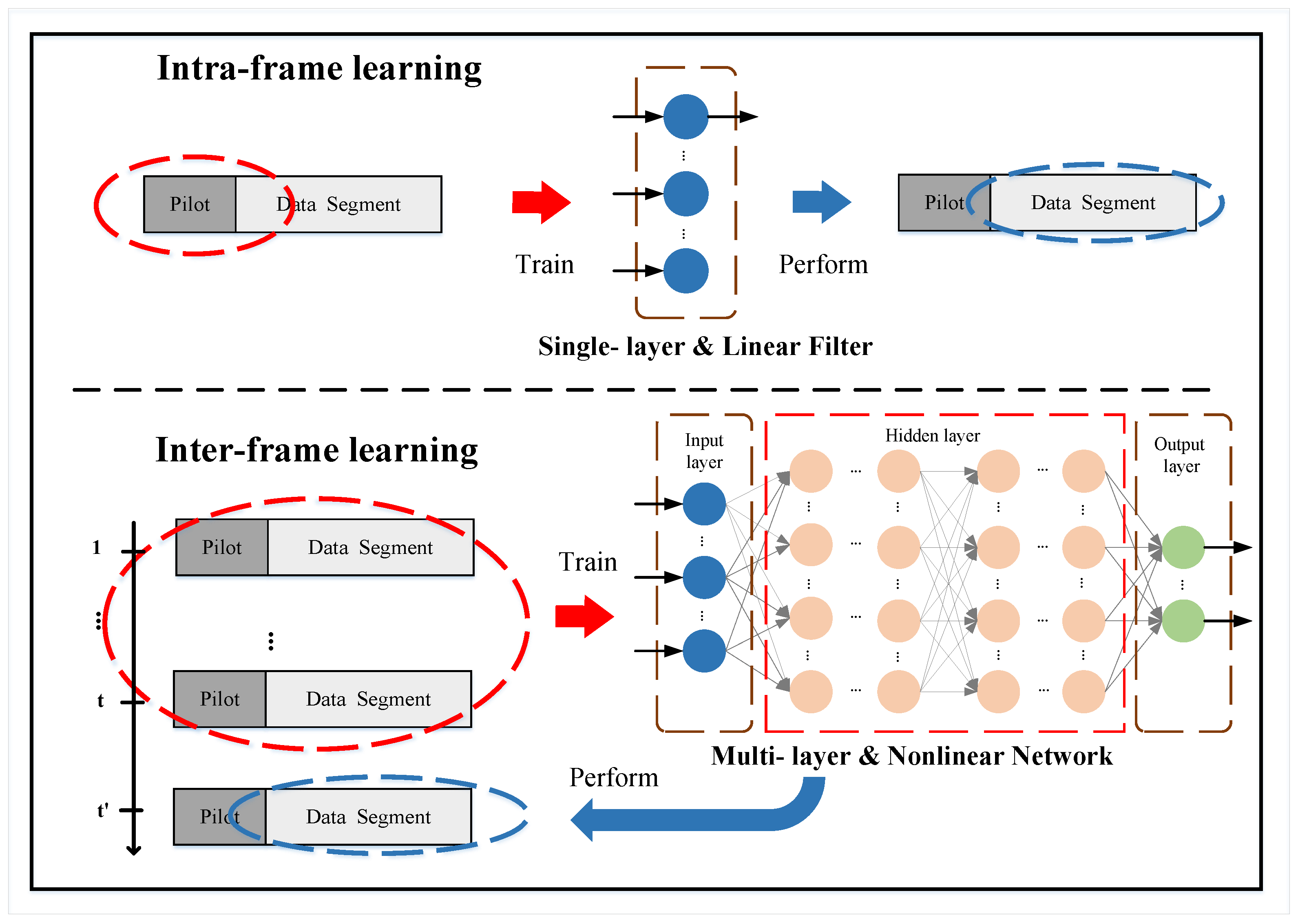
For convenience, we provide a summary of learning to equilization. The previous symbols can be used to equalize the received signal. For example, the symbol $x_k$ can be estimated by using the sequence $\{y_k,y_{k-1},\dots ,y_1\}$, despite the ISI caused by channel multi-path. The view of learning can be divided into intra-frame and inter-frame learning methods. A comparison of the intra-frame learning and the inter-frame learning is shown in Figure 2.

3.1. Intra-Frame Learning-Based Adaptive Equalizer

Intra-frame learning methods use only the pilots contained in a communication round to train the filter weight w. Only the online training process is available throughout the entire learning stage. The most typical algorithm is the classical adaptive filter method. The classical adaptive equalization methods are in-frame learning approaches. The specific process of the intra-frame learning is as follows: assume $\mathit{X}=\{x_1,\dots ,x_k,\dots ,x_K\}$ is the data sequence sent from transmitter, with K modulated symbols, and $\mathit{Y}=\{y_1,\dots ,y_k,\dots ,y_K\}$ is the corresponding observed data at the reiceiver. 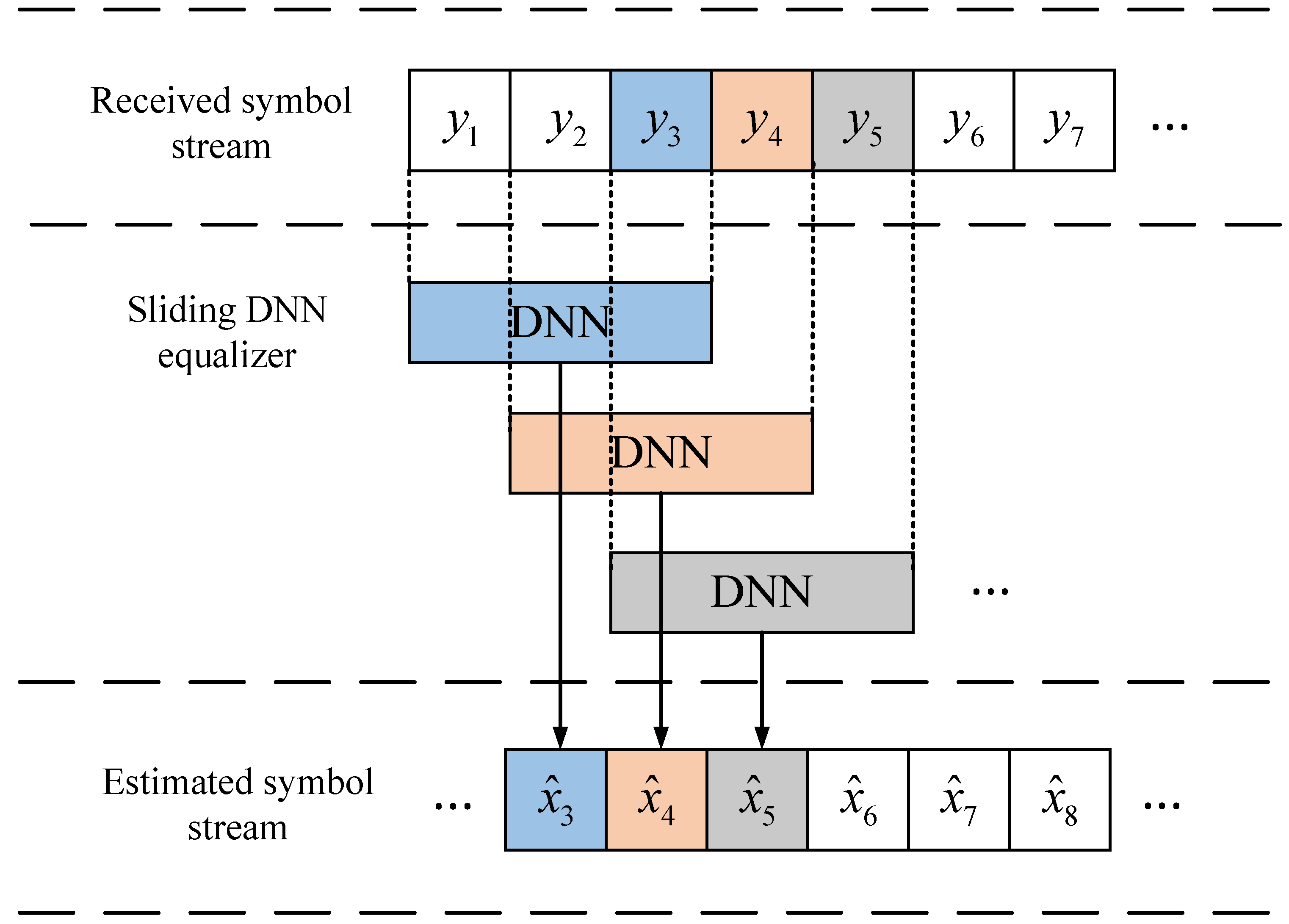A pair of training data and label can then be noted as $\{{\mathit{Y}}_{k-m,k},{\mathit{X}}_k\}$ with ${\mathit{Y}}_{k-m,k}=\{y_{k-m},\dots ,y_{k-1},y_k\}$, ${\mathit{X}}_k=\left\{x_k\right\}$, where k means the k-th symbol of the transmitted sequence and m represents the number of observation symbols for the k-th symbol, also known as the filter length. The sliding architecture is shown in Figure 3.

In this class of algorithms, only a simple network is considered. The simple framework can be easily trained on sequences and has a strong mathematical basis. The drawback is that the performance is unsatisfactory for tough channel conditions. The most famous adaptive equalization method is the LMS algorithm, which has a nonlinear feedback architecture. The LMS algorithm can be divided into two steps. The first step is the forward part, which equalizes the received signal and estimates the error. The second step is the adaptation process, which updates the current equalizer value based on the error. The forward architecture is a winner filter. The linear scheme makes it easy to analyze using mathematical methods. The winner filter can be represented in discrete form, and the input signal can be formulated as a discrete-time sequence. The output is guaranteed as an equalized symbol. According to optimization theory, the LMS algorithm updates the filter coefficients at each time step using the steepest descent method.

3.2. Inter-Frame Learning-Based Deep Learning Equalizer

Inter-frame learning methods contain both online and offline training phases that utilize this information. The inter-frame learning viewpoint is consistent with deep learning methods. Based on the LMS methods, we introduce a fully connected (FC) network-based framework, called FC-DNN, to equalize the SC signal in a sliding manner. We denote the FC-DNN equalizer as $f\left(\mathit{\theta }\right)$, where $\mathit{\theta }\in {\mathbb{R}}^n$ are the parameters of the neural network. Define $\mathit{y}$ as the network input and $\mathit{x}$ as the recovered symbols, respectively, where $x_l\in \{-1,1\}$. The input vector has dimensions $2M\times 1$, which concatenates the real and imaginary parts of the input signal $\mathit{y}$, where M is the filter length. The input is processed through a sequence of deterministic, layered transformations. The NN procedure is a cascade of linear transformations followed by element-wise non-linearities, progressively mapping the input to the desired output space using the network’s learned parameters.

Therefore, the DNN equalizer $f\left(\mathit{\theta }\right)$ can be expressed as

$$\begin{array}{c}\hfill \widehat{\mathit{x}}=f\left(\mathit{\theta }\right)=f_{tanh}^{\left(V\right)}(\dots f_{Relu}^{\left(v\right)}(\dots f_{Relu}^{\left(1\right)}\left(\mathit{y}\right))),\end{array}$$

(4)

where V is the number of layers, and the v-th layer contains a total of $N_v$ neurons, each connected to all neurons in the v-th layer through the connection weight matrix. The parameters of the network are optimized during the offline learning phase.

The input of the first layer is the samples of $y\left[k\right]$, which are selectively chosen from the observed signals through pre-processing. This dataset is then used to train the FC-DNN equalizer, which classifies $y\left[k\right]$ as $s_1$ or $s_2$. The output of the hidden layers are activated by $f_{Relu}\left(z_v\right)=max(0,z_v)$, which is a non-linear function, to provide a normalized output and keep the output within $[0,+\infty ]$, and $z_v$ represents the output of the v-th hidden layer. The width of the l-th layer is denoted $d_v$. Note that $w_l$ is the parameter of the l-th layer. Therefore, we can use $\mathit{\theta }=\{(w_1,b_1),\dots ,(w_v,b_v),\dots ,(w_V,b_V)\}\in \mathbb{R}$ to express the set of whole network hyper-parameters, where $w_v$ means the v-th layer weigth and $b_v$ represents the v-th layer bias with $v\in \{1,\dots ,V\}$. Due to the ReLU activation function, each neuron’s output can be represented by two limit states, denoted as $f_l\left({\mathit{z}}_{\mathit{i}}\right)\in \{0,1\}$. The output layer consists of a single neuron that outputs the estimates of the binary bits to be detected.

The receiver can be trained by optimizing the loss function

$$L(x_k,{\widehat{x}}_k;\mathit{\theta })={\displaystyle \frac{1}{N}}\sum _{k=1}^K{|x_k-{\widehat{x}}_k|}^2,$$

(5)

where ${\widehat{x}}_k$ denotes the output of the basic DNN scheme.

By employing Formula (5), the FC-DNN equalizer $f\left(\mathit{\theta }\right)$ arrives at an optimum set of connection weights ${\mathit{\theta }}_{opt}$ which minimizes the optimal average cost function. Then, the well-trained DNN $f\left({\mathit{\theta }}_{opt}\right)$ can be employed for signal equalization using Formula (4).

3.3. Comparison of the Complexity of Intra-Frame Learning and Inter-Frame Learning Equalizer

The complexity comparisons between intra-frame and inter-frame learning are shown in

Table 1. Comparison of the complexity of the LMS, NLMS, and DNN equalizers.

Algorithm	Addition	Multiplication	Memory
LMS	N	N + 1	N
NLMS	2N	2N + 1	N
DNN	${\displaystyle \sum _{v=2}^V}{N}_v\times N_{v-1}$	${\displaystyle \sum _{v=2}^V}{N}_v\times N_{v-1}$	${\sum }_{v=1}^V{N}_v$

, including addition, multiplication, and memory. In this article, the LMS and NLMS were selected as representative algorithms for intra-frame learning, while the DNN was chosen as a representative for inter-frame learning. There is no doubt that the complexity and storage parameters of inter-frame learning methods are higher than those of classical adaptive equalizers. Concretely, the LMS and NLMS algorithms, due to their simple structures, exhibit computational and memory requirements that scale linearly with the filter length N, making them highly efficient. Among them, NLMS introduces a normalization step, trading approximately twice the computational cost of LMS for more stable convergence performance. In contrast, the complexity of DNNs depends entirely on their network scale, with both computational load and memory usage growing rapidly with the number and width of network layers, often reaching quadratic or even higher orders. Thus, despite its powerful capabilities, the DNN requires significantly more computational resources than the former two algorithms.

4. The Proposed Meta-Learning-Based Inter-Frame Learning Strategy

In a time-varying condition, each communication round at a different slot will be distorted by various channel impulse responses. Therefore, the well-trained neural network (NN) should be fine-tuned to adapt to the channel for precise communication. In a classical adaptive filter algorithm, the filter parameters are updated based on a pilot or training sequence. From the same perspective, we aim to use the pilot to optimize the DL equalizer’s parameters for improved performance. To further improve the DL equalizer $f\left(\mathit{\theta }\right)$’s BER performance, we proposed a meta-learning-based training strategy for the SC system in the time domain using inter-frame learning, dubbed Meta-DNN. A flowchart of the meta-learning-based training strategy is shown in Figure 4. In real-world communication environments, the trained parameters need to be fine-tuned to adapt to the new environment. Hence, the meta-learning scheme is employed for inter-frame learning. The communication frame contains a pilot segment and a data segment. We divide them into two categories: the support set and the query set. The support set contains a pilot symbol of multiple communication rounds, and the query set includes a data symbol generated from multiple communication rounds. The support set for meta-learning can be denoted as $D_t^{Pilot}$, where $D_t^{Pilot}=\left\{((y_{k-m}^P,\dots ,y_{k-1}^P,y_k^P),x_k^P)\right\}$ is the received pilot signal pairs of the t-th time slot. Moreover, the query set is noted as $D_t^{Data}$, where $D_t^{Data}=\left\{((y_{k-m}^Q,\dots ,y_{k-1}^Q,y_k^Q),x_k^Q)\right\}$ are the received data signal pairs of the t-th time slot. The meta-learning-based inter-frame learning strategy is described in Algorithm 1.

Algorithm 1 The meta-learning-based inter-frame learning strategy.

Require: Support set generated by pilot symbol $D_t^{Pilot}$ and the query set generated by data symbol $D_t^{Data}$, the update steps T, step size $\alpha$ and $\beta$.   1: Initialize: $\mathit{\theta }$   2: Online training stage, both support set and query set are employed for updating   3: for $t=1$ to T do   4:    Using $D_t^{Pilot}$ update the parameters according to   5:    ${\mathit{\varphi }}^t\left(\mathit{\theta }\right)={\mathit{\theta }}^t-\alpha {\nabla }_{\mathit{\theta }}L({\mathit{\theta }}^t,D_t^{Pilot})$;   6:   Then, using $D_t^{Data}$ update the parameter according to   7:    ${\mathit{\theta }}^{t+1}={\mathit{\theta }}^t-\beta {\nabla }_{\mathit{\theta }}L({\mathit{\varphi }}^t\left({\mathit{\theta }}^{\mathit{t}}\right),D_t^{Data});$   8:    obtain the ${\mathit{\theta }}^{t+1}$   9: end for 10: Offline adaption stage, only support set is used to fine-tune the parameters according to Formula (7). Ensure: ${\mathit{\theta }}_{\mathit{opt}}$

The neural network was first updated using the support data $D_t^{Pilot}$, which were generated from different time slot t communications. Given the limited pilot length, the sliding step size is set to 1 to obtain more fine-tuning data for the query data. For the proposed algorithm, given the model parameters of the DL equalizer, we assume the DL equalizer can update its own parameters by few-step learning procedures according to the gradient descent based on $D_t^{Pilot}$, namely

$$\begin{array}{c}\hfill {\mathit{\varphi }}^t\left(\mathit{\theta }\right)={\mathit{\theta }}^t-\alpha {\nabla }_{\mathit{\theta }}L({\mathit{\theta }}^t,D_t^{Pilot}),\end{array}$$

(6)

where $\alpha$ is the adaptation learning rate.

Then, the loss $L({\mathit{\varphi }}^t,D_t^{Pilot})$ is evaluated according to Formula (5) and $\mathit{\theta }$ is updated by using the query data $D_t^{Data}$ ulteriorly according to

$$\begin{array}{c}\hfill {\mathit{\theta }}^{t+1}={\mathit{\theta }}^t-\beta {\nabla }_{\mathit{\theta }}L({\mathit{\varphi }}^t\left({\mathit{\theta }}^{\mathit{t}}\right),D_t^{Data}).\end{array}$$

(7)

where $\beta$ is the update learning rate. It is worth mentioning that during online training, both pilot symbol $D_t^{Pilot}$ and data symbol $D_t^{Data}$ are used to train the DL network. On the contrary, during the offline testing phase, only pilot data is used to update the network to adapt to data under different conditions.

5. Simulation and Discussion

In our experiments, PyTorch 1.2.0 is chosen as the development framework. The SC system with 1024 bits is considered. 4-QAM is used as the modulation scheme. SC blocks contain the pilots and transmitted symbols. We adopt the mean squared error (MSE) loss function and the adaptive moment estimation (Adam) optimizer with a $0.001$ learning rate. A four-layer FC-DNN structure with one input layer, two hidden layers, and one output layer is used, where the number of neurons in each layer is 160, 80, 40, and 1, respectively. In our experiments, each frame contains $M=200$ pilots and 1000 QPSK symbols. The local adaptation rate $\alpha$ is 0.001, and the update rate $\beta$ is 0.0001. The step size of the LMS and NLMS is $2\times {10}^{-5}$. The Norway–Oslofjord (NOF) and Norway–Continental Shelf (NCS) channels are used in this section [27] as the sea-trail-measured channels. The center frequency is 14 kHz. The maximum Doppler shifts of the NOF and NCS channels are $3.9$ Hz and $15.7$ Hz, respectively. The delay coverage of the NOF and NCS channels is 128 ms and 32 ms, respectively. Meanwhile, the channel response can be replayed as the QS channel and the TV channel. Hence, four conditions are considered in the simulations:, namely QS-NOF, QS-NCS, TV-NOF, and TV-NCS. In each channel type, $80\%$ is used for training and $20\%$ for testing. The training epochs are set to 100 or 500, and the batch size is 10 frames per epoch, each containing at least 2000 pilot symbols and 20,000 data symbols. Meanwhile, the channel response will change from frame to frame.

5.1. Pre-Equalization Methods

The comparison algorithms are the normalized LMS (NLMS) algorithm and the matching pursuit (MP) algorithm. Meanwhile, we introduce a pre-equalization method to eliminate the partial channel influence. Therefore, considering the pure DL receiver requires a longer training period, we employ a pre-equalization approach to perform pre-processing and obtain a better initial value. Pre-equalization can provide a better initial value and accelerate convergence during training. We combine our proposed FC-DNN equalizer and the NLMS time-domain equalizer to form a hybrid equalization procedure, which is a novel and effective approach for communication systems, as it can benefit from two equalizers at different stages of the equalization process.

5.2. BER Performance

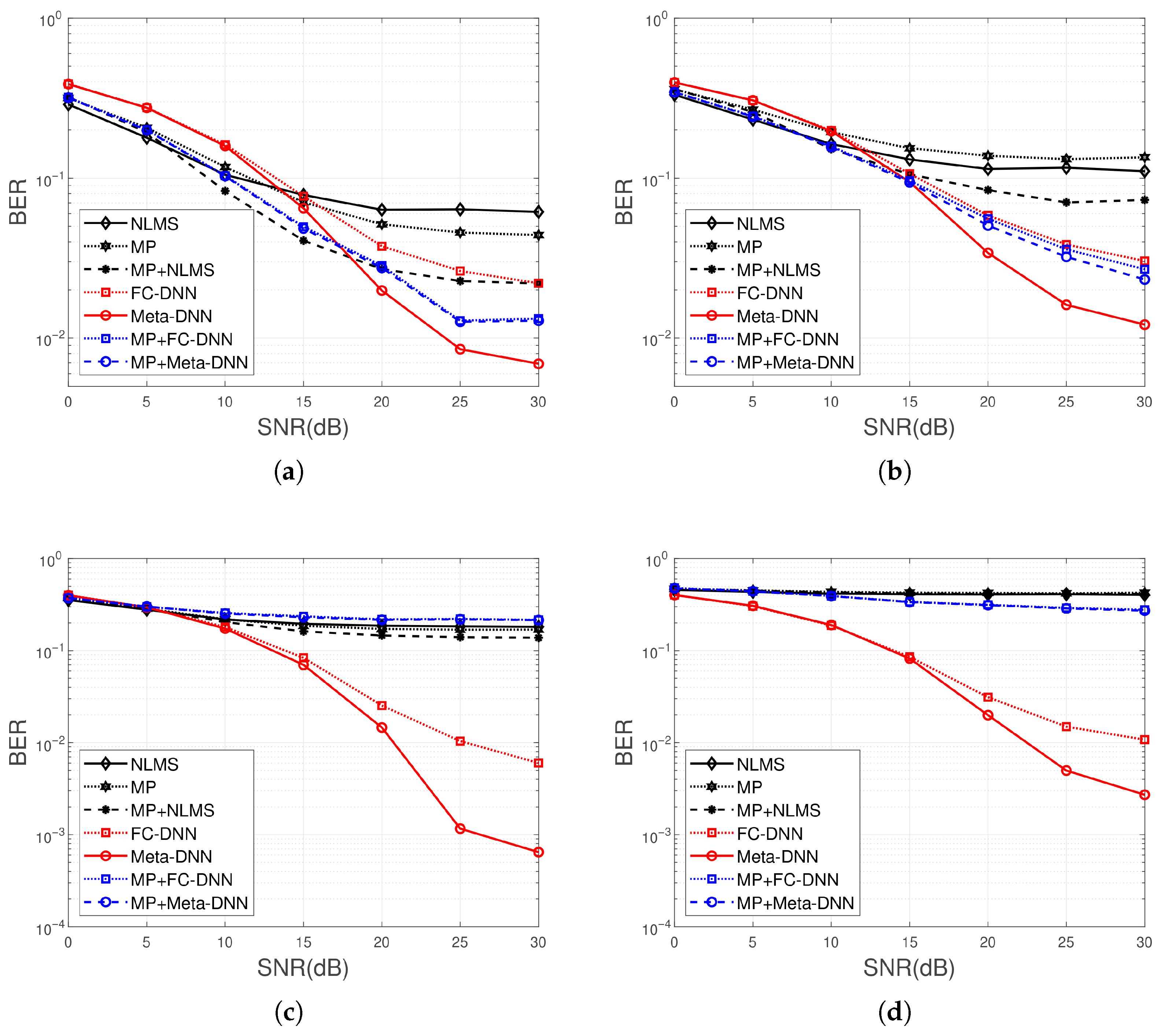
Figure 5 systematically compares the BER performance of seven equalization algorithms, including NLMS, MP, MP with NLMS, FC-DNN, Meta-DNN, MP with FC-DNN, and MP with Meta-DNN, across typical quasi-static and time-varying scenarios. The results demonstrate that under quasi-static channel conditions, all algorithms exhibit a steady decline in BER as SNR increases. Among them, DNN-based algorithms, particularly Meta-DNN, show significant advantages in the low-SNR region, reducing BER more than traditional methods do. In time-varying channels, the performance of adaptive algorithms generally degrades. Notably, the MP with the Meta-DNN combination maintains optimal performance, highlighting its strong robustness against channel time variations. Traditional methods, such as NLMS, perform worst in TV-NCS channels, with BER failing to drop below ${10}^{-2}$. MP with Meta-DNN consistently achieves the best performance across all channel conditions, reaching a BER of ${10}^{-3}$ at 20 dB SNR over TV-NCS channels. Standalone Meta-DNN slightly underperforms MP with Meta-DNN but still significantly outperforms FC-DNN. MP with FC-DNN approaches Meta-DNN performance in static channels but shows a noticeable gap in time-varying scenarios. The traditional MP with the NLMS scheme only approaches DNN-based performance in static channels at a high SNR. NLMS and MP consistently perform worst, with BER remaining around ${10}^{-1}$ over the time-varying NCS channel. The result confirms the superior adaptability of Meta-DNN-based methods, particularly in dynamic channel environments, while traditional approaches struggle to maintain reliable performance.

5.3. Training Epoch Performance

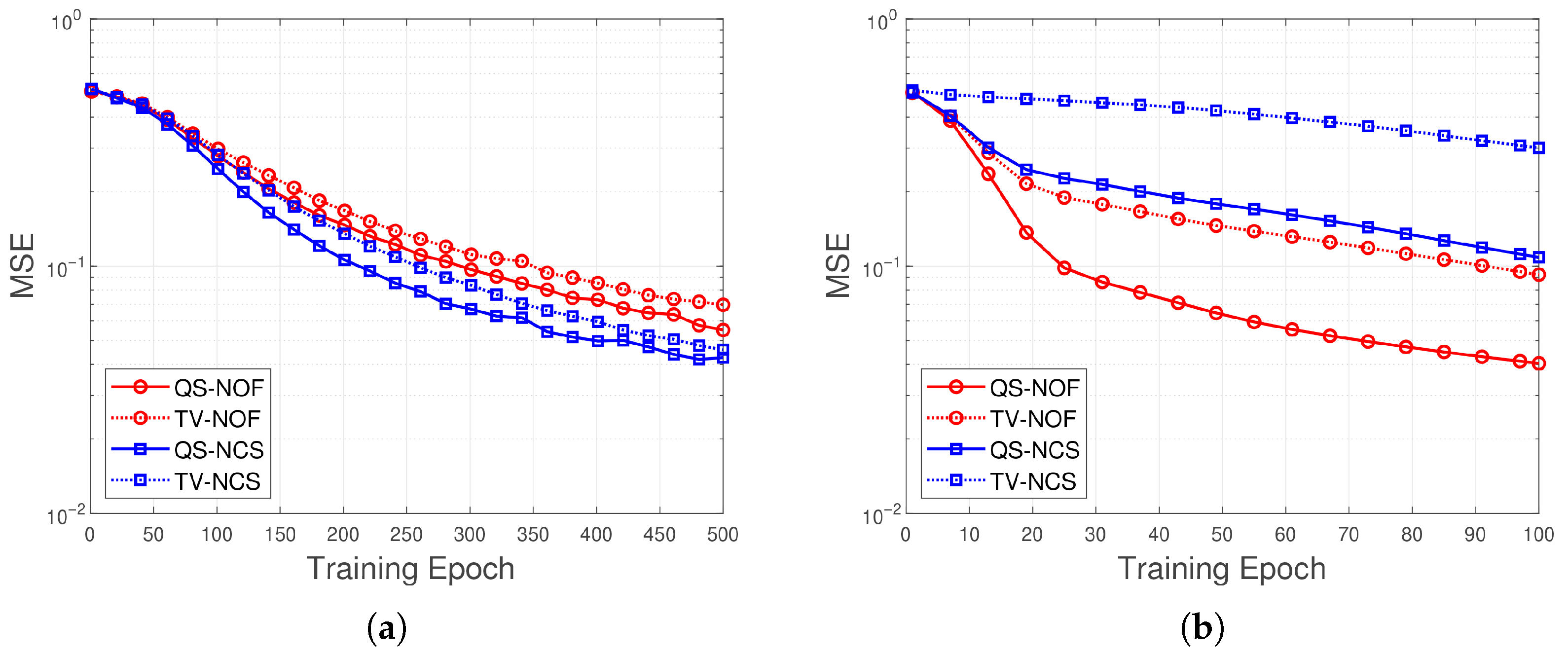
Figure 6 presents the learning-based receiver without pre-processing, also named the pure learning-based receiver, and the learning-based receiver with pre-processing. From Figure 6a, we know that the TV channel needs more training epochs than the QS channel. We also compare the training speed across two channel types. The learning process under the mild channel, NOF, exhibits a faster learning speed compared to that under the tough channel, NCS. From Figure 6b, the pre-equalization-based approach has fewer training epochs. It is because equalization is applied before the DL equalizer is used, which improves the initialization of the training data. Therefore, it speeds up learning convergence. However, there is a drawback: when the signal is distorted by a severe channel, the classical pre-equalization method cannot restore the signal to a relatively normal initial state, even under adverse conditions. It results in a higher MSE for the pre-equalization-based training process compared to the pure learning approach. The comparison of the MSE convergence characteristics of the proposed method under four typical channel environments reveals the key impact of channel characteristics on model training. Experimental results show that MSE decreases monotonically across all channel conditions. However, there are significant differences: in the quasi-static NOF channel (QS-NOF), MSE converges fastest and performs best, eventually stabilizing at the order of ${10}^{-2}$, while in the time-varying channel (TV-NOF/TV-NCS), MSE is always high, especially in short-term training, with significant fluctuations. Specifically, the training process can be divided into two stages: in the early stage, 0–100 epochs, the gradient descent efficiency of the QS-NOF channel is five times that of the TV-NCS channel; in the middle stage, 100–500 epochs, QS-NOF reaches stability in 200 rounds, while TV-NOF needs 400 rounds to approach convergence, and TV-NCS has never fully converged. Further analysis reveals that the impact of time variability on MSE is $1.6$ times that of NCS characteristics, directly resulting in a final MSE for TV-NCS that is higher than that for QS-NOF. Based on these findings, it is recommended to adopt a channel-aware training strategy in engineering practice: for an ideal environment, it can be used as a benchmark for algorithm performance verification; for time-varying channels, it is recommended to use a dynamic learning rate and extend the training cycle to more than 600 rounds; for NCS channels, it is necessary to add a delay spread compensation module to the network and improve the nonlinear activation function. These optimization measures will effectively enhance the model’s adaptability and convergence performance across different channel conditions.

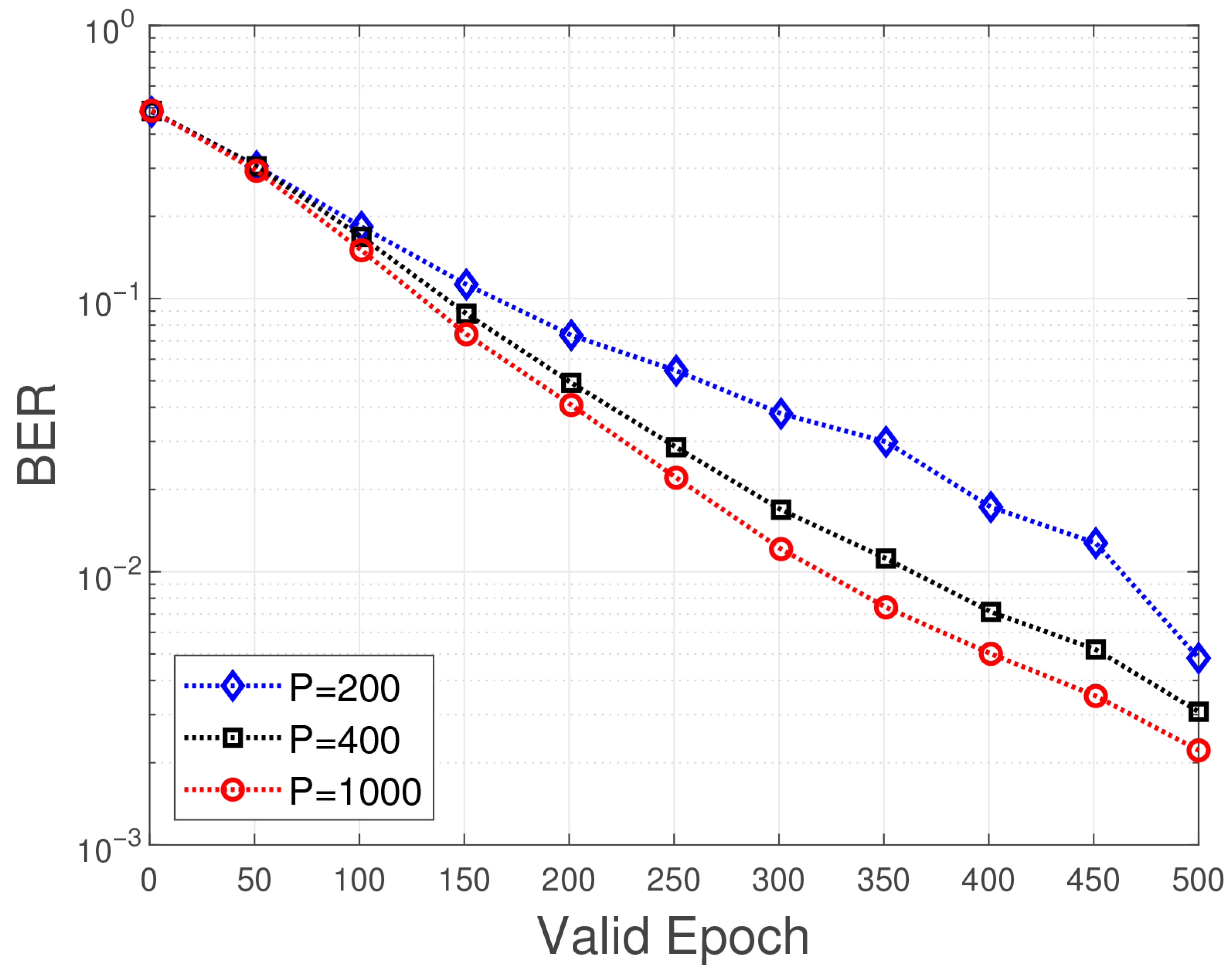
5.4. Pilot Number Effect

Figure 7 shows the performance impact of different training sequence lengths, also known as pilot numbers, on the BER as the number of training rounds changes under the condition of time-invariant channels. Pilots number $P=200$, $P=400$, and $P=1000$ are all considered. The BER decreases significantly with increasing the number of training rounds, and all curves show a monotonically decreasing trend, consistent with the expectation that the DNN model is gradually optimized during the training process. The longer the training sequence P, the faster the BER decreases. When P = 1000, the BER curve decreases the steepest, and the BER is close to ${10}^{-3}$ at about 150 rounds of training, finally stabilizing at the lowest level. The convergence speed of P = 400 and P = 200 slows down successively. In particular, P = 200 requires more than 300 rounds to achieve the performance of P = 1000 at 150 rounds. The challenge of time-invariant Rayleigh channels and multi-path fading requires the DNN to have strong nonlinear fitting capabilities, and increasing P directly improves the model’s representation ability, thereby approaching the theoretical optimal solution faster. However, as P increases, so does the redundancy overhead and network complexity. P = 400 can be used as a balanced choice, with a final BER close to P = 1000, a moderate number of training rounds, and higher spectrum efficiency. P = 200 is suitable only for scenarios with strict resource constraints and where significant performance loss can be tolerated. The more pilots, the lower the BER we can achieve. However, the disadvantage is that too many pilots will slow down the communication rate. Therefore, we have a balance between the BER and the communication rate.

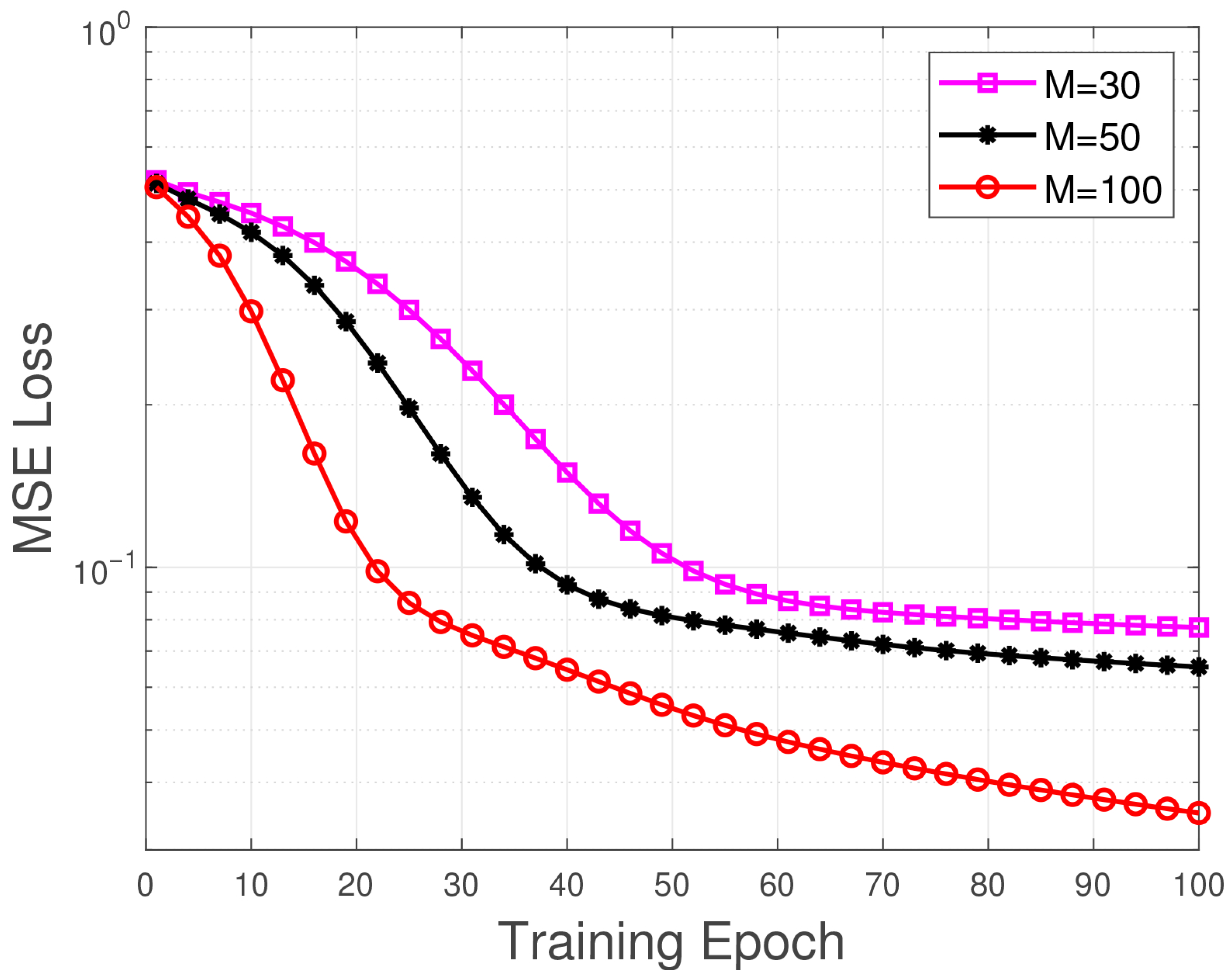
5.5. Filter Length Effect

Figure 8 clearly shows the effect of filter length, including M = 30, M = 50, and M = 100, on the MSE loss during neural network training. As demonstrated, a longer filter length is associated with a lower MSE. The MSE loss across all configurations decreases significantly with increasing training epochs before eventually stabilizing, consistent with typical training convergence. Faster convergence is achieved with larger M values. The curve for M = 100 drops most steeply and stabilizes at around 20 epochs, whereas the convergence for M = 30 is the slowest, requiring more epochs to reach a comparable loss level. At convergence, the lowest BER, approximately ${10}^{-1}$, is attained by M = 100, indicating that the convergence of the second-stage equalizer can be accelerated by increasing the length of the first-stage filter. Although the final loss values for M = 30 and M = 50 are similar, M = 50 holds a clear advantage in the early training phase. A moderate increase in filter length can optimize the initial optimization.

5.6. Constellation Performance

Figure 9 presents the output constellations of a hybrid equalizer over the NOF channel under 25 dB and 30 dB. In all cases, the first equalizer employs an MP channel estimator and an MMSE equalizer. The second equalizer, however, varies across the subfigures: Figure 9a,d use the NLMS algorithm; Figure 9b,e use a standard neural network (NN); and Figure 9c,f uses a meta-learning-based neural network. Our proposed NN-based algorithm as a secondary equalizer obtains a separated constellation in Figure 9b,e compared with the traditional hybrid algorithm combined with the MP channel estimation and MMSE equalization. In particular, the NNs combined with meta-learning can get the most separated constellation in Figure 9c,f than the NNs without transfer learning. By comparison, the equalization algorithm using meta-learning exhibits better convergence in constellation diagrams. Moreover, we can also know that the constellation of NNs based on the receiver has better limitations within the range $[-1,1]$. It is because we use a nonlinear tanh function as the activation function of the output layer.

6. Conclusions

In this paper, we concluded the investigation into learning-based equalization for single-carrier UWA communications. Meanwhile, a sliding deep neural network equalizer was proposed to overcome severe channel distortion, accompanied by a pre-processing strategy designed to accelerate training. To address time-varying channels, an adaptive online equalization scheme, Meta-DNN, was introduced and enhanced by meta-learning. In this scheme, pilot–data relationships were utilized to enable efficient transfer and improvement of BER performance. The superior and robust performance of the proposed approaches is confirmed through extensive tests conducted under reproducible, multi-scenario channels. In the future, we will improve the generalization of the proposed equalization method and leverage more advanced networks to enhance BER performance further. In addition, we will focus on potential deployment strategies, such as model quantization and pruning, to reduce computational and memory requirements for real-time inference.