Study on the Structural Vibration Control of a 10 MW Offshore Wind Turbine with a Jacket Foundation Under Combined Wind, Wave, and Seismic Loads
Abstract
1. Introduction
2. Fully Coupled Analysis Theories of OWT with Jacket Foundation
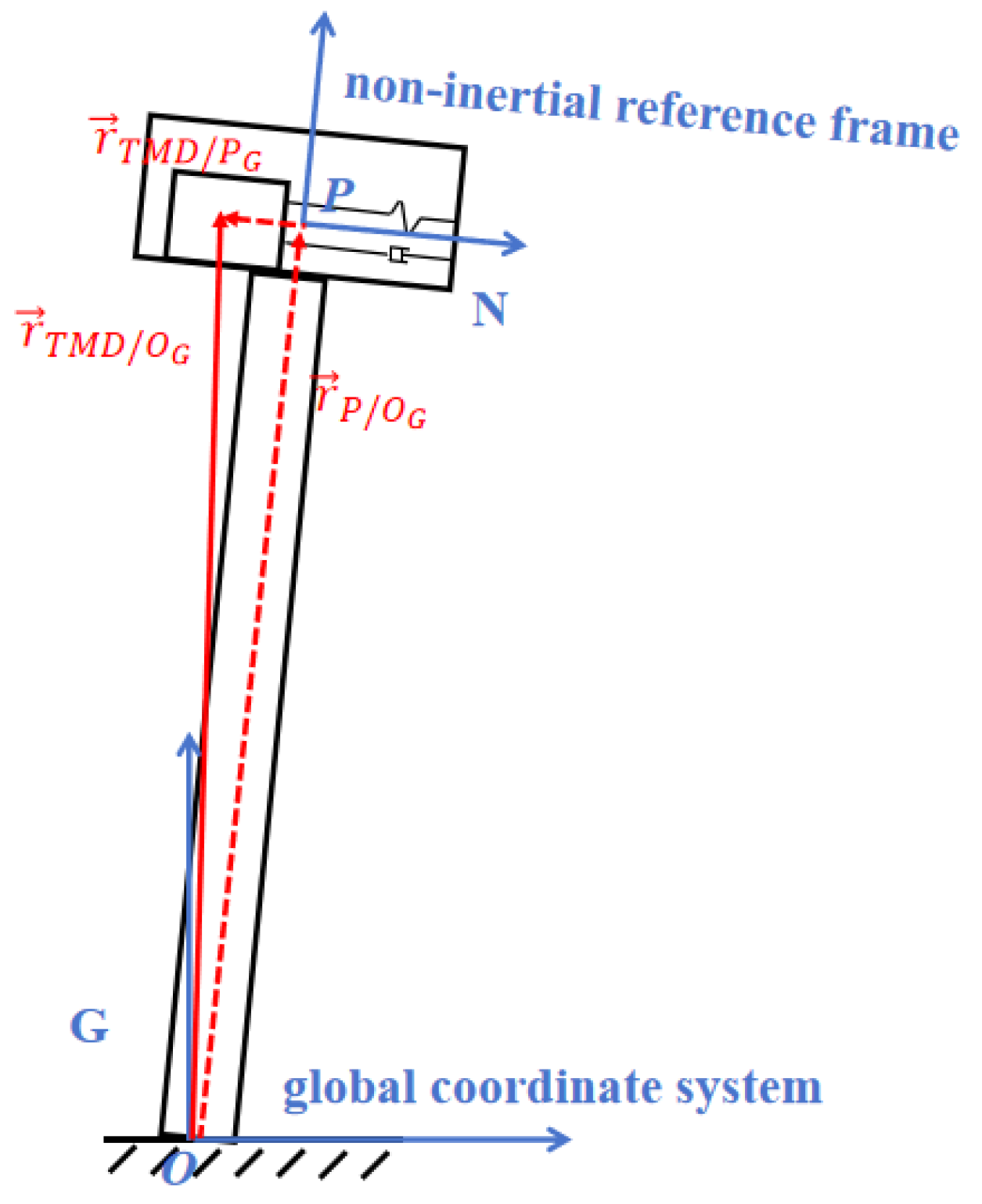
2.1. Kane’s Equations of Motion
2.2. Wind Loads
2.3. Wave Loads
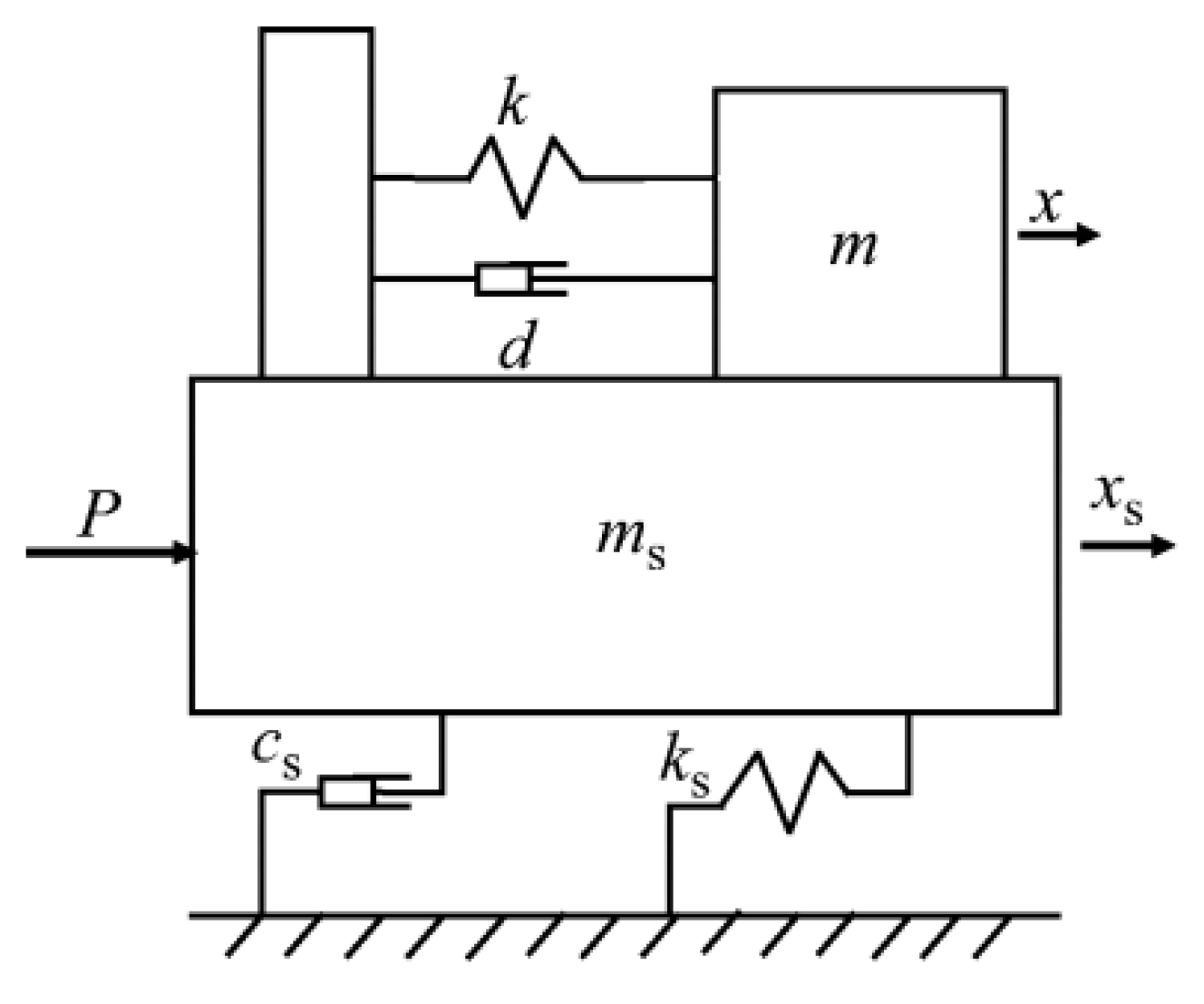
2.4. TMD Motion Equation
2.5. Seismic Load
2.6. Equation of Motion for Offshore Wind Turbine Structure Considering the Combined Effects of Wind, Waves, Earthquake, and TMD
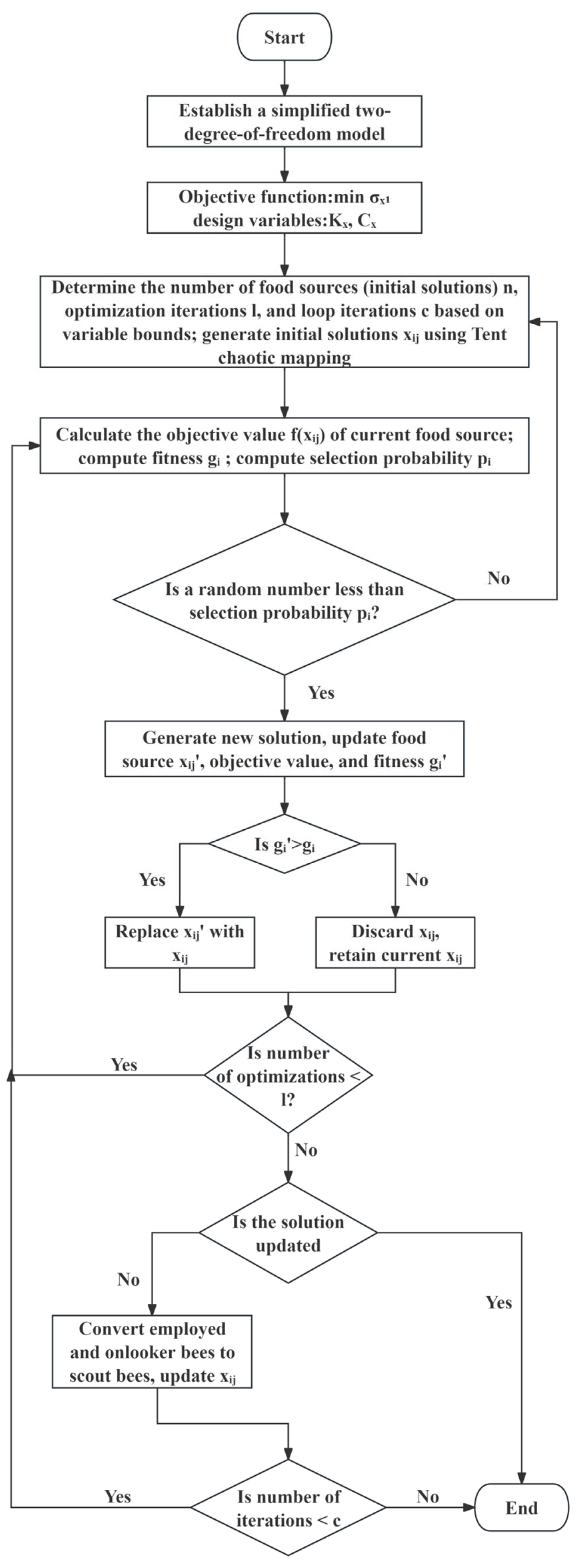
2.7. TMD Parameter Optimization Method Based on the Artificial Bee Colony Algorithm
3. OWT Parameters and Environmental Conditions
3.1. DTU 10MW Wind Turbine Parameters
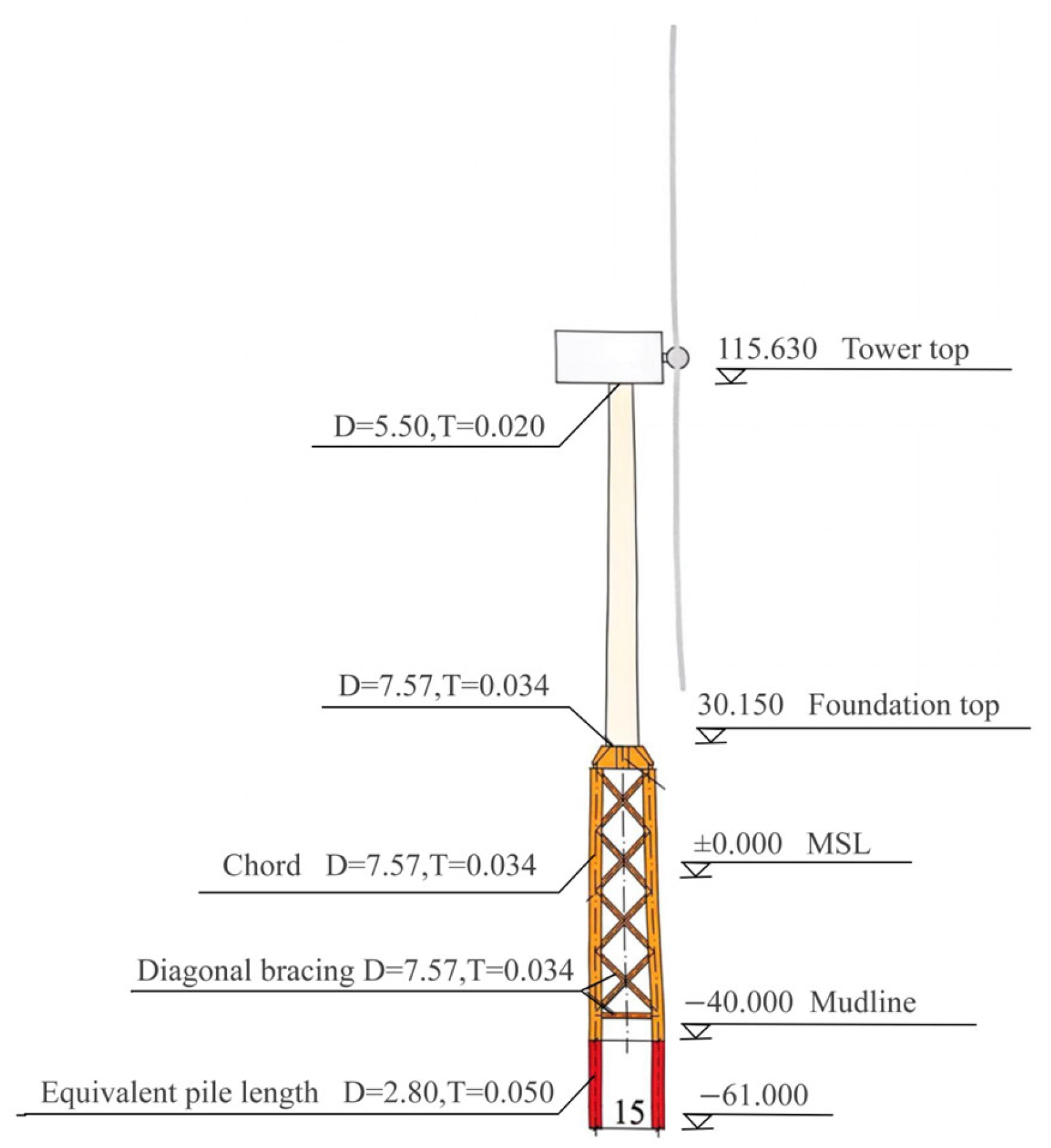
3.2. Jacket Foundation Parameters
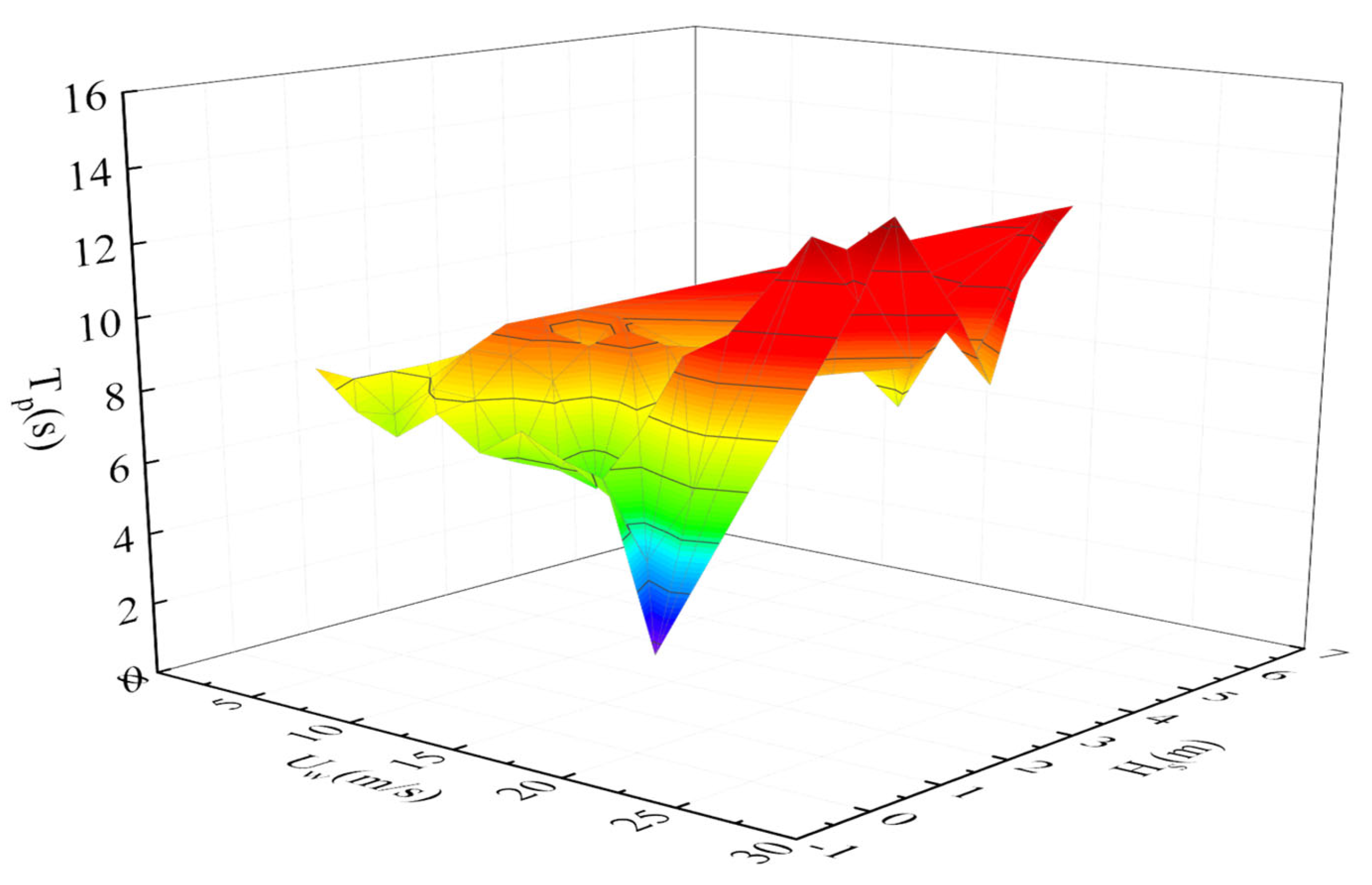
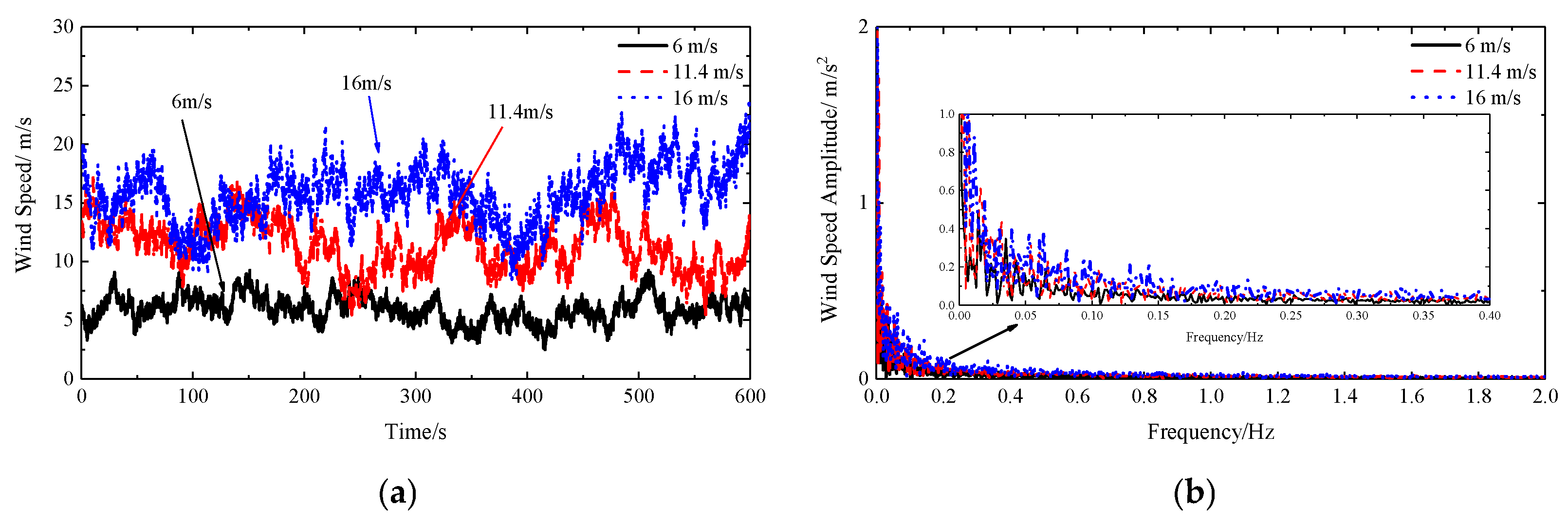
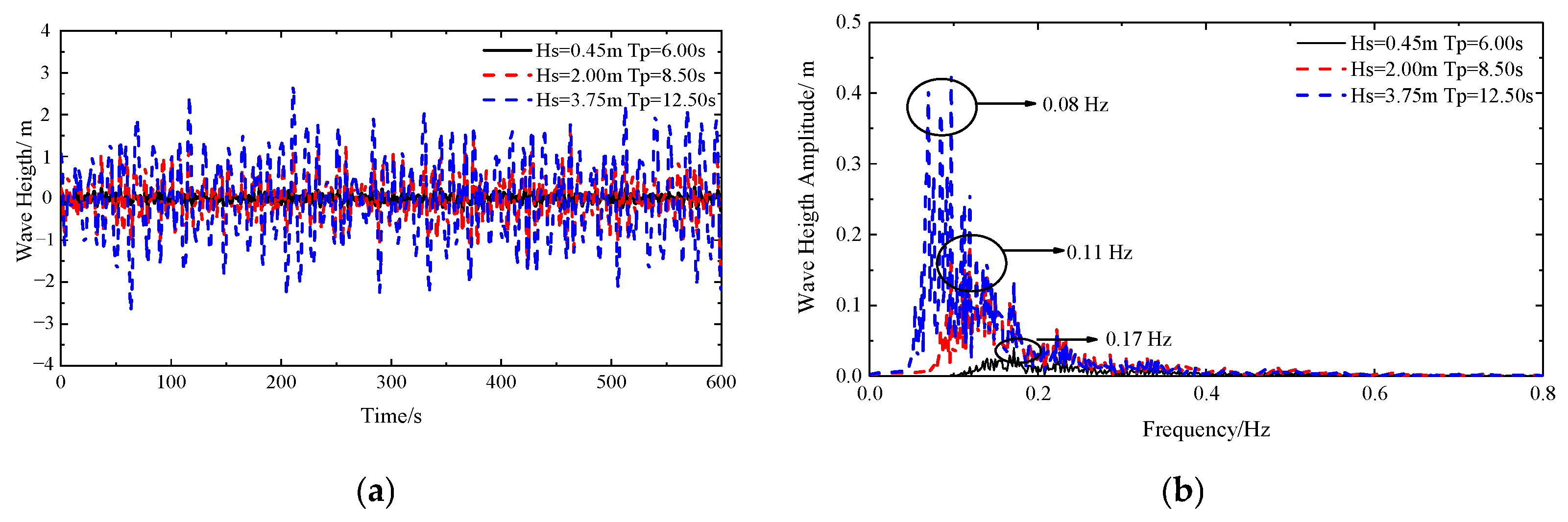
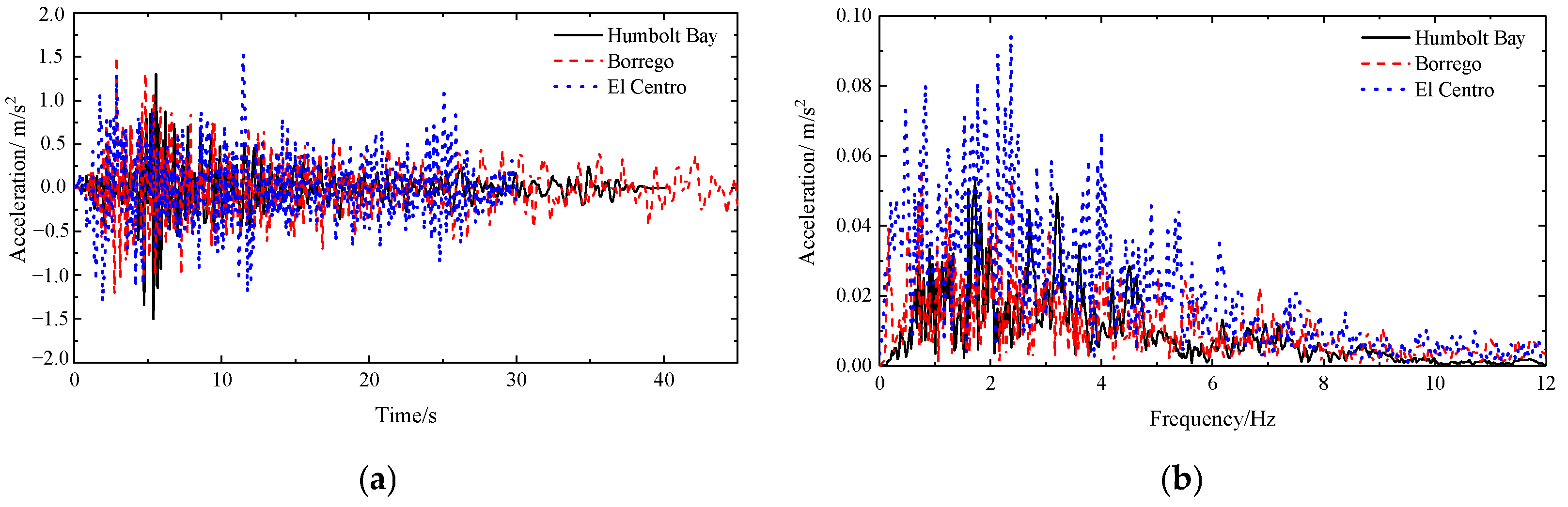
3.3. Marine Environment Conditions
4. TMD Parameter Analysis and Model Validation
4.1. TMD Parameter Analysis
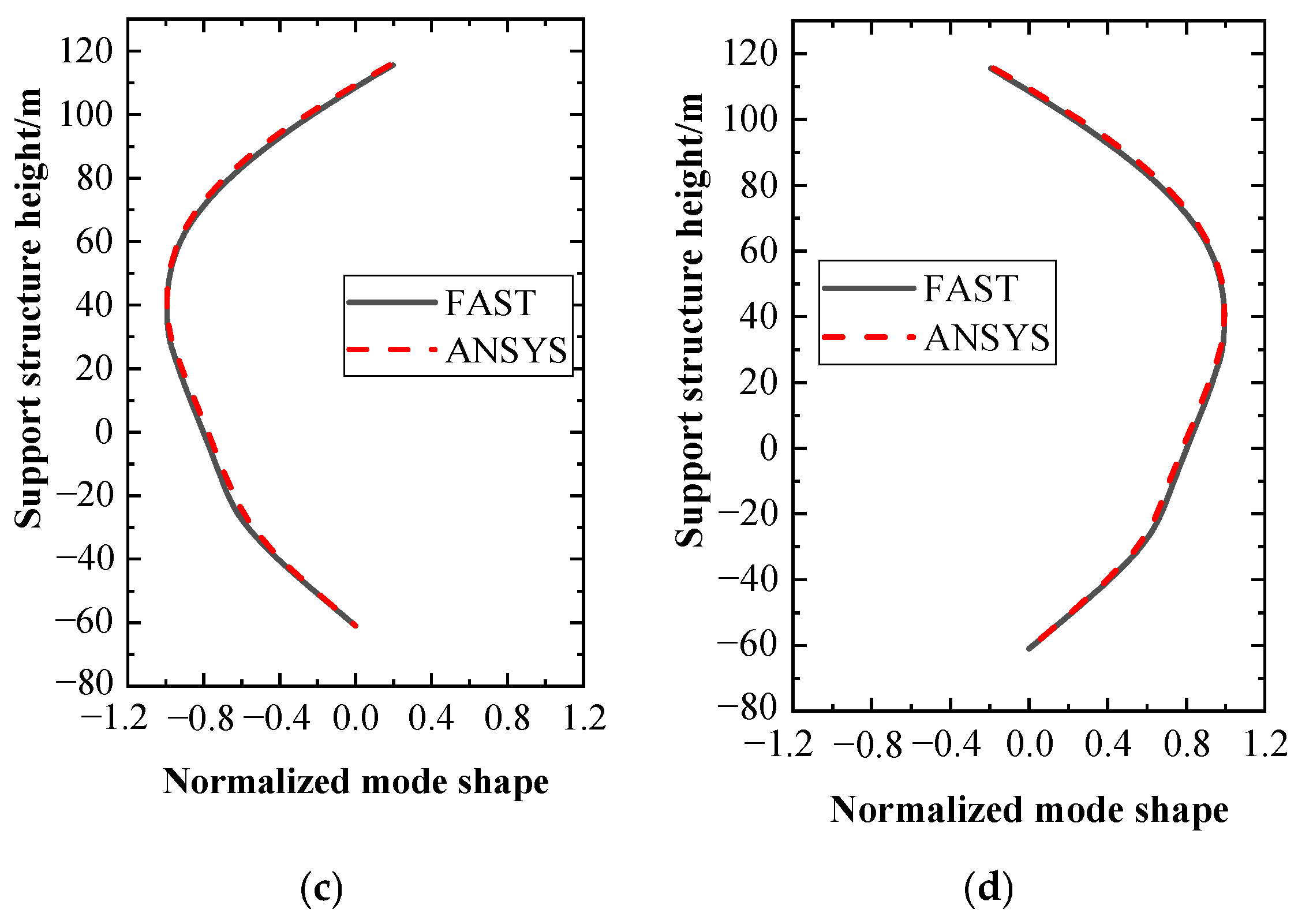
4.2. Model Validation
5. Vibration Mitigation Analysis of OWT Considering the Combined Wind, Wave, and Seismic Loads
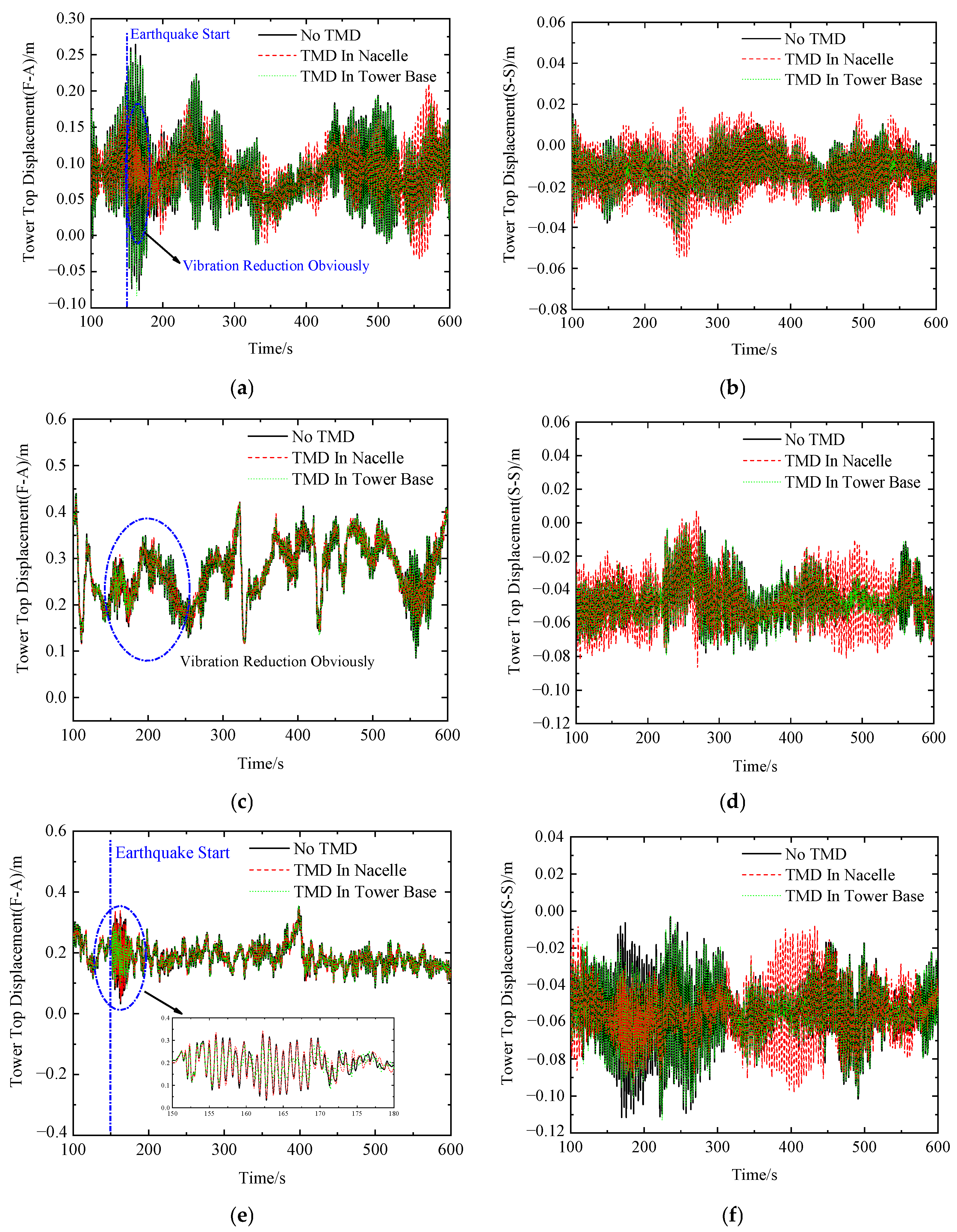
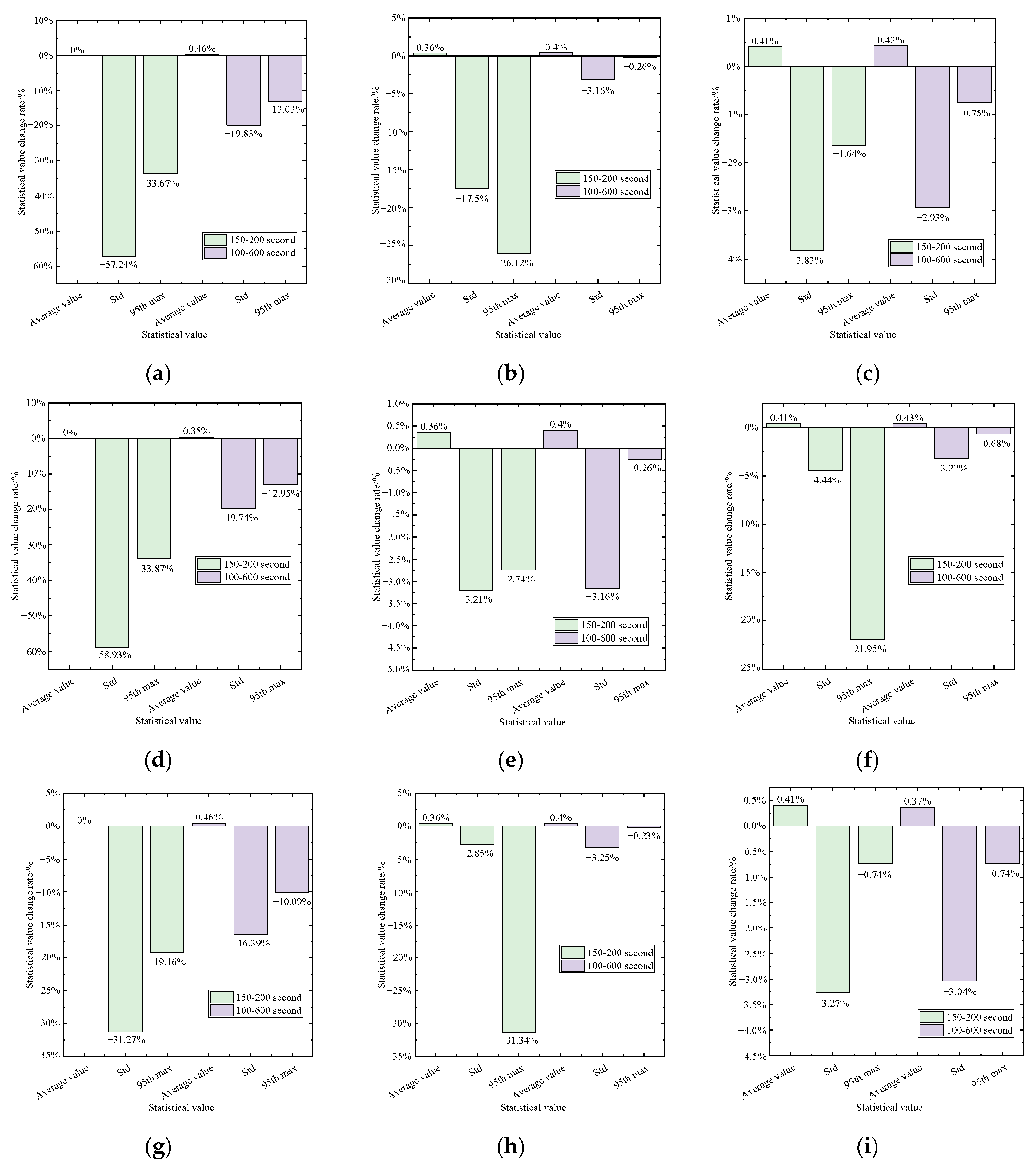
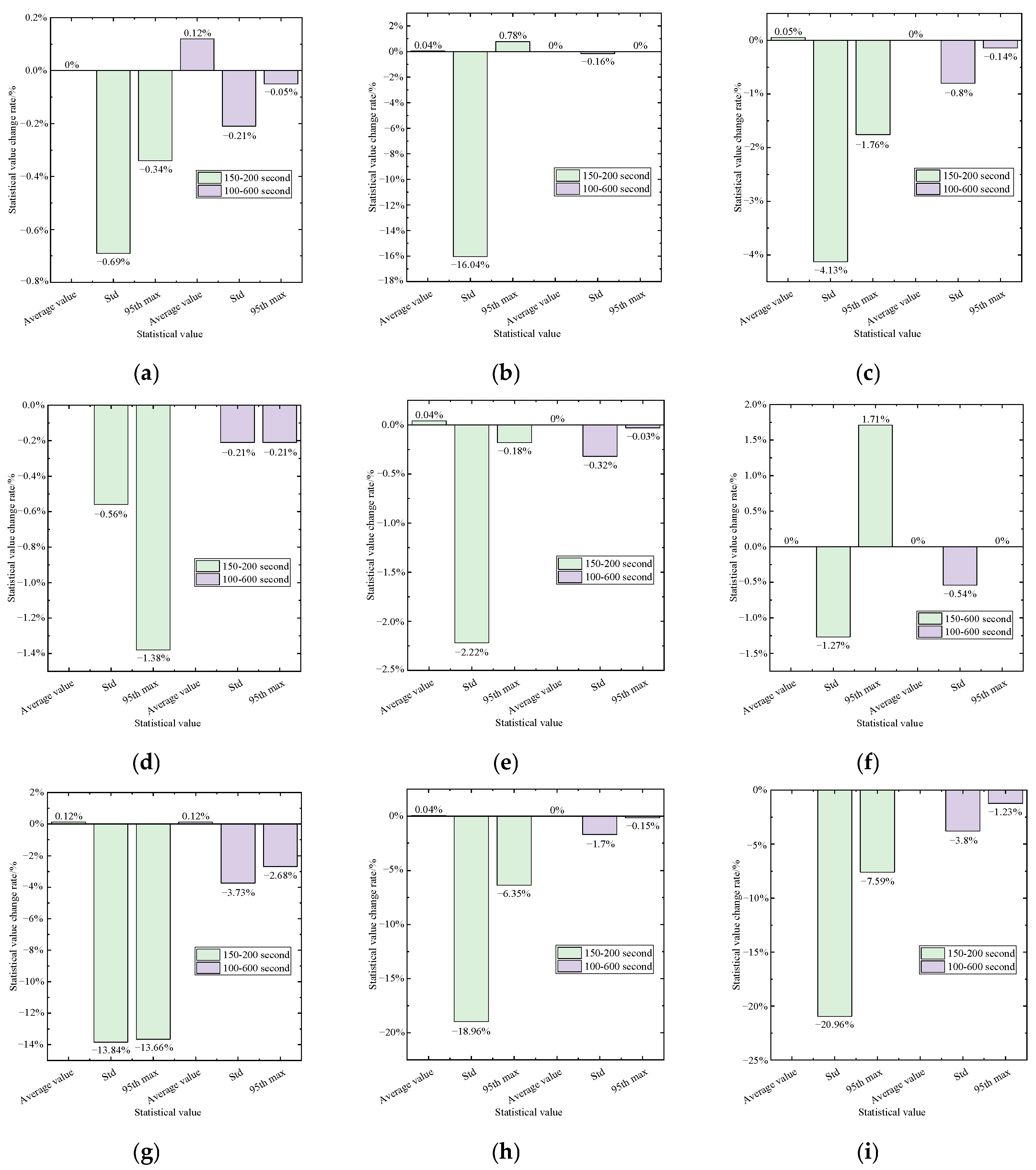
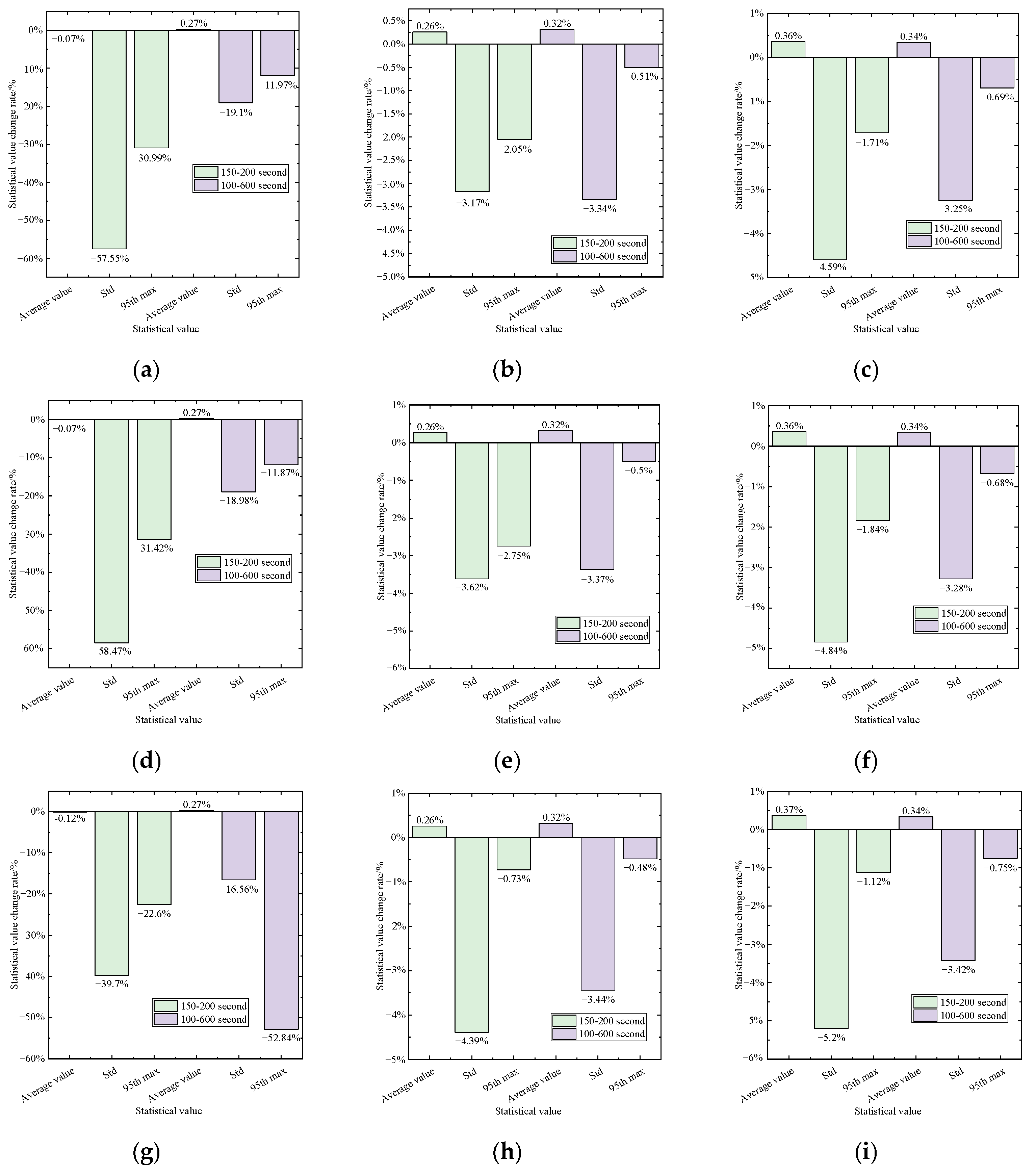
5.1. Tower-Top Displacement
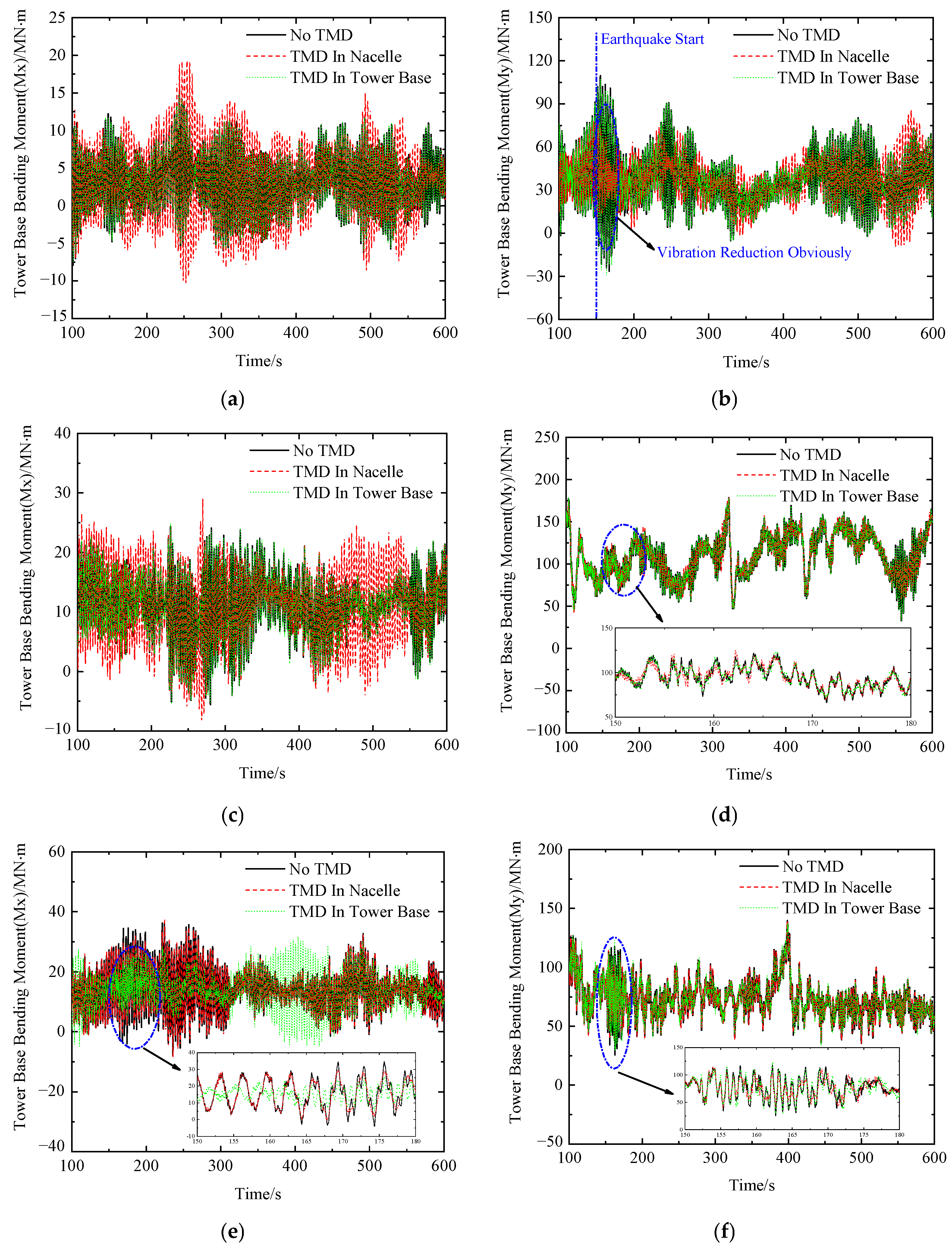
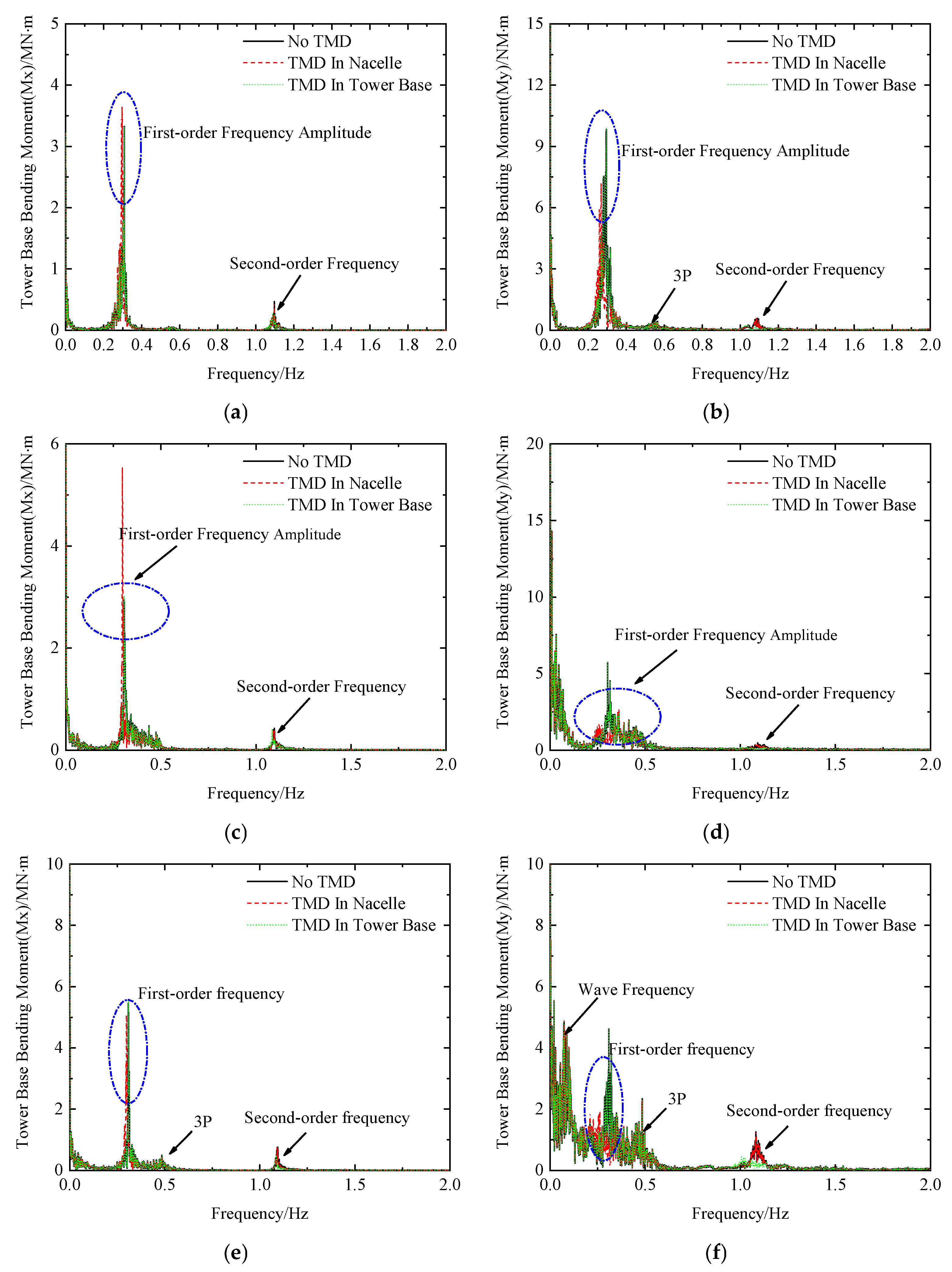
5.2. Tower-Base Bending Moment
6. Conclusions and Future Studies
- (1)
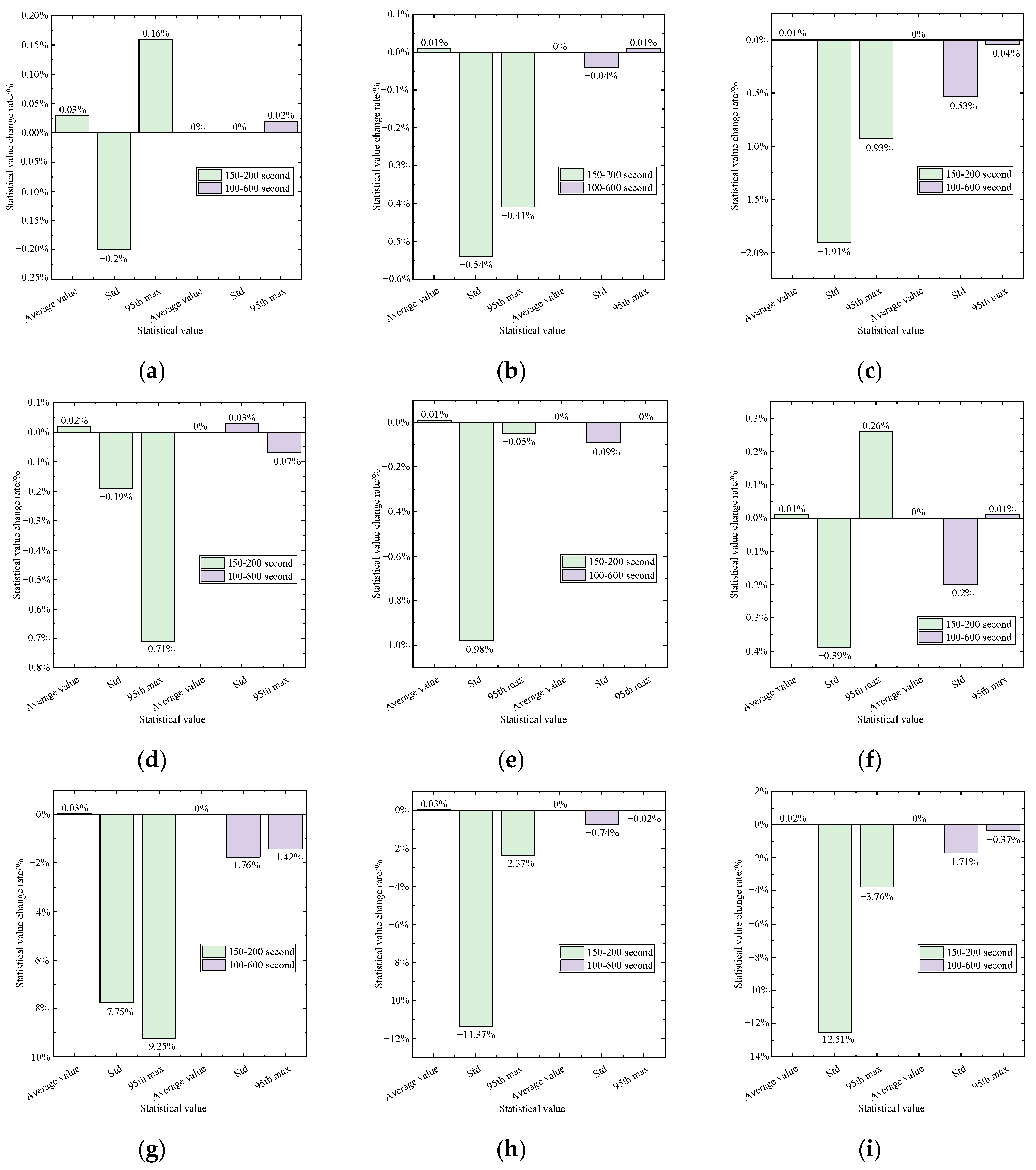
- Under combined wind, wave, and seismic loading, the application of a TMD significantly improves the vibration mitigation performance of the structure. Compared to placing the TMD at the tower base, positioning it within the nacelle yields better damping effectiveness.
- (2)
- Compared to the combined wind and wave loading condition, the TMD demonstrates enhanced vibration mitigation performance under combined wind, wave, and seismic loading. When seismic excitation is applied, significant variations are observed in both tower-top displacement and tower-base bending moment. The presence of the TMD primarily influences the standard deviation and 95th max, with reductions in standard deviation reaching 50% in certain cases, while its effect on the mean value remains minimal, generally below 1%.
- (3)
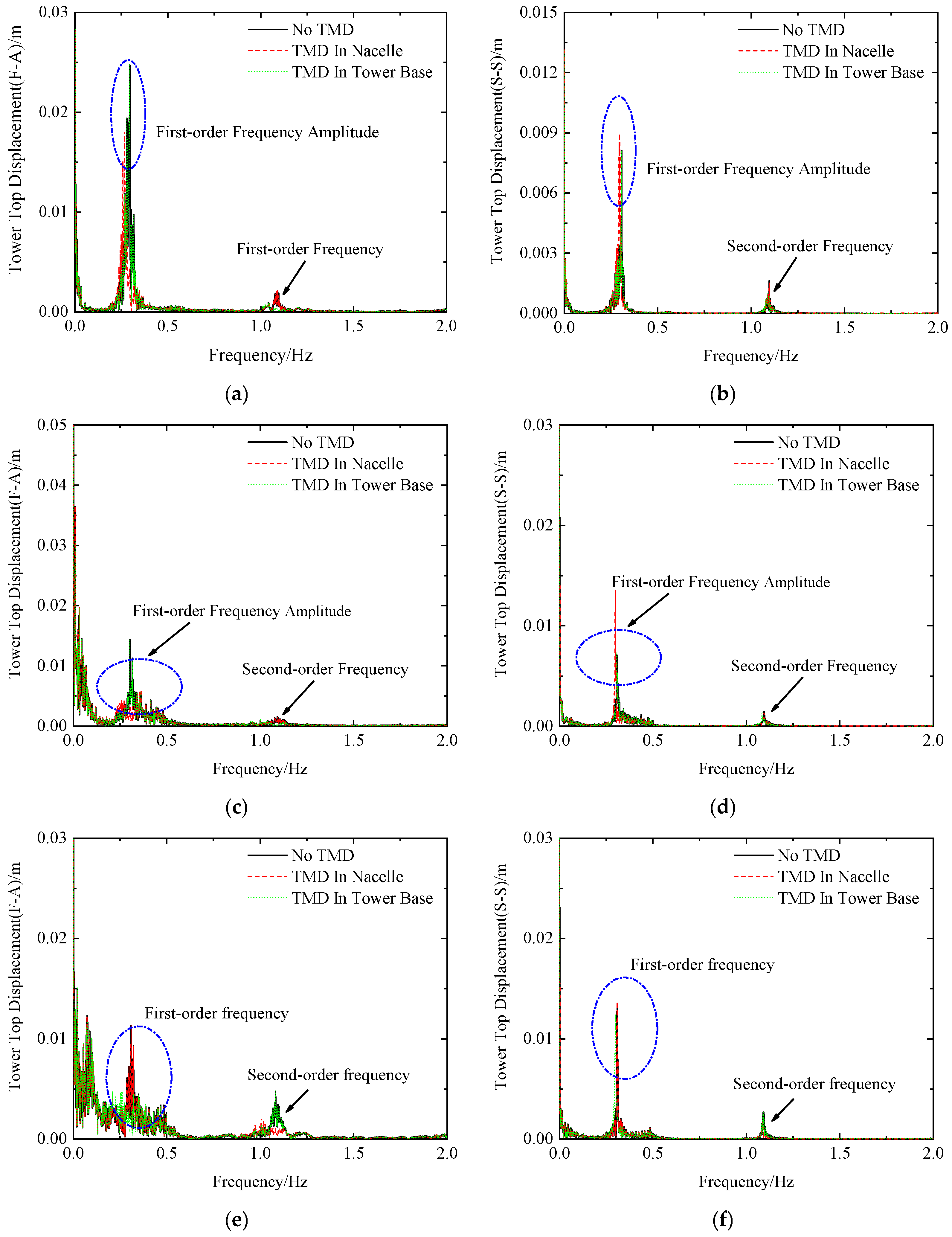
- Based on the frequency-domain analysis, it is observed that when the TMD is installed at the nacelle, it primarily affects the first-order natural frequency of the structure. Specifically, the first-order frequency amplitude in the X-direction is significantly reduced, whereas the corresponding amplitude in the Y-direction increases. In contrast, when the TMD is located at the tower base, its influence is mainly exerted on the second-order frequency. Since the structural response is predominantly governed by the first-order frequency, the impact of base-mounted TMDs on the time-domain response and statistical parameters is generally limited; however, under seismic excitations with broad frequency content and high spectral amplitudes such as the El Centro earthquake, the tower-base TMD demonstrates significant vibration mitigation effects.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bento, N.; Fontes, M. Emergence of floating offshore wind energy: Technology and industry. Renew. Sustain. Energy Rev. 2019, 99, 66–82. [Google Scholar] [CrossRef]
- Global Wind Energy Council. Global Wind Report; Global Wind Energy Council: Brussels, Belgium, 2024. [Google Scholar]
- Wu, X.; Hu, Y.; Li, Y.; Yang, J.; Duan, L.; Wang, T.; Adcock, T.; Jiang, Z.; Gao, Z.; Lin, Z.; et al. Foundations of offshore wind turbines: A review. Renew. Sustain. Energy Rev. 2019, 104, 379–393. [Google Scholar] [CrossRef]
- Jahani, K.; Langlois, R.G.; Afagh, F.F. Structural dynamics of offshore wind turbines: A review. Ocean Eng. 2022, 251, 111136. [Google Scholar] [CrossRef]
- Wang, J.; Golnary, F.; Li, S.; Weerasuriya, A.; Tse, K. A review on power control of wind turbines with the perspective of dynamic load mitigation. Ocean Eng. 2024, 311, 118806. [Google Scholar] [CrossRef]
- Salic, T.; Charpentier, J.; Benbouzid, M.; Boulluec, M. Control strategies for floating offshore wind turbine: Challenges and trends. Electronics 2019, 8, 1185. [Google Scholar] [CrossRef]
- Jonkman, J.; Butterfield, S.; Musial, W.; Scott, G. Definition of a 5-MW Reference Wind Turbine for Offshore System Development; NREL: Golden, CO, USA, 2009. [Google Scholar]
- Girsang, I.P.; Dhupia, J.S.; Muljadi, E.; Singh, M.; Jonkman, J. Modeling and control to mitigate resonant load in variable-speed wind turbine drivetrain. IEEE J. Emerg. Sel. Top. Power Electron. 2013, 1, 277–286. [Google Scholar] [CrossRef]
- Yang, F.; Song, Q.; Wang, L.; Zuo, S.; Li, S. Wind and wave disturbances compensation to floating offshore wind turbine using improved individual pitch control based on fuzzy control strategy. Abstr. Appl. Anal. 2014, 2014, 968384. [Google Scholar] [CrossRef]
- Abbas, N.J.; Zalkind, D.S.; Wright, A. A reference open-source controller for fixed and floating offshore wind turbines. Wind Energy Sci. 2022, 7, 53–73. [Google Scholar] [CrossRef]
- Abbas, N.J.; Jasa, J.; Zalkind, D.S.; Wright, A.; Pao, L. Control co-design of a floating offshore wind turbine. Appl. Energy 2024, 353, 122036. [Google Scholar]
- Kaynia, A.M.; Pedersen, D.; Askheim, H.; Romero-Sánchez, C. Implementation of seismic soil-structure interaction in OpenFAST and application to an offshore wind turbine on jacket structure. Mar. Struct. 2025, 103, 103832. [Google Scholar]
- Meng, F.; Lio, W.; Barlas, T. DTUWEC: An open-source DTU Wind Energy Controller with advanced industrial features. J. Phys. Conf. Ser. 2020, 1618, 022009. [Google Scholar] [CrossRef]
- Mozayan, S.; Saad, M.; Vahedi, H.; Fortin-Blanchette, H.; Soltani, M. Sliding mode control of PMSG wind turbine based on enhanced exponential reaching law. IEEE Trans. Ind. Electron. 2020, 63, 6148–6159. [Google Scholar] [CrossRef]
- Bagherieh, O.; Nagamune, R. Gain-scheduling control of a floating offshore wind turbine above rated wind speed. Control Theory Technol. 2015, 13, 160–172. [Google Scholar] [CrossRef]
- Shah, K.A.; Meng, F.; Li, Y.; Nagamune, R.; Zhou, Y.; Ren, Z.; Jiang, Z. A synthesis of feasible control methods for floating offshore wind turbine system dynamics. Renew. Sustain. Energy Rev. 2021, 151, 111525. [Google Scholar] [CrossRef]
- Civelek, Z.; Lüy, M.; Çam, E.; Barıșçı, N. Control of pitch angle of wind turbine by fuzzy PID controller. Intell. Autom. Soft Comput. 2016, 22, 463–471. [Google Scholar] [CrossRef]
- Wang, L.; Zuo, S.; Song, Y.; Zhou, Z. Variable torque control of offshore wind turbine on spar floating platform using advanced RBF neural network. Abstr. Appl. Anal. 2014, 2014, 903493. [Google Scholar] [CrossRef]
- Sun, Y.; Zhou, Q.; Sun, L.; Sun, L.; Kang, J.; Li, H. CNN–LSTM–AM: A power prediction model for offshore wind turbines. Ocean Eng. 2024, 301, 117598. [Google Scholar] [CrossRef]
- Kang, Y.; Kim, H.; Lee, S. Benefits of individual pitch control on offshore wind turbine submerged in upstream wake. Renew. Energy 2023, 217, 119127. [Google Scholar] [CrossRef]
- Namik, H.; Stol, K. Individual blade pitch control of a spar-buoy floating wind turbine. IEEE Trans. Control Syst. Technol. 2014, 22, 214–223. [Google Scholar] [CrossRef]
- Han, D.; Li, X.; Wang, W.; Su, X. Dynamic modeling and vibration control of barge offshore wind turbine using tuned liquid column damper in floating platform. Ocean Eng. 2023, 276, 114299. [Google Scholar] [CrossRef]
- Kim, H.; Kang, J. Application of semi-active TMD to tilted high-rise building structure subjected to seismic loads. Appl. Sci. 2021, 21, 1671–1679. [Google Scholar] [CrossRef]
- Ramezani, M.; Bathaei, A.; Ghorbani-Tanha, A.K. Application of artificial neural networks in optimal tuning of tuned mass dampers implemented in high-rise buildings subjected to wind load. Earthq. Eng. Eng. Vib. 2018, 17, 903–915. [Google Scholar] [CrossRef]
- Zhu, Z.; Lei, W.; Wang, Q.; Tiwari, N.; Hazra, B. Study on wind-induced vibration control of linked high-rise buildings by using TMDI. J. Wind Eng. Ind. Aerodyn. 2020, 205, 104306. [Google Scholar] [CrossRef]
- Lackner, M.A.; Rotea, M.A. Structural control of floating wind turbines. Mechatronics 2011, 21, 704–719. [Google Scholar] [CrossRef]
- Yan, S.; Wang, Y.; Wei, F.P.; Zhang, Z. Wind and wave-induced vibration reduction control for floating offshore wind turbine using delayed signals. J. Mar. Sci. Eng. 2024, 12, 1113. [Google Scholar] [CrossRef]
- Luo, Y.; Qian, F.; Su, H.; Wang, X.; Chen, A.; Zuo, L. Rigid-flexible coupling multi-body dynamics modeling of a semi-submersible floating offshore wind turbine. Ocean Eng. 2023, 281, 114648. [Google Scholar] [CrossRef]
- Li, T.; Liu, Z.; Liu, S.; Fan, Y.; Yang, Q.; Xiao, H. Numerical study on passive structural control of semi-submersible floating wind turbine considering non-collinear wind and waves. Ocean Eng. 2022, 266, 112745. [Google Scholar] [CrossRef]
- Stewart, G.M.; Lackner, M.A. The impact of passive tuned mass dampers and wind–wave misalignment on offshore wind turbine loads. Eng. Struct. 2014, 73, 54–61. [Google Scholar] [CrossRef]
- Zhang, J.W.; Liang, X.; Wang, L.Z.; Wang, B.X.; Wang, L.L. The influence of tuned mass dampers on vibration control of monopile offshore wind turbines under wind-wave loadings. Ocean Eng. 2023, 278, 114394. [Google Scholar] [CrossRef]
- Hua, Y.; Wang, J.; Chen, M.; Li, Z.; Sun, Y. Load mitigation for a barge-type floating offshore wind turbine via inerter-based passive structural control. Eng. Struct. 2018, 177, 198–209. [Google Scholar] [CrossRef]
- Zhang, T.; Wang, W.; Li, X.; Wang, B. Vibration mitigation in offshore wind turbine under combined wind-wave-earthquake loads using the tuned mass damper inerter. Renew. Energy 2023, 216, 119050. [Google Scholar] [CrossRef]
- Sun, C.; Jahangiri, V. Bi-directional vibration control of offshore wind turbines using a 3D pendulum tuned mass damper. Mech. Syst. Signal Process. 2018, 105, 338–360. [Google Scholar] [CrossRef]
- Jahangiri, V.; Sun, C. A novel three-dimensional nonlinear tuned mass damper and its application in floating offshore wind turbines. Ocean Eng. 2022, 250, 110703. [Google Scholar] [CrossRef]
- Luo, Y.; Sun, H.; Hall, L.; Lambert, D.; Okuda, R.; Wang, W.; Fang, B.; Zuo, L. Vibration control for a semi-submersible floating offshore wind turbine with optimal ultra-low frequency electromagnetic tuned inerter-mass dampers. Structures 2024, 63, 106296. [Google Scholar] [CrossRef]
- Jonkman, J.M. Dynamics Coupled Model with Coupled Spring Boundary and Loads Analysis of an Offshore Floating Wind Turbine; NREL: Golden, CO, USA, 2007. [Google Scholar]
- Morison, J.R.; Johnson, J.W.; Schaaf, S.A. The force exerted by surface waves on piles. J. Petrol. Technol. 1950, 2, 149–154. [Google Scholar] [CrossRef]
- Cava, W.L.; Lackner, M.A. Theory Manual for the Tuned Mass Damper Module in FAST v8; NREL: Golden, CO, USA, 2015. [Google Scholar]
- Karaboga, D.; Basturk, B. A powerful and efficient algorithm for numerical function optimization: Artificial bee colony (ABC) algorithm. J. Glob. Optim. 2007, 39, 459–471. [Google Scholar] [CrossRef]
- Karaboga, D.; Basturk, B. On the performance of artificial bee colony (ABC) algorithm. Appl. Soft Comput. 2008, 8, 687–696. [Google Scholar] [CrossRef]
- Akay, B.; Karaboga, D. A modified artificial bee colony algorithm for real-parameter optimization. Inf. Sci. 2012, 192, 120–142. [Google Scholar] [CrossRef]
- Thakur, S.; Abhinav, K.A.; Saha, N. Stochastic response reduction on offshore wind turbines due to flaps including soil effects. Soil Dyn. Earthq. Eng. 2018, 114, 174–185. [Google Scholar] [CrossRef]
- Jonkman, B.; Kilcher, L. TurbSim User’s Guide (Draft Version); NREL: Golden, CO, USA, 2012. [Google Scholar]
- Jonkman, J.; Robertson, A.; Hayman, G. HydroDyn User’s Guide and Theory Manual; NREL: Golden, CO, USA, 2013. [Google Scholar]
- McNamara, D.; Pandit, A.; Malekjafarian, A. Optimized design of multiple tuned mass dampers for vibration control of offshore wind turbines. Ocean Eng. 2024, 305, 117912. [Google Scholar] [CrossRef]
- Xie, S.; Jin, X.; He, J.; Gao, J.; Zhang, C.; Yan, Y. Applying multiple tuned mass dampers to control structural loads of bottom-fixed offshore wind turbines with inclusion of soil-structure interaction. Ocean Eng. 2020, 205, 107289. [Google Scholar] [CrossRef]
- Liu, Y.; Li, X.; Shi, W.; Wang, W.; Jiang, Z. Vibration control of a monopile offshore wind turbines under recorded seismic waves. Renew. Energy 2024, 226, 120455. [Google Scholar] [CrossRef]
- Wang, W.; Li, X.; Zhao, H.; Wang, B.; Li, Y. Vibration control of a pentapod offshore wind turbine under combined seismic wind and wave loads using multiple tuned mass damper. Appl. Ocean Res. 2020, 103, 102254. [Google Scholar] [CrossRef]


| Parameter | Value |
|---|---|
| Rated power | 10 MW |
| Rotor configuration and orientation | 3 blades, upwind |
| Control strategy | Variable speed, variable pitch |
| Mass of single blade, hub, nacelle | 41,732, 105,520, 446,036 kg |
| Rated thrust | 1500 kN |
| Rotor diameter, hub diameter | 178.3, 5.6 m |
| Hub height | 119 m |
| Cut-in, rated, cut-out wind speeds | 4.0, 11.4, 25.0 m/s |
| Cut-in, rated rotor speeds | 6.0, 9.6 rpm |
| Load Case No. | Wind-Wave Direction | Wind Speed (m/s) | Wave Height (m) | Peak Period (s) | Seismic Wave | Operational Condition | TMD Location |
|---|---|---|---|---|---|---|---|
| DLC1 | Aligned at 0° | 6.0 | 0.45 | 6.00 | Humbolt Bay | Operation | nacelle/tower base |
| DLC2 | 11.4 | 2.00 | 8.50 | nacelle/tower base | |||
| DLC3 | 16.0 | 3.75 | 12.50 | nacelle/tower base | |||
| DLC4 | 6.0 | 0.45 | 6.00 | Borrego | nacelle/tower base | ||
| DLC5 | 11.4 | 2.00 | 8.50 | nacelle/tower base | |||
| DLC6 | 16.0 | 3.75 | 12.50 | nacelle/tower base | |||
| DLC7 | 6.0 | 0.45 | 6.00 | El Centro | nacelle/tower base | ||
| DLC8 | 11.4 | 2.00 | 8.50 | nacelle/tower base | |||
| DLC9 | 16.0 | 3.75 | 12.50 | nacelle/tower base |
| Modal | ANSYS (Hz) | FAST (Hz) | Relative Error (%) |
|---|---|---|---|
| First in F-A | 0.290 | 0.298 | 2.68% |
| First in S-S | 0.290 | 0.298 | 2.68% |
| Second in F-A | 1.05 | 1.08 | 2.78% |
| Second in S-S | 1.05 | 1.08 | 2.78% |
| Load Case No. | TMD Location | Mean | Std. | 95%th Max | Mean | Std. | 95%th Max |
|---|---|---|---|---|---|---|---|
| 150–200 s | 100–600 s | ||||||
| DLC1 | No TMD | 0.0850 | 0.0725 | 0.2346 | 0.0865 | 0.0469 | 0.1903 |
| Nacelle | 0.0850 | 0.0310 | 0.1556 | 0.0869 | 0.0376 | 0.1655 | |
| Tower base | 0.0850 | 0.0720 | 0.2338 | 0.0866 | 0.0468 | 0.1902 | |
| DLC2 | No TMD | 0.2515 | 0.0480 | 0.3323 | 0.2743 | 0.0632 | 0.3885 |
| Nacelle | 0.2524 | 0.0396 | 0.2455 | 0.2754 | 0.0612 | 0.3875 | |
| Tower base | 0.2516 | 0.0403 | 0.3349 | 0.2743 | 0.0631 | 0.3885 | |
| DLC3 | No TMD | 0.1964 | 0.0339 | 0.2620 | 0.1868 | 0.0375 | 0.2790 |
| Nacelle | 0.1972 | 0.0326 | 0.2577 | 0.1876 | 0.0364 | 0.2769 | |
| Tower base | 0.1965 | 0.0325 | 0.2574 | 0.1868 | 0.0372 | 0.2786 | |
| DLC4 | No TMD | 0.0850 | 0.0711 | 0.2318 | 0.0866 | 0.0466 | 0.1900 |
| Nacelle | 0.0850 | 0.0292 | 0.1533 | 0.0869 | 0.0374 | 0.1654 | |
| Tower base | 0.0850 | 0.0707 | 0.2286 | 0.0866 | 0.0465 | 0.1896 | |
| DLC5 | No TMD | 0.2515 | 0.0405 | 0.3356 | 0.2743 | 0.0632 | 0.3886 |
| Nacelle | 0.2524 | 0.0392 | 0.3264 | 0.2754 | 0.0612 | 0.3876 | |
| Tower base | 0.2516 | 0.0396 | 0.3350 | 0.2743 | 0.0630 | 0.3885 | |
| DLC6 | No TMD | 0.1965 | 0.0315 | 0.2515 | 0.1868 | 0.0373 | 0.2784 |
| Nacelle | 0.1973 | 0.0301 | 0.1963 | 0.1876 | 0.0361 | 0.2765 | |
| Tower base | 0.1965 | 0.0311 | 0.2558 | 0.1868 | 0.0371 | 0.2784 | |
| DLC7 | No TMD | 0.0850 | 0.0809 | 0.2797 | 0.0865 | 0.0482 | 0.1942 |
| Nacelle | 0.0850 | 0.0556 | 0.2261 | 0.0869 | 0.0403 | 0.1746 | |
| Tower base | 0.0851 | 0.0697 | 0.2415 | 0.0866 | 0.0464 | 0.1890 | |
| DLC8 | No TMD | 0.2514 | 0.0596 | 0.3638 | 0.2743 | 0.0647 | 0.3891 |
| Nacelle | 0.2523 | 0.0579 | 0.2498 | 0.2754 | 0.0626 | 0.3882 | |
| Tower base | 0.2515 | 0.0483 | 0.3407 | 0.2743 | 0.0636 | 0.3885 | |
| DLC9 | No TMD | 0.1964 | 0.0520 | 0.2991 | 0.1868 | 0.0395 | 0.2840 |
| Nacelle | 0.1972 | 0.0503 | 0.2969 | 0.1875 | 0.0383 | 0.2819 | |
| Tower base | 0.1964 | 0.0411 | 0.2764 | 0.1868 | 0.0380 | 0.2805 | |
| Load Case No. | TMD Location | Mean | Std. | 95%th Max | Mean | Std. | 95%th Max |
|---|---|---|---|---|---|---|---|
| 150–200 s | 100–600 s | ||||||
| DLC1 | No TMD | 37.4145 | 28.4283 | 95.7504 | 37.0894 | 18.4138 | 78.2758 |
| Nacelle | 37.3874 | 12.0692 | 66.0747 | 37.1883 | 14.8976 | 68.9055 | |
| Tower base | 37.4272 | 28.3716 | 95.9072 | 37.0902 | 18.4145 | 78.2899 | |
| DLC2 | No TMD | 101.6430 | 15.8349 | 135.2358 | 110.2957 | 25.2618 | 156.2874 |
| Nacelle | 101.9068 | 15.3333 | 132.4681 | 110.6470 | 24.4185 | 155.4948 | |
| Tower base | 101.6570 | 15.7495 | 134.6816 | 110.2945 | 25.2522 | 156.2965 | |
| DLC3 | No TMD | 75.2627 | 13.1137 | 100.7264 | 73.6194 | 14.9428 | 111.7320 |
| Nacelle | 75.5349 | 12.5113 | 99.0051 | 73.8730 | 14.4567 | 110.9582 | |
| Tower base | 75.2738 | 12.8634 | 99.7868 | 73.6188 | 14.8638 | 111.6897 | |
| DLC4 | No TMD | 37.4184 | 27.9799 | 94.8522 | 37.0904 | 18.3298 | 78.1225 |
| Nacelle | 37.3916 | 11.6188 | 65.0457 | 37.1894 | 14.8512 | 68.8532 | |
| Tower base | 37.4258 | 27.9256 | 94.1754 | 37.0898 | 18.3348 | 78.0695 | |
| DLC5 | No TMD | 101.6446 | 15.7249 | 135.0917 | 110.2950 | 25.2603 | 156.2891 |
| Nacelle | 101.9119 | 15.1552 | 131.3715 | 110.6467 | 24.4084 | 155.5014 | |
| Tower base | 101.6576 | 15.5704 | 135.0228 | 110.2954 | 25.2375 | 156.2844 | |
| DLC6 | No TMD | 75.2702 | 12.6169 | 98.9661 | 73.6195 | 14.8996 | 111.6597 |
| Nacelle | 75.5443 | 12.0065 | 97.1414 | 73.8732 | 14.4114 | 110.9057 | |
| Tower base | 75.2798 | 12.5678 | 99.2185 | 73.6189 | 14.8697 | 111.6763 | |
| DLC7 | No TMD | 37.4298 | 28.9081 | 104.3831 | 37.0897 | 18.4802 | 78.2265 |
| Nacelle | 37.3851 | 17.4318 | 80.7891 | 37.1880 | 15.4191 | 36.8900 | |
| Tower base | 37.4410 | 26.6670 | 94.7320 | 37.0904 | 18.1548 | 77.1172 | |
| DLC8 | No TMD | 101.6117 | 20.3121 | 138.5718 | 110.2916 | 25.5905 | 156.3217 |
| Nacelle | 101.8791 | 19.4210 | 137.5667 | 110.6440 | 24.7104 | 155.5664 | |
| Tower base | 101.6426 | 18.0034 | 135.2906 | 110.2931 | 25.3999 | 156.2861 | |
| DLC9 | No TMD | 75.2479 | 17.4619 | 108.5187 | 73.6175 | 15.3834 | 112.3833 |
| Nacelle | 75.5248 | 16.5537 | 107.2995 | 73.8712 | 14.8566 | 111.5355 | |
| Tower base | 75.2616 | 15.2771 | 104.4341 | 73.6179 | 15.1204 | 111.9657 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, Z.; Xiong, T.; Gao, X.; Tian, D.; Liu, C.; Song, Y.; Wang, W.; Lu, D. Study on the Structural Vibration Control of a 10 MW Offshore Wind Turbine with a Jacket Foundation Under Combined Wind, Wave, and Seismic Loads. J. Mar. Sci. Eng. 2025, 13, 2112. https://doi.org/10.3390/jmse13112112
Hu Z, Xiong T, Gao X, Tian D, Liu C, Song Y, Wang W, Lu D. Study on the Structural Vibration Control of a 10 MW Offshore Wind Turbine with a Jacket Foundation Under Combined Wind, Wave, and Seismic Loads. Journal of Marine Science and Engineering. 2025; 13(11):2112. https://doi.org/10.3390/jmse13112112
Chicago/Turabian StyleHu, Zhongbo, Tao Xiong, Xiang Gao, Deshuai Tian, Changbo Liu, Yuguo Song, Wenhua Wang, and Dongzhe Lu. 2025. "Study on the Structural Vibration Control of a 10 MW Offshore Wind Turbine with a Jacket Foundation Under Combined Wind, Wave, and Seismic Loads" Journal of Marine Science and Engineering 13, no. 11: 2112. https://doi.org/10.3390/jmse13112112
APA StyleHu, Z., Xiong, T., Gao, X., Tian, D., Liu, C., Song, Y., Wang, W., & Lu, D. (2025). Study on the Structural Vibration Control of a 10 MW Offshore Wind Turbine with a Jacket Foundation Under Combined Wind, Wave, and Seismic Loads. Journal of Marine Science and Engineering, 13(11), 2112. https://doi.org/10.3390/jmse13112112






