Optimizing Informer with Whale Optimization Algorithm for Enhanced Ship Trajectory Prediction
Abstract
1. Introduction
2. Methodology
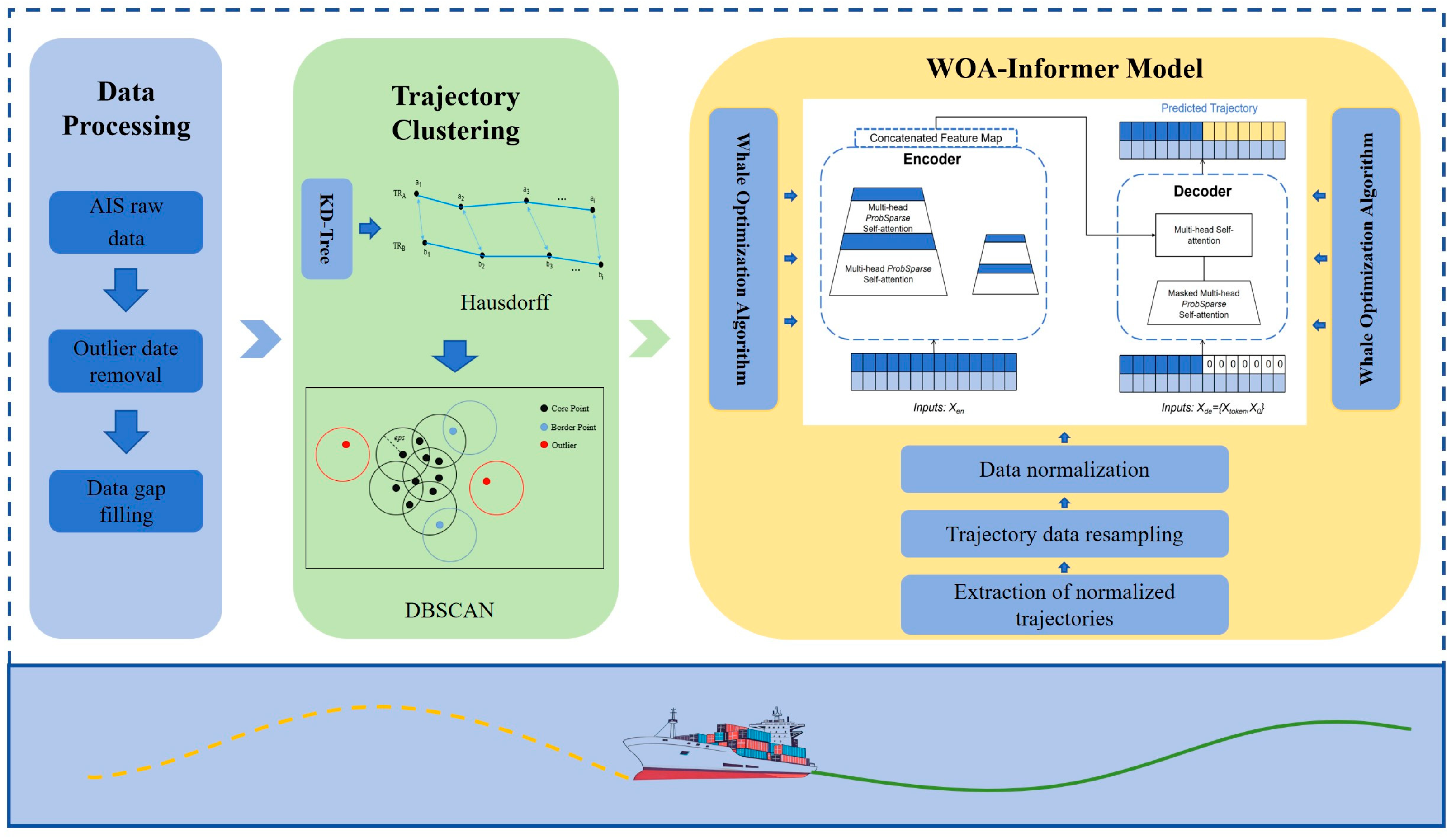
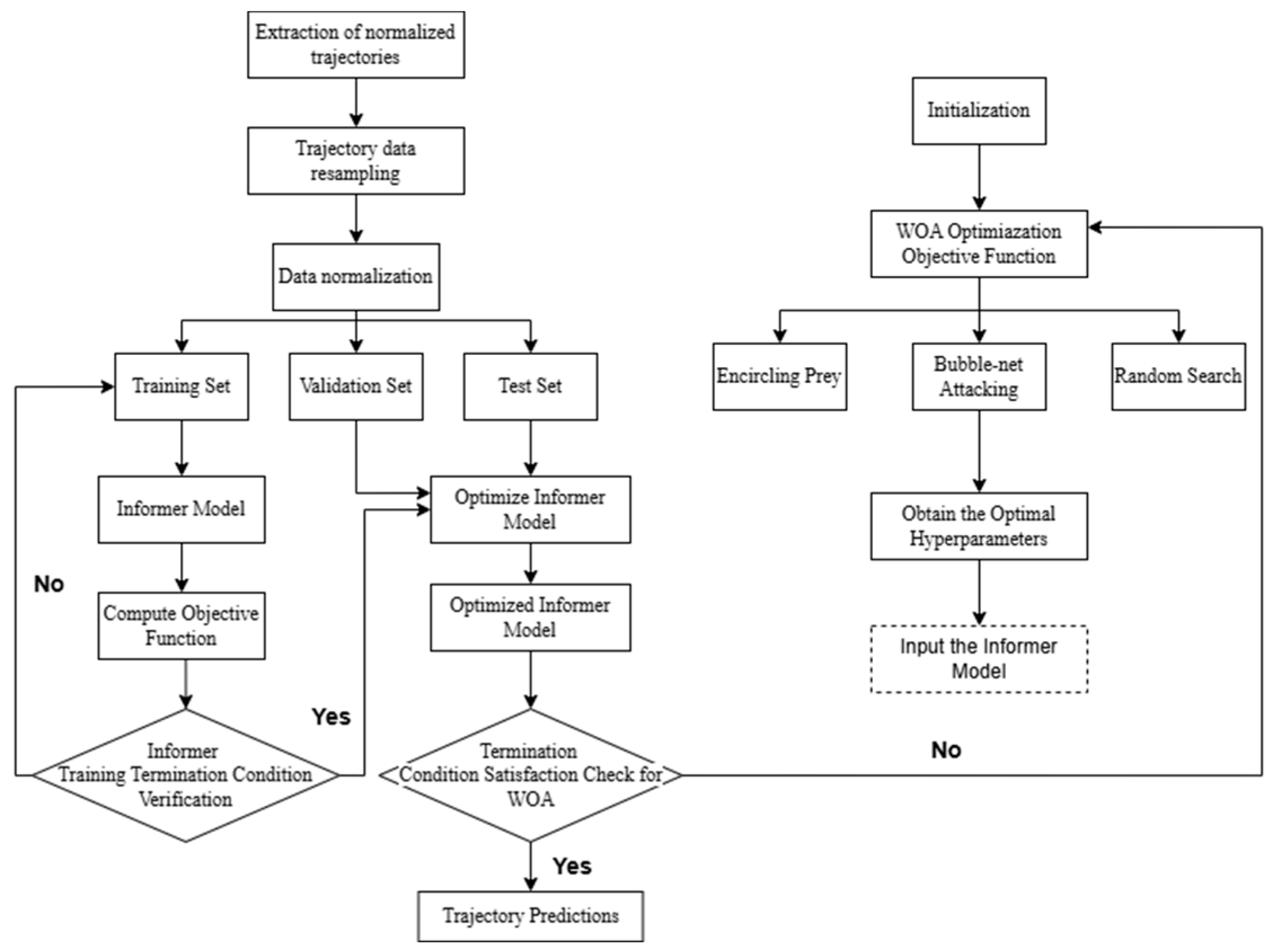
2.1. Overall Framework
| Algorithm 1. WOA-Informer Optimization Loop |
| Input: AIS trajectory data D |
| Output: Optimized Informer model |
| 1: Normalize and split D into Train, Val, and Test sets |
| 2: Initialize WOA population {P_i}, i = 1…N |
| 3: for each iteration t = 1…T do |
| 4: for each P_i do |
| 5: Train Informer with P_i; evaluate fitness E_i on Val set |
| 6: end for |
| 7: Update whales via encircling, bubble-net, and random search |
| 8: if termination condition met then break |
| 9: end for |
| 10: Train Informer with best P_best on Train + Val sets |
| 11: Test optimized model and output trajectory predictions |
2.2. AIS Data Preprocessing
- (1)
- Outlier date removal: Three primary types of outliers are addressed: incorrect values, duplicates, and drift values. Incorrect values correspond to parameters such as longitude, latitude, speed, and course that fall outside plausible ranges (e.g., longitude beyond [−180°, +180°] or latitude beyond [−90°, +90°]). Duplicates are identical AIS records appearing in consecutive time periods. Drift values denote sudden, large deviations occurring over short durations within otherwise continuous trajectories, contradicting typical ship motion patterns. Such outliers adversely affect subsequent analysis and must therefore be removed.
- (2)
- Trajectory pruning via thresholds: Empirical observations indicate that trajectory segments with an insufficient number of AIS points lack the requisite information to characterize ship navigation patterns adequately, thereby impairing subsequent analysis. Consequently, segments containing fewer than 200 points are discarded.
- (3)
- Missing data imputation: Signal interruptions in AISs can result in missing data over certain time intervals. Common imputation techniques include mean interpolation, Lagrange interpolation, and spline interpolation. Among these, cubic spline interpolation offers high precision and has been extensively validated for AIS data imputation [39]. This study therefore employs cubic spline interpolation for missing data reconstruction. The cubic spline interpolation formula is given by Equation (1), where denotes the spline function, denotes the node, and , , , denote the 4n unknown coefficients.
2.3. Trajectory Clustering
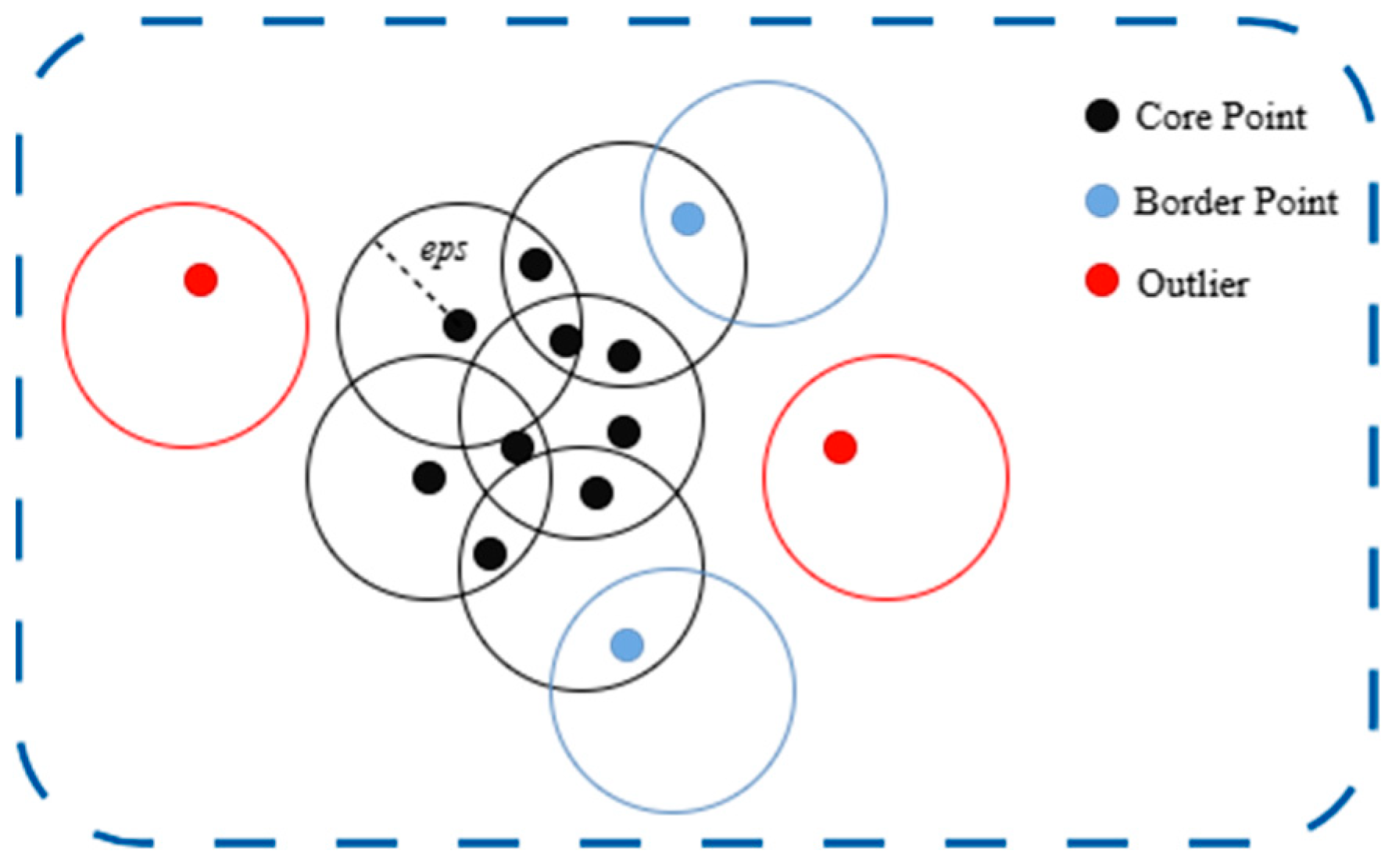
2.3.1. Density-Based Spatial Clustering of Applications with Noise Algorithm
- (1)
- Core point: A point is classified as a core point if it has at least points within its ε-neighborhood.
- (2)
- Border point: A point that has fewer than points within its -neighborhood, but is reachable from some core point, is classified as a border point.
- (3)
- Outlier: Any point that is neither a core point nor a border point is considered noise.
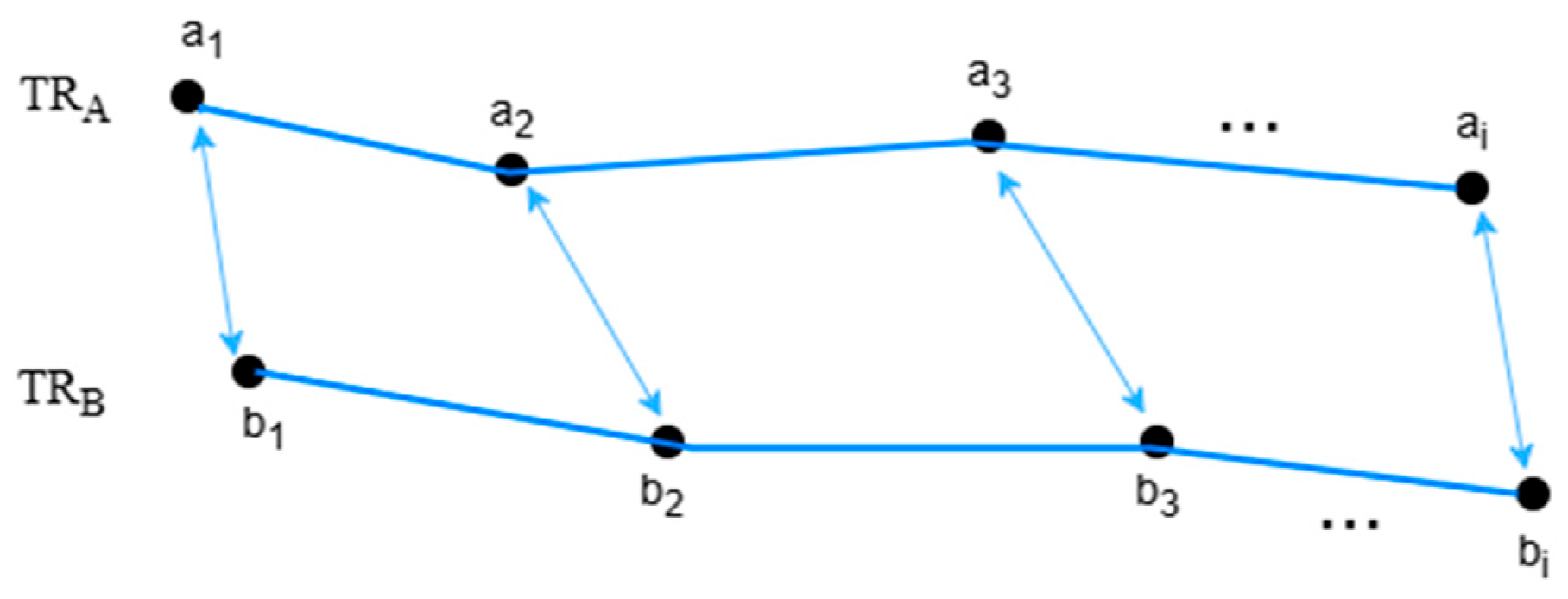
2.3.2. Hausdorff Distance
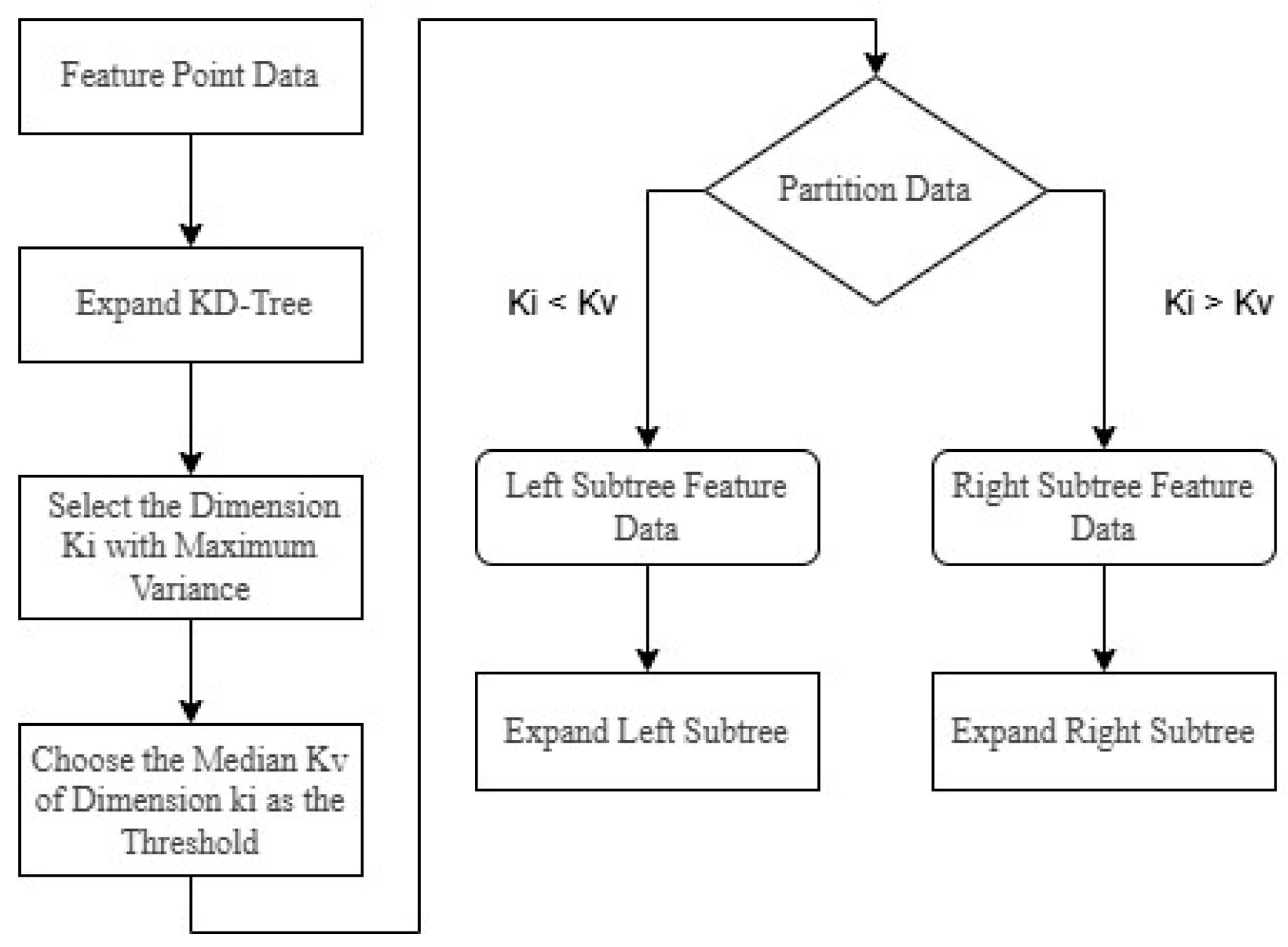
2.3.3. KD-Tree Algorithm
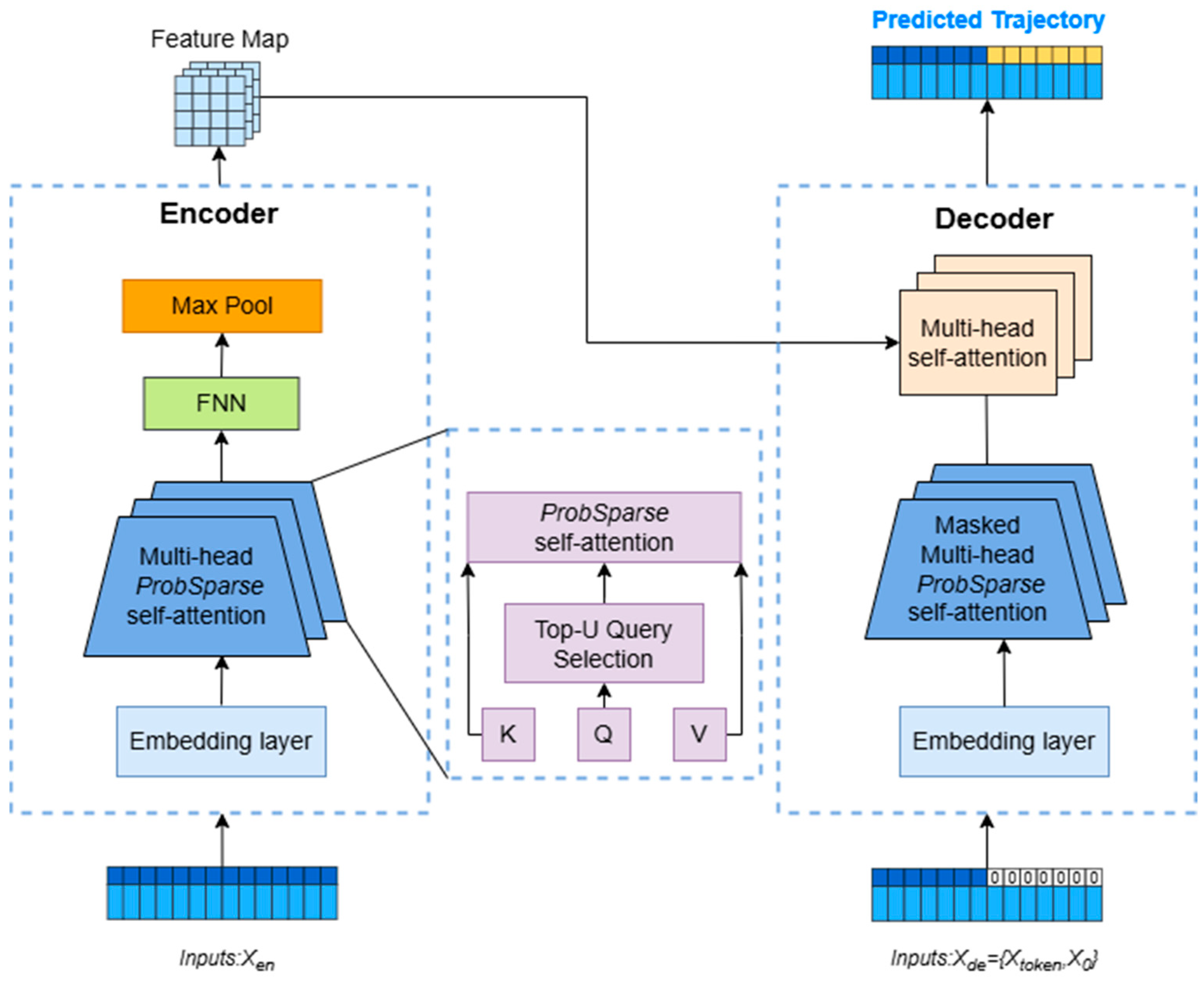
2.4. Informer Model
- (1)
- ProbSparse self-attention: This mechanism significantly reduces the time complexity of standard self-attention by sparsifying the attention matrix.
- (2)
- Self-attention distilling: This technique reduces layer dimensionality and parameter count while emphasizing salient features, improving efficiency in long-sequence processing.
- (3)
- Generative decoder: Unlike traditional step-by-step decoders, this variant generates the entire output sequence in a single forward pass, reducing error accumulation and improving efficiency.
2.4.1. Embedding Layer
2.4.2. Encoder
- (1)
- ProbSparse Attention Mechanism
- (2)
- Self-Attention Distilling
2.4.3. Decoder
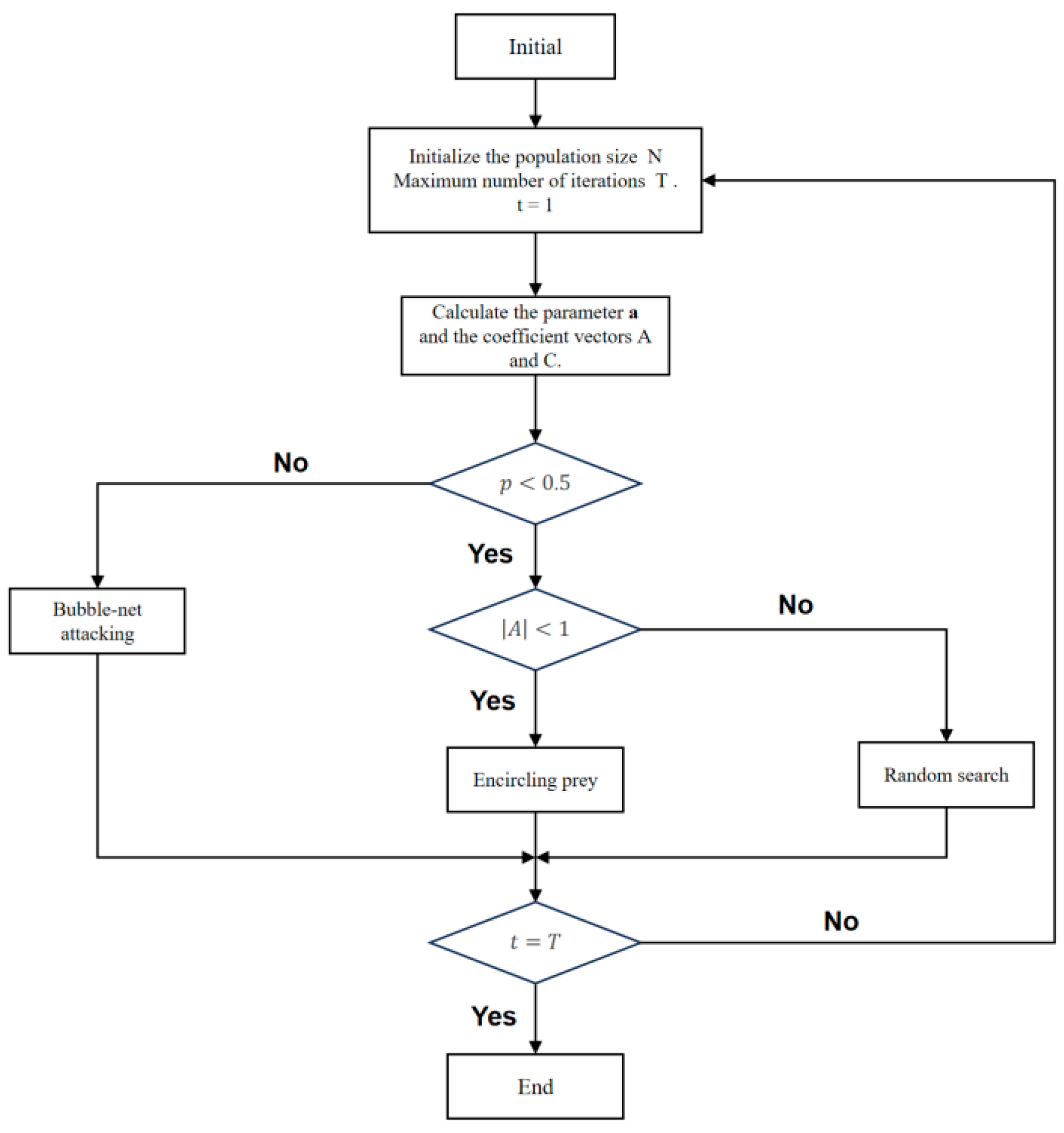
2.5. Whale Optimization Algorithm
- (1)
- Encircling prey phase: In nature, humpback whales can locate prey and encircle it. In optimization problems, where the global optimum is unknown a priori, the algorithm treats the current best solution as the target prey’s estimated position. Once this reference is established, other search agents update their positions toward it, modeled bywhere denotes the position of the best solution found at iteration , and are the current and next positions of a search agent, represents the enclosure distance, and and are coefficient vectors calculated as follows:where and are uniformly distributed random numbers in the range [0, 1], whose primary role is to introduce necessary stochasticity into the search process, aiding the population in escaping local optima and facilitating global exploration. And is a control parameter that decreases linearly from 2 to 0 over the course of the total iterations .
- (2)
- Bubble-net attacking phase: This phase models the spiral attacking maneuver of humpback whales by establishing a spiral update equation between the whale and the prey, formulated mathematically as:where represents the distance between the i-th whale individual and the optimal individual, is a constant parameter used to control the shape of the spiral, and is a random number between [0, 1].In addition, to simultaneously simulate the contraction encirclement mechanism and spiral update mechanism of whales, it is generally assumed that the two mechanisms have equal execution probabilities, whose mathematical expression is as follows:
- (3)
- Random search phase: To prevent the population from converging prematurely on local optima, the algorithm incorporates a random search strategy that enhances its exploration capabilities. This phase is mathematically represented as follows:where denotes the position vector of a randomly selected whale from the current population. It is important to note that the mathematical formulations for both the encircling prey and random search phases are similar. The choice between these two behaviors is contingent upon the value of the coefficient . Specifically, the encircling prey behavior is executed when , whereas the search for prey is triggered when .
3. Experimental Results and Analysis
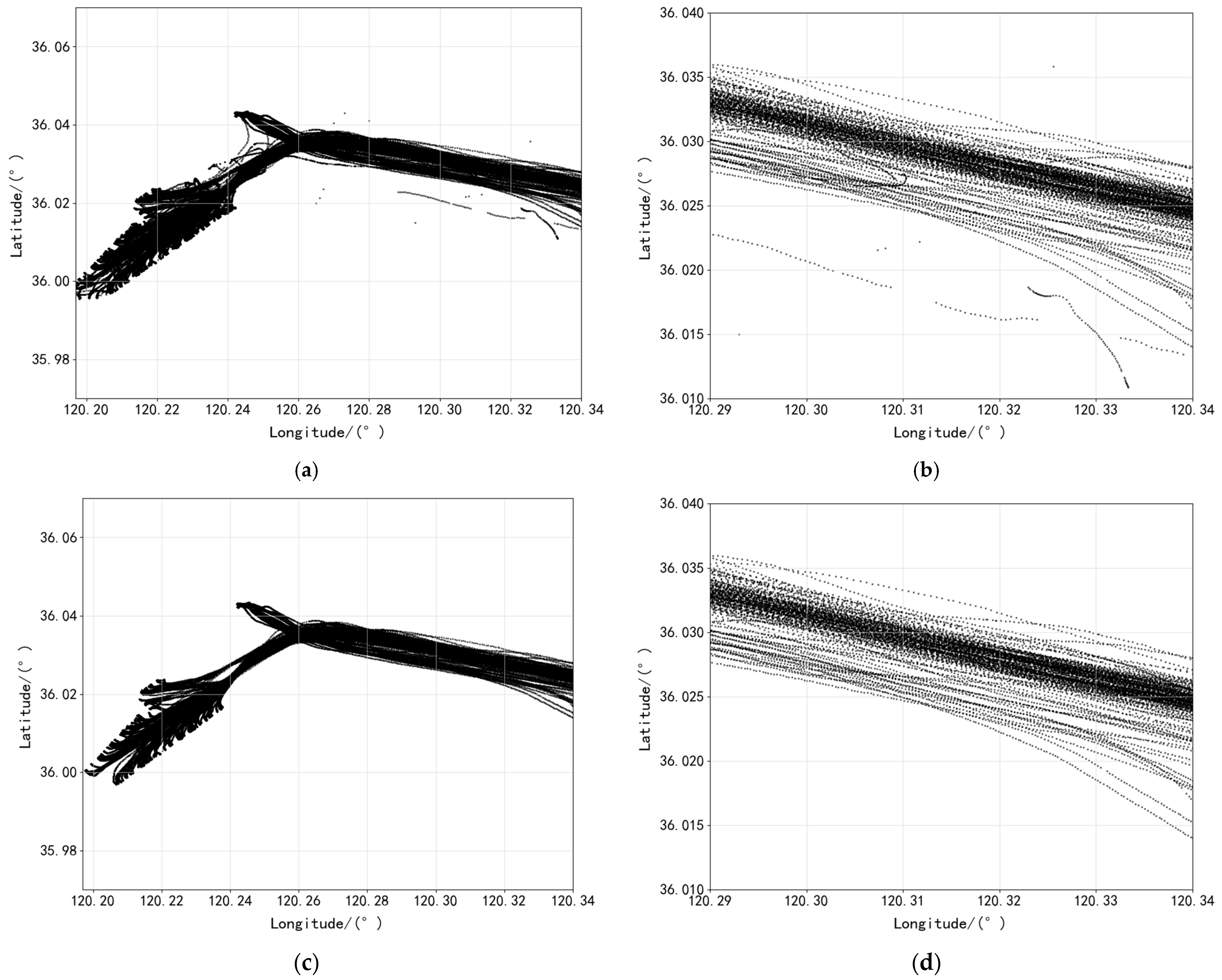
3.1. Data Preprocessing Analysis
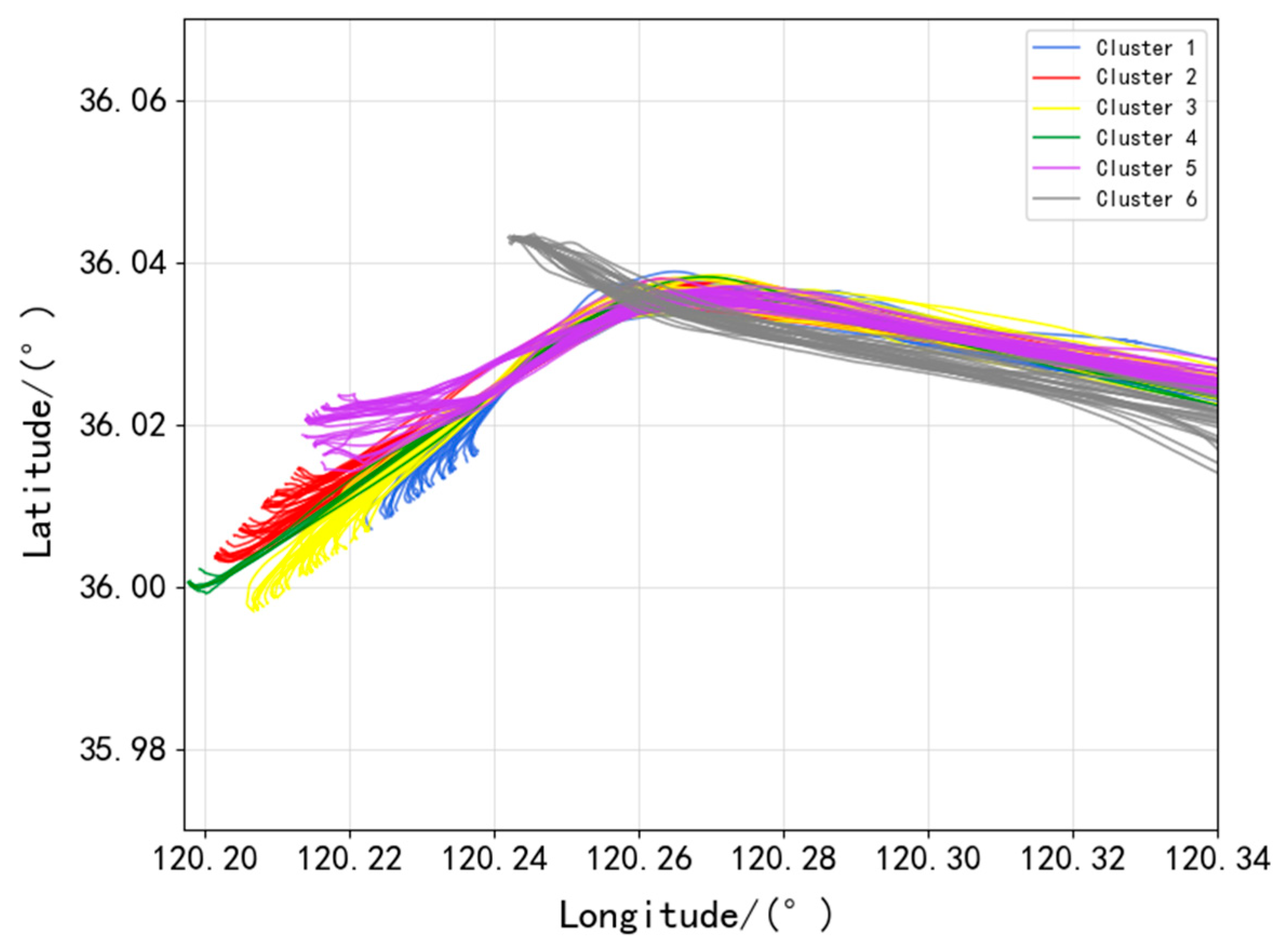
3.2. Trajectory Clustering Analysis
3.3. Prediction Result Analysis of WOA-Informer Model
3.3.1. Sample Dataset Construction and Evaluation Indicators
3.3.2. WOA Hyperparameter Selection and Optimization Results
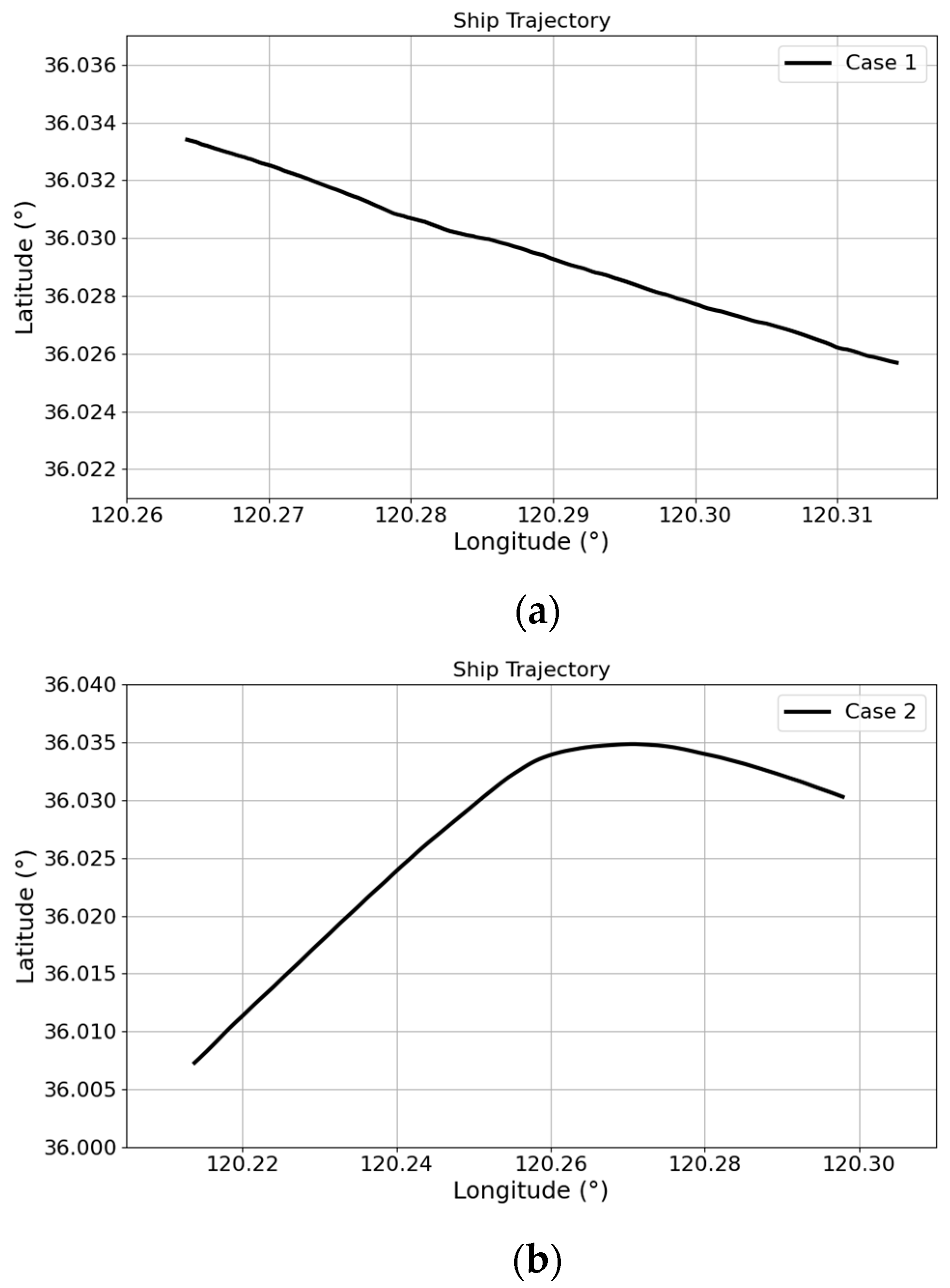
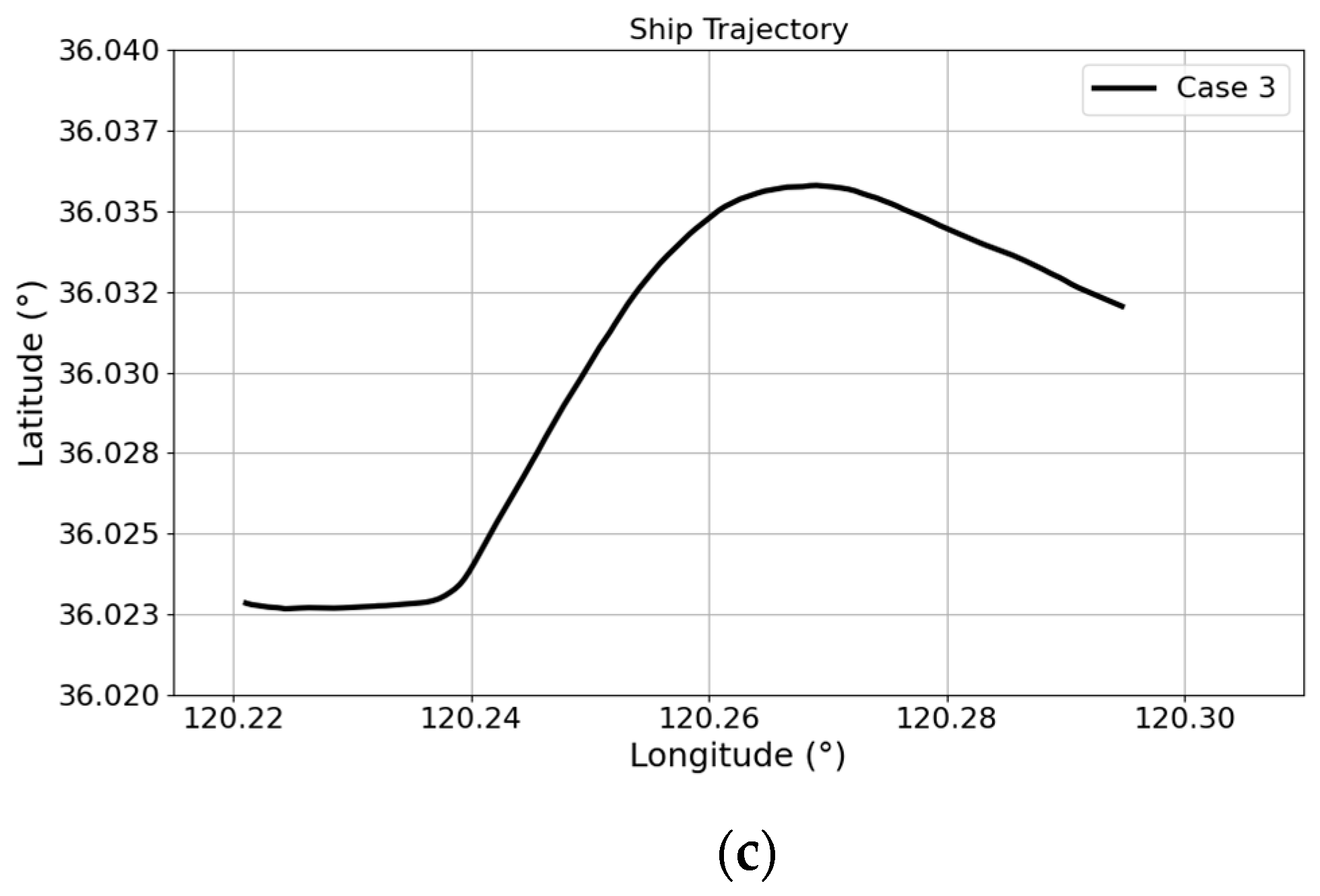
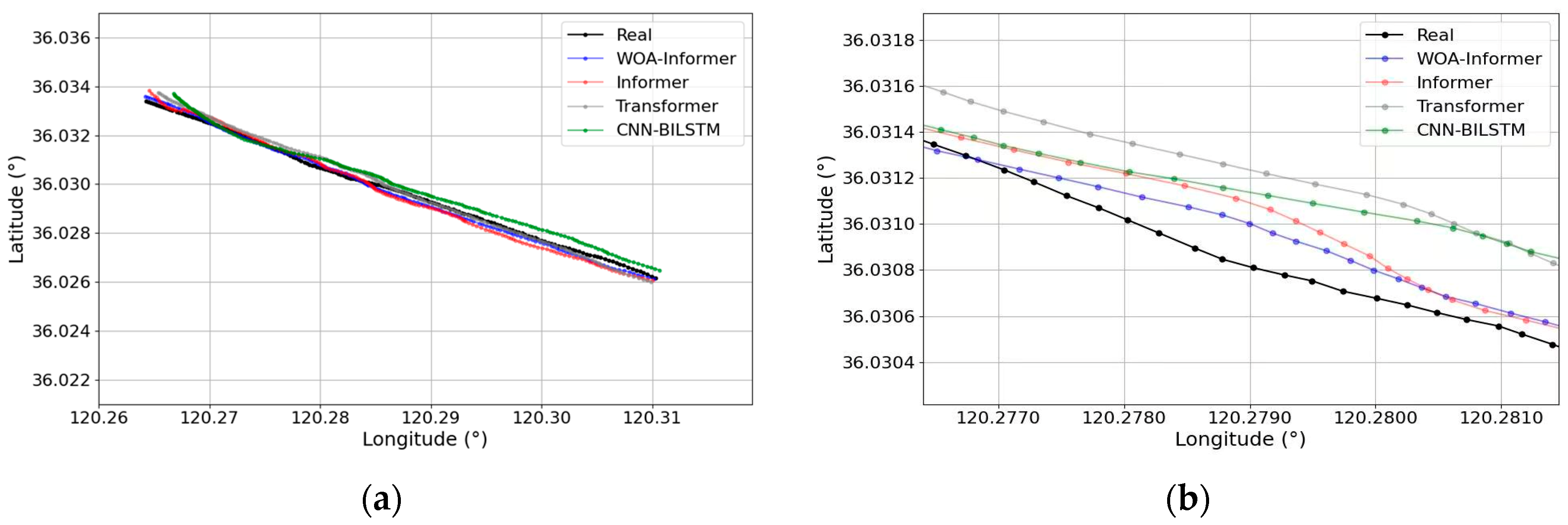
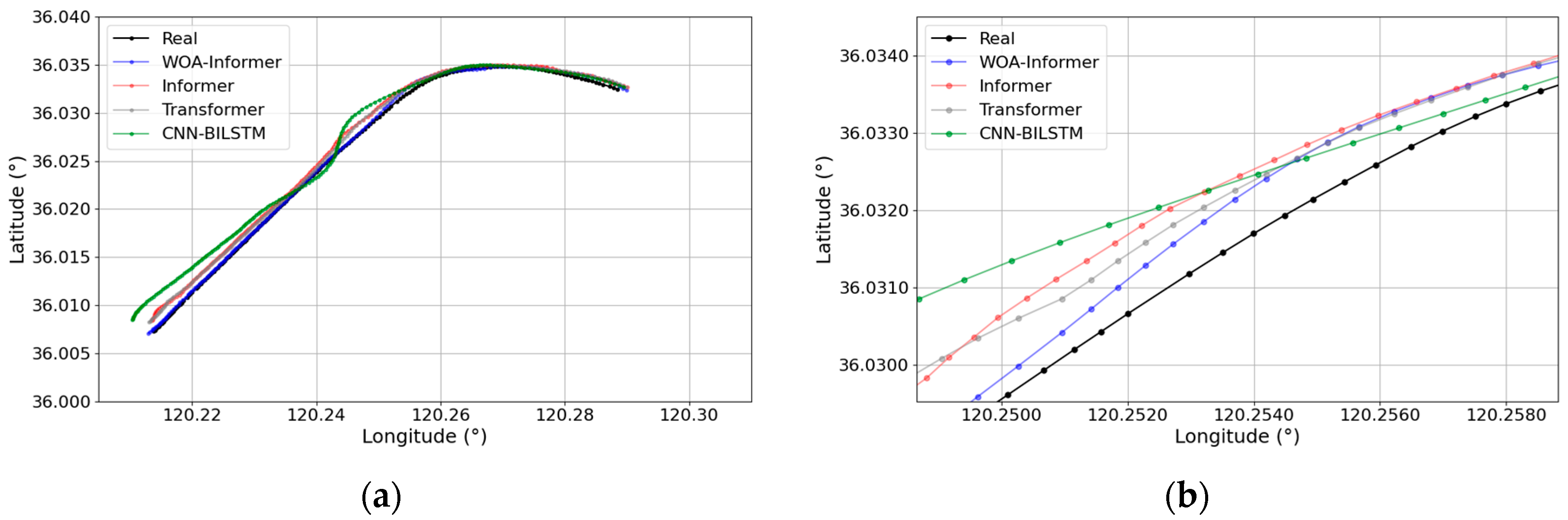
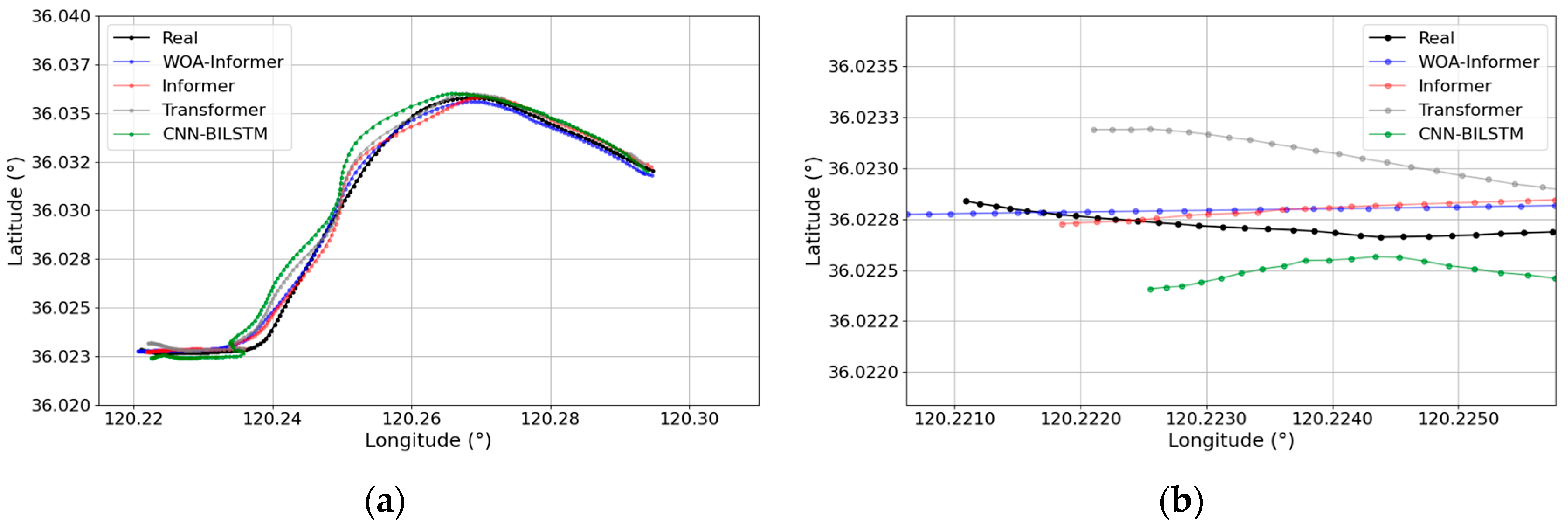
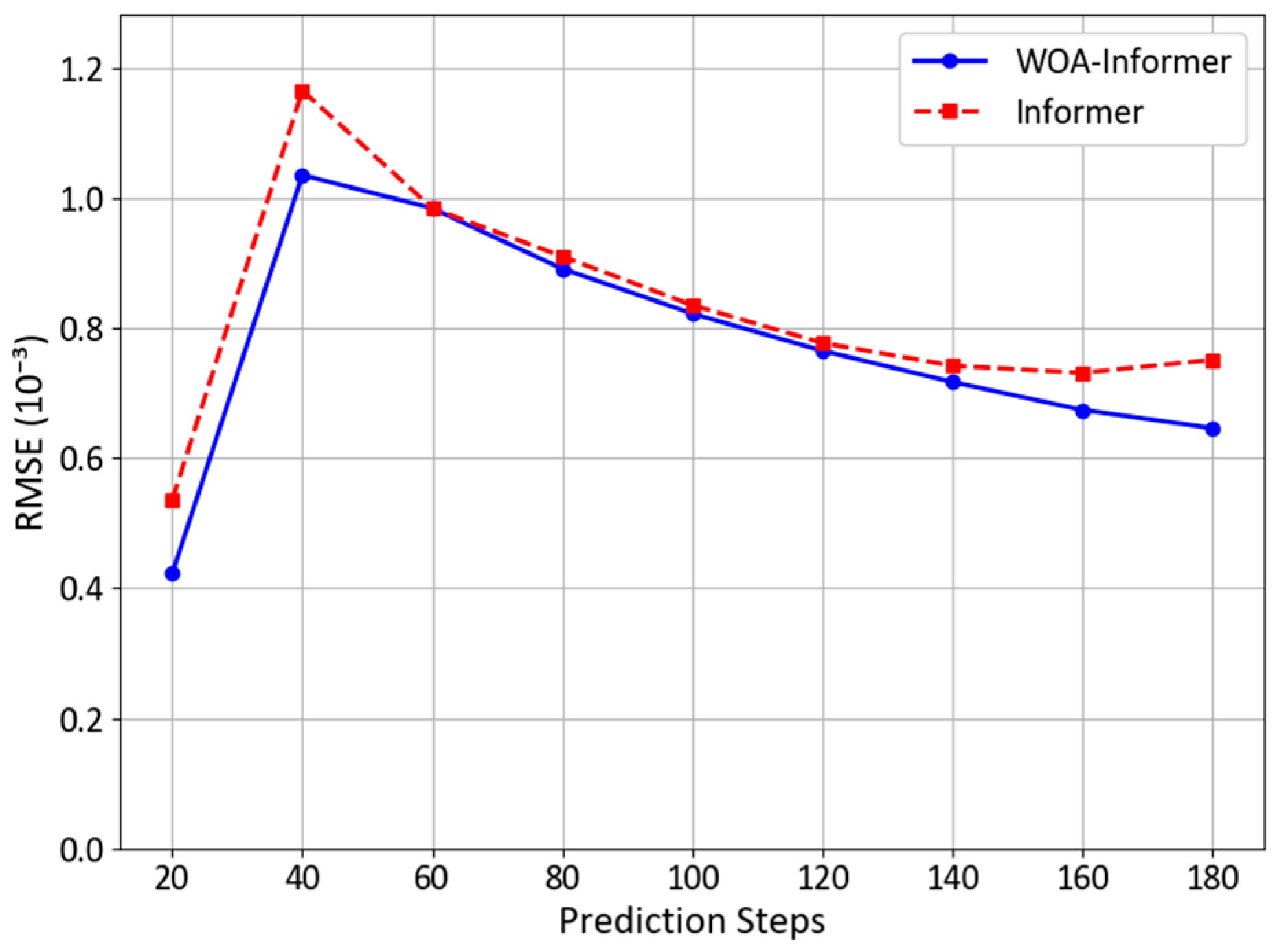
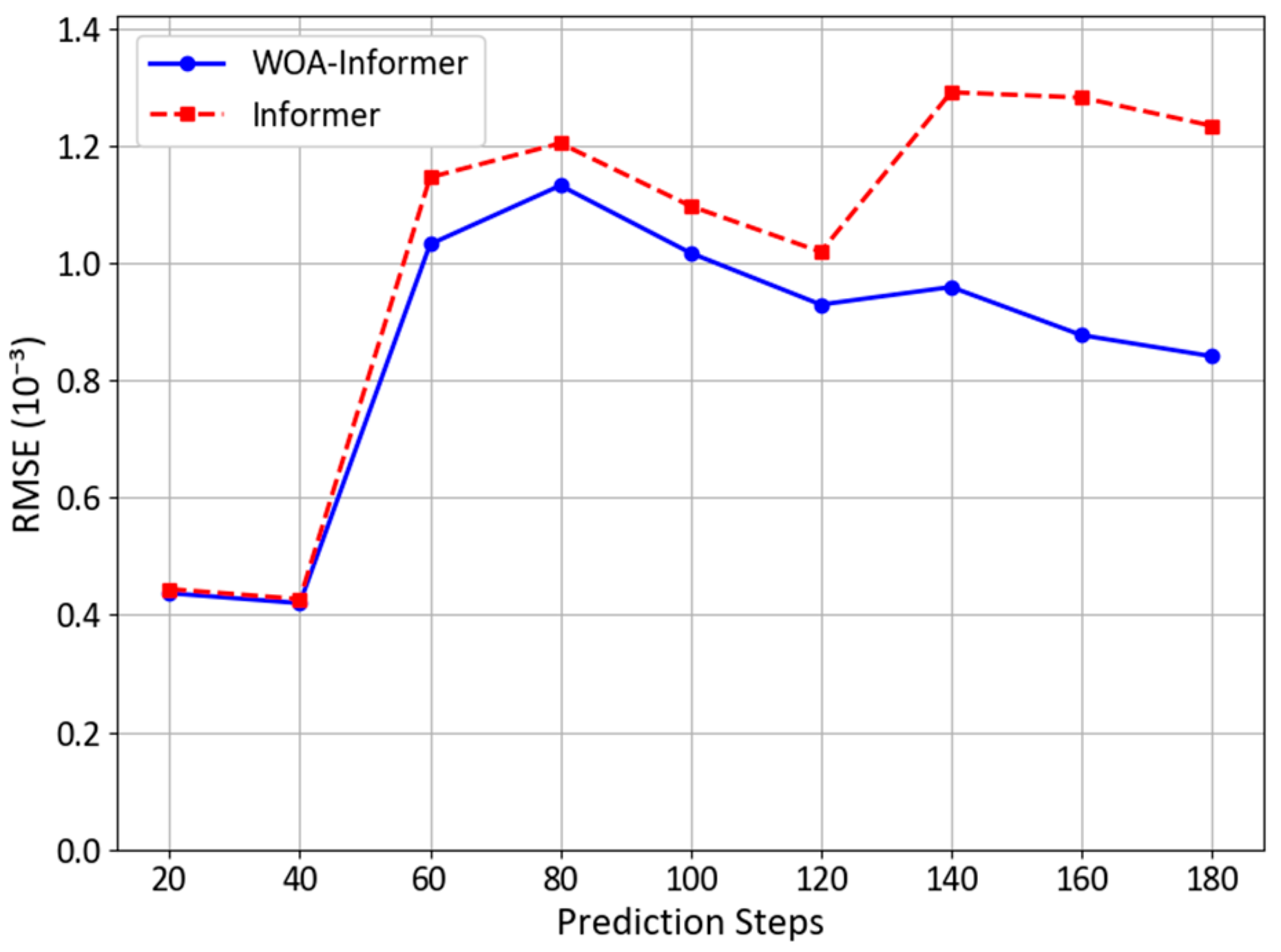
3.3.3. Prediction Results of WOA-Informer Model
4. Conclusions
- (1)
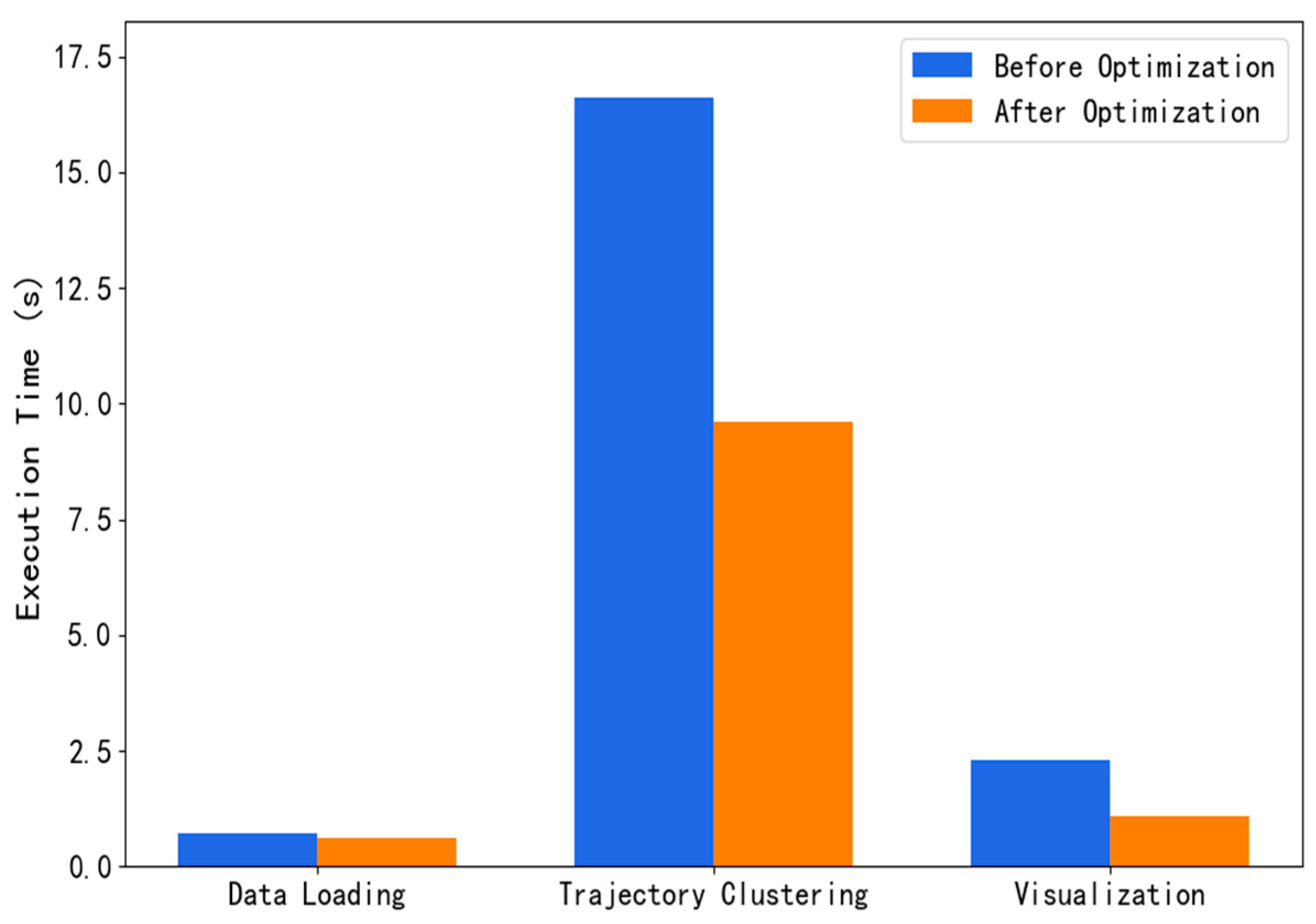
- Efficiency of trajectory clustering method: Addressing the multimodal characteristics of ship trajectories in port waters, this study employs a DBSCAN clustering algorithm based on Hausdorff distance, successfully identifying six distinct types of ship trajectory clusters. By incorporating a KD-Tree spatial index structure and GPU parallel computing, the computational time of the traditional clustering algorithm is reduced from 16.60 s to 9.61 s, achieving a 57.9% improvement in efficiency.
- (2)
- Significant improvement in prediction accuracy: The WOA-Informer model delivers optimal predictive performance across all three trajectory patterns. Compared to the unoptimized Informer model, it achieves average reductions of 23.1% in RMSE, 22.4% in MAE, 12% in MAPE, and 27.8% in Haversine distance. Particularly in complex turning scenarios (e.g., Trajectory Pattern 3), the model demonstrates enhanced adaptability to nonlinear motion, with errors converging more rapidly after turns, validating the efficacy of WOA in hyperparameter tuning.
- (3)
- Balanced computational efficiency optimization: Although introducing the WOA slightly increases the model’s training time, the ProbSparse attention mechanism ensures that its computational efficiency remains significantly higher than that of the CNN-BiLSTM and Transformer models. This balance between accuracy and efficiency enhances the model’s practical applicability for real-world engineering deployment.
4.1. Limitations
4.2. Future Research
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Seong, N.; Kim, J.; Lim, S. Graph-Based Anomaly Detection of Ship Movements Using CCTV Videos. J. Mar. Sci. Eng. 2023, 11, 1956. [Google Scholar] [CrossRef]
- Zhen, R.; Shao, Z.; Pan, J. Advance in character mining and prediction of ship behavior based on AIS data. J. Geo-Inf. Sci. 2021, 23, 2111–2127. [Google Scholar] [CrossRef]
- Wang, S.; Nie, H.; Shi, C. A Drifting Trajectory Prediction Model Based on Object Shape and Stochastic Motion Features. J. Hydrodyn. 2014, 26, 951–959. [Google Scholar] [CrossRef]
- Qiao, S.; Han, N.; Zhu, X.; Shu, H. A dynamic trajectory prediction algorithm based on Kalman filter. Acta Electonica Sin. 2018, 46, 418–423. [Google Scholar]
- Fossen, S.; Fossen, T.I. eXogenous Kalman Filter (XKF) for Visualization and Motion Prediction of Ships Using Live Automatic Identification System (AIS) Data. MIC 2018, 39, 233–244. [Google Scholar] [CrossRef]
- Moreira, L.; Vettor, R.; Guedes Soares, C. Neural Network Approach for Predicting Ship Speed and Fuel Consumption. J. Mar. Sci. Eng. 2021, 9, 119. [Google Scholar] [CrossRef]
- Bai, W.; Zhang, W.; Cao, L.; Liu, Q. Adaptive Control for Multi-Agent Systems with Actuator Fault via Reinforcement Learning and Its Application on Multi-Unmanned Surface Vehicle. Ocean Eng. 2023, 280, 114545. [Google Scholar] [CrossRef]
- Bai, W.; Chen, D.; Zhao, B.; D’Ariano, A. Reinforcement Learning Control for a Class of Discrete-Time Non-Strict Feedback Multi-Agent Systems and Application to Multi-Marine Vehicles. IEEE Trans. Intell. Veh. 2025, 10, 3613–3625. [Google Scholar] [CrossRef]
- Wang, Q.; Zhang, Q.; Wang, Y.; Hu, Y.; Guo, S. Event-Triggered Adaptive Finite Time Trajectory Tracking Control for an Underactuated Vessel Considering Unknown Time-Varying Disturbances. Transp. Saf. Environ. 2023, 5, tdac078. [Google Scholar] [CrossRef]
- Zhou, H.; Chen, Y.; Zhang, S. Ship Trajectory Prediction Based on BP Neural Network. J. Artif. Intell. 2019, 1, 29–36. [Google Scholar] [CrossRef]
- Kim, J.-S. Vessel Target Prediction Method and Dead Reckoning Position Based on SVR Seaway Model. Int. J. Fuzzy Log. Intell. Syst. 2017, 17, 279–288. [Google Scholar] [CrossRef]
- Liu, J.; Shi, G.; Zhu, K. Vessel Trajectory Prediction Model Based on AIS Sensor Data and Adaptive Chaos Differential Evolution Support Vector Regression (ACDE-SVR). Appl. Sci. 2019, 9, 2983. [Google Scholar] [CrossRef]
- Zhang, M.; Huang, L.; Wen, Y.; Zhang, J.; Huang, Y.; Zhu, M. Short-Term Trajectory Prediction of Maritime Vessel Using k-Nearest Neighbor Points. J. Mar. Sci. Eng. 2022, 10, 1939. [Google Scholar] [CrossRef]
- Gao, L.; Wu, j.; Yang, Z.; Xu, C.; Feng, Z.; Chen, J. Long-term Prediction of Ship Trajectories Using TCNformer Based on Spatiotemporal Feature Fusion. J. Nav. Aviat. Univ. 2024, 39, 437–444. [Google Scholar] [CrossRef]
- Gao, D.; Zhu, Y.; Zhang, J.; He, Y.; Yan, K.; Yan, B. A Novel MP-LSTM Method for Ship Trajectory Prediction Based on AIS Data. Ocean Eng. 2021, 228, 108956. [Google Scholar] [CrossRef]
- Wang, Y.; Liao, W.; Chang, Y. Gated Recurrent Unit Network-Based Short-Term Photovoltaic Forecasting. Energies 2018, 11, 2163. [Google Scholar] [CrossRef]
- Qian, L.; Zheng, Y.; Li, L.; Ma, Y.; Zhou, C.; Zhang, D. A New Method of Inland Water Ship Trajectory Prediction Based on Long Short-Term Memory Network Optimized by Genetic Algorithm. Appl. Sci. 2022, 12, 4073. [Google Scholar] [CrossRef]
- Li, W.; Lian, Y.; Liu, Y.; Shi, G. Ship Trajectory Prediction Model Based on Improved Bi-LSTM. ASCE-ASME J. Risk Uncertain. Eng. Syst. Part A-Civ. Eng. 2024, 10, 04024033. [Google Scholar] [CrossRef]
- Zhao, J.; Yan, Z.; Zhou, Z.; Chen, X.; Wu, B.; Wang, S. A Ship Trajectory Prediction Method Based on GAT and LSTM. Ocean Eng. 2023, 289, 116159. [Google Scholar] [CrossRef]
- Ju, C. Research on Vessel Track Prediction Based on CNN-GRU. Master’s Thesis, Dalian Maritime University, Dalian, China, 2023. [Google Scholar] [CrossRef]
- Dong, X.; Raja, S.S.; Zhang, J.; Wang, L. Ship Trajectory Prediction Based on CNN-MTABiGRU Model. IEEE Access 2024, 12, 115306–115318. [Google Scholar] [CrossRef]
- Jia, C.; Ma, J.; Kouw, W.M. Multiple Variational Kalman-GRU for Ship Trajectory Prediction With Uncertainty. IEEE Trans. Aerosp. Electron. Syst. 2025, 61, 3654–3667. [Google Scholar] [CrossRef]
- Lin, Z.; Yue, W.; Huang, J.; Wan, J. Ship Trajectory Prediction Based on the TTCN-Attention-GRU Model. Electronics 2023, 12, 2556. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is All you Need. arXiv 2017, arXiv:1706.03762. [Google Scholar]
- Yang, Z.; Dai, Z.; Yang, Y.; Carbonell, J.; Salakhutdinov, R.; Le, Q.V. XLNet: Generalized Autoregressive Pretraining for Language Understanding. In Proceedings of the Advances in Neural Information Processing Systems 32 (NIPS 2019), Vancouver, BC, Canada, 8–14 December 2019; Wallach, H., Larochelle, H., Beygelzimer, A., d’Alche-Buc, F., Fox, E., Garnett, R., Eds.; NIPS Foundation: San Diego, CA, USA, 2019; Volume 32. [Google Scholar]
- Xu, R.; Qi, Y.; Shi, L. Prediction of Ship Track Based on Transformer Model and Kalman Filter. Comput. Appl. Softw. 2021, 38, 106–111. [Google Scholar] [CrossRef]
- Xue, H.; Wang, S.; Xia, M.; Guo, S. G-Trans: A Hierarchical Approach to Vessel Trajectory Prediction with GRU-Based Transformer. Ocean Eng. 2024, 300, 117431. [Google Scholar] [CrossRef]
- Wang, P.; Pan, M.; Liu, Z.; Li, S.; Chen, Y.; Wei, Y. Ship Trajectory Prediction in Complex Waterways Based on Transformer and Social Variational Autoencoder (SocialVAE). J. Mar. Sci. Eng. 2024, 12, 2233. [Google Scholar] [CrossRef]
- Liu, Y.; Xiong, W.; Chen, N.; Yang, F. VTLLM: A Vessel Trajectory Prediction Approach Based on Large Language Models. J. Mar. Sci. Eng. 2025, 13, 1758. [Google Scholar] [CrossRef]
- Zhou, H.; Zhang, S.; Peng, J.; Zhang, S.; Li, J.; Xiong, H.; Zhang, W. Informer: Beyond efficient transformer for long sequence time-series forecasting. In Proceedings of the AAAI Conference on Artificial Intelligence 2021, Virtual, 2–9 February 2021; Volume 35, pp. 11106–11115. [Google Scholar]
- Xiong, C.; Shi, H.; Li, J.; Wu, X.; Gao, R. Informer-Based Model for Long-Term Ship Trajectory Prediction. J. Mar. Sci. Eng. 2024, 12, 1269. [Google Scholar] [CrossRef]
- Chen, L.; Zhou, N.; Li, S.; Liu, K.; Wang, K.; Zhou, Y. A Method of Ship Trajectory Prediction Based on a C-Informer Model. J. Transp. Inf. Saf. 2023, 41, 51–60+141. Available online: http://www.jtxa.net/cn/article/doi/10.3963/j.jssn.1674-4861.2023.06.006 (accessed on 14 October 2025).
- Rath, P.; Mallick, P.K.; Tripathy, H.K.; Mishra, D. A Tuned Whale Optimization-Based Stacked-LSTM Network for Digital Image Segmentation. Arab. J. Sci. Eng. 2023, 48, 1735–1756. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The Whale Optimization Algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Luo, J.; Gong, Y. Air Pollutant Prediction Based on ARIMA-WOA-LSTM Model. Atmos. Pollut. Res. 2023, 14, 101761. [Google Scholar] [CrossRef]
- Jia, H.; Yang, Y.; An, J.; Fu, R. A Ship Trajectory Prediction Model Based on Attention-BILSTM Optimized by the Whale Optimization Algorithm. Appl. Sci. 2023, 13, 4907. [Google Scholar] [CrossRef]
- Xie, H.; Ding, R.; Qiao, G.; Dai, C.; Bai, W. Research on Ship Traffic Flow Prediction Using CNN-BIGRU and WOA With Multi-Objective Optimization. IEEE Access 2024, 12, 138372–138385. [Google Scholar] [CrossRef]
- Han, Q.; Yang, X.; Song, H.; Sui, S.; Zhang, H.; Yang, Z. Whale optimization algorithm for ship path optimization in large-scale complex marine environment. IEEE Access 2020, 8, 57168–57179. [Google Scholar] [CrossRef]
- Jiang, D.; Shi, G.; Li, N.; Ma, L.; Li, W.; Shi, J. TRFM-LS: Transformer-Based Deep Learning Method for Vessel Trajectory Prediction. J. Mar. Sci. Eng. 2023, 11, 880. [Google Scholar] [CrossRef]
- Botts, C.H. A Novel Metric for Detecting Anomalous Ship Behavior Using a Variation of the DBSCAN Clustering Algorithm. SN Comput. Sci. 2021, 2, 412. [Google Scholar] [CrossRef]
- Chen, Y.; He, F.; Wu, Y.; Hou, N. A Local Start Search Algorithm to Compute Exact Hausdorff Distance for Arbitrary Point Sets. Pattern Recognit. 2017, 67, 139–148. [Google Scholar] [CrossRef]
- Erdinç, B.; Kaya, M.; Şenol, A. MCMSTStream: Applying Minimum Spanning Tree to KD-Tree-Based Micro-Clusters to Define Arbitrary-Shaped Clusters in Streaming Data. Neural Comput. Appl. 2024, 36, 7025–7042. [Google Scholar] [CrossRef]
- Zhao, L.; Shi, G. A Trajectory Clustering Method Based on Douglas-Peucker Compression and Density for Marine Traffic Pattern Recognition. Ocean Eng. 2019, 172, 456–467. [Google Scholar] [CrossRef]
- Shaygan, M.; Meese, C.; Li, W.; Zhao, X.G.; Nejad, M. Traffic Prediction Using Artificial Intelligence: Review of Recent Advances and Emerging Opportunities. Transp. Res. Part C Emerg. Technol. 2022, 145, 103921. [Google Scholar] [CrossRef]
- Chen, X.; Wu, H.; Han, B.; Liu, W.; Montewka, J.; Liu, R.W. Orientation-Aware Ship Detection via a Rotation Feature Decoupling Supported Deep Learning Approach. Eng. Appl. Artif. Intell. 2023, 125, 106686. [Google Scholar] [CrossRef]

| Environment | Specific Configuration |
|---|---|
| Operating System | Windows 11 |
| CPU | i5-12450H |
| GPU | RTX 3060 |
| Programming Language | Python 3.11.7 |
| Compiler | PyCharm 2021 |
| Framework | PyTorch 2.5.1 |
| MMSI | Base Date Time | LAT (°) | LON (°) | SOG (kn) | COG (°) |
|---|---|---|---|---|---|
| 352986146 | 2024-11-08T10:39:36 | 36.02465 | 120.33908 | 8.9 | 281.6 |
| 352986146 | 2024-11-08T10:41:05 | 36.02541 | 120.33456 | 9.0 | 281.5 |
| 352986146 | 2024-11-08T10:43:34 | 36.02672 | 120.32659 | 10.1 | 281.3 |
| 352986146 | 2024-11-08T10:45:07 | 36.02763 | 120.32127 | 10.8 | 281.8 |
| 352986146 | 2024-11-08T10:46:34 | 36.02864 | 120.31562 | 11.4 | 282.1 |
| Hyperparameters | Set Range | Step Size |
|---|---|---|
| Learning rate | [0.0001, 0.1] | 0.0001 |
| Batch size | [2, 128] | 1 |
| Encoder layers | [1, 6] | 1 |
| Decoder layers | [1, 6] | 1 |
| Dropout | [0.005, 0.4] | 0.01 |
| Hyperparameters | Case 1. Result | Case 2. Result | Case 3. Result |
|---|---|---|---|
| Learning rate | 0.0047 | 0.0036 | 0.0023 |
| Batch size | 38 | 29 | 23 |
| Encoder layers | 2 | 2 | 3 |
| Decoder layers | 1 | 2 | 2 |
| Dropout | 0.13 | 0.19 | 0.24 |
| Model | Hyperparameter | Hyperparameter Set |
|---|---|---|
| CNN-BILSTM | Filter size Regularization Activation function Attention type | 4 L2 Relu/Sigmoid None |
| Transformer | Encoder–Decoder Layers Head number Activation function Attention type | [2, 1] 8 Gelu Self-attention |
| Informer | Encoder–Decoder Layers Head number Activation function Attention type | [2, 1] 8 Gelu ProbSparse attention |
| Model | RMSE (10−3) | MAE (10−3) | MAPE (10−3) | HAV (m) |
|---|---|---|---|---|
| CNN-BILSTM | 0.927 | 0.678 | 0.692 | 107.7 |
| Transformer | 0.563 | 0.435 | 0.522 | 66.90 |
| Informer | 0.447 | 0.303 | 0.384 | 50.24 |
| WOA-Informer | 0.342 | 0.288 | 0.462 | 43.21 |
| Model | RMSE (10−3) | MAE (10−3) | MAPE (10−3) | HAV (m) |
|---|---|---|---|---|
| CNN-BILSTM | 1.554 | 1.105 | 1.352 | 168.23 |
| Transformer | 0.721 | 0.567 | 0.897 | 91.95 |
| Informer | 0.751 | 0.565 | 0.922 | 95.77 |
| WOA-Informer | 0.646 | 0.431 | 0.527 | 69.19 |
| Model | RMSE (10−3) | MAE (10−3) | MAPE (10−3) | HAV (m) |
|---|---|---|---|---|
| CNN-BILSTM | 1.626 | 1.151 | 1.604 | 189.64 |
| Transformer | 1.288 | 0.845 | 0.986 | 137.81 |
| Informer | 1.234 | 0.728 | 0.794 | 122.67 |
| WOA-Informer | 0.841 | 0.520 | 0.687 | 82.87 |
| Model | Pattern 1 Execution Time (s) | Pattern 2 Execution Time (s) | Pattern 3 Execution Time (s) |
|---|---|---|---|
| CNN-BILSTM | 52.457 | 47.651 | 58.658 |
| Transformer | 27.186 | 24.256 | 32.156 |
| Informer | 18.269 | 17.147 | 20.015 |
| WOA-Informer | 22.132 | 19.893 | 25.867 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, H.; Wang, J.; Shi, Z.; Xue, S. Optimizing Informer with Whale Optimization Algorithm for Enhanced Ship Trajectory Prediction. J. Mar. Sci. Eng. 2025, 13, 1999. https://doi.org/10.3390/jmse13101999
Xie H, Wang J, Shi Z, Xue S. Optimizing Informer with Whale Optimization Algorithm for Enhanced Ship Trajectory Prediction. Journal of Marine Science and Engineering. 2025; 13(10):1999. https://doi.org/10.3390/jmse13101999
Chicago/Turabian StyleXie, Haibo, Jinliang Wang, Zhiqiang Shi, and Shiyuan Xue. 2025. "Optimizing Informer with Whale Optimization Algorithm for Enhanced Ship Trajectory Prediction" Journal of Marine Science and Engineering 13, no. 10: 1999. https://doi.org/10.3390/jmse13101999
APA StyleXie, H., Wang, J., Shi, Z., & Xue, S. (2025). Optimizing Informer with Whale Optimization Algorithm for Enhanced Ship Trajectory Prediction. Journal of Marine Science and Engineering, 13(10), 1999. https://doi.org/10.3390/jmse13101999






