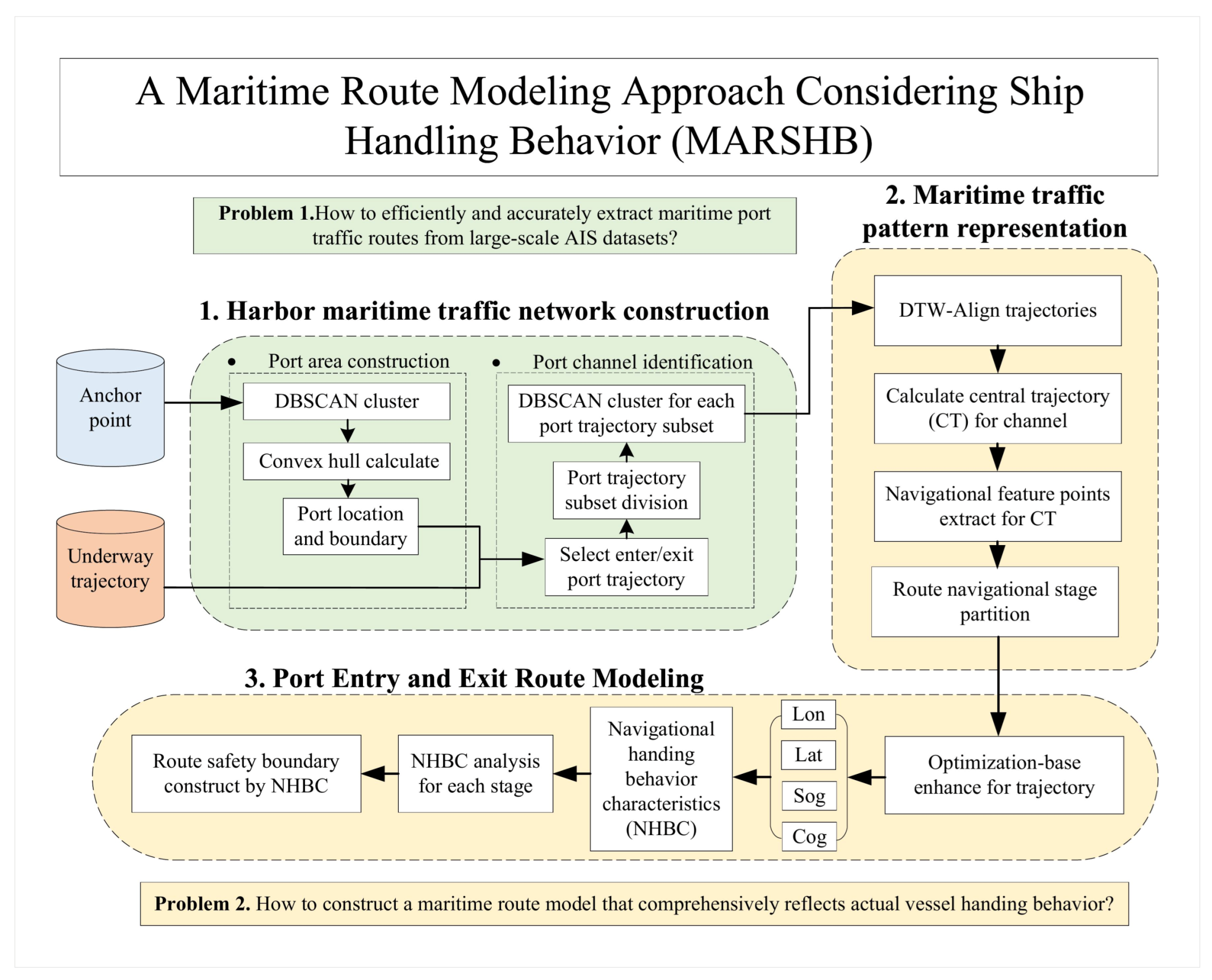
Multidimensional Maritime Route Modeling Method for Complex Port Waters Considering Ship Handling Behavior Diversity
Abstract
1. Introduction
- Aiming at port areas with heavy maritime traffic, an efficient and accurate method was designed to extract port routes with diverse traffic flow characteristics in complex environments, effectively addressing the challenge of balancing efficiency and accuracy in high-density data settings.
- A characterization method for maritime traffic patterns based on the navigational stage division was proposed. By integrating vessel handling behaviors—such as speed adjustments, obstacle avoidance, and berthing—with spatial features, this approach offers a more comprehensive understanding of ship dynamics in port entry and exit channels. It addresses the limitation in existing studies, which often focus heavily on spatial aspects while underrepresenting real-world operational behaviors.
- A route safety boundary that integrates spatial features and handling behavior standards was designed. After combining with vessel behavior guidelines, the route model achieves an upgrade from “spatial description” to “behavioral description.”
2. Related Work
2.1. Vector-Based Route Modeling Methods
2.2. Grid-Based Route Modeling Methods
2.3. Statistical Route Modeling Methods
2.4. General Remarks
3. Study Area and Data
3.1. Study Area
3.2. Anchorage Point Data
3.3. Ship Trajectory Data
4. Method
4.1. Harbor Maritime Route Network Construction
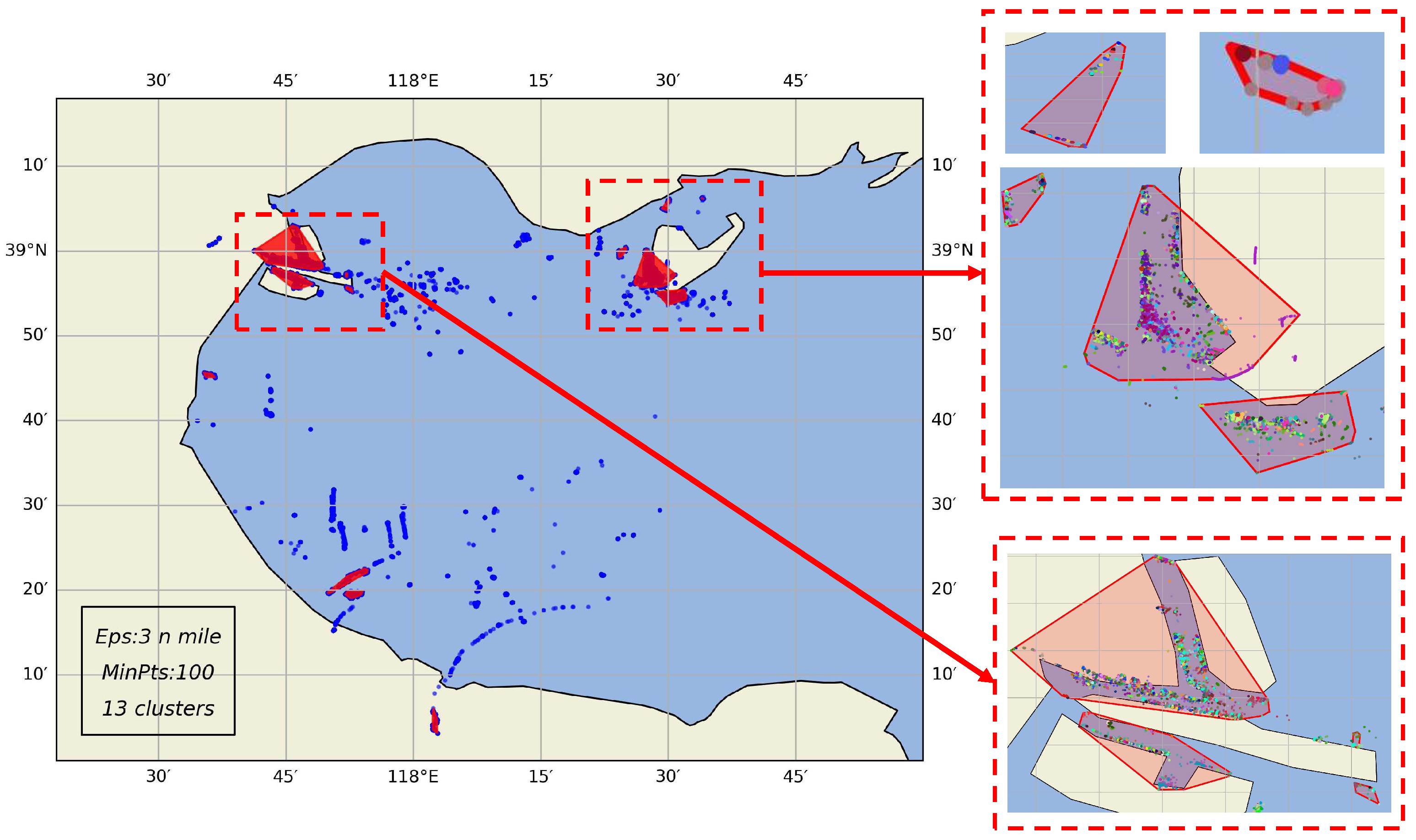
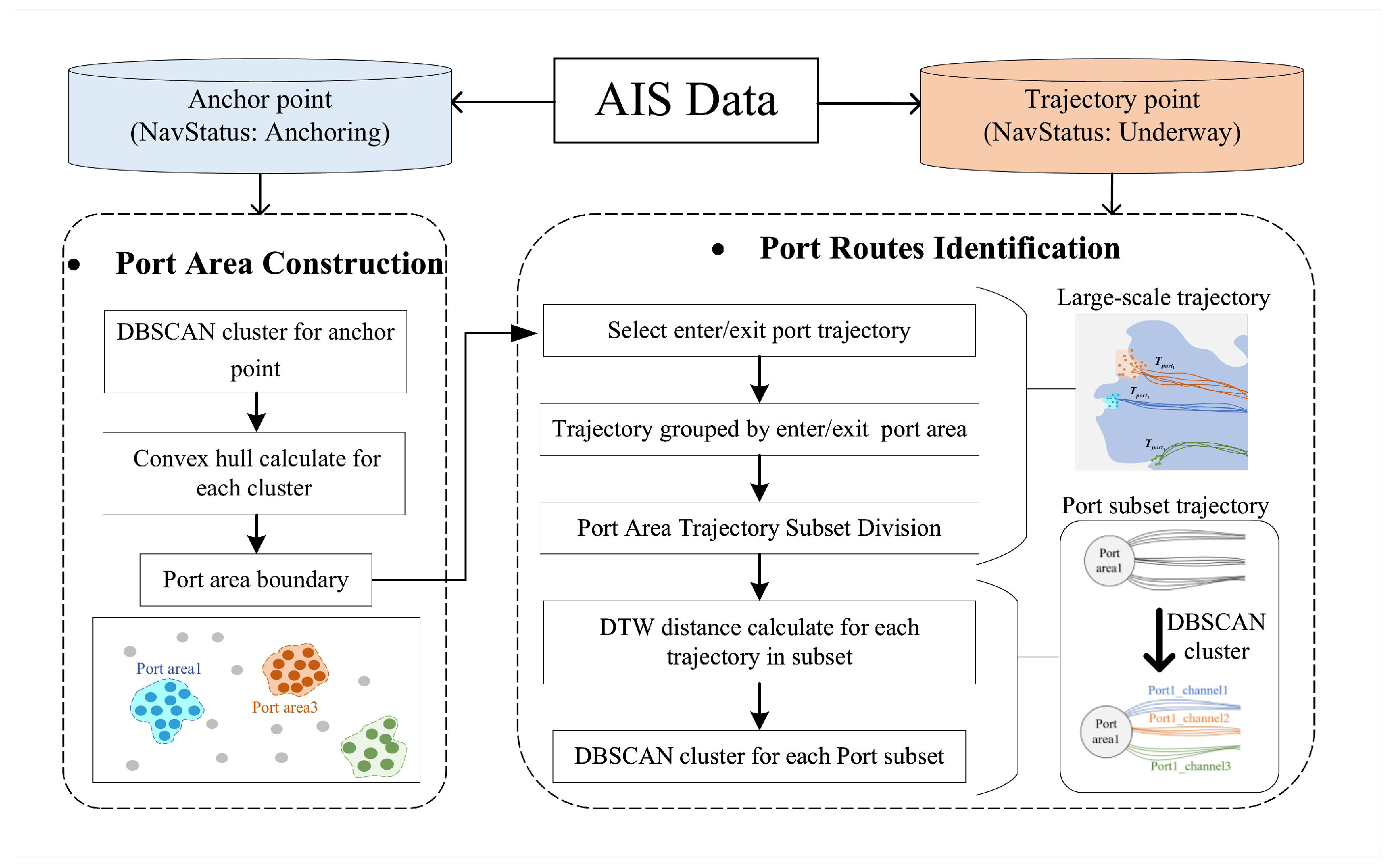
4.1.1. Port Area Construction
4.1.2. Harbor Routes Extraction
- (a)
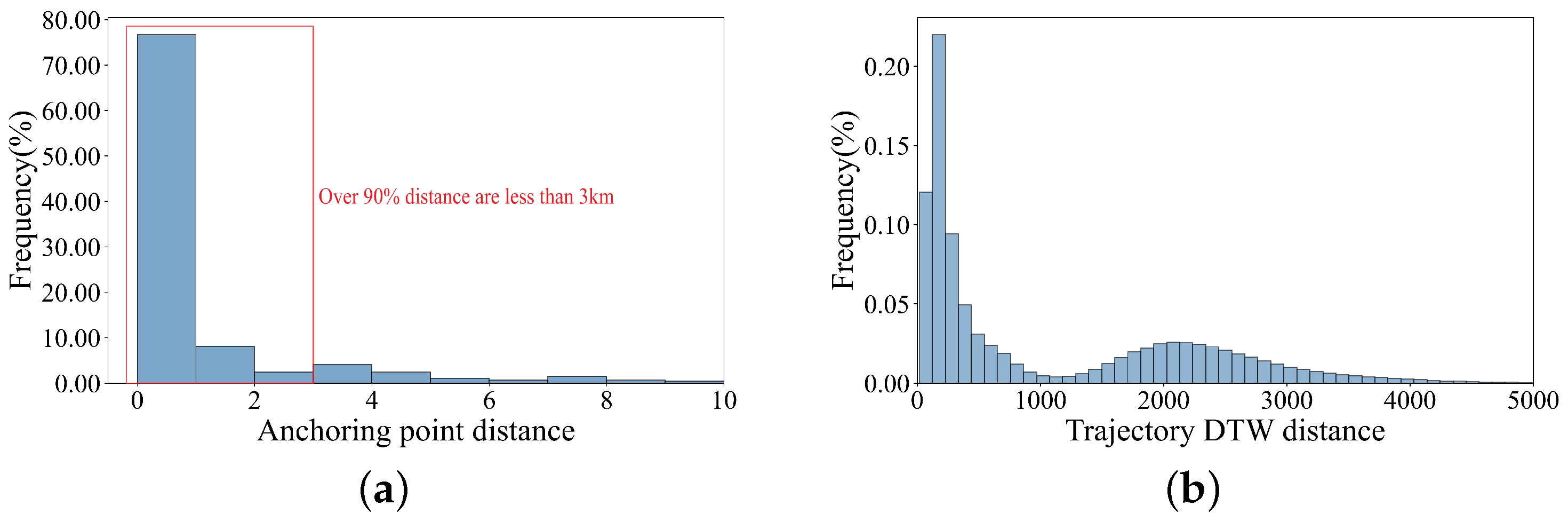
- Trajectory definition: The trajectory data set can be defined as , where represents the n-th trajectory. Trajectory points, including longitude, latitude, speed, course and time information, and the j-th trajectory point, can be expressed as . To reduce data redundancy and improve the efficiency of subsequent analysis, the DP algorithm was used to compress the trajectory segments [53]. The threshold for compression was set to 0.8 times the ship’s length, as recommended by [54].
- (b)
- Subset division of port area trajectories: Trajectory segments whose starting point or ending point lies within a port area are selected. These trajectories are then divided into subsets according to their associated port. Formally, for the i-th port area, the subset can be written aswhere denotes the set of trajectories related to the i-th port, is a trajectory, and and are the starting and ending points of .
- (c)
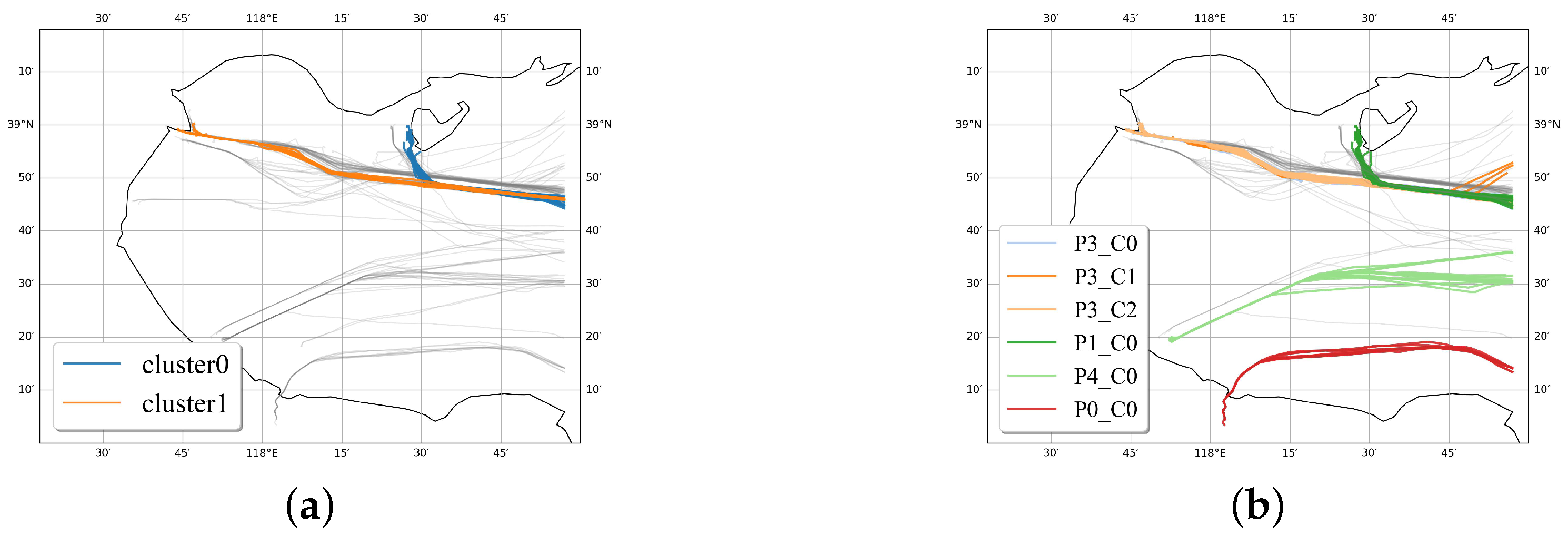
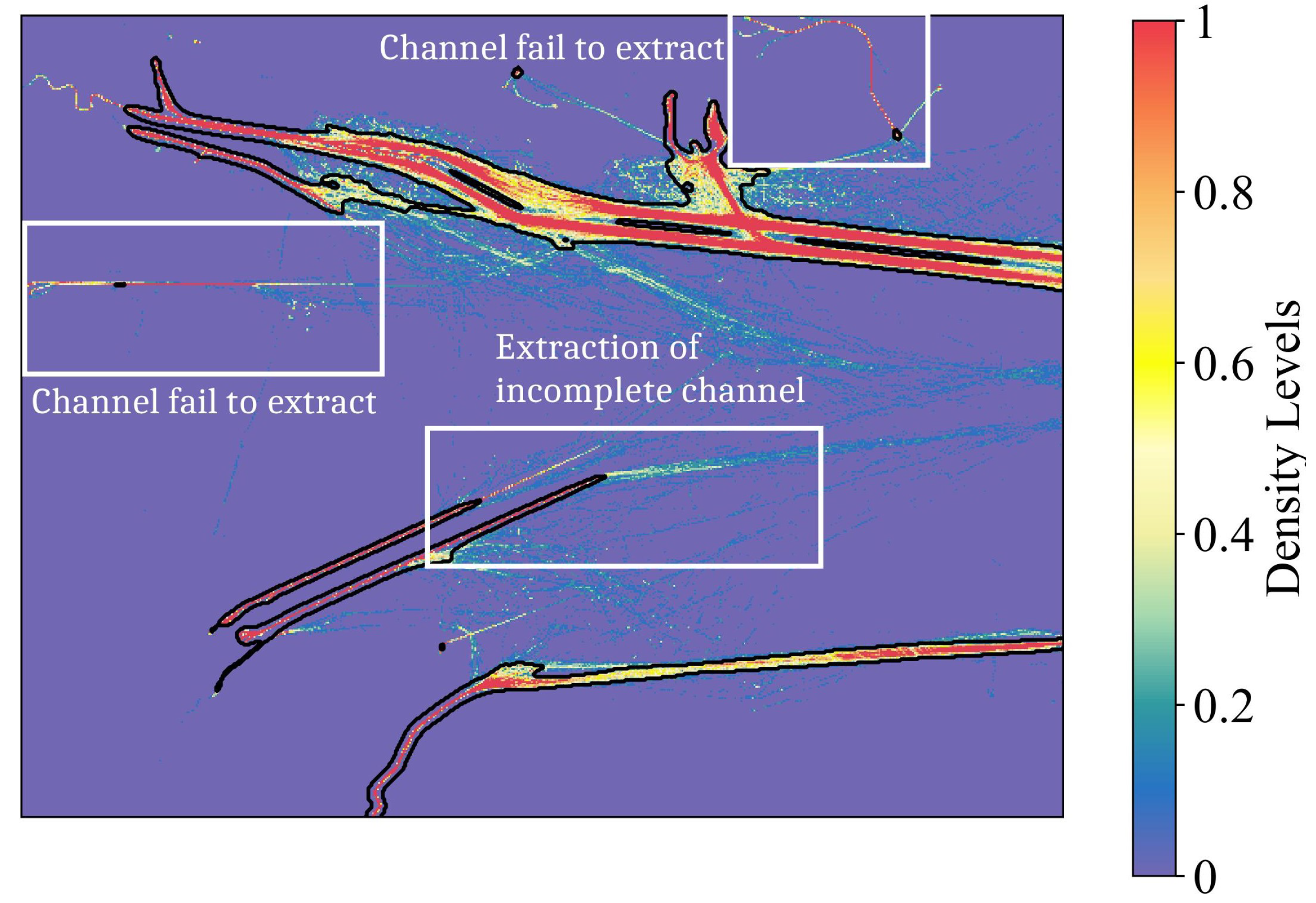
- Adaptive threshold clustering: Within each port subset, trajectories are compared using the Dynamic Time Warping (DTW) distance, and DBSCAN [55] is used to cluster similar trajectories into navigation routes. A minimum of five trajectories per cluster is required to ensure representativeness, following [56]. The key challenge is that trajectory density varies across ports: dense areas may easily form clusters, while sparse areas risk being ignored if the threshold is fixed [57]. To address this, we introduce an adaptive parameter setting. For each trajectory, we compute its average distance to the five nearest neighbors:where denotes the DTW distance. The clustering threshold eps is then chosen as the maximum of these local density estimates:Finally, the output clusters represent the major navigational routes of the port:
4.2. Maritime Traffic Pattern Representation
4.2.1. Representative Path Calculation
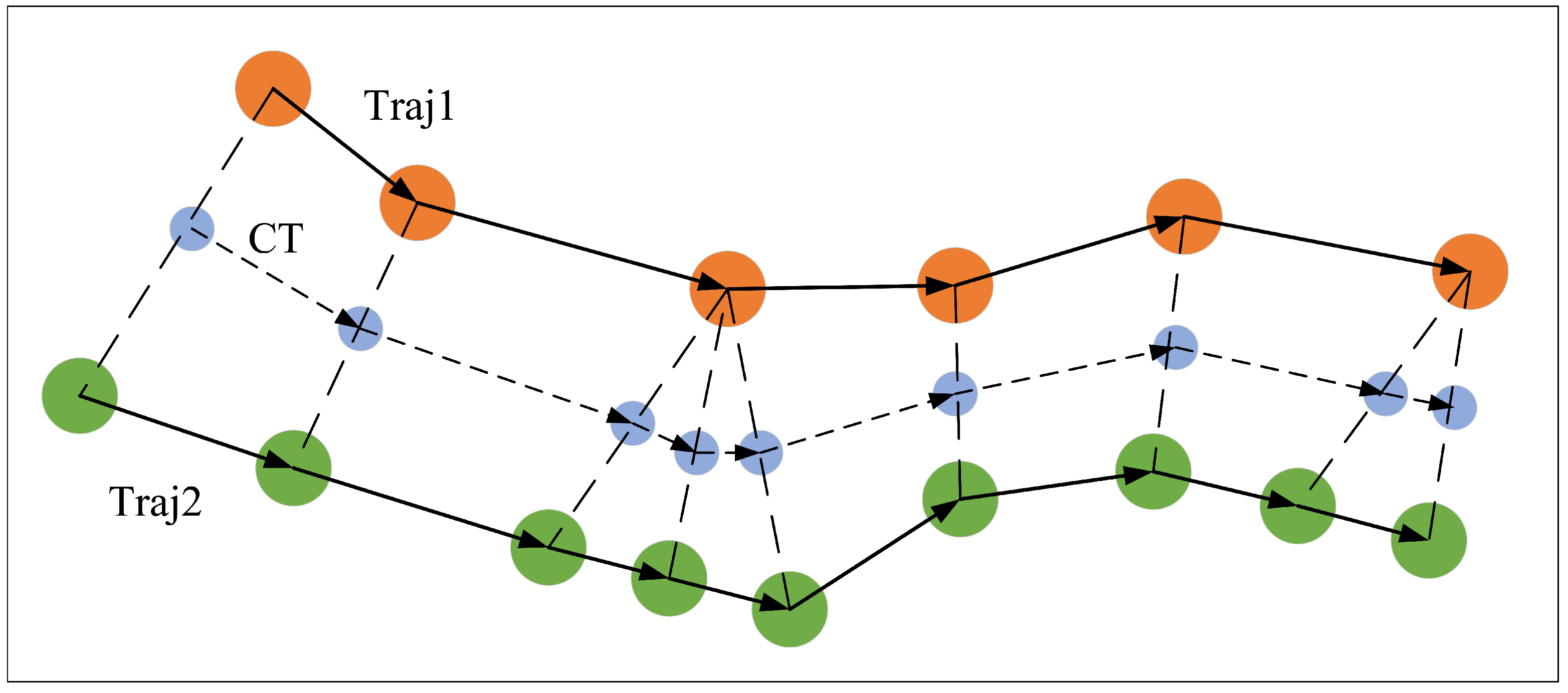
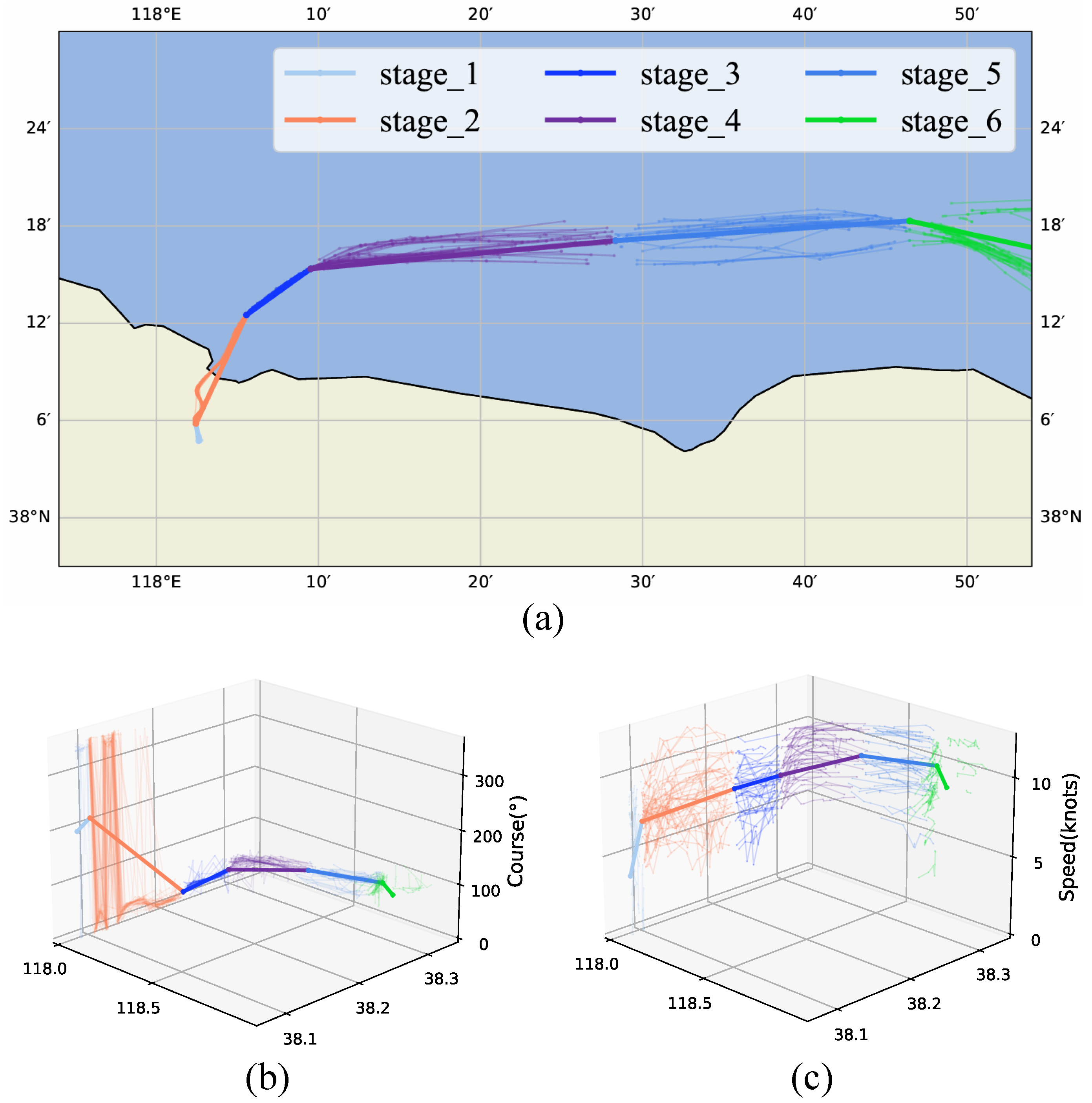
4.2.2. Route’s Navigation States Segmentation
| Algorithm 1 Feature Point Extraction. |
Input: Representative centerline trajectory CT, speed feature point threshold sth, course feature point threshold cth, trajectory compression threshold dpth Output: Feature Point FP # Find Handling Feature Point
# Find Position Feature Point
|
4.3. Port Access Route Modeling
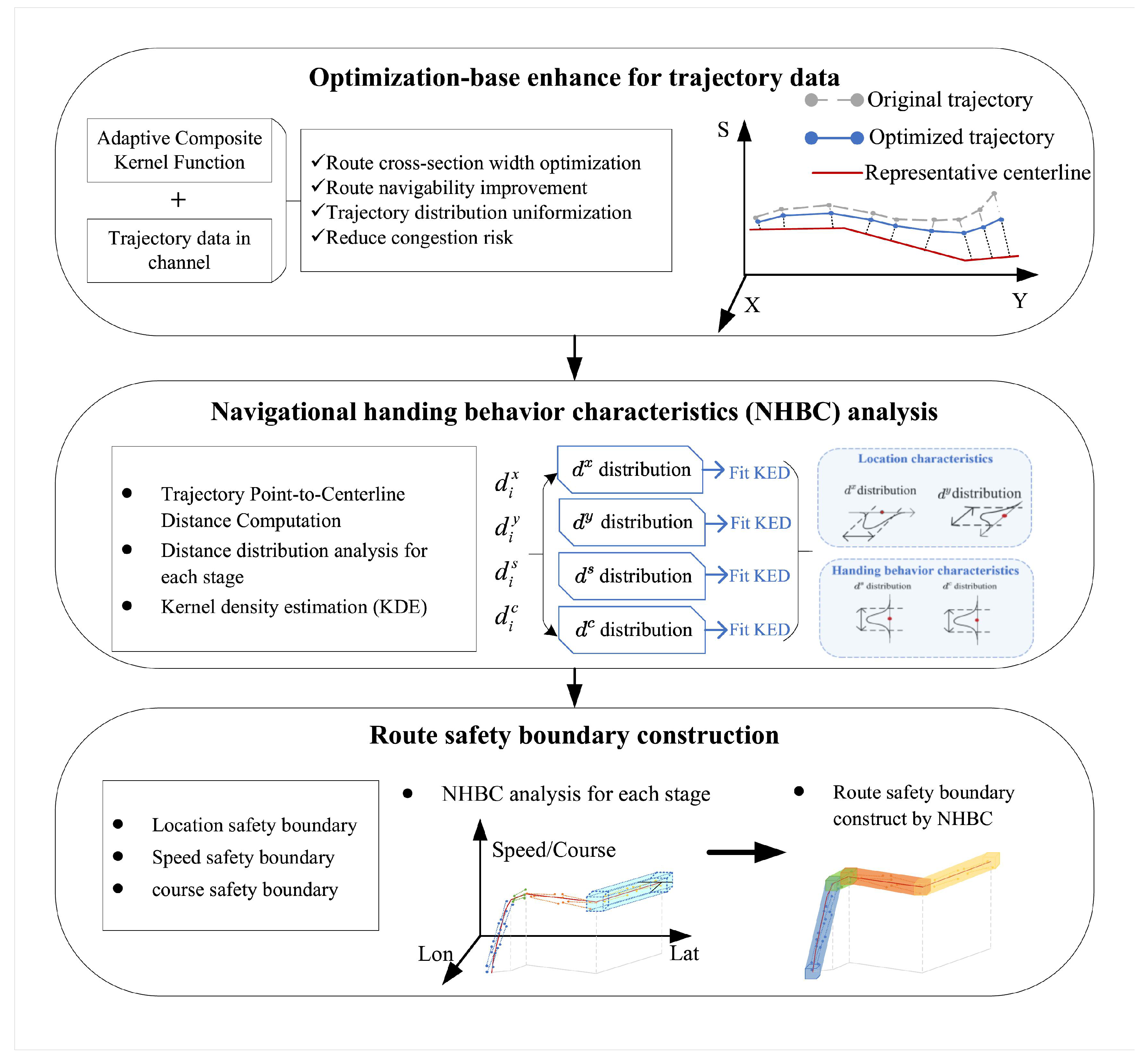
4.3.1. Route Trajectory Data Optimization
- Step 1
- Projection: Each trajectory point is first projected onto the route centerline to obtain a reference point.
- Step 2
- Similarity evaluation: The consistency between the original point and its projection is evaluated in four dimensions: longitude (x), latitude (y), speed (s), and course (c).
- Step 3
- Adjustment: If the point is similar to its projection across these dimensions, it is pulled closer to the centerline. This reduces excessive width in open waters and ensures a more compact distribution near ports.
4.3.2. Route Safety Boundary Establishing
- Step 1
- Compute the Distance from Projected Points to the Centerline: For each optimized trajectory point , we calculate its deviation from the projected point on the centerline . The overall deviation iswhich can also be decomposed into x, y, s, and c components.
- Step 2
- Fit KDE Probability Distribution for Each Stage: For each stage, we collect the deviation components of all trajectory points and estimate their probability distributions using kernel density estimation (KDE). For example, in the x-dimension,where is the kernel function and h is the bandwidth.
- Step 3
- Safety Boundary Description by Probability Density Curves: From the cumulative distribution function (CDF) of each dimension, we determine threshold values corresponding to a high confidence level (99.7%). These thresholds define the maximum acceptable deviation in position, speed, and course within that stage.
- Step4
- Construct the Safety Boundary Box for Each Stages: Each stage is assigned a safety boundary box centered at its starting point, extending by the threshold values in all four dimensions. The overall safety boundary of the route is the union of these stage-wise boxes.
5. Case Study and Results
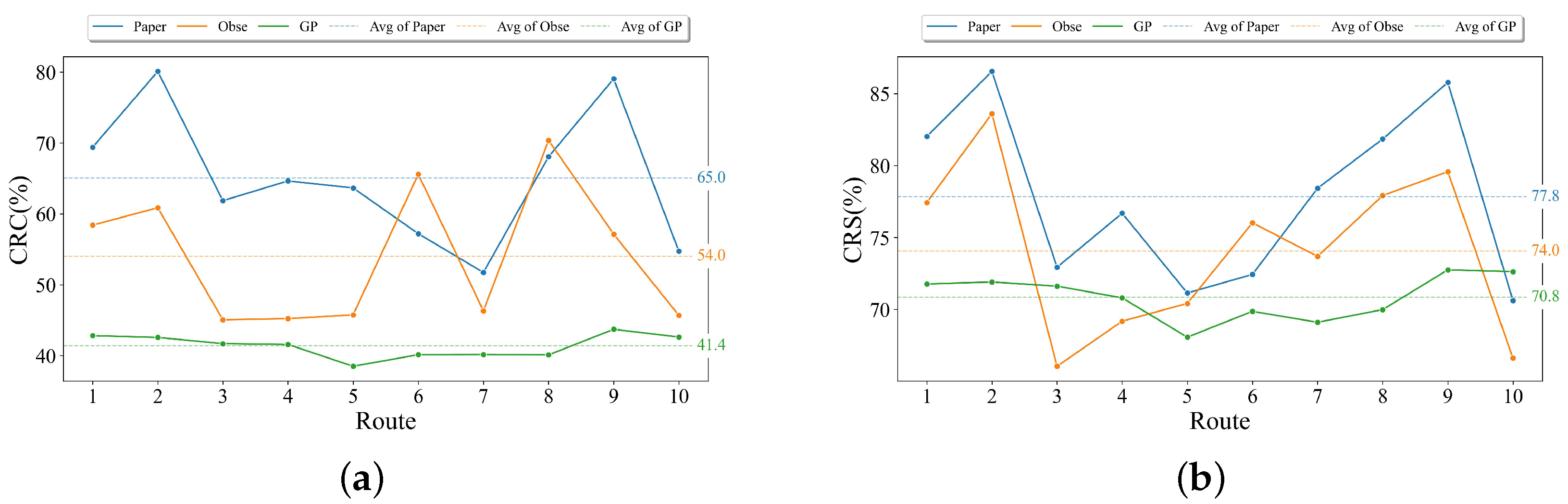
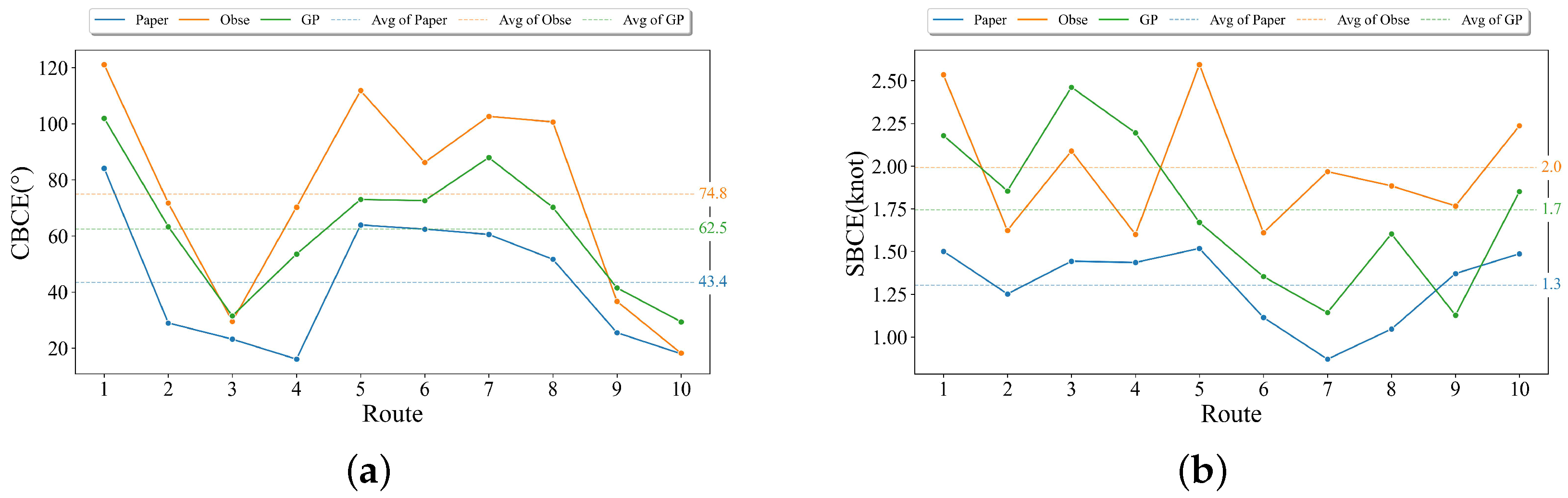
5.1. Evaluation Metrics
- (1)
- Speed Range Coverage (SRC) and Course Range Coverage (CRC): The SRC and CRC metrics are used to evaluate how well the model-generated safe speed and course ranges encompass historical data:where and are the numbers of points within the safe speed and course ranges, and denotes the total number of points. A higher coverage rate suggests that the model-generated safe speed and course range better encompassed historical data.
- (2)
- Speed Boundary Consistency Error (SBCE) and Course Boundary Consistency Error (CBCE): SBCE and CBCE are used to evaluate the consistency between the model-generated safety handling behavior boundaries and the speed/course distribution in historical data:Projection Calculation: For each point, compute its projection onto the centerline.Speed Boundary Retrieval: Based on the projected point’s position, retrieve the speed and course limits () from the safety handling behavior boundaries generated by the model.Minimum Distance Calculation: For each data point’s speed and course , the minimum distances and to the safety boundaries are calculated.Average Minimum Distance Calculation: Compute the average of the minimum distances across all data points, which yields SBCE and CBCE:where N is the total number of data points. A smaller SBCE and CBCE value indicates a higher consistency between the safety handling behavior boundaries generated by the model and historical data.
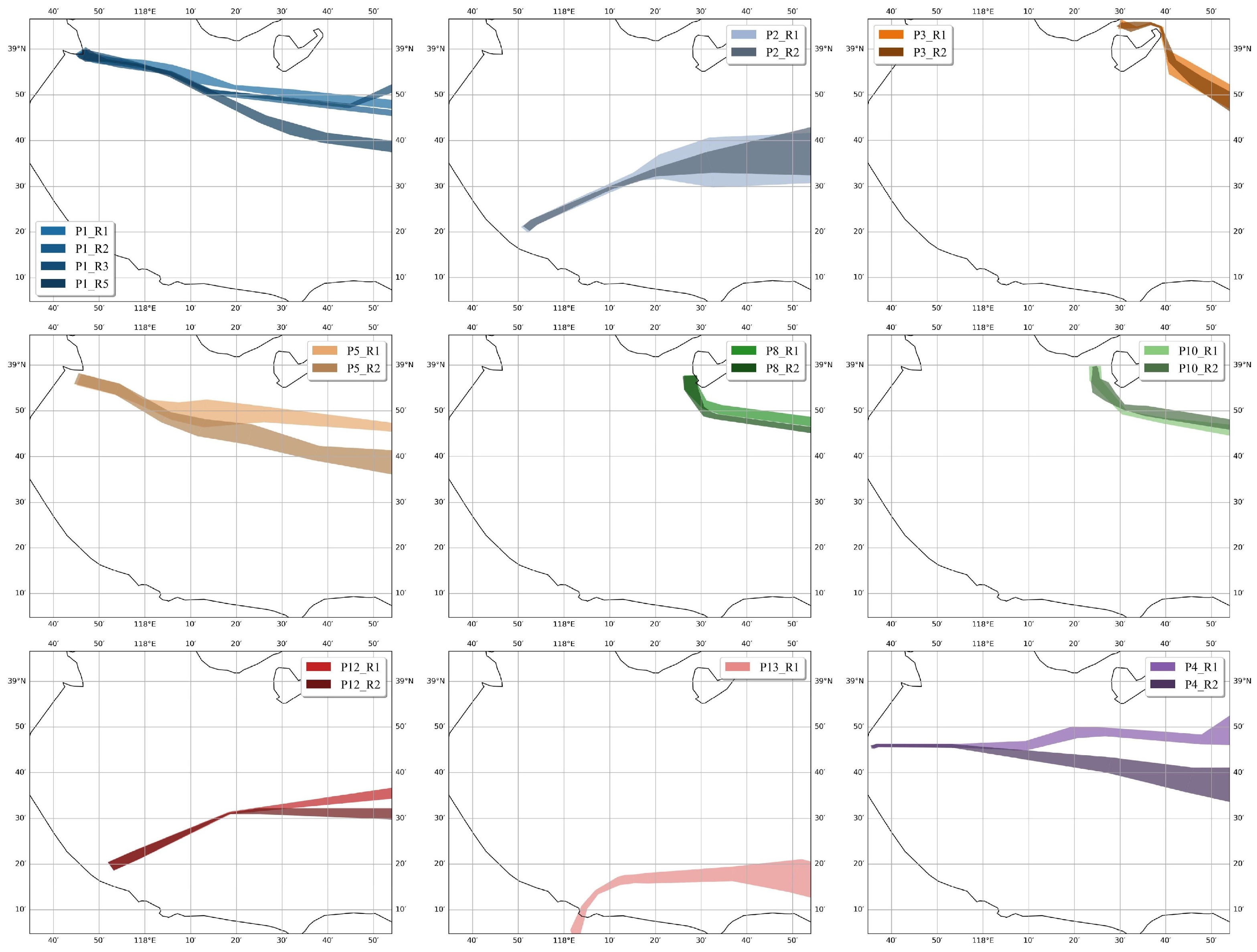
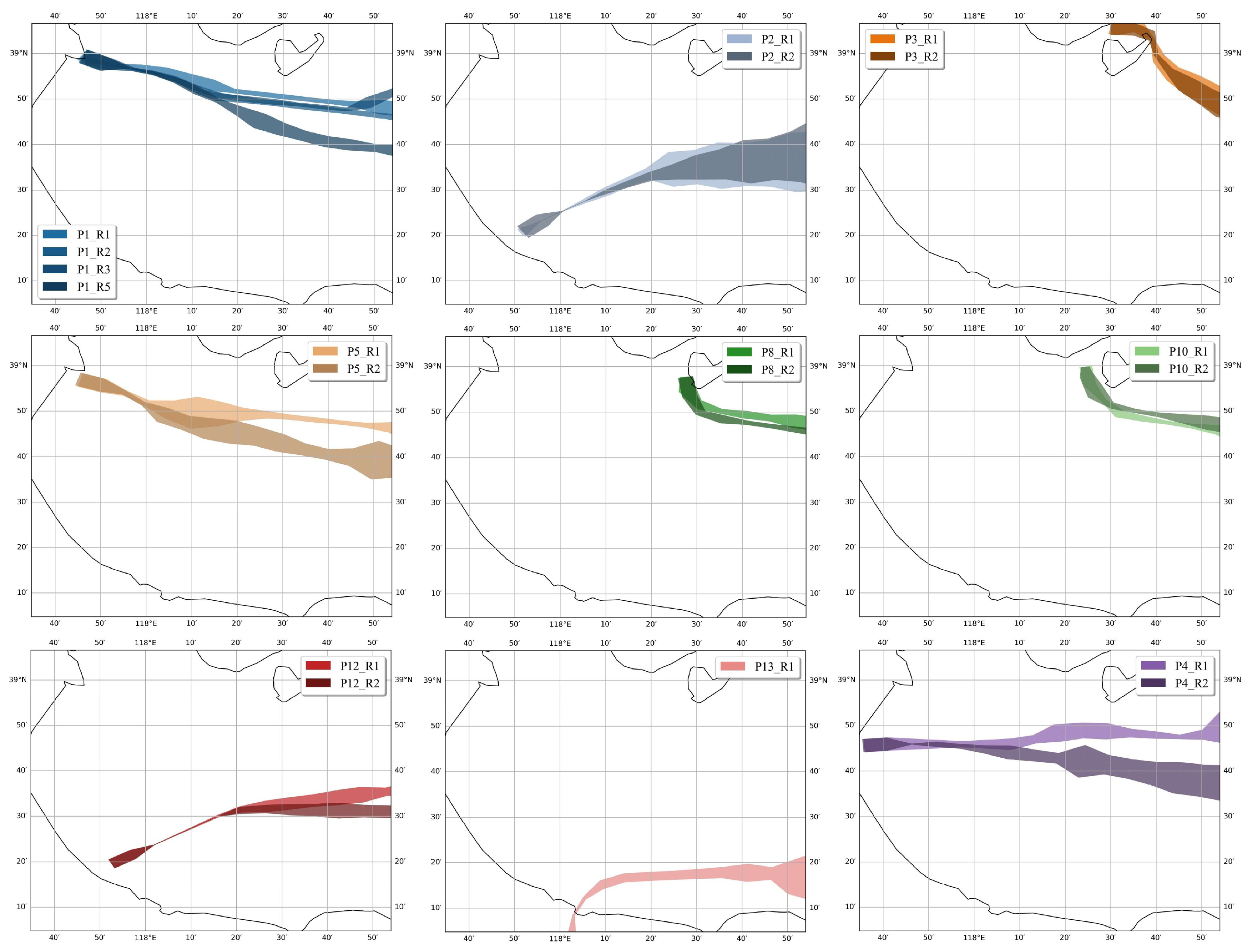
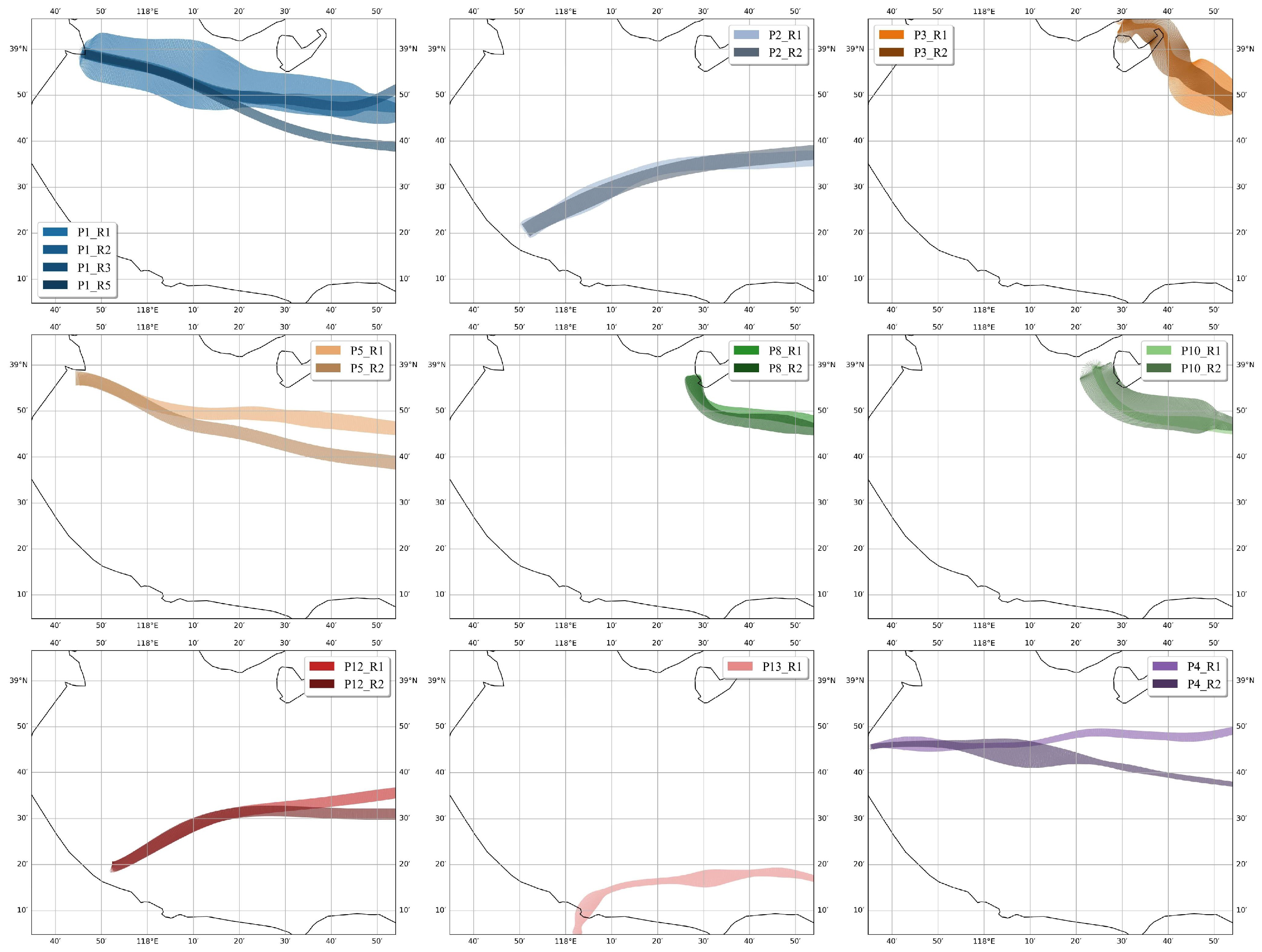
5.2. Maritime Route Network Construction Results
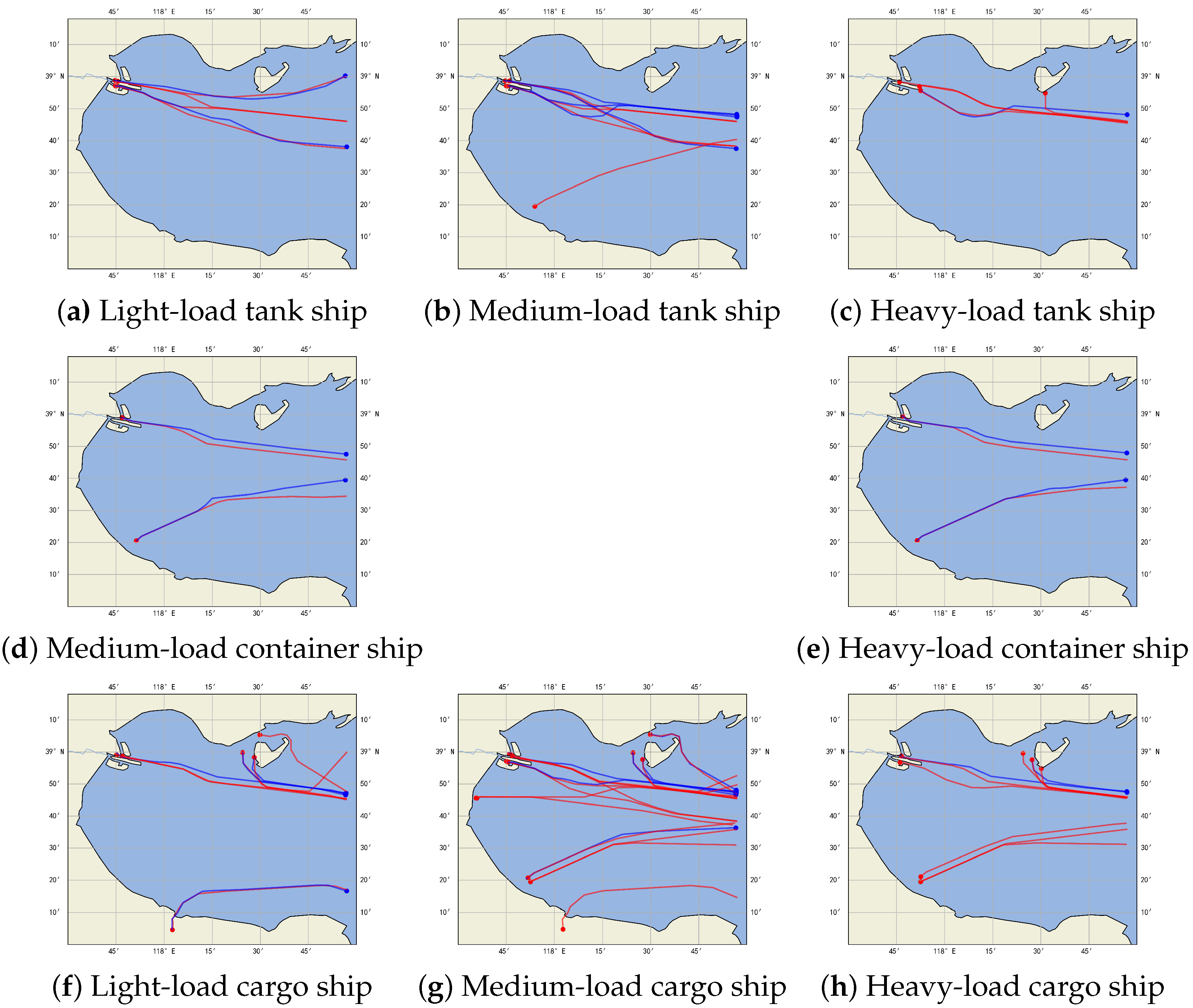
5.3. Maritime Traffic Pattern Characterization Results
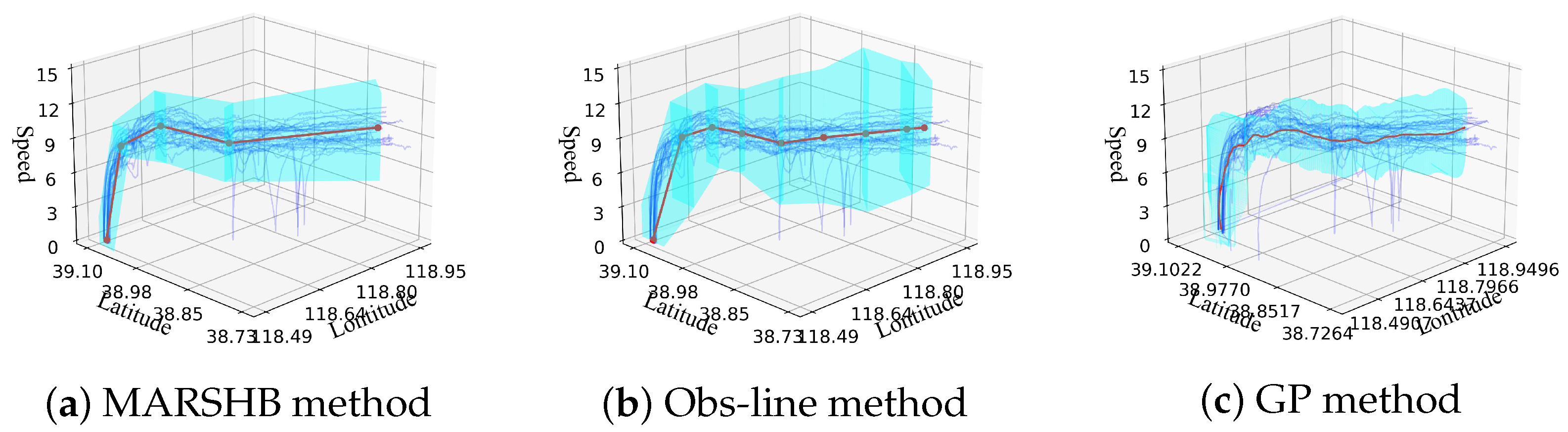
5.4. Route Safety Boundary Construction Results
6. Discussion
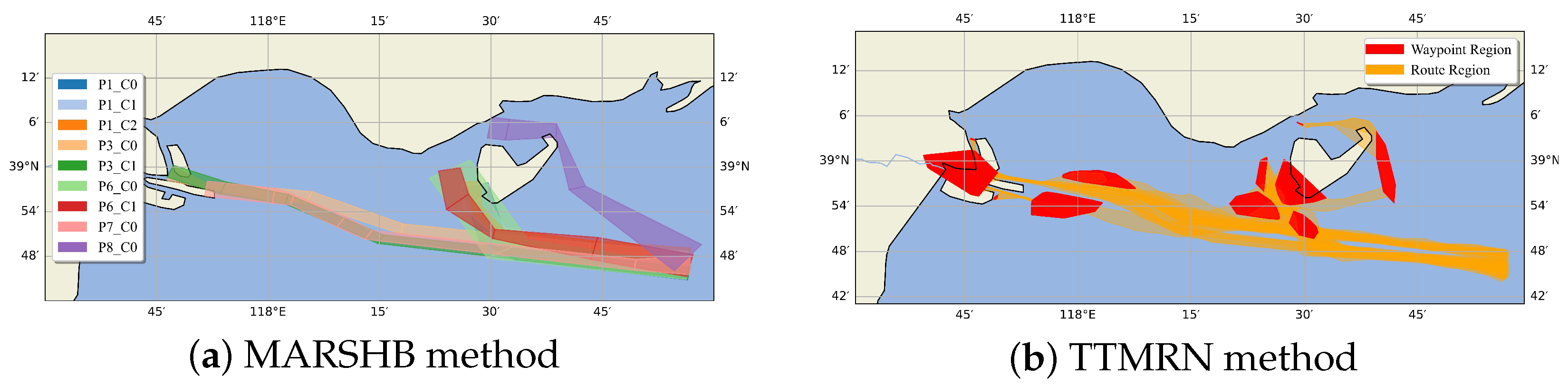
6.1. Accuracy of the Model in Capturing Spatial Distribution of Port Route
6.2. Accuracy of the Model in Representing Dynamic Characteristics
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Rong, H.; Teixeira, A.; Guedes Soares, C. A framework for ship abnormal behaviour detection and classification using AIS data. Reliab. Eng. Syst. Saf. 2024, 247, 110105. [Google Scholar] [CrossRef]
- Peng, P.; Claramunt, C.; Cheng, S.; Yang, Y.; Lu, F. A multi-layer modelling approach for mining versatile ports of a global maritime transportation network. Int. J. Digit. Earth 2023, 16, 2129–2151. [Google Scholar] [CrossRef]
- Liu, X.; He, Y.; Zhang, K.; Mou, J.; Zhang, K.; Zhao, X. Research on the decision-making method for autonomous navigation for the ocean-going ship in the ships’ routeing waters. Ocean Eng. 2025, 323, 120641. [Google Scholar] [CrossRef]
- Chen, D.; Zhu, M.; Yang, H.; Wang, X.; Wang, Y. Data-driven traffic simulation: A comprehensive review. IEEE Trans. Intell. Veh. 2024, 9, 4730–4748. [Google Scholar] [CrossRef]
- Zhang, M.; Zhang, D.; Fu, S.; Kujala, P.; Hirdaris, S. A predictive analytics method for maritime traffic flow complexity estimation in inland waterways. Reliab. Eng. Syst. Saf. 2022, 220, 108317. [Google Scholar] [CrossRef]
- Liu, L.; Shibasaki, R.; Zhang, Y.; Kosuge, N.; Zhang, M.; Hu, Y. Data-driven framework for extracting global maritime shipping networks by machine learning. Ocean Eng. 2023, 269, 113494. [Google Scholar] [CrossRef]
- Ribeiro, C.V.; Paes, A.; de Oliveira, D. AIS-based maritime anomaly traffic detection: A review. Expert Syst. Appl. 2023, 231, 120561. [Google Scholar] [CrossRef]
- Liu, D.; Rong, H.; Soares, C.G. Shipping route modelling of AIS maritime traffic data at the approach to ports. Ocean Eng. 2023, 289, 115868. [Google Scholar] [CrossRef]
- Rong, H.; Teixeira, A.; Guedes Soares, C. Ship trajectory uncertainty prediction based on a Gaussian Process model. Ocean Eng. 2019, 182, 499–511. [Google Scholar] [CrossRef]
- Rong, H.; Teixeira, A.; Guedes Soares, C. Maritime traffic probabilistic prediction based on ship motion pattern extraction. Reliab. Eng. Syst. Saf. 2022, 217, 108061. [Google Scholar] [CrossRef]
- Yan, Z.; Xiao, Y.; Cheng, L.; He, R.; Ruan, X.; Zhou, X.; Li, M.; Bin, R. Exploring AIS data for intelligent maritime routes extraction. Appl. Ocean Res. 2020, 101, 102271. [Google Scholar] [CrossRef]
- Cao, Y.; Liang, S.; Sun, L.; Liu, J.; Cheng, X.; Wang, D.; Chen, Y.; Yu, M.; Feng, K. Trans-Arctic shipping routes expanding faster than the model projections. Glob. Environ. Change 2022, 73, 102488. [Google Scholar] [CrossRef]
- Han, D.; Cheng, X.; Chen, H.; Xiao, C.; Wen, Y.; Sui, Z. Simulation Modeling for Ships Entering and Leaving Port in Qiongzhou Strait Waters: A Multi-Agent Information Interaction Method. J. Mar. Sci. Eng. 2024, 12, 1560. [Google Scholar] [CrossRef]
- Yan, Z.; Yang, G.; He, R.; Shi, K.; Yang, H. Reconstructing trajectories and extracting shipping routes between ports based on AIS data. Appl. Ocean Res. 2025, 161, 104709. [Google Scholar] [CrossRef]
- Chen, X.; Wu, P.; Zhang, Y.; Wang, X.; Xian, J.; Zhang, H. Smart Maritime Transportation-Oriented Ship-Speed Prediction Modeling Using Generative Adversarial Networks and Long Short-Term Memory. J. Mar. Sci. Eng. 2025, 13, 1045. [Google Scholar] [CrossRef]
- Xiao, Z.; Fu, X.; Zhang, L.; Goh, R.S.M. Traffic pattern mining and forecasting technologies in maritime traffic service networks: A comprehensive survey. IEEE Trans. Intell. Transp. Syst. 2019, 21, 1796–1825. [Google Scholar] [CrossRef]
- Xiao, Z.; Zhang, X.; Fu, X.; Zhang, L.; Xu, H.; Liu, R.W.; Chong, C.S.; Qin, Z. Innovating Waterway Route Planning as a Service for Marine Traffic Applications. IEEE Trans. Intell. Veh. 2024. [Google Scholar] [CrossRef]
- Pallotta, G.; Vespe, M.; Bryan, K. Traffic route extraction and anomaly detection from AIS data. In Proceedings of the International COST MOVE Workshop on Moving Objects at Sea, Brest, France, 27–28 June 2013; pp. 1–4. [Google Scholar]
- Zhou, C.; Xiang, J.; Huang, H.; Yan, Y.; Huang, L.; Wen, Y.; Xiao, C. TTMRN: A topological-geometric two-layer maritime route network modeling for ship intelligent navigation. Ocean Eng. 2023, 287, 115884. [Google Scholar] [CrossRef]
- Potočnik, P. Model Predictive Control for Autonomous Ship Navigation with COLREG Compliance and Chart-Based Path Planning. J. Mar. Sci. Eng. 2025, 13, 1246. [Google Scholar] [CrossRef]
- Liu, R.W.; Zhou, S.; Liang, M.; Gao, R.; Wang, H. From ports to routes: Extracting multi-scale shipping networks using massive AIS data. Ocean Eng. 2024, 311, 118969. [Google Scholar] [CrossRef]
- Xing, B.; Zhang, L.; Liu, Z.; Sheng, H.; Bi, F.; Xu, J. The study of fishing vessel behavior identification based on ais data: A case study of the east china sea. J. Mar. Sci. Eng. 2023, 11, 1093. [Google Scholar] [CrossRef]
- Kim, H.C.; Son, W.J.; Lee, J.S.; Cho, I.S. Identification of maritime areas with high vessel traffic based on polygon shape similarity. IEEE Access 2024, 12, 92253–92267. [Google Scholar] [CrossRef]
- Li, P.; Hu, Q. A grid-based method for unsupervised speed pattern recognition using AIS data. Ocean Eng. 2025, 328, 121050. [Google Scholar] [CrossRef]
- Zhang, L.; Chen, P.; Li, M.; Chen, L.; Mou, J. A data-driven approach for ship-bridge collision candidate detection in bridge waterway. Ocean Eng. 2022, 266, 113137. [Google Scholar] [CrossRef]
- Liang, M.; Liu, K.; Gao, R.; Li, Y. Integrating GPU-accelerated for fast large-scale vessel trajectories visualization in maritime IoT systems. IEEE Trans. Intell. Transp. Syst. 2025, 26, 4048–4065. [Google Scholar] [CrossRef]
- Kyaw, P.T.; Paing, A.; Thu, T.T.; Mohan, R.E.; Le, A.V.; Veerajagadheswar, P. Coverage path planning for decomposition reconfigurable grid-maps using deep reinforcement learning based travelling salesman problem. IEEE Access 2020, 8, 225945–225956. [Google Scholar] [CrossRef]
- Liu, Z.; Gao, H.; Zhang, M.; Yan, R.; Liu, J. A data mining method to extract traffic network for maritime transport management. Ocean Coast. Manag. 2023, 239, 106622. [Google Scholar] [CrossRef]
- Tang, C.; Chen, M.; Zhao, J.; Liu, T.; Liu, K.; Yan, H.; Xiao, Y. A novel ship trajectory clustering method for Finding Overall and Local Features of Ship Trajectories. Ocean Eng. 2021, 241, 110108. [Google Scholar] [CrossRef]
- Farahnakian, F.; Nicolas, F.; Farahnakian, F.; Nevalainen, P.; Sheikh, J.; Heikkonen, J.; Raduly-Baka, C. A comprehensive study of clustering-based techniques for detecting abnormal vessel behavior. Remote Sens. 2023, 15, 1477. [Google Scholar] [CrossRef]
- Zhang, R.; Wu, H.; Yin, Z.; Xiao, Z.; Cheng, Q.; Liu, K. Predictive clustering of vessel behavior based on hierarchical trajectory representation. IEEE Trans. Intell. Transp. Syst. 2024, 25, 19496–19506. [Google Scholar] [CrossRef]
- Liu, Z.; Yang, H.; Xiong, C.; Xu, F.; Gan, L.; Yan, T.; Shu, Y. Research on the optimization of ship trajectory clustering based on the OD–Hausdorff distance. J. Mar. Sci. Eng. 2024, 12, 1398. [Google Scholar] [CrossRef]
- Lee, B.; Silveira, P.; Loureiro, H.; Teixeira, A. A framework for characterizing the marine traffic of the continental coast of Portugal using historical AIS data. In Trends in Maritime Technology and Engineering; CRC Press: Boca Raton, FL, USA, 2022; pp. 113–120. [Google Scholar]
- Yin, Z.C.; Wei, J.J.; Ying, S.; Jia, P.N. Time-awareness in kernel density estimation for movement data. Int. J. Geogr. Inf. Sci. 2025, 1–18. [Google Scholar] [CrossRef]
- Zhang, X.; Zhou, S.; Jiang, Z.; Chu, X.; Yu, C. A novel ship trajectory clustering model integrated with spatiotemporal attributes. Ocean Eng. 2025, 336, 121774. [Google Scholar] [CrossRef]
- Yang, J.; Zhao, S.; Wang, M.; Sun, Y.; Wu, C. A noval method for constructing a hierarchical maritime topological route network based on the spatiotemporal features of vessel trajectories. Ocean Eng. 2025, 340, 122383. [Google Scholar] [CrossRef]
- Zhang, F.; Wen, Y.; Banda, O.V.; Chen, M.; Du, L. Maritime traffic network extraction and vessel flow prediction in complex inland port clusters. Ocean Eng. 2025, 341, 122791. [Google Scholar] [CrossRef]
- Gao, Y.; Fang, Z.; Xu, J.; Gong, S.; Shen, C.; Chen, L. An efficient and distributed framework for real-time trajectory stream clustering. IEEE Trans. Knowl. Data Eng. 2023, 36, 1857–1873. [Google Scholar] [CrossRef]
- Eljabu, L.; Etemad, M.; Matwin, S. Spatial clustering method of historical ais data for maritime traffic routes extraction. In Proceedings of the 2022 IEEE International Conference on Big Data (Big Data), Osaka, Japan, 17–22 December 2022; pp. 893–902. [Google Scholar]
- Huang, I.L.; Lee, M.C.; Chang, L.; Huang, J.C. Development and Application of an Advanced Automatic Identification System (AIS)-Based Ship Trajectory Extraction Framework for Maritime Traffic Analysis. J. Mar. Sci. Eng. 2024, 12, 1672. [Google Scholar] [CrossRef]
- Wani, A.A. Comprehensive analysis of clustering algorithms: Exploring limitations and innovative solutions. PeerJ Comput. Sci. 2024, 10, e2286. [Google Scholar] [CrossRef]
- Li, H.; Yang, Z. Incorporation of AIS data-based machine learning into unsupervised route planning for maritime autonomous surface ships. Transp. Res. Part E Logist. Transp. Rev. 2023, 176, 103171. [Google Scholar] [CrossRef]
- Cheng, X.; Wen, Y.; Sui, Z.; Huang, L.; Lin, H. Multi-granularity spatiotemporal object modelling of waterborne traffic elements. Comput. Ind. 2025, 164, 104185. [Google Scholar] [CrossRef]
- Dong, X.C.; Wang, G.X. Coal logistics competency strategies for ports in the Tianjin and Hebei regions around the Bohai Bay in China. Energy Procedia 2012, 17, 436–443. [Google Scholar] [CrossRef]
- Wang, G.W.; Zeng, Q.; Li, K.; Yang, J. Port connectivity in a logistic network: The case of Bohai Bay, China. Transp. Res. Part E Logist. Transp. Rev. 2016, 95, 341–354. [Google Scholar] [CrossRef]
- Ou, J.; Wang, S.; Liu, J.; Zhu, Y.; Li, H.; Zhao, W.; Deng, C. Multi-stage trajectory compression via speed information for preserving maritime traffic information integrity. Ocean Eng. 2025, 330, 121073. [Google Scholar] [CrossRef]
- Xia, Z.; Wang, W.; Guo, Z.; Peng, Y.; Xu, X. Navigation mode extraction and trajectory repair of complex waters in multi-harbor port: An optimal semi-supervised clustering method. Ocean Eng. 2024, 313, 119439. [Google Scholar] [CrossRef]
- Yan, Z.; Cheng, L.; He, R.; Yang, H. Extracting ship stopping information from AIS data. Ocean Eng. 2022, 250, 111004. [Google Scholar] [CrossRef]
- Alderton, P.M.; Saieva, G. Port Management and Operations; Taylor & Francis: Abingdon, UK, 2013. [Google Scholar]
- Xia, Z.; Tian, Q.; Feng, T.; Guo, Z.; Peng, Y.; Jiang, Y.; Wang, W. Integration management of vessel transportation in complex waterway network of port clusters: A column generation-based solution approach. Expert Syst. Appl. 2025, 268, 126242. [Google Scholar] [CrossRef]
- Bai, X.; Xie, Z.; Xu, X.; Xiao, Y. An adaptive threshold fast DBSCAN algorithm with preserved trajectory feature points for vessel trajectory clustering. Ocean Eng. 2023, 280, 114930. [Google Scholar] [CrossRef]
- Barber, C.B.; Dobkin, D.P.; Huhdanpaa, H. The quickhull algorithm for convex hulls. ACM Trans. Math. Softw. (TOMS) 1996, 22, 469–483. [Google Scholar] [CrossRef]
- Douglas, D.H.; Peucker, T.K. Algorithms for the reduction of the number of points required to represent a digitized line or its caricature. Cartogr. Int. J. Geogr. Inf. Geovisualization 1973, 10, 112–122. [Google Scholar] [CrossRef]
- Zhang, S.k.; Liu, Z.j.; Cai, Y.; Wu, Z.l.; Shi, G.y. AIS trajectories simplification and threshold determination. J. Navig. 2016, 69, 729–744. [Google Scholar] [CrossRef]
- Ester, M.; Kriegel, H.; Sander, J.; Xu, X. A density-based algorithm for discovering clusters in large spatial databases with noise. In Proceedings of the Second International Conference on Knowledge Discovery and Data Mining, Portland, OR, USA, 2–4 August 1996; Volume 96, pp. 226–231. [Google Scholar]
- Yang, J.; Liu, Y.; Ma, L.; Ji, C. Maritime traffic flow clustering analysis by density based trajectory clustering with noise. Ocean Eng. 2022, 249, 111001. [Google Scholar] [CrossRef]
- Zissis, D.; Chatzikokolakis, K.; Spiliopoulos, G.; Vodas, M. A distributed spatial method for modeling maritime routes. IEEE Access 2020, 8, 47556–47568. [Google Scholar] [CrossRef]
- Sheng, K.; Liu, Z.; Zhou, D.; He, A.; Feng, C. Research on ship classification based on trajectory features. J. Navig. 2018, 71, 100–116. [Google Scholar] [CrossRef]
- Zhang, X.; Guo, W.; Yang, Z.; Wang, J.; Wang, C. Optimization of integrated accurate ride-tide planning and vessel scheduling in multi-functional ports with long channels. Expert Syst. Appl. 2025, 273, 126894. [Google Scholar] [CrossRef]
- Liu, L.; Zhang, Y.; Hu, Y.; Wang, Y.; Sun, J.; Dong, X. A hybrid-clustering model of ship trajectories for maritime traffic patterns analysis in port area. J. Mar. Sci. Eng. 2022, 10, 342. [Google Scholar] [CrossRef]
- Rong, H.; Teixeira, A.; Soares, C.G. Evaluation of near-collisions in the Tagus River Estuary using a marine traffic simulation model. Zesz. Nauk. Akad. Morskiej Szczecinie 2015, 43, 68–78. [Google Scholar]



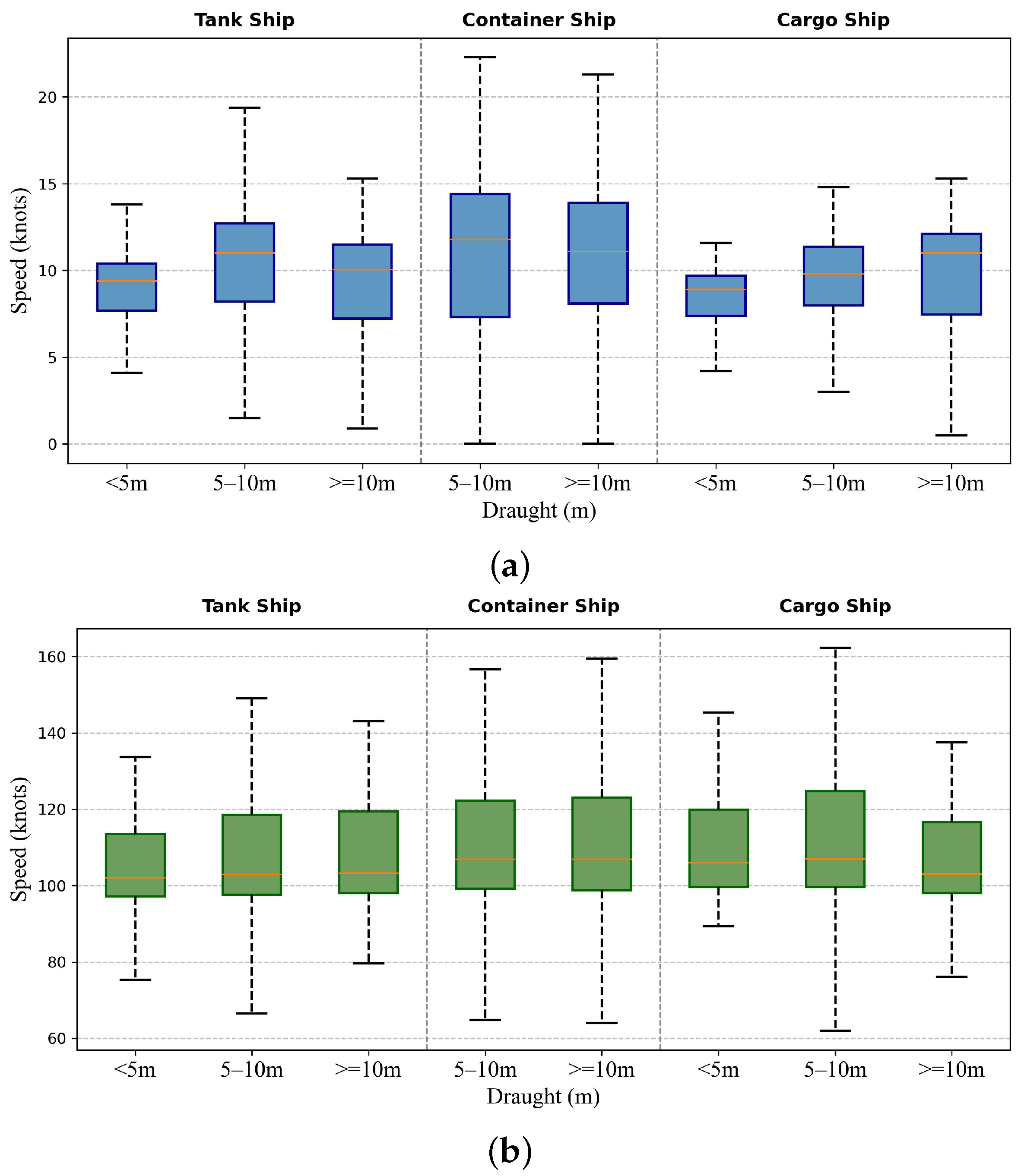
| Ship Type | Light Load | Medium Load | Heavy Load | Total |
|---|---|---|---|---|
| Tank | 751 | 757 | 203 | 1711 |
| Container | 8 | 978 | 949 | 1935 |
| Cargo | 3208 | 6209 | 2073 | 11,490 |
| Port | Longitude | Latitude | Anchor Points | Max Radius |
|---|---|---|---|---|
| Port1 | 117.76 | 38.99 | 223,800 | 7.26 |
| Port2 | 117.86 | 38.35 | 31,664 | 5.13 |
| Port3 | 118.50 | 39.09 | 6026 | 1.41 |
| Port4 | 117.60 | 38.76 | 6934 | 1.31 |
| Port5 | 117.76 | 38.95 | 50,206 | 4.30 |
| Port6 | 117.87 | 38.93 | 4549 | 1.44 |
| Port7 | 117.87 | 38.95 | 1698 | 0.86 |
| Port8 | 118.47 | 38.96 | 163,102 | 5.36 |
| Port9 | 118.50 | 38.91 | 18,784 | 2.99 |
| Port10 | 118.41 | 39.00 | 16,185 | 1.59 |
| Port11 | 118.57 | 39.10 | 502 | 0.23 |
| Port12 | 117.88 | 38.32 | 55,079 | 2.06 |
| Port13 | 118.04 | 38.08 | 8945 | 3.02 |
| Method | Spatial Capture Capability | Pattern Capture Capability | Applicable Scenarios |
|---|---|---|---|
| TTMRN | Medium (accurate near-port turning and berthing) | Medium (Clear local behavior, weak cross-waterway diversion) | Long-distance clearly pattern |
| KDE | High (accurate in dense main channels) | Low (secondary channels hard to identify) | High-density areas |
| MARSHB | High (covers main and branch channels) | High (captures diversion and multi-mode behavior) | Complex port multiple path |
| Method | CRC (%) | SRC (%) | SBCE (knot) | CBCE (°) |
|---|---|---|---|---|
| MARSHB | 65.0 | 77.8 | 1.3 | 43.4 |
| GP Method | 54.0 | 74.0 | 2.0 | 74.8 |
| Obs Method | 41.4 | 70.8 | 1.7 | 62.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ou, J.; Wang, S.; Liu, J.; Li, H.; Zhao, W.; Jiang, C. Multidimensional Maritime Route Modeling Method for Complex Port Waters Considering Ship Handling Behavior Diversity. J. Mar. Sci. Eng. 2025, 13, 1963. https://doi.org/10.3390/jmse13101963
Ou J, Wang S, Liu J, Li H, Zhao W, Jiang C. Multidimensional Maritime Route Modeling Method for Complex Port Waters Considering Ship Handling Behavior Diversity. Journal of Marine Science and Engineering. 2025; 13(10):1963. https://doi.org/10.3390/jmse13101963
Chicago/Turabian StyleOu, Junmei, Shuangxin Wang, Jingyi Liu, Hongrui Li, Wenyu Zhao, and Chenglong Jiang. 2025. "Multidimensional Maritime Route Modeling Method for Complex Port Waters Considering Ship Handling Behavior Diversity" Journal of Marine Science and Engineering 13, no. 10: 1963. https://doi.org/10.3390/jmse13101963
APA StyleOu, J., Wang, S., Liu, J., Li, H., Zhao, W., & Jiang, C. (2025). Multidimensional Maritime Route Modeling Method for Complex Port Waters Considering Ship Handling Behavior Diversity. Journal of Marine Science and Engineering, 13(10), 1963. https://doi.org/10.3390/jmse13101963






