Real-Time Digital Twin for Structural Health Monitoring of Floating Offshore Wind Turbines
Abstract
1. Introduction
2. Literature Review
2.1. Background and Motivation
2.2. Recent Advances
2.3. Research Gap and Proposed Solution
- IoT Infrastructure: A scalable platform streaming sensor data from both environmental and turbine systems, handling high-frequency measurements with quality assurance and anomaly detection.
- Physics-Based ROM: A reduced-order aero-servo-hydro-elastic model derived from a tightly coupled, time-domain finite-element solver, retaining primary structural modes while providing modal response-amplitude operators (MRAOs). These transfer functions, based on the methodology of Servan-Camas & García-Espinosa (2023, 2025), efficiently map hydrodynamic, aerodynamic, control, and mooring loads to generalized modal coordinates [18,19].
- Real-Time Engine: A Python-based processor computing critical responses— displacements, stresses, and fatigue indicators—with update rates suitable for operational decision support.
2.4. Paper Organization
3. Methodology
3.1. Seakeeping Governing Equations
- Free Surface (): On the free surface with elevation , two conditions hold:
- A kinematic condition ensuring that the free surface moves with the fluid:
- A dynamic condition (from Bernoulli’s equation) that balances the pressure:where g is gravitational acceleration and is the free surface pressure.
- Body Surface (): On the wetted surface of the structure, a no-penetration condition is imposed:where is the fluid velocity, is the body velocity, and n is the unit normal.
- Seabed (): At the rigid seabed, the no-penetration condition is as follows:
3.2. Fluid–Structure Governing Equations
- Surface tractions on : external pressures from waves or wind are applied as traction loads, , over the wetted hull and the exposed tower walls,
- Point loads at the hub: the linearized aerodynamic model supplies a resultant force and moment acting at the end of a rigid bar that represents the rotor axis; these are assembled directly into the global load vector,
- Mooring-line reactions: linearized mooring forces (Equation (17)) act at the fairlead attachment points.
- Pressure (stress) continuity: The fluid pressure and structural stress must satisfy the following:where is the normal from the solid (with from the fluid).
- Kinematic (no-penetration) continuity: The structural normal velocity equals the fluid particle velocity:
3.3. Aerodynamic and Mooring Linear Models
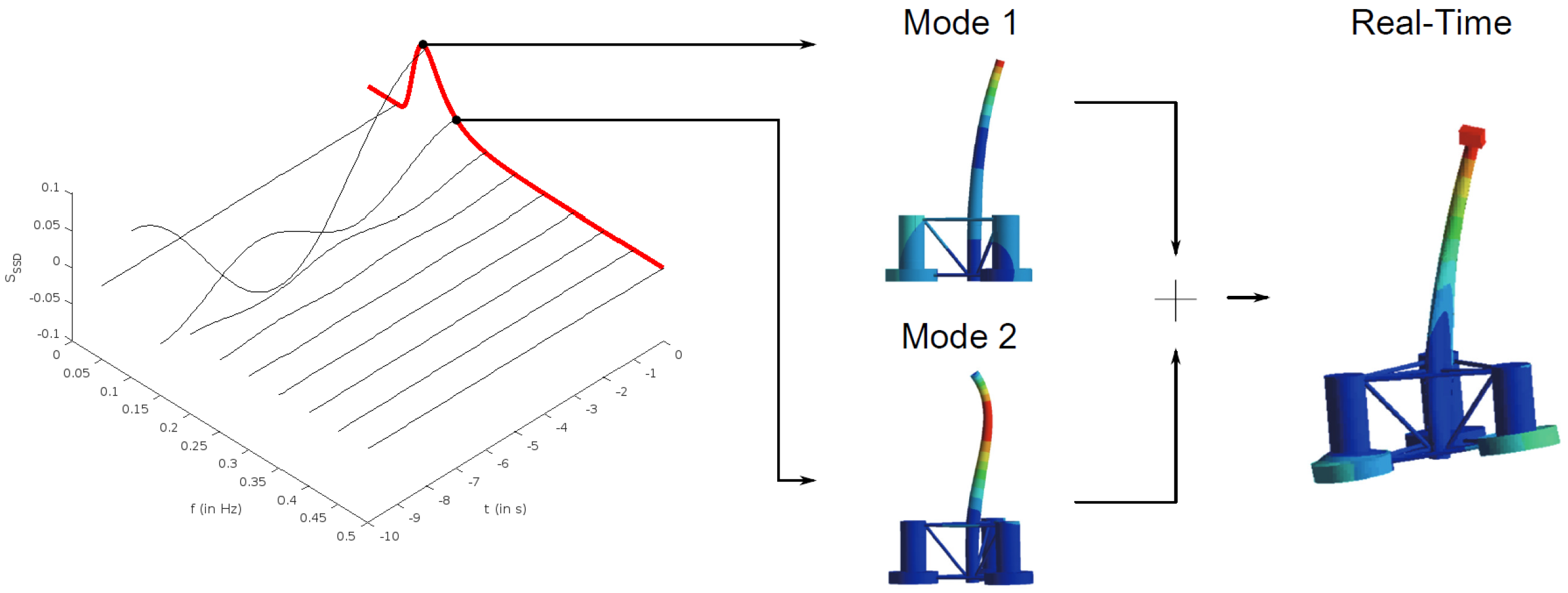
3.4. Real-Time Structural Solvers in SHM Digital Twins
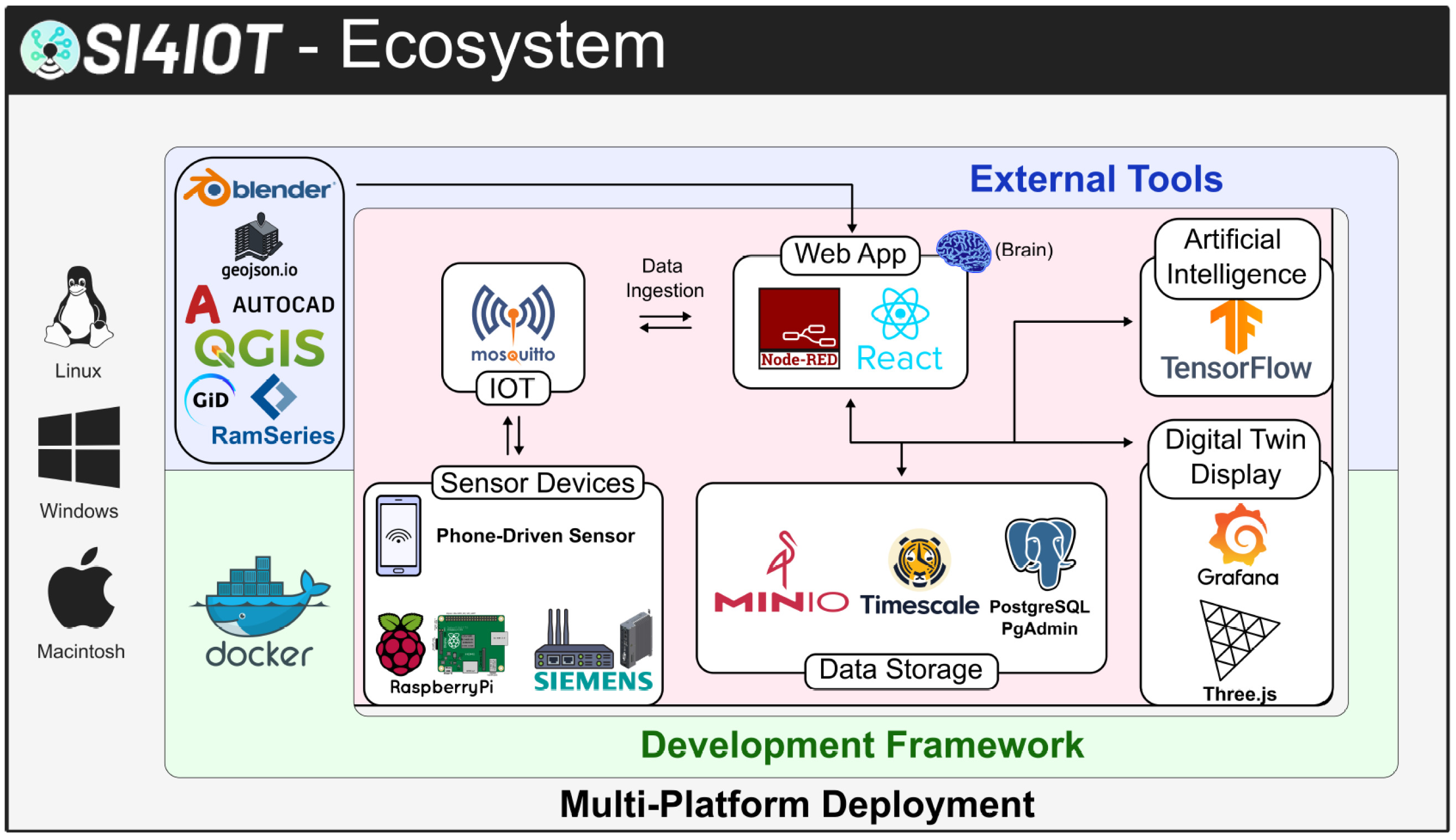
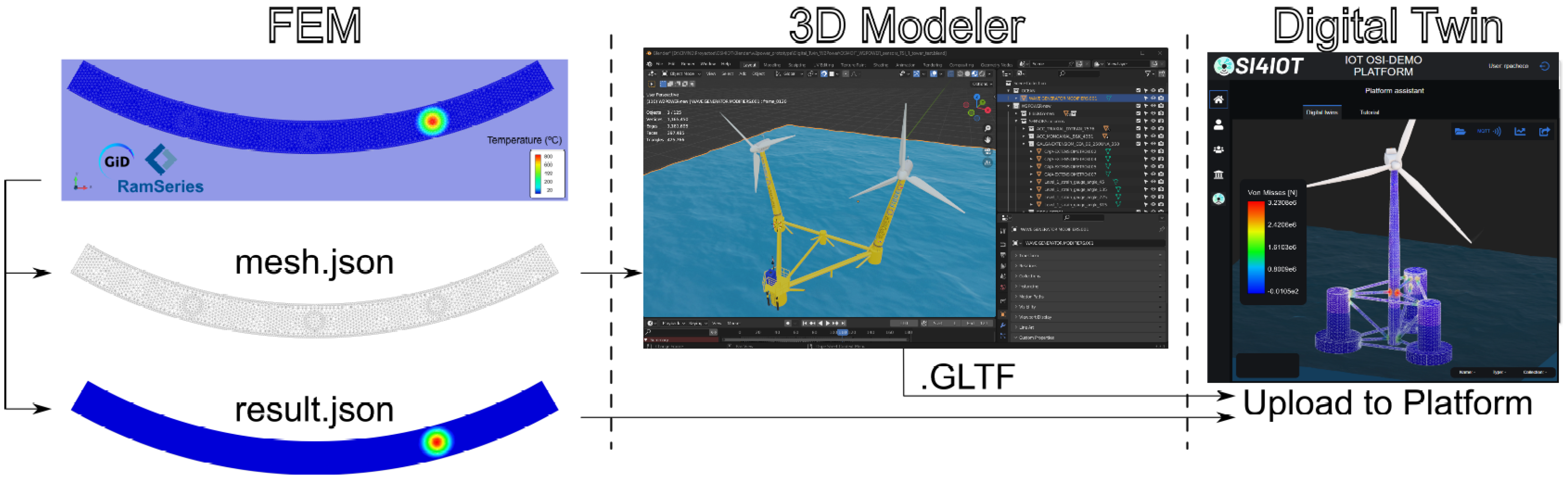
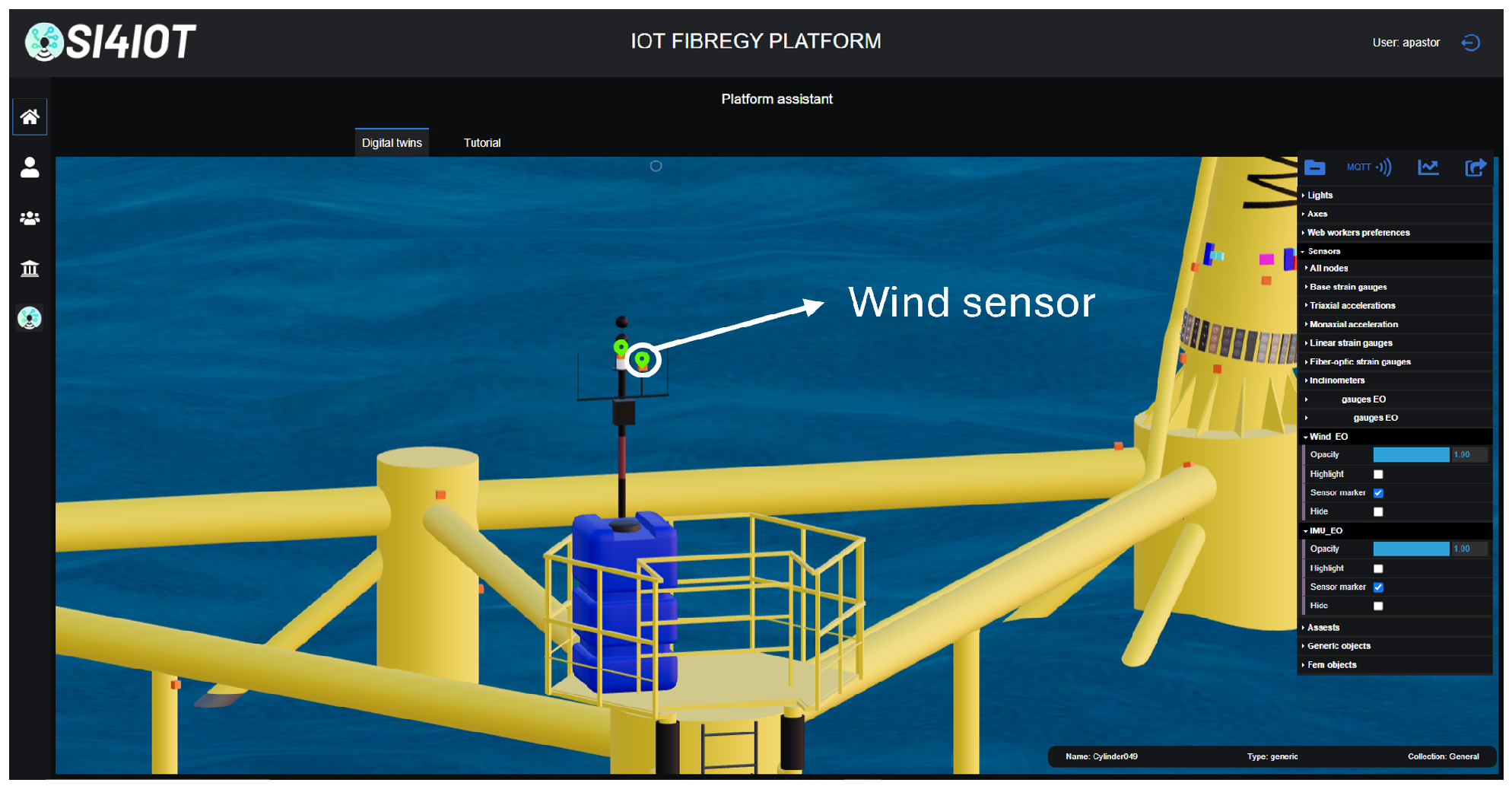
4. Digital Twin for Structural Health Monitoring
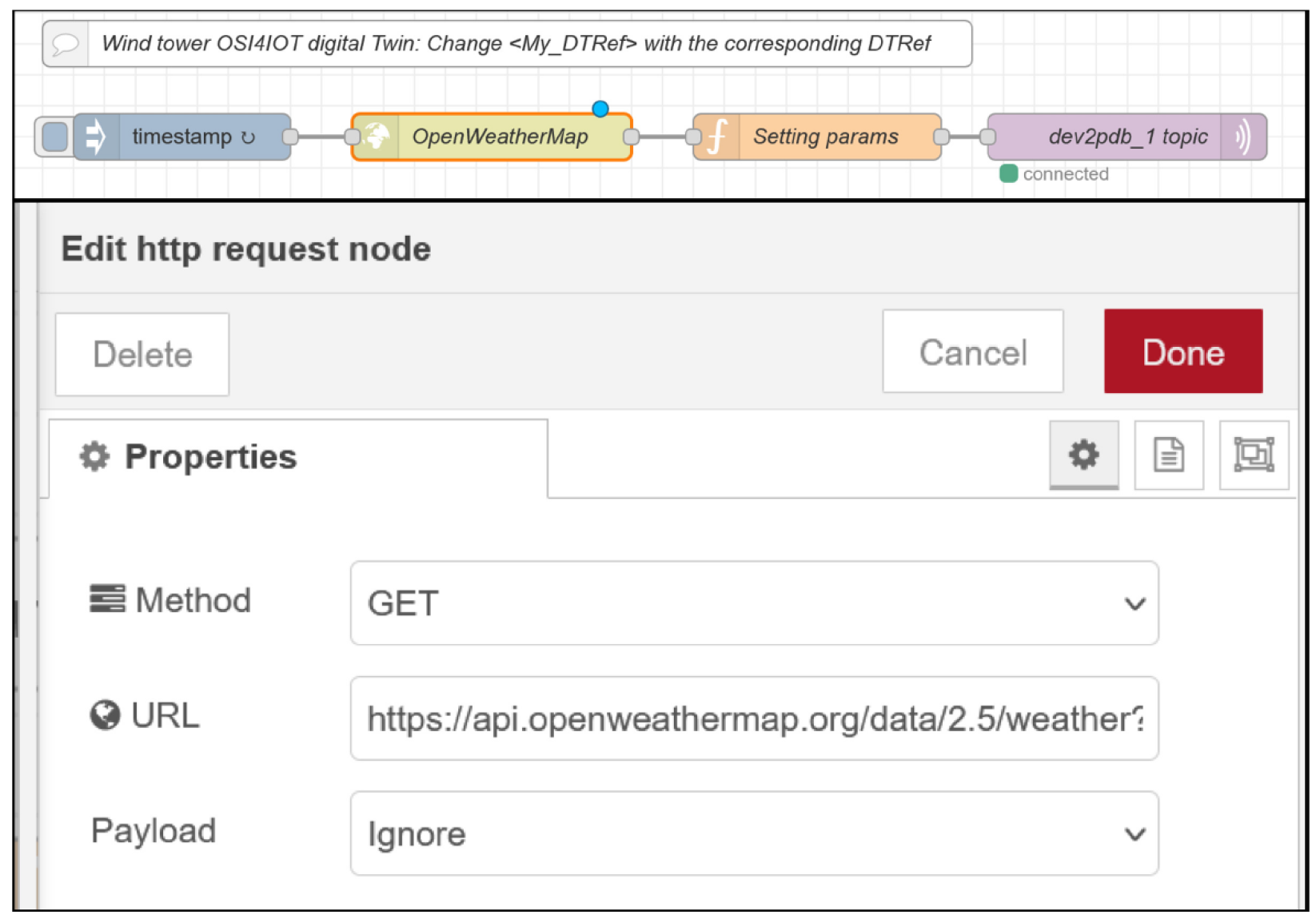
- Data ingestion: Sensors publish via MQTT (Mosquitto); forecasts fetched via OPeNDAP/HTTP on schedule.
- Quality control: Node-RED flows perform gap filling, outlier filtering, resampling, and unit tagging.
- Storage: Curated time series are written to TimescaleDB with asset/sensor metadata.
- Compute: The Python (version 3.12) DT service subscribes to metocean/operational topics, generates spectra, runs the MRAO-based ROM, and computes displacements, stresses, and fatigue.
- Publishing: Computed KPIs are written back to TimescaleDB (and optionally republished on MQTT).
- Visualization and alerts: Grafana dashboards and the web 3D viewer render signals; thresholds trigger alarms.
5. Case Study
- (1)
- Reference operating condition (RC)—used for the structural–response validation (displacements and stresses via ROM–FEM comparison). A hub–height mean wind speed is represented by an NPD spectrum (40 frequency components, 0.00027–2.8 Hz). The accompanying sea state is a unidirectional JONSWAP spectrum with significant height m and peak period s propagating from . Currents are neglected.
- (2)
- Fatigue environmental conditions (FEC)—used for the hot-spot analysis. An array of 1000 metocean scenarios is generated by combining: wind speed –25 m s−1 (5 discrete bins), significant wave height –8 m (4 bins), spectral peak period –20 s (5 bins), and wave incidence direction –330° (10 bins at 30° spacing). The Cartesian product of these bins () yields the 1000 distinct load cases employed to calculate fatigue damage at the selected hot-spot locations.
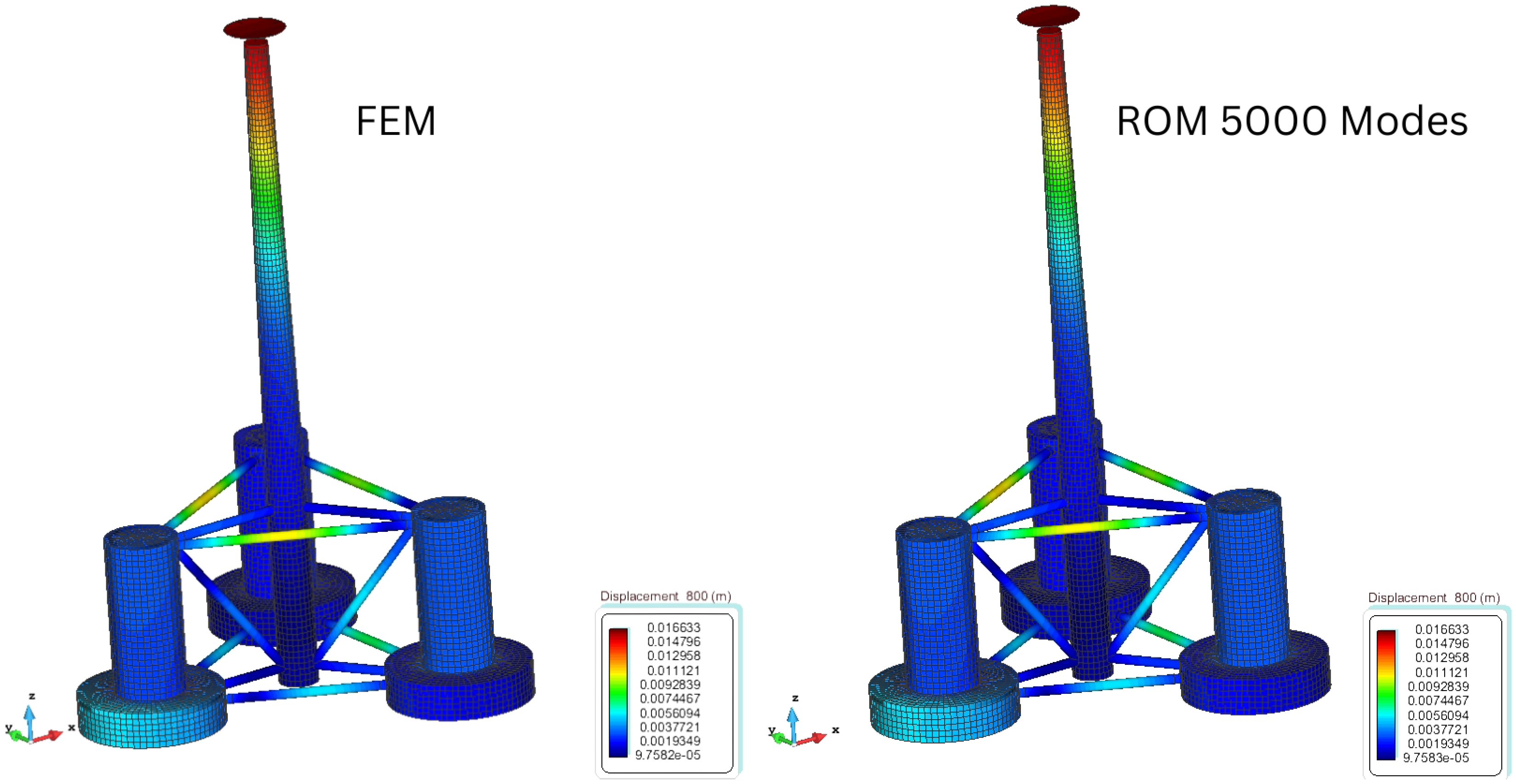
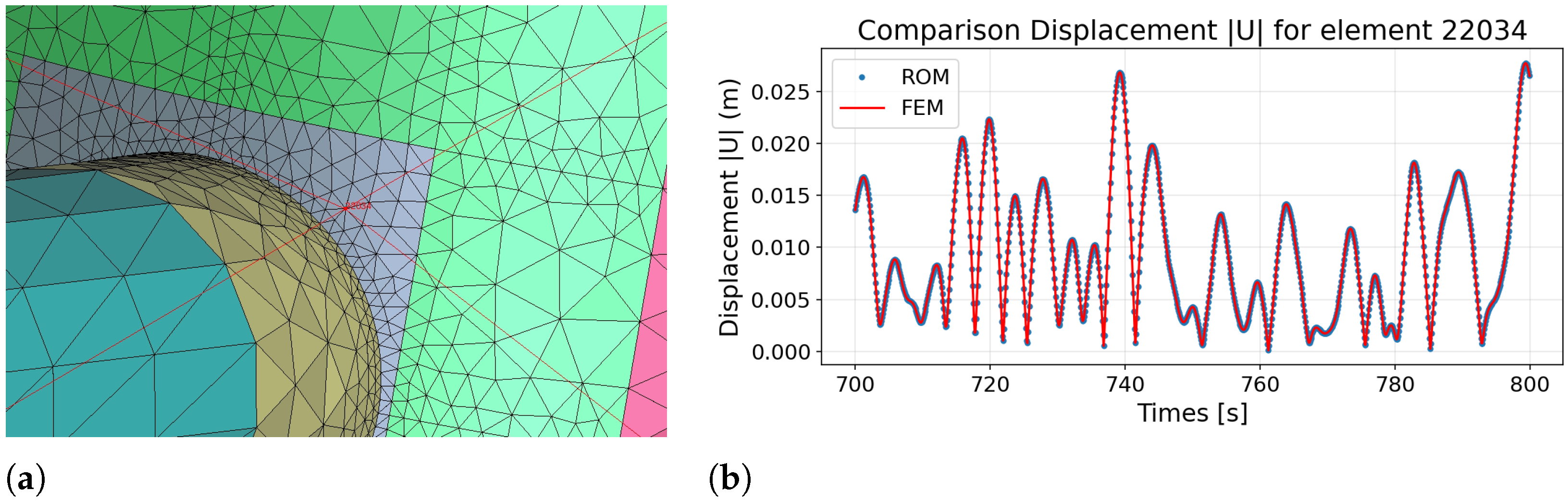
5.1. Structural Response
5.2. Stress
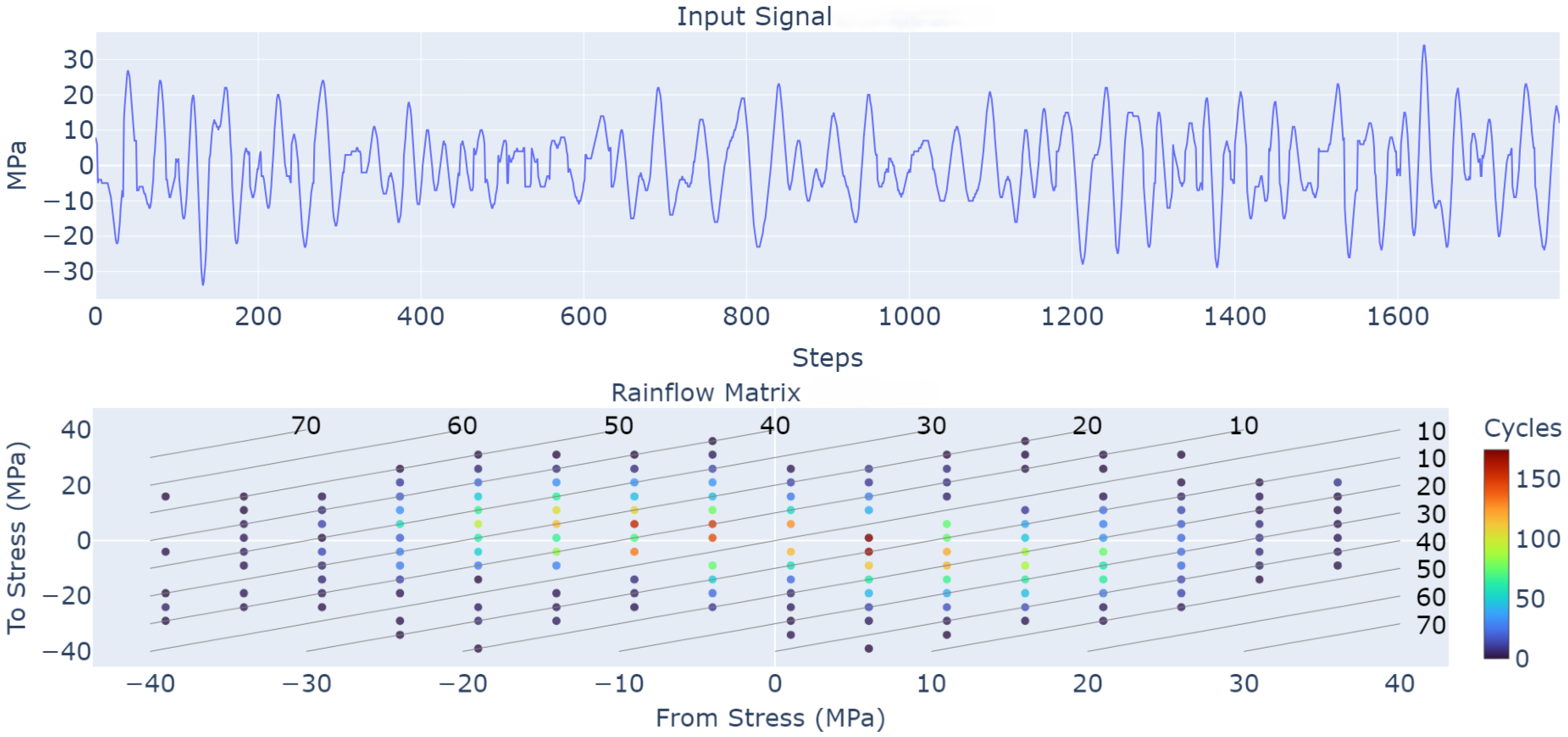
5.3. Fatigue
5.4. Real-Time Simulation Performance
5.4.1. Displacement Analysis
5.4.2. Stress Analysis
5.4.3. Fatigue Analysis
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Taze, I.E.; Hoda, M.A.; Míquelez, I.; Maddaloni, P.; Azam, S.E. A Review of Digital Twinning Applications for Floating Offshore Wind Turbines: Insights, Innovations, and Implementation. Energies 2025, 18, 3369. [Google Scholar] [CrossRef]
- León-Medina, J.X.; Tibaduiza, D.A.; Parés, N.; Pozo, F. Digital twin technology in wind turbine components: A review. Intell. Syst. Appl. 2025, 20, 200535. [Google Scholar] [CrossRef]
- Augustyn, D.; Ulriksen, M.D.; Sørensen, J.D. Reliability Updating of Offshore Wind Substructures by Use of Digital Twin Information. Energies 2021, 14, 5859. [Google Scholar] [CrossRef]
- Jorgensen, J.; Hodkiewicz, M.; Cripps, E.; Hassan, G.M. Requirements for the Application of the Digital Twin Paradigm to Offshore Wind Turbine Structures for Uncertain Fatigue Analysis. Comput. Ind. 2023, 145, 103806. [Google Scholar] [CrossRef]
- Yu, Q.; Xu, J. Fatigue reliability assessment of floating offshore wind turbines under correlated wind–wave–current loads. Ocean. Eng. 2024, 313, 119442. [Google Scholar] [CrossRef]
- Gaidai, O.; Yakimov, V.; Wang, F.; Zhang, F.; Balakrishna, R. Floating wind turbines structural details fatigue life assessment. Sci. Rep. 2023, 13, 19665. [Google Scholar] [CrossRef]
- Moghadam, F.K.; de S. Rebouças, G.F.; Nejad, A.R. Digital Twin Modeling for Predictive Maintenance of Gearboxes in Floating Offshore Wind Turbine Drivetrains. Forsch. Ingenieurwesen 2021, 85, 273–286. [Google Scholar] [CrossRef]
- Mehlan, F.C.; Nejad, A.R.; Gao, Z. Digital Twin Based Virtual Sensor for Online Fatigue Damage Monitoring in Offshore Wind Turbine Drivetrains. J. Offshore Mech. Arct. Eng. 2022, 144, 060901. [Google Scholar] [CrossRef]
- Walker, J.G.; Coraddu, A.; Collu, M.; Oneto, L. Digital Twins of the Mooring Line Tension for Floating Offshore Wind Turbines to Improve Monitoring, Lifespan, and Safety. J. Ocean Eng. Mar. Energy 2022, 8, 1–16. [Google Scholar] [CrossRef]
- Branlard, E.; Jonkman, J.; Brown, C.; Zhang, J. A digital twin solution for floating offshore wind turbines validated using a full-scale prototype. Wind. Energy Sci. 2024, 9, 1–24. [Google Scholar] [CrossRef]
- Bull, T.S.; Muff, D.V.; Wagner, P.R.; Zhang, W.H.; Faber, M.H.; Schubert, M.; Riber, H.J. Probabilistic Digital Twin-Informed Risk-Based Inspection Planning for Offshore Wind Turbine Structures. Struct. Health Monit. 2025; in press. [Google Scholar] [CrossRef]
- Mousavi, Z.; Varahram, S.; Ettefagh, M.M.; Sadeghi, M.H.; Feng, W.Q.; Bayat, M. A digital twin-based framework for damage detection of a floating wind turbine structure under various loading conditions based on deep learning approach. Ocean. Eng. 2024, 292, 116563. [Google Scholar] [CrossRef]
- Simpson, T.; Dervilis, N.; Couturier, P.; Maljaars, N.; Chatzi, E. Reduced order modeling of non-linear monopile dynamics via an AE-LSTM scheme. Front. Energy Res. 2023, 11, 1128201. [Google Scholar] [CrossRef]
- Xia, J.; Zou, G. Operation and Maintenance Optimization of Offshore Wind Farms Based on Digital Twin: A Review. Ocean. Eng. 2023, 268, 113322. [Google Scholar] [CrossRef]
- Chen, B.Q.; Liu, K.; Yu, T.; Li, R. Enhancing Reliability in Floating Offshore Wind Turbines through Digital Twin Technology: A Comprehensive Review. Energies 2024, 17, 1964. [Google Scholar] [CrossRef]
- Kandemir, E.; Hasan, A.; Kvamsdal, T.; Alaliyat, S.A. Predictive Digital Twin for Wind Energy Systems: A Literature Review. Energy Inform. 2024, 7, 68. [Google Scholar] [CrossRef]
- Pacheco-Blazquez, R.; Garcia-Espinosa, J.; Di Capua, D.; Pastor Sanchez, A. A Digital Twin for Assessing the Remaining Useful Life of Offshore Wind Turbine Structures. J. Mar. Sci. Eng. 2024, 12, 573. [Google Scholar] [CrossRef]
- Garcia-Espinosa, J.; Servan-Camas, B.; Calpe-Linares, M. High Fidelity Hydro-elastic Analysis Using Modal Matrix Reduction. J. Mar. Sci. Eng. 2023, 11, 1168. [Google Scholar] [CrossRef]
- Servan-Camas, B.; Berdugo-Parada, I.; Garcia-Espinosa, J.; Pastor-Sanchez, A. Modal Matrix Reduction for Fully Coupled Integrated Load Analysis of Floating Structures. Mar. Struct. 2025, 103, 103845. [Google Scholar] [CrossRef]
- Servan-Camas, B.; Gutierrez-Romero, J.E.; Garcia-Espinosa, J. A Time-Domain Second-Order FEM Model for the Wave Diffraction-Radiation Problem. Validation with a Semisubmersible Platform. Mar. Struct. 2018, 58, 278–300. [Google Scholar] [CrossRef]
- International Renewable Energy Agency. Future of Wind: Deployment, Investment, Technology, Grid Integration and Socio-Economic Aspects; Technical Report; IRENA: Abu Dhabi, United Arab Emirates, 2019. [Google Scholar]
- Global Offshore Wind Alliance. Offshore Wind: From 83 GW Today to 2,000 GW by 2050; IRENA and GOWA Initiative; IRENA: Abu Dhabi, United Arab Emirates, 2025. [Google Scholar]
- Center for Sustainable Systems, University of Michigan. Wind Energy Factsheet; Pub. No. CSS07-09; University of Michigan: Ann Arbor, MI, USA, 2024. [Google Scholar]
- Averroes.ai. Wind Turbine Maintenance & Inspection: Offshore, Cost, Blades; Averroes.ai: San Mateo, CA, USA, 2024. [Google Scholar]
- SANY Heavy Energy. SANY Heavy Energy Realizes High-Precision Wind Turbine Simulation with Siemens Simcenter 3D; Case Study: 10% LCOE Reduction Through Digital Twin Implementation; SANY Heavy Energy: Changsha, China, 2023. [Google Scholar]
- Dimitrov, N.; Jacquet, C.; Marelli, S. Innovative models slash offshore wind energy costs by 9%. TechXplore 2024. [Google Scholar]
- Servan-Camas, B.; Di-Capua, D.; Garcia-Espinosa, J.; Sa-Lopez, D. Fully 3D ship hydro-elasticity: Monolithic versus partitioned strategies for tight coupling. Mar. Struct. 2021, 80, 103098. [Google Scholar] [CrossRef]
- Bathe, K.J. Finite Element Procedures; K.J. Bathe: Watertown, MA, USA, 2016. [Google Scholar]
- Branlard, E.; Jonkman, J.; Dana, S.; Doubrawa, P. A digital twin based on OpenFAST linearizations for real-time load and fatigue estimation of land-based turbines. J. Phys. Conf. Ser. 2020, 1618, 022030. [Google Scholar] [CrossRef]
- ASTM E1049-85(2017); Standard Practices for Cycle Counting in Fatigue Analysis. ASTM: West Conshohocken, PA, USA, 2017. [CrossRef]
- Software, S.D.I. Calculating Damage with Miner’s Rule. 2023. Available online: https://community.sw.siemens.com/s/article/calculating-damage-with-miner-s-rule (accessed on 10 September 2025).
- Ltd, O. Fatigue Analysis: S–N and T–N Curves. 2025. Available online: https://www.orcina.com/webhelp/OrcaFlex/Content/html/Fatigueanalysis,S-NandT-Ncurves.htm (accessed on 10 September 2025).
- Siemens. Rainflow Counting Method. 2019. Available online: https://community.sw.siemens.com/s/article/rainflow-counting (accessed on 10 September 2025).
- React Documentation Team. React—The JavaScript Library for Building User Interfaces. 2025. Available online: https://legacy.reactjs.org/ (accessed on 10 September 2025).
- Node-RED Team. Node-RED. 2025. Available online: https://nodered.org/ (accessed on 10 September 2025).
- Eclipse Mosquitto Project. Eclipse Mosquitto. 2025. Available online: https://projects.eclipse.org/projects/iot.mosquitto (accessed on 10 September 2025).
- Timescale, Inc. TigerData—The Fastest Postgres Cloud for Real-Time Analytics, Time Series, AI & Vector Workloads; d/b/a TigerData; Timescale, Inc.: New York, NY, USA, 2025. [Google Scholar]
- Grafana Labs. Grafana—Dashboard Anything. Observe Everything; Grafana Labs: New York, NY, USA, 2025. [Google Scholar]
- PyTorch Foundation. PyTorch—An Open Source Machine Learning Framework; PyTorch Foundation: San Francisco, CA, USA, 2025. [Google Scholar]
- Compass Ingeniería y Sistemas, S.A. Structural Analysis—Tdyn RamSeries; Compass Ingeniería y Sistemas, S.A.: Barcelona, Spain, 2025. [Google Scholar]
- Blender Foundation. Blender—Free and Open Source 3D Creation Software; Blender Foundation: Amsterdam, The Netherlands, 2025. [Google Scholar]
- OpenWeather Ltd. OpenWeatherMap—Global weather data & APIs; OpenWeather Ltd.: London, UK, 2025. [Google Scholar]
- Puertos del Estado. Portus—Marine and Ocean-Meteorological Data for Spain’s Port System; Puertos del Estado: Madrid, Spain, 2025. [Google Scholar]
- Copernicus Programme/European Commission. Copernicus—The European Union’s Earth Observation Programme. 2025. Available online: https://www.copernicus.eu/sites/default/files/Brochure_Copernicus_2019%20updated_0.pdf (accessed on 10 September 2025).
- EnerOcean, S.L. W2Power—The Future of Floating. Now. 2025. Available online: https://enerocean.com/w2power/ (accessed on 10 September 2025).
- FIBREGY Consortium. FIBREGY—Composites for a Sustainable Environment. 2025. Available online: https://fibregy.eu/ (accessed on 10 September 2025).
- OPeNDAP, Inc. OPeNDAP—Open-source Project for a Network Data Access Protocol; OPeNDAP, Inc.: Butte, MT, USA, 2025. [Google Scholar]
- DeepCWind Company. DeepCWind Company—Accelerating the Future of Floating Offshore Wind; DeepCWind Company: Orono, ME, USA, 2025. [Google Scholar]
- Bureau Veritas Marine & Offshore. Guidelines for Fatigue Assessment of Ships and Offshore Units (Rule Note NI 611); Bureau Veritas Marine & Offshore: Courbevoie, France, 2020. [Google Scholar]
- IEC 61400-3-2:2025; Wind Turbines—Part 3-2: Design Requirements for Floating Offshore Wind Turbines. International Electrotechnical Commission: London, UK, 2025.




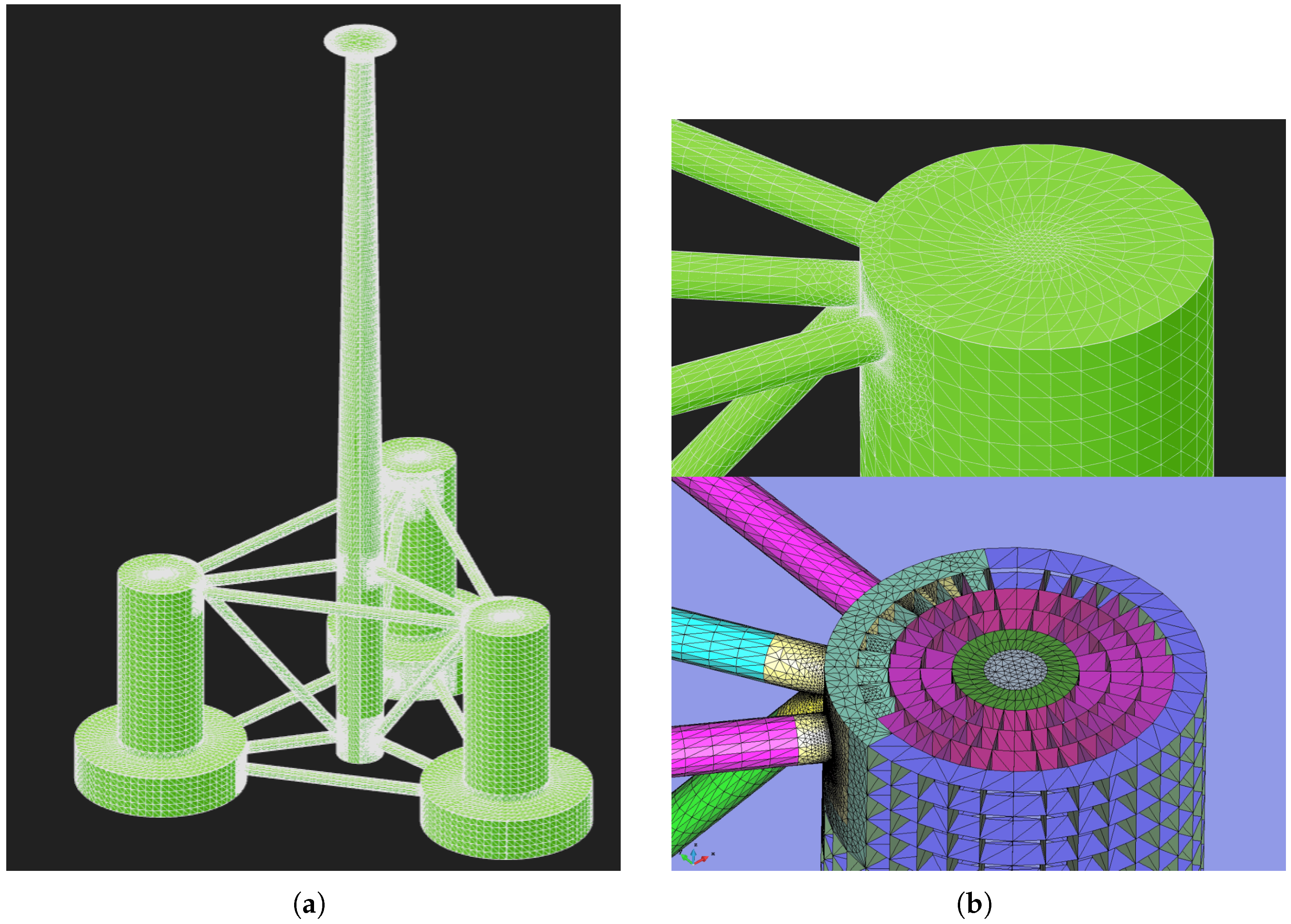
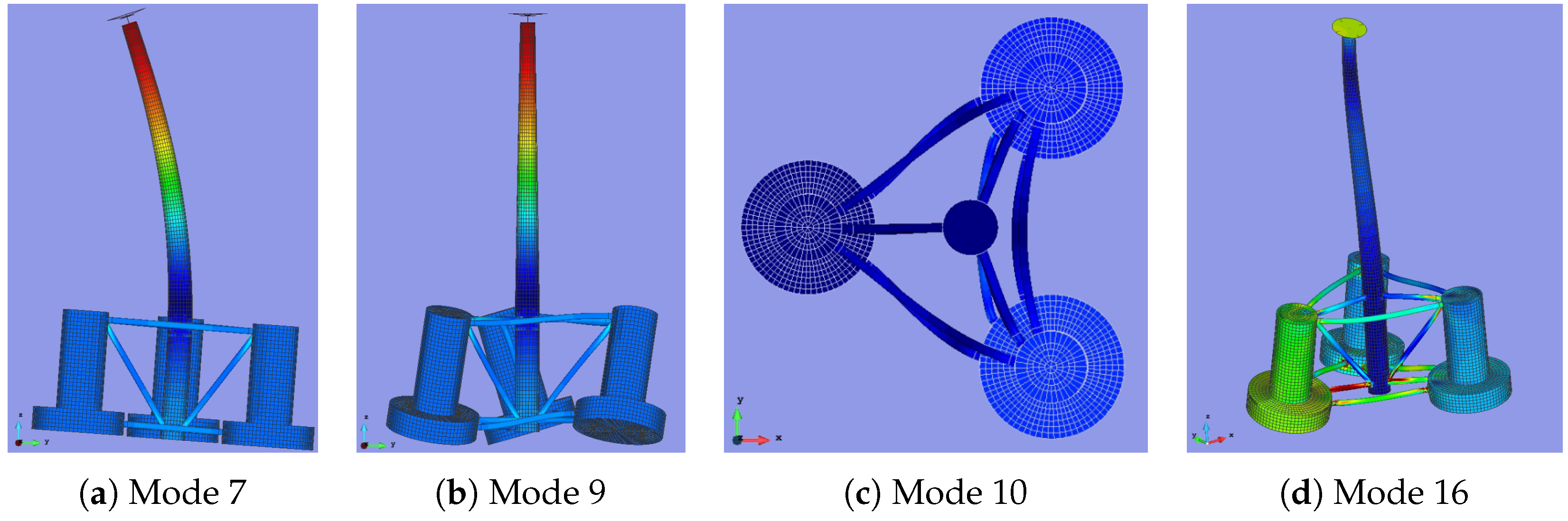




| Characteristic | Value | Unit |
|---|---|---|
| Wind turbine rating | 5 | MW |
| Platform mass (incl. ballast) | 14,077 | t |
| Center of mass below SWL | 11.06 | m |
| Center of buoyancy below SWL | 13.15 | m |
| Draft | 20 | m |
| Main column diameter | 6.25 | m |
| Offset column upper diameter | 12 | m |
| Offset column base diameter | 24 | m |
| Column spacing (triangle side) | 50 | m |
| Mooring lines | 3 | – |
| Mooring line length | 835.5 | m |
| Anchor radius | 837.6 | m |
| Fairlead radius | 40.87 | m |
| Roll inertia | kg·m2 | |
| Pitch inertia | kg·m2 | |
| Yaw inertia | kg·m2 | |
| Hub height | 90 | m |
| Water depth | 200 | m |
| Mooring system | Catenary | – |
| ROM | FEM | ||
|---|---|---|---|
| CPU | GPU | CPU | |
| Simulation Time | 14.45 min | 0.69 min | 2 235 min |
| Update Rate | 104.5 million DOFs/s | 2.43 billion DOFs/s | 0.68 million DOFs/s |
| CPU | GPU | |
|---|---|---|
| Simulation Time | 46.4 min | 3.81 min |
| Update Rate | 293.5 million points/s | 3.57 billion points/s |
| CPU | GPU | |
|---|---|---|
| Simulation Time | 98 min | 37 min |
| Processing Rate | 340.1 stress histories/s | 901.4 stress histories/s |
| CPU | GPU | |
|---|---|---|
| Time per Hotspot (1000 Scenarios) | 2.94 s | 1.10 s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pastor-Sanchez, A.; Garcia-Espinosa, J.; Di Capua, D.; Servan-Camas, B.; Berdugo-Parada, I. Real-Time Digital Twin for Structural Health Monitoring of Floating Offshore Wind Turbines. J. Mar. Sci. Eng. 2025, 13, 1953. https://doi.org/10.3390/jmse13101953
Pastor-Sanchez A, Garcia-Espinosa J, Di Capua D, Servan-Camas B, Berdugo-Parada I. Real-Time Digital Twin for Structural Health Monitoring of Floating Offshore Wind Turbines. Journal of Marine Science and Engineering. 2025; 13(10):1953. https://doi.org/10.3390/jmse13101953
Chicago/Turabian StylePastor-Sanchez, Andres, Julio Garcia-Espinosa, Daniel Di Capua, Borja Servan-Camas, and Irene Berdugo-Parada. 2025. "Real-Time Digital Twin for Structural Health Monitoring of Floating Offshore Wind Turbines" Journal of Marine Science and Engineering 13, no. 10: 1953. https://doi.org/10.3390/jmse13101953
APA StylePastor-Sanchez, A., Garcia-Espinosa, J., Di Capua, D., Servan-Camas, B., & Berdugo-Parada, I. (2025). Real-Time Digital Twin for Structural Health Monitoring of Floating Offshore Wind Turbines. Journal of Marine Science and Engineering, 13(10), 1953. https://doi.org/10.3390/jmse13101953







