Abstract
This paper presents the results of seakeeping tests conducted on the Tritor, a remotely controlled autonomous unmanned surface vehicle (USV) featuring a trimaran hull design known as the Three Slender Cylinders Hull (3SCH) and equipped with electric propulsion. Previous research focused on the vehicle’s design, prototype development, and initial functional testing. Tritor is characterised by its simple design and construction, reliable propulsion system, and excellent stability and manoeuvrability. Its control and navigation systems have demonstrated effective performance in both remote-controlled and fully autonomous modes. In the present study, seakeeping tests were carried out in a towing tank, with repeated trials conducted at various speeds and wavelengths. The selected wavelengths were close to the vehicle’s length, where the most significant responses were expected. Test speeds ranged from 1.0 to 2.5 m per second, based on prior operational experience with the vehicle. Due to the constraints of the towing tank, all wave directions were limited to head seas. Measurements included heave and pitch motions. Vertical accelerations at the vehicle’s centre of gravity were derived from the heave data and used as a key indicator of seakeeping performance. The results were evaluated against established seakeeping criteria related to vessel operability and structural safety.
1. Introduction
The key innovations in the present study are based on a novel trimaran hull form known as Three Slender Cylinder Hull (3SCH), which main characteristics of having a mid-cylinder placed underwater and two side cylinders on the surface. The main idea behind this novel form is to achieve improved seakeeping performance of the vehicle. This study is based purely on intuitive and experimental work carried out during the development and testing of the vehicle, both in real conditions and a towing tank. The proposed form was designed with two primary objectives: the first is to achieve high transverse stability, and the second is to minimise vertical accelerations. These two parameters are among the most critical when evaluating a vessel’s seakeeping performance. The first objective was met by positioning the side cylinders widely apart. The vehicle’s length-to-beam (L/B) ratio is 1.9, which is unachievable with conventional monohulls, catamarans, or even traditional trimaran configurations. It can be concluded that the 3SCH form features a unique buoyancy distribution that ensures a high level of transverse stability, which is difficult to attain with any other known hull form. The second objective, reducing vertical accelerations, was primarily achieved by positioning the mid-cylinder underwater. In this configuration, the cylinder acts to dampen vertical motions and accelerations by generating drag forces that oppose vertical movement. An additional benefit of the proposed design is reduced overall drag, since the submerged mid-cylinder does not contribute to wave-induced drag. Furthermore, this form eliminates slamming, as the mid-hull is placed below the waterline, an outcome confirmed through testing.
A naval architect’s work often focuses on improving a ship’s seakeeping performance and finding new technical solutions that are better than the previous ones. The development of the 3SCH hull form represents one such effort, with the primary goal of achieving better seakeeping characteristics of a ship as a platform in terms of reducing motions and accelerations. Seakeeping towing tank tests are conducted to validate the initial hypothesis that the new 3SCH hull form offers better performance compared to traditional monohulls, catamarans, and trimarans. These tests are designed to generate results that can be evaluated against established seakeeping criteria, enabling a clear and objective comparison. Therefore, in the literature review, the authors have chosen papers that deal with seakeeping towing tank tests and/or CFD calculations of monohull and multihull models.
Ref. [1] presents the initial work on the design, prototype development, and preliminary functional testing of the Tritor vehicle. In ref. [2], the seakeeping and resistance tests of a high-speed monohull were performed in a towing tank. The authors enhanced the vessel’s seakeeping performance by incorporating spray rails into the design. Work [3] presents experimental and numerical evaluations of three ship configurations—monohull, catamaran, and trimaran—focusing on seakeeping and other hydrodynamic characteristics. Results showed that each platform has advantages and disadvantages, and results are in close correlation with other published results for comparable platforms. Ref. [4] presents the results of seakeeping tests for a fast catamaran. Results established a high-value database for experimental and computational fluid dynamics (CFD) studies of fast catamarans. A numerical method for evaluating the seakeeping performance of a trimaran was developed in [5] and validated against experimental results. The method has been applied in numerous practical cases and has proven effective for calculating the seakeeping characteristics of high-speed multihull vessels. Ref. [6] represents seakeeping performance analyses conducted on four selected vessels. In parallel, experimental towing tank tests were performed. The strip theory exhibited a degree of inaccuracy, but this work was interesting due to its experimental results. The seakeeping characteristic optimisation of a displacement catamaran was conducted using the three-strip method codes [7]. The optimisation was limited to the head seas, and the results were compared with the results of the parent existing ship. In [8], the performance of a high-speed catamaran was investigated in all wave directions by applying three-dimensional potential flow theory. The results were compared with the experiment of free-running model tests. They showed that the translating pulsating source method provided more reliable predictions for head seas than the pulsating source method.
The ref. [9] shows the resistance and seakeeping characteristics of rescue vessels. It was designed as a double-M craft, with the main hull modelled after the Delft 372 catamaran, chosen due to its extensive experimental seakeeping studies. The ref. [10] presents the comparison of experimental and numerical results for a multi-hull form in head seas. The patrol ship’s motions and resistance were analysed in a towing tank [11]. The vessel has a higher vertical centre of gravity than expected, and large responses were observed. The full-scale seakeeping test results for the coastal patrol vessel are detailed in [12]. The results were compared with numerical calculations and set seakeeping criteria. Overall, the seakeeping performance of the vessel was satisfactory. There was disagreement about the numerical results for rolling response because the numerical model could not consider the influence of viscous forces. The ref. [13] shows the seakeeping performance of high-speed catamarans using two CFD calculation models. The numerical results showed good agreement with the experimental data, except for pitch motion, which was influenced by the nonlinear effects of the centre bow, causing large pitch motions. Wave-piercing high-speed catamaran seakeeping performances were analysed in [14] through two different numerical methods to install the motion-suppressing device. The results were compared with experimental data to ensure the verification and accuracy of the computational methods. The seakeeping performance of heave, pitch and vertical accelerations in head regular waves was investigated using numerical and experimental approaches [15]. The results showed that motion responses were reduced with the use of a T-foil and reasonably good agreement between numerical and experimental results. The ref. [16] presents the motions towing tank testing of a fast catamaran for the Office of Naval Research as a Littoral Surface Craft. Numerical calculations predicted excellent seakeeping performance for the vehicle. Extensive towing tank tests were performed to validate the numerical results.
Section 5 of the ref. [17] discusses seakeeping tests conducted in the towing tank using a model of a ship for compressed natural gas transport. The tests aimed to ascertain the seakeeping performance of the vehicle for the head, beam, and stern quartering waves. The vertical motions of the DTMB 5415 ship were investigated using two different numerical methods [18]. The first was linear strip theory, and the second was nonlinear viscous Unsteady Reynolds Averaged Navier–Stokes (URANS). The numerical and experimental data were compared, and the URANS method showed a better fit to experimental data as expected. The ref. [19] analyses the key factors that influence the hydrodynamic behaviour of multihull vessels and their suitability for a new class of ship. The seakeeping characteristics of multihulls should be compared to monohulls to prove multihulls’ better behaviour at sea. It concludes that, in addition to numerical tools, it is necessary to perform testing of the scale models in a towing tank to optimise multihull hydrodynamic characteristics. Ref. [20] is a book from the University of Rijeka that deals with the seakeeping of marine objects. The formula for root mean square values is taken from this reference. NATO standards [21] provide a common procedure for seakeeping in the ship design process as well as general and specific seakeeping criteria for naval vessels. The criteria for vertical accelerations and rolling angle were adopted from this reference. In [22], the current criteria for seakeeping are reviewed for different types of ships. The criteria for vertical acceleration at the bridge of a fast small craft were adopted from the mentioned reference. The video of one run of the Tritor vehicle in a towing tank is uploaded on the YouTube platform [23], while the tests in real conditions on lakes and rivers are given in [24]. Ref. [25] presents the catamaran unmanned surface vehicle, its autonomy capability development, path planning strategies for different types of missions, and sea trials of the vehicles.
The resistance in calm water and seakeeping performance of a trimaran planning hull on regular waves were tested in a towing tank [26]. The conclusion is that the motion responses have characteristics of high-speed vessels, and by increasing the velocity, the maximum motion response occurs at higher encounter frequencies. Ref. [27] proposes an optimisation method for the outrigger layout of wave-piercing trimarans, focusing on seakeeping and resistance characteristics. The method is based on a genetic algorithm and a Pareto-optimal front, resulting in a trimaran design with improved resistance and seakeeping performance. Ref. [28] presents a parametric multi-objective optimisation of an unmanned surface vehicle (USV). The optimisation objectives include wave resistance, vertical acceleration at the centre of gravity, and pitch amplitude. The optimisation was applied to a 7-metre USV hull, resulting in improved resistance and seakeeping performance. Ref. [29] provides an overview of recent research on USV hull design, comparing actual USVs in terms of their suitability for different sea state levels and examining how various hull design parameters affect USV performance. Ref. [30] provides insight into the development of a heading controller for USVs. Ref. [31] presents a comparison of a trimaran autonomous surface vehicle (ASV) with monohull and catamaran configurations. Ref. [32] presents experimental tests of four small waterplane area twin hull (SWATH) models in both calm water and regular waves. Seakeeping performance is evaluated in terms of heave, pitch, and vertical accelerations, presented in non-dimensional form. References [33,34,35,36,37,38] report seakeeping test results for various platforms, including monohulls, catamarans, and trimarans. These studies primarily present vertical accelerations at the centre of gravity and pitch motions expressed as RMS values. An attempt was made to compare these results with those of the Tritor vehicle. However, due to the substantial geometric and hydrodynamic differences between the Tritor and the referenced platforms, and the lack of a sufficiently rigorous scientific basis for comparison, this approach was ultimately abandoned, as discussed in Section 4.
This paper investigates the seakeeping characteristics of a novel 3SCH hull form in head sea conditions. Towing tank tests were conducted under various wave heights, speeds, and wavelengths. The resulting data were analysed and compared against established seakeeping criteria. Section 2 describes the main features of the towing tank facility, the testing methodology, the characteristics of the Tritor vehicle, and the key testing parameters, including wavelengths, speeds, wave heights, and other relevant conditions. Section 3 presents the results of the towing tank experiments, including motion amplitudes in heave and pitch. Vertical accelerations at the vehicle’s centre of gravity were derived from heave motion data. Section 5 presents a discussion, conclusion, and evaluation of the new 3SCH form, based on the results and comparison to the seakeeping criteria, and provides recommendations for future work in this area.
2. Towing Tank Characteristics and Tritor Vehicle Specification
Seakeeping tests of the Tritor vehicle were carried out in the towing tank at the Faculty of Mechanical Engineering and Naval Architecture, University of Zagreb (UNIZG), as shown in Figure 1. The towing tank was opened in 2022 as part of the Regional Centre for Laboratory Research in Hydromechanics—ORCHID, which was funded by EU grants. The main dimensions of the towing tank are:

Figure 1.
The towing tank of the UNIZG.
- length: 32.8 m;
- breadth: 3.7 m;
- height: 1.8 m;
- water level: 1.5 m;
- water volume: 190 m3.
The towing tank is part of a comprehensive laboratory system that includes the tank itself, a towing carriage for model propulsion, generators for both regular and irregular waves, a range of instruments and sensors, and a wave-absorbing beach. The facility supports testing of ship and marine structure models in calm water to measure resistance forces, as well as in wave conditions to evaluate seakeeping performance. Test results can be digitally recorded, and video documentation of experiments is also available. Instruments and sensors, positioned at the towing point, are as follows:
- Heave sensor—the sensing element is a linear motion position conductive plastic sensor. The sensor is capable of measuring heave motions within a range of ±150 mm.
- Analogue traction force sensor—the measuring cell is made of AISI 420. It is a cell with a full-scale value of 150 N.
- Angular device—based on a Hall effect rotary position sensor series, detection is made without contact, separating the magnet from the sensor body. The device measures maximum angles of ±30 degrees.
- A high-resolution camera is positioned on the carriage.
Regular sinusoidal waves were generated using a prismatic plunger-type wave generator whose heights were measured via wave probes. The vehicle was fixed to a towing post, positioned as close as possible to the vehicle’s centre of gravity, at the deck and free to heave and pitch. The stern part was fixed to a balanced anti-yaw mechanism.
The Tritor vehicle represents a conceptual hull form based on the Three Slender Cylinders Hull (3SCH) configuration. Before these experiments, the vehicle was tested under real conditions on lakes and rivers, as documented in [1]. During these trials, the vehicle demonstrated excellent stability and minimal roll amplitude, even while executing sharp turns.
The vehicle also demonstrated very favourable behaviour in wave conditions, with no slamming observed on the side cylinders. The core concept behind the development of this hull form is outlined in [1], where it was hypothesised that the design would exhibit high seakeeping performance. The towing tank tests presented in this paper aim to validate that hypothesis.
Figure 2, Figure 3, Figure 4 and Figure 5 present the vehicle’s 3D views, as well as its side, top, and front views. The vehicle’s coordinate system is depicted in Figure 2. All symbols used in that figure are defined in Table 1, which also lists the vehicle’s geometric and mass properties. The main particulars of the vehicle are as follows:
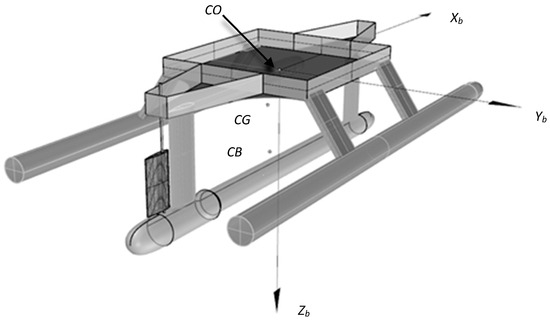
Figure 2.
Vehicle body coordinate system (CO origin in the centre of the rectangular deck).
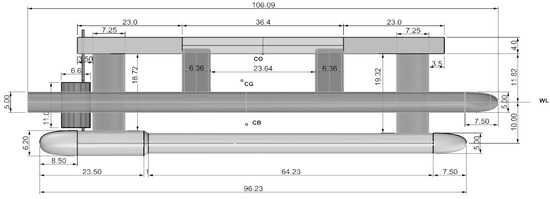
Figure 3.
Vehicle side view, vehicle dimensions in cm.
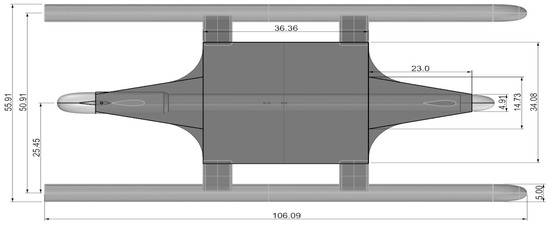
Figure 4.
Vehicle top view, vehicle dimensions in cm.
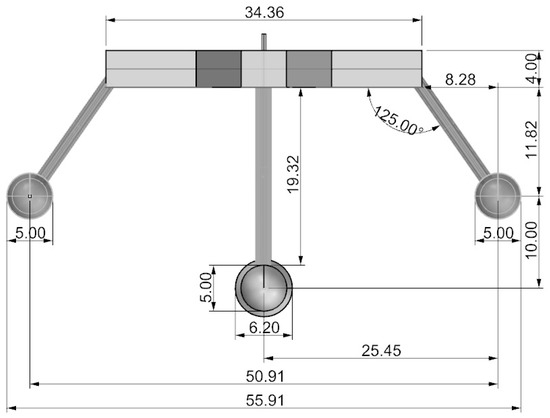
Figure 5.
Vehicle front view, vehicle dimensions in cm.

Table 1.
Vehicle geometry and mass characteristics.
- length: 107 cm;
- breadth: 55 cm;
- draft: 12.5 cm;
- displacement mass: 4.238 kg;
- maximum payload: 1.5 kg.
The seakeeping tests were conducted on regular waves (Figure 6). The tests on waves were conducted for two different wave heights, namely 40 and 60 millimetres, for four and three speed ranges, and three different wavelengths for each wave height. The seakeeping parameters are shown in Table 2. The tests on waves resulted in the resistance force of the vehicle as well as heave and pitch seakeeping responses. During the tests, the force gauge values were measured. However, since no tests were conducted in calm water, it was not possible to make meaningful comparisons. As a result, these measurements were not included in the paper. The authors intend to conduct additional tests on the Tritor vehicle, which will likely include force gauge measurements in both calm water and wave conditions, with an analysis of speed loss due to waves.

Figure 6.
Conducting tests in a towing tank.

Table 2.
The seakeeping test parameters.
Vertical accelerations in the vehicle’s centre of gravity were calculated based on data of the heave motions. Before testing, the Tritor vehicle was balanced with weights to obtain the designed displacement, and it was slightly stern trimmed. Since the initial towing point, positioned on the Tritor’s deck, was too high, this caused an overwhelming pitch during the runs; consequently, the deck was opened and the towing point lowered. It would be more favourable to conduct additional runs, especially regarding the broader spectrum of wavelengths; however, due to limited resources, the scope was constrained to the presented scope.
3. Results and Analyses of Seakeeping Tests
Because the vehicle is small and intended to operate in confined water bodies (lakes, rivers, and nearshore zones), performing full spectral analyses in situ would be very difficult. Accordingly, the authors chose to rely on empirical testing and presented the results of practical experiments in the paper.
The authors acknowledge that the testing presented in this paper does not fully comply with ITTC standards due to constraints of the towing tank, equipment, and resources. However, the rationale behind the selection of wave heights and wavelengths is explained below. A wave height of 40 mm was chosen to represent typical operational conditions in which the vehicle is expected to perform normally. A 60 mm wave height was selected as the upper operational limit, where the vehicle could experience significant loading. An 80 mm wave height was initially planned to represent extreme wave conditions; however, this was abandoned due to the limited availability of the towing tank. Wave heights were determined based on preliminary experimentation in the towing tank.
Initially, the plan was to test approximately 10 different wavelengths. However, due to time constraints, the number was reduced to five. These wavelengths were selected in relation to the vehicle’s length: one wavelength was equal to the vehicle length (L), two were shorter (0.5 L and 0.75 L), and two were longer (1.5 L and 2.0 L). Ultimately, the number of tested wavelengths was further reduced to four, as shown in Table 2.
These specific wavelengths and heights were chosen because they are expected to result in the most significant responses from the vehicle. For the longest wavelengths, the wave height to length ratio is close to the ITTC guideline of 1/50. The ratio of wave height to wavelength is presented in Table 3.

Table 3.
Wave height to length ratio.
Up to four different speeds were tested to assess the vehicle’s performance under varying dynamic conditions. The speed, Froude and Reynolds numbers are presented in Table 4.

Table 4.
Speed, Froude and Reynolds numbers.
For presenting the vehicle’s responses, non-dimensional transfer functions for heave and pitch motions were used, and Root Mean Square (RMS) values for vertical acceleration. The RMS method was specifically utilised to quantify vertical acceleration, providing a standardised metric that aligns with established criteria for vehicle performance assessment. The calculations of RMS values were performed using Equation (1). The authors believe this equation is pertinent for evaluating the vertical acceleration response at the vehicle’s centre of gravity, ensuring consistency with recognised methodologies in the field.
The vehicle could handle much higher speeds than 2.5 m/s, but the high towing point risked generating longitudinal moments, potentially leading to large pitch motions and even flipping the vehicle.
For each run, the computer recorded the following data related to the tests:
- time in ms,
- speed in m/s,
- position in m,
- wave height in mm,
- towing force in Newtons,
- heave amplitude in mm,
- pitch amplitude in degrees,
All tests were conducted with head waves owing to constraints in test facilities. Vertical accelerations in the vehicle’s centre of gravity were calculated from the heave motions. Heave and pitch motions were recorded at a frequency of 100 samples per second. These data files were imported into Excel, where the heave and pitch curves were initially plotted, as illustrated in Figure 7.
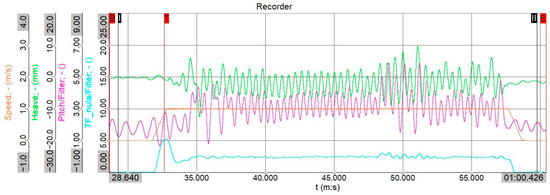
Figure 7.
Example of a recorded run, wave height 40 mm, wavelength 1101 mm, speed 1 m/s.
Subsequently, the curves were analysed to identify instability caused by the vehicle’s acceleration and deceleration. Data segments exhibiting instability were excluded from analysis, retaining only the stable interval, for example, from 38 to 48 seconds, as shown in Figure 7. This filtered dataset comprised approximately 1000 rows. For each time increment (1/100 of a second) or table row, the speed was calculated by deriving displacement over time. For example, the heave speed was obtained by subtracting two consecutive heave displacement values and dividing by the elapsed time of 0.01 seconds. This procedure was then repeated on the speed data to calculate acceleration, as acceleration is the derivative of speed over time. Next, the average acceleration was computed using all available records. Finally, the root mean square (RMS) value was calculated following Equation (1).
σ = rms—root mean square;
N—total number of samples;
—motion (heave or pitch) sample values;
—motion samples average value.
Processed root mean square (RMS) values for heave, pitch, and vertical accelerations at the vehicle’s centre of gravity, and average values for heave and pitch are presented in Table 5. The average pitch is slightly higher, which can be explained by the initial vehicle trim of approximately 2 degrees. This initial trim was applied out of concern that the vehicle might capsize at high speeds. If a 2-degree trim is subtracted from the values shown in Table 5, the resulting pitch values would be much more acceptable. Higher values of heave and pitch at high speeds were anticipated, as a wave height of 60 mm is significant for a vehicle of this scale. Additionally, head seas represent the most demanding condition for the vehicle. From the authors’ perspective, vertical accelerations are the most important seakeeping criterion and were therefore prioritised over heave and pitch motions.

Table 5.
The seakeeping test results.
To support visual interpretation of the data, associated result graphs are provided in Figure 8, Figure 9, Figure 10, Figure 11 and Figure 12.
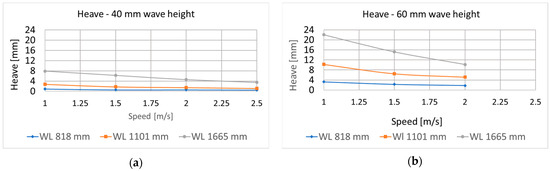
Figure 8.
Heave motion responses for 40 (a) and 60 (b) mm wave height.
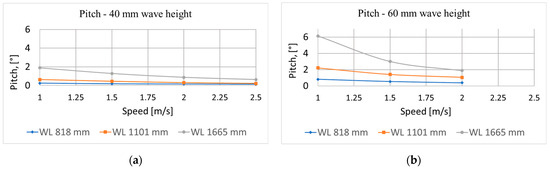
Figure 9.
Pitch motion responses for 40 (a) and 60 (b) mm wave height.
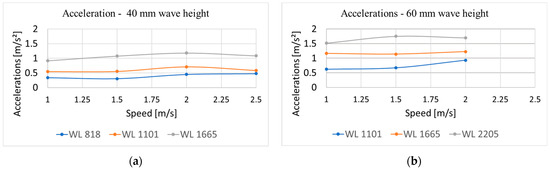
Figure 10.
Vertical accelerations of the vehicle for 40 (a) and 60 (b) mm wave height.
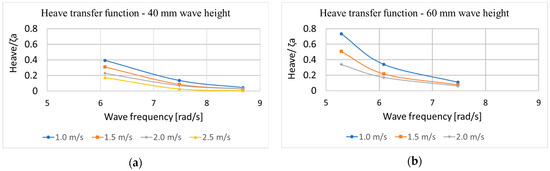
Figure 11.
Heave motion transfer function for 40 (a) and 60 (b) mm wave height.
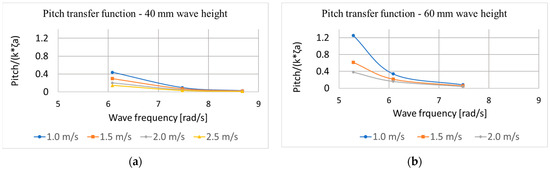
Figure 12.
Pitch transfer function for 40 (a) and 60 (b) mm wave height.
- Figure 8 shows heave motion responses for wave heights of 40 mm and 60 mm across various speeds and wavelengths.
- Figure 9 illustrates pitch motion responses under the same wave conditions.
- Figure 10 presents vertical accelerations at the vehicle’s centre of gravity for different speeds and wavelengths.
- Figure 11 displays heave motion transfer functions for both wave heights and varying speeds and wavelengths, where ζa is the wave amplitude.
- Figure 12 presents pitch motion transfer functions under the same conditions, where ζa is the wave amplitude, and k is the wave number.
The heave response results for a 40 mm wave height exhibit two expected trends. First, as the vehicle’s speed increases, heave motion decreases. This aligns with established behaviour, where maximum wave-induced motions typically occur at zero speed and reduce as speed increases due to the vehicle gaining dynamic stability. Second, heave motion increases with greater wavelengths. However, it is expected to stabilise beyond a certain point, as on sufficiently long waves the heave amplitude approaches the wave amplitude. Similar patterns were observed for the 60 mm wave height case, and pitch motion trends closely followed those of heave. As for vertical accelerations, they increased with both vehicle speed and wavelength. However, with further increases in wavelength, accelerations are expected not to rise further for the same reason mentioned earlier. Heave and pitch transfer functions followed expected trends. While it would have been beneficial to include more test points at longer wavelengths (i.e., lower wave frequencies), this was not feasible due to resource constraints.
Vertical acceleration values were compared with established criteria. According to NATO STANAG 4154 [21], the default vertical acceleration limit at the bridge is 0.2 g (RMS). Additionally, ref. [22] specifies limits for fast small craft at 0.65 g (RMS) at the forepeak (FP) and 0.275 g (RMS) at the bridge. In the case of the Tritor vehicle, the average vertical acceleration at the centre of gravity was 0.0699 g for a 40 mm wave height and 0.121 g for a 60 mm wave height. The maximum recorded value across all tests was 1.751 m/s2, equivalent to 0.179 g (RMS). This value corresponds to the centre of gravity, and the value at the bridge location would be slightly higher but still within acceptable limits, as the bridge is positioned close to the centre of gravity on this platform. An initial plan to conduct comparative seakeeping tests with conventional hull forms (monohull or catamaran) was not realised due to the difficulty in sourcing suitable models. Another important seakeeping criterion is the roll angle, which is limited to 4 degrees (RMS) in both [21,22] for fast small craft. While roll motion tests were not possible in the towing tank due to its limitation to head-sea wave conditions, free-running trials in real conditions revealed that the observed rolling amplitude did not exceed 1.5–2.0 degrees. This suggests that the 3SCH form also satisfies this criterion effectively.
The vertical acceleration data at the centre of gravity from the parametric optimisation of the deep-V hull USV in ref. [28] are compared with those of the Tritor vehicle in Table 6. All geometric details of the USV described are available in the same reference. The Froude number used for the USV hull form optimisation was 0.8925, which is comparable to the maximum Froude number of 0.775 used in the Tritor vehicle’s towing tank tests.

Table 6.
Comparison of vertical accelerations of the vehicle Tritor and the deep V hull USV.
4. Feasibility of Benchmarking the Tritor Against Other Platforms
After comparing Tritor’s seakeeping parameters with established criteria, the authors attempted to benchmark the seakeeping performance of the Tritor vehicle against other platforms, including monohulls, catamarans, and trimarans [33,34,35,36,37,38]. This effort was motivated by the need to place the results of the novel Three Slender Cylinders Hull (3SCH) form within a broader naval architectural context. In practice, however, identifying directly comparable platforms proved challenging. The Tritor’s unconventional configuration has no close analogues in the literature, which limited the availability of suitable reference data. Furthermore, most published seakeeping studies present results in terms of Response Amplitude Operators (RAOs) and spectral analyses. In contrast, the approach adopted in this study relied on empirical towing tank tests, followed by the calculation of average and root mean square (RMS) parameters. While RMS values provide meaningful insights into the dynamic responses of the Tritor, this methodology differs from the conventional RAO-based framework, making direct comparisons with literature data difficult.
Although preliminary results suggested that the Tritor performs favourably, particularly with respect to vertical accelerations and pitch motions, the differences in methodology and the lack of strictly analogous platforms render such conclusions tentative. Nevertheless, the authors maintain that the empirical RMS-based approach, though unconventional, produced results consistent with the study’s main objectives and yielded valuable indications of Tritor’s seakeeping potential. The authors believe that the methodology demonstrated a reasonable degree of validity within the experimental constraints and, most importantly, provided a solid foundation for future research. Future work will address the identified limitations through additional towing tank experiments with larger-scale models, the application of spectral and RAO-based analyses to improve compatibility with existing literature and controlled comparative tests involving conventional monohull and multihull platforms. These steps are expected to further substantiate the favourable seakeeping characteristics observed in the Tritor vehicle.
5. Discussion
The authors emphasise the significance of the seakeeping of unmanned vehicles, noting its strong correlation with onboard equipment and sensors. The ref. [21] outlines seakeeping criteria for naval platforms, categorising them into human, hull, and weapon systems/sensors criteria. The paper focuses on head wave responses, analysing heave, pitch motions, and vertical accelerations at the centre of gravity, within the constraints of the test facilities and vehicle size. Among these, vertical accelerations were deemed the most critical, guiding the research’s focus. Despite challenges, including the inability to measure phase shifts for specific point calculations, the study’s validity is supported by transfer functions exhibiting expected shapes, confirming the research’s reliability and relevance.
The Tritor is a novel conceptual vessel featuring a unique hull design composed of three slender cylindrical structures: a central hull submerged below the waterline and two outer hulls positioned above the water. The vehicle was initially tested in real conditions, such as free driving conditions on lakes and rivers. It demonstrated high performance, particularly in minimising rolling motions and exhibiting strong seakeeping capabilities in wave conditions. In this work, the vehicle was tested in a towing tank to prove its observed high seakeeping capabilities from initial trials. The main parameter significant for seakeeping characteristics estimation is the vertical acceleration of the vehicle’s centre of gravity. To the author’s knowledge, there is currently no specific standard or publication that addresses seakeeping operational criteria for unmanned surface vehicles (USVs). Therefore, the authors propose that existing seakeeping criteria for military and civilian vessels can be applied for this purpose. This approach is justified by the fact that, in the case of USVs, seakeeping criteria primarily affect the structure of the vehicle and its onboard equipment. The only significant difference compared to manned vessels is that such criteria for manned ships also apply to the crew. A relevant military standard that outlines detailed seakeeping criteria for naval vessels is [21]. This standard provides both general and specific seakeeping criteria applicable to the hull, onboard equipment, and crew. From this standard, the authors have adopted the seakeeping criterion for vertical acceleration at the centre of gravity, which is set at 0.2 g RMS. Comparable civilian seakeeping criteria are discussed in [22], from which the authors have adopted the vertical acceleration limit for fast small craft, namely 0.275 g RMS. The performance of onboard sensors in USVs is highly sensitive to vehicle motions and accelerations. In military vessels, vertical acceleration is one of the key criteria, with the accepted limit again set at 0.2 g RMS. This implies that sensitive onboard equipment may not function reliably if vertical accelerations exceed this threshold. The average vertical acceleration of the centre of gravity of the vehicle Tritor for a wave height of 40 mm was 0.0699 g (RMS), and 0.121 g (RMS) for a wave height of 60 mm. Considering all tests, the maximum vertical acceleration at the vehicle’s centre of gravity was 0.179 g (RMS). Both the maximum and average vertical accelerations are substantially lower than the thresholds established by two widely recognised criteria for ship operability. The authors agree that vertical accelerations are influenced by both heave and pitch motions; however, for vertical accelerations at the centre of gravity of the vehicle, the heave motion has a dominant effect. Additionally, it was more straightforward to compare the results with the seakeeping criteria for vertical accelerations at the vehicle’s centre of gravity, as referenced in [21,22]. Furthermore, when using the Tritor as an unmanned surface vehicle, most of the equipment would be positioned near the centre of gravity rather than at the bow or stern. Therefore, accelerations at the fore (FP) and aft (AP) positions are not critical for assessing the vehicle’s seakeeping characteristics. The authors initially intended to calculate vertical accelerations at the fore (FP) and aft (AP) positions. Unfortunately, the available measuring equipment, computer, and sensors were not capable of capturing the phase shift between heave and pitch. As a result, it was not possible to quantify the influence of pitch on vertical accelerations. Based on the encouraging results obtained so far, the authors plan to conduct further tests using a larger-scale Tritor vehicle (5–7 m in length). These tests will be more comprehensive and will include acceleration measurements at various locations using accelerometers.
The second key seakeeping parameter relates to roll motion. The roll amplitude of the vehicle during real condition (free driving) tests was assessed solely through the authors’ visual observation while operating the vehicle, and does not constitute a measured value. Based on these free driving tests, the authors believe that the vehicle exhibits a significantly lower roll amplitude compared to the established naval and civilian criterion of 4 degrees. Considering the results of initial tests of real conditions and the tests conducted in a towing tank, it can be concluded that the Tritor form has potentially high seakeeping characteristics. Further work in this area is aiming towards a larger vehicle of 3CSH form, which is expected to confirm the achieved results. The primary scientific contribution of this study lies in the experimental investigation of an innovative ship hull form, aimed at achieving substantial enhancements in seakeeping performance.
The authors acknowledge inherent uncertainties in the experimental research presented herein, which pertain primarily from constraints related to the test facility’s dimensions and the scale of the vehicle employed. Given the limited size of the test facility, there is a substantial likelihood that the proximity of the tank walls influenced the test results. However, it is assessed that this influence is not significant enough to render the results unacceptable. While this limitation cannot be mitigated within the current study, the authors propose three approaches for future research to address these uncertainties:
- Development of a larger vehicle: Making a scaled-up vehicle, approximately 5.0 to 7.0 m in length, to be tested in an appropriately sized facility and under real conditions. This approach aims to minimise boundary effects and enhance the reliability of the results.
- Advanced hydrodynamic analysis: Employing sophisticated computational tools to conduct detailed hydrodynamic analyses, focusing on seakeeping in wave conditions. This method would provide a more comprehensive understanding of the vehicle’s performance under various maritime scenarios.
- Conduct comparative seakeeping tests with conventional hulls (monohull or catamaran).
By pursuing these approaches, the authors intend to refine the experimental framework and reduce the uncertainties associated with the current study.
Author Contributions
Conceptualisation, methodology, software, validation, and original draft preparation, L.A.; resources, formal analysis, visualisation, supervision, S.V. and B.J.; project administration, investigation, review, and editing, B.J. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data available on request due to restrictions.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Ljulj, A.; Slapničar, V.; Brigić, J. Unmanned Surface Vehicle Tritor. Brodogradnja 2022, 73, 135–150. [Google Scholar] [CrossRef]
- Seo, J.; Choi, H.-K.; Jeong, U.-C.; Lee, D.K.; Rhee, S.H.; Jung, C.-M.; Yoo, J. Model Tests on Resistance and Seakeeping Performance of Wave-Piercing High-Speed Vessel with Spray Rails. Int. J. Nav. Archit. Ocean Eng. 2016, 8, 442–455. [Google Scholar] [CrossRef]
- Utama, I.; Jamaluddin, A.; Hutauruk, R.M. A Study into Selection of Mono-and Multi-Hull Vessel for Better Sea Transportation System. In Proceedings of the 4th International Product Design and Development in Conjunction with the 4th AUN/SEED-Net Regional Conference of Manufacture Yogyakarta, Yogyakarta, Indonesia, 9–10 November 2011. [Google Scholar]
- Broglia, R.; Bouscasse, B.; Jacob, B.; Olivieri, A.; Zaghi, S.; Stern, F. Calm Water and Seakeeping Investigation for a Fast Catamaran. In Proceedings of the 11th International Conference on Fast Sea Transportation FAST 2011, Honolulu, HI, USA, 26–29 September 2011. [Google Scholar]
- Sato, Y. CFD Simulation of Resistance and Seakeeping Performance for Multi-Hull Vessels. In Proceedings of the Symposium on Analyses of Strongly Nonlinear Flows Around Moving Boundaries, Fukuoka, Japan, 7–8 December 2006. [Google Scholar]
- Niklas, K.; Karczewski, A. Determination of Seakeeping Performance for a Case Study Vessel by the Strip Theory Method. Pol. Marit. Res. 2020, 27, 4–16. [Google Scholar] [CrossRef]
- Belga, C.R. Seakeeping Optimization of a Fast Displacement Catamaran on the Bases of Strip Theory Codes. Master’s Thesis, Tecnico Lisboa, Lisbon, Portugal, 2017. [Google Scholar]
- Hudson, D.; Molland, A.; Price, W.G.; Temarel, P. Seakeeping Performance of High Speed Catamaran Vessels in Head and Oblique Waves. In Proceedings of the 6th International Conference on Fast Sea Transportation FAST 2001, Southampton, UK, 4–6 September 2001. [Google Scholar]
- Ozturk, D.; Delen, C.; Mancini, S.; Serifoglu, M.O.; Hizarci, T. Full-Scale CFD Analysis of Double-M Craft Seakeeping Performance in Regular Head Waves. J. Mar. Sci. Eng. 2021, 9, 504. [Google Scholar] [CrossRef]
- Kerdraon, P.; Horel, B.; Bot, P.; Letourneur, A.; David Le Touzé, D. High Froude Number Experimental Investigation of the 2 DOF Behavior of a Multihull Float in Head Waves. J. Sail. Technol. 2021, 6, 1–20. [Google Scholar] [CrossRef]
- Firdaus, N.; Ali, B. Hydrodinamic Analysis of Patrol Vessel Based on Seakeeping and Resistance Performance. J. Ocean Mech. Aerosp. 2018, 60, 1–6. [Google Scholar]
- Ljulj, A.; Slapničar, V. Seakeeping Performance of a New Coastal Patrol Ship for the Croatian Navy. J. Mar. Sci. Eng. 2020, 8, 518. [Google Scholar] [CrossRef]
- Fang, C.-C.; Chan, H.-S. Investigation of Seakeeping Characteristics of High-Speed Catamarans in Waves. J. Mar. Sci. Technol. 2004, 12, 2. [Google Scholar] [CrossRef]
- Lin, C.T.; Lin, T.Y.; Lin, C.W.; Hsieh, Y.W.; Lu, L.; Hsin, C.Y. Investigation of the Seakeeping Performance of Twin Hull Vessels by Different Computational Methods. In Proceedings of the 10th International Workshop on Ship and Marine Hydrodynamics, Keelung, Taiwan, 5–8 November 2017. [Google Scholar]
- Li, A.; Li, Y. Numerical and Experimental Study on Seakeeping Performance of a Hihg-Speed Trimaran with T-Foil in Head Waves. Pol. Marit. Res. 2019, 26, 65–77. [Google Scholar] [CrossRef]
- Dudson, E.; Rambech, H.J. Optimisation of the Catamaran Hull to Minimise Motions and Maximise Operability. In Proceedings of the 7th International Conference on Fast Sea Transportation FAST2003, Ischia, Italy, 7–10 October 2003. [Google Scholar]
- Perosa, O. D5.2—Model Experimental Tests Results. GASVESSEL: Compressed Natural Gas Transport System (Horizon 2020, GA 723030). European Commission, CORDIS Public Deliverables. 2020. Available online: https://www.gasvessel.eu/wp-content/uploads/2017/11/D1.2-Project-Management-Plan.pdf (accessed on 12 June 2025).
- Cakici, F.; Sukas, O.F.; Kinaci, O.K.; Alkan, A.D. Prediction of the vertical motions of dtmb 5415 ship using different numerical approaches. Brodogradnja 2017, 68, 29–44. [Google Scholar] [CrossRef]
- Perez, R.; Riola, J.M. Contribution to the Seakeeping Analysis of Multihull Warships. Brodogradnja 2019, 70, 35–50. [Google Scholar] [CrossRef]
- Prpić-Oršić, J.; Čorić, V. Pomorstvenost Plovnih Objekata—Vessels’ Seakeeping; Zigo: Rijeka, Croatia, 2006; ISBN 953-7142-15-9. [Google Scholar]
- North Atlantic Treaty Organization. NATO STANAG 4154-Common Procedure for Seakeeping in the Ship Design Process; North Atlantic Treaty Organization: Washington, DC, USA, 2000. [Google Scholar]
- Zu, M.; Garme, K.; Rosén, A. Seakeeping Criteria Revisited. Ocean Eng. 2024, 297, 116785. [Google Scholar] [CrossRef]
- Unmanned Surface Vehicle Tritor Seakeeping Tests in Towing Tank. Available online: https://www.youtube.com/watch?v=sw_GS_CVrbk (accessed on 12 June 2025).
- Unmanned Surface Vehicle—Tritor Tests in Real Conditions on Lakes and Rivers. Available online: https://www.youtube.com/watch?v=p25tQpVGPXY (accessed on 12 June 2025).
- Liu, C.; Xiang, X.; Huang, J.; Yang, S.; Shaoze, Z.; Su, X.; Zhang, Y. Development of USV Autonomy: Architecture, Implementation and Sea Trials. Brodogradnja 2022, 73, 89–107. [Google Scholar] [CrossRef]
- Ma, W.; Sun, D.H.; Sun, D.H.; Zou, D.J.; Zhuang, J. Test Studies of the Resistance and Seakeeping Performance of a Trimaran Planing Hull. Pol. Marit. Res. 2015, 22, 22–27. [Google Scholar] [CrossRef]
- Lv, H.; Wei, C.; Liang, X.; Yi, H. Optimisation of wave-piercing trimaran outrigger layout with comprehensive consideration of resistance and seakeeping. Ocean Eng. 2022, 250, 111050. [Google Scholar] [CrossRef]
- Guan, G.; Wang, L.; Geng, J.; Zhuang, Z.; Yang, Q. Parametric automatic optimal design of USV hull form with respect to wave resistance and seakeeping. Ocean Eng. 2021, 235, 109462. [Google Scholar] [CrossRef]
- Mohamad, H.M.G.; Mohd, H.A.S.; Wan, R. Unmanned surface vehicles: From a hull design perspective. Ocean Eng. 2024, 312, 118977. [Google Scholar] [CrossRef]
- Wang, J.; Wang, J.; Liang, X.; Liu, J.; Cheng, S.; Yi, H. Real-sea validation of a model predictive controller’s inherent robustness for medium-scale unmanned trimaran heading. Ocean Eng. 2024, 313, 119513. [Google Scholar] [CrossRef]
- Silva, I.S.; Campopiano, F.; Lopes, G.S.V.; Uenojo, A.K.; Silva, H.T.; Pellini, E.L.; Alvarez, A.A.; Barros, E.A. Development of a Trimaran ASV. IFAC Pap. 2018, 51, 8–13. [Google Scholar] [CrossRef]
- Begovic, E.; Bertorello, C.; Bove, A.; De Luca, F. Experimental study on hydrodynamic performance of SWATH vessels in calm water and in head waves. Appl. Ocean Res. 2019, 85, 88–106. [Google Scholar] [CrossRef]
- Wellicome, J.F.; Temarel, P.; Bove, A.; Molland, A.F.; Courser, P.R. Experimental Measurements of the Seakeeping Characteristics of Fast Displacement Catamarans in Long-Crested Head-Seas. University of Southampton 1995, Ship Science Report 89. Available online: https://eprints.soton.ac.uk/46427/1/111.pdf (accessed on 12 June 2025).
- Windyandari, A.; Sugeng, S.; Sulaiman; Ridwan, M.; Yusim, A.K. Seakeeping Behavior of Hexagonal Catamaran Hull Form as an Alternative Geometry Design of Flat-Sided Hull Vessel. J. Appl. Eng. Sci. 2023, 21, 1016–1030. [Google Scholar] [CrossRef]
- Oh, I. A Study on the Motion Characteristics of a High-Speed Catamaran. J. Korean Stud. 1997, 11, 116–123. Available online: https://koreascience.kr/article/JAKO199711920579214.pdf (accessed on 12 June 2025).
- Zakki, A.F.; Windyandari, A.; Suharto; Ramadhan, A. Comparative Study on Catamaran and Monohull for the Hull Form Design of Livestock Carrier. J. Eng. Sci. Technol. 2019, 14, 20174–22089. Available online: https://jestec.taylors.edu.my/Vol%2014%20issue%204%20August%202019/14_4_23.pdf (accessed on 12 June 2025).
- Fernandez, R.P. Seakeeping in the navigation—Example in Trimaran ships. Int. J. Tfraffic Transp. Eng. 2012, 2, 221–235. Available online: http://ijtte.com/uploads/2012-10-01/5ebd8343-a147-4068IJTTE%20vol2%20no3%20(5).pdf (accessed on 12 June 2025). [CrossRef] [PubMed][Green Version]
- Dean, R.G.; Dalrymple, R.A. Water Wave Mechanics for Engineers and Scientists; World Scientific: Singapore, 2000. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).