From Numerical Models to AI: Evolution of Surface Drifter Trajectory Prediction

Abstract

Surface drifter trajectory prediction is essential for applications in environmental management, maritime safety, and climate studies. This survey paper reviews research from the past two decades, and systematically classifies the evolution of methodologies into six successive generations, including numerical models, data assimilation, statistical and probabilistic approaches, machine learning, deep learning, and hybrid or AI-based data assimilation (1st–5.5th Generation). To our knowledge, this is the first systematic generational classification of trajectory prediction methods. Each generation revealed distinct strengths and limitations. Numerical models ensured physical consistency but suffered from accumulated forecast errors in observation-sparse regions. Data assimilation improved short-term accuracy as observing networks expanded, while machine learning and deep learning enhanced short-range forecasts but faced challenges such as error accumulation and insufficient physical constraints in longer horizons. More recently, hybrid frameworks and AI-based data assimilation have emerged, combining physical models with deep learning and traditional statistical techniques, thereby opening new possibilities for accuracy improvements. By comparing methodologies across generations, this survey provides a roadmap that helps researchers and practitioners select appropriate approaches depending on observation density, forecast lead time, and application objectives. Finally, this paper highlights that future systems should shift focus from deterministic tracks toward credible uncertainty estimates, region-aware designs, and physically consistent prediction frameworks.

1. Introduction

In the ocean, predicting the future trajectories of unpowered floating objects such as pollutants, people, or vessels is a critical challenge for environmental management and maritime safety. However, directly releasing such objects into the ocean for data collection is impractical. Consequently, the deployment of surface drifters has become the practical and widely adopted alternative. A surface drifter is an autonomous floating instrument equipped with satellite positioning and communication modules. It drifts with near-surface currents while collecting real-time data such as position, current velocity, and sea surface temperature.

Since the commercialization of the Argos satellite system, drifters have become a standard component of the global ocean observing system and are operated under the international Global Drifter Program (GDP) [1]. As of 31 October 2022, the GDP had accumulated nearly 200 million position records and velocity estimates worldwide [2]. This vast dataset serves as a critical resource for a wide range of scientific and operational applications, including marine debris tracking, iceberg monitoring, global ocean circulation mapping, climate–atmosphere interaction studies, and satellite altimeter calibration [3].

Nevertheless, these drifter records are limited to past states, and past positions alone are insufficient for predicting future changes or supporting real-time response. When marine disasters such as oil spills or harmful algal blooms occur, effectively containing pollutant dispersion or reducing the search radius in search and rescue (SAR) operations requires accurate forecasts of drift pathways from hours to several days in advance. Trajectory prediction addresses this gap by using drifter observations together with environmental forcing data to estimate future positions and dispersion pathways. Drifter data become practically useful in such applications only when supported by robust trajectory prediction techniques. In other words, trajectory prediction is the process that converts drifter observations into actionable information and thereby enhances the value of measurements. For this reason, surface drifter trajectory prediction has become a core technology across many marine fields today.

Although research on trajectory prediction has continued and forecast accuracy has steadily improved, surface currents constitute a high-dimensional, nonlinear system in which wind, waves, bathymetry, seasonal cycles, and climatic factors interact, leaving substantial prediction errors and uncertainties. Even methods that report strong performance in specific studies may yield widely varying results depending on region, drifter type, or forcing conditions, making outcomes deviate from expectations. Therefore, experimental designs must be carefully tailored to the researcher’s context and objectives, based on sufficient understanding of the regions, datasets, aims, strengths, and limitations addressed in prior work.

For these reasons, this survey systematically reviews research on surface drifter trajectory prediction conducted over the past two decades and analyzes the principal techniques employed. To our knowledge, this is the first attempt to classify the evolution of methods into six successive generations, spanning numerical models, data assimilation, statistical and probabilistic approaches, machine learning (ML), deep learning (DL), and hybrid or AI-based frameworks. By discussing their strengths, limitations, and application contexts, this survey paper provides a roadmap that can guide researchers and practitioners in selecting appropriate methodologies and designing future studies.

The remainder of this paper is organized as follows. Section 2 examines the practical utility of drifters through representative applications such as marine pollution response, SAR, and ocean–atmosphere–climate studies. Section 3 defines drifters and trajectory prediction, outlines the key inputs and environmental drivers required for accurate forecasting, and introduces representative performance metrics. Section 4 reviews the development of prediction methodologies since the 2000s and analyzes the underlying drivers of each stage. Because readers may pursue different operational objectives, such as containing oil dispersion, saving lives, or optimizing search routes, we subdivide the trajectory prediction problem by objective and present studies organized by methods applied to each sub-objective. Section 5 then synthesizes research trends and findings, discusses conclusions and future challenges, and presents a summary table of major models and techniques. In short, this survey systematically reviews and synthesizes overall trends and core themes in drifter trajectory prediction, with the aim of serving as a reference for both researchers and practitioners. For clarity, the full names of the models, methods, and acronyms mentioned in this section are provided in the Summary of Key Acronyms, which follows the Conclusions and Future Directions section.

2. Application Case Studies

In this section, we examine three representative application areas of trajectory prediction based on observational data. Our aim is to understand why surface drifters are indispensable in each domain and to present concrete case studies illustrating their use in research and operational settings.

2.1. Prediction of Marine Pollutant Dispersion (Oil Spills, Harmful Algal Blooms, Marine Debris)

Various forms of pollutants, such as oil from tanker accidents, leaks during offshore drilling, harmful algal blooms, and marine debris, are dispersed widely across the ocean under the combined influence of physical drivers including currents, wind, and waves. If these dispersion pathways are not accurately predicted in advance, the strategic deployment of containment equipment becomes difficult, leading to inefficient use of resources and delayed response, which in turn exacerbates environmental and economic damage [4,5,6]. To address this challenge, drifter-based trajectory prediction models provide spatiotemporal dispersion pathways for pollutants, thereby offering a foundation for pre-positioning containment equipment at optimal locations. In particular, prediction models that assimilate drifter observations can substantially improve short-term forecast accuracy and serve as critical tools for real-time response and operational planning [7].

A representative real-world application of such drifter-based dispersion modeling was the Prestigeoil spill off the Galician coast of Spain in November 2002. Immediately after the accident, major research institutions, including the Spanish National Research Council, urgently deployed SC40 drifters in the waters off Galicia and across the Bay of Biscay to monitor near-surface current trajectories in real time [8]. The collected drifter trajectory data were coupled with the national coastal numerical prediction system operating at the time and used to calibrate linear Lagrangian models and high-resolution circulation models (e.g., PICHI, NRLPOM). Through this process, the drifter data played a key role in identifying critical oil-dispersion branch points and in developing response strategies based on predicted trajectories, thereby helping to mitigate shoreline contamination and enhance the efficiency of containment operations [9].

2.2. Search and Rescue and Backtracking of Floating Objects

Whereas marine-pollution response focuses on minimizing environmental and economic losses, SAR aims to minimize loss of life by characterizing the last known position of the distressed object (e.g., person, vessel, or debris), together with object type and external forcing factors, and then identifying the search area with the highest probability of success [10]. Because SAR operations are conducted across vast ocean areas under high uncertainty, failure to predict the drift path of distressed objects in advance greatly expands the search domain, significantly reducing the efficiency of resource deployment and the speed of the initial response. To overcome this challenge, surface drifter trajectory prediction has been integrated into SAR systems, enabling a substantial reduction in the search radius. Breivik & Allen [10] demonstrated that combining predicted currents, wind, and waves with drifter observations in an ensemble particle-tracking model produces probability density functions for SAR targets that can reduce the search area. On the other hand, backtracking is a technique that uses the observed position of a floating object at a given time to reconstruct its past trajectory and identify the initial release or accident site [11]. The BAKTRAK algorithm of Breivik et al. [11] repeatedly runs a forward surface drifter trajectory model while retaining only particles that converge to the observation point, thereby estimating the initial position with high accuracy; this allows backtracking to the accident site and supports causal analysis. Thus, drifter-based trajectory prediction has become a key technology for maximizing the efficiency of resource deployment in SAR and backtracking, enhancing rescue success rates, and improving the reliability of accident forensics.

2.3. Supporting Ocean–Atmosphere–Climate Interaction Studies

Ocean–atmosphere–climate models are numerical models that quantitatively represent interactions between the atmosphere and the ocean. Because they numerically describe the underlying physical and dynamical processes, these models require verification and calibration to evaluate their accuracy. Surface drifters provide high-resolution Lagrangian records of ocean circulation, supplying essential data for validating current fields, sea surface temperature, and salinity in numerical models [1]. Lumpkin & Pazos [12] proposed a reference framework for large-scale ocean–climate interaction studies by decomposing gridded time series of GDP drifter data into annual and semiannual harmonic components and residuals. In addition, Molcard et al. [13] showed that constraining the surface circulation fields of low-resolution ocean models (e.g., ECCO) with GDP drifter observations enables both the evaluation and improvement of model current accuracy. Sun & Penny [14] further demonstrated that, in an OSSE setting with a double-gyre model (a simplified representation of two major ocean gyres), assimilating drifter position observations can significantly improve forecasts of sea surface height and sea surface temperature. Thus, surface drifters provide indispensable Lagrangian observations for analyzing the mechanisms of the coupled ocean–atmosphere–climate system, and by combining these data with Eulerian fields and numerical modeling techniques, they play a central role in validating and calibrating numerical prediction models [3]. Moreover, the process of trajectory prediction itself can serve as an effective diagnostic of whether ocean transport, atmospheric forcing, and turbulence structures are being accurately represented. The closer the predicted trajectories are to the actual drift paths, the stronger the indirect evidence that a given numerical model correctly captures ocean–atmosphere interactions. Accordingly, improvements in drifter trajectory prediction accuracy translate into the enhanced predictability and credibility of the climate system, playing an important role in evaluating climate-change scenarios and in the development of coupled ocean–atmosphere models.

3. Surface Drifters and Trajectory Prediction

Trajectory prediction ultimately supports practical applications such as those introduced in Section 2. Because releasing real pollutants, people, or vessels into the ocean is impossible for experimentation, researchers instead employ surface drifters as safe and controllable observational proxies. This section first defines surface drifters, then introduces the concept of trajectory prediction, identifies the key inputs and environmental drivers influencing drift, and finally summarizes the performance metrics commonly used to evaluate prediction accuracy.

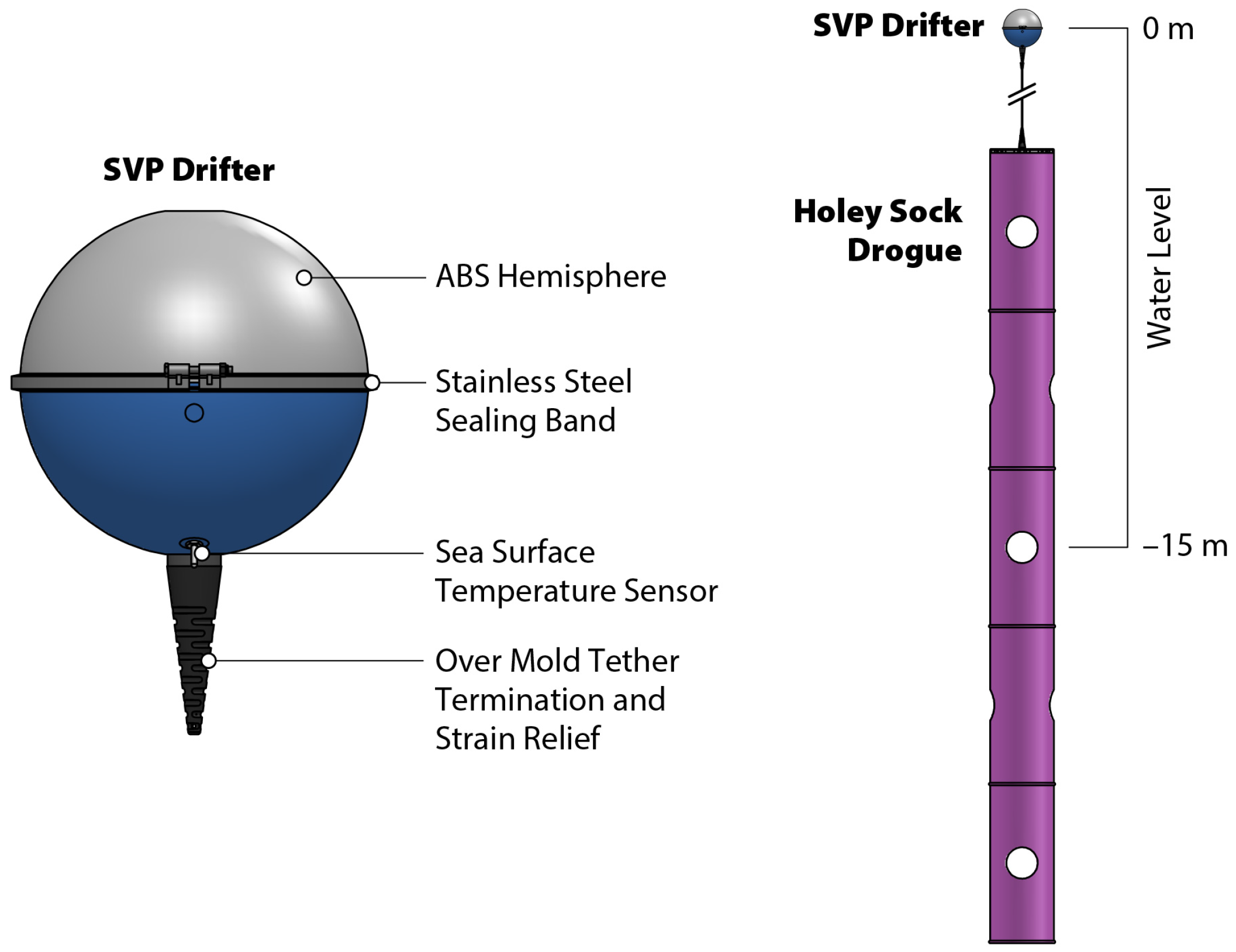
3.1. Surface Drifters

A surface drifter is a Lagrangian instrument equipped with GPS or satellite communications that moves along the sea surface and records trajectories as high-frequency position data [15]. Drifters are commonly categorized into two types, drogue-equipped and undrogued, as shown in Figure 1.

A drogue is an underwater structure, typically a set of panels or a net, deployed at a fixed depth (usually around 15 m) beneath the drifter that substantially increases current-induced drag. This design enables the drifter to follow ocean currents more faithfully while minimizing the influence of wind and waves [12]. Consequently, drogue-equipped drifters are widely used in current-dynamics studies and for calibrating trajectory prediction models, whereas undrogued drifters, lacking a drogue, respond sensitively to all external forcings, including wind, waves, and small-scale eddies.

These undrogued drifters are useful for studying the composite surface transport of pollutants such as oil slicks and marine debris, and they are often employed in field experiments as low-cost, easy-to-deploy platforms [12].

In addition to drifters, buoys are frequently used in ocean observation and forecasting. Conventional buoys are moored to the seafloor and serve as fixed-point instruments that collect the time series of salinity, wave height, temperature, pressure, wind direction, and wind speed. However, the studies mentioned in this survey that used buoys focused on non-moored devices, which drift freely with currents and winds and, like drifters, provide Lagrangian trajectory observations. Accordingly, in this work, we include such unpowered drifting buoys (unpowered floating platforms deployed for data collection) as part of an extended definition of drifters and incorporate studies utilizing these data within the scope of the survey.

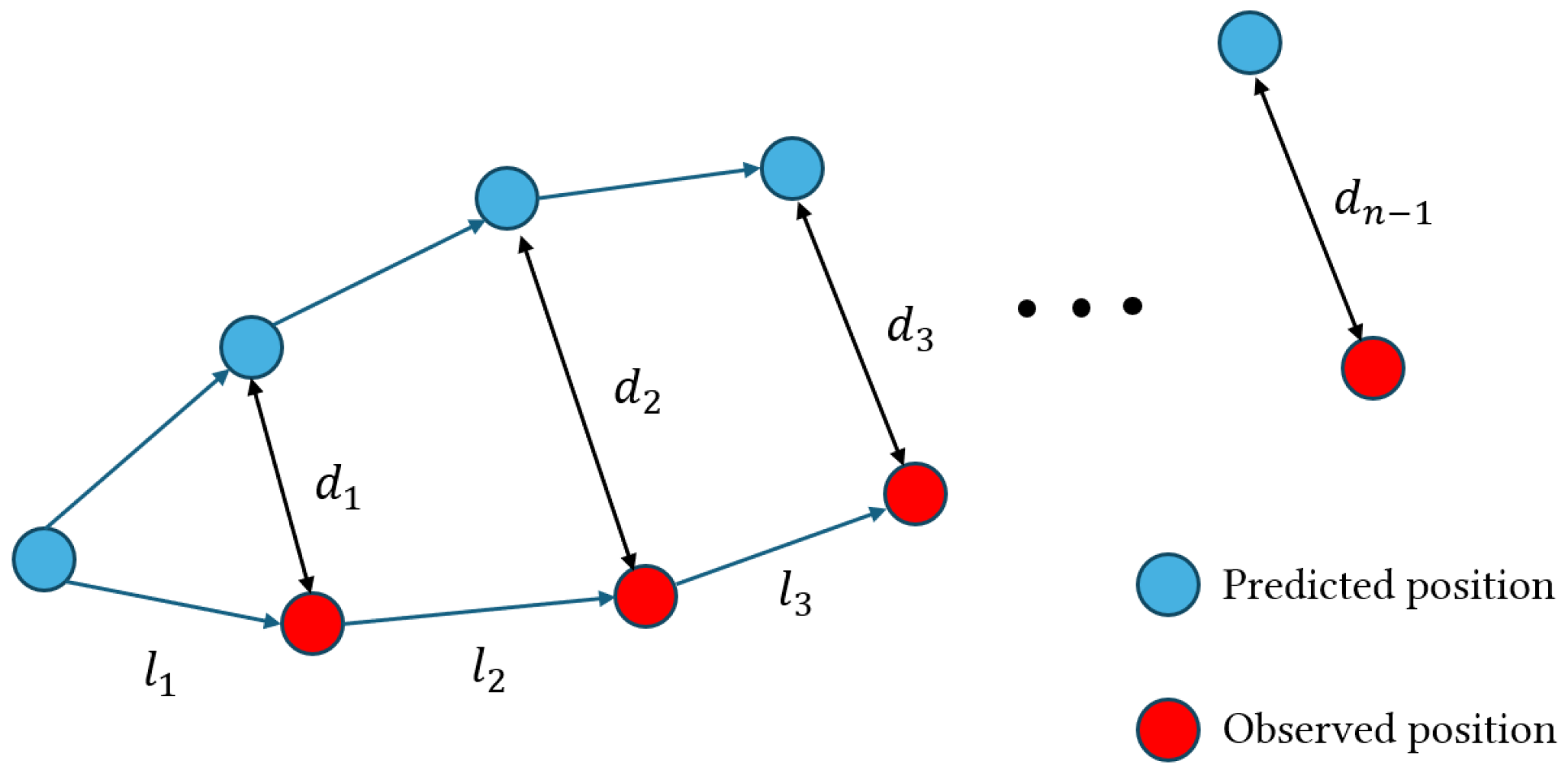
3.2. Trajectory Prediction

The surface drifter trajectory prediction estimates a drifter’s future path by combining its recorded positions with contemporaneous environmental information such as currents, winds, and waves. In practice, the method interprets both the time series of past coordinates and the surrounding spatiotemporal fields to generate forecasts over lead times ranging from hours to days. Depending on the modeling approach, forecasts may take the form of a single deterministic trajectory (e.g., position updates every hour) or a probabilistic distribution that reflects uncertainty in possible drift paths. To achieve this, a wide range of techniques are employed, including numerical models, data assimilation, statistical and probabilistic methods, ML, and DL.

3.3. Key Inputs and Environmental Drivers

The accurate prediction of a surface drifter’s path requires faithfully representing the forces acting on the drifter and incorporating them into the model. Time-stamped GPS coordinates (Lagrangian observations) capture the realized trajectory of the drifter and are indispensable for prediction. However, Lagrangian tracks alone cannot fully account for external drivers such as wind, currents, and topographic effects. To address this, reanalysis-based physical fields are used in tandem to enhance predictive accuracy. These fields assimilate satellite, buoy, and in situ observations into numerical models to reconstruct past ocean–atmosphere states on a four-dimensional grid (e.g., ERA5 with 1-h temporal resolution and 0.25° spatial resolution) [16]. ERA5 provides variables such as air temperature, pressure, wind speed, and wind direction; its ERA5-Wave module further includes significant wave height, average and maximum wave period, wave direction, and swell spectra, which are valuable for estimating Stokes drift. Moreover, by incorporating ocean reanalyses such as HYCOM and GLORYS, three-dimensional current, temperature, and salinity fields can be obtained [17,18]. Such reanalysis products can (i) represent external forcings in Lagrangian particle tracking, (ii) serve as additional input channels to DL predictors, or (iii) provide first-guess fields in data assimilation, against which observation–model innovations are computed. Bertin et al. [19] demonstrated that jointly exploiting Lagrangian trajectory data and Eulerian environmental fields can reduce prediction error by about 50%. Finally, auxiliary variables such as bathymetry may be added to address special cases, though they can degrade performance or increase computational cost. Thus, variable selection and cross-validation are essential to confirm their utility. In summary, drifter observations can be regarded as the backbone of trajectory prediction, reanalysis fields may be viewed as complementing external forcings, and auxiliary variables can be considered as providing opportunities for fine-tuning model performance.

3.4. Evaluation Metrics

Because evaluation depends on the research objective and on the characteristics and quality of the data, it is important to choose metrics appropriate to one’s specific context. Representative metrics used for surface drifter trajectory prediction include the following.

3.4.1. MAE (Mean Absolute Error)

MAE is defined as the mean of the absolute differences between predicted and observed positions.

$$\mathrm{MAE}={\displaystyle \frac{1}{N}}{\sum }_{i=1}^N\left|{\widehat{x}}_i-x_i\right|$$

(1)

where ${\widehat{x}}_i=({\widehat{Lat}}_i,{\widehat{Lon}}_i)$ is the predicted position at time i, $x_i=(La{t}_i,Lo{n}_i)$ is the observed position at time i, and N is the total number of time steps. MAE preserves the physical unit of the output, making it easy to interpret, and is relatively robust to outliers. However, because all errors are averaged uniformly, it does not specifically penalize very large errors. As the formula suggests, one may design a single model to predict latitude and longitude jointly, or design separate models for each.

3.4.2. MSE (Mean Squared Error)

MSE is the mean of squared errors and imposes greater penalties on large errors.

$$\mathrm{MSE}={\displaystyle \frac{1}{N}}{\sum }_{i=1}^N{|{\widehat{x}}_i-x_i|}^2$$

(2)

Because of the squaring, doubling the error quadruples the penalty, making MSE sensitive to large deviations. This encourages models to reduce catastrophic failures, but a few outliers may dominate the loss.

3.4.3. RMSE (Root Mean Square Error)

RMSE is the square root of MSE and thus restores the original distance unit of the error.

$$\mathrm{RMSE}=\sqrt{\mathrm{MSE}}=\sqrt{{\displaystyle \frac{1}{N}}{\sum }_{i=1}^N{|{\widehat{x}}_i-x_i|}^2}$$

(3)

RMSE shares MSE’s penalty properties while remaining easier to interpret and compare in physical units.

3.4.4. NCLS (Normalized Cumulative Lagrangian Separation)

Introduced by Liu & Weisberg [20], NCLS accumulates the separation between the predicted and observed trajectories over time and normalizes it by the distance the observed drifter travels over the same period. In other words, it compares how far the prediction strays from reality to how much the observed trajectory itself moved.

$$\mathrm{NCLS}\left(N\right)={\displaystyle \frac{{\sum }_{i=1}^N{d}_i}{{\sum }_{i=1}^N{\ell }_i}}$$

(4)

where $d_i=\parallel {\widehat{x}}_i-x_i\parallel$ is the prediction–observation separation distance, ${\ell }_i=\parallel x_i-x_{i-1}\parallel$ is the distance traveled by the observation between $i-1\to i$, ${\widehat{x}}_i$ is the predicted position at time i, $x_i$ is the observed position at time i, and N is the total number of time steps.

Interpretation

• $\mathrm{NCLS}<1$: cumulative separation is shorter than the observed path length(better);
• $\mathrm{NCLS}=1$: equal(neutral benchmark);
• $\mathrm{NCLS}>1$: separation exceeds the observed path length(worse).

Converting NCLS to a skill score(SS) [20] gives

$$\mathrm{SS}=1-\mathrm{NCLS}=1-{\displaystyle \frac{{\sum }_{i=1}^N{d}_i}{{\sum }_{i=1}^N{\ell }_i}}$$

(5)

• $\mathrm{SS}>0$: model error is smaller than the benchmark(observed path) error;
• $\mathrm{SS}=0$: equal;
• $\mathrm{SS}<0$: model error exceeds the benchmark.

As Figure 2 and Equation (4) illustrate, NCLS removes scale effects by normalizing the cumulative timewise error by the observed path length. It is therefore suitable for comparing long-horizon predictive stability, and expressing it as a skill score (Equation (5)) facilitates model-to-model comparisons at a glance.

3.4.5. Other Evaluation Metrics

Beyond the four core metrics above, additional measures are employed depending on research goals and data characteristics. These can be broadly grouped into three categories: (i) trajectory error metrics; (ii) field validation metrics; and (iii) generative model metrics.

(i)

Trajectory Error Metrics

The Liu Index, essentially a normalized measure of Lagrangian trajectory separation, quantifies trajectory prediction error from a relative, cumulative perspective and has recently been adopted in drifter-based DL studies [21]. This metric complements NCLS and skill scores by offering an alternative normalization scheme that highlights long-term divergence between predicted and observed trajectories.

(ii)

Field Validation Metrics

The Anomaly Correlation Coefficient (ACC), the Coefficient of Efficiency (CE), and the Nash–Sutcliffe Efficiency (NSE) are used for validating the accuracy of meso- to large-scale atmospheric and oceanic fields [22,23,24]. Additionally, the Lagrangian time scale (LTS), which characterizes the decorrelation timescale of velocity, gauges the flow’s memory and is used to assess the degree of model–data phase locking [21].

(iii)

Generative Model Metrics

In recent DL applications that reconstruct or augment ocean-state fields, perceptual and distributional metrics have been introduced. The Structural Similarity Index Measure (SSIM) assesses the structural fidelity of reconstructed fields, while the Fréchet Inception Distance (FID) measures the statistical distance between generated and reference distributions [25]. These metrics are especially relevant when evaluating the realism and quality of outputs from generative or restorative models.

In summary, trajectory-focused metrics (e.g., Liu Index) directly quantify drift-path errors, field-validation metrics (e.g., ACC, CE, NSE, LTS) assess consistency with physical fields, and generative-model metrics (e.g., SSIM, FID) evaluate the realism of AI-driven reconstructions. Selecting appropriate metrics depends on whether the research emphasis is on trajectory prediction accuracy, physical field validation, or the quality assessment of AI-generated outputs.

Furthermore, because prediction methodologies have evolved through successive generations, each stage tends to emphasize particular metrics that best capture its strengths and limitations. For instance, early numerical and assimilation-based methods (1st–2nd Gen) mainly relied on absolute error measures, whereas ML and DL approaches (3rd Gen) highlighted stability-oriented metrics such as NCLS and Skill Score. CNN-based and attention-based hybrids (4th–5th Gen) increasingly incorporated flow memory and large-scale validation indices, while the latest AI-based end-to-end systems (5.5th Gen) require perceptual and distributional measures to evaluate realism. This mapping is summarized in

Table 1. Generation-specific evaluation metrics for surface drifter trajectory prediction.

Generation	Representative Metrics	Rationale
1st–2nd Gen	MAE, RMSE	Focused on direct position error in numerical and early assimilation studies.
3rd Gen	NCLS, Skill Score	Emphasized cumulative separation and long-horizon predictive stability in ML and DL applications.
4th–5th Gen	Liu Index, ACC, LTS	Captured spatiotemporal consistency, flow memory, and large-scale circulation validation for CNN and attention-based models.
5.5th Gen	SSIM, FID	Addressed realism and distributional fidelity of AI-driven end-to-end generative or surrogate models.

.

4. Major Trends in Generation-Specific Research Methods

Over the past two decades, trajectory prediction research has advanced in parallel with innovations in data availability and computational resources, leading to paradigm shifts across numerical models, statistical and probabilistic methods, artificial intelligence, hybrid approaches, and AI-based data assimilation. Each methodological shift was motivated by the need to reduce the unresolved errors of its era, while simultaneously revealing new limitations.

In this section, we divide the evolution of methods, driven by changes in observational infrastructure, into six generations. Within each generation, we further classify studies by objective to organize the prediction techniques employed. This categorization is a conceptual framework adopted for analytical convenience; in practice, the boundaries between categories often overlap or become blurred for several reasons. For example, a numerically predicted trajectory may be further refined by a DL model, blurring methodological distinctions depending on purpose and architecture. In addition, the dominant physical drivers vary across regions, and the characteristics of the observational floaters employed (drifters, buoys, unpowered surface vehicles, etc.) also differ. Even when studying the same region and using the same floater type, it is difficult to match spatiotemporal conditions exactly. As a result, performance can vary substantially even when the same method is applied, requiring caution in direct comparisons or uniform classifications.

Beginning with the perceptron in 1959, research in ML focused primarily, up to the early 2000s, on relatively shallow models such as linear regression and support vector machines [26]. In Figure 3, the interval labeled as the 1st Generation (1st Gen) (2000–2005) corresponds to the stage before these traditional ML concepts were directly applied to oceanic numerical models. At that time, three-dimensional numerical models with turbulence parameterizations, together with Kalman-family data assimilation, dominated Lagrangian trajectory prediction. Key limitations identified at this stage included restrictive assumptions of linearity and Gaussianity, as well as the accumulation of forecast errors in regions with sparse observations.

Around 2005, the rapid expansion of satellite altimetry and drifter deployments raised the need to explicitly quantify uncertainty based on observations. The Second Generation (2nd Gen) denotes the period when probabilistic and statistical models such as Markov chains and ARMA were combined with large observational datasets to quantify predictive uncertainty using ensemble spread. This represented a transition from deterministic trajectories to probabilistic forecasts with explicitly defined confidence intervals.

Meanwhile, with the advent of layer-wise pretraining in 2006, DL emerged as a distinct discipline, and interest surged after AlexNet’s decisive ImageNet victory in 2012 [27,28]. As AI research grew explosively after 2015, early LSTM and CNN models began to be introduced between 2019 and 2020 as post-processors to reduce numerical-model residual errors, forming the Third Generation (3rd Gen) [29]. This stage may be considered an initial exploratory phase in the application of DL: rather than replacing traditional models outright, ML and DL were experimentally applied to drifter trajectory prediction to test their potential.

Architecture innovations such as the Transformer marked the beginning of a rapid transition to the 4th Generation (4th Gen) [30]. The hallmark of this stage is the hybrid approach, in which CNN/GCN- and attention-based models are coupled with traditional assimilation and physics-based models, either in parallel or in serial configurations, to incrementally mitigate residual errors. Large-scale DL models introduced during this period, such as FourCastNet, GraphCast, and PathNet, achieved both reduced computational cost and improved short-range forecast skill, representing a significant advancement in operational applicability.

The 5th Generation (5th Gen) The fifth generation marks the heyday of DL, where CNN-based models became the standard for short-range trajectory prediction, and Transformer and diffusion models began to be applied in research. Studies in this stage also explored attention-augmented CNN-RNN hybrids, physics-informed frameworks, and lightweight heuristic alternatives, consolidating DL as the dominant predictive paradigm while assimilation methods mainly served as stabilizing tools.

Finally, the 5.5th Generation (5.5th Gen), emerging around 2025, is defined as end-to-end (E2E) AI forecasting. In this stage, DL encoders are designed to directly ingest diverse observational datasets such as satellite radiances, GNSS-RO, and radar observations. Within a unified latent space, AI systems jointly perform observation processing, data assimilation, and forecasting in a single pipeline. Representative examples include the FuXi Weather system, which employs a PointPillars encoder for satellite brightness temperatures and GNSS-RO observations [24], the hybrid FourCastNet–3DVAR cycling system for global atmospheric fields [23], and the Aardvark Weather model, which performs E2E forecasts directly from multi-source observations without explicit reliance on numerical models [31]. These approaches illustrate a paradigm shift where AI unifies the entire observation–assimilation–forecast cycle, enabling forecasts that are both physically consistent and computationally efficient. The main flow of research across generations is summarized in Figure 3.

4.1. Numerical Models and Kalman-Series Assimilation (First Generation)

In the early 2000s, attempts to predict Lagrangian particle (drifter) trajectories frequently combined three-dimensional ocean circulation models, such as ROMS, HYCOM, and POM, with Kalman-family assimilation methods. These approaches had the advantage of preserving the governing physical equations while correcting errors in real time; however, (i) the assumptions of linearity and Gaussian error distributions often proved invalid in strongly turbulent ocean regimes; and (ii) in observation-sparse regions, filters became ineffective, leading to the rapid accumulation of initialization and boundary-condition errors.

4.1.1. Numerical Model Applications in Oil-Spill Response

The operational feasibility of trajectory prediction systems for rapid decision support in real oil-spill scenarios and their sensitivity to factors such as the temporal resolution of wind and wave forcing were evaluated in early case studies. Garcia-Ladona et al. [8] investigated the 2002 Prestige tanker spill, driving oil-dispersion models (GNOME, PICHI) with wind and wave forecasts from numerical models (HIRLAM, ARPS, WAM). Drag coefficients were empirically tuned using in situ buoy and satellite observations and the predicted trajectories showed general agreement with observed buoy tracks. This suggested the feasibility of such systems for real-time incident response forecasting.

Collectively, these studies illustrate the defining feature of the 1st Gen. While numerical models coupled with Kalman-type corrections achieved physical consistency and short-term accuracy gains, their effectiveness was highly dependent on drifter density. In observation-sparse regions, forecast errors still accumulated rapidly, highlighting a structural limitation that later motivated the shift toward probabilistic and data-rich approaches in the 2nd Gen.

4.1.2. Probabilistic Correction Based on Drifter Density

The spatial density and placement of drifter observations strongly influence the skill of Gauss–Markov–Kalman corrections and the reduction in predictive uncertainty, thereby informing the design of optimal observing systems. Özgökmen et al. [32] used an idealized MICOM double-gyre experiment with massive virtual deployments, predicting positions with an AR(1) Gauss–Markov model (a first-order autoregressive process in which the current state depends linearly on the previous state plus random noise) and a simple Kalman filter. They demonstrated that increasing the number of neighboring buoys ($N_R$, defined as the number of drifters assimilated into the local correction) reduced RMSE in proportion to $N_R^{-1/2}$, thereby theoretically establishing drifter density as a dominant control on predictive uncertainty. Castellari et al. [33] applied the same Gauss–Markov and Kalman framework to Adriatic Sea drifter data, confirming that even $N_R\ge 1$ led to a measurable reduction in forecast error. Despite differences in data sources (model-based vs. observational) and study domains, both studies reached the common conclusion that denser observing networks enhance the accuracy of probabilistic correction.

4.1.3. Summary

All three studies underscore the importance of observational density. Garcia-Ladona, Özgökmen, and Castellari each identified the number of neighboring drifters, $N_R$, as a key variable governing trajectory prediction accuracy. However, in practice, increasing observational density is not easy. In regions such as the open ocean or polar seas, deploying and maintaining dense drifter networks is costly and logistically difficult. As a result, initial-condition uncertainties persist in practice, and prediction errors accumulate despite methodological advances. These study results are summarized in

Table 2. Representative studies in the 1st Gen.

Authors (Year)	Data/Region	Models/Methods	Key Findings/Applications
Garcia-Ladona et al. (2005) [8]	Prestige spill: in situ buoys and satellite data	GNOME, PICHI; HIRLAM, ARPS, WAM	Manual calibration of drag coefficients improved forecast accuracy; demonstrated feasibility for real-time spill response
Özgökmen et al. (2000) [32]	MICOM double-gyre virtual buoys	AR(1) Gauss–Markov and Kalman filter; assimilation of $N_R$ neighbors	$N_R\uparrow \Rightarrow$ RMSE $\propto N_R^{-1/2}$; theoretical validation
Castellari et al. (2001) [33]	Adriatic Sea observed drifters	Gauss–Markov and Kalman filter	Increasing $N_R$ reduced 24 h RMSE; improved short-term coastal trajectory forecasts

, which shows that denser observations help mitigate long-term divergence driven by nonlinearity and boundary-condition errors.

4.2. Statistical and Probabilistic Models and the Expansion of Observations (Second Generation)

Since the mid-2000s, surface drifter observations accumulated rapidly. After reaching its target of 1250 units in September 2005, the GDP continued deployments, and by 2024, exceeded a cumulative total of 30,000 [34].

At the same time, satellite altimeters such as Jason-1, CryoSat-2, and SARAL/AltiKa were launched and became operational, enabling scans of sea surface height over mid-latitude regions at roughly 7 km spacing every ten days. With the increasing abundance of observations, researchers began quantifying forecast uncertainty. This survey identifies four major approaches. First, the Markov chain method records the probability of a particle moving from one grid cell to another in a transition matrix and computes the distribution after time t by raising the matrix to the tth power. Second, the Monte Carlo particle-dispersionapproach randomly releases thousands of virtual particles around the initial position and simulates ensembles of trajectories under observed wind and current fields, thereby estimating dispersion statistics such as the mean, variance, and percentiles. Third, AR/ARIMA time-series models construct linear regression, style predictors from past data, providing both the next-step prediction and its associated forecast error bounds (±1 standard deviation). Fourth, 3DVAR and 4DVAR data assimilation schemes optimize the initial state by comparing observations with the model background (3DVAR) or by assimilating a continuous time window of observations (4DVAR), which also enables an estimation of error covariances. These methods yield state-variable probability distributions together with quantified uncertainties. All four approaches provide probability distributions or error bounds for predictions, making them highly effective in applications such as pollutant-dispersion tracking and SAR, where prioritizing search regions is critical.

Collectively, these approaches marked a clear departure from the deterministic forecasts of the 1st Gen. By explicitly quantifying uncertainty through probability distributions and confidence intervals, 2nd Gen methods enabled decision makers to evaluate not only the most likely trajectory but also the range of possible outcomes. This probabilistic framing distinguished the 2nd Gen as a precision-oriented refinement of trajectory prediction, directly reflecting the rapid growth of observational data during this period.

4.2.1. Lagrangian Validation for Diagnosing Numerical-Model Limits

This approach aims to identify structural limitations and sensitivities (e.g., resolution, tidal processes) in numerical models by directly comparing drifter observations with model-integrated trajectories. Huntley et al. [35] compared SVP drifter tracks deployed in the field with results obtained by integrating offline velocities from the EAS16 ocean model. Using Lagrangian metrics (trajectory separation distance and Time-in-Circle, which measures the duration a predicted drifter remains within a specified radius of the observed position), they assessed the impacts of tides, spatial and temporal resolution, and deployment timing on forecast errors, while quantifying the gain in predictive skill, showing in particular that forecast skill degraded when the temporal resolution was coarser than 8 h, thereby revealing structural limits of model-centric approaches.

4.2.2. Improving Short-Range Skill via Drifter-Based Data Assimilation

The goal here is to assimilate drifter positions and velocities (using 4DVAR or particle filters) to adjust the initial state and surface currents, thereby improving short-term trajectory forecasts. Muscarella et al. [36] assimilated surface velocities inferred from drifter positions in the Gulf of Mexico into an NCOM–4DVAR system. Compared with experiments using only SST, ARGO, and XBT (Expendable Bathythermograph, a probe that measures vertical ocean temperature profiles), they reproduced the position and shape of the Loop Current ring more accurately and substantially reduced the growth rate of the mean trajectory error. Holm et al. [7] combined a shallow-water model with a GPU-parallelized Implicit Equal-Weights Particle Filter (IEWPF) to assimilate synthetic drifter velocities. Even with observations covering only 0.1% of the state space, the 12 h forecast RMSE decreased markedly, with the improvements being most pronounced in turbulent regimes.

4.2.3. Summary

All three studies reported the common limitation that forecast errors increase rapidly with longer horizons. The studies summarized in

Table 3. Representative studies in the 2nd Gen.

Authors (Year)	Data/Region	Models/Methods	Key Results/Objectives
Huntley et al. (2011) [35]	SVP drifters and EAS16 (Kuroshio front and shelf)	Sensitivity to tides and resolution via Lagrangian metrics	Forecast skill degraded when temporal resolution > 8 h; retained only within 24–36 h
Muscarella et al. (2015) [36]	Gulf of Mexico drifter positions and velocities plus SST, ARGO and XBT	NCOM–4DVAR (4-day cycle)	Assimilating drifter velocities ⇒ improved Loop Current ring depiction; substantially slower growth of trajectory error
Holm et al. (2020) [7]	Synthetic drifter and buoy velocities	Shallow-water model and IEWPF (GPU)	Even 0.1% observational coverage reduced 12 h RMSE; most pronounced improvements in turbulent regimes

demonstrate that higher spatial and temporal resolution mitigates this error growth rate. Accordingly, 2nd Gen systems can be regarded as precision-oriented refinements of prediction systems. They reflect the probabilistic nature of forecasts based on drifter data and supplement and correct numerical models through statistical methods and data assimilation. Nevertheless, in sparsely observed regions, large initial-condition uncertainties remain, and in practice this problem is fundamentally difficult to resolve due to the high cost and logistical limitations of expanding observational networks.

In summary, the 2nd Gen provided probabilistic forecasts and short-range accuracy gains as a precision-oriented refinement, but reliance on dense observations and instability beyond one to two days remained structural constraints. The need to reduce these unresolved errors, together with widespread GPU acceleration and high-resolution reanalyses such as ERA5, motivated the adoption of ML/DL approaches in the 3rd Gen.

4.3. Introduction of Machine Learning and Deep Learning (Third Generation)

Around 2019, with widespread GPU acceleration and the establishment of high-resolution reanalysis datasets such as ERA5, ML and DL models began to be applied to trajectory prediction. Researchers trained directly on time-series data such as drifter positions, wind speed, and sea surface height rather than relying solely on numerical-model outputs, with several studies reporting significantly reduced 1-day lead and lag RMSEs (i.e., errors measured one day before and after the forecast reference time) compared with numerical models. This marked a transition from probabilistic but model-tied forecasts in the 2nd Gen to data-driven sequence models that learned spatiotemporal dynamics directly from observations. However, RNN-based approaches revealed two major limitations: they exhibited instability in capturing long temporal dependencies, and the physical mechanisms underlying their predictions remained difficult to interpret, and thus the long-standing black-box critique persisted.

4.3.1. Machine Learning, Deep Learning, and Evolutionary Computation

Nam et al. [37] compared a numerical model (MOHID) with ML regressors (SVR, RBFN, etc.), DL models (e.g., LSTM), and evolutionary algorithms (DE, PSO, CMA-ES), using Korean coastal drifter data as input. Employing drifter positions, wind velocity, and flow velocity as predictors with cross-validation, RBFN reduced MAE by 35.2% relative to MOHID, while LSTM achieved a 6.24% improvement in NCLS. Evolutionary algorithms (CMA-ES, DE, PSO) also improved both MAE and NCLS over MOHID, achieving performance above the numerical-model baseline, though their accuracy gains were more modest than those of RBFN or LSTM. Together, these independently applied approaches, including evolutionary computation, lightweight ML, and sequence-model-based DL, demonstrated clear potential to match or surpass traditional numerical models.

4.3.2. Hybrid RNNs for Physics-Model Bias Correction

This hybrid approach employs an LSTM to learn the residuals left by a physics-based model (e.g., wind/wave effects) and then post-processes the numerical predictions to correct residual biases. Aksamit et al. [38] computed physics-based trajectories by solving the Maxey–Riley equation with AVISO geostrophic velocities and ERA5 winds, then used an LSTM to correct wind-drag and wave effects not captured by the physics model. In submesoscale mixing regimes, this hybrid method achieved notable improvements in both the RMSE and skill score.

4.3.3. Summary

Nam et al. demonstrated that evolutionary computation, compact ML, and sequence-model DL can independently serve as viable alternatives or complementary tools to numerical models, while Aksamit et al. showed that a hybrid RNN architecture, consisting of a physics model plus LSTM correction, can deliver practical improvements in predictive skill under real-world conditions. However, both studies also highlighted persistent the limitations of RNN-based architectures: sensitivity to the training-data distribution and limited generalization. The representative works discussed in this section are summarized in

Table 4. Representative studies in the 3rd Gen.

Authors (Year)	Data/Region	Models/Methods	Key Results/Objectives
Nam et al. (2020) [37]	Korean coastal drifters (2015–2016); wind; currents	SVR, GP, RBFN, LSTM; DE, PSO and CMA-ES	RBFN MAE 0.0556 (−35%), LSTM NCLS 0.8762 ($+6.24$%) → outperformed MOHID baseline
Aksamit et al. (2019) [38]	AVISO velocities and ERA5 winds (North Atlantic)	Maxey–Riley physics model with LSTM correction	RMSE↓ and skill score↑ in submesoscale regimes; demonstrated the effectiveness of the hybrid approach

. In operational settings, long-term drifter records are often difficult to obtain consistently, and the distribution of training data varies significantly across regions and seasons. This sensitivity to data distribution leads to large performance differences depending on the study area, making robust generalization in real-world applications particularly challenging.

In summary, the 3rd Gen demonstrated the feasibility of replacing or augmenting physics-based models with ML/DL to achieve short-term gains. Yet the black-box nature, sensitivity to regional data distribution, and instability beyond one or two days reveal structural weaknesses. These challenges motivated the integration of attention mechanisms and hybrid assimilation strategies in the subsequent 4th Gen.

4.4. Rise of Machine Learning and Deep Learning (4th Generation)

Since the late 2000s, GPS drifter observations have accumulated on a large scale, and high-resolution reanalysis products such as ERA5, HYCOM, and GLORYS12V1 have become widely available. At the same time, CNN-based studies proliferated in other fields, and trajectory prediction research increased in parallel.

4.4.1. CNN-Based Trajectory Prediction

These studies aim to replace or complement traditional Lagrangian integration with deep spatiotemporal regression networks and to improve short-range trajectory prediction accuracy. Botvynko et al. [21] designed DriftNet (CNN-ConvLSTM) using GLORYS12V1 velocities and GDP drifter tracks, achieving improvements in RMSE, the Liu index, and the Lagrangian Time Scale (LTS). Grossi [39] applied an SST-GCNN to GLAD drifter observations, achieving Day-5 forecast errors of about 50 ± 35 km, roughly 25 km lower than ARIMA. Earlier, HYCOM synthetic trajectories had been used to test simpler ANNs, not to train the SST-GCNN. Zeng et al. [40] applied a ResNet–GRU–Attention model to multifunctional buoy time series, lowering the MAE relative to GRU and LSTM. Jenkins et al. [41] generated probabilistic trajectory PDFs from numerical velocities and regressed the next-step ${\mathrm{P}\mathrm{D}\mathrm{F}}_{t+1}$ with a U-Net, thereby learning distributional evolution without explicit ensembles. All four studies shared the common goal of directly regressing trajectories (or distributions) to replace or complement traditional Lagrangian integration, extracting spatial patterns with CNN filters and temporal or probabilistic structures with deep models. They typically fuse Eulerian and Lagrangian inputs at the model-ingestion stage (e.g., GLORYS, HYCOM fields with buoy time series). Although lead times were short (6 h–2 d), they reported 15–30% gains in RMSE and the Liu index.

4.4.2. Parameter Estimation and Observation-Based Wave Prediction

The research can broadly be viewed as following two main directions. The first is estimating physical constants that were fixed in numerical models, such as wind-drag and diffusion coefficients, using ML. The second is directly predicting ocean wave variables from observations. Liu et al. [42] inverted the Wind Drift Factor (WDF) from globally distributed unmoored-buoy data and trained SVR-PM, achieving more accurate predictions than fixed coefficient schemes. This line of work focuses on reducing uncertainty by regressing parameters that numerical models have historically treated as constants. By inverting target parameters from observations and validating against real incidents, the study reported a reduced error and tighter predicted impact areas compared with fixed-coefficient baselines. Domala et al. [43] used NOAA buoy measurements (WDIR, WSPD, GST, PRES, ATMP, etc.) to predict significant wave height, wave speed, and average wave period. Comparing FBProphet with ensemble ML methods (random forest, gradient boosting, and XGBoost), the study found that random forest and XGBoost generally delivered the best performance, with XGBoost being the fastest. This approach highlights the direct data-driven prediction of wave parameters from buoy observations, in contrast to traditional numerical-model-based approaches.

4.4.3. Learning-Free Hybrid Models

Alongside learning-based approaches, learning-free hybrid approaches combining numerical models, statistical analysis, and optimization have also been shown to improve trajectory skill. Pan et al. [44] constructed a space–air–sea–ground integrated monitoring network-based forecasting system, coupling Lagrangian drift and oil-spill models with operational ROMS and WRF forecasts, while HYCOM currents were included for ensemble purposes. Updating the simulations with satellite and airborne SAR–derived positions markedly improved the accuracy of the forecast trajectories. Lee et al. [45] applied PCA and a genetic algorithm (GA) to simulated particle trajectories, achieving a mean position error of 0.053°. The study also reported an average data error of 3.2%.

4.4.4. Summary

Leveraging high-resolution reanalyses and large-volume drifter observations, 4th Gen studies explored diverse strategies to replace or complement traditional Lagrangian integration. CNN-family networks effectively captured spatial patterns, while coupling with temporal models further improved forecast performance. Some studies employed ML to infer fixed numerical-model parameters (e.g., wind-drag coefficients) from observations, whereas others directly predicted wave variables from observational records. In addition, learning-free hybrids, which combine numerical modeling, optimization, and statistical methods, demonstrated practical improvements in accuracy. The representative studies discussed above are summarized in

Table 5. Representative studies in the 4th Gen.

Authors (Year)	Data/Region	Models/Methods	Key Results/Objectives
Botvynko et al. (2023) [21]	GLORYS12V1; GDP drifters	DriftNet (CNN-ConvLSTM)	RMSE and Liu index improved; potential for velocity inverse problem
Grossi (2021) [39]	GLAD drifters (HYCOM synthetic trajectories used earlier for ANN tests)	SST-GCNN	Day-5 forecast error ≈ 50 ± 35 km,  25 km lower than ARIMA
Zeng et al. (2022) [40]	Chinese coastal buoys	ResNet-GRU-Attention	MAE lower than GRU and LSTM
Jenkins et al. (2023) [41]	PDF trajectories from numerical velocities	U-Net (PDFt+1 ← PDFt)	Learned distributional evolution without ensembles
Liu et al. (2023) [42]	GDP undrogued buoys	SVR-PM (WDF)	More accurate than fixed coefficient schemes; higher SAR overlap
Domala et al. (2022) [43]	NOAA buoy wave and meteorology	XGBoost, etc. (comparison)	XGBoost best in $R^2$, RMSE, MAE
Pan et al. (2021) [44]	Sanchi incident; SAR and buoy; ROMS, WRF and HYCOM	Real-time ensemble Lagrangian	Observation-forecast integration; highest precision
Lee et al. (2020) [45]	32k-particle simulation	PCA and GA	Mean position error 0.053° (3.2%)

. Nevertheless, these approaches remain limited in practice. Most studies have focused on short lead times and forecast that skill degrades rapidly beyond this horizon. In addition, model performance is highly sensitive to the availability and quality of high-resolution observations, which means that, in regions with sparse data the accuracy gains are much harder to realize. Finally, the reliance on intensive computational resources and the lack of explicit physical constraints pose further challenges for real-time operational deployment.

4.5. Heyday of Deep Learning and Method Diversification (5th Generation)

Around 2024, CNN-based DL became the de facto standard for trajectory and pollutant dispersion prediction. Transformer and diffusion models were also explored, aiming to capture long-range spatiotemporal interactions and improve spatiotemporal sequence forecasting. However, concerns over black-box behavior, overfitting, and violations of physical constraints gave rise to three concurrent strands of research. These are (i) attention-augmented CNN-RNN models, (ii) physics-informed or physics–numerical-model fusion, and (iii) lightweight ML and heuristic alternatives.

4.5.1. CNN-RNN and Attention Variants

These methods extract spatial patterns with CNNs and temporal dependencies with RNNs, then apply attention to highlight key spatiotemporal features, thereby capturing both long- and short-term dependencies. Ning et al. [46] trained on Argo GDAC and AVISO with SRU and TSFFAM attention, reducing position RMSE relative to LSTM. Botvynko et al. [47] applied DriftNet (CNN-ConvLSTM) to GLORYS, observed, and synthetic trajectories, outperforming both numerical and earlier DL models. Song et al. [48] processed 15 environmental variables with a CNN-BiGRU–Attention model, lowering RMSE at longer lead times compared with BiLSTM and Transformer. Chen et al. [49] proposed DriftNet, introducing a Target-Area Differential Attention (TADA) mechanism and a Direction–Distance Loss (DDL) to jointly reduce spatial and directional errors, achieving over 50% improvement in ${\mathrm{N}\mathrm{C}\mathrm{E}\mathrm{S}\mathrm{D}}_{72}$ (a normalized cumulative separation distance metric similar to NCLS) compared with physical and traditional ML models in the Taiwan Strait. All four studies share a common structure in which CNN filters extract spatial patterns and RNNs capture temporal dependencies, while three of them further apply attention mechanisms to weight important spatiotemporal cues. They also merge satellite altimetry and reanalysis currents with observed drifters, thus jointly learning from Eulerian and Lagrangian sources.

4.5.2. Physics-Informed and Numerical-Model Fusion

This line of research focuses on embedding physical constraints at the loss, input, or post-processing stages to retain computational efficiency while strengthening physical consistency and uncertainty quantification. Lyu et al. [25] trained a DiffusionLSTM on MODIS (MODSD) remote sensing sequences and coupled it with OpenOil simulations driven by GLORYS and reanalysis winds, generating short-interval oil spill images. Compared with ConvLSTM and GAN-LSTM, the framework achieved a lower FID and higher SSIM. Beiser et al. [50] applied EnKF and PF within a GPU-accelerated shallow-water ensemble framework to assimilate observations and quantify uncertainty in local drift forecasts, using ensemble statistics (and KDE) to represent predictive distributions. Fajardo-Urbina et al. [51] proposed a ConvLSTM surrogate trained with forcing and outputs from GETM simulations to predict tidal-cycle advection and dispersion statistics, providing results within seconds and being over 30 times faster than a traditional LPTM. Bang et al. [52] trained a PINN-Sparse Regression model on HYCOM synthetic trajectories, reducing RMSE relative to interpolation (IDW/Kriging) and increasing MS-SSIM. Together, these works show that embedding physical laws or numerical-model outputs at various stages can combine DL efficiency with physical consistency. Notably, they add capabilities such as uncertainty quantification (EnKF and PF), PDE-term estimation (PINN-SR), and video-sequence restoration (DiffusionLSTM).

4.5.3. Lightweight Machine Learning and Heuristic Alternatives

Instead of complex deep networks, these studies employ interpretable, lightweight models and heuristics for real-world settings where data are limited or a rapid response is required. Kim et al. [53] generated numerous features, selected six via a GA, and ensembled LR, SVR, LGBM, achieving over 75% accuracy improvement compared with a baseline. Tombul et al. [54] used a wind-current weighted moving-average model based on ERA5 and CMEMS, enabling rapid trajectory tracking with errors within 30 km. Both studies emphasize interpretability and computational efficiency over deep complexity, with Kim aiming for parsimonious inputs with strong predictive performance through GA-based feature selection plus ensembling, whereas Tombul pursues simplified structure with high computational speed through physical heuristics—both highlighting promise for real-time or data-constrained applications.

4.5.4. Summary

All three strands mitigate data scarcity by the leveraging combinations of satellite altimetry, reanalysis currents, and observed drifters, with some also incorporating synthetic trajectories. They consistently report improved evaluation metrics (e.g., RMSE, NCLS, Skill Score) compared with prior baselines. CNN-RNN and Attention Variants emphasize efficient data-driven learning, while physics-informed fusion enhances physical consistency and quantifies uncertainty. Although most studies are DL-centric, lightweight ML and heuristics counterbalance DL’s dominance by prioritizing interpretability and computational efficiency. Furthermore, the representative results of these studies are systematically summarized in

Table 6. Representative studies in the 5th Gen.

Authors (Year)	Data/Region	Models/Methods	Key Results
Ning et al. (2024) [46]	Argo GDAC; AVISO altimetry	SRU; TSFFAM attention	Reduced position RMSE vs. LSTM
Botvynko et al. (2025) [47]	GLORYS12V1; synthetic and observed trajectories	CNN-ConvLSTM	Outperformed prior numerical and DL methods
Song et al. (2024) [48]	GDP drifters	CNN-BiGRU–Attention	Higher $R^2$ and lower RMSE than BiLSTM and Transformer
Chen et al. (2025) [49]	Taiwan Strait; ROMS reanalysis and observed drifters	TADA and DDL	>50% improvement in ${\mathrm{N}\mathrm{C}\mathrm{E}\mathrm{S}\mathrm{D}}_{72}$ vs. physical and ML baselines
Lyu et al. (2024) [25]	MODIS NIR; GLORYS; OpenOil	DiffusionLSTM; OpenOil	Higher SSIM, lower FID, 2.5 km error reduction
Beiser et al. (2024) [50]	NorKyst; drifters	Shallow-water ensemble; EnKF and PF	Probabilistic drift forecasts and quantified uncertainty
Fajardo-Urbina et al. (2024) [51]	Dutch Wadden Sea; GETM-based residual transport (A, D)	ConvLSTM surrogate with simplified LPTM	Tidal-cycle advection/dispersion predicted in seconds;  30× faster than LPTM
Bang et al. (2024) [52]	HYCOM synthetic drifters	PINN-sparse regression	Lower RMSE vs. IDW and Kriging; higher MS-SSIM
Kim et al. (2024) [53]	GDP and OpenDrift	GA-selected 6 features → LR, SVR and LGBM ensemble	>75% accuracy improvement over baseline
Tombul et al. (2023) [54]	ERA5 winds; CMEMS currents	Wind-current weighted moving average	Simple implementation; error ≤ 30 km

, providing a concise comparison of data, methods, and outcomes across different approaches. Nevertheless, important limitations remain in practice. Pure deep learning approaches often lack explicit physical consistency, which forces operators to conduct additional post-verification to ensure that predictions are physically plausible. This challenge is compounded by the fact that dominant physical processes differ across regions (e.g., tides in coastal seas, mesoscale eddies in the open ocean, or ice dynamics in polar waters), making generalization particularly difficult. To address these issues, physics-informed and hybrid models have been introduced, but they are still computationally demanding. Meanwhile, lightweight ML and heuristic alternatives offer greater efficiency and interpretability, yet their simplified assumptions often sacrifice accuracy, especially under complex and rapidly evolving ocean conditions. As a result, although these methods have significantly improved short-term accuracy, their robust and reliable deployment in real-world operations is still constrained by unresolved challenges.

4.6. Data–AI Integration (5.5th Generation)

Until recently, most studies have focused on leveraging numerical models, in situ drifters, buoy records, or simulated particle trajectories, and on the methods applied to exploit these datasets. More recently, however, research has advanced beyond merely using existing data as predictors. AI is beginning to play a direct role in data assimilation, learning nonlinear mappings between observations and forecasts and correcting the initial state of numerical models. In other words, while 5th Gen techniques (LSTM, CNN, Transformer, etc.) explored how best to utilize available data for prediction, a parallel line of research seeks to improve the reliability of initial conditions by processing observations into more accurate analyses. Accordingly, we define a new stage in which AI directly intervenes not only in the use of observational data but also in their interpretation and correction; we refer to this as the 5.5th Gen. In particular, recent DL models are being used to integrate observations into physics-based numerical models, with growing efforts to replace or complement traditional variational and Kalman-filter approaches. This approach has become increasingly powerful as the resolution and diversity of observations (e.g., satellite products, reanalyses) have grown, attracting attention across the ocean–atmosphere–climate system for improving forecasts in sparsely observed regions, reducing computational costs, and maintaining physical consistency.

4.6.1. Online Deep Learning-Filter Coupled Systems

A DL model first produces a background forecast, and then a filter (e.g., EnKF, 3DVAR) updates the analysis in real time by assimilating observations in the network’s latent space. This removes the need for traditional observation operators (e.g., RTTOV), allowing highly nonlinear data— native-gridded satellite radiances and proxy records—to be ingested directly. Sun et al. [24] (2025) combined a CNN surrogate model (Net) with an IHEnKF filter online, using CESM-LME ensembles and PAGES 2k proxies as inputs. With a hybrid weight of 0.7, the Net and Analog experiment (Exp_NETANA) outperformed the LIM-based baseline (Exp_LIM) in both global-mean CE and RMSE, with even larger gains in data-sparse regions.

4.6.2. Cycling Integration of Deep Learning Forecast and Assimilation

A DL assimilation network ingests large-volume observations, such as native-gridded satellite radiances and GNSS-RO, to produce analyses every 6–8 h, while a companion deep learning model generates forecasts beyond 10 days. Because analysis and forecasting are closed within a single framework, computational costs decrease substantially compared with traditional numerical models. Sun et al. [22] sparsified FY-3E/Metop-C satellite brightness temperatures and GNSS-RO with a PointPillars encoder to generate 6-hourly analyses, and FuXi then produced 10-day forecasts. The useful lead time for Z500 (ACC $\ge 0.6$) increased from 9.25 to 9.50 days versus ECMWF HRES; for T2M, whereas HRES loses skill in roughly 2 days, FuXi Weather maintained ACC $>0.6$ throughout 10 days.

4.6.3. Deep Learning Surrogates with Traditional Filters (Hybrid)

In this approach, a high-resolution DL surrogate model (e.g., FourCastNet) provides the background, while the analysis step continues to use a traditional 3DVAR/EnKF algorithm. The working hypothesis, supported by both theoretical analysis and empirical validation, is to secure short-lead accuracy and retain filter stability, though divergence can occur when the observation density is low. Adrian et al. [23] ran a year-long cycling 3DVAR with FourCastNet 6 h backgrounds; across 20 atmospheric variables, the 3DVAR analysis delivered lower RMSE and higher ACC than observation-only interpolation (initial guess), and the resulting FourCastNet short-range forecasts (0–48 h) also showed reduced errors and improved the initialization of extreme events.

4.6.4. End-to-End Observation-Based Models: Full Replacement of Numerical Models

E2E systems replace each stage of conventional NWP, including data assimilation, numerical integration, and post-processing, with a single deep learning model; at forecast time, they operate directly from observations without relying on numerical-model outputs or initial conditions. In other words, numerical models are used only as a training reference, while operational forecasts are driven solely by observations. Allen et al. [31] proposed the Aardvark Weather system. Given observations from the past 1–24 h, including satellite remote sensing (ASCAT, AMSU, IASI, etc.) and surface networks (HadISD, ICOADS, IGRA), the model’s Encoder–Processor–Decoder pipeline performs initial-state construction, gridded forecasting, and local forecasting. The outputs include global forecasts on a 1.5° grid and point forecasts (2 m temperature, 10 m wind) at thousands of sites, with errors lower than those of GFS and approaching the performance of ECMWF HRES. They also demonstrated region-specific optimization via pretraining and fine-tuning.

4.6.5. Summary

Collectively, 5.5th Gen studies reconstruct or augment every stage of the traditional observation–assimilation–forecast pipeline with AI, learning nonlinear mappings between observations and forecasts to improve both initial-condition accuracy and forecast reliability. DL models (i) directly ingest complex datasets (e.g., satellites, proxies) without explicit observation operators, (ii) fuse with Kalman filters/3DVAR in latent space to reduce RMSE even in sparsely observed regions, (iii) hybridize high-resolution surrogates with traditional filters to secure long-horizon stability, and (iv) advance to E2E systems that generate global forecasts from observations alone. Reported outcomes include extended Z500 Anomaly Correlation Coefficient (ACC) duration (≈0.25 day), the improved initialization of extreme events, reduced global RMSE, and lower computational cost. In short, the 5.5th Gen represents a new paradigm where AI unifies data assimilation and forecasting into an end-to-end framework, maintaining physical consistency while addressing the dual challenges of sparse observations and massive sensor data. The representative works are summarized in

Table 7. Representative studies in the 5.5th Gen.

Authors (Year)	Data/Region	Models/Methods	Key Results/Objectives
Sun et al. (2025) [24]	CESM-LME simulations; PAGES 2k proxies (global)	CNN surrogate; IHEnKF online DL–filter coupling	Higher CE and lower RMSE vs. LIM; larger gains where proxies are sparse; complements low-density data
Sun et al. (2025) [22]	FY-3E and Metop-C BT; GNSS-RO (global)	PointPillars encoder; FuXi forecaster cycling DL forecast–assimilation	Z500 ACC 0.6 duration 9.25 → 9.50 days; T2M ACC > 0.6 (10 days); reduced compute cost
Adrian et al. (2025) [23]	ERA5 background; downsampled obs (global)	FourCastNet background; 3DVAR DL surrogate with traditional filter	Year-long cycling: RMSE↓, ACC↑; 0–48 h forecast errors reduced; better extreme-event initialization
Allen et al. (2025) [31]	Satellites (ASCAT, AMSU and IASI, etc.); surface (HadISD, ICOADS and IGRA) (global)	End-to-end observation-based encoder–processor–decoder	Global 1.5° and site forecasts; lower RMSE than GFS; near-HRES skill; observation-only forecasting

, highlighting variations in data usage, methodological design, and forecast improvements across AI-based assimilation frameworks. Despite these advances, several important challenges remain. The robustness of end-to-end AI systems is still constrained by the diversity and quality of training data, which raises concerns about their generalization across regions with different dominant physical processes. Moreover, ensuring physical consistency in highly nonlinear regimes continues to require careful validation, and the integration of AI-based frameworks with existing operational infrastructures is far from trivial. Finally, while computational costs are often reduced compared to full numerical models, training and maintaining large-scale AI systems still demands substantial resources, which can hinder their deployment in real-time forecasting environments.

4.7. Comparative Summary Across Generations

Table 8. Comparative summary of different generations of surface drifter trajectory prediction methods.

Generation	Advantages	Limitations	Data Requirements
1st	Physically consistent, interpretable	Error growth in sparse regions, sensitive to initial conditions	Drifter coverage, basic wind/wave/current forcing
2nd	Probabilistic forecasts, uncertainty quantification	Limited long-range skill, dependent on observation density	Dense drifter networks, ensemble/statistical models
3rd	Improved short-range accuracy with ML/DL	Black-box, weak generalization across regions	Drifter time series with reanalysis (e.g., ERA5, HYCOM)
4th	Hybrid CNN/attention with residual correction	High computational cost, data-intensive	Fusion of reanalysis products and in situ observations
5th	High short-range accuracy, scalable DL	Risk of overfitting, limited physical constraints	Large multi-source datasets (drifters, reanalysis, satellite altimetry, winds, waves)
5.5th	End-to-end pipeline integrating obs.–assim.–forecast	Still emerging, requires massive/diverse data	Multi-source satellites (GNSS-RO, radar) and drifters

provides a concise overview of the advantages, limitations, and data requirements across six generations of surface drifter trajectory prediction methods. This summary complements the detailed generation-specific discussions presented above and helps readers quickly compare the trade-offs among different approaches. In particular, by highlighting how each generation has overcome the constraints of observational infrastructure and computational resources, the table offers a clear perspective on the progression of methodologies. It thereby serves as a practical guide for researchers to select the most suitable approach for specific contexts such as observation density, computational environment, or application objectives.

5. Conclusions and Future Directions

This survey reorganizes the scattered literature on surface drifter trajectory prediction, an area where no standard practice has yet been established, by method and objective, and provides a roadmap of prior work. First, by dividing the continuous spectrum of studies into 1st–5.5th Gen and comparing the principal techniques and results of each, we enable researchers to identify where their work sits and where potential gaps remain. Second, by highlighting studies that address physical consistency and quantitative uncertainty, topics of growing importance, we emphasize the need to move beyond reliance on a single error metric toward evaluations grounded in physical constraints and probabilistic skill. Third, by reviewing the latest advances in AI-based data assimilation and E2E forecasting (5.5th Gen), we point to promising directions for the next mainstream research trends. Taken together, this integrated perspective can accelerate collaboration between the physics and AI communities and, more importantly, provide a common foundation for next-generation trajectory prediction systems that prioritize credible uncertainty over unattainable perfection. To our knowledge, this is the first attempt to systematically classify surface drifter trajectory studies by generation and to synthesize their outcomes, offering foundational material for researchers selecting methods and designing future studies.

Early studies relied on numerical models but soon faced limitations due to mismatches between model linearity and the nonlinear dynamics of regional oceans. As observational datasets expanded, data assimilation was introduced to constrain forecasts back towards observations whenever errors arose. Nevertheless, in regions with strong turbulence and sparse observations, forecast uncertainty remained high. RNNs based on LSTM and GRU architectures (3rd Gen) directly captured temporal patterns and improved short-range accuracy, but they neglected spatial structures and thus struggled near coastlines and in eddy-rich regimes. To address this, the 4th Gen introduced hybrid strategies combining CNN-based spatial feature extraction with dynamic corrections, while the 5th Gen broadened the methodological spectrum with attention-augmented CNN-RNNs, PINNs, and lightweight ML approaches.

Importantly, researchers have not universally designed models that map drifter data to a single deterministic future position. Instead, they proposed alternatives, such as models that output probability distributions, correct physical biases, or redefine the prediction target, thereby reconfiguring the traditional goal of point-wise forecasting. These efforts suggest an implicit consensus that perfect trajectory prediction for floating bodies is fundamentally unattainable. Given the noisy nature of reanalysis inputs, such perfection remains infeasible at present. Accordingly, future work should prioritize generating credible bounds on forecast error rather than exact tracks.

In our view, three directions appear especially promising. First, probabilistic or Bayesian DL should be adopted to predict not only future positions but also the associated uncertainty distributions [55]. Second, physics-informed networks such as PINNs should be used to enforce governing laws, enabling self-correction when predictions violate physical constraints [52]. For instance, particle equations of motion could be imposed to prevent divergence in long-term forecasts. Third, regional characteristics such as current strength, turbulence intensity, and bathymetric curvature should be quantified and incorporated as input features, allowing for region-specific models that better capture spatial heterogeneity [56].

Despite these promising directions, several open challenges remain. Most critically, data sparsity continues to limit model reliability in regions with few drifter deployments or heterogeneous observational coverage. In addition, the high computational cost of advanced DL and PINN models poses obstacles to real-time deployment in time-sensitive applications. Finally, ensuring physical consistency in AI-driven forecasts remains unresolved, as purely data-driven methods may violate governing ocean dynamics. Addressing these challenges will be essential for translating methodological advances into robust and operationally credible trajectory prediction systems. Beyond methodological perspectives, practical considerations also deserve attention. Numerical and assimilation models provide strong physical consistency but often face challenges in operational feasibility due to their high computational demands. Deep learning approaches enable rapid inference once trained, supporting real-time performance, yet retraining costs and sensitivity to regional data distribution remain significant constraints. Furthermore, statistical and ML methods depend heavily on dense drifter networks, whereas hybrid and AI-based assimilation frameworks can mitigate data gaps by fusing multi-source observations but still struggle in sparsely observed regions. These factors highlight that next-generation trajectory prediction systems must balance accuracy with feasibility, timeliness, and data availability to ensure reliable real-world deployment.

Finally, a real-time ensemble framework that integrates multiple predictors and displays both forecast errors and worst-case drift pathways would enable operators to interpret and adjust results on the fly, paving the way toward next-generation trajectory prediction systems. In addition to these scientific and methodological directions, it is also essential to recognize the practical constraints of real-time operational deployment. High-resolution DL or PINN models can be computationally expensive, challenging the low-latency requirements of time-critical applications such as SAR. Similarly, while reanalysis products (e.g., HYCOM, GLORYS) provide valuable large-scale context, their latency and limited near-real-time availability constrain direct operational use. Therefore, the need for robust data pipelines that can reliably process diverse real-time observations becomes essential. Moreover, building standardized operational frameworks that integrate model inference, data assimilation, and decision-support visualization remains a significant engineering challenge. Addressing these computational, data-access, and pipeline-integration constraints is therefore indispensable for transitioning advanced prediction methods from research prototypes into reliable, real-world operational systems.

In short, integrating these three pillars (region-tailored design, physical consistency, and uncertainty awareness) is essential for realizing robust, credible, and operationally useful trajectory prediction frameworks.