Investigation of Sediment Erosion of the Top Cover in the Francis Turbine Guide Vanes at the Genda Power Station

Abstract

This study utilizes the Standard k-ε turbulence model and ANSYS CFX software to tackle silt erosion in the top cover clearances of guide vane of the Francis turbine at Genda Power Station (Minjiang River Basin section, 103°17′ E and 31°06′ N) under sediment-laden flow conditions. A numerical simulation of a solid–liquid two-phase flow along the whole flow route was performed under rated operating circumstances to examine the impact of varying guide vane end clearance heights (0.3 mm, 0.5 mm, and 1.0 mm) on internal flow patterns and sediment erosion characteristics. The simulation parameters employed an average sediment concentration of 2.9 kg/m³ and a median particle size of 0.058 mm, indicative of the flood season. The findings demonstrate that augmenting the clearance height intensifies leaky flow and secondary flow, resulting in a 0.49% reduction in efficiency. As the gap expanded from 0.3 mm to 1.0 mm, the leakage flow velocity notably increased to 40 m/s, exacerbating flow separation, enlarging the vortex structures in the vaneless space, and augmenting the sediment velocity gradient and concentration, consequently heightening the risk of erosion. An experimental setup was devised based on the numerical results, and the dynamic resemblance between the constructed test section and the prototype turbine was confirmed for flow velocity, concentration, and Reynolds number. Tests on sediment erosion revealed that the erosion resistance of the anti-sediment erosion material 04Cr13Ni5Mo markedly exceeded that of the base cast steel, especially in high-velocity areas. This study delivers a systematic, quantitative analysis of clearance effects on flow and erosion, along with an experimental wear model specifically for the Gengda Power Station, thereby providing direct theoretical support and engineering guidance for its wear protection strategy and maintenance planning.

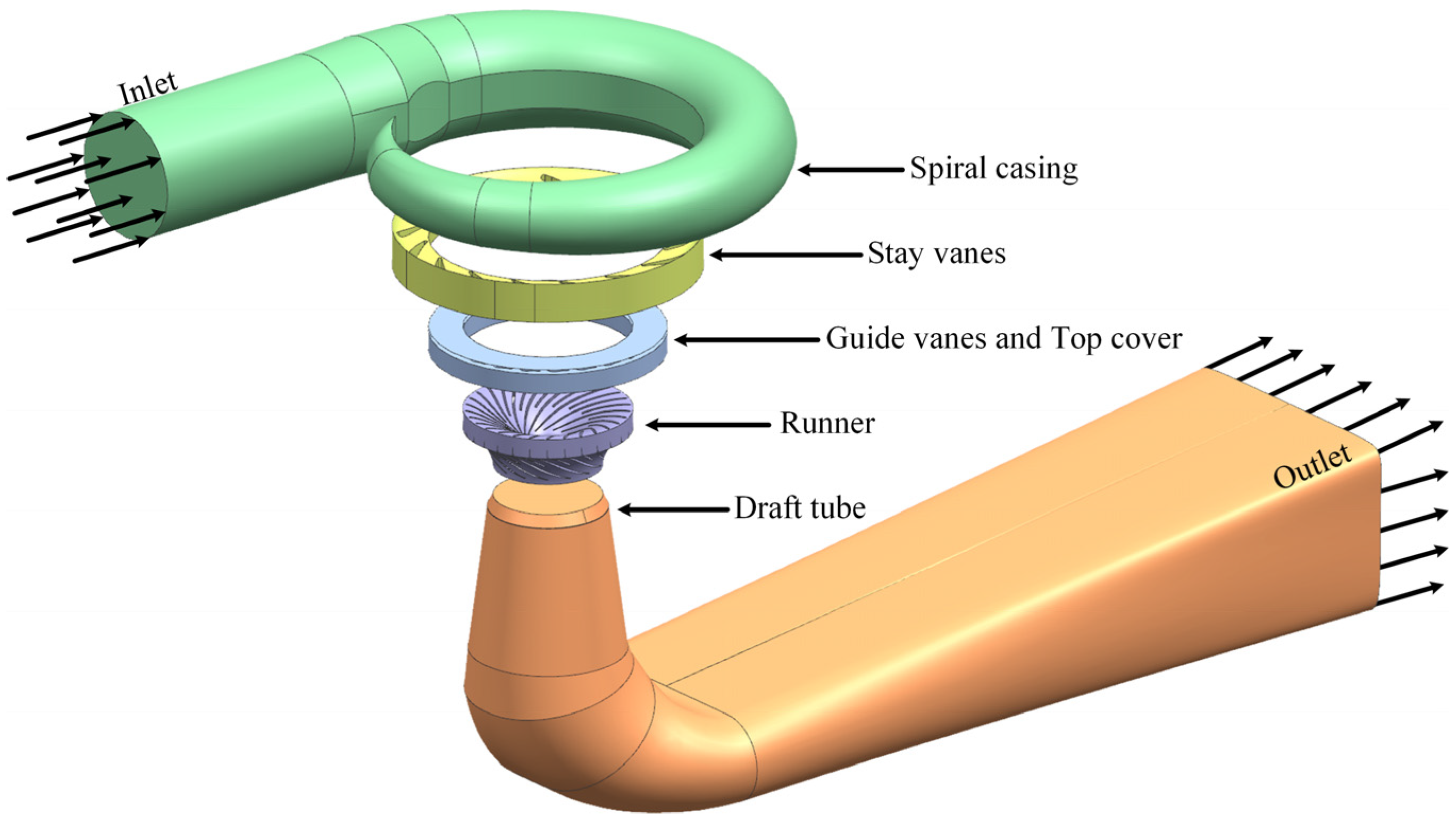
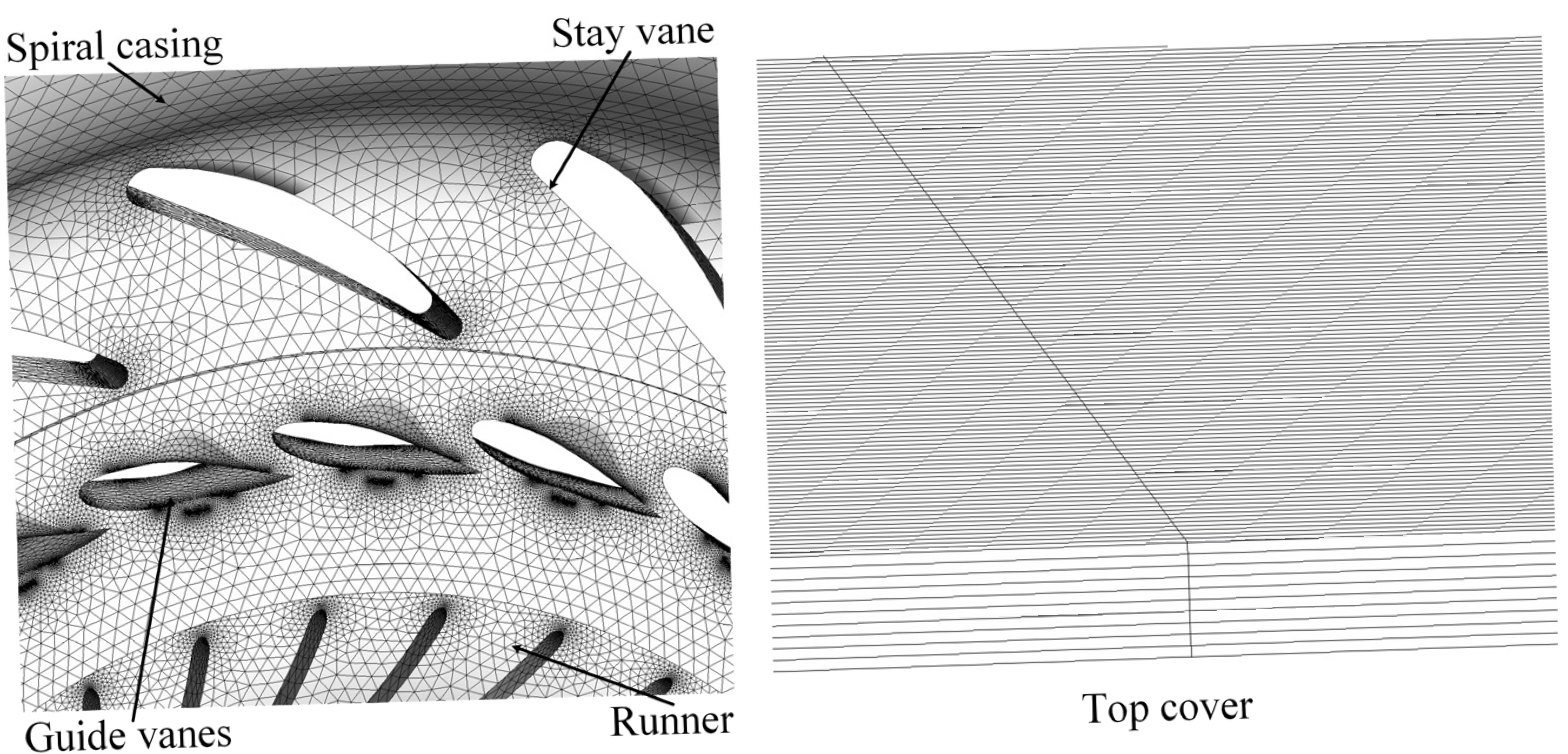
1. Introduction

The safe, steady, and efficient operation of hydraulic turbines is essential to the overall functionality of hydropower-producing facilities. Sediment-laden rivers, sediment erosion, or the combined impact of sediment erosion and cavitation significantly contribute to the deterioration of flow-passing components of turbines, resulting in performance degradation, efficiency loss, reduced service life, and potential structural damage. The Francis turbines, owing to their extensive employment, experience severe sediment erosion in the guiding vane area, characterized by elevated flow velocities and complicated flow patterns. The guide vane top cover, a key sealing and supporting component, is particularly susceptible to erosion failure due to the constant impact of high-velocity sediment-laden flow. This not only raises maintenance expenses and downtime but also poses a direct threat to the safe and stable functioning of the power station.

Recent years have witnessed substantial advancements in the study of solid–liquid two-phase flow and sediment erosion in hydraulic turbines. Liu Xiaobing [1] developed a k-ε two-equation turbulence model and a volume fraction turbulence model to simulate turbulent solid–liquid two-phase flow and to estimate wall sediment erosion in hydraulic machinery channels. Min Su Roh et al. [2] formulated an optimization model for the blade angles of Francis turbines, utilizing response surface methods and numerical simulations, resulting in an efficiency enhancement of up to 1.42% while sustaining an output power of 30 MW. Biraj Singh Thapa et al. [3] developed an improved empirical model for sediment erosion in Francis turbine runners, establishing a predictive method that demonstrates good agreement with field measurement data. Ujjwal et al. [4] conducted a numerical analysis of a Francis turbine to identify places susceptible to erosion and examine the correlation between sediment characteristics and sediment erosion. Wei Xinyu et al. [5] investigated sediment erosion in turbines functioning in hilly rivers, demonstrating the relationship between inter-blade vortices and erosion distribution based on actual sediment gradation and flow characteristics. Acharya N. et al. [6] integrated numerical simulation with experimental validation to systematically investigate leakage vortices and corresponding sediment erosion mechanisms in the guide vane and rotor-stator gaps of a Francis turbine at the Bhilangana III Hydroelectric Project in India, emphasizing the influence of these flow structures on overall turbine performance. Poudel R. et al. [7] performed experiments on a Francis model turbine within a non-circulating sediment test rig, employing visual coating techniques to qualitatively assess erosion on the runner and guide vanes across diverse operating conditions, while quantitatively measuring cumulative erosion rates and mass loss percentages for a brass runner subjected to elevated sediment concentrations. Zhao Zilong et al. [8] suggested a passive flow control technique utilizing biomimetic protuberances. Utilizing integrated numerical and experimental methodologies, they evidenced that these structures can diminish sediment erosion by over 50% by inhibiting inter-blade vortex formation, generating small-scale vortices, and expediting vortex dissipation. Longgang Sun et al. [9] utilized numerical simulations to examine the effects of sediment concentration, particle size, and operational parameters on sediment erosion in high-head Francis turbines, proposing a multi-condition, multi-objective optimization design methodology that balances erosion resistance and hydraulic efficiency. B. Rajkarnikar et al. [10] developed a rotating disc apparatus specifically designed for testing sediment erosion on Francis turbine runner blades under high-sediment flow conditions in Nepal, thereby validating the susceptibility of conventional design methodologies to material damage in such operating environments. Wang et al. [11] employed the Tabakoff-Grant erosion model and the ZGB cavitation model to investigate the factors contributing to erosion in guide vane of high-head power stations and suggested solutions to mitigate sediment erosion. Zhao Zilong et al. [12] employed a dynamic mesh-based Eulerian–Lagrangian methodology to elucidate the mechanism by which the interaction between leakage flow and main flow generates leakage vortices, resulting in significant erosion in critical regions such as the top cover, thereby clarifying the coupling effect between erosion deformation and alterations in the flow field. Song Xiji et al. [13] enhanced the gap erosion model and illustrated that particle size substantially influences particle impact characteristics in gap flow, intensifying erosion around the guide vane jet and runner crown, thus predominating energy dissipation. Zhou Ziyao et al. [14] developed a single-channel sediment erosion testing apparatus utilizing numerical simulation and similarity theory, investigating the solid–liquid two-phase flow characteristics and sediment erosion mechanisms in the Francis-99 turbine under sediment-laden conditions, and performed sediment erosion tests on its guiding components. Pang Jiayang et al. [15] employed a k-ε multiphase turbulence model to numerically simulate sediment-laden flow in both long- and short-blade Francis turbines for high-head applications in the Min River, and developed a calculation formula for the sediment erosion rate of 0Cr13Ni5Mo material flow-passing components based on experimental investigations. Rakish Shrestha et al. [16] has systematically reviewed experimental research methodologies and findings on sediment erosion in hydraulic machinery, identifying Francis turbine guide vanes and runners as critical components susceptible to erosion, thereby synthesizing quantitative models for erosion prediction and associated experimental simplification strategies.

To limit sediment erosion, the industry has taken numerous methods, including better hydraulic design, the use of wear-resistant materials, altered operational tactics, and improved sediment evacuation facilities. Among these, the precise control of the internal flow field within the turbine is recognized as a significant technical avenue. Ravi Koirala et al. [17] conducted a computational analysis of the impact of guide vane clearance on the overall performance of a Francis turbine and integrated the findings with empirical correlations to forecast clearance leakage flow. Chitrakar S. et al. [18] conducted a literature survey that elucidated the interplay between sediment erosion and secondary flow effects, which together result in heightened losses, vibrations, fatigue, and turbine failure. They deliberated on mitigating cumulative impacts by regulating either sediment erosion or secondary flow in turbines and underscored the necessity of comprehending the interplay between these two phenomena. Ravi Koirala et al. [19] employed numerical simulations and rotating disc experiments to demonstrate that non-symmetric airfoil guide vanes can effectively balance erosion resistance requirements with performance stability in Francis turbines operating under sediment-laden flow conditions, thereby providing an optimized design solution for hydropower plants facing severe abrasion issues. Thapa et al. [20] revealed that sediment erosion can lead to an increase in the clearance between the guide vanes and the top cover in low-specific-speed Francis turbines. Due to the pressure gradient between the surfaces of the guide vanes, leakage flow is generated within this gap. Khullar et al. [21] investigated the impact of non-uniform variations in the clearance between the guide vanes and the top cover on both erosion and leakage flow. Gautam S. et al. [22] conducted a numerical simulation utilizing the replacement gap approach, indicating that the vortex intensity induced by the guide vane clearance leakage flow in a Francis turbine increases with the enlargement of the clearance. They also found that asymmetric guide vanes can lessen the vortex velocity. The pressure pulsations induced by this leakage flow exhibit a frequency of half the rotational frequency and are identified as the principal cause of sediment erosion in the runner of low-specific-speed units. Jin Zhiqiang et al. [23] applied the Eulerian-Lagrangian technique coupled with the Tabakoff erosion model, indicating that a smaller guide vane aperture in a Francis turbine leads to a more substantial impact on the vortex structures and particle distribution within the runner. Biraj Singh Thapa et al. [24] conducted research on a guide vane cascade, discovering that when the guide vane clearance in a Francis turbine climbs to 2 mm, the leakage flow interacts with the main flow, generating vortices that enter the runner. This leads in the relative velocity at the crown at the runner inlet increasing up to thrice, highlighting the significant influence of clearance expansion on the runner’s flow characteristics. Saroj Gautam et al. [25] concentrated on a low-specific-speed Francis turbine in an Indian power station. Through numerical simulations, they identified the guide vane clearance leakage flow as the main cause of erosion at the runner blade inlet and confirmed a positive association between the size and shape of quartz particles and the erosion rate. Jianjun Feng et al. [26] compared CFD results with model experiments, demonstrating that the disc friction loss in a Francis turbine runner increases with the unit speed, with a bigger contribution from the shroud surface. While an increase in clearance reduces the total friction loss, it results in a drop in efficiency. Their findings proved the accuracy of CFD in estimating hydraulic efficiency around the optimal efficiency point. Ravi Koirala et al. [27], through guide vane cascade studies, observed that, after sediment erosion begins on Francis turbine guide vanes, the pressure on both sides of the blade and at the outlet increases dramatically. This illustrates the important importance of erosion morphology on the flow parameters in the guide vane region. Sailesh Chitrakar et al. [28] investigated the issue of guide vane clearance wear in a Francis turbine at a power station in Nepal. Ravi Koirala et al. [29] carefully examined the erosion of Francis turbine guide vanes in sediment-laden water, uncovering intricate flow modifications generated by erosion, such as lateral clearance flow and trailing edge leakage, and their impact on hydraulic performance. Kumar Sahu Rohit et al. [30] performed a comprehensive analysis of the erosion mechanism of Francis turbine guide vanes in sediment-laden flow. They highlighted flow anomalies generated by erosion, including secondary flows and horseshoe vortices, and their implications on unit efficiency, combining findings from field observations, experiments, and numerical models. Their research demonstrates that regions dominated by complex secondary flows and tip leakage flows are prone to forming zones characterized by high flow velocity, intense shear, and low pressure. These conditions can induce cavitation and exacerbate impact wear from sediment particles, making such areas critical targets for erosion mitigation strategies.

In contrast to previous studies, this paper systematically investigates the effects of guide vane top cover clearance height (0.3, 0.5, 1.0 mm) on the internal flow field and sediment wear of the top cover plate in the Francis turbine of the Gengda Power Station under sediment-laden flow. Based on full-passage numerical simulation results, an experimental test section satisfying dynamic similarity was designed, and comparative wear tests were conducted on the base material (cast steel) and the wear-resistant plate material (04Cr13Ni5Mo). Furthermore, a mathematical model for the sediment wear rate was established, tailored to the specific operating conditions and material properties of this power station, for engineering life prediction.

2. Numerical Calculation

2.1. Numerical Model

2.1.1. Solid–Liquid Two-Phase Flow Equation

The sediment-laden flow is represented as an isothermally incompressible Newtonian fluid with minimal heat transfer. It is presumed that the sand particles are spherical and uniform in size, and that neither the sand nor the water experiences any phase transition. In these circumstances, both phases are regarded as interpenetrating continua that occupy the same macroscopic domain while residing in separate microscopic volumes. The governing equations for solid–liquid two-phase flow are formulated within the Eulerian framework as follows:

Equation of continuity in the liquid phase:

$${\displaystyle \frac{\partial }{\partial t}}\left({\varphi }_f\right)+{\displaystyle \frac{\partial }{\partial x_i}}\left({\varphi }_f{u}_{fi}\right)=0$$

(1)

Equation of continuity in the solid phase:

$${\displaystyle \frac{\partial }{\partial t}}\left({\varphi }_p\right)+{\displaystyle \frac{\partial }{\partial x_i}}\left({\varphi }_p{u}_{pi}\right)=0$$

(2)

Momentum equation in the liquid phase:

$${\displaystyle \frac{\partial }{\partial t}}\left({\varphi }_f{u}_{fi}\right)+{\displaystyle \frac{\partial }{\partial x_k}}\left({\varphi }_f{u}_{fi}{u}_{fk}\right)=-{\displaystyle \frac{1}{{\rho }_f}}{\varphi }_f{\displaystyle \frac{\partial P}{\partial x_i}}+{\nu }_f{\displaystyle \frac{\partial }{\partial x_k}}\left[{\varphi }_f\left({\displaystyle \frac{\partial u_{fi}}{\partial x_k}}+{\displaystyle \frac{\partial u_{fk}}{\partial x_i}}\right)\right]-{\displaystyle \frac{B}{{\rho }_f}}{\varphi }_f{\varphi }_p\left(u_{fi}-u_{pi}\right)+{\varphi }_f{g}_i$$

(3)

Momentum equation in the solid phase:

$${\displaystyle \frac{\partial }{\partial t}}\left({\varphi }_p{u}_{pi}\right)+{\displaystyle \frac{\partial }{\partial x_k}}\left({\varphi }_p{u}_{pi}{u}_{pk}\right)=-{\displaystyle \frac{1}{{\rho }_p}}{\varphi }_p{\displaystyle \frac{\partial P}{\partial x_i}}+{\nu }_p{\displaystyle \frac{\partial }{\partial x_k}}\left[{\varphi }_p\left({\displaystyle \frac{\partial u_{pi}}{\partial x_k}}+{\displaystyle \frac{\partial u_{pk}}{\partial x_i}}\right)\right]-{\displaystyle \frac{B}{{\rho }_p}}{\varphi }_p{\varphi }_f\left(u_{pi}-u_{fi}\right)+{\varphi }_p{g}_i$$

(4)

where t denotes time; x represents the spatial coordinate; u indicates velocity; ν signifies the kinematic viscosity coefficient; ϕ stands for volume fraction, where ϕ_p + ϕ_f = 1; P refers to pressure; g symbolizes gravitational acceleration; ρ represents density; B denotes the interphase interaction coefficient, B = 18(1 + B₀)ρ_fν_f/$d_p^2$; d_p indicates particle diameter; the subscripts f and p correspond to the liquid phase and solid phase, respectively; and the indices i and k are tensor coordinates.

2.1.2. Turbulent Flow Model

The Standard k-ε model is among the most prevalent two-equation turbulence models in Computational Fluid Dynamics (CFD). The Reynolds-Averaged Navier–Stokes (RANS) model is formulated to simulate turbulence effects on the primary flow field via a time-averaging methodology.

Turbulent kinetic energy k equation:

$${\displaystyle \frac{\partial }{\partial t}}\left({\varphi }_{f}k\right)+{\displaystyle \frac{\partial }{\partial x_j}}\left({\varphi }_{f}k{V}_{fj}\right)={\displaystyle \frac{\partial }{\partial x_j}}\left[{\varphi }_f\left({\nu }_f+{\displaystyle \frac{{\nu }_t}{{\sigma }_k}}\right){\displaystyle \frac{\partial k}{\partial x_j}}\right]+G_k+G_b-{\varphi }_f\epsilon -Y_m$$

(5)

Turbulent kinetic energy dissipation rate ε equation:

$${\displaystyle \frac{\partial }{\partial t}}\left({\varphi }_f\epsilon \right)+{\displaystyle \frac{\partial }{\partial x_j}}\left({\varphi }_f\epsilon V_{fj}\right)={\displaystyle \frac{\partial }{\partial x_j}}\left[{\varphi }_f\left({\nu }_f+{\displaystyle \frac{{\nu }_t}{{\sigma }_{\epsilon }}}\right){\displaystyle \frac{\partial \epsilon }{\partial x_j}}\right]+C_{1\epsilon }(G_k+{\varphi }_f{C}_{3\epsilon }{G}_b){\displaystyle \frac{\epsilon }{k}}-{\varphi }_f{C}_{2\epsilon }{\displaystyle \frac{{\epsilon }^2}{k}}$$

(6)

where C_1ε = 1.44, C_2ε = 1.92, C_3ε = 1.2, σ_k = 1.0, σ_ε = 1.3, G_k denotes the turbulent kinetic energy produced by the average velocity gradient, G_b signifies the turbulent kinetic energy arising from buoyancy, and Y_m represents the contribution of the dissipation rate resulting from the diffusion of the transition [31].

This study utilized the Standard k-ε turbulence model in conjunction with typical wall functions to simulate flow in the near-wall region. This model has commendable stability and computing efficiency in simulating turbulence within the primary flow field; however, it reveals specific limits in addressing the areas characterized by significant adverse pressure gradients or flow separation. Future research may implement more sophisticated turbulence models, such as the SST k-ω model, to improve the precision of near-wall flow forecast.

2.2. Model and Mesh Generation

The research examines the turbine unit at Genda Power Station, particularly the HLA542b-LJ-215 model, with its essential parameters outlined in

Table 1. The Francis turbine basic parameters.

Parameter	Value	Parameter	Value
Design head (m)	283	Design flow (m3/s)	16
Runner diameter (m)	0.630	Rated speed (rpm)	500
Stay vane	16	Guide vane	24
Runner’s long blade	15	Runner’s short blade	15

.

A comprehensive flow passage model was developed based on the design specifications of Genda Power Station to precisely analyses the flow processes of sediment-laden water within the turbine. The model comprises the spiral casing, stay vanes, guide vanes, runner, and draft tube. The simulation was conducted under specified operating parameters, and the three-dimensional hydraulic model of the turbine under these conditions is depicted in Figure 1.

Due to the paramount significance of efficiency in turbine operation, the complete flow channel was discretized utilizing unstructured tetrahedral meshes, however the top cover clearance of the guide vane was meshed with structured hexahedral elements. Figure 2 presents a partial view of the mesh model for the turbine at Genda Power Station.

Fifteen mesh configurations with cell counts between 3.79 million and 15.37 million were created for three distinct guide vane end clearances (0.3 mm, 0.5 mm, and 1.0 mm). A grid independence analysis was performed utilizing turbine efficiency as the assessment criterion. The findings demonstrate that efficiency stabilizes at about 10.49 million, 10.61 million, and 10.59 million cells for the corresponding clearances, indicating that additional mesh refinement has minimal effect on computational correctness. The final chosen mesh sizes, balancing simulation accuracy and computing expense, were 10.49 million cells for the 0.3 mm clearance, 10.61 million for the 0.5 mm clearance, and 10.59 million for the 1.0 mm clearance. Figure 3 illustrates the validation of grid independence.

The distribution of grid numbers for the final selected mesh across various components (volute, guide vanes, runner, etc.) is presented in

Table 2. Number of meshes for different components of the Francis turbine.

Parameter	Value	Parameter	Value
Spiral casing	808,766	Runner	2,056,391
Stay vane	581,758	Draft tube	3,228,665
Guide vane (0.3 mm)	2,884,650	Top cover (0.3 mm)	928,800
Guide vane (0.5 mm)	2,386,836	Top cover (0.5 mm)	1,544,400
Guide vane (1.0 mm)	2,364,718	Top cover (1.0 mm)	1,548,000

.

2.3. Boundary Conditions

This research utilized ANSYS CFX 2022 software alongside the Standard k-ε turbulence model to perform numerical simulations of sand-water two-phase flow under specified operating circumstances across the entire flow pathway of the Francis turbine at Genda Power Station. Two stage-specific rotor-stator interfaces were established: one between the runner and the guide vanes, and another between the runner and the draft tube. The inlet boundary condition was established as a total pressure inlet, orientated perpendicular to the spiral case inlet cross-section, with a value of 2.6 MPa derived from operational monitoring data. The outlet was characterized as a pressure outlet, positioned perpendicular to the draft tube exit, with a static pressure of 67,477 Pa established based on the draft tube suction head. All wall boundaries were regarded as no-slip surfaces.

The models utilized an average sediment concentration of 2.9 kg/m³ and a median particle size of 0.058 mm, indicative of flood season conditions. The research specifically highlighted the impact of varying guide vane end clearances (0.3 mm, 0.5 mm, and 1.0 mm) on internal flow dynamics and sediment-related sediment erosion properties.

2.4. Sensitivity Analysis of Turbulence Model

The Standard k-ε (SKE) model is widely used in engineering simulations due to its excellent robustness and computational efficiency. However, this model is known to have limitations when simulating complex flows involving strong adverse pressure gradients, flow separation, and significant streamline curvature [32]. To evaluate the impact of turbulence model selection on the findings of this study, a sensitivity analysis was conducted for the 0.5 mm gap case using the Shear Stress Transport (SST) k-ω turbulence model.

A comparison of the global performance parameters calculated by the two models is presented in

Table 3. Sensitivity analysis of turbulence model to global performance parameters.

Turbulent Model	Torque/(N·m)	Flow Rate/(m3/s)	Head/(m)	Efficiency/(%)
Standard k-ε	729,615	16.27	255.25	93.79
SST k-ω	731,200	16.22	255.30	93.85

. From the perspective of global parameters, the efficiency and flow rate predicted by both models are in very close agreement, with discrepancies within 0.1%. This indicates that for the operating conditions examined in this study, the SKE model provides predictions consistent with those of the SST model from the standpoint of macroscopic energy conversion.

2.5. Comparison Validation

Based on the actual operational efficiency of the Gengda Power Station under rated conditions, a comparison was made with the numerical simulation findings (details in

Table 4. Calculation parameters of each working condition.

Clearance Height	Actual	Numerical	Difference
0.3 mm	93.1%	94.1%	1.07%
0.5 mm	92.6%	93.8%	1.30%
1.0 mm	92.1%	93.6%	1.63%

). The disparities between the numerically estimated and experimentally determined efficiencies are 1.07% for the 0.3 mm clearance height case, 1.30% for the 0.5 mm clearance height case, and 1.63% for the 1.0 mm clearance height case. The efficiencies produced by numerical simulation are consistently higher than the actual values. This divergence develops because the turbulence model struggles to effectively represent some flow properties (such as flow separation), leading to an underestimating of energy losses and thus forecasting greater efficiency numbers.

2.6. Numerical Results

2.6.1. Efficiency Change Analysis

The computational outcomes of turbine efficiency at three distinct guide vane end clearances (0.3 mm, 0.5 mm, and 1.0 mm) are encapsulated in

Table 5. Turbine efficiency calculation under different guide vane end clearances.

Clearance Height/(mm)	Torque/(N·m)	Angular Velocity/(rad/s)	Head/(m)	Flow Rate/(m3/s)	Efficiency /(%)
0.3	728,000	52.36	255.28	16.17	94.12
0.5	729,615	52.36	255.25	16.27	93.79
1.0	733,672	52.36	255.20	16.39	93.63

. An analysis of the three cases indicates that as clearance escalates from 0.3 mm to 1.0 mm, both angular velocity and head remain largely constant. Simultaneously, the torque escalates from 728,000 N·m to 733,672 N·m (+0.78%), and the flow rate rises from 16.17 m³/s to 16.39 m³/s (+1.36%). The efficiency diminishes from 94.12% to 93.63%, indicating a reduction of 0.52%. In particular, relative to the 0.3 mm clearance scenario, efficiency decreases by 0.33% at 0.5 mm and by 0.49% at 1.0 mm.

The principal cause of this efficiency decline is the secondary flow losses resulting from leaks. A wider clearance facilitates enhanced flow and torque; yet, the augmented leakage flow fosters secondary flow structures, including horseshoe vortices. The energy squandered by these vortex forms amplifies turbulent kinetic energy losses, thereby diminishing the ratio of effective power output.

2.6.2. Internal Flow Analysis

The streamwise length from the leading to the trailing edge on both sides of the guide vane end clearance is delineated and standardized to a range of 0 to 1. Figure 4 illustrates the pressure distributions on both sides of the clearance for three distinct gap sizes: 0.3 mm, 0.5 mm, and 1.0 mm.

The leakage flow through the guide vane end clearance is primarily a pressure-driven shear flow at elevated Reynolds numbers, with its intensity influenced by the pressure differential across the gap and the height of the clearance. Under all three clearance conditions, the pressure profiles demonstrate analogous trends. The pressure diminishes progressively from the leading edge to the trailing edge in the streamwise direction. On the suction side, the pressure initially falls and then climbs along the same path. The peak pressure is situated along the leading edge of the pressure side, whereas the lowest pressure is found in the mid-region of the suction side. The highest-pressure differentials across the clearances for the 0.3 mm, 0.5 mm, and 1.0 mm gaps are 0.967 MPa, 0.953 MPa, and 0.924 MPa, respectively. As the clearance expands, the pressure differential across the gap diminishes marginally, while the overall fluctuation remains quite minor.

On the suction side, the pressure begins to recover at a streamwise location of approximately 0.6. This nonlinear phenomenon is attributed to the intense shear between the tip leakage flow and the main flow in the mid-to-downstream region, which generates vortical structures leading to local flow separation and reattachment. The combined effect of the low-pressure zone at the vortex core and the pressure recovery in the near-wall reattachment region results in the characteristic “trough” and “recovery” observed in the pressure distribution curve.

Figure 5 depicts the streamline distributions for three distinct guide vane end clearances: 0.3 mm, 0.5 mm, and 1.0 mm. As the clearance expands, the leakage flow escalates, resulting in significant divergence of streamlines within the gap region. Distinct vortex formations are found, particularly under the 1.0 mm clearing condition.

The 0.3 mm clearance results in streamlines tightly adhering to the guide vane surface, signifying attached wall-bounded flow with minimal flow separation. A feeble jet exists within the near-wall low-speed layer, and the interaction between leaky flow and the primary flow is negligible, with no discernible vortex formation. A localized high-velocity jet emerges at the exit of the 0.5 mm clearance height. This jet, at an impingement angle of roughly 30°, strikes the primary flow on the pressure side of the guide vane, resulting in streamline divergence and initial flow separation. Under the 1.0 mm clearance condition, the leakage jet velocity attains 40 m/s at the gap outlet, followed by distinct vortex formations. Flow separation in the vaneless region significantly worsens, accompanied by a considerable enlargement of the separation zone.

Figure 6 depicts the distributions of turbulent kinetic energy (TKE) for three distinct guide vane end clearances: 0.3 mm, 0.5 mm, and 1.0 mm. The pressure differential induces leakage flow through the clearing, which interacts with the primary flow through shear, producing vortex formations that travel along the streamlines’ courses. A unique horseshoe vortex develops in the leading-edge area of the guiding vane.

The flow field structures under the three clearance conditions are similar, but differences exist in the magnitude and concentration regions of TKE. As shown in the Figure 6, the extent and intensity of the high-TKE regions (red) increase significantly with the enlargement of the gap. Under the 0.3 mm clearance condition, the high-TKE distribution is relatively dispersed. As the clearance increases to 1.0 mm, the flow separation intensifies, and the high-TKE region becomes more concentrated, primarily aggregating near the pressure side and the trailing edge of the guide vane. This indicates stronger and larger-scale vortex structures. The vortex core breaks down while developing downstream, generating more small-scale turbulence, which exacerbates energy dissipation and potential wear risk.

The distribution of TKE directly reflects the energy dissipation inside the flow. As the distance increases, the high-TKE region transforms from a dispersed state to a concentrated one, notably in the guide vane trailing edge region. This concentration suggests amplified shear between the leaky flow and the main flow, resulting in stronger and more coherent vortex formations. The production and subsequent breakdown of these vortices consume a considerable percentage of the flow energy, transforming it into TKE, which is ultimately dissipated as heat. This additional energy loss, driven by the tip leakage flow, provides one of the key reasons for the decline in turbine efficiency with increasing gap size (as indicated in Table 5).

2.6.3. Analysis of Sediment Abrasion

The sediment velocity refers to the mean velocity of the sediment particle phase within the Eulerian framework, which is obtained by solving the solid-phase momentum equation (Equation (4)). Figure 7 depicts the sediment velocity distributions for three distinct guide vane end clearances: 0.3 mm, 0.5 mm, and 1.0 mm. With a tiny clearance of 0.3 mm, the leakage flow is rather feeble, leading to a restricted area of elevated sediment velocity and a gentle velocity gradient. The region of elevated sediment velocity is primarily located near the pressure side of the guide vane, adjacent to the skirt area.

As the clearance expands, the leakage flow markedly intensifies, resulting in the formation of substantial vortex structures. This results in a significant rise in the velocity gradient and an enlargement of the high-sediment-velocity area. In the substantial clearing condition (1.0 mm), the sediment velocity attains 40 m/s, significantly intensifying sediment erosion in the gap region. The heightened velocity gradient bestows greater kinetic energy upon sediment particles, leading to intensified erosion and abrasion.

Under the 1.0 mm clearance condition, the sediment velocity is observed to peak at approximately 0.6 of the streamwise location before beginning to decline. This trend corresponds to the pressure recovery on the suction side starting at the same position, as shown in Figure 4. The underlying physics involves the deceleration of the leakage jet after it exits the gap due to obstruction by the main flow, whereby its kinetic energy is converted into pressure energy. This energy conversion causes a subsequent decrease in the velocity of the entrained sediment particles. Concurrently, the combined effect of the local pressure recovery (Figure 4) and the intense vortex motion (Figure 5) alter particle trajectories, with some particles being entrained into the vortex core, resulting in a reduction of their time-averaged velocity.

Figure 8 illustrates the silt concentration distributions for three guide vane end clearances: 0.3 mm, 0.5 mm, and 1.0 mm. Under the 0.3 mm clearance condition, low concentration prevails across the majority of the domain. A uniformly distributed band of moderate concentration is noted near the end surface of the guide vane, whereas a high-velocity zone along the leading edge on the pressure side, adjacent to the skirt, displays a markedly increased sediment concentration of up to 10.6 kg/m³. This indicates the existence of unique vortex formations that capture and gather sediment particles, a phenomenon resulting from the interaction between leakage flow and the primary flow. The sediment concentration pattern for the 0.5 mm clearance closely approaches that of the 0.3 mm instance; however, the concentration within the clearance zone is significantly elevated. In the 1.0 mm clearance scenario, the area of elevated concentration diminishes, and the peak concentration value is lowered. Despite the silt distribution becoming more uniform in the expanded gap, the average sediment concentration in the clearance region exceeds that of the 0.3 mm and 0.5 mm scenarios. The heightened concentration amplifies sediment erosion in the interstitial region.

3. Experimental Study

Full-flow passage numerical simulations of the sediment-laden flow under the specified parameters yielded the sand-water velocity distribution, streamline patterns around the guide vanes, and sediment concentration on the top cover surface. An experimental setup was devised to perform sediment erosion studies based on the flow parameters within the guide vane passage. The experimental model’s design guaranteed that flow conditions mirrored those of the actual flow channel, hence ensuring consistency between experimental results and real-world performance.

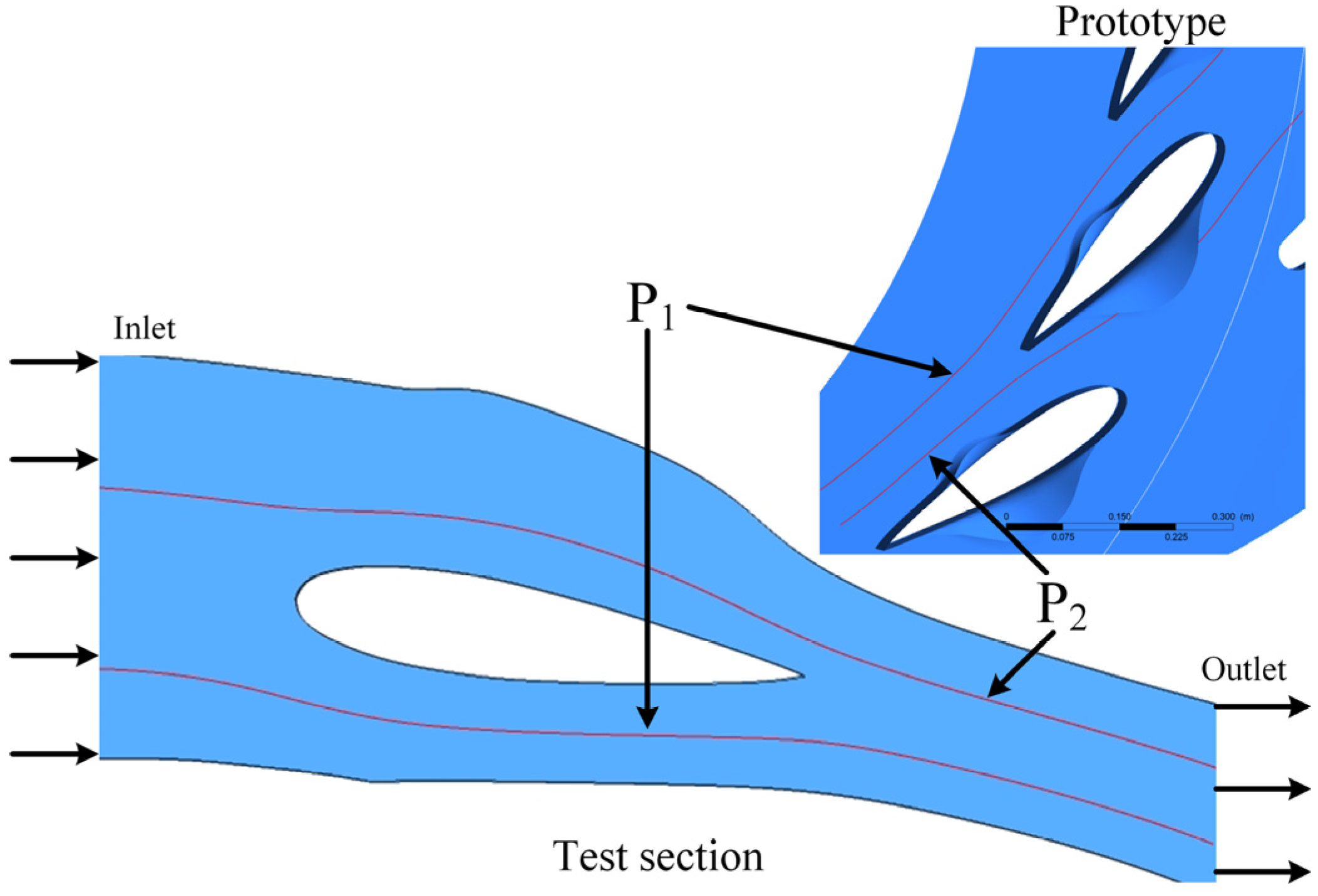
A test section mimicking the top cover flow passage under rated operating conditions for sediment erosion testing on the guide vanes’ top cover of the Genda Power Station turbine was constructed based on geometric and kinematic similarity principles. This methodology guaranteed that the test segment precisely reflected the flow dynamics in the prototype turbine.

The velocity and sediment concentration distributions on the top cover surface in the guide vane region of the prototype turbine at rated circumstances were determined by full-passage CFD simulations. Based on these distributions and following the dynamic similarity criteria, the test section was designed to ensure that the flow conditions (velocity, sediment concentration, Reynolds number) within it were similar to those in the critical regions of the prototype. The influence of the clearance height is thus indirectly represented in the tests by adjusting these flow field parameters. The tests try to replicate material wear behavior under certain flow circumstances, rather than explicitly reproducing the geometric structures of varied clearance heights.

3.1. Test Section Design

The top cover’s foundation material in the guiding vane region of the Genda Power Station turbine is cast steel, whilst the sediment erosion-resistant plate utilized for repairs is composed of 04Cr13Ni5Mo. The experimental apparatus was constructed using the specified materials.

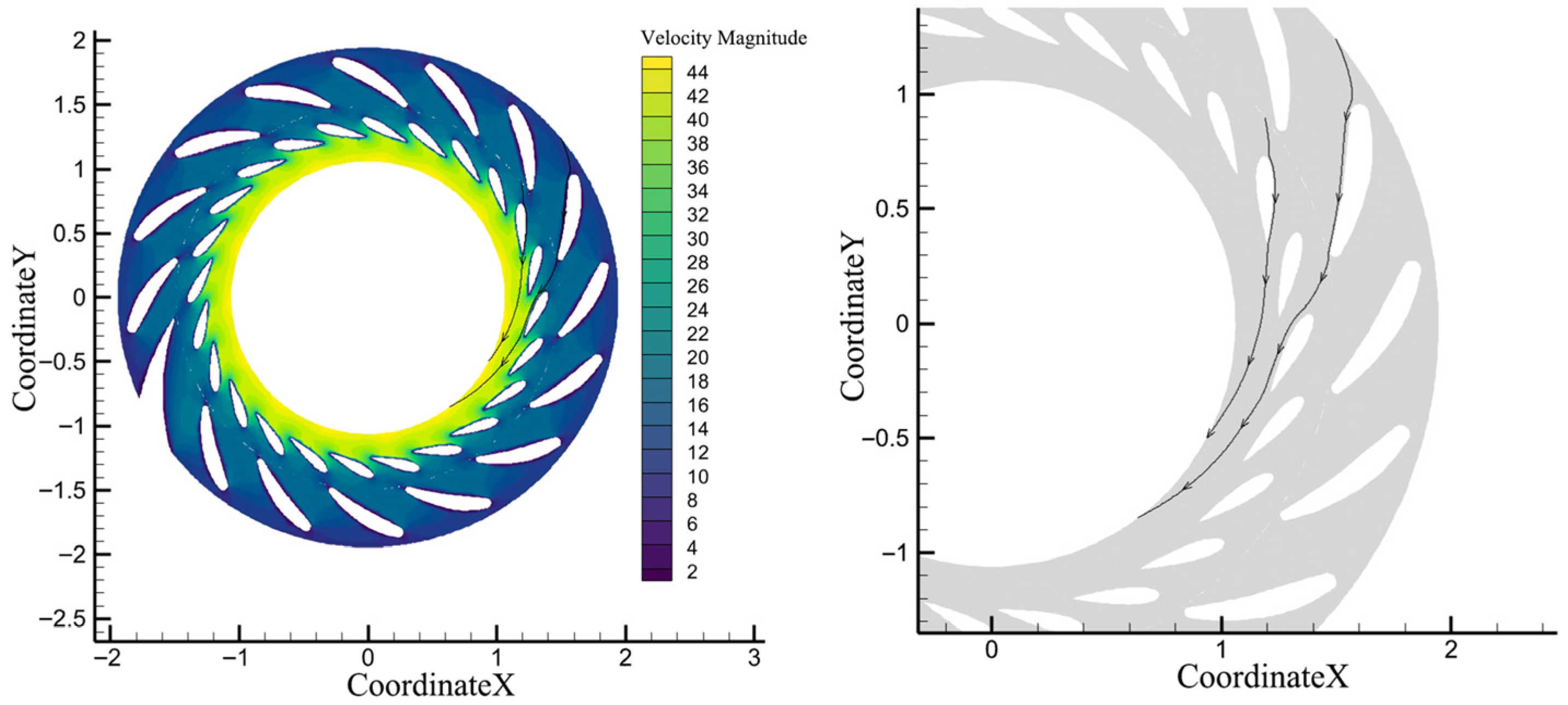
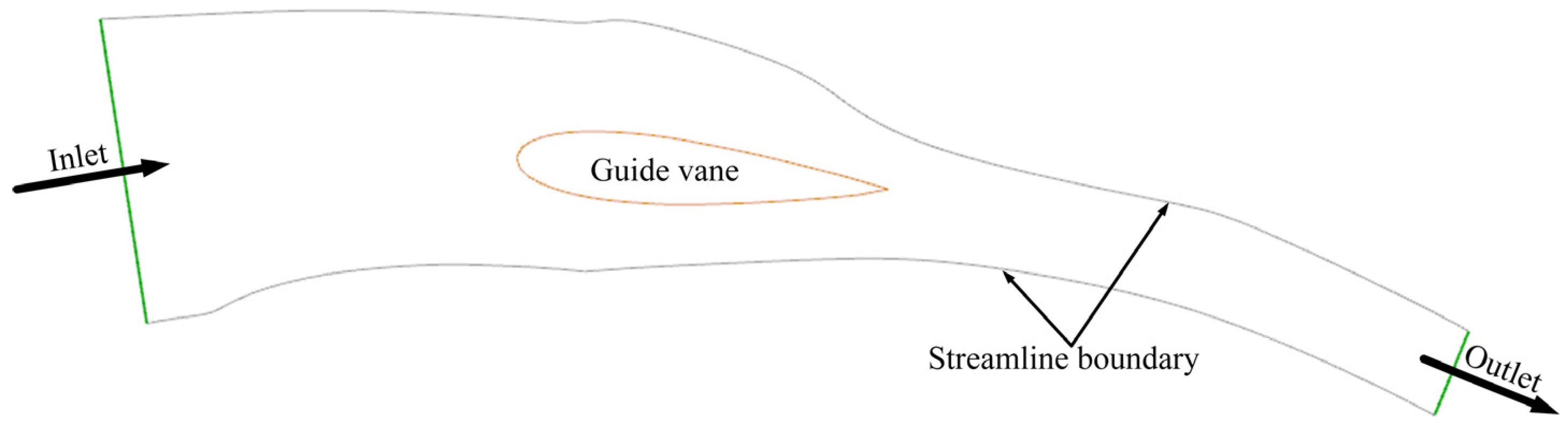
Erosion of the sediment on the flow-passing surface of the top cover largely occurs due to the impact and abrasion of sediment-laden flow within the guide vane passage. Two example streamlines from the guide vane domain were extracted based on numerical simulation results of the full-flow passage under rated conditions, as illustrated in Figure 9. The delineations of these streamlines were employed to establish the flow boundaries of the test section, so assuring hydraulic equivalence between the experimental apparatus and the actual turbine.

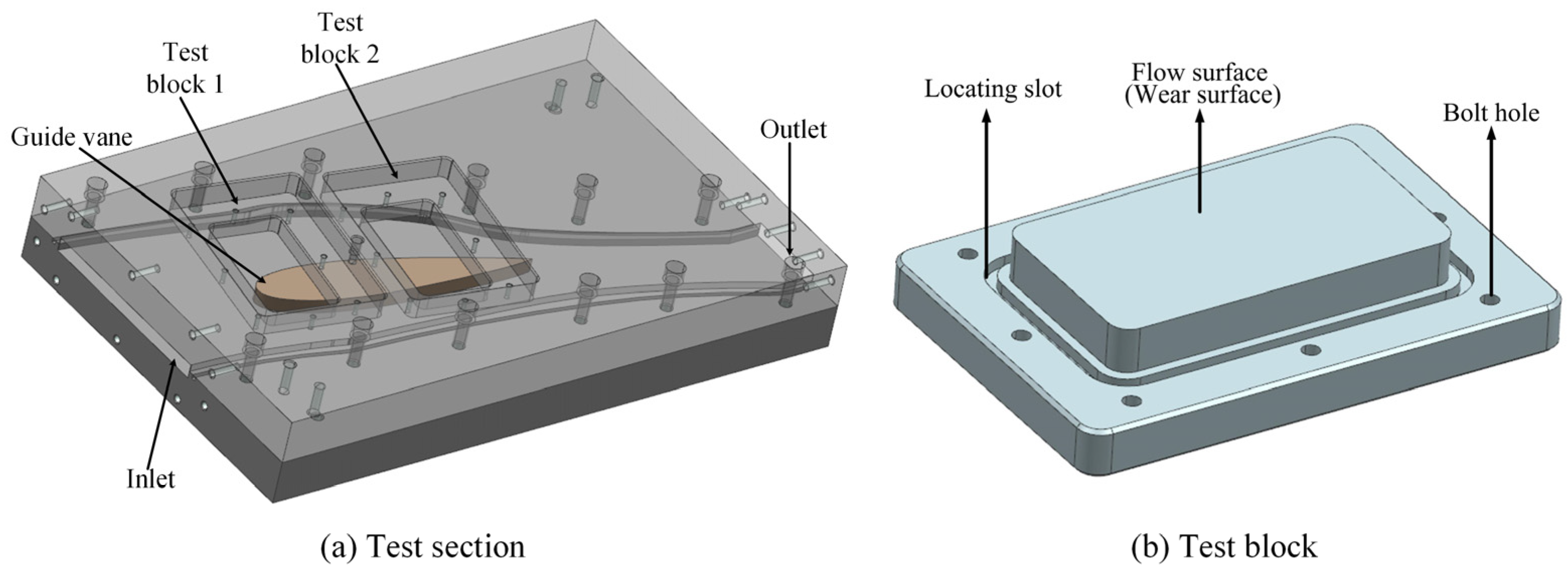
The geometric model of the turbine guide vane was utilized to construct the guide vane within the flow path of the test section. The model, along with the delineated wall limits, formed the test section for assessing the efficacy of the sediment erosion-resistant plate. Figure 10 presents a cross-sectional view of the test portion.

The numerical simulation results of the prototype turbine indicated that the average inlet velocity of the test section was 14 m/s, with the design flow rate of the test system established at 280 m³/h. The intake height of the test section was set to be 20 mm to ensure that the inlet velocity matches that of the corresponding cross-section of the prototype.

Test block 1 was produced from sediment erosion-resistant plate material (04Cr13Ni5Mo), whereas Test block 2 was constructed from the top cover base material (cast steel). A 0.3 mm end-face clearance was preserved between the test blocks and the guide vane, in accordance with the real layout of the prototype turbine. Figure 11 illustrates the three-dimensional model of the test section and the test blocks.

3.2. Rationality Verification of Test Section Design

To validate the rationality of the test section design, it is essential to ensure the dynamic similarity of the sediment-laden flow parameters between the test section and the prototype turbine flow passage (obtained via full-passage numerical simulation). This section evaluates the similarity between the two by comparing the flow velocity, sediment concentration, and Reynolds number at corresponding locations in the test section and the prototype flow passage (numerical model).

Figure 12 illustrates that the validation segment of the test section was developed using two extracted streamlines (P₁ and P₂) from the prototype flow passage. The streamlines were integrated into the test section model to acquire appropriate data. To statistically assess the flow similarity between the test section and the prototype, a comparison was conducted along a normalized trajectory from the inlet (designated as position “0”) to the outlet (designated as position “1”). Sequential locations were picked along this course, and essential characteristics such as sediment velocity, sediment concentration, and Reynolds number were compared and analyzed at each position.

3.2.1. Comparison of Sediment Velocity

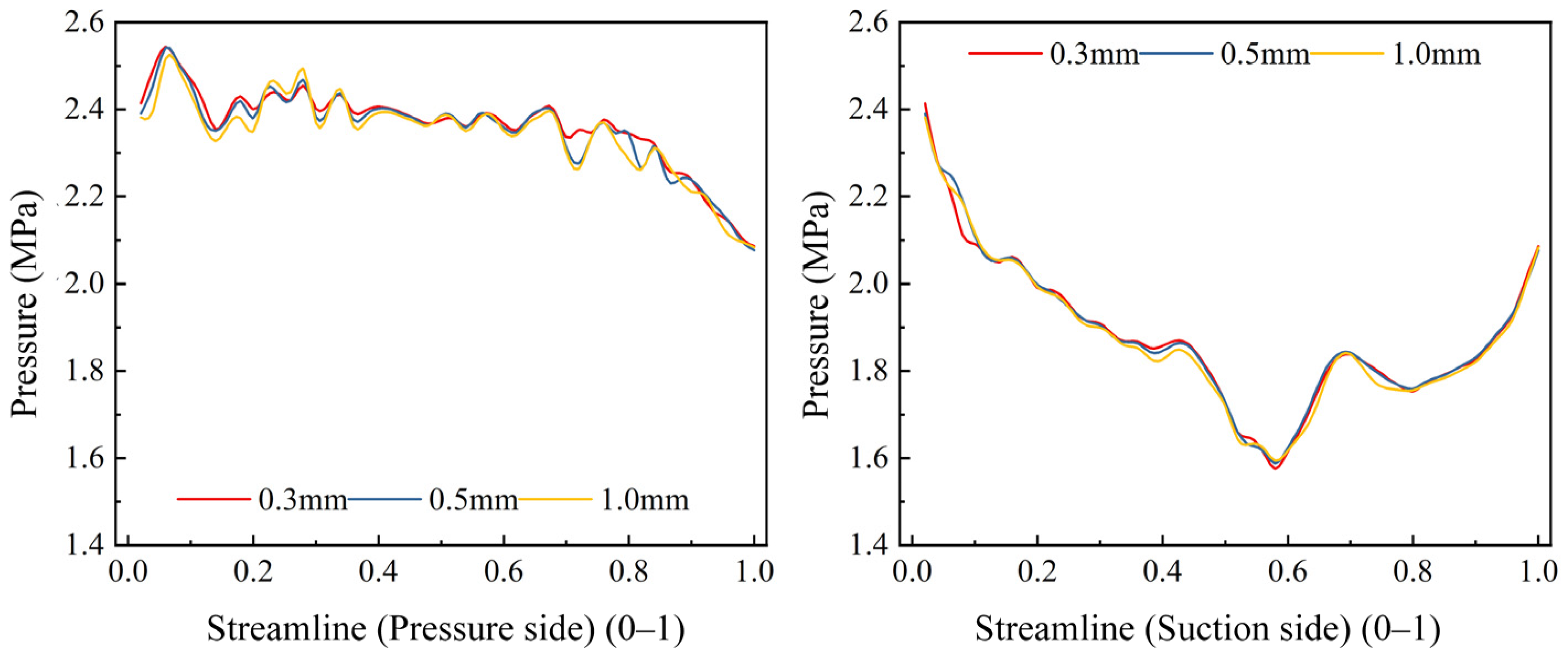
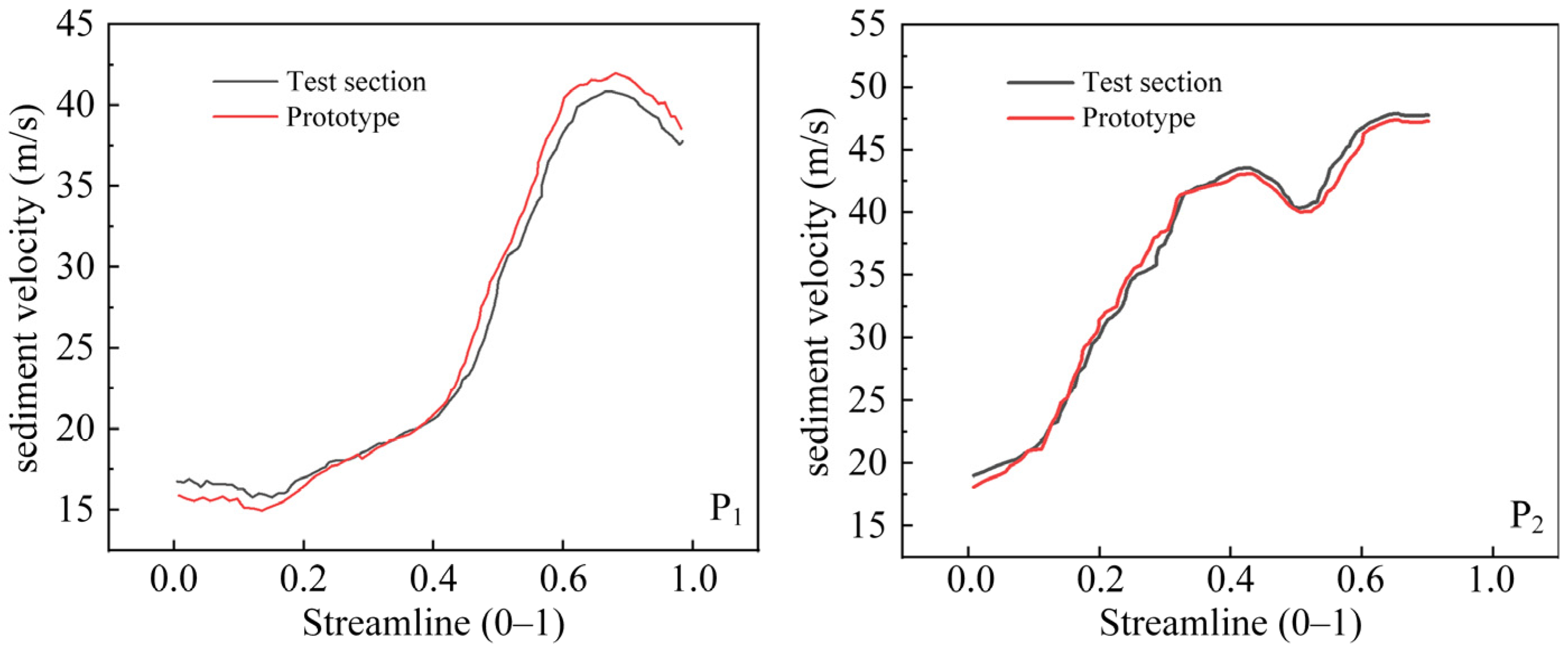
The curves in the figure are derived from the numerical simulation results, obtained by extracting and comparing data from corresponding streamlines in the prototype flow passage and the test section. Sediment velocity is a critical factor governing its kinetic energy upon impact with the wall surface, and is thus directly related to the erosive impact. Figure 13 presents a quantitative comparison of sediment velocity between the test section and the prototype turbine. The sediment velocity curves for streamlines P₁ and P₂ exhibit strong concordance between the test section and the prototype, demonstrating consistent fluctuation patterns and similar magnitude ranges.

3.2.2. Comparison of Sediment Concentration

The curves in the figure are derived from the numerical simulation results, obtained by extracting and comparing data from corresponding streamlines in the prototype flow passage and the test section. Figure 14 illustrates the comparison of sediment concentration. The sediment concentration variation trends along both P₁ and P₂ streamlines are broadly consistent between the test section and the prototype. The test segment demonstrates a slightly elevated sediment content compared to the prototype at P₁, while exhibiting a considerably reduced concentration at P₂. The disparities in silt concentration between the test section and the prototype are negligible along both streamlines.

3.2.3. Comparison of Reynolds Number

The Reynolds number (Re) is an essential similarity criteria in fluid mechanics, fulfilling three primary functions: (1) It establishes the flow regime—laminar flow at Re < 2300, turbulent flow at Re > 4000, and transitional flow in the intermediate range; (2) It forecasts resistance characteristics by directly affecting the variation of drag coefficients in the flow around objects; (3) It directs model testing by ensuring dynamic similarity between prototype and model through the equivalence of Reynolds numbers.

The formula for calculating the Reynolds number (Re) is as follows:

$$\mathit{Re}={\displaystyle \frac{Vd}{\nu }}$$

(7)

where V, v, and d denote the flow velocity, kinematic viscosity coefficient, and characteristic length of the fluid, respectively.

The formula for calculating the ratio K between the Reynolds number Re₁ of the test section and Re₂ of the prototype section is given as follows:

$$K={\displaystyle \frac{V_1{d}_1{\nu }_2}{V_2{d}_2{\nu }_1}}$$

(8)

where the subscript “1” indicates parameters of the test section, and the subscript “2” signifies parameters of the prototype portion, with d₁ = d₂. It is important to observe that for low sediment concentrations, the viscosity of the sediment-laden flow is directly proportional to the sediment concentration.

Thus, Equation (9) may be simplified into the following form:

$$K={\displaystyle \frac{V_1{S}_2}{V_2{S}_1}}$$

(9)

where S₁ and S₂ denote the sediment concentration in the test section and the prototype section, respectively.

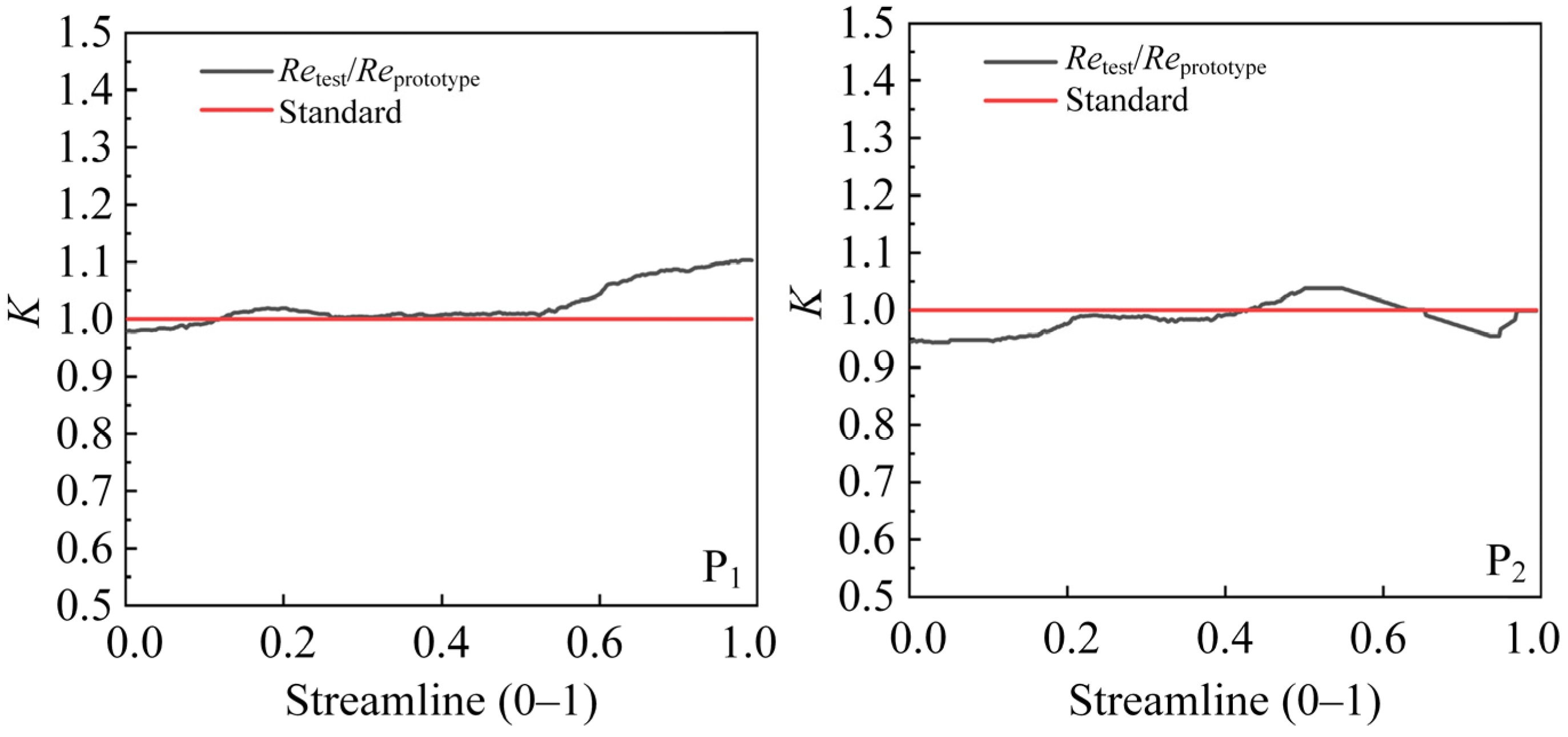
Figure 15 illustrates the correlation between the similarity coefficient K and the positions along streamlines P₁ and P₂. The K-values at all places throughout the three comparative segments are approximately 1, signifying little discrepancies in Reynolds numbers between the test section and the prototype turbine at each respective position. This verifies that the flow in the test section meets the Reynolds number similarity condition in relation to the prototype.

3.3. Test System

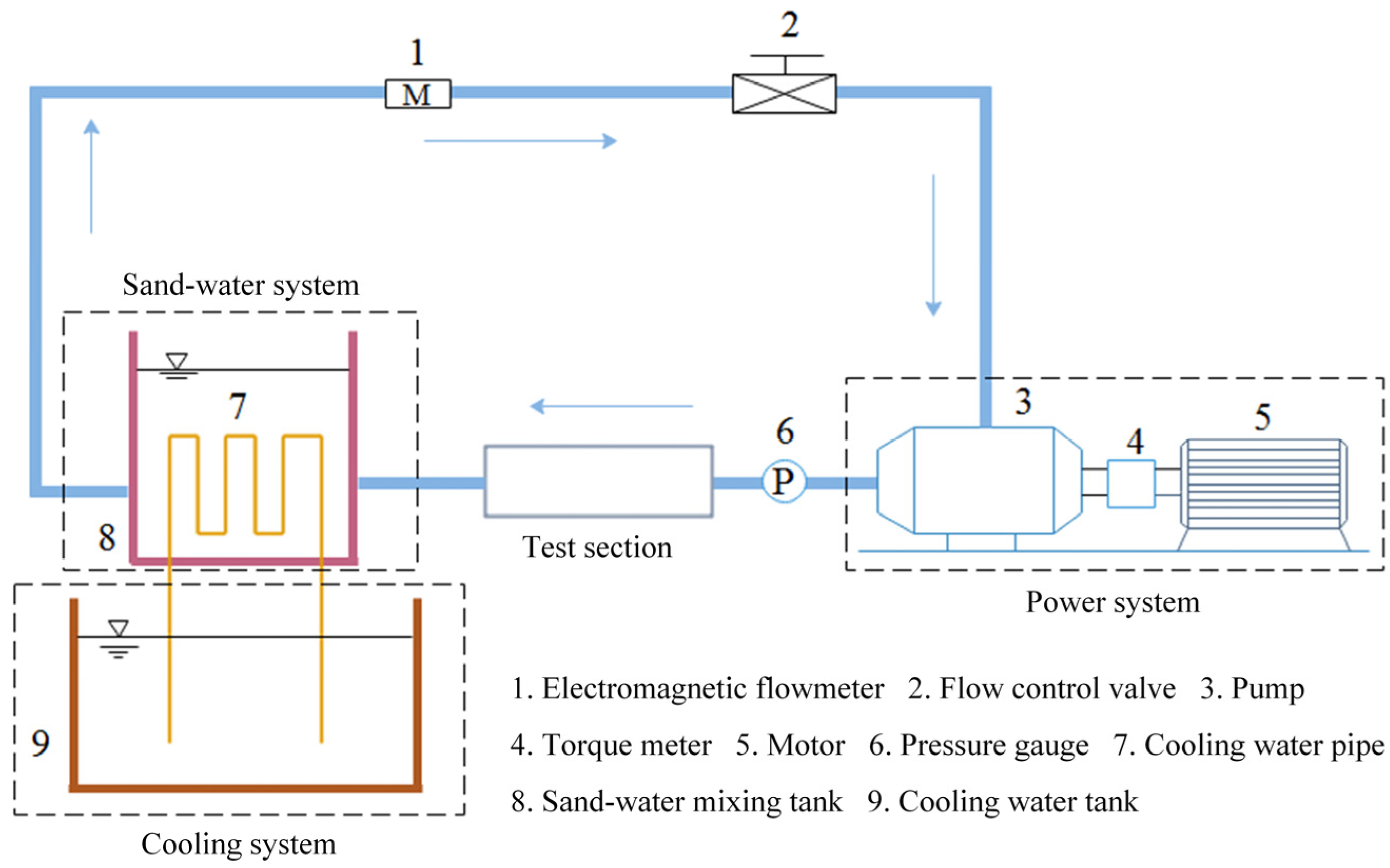
Figure 16 depicts the developed sediment erosion test system. The system comprises four primary components: a power unit, a sediment mixing apparatus, a cooling module, and the test section. The power unit features a high-capacity 630 kW motor, capable of generating a system pressure corresponding to a 376 m water column and a rated flow rate of 482 m³/h. The sediment mixing apparatus employs high-velocity water impact to attain homogeneous suspension of sediments. The cooling system utilizes a serpentine pipe to circulate groundwater for thermal exchange. The test section, as the fundamental element, possesses a modular design that allows for tailored modifications based on particular research requirements, facilitating experiments under diverse operating situations. The system employs a modular architecture, with all functional units collaborating to create a dependable experimental platform for hydraulic turbine research. Based on the study objectives, several test sections and test blocks might be constructed to fulfil particular experimental criteria. Figure 17 illustrates the comprehensive setup of the sediment erosion test section.

3.4. Measurement Method of Test Results

The laser rangefinder is a high-precision device for measuring distances, utilizing laser modulation technology. The operational principle entails producing modulated pulsed laser beams (either single or sequential pulses) and employing a highly sensitive photodetector to capture the reflected signal from the target, thus precisely calculating the round-trip time of flight.

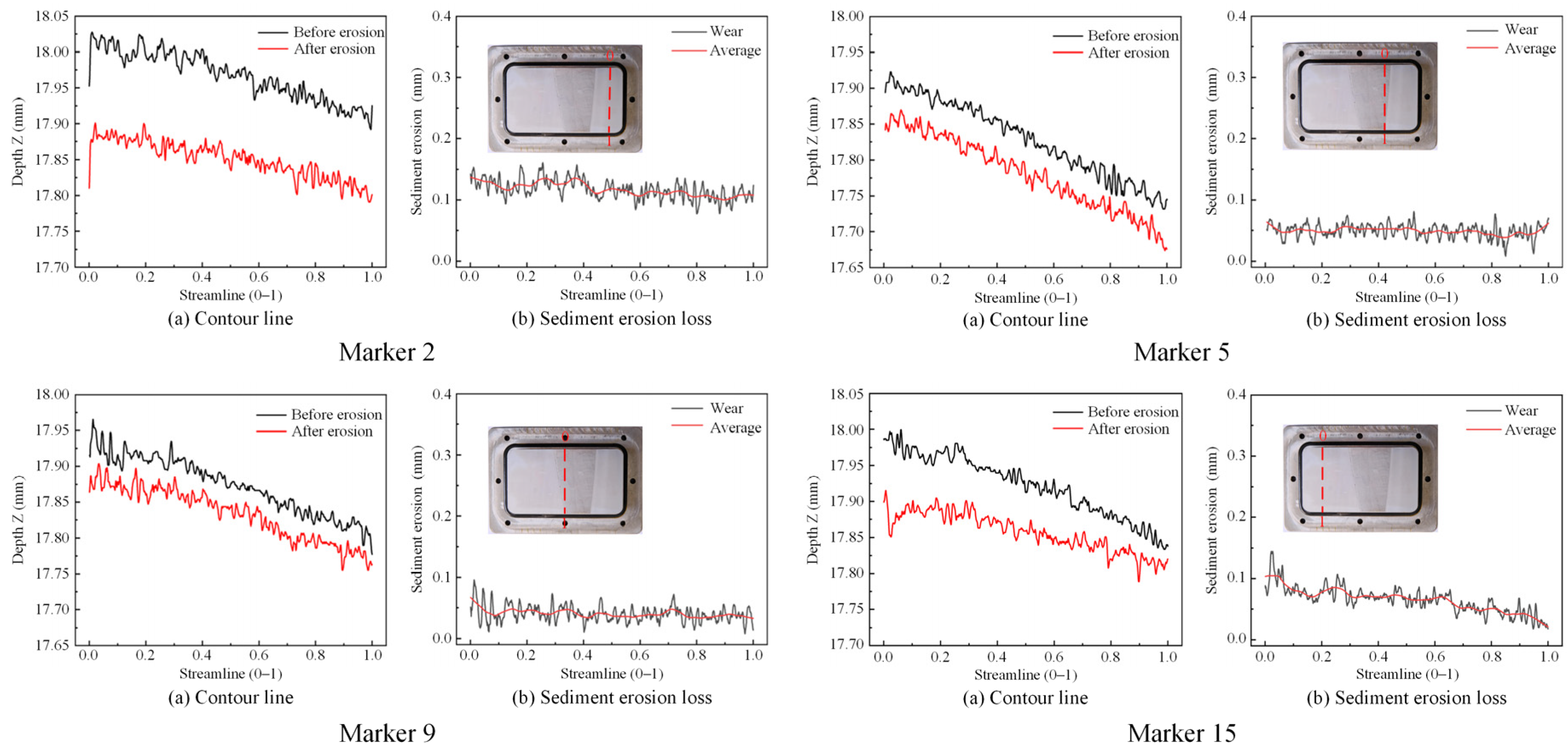
Multiple measurement lines were delineated on the non-test surface of the test block to function as reference benchmarks prior to and following the experiment. The non-test surface is impervious to silt erosion, maintaining its condition during the experiment, so assuring that measurements are conducted at the same sites before and after the test. The measurement’s initial point is designated as “0,” while the terminal position is labelled “1.” Figure 18 illustrates the locations of the engraved lines and the measurement bounds.

The recorded data illustrates the surface profile of the abraded test surface. By overlaying the pre- and post-test profiles within a unified coordinate system, the erosion depth at each location along the measurement line can be quantitatively assessed.

4. Results of Sediment Erosion Test

4.1. Sediment Erosion Distribution

Superimposing the pre- and post-test surface profiles of the test block inside a unified coordinate system allows the vertical difference between the two profiles to immediately indicate the sediment erosion depth at each measurement point.

Figure 19 illustrates the contour lines and sediment erosion loss distribution along the partial measurement lines of Test block 1. The sediment erosion depths on the left and right sides of the guide vane exhibit considerable disparity. The sediment erosion along Lines 1–4 is typically approximately 0.1 mm, which exceeds that along Lines 10–17. This mismatch is due to the variation in flow velocity between the pressure side and suction side of the guide vane. Lines 1–4 are situated in the high-velocity zone on the pressure side, where elevated flow velocity results in exacerbated erosion.

The limited space between the guide vane end face and the test block leads to a lower silt concentration in this location, hence diminishing sediment erosion on the test block’s corresponding region. As only portions of Lines 4–11 fall inside the end face influence zone, the sediment erosion depth along these lines diminishes sharply in the area coinciding with the vane end. Conversely, sediment erosion depth stays consistently uniform along Lines 1–3 and 12–17, which are beyond the effect region of the end face.

Figure 20 illustrates the contour lines and sediment erosion loss distribution along the partial measurement lines of Test Block 2. Consistent with Test block 1, the sediment erosion depth in the high-velocity section (Lines 1–4) of Test block 2 typically surpasses 0.1 mm, exceeding that observed in the low-velocity region (Lines 10–17). The guide vane end face affects Lines 5–9 of Test block 2, which are completely situated inside the end face zone, leading to reduced sediment erosion in this location relative to other sections of the test block. Conversely, Lines 1–3 and 12–17 are unaffected by the end face, demonstrating a rather consistent sediment erosion depth across each line.

Figure 19 and Figure 20 exhibit the wear depth distributions on the two material test blocks. It can be readily noted that in the high-flow velocity regions corresponding to the pressure side of the guide vane (measurement lines 1–4), the wear depth is often greater than that in the low-flow velocity regions on the suction side (measurement lines 10–17). Furthermore, in the area just below the guide vane end face (parts of lines 4–11 on test block 1 and lines 5–9 on test block 2), a significant stratification of wear depth develops due to the relatively reduced silt concentration within the gap. This suggests that both flow velocity and local sediment concentration are major factors simultaneously affecting the wear distribution. The overall wear depth on test block 2 (cast steel) is larger than that on test block 1 (04Cr13Ni5Mo), providing unambiguous proof of the efficiency of the wear-resistant material.

4.2. Sediment Erosion and Flow Velocity

A link between flow velocity and erosion was established based on computationally estimated sediment-laden water flow velocity distributions over the test block surface and empirically recorded sediment erosion depths. Figure 21 illustrates the velocity-sediment erosion correlations for Test block 1 and Test block 2. Distinct correlation curves were discovered due to variations in flow velocity between the left and right sides of the guide vane. These were classified into high-velocity and low-velocity zones.

In both zones, the sediment erosion depth of the sediment erosion-resistant plate material (04Cr13Ni5Mo) was consistently inferior to that of the base material (cast steel) at equivalent flow velocities. The anti-erosion efficacy of the sediment erosion-resistant plate is substantial, especially accentuated in the high-velocity zone.

4.3. Sediment Erosion Model

The formula for the sediment erosion rate of flow-passing components in hydraulic turbines is as follows [15]:

$$E=k_s{k}_m{C}_V^m{W}^n$$

(10)

where E signifies the erosion rate of the surface material per unit time; k_S and k_m denote the characteristic coefficients of the sediment particles and the flow-passing material, respectively; C_V denotes the mean sediment concentration; the exponent m is typically assumed to be 1; W represents the magnitude of the relative velocity between the sediment-laden flow and the surface component; and n signifies the velocity exponent.

In this experiment, with the average sediment concentration C_V maintained at 2.9 kg/m³ and the characteristics of the sediment and material remaining constant, the equation can be simplified under the specified sediment concentration conditions as follows:

$$E=K{W}^n$$

(11)

The duration for each wear test was set at 170 h, with each material tested for a minimum of three replicates under identical conditions to ensure result repeatability and reliability. The sediment erosion rate E (μm/h) was determined by dividing the sediment erosion depth by the duration of the test. The correlation between flow velocity and sediment erosion rate was then established using nonlinear fitting with post-processing software, yielding fitted curves that illustrate the dependence of sediment erosion rate on the sediment-laden flow velocity surrounding the test blocks. Figure 22 displays the fitted curves demonstrating the relationship between sediment erosion rate and flow velocity for Test block 1 and Test block 2.

This study derived sediment erosion calculation formulas for various regions and materials of the top cover by combining experimental results of sediment erosion in the hydraulic turbine with numerical simulations of sediment-laden flow, utilizing nonlinear curve fitting to establish a sediment erosion model. The formulated sediment erosion model, together with its associated coefficients, is encapsulated in

Table 6. Test the coefficient of the fitting formula for the sediment erosion rate of the top cover.

Material	K	n	Sediment Erosion Model
04Cr13Ni5Mo	9.11 × 10−5	2.44	E = 9.11 × 10−5W2.44
cast steel	1.35 × 10−4	2.45	E = 1.35 × 10−4W2.45

. The velocity exponents n obtained in this study (2.44 for 04Cr13Ni5Mo and 2.45 for cast steel) fall within the common range reported in the literature (typically 2.0–3.0), which aligns with the understood erosion mechanism of sediment particles impacting metallic materials.

This erosion model was developed based on the specific operating conditions, sediment characteristics (concentration: 2.9 kg/m³, median particle size: 0.058 mm), and materials of the Gengda Power Station, granting its coefficients a context-specific applicability. When applied to other power stations, the model requires correction and validation against their respective specific parameters.

4.4. Comparison of Numerical Simulation and Experimental Erosion Morphology

A comparison between the high-flow velocity and high-turbulent kinetic energy regions from CFD simulations and the experimentally determined wear distributions demonstrates a strong spatial agreement. The numerical simulation anticipated a high-velocity jet and a high-pressure zone near the crown on the pressure side of the guide vane, which corresponds perfectly to the spot where significant wear was found experimentally. This consistency illustrates that, despite model simplifications, the current CFD methodology can successfully identify locations at high risk of wear, hence offering significant information for anti-wear design.

5. Conclusions

This study examined the impact of incrementally enlarging guide vane end clearances on internal flow and sediment-induced erosion in a Francis turbine at Genda Power Station under sediment-laden conditions, employing a hybrid methodology of numerical simulation and experimental testing. A sediment erosion model for pertinent materials was established using sediment erosion tests. The primary conclusions are as follows:

(1) As the guide vane end clearance grew from 0.3 mm to 1.0 mm, the leakage flow increased (flow rate +1.36%, torque +0.78%). Nonetheless, secondary flows generated by the leakage, which deplete turbulent kinetic energy, resulted in a decrease in efficiency from 94.12% to 93.63% (a decline of 0.49%). The augmented clearance resulted in an elevated sediment velocity gradient, enhancing particle kinetic energy and substantially increasing erosion hazards. Furthermore, silt concentration within the clearance augmented with wider gaps. Under the 1.0 mm clearance condition, the overall sediment concentration in the gap exceeded that of lesser clearance scenarios, hence intensifying sediment erosion.

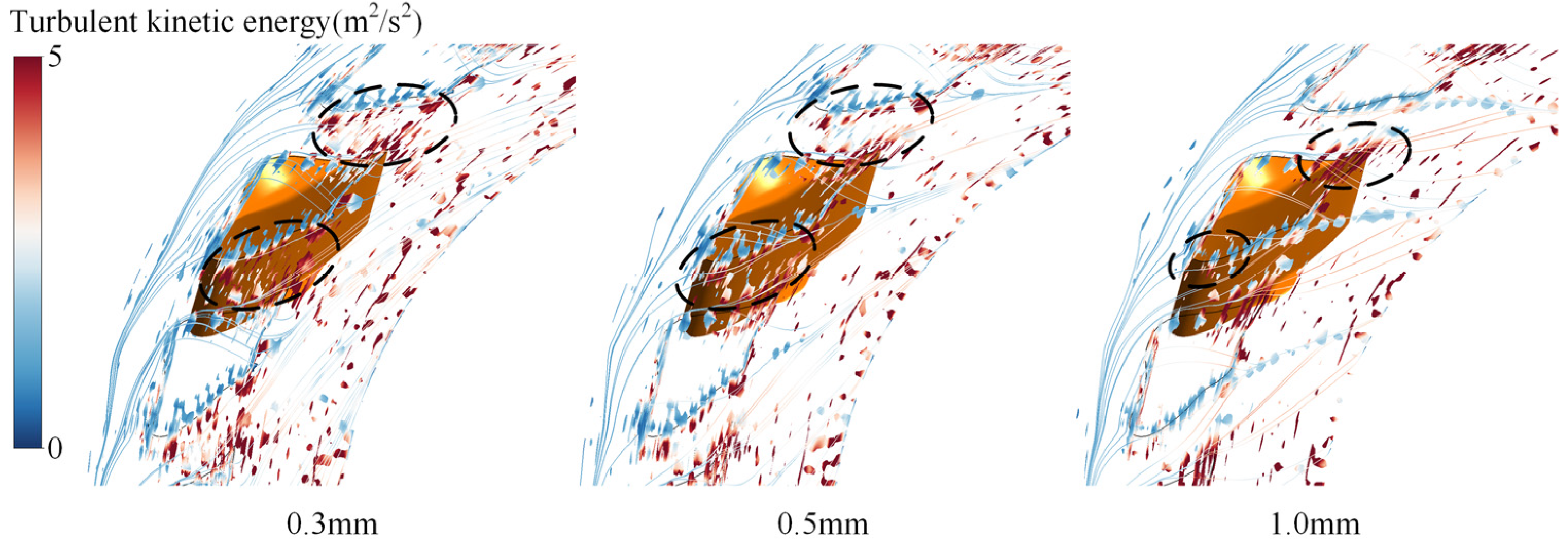
(2) The increase in guide vane end clearance resulted in a small reduction in the pressure differential across the gap. At a 0.3 mm clearance, streamlines conformed closely to the vane surface, exhibiting no notable flow separation. A 0.5 mm clearance resulted in a high-velocity jet with an impingement angle of roughly 30° at the gap exit, causing local flow separation. At a clearance of 1.0 mm, the augmented leakage flow affected the primary stream, leading to vortex formations and a marked rise in flow separation within the vaneless region. Increasing the clearance resulted in the high-turbulent-kinetic-energy region transitioning from a distribution across guide vanes to a concentration along the trailing edge, with more frequent vortex collapse exacerbating small-scale turbulence.

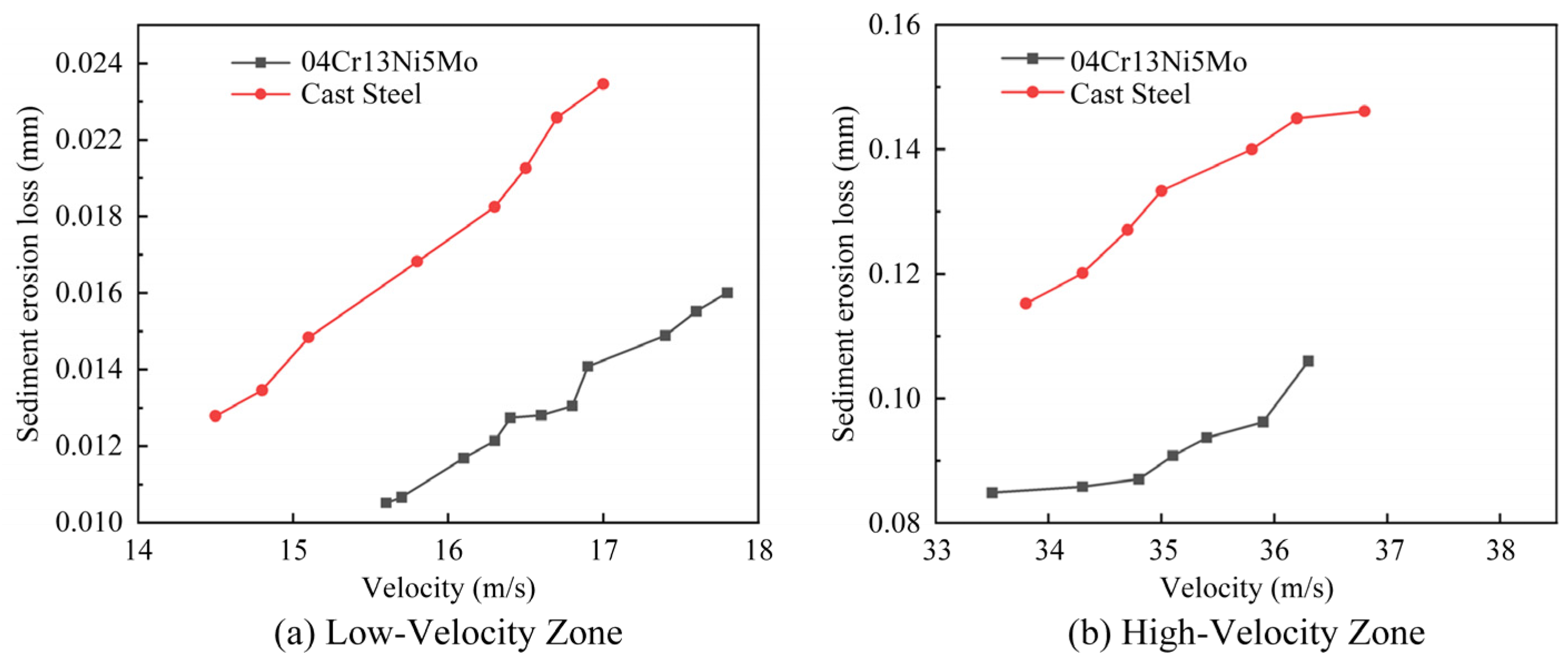
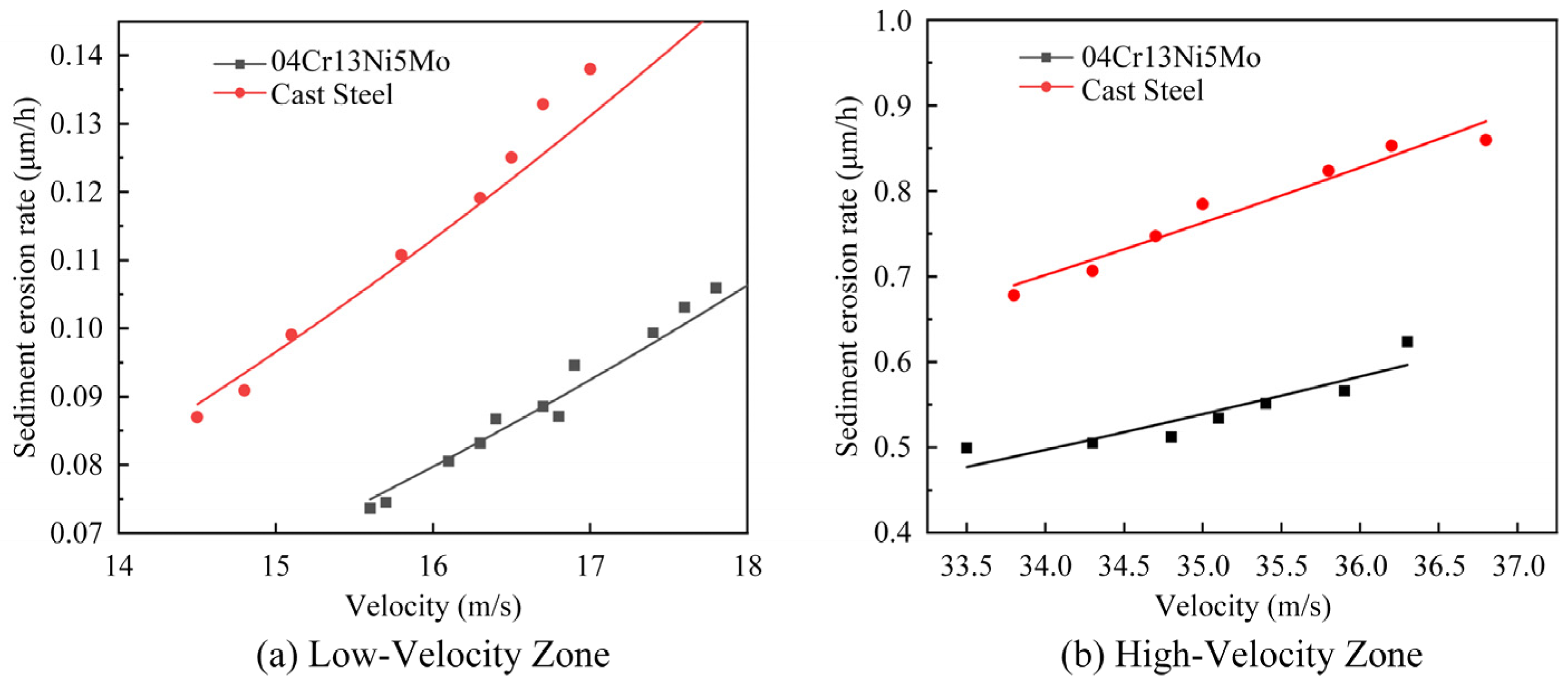
(3) The sediment erosion-resistant material (04Cr13Ni5Mo) exhibited markedly superior performance compared to the basis material (cast steel), especially in high-velocity areas. The sediment erosion rate demonstrated a power-function correlation with flow velocity. Models for sediment erosion rates were developed for various materials and regions: for the sediment erosion-resistant plate (04Cr13Ni5Mo), the erosion rate is expressed as E = 9.11 × 10⁻⁵W^2.44, while for the base material (cast steel), it is E = 1.35 × 10⁻⁴W^2.45. These models offer a mathematical foundation for anti-erosion design.

(4) It is recommended that the guide vane top cover clearance be strictly controlled at the lower design limit during maintenance to suppress leakage flow, reduce efficiency loss, and mitigate wear risk. For high-pressure and high-velocity regions, the application of 04Cr13Ni5Mo erosion-resistant steel plates is advised to replace the base cast steel, thereby significantly extending the maintenance interval. The established wear model can provide a quantitative reference for material selection and life prediction in similar power stations.

(5) This study has certain acknowledged limitations. The wear tests were performed under steady-state circumstances and consequently do not account for the influence of transient load fluctuations observed in real-world operation. Consequently, the applicability of the established wear model, which is calibrated to the specific sediment features and materials of the Gengda Power Station, may be limited, and its extrapolation requires careful study. Addressing these restrictions will be a significant focus of future development.