Structural Responses of the Net System of a Bottom-Mounted Aquaculture Farm in Waves and Currents
Abstract
1. Introduction
2. Material and Methods
2.1. Numerical Method
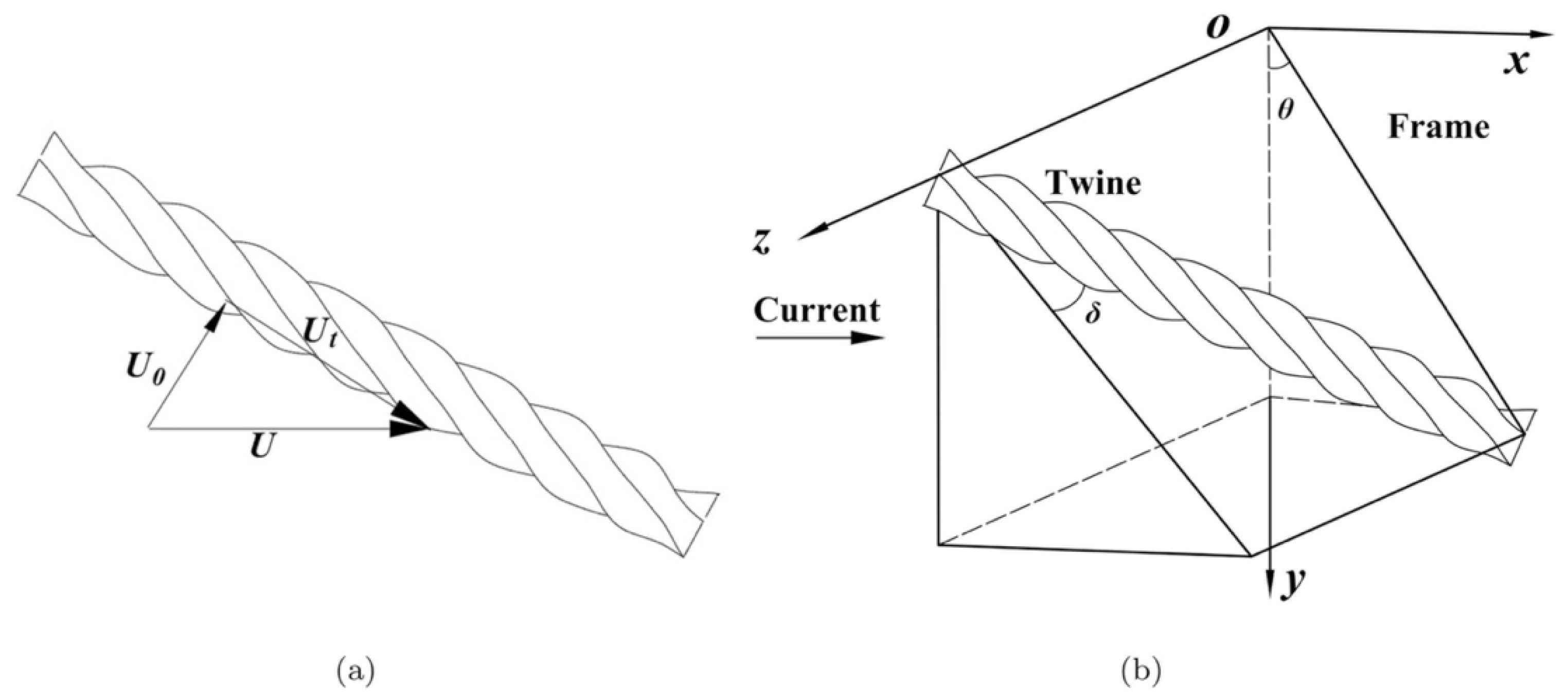
2.1.1. Governing Equations for the Structural Responses of Nets
2.1.2. Hydrodynamic Loads on Nets: Morison Model
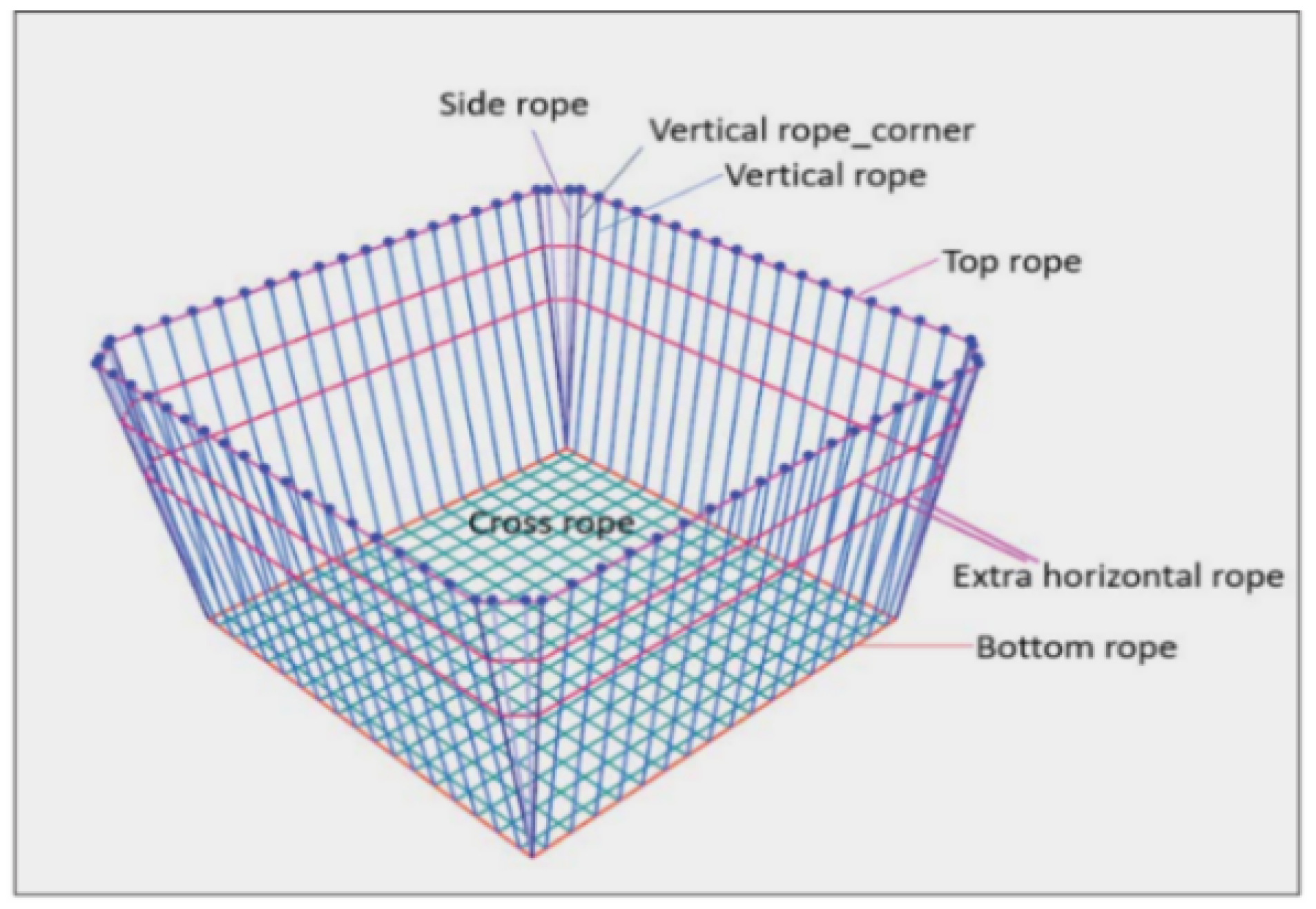
2.2. Investigated Net Systems
2.3. Environmental Loadings and Cases Set-Up
3. Results and Discussions
3.1. Hydrodynamic Loads on the Net Systems
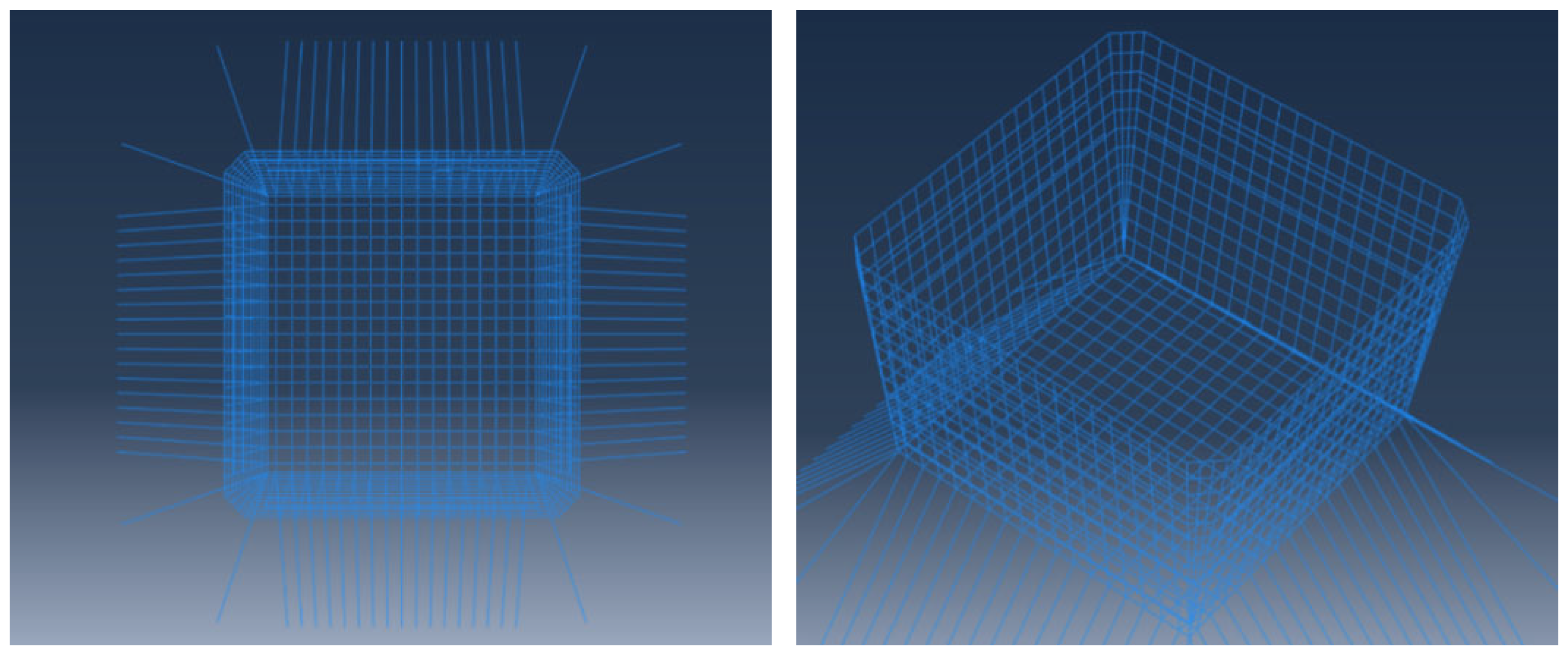
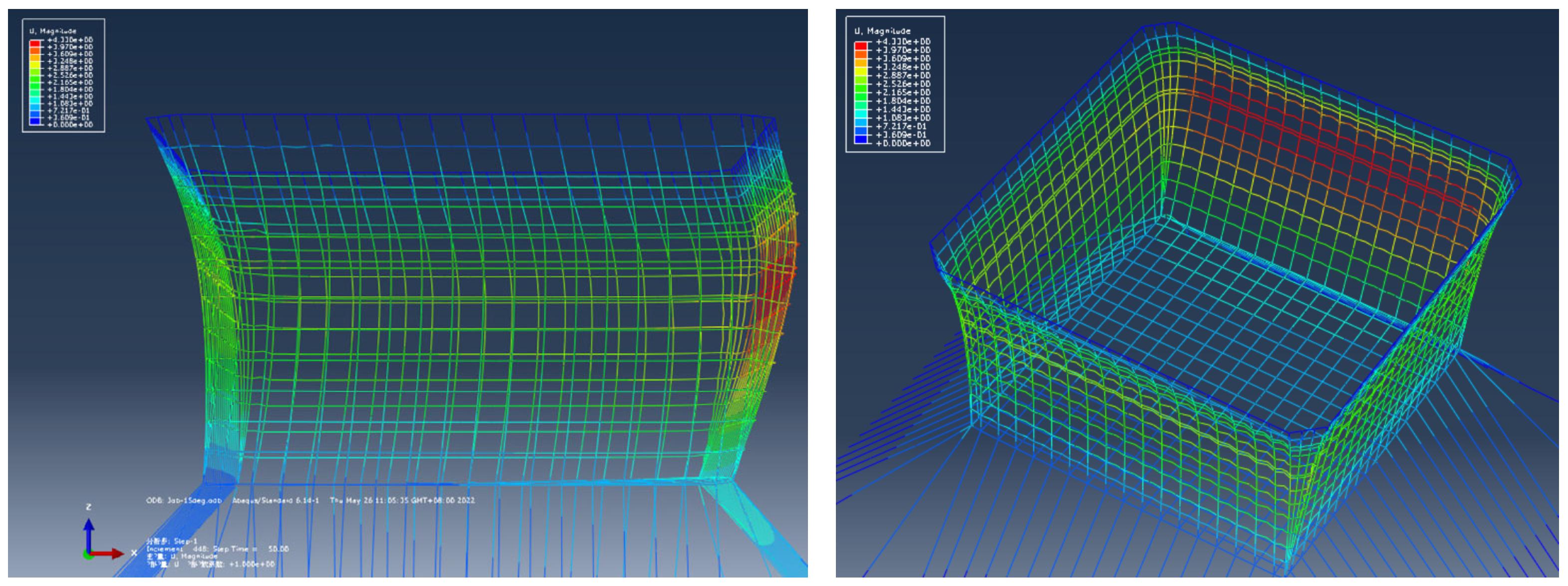
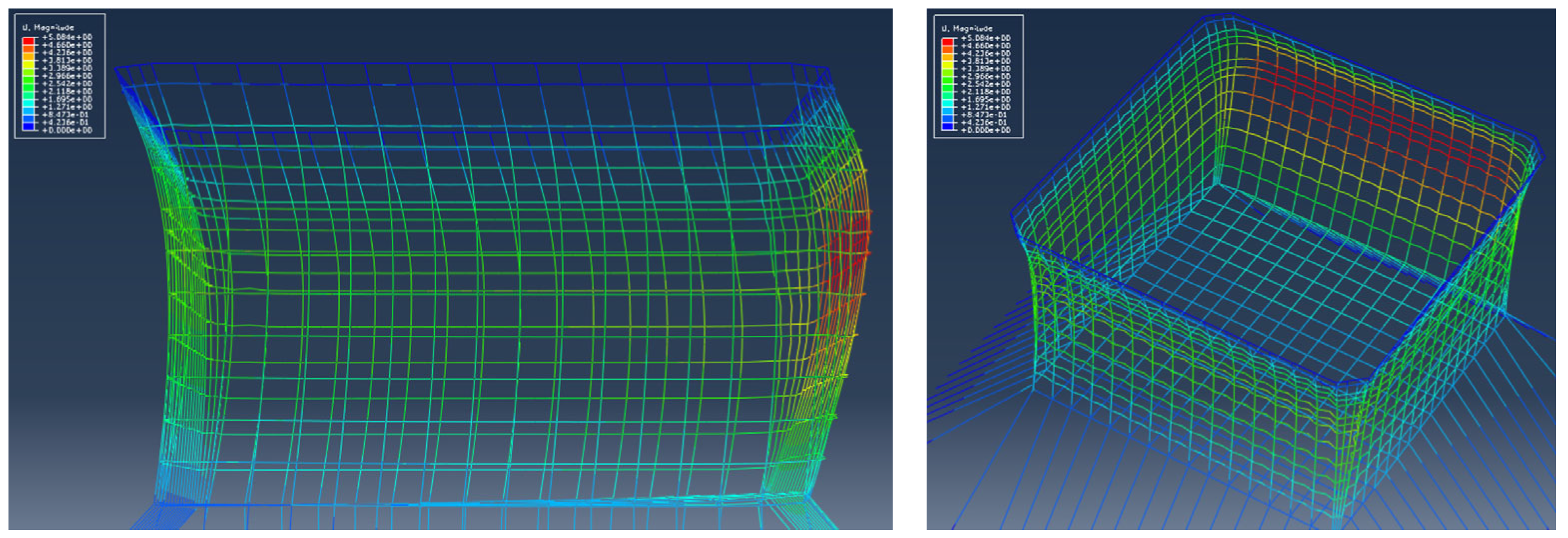
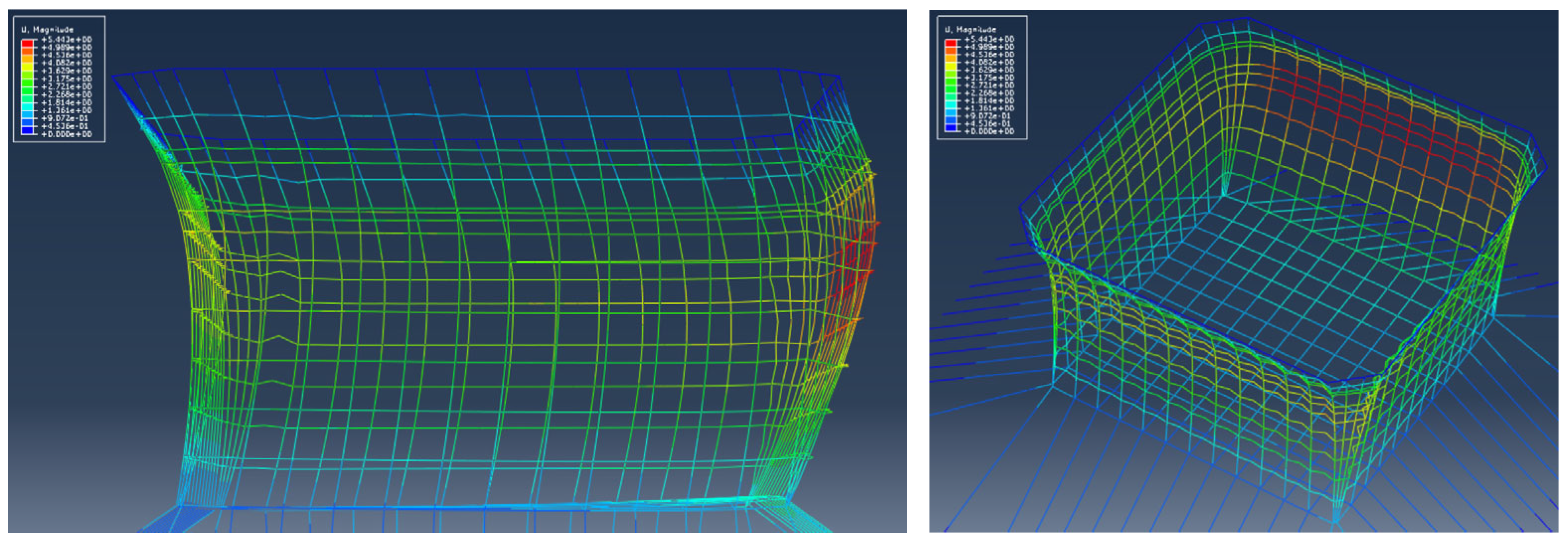
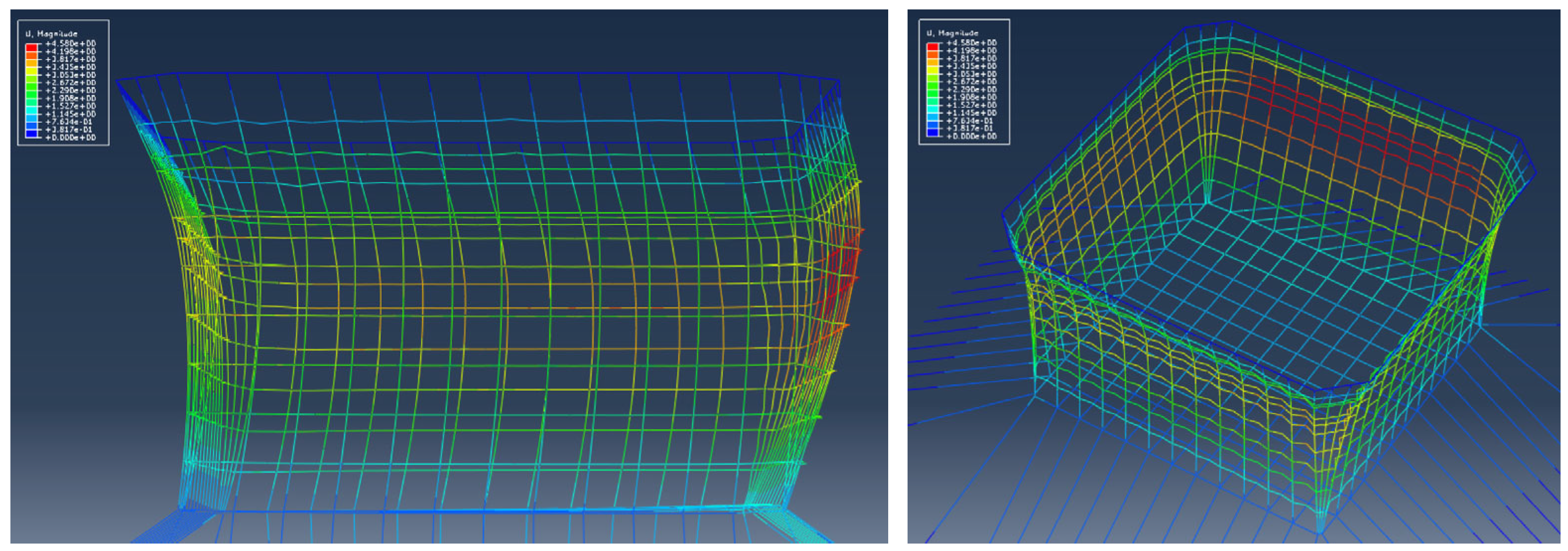
3.2. Deformation of the Net Systems
3.3. Discussions on the Comparisons and the Design Trade-Offs of the Three Schemes
4. Conclusions and Outlook
- It is demonstrated that Scheme 1 offers the best balance between the structural safety and functional efficiency for the deployments in the Bohai Sea, making it the recommended design. Scheme 1 trades off maximum volume expansion for optimal load management, minimal deformation, and the highest overall structural reliability.
- Scheme 1 offers a critical safety advantage by significantly reducing the risk of collisions, with a minimum clearance of −0.46 m. In contrast, Scheme 2 and Scheme 3 exhibit much higher collision risks, with minimum clearances of −1.66 m and −1.63 m, respectively, under 100 year storm conditions. Additionally, the peak bottom tension rope load for Scheme 1 is 37.9 tons, which is 14% lower than Scheme 3 (46.1 tons) and 18% lower than Scheme 2 (44.2 tons). This demonstrates that Scheme 1 is more compatible with standard mooring systems and provides higher engineering safety margins.
- Scheme 1 has shown the capacity of withstanding combined wave heights of 8.4 m and currents of 1.5 m/s at the critical angle of 15° between the wave and current directions. Its maximum displacement of 4.0 m is 21.3% lower than that of Scheme 3, which has a displacement of 5.08 m, providing a significant margin for deformation. The design of Scheme 1 offers sufficient safety margins to account for potential increases in load due to biofouling.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, Y.; Ni, Q.; Liu, H.; Zhang, C. Status quo of industrialized aquaculture of Atlantic salmon in Norway and its implications for China. Trans. Chin. Soc. Agric. Eng. (Trans. CSAE) 2020, 36, 310–315, (In Chinese with English Abstract). [Google Scholar]
- Zhang, C.; Liu, H.; Xu, H.; Zhang, Y.; Miao, M. Status quo of industrialized aquaculture of tuna in Japan and the enlightenment to China. Fish. Mod. 2021, 48, 10–17, (In Chinese with English Abstract). [Google Scholar]
- Fredriksson, D.W.; Swift, M.R.; Irish, J.D.; Tsukrov, I.; Celikkol, B. Fish Cage and Mooring System Dynamics Using Physical and Numerical Models with Field Measurements. Aquac. Eng. 2003, 27, 117–146. [Google Scholar] [CrossRef]
- Li, X.; Li, J.; Wang, Y.; Fu, L.; Fu, Y.; Li, B.; Jiao, B. Aquaculture Industry in China: Current State, Challenges, and Outlook. Rev. Fish. Sci. 2011, 19, 187–200. [Google Scholar] [CrossRef]
- Yu, J.; Cheng, X.; Fan, Y.; Ni, X.; Chen, Y.; Ye, Y. Mooring Design of Offshore Aquaculture Platform and Its Dynamic Performance. Ocean. Eng. 2023, 275, 114146. [Google Scholar] [CrossRef]
- Chu, Y.I.; Wang, C.M.; Park, J.C.; Lader, P.F. Review of Cage and Containment Tank Designs for Offshore Fish Farming. Aquaculture 2020, 519, 734928. [Google Scholar] [CrossRef]
- Chen, C.; Wang, H.; Zhang, X.; Zhang, X. Hydrodynamic Interactions between the Cylinder and Nets of a Typical Offshore Aquaculture Structure in Steady Current: Numerical Investigation and Coupling Mechanism. Mar. Struct. 2024, 97, 103657. [Google Scholar] [CrossRef]
- Wang, G.; Martin, T.; Huang, L.; Bihs, H. Modelling the Flow around and Wake behind Net Panels Using Large Eddy Simulations. Ocean. Eng. 2021, 239, 109846. [Google Scholar] [CrossRef]
- Wang, G.; Martin, T.; Huang, L.; Bihs, H. An Improved Screen Force Model Based on CFD Simulations of the Hydrodynamic Loads on Knotless Net Panels. Appl. Ocean. Res. 2022, 118, 102965. [Google Scholar] [CrossRef]
- Loland, G. Current Forces on and Flow through Fish Farms. PhD Thesis, Norweigian University of Science and Technology, Trondheim, Norway, 1991. [Google Scholar]
- Loland, G. Current Forces on, and Water Flow through and around, Floating Fish Farms. Aquacult. Int. 1993, 1, 72–89. [Google Scholar] [CrossRef]
- Tang, H.; Hu, F.; Xu, L.; Dong, S.; Zhou, C.; Wang, X. Variations in Hydrodynamic Characteristics of Netting Panels with Various Twine Materials, Knot Types, and Weave Patterns at Small Attack Angles. Sci. Rep. 2019, 9, 1923. [Google Scholar] [CrossRef]
- Tsukrov, I.; Drach, A.; DeCew, J.; Robinson Swift, M.; Celikkol, B. Characterization of Geometry and Normal Drag Coefficients of Copper Nets. Ocean. Eng. 2011, 38, 1979–1988. [Google Scholar] [CrossRef]
- Lader, P.F.; Fredheim, A. Dynamic Properties of a Flexible Net Sheet in Waves and Current—A Numerical Approach. Aquac. Eng. 2006, 35, 228–238. [Google Scholar] [CrossRef]
- Lader, P.F.; Olsen, A.; Jensen, A.; Sveen, J.K.; Fredheim, A.; Enerhaug, B. Experimental Investigation of the Interaction between Waves and Net Structures—Damping Mechanism. Aquac. Eng. 2007, 37, 100–114. [Google Scholar] [CrossRef]
- Song, W.; Liang, Z.; Huang, L.; Lv, Y.; Chen, B. Hydrodynamic feature of fishing net under wave action in flume experiment. Oceanol. Limnol. Sin. 2007, 38, 15–21. [Google Scholar]
- Ito, S.; Kinoshita, T.; Kitazawa, D.; Bao, W.; Itakura, H.; Nishizawa, S. Experimental Investigation and Numerical Modeling of Hydrodynamic Force Characteristics of a Heaving Net. In Proceedings of the 29th International Conference on Ocean, Offshore and Arctic Engineering, Shanghai, China, 6–11 June 2010; ASMEDC: Shanghai, China, 2010; Volume 3, pp. 87–96. [Google Scholar]
- Ito, S.; Kinoshita, T.; Kitazawa, D.; Bao, W.; Itakura, H. Experimental Investigation and Numerical Modeling of Hydrodynamic Force Characteristics and Deformation of an Elastic Net. In Proceedings of the ASME 2011 30th International Conference on Ocean, Offshore and Arctic Engineering, Rotterdam, The Netherlands, 19–24 June 2011; ASMEDC: Rotterdam, The Netherlands, 2011; Volume 5: Ocean Space Utilization; Ocean Renewable Energy, pp. 23–33. [Google Scholar]
- Balash, C.; Colbourne, B.; Bose, N.; Raman-Nair, W. Aquaculture Net Drag Force and Added Mass. Aquac. Eng. 2009, 41, 14–21. [Google Scholar] [CrossRef]
- Swift, M.R.; Fredriksson, D.W.; Unrein, A.; Fullerton, B.; Patursson, O.; Baldwin, K. Drag Force Acting on Biofouled Net Panels. Aquac. Eng. 2006, 35, 292–299. [Google Scholar] [CrossRef]
- Lader, P.; Fredriksson, D.W.; Guenther, J.; Volent, Z.; Blocher, N.; Kristiansen, D.; Gansel, L.; Decew, J. Drag on Hydroid-Fouled Nets—An Experimental Approach. China Ocean Eng. 2015, 29, 369–389. [Google Scholar] [CrossRef]
- Tsukrov, I.; Eroshkin, O.; Fredriksson, D.; Swift, M.R.; Celikkol, B. Finite Element Modeling of Net Panels Using a Consistent Net Element. Ocean. Eng. 2003, 30, 251–270. [Google Scholar] [CrossRef]
- Lee, C.-W.; Kim, Y.-B.; Lee, G.-H.; Choe, M.-Y.; Lee, M.-K.; Koo, K.-Y. Dynamic Simulation of a Fish Cage System Subjected to Currents and Waves. Ocean. Eng. 2008, 35, 1521–1532. [Google Scholar] [CrossRef]
- Lader, P.F.; Enerhaug, B.; Fredheim, A.; Krokstad, J. Modelling of 3D Net Structures Exposed to Waves and Current. In Proceedings of the 3rd International Conference on Hydroelasticity in Marine Technology, Oxford, UK, 15–17 September 2003; Department of Engineering Science, The University of Oxford: Oxford, UK, 2003; pp. 19–26. [Google Scholar]
- Moe, H.; Olsen, A.; Hopperstad, O.S.; Jensen, Ø.; Fredheim, A. Tensile Properties for Netting Materials Used in Aquaculture Net Cages. Aquac. Eng. 2007, 37, 252–265. [Google Scholar] [CrossRef]
- Moe, H.; Dempster, T.; Sunde, L.M.; Winther, U.; Fredheim, A. Technological Solutions and Operational Measures to Prevent Escapes of Atlantic Cod (Gadus morhua) from Sea Cages. Aquac. Res. 2007, 38, 91–99. [Google Scholar] [CrossRef]
- Bian, C.; Jiang, W.; Pohlmann, T.; Sündermann, J. Hydrography-Physical Description of the Bohai Sea. J. Coast. Res. 2016, 74, 1–12. [Google Scholar] [CrossRef]
- Wan, R.; Huang, W.Q.; Song, X.F.; Hu, F.X.; Tokai, T. Statics of a Gillnet Placed in a Uniform Current. Ocean. Eng. 2004, 31, 1725–1740. [Google Scholar] [CrossRef]
- Zhao, Y.-P.; Li, Y.-C.; Dong, G.-H.; Gui, F.-K.; Teng, B. Numerical Simulation of the Effects of Structure Size Ratio and Mesh Type on Three-Dimensional Deformation of the Fishing-Net Gravity Cage in Current. Aquac. Eng. 2007, 36, 285–301. [Google Scholar] [CrossRef]
- Moe, H.; Fredheim, A.; Hopperstad, O.S. Structural Analysis of Aquaculture Net Cages in Current. J. Fluids Struct. 2010, 26, 503–516. [Google Scholar] [CrossRef]
- Huang, L.; Li, Y.; Wang, G.; Wang, Y.; Wu, Q.; Jia, M.; Wan, R. An Improved Morison Hydrodynamics Model for Knotless Nets Based on CFD and Metamodelling Methods. Aquac. Eng. 2022, 96, 102220. [Google Scholar] [CrossRef]
- Hilber, H.M.; Hughes, T.J.R. Collocation, Dissipation and [Overshoot] for Time Integration Schemes in Structural Dynamics. Earthq. Eng. Struct. Dyn. 1978, 6, 99–117. [Google Scholar] [CrossRef]
- Choc, Y.-I.; Casarell, M.J. Hydrodynamic Resistance of Towed Cables. J. Hydronautics 1971, 5, 126–131. [Google Scholar] [CrossRef]
- DeCew, J.; Tsukrov, I.; Risso, A.; Swift, M.R.; Celikkol, B. Modeling of Dynamic Behavior of a Single-Point Moored Submersible Fish Cage under Currents. Aquac. Eng. 2010, 43, 38–45. [Google Scholar] [CrossRef]
- Zhao, Y.-P.; Li, Y.-C.; Dong, G.-H.; Gui, F.-K.; Teng, B. A Numerical Study on Dynamic Properties of the Gravity Cage in Combined Wave-Current Flow. Ocean. Eng. 2007, 34, 2350–2363. [Google Scholar] [CrossRef]
- Li, N.; Li, X.; Shi, W.; Liu, C. Numerical simulation of hydrodynamic characteristics of the plane net under waves and current. J. Shanghai Ocean. Univ. 2024, 33, 509–519, (In Chinese with English Abstract). [Google Scholar]



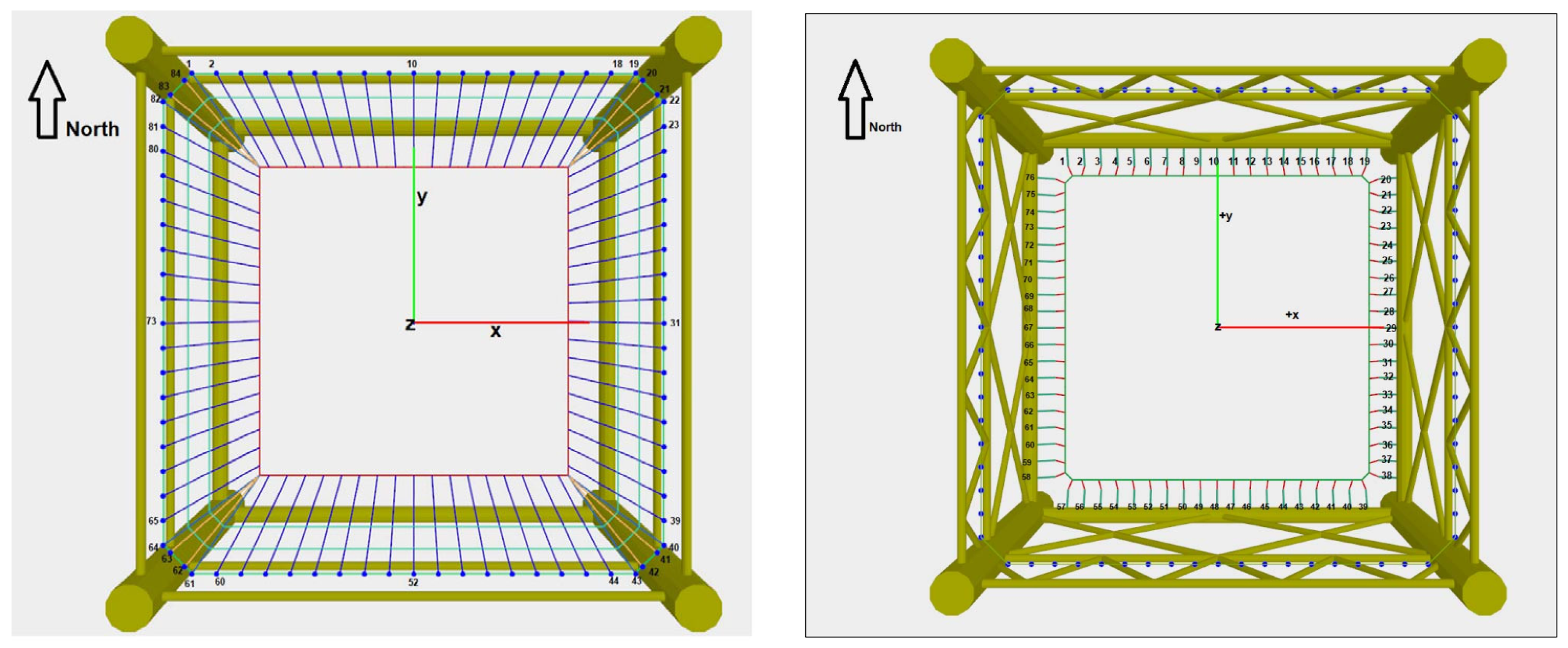
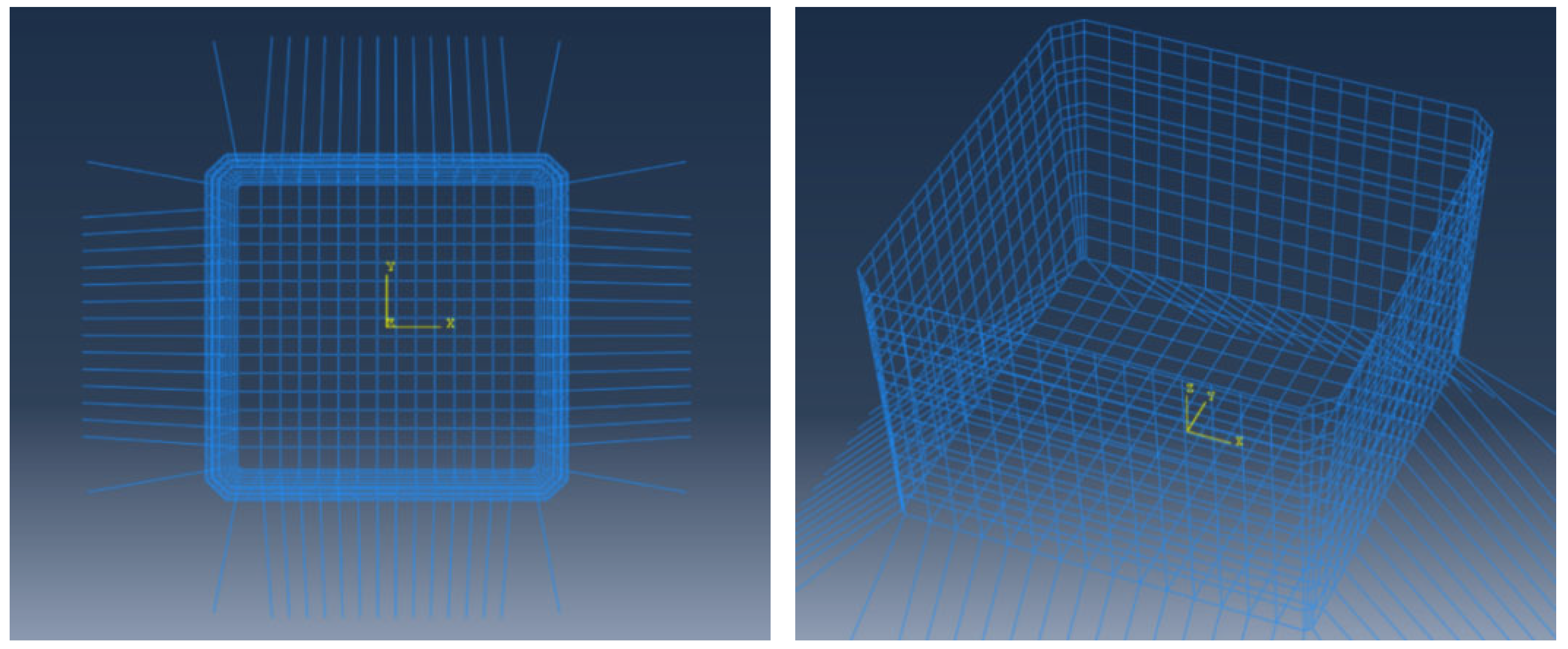
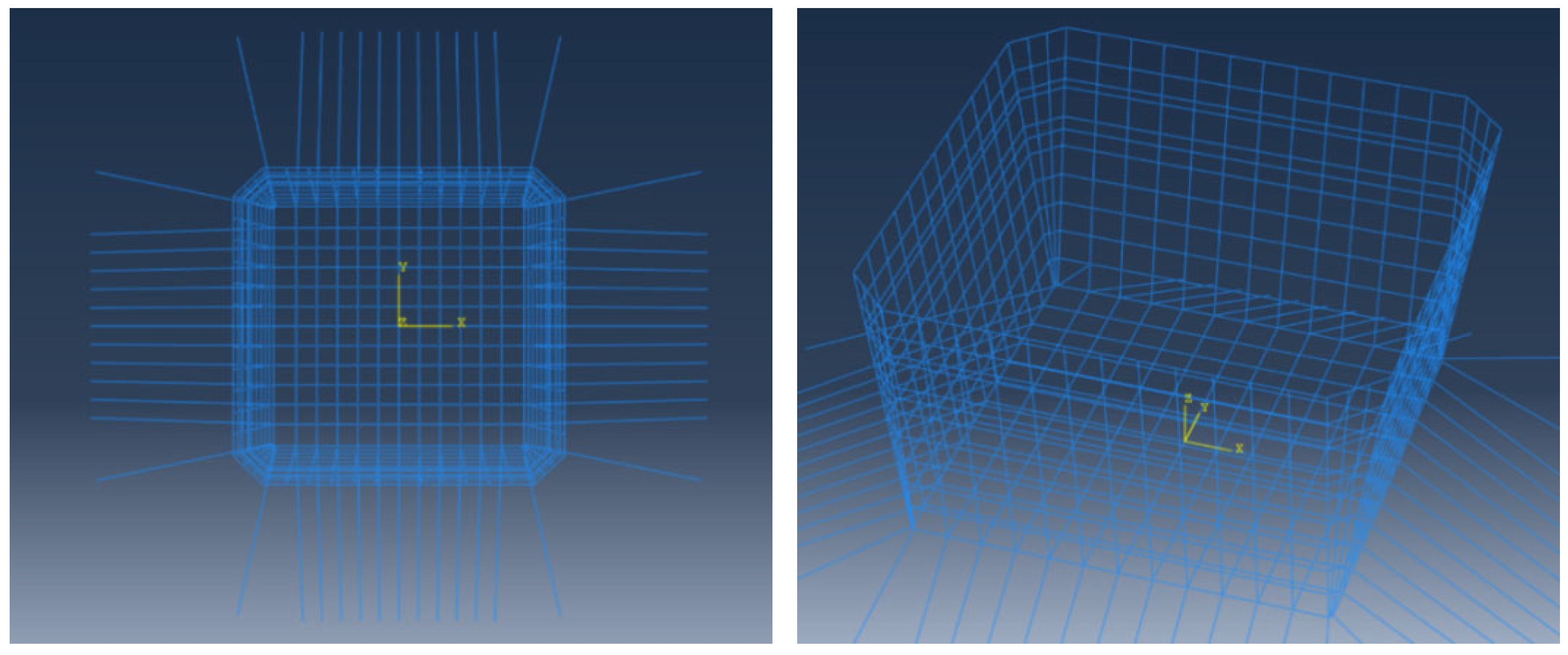


| Schemes | Design Objective | Modifications Compared with Scheme 1 |
| 2 | Increase aquaculture volume and utilization rate |
|
| 3 | Optimize load distribution while maintaining aquaculture volume |
|
| Environmental Load | Survival Condition (100-Year Recurrence) | Normal Operational Condition (1-Year Recurrence) | Remarks |
|---|---|---|---|
| Ambient temperature (°C) | −10.0–36.0 | Air temperature | |
| Air humidity | Summer humidity 70% | / | |
| Water depth (m) | 32.5 | Water depth at low tide | |
| Tidal range (m) | 2 | / | |
| Storm surge water level rise (m) | 2 | / | |
| Wind speed (m/s) | 36.0 | 17.1 | 1 min average wind speed at 10 m above sea level |
| Maximum wave height (m) | 8.4 | 5.8 | / |
| Wave period (s) | 12.5 | 10.3 | / |
| Surface current velocity (m/s) | 1.5 | 1.5 | / |
| Bottom current velocity (m/s) | 1.0 | 1.0 | / |
| Ice formation risk | No | No | / |
| Scheme No. | Working Condition Type | Case No. | Wave–Current Direction (deg) | Water Depth | Wave Height (m) | Wave Period (T) | Current Velocity (m/s) |
|---|---|---|---|---|---|---|---|
| Scheme 1 | Survival condition | case1-1 | 0 | 36.5 | 8.4 | 12.5 | 1.5/1.0 |
| case1-2 | 15 | 36.5 | 8.4 | 12.5 | 1.5/1.0 | ||
| case1-3 | 30 | 36.5 | 8.4 | 12.5 | 1.5/1.0 | ||
| case1-4 | 45 | 36.5 | 8.4 | 12.5 | 1.5/1.0 | ||
| Operational condition | case1-5 | 0 | 34.5 | 5.8 | 10.3 | 1.5/1.0 | |
| case1-6 | 15 | 34.5 | 5.8 | 10.3 | 1.5/1.0 | ||
| case1-7 | 30 | 34.5 | 5.8 | 10.3 | 1.5/1.0 | ||
| case1-8 | 45 | 34.5 | 5.8 | 10.3 | 1.5/1.0 | ||
| Survival condition | case1-9 | 0 | 34.5 | 8.4 | 12.5 | 1.5/1.0 | |
| case1-10 | 15 | 34.5 | 8.4 | 12.5 | 1.5/1.0 | ||
| case1-11 | 30 | 34.5 | 8.4 | 12.5 | 1.5/1.0 | ||
| case1-12 | 45 | 34.5 | 8.4 | 12.5 | 1.5/1.0 | ||
| Operational condition | case1-13 | 0 | 32.5 | 5.8 | 10.3 | 1.5/1.0 | |
| case1-14 | 15 | 32.5 | 5.8 | 10.3 | 1.5/1.0 | ||
| case1-15 | 30 | 32.5 | 5.8 | 10.3 | 1.5/1.0 | ||
| case1-16 | 45 | 32.5 | 5.8 | 10.3 | 1.5/1.0 | ||
| Scheme 2 | Survival condition | case2-1 | 0 | 36.5 | 8.4 | 12.5 | 1.5/1.0 |
| case2-2 | 15 | 36.5 | 8.4 | 12.5 | 1.5/1.0 | ||
| case2-3 | 30 | 36.5 | 8.4 | 12.5 | 1.5/1.0 | ||
| case2-4 | 45 | 36.5 | 8.4 | 12.5 | 1.5/1.0 | ||
| Operational condition | case2-5 | 0 | 34.5 | 5.8 | 10.3 | 1.5/1.0 | |
| case2-6 | 15 | 34.5 | 5.8 | 10.3 | 1.5/1.0 | ||
| case2-7 | 30 | 34.5 | 5.8 | 10.3 | 1.5/1.0 | ||
| case2-8 | 45 | 34.5 | 5.8 | 10.3 | 1.5/1.0 | ||
| Scheme 3 | Survival condition | case3-1 | 0 | 36.5 | 8.4 | 12.5 | 1.5/1.0 |
| case3-2 | 15 | 36.5 | 8.4 | 12.5 | 1.5/1.0 | ||
| case3-3 | 30 | 36.5 | 8.4 | 12.5 | 1.5/1.0 | ||
| case3-4 | 45 | 36.5 | 8.4 | 12.5 | 1.5/1.0 | ||
| Operational condition | case3-5 | 0 | 34.5 | 5.8 | 10.3 | 1.5/1.0 | |
| case3-6 | 15 | 34.5 | 5.8 | 10.3 | 1.5/1.0 | ||
| case3-7 | 30 | 34.5 | 5.8 | 10.3 | 1.5/1.0 | ||
| case3-8 | 45 | 34.5 | 5.8 | 10.3 | 1.5/1.0 |
| Working Condition | Case No. | Wave and Current Direction (deg) | Water Depth (m) | Maximum Load of Side Netting Vertical Ropes (Tons) | Maximum Load of Corner Vertical Ropes (Tons) |
|---|---|---|---|---|---|
| Survival condition | case1-1 | 0 | 36.5 | 20.3 | 15.3 |
| case1-2 | 15 | 36.5 | 26.3 | 17.2 | |
| case1-3 | 30 | 36.5 | 24.4 | 16.0 | |
| case1-4 | 45 | 36.5 | 21.8 | 14.0 | |
| Operational condition | case1-5 | 0 | 34.5 | 15.6 | 11.5 |
| case1-6 | 15 | 34.5 | 20.1 | 12.9 | |
| case1-7 | 30 | 34.5 | 18.8 | 12.3 | |
| case1-8 | 45 | 34.5 | 16.9 | 10.8 | |
| Survival condition | case1-9 | 0 | 34.5 | 19.1 | 14.3 |
| case1-10 | 15 | 34.5 | 25.0 | 16.1 | |
| case1-11 | 30 | 34.5 | 23.3 | 15.2 | |
| case1-12 | 45 | 34.5 | 20.8 | 13.4 | |
| Operational condition | case1-13 | 0 | 32.5 | 14.6 | 10.9 |
| case1-14 | 15 | 32.5 | 19.1 | 12.2 | |
| case1-15 | 30 | 32.5 | 17.8 | 11.7 | |
| case1-16 | 45 | 32.5 | 15.9 | 10.3 |
| Working Condition | Case No. | Wave and Current Direction (deg) | Water Depth (m) | The maximum Load of the Tension Ropes at the Four Bottom Corners (Tons) | The Maximum Load of Other Tension Ropes at the Bottom (Tons) |
|---|---|---|---|---|---|
| Survival condition | case1-1 | 0 | 36.5 | 30.3 | 27.8 |
| case1-2 | 15 | 36.5 | 37.9 | 36.4 | |
| case1-3 | 30 | 36.5 | 36.5 | 35.3 | |
| case1-4 | 45 | 36.5 | 30.7 | 31.7 | |
| Operational condition | case1-5 | 0 | 34.5 | 23.7 | 21.9 |
| case1-6 | 15 | 34.5 | 29.8 | 28.5 | |
| case1-7 | 30 | 34.5 | 28.8 | 27.6 | |
| case1-8 | 45 | 34.5 | 24.3 | 24.8 | |
| Survival condition | case1-9 | 0 | 34.5 | 29.7 | 26.9 |
| case1-10 | 15 | 34.5 | 37.4 | 35.7 | |
| case1-11 | 30 | 34.5 | 35.9 | 34.5 | |
| case1-12 | 45 | 34.5 | 30.1 | 31.0 | |
| Operational condition | case1-13 | 0 | 32.5 | 22.9 | 20.9 |
| case1-14 | 15 | 32.5 | 28.9 | 27.3 | |
| case1-15 | 30 | 32.5 | 27.8 | 26.3 | |
| case1-16 | 45 | 32.5 | 23.4 | 23.5 |
| Working Condition | Case No. | Wave and Current Direction (deg) | Water Depth | Maximum Load of Side Netting Vertical Ropes (Tons) | Maximum Load of Corner Vertical Ropes (Tons) |
|---|---|---|---|---|---|
| Survival condition | case2-1 | 0 | 36.5 | 24.5 | 19.5 |
| case2-2 | 15 | 36.5 | 31.7 | 22.6 | |
| case2-3 | 30 | 36.5 | 29.2 | 21.2 | |
| case2-4 | 45 | 36.5 | 25.9 | 17.8 | |
| Operational condition | case2-5 | 0 | 34.5 | 18.8 | 15.0 |
| case2-6 | 15 | 34.5 | 24.3 | 17.4 | |
| case2-7 | 30 | 34.5 | 22.6 | 16.3 | |
| case2-8 | 45 | 34.5 | 20.2 | 14.0 |
| Working Condition | Case No. | Wave and Current Direction (deg) | Water Depth (m) | The Maximum Load of the Tension Ropes at the Four Bottom Corners (Tons) | The Maximum Load of Other Tension Ropes at the Bottom (Tons) |
|---|---|---|---|---|---|
| Survival condition | case2-1 | 0 | 36.5 | 36.4 | 32.6 |
| case2-2 | 15 | 36.5 | 44.2 | 42.3 | |
| case2-3 | 30 | 36.5 | 42.2 | 40.1 | |
| case2-4 | 45 | 36.5 | 34.4 | 35.6 | |
| Operational condition | case2-5 | 0 | 34.5 | 28.3 | 25.8 |
| case2-6 | 15 | 34.5 | 34.9 | 33.5 | |
| case2-7 | 30 | 34.5 | 33.5 | 31.7 | |
| case2-8 | 45 | 34.5 | 27.6 | 28.2 |
| Working Condition | Case No. | Wave and Current Direction (deg) | Water Depth | Maximum Load of Side Netting Vertical Ropes (Tons) | Maximum Load of Corner Vertical Ropes (Tons) |
|---|---|---|---|---|---|
| Survival condition | case3-1 | 0 | 36.5 | 21.6 | 17.8 |
| case3-2 | 15 | 36.5 | 27.5 | 20.8 | |
| case3-3 | 30 | 36.5 | 25.5 | 19.9 | |
| case3-4 | 45 | 36.5 | 23.4 | 22.3 | |
| Operational condition | case3-5 | 0 | 34.5 | 16.8 | 13.6 |
| case3-6 | 15 | 34.5 | 19.5 | 14.4 | |
| case3-7 | 30 | 34.5 | 19.5 | 15.0 | |
| case3-8 | 45 | 34.5 | 18.2 | 16.8 |
| Working Condition | Case No. | Wave and Current Direction (deg) | Water Depth (m) | The Maximum Load of the Tension Ropes at the Four Bottom Corners (Tons) | The Maximum Load of Other Tension Ropes at the Bottom (Tons) |
|---|---|---|---|---|---|
| Survival condition | case3-1 | 0 | 36.5 | 37.7 | 34.7 |
| case3-2 | 15 | 36.5 | 46.1 | 44.3 | |
| case3-3 | 30 | 36.5 | 43.9 | 42.3 | |
| case3-4 | 45 | 36.5 | 42.7 | 39.8 | |
| Operational condition | case3-5 | 0 | 34.5 | 30.1 | 28.2 |
| case3-6 | 15 | 34.5 | 33.9 | 32.6 | |
| case3-7 | 30 | 34.5 | 35.0 | 33.7 | |
| case3-8 | 45 | 34.5 | 34.3 | 31.7 |
| Working Condition | Case No. | Wave and Current Direction (deg) | Water Depth (m) | Maximum Netting Displacement (m) | Peak x-Direction Displacement (m) | Minimum Distance to Diagonal Brace (m) |
|---|---|---|---|---|---|---|
| Survival condition | case1-1 | 0 | 36.5 | 3.3 | 27.3 | 0.23 |
| case1-2 | 15 | 36.5 | 4.0 | 28.0 | −0.46 | |
| case1-3 | 30 | 36.5 | 3.7 | 27.7 | −0.12 | |
| case1-4 | 45 | 36.5 | 3.1 | 27.1 | 0.40 | |
| Operational condition | case1-5 | 0 | 34.5 | 2.7 | 26.7 | 0.84 |
| case1-6 | 15 | 34.5 | 3.4 | 27.3 | 0.21 | |
| case1-7 | 30 | 34.5 | 3.1 | 27.0 | 0.52 | |
| case1-8 | 45 | 34.5 | 2.6 | 26.6 | 0.97 | |
| Survival condition | case1-9 | 0 | 34.5 | 3.3 | 27.2 | 0.35 |
| case1-10 | 15 | 34.5 | 4.0 | 27.9 | −0.36 | |
| case1-11 | 30 | 34.5 | 3.7 | 27.6 | −0.01 | |
| case1-12 | 45 | 34.5 | 3.1 | 27.0 | 0.52 | |
| Operational condition | case1-13 | 0 | 32.5 | 2.6 | 26.5 | 1.06 |
| case1-14 | 15 | 32.5 | 3.3 | 27.1 | 0.41 | |
| case1-15 | 30 | 32.5 | 3.0 | 26.8 | 0.73 | |
| case1-16 | 45 | 32.5 | 2.5 | 26.4 | 1.17 |
| Working Condition | Case No. | Wave and Current Direction (deg) | Water Depth (m) | Maximum Netting Displacement (m) | Peak x-Direction Displacement (m) | Minimum Distance to Diagonal Brace (m) |
|---|---|---|---|---|---|---|
| Survival condition | case2-1 | 0 | 36.5 | 3.95 | 28.48 | −0.93 |
| case2-2 | 15 | 36.5 | 4.70 | 29.21 | −1.66 | |
| case2-3 | 30 | 36.5 | 4.28 | 28.79 | −1.24 | |
| case2-4 | 45 | 36.5 | 3.71 | 28.23 | −0.68 | |
| Operational condition | case2-5 | 0 | 34.5 | 3.36 | 27.87 | −0.32 |
| case2-6 | 15 | 34.5 | 4.06 | 28.56 | −1.01 | |
| case2-7 | 30 | 34.5 | 3.67 | 28.17 | −0.62 | |
| case2-8 | 45 | 34.5 | 3.14 | 27.65 | −0.10 |
| Working Condition | Case No. | Wave and Current Direction (deg) | Water Depth (m) | Maximum Netting Displacement (m) | Peak x-Direction Displacement (m) | Minimum Distance to Diagonal Brace (m) |
|---|---|---|---|---|---|---|
| Survival condition | case3-1 | 0 | 36.5 | 4.36 | 28.49 | −0.94 |
| case3-2 | 15 | 36.5 | 5.08 | 29.18 | −1.63 | |
| case3-3 | 30 | 36.5 | 4.66 | 28.78 | −1.23 | |
| case3-4 | 45 | 36.5 | 3.97 | 28.11 | −0.56 | |
| Operational condition | case3-5 | 0 | 34.5 | 3.91 | 28.04 | −0.49 |
| case3-6 | 15 | 34.5 | 3.93 | 28.06 | −0.51 | |
| case3-7 | 30 | 34.5 | 4.04 | 28.13 | −0.58 | |
| case3-8 | 45 | 34.5 | 3.41 | 27.52 | 0.03 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, F.; Zhu, H.; Sun, G.; Zhang, Y.; Wang, Y.; Wang, G. Structural Responses of the Net System of a Bottom-Mounted Aquaculture Farm in Waves and Currents. J. Mar. Sci. Eng. 2025, 13, 1900. https://doi.org/10.3390/jmse13101900
Liu F, Zhu H, Sun G, Zhang Y, Wang Y, Wang G. Structural Responses of the Net System of a Bottom-Mounted Aquaculture Farm in Waves and Currents. Journal of Marine Science and Engineering. 2025; 13(10):1900. https://doi.org/10.3390/jmse13101900
Chicago/Turabian StyleLiu, Fuxiang, Haitao Zhu, Guoqing Sun, Yuqin Zhang, Yanyan Wang, and Gang Wang. 2025. "Structural Responses of the Net System of a Bottom-Mounted Aquaculture Farm in Waves and Currents" Journal of Marine Science and Engineering 13, no. 10: 1900. https://doi.org/10.3390/jmse13101900
APA StyleLiu, F., Zhu, H., Sun, G., Zhang, Y., Wang, Y., & Wang, G. (2025). Structural Responses of the Net System of a Bottom-Mounted Aquaculture Farm in Waves and Currents. Journal of Marine Science and Engineering, 13(10), 1900. https://doi.org/10.3390/jmse13101900







