Prediction of the Bearing Capacity Envelope for Spudcan Foundations of Jack-Up Rigs in Hard Clay with Varying Strengths
Abstract
1. Introduction
2. Numerical Modeling and Verification
2.1. Numerical Model
2.1.1. Spudcan Dimensions and Loads
2.1.2. Soil Properties
2.1.3. Soils Size and Constitutive Model
2.2. Loading Techniques for Bearing Capacities
2.2.1. Swipe and Probe Loadings
2.2.2. Use of Loading Techniques
2.3. Verification
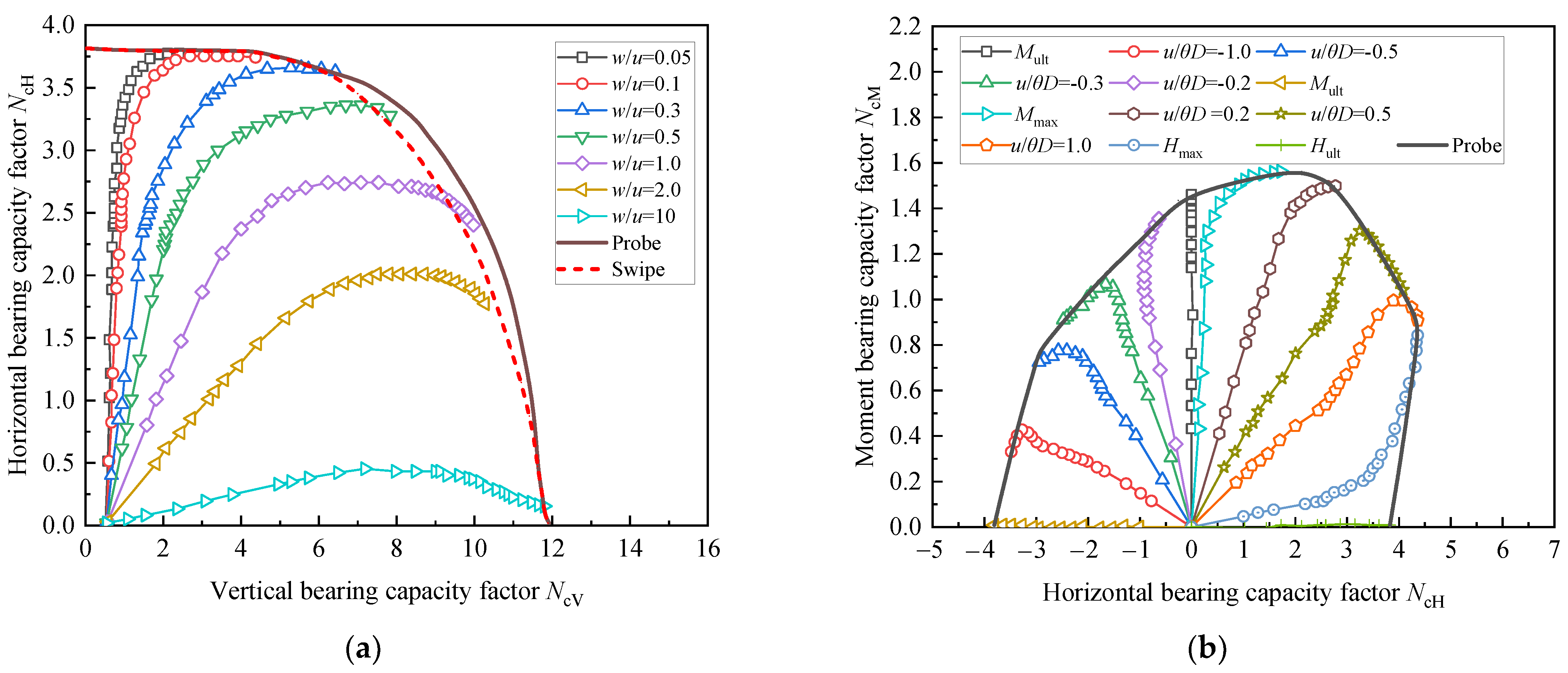
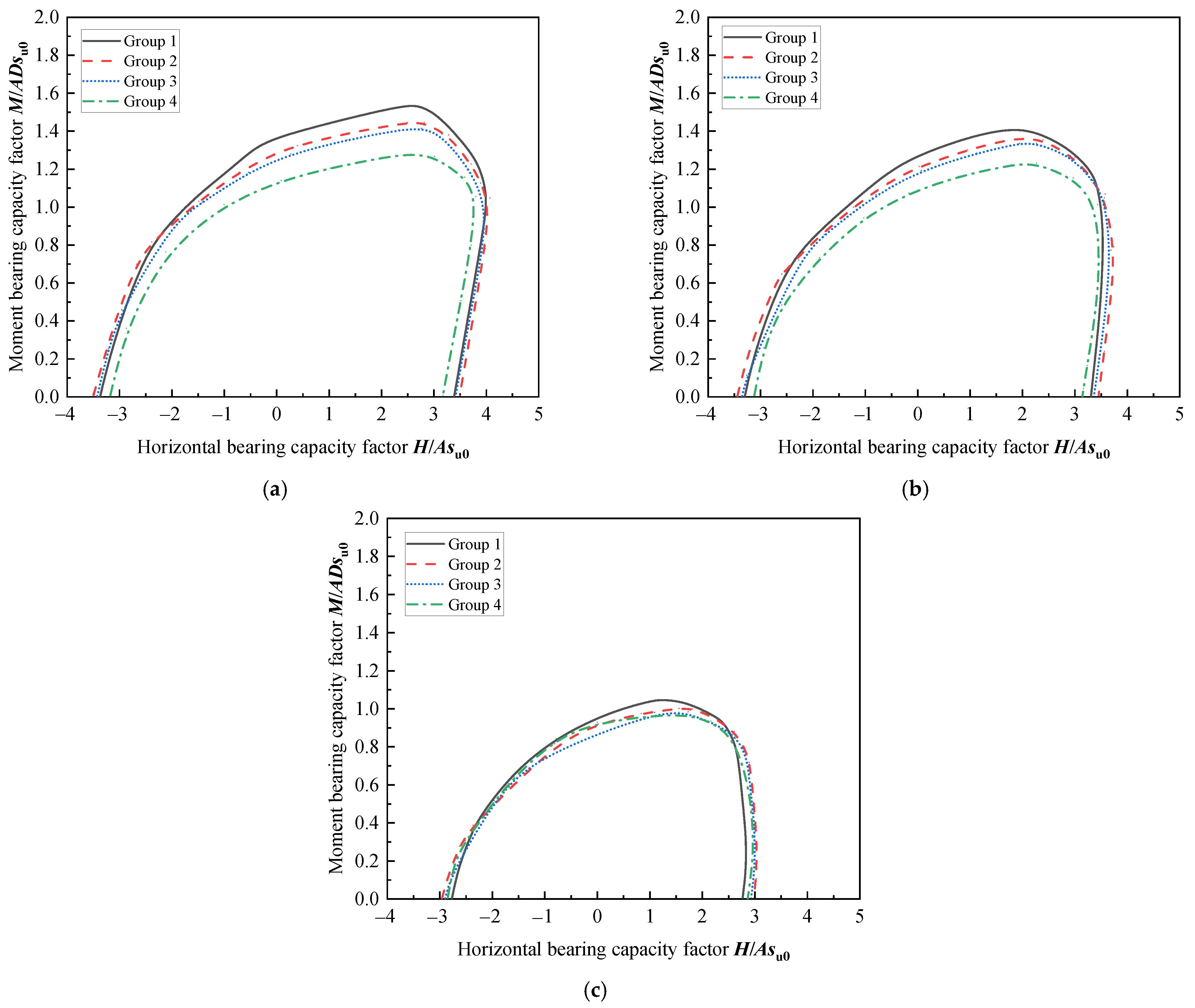
3. Capacities of Spudcan in Clay with Variable Strength
4. Prediction of Failure Envelope
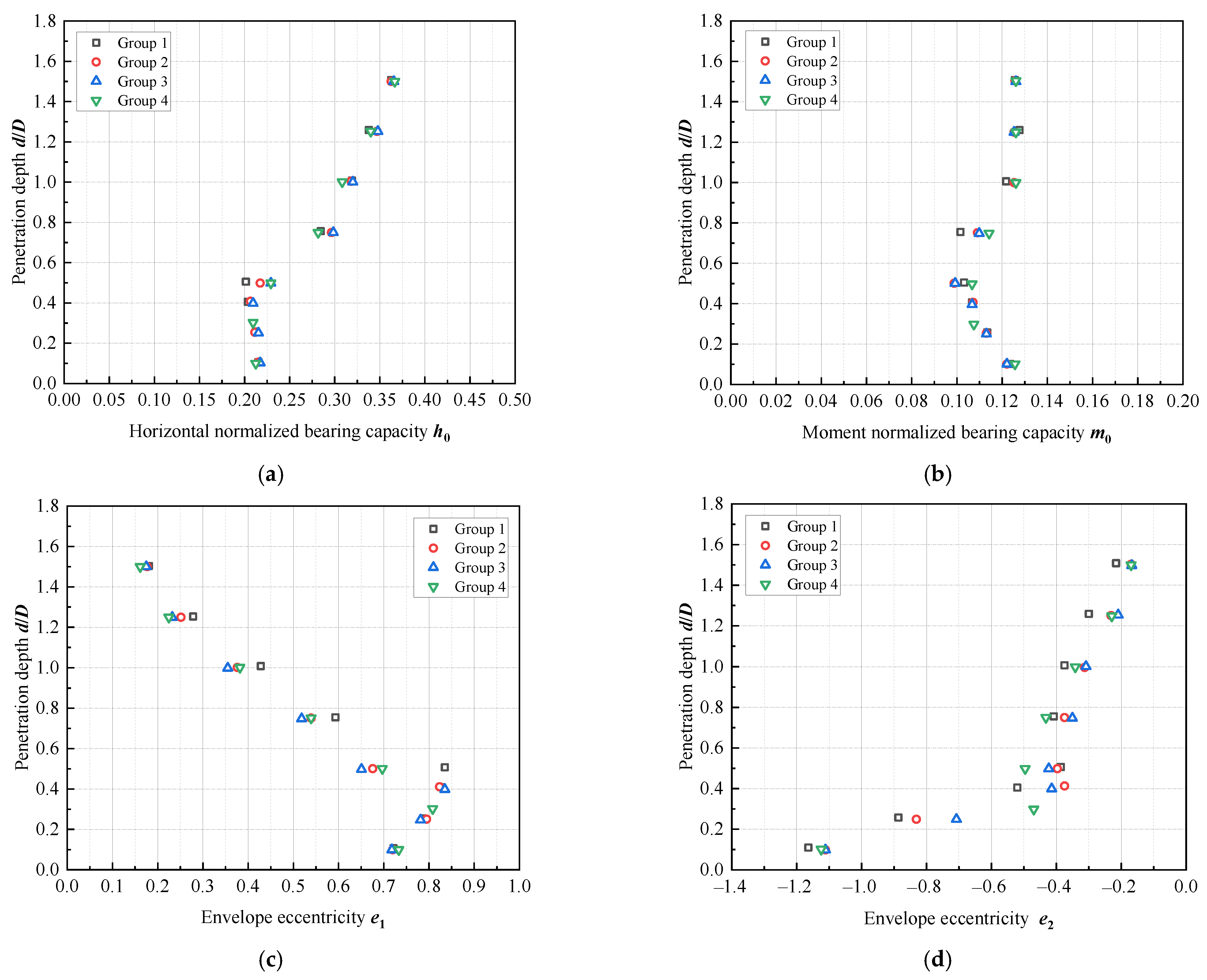
4.1. Prediction Equation
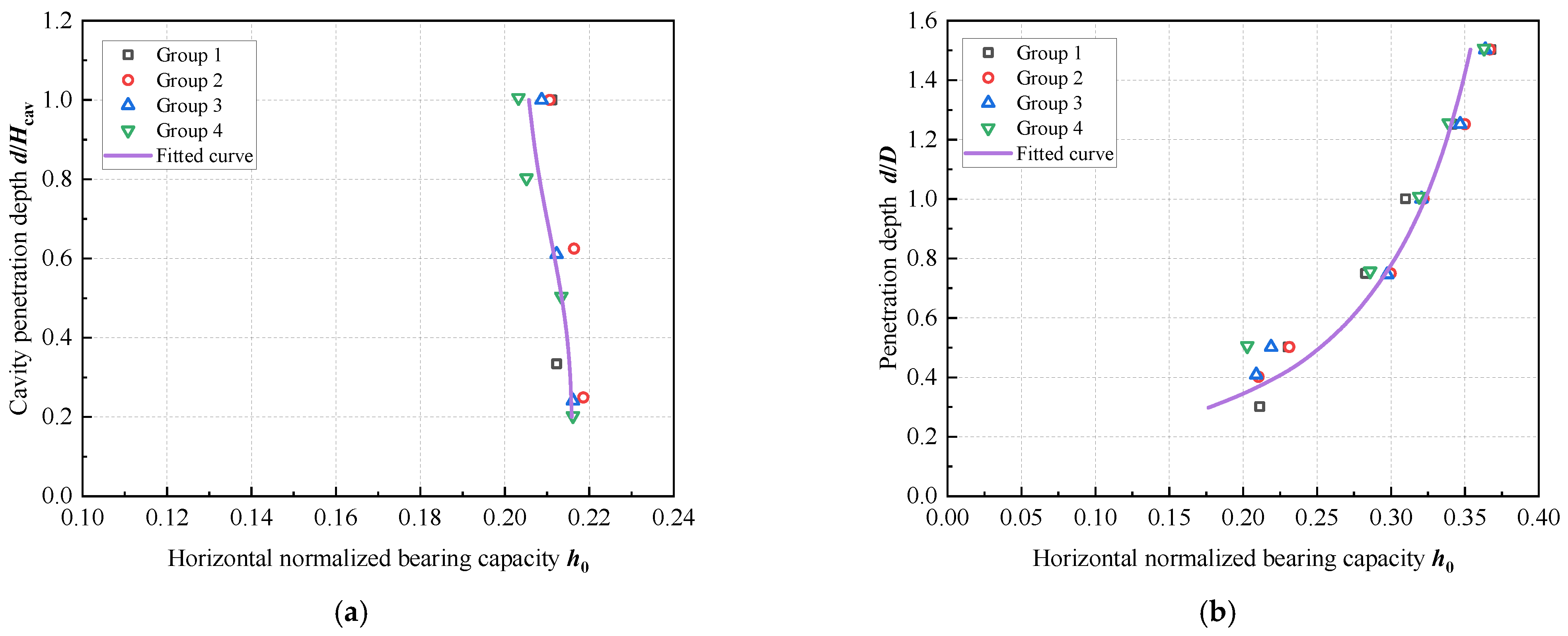
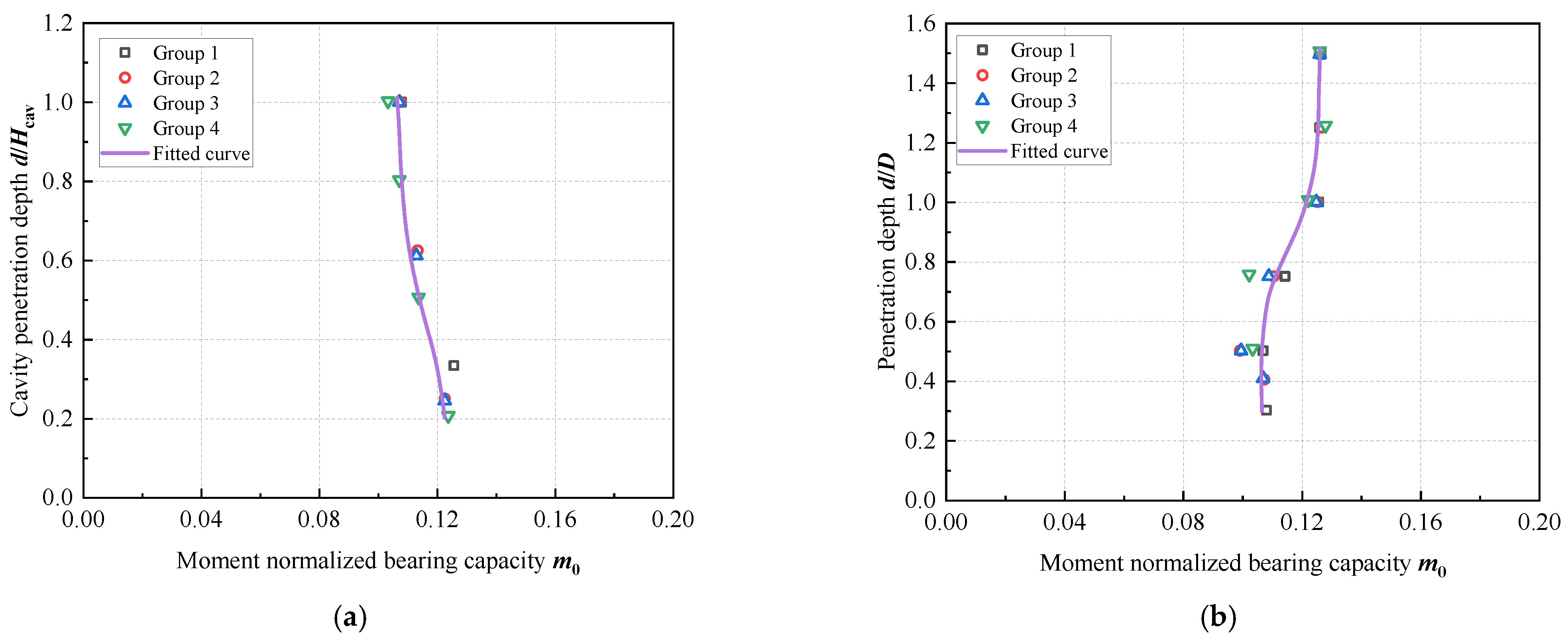
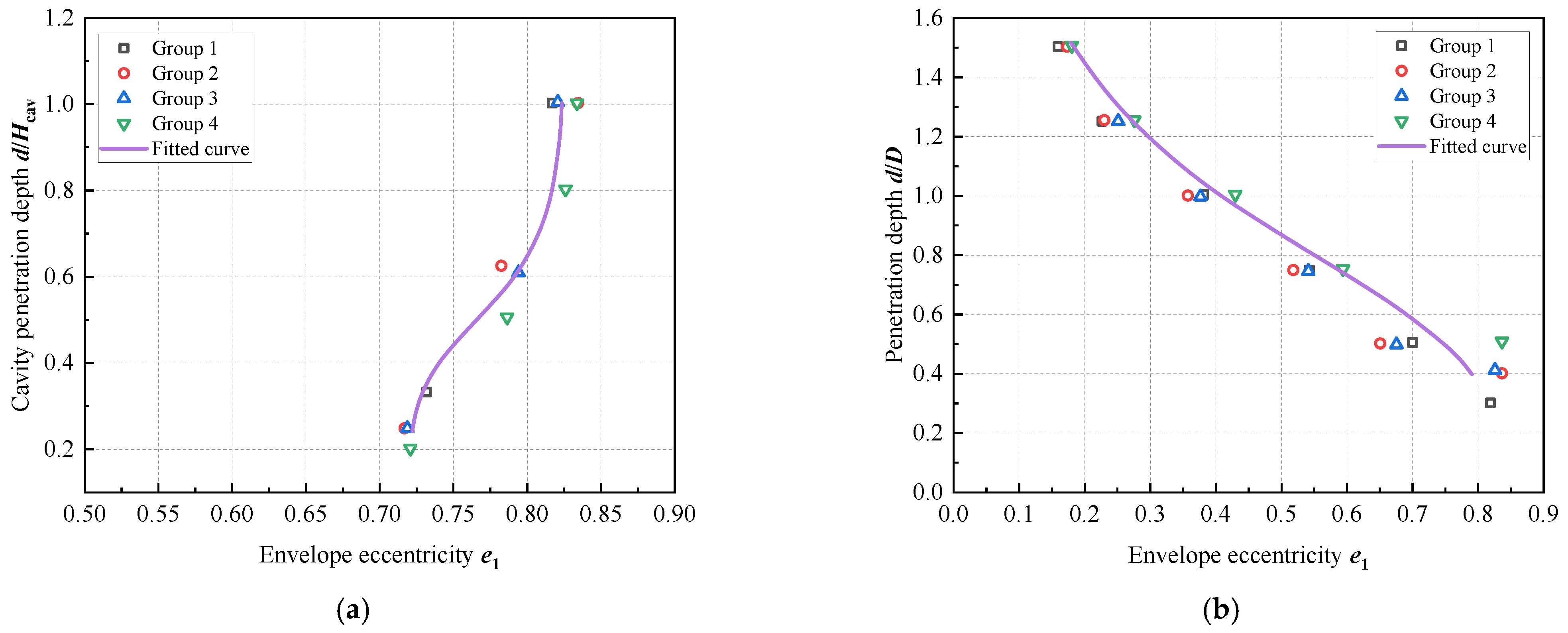
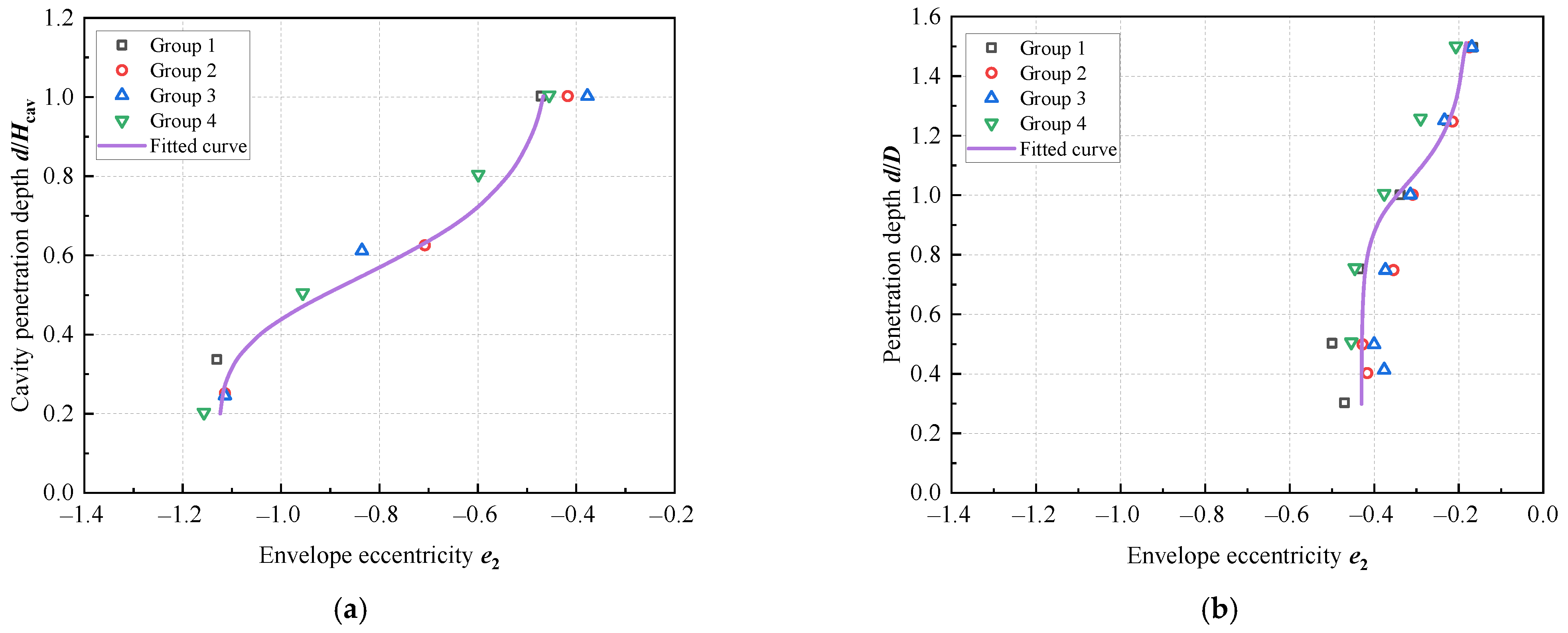
4.2. Parameter Fitting
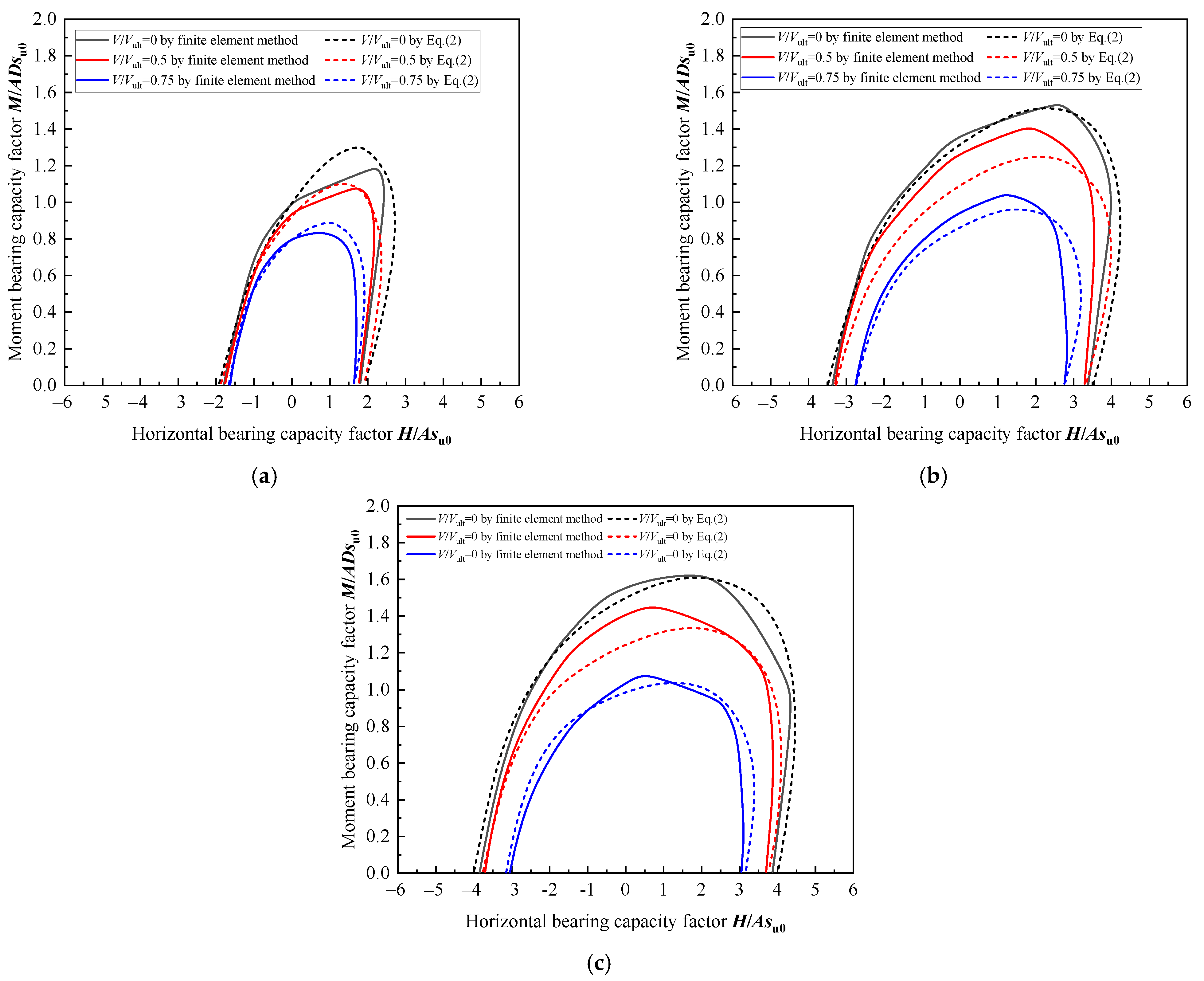
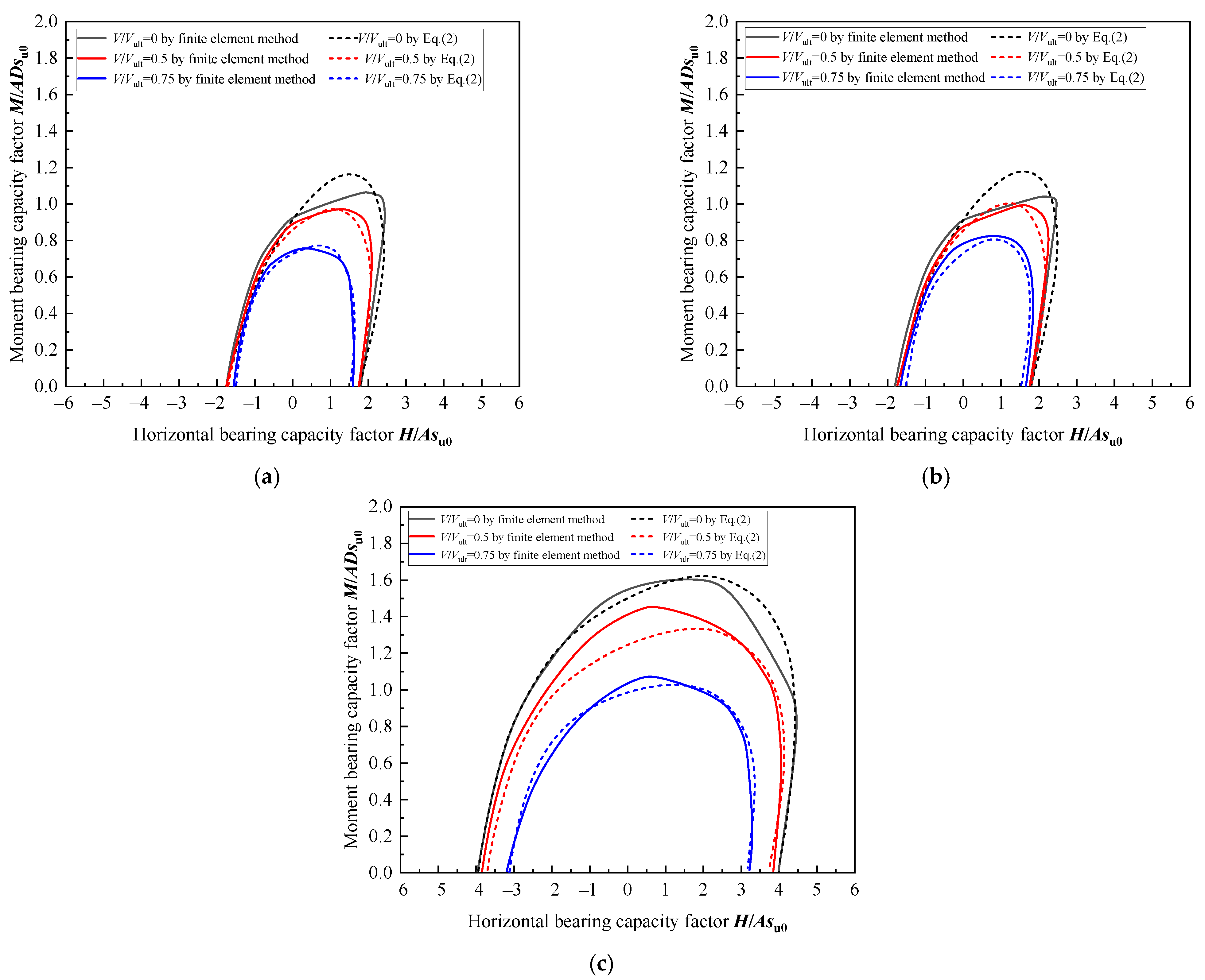
4.3. Verification of Prediction Results
5. Conclusions and Limitations
- (1)
- By employing a finite element method in conjunction with the combined Swipe (for the V-M load plane) and Probe (for the V-H and H-M load planes) loading techniques, the combined capacities of the spudcan in hard clay are accurately predicted. The results show reasonable agreement with the existing centrifuge data, theoretical solutions, and small-deformation results, with errors within 3%.
- (2)
- The size of the failure envelope is highly sensitive to soil strength and cavity depth. Higher undrained shear strength in hard clay corresponds to greater bearing capacity and reduced soil displacement at failure. Under combined V-H-M loading, deeper cavities (Hcav/D ≥ 0.5) reduce the envelope size.
- (3)
- The proposed equation of the failure envelope for the V-H-M includes the normalization coefficient h0 and m0, and the shape parameters e1 and e2 fitted against the spudcan depth. Comparisons with numerical results show that the error of the equation suggested is less than 10% when V/Vult = 0.5 and 0.75. Moreover, as the spudcan depth and soil strength are increased, the accuracy of the prediction may be improved further.
- (4)
- The proposed equation is validated for a specific range of soil strength and cavity conditions, and its applicability to more complex scenarios requires further verification. The Tresca model may oversimplify soil behavior under cyclic loading. Future research should include physical model tests (e.g., centrifuge experiments) and advanced constitutive models to account for cyclic degradation and rate effects. The methodology could also be extended to applications like offshore wind turbine foundations, which involve complex environmental loads.
- (5)
- This study validates the proposed method for shallow to moderate penetration depths in hard clays. The method may be less suitable for conditions involving strong strain softening, partial interface slip, or highly irregular cavity geometries. The model’s idealization of a cylindrical cavity with a perfectly bonded interface may overestimate capacity in scenarios with significant soil disturbance or interface slip. For preliminary design, the calculated capacities should be considered potentially non-conservative, and engineers must apply appropriate safety factors to mitigate the risk of overestimation.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Suryasentana, S.K.; Dunne, H.P.; Martin, C.M.; Burd, H.J.; Byrne, B.W.; Shonberg, A. Assessment of numerical procedures for determining shallow foundation failure envelopes. Geotechnique 2019, 70, 60–70. [Google Scholar] [CrossRef]
- Teh, K.L.; Cassidy, M.J.; Leung, C.F.; Chow, Y.K.; Randolph, M.F.; Quah, C.K. Revealing the Bearing Capacity Mechanisms of a Penetrating Spudcan through Sand Overlying Clay. Geotechnique 2008, 58, 793–804. [Google Scholar] [CrossRef]
- Hossain, M.S.; Randolph, M.F.; Hu, Y.; White, D.J. Cavity Stability and Bearing Capacity of Spudcan Foundations on Clay. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 1 May 2006. [Google Scholar]
- SNAME. T&R Bulletin 5-05 A: Guidelines for Site Specific Assessment of Mobile Jack-Up Units. 2008. Available online: https://sname.org/node/1810 (accessed on 5 September 2025).
- Zhang, Y.; Bienen, B.; Cassidy, M.J.; Gourvenec, S. The Undrained Bearing Capacity of a Spudcan Foundation under Combined Loading in Soft Clay. Mar. Struct. 2011, 24, 459–477. [Google Scholar] [CrossRef]
- Li, L.; Li, J.; Huang, J.; Gao, F.P. Bearing Capacity of Spudcan Foundations in a Spatially Varying Clayey Seabed. Ocean Eng. 2017, 143, 97–105. [Google Scholar] [CrossRef]
- Wu, Y.; Zhang, H.; Shu, S. Probabilistic Bearing Capacity of Spudcan Foundations under Combined Loading in Spatially Variable Soils. Ocean Eng. 2022, 248, 110738. [Google Scholar] [CrossRef]
- Choi, J.; Jang, B.S.; Ju, H.; Han, S. Undrained Bearing Capacity of Spudcan in Soft-over-Stiff Clay after Penetration. Ocean Eng. 2021, 235, 109369. [Google Scholar] [CrossRef]
- Tho, K.K.; Leung, C.F.; Chow, Y.K.; Swaddiwudhipong, K. Improved Prediction of Spudcan Penetration Resistance by an Observation-Optimized Model. Int. J. Geomech. 2010, 12, 64–73. [Google Scholar] [CrossRef]
- Shu, S.; Gao, Y.; Wu, Y. Probabilistic bearing capacity analysis of spudcan foundation in soil with linearly increasing mean undrained shear strength. Ocean Eng. 2020, 204, 106800. [Google Scholar] [CrossRef]
- Bandyopadhyay, P.; Teng, F.C. Analysis of pile-soil-excavation interaction and load transfer mechanism in multi-layered soil for an in-service pile group. Comput. Geotech. 2024, 171, 106378. [Google Scholar] [CrossRef]
- Qiu, G.; Grabe, J. Numerical Investigation of Bearing Capacity Due to Spudcan Penetration in Sand Overlying Clay.Pdf. Can. Geotech. J. 2012, 49, 1393–1407. [Google Scholar] [CrossRef]
- Li, X.; Zhang, A.; Zhang, Q.; Li, D. Predicting the Ultimate Bearing Capacity of Spudcan in Stiff-over-Soft Clay Based on a Failure Model Varying with Soil Parameter. Appl. Ocean Res. 2024, 148, 104026. [Google Scholar] [CrossRef]
- Wang, Y.; Cassidy, M.J.; Bienen, B. Numerical Investigation of Bearing Capacity of Spudcan Foundations in Clay Overlying Sand under Combined Loading. J. Geotech. Geoenviron. Eng. 2020, 146, 04020117. [Google Scholar] [CrossRef]
- Liu, Y.; Zheng, J.; Wang, D.; Liu, K. Capacity of Spudcan Foundation on Dense Sand Overlying Clay under Combined Loading. Ocean Eng. 2022, 266, 112980. [Google Scholar] [CrossRef]
- Yin, Q.; Dong, S. Combined Bearing Capacity of Spudcans on a Double Layer Deposit of Strong-Over-Weak Clays. J. Ocean Univ. China 2019, 18, 133–143. [Google Scholar] [CrossRef]
- Zhang, Y.; Bienen, B.; Cassidy, M.J.; Gourvenec, S. Undrained Bearing Capacity of Deeply Buried Flat Circular Footings under General Loading. J. Geotech. Geoenviron. Eng. 2012, 138, 385–397. [Google Scholar] [CrossRef]
- Hossain, M.S.; Hu, Y.; Randolph, M.F.; White, D.J. Limiting Cavity Depth for Spudcan Foundations Penetrating Clay. Geotechnique 2005, 55, 679–690. [Google Scholar] [CrossRef]
- Dassault Systèmes Simulia Corp. Abaqus, Version 6.11; Dassault Systèmes Simulia Corp.: Providence, RI, USA, 2011.
- Menzies, D.; Roper, R. Comparison of Jackup Rig Spudcan Penetration Methods in Clay. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 5 May 2008. [Google Scholar]
- Shuttle, D. Cylindrical cavity expansion and contraction in Tresca soil. Geotechnique 2007, 57, 305–308. [Google Scholar] [CrossRef]
- Purwana, O.A.; Leung, C.F.; Chow, Y.K.; Foo, K.S. Influence of Base Suction on Extraction of Jack-up Spudcans. Geotechnique 2005, 55, 741–753. [Google Scholar] [CrossRef]
- Martin, C.M.; Houlsby, G.T. Combined Loading of Spudcan Foundations on Clay: Laboratory Tests. Geotechnique 2000, 50, 325–338. [Google Scholar] [CrossRef]
- Tan, F.S. Centrifuge and Theoretical Modelling of Conical Footings on Sand. Doctoral Dissertation, University of Cambridge, Cambridge, UK, 1990. [Google Scholar]
- Li, L.; Li, J.; Huang, J.; Liu, H.; Cassidy, M.J. The Bearing Capacity of Spudcan Foundations under Combined Loading in Spatially Variable Soils. Eng. Geol. 2017, 227, 139–148. [Google Scholar] [CrossRef]
- Gourvenec, S.; Randolph, M. Effect of Strength Non-Homogeneity on the Shape of Failure Envelopes for Combined Loading of Strip and Circular Foundations on Clay. Geotechnique 2003, 53, 575–586. [Google Scholar] [CrossRef]
- Hossain, M.S.; Randolph, M.F. New Mechanism-Based Design Approach for Spudcan Foundations on Single Layer Clay. J. Geotech. Geoenviron. Eng. 2009, 135, 1264–1274. [Google Scholar] [CrossRef]
- Martin, C.M.; Randolph, M. Applications of Lower and Upper Bound Theorems of Plasticity to Collapse of Circular Foundations. In Computer Methods and Advances in Geomechanics; Taylor & Francis: Abingdon, UK, 2001; Volume 2, pp. 1417–1428. [Google Scholar]
- Elkhatib, S. The Behaviour of Drag-in Plate Anchors in Soft Cohesive Soils. Doctoral Dissertation, University of Western Australia, Crawley, Australia, 2006. [Google Scholar]
- Hu, P.; Cassidy, M. Two-Dimensional Bearing Capacity of a Spudcan in Clay After Penetrating Through Top Sand. Int. J. Offshore Polar Eng. 2020, 30, 493–500. [Google Scholar] [CrossRef]
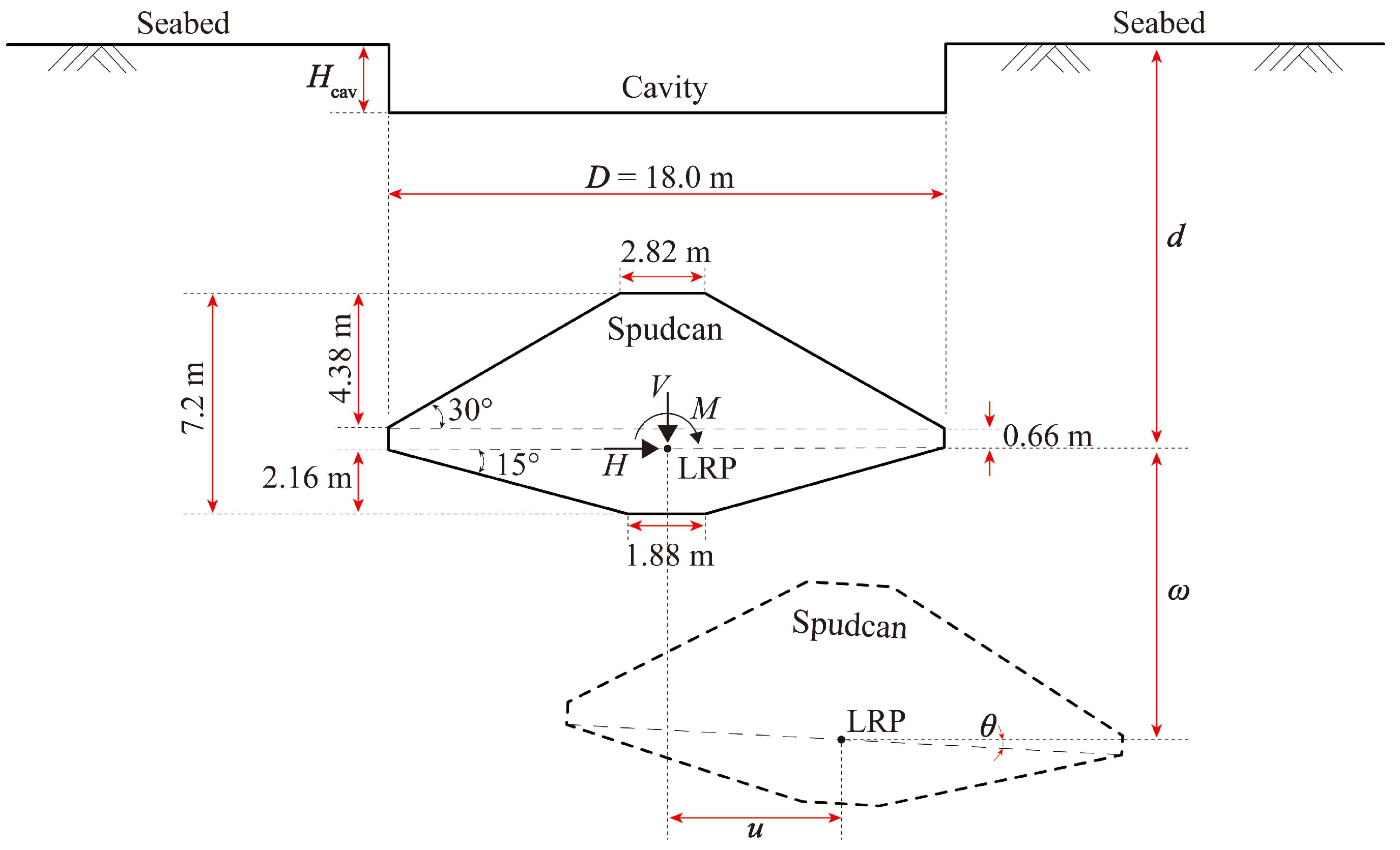
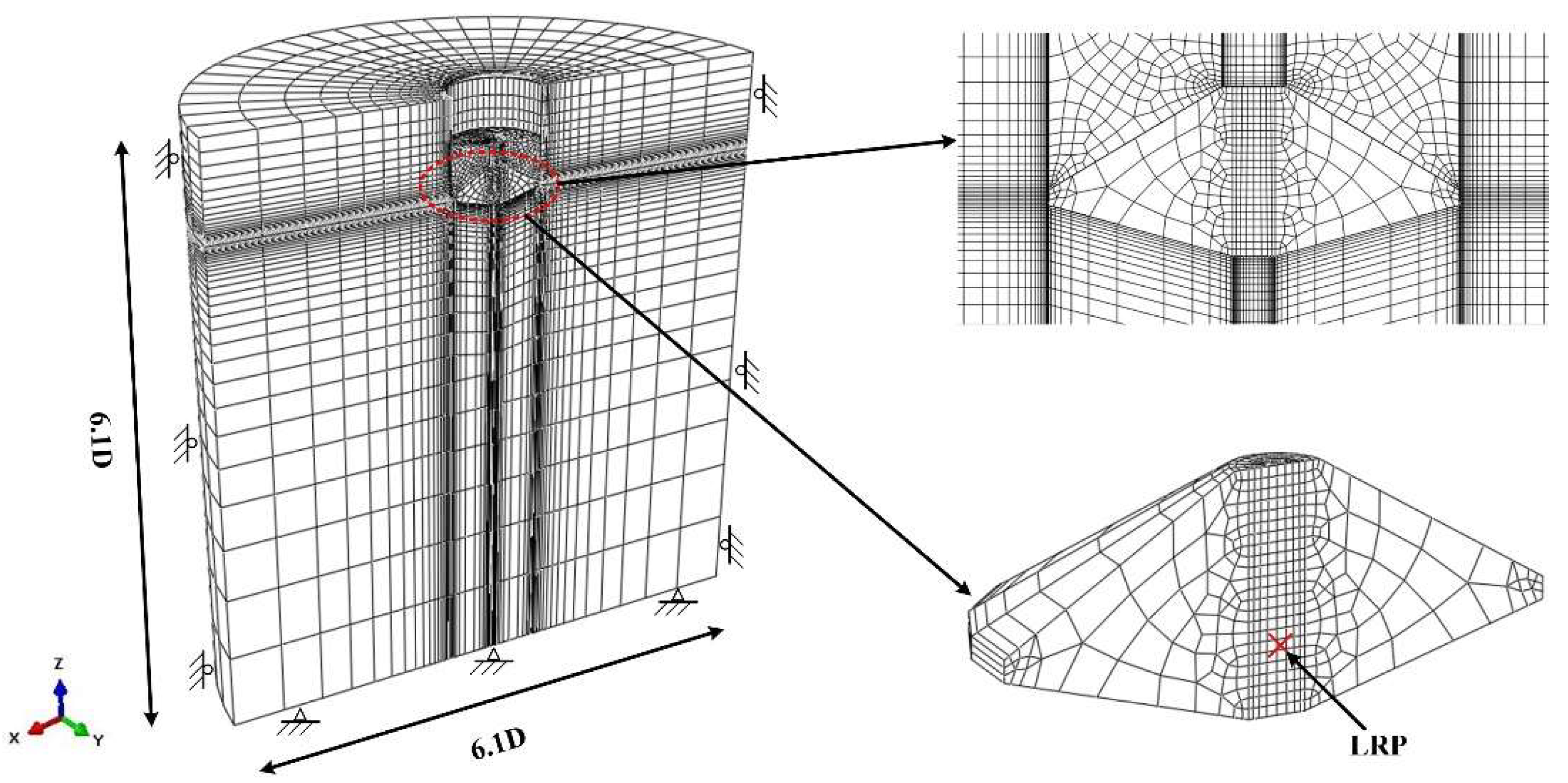
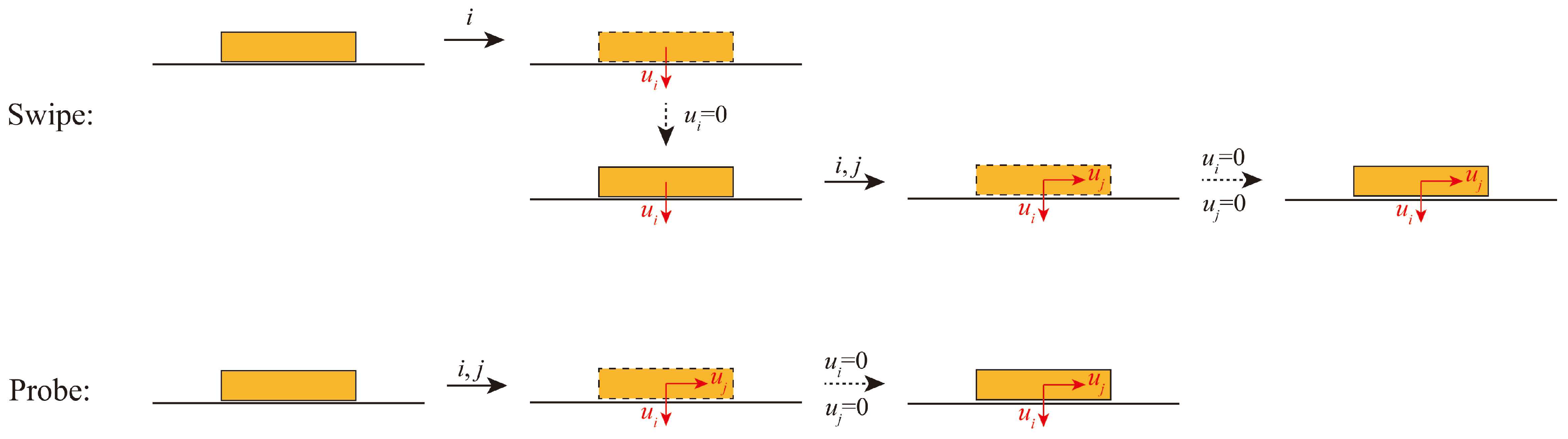

| Vertical | Horizontal | Moment | |
|---|---|---|---|
| Load (N or N·m) | V (N) | H (N) | M (N·m) |
| Unidirectional bearing capacity (N or N·m) | Vult (N) | Hult (N) | Mult (N·m) |
| Bearing capacity factor (-) | NcV = Vult/Asu0 | NcH = Hult/Asu0 | NcM = Mult/ADsu0 |
| Normalized bearing capacity (-) | n/a | h0 = Hult/Vult | m0 = Mult/DVult |
| Displacement (m or rad) | w (m) | u (m) | θ (rad) |
| Group | sum (kPa) | k (kPa/m) | Cavity Ratio Hcav/D |
|---|---|---|---|
| 1 | 10 | 1.5 | 0.3 |
| 2 | 18 | 1.2 | 0.4 |
| 3 | 20 | 1.5 | 0.41 |
| 4 | 25 | 2.0 | 0.5 |
| Group (V-H) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| w/u (-) | 0.05 | 0.1 | 0.3 | 0.5 | 1.0 | 2.0 | 10.0 | n/a | n/a | n/a | n/a | n/a |
| Group (H-M) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| u/θD (-) | −∞ (−Hult) | −0.2 | −0.3 | −0.5 | −1.0 | 0 (Mult) | 0 (Mmax) | 0.2 | 0.5 | 1.0 | +∞ (Hmax) | +∞ (Hult) |
| Existing Research | Methods | Types | NcV | NcH | NcM |
|---|---|---|---|---|---|
| Hossain et al. [18] | Centrifuge test | Spudcan | 11.0–12.0 | n/a | n/a |
| Hossain et al. [3] | Small-deformation simulation | Spudcan | 13.1 | n/a | n/a |
| Hossain et al. [27] | Large-deformation simulation | Spudcan | 11.3 | n/a | n/a |
| Martin & Randolph [28] | Theoretical analysis | Thin plate | 13.11 | n/a | n/a |
| Eilkhatib [29] | Theoretical analysis | Thin plate | n/a | n/a | 1.57 |
| Zhang et al. [5] | Small-deformation simulation | Spudcan | 12.99 | 4.93 | 1.61 |
| This study | Small-deformation simulation | Spudcan | 12.73 | 4.94 | 1.60 |
| Parameter | Value | Parameter | Value | Parameter | Value | Parameter | Value |
|---|---|---|---|---|---|---|---|
| h0s | 0.216 | m0s | 0.123 | e1s | 0.72 | e2s | 1.124 |
| h0cav | 0.208 | m0cav | 0.106 | e1cav | 0.827 | e2cav | −0.43 |
| h0d | 0.367 | m0d | 0.126 | e1d | 0.171 | e2d | −0.182 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, M.; Yang, X.; Chen, Y.; Wang, D.; Sun, H. Prediction of the Bearing Capacity Envelope for Spudcan Foundations of Jack-Up Rigs in Hard Clay with Varying Strengths. J. Mar. Sci. Eng. 2025, 13, 1899. https://doi.org/10.3390/jmse13101899
Wang M, Yang X, Chen Y, Wang D, Sun H. Prediction of the Bearing Capacity Envelope for Spudcan Foundations of Jack-Up Rigs in Hard Clay with Varying Strengths. Journal of Marine Science and Engineering. 2025; 13(10):1899. https://doi.org/10.3390/jmse13101899
Chicago/Turabian StyleWang, Mingyuan, Xing Yang, Yangbin Chen, Dong Wang, and Huimin Sun. 2025. "Prediction of the Bearing Capacity Envelope for Spudcan Foundations of Jack-Up Rigs in Hard Clay with Varying Strengths" Journal of Marine Science and Engineering 13, no. 10: 1899. https://doi.org/10.3390/jmse13101899
APA StyleWang, M., Yang, X., Chen, Y., Wang, D., & Sun, H. (2025). Prediction of the Bearing Capacity Envelope for Spudcan Foundations of Jack-Up Rigs in Hard Clay with Varying Strengths. Journal of Marine Science and Engineering, 13(10), 1899. https://doi.org/10.3390/jmse13101899







