Integrated Scheduling of Handling and Spraying Operations in Smart Coal Ports: A MAPPO-Driven Adaptive Micro-Evolutionary Algorithm Framework
Abstract
1. Introduction
- (1)
- This study achieves a comprehensive analysis of coal ports’ operational processes, integrating train splitting, handling equipment scheduling, stockyard allocation, and dust suppression spraying operations. Focusing on the resource consumption characteristics of spraying operations, it quantifies water and electricity consumption by combining environmental factors with intrinsic coal properties like moisture content and coal type and incorporates these quantitative results into the optimization objectives. Specifically, the established mixed-integer linear programming model takes minimizing the total operating time of trains and ships and reducing resource consumption costs as dual goals, breaking through the limitations of traditional segmented optimization that separates equipment scheduling from spraying operations and realizing the overall optimization of efficiency and resource conservation.
- (2)
- A novel hybrid optimization algorithm is developed, which combines the global search capability of the micro-evolutionary algorithm (MEA) framework with the adaptive decision-making ability of multi-agent proximal policy optimization (MAPPO). The algorithm adopts a two-layer chromosome encoding structure to capture key decision variables such as unloading and loading line selection, ass well as operation sequence, ensuring comprehensive coverage of the solution space while reducing encoding complexity. The dominance recording matrix (DRM) dynamically extracts and records dominant gene structures from elite individuals, providing directional guidance for evolution operations. Three specialized agents for crossover, mutation, and neighborhood search perceive population states and environmental feedback, collaboratively adjust evolutionary operators in real time, and balance exploration and exploitation through adaptive strategy adjustment, enabling an efficient solution of large-scale multi-objective scheduling problems.
- (3)
- The effectiveness and applicability of the proposed algorithm are verified through in-depth case studies and multi-scale comparative experiments. In the case study of a major Chinese coal port, two typical solutions on the Pareto front, namely the efficiency-maximizing solution and the optimal compromise solution, are analyzed in detail, and the trade-off relationship between their operational time and resource consumption is quantified, which reflects the algorithm’s ability to balance dual objectives. Moreover, comparative experiments with four benchmark algorithms on ten different scale instances show that the proposed algorithm has obvious advantages in hypervolume (HV) and inverted generational distance (IGD), which confirms its strong convergence and high solution quality in different operation scales, and fully demonstrates its practical application value.
2. Literature Review
2.1. Intelligent Scheduling in Port Operations
2.2. Green Strategies in Port Operations
2.3. Reinforcement Learning in Port Operations
3. Problem Description and Model Formulation
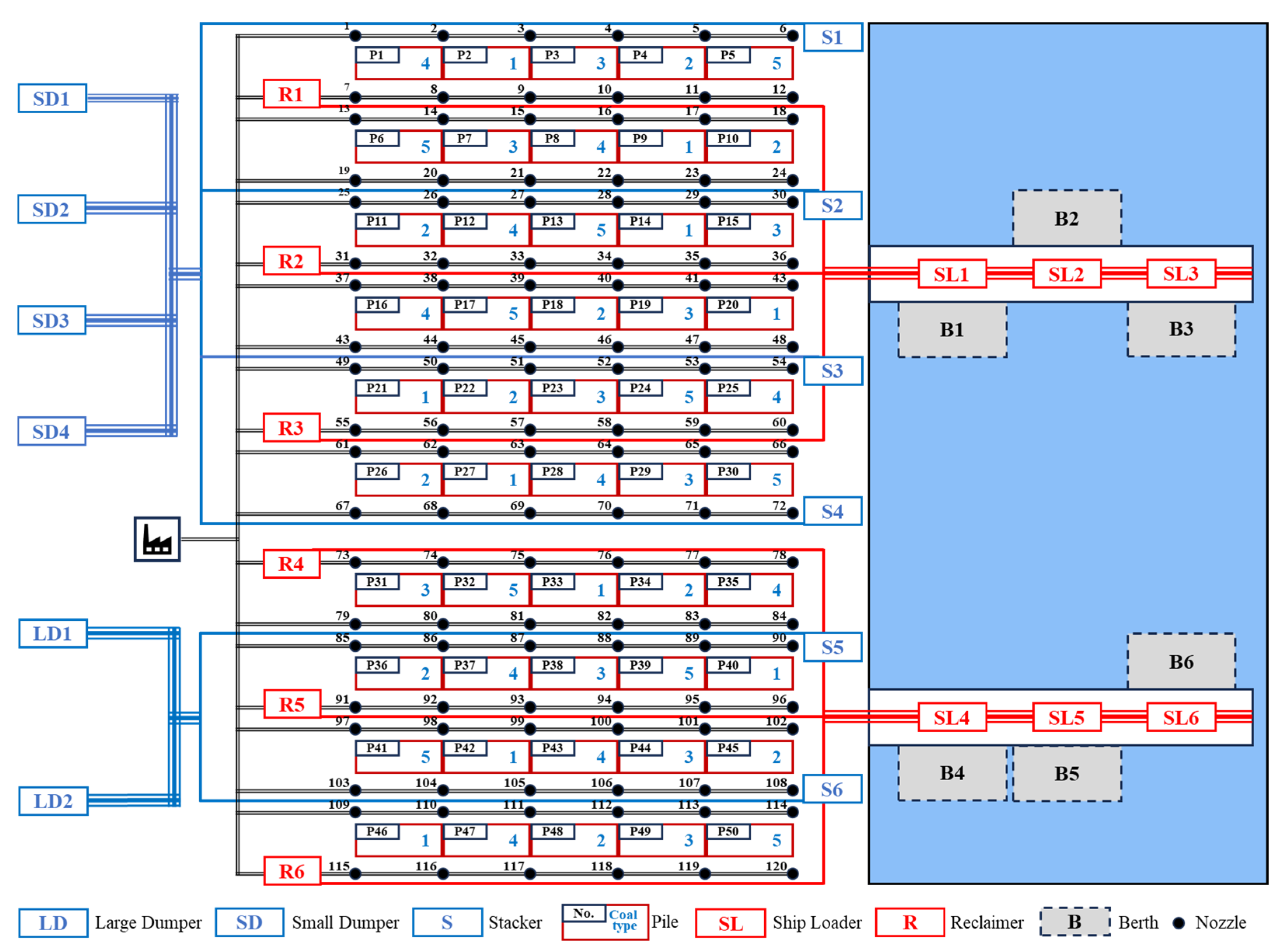
3.1. Problem Description
3.2. Model Formulation
- (1)
- Each piece of equipment serves only one operational line at any given time without interruption.
- (2)
- Equipment productivity remains constant, with synchronized start and stop times for all equipment within the same operational line.
- (3)
- Each pile is dedicated to storing a single coal type exclusively.
- (4)
- Handling duration is determined by both operation volume and pile location.
- (5)
- Every berth is equipped with its corresponding ship loader.
- (1)
- Train splitting and unloading-stacking constraints
- (2)
- Reclaiming-loading constraints
- (3)
- Spraying operation constraints
4. Algorithm Design
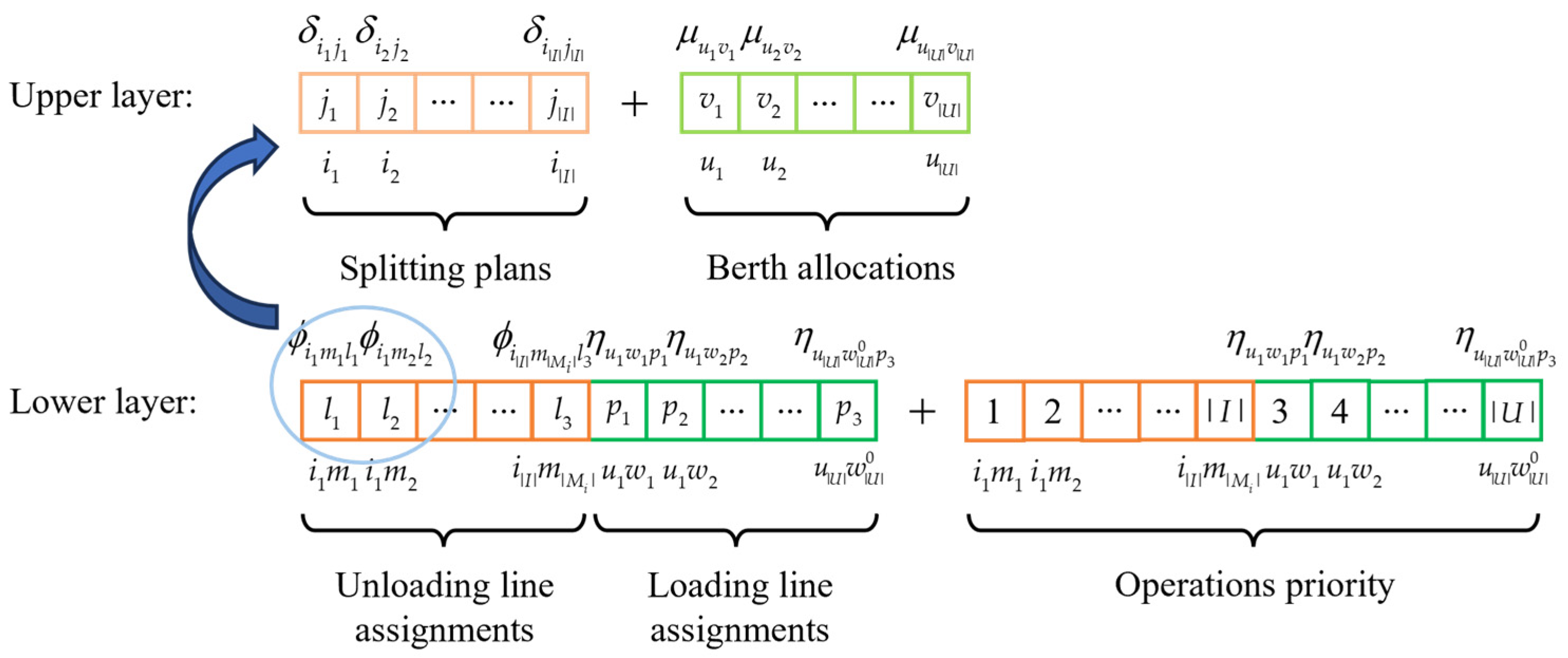
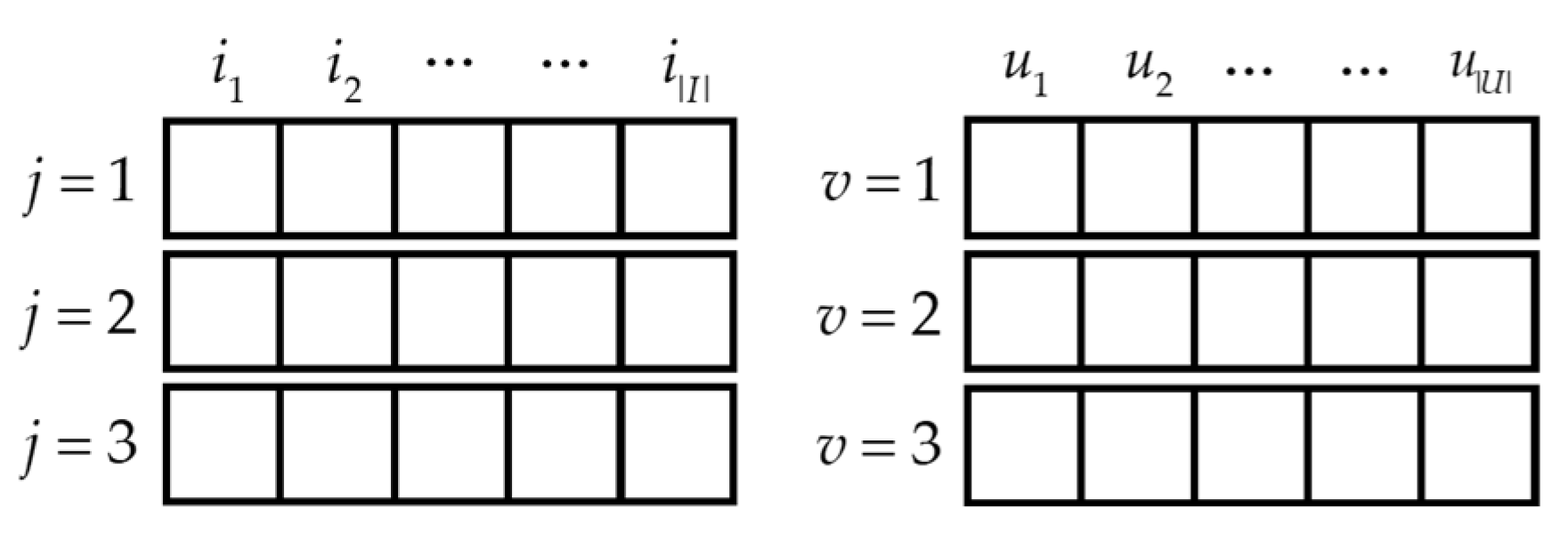
4.1. Encoding and Gene Structure
4.2. Dominance Recording Matrix
4.3. MAPPO-Based Adaptive Evolutionary Strategy
4.3.1. State Representation
4.3.2. Action Space
4.3.3. Reward Function
4.4. Algorithm Framework
5. Case Study
5.1. Case Introduction
5.2. Results Analysis
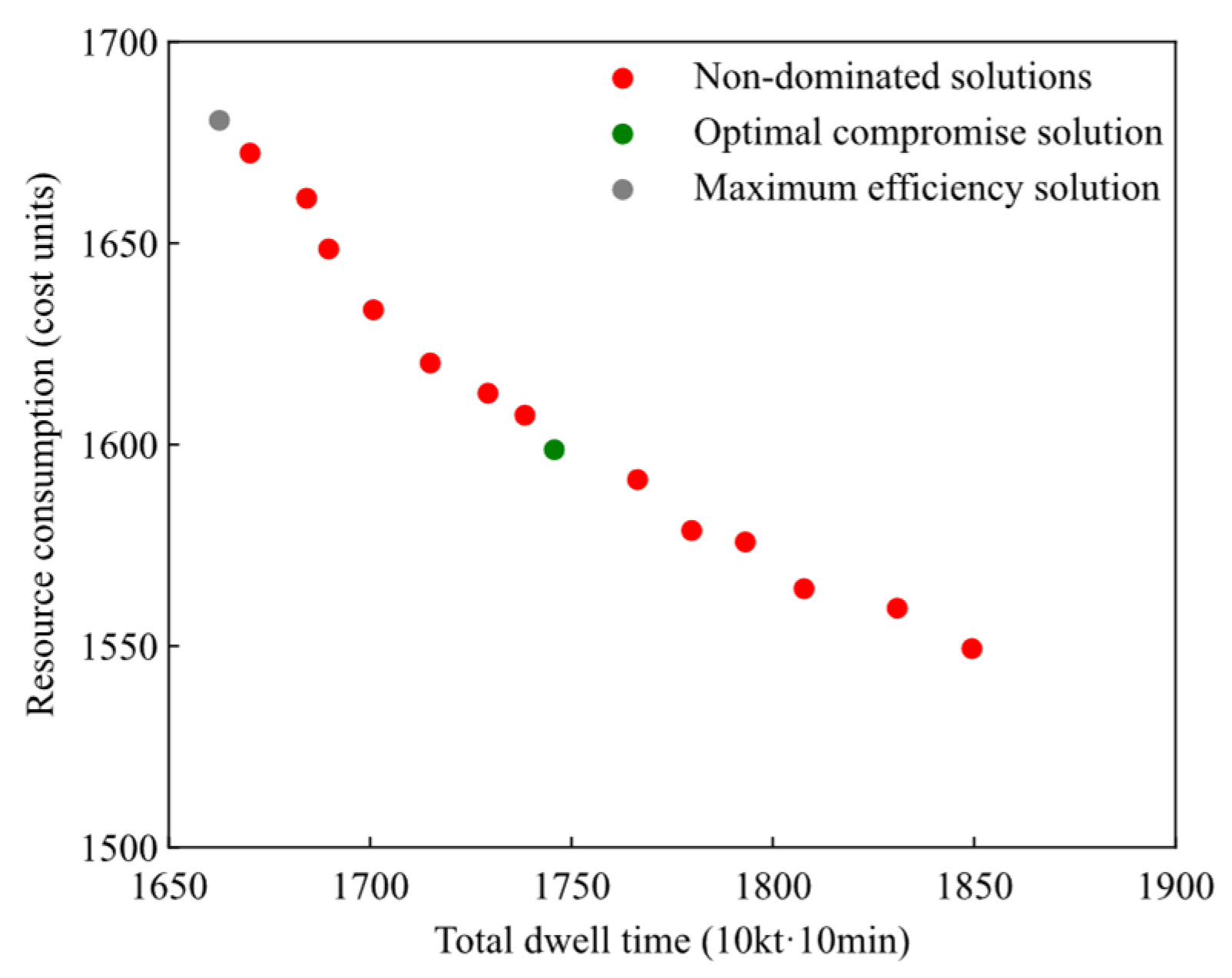
5.2.1. Computational Results
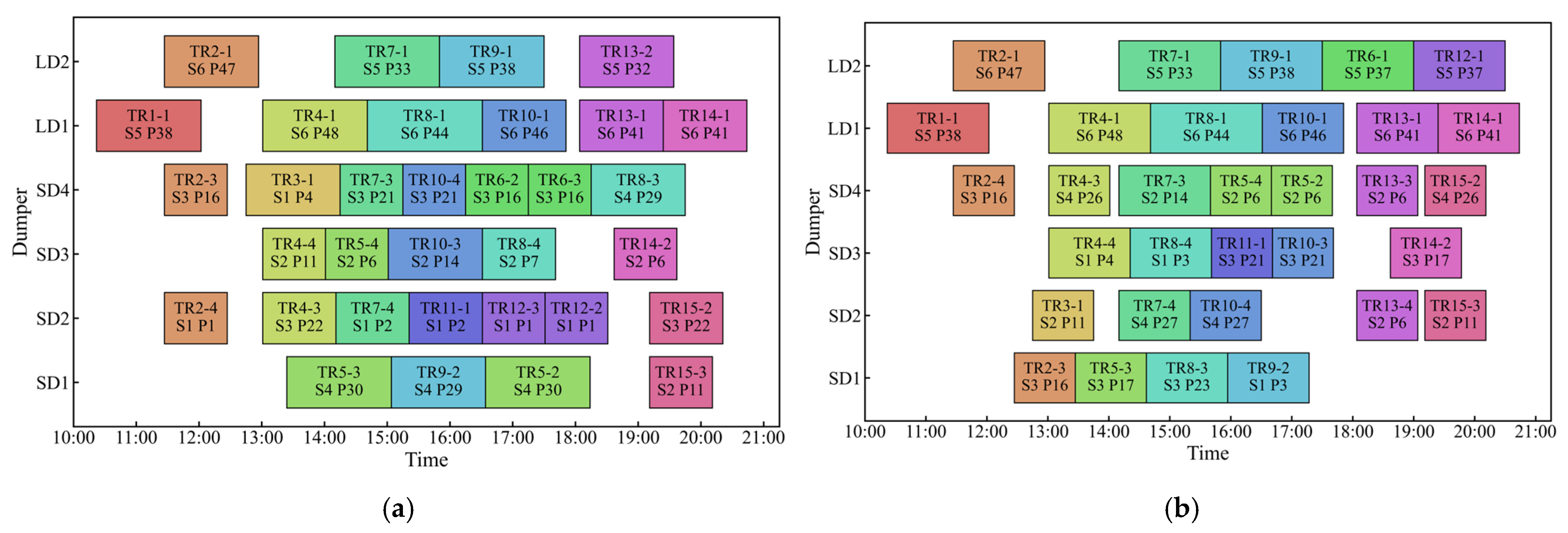
- (1)
- Analysis of unloading operations
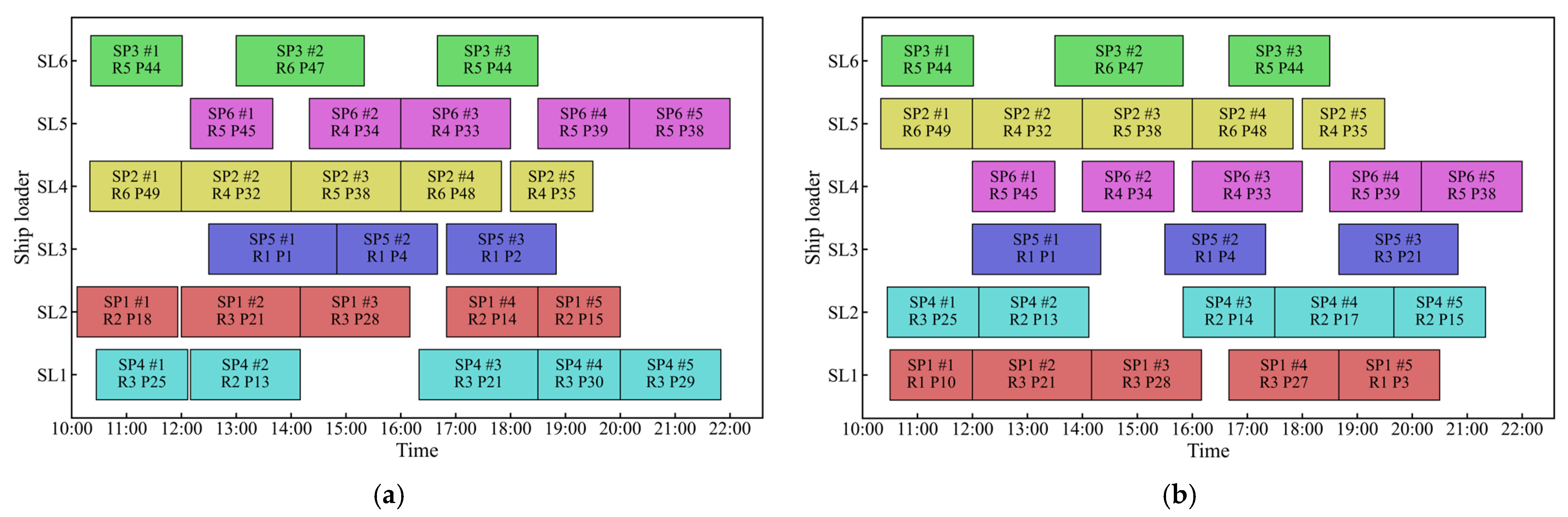
- (2)
- Analysis of loading operations
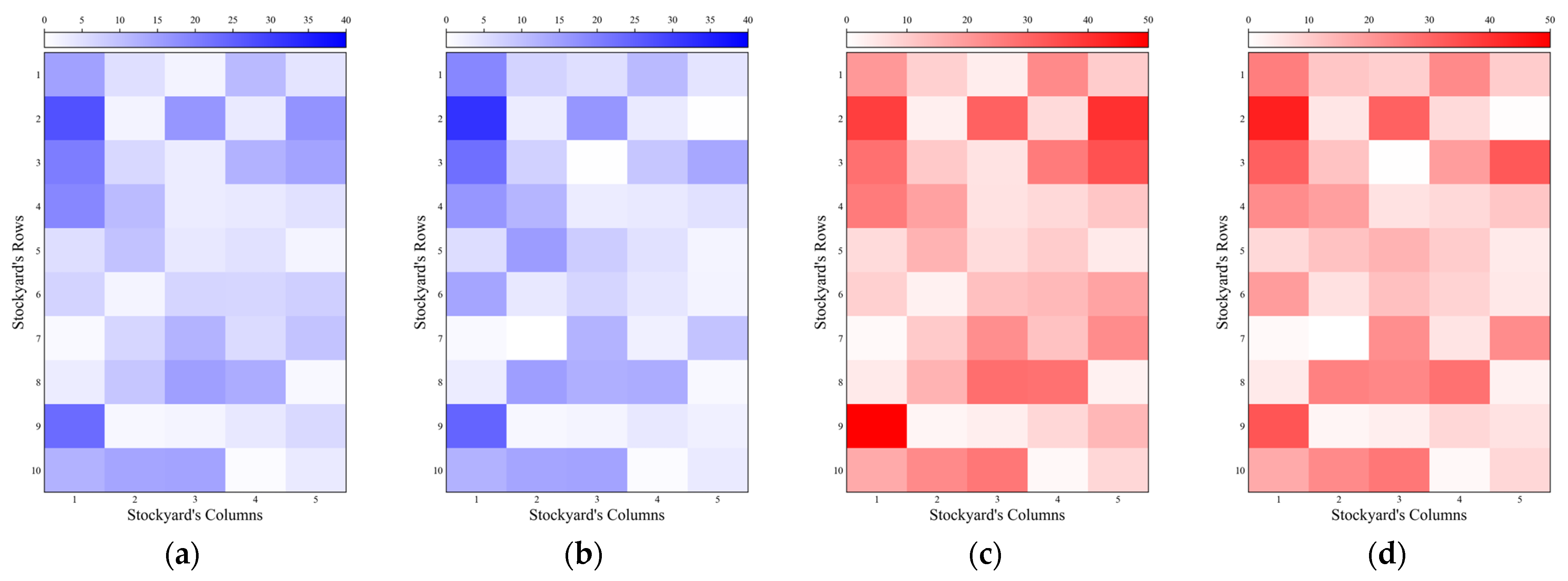
- (3)
- Analysis of stockyard allocation and resource consumption
5.2.2. Algorithm Performance
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- International Energy Agency. Coal 2024: Analysis and Forecast to 2026. Available online: https://www.iea.org/reports/coal-2024/executive-summary (accessed on 26 July 2025).
- Liu, J.; Lyu, Y.; Wu, J.; Wang, J. Adoption Strategies of Carbon Abatement Technologies in the Maritime Supply Chain: Impact of Demand Information Sharing. Int. J. Logist.-Res. Appl. 2025, 28, 70–97. [Google Scholar] [CrossRef]
- Lv, Y.; Zou, M.; Li, J.; Liu, J. Dynamic Berth Allocation under Uncertainties Based on Deep Reinforcement Learning towards Resilient Ports. Ocean Coast. Manag. 2024, 252, 107113. [Google Scholar] [CrossRef]
- Xia, Z.; Guo, Z.; Wang, W.; Jiang, Y. Joint Optimization of Ship Scheduling and Speed Reduction: A New Strategy Considering High Transport Efficiency and Low Carbon of Ships in Port. Ocean Eng. 2021, 233, 109224. [Google Scholar] [CrossRef]
- Li, H.; Zhao, J.; Jia, P.; Ou, H.; Zhao, W. Optimization of Bulk Cargo Terminal Unloading and Outbound Operations Based on a Deep Reinforcement Learning Framework. J. Mar. Sci. Eng. 2025, 13, 105. [Google Scholar] [CrossRef]
- Golias, M.; Portal, I.; Konur, D.; Kaisar, E.; Kolomvos, G. Robust Berth Scheduling at Marine Container Terminals via Hierarchical Optimization. Comput. Oper. Res. 2014, 41, 412–422. [Google Scholar] [CrossRef]
- Gambardella, L.M.; Mastrolilli, M.; Rizzoli, A.E.; Zaffalon, M. An Optimization Methodology for Intermodal Terminal Management. J. Intell. Manuf. 2001, 12, 521–534. [Google Scholar] [CrossRef]
- Chen, L.; Bostel, N.; Dejax, P.; Cai, J.; Xi, L. A Tabu Search Algorithm for the Integrated Scheduling Problem of Container Handling Systems in a Maritime Terminal. Eur. J. Oper. Res. 2007, 181, 40–58. [Google Scholar] [CrossRef]
- Hsu, H.-P.; Tai, H.-H.; Wang, C.-N.; Chou, C.-C. Scheduling of Collaborative Operations of Yard Cranes and Yard Trucks for Export Containers Using Hybrid Approaches. Adv. Eng. Inform. 2021, 48, 101292. [Google Scholar] [CrossRef]
- Zeng, Q.; Yang, Z. Integrating Simulation and Optimization to Schedule Loading Operations in Container Terminals. Comput. Oper. Res. 2009, 36, 1935–1944. [Google Scholar] [CrossRef]
- Cao, Y.; Yang, A.; Liu, Y.; Zeng, Q.; Chen, Q. AGV Dispatching and Bidirectional Conflict-Free Routing Problem in Automated Container Terminal. Comput. Ind. Eng. 2023, 184, 109611. [Google Scholar] [CrossRef]
- Li, L.; Li, Y.; Liu, R.; Zhou, Y.; Pan, E. A Two-Stage Stochastic Programming for AGV Scheduling with Random Tasks and Battery Swapping in Automated Container Terminals. Transp. Res. Part E-Logist. Transp. Rev. 2023, 174, 103110. [Google Scholar] [CrossRef]
- Homayouni, S.M.; Tang, S.H.; Ismail, N.; Ariffin, M.K.A.M.; Samin, R. A Hybrid Genetic-Heuristic Algorithm for Scheduling of Automated Guided Vehicles and Quay Cranes in Automated Container Terminals. In Proceedings of the CIE: 2009 International Conference on Computers and Industrial Engineering, Troyes, France, 6–9 July 2009; Volume 1–3, pp. 96–101. [Google Scholar]
- Chen, X.; Liu, S.; Zhao, J.; Wu, H.; Xian, J.; Montewka, J. Autonomous Port Management Based AGV Path Planning and Optimization via an Ensemble Reinforcement Learning Framework. OCEAN Coast. Manag. 2024, 251, 107087. [Google Scholar] [CrossRef]
- Liang, C.; Zhang, Y.; Dong, L. A Three Stage Optimal Scheduling Algorithm for AGV Route Planning Considering Collision Avoidance under Speed Control Strategy. Mathematics 2023, 11, 138. [Google Scholar] [CrossRef]
- Yang, Y.; Sun, S.; He, S.; Jiang, Y.; Wang, X.; Yin, H.; Zhu, J. Research on the Multi-Equipment Cooperative Scheduling Method of Sea-Rail Automated Container Terminals under the Loading and Unloading Mode. J. Mar. Sci. Eng. 2023, 11, 1975. [Google Scholar] [CrossRef]
- Chen, H.; Liu, W.; Oldache, M.; Pervez, A. Research on Train Loading and Unloading Mode and Scheduling Optimization in Automated Container Terminals. J. Mar. Sci. Eng. 2024, 12, 1415. [Google Scholar] [CrossRef]
- Munuzuri, J.; Lorenzo-Espejo, A.; Pegado-Bardayo, A.; Escudero-Santana, A. Integrated Scheduling of Vessels, Cranes and Trains to Minimize Delays in a Seaport Container Terminal. J. Mar. Sci. Eng. 2022, 10, 1506. [Google Scholar] [CrossRef]
- de Andrade, J.L.M.; Menezes, G.C. A Column Generation-Based Heuristic to Solve the Integrated Planning, Scheduling, Yard Allocation and Berth Allocation Problem in Bulk Ports. J. Heuristics 2023, 29, 39–76. [Google Scholar] [CrossRef]
- Tang, X.; Jin, J.G.; Shi, X. Stockyard Storage Space Allocation in Large Iron Ore Terminals. Comput. Ind. Eng. 2022, 164, 107911. [Google Scholar] [CrossRef]
- Ouhaman, A.A.; Benjelloun, K.; Kenne, J.P.; Najid, N. The Storage Space Allocation Problem in a Dry Bulk Terminal: A Heuristic Solution. IFAC Pap. 2020, 53, 10822–10827. [Google Scholar] [CrossRef]
- van Vianen, T.; Ottjes, J.; Lodewijks, G. Simulation-Based Rescheduling of the Stacker-Reclaimer Operation. J. Comput. Sci. 2015, 10, 149–154. [Google Scholar] [CrossRef]
- Xin, J.; Negenborn, R.R.; van Vianen, T. A Hybrid Dynamical Approach for Allocating Materials in a Dry Bulk Terminal. IEEE Trans. Autom. Sci. Eng. 2018, 15, 1326–1336. [Google Scholar] [CrossRef]
- Bouzekri, H.; Alpan, G.; Giard, V. Integrated Laycan and Berth Allocation Problem with Ship Stability and Conveyor Routing Constraints in Bulk Ports. Comput. Ind. Eng. 2023, 181, 109341. [Google Scholar] [CrossRef]
- Babu, S.A.K.I.; Pratap, S.; Lahoti, G.; Fernandes, K.J.; Tiwari, M.K.; Mount, M.; Xiong, Y. Minimizing Delay of Ships in Bulk Terminals by Simultaneous Ship Scheduling, Stockyard Planning and Train Scheduling. Marit. Econ. Logist. 2015, 17, 464–492. [Google Scholar] [CrossRef]
- Fereidoonian, F.; Sadjadi, S.J.; Heydari, M.; Mirzapour Al-e-Hashem, S.M.J. A Timely Efficient and Emissions-Aware Multiobjective Truck-Sharing Integrated Scheduling Model in Container Terminals. Proc. Inst. Mech. Eng. Part M-J. Eng. Marit. Environ. 2024, 238, 982–1008. [Google Scholar] [CrossRef]
- Zheng, Y.; Xu, M.; Wang, Z.; Xiao, Y. A Genetic Algorithm for Integrated Scheduling of Container Handing Systems at Container Terminals from a Low-Carbon Operations Perspective. Sustainability 2023, 15, 6035. [Google Scholar] [CrossRef]
- Peng, Y.; Wang, W.; Liu, K.; Li, X.; Tian, Q. The Impact of the Allocation of Facilities on Reducing Carbon Emissions from a Green Container Terminal Perspective. Sustainability 2018, 10, 1813. [Google Scholar] [CrossRef]
- Niu, Y.; Yu, F.; Yao, H.; Yang, Y. Multi-Equipment Coordinated Scheduling Strategy of U-Shaped Automated Container Terminal Considering Energy Consumption. Comput. Ind. Eng. 2022, 174, 108804. [Google Scholar] [CrossRef]
- Peng, W.; Wang, D.; Qiu, H.; Chu, F.; Yin, Y. Integrated Optimization on Double-Side Cantilever Yard Crane Scheduling and Green Vehicle Path Planning at U-Shaped Yard. IEEE Trans. Intell. Transp. Syst. 2025, 26, 3684–3699. [Google Scholar] [CrossRef]
- He, J.; Huang, Y.; Yan, W. Yard Crane Scheduling in a Container Terminal for the Trade-off between Efficiency and Energy Consumption. Adv. Eng. Inform. 2015, 29, 59–75. [Google Scholar] [CrossRef]
- Lu, H.; Lu, X. Joint Optimization of Berths and Quay Cranes Considering Carbon Emissions: A Case Study of a Container Terminal in China. J. Mar. Sci. Eng. 2025, 13, 148. [Google Scholar] [CrossRef]
- Jiang, X.; Zhong, M.; Shi, J.; Li, W. Optimization of Integrated Scheduling of Restricted Channels, Berths, and Yards in Bulk Cargo Ports Considering Carbon Emissions. Expert Syst. Appl. 2024, 255, 124604. [Google Scholar] [CrossRef]
- Wang, W.; Guo, J.; Tian, Q.; Peng, Y.; Cao, Z.; Liu, K.; Peng, S. Stockyard Allocation in Dry Bulk Ports Considering Resource Consumption Reduction of Spraying Operations. Transp. Res. Part E-Logist. Transp. Rev. 2025, 193, 103816. [Google Scholar] [CrossRef]
- Gong, L.; Huang, Z.; Xiang, X.; Liu, X. Real-Time AGV Scheduling Optimisation Method with Deep Reinforcement Learning for Energy-Efficiency in the Container Terminal Yard. Int. J. Prod. Res. 2024, 62, 7722–7742. [Google Scholar] [CrossRef]
- Yue, L.; Fan, H. Dynamic Scheduling and Path Planning of Automated Guided Vehicles in Automatic Container Terminal. IEEE-CAA J. Autom. Sin. 2022, 9, 2005–2019. [Google Scholar] [CrossRef]
- Zeng, Q.; Yang, Z.; Hu, X. A Method Integrating Simulation and Reinforcement Learning for Operation Scheduling in Container Terminals. Transport 2011, 26, 383–393. [Google Scholar] [CrossRef]
- Zhong, R.; Wen, K.; Fang, C.; Liang, E. Real-Time Multi-Resource Jointed Scheduling of Container Terminals with Uncertainties Using a Reinforcement Learning Approach. In Proceedings of the 2022 13th Asian Control Conference, ASCC, Jeju, Republic of Korea, 4–7 May 2022; pp. 110–115. [Google Scholar]
- Che, A.; Wang, Z.; Zhou, C. Multi-Agent Deep Reinforcement Learning for Recharging-Considered Vehicle Scheduling Problem in Container Terminals. IEEE Trans. Intell. Transp. Syst. 2024, 25, 16855–16868. [Google Scholar] [CrossRef]
- Tang, G.; Guo, Y.; Qi, Y.; Fang, Z.; Zhao, Z.; Li, M.; Zhen, Z. Real-Time Twin Automated Double Cantilever Rail Crane Scheduling Problem for the U-Shaped Automated Container Terminal Using Deep Reinforcement Learning. Adv. Eng. Inform. 2025, 65, 103193. [Google Scholar] [CrossRef]
- Zhu, J.; Zhang, W.; Yu, L.; Guo, X. A Novel Multi-Attention Reinforcement Learning for the Scheduling of Unmanned Shipment Vessels (USV) in Automated Container Terminals. OMEGA-Int. J. Manag. Sci. 2024, 129, 103152. [Google Scholar] [CrossRef]
- Li, B.; Yang, C.; Yang, Z. Multiple Container Terminal Berth Allocation and Joint Operation Based on Dueling Double Deep Q-Network. J. Mar. Sci. Eng. 2023, 11, 2240. [Google Scholar] [CrossRef]
- Li, C.; Wu, S.; Li, Z.; Zhang, Y.; Zhang, L.; Gomes, L. Intelligent Scheduling Method for Bulk Cargo Terminal Loading Process Based on Deep Reinforcement Learning. Electronics 2022, 11, 1390. [Google Scholar] [CrossRef]
- Ai, T.; Huang, L.; Song, R.J.; Huang, H.F.; Jiao, F.; Ma, W.G. An Improved Deep Reinforcement Learning Approach: A Case Study for Optimisation of Berth and Yard Scheduling for Bulk Cargo Terminal. Adv. Prod. Eng. Manag. 2023, 18, 303–316. [Google Scholar] [CrossRef]
- Cui, Y.; Geng, Z.; Zhu, Q.; Han, Y. Review: Multi-Objective Optimization Methods and Application in Energy Saving. Energy 2017, 125, 681–704. [Google Scholar] [CrossRef]



| Heavy-Haul Train | Splitting Plan |
|---|---|
| 5000 t | ① 5 kt |
| 10,000 t | ① 10 kt |
| ② 5 kt + 5 kt | |
| 15,000 t | ① 10 kt + 5 kt |
| ② 5 kt + 5 kt + 5 kt | |
| 20,000 t | ① 10 kt + 10 kt |
| ② 10 kt + 5 kt + 5 kt | |
| ③ 5 kt + 5 kt + 5 kt + 5 kt |
| Notation | Definition |
|---|---|
| Set of inbound trains, indexed by . | |
| Set of splitting plans for inbound train , indexed by . | |
| Set of all potential unit trains for inbound train , indexed by . | |
| Set of all potential unit trains for inbound train in splitting plan , indexed by . | |
| Set of candidate unloading operational lines for unit train of inbound train , indexed by . | |
| Set of candidate dumpers for unit train of inbound train , indexed by . | |
| Set of all unloading operational lines corresponding to dumper , indexed by . | |
| Set of candidate stackers for unit train of inbound train , indexed by . | |
| Set of all unloading operational lines corresponding to stacker , indexed by . | |
| Set of candidate piles for unit train of inbound train , indexed by . | |
| Set of all unloading operational lines corresponding to pile , indexed by . | |
| Set of arriving ships, indexed by . | |
| Set of candidate berths for ship , indexed by . | |
| Set of loading operations for ship , indexed by . | |
| Set of candidate loading operational lines for loading operation of ship , indexed by . | |
| Set of all loading operational lines corresponding to pile , indexed by . | |
| Set of candidate piles for loading operation of ship , indexed by . | |
| Set of candidate reclaimers for loading operation of ship , indexed by . | |
| Set of all loading operational lines corresponding to reclaimer , indexed by . | |
| Set of ship loaders, indexed by . | |
| Set of nozzles, indexed by . | |
| Set of piles corresponding to nozzle , indexed by . | |
| Set of time within the scheduling period, indexed by . | |
| Set of spraying operation time within the scheduling period, indexed by . | |
| Formation type of unit train of inbound train , . | |
| Formation type of heavy-haul train , . | |
| Ship loader corresponding to loading operational line . | |
| Ship loader corresponding to berth . | |
| Earliest unloading start time for unit train of inbound train . | |
| Unloading-stacking time for unit train of inbound train on unloading operational line . | |
| Arrival time for ship . | |
| Reclaiming-loading time for loading operation of ship on loading operational line . | |
| The last loading operation of ship . | |
| Initial coal amount in pile . | |
| Maximum storage capacity of pile . | |
| Unloading coal volume for unit train of inbound train . | |
| Deadweight tonnage of ship . | |
| Loading coal volume for loading operation of ship . | |
| Number of nozzles corresponding to each pile. | |
| Spraying coefficient per unit coal at time . | |
| Intrinsic coal characteristic coefficient of pile at time . | |
| Electricity consumption coefficient per unit water for nozzle . | |
| Unit electricity cost. | |
| Unit water cost. | |
| Cost for unit train of inbound train on unloading operational line . | |
| Cost for loading operation of ship on loading operational line . | |
| A large enough positive number. |
| Variable | Definition |
|---|---|
| Decision binary variable equals 1 if inbound train selects splitting plan ; 0 otherwise. | |
| Decision binary variable equals 1 if inbound train splits into unit train ; 0 otherwise. | |
| Decision binary variable equals 1 if unit train of inbound train selects unloading operational line ; 0 otherwise. | |
| Binary variable equals 1 if unit train of inbound train selects dumper for unloading; 0 otherwise. | |
| Binary variable equals 1 if unit train of inbound train unloads before unit train of inbound train at dumper ; 0 otherwise. | |
| Start time of unloading-stacking operation for unit train of inbound train . | |
| Binary variable equals 1 if coal from unit train of inbound train selects stacker ; 0 otherwise. | |
| Binary variable equals 1 if coal from unit train of inbound train is stacked before coal from unit train of inbound train at stacker ; 0 otherwise. | |
| Binary variable equals 1 if coal from unit train of inbound train is stored in pile ; 0 otherwise. | |
| Binary variable equals 1 if coal from unit train of inbound train is stacked before coal from unit train of inbound train in pile ; 0 otherwise. | |
| Decision binary variable equals 1 if ship selects berth ; 0 otherwise. | |
| Decision binary variable equals 1 if loading operation of ship selects loading operational line ; 0 otherwise. | |
| Start time of reclaiming-loading operation for loading operation of ship . | |
| Binary variable equals 1 if loading operation of ship reclaims from pile ; 0 otherwise. | |
| Binary variable equals 1 if loading operation of ship before loading operation of ship from pile ; 0 otherwise. | |
| Binary variable equals 1 if loading operation of ship selects reclaimer ; 0 otherwise. | |
| Binary variable equals 1 if loading operation of ship before loading operation of ship at reclaimer ; 0 otherwise. | |
| Binary variable equals 1 if loading operation of ship selects ship loader ; 0 otherwise. | |
| Binary variable equals 1 if ship arrives before ship at berth ; 0 otherwise. | |
| Binary variable equals 1 if unit train of inbound train stacks coal in pile at time ; 0 otherwise. | |
| Binary variable equals 1 if loading operation of ship reclaims from pile at time ; 0 otherwise. | |
| Binary variable equals 1 if unit train of inbound train operates on pile before loading operation of ship ; 0 otherwise. | |
| Amount of stored coal in pile at time . | |
| The amount of water consumed by nozzle in pile at time . | |
| The amount of water consumed by nozzle at time . |
| No. | Time | Formulation | Coal Type | No. | Time | Formulation | Coal Type | No. | Time | Formulation | Coal Type |
|---|---|---|---|---|---|---|---|---|---|---|---|
| TR1 | 10:12 | 10 kt | 3 | TR6 | 13:52 | 10 kt | 4 | TR11 | 15:13 | 5 kt | 1 |
| TR2 | 11:27 | 20 kt | 4 | TR7 | 14:10 | 20 kt | 1 | TR12 | 16:08 | 10 kt | 4 |
| TR3 | 12:45 | 5 kt | 2 | TR8 | 14:19 | 20 kt | 3 | TR13 | 18:04 | 20 kt | 5 |
| TR4 | 13:01 | 20 kt | 2 | TR9 | 14:33 | 15 kt | 3 | TR14 | 18:37 | 15 kt | 5 |
| TR5 | 13:24 | 15 kt | 5 | TR10 | 14:50 | 20 kt | 1 | TR15 | 19:11 | 10 kt | 2 |
| No. | Time | Loading Operation |
|---|---|---|
| SP1 | 10:06 | #1: 2/8500 t, #2: 1/8800 t, #3: 4/9400 t, #4: 1/8900 t, #5: 3/8500 t |
| SP2 | 10:20 | #1: 3/8300 t, #2: 5/8500 t, #3: 3/9200 t, #4: 2/8700 t, #5: 4/8400 t |
| SP3 | 10:22 | #1: 3/9000 t, #2: 4/9700 t, #3: 3/9200 t |
| SP4 | 10:27 | #1: 4/9500 t, #2: 5/9800 t, #3: 1/8700 t, #4: 5/9200 t, #5: 3/9300 t |
| SP5 | 10:43 | #1: 4/9000 t, #2: 4/9500 t, #3: 1/8900 t |
| SP6 | 11:17 | #1: 2/9200 t, #2: 2/8800 t, #3: 1/9500 t, #4: 5/9000 t, #5: 3/8500 t |
| Istance (Train, Ship) | HV | IGD | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| MEA-MAPPO | NSGA-II | IDQN | MA-A2C | MA-PPO | MEA-MAPPO | NSGA-II | IDQN | MA-A2C | MA-PPO | |
| I1 (15, 6) | 1.0573 | 0.8768 | 0.8302 | 0.9126 | 0.9053 | 0.0365 | 0.1493 | 0.2064 | 0.0892 | 0.0921 |
| I2 (16, 6) | 1.1483 | 0.7639 | 0.8252 | 0.8583 | 0.9205 | 0.0339 | 0.2904 | 0.2128 | 0.1976 | 0.1082 |
| I3 (17, 7) | 1.0885 | 0.8022 | 0.6816 | 0.7475 | 0.7794 | 0.0952 | 0.1866 | 0.3271 | 0.2793 | 0.2365 |
| I4 (18, 7) | 1.2062 | 0.9303 | 0.6573 | 0.8434 | 0.7252 | 0.0263 | 0.1437 | 0.4065 | 0.2070 | 0.3527 |
| I5 (19, 7) | 1.1704 | 0.8145 | 0.8957 | 0.8608 | 0.9032 | 0.0176 | 0.2672 | 0.1973 | 0.2164 | 0.1793 |
| I6 (20, 8) | 1.0948 | 0.6996 | 0.8489 | 0.7313 | 0.8177 | 0.0383 | 0.3974 | 0.2065 | 0.3325 | 0.2204 |
| I7 (21, 8) | 1.1501 | 0.6620 | 0.9037 | 0.7158 | 0.8640 | 0.0409 | 0.4083 | 0.1818 | 0.3578 | 0.2419 |
| I8 (23, 9) | 1.0949 | 0.7413 | 0.6801 | 0.9195 | 0.7518 | 0.0336 | 0.3056 | 0.3549 | 0.1691 | 0.2878 |
| I9 (24, 9) | 1.2620 | 0.8174 | 0.7342 | 0.7810 | 0.8393 | 0.0127 | 0.2722 | 0.3780 | 0.3309 | 0.2442 |
| I10 (26, 10) | 1.1363 | 0.7221 | 0.6128 | 0.8290 | 0.8424 | 0.0231 | 0.3874 | 0.4669 | 0.2547 | 0.2165 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Y.; He, S.; Tang, H.; Long, Z.; Xiang, A. Integrated Scheduling of Handling and Spraying Operations in Smart Coal Ports: A MAPPO-Driven Adaptive Micro-Evolutionary Algorithm Framework. J. Mar. Sci. Eng. 2025, 13, 1840. https://doi.org/10.3390/jmse13101840
Wu Y, He S, Tang H, Long Z, Xiang A. Integrated Scheduling of Handling and Spraying Operations in Smart Coal Ports: A MAPPO-Driven Adaptive Micro-Evolutionary Algorithm Framework. Journal of Marine Science and Engineering. 2025; 13(10):1840. https://doi.org/10.3390/jmse13101840
Chicago/Turabian StyleWu, Yidi, Shiwei He, Haozhou Tang, Zeyu Long, and Aibing Xiang. 2025. "Integrated Scheduling of Handling and Spraying Operations in Smart Coal Ports: A MAPPO-Driven Adaptive Micro-Evolutionary Algorithm Framework" Journal of Marine Science and Engineering 13, no. 10: 1840. https://doi.org/10.3390/jmse13101840
APA StyleWu, Y., He, S., Tang, H., Long, Z., & Xiang, A. (2025). Integrated Scheduling of Handling and Spraying Operations in Smart Coal Ports: A MAPPO-Driven Adaptive Micro-Evolutionary Algorithm Framework. Journal of Marine Science and Engineering, 13(10), 1840. https://doi.org/10.3390/jmse13101840







