Advanced Control for Shipboard Cranes with Asymmetric Output Constraints
Abstract
1. Introduction
- Due to unforeseen disturbances such as persistent waves, the ship’s motion can significantly amplify the crane’s cargo swing during operation. Therefore, this paper designs the controller and conducts theoretical analysis using the original complex nonlinear dynamic model to ensure more reliable performance.
- This method achieves asymmetric motion constraints for the boom and rope by appropriately modifying conventional symmetric barrier functions, ensuring the validity of the rope length under the same sign constraints. For the swing constraints of the unactuated payload, unlike traditional approaches, the proposed method introduces an auxiliary signal to embed the relevant constraint terms into the controller, supported by rigorous theoretical analysis through proof using a reductio ad absurdum argument. Consequently, in contrast to most existing crane-related studies [14,15,16,17,18,19,20,21,22,23,24], which assume the swing angle is confined within a conservative range of (−π/2, π/2), the proposed method removes this assumption. Instead, it flexibly constrains the swing angle within a reasonable range according to practical requirements, making it more adaptable and effective for cargo loading, unloading, and transportation tasks.
- Moreover, the proposed auxiliary signal ingeniously integrates information such as boom luffing velocity and payload swing angle-related information, demonstrating superior swing suppression capabilities compared to existing methods. Theoretical analysis and simulation results further verify that the proposed method can accurately position the payload and effectively limit its swing amplitude, which is of significant importance for the challenging operational environment of shipboard cranes.
2. Problem Statement
2.1. Dynamics for Shipboard Boom Cranes
2.2. Control Objective
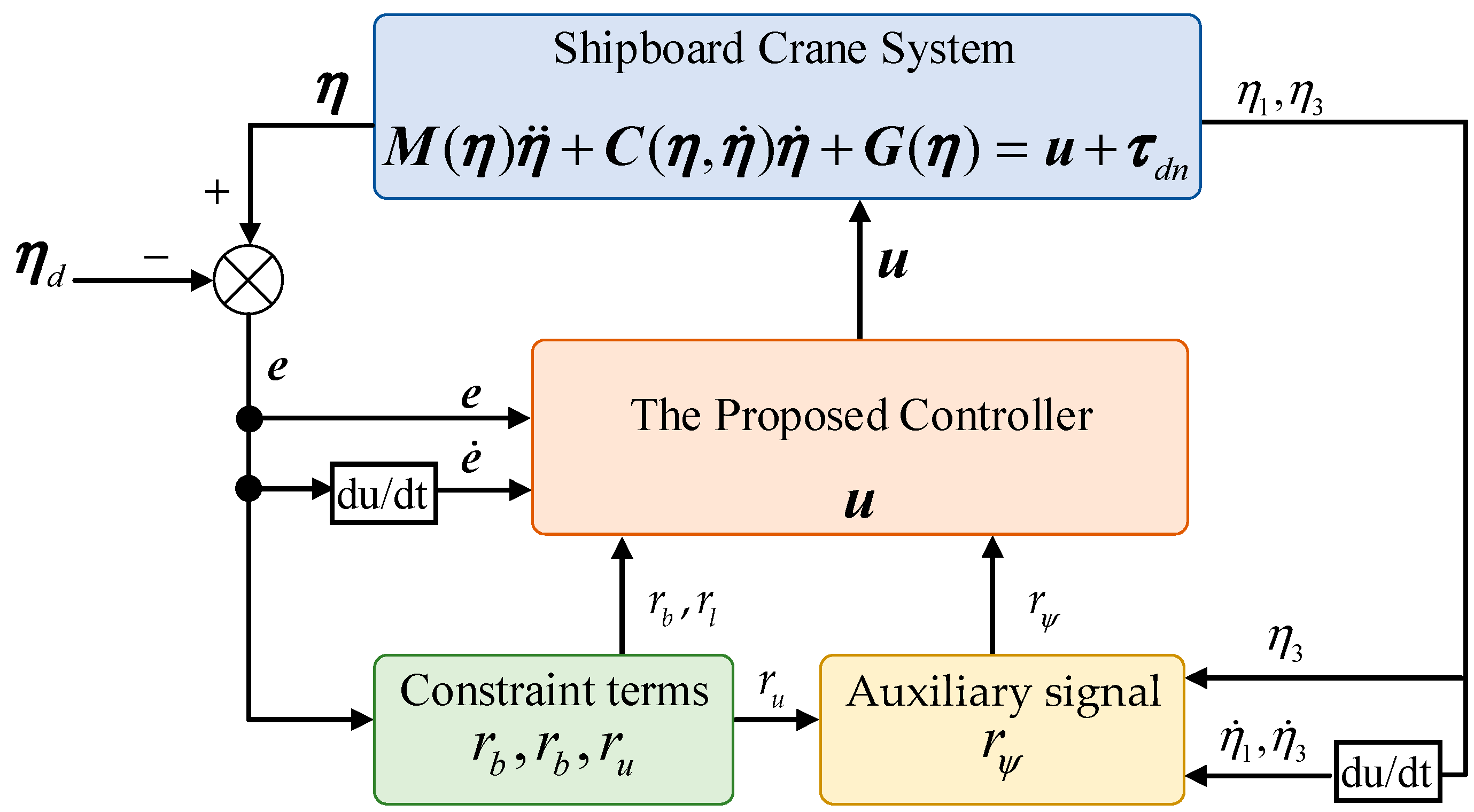
3. Controller Design and Stability Analysis
3.1. Controller Design
3.2. Stability Analysis
- Assume that or reach its preset upper or lower limit at time . In this case, the logarithmic terms corresponding to these states in would approach infinity, leading to being infinite. This conclusion contradicts the result (36). Using a reductio ad absurdum argument, the states and are always able to comply with their constraints, that is,
- Assuming that violates any constraint within a very small adjacent time , referring to (28) and (29), will be infinite. And for , the solution of the differential Equation (31) is
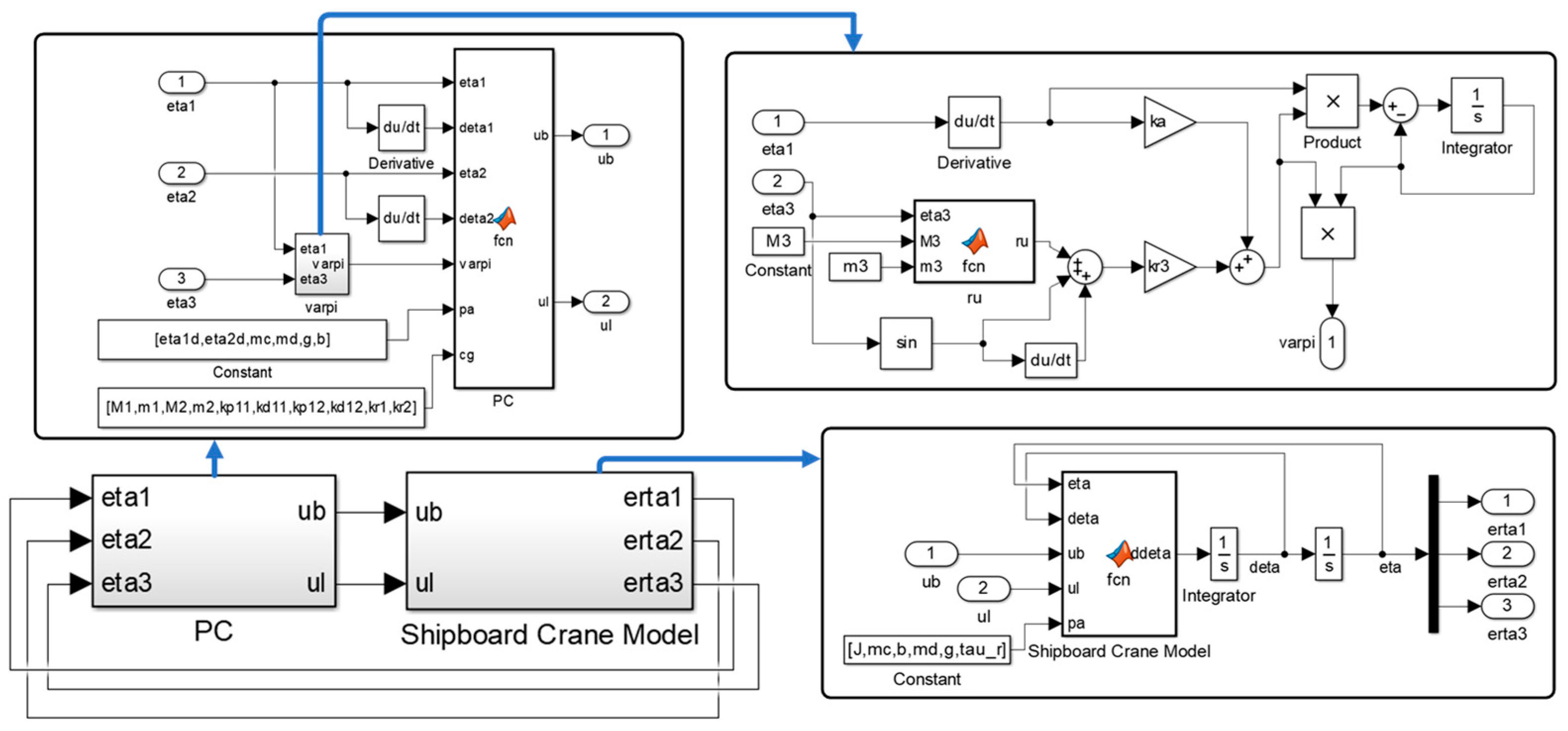
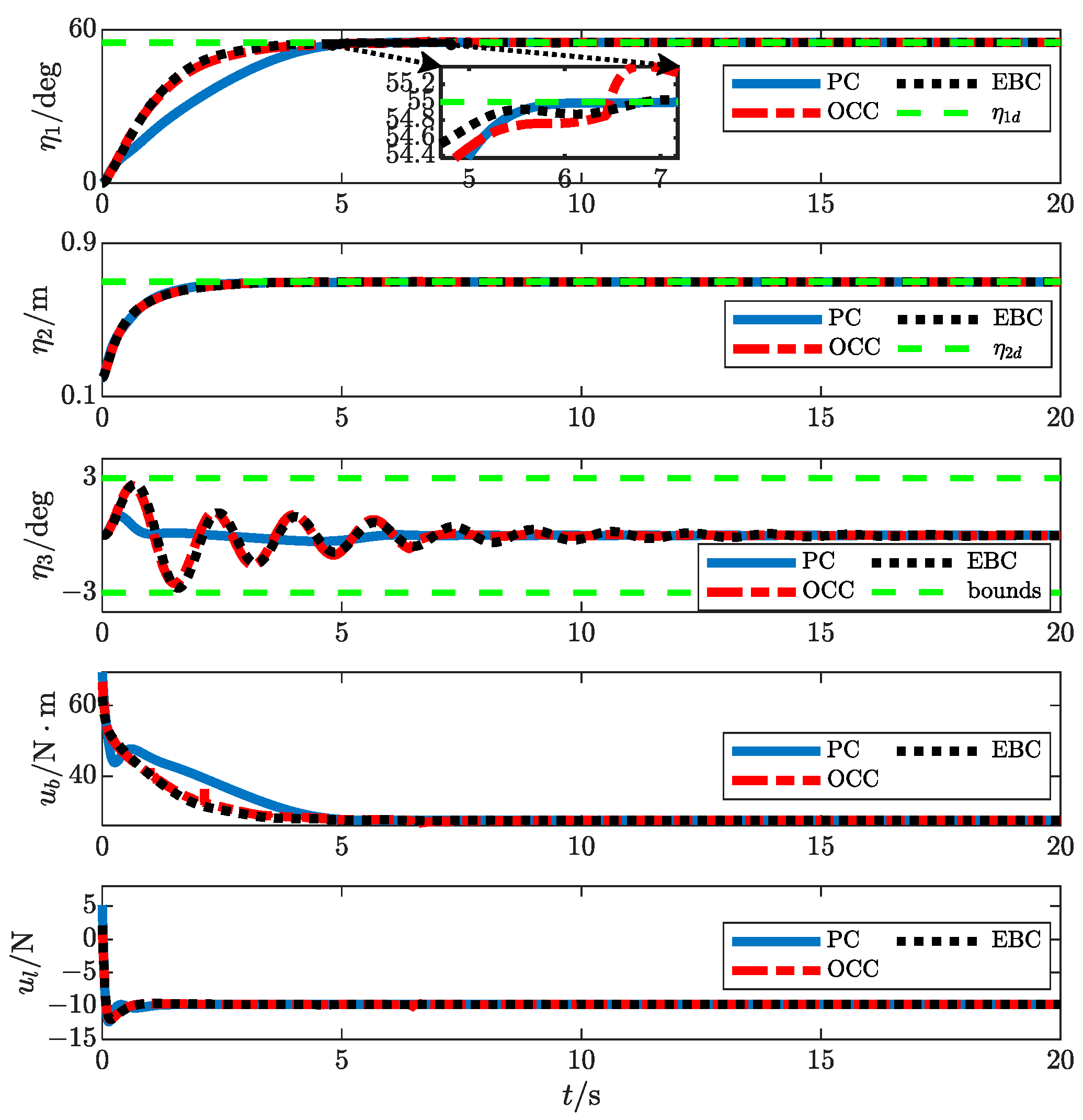
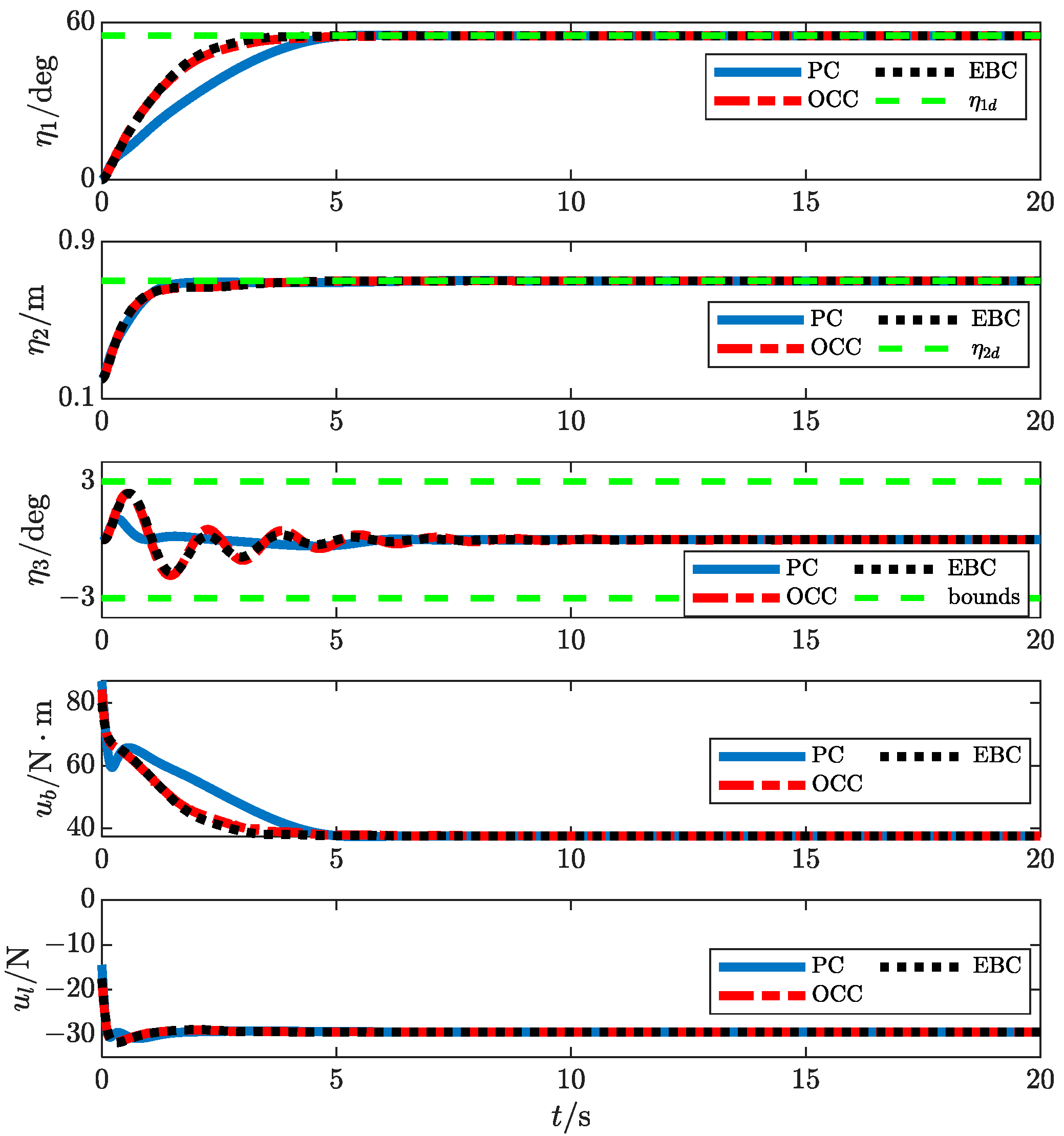
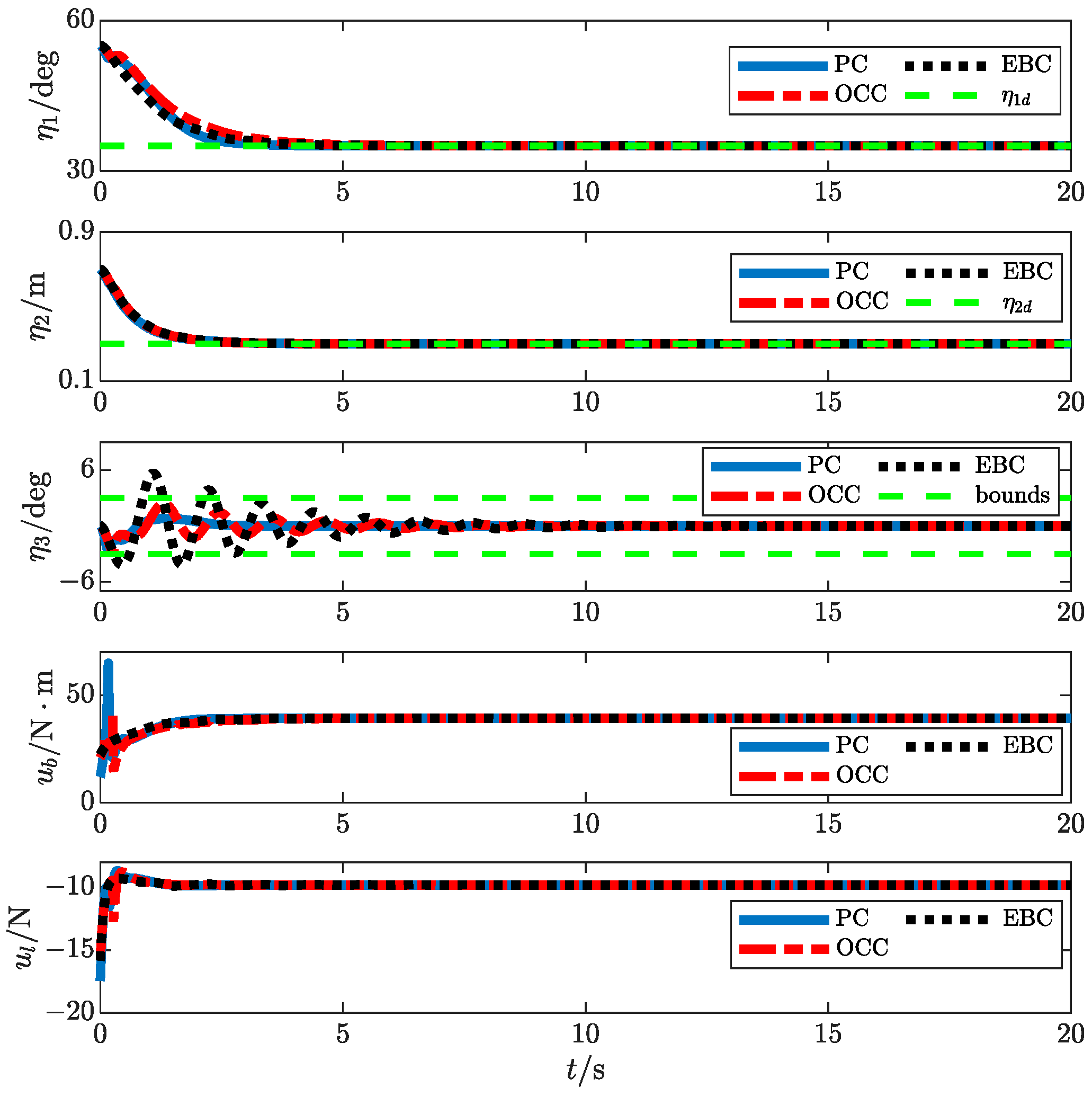
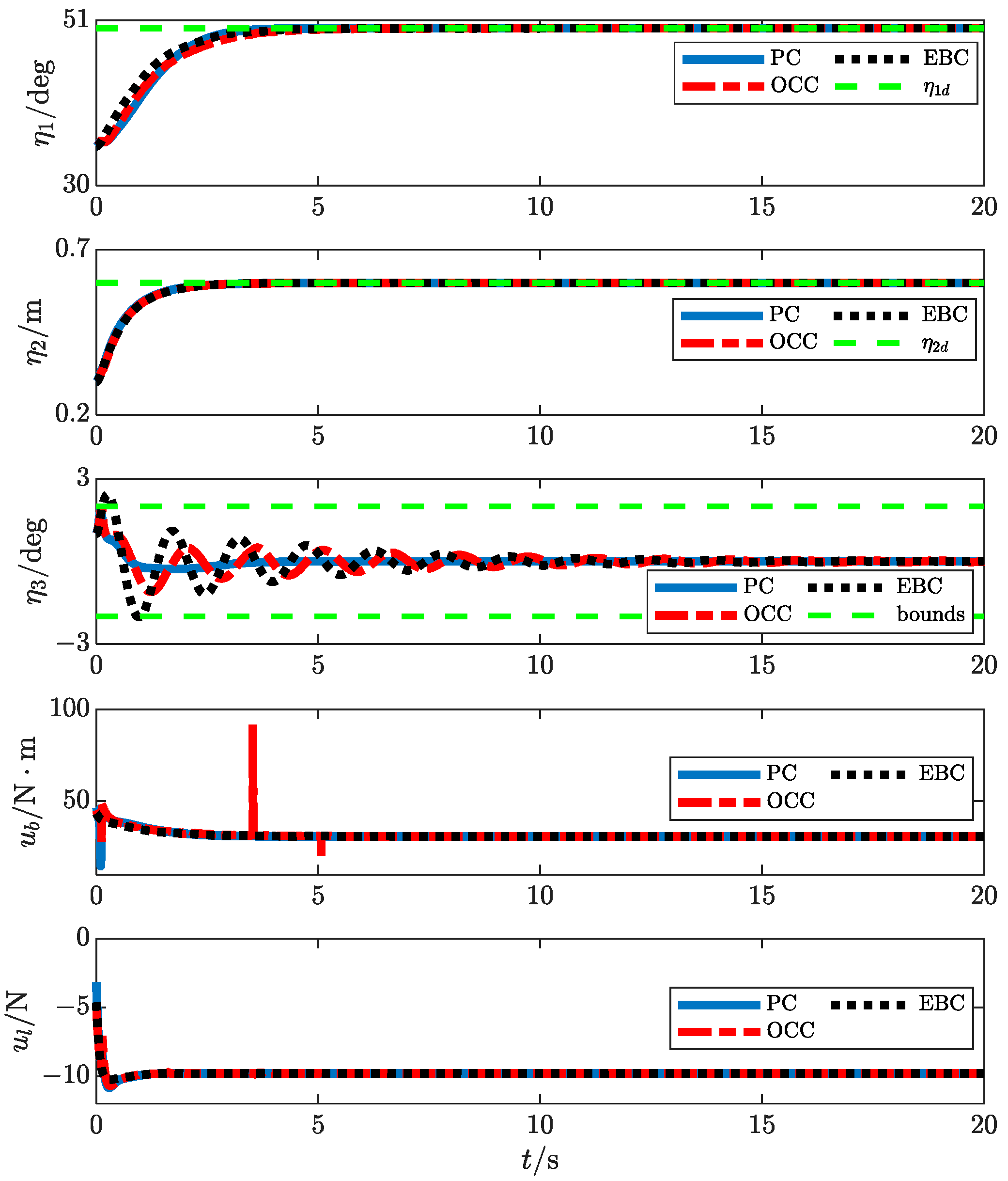
4. Simulation Results
- : The time required for the positioning error of the rope length to converge within the range of
- : The payload swing amplitude’s peak value during the control process.
- : The time required for the payload swing angle to converge within the range of
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Küchler, S.; Mahl, T.; Neupert, J.; Schneider, K.; Sawodny, O. Active control for an offshore crane using prediction of the vessel’s motion. IEEE/ASME Trans. Mechatron. 2010, 16, 297–309. [Google Scholar] [CrossRef]
- Rong, B.; Rui, X.; Lu, K.; Tao, L.; Wang, G.; Yang, F. Dynamics analysis and wave compensation control design of ship’s seaborne supply by discrete time transfer matrix method of multibody system. Mech. Syst. Signal Process. 2019, 128, 50–68. [Google Scholar] [CrossRef]
- Shi, J.; Hu, M.; Zhang, Y.; Chen, X.; Yang, S.; Hallak, T.S.; Chen, M. Dynamic Analysis of Crane Vessel and Floating Wind Turbine during Temporary Berthing for Offshore On-Site Maintenance Operations. J. Mar. Sci. Eng. 2024, 12, 1393. [Google Scholar] [CrossRef]
- Huang, J.; Wang, W.; Zhou, J. Adaptive control design for underactuated cranes with guaranteed transient performance: Theoretical design and experimental verification. IEEE Trans. Ind. Electron. 2021, 69, 2822–2832. [Google Scholar] [CrossRef]
- Liu, Z.; Fu, Y.; Sun, N.; Yang, T.; Fang, Y. Collaborative antiswing hoisting control for dual rotary cranes with motion constraints. IEEE Trans. Ind. Inform. 2021, 18, 6120–6130. [Google Scholar] [CrossRef]
- Ramli, L.; Mohamed, Z.; Abdullahi, A.M.; Jaafar, H.I.; Lazim, I.M. Control strategies for crane systems: A comprehensive review. Mech. Syst. Signal Process. 2017, 95, 1–23. [Google Scholar] [CrossRef]
- Wang, T.; Lin, C.; Li, R.; Qiu, J.; He, Y.; Zhou, Z.; Qiu, G. Nonlinear enhanced coupled feedback control for bridge crane with uncertain disturbances: Theoretical and experimental investigations. Nonlinear Dyn. 2023, 111, 19021–19032. [Google Scholar] [CrossRef]
- Sun, N.; Fang, Y. New energy analytical results for the regulation of underactuated overhead cranes: An end-effector motion-based approach. IEEE Trans. Ind. Electron. 2012, 59, 4723–4734. [Google Scholar] [CrossRef]
- Sun, N.; Fang, Y.; Wu, X. An enhanced coupling nonlinear control method for bridge cranes. IET Control Theory Appl. 2014, 8, 1215–1223. [Google Scholar] [CrossRef]
- Zhang, S.; He, X.; Zhu, H.; Li, X.; Liu, X. PID-like coupling control of underactuated overhead cranes with input constraints. Mech. Syst. Signal Process. 2022, 178, 109274. [Google Scholar] [CrossRef]
- Wang, T.; Tan, N.; Qiu, J.; Zheng, Z.; Lin, C.; Wang, H. A novel model-free adaptive terminal sliding mode controller for bridge cranes. Meas. Control 2023, 56, 1217–1230. [Google Scholar] [CrossRef]
- Maghsoudi, M.; Ramli, L.; Sudin, S.; Mohamed, Z.; Husain, A.; Wahid, H. Improved unity magnitude input shaping scheme for sway control of an underactuated 3D overhead crane with hoisting. Mech. Syst. Signal Process. 2019, 123, 466–482. [Google Scholar] [CrossRef]
- Chen, Q.; Cheng, W.; Liu, J.; Du, R. Partial state feedback sliding mode control for double-pendulum overhead cranes with unknown disturbances. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2022, 236, 3902–3911. [Google Scholar] [CrossRef]
- Chen, H.; Fang, Y.; Sun, N. A swing constraint guaranteed MPC algorithm for underactuated overhead cranes. IEEE/ASME Trans. Mechatron. 2016, 21, 2543–2555. [Google Scholar] [CrossRef]
- Cao, Y.; Li, T. Review of antiswing control of shipboard cranes. IEEE/CAA J. Autom. Sin. 2020, 7, 346–354. [Google Scholar] [CrossRef]
- Ngo, Q.H.; Hong, K.-S. Sliding-mode antisway control of an offshore container crane. IEEE/ASME Trans. Mechatron. 2010, 17, 201–209. [Google Scholar] [CrossRef]
- Saghafi Zanjani, M.; Mobayen, S. Anti-sway control of offshore crane on surface vessel using global sliding mode control. Int. J. Control. 2022, 95, 2267–2278. [Google Scholar] [CrossRef]
- Kim, G.-H.; Hong, K.-S. Adaptive sliding-mode control of an offshore container crane with unknown disturbances. IEEE/ASME Trans. Mechatron. 2019, 24, 2850–2861. [Google Scholar] [CrossRef]
- Lu, B.; Fang, Y.; Lin, J.; Hao, Y.; Cao, H. Nonlinear antiswing control for offshore boom cranes subject to ship roll and heave disturbances. Autom. Constr. 2021, 131, 103843. [Google Scholar] [CrossRef]
- Sun, N.; Yang, T.; Chen, H.; Fang, Y. Dynamic feedback antiswing control of shipboard cranes without velocity measurement: Theory and hardware experiments. IEEE Trans. Ind. Inform. 2018, 15, 2879–2891. [Google Scholar] [CrossRef]
- Wu, Y.; Sun, N.; Chen, H.; Fang, Y. New adaptive dynamic output feedback control of double-pendulum ship-mounted cranes with accurate gravitational compensation and constrained inputs. IEEE Trans. Ind. Electron. 2021, 69, 9196–9205. [Google Scholar] [CrossRef]
- Guo, B.; Chen, Y. Fuzzy robust fault-tolerant control for offshore ship-mounted crane system. Inf. Sci. 2020, 526, 119–132. [Google Scholar] [CrossRef]
- Jang, J.H.; Kwon, S.-H.; Jeung, E.T. Pendulation reduction on ship-mounted container crane via TS fuzzy model. J. Cent. South Univ. 2012, 19, 163–167. [Google Scholar] [CrossRef]
- Yang, T.; Sun, N.; Chen, H.; Fang, Y. Neural network-based adaptive antiswing control of an underactuated ship-mounted crane with roll motions and input dead zones. IEEE Trans. Neural Netw. Learn. Syst. 2019, 31, 901–914. [Google Scholar] [CrossRef]
- Li, Z.; Hou, C.; Liu, C. Radical Basis Neural Network Based Anti-swing Control for 5-DOF Ship-Mounted Crane. In Proceedings of the International Conference on Neural Computing for Advanced Applications, Guilin, China, 5–7 July 2024; pp. 18–29. [Google Scholar]
- Cao, Y.; Li, T.; Hao, L.-Y. Lyapunov-based model predictive control for shipboard boom cranes under input saturation. IEEE Trans. Autom. Sci. Eng. 2022, 20, 2011–2021. [Google Scholar] [CrossRef]
- Sun, M.; Ji, C.; Luan, T.; Wang, N. LQR pendulation reduction control of ship-mounted crane based on improved grey wolf optimization algorithm. Int. J. Precis. Eng. Manuf. 2023, 24, 395–407. [Google Scholar] [CrossRef]
- Chen, H.; Sun, N. Nonlinear control of underactuated systems subject to both actuated and unactuated state constraints with experimental verification. IEEE Trans. Ind. Electron. 2019, 67, 7702–7714. [Google Scholar] [CrossRef]
- Li, E.; Liang, Z.-Z.; Hou, Z.-G.; Tan, M. Energy-based balance control approach to the ball and beam system. Int. J. Control 2009, 82, 981–992. [Google Scholar] [CrossRef]
- Lu, B.; Fang, Y.; Sun, N.; Wang, X. Antiswing control of offshore boom cranes with ship roll disturbances. IEEE Trans. Control Syst. Technol. 2017, 26, 740–747. [Google Scholar] [CrossRef]
- Qian, Y.; Hu, D.; Chen, Y.; Fang, Y.; Hu, Y. Adaptive neural network-based tracking control of underactuated offshore ship-to-ship crane systems subject to unknown wave motions disturbances. IEEE Trans. Syst. Man Cybern. Syst. 2021, 52, 3626–3637. [Google Scholar] [CrossRef]
- Wang, Y.; Yang, T.; Zhai, M.; Fang, Y.; Sun, N. Ship-Mounted Cranes Hoisting Underwater Payloads: Transportation Control With Guaranteed Constraints on Overshoots and Swing. IEEE Trans. Ind. Inform. 2023, 19, 9968–9978. [Google Scholar] [CrossRef]
- Khalil, H.K. Nonlinear Systems, 3rd ed.; Upper Saddle River Nj Prentice Hall Inc.: Saddle River, NJ, USA, 2002. [Google Scholar]
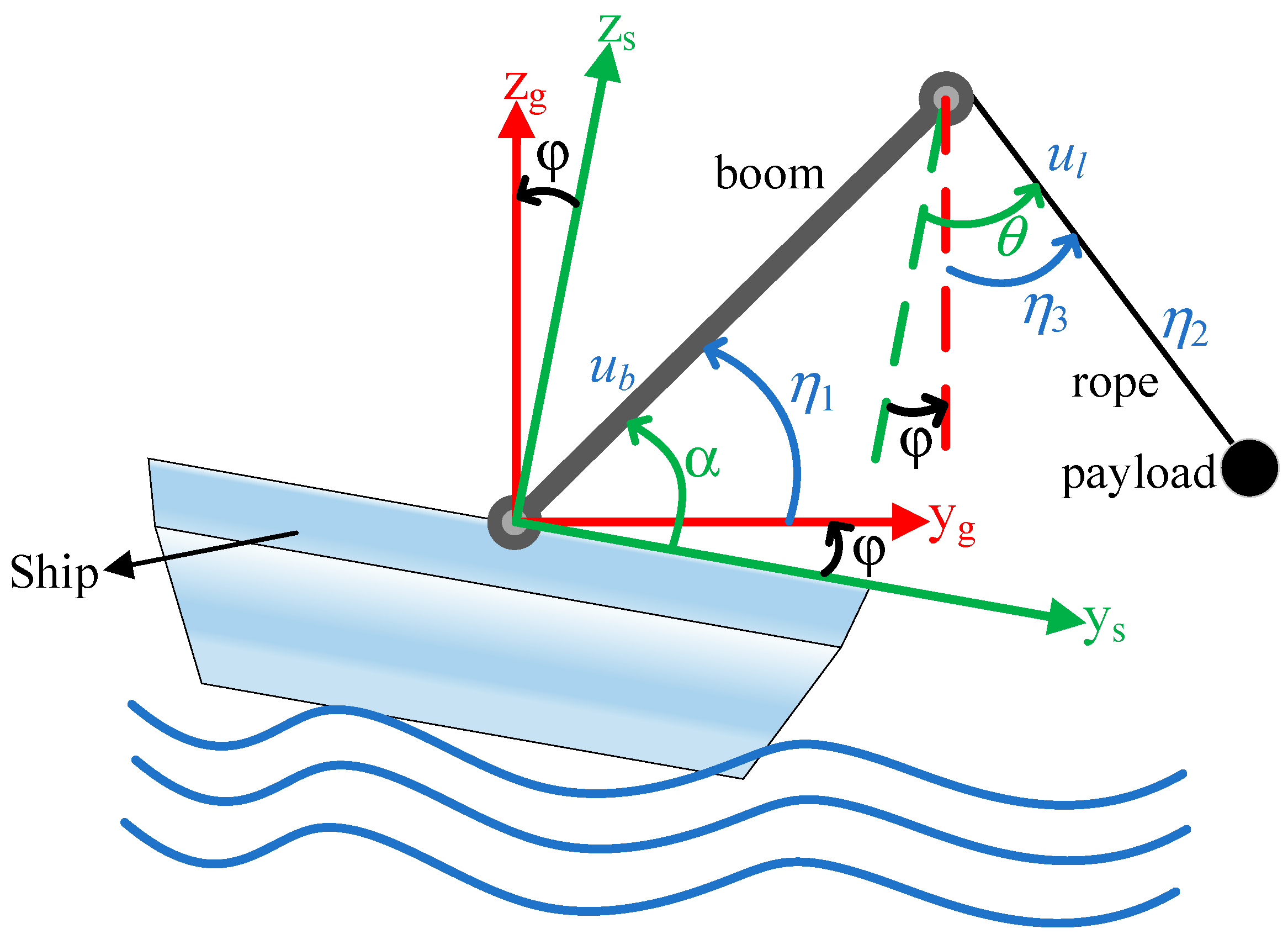
| Symbols | Parameters/Variables | Units |
|---|---|---|
| Boom luffing angle | ||
| Payload swing angle | ||
| Ship rolling angle | ||
| Time-varying rope length | ||
| Control input acting on the boom | ||
| Control input acting on the rope | ||
| Payload mass | ||
| The product of the boom mass and the distance between the boom barycenter and the point O | ||
| Boom length | ||
| Boom rotational inertia | ||
| Gravity constant |
| Controllers | Control Gains |
|---|---|
| PC | |
| EBC | |
| OCC |
| Controller | |||
|---|---|---|---|
| PC | 3.9 | 1 | 5.7 |
| EBC | 3.8 | 2.7 | 16.6 |
| OCC | 3.8 | 2.6 | 10 |
| Controller | |||
|---|---|---|---|
| PC | 6 | 1.1 | 5.8 |
| EBC | 4.4 | 2.4 | 7.2 |
| OCC | 4.4 | 2.4 | 9.7 |
| Controller | |||
|---|---|---|---|
| PC | 3.3 | 2.7 | 3.3 |
| EBC | 3.3 | 5.6 | 12.2 |
| OCC | 3.3 | 2.9 | 10.7 |
| Controller | |||
|---|---|---|---|
| PC | 3 | 1.8 | 3.5 |
| EBC | 3 | 2.4 | 14.7 |
| OCC | 3 | 1.9 | 16 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, M.; Xu, M.; Gao, Y.; Wang, T.; Deng, A.; Liu, Z. Advanced Control for Shipboard Cranes with Asymmetric Output Constraints. J. Mar. Sci. Eng. 2025, 13, 91. https://doi.org/10.3390/jmse13010091
Cao M, Xu M, Gao Y, Wang T, Deng A, Liu Z. Advanced Control for Shipboard Cranes with Asymmetric Output Constraints. Journal of Marine Science and Engineering. 2025; 13(1):91. https://doi.org/10.3390/jmse13010091
Chicago/Turabian StyleCao, Mingxuan, Meng Xu, Yongqiao Gao, Tianlei Wang, Anan Deng, and Zhenyu Liu. 2025. "Advanced Control for Shipboard Cranes with Asymmetric Output Constraints" Journal of Marine Science and Engineering 13, no. 1: 91. https://doi.org/10.3390/jmse13010091
APA StyleCao, M., Xu, M., Gao, Y., Wang, T., Deng, A., & Liu, Z. (2025). Advanced Control for Shipboard Cranes with Asymmetric Output Constraints. Journal of Marine Science and Engineering, 13(1), 91. https://doi.org/10.3390/jmse13010091







