Hydroelasto-Plastic Response of a Ship Model in Freak Waves: An Experimental and Numerical Investigation
Abstract
1. Introduction
1.1. Background
1.2. Recent Studies on Hydroelasto-Plasticity Generated by Freak Waves
1.2.1. Generation of Freak Wave
1.2.2. FSI of Freak Wave and Ship Structure
1.2.3. Hydroelasto-Plasticity
1.3. Challenges of Studying Hydroelasto-Plastic Responses Caused by Freak Waves
- (1)
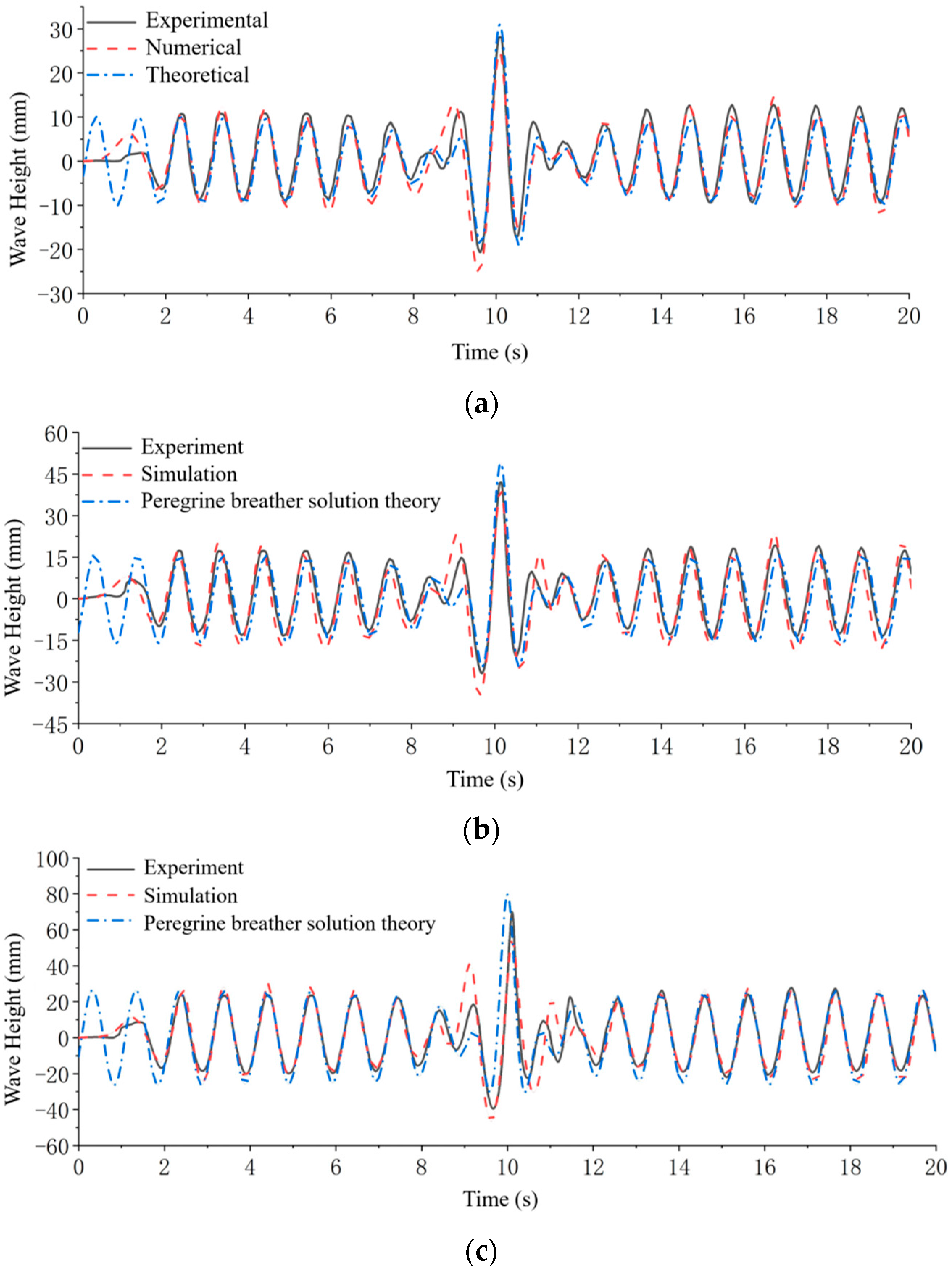
- Generation of freak waves in both experiment and simulation: Both experimental and numerical methods will be used to study the structural collapsed response of ship structure in freak waves. Therefore, freak waves must be generated in the experimental wave tank and integrated into the FSI numerical approach. While waves can be superimposed or constructed using the Peregrine breather solution theory based on the NLS equation, the latter offers a more stable and nonlinear representation of freak waves, making it the preferred method.
- (2)
- Conducting a hydroelasto-plastic model experiment in freak waves: Any numerical hydroelasto-plastic approach must be validated through a model experiment. Traditional hydroelastic ship structures, which use a beam to test VBM, often struggle with small wave heights, making it difficult to generate a structurally collapsed response. This study proposes a specialized hydroelasto-plastic ship structure with a buckling hinge at midship and rigid strips at the ends, enabling structural collapse simulations. This model differs from previous experiments confined to regular waves [27,28] and represents a novel approach.
- (3)
- Development of an appropriate FSI numerical approach: CFD platform STAR-CCM+ offers the capability to model nonlinear wave patterns if the velocity field is determined, such as through Peregrine breather solution theory [29]. Additionally, STAR-CCM+ can be combined with the nonlinear FEM solver ABAQUS, considering structural plasticity and instability, to establish a one-way or two-way hydroelasto-plastic numerical approach.
- (4)
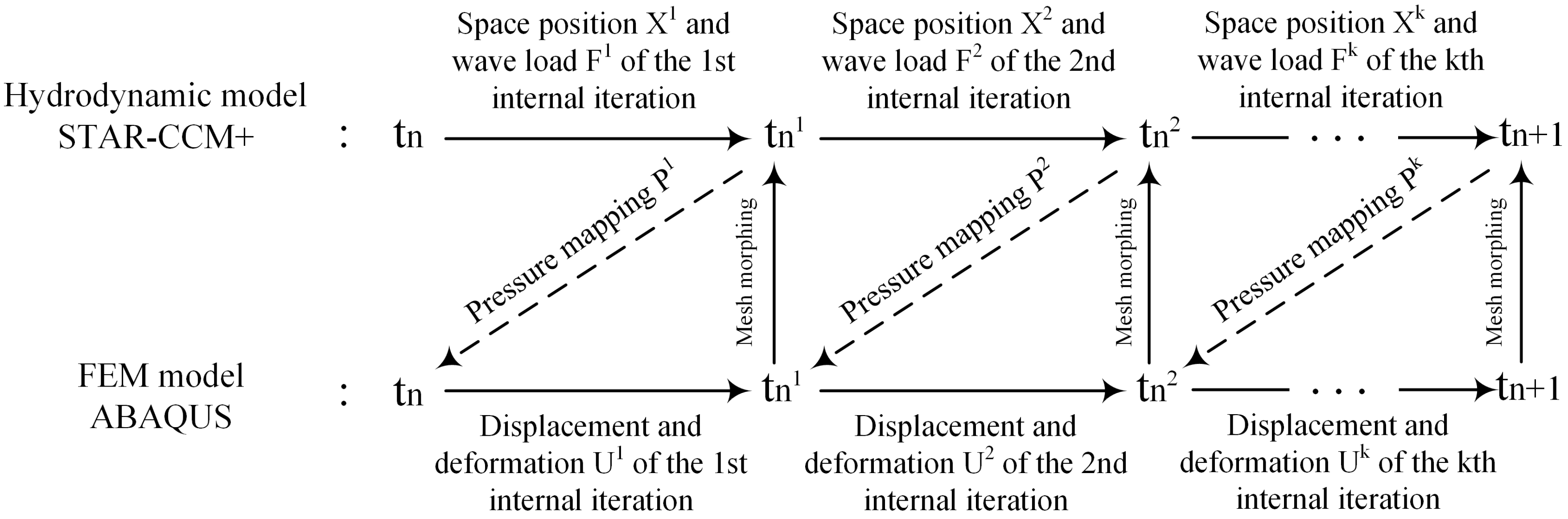
- Implementation of two-way FSI of CFD and nonlinear FEM: FSI can be performed as either one-way or two-way coupling. One-way FSI involves a single data transfer, where wave pressures calculated by CFD are applied to the FEM model without considering the effect of structural deformation on fluid pressures. Two-way FSI involves two data transfers, allowing co-simulation of wave pressures and structural nonlinearities, thus considering the effect of both wave load and structural deformation. Previous analysis found two-way FSI to be more accurate than one-way FSI [27], leading to employing two-way FSI in this study.
1.4. Objectives of This Paper
2. Hydroelasto-Plastic Model Experiment of a Ship Structure in Freak Waves
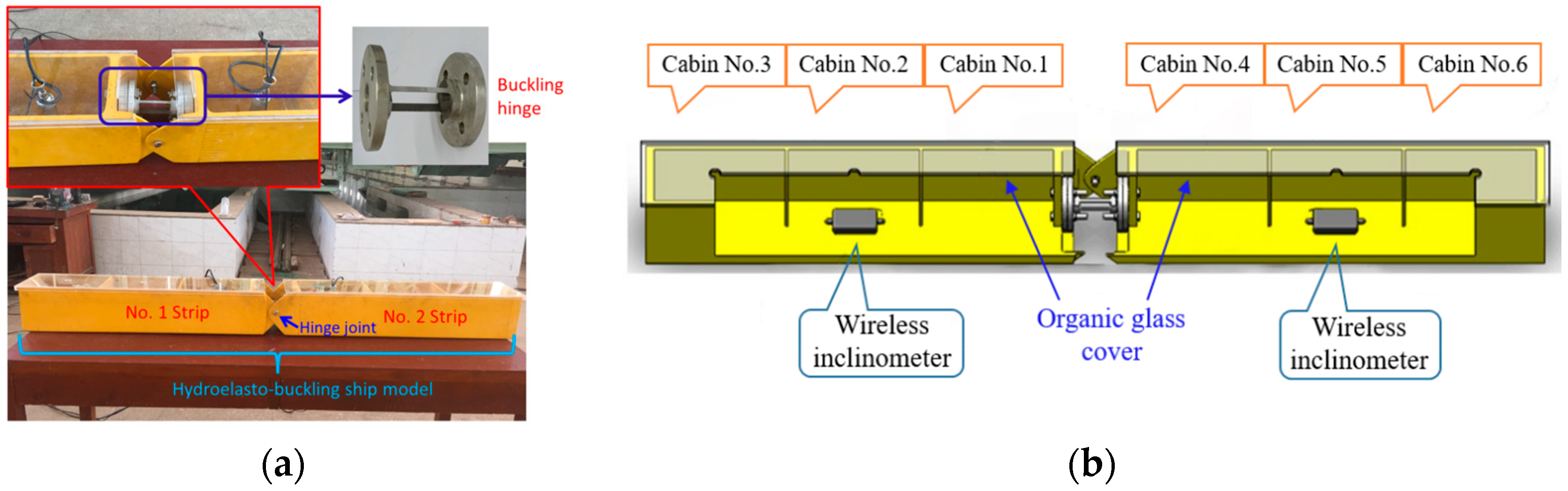
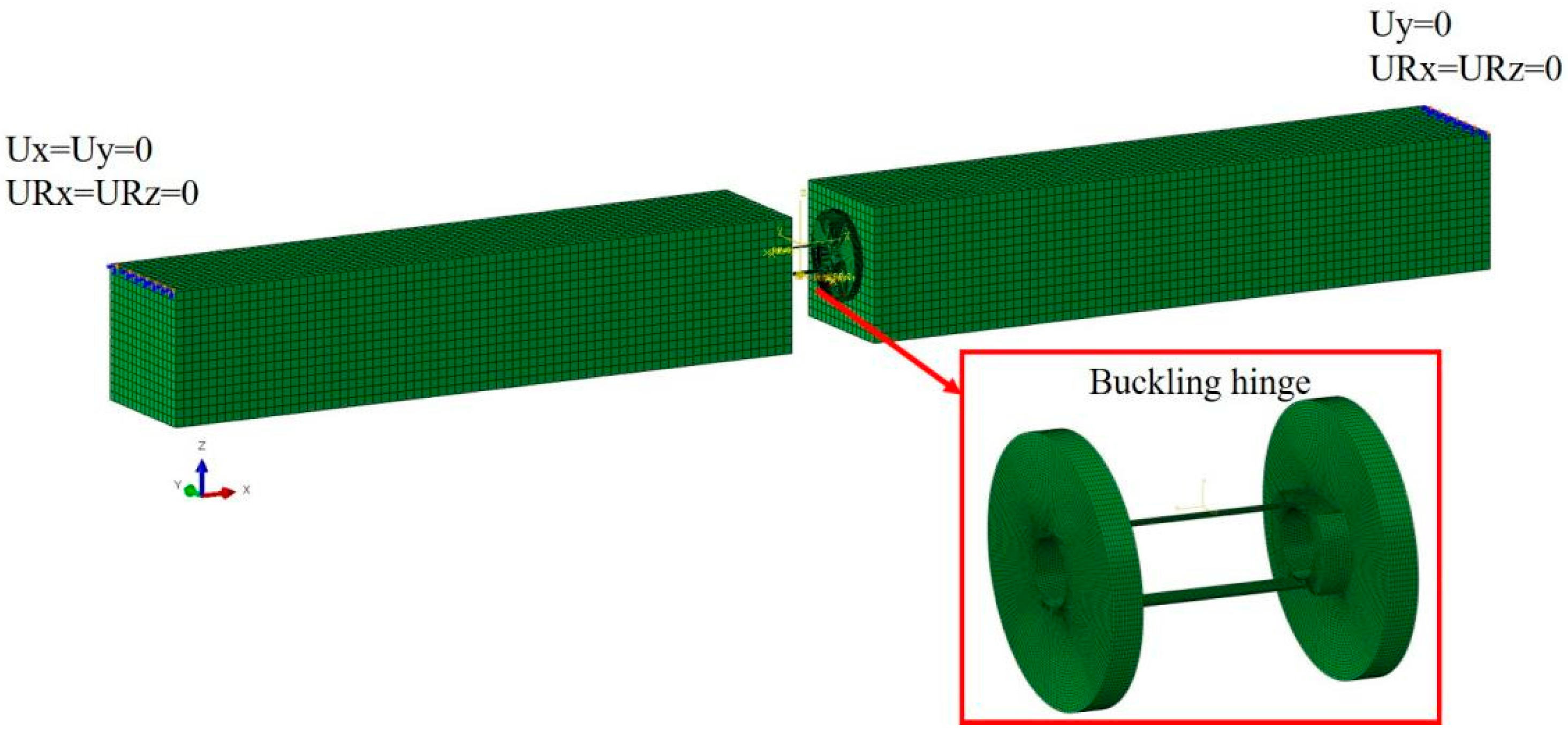
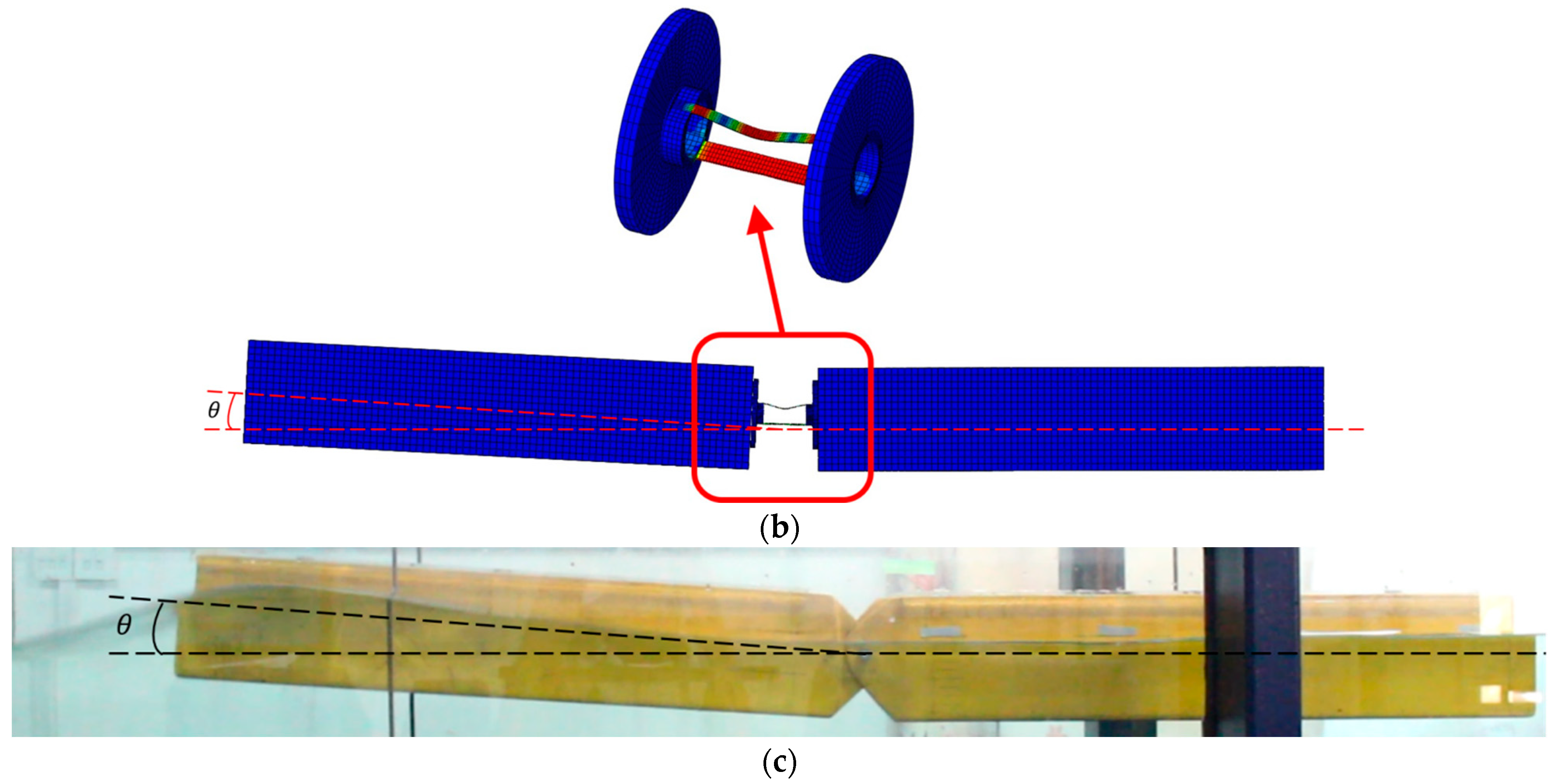
2.1. Model Description
2.2. Experimental Facilities
2.3. Experimental Cases
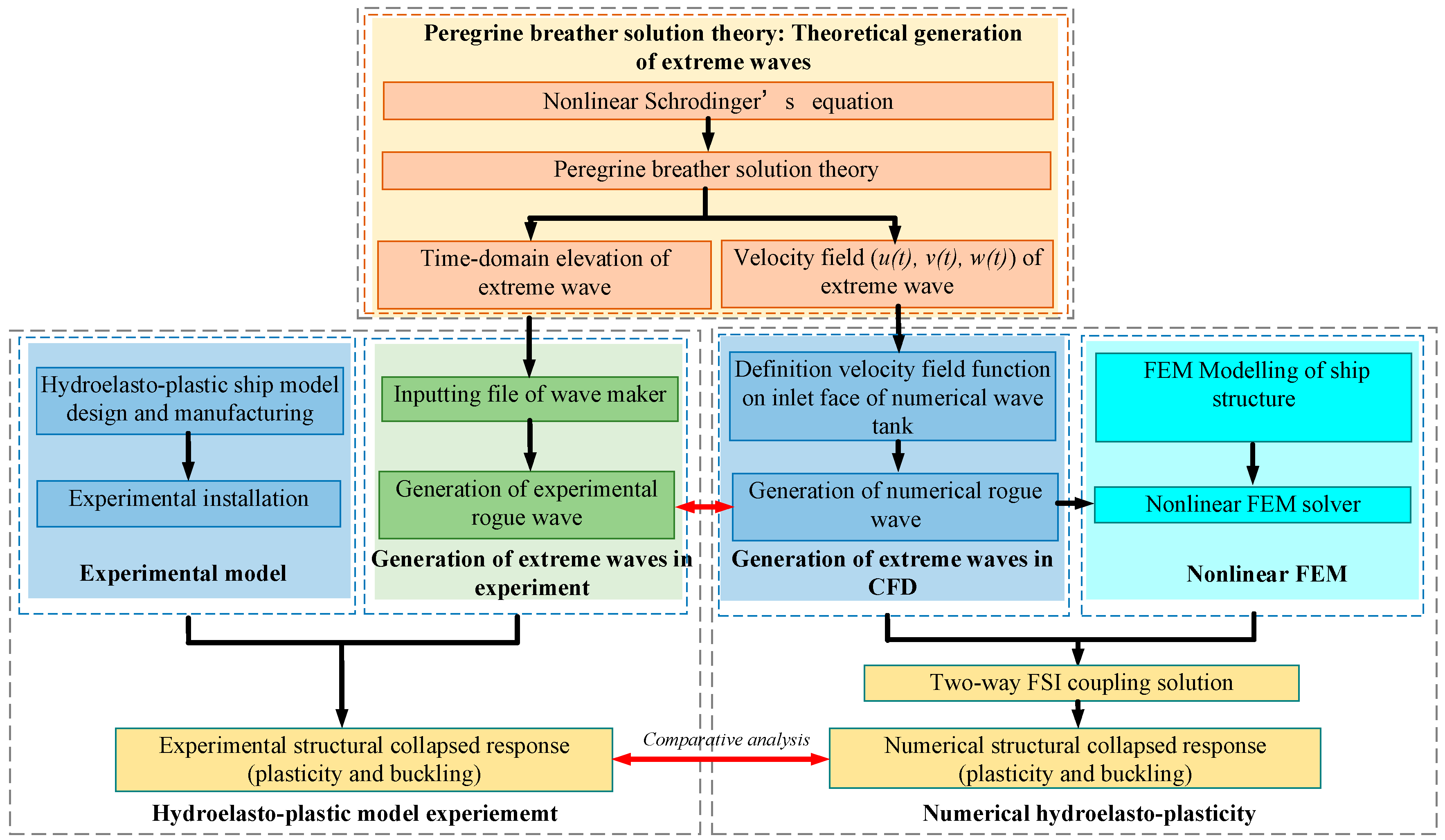
3. Numerical Methodology
3.1. Hydroelasto-Plastic Numerical Framework
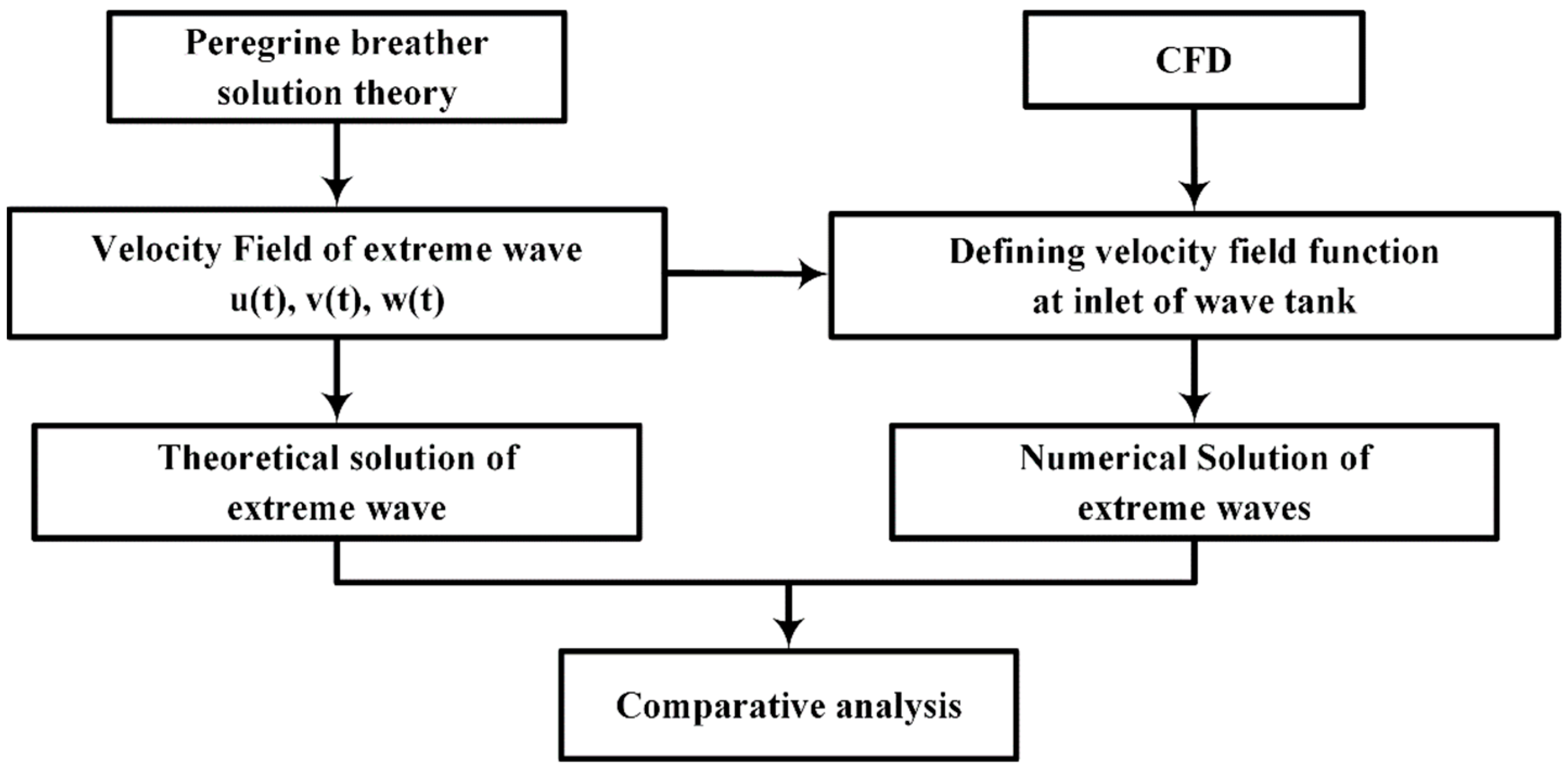
3.2. Peregrine Breather Solution Theory Solved from Nonlinear Schrödinger’s Equation
3.3. Nonlinear FEM
3.4. Two-Way Hydroelasto-Plastic Coupling CFD and Nonlinear FEM
4. Numerical Modelling
4.1. Generation of Numerical Freak Wave
4.2. CFD Model
4.3. Numerical Nonlinear FEM Model
5. Results Analysis
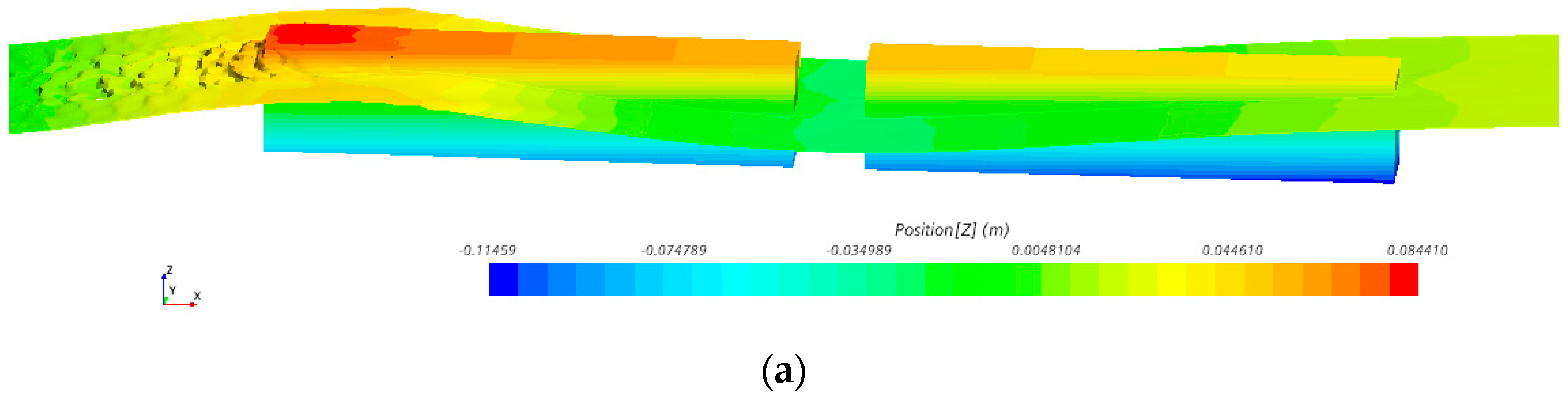
5.1. Wave Elevation Analysis
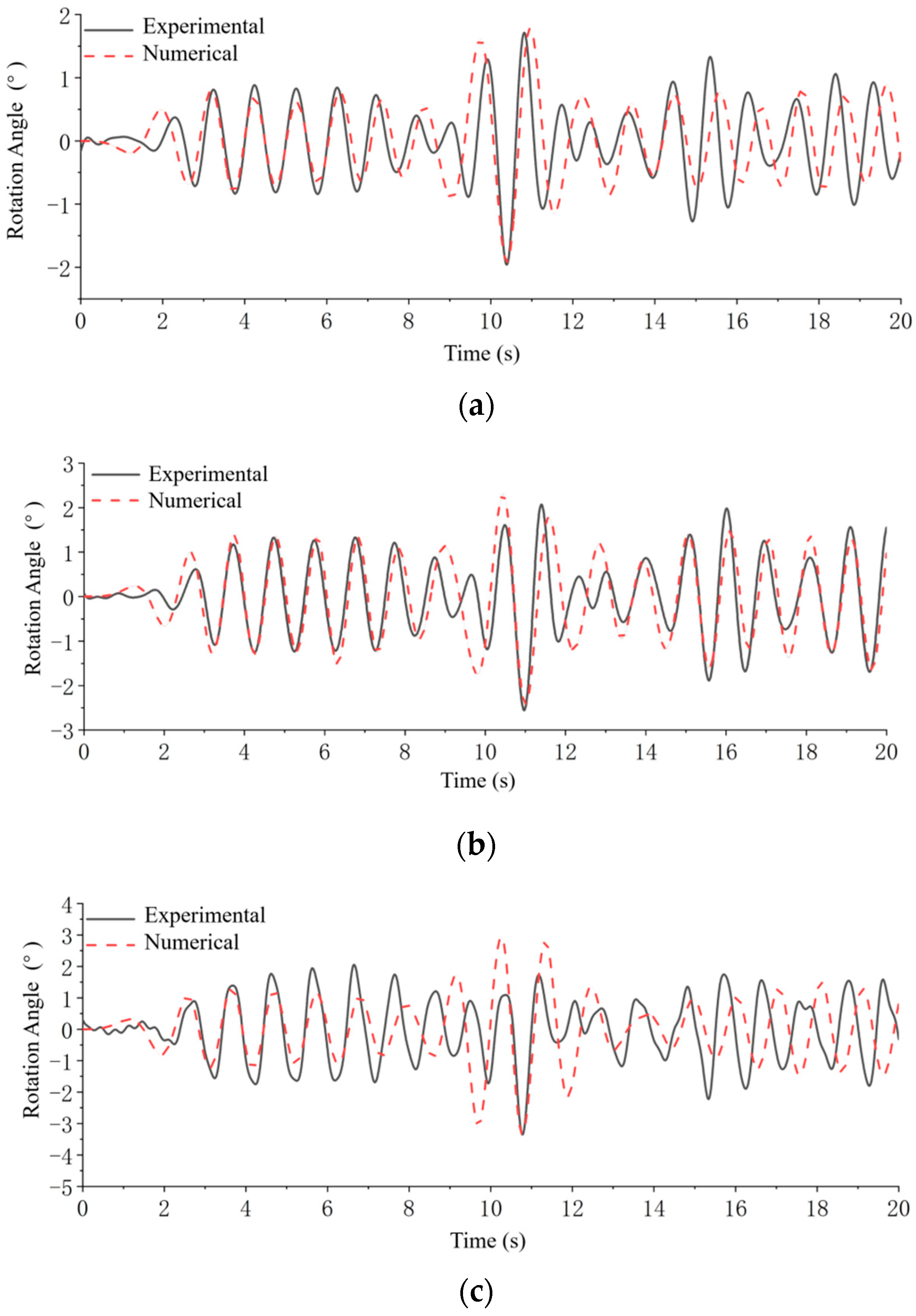
5.2. Rotational Deformation Analysis
6. Discussion
7. Conclusions
- (1)
- Peregrine breather solution theory, derived from the NLS equation, offers a nonlinear and stable means for generating both numerical and experimental freak waves.
- (2)
- The hydroelasto-plastic model experiment of ship structure under tank freak waves is realized using a relative strength model design. The appropriate selection of a buckling hinge and the application of tank freak wave obtained from the Peregrine breather solution theory is pivotal to this process.
- (3)
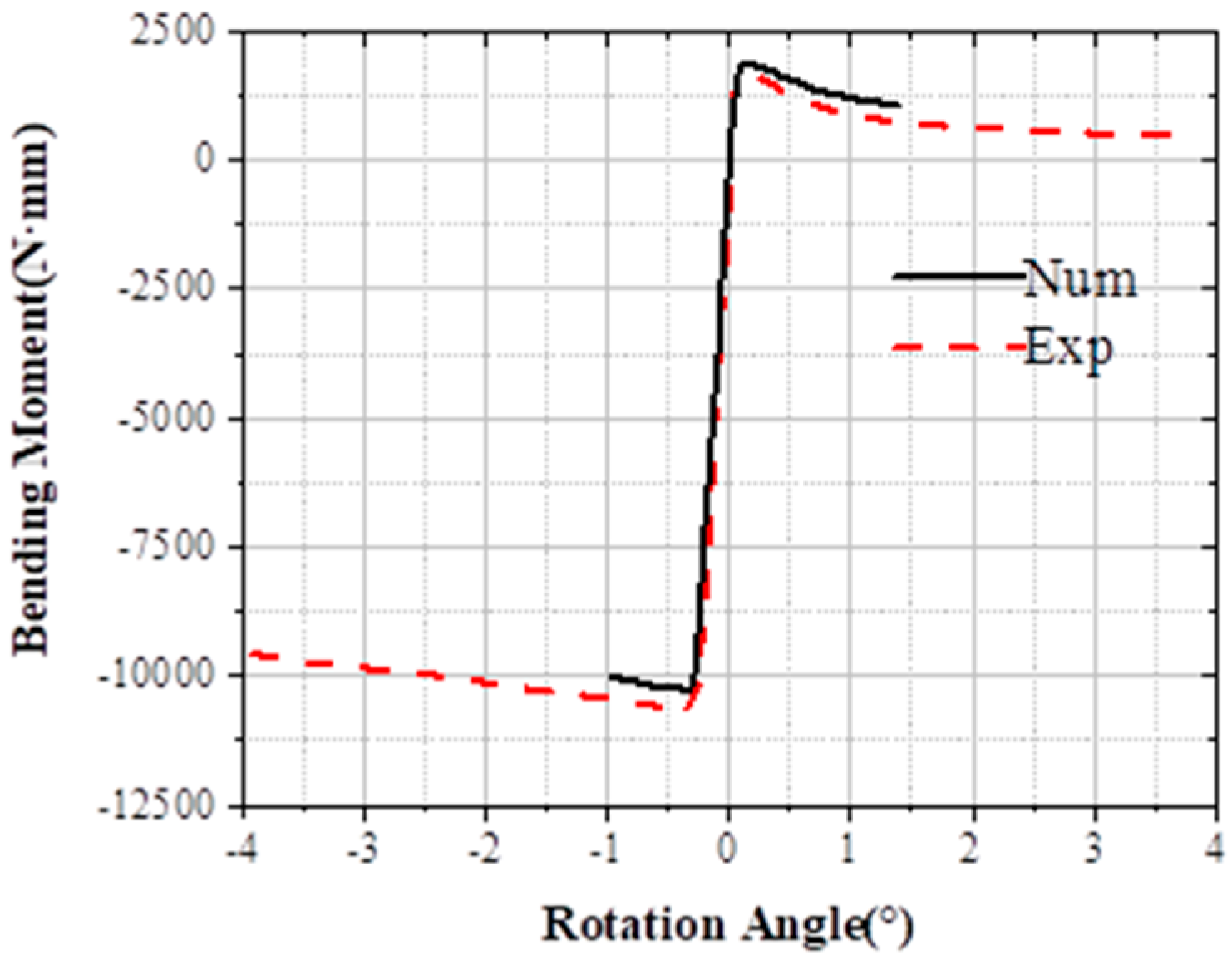
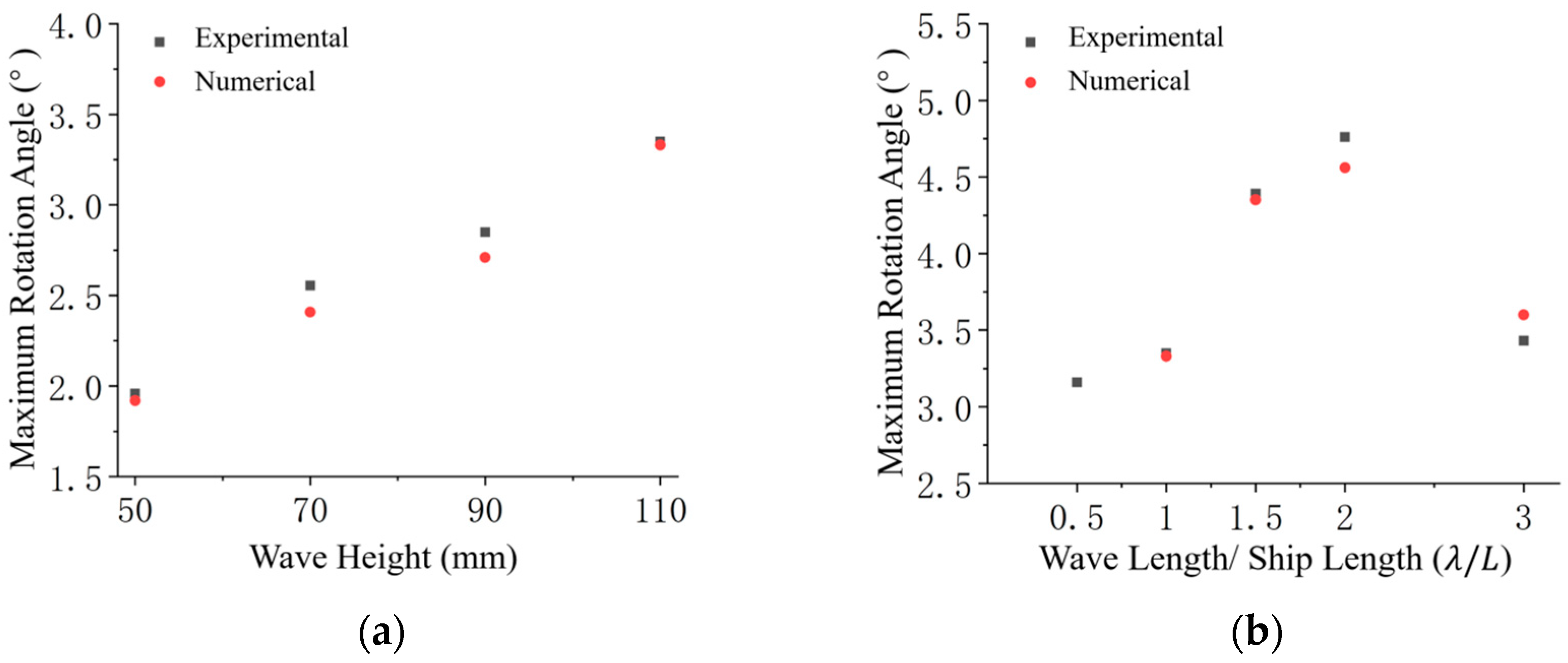
- This paper introduces a numerical hydroelasto-plastic framework that integrates Peregrine breather solution theory with an FSI approach, utilizing CFD and nonlinear FEM. This method is validated against experimental data, yielding strong agreements between the numerical and experimental results. A key observation is a large sagging rotational deformation, reaching a maximum value of 4.6 degrees (substantially greater than elastic rotation), indicating actual structural collapse in this study. Both numerical and experimental approaches successfully capture this significant collapsed rotation.
- (4)
- Computational time and meshing techniques are important challenges to carrying out hydroelasto-plastic response calculation for ocean structure. The numerical approach used in this paper involves solutions of CFD and nonlinear FEM; it needs to take a large amount of time and cost. Moreover, meshing qualities of CFD and FEM are still important to realize FSI numerical investigation, grid sizes of the CFD model and element sizes of FEM meshes need to be kept close.
- (5)
- The numerical and experimental results demonstrate that the maximum angular deformation of the midship increases with wave height. When the wave-length to model-length ratio is less than 2, the maximum midship rotation angle rises with this ratio. The peak angular deformation occurs when the wavelength is approximately twice the length of the structure. Beyond a wavelength/structural length ratio of 2, the maximum angular deformation decreases with an increase in this ratio.
- (6)
- While the numerical hydroelasto-plastic approach has proven effective in simulating the hydroelasto-plastic model experiment, future work may extend this methodology to explore the collapsed structural response of real ship structures under oceanic freak waves.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Haver, S.; Vestbostad, T.M.; Andersen, O.J.; Jakobsen, J.B. Freak waves and their conditional probability problem. In Proceedings of the Fourteenth International Ship and Polar Engineering Conference, Toulon, France, 23–28 May 2004. [Google Scholar]
- Haver, S. Freak Waves; Ifremer: Brest, France, 2001; pp. 129–140. [Google Scholar]
- Haver, S. Freak Wave Event at Draupner Jacket January 1 1995; Statoil Technical: Stavanger, Norway, 2003. [Google Scholar]
- Gunson, J.; Lehner, S.; Bitner-Gregersen, E. Extreme Wave Conditions from Wave Model Hindcasts and from Synthetic Aperture Radar Images. In Proceedings of the International Conference on Design and Operation for Abnormal Conditions II, London, UK, 6–7 November 2001. [Google Scholar]
- Müller, P.; Garrett, C.; Osborne, A. Freak waves. Oceanography 2005, 18, 66. [Google Scholar] [CrossRef]
- Anders, M. Update on incident involving the containership MOL Confort. Am. J. Transp. 2013, 558, 19. [Google Scholar]
- Vikram, M. Ukrainian Cargo Ship Arvin Sinks off Black Sea. Available online: https://maritime.direct/en/2021/01/18/ukrainian-cargo-ship-arvin-sinks-off-black-sea/ (accessed on 18 January 2021).
- Kriebel, D.L.; Alsina, M.V. Simulation of freak waves in a background random sea. In Proceedings of the Tenth International Ship and Polar Engineering Conference, Seattle, WA, USA, 27 May–2 June 2000. [Google Scholar]
- Kim, N.; Kim, C.H. Investigation of a dynamic property of Draupner freak wave. Int. J. Ship Polar Eng. 2003, 13, 1–12. [Google Scholar]
- Sheng, Y. Numerical Simulation of Freak Wave and the Interactions Between Freak Wave and Ship Structure. Master’s Thesis, Shanghai Jiaotong University, Shanghai, China, 2013. [Google Scholar]
- Waseda, T.; Rheem, C.K.; Sawamura, J.; Yuhara, T.; Kinoshita, T.; Tanizawa, K.; Tomita, H. Freak wave generation in Laboratory Wave Tank. In Proceedings of the 15th International Ship and Polar Engineering Conference, Seoul, Republic of Korea, 19–24 June 2005. [Google Scholar]
- Hu, Z.; Tang, W.; Xue, H.; Zhang, X. Numerical study of Freak waves as nonlinear Schrödinger breather solutions under finite water depth. Wave Motion 2015, 52, 81–90. [Google Scholar] [CrossRef]
- Chabchoub, A.; Hoffmann, N.; Akhmediev, N. Freak wave observation in a water wave tank. Phys. Rev. Lett. 2011, 106, 204502. [Google Scholar] [CrossRef] [PubMed]
- Zakharov, V.E.; Dyachenko, A.I.; Prokofiev, A.O. Freak waves as nonlinear stage of Stokes wave modulation instability. Eur. J. Mech. B Fluids 2006, 25, 677–692. [Google Scholar] [CrossRef]
- Didenkulova, I.I.; Nikolkina, I.F.; Pelinovsky, E.N. Freak waves in the basin of intermediate depth and the possibility of their formation due to the modulational instability. JETP Lett. 2013, 97, 194–198. [Google Scholar] [CrossRef]
- Clauss, G.F.; Kauffeldt, A.; Klein, M. Systematic investigation of loads and motions of a bulk carrier in extreme seas. In Proceedings of the 28th International Conference on Ship Mechanics and Arctic Engineering, Honolulu, HI, USA, 31 May–5 June 2009; Volume 43444, pp. 277–287. [Google Scholar]
- Shi, J.S.; Takuji, W.; Katsuyuki, S.; Takeshi, K.; Tetsuo, Y. Wave Loads on Container Ship in Freak Waves; The Japan Society of Naval Architects and Ocean Engineers: Tokyo, Japan, 2006. [Google Scholar]
- Kinoshita, T. Longitudinal Loads on a Container Ship in Extreme Regular Sea and Freak Wave. In Proceedings of the 4th International Conference on Hydroelasticity in Marine Technology, Wuxi, China, 10–14 September 2006. [Google Scholar]
- Holst, A.; Gunnar, D.; Celine, F. CFD Analysis of Wave-Induced Loads on Tidal Turbine Blades. IEEE J. Ocean. Eng. 2015, 40, 506–521. [Google Scholar] [CrossRef]
- Wang, J.; Hao, Q.; Zhe, H.; Lin, M. Three-dimensional study on the interaction between a container ship and freak waves in beam sea. Int. J. Nav. Archit. Ocean. Eng. 2022, 15, 100509. [Google Scholar] [CrossRef]
- Liu, Y. Hydroelastic Response of Large Floating Structure in Nonlinear Waves. Master’s Thesis, Jiangsu University of Technology, Zhenjiang, China, 2020. [Google Scholar]
- Masaoka, K.; Okada, H. A numerical approach for ship hull girder collapse behavior in waves. In Proceedings of the Thirteenth International Ship and Polar Engineering Conference, Honolulu, HI, USA, 25–30 May 2003. [Google Scholar]
- Iijima, K.; Kimura, K.; Xu, W.; Fujikubo, M. Hydroelasto-plasticity approach to predicting the post- ultimate strength behavior of a ship’s hull girder in waves. J. Mar. Sci. Technol. 2011, 16, 379–389. [Google Scholar] [CrossRef]
- Lee, S.; You, J.; Lee, H.; Lim, T.; Park, S.; Seo, J.; Rhee, S.; Rhee, K. Experimental Study on the Six Degree-of-Freedom Motions of a Damaged Ship Floating in Regular Waves. IEEE J. Ocean. Eng. 2016, 41, 40–49. [Google Scholar]
- Liu, W.; Song, X.; Wu, W.; Suzuki, K. Strength of a Container Ship in Freak waves Obtained by Nonlinear Hydroelasto-plasticity Dynamic Analysis and Finite Element Modeling. J. Ship Mech. Arct. Eng. 2016, 138, 031602. [Google Scholar]
- Liu, W.; Huang, Y.; Li, Y.; Song, X.; Wei, F.; Wu, X. Numerical and experimental investigation on nonlinear cyclic collapse response of ship model in regular waves. J. Ship Mech. Arct. Eng. 2021, 143, 041702. [Google Scholar] [CrossRef]
- Liu, W.; Luo, W.; Yang, M.; Xia, T.; Huang, Y.; Wang, S.; Li, Y. Development of a fully coupled numerical hydroelasto-plastic approach for ship structure. Ocean Eng. 2022, 258, 111713. [Google Scholar] [CrossRef]
- Liu, W.; Song, X.; Pei, Z.; Li, Y. A Hydroelasto-buckling Experiment Study of Ship Model in Single Wave. Ocean Eng. 2017, 142, 102–114. [Google Scholar] [CrossRef]
- Mei, C.C. The Applied Dynamics of Ocean Surface Waves; World Scientific: Singapore, 1989; Volume 1. [Google Scholar]






| Case | Wave Height (m) | Wavelength/Model Length | Wavelength (m) | Period (s) |
|---|---|---|---|---|
| H1 | 0.05 | 1 | 1.6 | 1.0123 |
| H2 | 0.07 | 1 | 1.6 | 1.0123 |
| H3 | 0.09 | 1 | 1.6 | 1.0123 |
| H4 | 0.11 | 1 | 1.6 | 1.0123 |
| L2 | 0.11 | 1.5 | 2.4 | 1.2398 |
| L3 | 0.11 | 2 | 3.2 | 1.4316 |
| L4 | 0.11 | 3 | 4.8 | 1.7534 |
| Ultimate Sagging BM (N·mm) | Critical Rotational Angle (°) | Ultimate Hogging BM (N·mm) | Critical Rotational Angle (°) | |
|---|---|---|---|---|
| Experiment | 1850 | 0.121 | −10269 | −0.3048 |
| Simulation | 1792 | 0.101 | −10631 | −0.3811 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, W.; Mo, Y.; Xiong, L.; Xu, H.; Song, X.; Li, Y. Hydroelasto-Plastic Response of a Ship Model in Freak Waves: An Experimental and Numerical Investigation. J. Mar. Sci. Eng. 2024, 12, 1555. https://doi.org/10.3390/jmse12091555
Liu W, Mo Y, Xiong L, Xu H, Song X, Li Y. Hydroelasto-Plastic Response of a Ship Model in Freak Waves: An Experimental and Numerical Investigation. Journal of Marine Science and Engineering. 2024; 12(9):1555. https://doi.org/10.3390/jmse12091555
Chicago/Turabian StyleLiu, Weiqin, Yining Mo, Luonan Xiong, Haodong Xu, Xuemin Song, and Ye Li. 2024. "Hydroelasto-Plastic Response of a Ship Model in Freak Waves: An Experimental and Numerical Investigation" Journal of Marine Science and Engineering 12, no. 9: 1555. https://doi.org/10.3390/jmse12091555
APA StyleLiu, W., Mo, Y., Xiong, L., Xu, H., Song, X., & Li, Y. (2024). Hydroelasto-Plastic Response of a Ship Model in Freak Waves: An Experimental and Numerical Investigation. Journal of Marine Science and Engineering, 12(9), 1555. https://doi.org/10.3390/jmse12091555





