Abstract
The capability of the in-house transient wave-multibody computational tool, ITU-WAVE, is extended to predict the wave power absorption with Wave Energy Converters (WECs) arrays placed in front of a vertical breakwater. The hydrodynamic forces are approximated by solving boundary integral equation at each time interval. The reflection of incoming waves due to a vertical wall is predicted with method of images. The constructive or destructive performance of WECs arrays with different array configurations is measured with mean interaction factor. The behaviour of the hydrodynamic forces of each WEC due to a vertical wall effect shows considerable differences than those of WECs arrays without a vertical wall. When the wave power absorption with WECs arrays with and without a vertical wall effect are compared, the numerical results show that WECs placed in front of a vertical wall have much greater effects on wave power absorption. This can be attributed to the hydrodynamic interaction, standing waves, and nearly trapped waves in the gap between a vertical wall and WECs arrays. The analytical and other numerical results are used for the validation of present ITU-WAVE computational results for exciting and radiation forces, and mean interaction factor of WECs arrays which show satisfactory agreements.
1. Introduction
The performances of isolated WECs for wave power absorption can be improved using different array configurations of rectangular, square, or linear forms. In addition, single or multimode of motions (e.g., surge, heave, pitch), separation distance between WECs [1], heading angles (e.g., head seas, beam seas), Power-Take-Off systems or control strategies play a significant role on the performances of WECs arrays. Wave power absorptions could also significantly be improved by replacing isolated device with WECs arrays [1]. The array configuration results in increasing absorbed wave power due to wave interaction and standing waves between a vertical wall and WECs. Wave power could be exploited either in nearshore or offshore environments. The efficiency of WECs arrays and absorbed wave power could be further improved by replacing WECs arrays in front of the marine structures (e.g., a vertical wall) [2,3] or integrating them with breakwaters. The overall costs of WECs arrays in the offshore environment increase considerably due to the cost of the maintenance, installations, and operations. However, the overall cost could be decreased significantly by sharing it with existing marine structure and replacing WECs arrays in front of a breakwater or integrating them [4] with a vertical wall.
When wave power absorption of WECs arrays is compared that of isolated WEC, the experimental [5] and numerical [1,6] analyses show that WECs arrays are superior to isolated WEC. The nearly trapped waves and hydrodynamic interactions in the gap are the reasons for the considerably improved wave power absorption with WECs array configurations. The competitiveness of WECs arrays can be further improved and enhanced by exploiting the optimum hydrodynamic interaction in the gap of array system. A vertical wall effect on the efficiency and behaviour of WECs arrays due to the wave interaction in the gap between WECs arrays and between a vertical wall and WECs are investigated numerically and experimentally [2,7]. The effects of a vertical wall for maximum absorbed wave power are strongly influenced with the separation distance between a vertical wall and WECs arrays as well as between WECs [8]. The integration of WECs with breakwater has significant influence in the behaviour and performance of WECs arrays with the configurations of floating and stationary systems (e.g., oscillating buoys, overtopping, oscillating water columns) [5].
The effects of a breakwater on hydrodynamic performance and flow behaviour around WECs arrays could be considered with method of images in which a breakwater is used as the line of symmetry. This method is used to approximate hydrodynamic coefficients in front of a vertical wall or in a channel [6,9]. A vertical wall could be considered as either a wall with an infinite length [10] or a wall with a finite length [7]. The perfect reflection of the incoming waves is achieved with an infinite wall length whilst the effects on hydrodynamic variables of WECs arrays are taken with a finite wall length assumption into account. The integral equation which includes method of images to approximate hydrodynamic parameters is obtained by three preferred and most used methods considering three-dimensional effects and taking the hydrodynamic interactions in the gap of WECs arrays and between a vertical wall and WECs arrays into account automatically. Two of them are numerical methods in which the geometry of WECs arrays could be arbitrary whilst the third one is an analytical method. One of the numerical methods is the Rankine panel method [11,12] whilst the other one is wave Green function which uses Boundary Integral Equation Method (BIEM) [1,13,14] for the solution. Point ab-sorber [15], plane wave analysis [16], and direct matrix method [17] are widely used analytical methods that are preferred when the geometry of WECs arrays is defined analytically (e.g., vertical cylinder, sphere).
The novel elements of the effects of the breakwater on wave power absorption from ocean waves are not studied extensively although much attention is given to wave power absorption and hydrodynamic performances without breakwater effects. The effects of a breakwater or vertical wall increase the efficiency and absorbed wave power considerably due to strong hydrodynamic interactions and standing waves between WECs and breakwater. In addition, most of the papers in the open literature consider the predictions of the exciting force calculations whilst the analyses of the radiation force prediction are not studied extensively. These knowledge gaps are studied and will be filled in the present paper. The other novel element and contribution to the knowledge of the present paper is the solution and prediction of the exciting and radiation forces using transient wave Green function, which has not been studied before, for wave power absorption with WECs arrays placed in front of a breakwater.
The hydrodynamic performances and wave power absorptions with WECs arrays are studied extensively in the literature. However, the limited numbers of papers exist to exploit the novelty of the wave power absorption with WECs in front of a vertical wall. The exploitation of a vertical wall increases the efficiency of WECs arrays due to strong hydrodynamic interactions between a vertical wall and WECs arrays. In addition, most of the existence literature is mainly focused on the exciting force predictions without giving much attention to the radiation force calculations. The present paper aims to contribute and fill these knowledge gap in the literature. Furthermore, to the best of author’s knowledge, the numerical analysis of radiation and exciting forces with direct time domain methods using three-dimensional transient wave Green function for the predictions of wave power absorption with WECs arrays in front of a vertical wall are not studied before in the literature in the context of the potential theory and linear formulation. This is another contribution to knowledge and the novel part of the present study.
The hydrodynamic parameters of diagonal and interaction exciting and radiation IRFs in the present paper are predicted by time marching of time-dependent integral equation with BIEM method [13,18,19] and method of images, which consider an infinite wall length assumption whilst the superpositions of Impulse Response Functions (IRFs) of diffraction and Froude–Krylov are used for prediction of IRFs of the exciting force. The isolated WEC, linear (1 × 3, 1 × 5), square (2 × 2, 3 × 3, 5 × 5), and rectangular (2 × 3, 2 × 5, 3 × 5, 5 × 3) WECs arrays with or without a breakwater effect are used to predict hydrodynamic parameters in heave and sway modes. The exciting force IRFs are used to predict the frequency-dependent exciting force amplitude through Fourier transform which has a link between the frequency and time domain variables whilst the radiation IRFs are used for the radiation added mass and damping coefficients. The numerical results of the present three-dimensional ITU-WAVE computational tool are then validated against other numerical and analytical results which show acceptable level of agreements. The superpositions of instantaneous wave power due to the time-dependent exciting and radiation forces are used to obtain the absorbed wave power with time average approximation. The transient effects on the predicted absorbed wave power in direct time domain analysis are avoided by considering only the last half of time domain simulations which achieve the steady-state condition.
2. Materials and Methods
The numbers (1, 2, 3,…,10) in Figure 1 are used to show the location of 2 × 5 array system with a vertical wall. is used for heading angle whilst the separation distance between WECs arrays is given with . The separation distance between 2 × 5 WEC arrays and a vertical wall is given with . The WECs arrays with free surface intersection is given with whilst is used for free surface. is used to represent the surface at infinity.
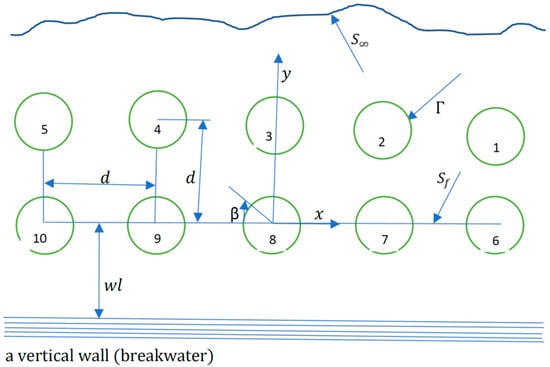
Figure 1.
Positions of WECs in 2 × 5 arrays with a vertical wall (breakwater) and a coordinate system in xy-plane.
Potential theory to solve the hydrodynamic parameters of WECs arrays with effects of a vertical wall in time domain is studied in the present work to approximate the velocity potential in time. Potential theory results in the assumptions that fluid flow is irrotational implying no fluid separations, and fluid is incompressible and inviscid implying no lifting effects. The velocity potential gradient is used to approximate the flow velocity which results from the potential theory assumption.
2.1. Time Domain Equation of Motion of WECs Arrays
The simulation of the equation of motion in time domain with effect of a breakwater on WECs in an array system is achieved through contribution from time-dependent exciting forces acting external forces, time-dependent radiation forces acting hydrodynamic restoring forces and representing wave damping, damping due to PTO system acting control forces, hydrostatic restoring forces due to wave motion and PTO system, and inertia mass and added mass at infinity in Equation (1) [20]. The pressure disturbances around WECs arrays are created due to incoming waves which are represented with right-hand side convolution integral in Equation (1). The pressure changes also result in the disturbances of the free surface which is represented with left-hand side convolution integral in Equation (1).
where (surge, sway, heave, roll, pitch, yaw mode of motions, respectively) on upper and lower boundary of summation symbol is used to present rigid behavior of each WEC. The number of WECs arrays is represented with . The acceleration, velocity, and displacement of each WEC are given , , and , respectively, where time derivatives of the displacements are given with dots. The elements of inertia mass matrix and those of restoring coefficients in Equation (2) are represented with and which correspond to an isolated WEC’s inertia mass and restoring coefficient, respectively. As each WEC in an array system has the same radius R, all elements of hydrostatic restoring coefficient matrix and those of inertia mass matrix are the same.
The geometry-dependent, and time- and frequency-independent variables of infinite added mass, damping coefficient, and restoring coefficient in Equation (3) are given with and which are relate acceleration, velocity, and displacement, respectively. The influence of each WEC is given with diagonal terms whilst the interaction of each WEC with each other is given with off-diagonal terms. The hydrodynamic relevant forces are presented with the time- and geometry-dependent IRF [21].
A uni-directional impulsive incident wave elevation in body coordinate system at origin of Figure 1 with arbitrary incident wave angle in Equation (4) result in exciting force IRFs on the body [22]. The exciting force IRFs are obtained by summation of diffraction IRFs due to reflected waves from array of each WEC and Froude–Krylov IRFs due to incoming incident waves.
The damping and restoring matrix of PTO system in Equation (5) are frequency-dependent and time-independent variables. The damping coefficient at resonant frequency is selected as PTO damping matrix elements of . The maximum wave power [23] is absorbed at resonance condition in which each WEC’ natural frequency in an array system equals to incident wave frequency. As there is no hydrostatic restoring force in sway mode for a floating system, the present paper assumes that the elements of PTO restoring matrix in sway mode have the same as those of heave mode. The same displacement and natural frequency are achieved with this assumption in heave and sway modes which also results in the direct comparison of the performance of each WEC in heave and sway modes with respect to maximum power absorption.
where represents each isolated WEC’ natural frequency in an array system. The time domain simulation of equation of motion Equation (1) [2,13,18,19] is achieved Runge–Kutta method with fourth-order version after determining the parameters in Equations (2)–(5).
2.2. Mean and Instantaneous Wave Power
PTO system at each mode is used to convert the absorbed instantaneous wave power in Equation (6) to electrical energy with WECs arrays which takes the effects of a vertical wall into account. The instantaneous wave power is obtained with the superposition of wave power generated by exciting and radiation forces.
where the incident coming waves and waves diffracted from each WEC in front of a breakwater result in the generation of instantaneous exciting forces in Equation (7) whilst the oscillations and interactions of each WEC in Equation (8) result in the generation of instantaneous radiation forces [1,2].
The absorbed instantaneous exciting wave power at any heading angles, which are the functions of the exciting force in Equation (7) and the velocity of each WEC, are the total wave power absorbed from incident wave. The instantaneous radiation wave power at any mode of motion in Equation (8), which are obtained multiplying radiation forces with velocity of the each WEC, represent the wave power which is returned to sea with radiation of absorbed wave power. The time averaged over period in Equation (9) is used to obtain the mean absorbed wave power with PTO system.
The superposition of the mean wave power in mode with N number of WEC in an array system in Equation (10) is used to obtain the total mean wave power absorption .
2.3. Constructive and Destructive Effects with Mean Interaction Factor
The frequency-dependent mean interaction factor is used to predict the gain factor at any incident wave frequency and mode of motion. Mean interaction factor at arbitrary heading angles is the ratio of wave power absorbed by N interacting WECs to N number of isolated WEC. The separation distance between WECs and a breakwater, control strategies, geometry of WECs, incident wave angles, determine the destructive ( or constructive effect. Mean interaction factor in Equation (11) is given as [24].
where total WECs number in an array system is given with N. The average wave power absorbed with an isolated WEC is given with at the resonant frequency . represents total mean absorbed wave power at mode and wave frequency . The mean values of and are used to predict at the incoming wave frequency and at the resonant frequency , respectively.
2.4. Transient Boundary Integral Equation for WECs Arrays
The transient boundary integral equation is used to solve the initial value problem with transient wave Green function which satisfies the condition at infinity, free surface boundary condition, and initial conditions automatically. This implicitly means that the surface of WECs arrays needs to be discretised to satisfy the body boundary condition [25]. The potential theory and transient wave Green function with application of Green theorem over surface of WECs arrays in Equation (12) are used to obtain transient boundary integral equation for the source strength [1,2].
And transient potential over each WEC in an array system is given in Equation (13)
where and are used for field points and source or integration points, respectively. represents transient wave Green function in which is used for time-independent Rankine part and analytically solved and integrated over discretised quadrilateral elements [26]. . is used for transient part due to oscillation of floating systems representing free surface effect. is solved analytically and then numerically integrated with two-dimensional 2 × 2 Gaussian quadrature over quadrilateral elements [18,19,22,27]. and are Dirac delta function and Heaviside unit step function, respectively. The influence of discretised surface against each other is given with underneath of free surface, and image part against free surface is presented with . ( in Equation (12) is the transient source strength, and ( in Equation (13) is the transient potential where the number of WECs in an array system is given with N.
3. Results
The present ITU-WAVE in-house computational tool [2,18] is used for the predictions of exciting force amplitudes, radiation and exciting IRFs, damping and added-mass coefficients, response amplitude operator, and mean interaction factor. Vertical cylinder and sphere WECs arrays are used to approximate the effects of a vertical wall on hydrodynamic performances of each WEC.
3.1. Validation of ITU-WAVE Numerical Results
3.1.1. Added Mass and Damping Coefficients
The in-house ITU-WAVE computational results of interaction hydrodynamic coefficients of added mass . and damping between WEC1 and WEC 4 using vertical cylinder of 1 × 5 arrays in sway mode in Figure 2a,b are validated against analytical results of nondimensional added mass and damping coefficients, respectively [10]. The analytical and in-house ITU-WAVE computational results are in satisfactory agreement as observed from Figure 2a,b. In , subscript is used for mode of motion (e.g., 2 is for sway mode) whilst superscript is used for interaction between WECs (e.g., 14 is the interaction between WEC1 and WEC4).
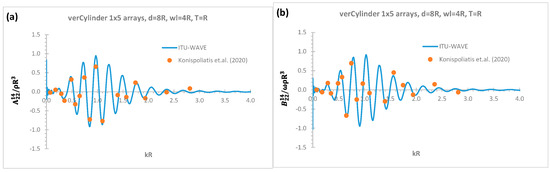
Figure 2.
Nondimensional interaction sway radiation force coefficients between WEC1 and WEC4 [10]; (a) ; (b) .
The interaction added mass and damping coefficients between WEC1 and WEC5 of truncated vertical cylinder of 1 × 5 arrays in sway mode are given with Figure 3a,b, respectively, in which the present numerical results of ITU-WAVE are validated against analytical results which shows good agreement [10]. It can be observed from Figure 2 and Figure 3 for added mass and damping coefficients that when the separation distance between WECs increases, the amplitudes of the oscillations increase at higher incident wave frequencies in Figure 3 compared to Figure 2.
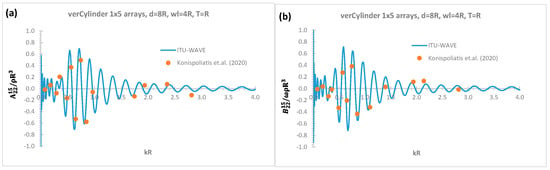
Figure 3.
Nondimensional interaction sway radiation force coefficients between WEC1 and WEC5 [10]; (a) ; (b) .
3.1.2. Exciting Force Amplitude
In addition to validation of radiation damping and added mass coefficients with analytical results, ITU-WAVE numerical results of truncated vertical cylinder of square 2 × 2 arrays for exciting force amplitudes in surge mode in Figure 4a,b are also validated against the analytical results [3] at the heading angle 270° for WEC1 & WEC2 () and WEC3 and WEC4 (), respectively. In , subscript represents the mode of motion for exciting force (e.g., 1E is exciting force for surge mode) whilst superscript represents WECs (e.g., 1 is for 1st WEC and 2 is for 2nd WEC in the array system). The compared present numerical results of exciting force amplitude are also in good agreement with analytical results.
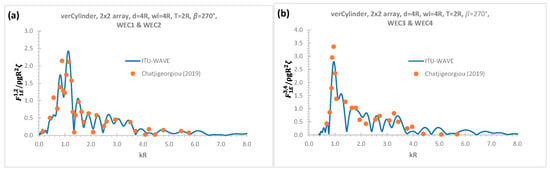
Figure 4.
Nondimensional amplitudes of exciting forces in surge mode [3]; (a) ; (b) .
3.1.3. Mean Interaction Factor
Mean interaction factor of a vertical cylinder with hemisphere bottom of rectangular 2 × 5 arrays at heading angle 90° in heave mode is used to validate ITU-WAVE numerical results against analytical result [28] in Figure 5. The present numerical result and analytical result show satisfactory agreement as observed from Figure 5. The contributions of 1st row (WEC1-WEC5) and 2nd row (WEC6-WEC10) of rectangular 2 × 5 arrays in Figure 5 are presented together with overall mean interaction factor, which is the superposition of 1st and 2nd rows, to show the effects of each row. WECs in the 2nd row is closer to a vertical wall as presented in Figure 1. When mean interaction factors of 1st and 2nd rows of 2 × 5 rectangular arrays are compared, it can be observed in Figure 5 that 2nd row has much better constructive effects due to the nearly trapped waves and wave interactions in the gap of 1st and 2nd rows. The dominant constructive effects happen around the nondimensional resonant frequency of 0.5; however, away from natural frequency, the destructive effects start to become dominant around the nondimensional incident wave frequency of 0.6. When the nondimensional lower and upper frequency ranges are considered, the same amount of wave power which oscillates around = 1.0 is absorbed with isolated WEC and WECs arrays in the lower frequency range up to nondimensional wave frequency of 0.4. However, at the upper frequency range, more wave power is exploited with WECs in 2 × 5 rectangular array system compared to isolated WEC.
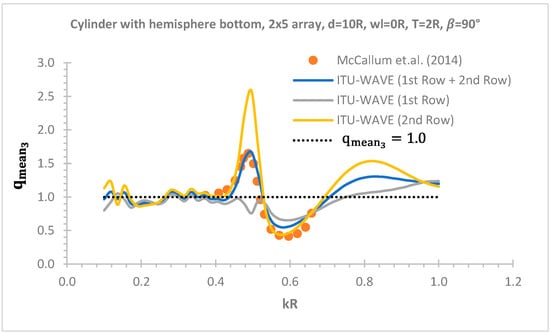
Figure 5.
Mean interaction factor of rectangle 2 × 5 arrays [28].
3.2. Exciting and Radiation Force IRFs
3.2.1. Exciting Force IRFs
The nondimensional exciting force IRFs of 5th row of sphere 5 × 5 arrays with radius R are presented in Figure 6 which shows with and without vertical wall effects. WEC22 and WEC24 as well as WEC21 and WEC25 are symmetric with respect to heading angle 90° and WEC23 is placed at the centre of 5 × 5 array configuration. The symmetric configuration with respect to heading angle 90° of 5th row of WECs in 5 × 5 array system results in the same exciting force IRFs in heave mode for WEC22 and WEC24 as well as WEC21 and WEC25. The area under IRFs represents wave energy implying available wave power that could be absorbed by WECs in an array system. A vertical effect in an array system results in greater bandwidth and amplitudes of IRFs in Figure 6 over a range of time.
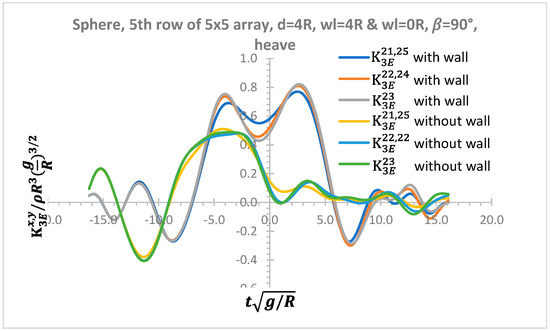
Figure 6.
Nondimensional heave IRF of exciting force for 5th row of 5 × 5 arrays with and without a vertical wall effect.
The effects without and with a vertical wall on exciting force IRFs in Figure 7a,b are presented at the centre of each row of rectangular 3 × 5 sphere arrays in heave mode, respectively. The effects of a vertical breakwater on IRFs of the exciting forces bandwidth are superior to those of without a breakwater effect. This implies that there is more available wave energy to be absorbed with arrays placed in front of a vertical breakwater. It can be also observed from Figure 7b that WEC at the centre of 1st row at heading angle 90° has greater bandwidth compared to WEC at the centre of 3rd row.
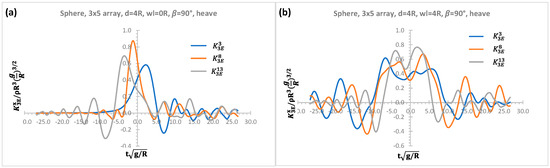
Figure 7.
Nondimensional IRFs of exciting force in heave mode at the centre of each row of 3 × 5 arrays; (a) without a vertical breakwater; (b) with a vertical breakwater.
3.2.2. Radiation Force IRFs
The effects without and with a vertical wall on radiation interaction force IRFs between WEC1 and WECs at the centre of 1st row (WEC3) and 3rd row (WEC13) in Figure 8a,b, respectively, are presented for linear 3 × 5 sphere arrays in heave mode of motion. The amplitudes of the interaction heave IRFs increase over time with increasing separation distances between WECs in an array system in the case of effects of a vertical wall. As pointed out before, the greater amplitudes of radiation IRFs imply more wave energy is stored under the area of the radiation IRFs to be exploited with effects of a vertical wall.
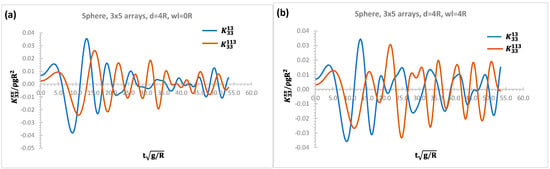
Figure 8.
Nondimensional heave radiation interaction IRFs of 3 × 5 arrays; (a) without a vertical wall; (b) with a vertical wall.
3.3. Response of Each WEC in an Array System—RAOs
The effects of a vertical breakwater on sway and heave RAOs for sphere with linear 1 × 3 arrays at heading angle 90° are presented in Figure 9a,b, respectively. As WECs in 1 × 3 arrays is symmetric with respect to the centre of the coordinates system, heave RAOs () and sway RAOs () are the same. In , subscript represents mode of motion (e.g., 3 is for heave) whilst superscript represents positions of WECs in an array system (e.g., 1, 3 are for WEC1 and WEC3, respectively).
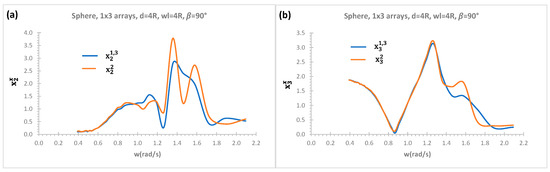
Figure 9.
Effects of a vertical wall on each WEC’s RAO for 1 × 3 arrays of sphere; (a) sway; (b) heave.
RAOs of 1st and 2nd rows in heave and sway modes at incident wave angle 90° for sphere 2 × 3 arrays with effects of a vertical wall are presented in Figure 10a,b for sway mode, and Figure 10c,d for heave mode. In 2 × 3 arrays, 2nd row is closer to vertical wall whilst 1st row meets the incoming wave first at a heading angle of 90°. RAOs in both heave and sway modes have finite resonance conditions over a range of the absolute wave frequencies due to the wave interactions, standing waves, and nearly trapped waves between WECs arrays and a vertical wall in Figure 10. As the some of the trapped wave energy in the gap of the array system is radiated back to sea, these resonances are finite in both heave and sway modes. The standing wave frequencies are the main reason for the stronger excitations of the wave motion in the gap of 2 × 3 array system. In addition, the incident waves could have complete transmission or reflection with a vertical wall at the frequencies of the standing waves and wave motion is resonant in the gap [29,30]. The effects of standing waves, wave motion, and nearly trapped waves in the gap can be observed in both sway and heave mode RAOs in 2nd row as the amplitude of 2nd row of RAOs, which is closer to a vertical breakwater, in Figure 10b,d are greater compared to 1st row RAOs in Figure 10a,c, respectively, although it is not much greater compared to heave mode. The 1st row RAOs of WEC1 and WEC3 have equal amplitudes due to symmetric configurations of WECs with respect to the centre of the coordinate system in both sway () and heave () modes in Figure 10a,c, respectively, whilst 2nd row RAOs of WEC4 and WEC6 are the same again due to the same symmetric condition in both sway () and heave () modes in Figure 10b,d, respectively.
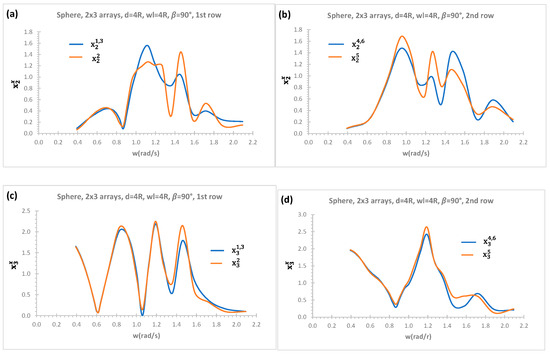
Figure 10.
Effects of a vertical wall on each WEC’s RAO for 2 × 3 arrays of sphere; (a) 1st row sway; (b) 2nd row sway; (c) 1st row heave; (d) 2nd row heave.
3.4. Wave Power Absorption with 2 × 3 Arrays
Figure 11 represents the effect of the incident wave angle 90° on RAOs (, ) in Figure 11a and absorbed wave power (, ) in Figure 11b for the isolated WEC in sway and heave modes. In and , subscripts represent mode of motion (e.g., 2 is used for sway mode). It is known that the hydrostatic restoring force coefficient in sway mode does not exist for floating systems. Assuming PTO restoring force coefficient of sway mode equals that of heave mode in the present study. If the restoring force coefficients are the same in sway and heave modes, this implies that the floating system of an isolated sphere WEC will have the same displacements and its hydrodynamic performances can be directly compared to determine which mode of motion perform better for absorbed wave power. When the natural frequency of floating system of an isolated sphere WEC ( rad/s, kR = 0.194) and incident wave frequency equal each other, the floating system is in resonance conditions at which the maximum wave power is absorbed, as shown in the present numerical study in Figure 11b and theoretical studies [23]. When the performances of an isolated sphere WEC in sway and heave modes are compared, it can be observed from Figure 11b that sway mode shows better performance at around resonant frequency region and higher incident wave frequency range whilst mode of heave shows better performances in lower frequency ranges in which swell waves are present implying more wave power are available to be absorbed at this lower frequency range.
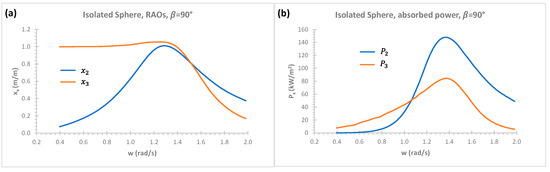
Figure 11.
Heave and sway modes of isolated sphere; (a) , ; (b) .
Figure 12a,b in heave and sway modes with vertical wall effect represent the absorbed wave power with sphere 2 × 3 arrays at heading angle 90°. The contribution from 1st row, 2nd row and overall wave power absorption, which is obtained with the superposition of 1st and 2nd rows of sphere 2 × 3 arrays, is also presented in sway and heave modes in Figure 12a,b, respectively. The absorbed wave power in sway mode is given with respect to absolute incident wave frequency and has wider bandwidth in Figure 12a whilst the wave power absorption in Figure 12b is mostly concentrated around absolute wave frequency of rad/s (kR = 0.147) in heave mode for 2nd row. The wave power in sway mode at lower incident wave frequency performs better compared to heave mode. Maximum wave power absorption from 1st and 2nd rows is mixed in heave mode in Figure 12b. The performance of 1st row are distributed over incident wave frequencies whilst 2nd row generates more wave power at resonant frequency region in heave mode in Figure 12b. The wave power absorption has wider absorption bandwidth with both 1st and 2nd rows in sway mode.
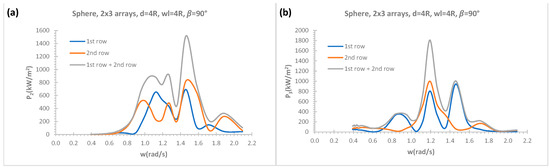
Figure 12.
Effects of a vertical wall with 2 × 3 arrays on wave power absorption; (a) (b) .
3.5. Effects of a Vertical Wall on Mean Interaction Factors
Figure 13a,b present mean interaction factors of 2 × 3 and 3 × 3 arrays with separation distance between WECs 4R for each row in heave mode at heading angle 90° discarding the effect of a vertical wall. The incident wave meets the 1st row first at heading angle 90°. The constructive effects for WECs arrays are dominant with increasing row numbers as it can be observed in 2nd row of 2 × 3 arrays in Figure 13a and 3rd row of 3 × 3 arrays in Figure 13b. When the row numbers are increased, whilst keeping column number the same in an array system, the destructive effects become more dominant at lower row numbers at higher absolute wave frequency. This can be observed when the mean interaction factor of 1st row of 2 × 3 arrays in Figure 13a are compared with those of 1st row of 3 × 3 arrays in Figure 13b.
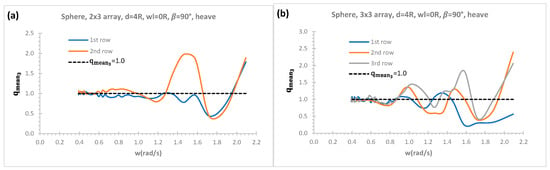
Figure 13.
Heave mean interaction factors of each row without a vertical wall effect; (a) 2 × 3; (b) 3 × 3 arrays.
The effects of a vertical breakwater on mean interaction factors in heave mode at heading angle 90° in Figure 14a,b are presented for sphere 2 × 3 arrays and 3 × 3 arrays, respectively, which are the same configurations that are considered in Figure 13a,b without a vertical wall effect. In the case of rectangular sphere 2 × 3 arrays, 2nd row is closer to a vertical wall whilst it is 3rd row in the case of square 3 × 3 arrays. The 1st row in Figure 14a,b shows mixed constructive and destructive effects in a range of incident wave frequencies. However, WECs closer to vertical breakwater, which is 2nd row in Figure 14a and 3rd row in Figure 14b, show different behaviours as the dominant mean interaction factors in both 2 × 3 and 3 × 3 arrays configurations are at around incident wave frequency of (kR = 0.147) whilst they show mixed of constructive and destructive effects at lower and higher incident wave frequencies range. When the effects of a vertical wall on the amplitudes of mean interaction factors in Figure 13a and Figure 14a for 2 × 3 arrays as well as Figure 13b and Figure 14b for 3 × 3 arrays are compared, it can be observed that a vertical breakwater has greater effects on the amplitudes of mean interaction factor in Figure 14a,b over those without vertical breakwater effect in Figure 13a,b. This implies that more wave power is available to be absorbed in the case of WECs arrays with a vertical breakwater.
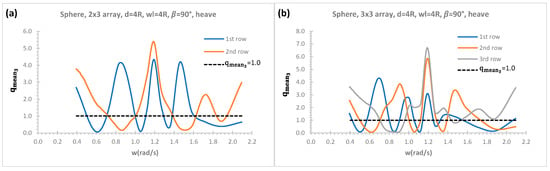
Figure 14.
Effects of a vertical wall on heave mean interaction factors of each row; (a) 2 × 3 arrays; (b) 3 × 3 arrays.
Figure 15a,b are used to present heave mean interaction factors at heading angle 90° with respect to absolute wave frequencies for 1 × 3, 3 × 3, 5 × 3 arrays keeping column constant and increasing row numbers without and with the effects of a vertical wall, respectively. Sphere 1 × 3 array shows significant constructive effect around absolute wave frequencies of 1.2–1.6 rad/s compared to other configurations in Figure 15a in the case of without a vertical wall effect. Mean interaction factor oscillates around 1 up to 1.2 rad/s implying wave power absorption with N number of interacted arrays and isolated N number of WEC are approximately the same. When the row numbers are increased keeping the column number constant, there are a mix of constructive and destructive effects with 3 × 3 arrays as the constructive effects are dominant at lower incident wave frequencies which has more wave power to be absorbed with WECs. It can be observed that 5 × 3 arrays do not show constructive effect with respect to absolute wave frequencies after absolute wave frequency of 1.1 rad/s (kR = 0.123) in Figure 15a, although it has considerably high constructive effects at lower wave frequencies. The effects of a vertical wall on all array configurations show dominant constructive effects with respect to absolute wave frequencies in Figure 15b. The arrays of 1 × 3, 3 × 3 in Figure 15b show considerably higher constructive effects around 1.2 rad/s (kR = 0.147) and mean interaction factor reaches up to between 4 and 5 whilst 5 × 3 array also has significant constructive effect in a range of incident wave frequencies. However, when the row numbers are increased, although arrays show the constructive effect, the magnitude of mean interaction factors are considerably reduced (e.g., 5 × 3 arrays) in Figure 15b. When mean interaction factor without and with the influence of a vertical wall in Figure 15a,b are compared, the constructive effects due to a vertical breakwater effect show significantly higher superiority over without a vertical effect with respect to absolute wave frequencies especially lower and mid-range of absolute wave frequencies.
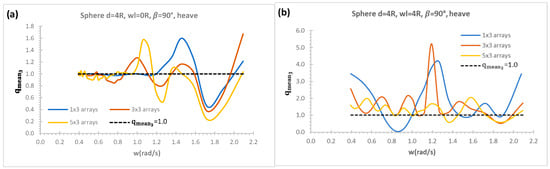
Figure 15.
Heave mean interaction factors in a range of row numbers; (a) without a vertical wall; (b) with a vertical wall.
4. Conclusions
The transient in-house computational tool ITU-WAVE, which has a wide range of applications for wave-multibody interactions of floating systems of rigid and elastic isolated or array configurations, is used to predict absorbed wave power with and without a vertical wall effect to determine the behaviours of WECs in an array system. The radiation and exciting IRFs, which are directly calculated in time domain with the time marching of boundary integral equation method and method of images, are used to approximate the absorbed wave power due to the superpositions of wave power from the radiation and exciting forces.
The absorbed wave power is significantly improved and increased with effects of a vertical wall which enhances the absorption considerably. The enhancements of wave power absorption results from the wave motion, standing waves, and nearly trapped waves between WECs arrays and a vertical wall as well as between WECs in an array system. The numerical analyses show that the influence of a vertical wall increases the wave power absorption considerably, being approximately 2.5-times greater than those without vertical wall effect at around absolute wave frequency of 1.2 rad/s (kR = 0.147). In addition, the constructive effects are dominant at lower- and mid-range incident wave frequencies.
The numerical results of the present in-house ITU-WAVE are validated against analytical and other numerical results for interaction and diagonal added mass, and damping coefficients with 1 × 5 WECs arrays of truncated vertical cylinder, exciting force amplitudes with 2 × 2 WECs arrays of truncated vertical cylinder, and mean interaction factor with 2 × 5 WECs arrays of vertical cylinder with hemisphere bottom. The comparison of the present numerical results of ITU-WAVE with analytical and other numerical results shows satisfactory agreements.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data is contained within the article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kara, F. Time domain prediction of power absorption from ocean waves with wave energy converters arrays. Renew. Energy 2016, 92, 30–46. [Google Scholar] [CrossRef]
- Kara, F. Effects of a vertical wall on wave power absorption with wave energy converters arrays. Renew. Energy 2022, 196, 812–823. [Google Scholar] [CrossRef]
- Chatjigeorgiou, I.K. Semi-analytical solution for the water wave diffraction by arrays of truncated circular cylinders in front of a vertical wall. Appl. Ocean. Res. 2019, 88, 147–159. [Google Scholar] [CrossRef]
- Mustapa, M.A.; Yaakob, O.B.; Ahmed, Y.M.; Rheem, C.-K.; Koh, K.K.; Adnan, F.A. Wave energy device and breakwater integration: A review. Renew. Sustain. Energy Rev. 2017, 77, 43–58. [Google Scholar] [CrossRef]
- Ning, D.Z.; Zhao, X.L.; Goteman, M.; Kang, H.G. Hydrodynamic performance of a pile-restrained WEC-type floating breakwater: An experimental study. Renew Energy 2016, 95, 531–541. [Google Scholar] [CrossRef]
- Zhao, X.L.; Ning, D.Z.; Liang, D.F. Experimental investigation on hydrodynamic performance of a breakwater integrated WEC system. Ocean. Eng. 2019, 171, 25–32. [Google Scholar] [CrossRef]
- Loukogeorgaki, E.; Boufidi, I.; Chatjigeorgiou, I.K. Performance of an array of oblate spheroidal heaving wave energy converters in front of a wall. Water 2020, 12, 188. [Google Scholar] [CrossRef]
- Schay, J.; Bhattacharjee, J.; Soares, C.G. Numerical Modelling of a Heaving Point Absorber in front of a Vertical Wall. In Proceedings of the ASME 32nd International Conference on Ocean, Offshore and Arctic Engineering, Nantes, France, 9–14 June 2013. [Google Scholar]
- Newman, J.N. Channel wall effects in radiation-diffraction analysis. In Proceedings of the 31st International Workshop on Water Waves and Floating Bodies, Plymouth, MI, USA, 3–6 April 2016. [Google Scholar]
- Konispoliatis, D.N.; Mavrakos, S.A.; Katsaounis, G.M. Theoretical evaluation of the hydrodynamic characteristics of arrays of vertical axisymmetric floaters of arbitrary shape in front of a vertical breakwater. J. Mar. Sci. Eng. 2020, 8, 62. [Google Scholar] [CrossRef]
- Kring, D.C.; Sclavounos, P.D. Numerical stability analysis for time-domain ship motion simulations. J. Ship Res. 1995, 39, 313–320. [Google Scholar]
- Nakos, D.; Kring, D.; Sclavounos, P.D. Rankine Panel Method for Transient Free Surface Flows. In Proceedings of the 6th International Symposium on Numerical Hydrodynamics, Iowa City, IA, USA, 2–5 August 1993; pp. 613–632. [Google Scholar]
- Kara, F. Hydroelastic behaviour and analysis of marine structures. J. Sustain. Mar. Struct. 2021, 2, 14–24. [Google Scholar] [CrossRef]
- Chang, M.S. Computation of Three-Dimensional Ship Motions with Forward Speed. In Proceedings of the 2nd International Symposium on Numerical Ship Hydrodynamics, University of California, Berkeley, CA, USA; 1977; pp. 124–135. Available online: https://www.scribd.com/document/268162212/ADA169794-Second-International-Conference-on-Numerical-Ship-Hydrodynamics-September-1977-University-of-California-Berkeley (accessed on 27 July 2024).
- Budal, K. Theory for absorption of wave power by a system of interacting bodies. J. Ship Res. 1977, 21, 248–253. [Google Scholar] [CrossRef]
- Ohkusu, M. Wave action on groups of vertical circular cylinders. J. Soc. Nav. Archit. Jpn. 1972, 131, 53–64. [Google Scholar] [CrossRef]
- Kagemoto, H.; Yue, D.K.P. Interactions among multiple three-dimensional bodies in water waves: An exact algebraic method. J. Fluid Mech. 1986, 166, 189–209. [Google Scholar] [CrossRef]
- Kara, F. Coupled dynamic analysis of horizontal axis floating offshore wind turbines with a spar buoy floater. Wind. Eng. 2023, 47, 607–626. [Google Scholar] [CrossRef]
- Kara, F. Time domain potential and source methods and their application to twin-hull high speed crafts. Ships Offshore Struct. 2023, 18, 191–204. [Google Scholar] [CrossRef]
- Cummins, W.E. The Impulse response function and ship motions. Shiffstechnik 1962, 9, 101–109. [Google Scholar]
- Ogilvie, T.F. Recent progress toward the understanding and prediction of ship motions. In Proceedings of the 5th Symposium on Naval Hydrodynamics, Office of Naval Research, Washington, DC, USA, 12 July 1964; pp. 3–128. [Google Scholar]
- King, B.W. Time Domain Analysis Of Wave Exciting Forces on Ships and Bodies. Ph.D. Thesis, The University of Michigan, Ann Arbor, MI, USA, 1987. [Google Scholar]
- Budal, K.; Falnes, J. Optimum Operation of Wave Power Converter; Internal Report; Norwegian University of Science and Technology: Trondheim, Norway, 1976. [Google Scholar]
- Thomas, G.P.; Evans, D.V. Arrays of three-dimensional wave-energy absorbers. J. Fluid Mech. 1981, 108, 67–88. [Google Scholar] [CrossRef]
- Wehausen, J.V.; Laitone, E.V. Surface Waves in Fluid Dynamics III in Handbuch der Physik 1960. Chapter 3. pp. 446–778. Available online: https://folk.ntnu.no/falnes/w_e/rpts_scnnd/1976greenbook.pdf (accessed on 27 July 2024).
- Hess, J.L.; Smith, A.M.O. Calculation of non-lifting potential flow about arbitrary three-dimensional bodies. J. Ship Res. 1964, 8, 22–44. [Google Scholar] [CrossRef]
- Liapis, S. Time Domain Analysis of Ship Motions. PhD thesis, The University of Michigan, Ann Arbor, MI, USA, 1986. [Google Scholar]
- McCallum, P.; Venugopal, V.; Forehand, D.; Sykes, R. On the performance of an array of floating wave energy converters for different water depths. In Proceedings of the ASME, 33rd International Conference on Ocean, Offshore and Arctic Engineering, San Francisco, CA, USA, 8–13 June 2014. [Google Scholar]
- Newman, J.N. Interactions of water waves with two closely spaced vertical obstacles. J. Fluid Mech. 1974, 66, 97–106. [Google Scholar] [CrossRef]
- Evans, D.V. A note on the total reflection or transmission of surface waves in the presence of parallel obstacles. J. Fluid Mech. 1975, 67, 465–472. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).