Development of a Spectrum-Based Scheme for Simulating Fine-Grained Sediment Transport in Estuaries
Abstract
1. Introduction
2. Methods
2.1. A Size-Resolved Flocculation Module
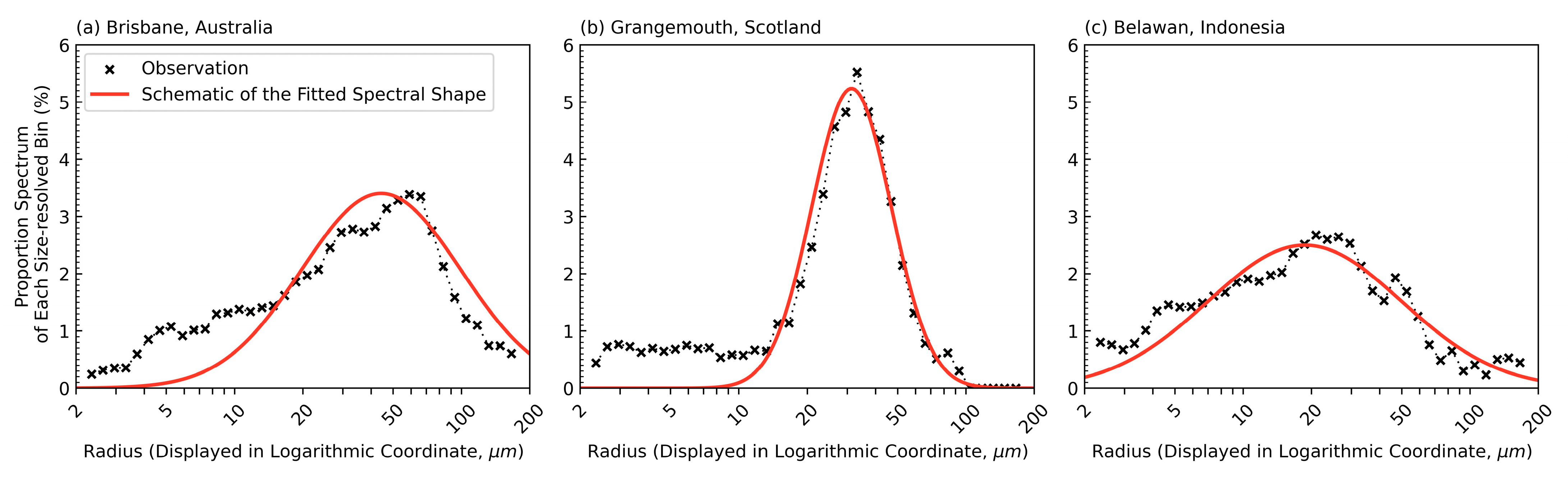
2.2. Spectrum-Based Scheme
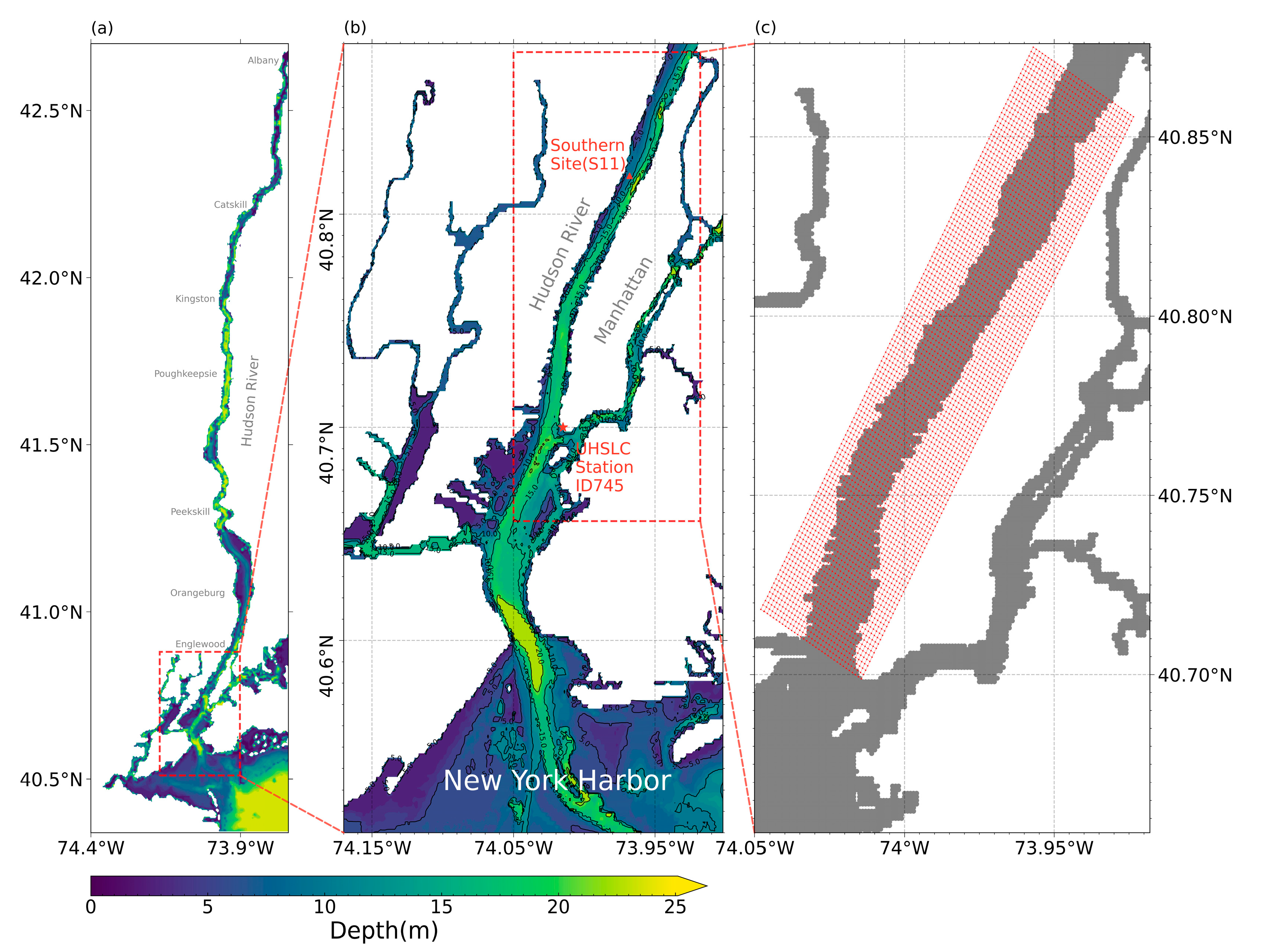
3. Numerical Experiments of the Hudson River Estuary
3.1. Model Setup
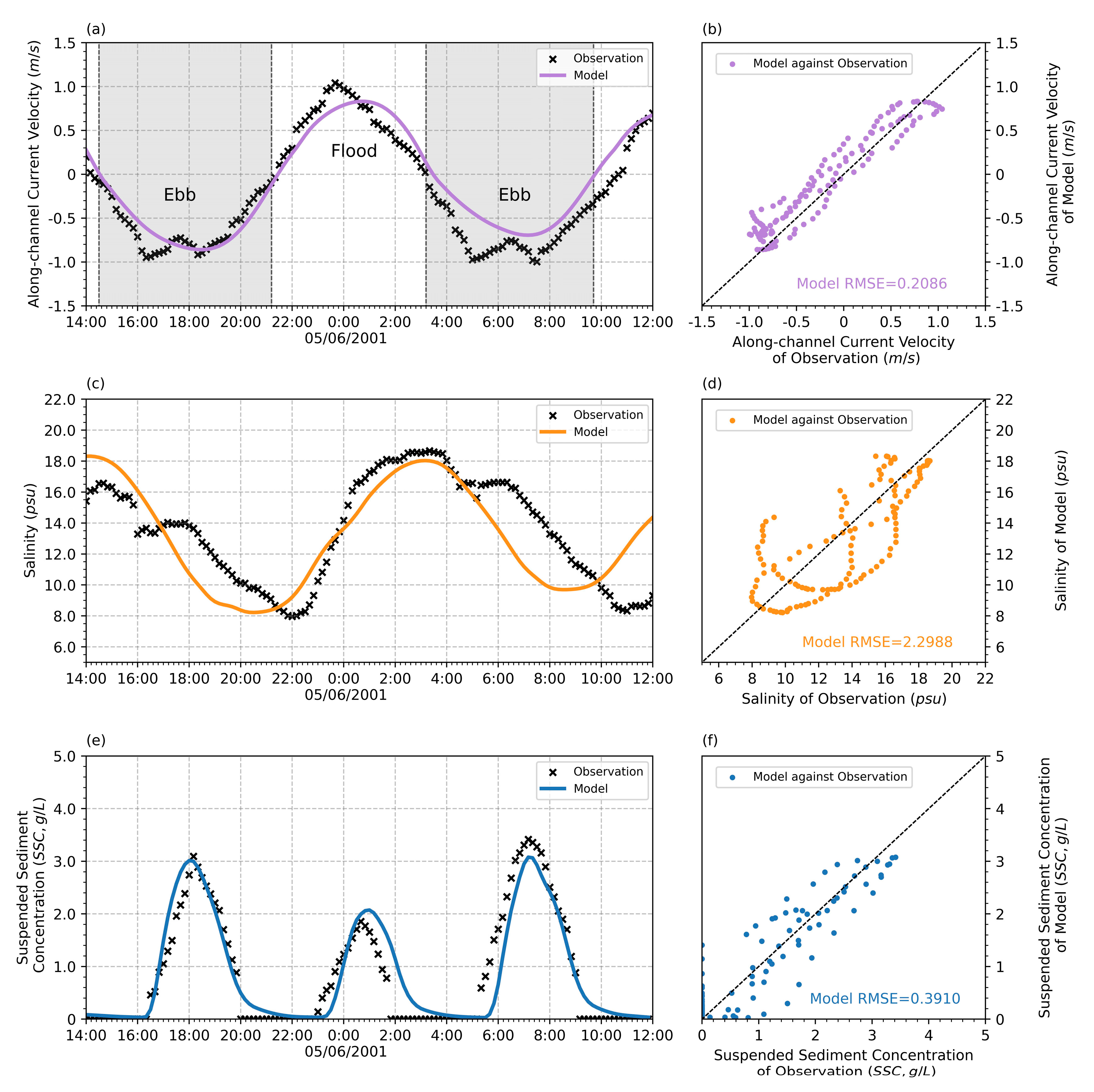
3.2. Validation of Salinity, Current Velocity, SSC, and Tides
4. Assessment of the Spectrum-Based Scheme
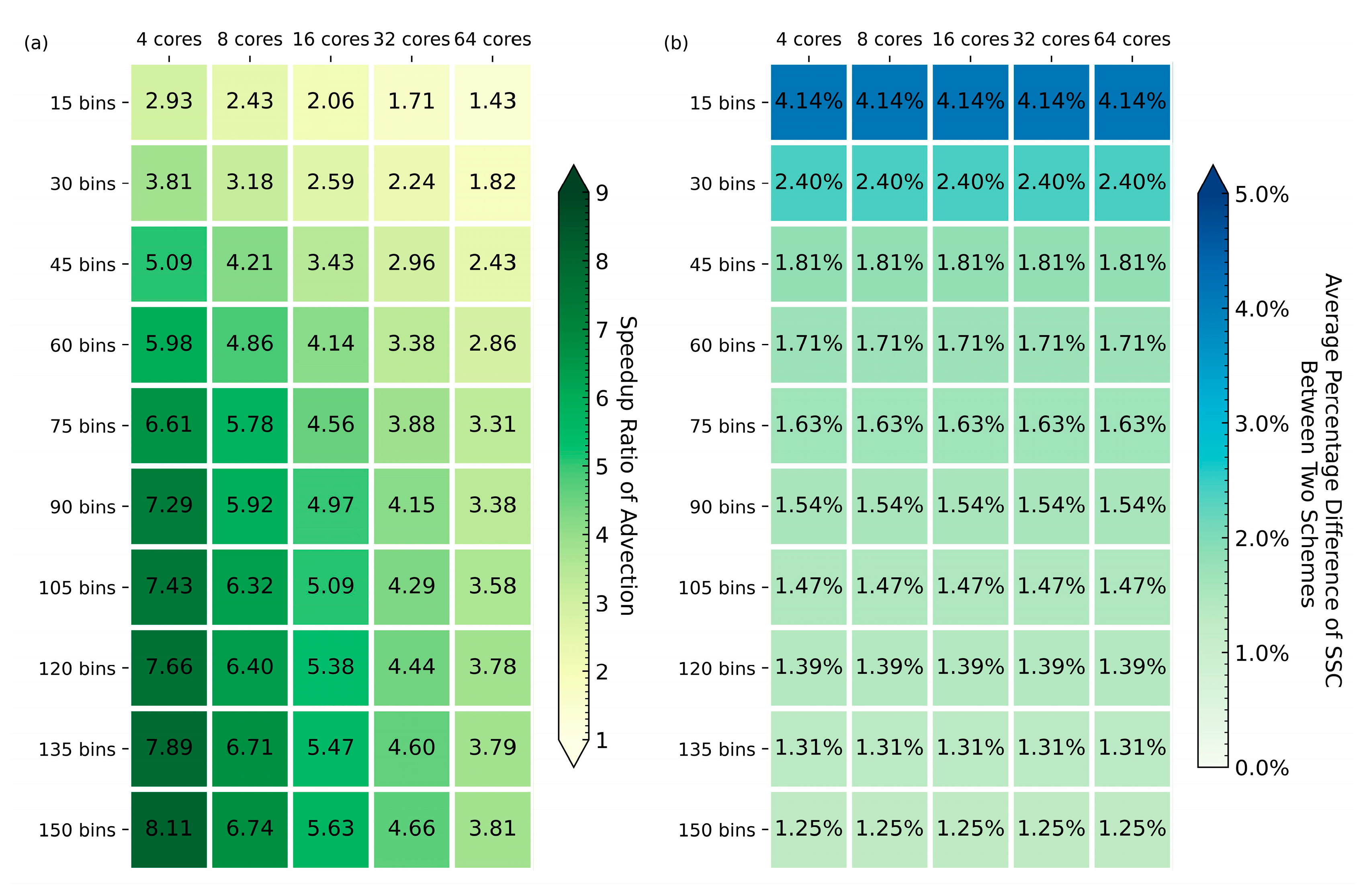
4.1. Comparison of SSC between the Bin-Based Scheme and the Spectrum-Based Scheme
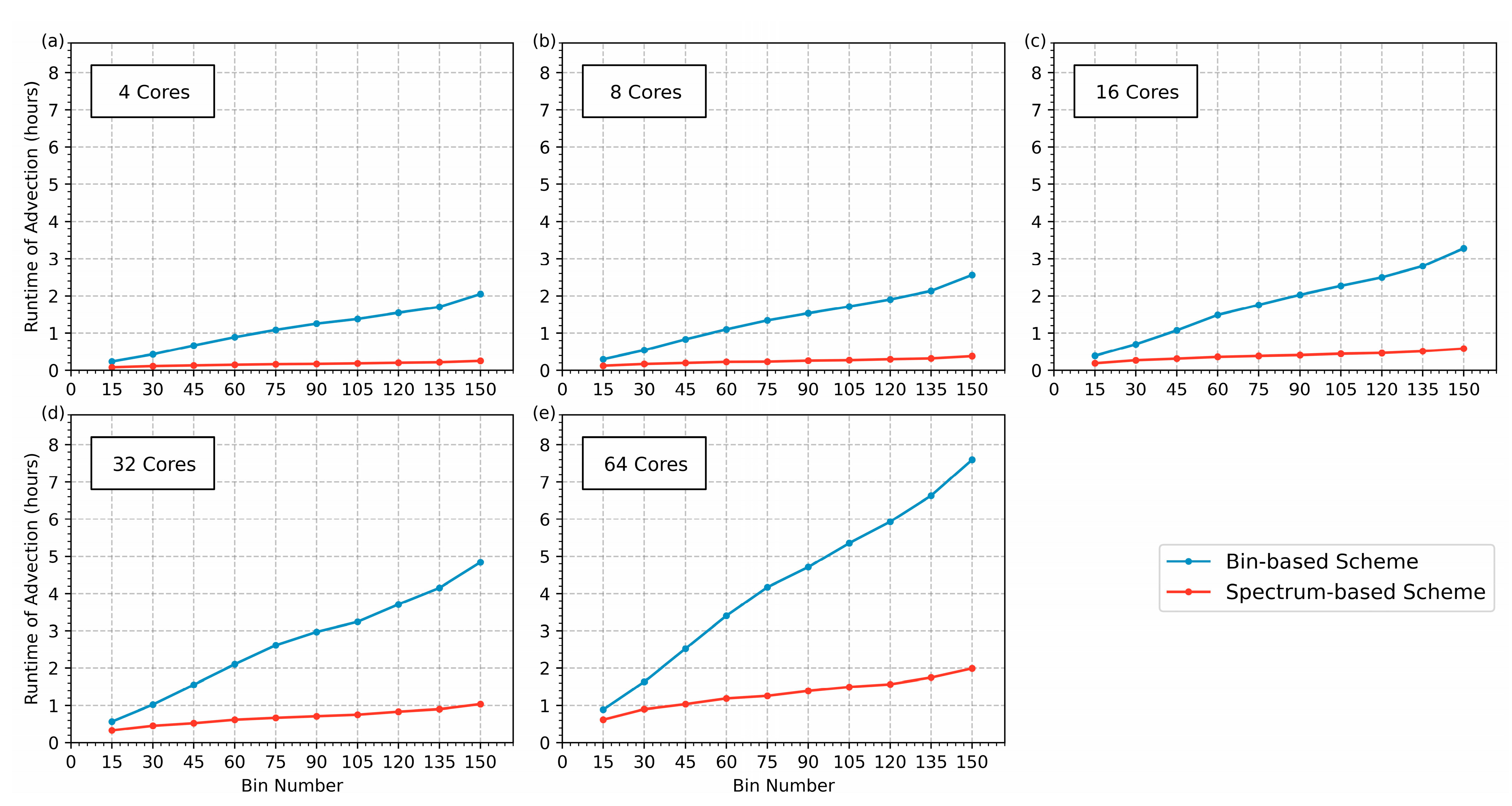
4.2. Evaluation of the Runtime of the Spectrum-Based Scheme
5. Conclusions and Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Table of the Setup
| Experiment | Bin Number | Core Number | New Scheme | Experiment | Bin Number | Core Number | New Scheme |
|---|---|---|---|---|---|---|---|
| Exp00 | 30 | 4 | Off | Exp50 | 90 | 4 | Off |
| Exp01 | 30 | 4 | On | Exp51 | 90 | 4 | On |
| Exp02 | 30 | 8 | Off | Exp52 | 90 | 8 | Off |
| Exp03 | 30 | 8 | On | Exp53 | 90 | 8 | On |
| Exp04 | 30 | 16 | Off | Exp54 | 90 | 16 | Off |
| Exp05 | 30 | 16 | On | Exp55 | 90 | 16 | On |
| Exp06 | 30 | 32 | Off | Exp56 | 90 | 32 | Off |
| Exp07 | 30 | 32 | On | Exp57 | 90 | 32 | On |
| Exp08 | 30 | 64 | Off | Exp58 | 90 | 64 | Off |
| Exp09 | 30 | 64 | On | Exp59 | 90 | 64 | On |
| Exp10 | 15 | 4 | Off | Exp60 | 105 | 4 | Off |
| Exp11 | 15 | 4 | On | Exp61 | 105 | 4 | On |
| Exp12 | 15 | 8 | Off | Exp62 | 105 | 8 | Off |
| Exp13 | 15 | 8 | On | Exp63 | 105 | 8 | On |
| Exp14 | 15 | 16 | Off | Exp64 | 105 | 16 | Off |
| Exp15 | 15 | 16 | On | Exp65 | 105 | 16 | On |
| Exp16 | 15 | 32 | Off | Exp66 | 105 | 32 | Off |
| Exp17 | 15 | 32 | On | Exp67 | 105 | 32 | On |
| Exp18 | 15 | 64 | Off | Exp68 | 105 | 64 | Off |
| Exp19 | 15 | 64 | On | Exp69 | 105 | 64 | On |
| Exp20 | 45 | 4 | Off | Exp70 | 120 | 4 | Off |
| Exp21 | 45 | 4 | On | Exp71 | 120 | 4 | On |
| Exp22 | 45 | 8 | Off | Exp72 | 120 | 8 | Off |
| Exp23 | 45 | 8 | On | Exp73 | 120 | 8 | On |
| Exp24 | 45 | 16 | Off | Exp74 | 120 | 16 | Off |
| Exp25 | 45 | 16 | On | Exp75 | 120 | 16 | On |
| Exp26 | 45 | 32 | Off | Exp76 | 120 | 32 | Off |
| Exp27 | 45 | 32 | On | Exp77 | 120 | 32 | On |
| Exp28 | 45 | 64 | Off | Exp78 | 120 | 64 | Off |
| Exp29 | 45 | 64 | On | Exp79 | 120 | 64 | On |
| Exp30 | 60 | 4 | Off | Exp80 | 135 | 4 | Off |
| Exp31 | 60 | 4 | On | Exp81 | 135 | 4 | On |
| Exp32 | 60 | 8 | Off | Exp82 | 135 | 8 | Off |
| Exp33 | 60 | 8 | On | Exp83 | 135 | 8 | On |
| Exp34 | 60 | 16 | Off | Exp84 | 135 | 16 | Off |
| Exp35 | 60 | 16 | On | Exp85 | 135 | 16 | On |
| Exp36 | 60 | 32 | Off | Exp86 | 135 | 32 | Off |
| Exp37 | 60 | 32 | On | Exp87 | 135 | 32 | On |
| Exp38 | 60 | 64 | Off | Exp88 | 135 | 64 | Off |
| Exp39 | 60 | 64 | On | Exp89 | 135 | 64 | On |
| Exp40 | 75 | 4 | Off | Exp90 | 150 | 4 | Off |
| Exp41 | 75 | 4 | On | Exp91 | 150 | 4 | On |
| Exp42 | 75 | 8 | Off | Exp92 | 150 | 8 | Off |
| Exp43 | 75 | 8 | On | Exp93 | 150 | 8 | On |
| Exp44 | 75 | 16 | Off | Exp94 | 150 | 16 | Off |
| Exp45 | 75 | 16 | On | Exp95 | 150 | 16 | On |
| Exp46 | 75 | 32 | Off | Exp96 | 150 | 32 | Off |
| Exp47 | 75 | 32 | On | Exp97 | 150 | 32 | On |
| Exp48 | 75 | 64 | Off | Exp98 | 150 | 64 | Off |
| Exp49 | 75 | 64 | On | Exp99 | 150 | 64 | On |
Appendix B. Derivation for Method of Moments to the Normal Distribution
- Step 1: Calculate the masswhere is the SSC density function of bin is the total bin number, and is the bin interval width in logarithmic coordinates. The mass will be used in the denominator to fit the probability density function of the normal distribution:
- Step 2: Calculate the meanThe following is the estimator of the mean , calculated as:
- Step 3: Calculate the varianceThe following is the estimator of the variance , calculated as:
- Step 4: Fit the normal distribution
References
- Elliott, M.; Whitfield, A.K. Challenging paradigms in estuarine ecology and management. Estuar. Coast. Shelf Sci. 2011, 94, 306–314. [Google Scholar] [CrossRef]
- Thrush, S.F.; Townsend, M.; Hewitt, J.E.; Davies, K.; Lohrer, A.M.; Lundquist, C.; Cartner, K.; Dymond, J. The many uses and values of estuarine ecosystems. In Ecosystem Services in New Zealand–Conditions Trends; Manaaki Whenua Press: Lincoln, New Zealand, 2013; pp. 226–237. [Google Scholar]
- Hoque, M.Z.; Cui, S.; Islam, I.; Xu, L.; Tang, J. Future impact of land use/land cover changes on ecosystem services in the lower meghna river estuary, Bangladesh. Sustainability 2020, 12, 2112. [Google Scholar] [CrossRef]
- Rakib, M.R.J.; Hossain, M.B.; Kumar, R.; Ullah, M.A.; Al Nahian, S.; Rima, N.N.; Choudhury, T.R.; Liba, S.I.; Yu, J.; Khandaker, M.U. Spatial distribution and risk assessments due to the microplastics pollution in sediments of Karnaphuli River Estuary, Bangladesh. Sci. Rep. 2022, 12, 8581. [Google Scholar] [CrossRef]
- Wang, Z.; Lin, K.; Liu, X. Distribution and pollution risk assessment of heavy metals in the surface sediment of the intertidal zones of the Yellow River Estuary, China. Mar. Pollut. Bull. 2022, 174, 113286. [Google Scholar] [CrossRef]
- Ballagh, F.E.A.; Rabouille, C.; Andrieux-Loyer, F.; Soetaert, K.; Elkalay, K.; Khalil, K. Spatio-temporal dynamics of sedimentary phosphorus along two temperate eutrophic estuaries: A data-modelling approach. Cont. Shelf Res. 2020, 193, 104037. [Google Scholar] [CrossRef]
- Ho, Q.N.; Fettweis, M.; Spencer, K.L.; Lee, B.J. Flocculation with heterogeneous composition in water environments: A review. Water Res. 2022, 213, 118147. [Google Scholar] [CrossRef] [PubMed]
- Zhao, C.; Zhou, J.; Yan, Y.; Yang, L.; Xing, G.; Li, H.; Wu, P.; Wang, M.; Zheng, H. Application of coagulation/flocculation in oily wastewater treatment: A review. Sci. Total Environ. 2021, 765, 142795. [Google Scholar] [CrossRef] [PubMed]
- Vercruysse, K.; Grabowski, R.C.; Rickson, R.J. Suspended sediment transport dynamics in rivers: Multi-scale drivers of temporal variation. Earth-Sci. Rev. 2017, 166, 38–52. [Google Scholar] [CrossRef]
- Burchard, H.; Schuttelaars, H.M.; Ralston, D.K. Sediment trapping in estuaries. Annu. Rev. Mar. Sci. 2018, 10, 371–395. [Google Scholar] [CrossRef]
- Choi, Y.E.; Oh, C.-O.; Chon, J. Applying the resilience principles for sustainable ecotourism development: A case study of the Nakdong Estuary, South Korea. Tour. Manag. 2021, 83, 104237. [Google Scholar] [CrossRef]
- Mitchell, S. Turbidity maxima in four macrotidal estuaries. Ocean Coast. Manag. 2013, 79, 62–69. [Google Scholar] [CrossRef]
- McManus, J. Salinity and suspended matter variations in the Tay estuary. Cont. Shelf Res. 2005, 25, 729–747. [Google Scholar] [CrossRef]
- Wang, H.; Yang, Z.; Li, Y.; Guo, Z.; Sun, X.; Wang, Y. Dispersal pattern of suspended sediment in the shear frontal zone off the Huanghe (Yellow River) mouth. Cont. Shelf Res. 2007, 27, 854–871. [Google Scholar] [CrossRef]
- McAnally, W.H.; Friedrichs, C.; Hamilton, D.; Hayter, E.; Shrestha, P.; Rodriguez, H.; Sheremet, A.; Teeter, A.; Mud, A.T.C.o.M.o.F. Management of fluid mud in estuaries, bays, and lakes. I: Present state of understanding on character and behavior. J. Hydraul. Eng. 2007, 133, 9–22. [Google Scholar] [CrossRef]
- Winterwerp, J.; Kranenburg, C. Erosion of fluid mud layers. II: Experiments and model validation. J. Hydraul. Eng. 1997, 123, 512–519. [Google Scholar] [CrossRef]
- Manning, A.; Langston, W.; Jonas, P. A review of sediment dynamics in the Severn Estuary: Influence of flocculation. Mar. Pollut. Bull. 2010, 61, 37–51. [Google Scholar] [CrossRef] [PubMed]
- Partheniades, E. A fundamental framework for cohesive sediment dynamics. Estuar. Cohesive Sediment Dyn. 1986, 14, 219–250. [Google Scholar] [CrossRef]
- Meakin, P. Formation of fractal clusters and networks by irreversible diffusion-limited aggregation. Phys. Rev. Lett. 1983, 51, 1119. [Google Scholar] [CrossRef]
- Ladd, A.J.; Verberg, R. Lattice-Boltzmann simulations of particle-fluid suspensions. J. Stat. Phys. 2001, 104, 1191–1251. [Google Scholar] [CrossRef]
- Teisson, C. Cohesive suspended sediment transport: Feasibility and limitations of numerical modeling. J. Hydraul. Res. 1991, 29, 755–769. [Google Scholar] [CrossRef]
- Krishnappan, B.G. Review of a semi-empirical modelling approach for cohesive sediment transport in river systems. Water 2022, 14, 256. [Google Scholar] [CrossRef]
- Nicholson, J.; O’Connor, B.A. Cohesive sediment transport model. J. Hydraul. Eng. 1986, 112, 621–640. [Google Scholar] [CrossRef]
- Xu, F.; Wang, D.-P.; Riemer, N. Modeling flocculation processes of fine-grained particles using a size-resolved method: Comparison with published laboratory experiments. Cont. Shelf Res. 2008, 28, 2668–2677. [Google Scholar] [CrossRef]
- Sherwood, C.R.; Aretxabaleta, A.L.; Harris, C.K.; Rinehimer, J.P.; Verney, R.; Ferré, B. Cohesive and mixed sediment in the regional ocean modeling system (ROMS v3. 6) implemented in the Coupled Ocean–Atmosphere–Wave–Sediment Transport Modeling System (COAWST r1234). Geosci. Model Dev. 2018, 11, 1849–1871. [Google Scholar] [CrossRef]
- Verney, R.; Lafite, R.; Brun-Cottan, J.C.; Le Hir, P. Behaviour of a floc population during a tidal cycle: Laboratory experiments and numerical modelling. Cont. Shelf Res. 2011, 31, S64–S83. [Google Scholar] [CrossRef]
- Teh, C.Y.; Budiman, P.M.; Shak, K.P.Y.; Wu, T.Y. Recent advancement of coagulation–flocculation and its application in wastewater treatment. Ind. Eng. Chem. Res. 2016, 55, 4363–4389. [Google Scholar] [CrossRef]
- Liu, J.; Liang, J.H.; Xu, K.; Chen, Q.; Ozdemir, C.E. Modeling sediment flocculation in Langmuir turbulence. J. Geophys. Res. Ocean. 2019, 124, 7883–7907. [Google Scholar] [CrossRef]
- Tarpley, D.R.; Harris, C.K.; Friedrichs, C.T.; Sherwood, C.R. Tidal variation in cohesive sediment distribution and sensitivity to flocculation and bed consolidation in an idealized, partially mixed estuary. J. Mar. Sci. Eng. 2019, 7, 334. [Google Scholar] [CrossRef]
- Figueroa, S.M.; Lee, G.h.; Chang, J.; Jung, N.W. Impact of estuarine dams on the estuarine parameter space and sediment flux decomposition: Idealized numerical modeling study. J. Geophys. Res. Ocean. 2022, 127, e2021JC017829. [Google Scholar] [CrossRef]
- Bott, A. A flux method for the numerical solution of the stochastic collection equation. J. Atmos. Sci. 1998, 55, 2284–2293. [Google Scholar] [CrossRef]
- Thorn, M. 6 Physical processes of siltation in tidal channels. In Hydraulic Modelling in Maritime Engineering; Thomas Telford Publishing: London, UK, 1982; pp. 65–73. [Google Scholar]
- Traykovski, P.; Geyer, R.; Sommerfield, C. Rapid sediment deposition and fine-scale strata formation in the Hudson estuary. J. Geophys. Res. Earth Surf. 2004, 109, F02004. [Google Scholar] [CrossRef]
- Xu, F.; Wang, D.-P.; Riemer, N. An idealized model study of flocculation on sediment trapping in an estuarine turbidity maximum. Cont. Shelf Res. 2010, 30, 1314–1323. [Google Scholar] [CrossRef]
- Smoluchowski, M. Mathematical theory of the kinetics of the coagulation of colloidal solutions. Z. Phys. Chem. 1917, 92, 129–168. [Google Scholar]
- Burd, A.; Jackson, G. Predicting particle coagulation and sedimentation rates for a pulsed input. J. Geophys. Res. Ocean. 1997, 102, 10545–10561. [Google Scholar] [CrossRef]
- Maggi, F. Flocculation Dynamics of Cohesive Sediment; Faculty of Civil Engineering and Geosciences, Delft University of Technology: Delft, The Netherlands, 2005. [Google Scholar]
- Hill, P.S.; Voulgaris, G.; Trowbridge, J.H. Controls on floc size in a continental shelf bottom boundary layer. J. Geophys. Res. Ocean. 2001, 106, 9543–9549. [Google Scholar] [CrossRef]
- Sternberg, R.; Berhane, I.; Ogston, A. Measurement of size and settling velocity of suspended aggregates on the northern California continental shelf. Mar. Geol. 1999, 154, 43–53. [Google Scholar] [CrossRef]
- Leussen, V. Estuarine Macroflocs and Their Role in Fine-Grained Sediment Transport. Ph. D. Thesis, University of Utrecht, Utrecht, The Netherlands, 1994.
- McCave, I. Size spectra and aggregation of suspended particles in the deep ocean. Deep Sea Res. Part A Oceanogr. Res. Pap. 1984, 31, 329–352. [Google Scholar] [CrossRef]
- Winterwerp, J.C. A simple model for turbulence induced flocculation of cohesive sediment. J. Hydraul. Res. 1998, 36, 309–326. [Google Scholar] [CrossRef]
- Zhang, J.j.; Li, X.y. Modeling particle-size distribution dynamics in a flocculation system. AIChE J. 2003, 49, 1870–1882. [Google Scholar] [CrossRef]
- Hall, A.R. Generalized method of moments. In A Companion to Theoretical Econometrics; Blackwell Publishing Ltd.: Oxford, UK, 2003; pp. 230–255. [Google Scholar] [CrossRef]
- Imbens, G.W. Generalized method of moments and empirical likelihood. J. Bus. Econ. Stat. 2002, 20, 493–506. [Google Scholar] [CrossRef]
- Jordi, A.; Wang, D.-P. sbPOM: A parallel implementation of Princenton Ocean Model. Environ. Model. Softw. 2012, 38, 59–61. [Google Scholar] [CrossRef]
- Nitsche, F.; Ryan, W.; Carbotte, S.; Bell, R.; Slagle, A.; Bertinado, C.; Flood, R.; Kenna, T.; McHugh, C. Regional patterns and local variations of sediment distribution in the Hudson River Estuary. Estuar. Coast. Shelf Sci. 2007, 71, 259–277. [Google Scholar] [CrossRef]
- Sinsabaugh, R.; Findlay, S. Microbial production, enzyme activity, and carbon turnover in surface sediments of the Hudson River estuary. Microb. Ecol. 1995, 30, 127–141. [Google Scholar] [CrossRef] [PubMed]
- Geyer, W.R.; Woodruff, J.D.; Traykovski, P. Sediment transport and trapping in the Hudson River estuary. Estuaries 2001, 24, 670–679. [Google Scholar] [CrossRef]
- Blumberg, A.F.; Mellor, G.L. A description of a three-dimensional coastal ocean circulation model. Three-Dimens. Coast. Ocean Models 1987, 4, 1–16. [Google Scholar] [CrossRef]
- Chau, K.-W. Manipulation of numerical coastal flow and water quality models. Environ. Model. Softw. 2003, 18, 99–108. [Google Scholar] [CrossRef]
- Vichi, M.; Pinardi, N.; Zavatarelli, M.; Matteucci, G.; Marcaccio, M.; Bergamini, M.; Frascari, F. One-dimensional ecosystem model tests in the Po Prodelta area (Northern Adriatic Sea). Environ. Model. Softw. 1998, 13, 471–481. [Google Scholar] [CrossRef]
- Liu, X.; Huang, W. Modeling sediment resuspension and transport induced by storm wind in Apalachicola Bay, USA. Environ. Model. Softw. 2009, 24, 1302–1313. [Google Scholar] [CrossRef]
- Mellor, G.L.; Yamada, T. Development of a turbulence closure model for geophysical fluid problems. Rev. Geophys. 1982, 20, 851–875. [Google Scholar] [CrossRef]
- Nittis, K.; Perivoliotis, L.; Korres, G.; Tziavos, C.; Thanos, I. Operational monitoring and forecasting for marine environmental applications in the Aegean Sea. Environ. Model. Softw. 2006, 21, 243–257. [Google Scholar] [CrossRef]
- Sun, Z.; Shao, W.; Yu, W.; Li, J. A study of wave-induced effects on sea surface temperature simulations during typhoon events. J. Mar. Sci. Eng. 2021, 9, 622. [Google Scholar] [CrossRef]
- Ralston, D.K.; Geyer, W.R. Episodic and long-term sediment transport capacity in the Hudson River estuary. Estuaries Coasts 2009, 32, 1130–1151. [Google Scholar] [CrossRef]
- Zhu, Y.; Lu, J.; Liao, H.; Wang, J.; Fan, B.; Yao, S. Research on cohesive sediment erosion by flow: An overview. Sci. China Ser. E Technol. Sci. 2008, 51, 2001–2012. [Google Scholar] [CrossRef]
- Yang, M.-Q.; Wang, G.-L. The incipient motion formulas for cohesive fine sediments. J. Basic Sci. Eng. 1995, 3, 99–109. [Google Scholar]
- Carrere, L.; Lyard, F.; Cancet, M.; Guillot, A. FES 2014, a new tidal model on the global ocean with enhanced accuracy in shallow seas and in the Arctic region. In Proceedings of the EGU General Assembly Conference Abstracts, Vienna, Austria, 12–17 April 2015; p. 5481. [Google Scholar]
- Lyard, F.H.; Allain, D.J.; Cancet, M.; Carrère, L.; Picot, N. FES2014 global ocean tide atlas: Design and performance. J. Ocean Sci. 2021, 17, 615–649. [Google Scholar] [CrossRef]
- Caldwell, P.; Merrifield, M.; Thompson, P. Sea level measured by tide gauges from global oceans–the Joint Archive for Sea Level holdings (NCEI Accession 0019568), Version 5.5, NOAA National Centers for Environmental Information. Cent. Environ. Inf. Dataset 2015, 10, V5V40S47W. [Google Scholar]
- Bayliss, A.; Turkel, E. Radiation boundary conditions for wave-like equations. Commun. Pure Appl. Math. 1980, 33, 707–725. [Google Scholar] [CrossRef]
- Marchesiello, P.; McWilliams, J.C.; Shchepetkin, A. Open boundary conditions for long-term integration of regional oceanic models. Ocean Model. 2001, 3, 1–20. [Google Scholar] [CrossRef]
- Smolarkiewicz, P.K. A fully multidimensional positive definite advection transport algorithm with small implicit diffusion. J. Comput. Phys. 1984, 54, 325–362. [Google Scholar] [CrossRef]
- Smagorinsky, J. The dynamical influence of large-scale heat sources and sinks on the quasi-stationary mean motions of the atmosphere. Q. J. R. Meteorol. Soc. 1953, 79, 342–366. [Google Scholar] [CrossRef]
- Willmott, C.J. On the validation of models. Phys. Geogr. 1981, 2, 184–194. [Google Scholar] [CrossRef]
- Warner, J.C.; Geyer, W.R.; Lerczak, J.A. Numerical modeling of an estuary: A comprehensive skill assessment. J. Geophys. Res. Ocean. 2005, 110, C05001. [Google Scholar] [CrossRef]
- Gu, C.; Li, H.; Xu, F.; Cheng, P.; Wang, X.H.; Xu, S.; Peng, Y. Numerical study of Jiulongjiang river plume in the wet season 2015. Reg. Stud. Mar. Sci. 2018, 24, 82–96. [Google Scholar] [CrossRef]
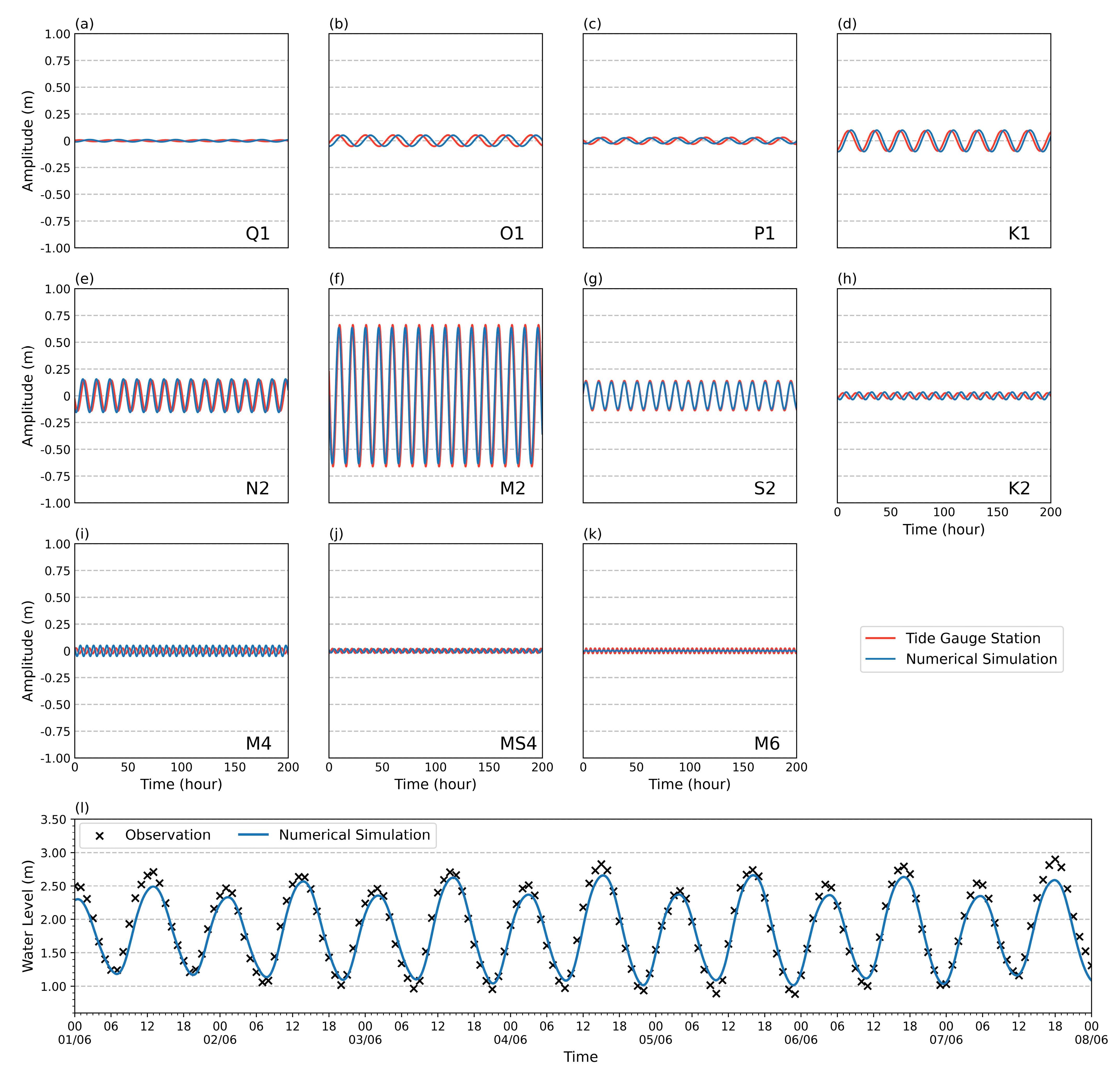


| Tidal Constituent | M2 | S2 | N2 | O1 | K1 | Average | |
|---|---|---|---|---|---|---|---|
| Frequency (Hour−1) | 0.0805 | 0.0833 | 0.0789 | 0.0387 | 0.0418 | ||
| Amplitude (m) | Observation | 0.6613 | 0.1390 | 0.1436 | 0.0517 | 0.0943 | |
| Simulation | 0.6359 | 0.1262 | 0.1546 | 0.0505 | 0.0998 | ||
| Bias | −0.0254 | −0.0127 | 0.0110 | −0.0012 | 0.0055 | ||
| APE | 3.84% | 9.17% | 7.66% | 2.34% | 5.85% | 5.77% | |
| Phase(°) | Observation | 289.8037 | 79.1998 | 256.7599 | 115.6710 | 156.9943 | |
| Simulation | 269.8934 | 73.3644 | 216.9272 | 183.1175 | 195.2466 | ||
| Bias | −19.9103 | −5.8354 | 39.8327 | 67.4465 | 38.2523 | ||
| APE | 5.53% | 1.62% | 11.06% | 18.74% | 10.63% | 9.51% | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fang, Z.; Xu, F. Development of a Spectrum-Based Scheme for Simulating Fine-Grained Sediment Transport in Estuaries. J. Mar. Sci. Eng. 2024, 12, 1189. https://doi.org/10.3390/jmse12071189
Fang Z, Xu F. Development of a Spectrum-Based Scheme for Simulating Fine-Grained Sediment Transport in Estuaries. Journal of Marine Science and Engineering. 2024; 12(7):1189. https://doi.org/10.3390/jmse12071189
Chicago/Turabian StyleFang, Zheng, and Fanghua Xu. 2024. "Development of a Spectrum-Based Scheme for Simulating Fine-Grained Sediment Transport in Estuaries" Journal of Marine Science and Engineering 12, no. 7: 1189. https://doi.org/10.3390/jmse12071189
APA StyleFang, Z., & Xu, F. (2024). Development of a Spectrum-Based Scheme for Simulating Fine-Grained Sediment Transport in Estuaries. Journal of Marine Science and Engineering, 12(7), 1189. https://doi.org/10.3390/jmse12071189






