Impact and Technical Solutions of Hydrodynamic and Thermodynamic Processes in Liquefied Natural Gas Regasification Process

Abstract

Transporting natural gas in liquid form increases opportunities for storage and export worldwide, thus making transportation more sustainable. However, liquefied natural gas (LNG) is in an unsteady state, leading to LNG conversion to the gas state occurring throughout the storage, loading, unloading, and transportation processes. To observe the transition of LNG to natural gas, mathematical models are developed to monitor technical parameters. This research analyses a floating storage and regasification unit for and adopts a mathematical model of the LNG regasification system, aiming for improved observation of hydrodynamic, dynamic, and thermo-physical properties. The complex mathematical model of the system was implemented using the Fortran programming language and MATLAB R28a. From the investigation of the total LNG regasification system, it could be concluded that increasing the outlet pressure of the system results in a decrease in the velocity of LNG. It was found that the total hydraulic energy losses of the total LNG regasification system were approximately 41.3 kW (with outlet pressure of 2 MPa), 12.75 kW (with outlet pressure of 5 MPa), and 4.24 kW (with outlet pressure of 7 MPa).

1. Introduction

Transporting natural gas in liquid form increases opportunities for storage and export worldwide, thus making transportation more sustainable. However, liquefied natural gas (LNG) is in an unsteady state, leading to LNG conversion to the gas state occurring throughout the storage, loading, unloading, and transportation processes [1].

This poses technical challenges for floating storage and regasification units (FSRUs), which are increasingly being used in the EU to solve energy supply bottlenecks. FSRUs are suitable as an interface between the gas tankers for transport and the natural gas distribution network on land for storage, transfer to another vessel, and regasification for re-injection into the natural gas network [2,3]. The parameters to be monitored in the various systems such as storage tanks and regasification plants are, for example, hydrostatic pressure in the tanks, vapour pressure, LNG density, LNG temperature, and phase change between liquid and gaseous states. Controlling the pressure in the storage tank is extremely important to avoid overfilling [4]. The biggest challenge of an FSRU is regasification to make the gas usable for end users. A regasification plant naturally consists of numerous pipes and pumps. The challenge is to pump LNG through pipelines, which is related to the possibility of two-phase flow due to heat ingress from the environment [5]. Two-phase flow formation is influenced by two processes: evaporation and condensation. Evaporation occurs when the temperature of a liquid exceeds the boiling point at a certain pressure. Condensation, on the other hand, is the opposite evaporation process, where vapours condense due to the removal of heat from a liquid. Condensation occurs when the vapour temperature drops below the saturation temperature. Consequently, a small amount of LNG can convert into gases, leading to a non-equilibrium state of the phases and causing pressure changes in the pipeline. This two-phase flow can result in intensive fluctuations and vibration in the pipe, necessitating close monitoring to guard against cavitation and potential disruption of the pumping equipment [6]. Additionally, it results in extra pipeline cooling, a factor not accounted for in daily maintenance routines. To ensure the reliable transportation of LNG through the pipeline to downstream regasification equipment, high-pressure pumps are employed to increase pressure, facilitating the attainment of supercritical conditions [7].

LNG transportation poses challenges due to its state as a cryogenic liquid, requiring high-pressure pumps to maintain it above supercritical conditions for pipeline transportation to LNG vaporisers. During the construction phases of the vaporiser, numerous calculations must be conducted to verify thermo-physical properties such as density, specific heat, thermal conductivity, and viscosity [8]. These properties are greatly affected by temperature and pressure changes. Initially, LNG behaves as a supercritical fluid without undergoing a phase change at supercritical pressure and the boiling temperature. However, when it reaches the pseudo-critical temperature, the thermo-physical properties undergo drastic changes, leading to non-uniform heat transfer in the heat exchangers’ channels [9]. To gain a better understanding of the impact of thermo-physical parameters on the vaporisation process, one can examine the frictional pressure drop. Particularly in the presence of a liquid and gas mixture, variations in physical properties are influenced by saturated pressure and a frictional pressure drop. Frictional pressure loss refers to the energy dissipated in fluid transportation through a pipe due to the friction between the fluid and pipe wall. As the saturated pressure increases, the two-phase frictional drops decrease, thereby affecting the flow pattern transition. Conversely, during the initiation of the heating process, the influence of heat fluxes on the frictional pressure drop becomes better with an increase in vapour quality [10]. The frictional pressure drop is determined by viscosity and density, while the heat transfer coefficient is influenced by specific heat capacity, thermal conductivity, and flow phase. Therefore, when a mixture contains two phases, observing the vaporisation process and determining thermo-physical parameters become more complicated. Most of the scientists use approximations, such as a piecewise-polynomial function of temperature for thermo-physical properties of supercritical LNG within a certain range of pressure or at constant pressure.

The phase transition significantly influences both the regasification process itself and the quality of natural gas production. The regasification process begins as LNG enters the heat exchanger, where it is heated by specialised mediums such as water, heat, ambient air, or specific fluids. The choice of heating medium dictates the construction of heat exchangers, which can be categorised into several types: the open rack vaporiser (ORV), ambient air vaporiser (AAV), intermediate fluid vaporiser (IFV), shell tube vaporiser (STV), and submerged combustion vaporiser (SCV) [11]. LNG does not come into direct contact with the medium; instead, heat transfers occur between the heat exchanger walls. Typically, intermediate fluid vaporiser technology is installed on the floating storage and regasification unit (FSRU) for converting LNG into its gaseous state. This technology primarily comprises various types of heat exchangers with different geometric parameters. One set of heat exchangers is employed for the heating medium, while another set is dedicated to LNG vaporisation.

The printed circuit heat exchanger (PCHE) is mainly used in the regasification process on the FSRU due to its high efficiency, compactness, and resilience to sloshing [9]. Another criterion for using the PCHE is its suitability for cryogenic fluids. Nevertheless, this type of heat exchanger exhibits a significant pressure drop and non-uniform flow rate in the microchannel inlets. The misdistribution of the flow rate can lead to an exceptionally large pressure drop in the core channels and minimal to no heat exchange in the surrounding channels [6]. For example, [8] analyses heat transfer characteristics of supercritical LNG in the zigzag channel of a PCHE operating in different conditions. The hydraulic performance is assessed using the SST k-ω turbulence model. The analysis results show that the local convection heat coefficient varies along the streamwise direction, with the peak value appearing at the pseudo-critical temperature. Additionally, the pressure drops increase along the streamwise path. The research demonstrates that both the heat transfer coefficient and the pressure drop increase with turbulent flow, attributed to changes in mass flux. The optimal hydraulic performance is achieved with bend angles less than 15° when the mass flux ranges from 207.2 kg/(m²·s) to 621.6 kg/(m² · s), and it improves further at bend angles of 10° and lower compared to 15° at mass fluxes exceeding 414.4 kg/(m² · s). Ref. [9] presents a 3D numerical model of a PCHE utilising the SST k-ω turbulent model. This model aims to enhance the understanding of the flow and heat transfer mechanisms of subcooled-liquid natural gas (S-LNG) in the sinusoidal wavy semi-circuit channel.

The focus of their research is to investigate the characteristics of flow and heat transfer of supercritical cryogenic fluids and their heat transfer mechanism between periods of wavy channels of a PCHE. Another scientist [12] developed a three-dimensional numerical model for counter-flow in a printed circuit heat exchanger. LNG is chosen as the cold source, and propane as the hot source. The model results indicate that a larger channel bending angle correlated with improved heat transfer and increased pressure drop. The best performance of the heat exchange process was observed when the channel bending angle was 15° [12]. A further scientist [2] investigated the local and global hydraulic properties of the PCHE’s geometric structure using supercritical LNG and nitrogen through numerical methods. One aspect of their research involves investigating flow separation and recirculation at corners, which limit heat transfer and increase pressure drop [2]. Ref. [3] concludes in their research that the structure of the heat exchanger will influence the pressure drop of each channel and subsequently affect the distribution of the gas–liquid mixture among multiple channels. The pressure drop of the fluid in a single channel includes the pressure drop upon entering the channel from the inlet header, the pressure drops along the channel, and the pressure drop loss when entering the outlet header from the channel [4]. Ref. [5] developed a correlation for the frictional drop and heat transfer coefficient of an LNG from ethane-contaminated methane compared to LNG from pure methane (the correlations are fitted under 6–9 MPa).

To observe the transition of LNG to natural gas, models are developed to monitor technical parameters. One of the most used models is the volume of the fluid model, as adopted by [13] for a Computational Fluid Dynamics (CFD) approach to study leaked LNG evaporation through a cargo tank membrane. The model of [13] accurately describes mass transfer from liquid to vapour and vapour to liquid during evaporation and condensation, which is improved and provided with certain conditions in [14]. The rate of evaporation and condensation is incorporated into the continuity equation. The development of the model was conducted by simulating the propane condensation process in the Fluent program [9,12]. Thus, using this model, liquid and gas volumes could be verified simultaneously. Additionally, governing equations for mass, momentum, continuity, and energy conservation are employed to indicate the alteration of surface area to volume ratio, which impacts the heat transfer characteristics and internal flow dynamics of the system [15]. These equations are primarily used for heat transfer in the heat exchangers during LNG regasification [12,14,16].

Theoretical analysis of scientists’ research expands our understanding by developing a mathematical model to assess the limitations of our investigated regasification system. In a prior study [17], a model was constructed that is capable of analysing high-speed hydrodynamic and dynamic processes at cryogenic temperatures (110 K). This model evaluates geometric parameters, including tank geometry, pumps, pipe geometric parameters, and roughness of internal surfaces, along with characteristics of pumps and electric motors. The findings from this model reveal that LNG flow in this system is unsteady and warrants monitoring for further regasification processes. In the current research, we select an FSRU for analysis and to develop a mathematical model of the LNG regasification system, aiming for improved observation of hydrodynamic, dynamic, and thermo-physical properties. The integration of the Lee model [13] into our new model enables the observation of phase changes of LNG and the duration of the regasification process.

2. Research Methodology

The research methodology consists of making assumptions for mathematical models, preparing data for the models, and creating the mathematical models. The following chapters introduce in detail the individual mathematical models of equipment.

2.1. Symbols and Notations

Table 1. Symbols and notations.

Symbol	Meaning
${\alpha }_{in}$	convective heat transfer coefficient, which is calculated according to the Dittus Boelter equation [18];
$Q_{LNG}$	volumetric flow rate, m3/s;
$Din$	inside diameter if the pipe is circular, m;
$v$	kinematic viscosity, m2/s;
$S$	pipe’s cross-sectional area, m2;
${\rho }_l$	density of LNG, kg/m3;
$\mu$	fluid dynamic viscosity, Pa s;
$c_p$	isobaric heat capacity, J/(kgK);
$k$	thermal conductivity of fluid, W/(mK);
${\alpha }_{out}$	external heat transfer coefficient characterising heat transfer from the environment to the outer surface of the insulation, W/(m2·K);
$\alpha$y1	fraction of the liquid phase;
$\alpha$y2	fraction of the gas phase;
$\mathrm{A}\left(\mathrm{x}\right)$	cross-sectional area of a pipe, m2;
p	LNG pressure, MPa;
$\mathsf{\Pi }\left(\mathrm{x}\right)$	the perimeter of the cross-section of the pipeline, m;
$\mathsf{\tau }$	tangential fluid stress on the inner surface of the pipeline, Pa;
$k_x$	thermal conductivity in the direction of the axis, W/(m · K);
$\dot{Q}$	the rate of heat generated per unit volume per unit time, W/m3;
T	temperature, K;
$h$	heat transfer coefficient, W/(m2 · K);
$T_{amb}$	ambient temperature, T;
$\theta$	discretisation parameter of time, µs;
${\mathrm{K}}_{0,\mathrm{LNG}}$	bulk modulus of elasticity of LNG, Pa;
${\mathrm{V}}_{0,\mathrm{LNG}}$	volume of LNG, m3;
${\mathrm{G}}_{\mathrm{in},\mathrm{LNG}}$	input of LNG mass flow rate to heat exchanger, kg/s;
${\mathsf{\zeta }}_{\mathrm{TR},\mathrm{in}1,\mathrm{LNG}}$	coefficient of transportation pressure losses, -;
${\rho }_{in,LNG}$	input LNG density, kg/m3;
${\rho }_{0,LNG}$	output LNG density of i section of heat exchanger channel, kg/m3;
${\mathsf{\zeta }}_{\mathrm{Loc},\mathrm{in}1,\mathrm{LNG}}$,	coefficient of local pressure losses in point 1;
${\mathsf{\zeta }}_{\mathrm{Loc},\mathrm{N},\mathrm{LNG} }$	coefficient of local pressure losses in the output of point N.

describes the symbols used in this work.

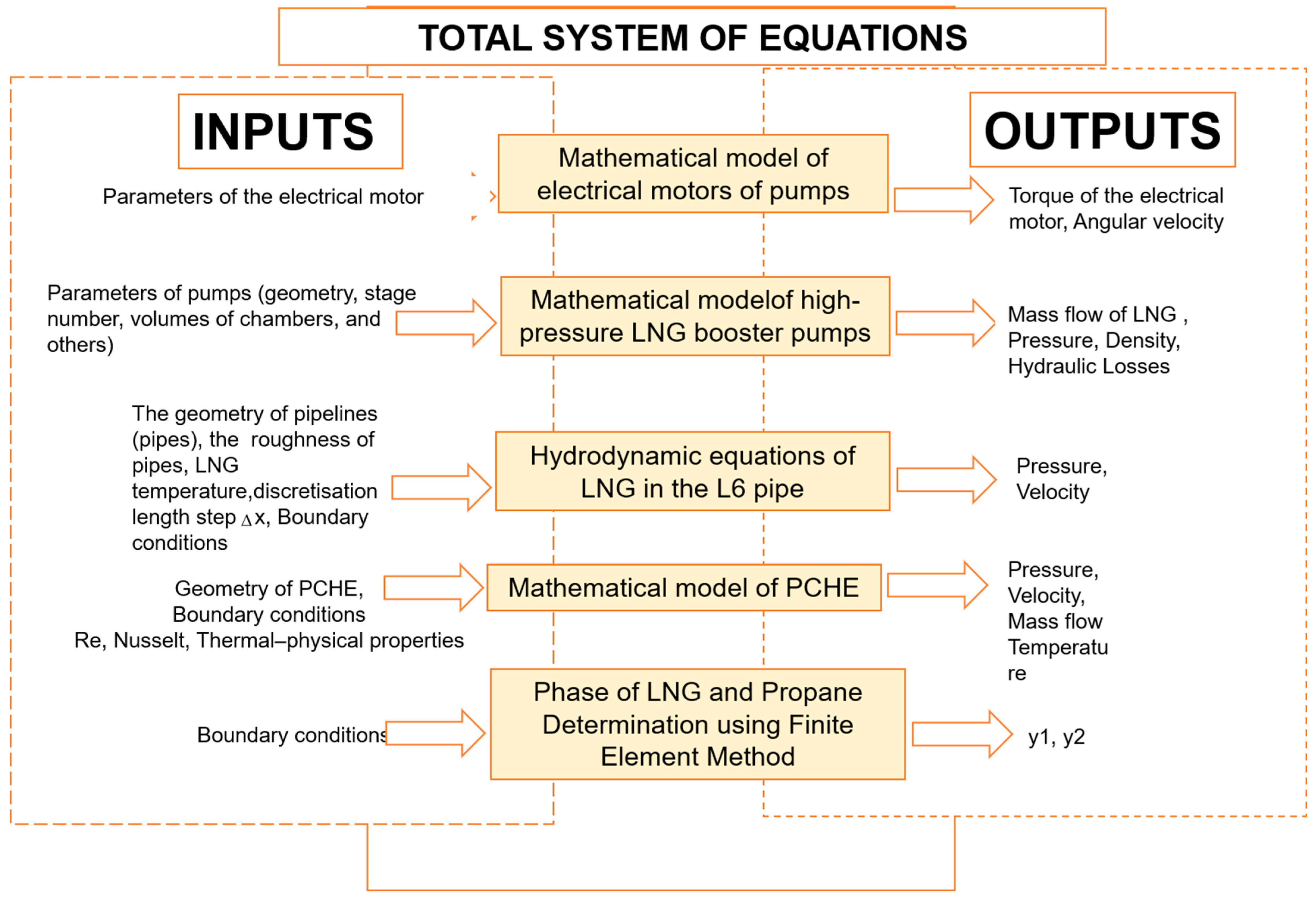
A mathematical model of the FSRU LNG regasification system was created to solve the total system equations with selected boundary conditions and determine the final system parameters. The principal scheme of the mathematical model for the regasification LNG system is introduced in Figure 1. Figure 1 presents the main principle of the total mathematical model of regasification systems. All inputs and outputs are selected and calculated according to the technical equipment’s specifications.

This paper addresses a large hydrodynamic and thermodynamic system, where a liquid flow of LNG is considered a pressurised fluid, and the propagation of pressure waves throughout the system is evaluated. The speed of sound in LNG depends on pressure and temperature. Pressure pulsation (pressure variation at each point of the system) in the considered system depends on the “electric motor-centrifugal multistage pump” system, system load (pressure at the end of the system), LNG physical and mechanical properties, and LNG temperature.

The temperature variation depends on the heat exchange with the environment, the thickness of the insulating layers of the pipes, heat conduction coefficients, heat transfer coefficients, and other parameters. Therefore, the presented mathematical model of the system accurately describes the physical processes involved because the system is considered a whole composed of separate elements. The time step for the integration of differential equations is small, about 10 μs.

The integrated system model has a major advantage: changing one system parameter affects the entire system’s parameters. However, it also has drawbacks: many variables and a long solution time. Nevertheless, solving this problem provides complete information about the functioning of each element of the system.

One-dimensional models were used to create a mathematical model of a single system. It is almost impossible to use three-dimensional models to estimate the density of LNG and consider the system as a single entity consisting of various devices (electric motors, pumps, etc.). Scientists who study similar processes often study the elements of the system separately.

The key assumptions used for the mathematical model are as follows:

• Hydrodynamic and thermodynamic processes can be described as one-dimensional systems.
• Thermo-physical properties of LNG and propane are used as functions of pressure and temperature in the mathematical model of the regasification system, based on the work of other researchers.
• All flow channels are used with the same geometry and with parallel flow in the PCHE.
• The composition of LNG is assumed to be more than 90 mol% methane.
• LNG is described as unsteady flow in the LNG regasification system.
• The outlet pressure of the LNG regasification system is variable in time, ranging from the initial pressure value to the maximum pressure values.
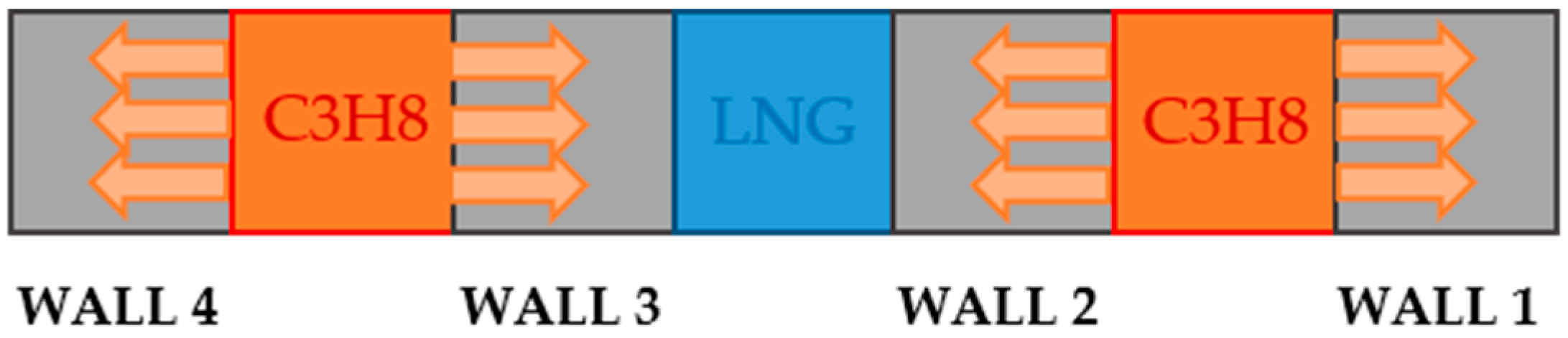
• A mathematical model of the PCHE is described as one LNG channel and two propane channels and 4 walls between these channels.

This study aimed to observe the quality of the LNG regasification process under different output pressure conditions. The investigation included varying outlet pressure to determine changes in velocity and phases (liquid and vapour) of LNG. The investigation is based on high-speed hydrodynamic and dynamic processes in the real LNG regasification system of FSRUs [19] in system start-up mode. This study encompasses the system’s start-up mode, with a particular emphasis on observing the moment when the system stabilises.

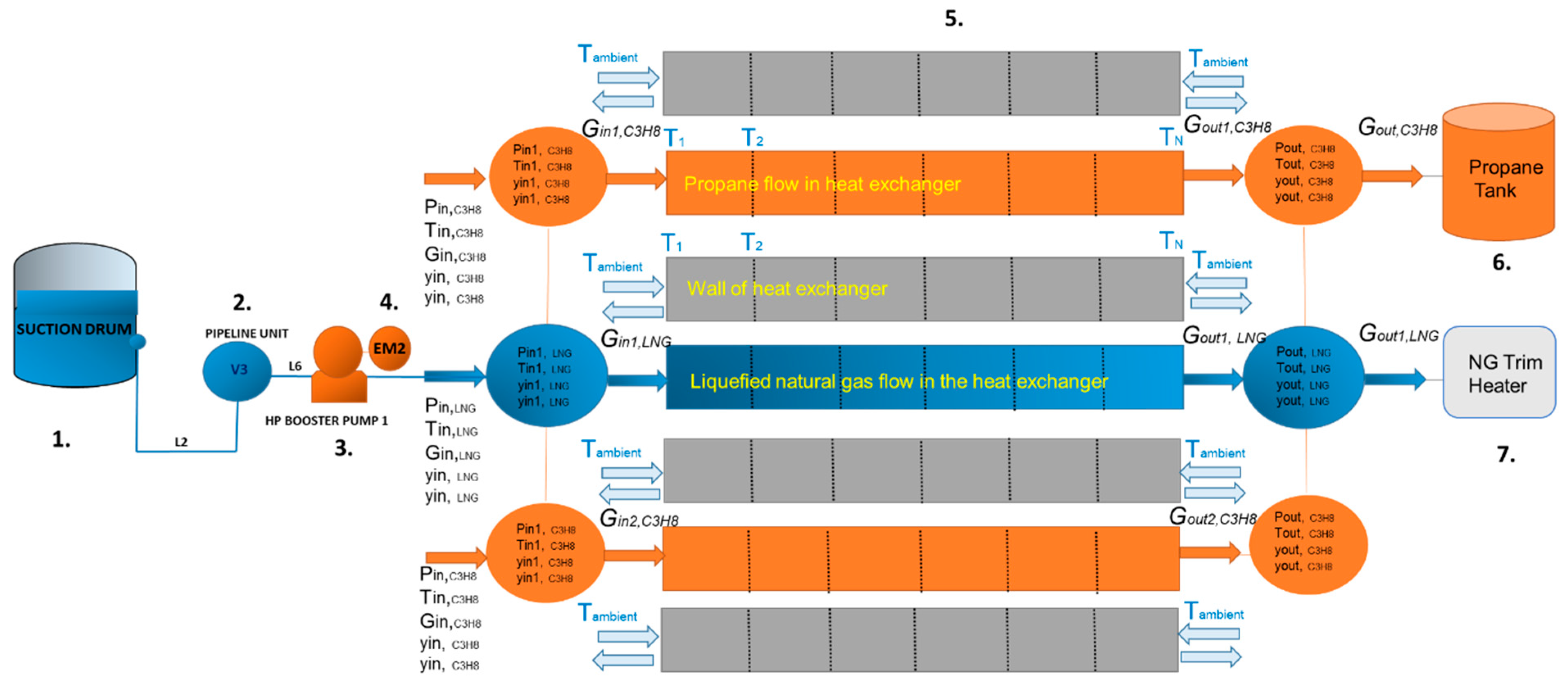
2.2. Description of the LNG Regasification System

The regasification process begins when the LNG flow is transferred by a high-pressure booster pump (3.) from the suction drum (1.) to the PCHE (3.) by the pipe L6 (Figure 1). A more detailed description of the suction drum (1), pipeline unit (2), high-pressure booster pump (3), and electric motor (4) is provided in previous research by [17,20]. This research focuses on the regasification process, specifically when LNG enters the PCHE (5). The PCHE consists of headers presented in blue and orange colours, LNG tubes, four walls, and two propane tubes (Figure 2).

In the PCHE, propane enters as a vapour and liquid mixture, and after regasification of the LNG, the propane condenses as a liquid at −20 °C. After LNG evaporation into the gas phase, the condensed propane is collected in the propane tank (6). As LNG extracts heat from the transferred propane and converts to a gas state, the natural gas is transferred to the natural gas (NG) trim heater (7) for final heating until reaching the reference temperature and pressure conditions for national grid requirements. The technical parameters (Pin—pressure, Tin—temperature, Gin—mass flow, y₁in—liquid phase, y₂in—vapour phase) observed in the mathematical model during the simulation time are introduced in the following sections.

The main parameters of the FSRU equipment are presented in

Table 2. Specifications of FSRU equipment (data from Klaipeda Terminal).

Equipment	Parameters
High-pressure booster pump	Maximum capacity: 510 m3/h. Electric motor power: 1000 kW. Number of pump stages: 13. Mass inertial moment of electric motor rotor and pump wheel: 2234 kg/m2.
LNG printed circuit heat exchanger	Diameter of inner channel: 1.20 mm. Number of channels (LNG): 66.590. Number of channels (C3H8): 180.653. Length of core: 0.646 m. Width of core: 0.540 m. Height of core: 1.520 m.

.

Technical data (lengths, diameters, etc.) were collected on pipeline systems to observe hydrodynamic and thermodynamic processes, as well as two-phase formation in the pipelines.

2.3. Mathematical Model of High-Pressure LNG Booster Pump and System of Equations of Pipelines Using Method of Characteristics

The mathematical model of the booster pump with an electrical motor was utilised for transferring LNG to the LNG PCHE. The description of the mathematical model of the booster pump with an electrical motor is provided in [17]. The main concern of this part is to determine the overall heat transfer coefficient (h) in pipes with insulation, as determined by Equation (1):

$$\mathrm{h}=\frac{1}{\frac{1}{{\alpha }_{in}}+\frac{ln\left(\frac{D_{out}}{D_{in}}\right)·D_{in}}{2·k_{pipe}}+\frac{ln\left(\frac{D_{ins}}{D_{out}}\right)·D_{in}}{2·k_{ins}}+\frac{D_{in}}{{\alpha }_{out}·D_{grp}}}$$

(1)

where ${\alpha }_{in}$—convective heat transfer coefficient, which is calculated according to the Dittus Boelter equation, which is used to determine the heat transfer inside the pipeline when Re > 10,000 [18]; index ins—insulator.

$$\mathrm{Re}=\frac{Q_{LNG}·Din}{v·A}$$

(2)

where $Q_{LNG}$—volumetric flow rate, m³/s; $D_{in}$—inside diameter if the pipe is circular, m; $v$—kinematic viscosity, m²/s; $A$—pipe’s cross-sectional area, m².

$${\alpha }_{in}=0.023·\frac{k^{1-n}·G_{LNG}{0}^{.8}·c_p^n}{{\mu }^{0.8-n}·D_{in}^{0.2}}$$

(3)

where n = 0.4 for fluids which are cooler than their environment [18]; ${\mathrm{c}}_{\mathrm{p}}$—isobaric heat capacity, J/(kg · K); ${\mathrm{G}}_{\mathrm{LNG}}$—mass flow rate, kg/s;$\mathsf{\mu }$—fluid dynamic viscosity, Pa · s; $D_{in}$—inside diameter if the pipe is circular; $\mathrm{k}$—thermal conductivity of fluid, W/(m · K); ${\mathsf{\alpha }}_{\mathrm{out}}$—external heat transfer coefficient characterising heat transfer from the environment to the outer surface of the insulation, W/(m² · K).

The flow of LNG is described by classical hydrodynamic equations. The equation of LNG continuity is written in differential form as follows:

$$\frac{\mathsf{\partial }}{\mathsf{\partial }\mathrm{t}}\left[\mathrm{A}\left(\mathrm{x}\right){\mathsf{\rho }}_{\mathrm{l}}\right]+\frac{\mathsf{\partial }}{\mathsf{\partial }\mathrm{x}}\left[\mathrm{A}\left(\mathrm{x}\right){\mathsf{\rho }}_{\mathrm{l}}\mathsf{\upsilon }\right]=0$$

(4)

where ${\rho }_l,\upsilon$—density and velocity of LNG, kg/m³ and m/s; $\mathrm{A}\left(\mathrm{x}\right)$—cross-sectional area of a pipe, m².

The equation of the liquid flow impulse (momentum) is

$$\frac{\mathsf{\partial }}{\mathsf{\partial }\mathrm{t}}\left[\mathrm{A}\left(\mathrm{x}\right){\mathsf{\rho }}_{\mathrm{l}}\mathsf{\upsilon }\right]+\frac{\mathsf{\partial }}{\mathsf{\partial }\mathrm{t}}\left[\mathrm{A}\left(\mathrm{x}\right) \left(\mathrm{p}+{\mathsf{\rho }}_{\mathrm{l}}{\mathsf{\upsilon }}^2\right)\right]+\mathsf{\Pi }\left(\mathrm{x}\right)\mathsf{\tau }+\mathrm{A}\left(\mathrm{x}\right){\mathsf{\rho }}_{\mathrm{l}}{\mathrm{a}}_{\mathrm{x}}={\mathrm{p}}_{\mathrm{l}}\frac{\mathsf{\partial }\mathrm{A}}{\mathsf{\partial }\mathrm{x}}$$

(5)

where p—LNG pressure, Pa; $\mathsf{\Pi }\left(\mathrm{x}\right)$—the perimeter of the cross-section of the pipeline, m; $\mathsf{\tau }$—tangential fluid stress on the inner surface of the pipeline, Pa.

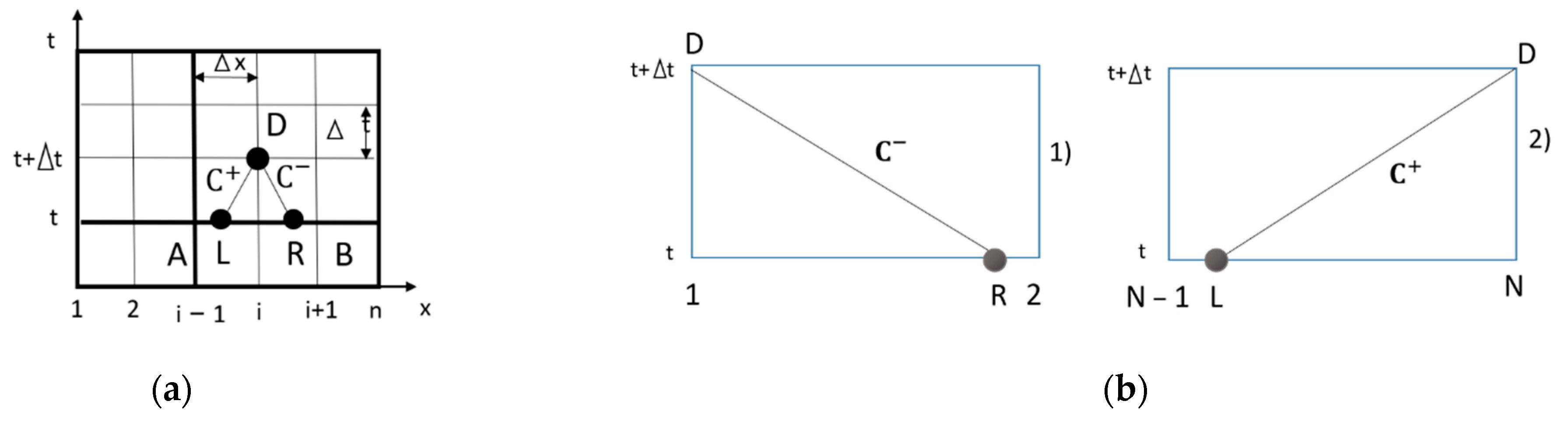
These equations are solved using the method of characteristics (MOC) [17,21,22,23] to determine the unknown variable velocity ($v$) and the pressure of ($p$) of LNG at a moment in time $t$ and certain time intervals t + ∆t at every point in the pipe, as shown in Figure 3.

Pressure and velocity at point D at that moment are determined from a nonlinear algebraic equation system:

$$\begin{gathered} C^{+}:{\Phi }_1=v_D-v_L+\frac{1}{2}\left({\rho }_D-{\rho }_L\right)\left[{\left(\frac{1}{{\rho }_{l}c}\right)}_L+{\left(\frac{1}{{\rho }_{l}c}\right)}_D\right]-\frac{∆t}{2}\left[{\left(\frac{f_1}{{\rho }_{l}c}\right)}_L+{\left(\frac{f_1}{{\rho }_{l}c}\right)}_D\right]- \\ \frac{∆t}{2}\left[{\left(f_2\right)}_L+{\left(f_2\right)}_D\right]=0, \\ {C}^{-}:{\Phi }_2=v_D-v_R+\frac{1}{2}\left({\rho }_D-{\rho }_R\right)\left[{\left(\frac{1}{{\rho }_{l}c}\right)}_R+{\left(\frac{1}{{\rho }_{l}c}\right)}_D\right]-\frac{∆t}{2}\left[{\left(\frac{f_1}{{\rho }_{l}c}\right)}_R+{\left(\frac{f_1}{{\rho }_{l}c}\right)}_D\right]- \\ \frac{∆t}{2}\left[{\left(f_2\right)}_R++{\left(f_2\right)}_D\right]=0, \end{gathered}$$

(6)

where $f_1\left(p,\upsilon \right)=\frac{c}{A\left(x\right)}\left({\rho }_l\upsilon \frac{\mathsf{\partial }A\left(x\right)}{\mathsf{\partial }x}\right)$; $f_2\left(\upsilon ,p\right)=\frac{\tau \Pi \left(x\right) }{{\rho }_{l}A\left(x\right)}$. The subscripts D, L, and R refer to the points in Figure 3.

The nonlinear algebraic Equation (6) is solved by the Newton–Raphson method [24,25]. At points L and R, variables p and $v$ are defined using a system of two nonlinear algebraic equations with unknown p_L, v_L and p_R, v_R:

$${\Phi }_3=p_L-p_C-\theta \left(p_A-p_C\right)\left[v_L+c\left(p_L\right)\right]=0$$

(7)

$${\Phi }_4=v_L-v_C-\theta \left(v_A-v_C\right)\left[v_L+c\left(p_L\right)\right]=0$$

(8)

and

$${\Phi }_5=p_R-p_C+\theta \left(p_B-p_C\right)\left[v_R-c\left(p_R\right)\right]=0$$

(9)

$${\Phi }_6=v_R-v_C+\theta \left(v_B-v_C\right)\left[v_R-c\left(p_R\right)\right]=0$$

(10)

where $=$ $\frac{∆t}{∆x}$.

The boundary conditions are used to connect the pipeline with the equipment of the system (LNG suction drum, pumps, heat exchanger, etc.), and are described below:

Boundary condition: when the point is known $x=0$, pressure is known variable $p\left(t\right)=p_D$, then LNG flow velocity is determined by the formula:

$${\Phi }_2\left(v_D\right)=0.$$

(11)

Boundary condition: when the point is known $x=0$, LNG flow velocity is known variable $v\left(t\right)=v_D$, then pressure is determined by the formula:

$${\Phi }_2\left(p_D\right)=0.$$

(12)

Boundary condition: when the point is known $x=L$, pressure is known variable $p\left(t\right)=p_D$, then LNG flow velocity is determined by the formula:

$${\Phi }_1\left(v_D\right)=0.$$

(13)

Boundary condition: when the point is known $x=L$, NG flow velocity is known variable $v\left(t\right)=v_D$, then pressure is determined by the formula:

$${\Phi }_1\left(p_D\right)=0.$$

(14)

2.4. Thermal Conductivity Equations Determining the Change in Temperature

The thermal conductivity equation is employed to observe the temperature changes of the system. The temperature distribution T through the wall of the equipment or the pipes is described by the Fourier differential equation [26]:

$$\rho ·c_p\left(\frac{\mathsf{\partial }T}{\mathsf{\partial }t}+v·\frac{\mathsf{\partial }T}{\mathsf{\partial }x}\right)=\frac{\mathsf{\partial }}{\mathsf{\partial }x}\left(k_x·\frac{\mathsf{\partial }T}{\mathsf{\partial }x}\right)+\dot{Q}$$

(15)

where $c_p$—specific heat;$k_x$—thermal conductivity in the direction of the axis; $\dot{Q}$—the rate of heat generated per unit volume per unit time; T—temperature; $v$—velocity in the x-direction.

The Fourier differential equation is solved using the Ritz method [27,28]. For this purpose, the following set of boundary conditions is defined for solving the Fourier differential equation.

Boundary conditions: Convective heat exchange with the environment takes place on the side surfaces of the pipe or tube. On the surface S, the known heat flow rate q in the x-direction is as follows [26]:

$$k_{x}S\left(\frac{\mathsf{\partial }T}{\mathsf{\partial }x}\right)+q=0$$

(16)

The rate of heat flow by convection on the surface is as follows (S):

$$k_x·S \left(\frac{\mathsf{\partial }T}{\mathsf{\partial }x}\right)+h·S \left(T-T_{amb}\right)=0$$

(17)

where $h$—heat transfer coefficient, W/(m² K)$; T_{amb}$—surrounding temperature; T—temperature.

A one-dimensional finite element is used to determine the temperature (T) of the pipe and tube (Figure 4):

The variation in temperature in finite element e is equal to

$$T\left(\xi ,t\right)=\left[N\left(\xi \right)\right]·\left\{T_e\left(t\right)\right\}$$

(18)

where $\left\{T_e\left(t\right)\right\}$—the temperature vector in the finite element node.

$${\left\{T_e\left(t\right)\right\}}^T=\left[T_1 T_2\right]$$

(19)

$\left[N\left(\xi \right)\right]$—the matrix of shape functions:

$$\left[N\left(\xi \right)\right]=\left[N_1\left(\xi \right),N_2\left(\xi \right)\right]=\left[1-\xi , \xi \right]$$

After applying Galerkin’s method [29], the system of finite element equations is established [30]:

$$\left[M_e\right]·\left\{\dot{T_e}\right\}+\left[K_e\right]·\left\{T\right\}=\left\{P_e\left(t\right)\right\}$$

(20)

The general system of LNG tube or pipe equations is equal to

$$\left[M\right]·\left\{\dot{T}\right\}+\left[K\right]·\left\{T\right\}=\left\{P\right\}$$

(21)

Using discretisation parameter θ instead of ½, the following is true:

$$\left(\left[M_t\right]+∆t\theta \left[K_t\right]\right)\left\{T_{t+∆t}\right\}=∆t\left(1-\theta \right)\left\{P_t\right\}+\theta \left\{P_{t+∆t}\right\}-∆t\left(1-\theta \right)\left[K_t\right]\left\{T_t\right\}+\left[M_t\right]\left\{T_t\right\}$$

(22)

$\theta$—discretisation parameter of time.

Three conditions are set to solve:

When $\theta =\frac{1}{2}$, the Crank–Nicolson method [31] is used for solving the heat and similar partial differential equations.

When $\theta =0$, Euler’s forward method [32] is used for solving ordinary differential equations.

When $\theta =1$, the backward differencing method [32] is used for the numerical integration of ordinary differential equations.

The parameter θ is needed in order to be able to numerically solve the differential equations of the first degree. The set value of the parameter θ depends on what kind of task can be solved. Three conditions are added to different meanings of θ. The choice was θ = 0.5, since the Crank–Nicolson method is widely used to deal with such equations and the solution step is small (10⁻⁵ m) so that we can examine high-speed hydrodynamic processes and assess the propagation of pressure waves in the medium.

2.5. Technical Parameter Observation in the Printed Circuit Heat Exchanger

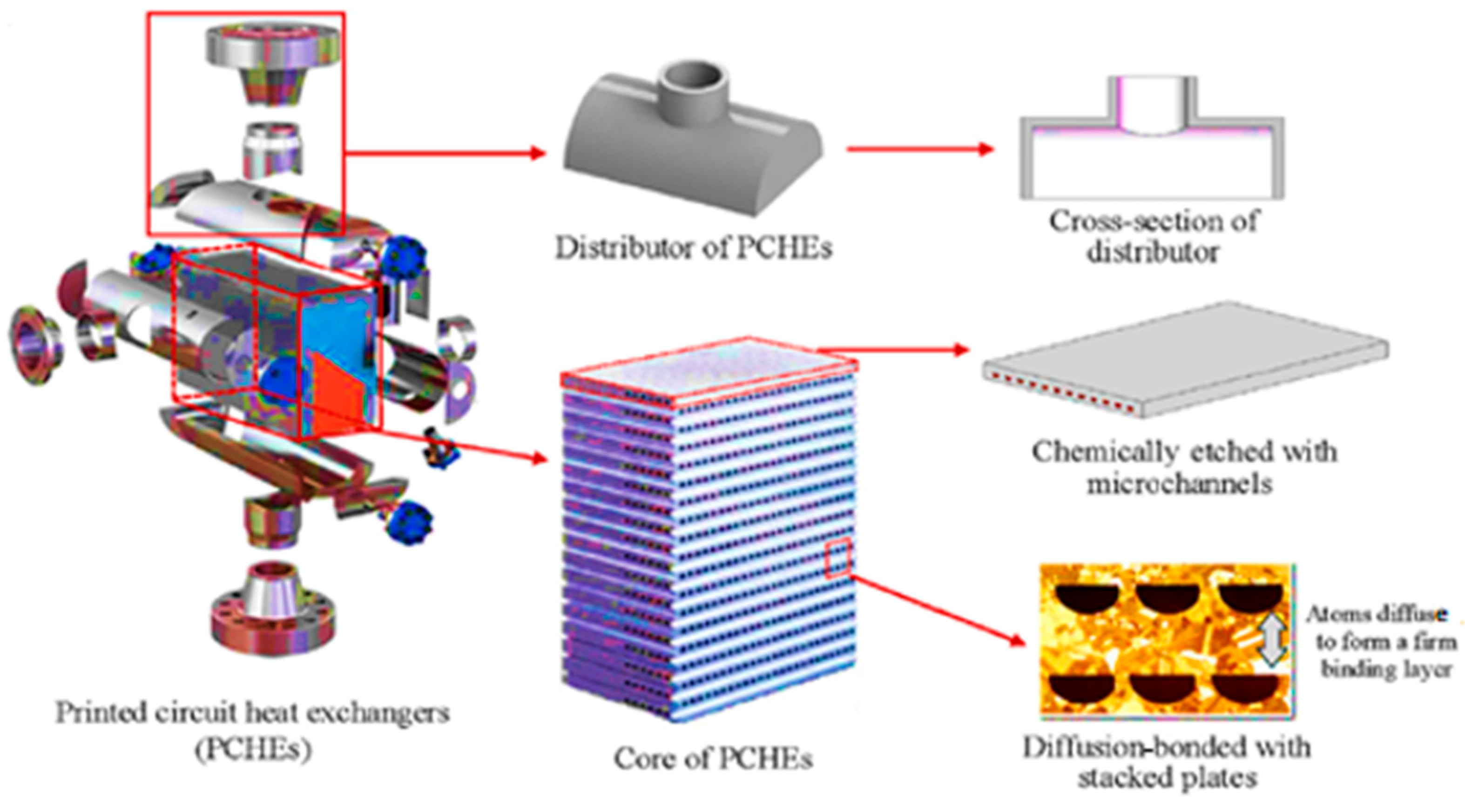
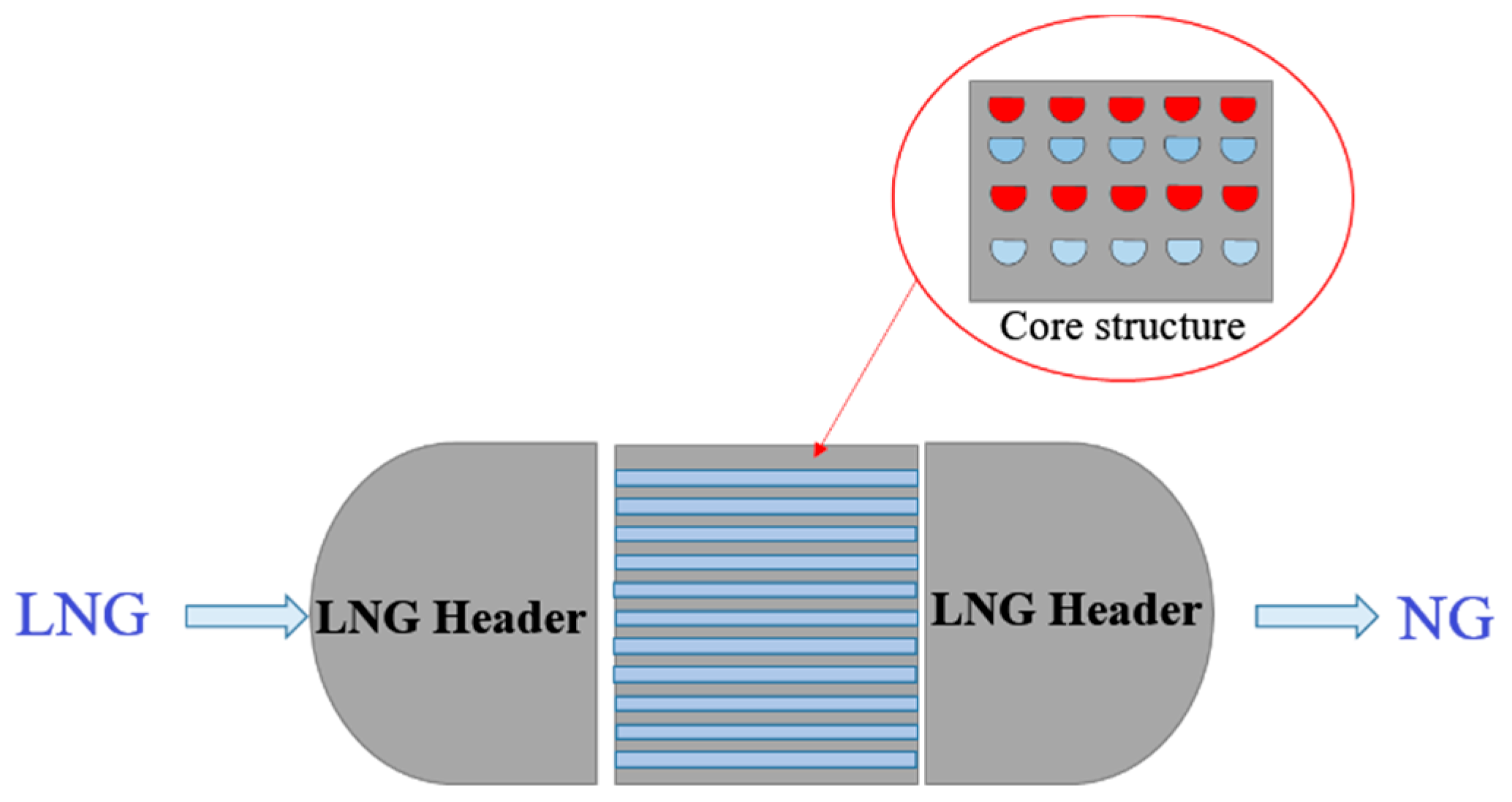
The PCHE is constructed of a stack of diffusion-bonded flat plates with flow channels. According to the technical sheets, the core dimensions of the test PCHE are 646 × 552 × 1520 (L × H × W) (Figure 5). The core serves as the main part of the heat exchanger, where many layers of metal with channels are joined together in the one-quadratic part.

Another important component of the PCHE is the header, which functions to distribute flow equally to channels of the core in parallel (Figure 6). According to the technical specifications, the working range of the PCHE is when LNG is heated to from −155/−135 °C to −10 °C. The parts of the PCHE are introduced in Figure 3.

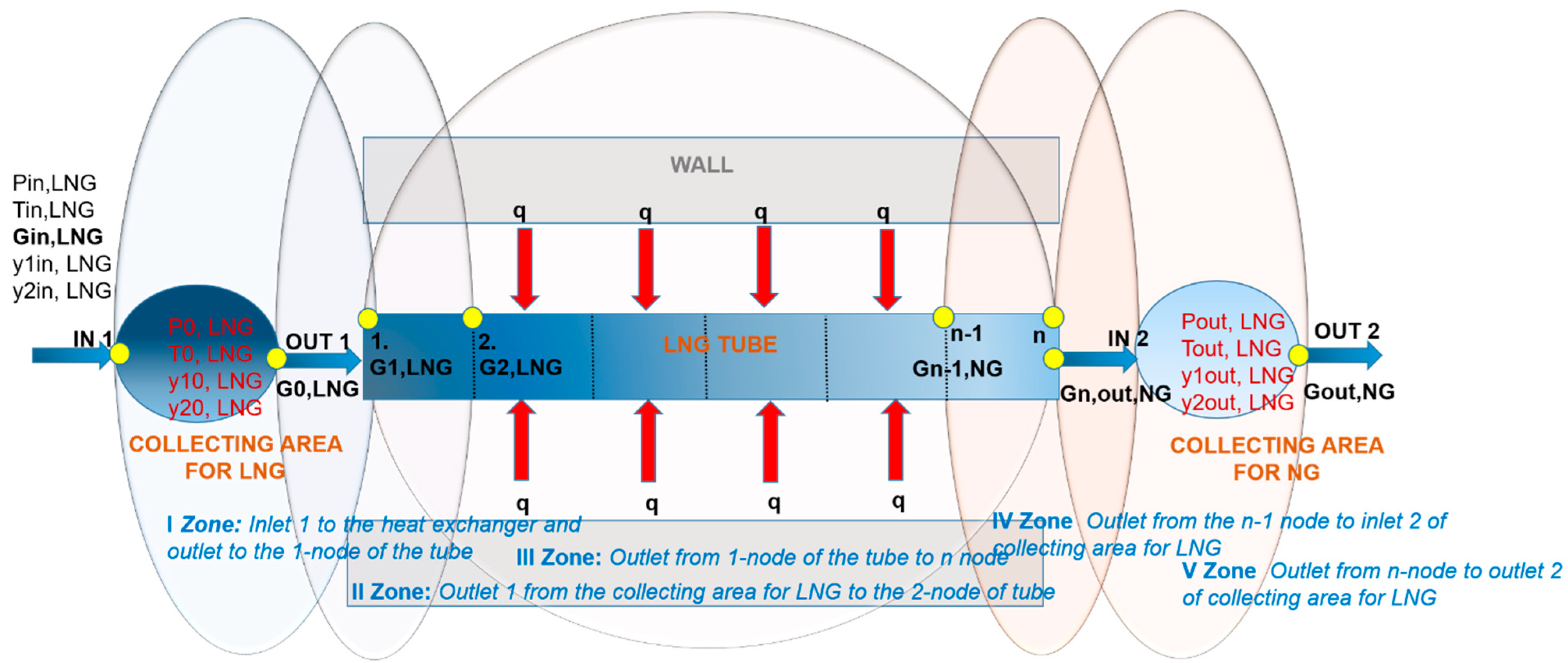
In the model, the flow heat exchange with the propane gas causes propane to condense on the propane side as LNG is evaporated on the LNG side. The mathematical model’s working range is divided into zones, which are introduced in Figure 7, and within these zones, different observations of technical parameter changes (p—pressure, T—temperature, G—mass flow rate, $\alpha$_y1—fraction of the liquid phase, and $\alpha$_y2—fraction of the gas phase) are made. Boundary conditions are selected inputs (p_in, T_in, G_in, α_xin, α_yin) that initiate the regasification process in the heat exchanger.

The first observations of technical parameter changes (p_in1,LNG, T_in1,LNG, G_in1,LNG, $\alpha$_yin1,LNG, $\alpha$_yin2,LNG) are described by equations in the I Zone for LNG:

The pressure observation is as follows:

$${\dot{\mathrm{P}}}_{0,\mathrm{LNG}}=\frac{{\mathrm{K}}_{0,\mathrm{LNG}}}{{\mathrm{V}}_{0,\mathrm{LNG}}}·\left(\frac{{\mathrm{G}}_{\mathrm{in},\mathrm{LNG}}}{{\mathsf{\rho }}_{\mathrm{in},\mathrm{LNG}}}-\frac{{\mathrm{G}}_{0,\mathrm{LNG}}}{{\mathsf{\rho }}_{0,\mathrm{LNG}}}\right)$$

(23)

where ${\mathrm{K}}_{0,\mathrm{LNG}}$—bulk modulus of elasticity of LNG, Pa; ${\mathrm{V}}_{0,\mathrm{LNG}}$—volume of LNG, m³; ${\mathrm{G}}_{\mathrm{in},\mathrm{LNG}}$—input of LNG mass flow rate to the heat exchanger, kg/s; ${\rho }_{in,LNG}$—input LNG density, kg/m³; ${\rho }_{0,LNG}$—output LNG density of i section of the heat exchanger tube, kg/m³;$G_{0,LNG}$—output of LNG mass flow rate to i section of the heat exchanger tube, kg/s.

The temperature observation is as follows:

$${\dot{\mathrm{T}}}_{0,\mathrm{LNG}}=-\frac{{\mathrm{h}}_{0,\mathrm{LNG}}·{\mathrm{S}}_{0,\mathrm{LNG}}·\left({\mathrm{T}}_{0,\mathrm{LNG}}-{\mathrm{T}}_{\mathrm{ambient}}\right)}{{\mathsf{\rho }}_{0,\mathrm{LNG}}·{\mathrm{V}}_{0,\mathrm{LNG}}·{\mathrm{c}}_{\mathrm{p},\mathrm{LNG}}}+\frac{{\mathrm{T}}_{\mathrm{in},\mathrm{LNG}}·{\mathrm{G}}_{\mathrm{in},\mathrm{LNG}}}{\left({\mathsf{\rho }}_{\mathrm{in},\mathrm{LNG}}·{\mathrm{V}}_{0,\mathrm{LNG}}\right)}-\frac{{\mathrm{T}}_{0,\mathrm{LNG}}·{\mathrm{N}}_{\mathrm{pipes}}{\mathrm{G}}_{\mathrm{in}1,\mathrm{LNG}}}{\left({\mathsf{\rho }}_{0,\mathrm{LNG}}·{\mathrm{V}}_{0,\mathrm{LNG}}\right)}$$

(24)

where $h_{0,LNG}$—heat transfer coefficient; ${\mathrm{V}}_{0,\mathrm{LNG}}$—volume of LNG in the header, m³; ${\mathrm{G}}_{\mathrm{in}1,\mathrm{LNG}}$—input of LNG mass flow rate to the heat exchanger, m³/s; ${\rho }_{in,LNG}$—input LNG density of i section of the heat exchanger tube, m³/kg; ${\rho }_{0,LNG}$—output LNG density of i section of the heat exchanger tube, m³/kg;$G_{in1,LNG}$—output of LNG mass flow rate to i section of the heat exchanger tube, m³/s; N_pipes—number of pipes;$·S_{0,LNG}$—the pipe’s cross-sectional area of the LNG tube (see Figure 7), m².

The mass flow observation is as follows:

$${\dot{\mathrm{G}}}_{\mathrm{in}1,\mathrm{LNG}}=\frac{{\mathrm{A}}_{\mathrm{pipe},\mathrm{LNG}}}{{\mathrm{L}}_{\mathrm{pipe}\_\mathrm{LNG}}}·\left(\begin{array}{c}{\mathrm{p}}_{1,\mathrm{LNG}}-0.5·N\_pipe·{\mathsf{\rho }}_{\mathrm{in}1,\mathrm{LNG}}·{\mathsf{\zeta }}_{\mathrm{TR},\mathrm{in}1,\mathrm{LNG}}{ \mathrm{v}}_{\mathrm{in}1,\mathrm{LNG}}·\left|v_{\mathrm{in}1,\mathrm{LNG}}\right|-{\mathrm{p}}_{\mathrm{N},\mathrm{LNG}}\end{array}\right)$$

(25)

The pressure determination is as follows:

$${\mathrm{p}}_{1,\mathrm{LNG}}={\mathrm{p}}_{0,\mathrm{LNG}}-0.5·{\mathrm{N}}_{\mathrm{pipe}}·{\mathsf{\rho }}_{\mathrm{in}1,\mathrm{LNG}}·{\mathsf{\zeta }}_{\mathrm{Loc},\mathrm{in}1,\mathrm{LNG}}{v}_{\mathrm{in}1,\mathrm{LNG}}·\left|v_{\mathrm{in}1,\mathrm{LNG}}\right|$$

(26)

$${\mathrm{p}}_{\mathrm{n},\mathrm{LNG}}={\mathrm{p}}_{\mathrm{out},\mathrm{LNG}}-0.5·{\mathrm{N}}_{\mathrm{pipe}}·{\mathsf{\rho }}_{\mathrm{out},\mathrm{LNG}}·{\mathsf{\zeta }}_{\mathrm{Loc},\mathrm{N},\mathrm{LNG}}{v}_{\mathrm{in}1,\mathrm{LNG}}·\left|v_{\mathrm{in}1,\mathrm{LNG}}\right|$$

(27)

where, in Equations (25)–(27), ${\mathsf{\zeta }}_{\mathrm{TR},\mathrm{in}1,\mathrm{LNG}}$—coefficient of transportation pressure losses; ${\mathsf{\zeta }}_{\mathrm{Loc},\mathrm{in}1,\mathrm{LNG}}$,${ \mathsf{\zeta }}_{\mathrm{Loc},\mathrm{N},\mathrm{LNG} }$—coefficients of local pressure losses in point 1 and point N.

When the temperature is higher than the saturation, temperature $T$ > $T_{sat.}$ Evaporation occurs [12,13,14]:

$$∆T_1=\frac{\left(T-T_{sat.}\right)}{T_{sat.}}$$

(28)

When the temperature is lower than the saturation temperature, $T$ > $T_{sat.}$ Condensation occurs [12,13,14]:

$$∆T_2=\frac{\left(T_{sat.}-T\right)}{T_{sat}.}$$

(29)

The liquid (y₁) and gas phases (y₂) of LNG are determined by the following equation:

$$y_1={\alpha }_L·{\rho }_L;y_2={\alpha }_g·{\rho }_g.$$

(30)

where y₁ and y₂—LNG densities of liquid and gas phases, m³/kg.

The volume fraction of the vapour phase and liquid fraction of the liquid phase ${\alpha }_L$ are determined by the following [14]:

$${\alpha }_L=\frac{V_L}{V_L+V_g}; {\alpha }_g=\frac{V_g}{V_L+V_g}, {\alpha }_L+{\alpha }_g=1$$

(31)

where $V_L, V_g$—volumes of liquid and gas, m³.

LNG densities of liquid and gas phases are determined from the system of Equation (32) written in matrix form:

$$\frac{d}{dt}\left\{y\right\}-\left[D\right]·\left\{y\right\}=0$$

(32)

where $\left\{y\right\}$—the unknown vector; ${\left\{y\right\}}^T=\left[y_1,y_2\right]$; Matrix $\left[\mathrm{D}\right]$ is as follows:

$$\left[\mathrm{D}\right]=\left[\begin{array}{cc}-coeff ∆T_{1}h\left(∆T_1\right)& coeff∆T_{2}h\left(∆T_2\right)\\ coeff ∆T_{1}h\left(∆T_1\right)& -coeff∆T_{2}h\left(∆T_2\right)\end{array}\right]$$

(33)

where $coeff$—the configurable mass transfer parameter, which is used in [13], 1/(s/K).

The final expression of the system of equations is

$$\frac{\mathsf{\partial }}{\mathsf{\partial }t}\left\{y\right\}+v \frac{\mathsf{\partial }}{\mathsf{\partial }x}\left\{y\right\}-\left[D\right]\left\{y\right\}=0$$

(34)

where $v$—LNG velocity.

The differential equations of [13] with partial derivatives describing the evaporation are solved by the finite element method, introduced in the following sub-chapter.

2.6. Phase of Liquefied Natural Gas Determination Using Finite Element Method

The differential equations of evaporation of Lee [13] are used in the finite element method (FEM) because these equations have partial derivatives. Using the FEM, a system of first-order differential equations is obtained, which is solved using the numerical method. The unknown vector $\left\{y\right\}$ in the finite element is approximated in the following [30]:

$$\left\{y\right\}=\left[N\left(\xi \right)\right]\left\{Y_e\right\}$$

(35)

The matrix of shape functions is as follows:

$$\left[N\left(\xi \right)\right]=\left[\begin{array}{ccc}{N}_1& 0& N_2\\ 0& N_1& 0\end{array} \begin{array}{c}0\\ N_2\end{array}\right]$$

(36)

$\left\{Y_e\right\}$—unknown vectors at the element nodes.

$$N_1\left(\xi \right)=\left(1-\xi \right); N_2\left(\xi \right)=\xi ; \xi = x/\mathrm{Le}$$

(37)

where Le—length of the finite element.

$${\left\{Y_e\right\}}^T=\left[y_{1,1},y_{2,1},y_{1,2},y_{2,2}\right]=\left[{\left\{y\right\}}_1^T,{\left\{y\right\}}_2^T\right]$$

(38)

Using Galerkin’s method, a system of finite element equations is obtained [30]:

$$\left[M_e\right]\left\{\dot{Y_e}\right\}+\left[K_e\right]\left\{Y_e\right\}=\left\{P_e\right\}$$

(39)

where

$$\left[M_e\right]={{\displaystyle \int }}_0^1{\left[N\right]}^T\left[N\right]L_e d\xi$$

(40)

$$\left[K_e\right]={{\displaystyle \int }}_0^1{\left[N\left(\xi \right)\right]}^{T}v\left(\xi \right)\frac{\mathsf{\partial }\left[N\left(\xi \right)\right]}{\mathsf{\partial }\xi }d\xi$$

(41)

$$v\left(\xi \right)=N_1\left(\xi \right)v_1+N_2\left(\xi \right)v_2$$

(42)

$v_1$ and $v_2$—fluid flow velocities at cell nodes.

$$\left\{P_e\right\}={{\displaystyle \int }}_0^1{\left[N\left(\xi \right)\right]}^T\left[D\right]\left[N\left(\xi \right)\right]L_e d\xi \left\{Y_e\right\}$$

(43)

The system of equations of finite element e is

$$\left[A_e\right]\left\{Y_{e,t+∆t}\right\}=\left\{B_e\right\}$$

(44)

where $\left[A_e\right]=\left[M_{e,t}\right]+∆t\theta \left[K_e\right]$;

$$\left\{B_e\right\}=\left[M_{e,t}\right]\left\{Y_{e,t}\right\}-∆t\left(1-\theta \right)\left[K_e\right]\left\{Y_{e,t}\right\}+∆t\left(\left(1-\theta \right)\left\{P_{e,t}\right\}+\theta \left\{P_{e,t+∆t}\right\}\right)$$

(45)

The general system of equations is equal:

$$\left[A_t\right]·\left\{Y_{t+∆t}\right\}=\left\{B_t\right\}$$

(46)

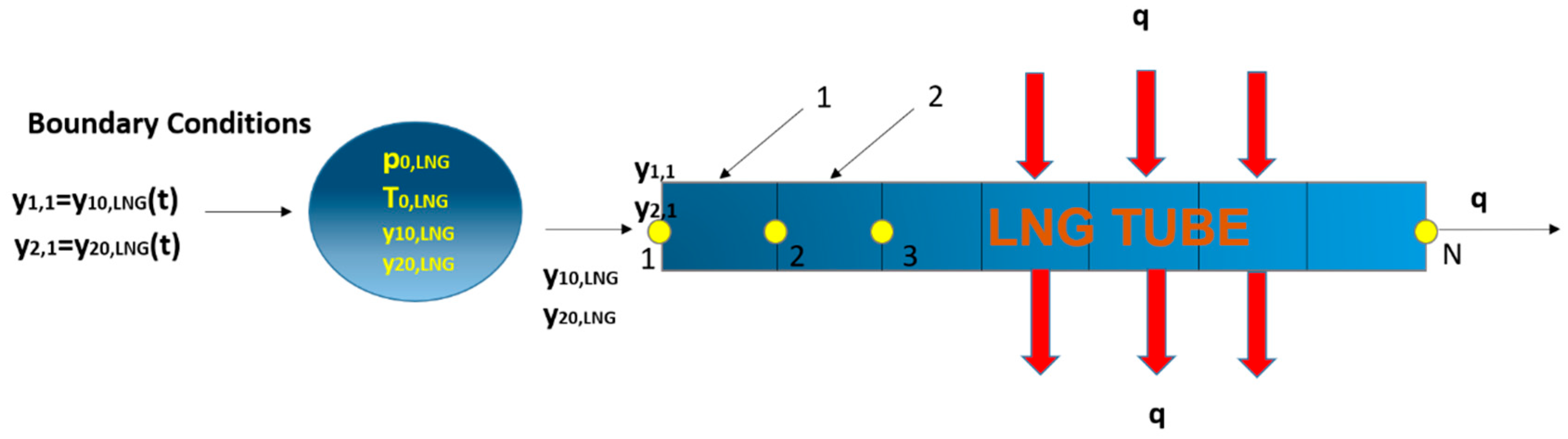
The boundary conditions for the FEM are described (Figure 8).

The introduction of the boundary conditions to the first node of the first finite element (system of equations) is as follows:

$$\left[\begin{array}{cccc}{a}_{11}& a_{12}& a_{13}& a_{14}\\ a_{21}& a_{22}& a_{23}& a_{24}\\ a_{31}& a_{32}& a_{33}& a_{34}\\ a_{41}& a_{42}& a_{43}& a_{44}\end{array}\right]\left\{\begin{array}{c}{y}_{1,1}\\ y_{2,1}\\ y_{1,2}\\ y_{2,2+∆t}\end{array}\right\}=\left\{\begin{array}{c}{B}_1\\ B_2\\ B_3\\ B_4\end{array}\right\}$$

(47)

The final step is as follows:

$$\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& a_{33}& a_{34}\\ 0& 0& a_{43}& a_{44}\end{array}\right]\left\{\begin{array}{c}{y}_{1,1}\\ y_{2,1}\\ y_{1,2}\\ y_{2,2+∆t}\end{array}\right\}=\left\{\begin{array}{c}{y}_{10,\mathrm{LNG}}\left(t\right)\\ y_{20,\mathrm{LNG}}\left(t\right)\\ B_3-a_{31}{y}_{10,\mathrm{LNG}}\left(t\right)-a_{32}{y}_{20,\mathrm{LNG}}\left(t\right)\\ B_4-a_{41}{y}_{10,\mathrm{LNG}}\left(t\right)-a_{42}{y}_{20,\mathrm{LNG}}\left(t\right)\end{array}\right\}$$

(48)

Detailed mathematical differential equations were developed for modelling the hydrodynamic behaviour of LNG in the PCHE. The full model was implemented using Microsoft Visual Studio.

3. Results of LNG Regasification System Dynamic and Hydrodynamic Processes

In the mathematical model, the solution time step is 10⁻⁶ s, the discretisation step of pipe L6 is 0.05 m, and the LNG and propane flows’ discretisation step of the PCHE tube is 0.01615 m. The simulation of a mathematical model for the LNG regasification process was conducted to verify changes in hydrodynamics (velocity and pressure) throughout the total regasification system (including the pump, in pipe L6, and headers and channels of the PCHE), changes in dynamics (angular velocity and pressure changes) as the multistage pump operates, and their impact on the overall system. The regasification process of LNG begins when the LNG starts transferring by a high-pressure pump to the LNG PCHE. This involves initiating the electric motor EM3, causing the LNG to be transferred by the HP booster pump 3 through pipe L6 to the LNG PCHE. 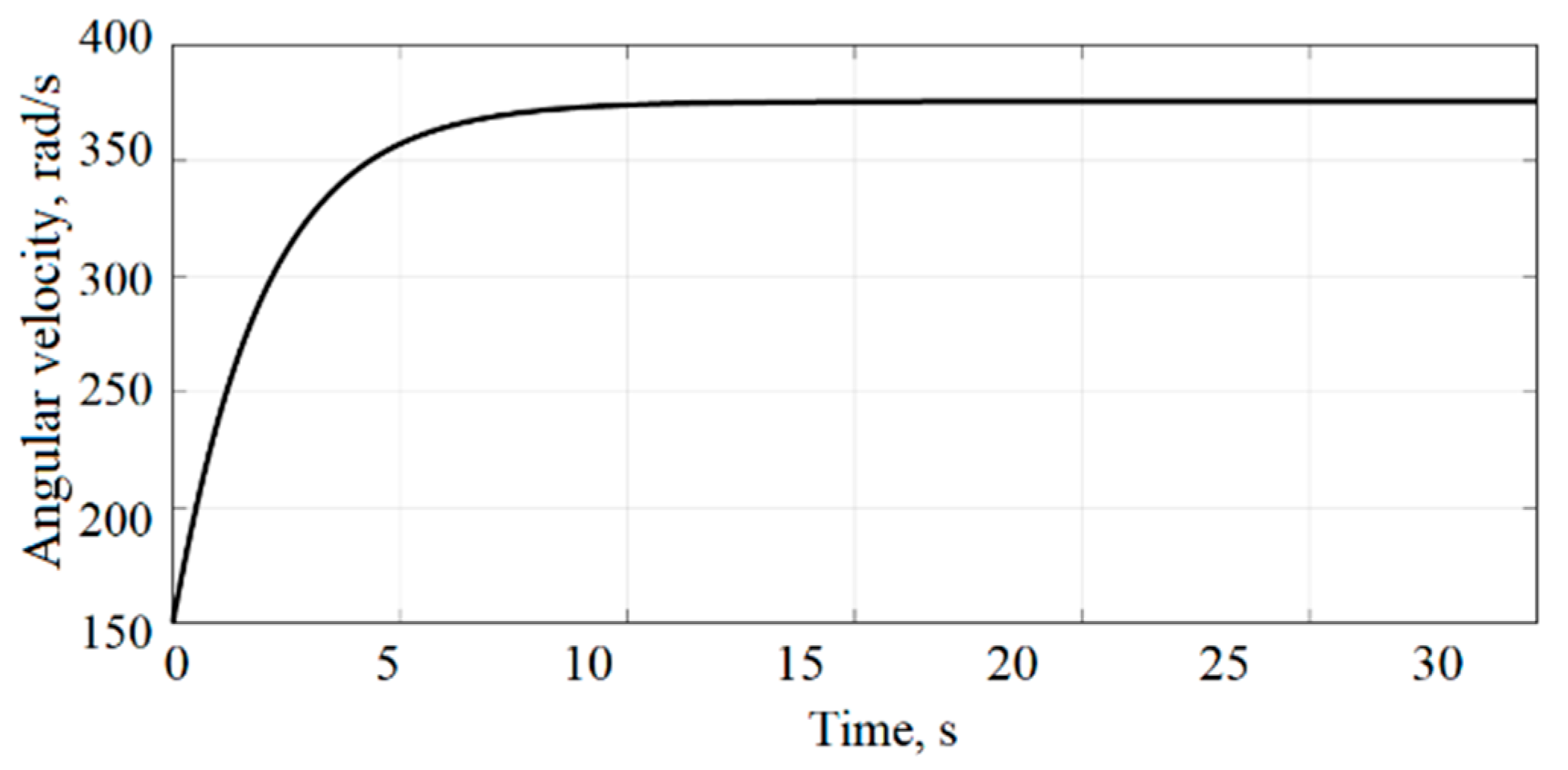Figure 9 shows the changes in angular velocity (ω_EM3). The angular velocity values stabilise after 10 s, with ω_EM3 reaching 376 rad/s.

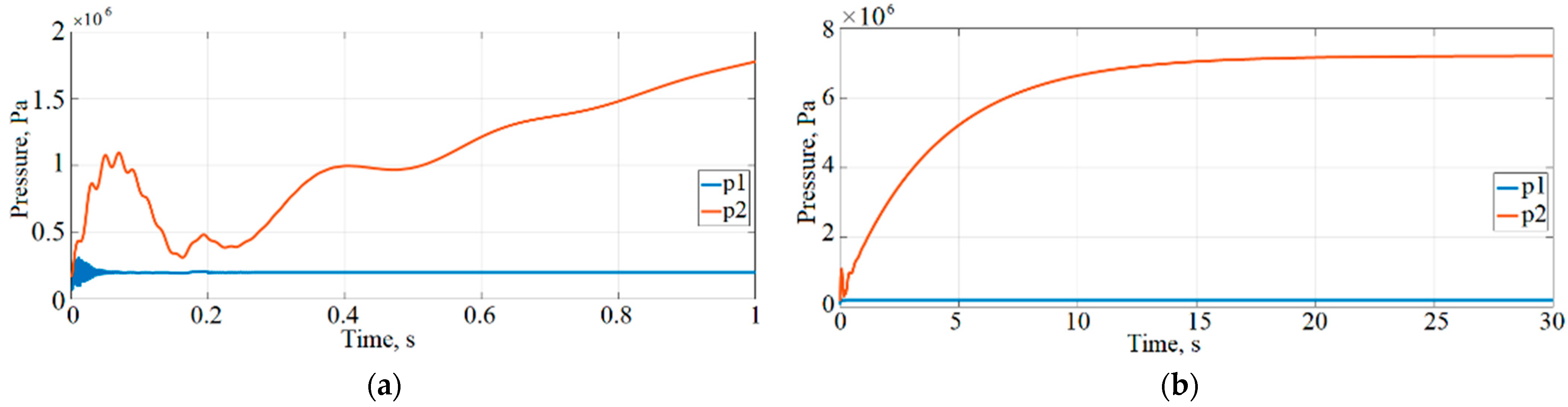
Figure 10a,b present observations of the pressure flow changes through the passages of HP booster pump 3. In Figure 10a, the blue line represents p₁, and the red line represents p₂, illustrating that LNG starts transferring from the L6 pipe to the input of HP booster pump 3 (pressure p₁) and the outlet of HP booster pump 3 (pressure p₂). Figure 10b shows pressure changes over the course of the simulation, indicating that from the beginning, pressure p₁ starts at a value of 0.1 · ${10}^6$ Pa and reaches around 7 · ${10}^6$ Pa after 30 s at p₂.

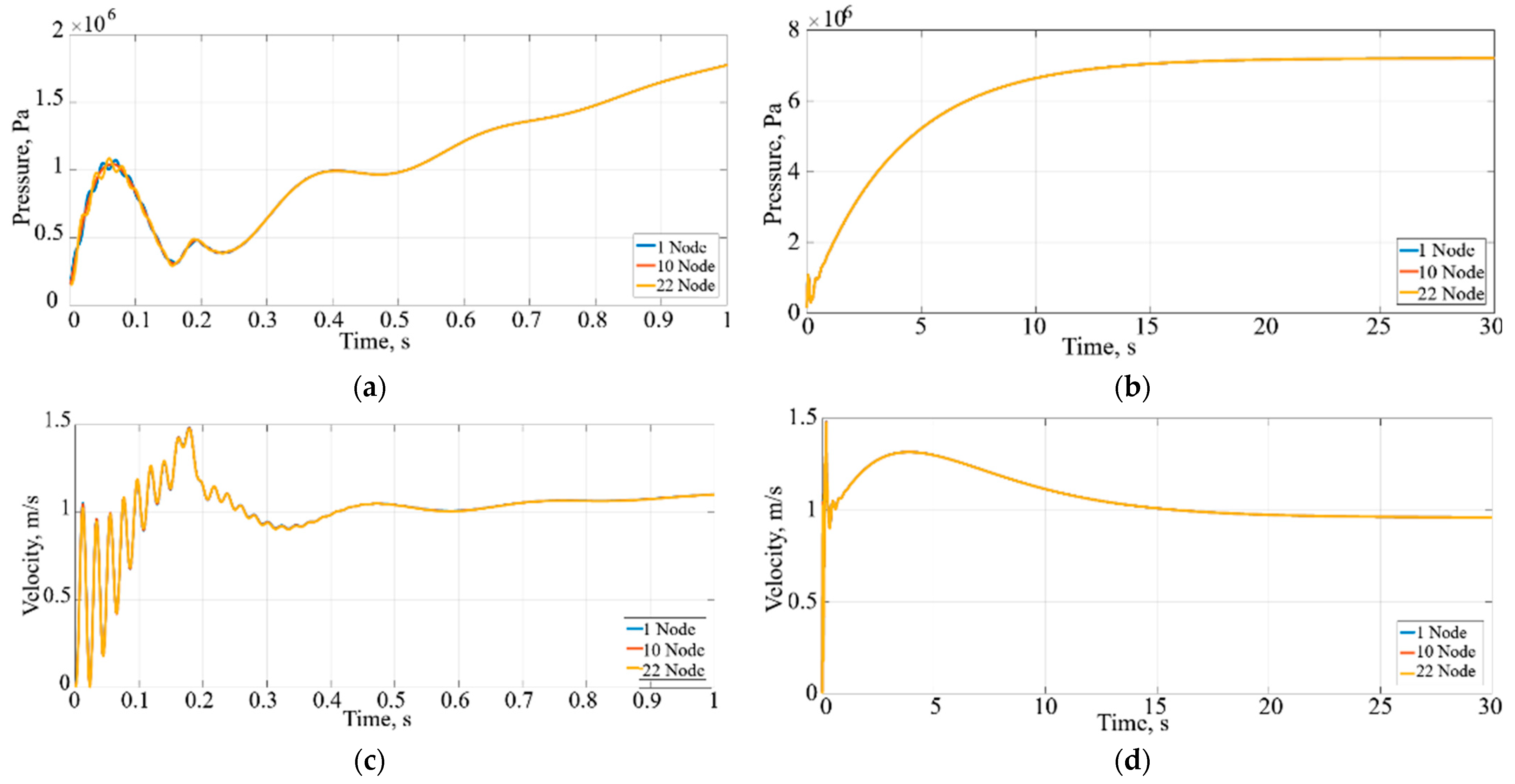
The LNG pressure and velocity changes in the L6 pipes are depicted in Figure 11. Figure 11a,b illustrate the changes in pressure values in the L6 pipe, as HP booster pump 3 starts at 0.1 ${10}^6$ Pa and reaches around 7 · ${10}^6$ Pa after 30 s.

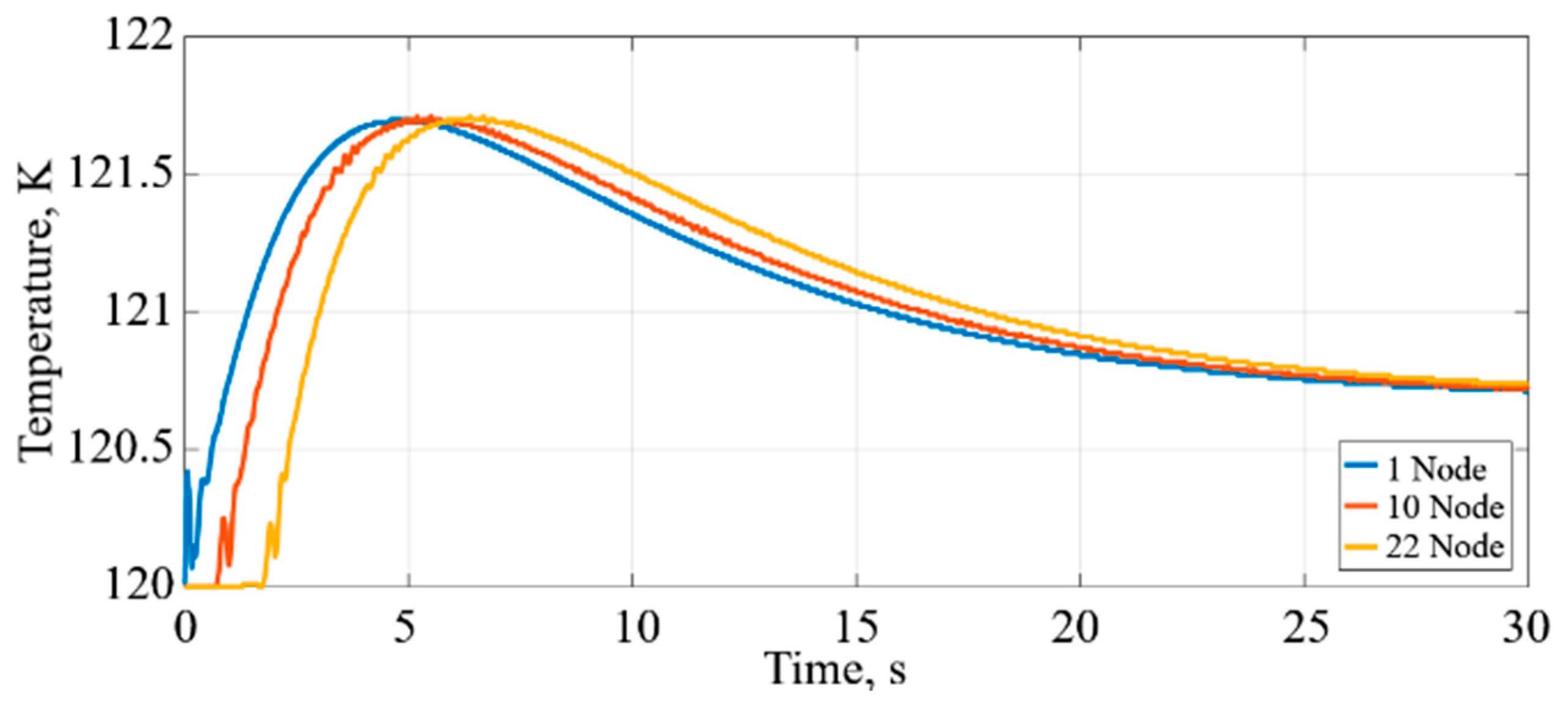
Figure 11c,d indicate that LNG velocity starts at 1 m/s and reaches 1.5 m/s after 0.18 s. After 15 s, the LNG velocity stabilises in the L6 pipe at around 1 m/s. Figure 12 indicates LNG temperature changes in the L6 pipe.

The variations in hydrodynamic (pressure and velocity, mass flow) and thermodynamic (temperature, heat transfer, phase change) processes at any time are presented at the system’s nodes, and are indicated by curves of different colours in Figure 12. The curves show different changes at other nodes and at each time. The LNG temperature changes are similar to those of HP booster pump 3. The LNG temperature value reaches approximately 120.7 K after 30 s.

Also, thermodynamic parameters were investigated, such as temperature and phases (densities of liquid and vapour) of headers and sections of LNG and propane channels in the PCHE, heat release through the walls into LNG, the heat transfer coefficient, and temperature changes between the walls of the PCHE. 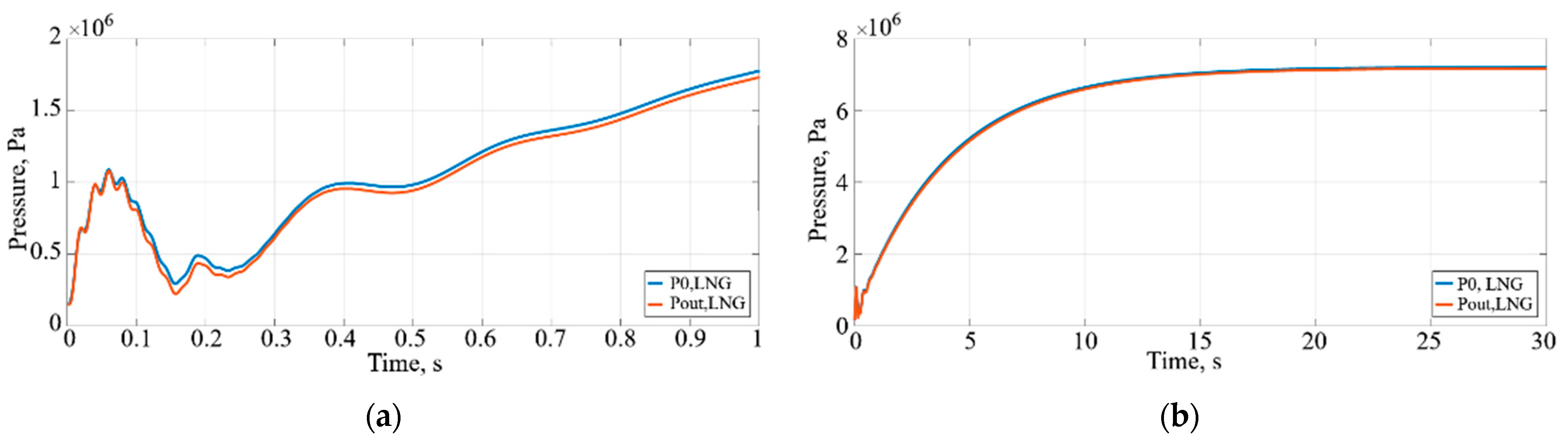The main focus of the simulation is to observe technical parameters (p_in1,LNG, T_in1,LNG, G_in1,LNG, y_in1,LNG, y_in2,LNG etc.) when LNG enters the PCHE. Firstly, to prevent the misdistribution of the LNG flow rate from causing a large pressure drop in the core channels, pressure changes (P_0,LNG, P_out,NG) are monitored in the headers. Figure 13a shows that in the headers, the pressure reaches 1.7 · ${10}^6$ Pa after 1 s. Figure 13b presents results indicating that after 4 s, the pressure reaches the critical value of 4.59 · ${10}^6$ Pa, and after 20 s, it reaches 7 · ${10}^6$ Pa. The calculated difference from Figure 13a between P_0,LNG band P_out,LNG after 1 s is around 50 kPa.

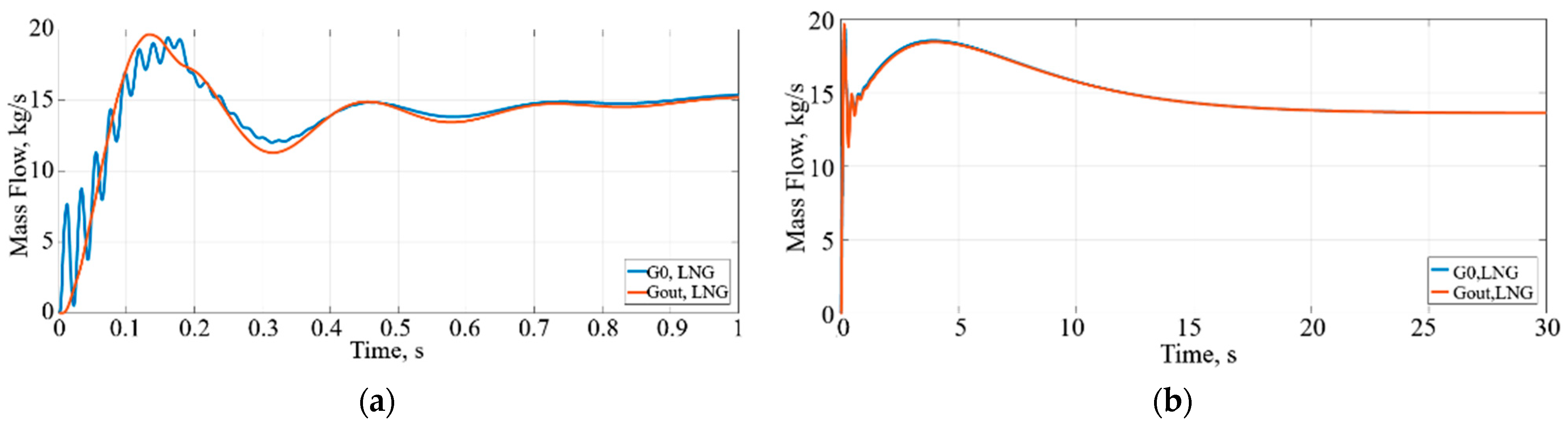
Mass flows (G_0,LNG, G_out,LNG) represent the input and output of headers. It can be seen from Figure 14a that the mass flow reaches its maximum of around 19 kg/s after 0.16 s, then starts decreasing until 0.3 s. After 20 s, the mass flow stabilises at 14 kg/s (Figure 14).

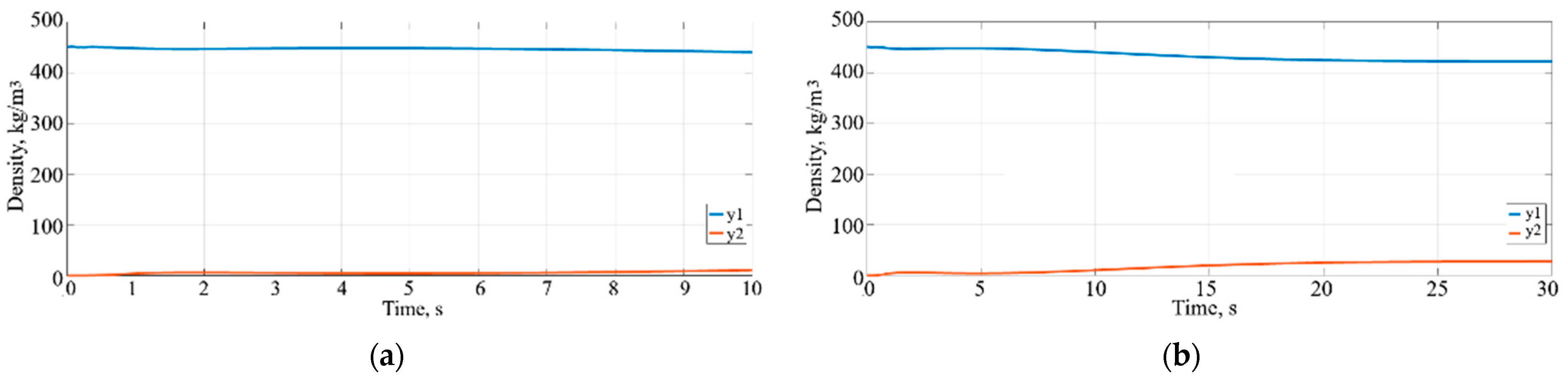
The phases of LNG liquid (y₁) and LNG vapour (y₂) are observed in the headers during the solution time. In Figure 15a, only the liquid phase is represented by the blue line. After 5 s, it starts decreasing, while the vapour phase (y₂) begins to increase (shown in red, as depicted in Figure 15b).

Figure 15b shows that the liquid density y₁ decreases from 460 kg/m³ to 410 kg/m³, while the vapour density increases from 0 to 50 kg/m³.

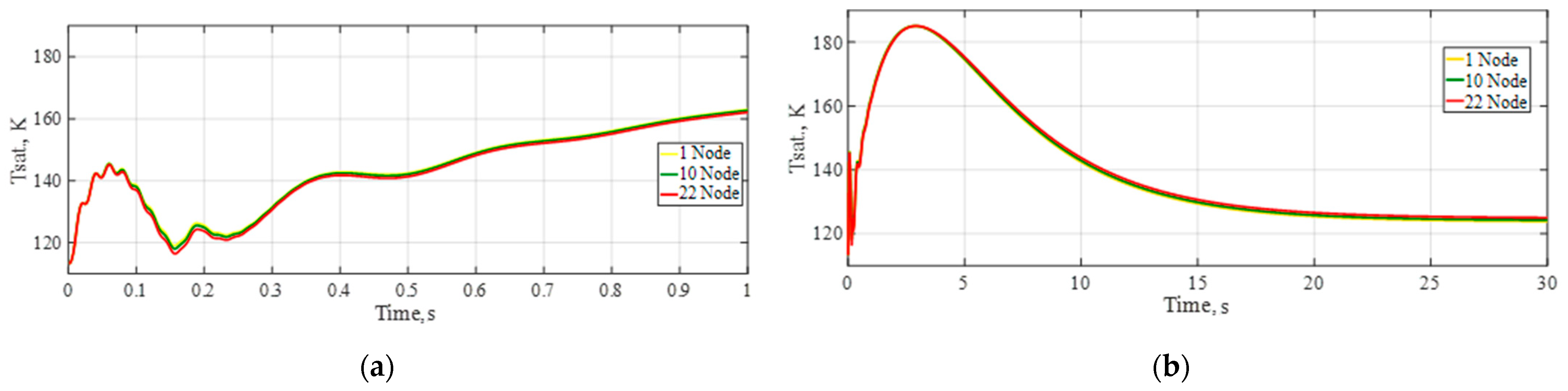
The main parameter is Tsat., which indicates the beginning of condensation and evaporation, depending on the temperature of LNG and pressure changes. The model of Lee [13] introduces equations that determine the vaporisation (evaporation) (Tl > Tsat.) and condensation processes (Tl < Tsat.). Figure 16 shows that about 4 s after reaching the critical temperature and pressure of LNG (the critical pressure being 4.59 · ${10}^6$ Pa), Tsat. starts decreasing from point 185 K. Additionally, when reaching critical conditions, LNG exhibits improved heat transfer characteristics [5].

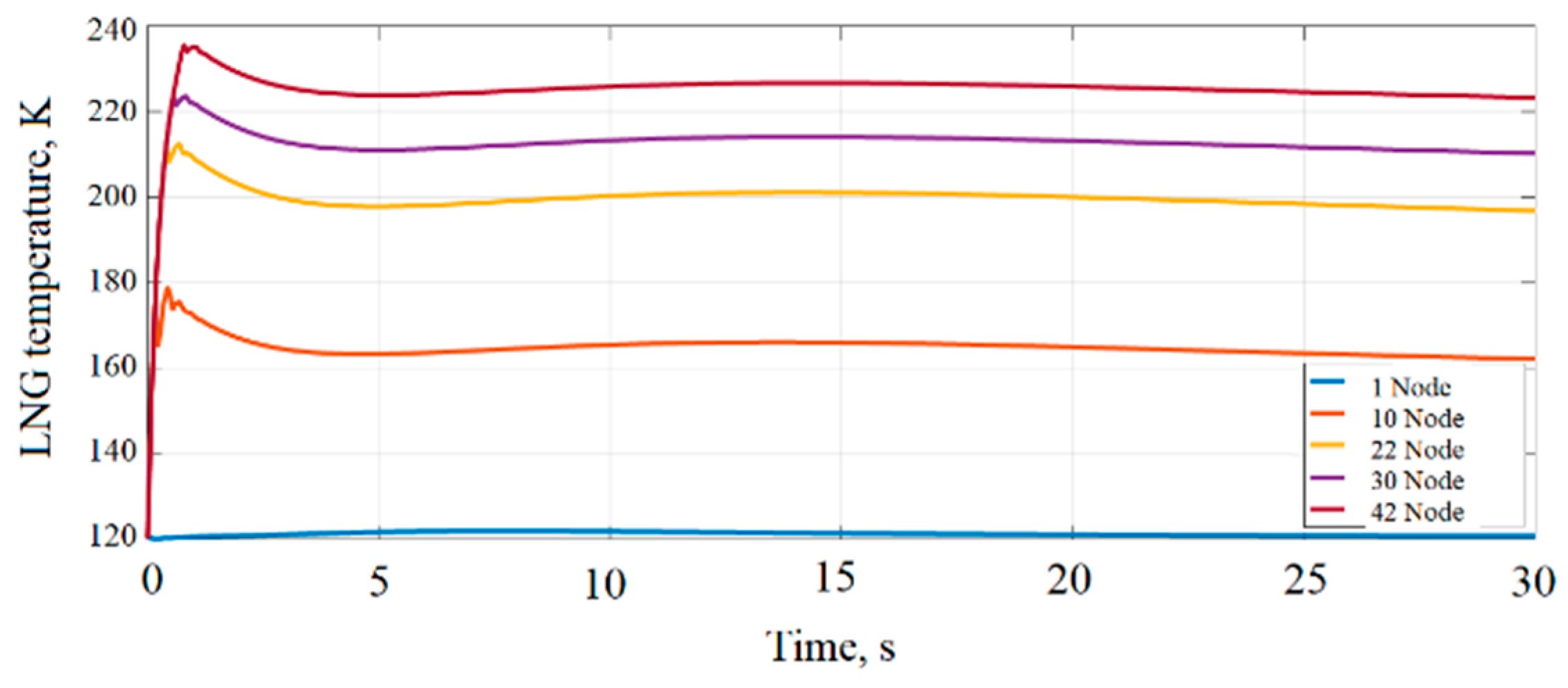
As can be seen in Figure 17, the liquid temperature varies between 120 and 222 K during the simulation time. This indicates that the evaporation process is taking place and no liquid is left.

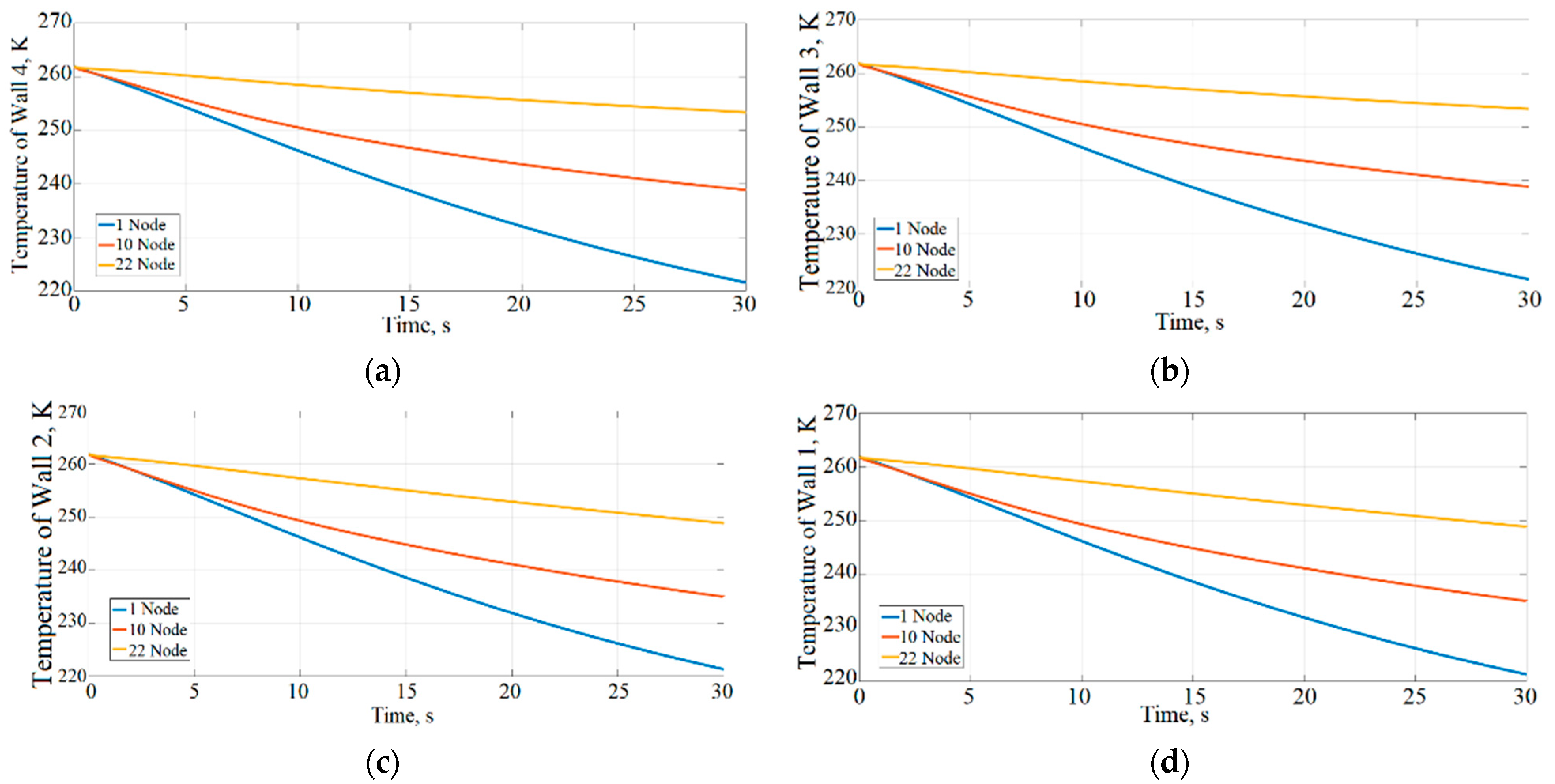
The wall temperature changes in the PCHE are introduced in Figure 18.

Since periodic flow and heat transfer occur on both tube sides (cold and hot), the temperature distribution has an impact on velocity distribution [12]. Observing the temperatures of walls, it can be seen in Figure 19a–d that temperatures decrease throughout the entire solution time, starting from a value of 262 K.

This results in a minor change in the heat transfer coefficient, which is influenced by the channel diameter, the thermal conductivity of the wall, and the Nusselt number.

Propane observations from the hot side were analysed to observe the reliable evaporation process, and the impact of the LNG evaporation process was examined. The propane saturation temperature changes in the PCHE tube are important parameters to indicate vaporisation or condensation processes. From the propane side channels, the propane temperature must be reduced below the saturation point to achieve condensation conditions.

Simulation with Different Pressure Value Variations

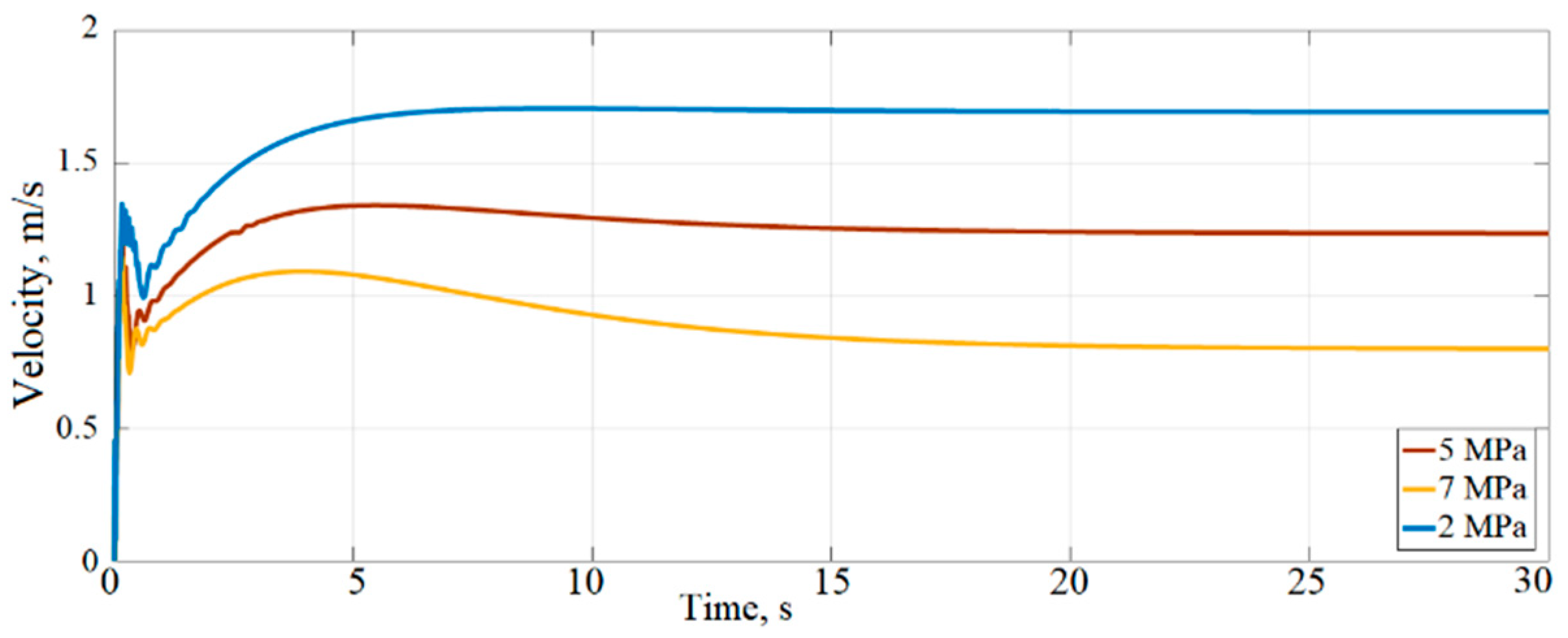
The simulation was conducted with a variation in pressure to verify LNG evaporation quality. In this case, coefficient values are determined as 11/K/s.

Figure 20 presents that at higher pressure, a lower velocity is observed (indicated by the yellow line). One of the impacts of the LNG regasification process is that at higher outlet pressure, there is higher viscosity and lower velocity, which could affect heat transfer between the walls [33,34]. On the other hand, a higher heat transfer value increases heat transfers and improves the quality of the LNG evaporation process. Also, at the same inlet temperature, as the outlet pressure increases, the frictional pressure drop decreases, and the heat transfer coefficient increases. For the decrease in the frictional pressure drop, the significant increase in density at higher pressure leads to a decrease in velocity, which greatly reduces the pressure drop [5].

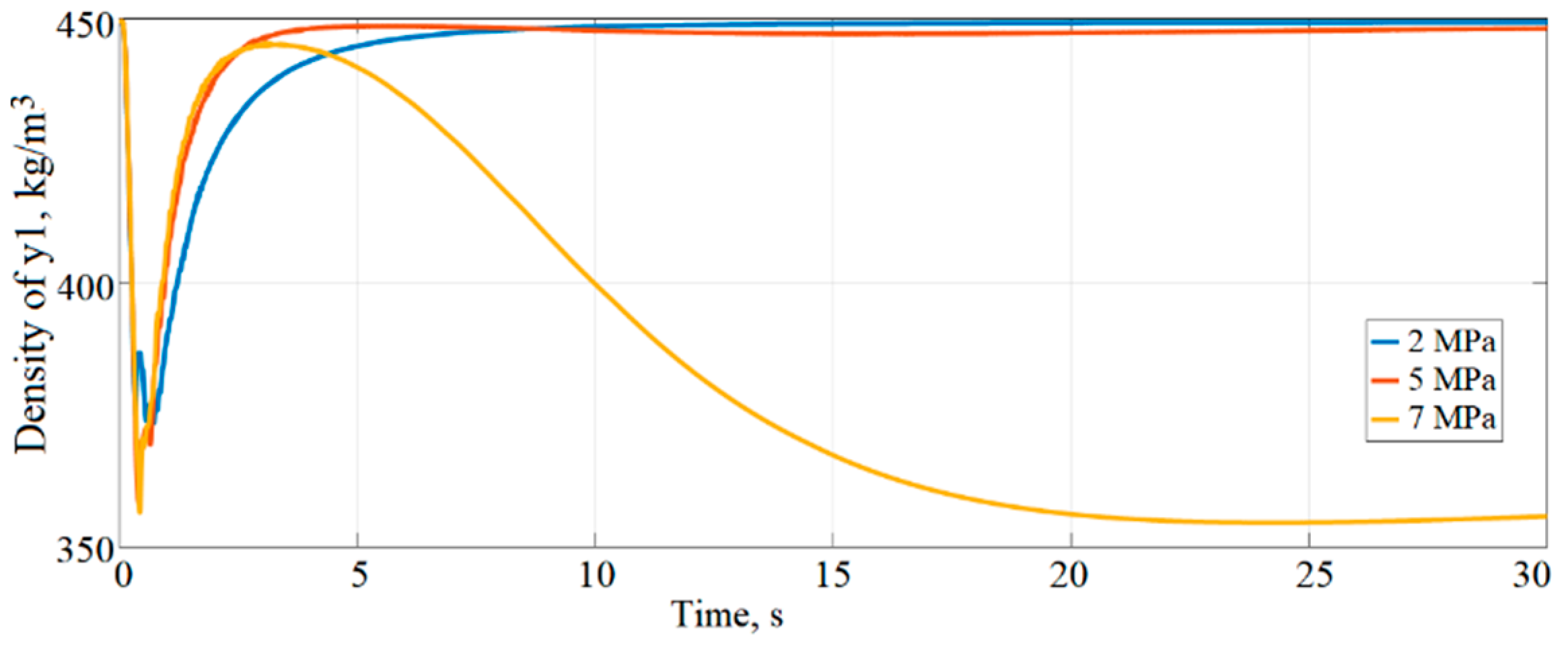
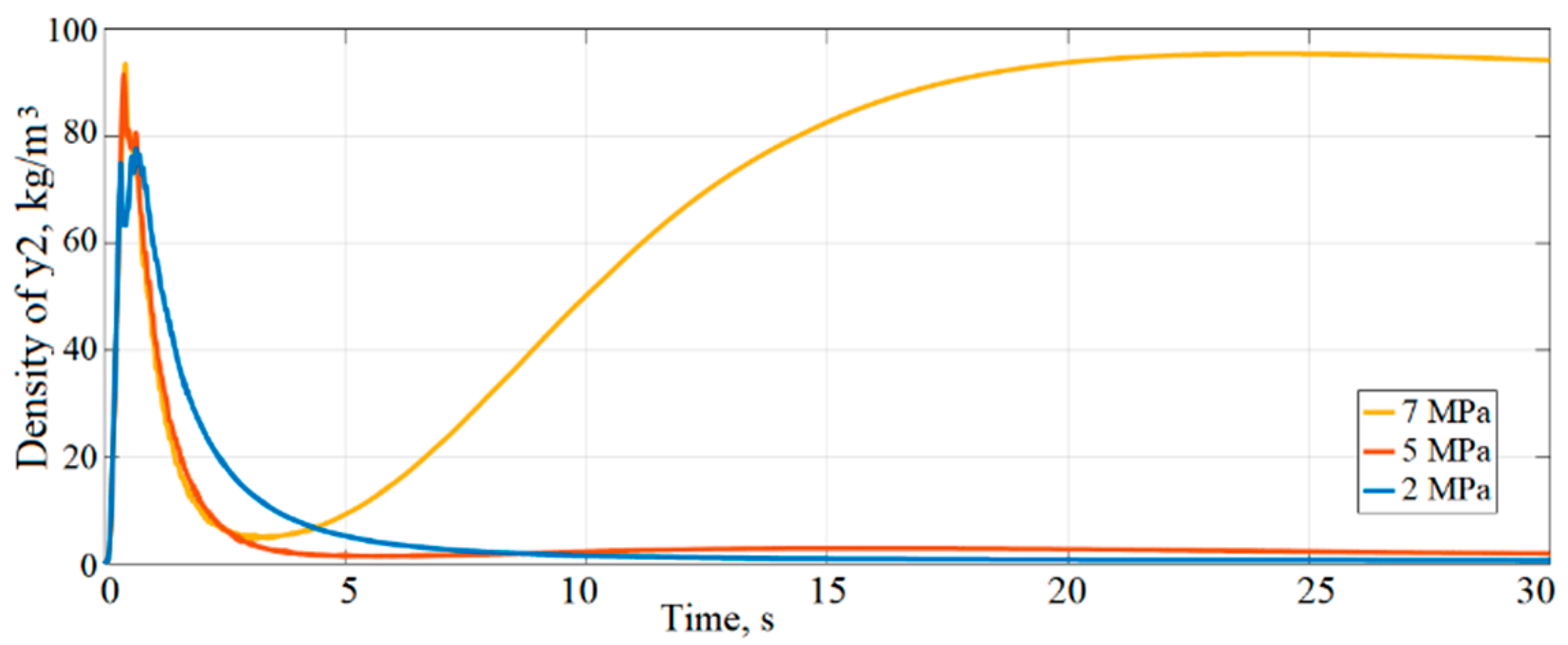
To observe the LNG evaporation process and understand how the outlet pressure impacts the quality of evaporation, the density of phases y₁ and y₂ is analysed. The phase transition, as depicted in Figure 21 and Figure 22, indicates that a higher outlet pressure leads to a more favourable phase transition. Consequently, with a pressure of 7 MPa during the simulation time, the liquid phase density changes from 450 kg/m³ to 356 kg/m³, whereas with an outlet pressure of 5 MPa, it remains near the same value at 448 kg/m³. To compare the beginning of the simulation, where the density value of vapour is 0, with the end of the solution time, it can be observed that the vapour density values are approximately 90 kg/m³ at the 7 MPa outlet pressure. Conversely, when the pressure is 2 or 5 MPa, the evaporation process is slow, and the density of vapour remains around 3 kg/m³.

As concluded previously, a higher pressure is needed to reach the critical pressure and temperature points faster, initiating the evaporation process and ensuring its efficiency.

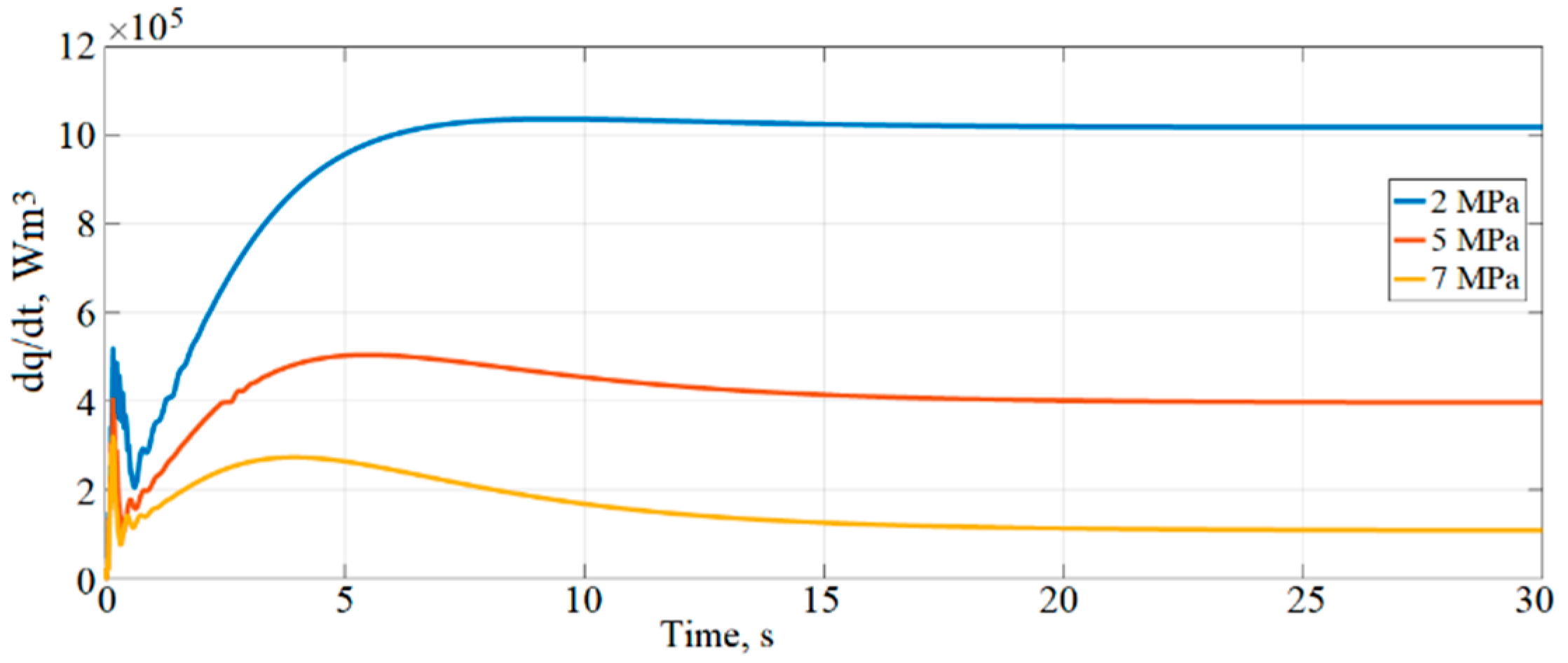
The variations in the heat release due to LNG fluid friction between the channel walls under different outlet pressures are shown in Figure 23. It can be seen that when the output pressure is 2 MPa, the highest heat release (10.10 W/m³) is determined during the simulation time due to the reason that, in this case, the velocity of LNG reaches the highest values, as shown in Figure 23.

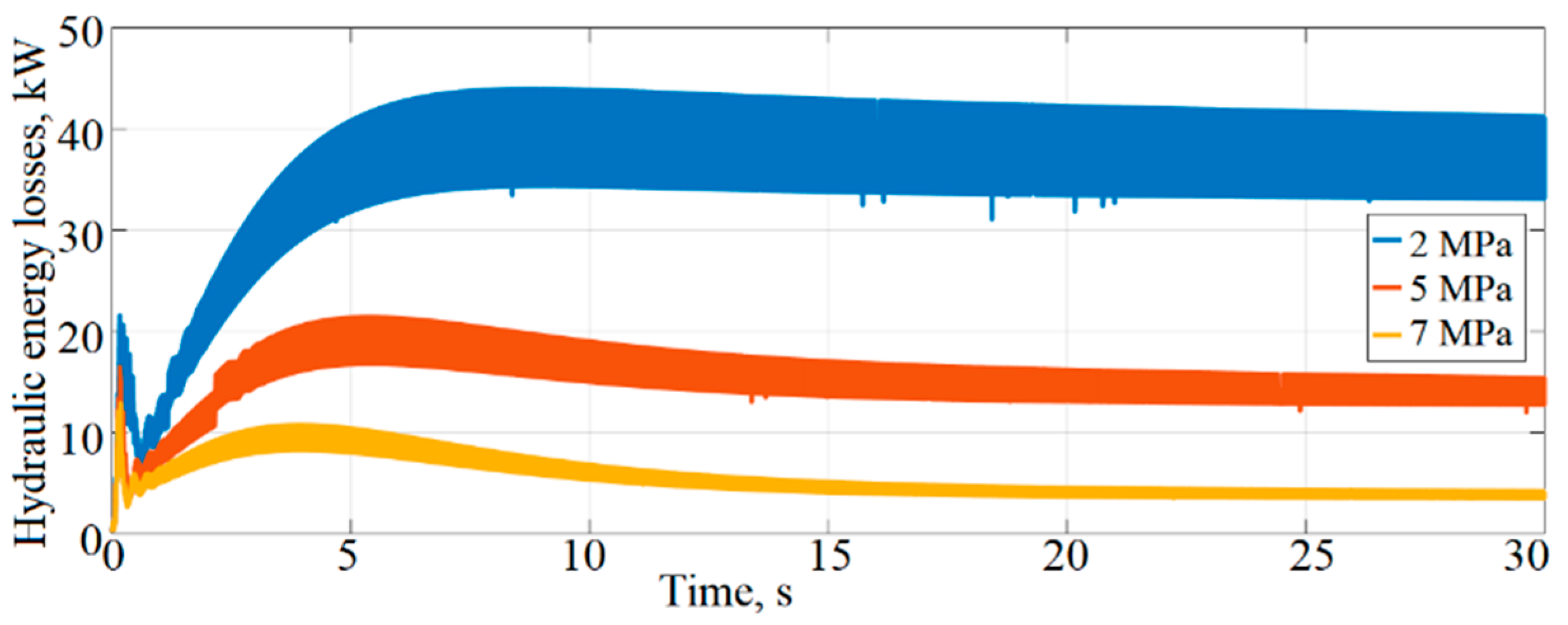
In other cases, when the output pressure is 5 and 7 MPa, heat release due to LNG fluid friction (dq/dt) is determined at 4.2 and 1.7 W/m³ at the end of the solution time. By observing the results in Figure 24 after 30 s, it can be obtained that hydraulic energy losses in the total LNG regasification system were achieved at ~41.3 kW when the outlet pressure was 2 MPa, ~12.75 kW when the outlet pressure was 5 MPa, and ~4.24 kW when the outlet pressure was 7 MPa. From the investigation, it could be concluded that increasing the outlet pressure of the system results in a decrease in the velocity of LNG. In this case, the evaporation process accelerates, and hydraulic losses decrease.

Upon observing all hydraulic energy losses in the system in comparison to the total power of the electric motor at the end of the simulation, it is determined that the hydraulic energy losses are as follows in

Table 3. Total hydraulic energy losses.

Outlet Pressure, MPa	Total Electric Motor Power, kW	Hydraulic Energy Losses, %
2	313	13
5	526	2
7	471	1

.

This constitutes 13% of the total LNG regasification system at an outlet pressure of 2 MPa with a total electric motor power of 313 kW, 2% at an outlet pressure of 5 MPa with a total power of 526 kW, and 1% at an outlet pressure of 7 MPa with a total electric motor power of 471 kW. This research shows that increasing the outlet pressure in the system leads to a decrease in the speed of the LNG flow in the heat exchanger and an increase in heat output exchange; i.e., the evaporation process is accelerated, and hydraulic losses are reduced.

4. Conclusions

This research investigates the hydrodynamic and dynamic processes in the real LNG regasification system of FSRUs (LNG Terminal of Klaipeda City) in system start-up (until 30 s) mode.

From the investigation of the total LNG regasification system, it could be concluded that increasing the outlet pressure of the system results in a decrease in the velocity of LNG. In this case, the evaporation process accelerates, and hydraulic losses decrease. It is found that the total hydraulic energy losses of the total LNG regasification system are approximately 41.3 kW (with outlet pressure of 2 MPa), 12.75 kW (with outlet pressure of 5 MPa), and 4.24 kW (with outlet pressure of 7 MPa).

Using a developed mathematical model, hydraulic energy losses in the total LNG regasification system are evaluated. When considering all hydraulic energy losses in the entire LNG regasification systems compared to the total power of the electric motor at the end of the simulation, it is found that hydraulic energy losses constitute 13% of the total LNG regasification system at an outlet pressure of 2 MPa with a total electric motor power of 313 kW, 2% at an outlet pressure of 5 MPa with a total power of 526 kW, and 1% at an outlet pressure of 7 MPa with a total electric motor power of 471 kW.

The implementation of the results of these studies of hydrodynamic and thermodynamic processes in the total LNG regasification systems allow for determination of and reductions in hydraulic energy losses inside the systems. The obtained results could be used to increase the accuracy of process analysis for various LNG construction projects or monitoring systems.