A Critical Review of Constitutive Models Applied to Ice-Crushing Simulations
Abstract
1. Introduction
2. Ice Strength Envelopes for Yield and Failure Criteria
3. Rheological Theories Applied in Constitutive Models for Ice Crushing Simulations
3.1. Viscoelasticity
3.2. Plasticity
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
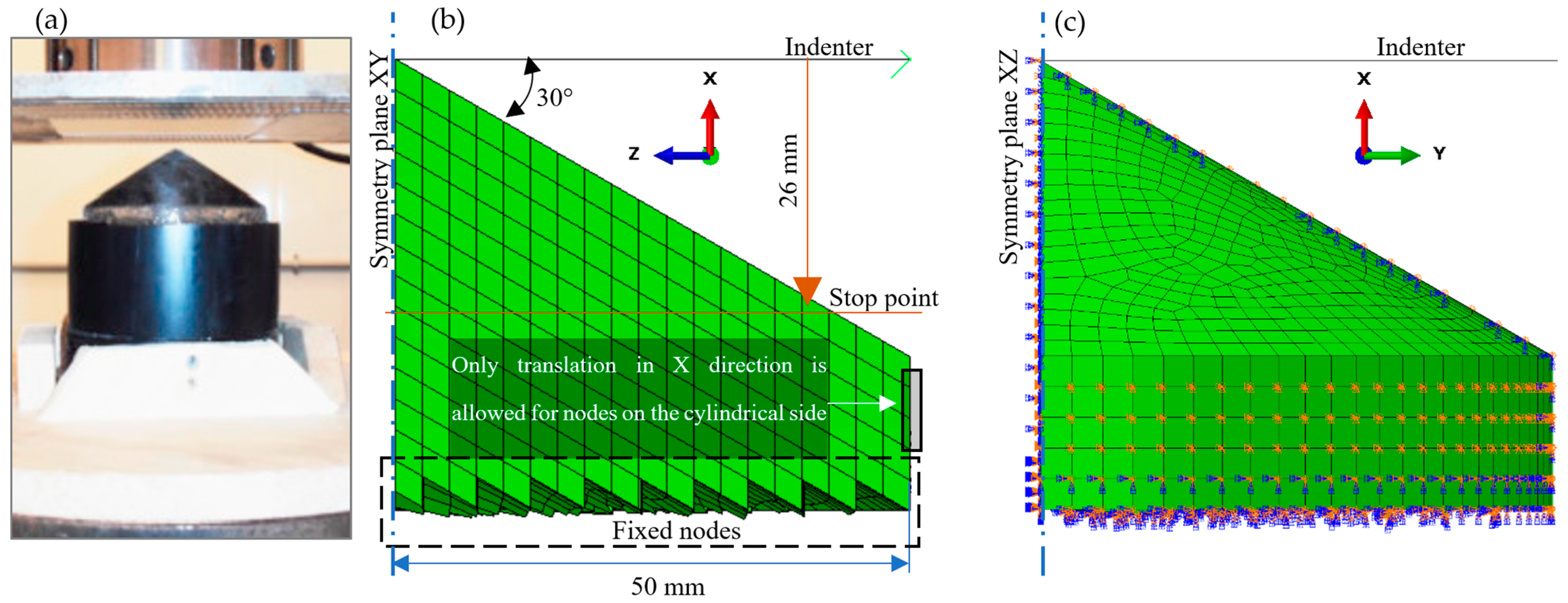
Appendix A. Conical Ice-Crushing Test: Physical and Numerical Model Setup
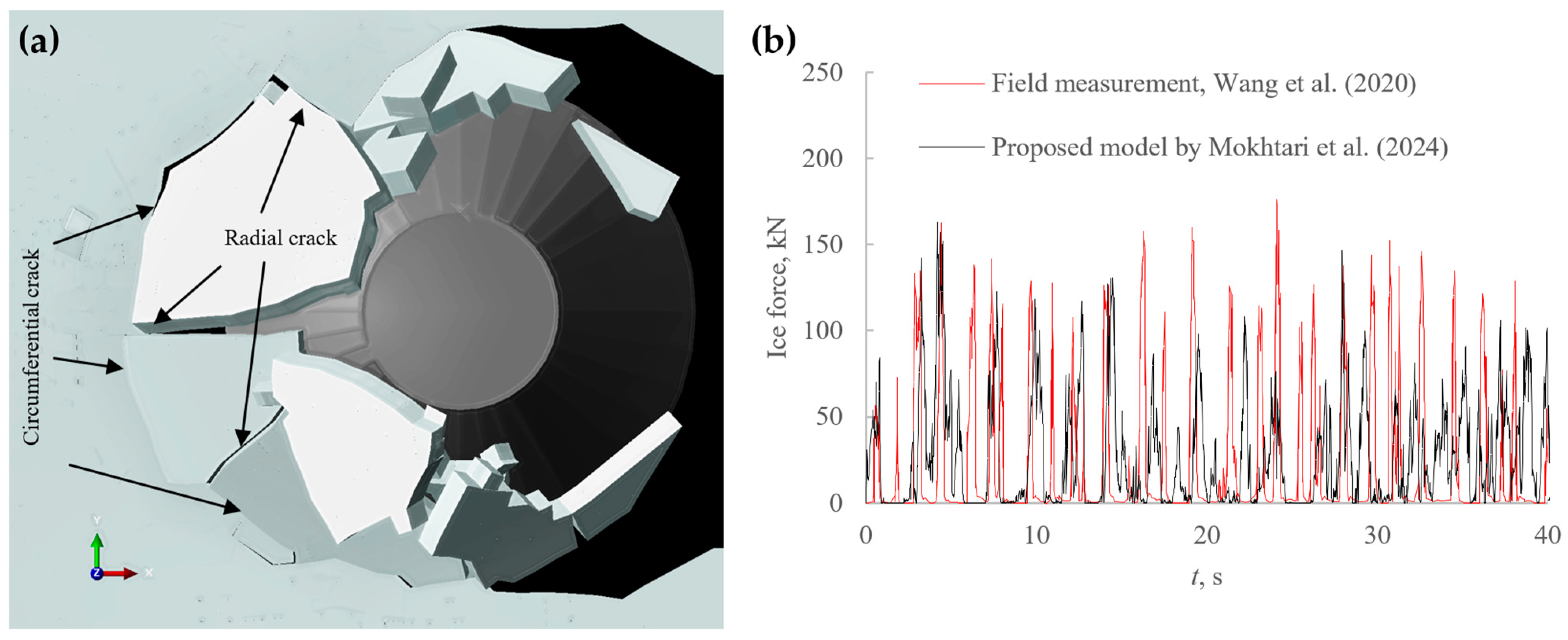
Appendix B. Performance Assessment of the Viscoelastic Damage Models [9]



References
- Meier, W.N.; Hovelsrud, G.K.; Van Oort, B.E.; Key, J.R.; Kovacs, K.M.; Michel, C.; Haas, C.; Granskog, M.A.; Gerland, S.; Perovich, D.K. Arctic sea ice in transformation: A review of recent observed changes and impacts on biology and human activity. Rev. Geophys. 2014, 52, 185–217. [Google Scholar] [CrossRef]
- Brosnan, I.G.; Leschine, T.M.; Miles, E.L. Cooperation or conflict in a changing Arctic? Ocean Dev. Int. Law 2011, 42, 173–210. [Google Scholar] [CrossRef]
- Hammer, T.C.; Hendrikse, H. Experimental study into the effect of wind-ice misalignment on the development of ice-induced vibrations of offshore wind turbines. Eng. Struct. 2023, 286, 116106. [Google Scholar] [CrossRef]
- Barooni, M.; Nezhad, S.K.; Ali, N.A.; Ashuri, T.; Sogut, D.V. Numerical study of ice-induced loads and dynamic response analysis for floating offshore wind turbines. Mar. Struct. 2022, 86, 103300. [Google Scholar] [CrossRef]
- King, T.; Ralph, F.; Fuglem, M.; Stuckey, P.; Thijssen, J.; Turnbull, I.; Huang, Y.; Talimi, V.; Liu, L.; Yulmetov, R. Ice Risk Analysis for Floating Wind Turbines, Offshore Newfoundland and Labrador. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 2–5 May 2022; p. D031S031R007. [Google Scholar]
- Schulson, E.M. Brittle failure of ice. Eng. Fract. Mech. 2001, 68, 1839–1887. [Google Scholar] [CrossRef]
- Jones, S.J. A review of the strength of iceberg and other freshwater ice and the effect of temperature. Cold Reg. Sci. Technol. 2007, 47, 256–262. [Google Scholar] [CrossRef]
- Shazly, M.; Prakash, V.; Lerch, B.A. High strain-rate behavior of ice under uniaxial compression. Int. J. Solids Struct. 2009, 46, 1499–1515. [Google Scholar] [CrossRef]
- Mokhtari, M.; Kim, E.; Amdahl, J. A non-linear viscoelastic material model with progressive damage based on microstructural evolution and phase transition in polycrystalline ice for design against ice impact. Int. J. Impact Eng. 2023, 176, 104563. [Google Scholar] [CrossRef]
- Mokhtari, M.; Kim, E.; Amdahl, J. A rate and pressure dependent elastoplastic material model for glacial ice colliding with marine structures. In Advances in the Analysis and Design of Marine Structures; CRC Press: London, UK, 2023. [Google Scholar]
- Derradji-Aouat, A. A unified failure envelope for isotropic fresh water ice and iceberg ice. In Proceedings of the ETCE/OMAE Joint Conference Energy for the New Millenium, New Orleans, LA, USA, 14–17 February 2000. [Google Scholar]
- Nadreau, J.-P.; Michel, B. Yield and failure envelope for ice under multiaxial compressive stresses. Cold Reg. Sci. Technol. 1986, 13, 75–82. [Google Scholar] [CrossRef]
- Li, H.; Feng, Y.; Ong, M.C.; Zhao, X.; Zhou, L. An Approach to Determine Optimal Bow Configuration of Polar Ships under Combined Ice and Calm-Water Conditions. J. Mar. Sci. Eng. 2021, 9, 680. [Google Scholar] [CrossRef]
- Sotthewes, K.; Bampoulis, P.; Zandvliet, H.J.; Lohse, D.; Poelsema, B. Pressure-induced melting of confined ice. ACS Nano 2017, 11, 12723–12731. [Google Scholar] [CrossRef]
- Jones, S.J. The Confined Compressive Strength of Polycrystalline Ice. J. Glaciol. 1982, 28, 171–178. [Google Scholar] [CrossRef]
- Patil, A.; Sand, B.; Cwirzen, A.; Fransson, L. Numerical prediction of ice rubble field loads on the Norströmsgrund lighthouse using cohesive element formulation. Ocean Eng. 2021, 223, 108638. [Google Scholar] [CrossRef]
- Li, L.; Gao, Q.; Bekker, A.; Dai, H. Formulation of ice resistance in level ice using double-plates superposition. J. Mar. Sci. Eng. 2020, 8, 870. [Google Scholar] [CrossRef]
- Patil, A.; Sand, B.; Fransson, L. Numerical simulations of shear properties of ice rubble: A shear box experiment. In Proceedings of the 22nd International Conference on Port and Ocean Engineering under Arctic Conditions, Espoo, Finland, 9–13 June 2013. [Google Scholar]
- Han, D.; Lee, H.; Choung, J.; Kim, H.; Daley, C. Cone ice crushing tests and simulations associated with various yield and fracture criteria. Ships Offshore Struct. 2017, 12, S88–S99. [Google Scholar] [CrossRef]
- Jeon, S.; Kim, Y. Numerical simulation of level ice–structure interaction using damage-based erosion model. Ocean Eng. 2021, 220, 108485. [Google Scholar] [CrossRef]
- Zhang, N.; Zheng, X.; Ma, Q. Updated smoothed particle hydrodynamics for simulating bending and compression failure progress of ice. Water 2017, 9, 882. [Google Scholar] [CrossRef]
- Zhang, N.; Zheng, X.; Ma, Q.; Hu, Z. A numerical study on ice failure process and ice-ship interactions by Smoothed Particle Hydrodynamics. Int. J. Nav. Archit. Ocean Eng. 2019, 11, 796–808. [Google Scholar] [CrossRef]
- Bhat, S.; Choi, S.; Wierzbicki, T.; Karr, D. Failure analysis of impacting ice floes. J. Offshore Mech. Arct. Eng. 1991, 113, 171–178. [Google Scholar] [CrossRef]
- Pariseau, W.G. Plasticity Theory For Anisotropic Rocks And Soil. In Proceedings of the 10th U.S. Symposium on Rock Mechanics (USRMS), Austin, TX, USA, 20–22 May 1968; pp. 267–295. [Google Scholar]
- Tsai, S.W.; Wu, E.M. A general theory of strength for anisotropic materials. J. Compos. Mater. 1971, 5, 58–80. [Google Scholar] [CrossRef]
- Glen, J.W. The creep of polycrystalline ice. Proceedings of the Royal Society of London. Series A. Math. Phys. Sci. 1955, 228, 519–538. [Google Scholar]
- Dillon, H.; Andersland, O. Physics of Snow and Ice. In Proceedings of the International Conference on Low Temperature Science. I. Conference on Physics of Snow and Ice, II. Conference on Cryobiology, Sapporo, Japan, 14–19 August 1966; pp. 313–328. [Google Scholar]
- Gold, L.W. The Failure Process in Columnar-Grained Ice. Ph.D. Thesis, McGill University, Montréal, QC, Canada, 1970. [Google Scholar]
- Barnes, P.; Tabor, D.; Walker, J. The friction and creep of polycrystalline ice. Proc. R. Soc. Lond. A Math. Phys. Sci. 1971, 324, 127–155. [Google Scholar]
- Sinha, N.K. Rheology of columnar-grained ice. Exp. Mech. 1978, 18, 464–470. [Google Scholar] [CrossRef]
- Sinha, N.K.; Ehrhart, P.; Carstanjen, H.; Fattah, A.; Roberto, J. Grain boundary sliding in polycrystalline materials. Philos. Mag. A 1979, 40, 825–842. [Google Scholar] [CrossRef]
- Jordaan, I.J.; McKenna, R.F. Constitutive relations for the creep of ice. In Proceedings of the International Association for Hydraulic Research (IAHR) Symposium on Ice, Sapporo, Japan, 23–27 August 1988; pp. 47–58. [Google Scholar]
- Jordaan, I.J.; McKenna, R.F. Modelling of progressive damage in ice. In Proceedings of the International Association for Hydraulic Research (IAHR) Symposium on Ice, Sapporo, Japan, 23–27 August 1988; pp. 582–624. [Google Scholar]
- Schapery, R.A. On viscoelastic deformation and failure behavior of composite materials with distributed flaws. In 1981 Advances in Aerospace Structures and Materials, Proceedings of the Winter Annual Meeting, Washington, DC, USA, 15–20 November 1981; NASA STI: Hampton, VA, USA, 1981; pp. 5–20. [Google Scholar]
- Schapery, R.A. Correspondence principles and a generalized J integral for large deformation and fracture analysis of viscoelastic media. Int. J. Fract. 1984, 25, 195–223. [Google Scholar] [CrossRef]
- Xiao, J. Finite Element Modelling of Damage Processes in Ice-structure Interaction. Master’s Thesis, Memorial University of Newfoundland, St. John’s, NL, Canada, 1991. [Google Scholar]
- Xiao, J. Damage and Fracture of Brittle Viscoelastic Solids with Application to Ice Load Models. Ph.D. Thesis, Memorial University of Newfoundland, St. John’s, NL, Canada, 1997. [Google Scholar]
- Liu, B. Numerical Modelling of Medium Scale Indentation Tests. Master’s Thesis, Memorial University of Newfoundland, St. John’s, NL, Canada, 1994. [Google Scholar]
- Li, C. Finite Element Analysis of Ice-Structure Interaction with a Viscoelastic Model Coupled with Damage Mechanics. Master’s Thesis, Memorial University of Newfoundland, St. John’s, NL, Canada, 2002. [Google Scholar]
- Moore, P.; Jordaan, I.; Taylor, R. Explicit finite element analysis of compressive ice failure using damage mechanics. In Proceedings of the 22nd International Conference on Port and Ocean Engineering under Arctic Conditions, Espoo, Finland, 9–13 June 2013; pp. 9–13. [Google Scholar]
- Turner, J. Constitutive Behaviour of Ice under Compressive States of Stress and Its Application to Ice-Structure Interactions. Ph.D. Thesis, Memorial University of Newfoundland, St. John’s, NL, Canada, 2018. [Google Scholar]
- Jordaan, I.J.; McKenna, R.F. Processes of deformation and fracture of ice in compression. In Ice-Structure Interaction: IUTAM-IAHR Symposium on Ice-Structure Interaction, St. John’s, Newfoundland, Canada, 1989; Springer: Berlin/Heidelberg, Germany, 1991; pp. 283–309. [Google Scholar]
- Jordaan, I.J.; Stone, B.M.; McKenna, R.F.; Fuglem, M.K. Effect of microcracking on the deformation of ice. Can. Geotech. J. 1992, 29, 143–150. [Google Scholar] [CrossRef]
- Singh, S.; Jordaan, I. Constitutive behaviour of crushed ice. Int. J. Fract. 1999, 97, 171–187. [Google Scholar] [CrossRef]
- Singh, S.; Jordaan, I. Triaxial tests on crushed ice. Cold Reg. Sci. Technol. 1996, 24, 153–165. [Google Scholar] [CrossRef]
- Singh, S.K. Mechanical Behaviour of Viscoelastic Material with Changing Microstructure. Ph.D. Thesis, Memorial University of Newfoundland, St. John’s, NL, Canada, 1993. [Google Scholar]
- Xiao, J.; Jordaan, I. Application of damage mechanics to ice failure in compression. Cold Reg. Sci. Technol. 1996, 24, 305–322. [Google Scholar] [CrossRef]
- Jordaan, I.J.; Matskevitch, D.G.; Meglis, I.L. Disintegration of ice under fast compressive loading. Int. J. Fract. 1999, 97, 279–300. [Google Scholar] [CrossRef]
- McKenna, R.F.; Jordaan, I.J.; Xiao, J. Analysis of damage and energy flow in the crushed layer during rapid ice loading. In Proceedings of the IAHR Symposium of Ice, Espoo, Finland, 20–23 August 1990; pp. 231–245. [Google Scholar]
- Jonas, J.; Muller, F. Deformation of Ice under High Shear Stress. Can. J. Earth Sci. 1969, 6, 963–968. [Google Scholar] [CrossRef]
- Shi, C.; Hu, Z.; Ringsberg, J.; Luo, Y. A nonlinear viscoelastic iceberg material model and its numerical validation. Proc. Inst. Mech. Eng. Part M J. Eng. Marit. Environ. 2017, 231, 675–689. [Google Scholar] [CrossRef]
- Gagnon, R.; Gammon, P. Triaxial experiments on iceberg and glacier ice. J. Glaciol. 1995, 41, 528–540. [Google Scholar] [CrossRef]
- Michel, B.; Toussaint, N. Mechanisms and theory of indentation of ice plates. J. Glaciol. 1977, 19, 285–300. [Google Scholar] [CrossRef]
- Ince, S.T.; Kumar, A.; Paik, J.K. A new constitutive equation on ice materials. Ships Offshore Struct. 2017, 12, 610–623. [Google Scholar] [CrossRef]
- Stone, B.M.; Jordaan, I.J.; Jones, S.J.; McKenna, R.F. Damage of isotropic polycrystalline ice under moderate confining pressures. In Proceedings of the 10th International Conference on Port and Ocean Engineering under Arctic Conditions, Lulea, Sweden, 12–16 June 1989; pp. 408–419. [Google Scholar]
- Ji, S.; Chen, X.; Wang, A. Influence of the loading direction on the uniaxial compressive strength of sea ice based on field measurements. Ann. Glaciol. 2020, 61, 86–96. [Google Scholar] [CrossRef]
- Mokhtari, M.; Kim, E.; Amdahl, J. Numerical Simulation of Concurrent Flexural and Crushing Failure of Level Ice. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering, Singapore, 9–14 June 2024. [Google Scholar]
- Sinha, N.K. Short-term rheology of polycrystalline ice. J. Glaciol. 1978, 21, 457–474. [Google Scholar] [CrossRef]
- Sinha, N.K. Creep model of ice for monotonically increasing stress. Cold Reg. Sci. Technol. 1983, 8, 25–33. [Google Scholar] [CrossRef]
- Sinha, N.K. Crack-enhanced creep in polycrystalline material: Strain-rate sensitive strength and deformation of ice. J. Mater. Sci. 1988, 23, 4415–4428. [Google Scholar] [CrossRef]
- Jordaan, I.J. Mechanics of ice–structure interaction. Eng. Fract. Mech. 2001, 68, 1923–1960. [Google Scholar] [CrossRef]
- Taylor, R.S. Analysis of Scale Effect in Compressive Ice Failure and Implications for Design. Ph.D. Thesis, Memorial University of Newfoundland, St. John’s, NL, Canada, 2010. [Google Scholar]
- O’Rourke, B.J.; Jordaan, I.J.; Taylor, R.S.; Gürtner, A. Experimental investigation of oscillation of loads in ice high-pressure zones, part 1: Single indentor system. Cold Reg. Sci. Technol. 2016, 124, 25–39. [Google Scholar] [CrossRef]
- Wang, Y.; Yao, X.; Teo, F.C.; Zhang, J. Cohesive Element Method to Level Ice-sloping Structure Interactions. Int. J. Offshore Polar Eng. 2020, 30, 385–394. [Google Scholar] [CrossRef]
- Mokhtari, M.; Kim, E.; Amdahl, J. Pressure-dependent plasticity models with convex yield loci for explicit ice crushing simulations. Mar. Struct. 2022, 84, 103233. [Google Scholar] [CrossRef]
- Gagnon, R. A numerical model of ice crushing using a foam analogue. Cold Reg. Sci. Technol. 2011, 65, 335–350. [Google Scholar] [CrossRef]
- Kim, J.-H.; Kim, Y. Numerical simulation of concrete abrasion induced by unbreakable ice floes. Int. J. Nav. Archit. Ocean Eng. 2019, 11, 59–69. [Google Scholar] [CrossRef]
- Obisesan, A.; Sriramula, S. Efficient response modelling for performance characterisation and risk assessment of ship-iceberg collisions. Appl. Ocean Res. 2018, 74, 127–141. [Google Scholar] [CrossRef]
- Price, A.; Quinton, B.W.; Veitch, B. Shared-energy prediction model for ship-ice interactions. In Proceedings of the SNAME Maritime Convention, Providence, RI, USA, 27–29 October 2021. [Google Scholar]
- Gagnon, R.; Wang, J. Numerical simulations of a tanker collision with a bergy bit incorporating hydrodynamics, a validated ice model and damage to the vessel. Cold Reg. Sci. Technol. 2012, 81, 26–35. [Google Scholar] [CrossRef]
- Cao, B.; Bae, D.-M.; Sohn, J.-M.; Prabowo, A.R.; Chen, T.H.; Li, H. Numerical analysis for damage characteristics caused by ice collision on side structure. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering, Busan, Republic of Korea, 18–24 June 2016; p. V008T007A019. [Google Scholar]
- Wang, B.; Yu, H.-C.; Basu, R. Ship and ice collision modeling and strength evaluation of LNG ship structure. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering, Estoril, Portugal, 15–20 June 2008; pp. 911–918. [Google Scholar]
- Gagnon, R. Results of numerical simulations of growler impact tests. Cold Reg. Sci. Technol. 2007, 49, 206–214. [Google Scholar] [CrossRef]
- Gagnon, R. Numerical rendition of ice crushing. In Proceedings of the 20th IAHR International Symposium on Ice, Lahti, Finland, 14–18 June 2010; pp. 14–18. [Google Scholar]
- Jordaan, I.; Wells, J.; Xiao, J.; Derradji-Aouat, A. Ice crushing and cyclic loading in compression. In Proceedings of the 19th IAHR Symposium on Ice, Vancouver, BC, Canada, 6–11 July 2008; pp. 801–813. [Google Scholar]
- Singh, S.K.; Jordaan, I.J.; Xiao, J.; Spencer, P.A. The flow properties of crushed ice. J. Offshore Mech. Arct. Eng. 1995, 117, 276–282. [Google Scholar] [CrossRef]
- Wells, J.; Jordaan, I.; Derradji-Aouat, A.; Taylor, R. Small-scale laboratory experiments on the indentation failure of polycrystalline ice in compression: Main results and pressure distribution. Cold Reg. Sci. Technol. 2011, 65, 314–325. [Google Scholar] [CrossRef]
- Kim, H. Simulation of compressive ‘cone-shaped’ ice specimen experiments using LS-DYNA. In Proceedings of the 13th International LS-DYNA Users Conference, Dearborn, MI, USA, 8–10 June 2014. [Google Scholar]
- Kim, H.; Daley, C.; Colbourne, B. A numerical model for ice crushing on concave surfaces. Ocean Eng. 2015, 106, 289–297. [Google Scholar] [CrossRef]
- Kim, H.; Quinton, B. Evaluation of moving ice loads on an elastic plate. Mar. Struct. 2016, 50, 127–142. [Google Scholar] [CrossRef]
- Deshpande, V.S.; Fleck, N.A. Isotropic constitutive models for metallic foams. J. Mech. Phys. Solids 2000, 48, 1253–1283. [Google Scholar] [CrossRef]
- ABAQUS Standard User’s Manual. Version 6.14; Dassault Systemes Simulia Corp.: Providence, RI, USA, 2014.
- Hallquist, J. LS-Dyna Keyword User’s Manual; Livermore Software Technology Corporation (LSTC): Livermore, CA, USA, 2006. [Google Scholar]
- Liu, Z.; Amdahl, J.; Løset, S. Plasticity based material modelling of ice and its application to ship–iceberg impacts. Cold Reg. Sci. Technol. 2011, 65, 326–334. [Google Scholar] [CrossRef]
- Mokhtari, M. Ice-Elastoplastic-Material-Model. Available online: https://github.com/NTNU-IMT/Ice-Elastoplastic-Material-Model (accessed on 8 January 2023).
- Mokhtari, M.; Kim, E.; Amdahl, J. Numerical Simulation of an Aluminium Panel Subject to Ice Impact Load Using a Rate and Pressure Dependent Elastoplastic Material Model for Ice. In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering, Melbourne, Australia, 11–16 June 2023; p. V006T007A016. [Google Scholar]
- Herrnring, H.; Kubiczek, J.M.; Ehlers, S.; Niclasen, N.O.; Burmann, M. Experimental investigation of an accidental ice impact on an aluminium high speed craft. In Progress in the Analysis and Design of Marine Structures; CRC Press: Boca Raton, FL, USA, 2017; pp. 697–704. [Google Scholar]



| Major Limitations | Elastoplasticity | Viscoelasticity | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Mohr–Coulomb | Drucker–Prager | Crushable Foam | Liu et al. [84] | Mokhtari et al. [10] | DMa by Xiao [37] | DMb by Turner [41] | iDM by Mokhtari et al. [9] | |||
| Limited to brittle range above transition strain rate | Y | Y | Y | Y | Y | |||||
| Strain rate-independent elastic stiffness | Y | Y | Y | Y | Y | |||||
| Does not account for the effects of pulverised ice viscous flow | Y | Y | Y | Y | Y | |||||
| Strain rate-independent strength | Y | Y | Y | Y | ||||||
| Does not include pressure softening of ice | Y | Y | ||||||||
| Cannot capture confining/hydrostatic pressure in ice | Y | |||||||||
| Limited to ductile range below transition strain rate | Y | |||||||||
| Inaccurate in simulating progressive crushing of ice | Y | Y | ||||||||
| Complex, parameter-intensive, and computationally expensive | Y | Y | Y | |||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mokhtari, M.; Leira, B.J. A Critical Review of Constitutive Models Applied to Ice-Crushing Simulations. J. Mar. Sci. Eng. 2024, 12, 1021. https://doi.org/10.3390/jmse12061021
Mokhtari M, Leira BJ. A Critical Review of Constitutive Models Applied to Ice-Crushing Simulations. Journal of Marine Science and Engineering. 2024; 12(6):1021. https://doi.org/10.3390/jmse12061021
Chicago/Turabian StyleMokhtari, Mojtaba, and Bernt Johan Leira. 2024. "A Critical Review of Constitutive Models Applied to Ice-Crushing Simulations" Journal of Marine Science and Engineering 12, no. 6: 1021. https://doi.org/10.3390/jmse12061021
APA StyleMokhtari, M., & Leira, B. J. (2024). A Critical Review of Constitutive Models Applied to Ice-Crushing Simulations. Journal of Marine Science and Engineering, 12(6), 1021. https://doi.org/10.3390/jmse12061021