Research on a Real-Time Prediction Method of Hull Girder Loads Based on Different Recurrent Neural Network Models
Abstract
1. Introduction
2. Hull Girder Loads Prediction Model
2.1. Basic Concepts of RNN
2.2. Input and Output Data
2.3. Data Pre-Processing
2.4. Evaluation Criterion
3. Physics-Based Numerical Simulation
3.1. Simulation Model
3.2. Simulation Load Case
4. Results and Discussion
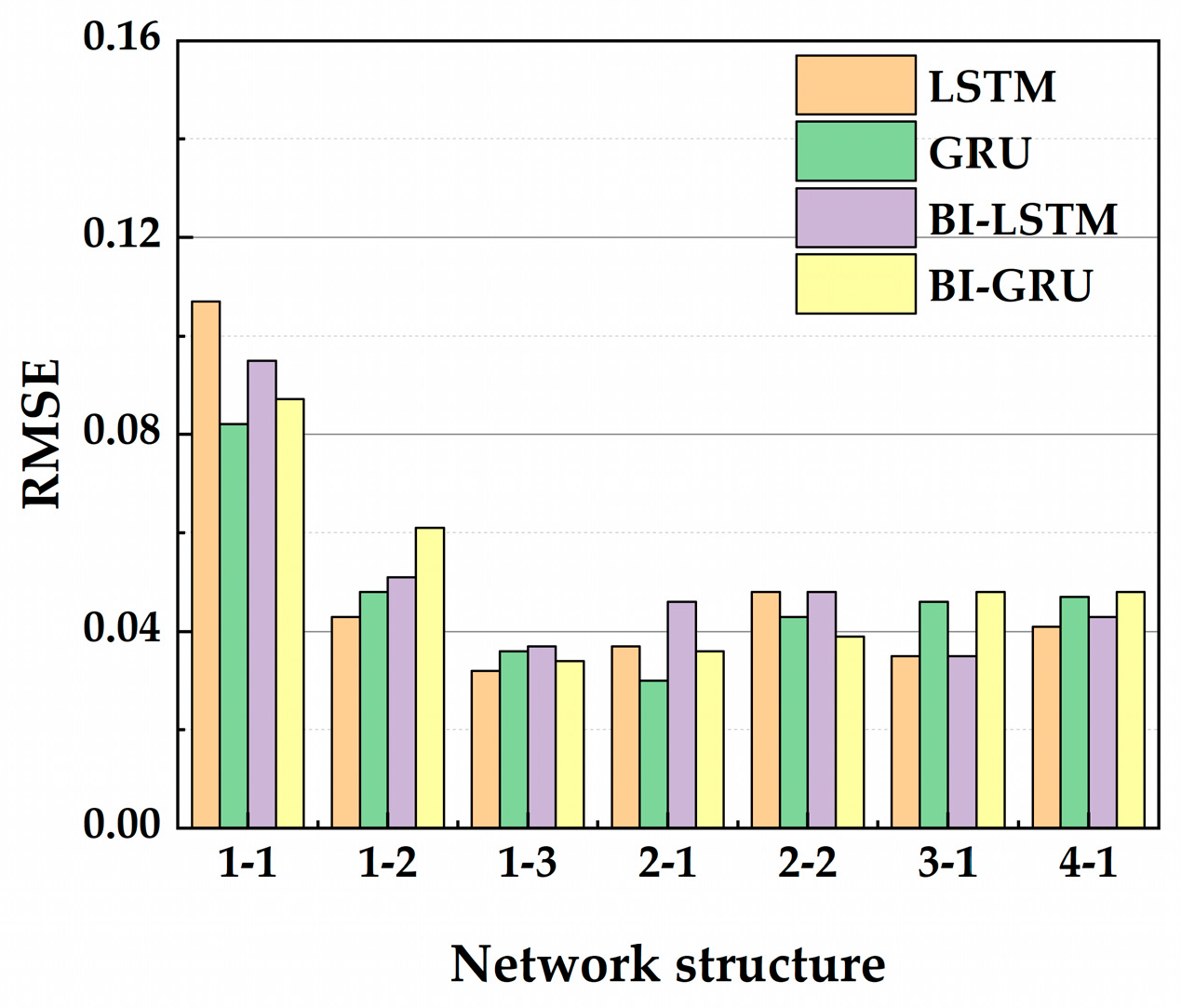
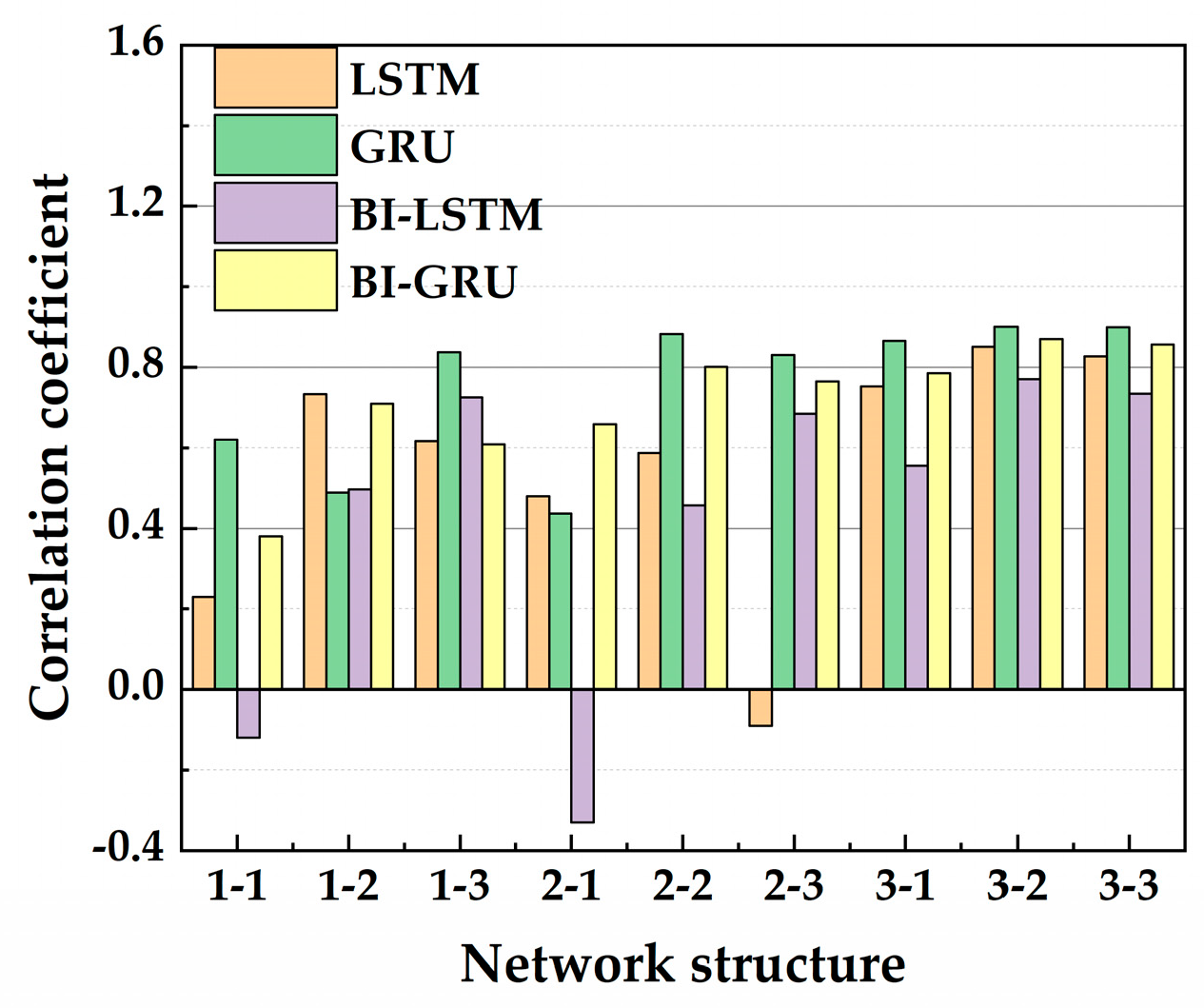
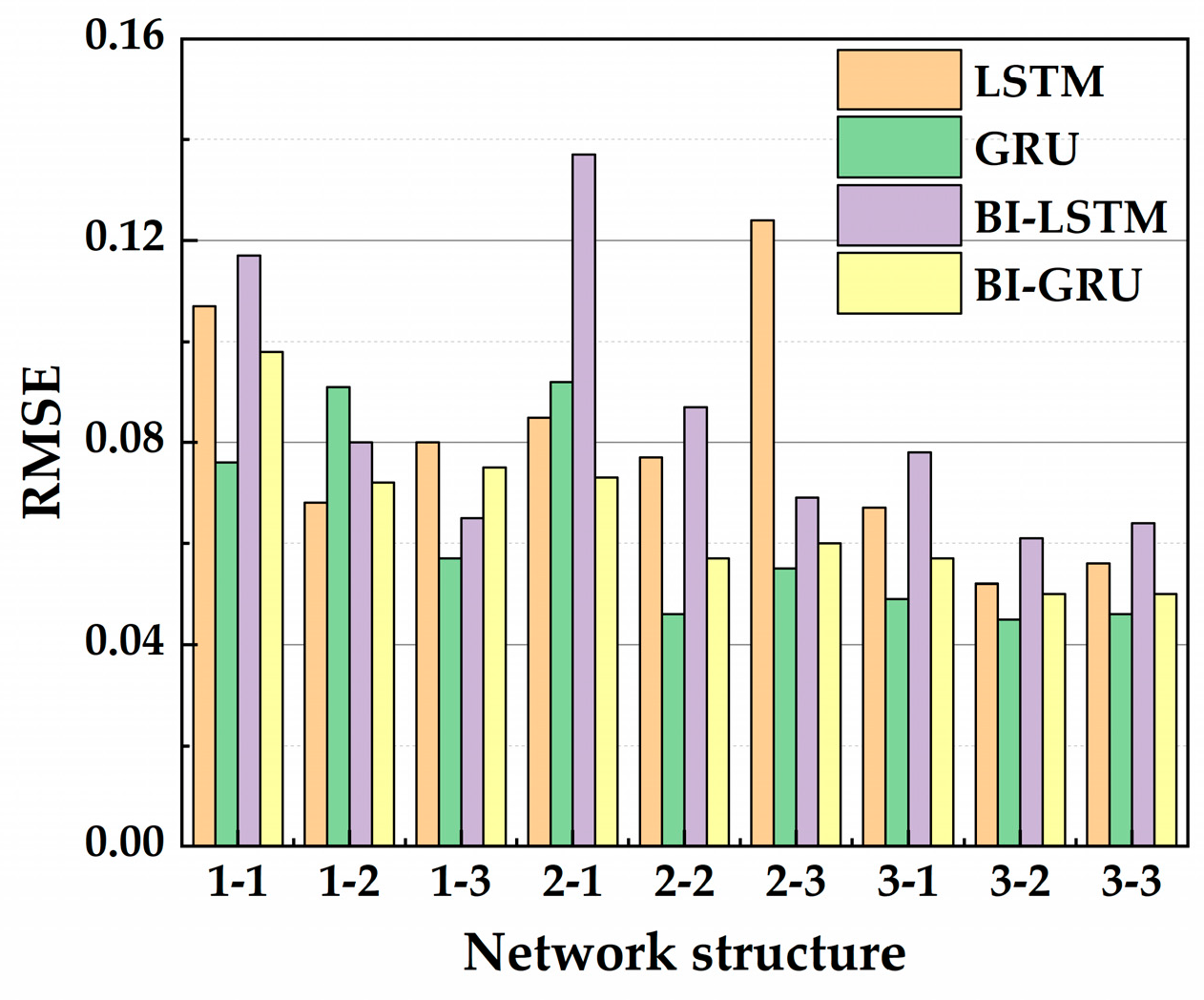
4.1. Determination of Network Structures of Different RNN Models
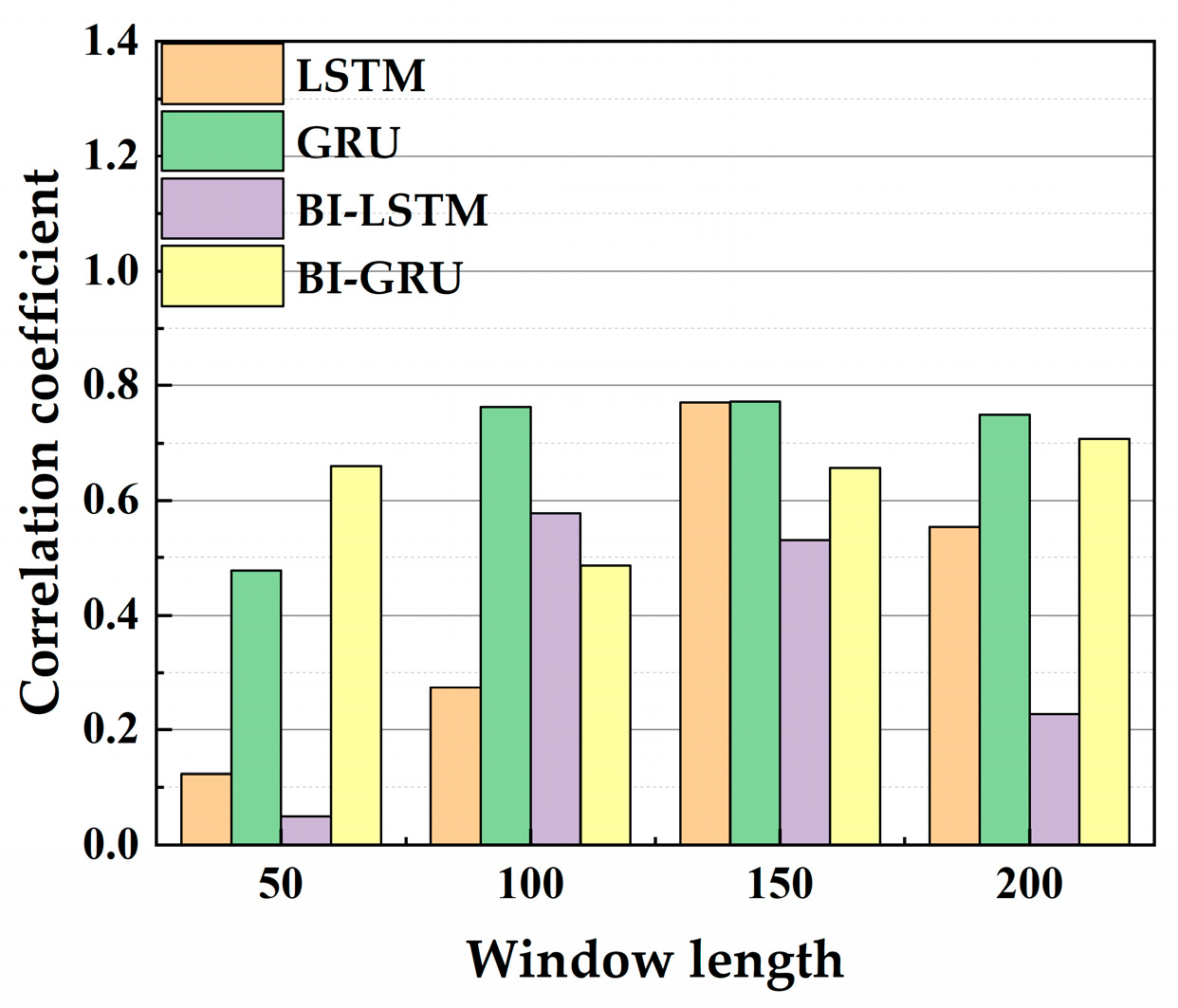
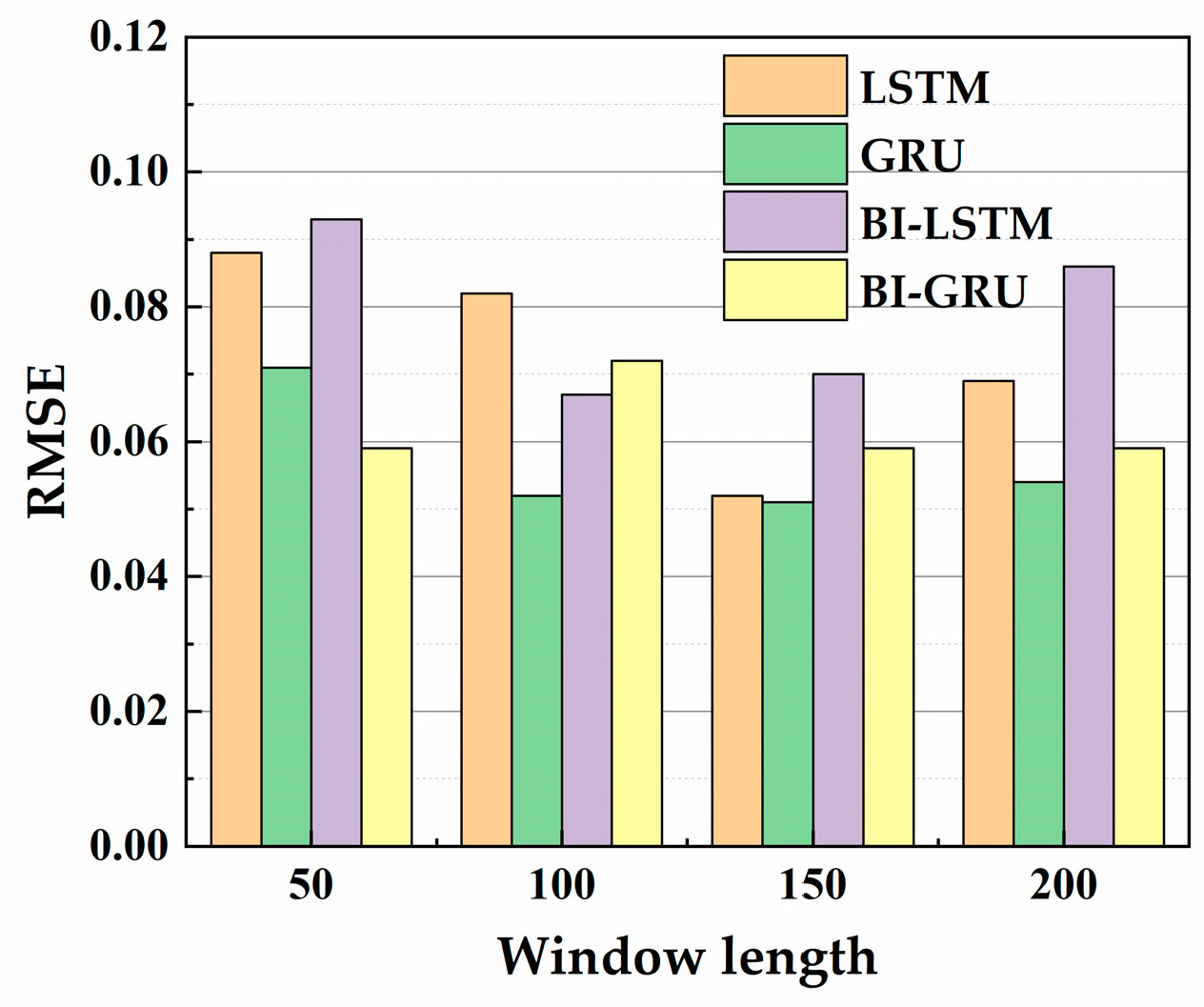
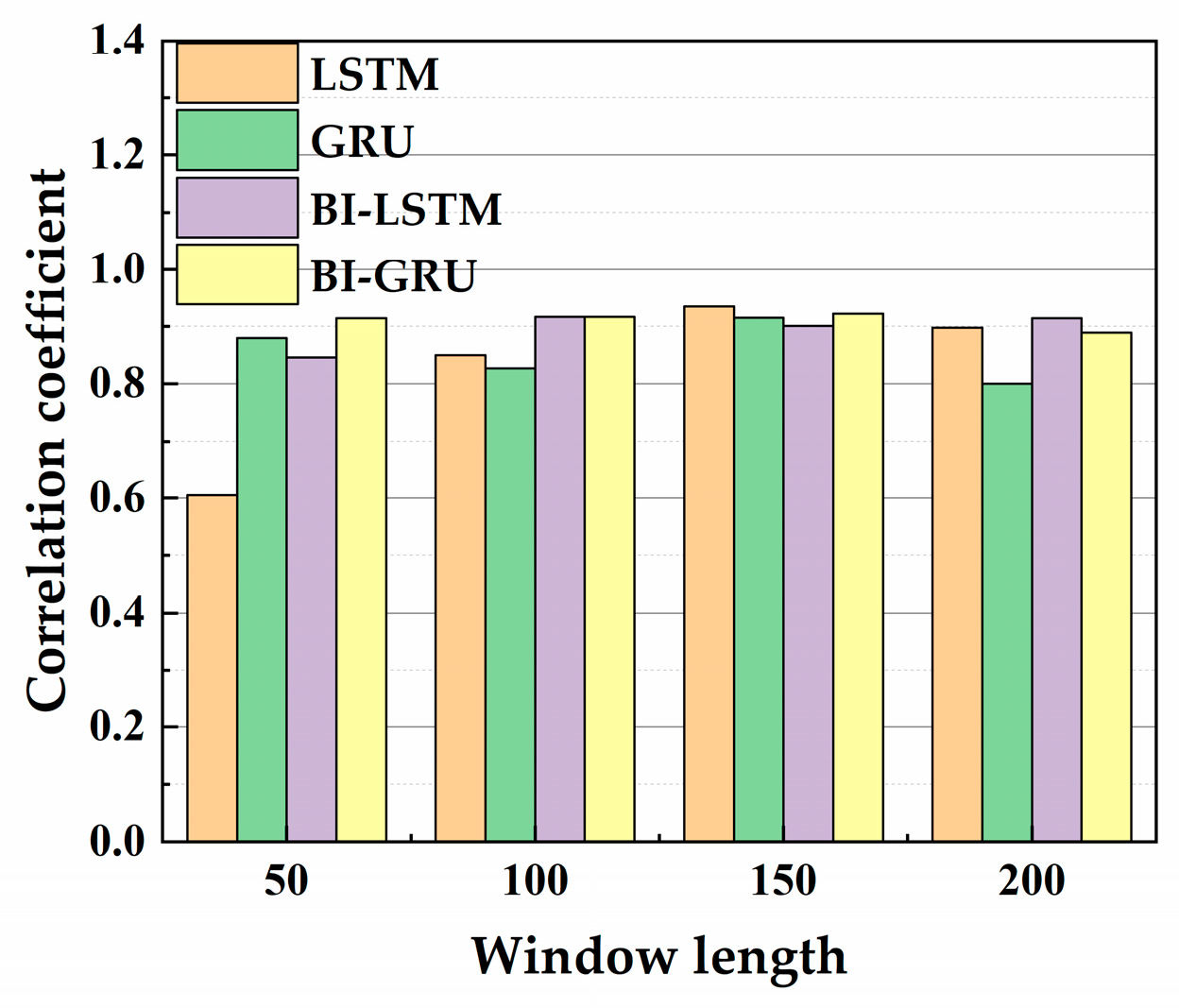
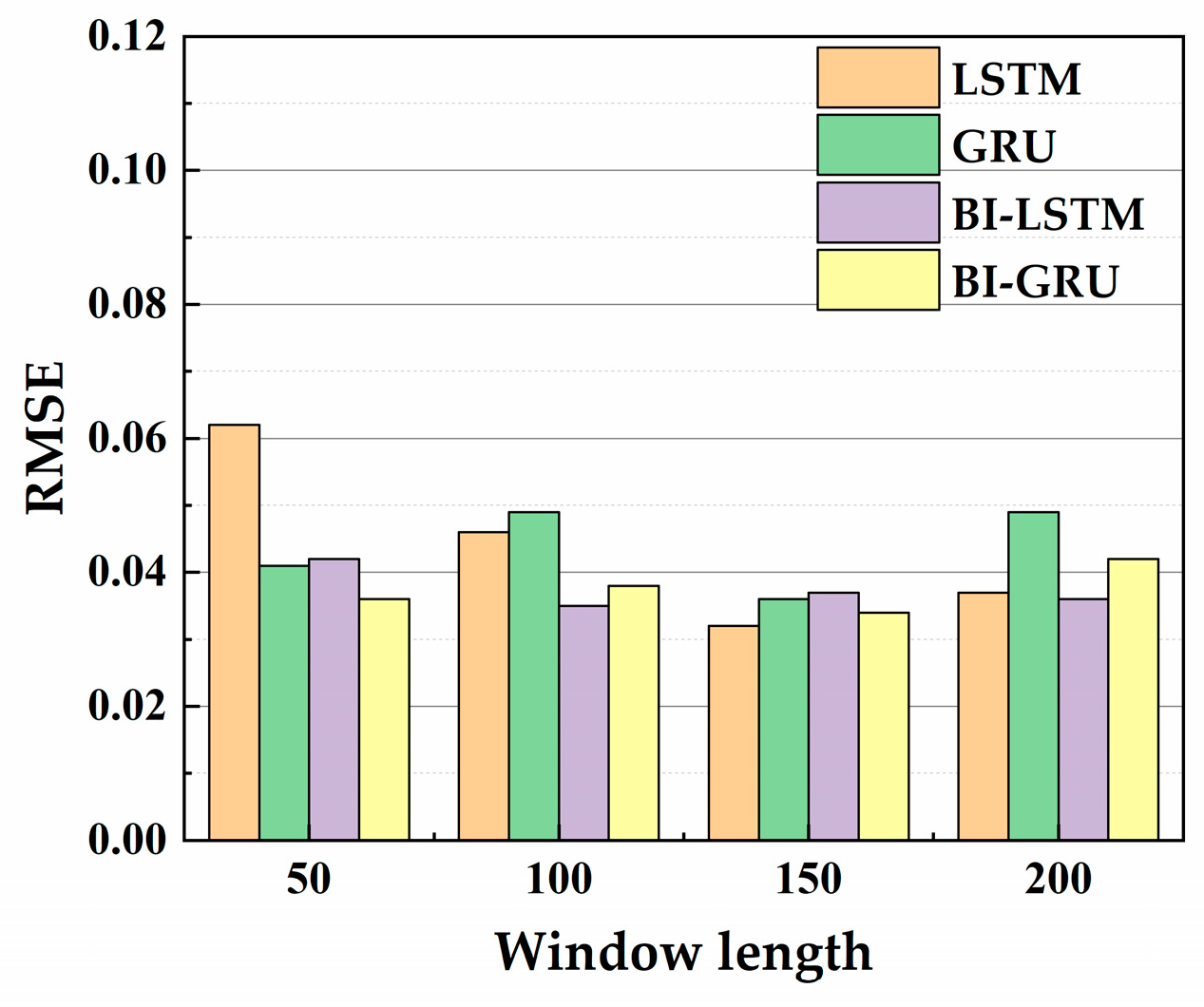
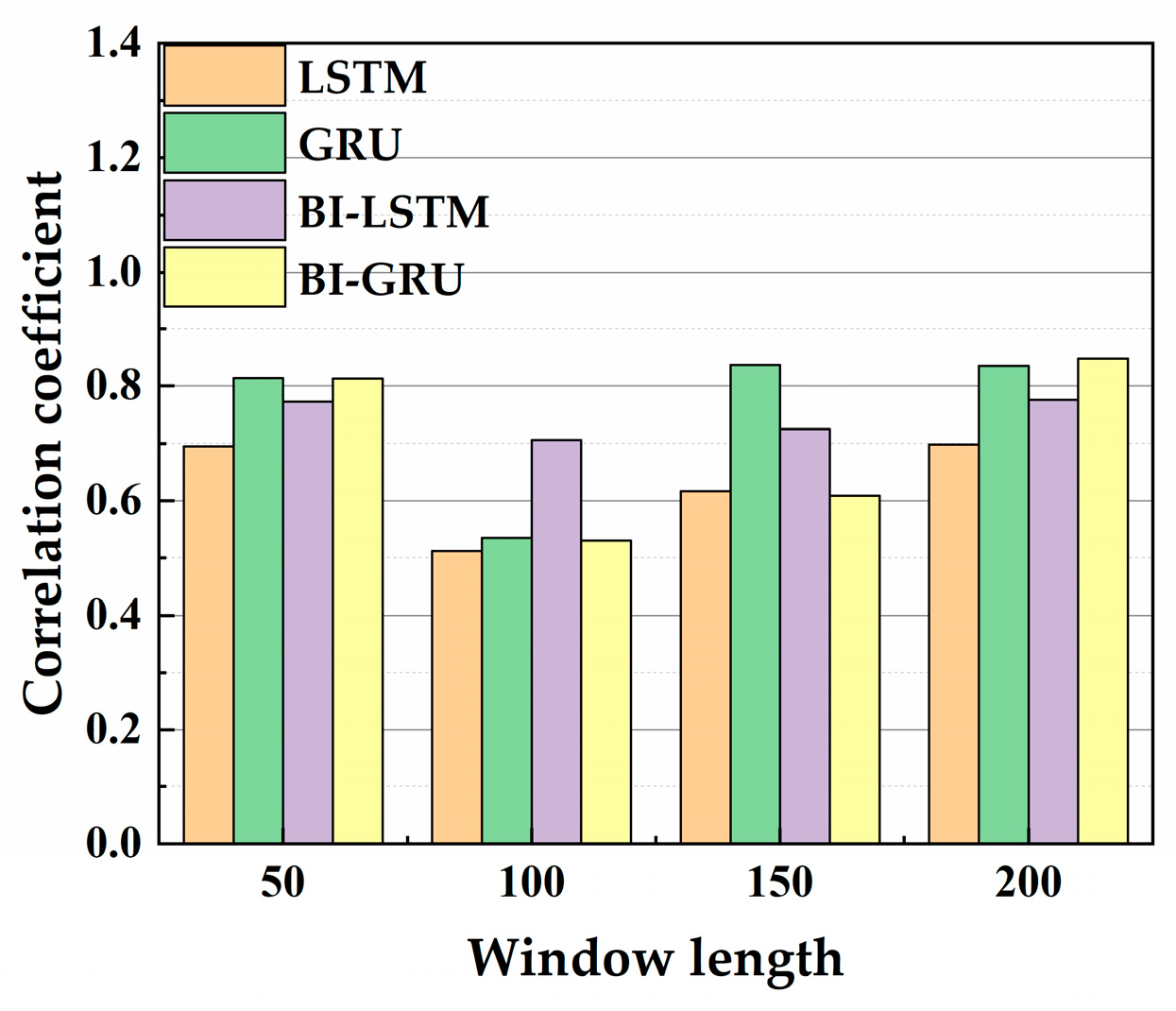
4.1.1. Determination of Window Length
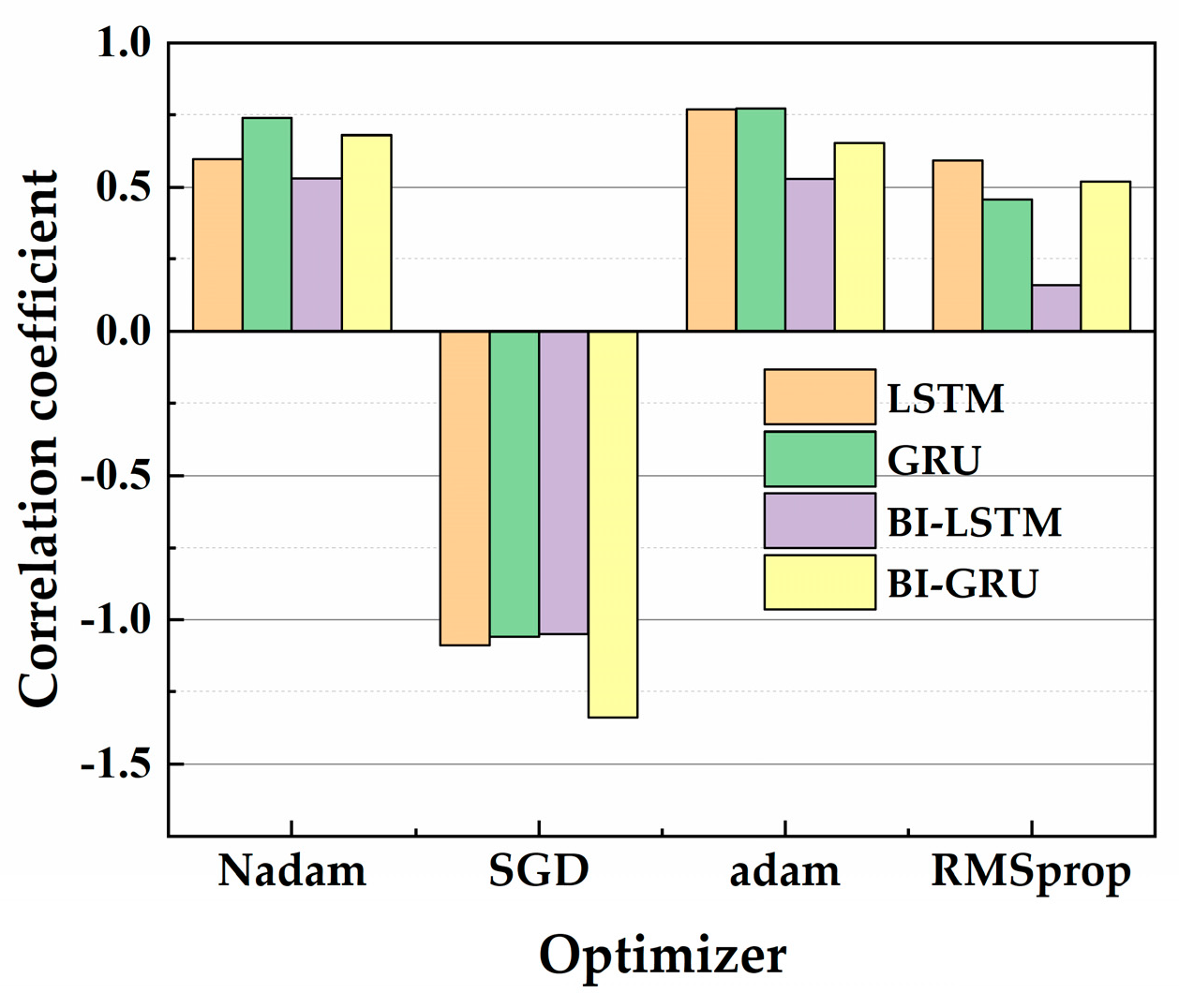
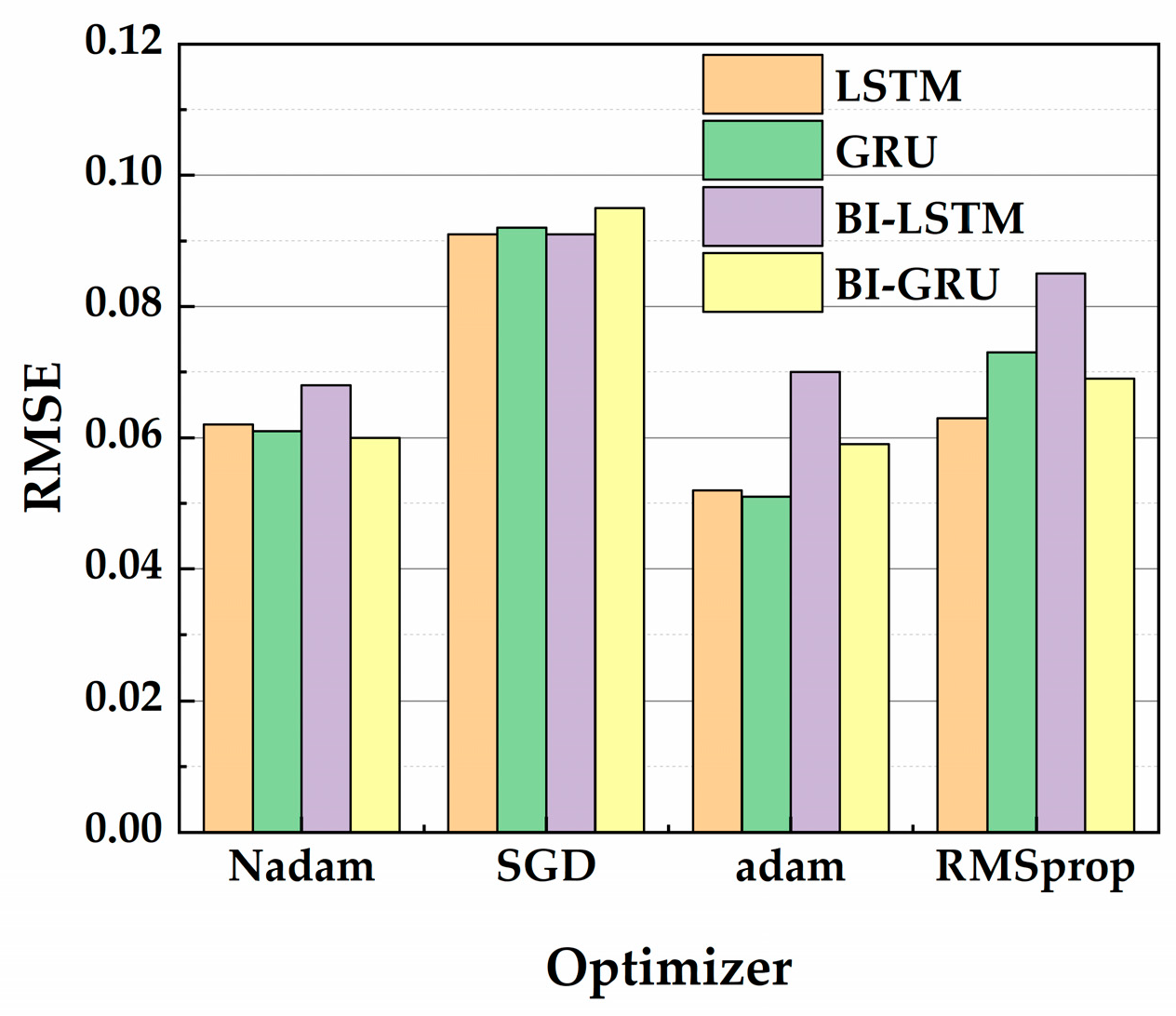
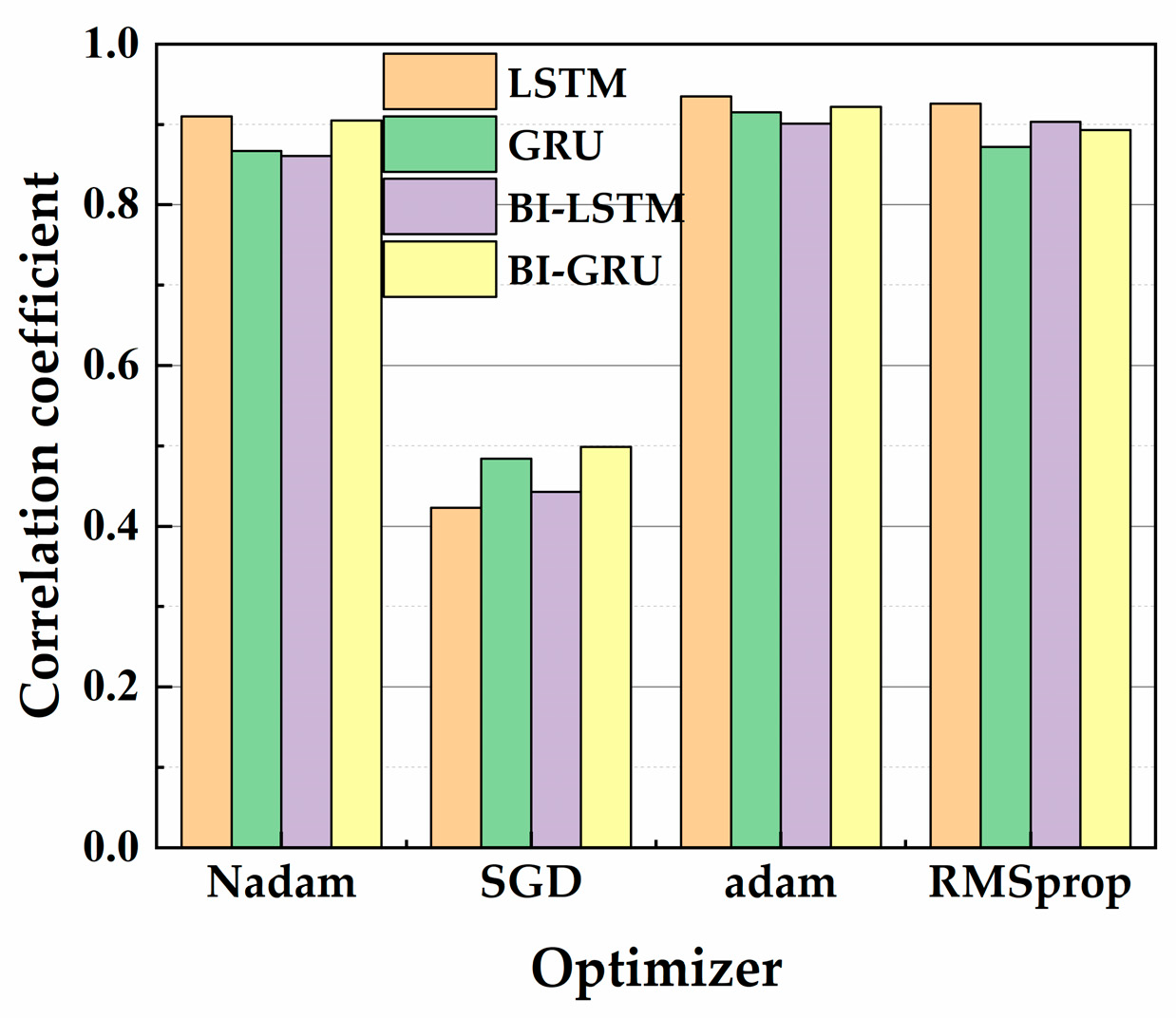
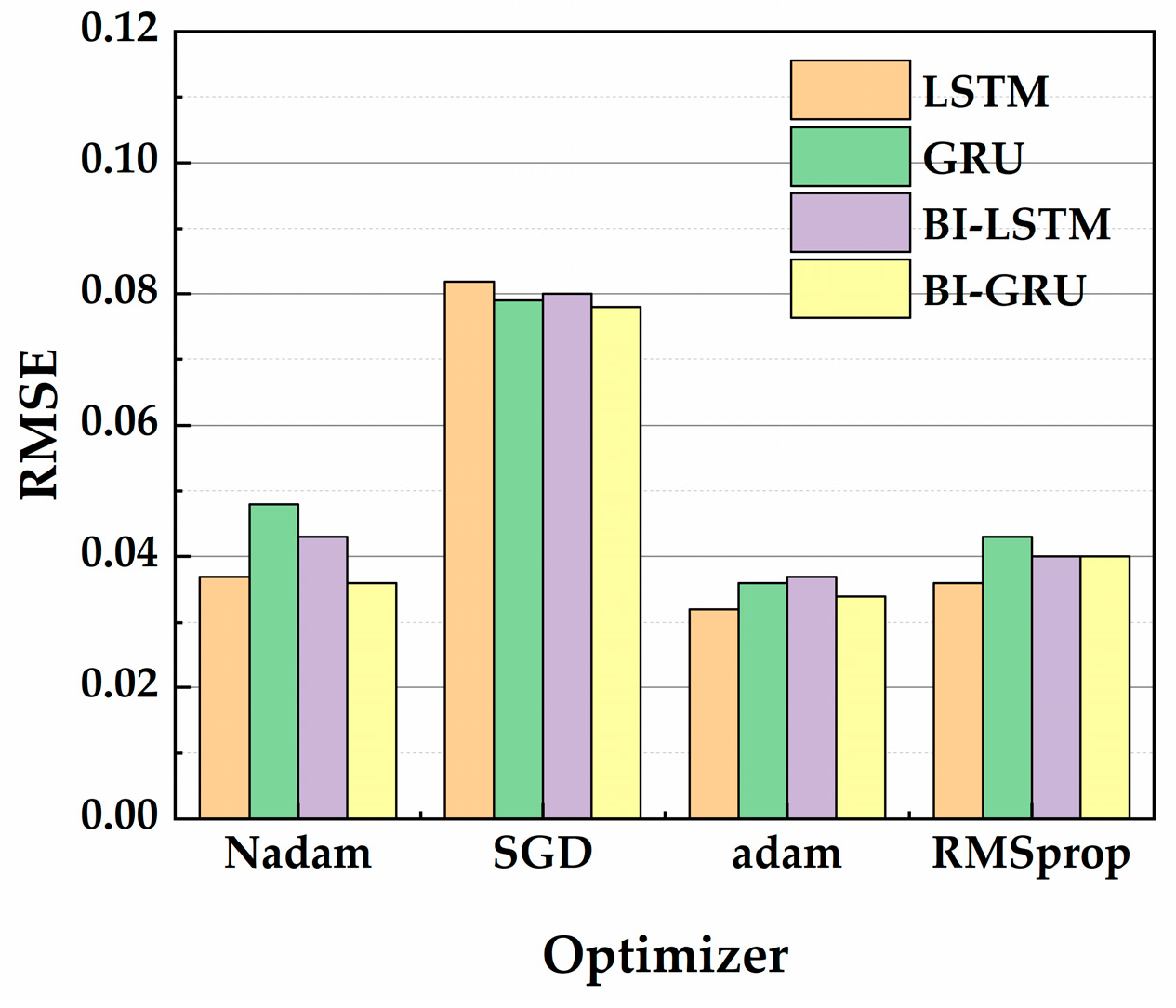
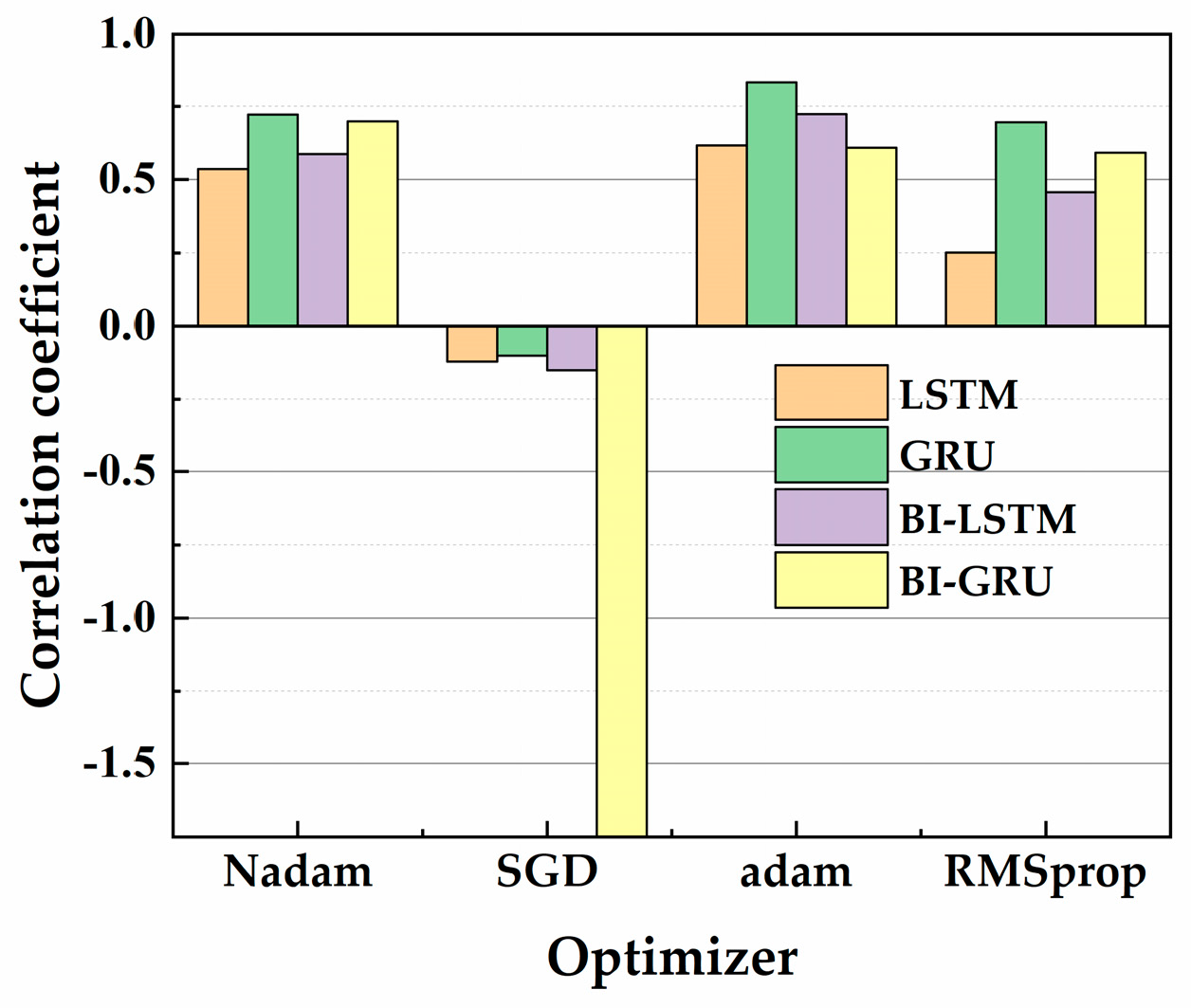
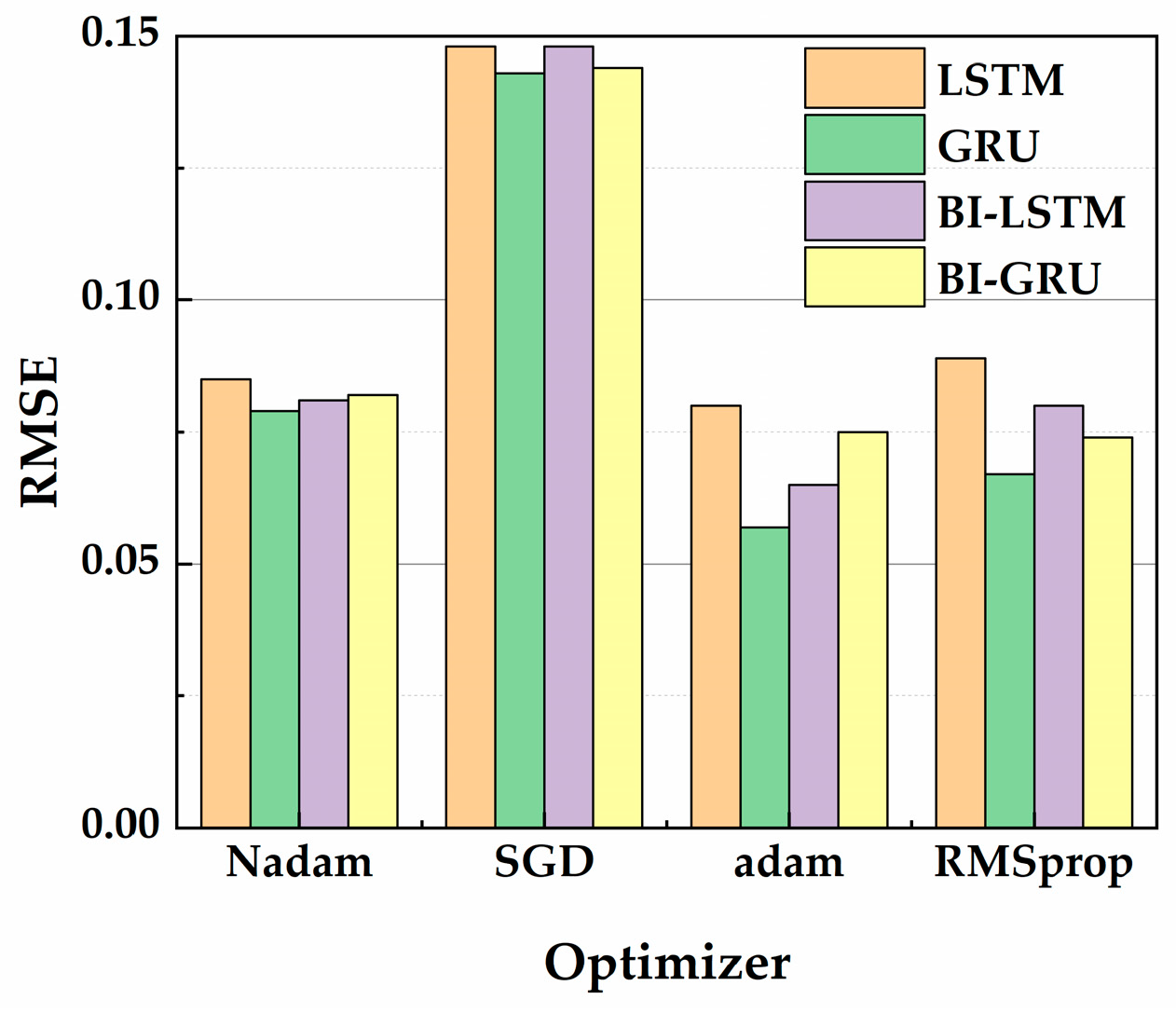
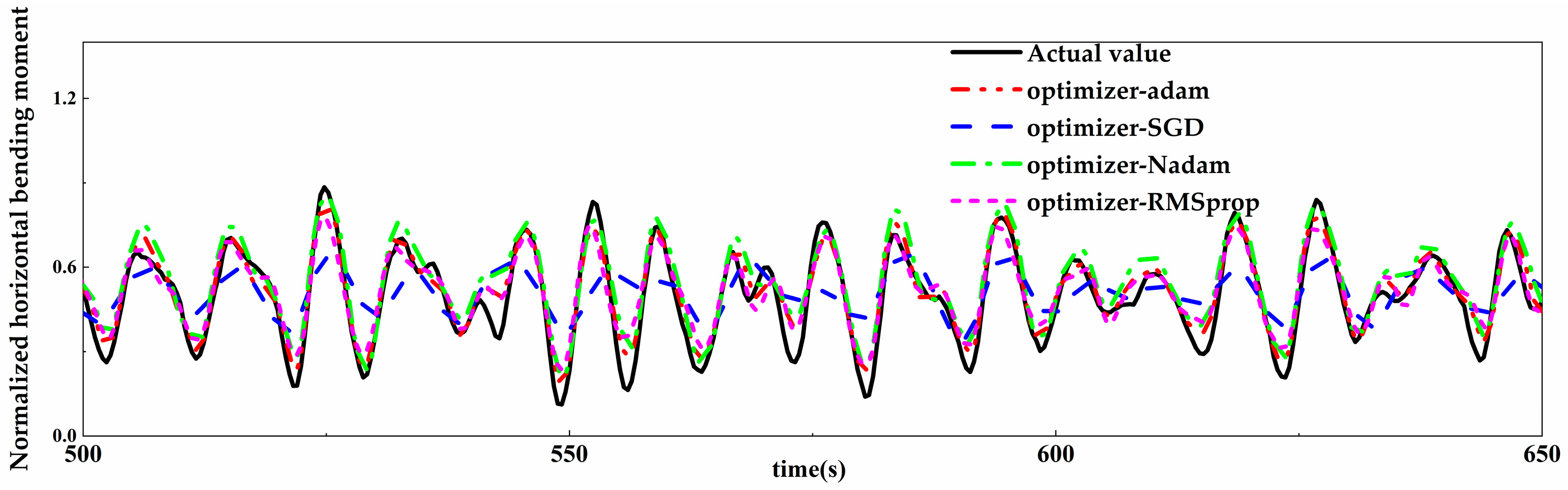
4.1.2. Determination of Optimizers
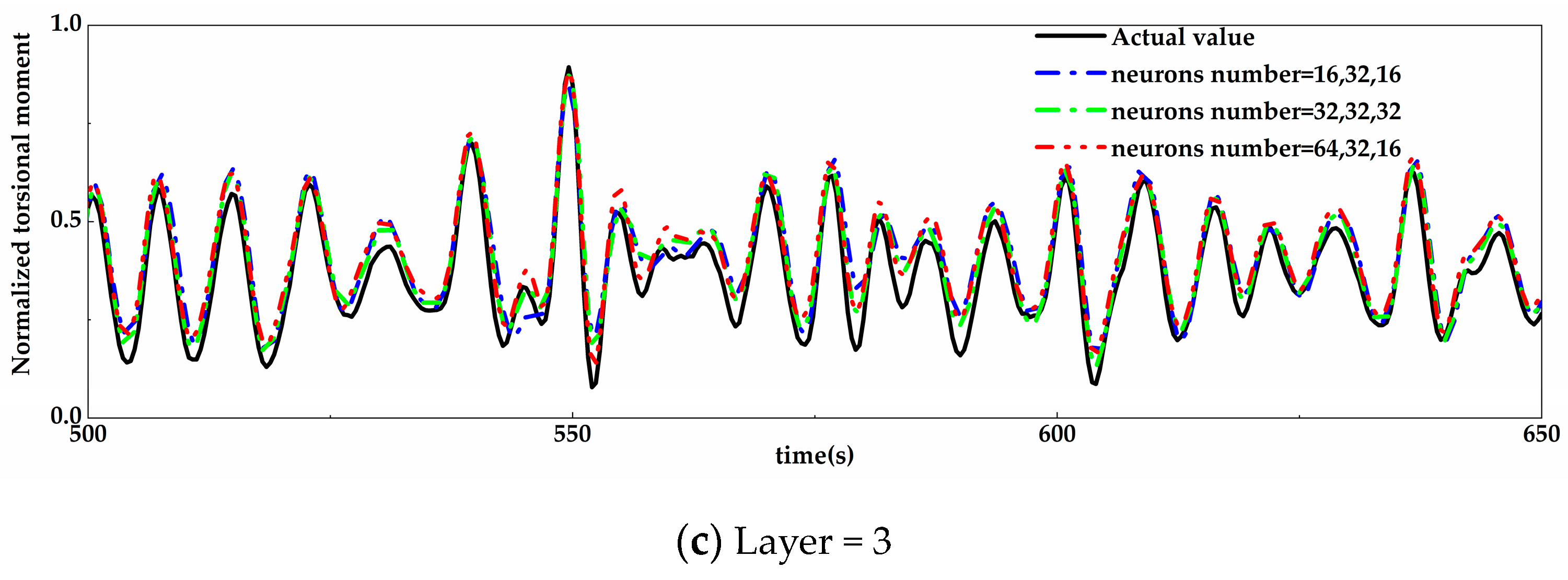
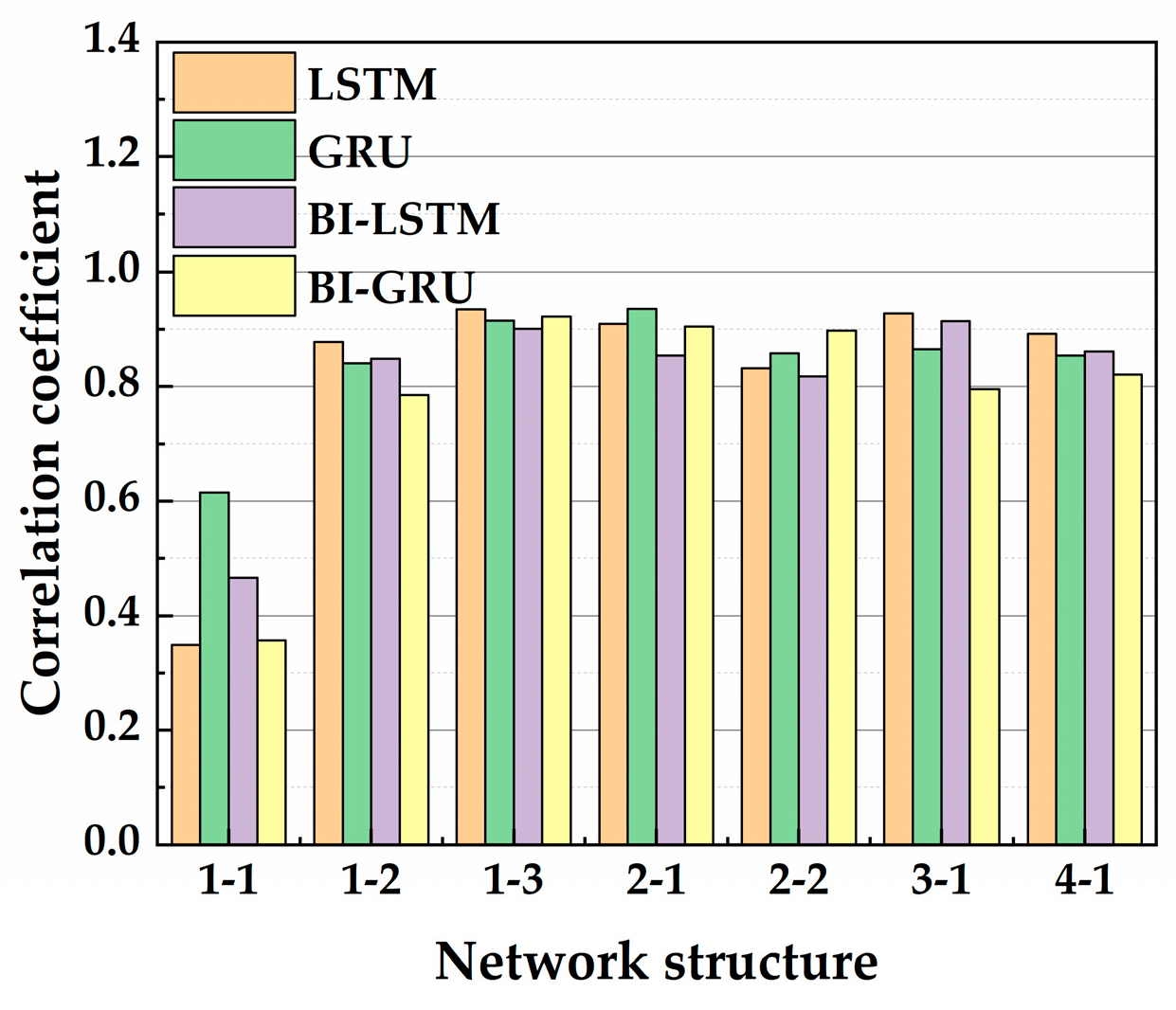
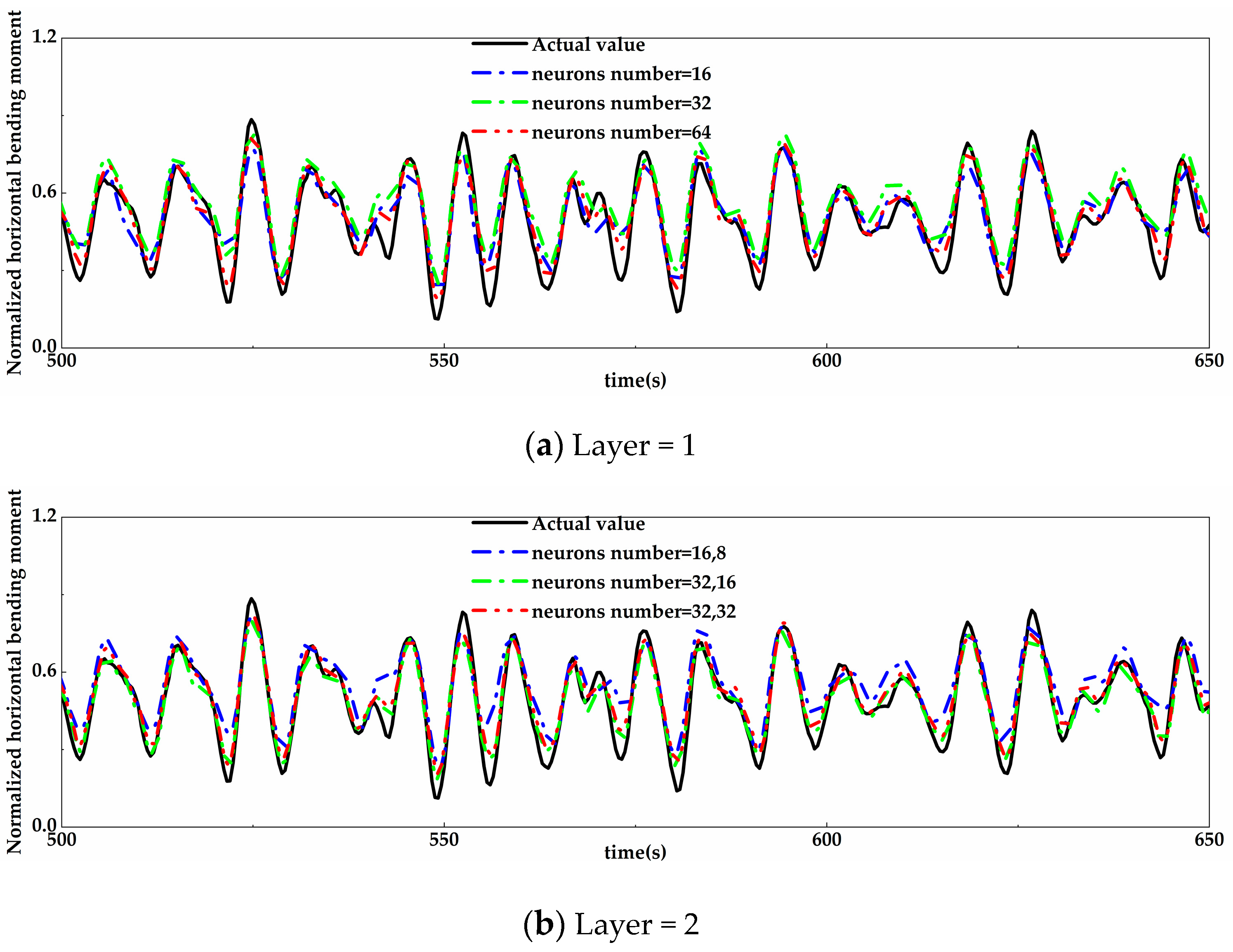
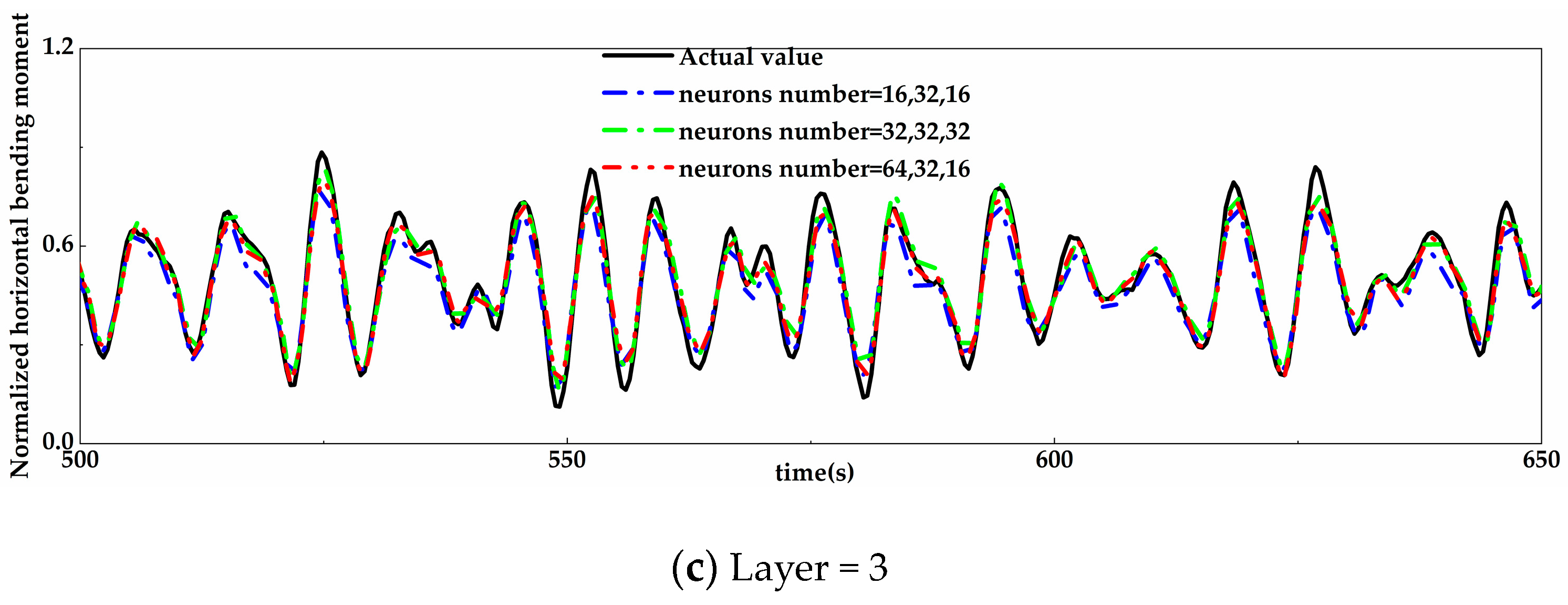
4.1.3. Coupling Determination of the Layer and Neuron Number
4.2. Prediction of Different Network Models Using Motion Data with The Same Noise
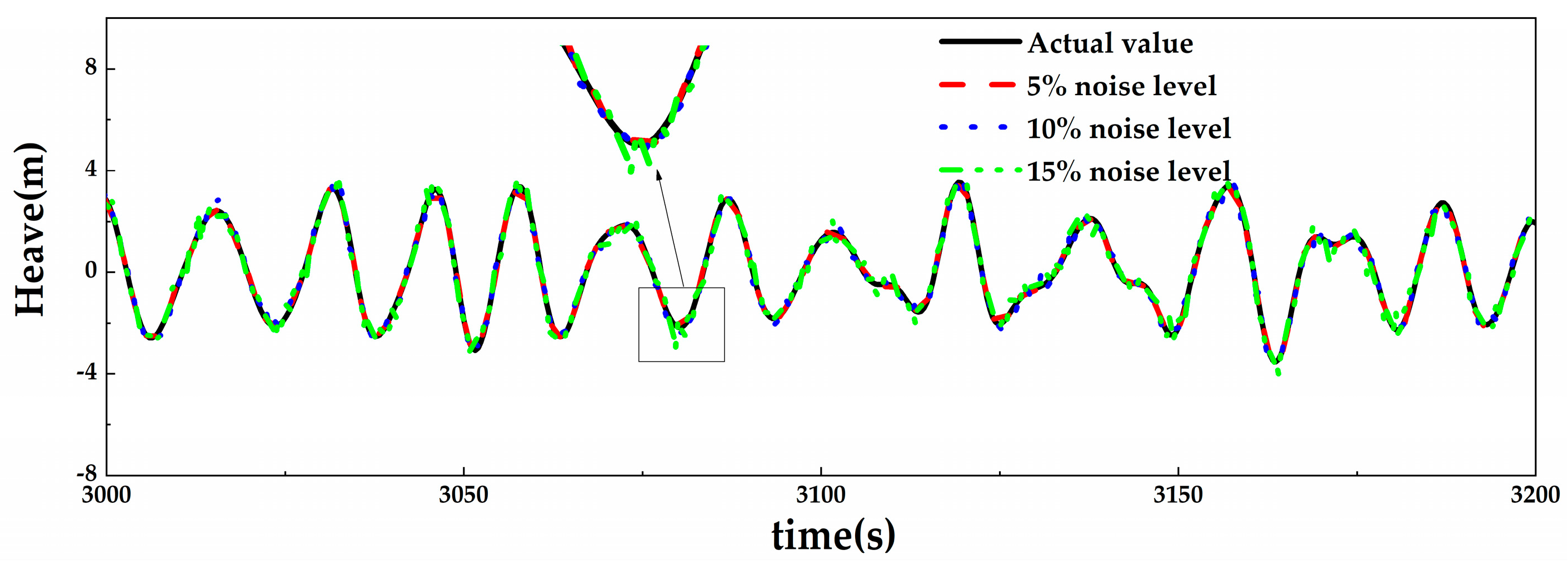
4.2.1. Numerical Noise
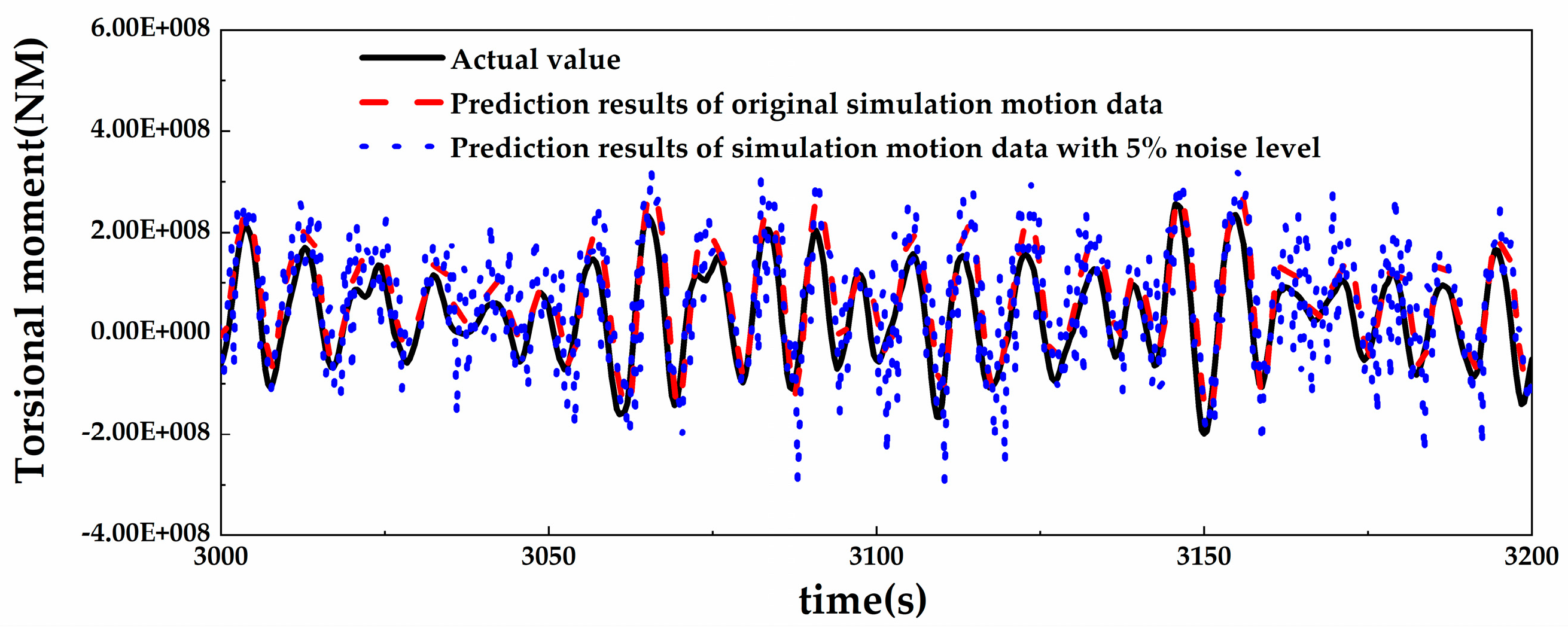
4.2.2. Filtering Technique
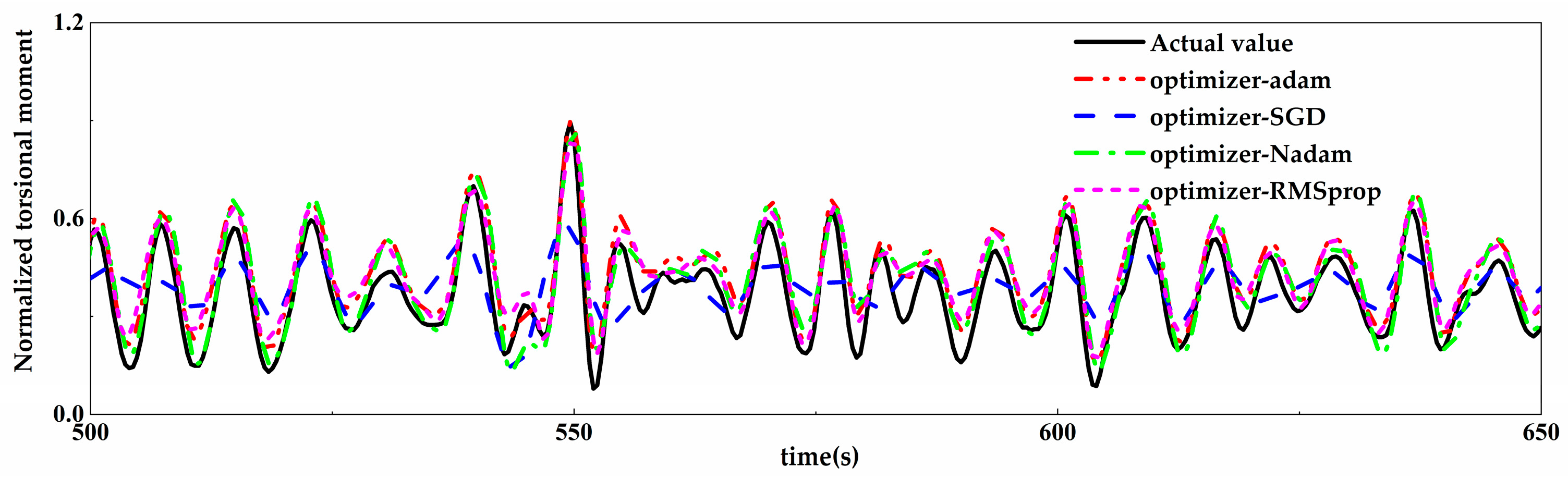
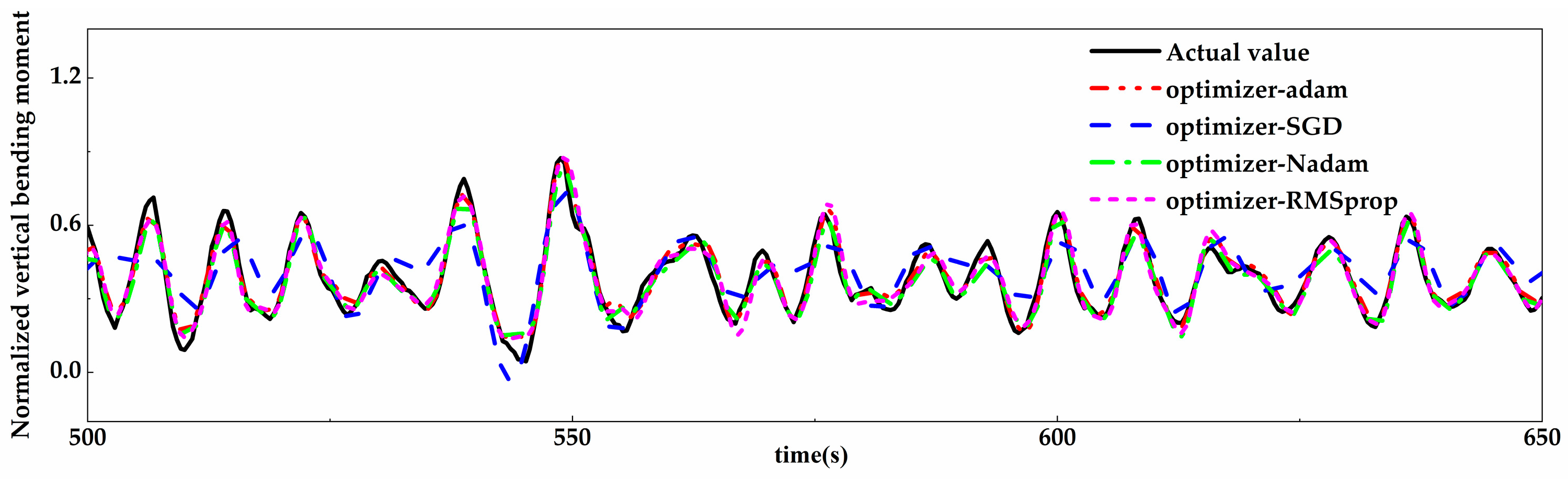
4.2.3. Prediction Results
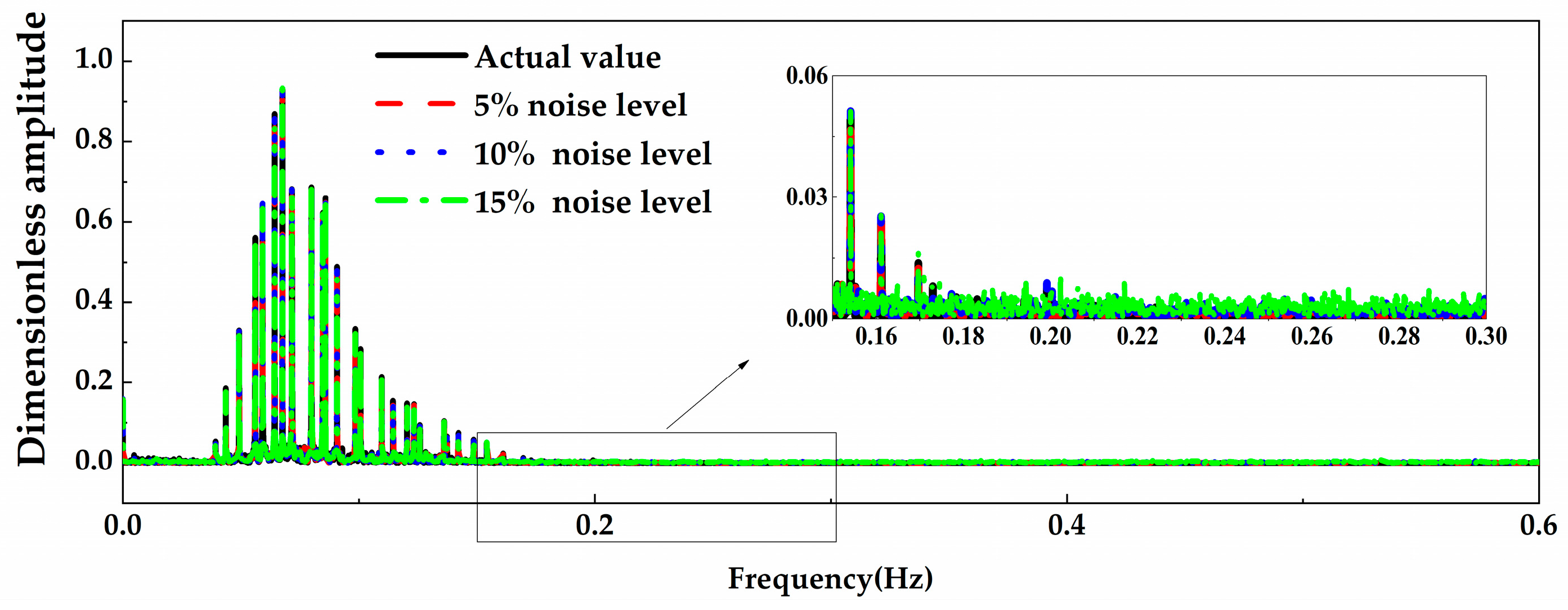
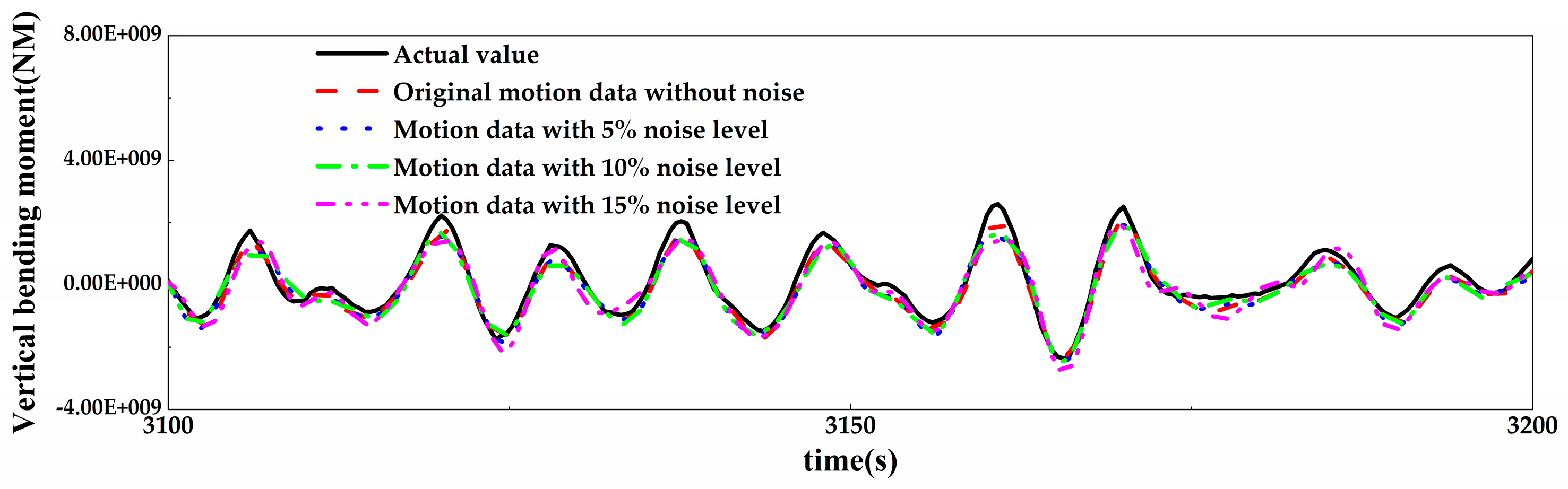
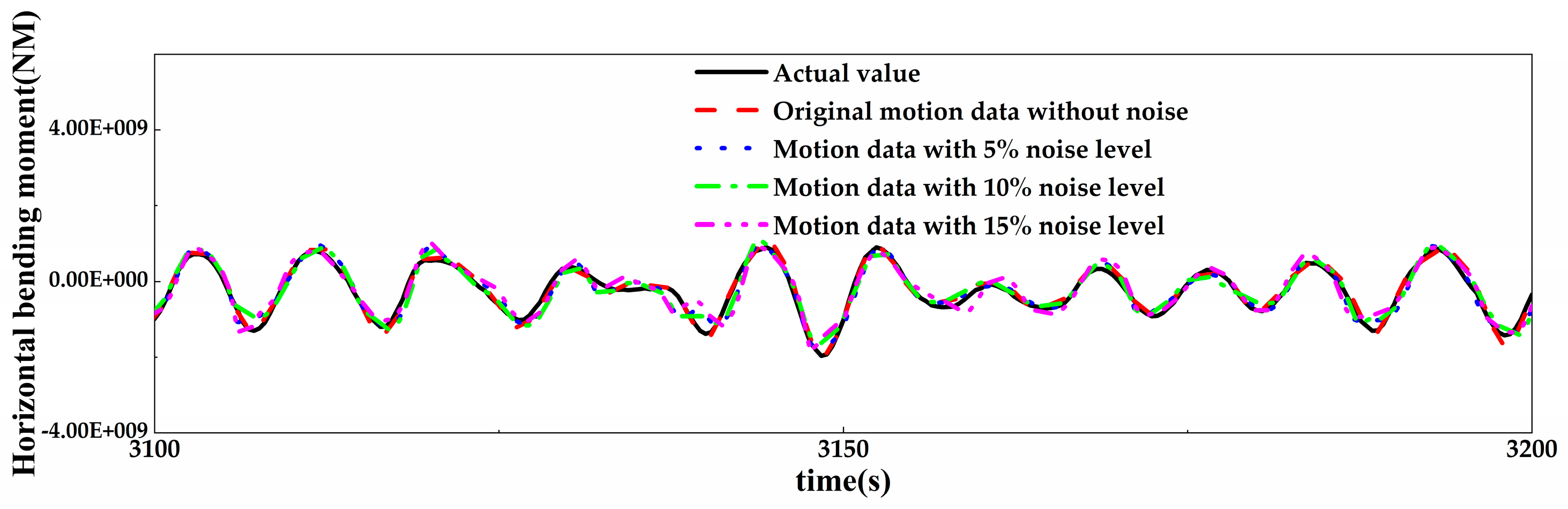
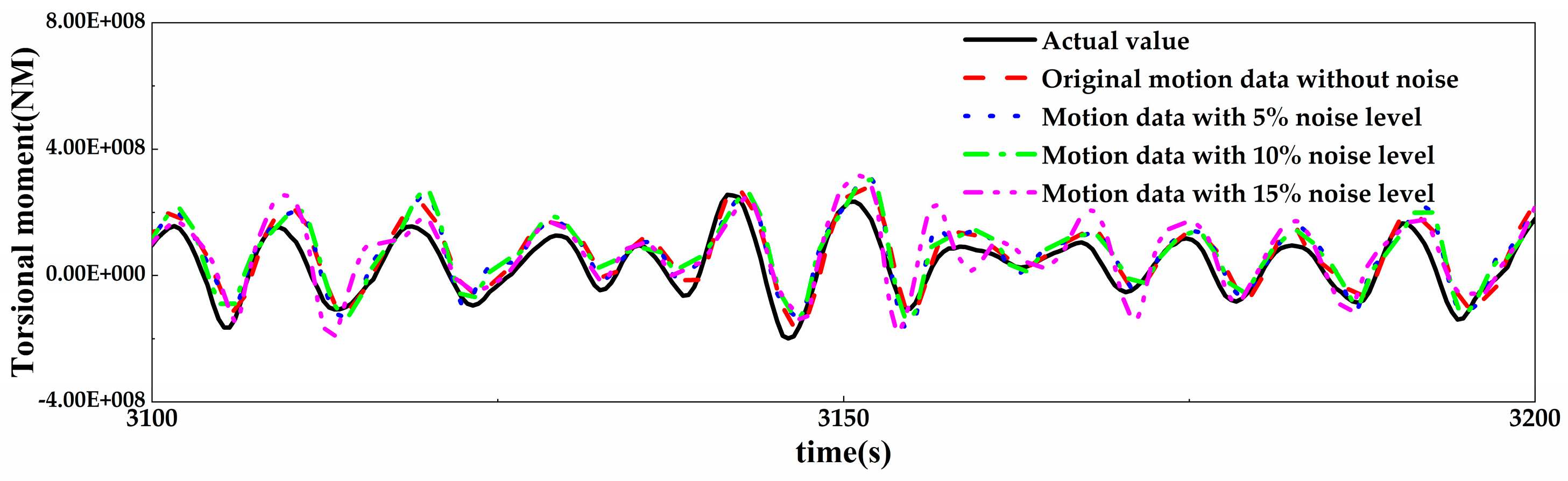
4.3. Prediction of the Same Network Models Using Motion Data with Different Noise
5. Conclusions
- (1)
- The method of controlling variables is used for hyperparameter optimization. Without considering data noise, the optimal network structures of the hull girder load prediction model are respectively obtained based on four improved recurrent neural networks (LSTM, GRU, BI-LSTM, and BI-GRU networks). It found that the most suitable type of recurrent neural network for different load components (TM, VBM, and HBM) is different. The three-layer GRU network with 32 neurons each is the optimal network structure for predicting TM and HBM, and the one-layer LSTM with 32 neurons is the optimal network structure for predicting VBM.
- (2)
- The real-time prediction model of hull girder load takes ship motion monitoring data as input in practical applications, and motion monitoring data inevitably contain certain noise. It is found that directly using motion monitoring data as input for the real-time prediction of hull girder loads will result in significant prediction errors. Therefore, a numerical filtering method is proposed to preprocess the motion monitoring data. The results indicate that the filtering preprocessing method can significantly improve the prediction accuracy of the model. Using the prediction model that considers the effect of motion data noise, the performance of four improved recurrent neural networks is further analyzed. It is also found that the three-layer GRU network with 32 neurons each is the optimal network structure for predicting TM and HBM, and the one-layer LSTM with 32 neurons is the optimal network structure for predicting VBM.
- (3)
- The prediction accuracy of the optimal network models for input data with different levels of noise is discussed. It found that although filtering was applied to the original noise data, the prediction accuracy of the model still decreased as the noise level increased. For both the original input data and noisy input data, the prediction accuracy of VBM and HBM is consistently more than 20% higher than that of TM.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Mohammed, E.A.; Benson, S.D.; Hirdaris, S.E.; Dow, R.S. Design safety margin of a 10,000 TEU container ship through ultimate hull girder load combination analysis. Mar. Struct. 2016, 46, 78–101. [Google Scholar] [CrossRef]
- Amlashi, H.K.K.; Moan, T. A proposal of reliability-based design formats for ultimate hull girder strength checks for bulk carriers under combined global and local loadings. J. Mar. Sci. Technol. 2011, 16, 51–67. [Google Scholar] [CrossRef]
- Almallah, I.; Lavroff, J.; Holloway, D.S.; Shabani, B.; Davis, M.R. Global load determination of high-speed wave-piercing catamarans using finite element method and linear least squares applied to sea trial strain measurements. J. Mar. Sci. Technol. 2020, 25, 901–913. [Google Scholar] [CrossRef]
- Torkildsen, H.E.; Grøvlen, Å.; Skaugen, A.; Wang, G.; Jensen, A.E.; Pran, K.; Sagvolden, G. Development and Applications of Full-Scale Ship Hull Health Monitoring Systems for the Royal Norwegian Navy. In Recent Developments in Non-Intrusive Measurement Technology for Military Application on Model- and Full-Scale Vehicles; RTO: Neuilly-sur-Seine, France, 2005. [Google Scholar]
- Fanelli, P.; Mercuri, A.; Trupiano, S.; Vivio, F.; Falcucci, G.; Jannelli, E. Live reconstruction of global loads on a powerboat using local strain FBG measurements. Procedia Struct. Integr. 2019, 24, 949–960. [Google Scholar] [CrossRef]
- Zhang, M.; Sun, L.H.; Xie, Y.G. A monitoring method of hull structural bending and torsional moment. Ocean. Eng. 2024, 291, 116344. [Google Scholar] [CrossRef]
- Tayyar, G.T. Overall hull girder nonlinear strength monitoring based on inclinometer sensor data. Int. J. Nav. Archit. Ocean. Eng. 2020, 12, 902–909. [Google Scholar] [CrossRef]
- Kefal, A.; Oterkus, E. Displacement and stress monitoring of a chemical tanker based on inverse finite element method. Ocean. Eng. 2016, 112, 33–46. [Google Scholar] [CrossRef]
- Xu, J.Z. Estimation of wave-induced ship hull bending moment from ship motion measurements. Mar. Struct. 2000, 14, 593–610. [Google Scholar] [CrossRef]
- Moreira, L.; Guedes Soares, C. Neural network model for estimation of hull bending moment and shear force of ships in waves. Ocean. Eng. 2020, 206, 107347. [Google Scholar] [CrossRef]
- Fonseca, N.; Soares, C.G. Experimental investigation of the nonlinear effects on the statistics of vertical motions and loads of a containership in irregular waves. J. Ship Res. 2004, 48, 148–167. [Google Scholar] [CrossRef]
- Xu, W.; Li, H.; Ying, Y.; Zhang, M. Prediction of Total Force and Moment of Ship Based on Improved BP Neural Network. In Proceedings of the 8th International Technical Conference on Frontiers of Hydraulic and Civil Engineering Technology, HCET 2023, Wuhan, China, 25–27 September 2023; pp. 1420–1435. [Google Scholar]
- Liu, R.X.; Li, H.; Zou, J.; Ong, M.C. Reconstruction and prediction of global whipping responses on a large cruise ship based on LSTM neural networks. Ocean. Eng. 2023, 285, 115393. [Google Scholar] [CrossRef]
- Su, Y.M.; Lin, J.F.; Zhao, D.G.; Guo, C.Y.; Wang, C.; Guo, H. Real-Time Prediction of Large-Scale Ship Model Vertical Acceleration Based on Recurrent Neural Network. J. Mar. Sci. Eng. 2020, 8, 777. [Google Scholar] [CrossRef]
- Li, S.Y.; Wang, T.T.; Li, G.Y.; Skulstad, R.; Zhang, H.X. Short-term ship roll motion prediction using the encoder-decoder Bi-LSTM with teacher forcing. Ocean. Eng. 2024, 295, 116917. [Google Scholar] [CrossRef]
- Fan, G.J.; Yu, P.Y.; Wang, Q.; Dong, Y.K. Short-term motion prediction of a semi-submersible by combining LSTM neural network and different signal decomposition methods. Ocean. Eng. 2023, 267, 113266. [Google Scholar] [CrossRef]
- Liu, Y.C.; Duan, W.Y.; Huang, L.M.; Duan, S.L.; Ma, X.W. The input vector space optimization for LSTM deep learning model in real-time prediction of ship motions. Ocean. Eng. 2020, 213, 107681. [Google Scholar] [CrossRef]
- Xie, Y.J.; Tang, H.S.; Low, Y.M. Deep gated recurrent unit networks for time-domain long-term fatigue analysis of mooring lines considering wave directionality. Ocean. Eng. 2023, 284, 115244. [Google Scholar] [CrossRef]
- Zhang, T.; Zheng, X.Q.; Liu, M.X. Multiscale attention-based LSTM for ship motion prediction. Ocean. Eng. 2021, 230, 109066. [Google Scholar] [CrossRef]
- Liu, H.D.; Liu, Y.; Li, B.; Qi, Z.G. Ship Abnormal Behavior Detection Method Based on Optimized GRU Network. J. Mar. Sci. Eng. 2022, 10, 249. [Google Scholar] [CrossRef]
- Li, H.H.; Xing, W.B.; Jiao, H.; Yang, Z.L.; Li, Y. Deep bi-directional information-empowered ship trajectory prediction for maritime autonomous surface ships. Transp. Res. Part E-Logist. Transp. Rev. 2024, 181, 103367. [Google Scholar] [CrossRef]
- Wang, Z.M.; Qiao, D.S.; Yan, J.; Tang, G.Q.; Li, B.B.; Ning, D.Z. A new approach to predict dynamic mooring tension using LSTM neural network based on responses of floating structure. Ocean. Eng. 2022, 249, 110905. [Google Scholar] [CrossRef]
- Qiao, D.S.; Li, P.; Ma, G.; Qi, X.L.; Yan, J.; Ning, D.Z.; Li, B.B. Realtime prediction of dynamic mooring lines responses with LSTM neural network model. Ocean. Eng. 2021, 219, 108368. [Google Scholar] [CrossRef]
- Xie, H.; Ren, H.; Deng, B.; Tang, H. Experimental drop test investigation into slamming loads on a truncated 3D bow flare model. Ocean. Eng. 2018, 169, 567–585. [Google Scholar] [CrossRef]
- Wang, Q.; Yu, P.; Fan, G.; Li, G. Experimental drop test investigation into cross deck slamming loads on a trimaran. Ocean. Eng. 2021, 240, 109999. [Google Scholar] [CrossRef]
- Lay-Ekuakille, A.; Vendramin, G.; Trotta, A. Spectral analysis of leak detection in a zigzag pipeline: A filter diagonalization method-based algorithm application. Measurement 2009, 42, 358–367. [Google Scholar] [CrossRef]
- Thirumala, K.; Umarikar, A.C.; Jain, T. An improved adaptive filtering approach for power quality analysis of time-varying waveforms. Measurement 2019, 131, 677–685. [Google Scholar] [CrossRef]






| Length | Width | Depth | Structural Draught | Speed | Block Coefficient |
|---|---|---|---|---|---|
| 278 m | 32.2 m | 23.3 m | 13 m | 23 kn | 0.7 |
| Load Case | Databases | Significant Wave (m) | Zero-Crossing (s) | Wave Direction (°) | Velocity (kn) |
|---|---|---|---|---|---|
| B_MULTI | Training and validating | 10.5 | 10.5 | 120 | 5 |
| 10.5 | 10.5 | 120 | 10 | ||
| 10.5 | 10.5 | 150 | 5 | ||
| 10.5 | 10.5 | 150 | 10 | ||
| 10.5 | 11.5 | 120 | 5 | ||
| 10.5 | 11.5 | 120 | 10 | ||
| 10.5 | 11.5 | 150 | 5 | ||
| 10.5 | 11.5 | 150 | 10 | ||
| 11.5 | 10.5 | 120 | 5 | ||
| 11.5 | 10.5 | 120 | 10 | ||
| 11.5 | 10.5 | 150 | 5 | ||
| 11.5 | 10.5 | 150 | 10 | ||
| 11.5 | 11.5 | 120 | 5 | ||
| 11.5 | 11.5 | 120 | 10 | ||
| 11.5 | 11.5 | 150 | 5 | ||
| 11.5 | 11.5 | 150 | 10 | ||
| Testing | 11 | 11 | 135 | 7.5 |
| Item | 1-1 | 1-2 | 1-3 | 2-1 | 2-2 | 2-3 | 3-1 | 3-2 | 3-3 |
|---|---|---|---|---|---|---|---|---|---|
| Network Layers | 1 | 1 | 1 | 2 | 2 | 2 | 3 | 3 | 3 |
| Number of neurons | 16 | 32 | 64 | 16-8 | 32-16 | 32-32 | 16-32-16 | 32-32-32 | 64-32-16 |
| Item | 1-1 | 1-2 | 1-3 | 2-1 | 2-2 | 3-1 | 4-1 |
|---|---|---|---|---|---|---|---|
| Network Layers | 1 | 1 | 1 | 2 | 2 | 3 | 4 |
| Number of neurons | 8 | 16 | 32 | 16-8 | 32-16 | 16-32-16 | 16-32-32-16 |
| Item | 1-1 | 1-2 | 1-3 | 2-1 | 2-2 | 2-3 | 3-1 | 3-2 | 3-3 |
|---|---|---|---|---|---|---|---|---|---|
| Network Layers | 1 | 1 | 1 | 2 | 2 | 2 | 3 | 3 | 3 |
| Number of neurons | 16 | 32 | 64 | 16-8 | 32-16 | 32-32 | 16-32-16 | 32-32-32 | 64-32-16 |
| model | LSTM | GRU | ||||
| window length | optimizer | network structure | window length | optimizer | network structure | |
| TM | 150 | adam | 3, 32-32-32 | 150 | adam | 3, 32-32-32 |
| VBM | 150 | adam | 1, 32 | 150 | adam | 2, 16-8 |
| HBM | 200 | adam | 3, 32-32-32 | 150 | adam | 3, 32-32-32 |
| model | BI-LSTM | BI-GRU | ||||
| window length | optimizer | network structure | window length | optimizer | network structure | |
| TM | 100 | Nadam | 1, 16 | 150 | adam | 1, 64 |
| VBM | 100 | RMSprop | 3, 16-32-16 | 150 | adam | 1, 32 |
| HBM | 200 | adam | 3, 32-32-32 | 200 | Nadam | 3, 32-32-32 |
| model | LSTM | GRU | ||||
| RMSE | MAPE | RMSE | MAPE | |||
| TM | 0.608 | 0.089 | 7.50% | 0.660 | 0.085 | 7.40% |
| VBM | 0.873 | 0.050 | 3.90% | 0.875 | 0.052 | 4.00% |
| HBM | 0.841 | 0.052 | 4.00% | 0.886 | 0.050 | 3.80% |
| model | BI-LSTM | BI-GRU | ||||
| RMSE | MAPE | RMSE | MAPE | |||
| TM | 0.583 | 0.090 | 8.30% | 0.612 | 0.092 | 8.50% |
| VBM | 0.876 | 0.051 | 4.00% | 0.873 | 0.050 | 4.00% |
| HBM | 0.838 | 0.057 | 4.20% | 0.845 | 0.054 | 4.30% |
| Model | Type | Window Length | Optimizer | Network Structure |
|---|---|---|---|---|
| TM | GRU | 150 | adam | 3, 32-32-32 |
| VBM | LSTM | 150 | adam | 1, 32 |
| HBM | GRU | 150 | adam | 3, 32-32-32 |
| Motion Data | TM | VBM | HBM | ||||||
|---|---|---|---|---|---|---|---|---|---|
| RMSE | MAPE | RMSE | MAPE | RMSE | MAPE | ||||
| Origin | 0.743 | 0.073 | 6.20% | 0.913 | 0.042 | 3.30% | 0.945 | 0.036 | 2.40% |
| 5% noise | 0.729 | 0.075 | 6.40% | 0.887 | 0.048 | 3.60% | 0.904 | 0.046 | 3.60% |
| 10% noise | 0.660 | 0.085 | 7.40% | 0.873 | 0.050 | 3.90% | 0.886 | 0.050 | 3.80% |
| 15% noise | 0.697 | 0.082 | 7.10% | 0.838 | 0.062 | 5.60% | 0.850 | 0.056 | 4.50% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Q.; Wu, L.; Li, C.; Chang, X.; Zhang, B. Research on a Real-Time Prediction Method of Hull Girder Loads Based on Different Recurrent Neural Network Models. J. Mar. Sci. Eng. 2024, 12, 746. https://doi.org/10.3390/jmse12050746
Wang Q, Wu L, Li C, Chang X, Zhang B. Research on a Real-Time Prediction Method of Hull Girder Loads Based on Different Recurrent Neural Network Models. Journal of Marine Science and Engineering. 2024; 12(5):746. https://doi.org/10.3390/jmse12050746
Chicago/Turabian StyleWang, Qiang, Lihong Wu, Chenfeng Li, Xin Chang, and Boran Zhang. 2024. "Research on a Real-Time Prediction Method of Hull Girder Loads Based on Different Recurrent Neural Network Models" Journal of Marine Science and Engineering 12, no. 5: 746. https://doi.org/10.3390/jmse12050746
APA StyleWang, Q., Wu, L., Li, C., Chang, X., & Zhang, B. (2024). Research on a Real-Time Prediction Method of Hull Girder Loads Based on Different Recurrent Neural Network Models. Journal of Marine Science and Engineering, 12(5), 746. https://doi.org/10.3390/jmse12050746







