Improving Water Quality in a Sea Bay by Connecting Rivers on Both Sides of a Harbor
Abstract
1. Introduction
2. Study Area and Water Quality Issues
2.1. Study Area
2.2. Water Quality Issue
3. Numerical Model
3.1. Model Description
3.2. Control Equations
- (1)
- Continuity equation:
- (2)
- Momentum equation:
3.3. Initial and Boundary Conditions
- (1)
- Initial conditions:
- (2)
- Boundary conditions:
3.4. Modeling Scenarios
4. Results and Discussion
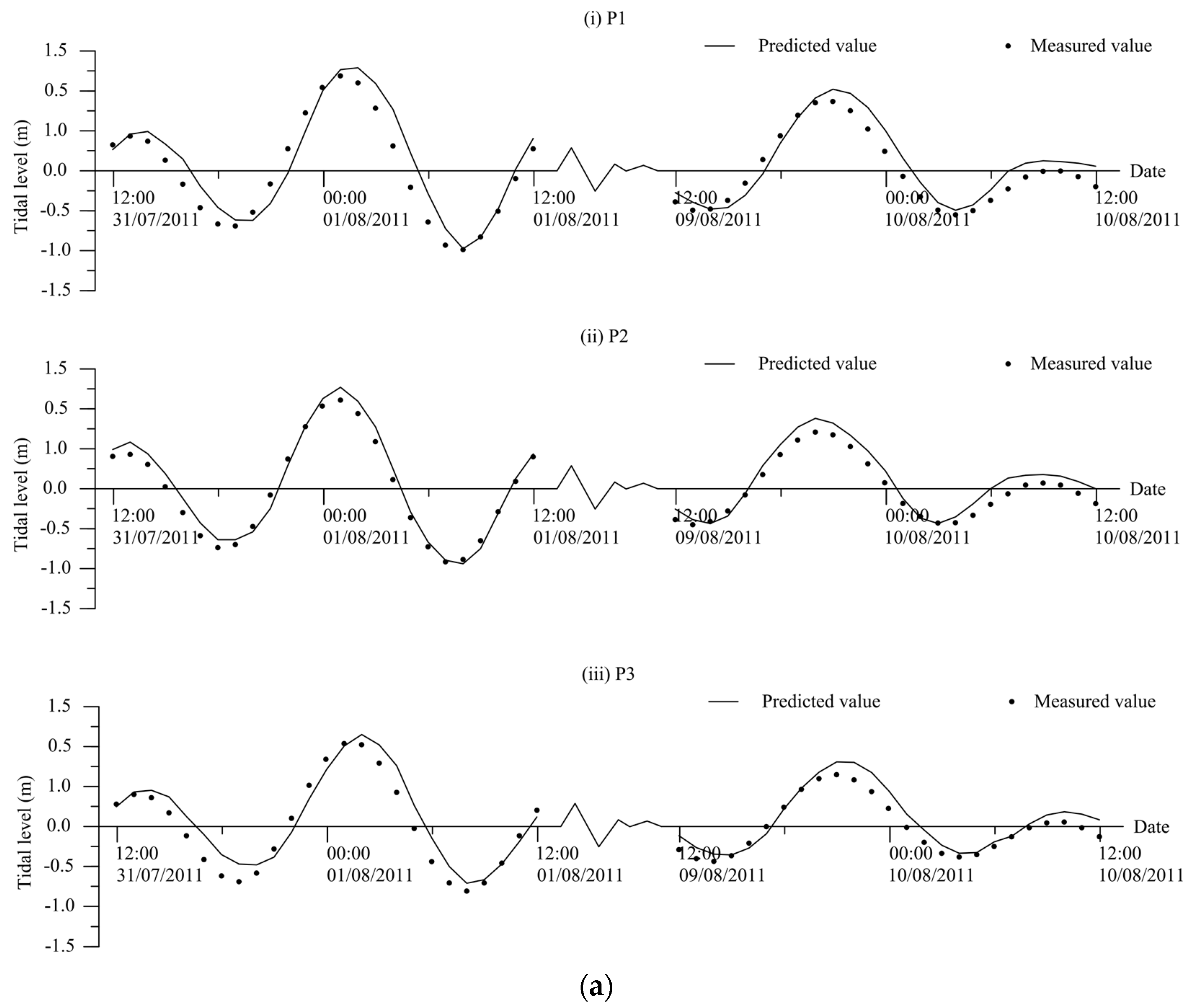
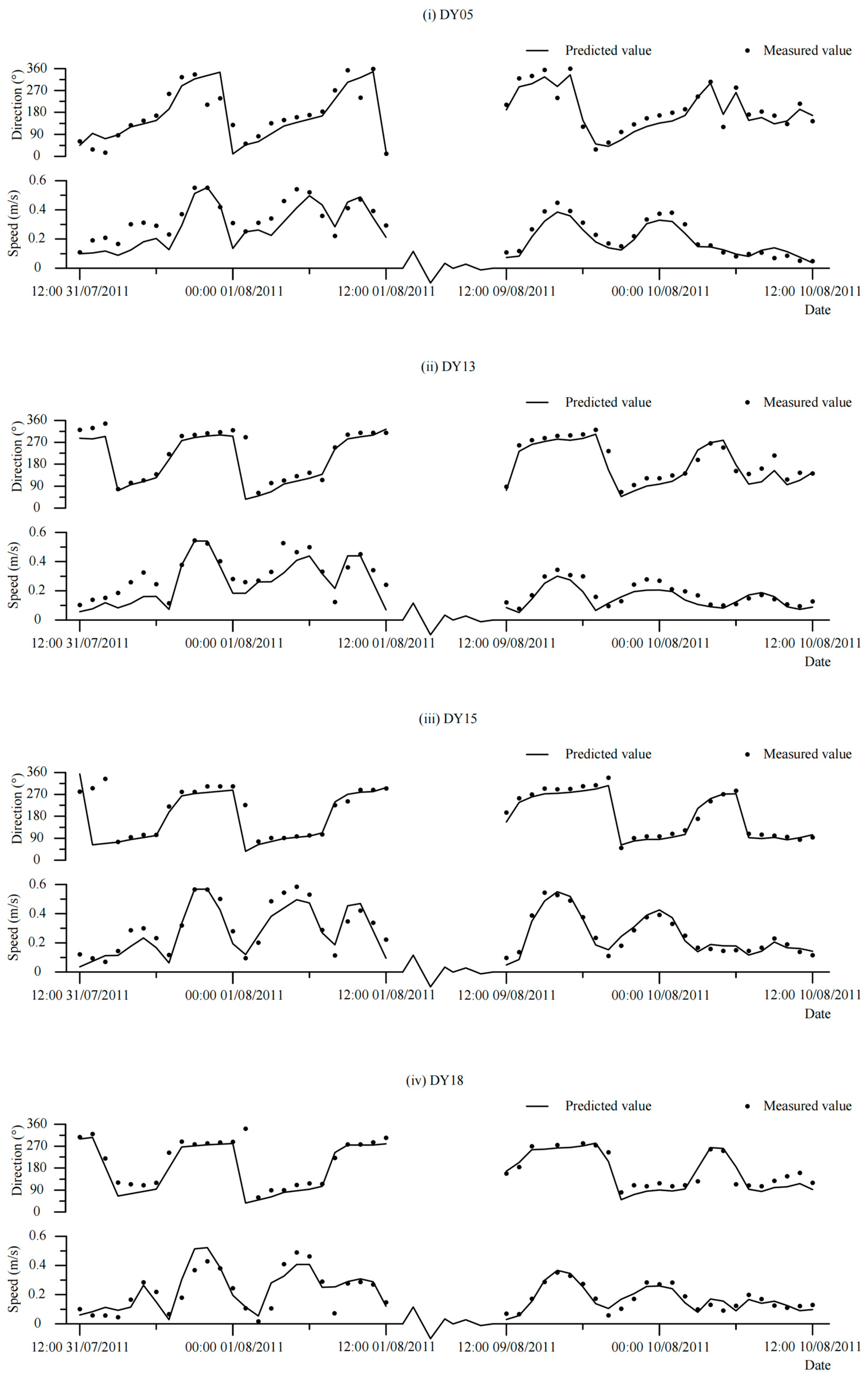
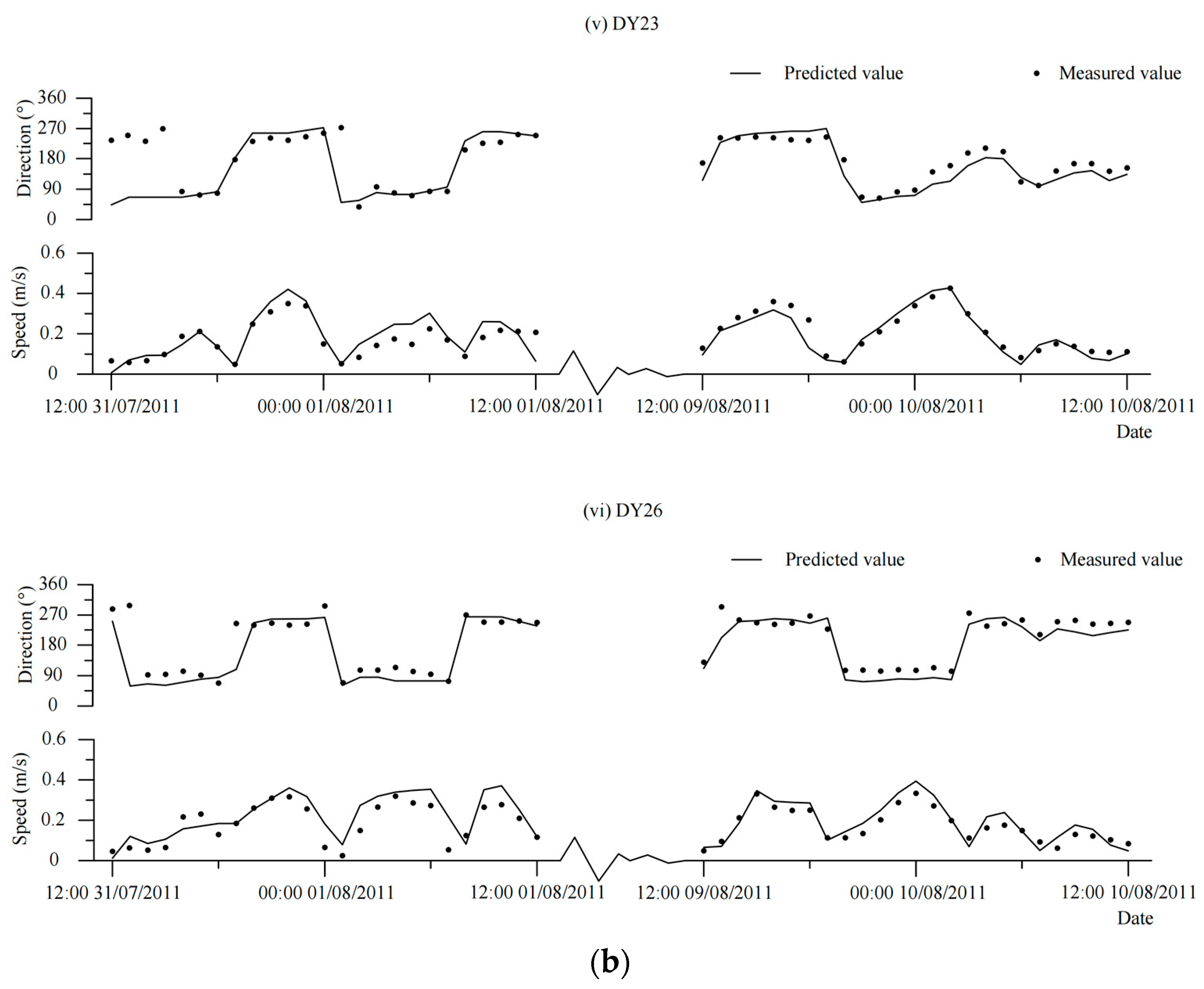
4.1. Model Validation
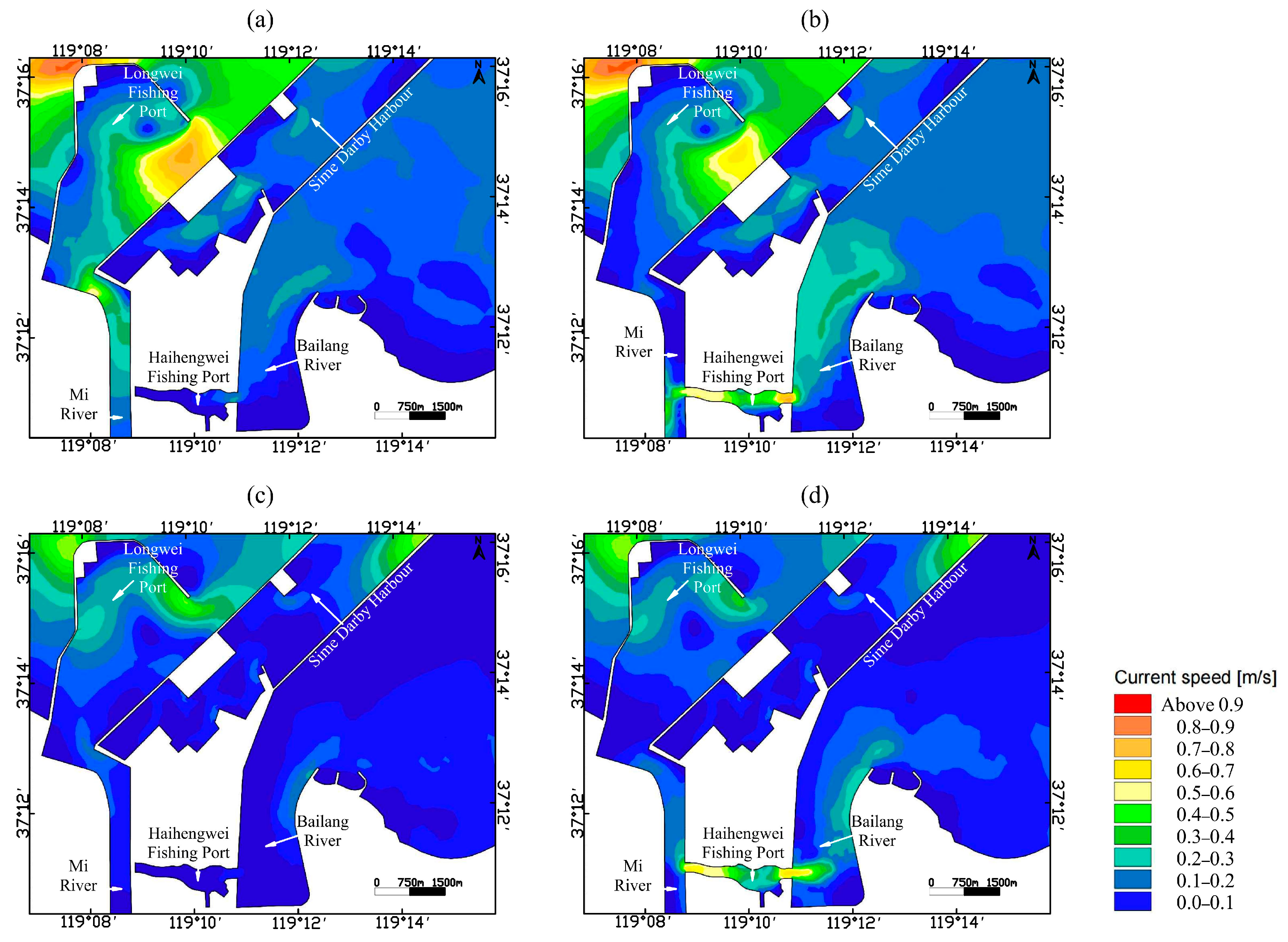
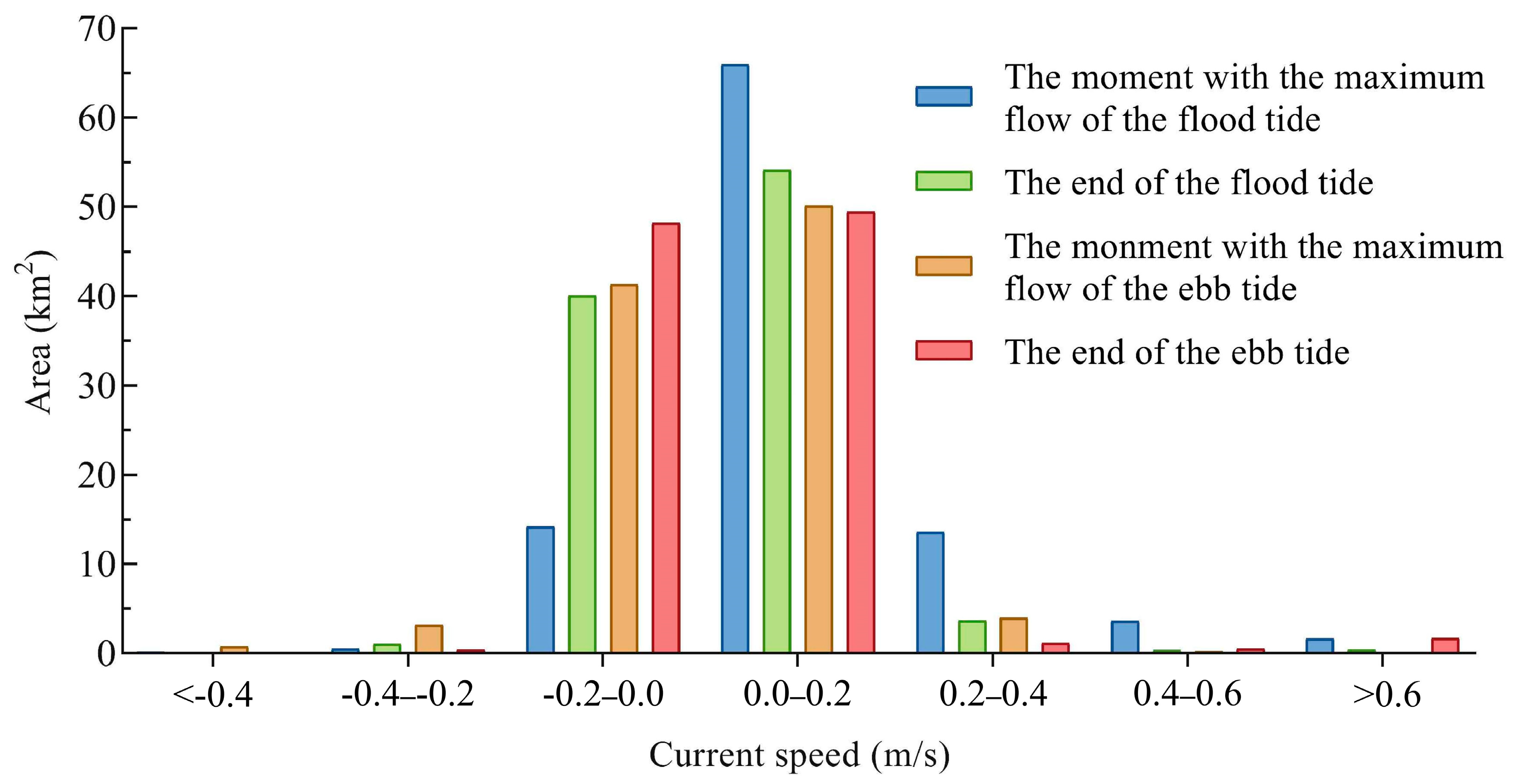
4.2. Tidal Current
4.3. Eulerian Residual Current
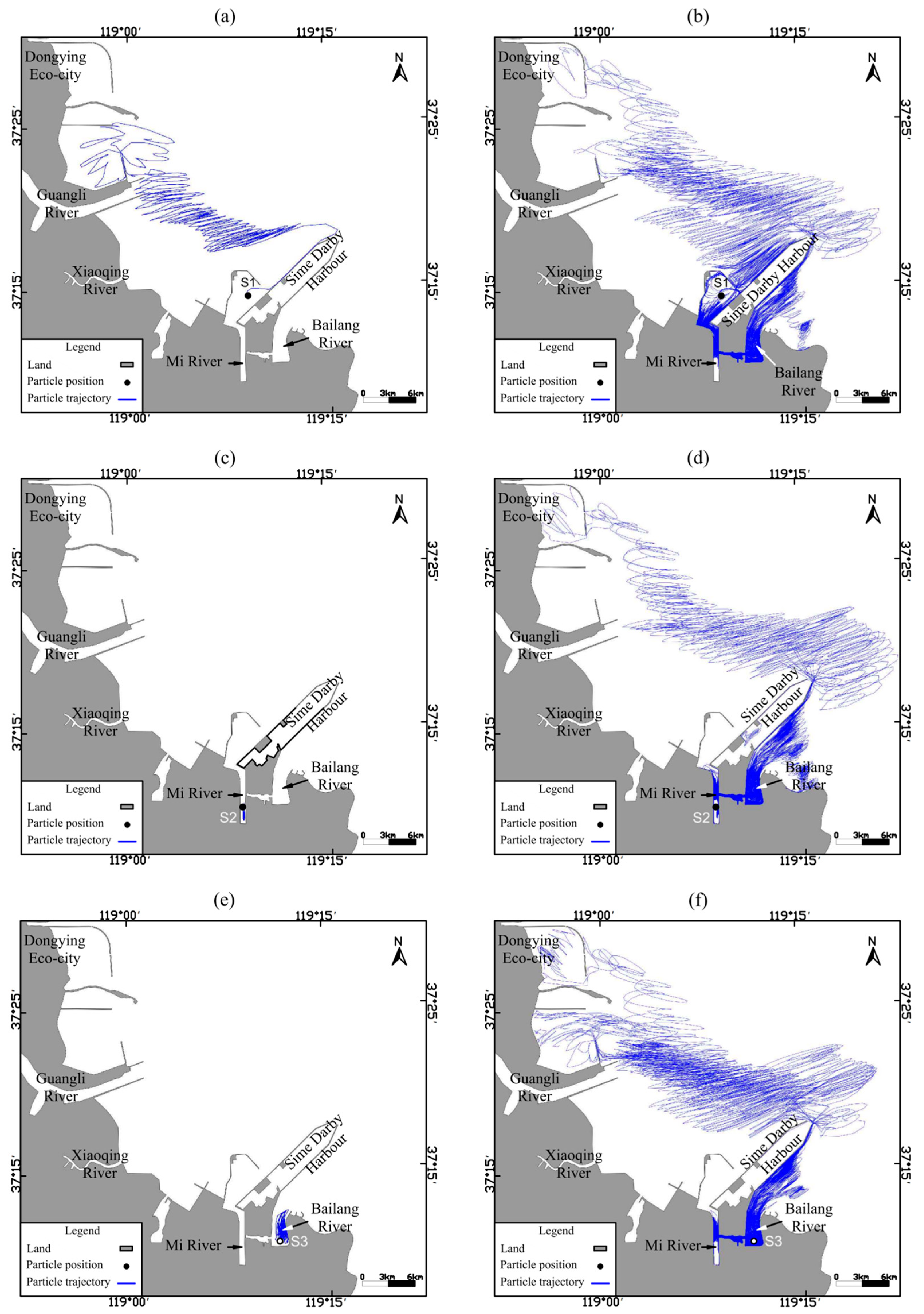
4.4. Lagrangian Particle Tracking
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kateb, A.E.; Stalder, C.; Rüggeberg, A.; Neururer, C.; Spangenberg, J.E.; Spezzaferri, S. Impact of industrial phosphate waste discharge on the marine environment in the Gulf of Gabes (Tunisia). PLoS ONE 2018, 13, 0197731. [Google Scholar] [CrossRef] [PubMed]
- Fasano, E.; Arnese, A.; Esposito, F.; Albano, L.; Masucci, A.; Capelli, C.; Cirillo, T.; Nardone, A. Evaluation of the impact of anthropogenic activities on arsenic, cadmium, chromium, mercury, lead, and polycyclic aromatic hydrocarbon levels in seafood from the Gulf of Naples, Italy. J. Environ. Sci. Health 2018, 53, 786–792. [Google Scholar] [CrossRef] [PubMed]
- Rahman, M.A.; Dawes, L.; Donehue, P.; Rahman, M.R. Cross-temporal analysis of disaster vulnerability of the southwest coastal communities in Bangladesh. Reg. Environ. Chang. 2021, 21, 67. [Google Scholar] [CrossRef]
- Xu, T.; You, X. Effects of large-scale embankments on the hydrodynamics and salinity in the Oujiang River Estuary, China. J. Mar. Sci. Technol. 2017, 22, 71–84. [Google Scholar] [CrossRef]
- Ebrahimi-sirizi, Z.; Riyahi-bakhtiyari, A. Petroleum pollution in mangrove forests sediments from Qeshm Island and Khamir Port—Persian Gulf, Iran. J. Environ. Monit. Assess. 2013, 185, 4019–4032. [Google Scholar] [CrossRef] [PubMed]
- Gao, F.; Zhang, C.; Jin, R.; Chen, S. The Development of Offshore Artificial Island Construction and Application of Key Hydrodynamic Technologies in China—Take Haihua Island Project as an Example. IOP Conf. Ser. Earth Environ. Sci. 2020, 580, 012093. [Google Scholar] [CrossRef]
- Guo, L.; Zhu, C.; Xu, F.; Xie, W.; Van Der Wegen, M.; Townend, I.; Wang, Z.B.; He, Q. Reclamation of tidal flats within tidal basins alters centennial morphodynamic adaptation to sea-level rise. J. Geophys. Res. Earth Surf. 2022, 127, 249857249. [Google Scholar] [CrossRef]
- Chi, W.; Zhang, X.; Zhang, W.; Bao, X.; Liu, Y.; Xiong, C.; Liu, J.; Zhang, Y. Impact of tidally induced residual circulations on chemical oxygen demand (COD) distribution in Laizhou Bay, China. Mar. Pollut. Bull. 2020, 151, 110811.1–110811.13. [Google Scholar] [CrossRef]
- Gao, X.; Zhuang, W.; Chen, C.; Zhang, Y. Sediment Quality of the SW Coastal Laizhou Bay, Bohai Sea, China: A Comprehensive Assessment Based on the Analysis of Heavy Metals. PLoS ONE 2015, 10, e0122190. [Google Scholar] [CrossRef]
- Hu, K.; Zhang, W.; Wang, X. Simulation of the Impact of Breakwaters on Hydrodynamic Environment in Laizhou Bay, China. J. Ocean Univ. China 2022, 21, 1557–1564. [Google Scholar] [CrossRef]
- Vona, I.; Gray, M.W.; Nardin, W. The Impact of Submerged Breakwaters on Sediment Distribution along Marsh Boundaries. Water 2020, 12, 1016. [Google Scholar] [CrossRef]
- Zhang, H.; Shen, Y.; Tang, J. Numerical investigation of successive land reclamation effects on hydrodynamics and water quality in Bohai Bay. Ocean Eng. 2023, 268, 113483. [Google Scholar] [CrossRef]
- Yang, Y.; Liang, S.; Li, K.; Liu, Y.; Lv, H.; Li, Y.; Wang, X. Administrative responsibility and land-sea synergistic regulating indicators for nutrient pollution: Linking terrigenous emission to water quality target in Laizhou Bay, China. Ecol. Indic. 2022, 13, 108884. [Google Scholar] [CrossRef]
- Komyakova, V.; Jaffrés, J.B.D.; Strain, E.M.A.; Cullen-Knox, C.; Fudge, M.; Langhamer, O.; Bender, A.; Yaakub, S.M.; Wilson, E.; Allan, B.J.M.; et al. Conceptualisation of multiple impacts interacting in the marine environment using marine infrastructure as an example. Sci. Total Environ. 2022, 830, 154748. [Google Scholar] [CrossRef] [PubMed]
- Ranjbar, M.H.; Jandaghi, A.M.; Nazarali, M. A modeling study of the impact of increasing water exchange rate on water quality of a semi-enclosed bay. Ecol. Eng. 2019, 136, 177–184. [Google Scholar] [CrossRef]
- Kazempour, Z.; Danesh, Y.M. Spatiotemporal dynamics of chlorophyll-a in the Gorgan Bay and Miankaleh Peninsula biosphere reserve: Call for action. Remote Sens. Appl. Soc. Environ. 2023, 30, 100946. [Google Scholar] [CrossRef]
- Serrano, D.; Flores-Verdugo, F.; Ramírez-Félix, E.; Kovacs, J.M.; Flores-de-Santiago, F. Modeling tidal hydrodynamic changes induced by the opening of an artificial inlet within a subtropical mangrove dominated estuary. Wetl. Ecol. Manag. 2020, 28, 103–118. [Google Scholar] [CrossRef]
- Tao, B.; Xu, J.; Zhang, M.; Chun-Ming, C. Seawater exchange rates for harbors based on the use of Mike 21 coupled with transport and particle tracking models. J. Coast. Conserv. 2021, 25, 33. [Google Scholar]
- Yan, J.; Chen, M.; Xu, L.; Liu, Q.; Shi, H.; He, N. Mike 21 Model Based Numerical Simulation of the Operation Optimization Scheme of Sedimentation Basin. Coatings 2022, 12, 478. [Google Scholar] [CrossRef]
- Xuan, T.L.; Cong, P.N.; Quoc, T.V.; Tran, Q.Q.; Wright, D.P.; Anh, D.T. Multi-scale modelling for hydrodynamic and morphological changes of breakwater in coastal Mekong Delta in Vietnam. J. Coast. Conserv. 2022, 26, 18. [Google Scholar] [CrossRef]
- Nguyen, P.; Gourbesville, P.; Audra, P.; Vo, N.D. Optimization of Channel Outlet in the Coastal Area—Application to Da Nang Bay, Viet Nam. Int. J. Environ. Sci. Dev. 2022, 13, 246–250. [Google Scholar] [CrossRef]
- Lefebvre, C.; Rojas, I.J.; Lasserre, J.; Villette, S.; Morin, B. Stranded in the high tide line: Spatial and temporal variability of beached microplastics in a semi-enclosed embayment (Arcachon, France). Sci. Total Environ. 2021, 797, 149144. [Google Scholar] [CrossRef]
- GB 3097-1997; Sea Water Quality Standard. Ministry of Ecology and Environment of the People’s Republic of China: Beijing, China, 1998.
- Li, X.; Huang, M.; Wang, R. Numerical simulation of Donghu Lake hydrodynamics and water quality based on remote sensing and MIKE 21. ISPRS Int. J. Geo-Inf. 2020, 9, 94. [Google Scholar] [CrossRef]
- Lambkin, D. A Review of the Bed Roughness Variable in MIKE 21 FLOW MODEL FM, Hydrodynamic (HD) and Sediment Transport (ST) Modules; English Heritage ALSF Project No. 5224; University of Southampton: Southampton, UK, 2010. [Google Scholar]
- Wang, W.; Hu, Z.; Li, M.; Zhang, H. Assessment of Tidal Current Energy Resources in the Pearl River Estuary Using a Numerical Method. Water 2023, 15, 3990. [Google Scholar] [CrossRef]
- Subramanian, R. Boundary Conditions in Fluid Mechanics; Clarkson University: Potsdam, NY, USA, 2019. [Google Scholar]
- Wang, R.; Herdman, L.M.; Erikson, L.; Barnard, P.; Hummel, M.; Stacey, M.T. Interactions of estuarine shoreline infrastructure with multiscale sea level variability. J. Geophys. Res. Ocean 2017, 122, 9962–9979. [Google Scholar] [CrossRef]
- Stashchuk, N.; Vlasenko, V.; Hosegood, P.; Nimmo-Smith, W.A. Tidally induced residual current over the Malin Sea continental slope. Cont. Shelf Res. 2017, 139, 21–34. [Google Scholar] [CrossRef]
- Yang, Z.; Wang, T. Tidal residual eddies and their effect on water exchange in Puget Sound. Ocean Dyn. 2013, 63, 995–1009. [Google Scholar] [CrossRef]
- Deng, F.; Jiang, W.; Valle-Levinson, A.; Feng, S. 3D Modal Solution for Tidally Induced Lagrangian Residual Velocity with Variations in Eddy Viscosity and Bathymetry in a Narrow Model Bay. J. Ocean Univ. China 2019, 18, 69–79. [Google Scholar] [CrossRef]
- Mardani, N.; Khanarmuei, M.; Suara, K.; Brown, R.; McCallum, A.; Sidle, R.C. Lagrangian data assimilation for improving model estimates of velocity fields and residual currents in a tidal estuary. Appl. Sci. 2021, 11, 11006. [Google Scholar]
- Cereja, R.; Brotas, V.; Nunes, S.; Rodrigues, M.; Cruz, J.P.; Brito, A.C. Tidal influence on water quality indicators in a temperate mesotidal estuary (Tagus Estuary, Portugal). Ecol. Indic. 2022, 136, 108715. [Google Scholar]
- DiLorenzo, J.L.; Filadelfo, R.J.; Surak, C.R.; Litwack, H.S.; Gunawardana, V.K.; Najarian, T.O. Tidal variability in the water quality of an urbanized estuary. Estuaries 2004, 27, 851–860. [Google Scholar] [CrossRef]
- Kong, X. Influence of inter-river water diversion on estuary pollution control: A case study of Liaodong Bay. Reg. Stud. Mar. Sci. 2024, 70, 103362. [Google Scholar] [CrossRef]
- Wu, Z.; Zhou, C.; Wang, P.; Fei, Z. Responses of tidal dynamic and water exchange capacity to coastline change in the Bohai Sea, China. Front. Mar. Sci. 2023, 10, 2296–7745. [Google Scholar] [CrossRef]
- Zhao, E.; Mu, L.; Qu, K.; Shi, B.; Ren, X.; Jiang, C. Numerical investigation of pollution transport and environmental improvement measures in a tidal bay based on a Lagrangian particle-tracking model. Water Sci. Eng. 2018, 11, 1674–2370. [Google Scholar] [CrossRef]
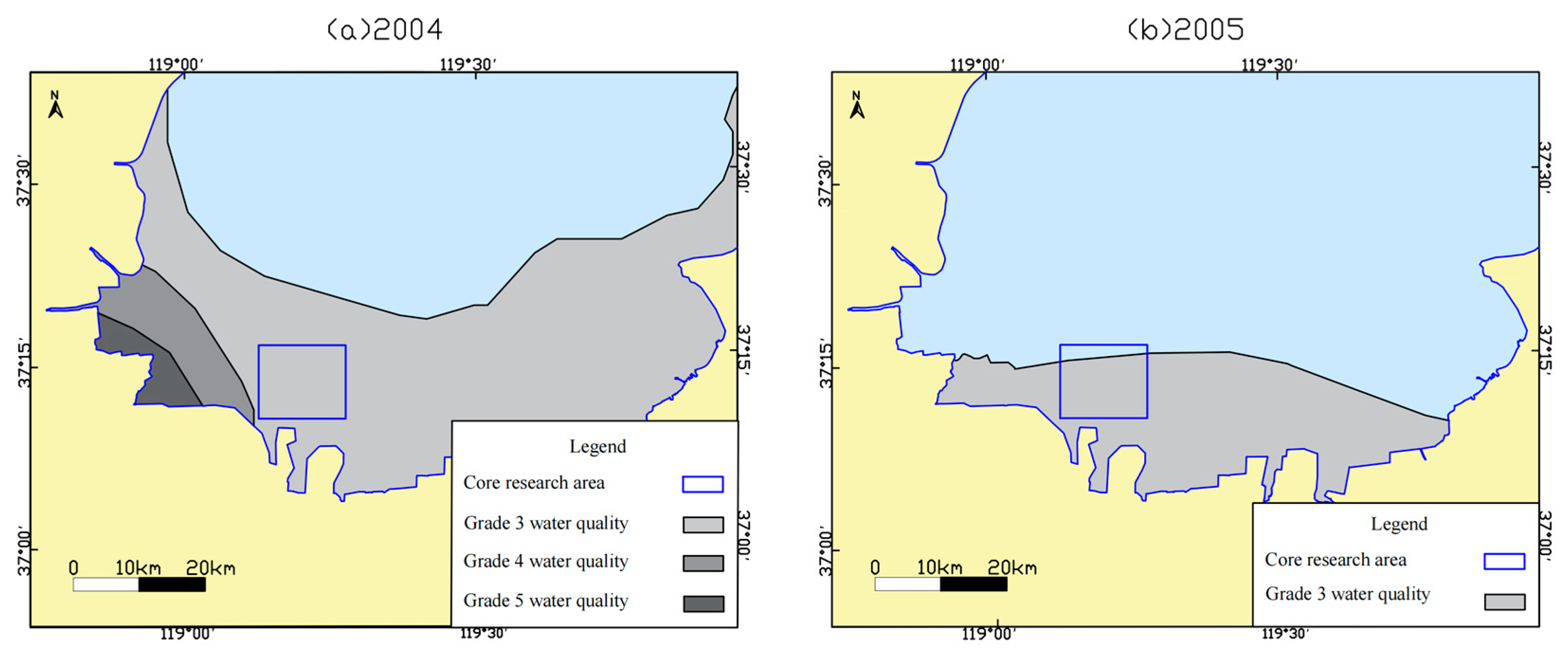


| Year | Water Area (km2) with Water Quality of | ||
|---|---|---|---|
| Grade 5 | Grade 4 | Grade 3 | |
| 2014 | 1116.5 | 2523.9 | 3572.9 |
| 2013 | 1112.9 | 1852.3 | 4989.5 |
| 2012 | 1621.1 | 2408.6 | 3602.9 |
| 2011 | — | — | — |
| 2010 | 312.1 | 766.3 | 1423.4 |
| 2009 | 336.1 | 1053.7 | 2351.4 |
| 2008 | 720.1 | 2166.8 | 3469.1 |
| 2007 | 1132.1 | 2942.2 | 4179.9 |
| 2006 | — | — | 620.1 |
| 2005 | — | — | 694.5 |
| 2004 | 100.0 | 186.2 | 2860.8 |
| Tidal Level | |||||
|---|---|---|---|---|---|
| Location | Tidal Periodicity | RMS (m) | RMSE (m) | R2 | |
| Measured Value | Predicted Value | ||||
| P1 | Spring tide | 0.65 | 0.67 | 0.23 | 0.91 |
| Neap tide | 0.45 | 0.49 | 0.15 | 0.93 | |
| P2 | Spring tide | 0.62 | 0.66 | 0.12 | 0.98 |
| Neap tide | 0.37 | 0.42 | 0.12 | 0.98 | |
| P3 | Spring tide | 0.57 | 0.56 | 0.19 | 0.92 |
| Neap tide | 0.34 | 0.38 | 0.13 | 0.95 | |
| Average | 0.50 | 0.53 | 0.16 | 0.95 | |
| Current Speed | |||||
| Location | Tidal Periodicity | RMS (m/s) | RMSE (m/s) | R2 | |
| Measured Value | Predicted Value | ||||
| DY05 | Spring tide | 0.24 | 0.21 | 0.06 | 0.80 |
| Neap tide | 0.24 | 0.21 | 0.04 | 0.94 | |
| DY13 | Spring tide | 0.21 | 0.19 | 0.06 | 0.76 |
| Neap tide | 0.19 | 0.16 | 0.05 | 0.82 | |
| DY15 | Spring tide | 0.27 | 0.26 | 0.07 | 0.74 |
| Neap tide | 0.29 | 0.29 | 0.04 | 0.93 | |
| DY18 | Spring tide | 0.34 | 0.37 | 0.08 | 0.82 |
| Neap tide | 0.19 | 0.19 | 0.03 | 0.86 | |
| DY23 | Spring tide | 0.31 | 0.34 | 0.08 | 0.81 |
| Neap tide | 0.24 | 0.23 | 0.04 | 0.90 | |
| DY26 | Spring tide | 0.34 | 0.37 | 0.09 | 0.68 |
| Neap tide | 0.19 | 0.22 | 0.04 | 0.90 | |
| Average | 0.25 | 0.25 | 0.06 | 0.83 | |
| Current Direction | |||||
| Location | Tidal Periodicity | RMS (°) | RMSE (°) | R2 | |
| Measured Value | Predicted Value | ||||
| DY05 | Spring tide | 175.31 | 192.50 | 55.56 | 0.70 |
| Neap tide | 215.22 | 202.97 | 28.41 | 0.90 | |
| DY13 | Spring tide | 171.04 | 164.44 | 49.59 | 0.71 |
| Neap tide | 208.17 | 194.36 | 31.24 | 0.91 | |
| DY15 | Spring tide | 205.42 | 227.88 | 62.40 | 0.69 |
| Neap tide | 208.54 | 198.95 | 18.30 | 0.91 | |
| DY18 | Spring tide | 198.65 | 203.11 | 35.21 | 0.88 |
| Neap tide | 189.42 | 183.28 | 29.00 | 0.97 | |
| DY23 | Spring tide | 220.04 | 245.38 | 57.01 | 0.76 |
| Neap tide | 179.02 | 170.82 | 26.43 | 0.89 | |
| DY26 | Spring tide | 193.66 | 204.48 | 32.45 | 0.91 |
| Neap tide | 215.38 | 201.52 | 30.28 | 0.88 | |
| Average | 198.32 | 199.14 | 37.99 | 0.84 | |
| Particle | Net Transport Distance (km) | Increase | ||
|---|---|---|---|---|
| Before Connection | After Connection | (km) | (%) | |
| S1 | 24.9 | 33.4 | 8.5 | 34.2 |
| S2 | 1.8 | 41.8 | 39.9 | 2.2 × 103 |
| S3 | 3.7 | 42.1 | 38.4 | 1.0 × 103 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chi, Y.; Zhang, W.; Liu, Y.; Zhang, X.; Chi, W.; Shi, B. Improving Water Quality in a Sea Bay by Connecting Rivers on Both Sides of a Harbor. J. Mar. Sci. Eng. 2024, 12, 442. https://doi.org/10.3390/jmse12030442
Chi Y, Zhang W, Liu Y, Zhang X, Chi W, Shi B. Improving Water Quality in a Sea Bay by Connecting Rivers on Both Sides of a Harbor. Journal of Marine Science and Engineering. 2024; 12(3):442. https://doi.org/10.3390/jmse12030442
Chicago/Turabian StyleChi, Yuning, Wenming Zhang, Yanling Liu, Xiaoyu Zhang, Wanqing Chi, and Bing Shi. 2024. "Improving Water Quality in a Sea Bay by Connecting Rivers on Both Sides of a Harbor" Journal of Marine Science and Engineering 12, no. 3: 442. https://doi.org/10.3390/jmse12030442
APA StyleChi, Y., Zhang, W., Liu, Y., Zhang, X., Chi, W., & Shi, B. (2024). Improving Water Quality in a Sea Bay by Connecting Rivers on Both Sides of a Harbor. Journal of Marine Science and Engineering, 12(3), 442. https://doi.org/10.3390/jmse12030442




