Research on Three-Closed-Loop ADRC Position Compensation Strategy Based on Winch-Type Heave Compensation System with a Secondary Component
Abstract
1. Introduction
2. Dynamic Model of Heave Compensation System
2.1. Mathematical Modeling
2.1.1. The Model of the Electro-Hydraulic Servo Valve
2.1.2. Variable Control Oil Cylinder
2.1.3. Secondary Component Displacement
2.1.4. Cable-Winding System
2.2. Simulation Model and Parameter Settings
- The system operated in an ideal constant-temperature and constant-pressure hydraulic environment. The hydraulic components and pipelines were sufficiently rigid, and there was no pressure loss along the pipeline.
- The hydraulic oil was considered to be incompressible, with a constant density and viscosity.
- Friction forces at various locations, such as the cable and valve spool, were assumed to be constant and did not vary with operating conditions and temperature changes.
3. Three-Closed-Loop ADRC Position Control Strategy Design
3.1. ADRC Controller Design and Composition
3.1.1. The Tracking Differentiator (TD)
3.1.2. Extended State Observer (ESO)
3.1.3. Nonlinear States Error Feedback (NLSEF)
3.1.4. Disturbance Estimation Compensation
3.1.5. Stability Analysis
3.2. Controller Design and Parameter Setting
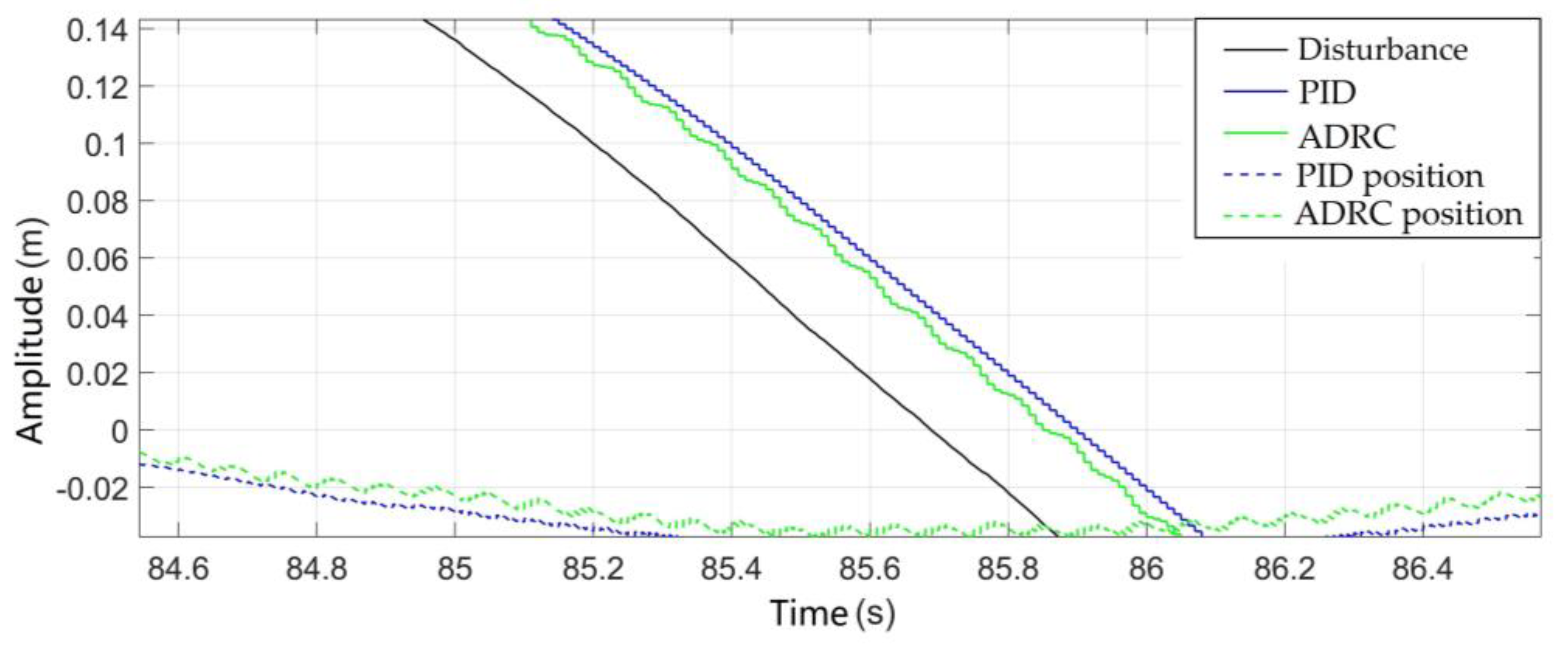
4. Simulation Experiment Research and Analysis
4.1. Step Disturbance Response Analysis
4.2. Sine Disturbance Response Analysis
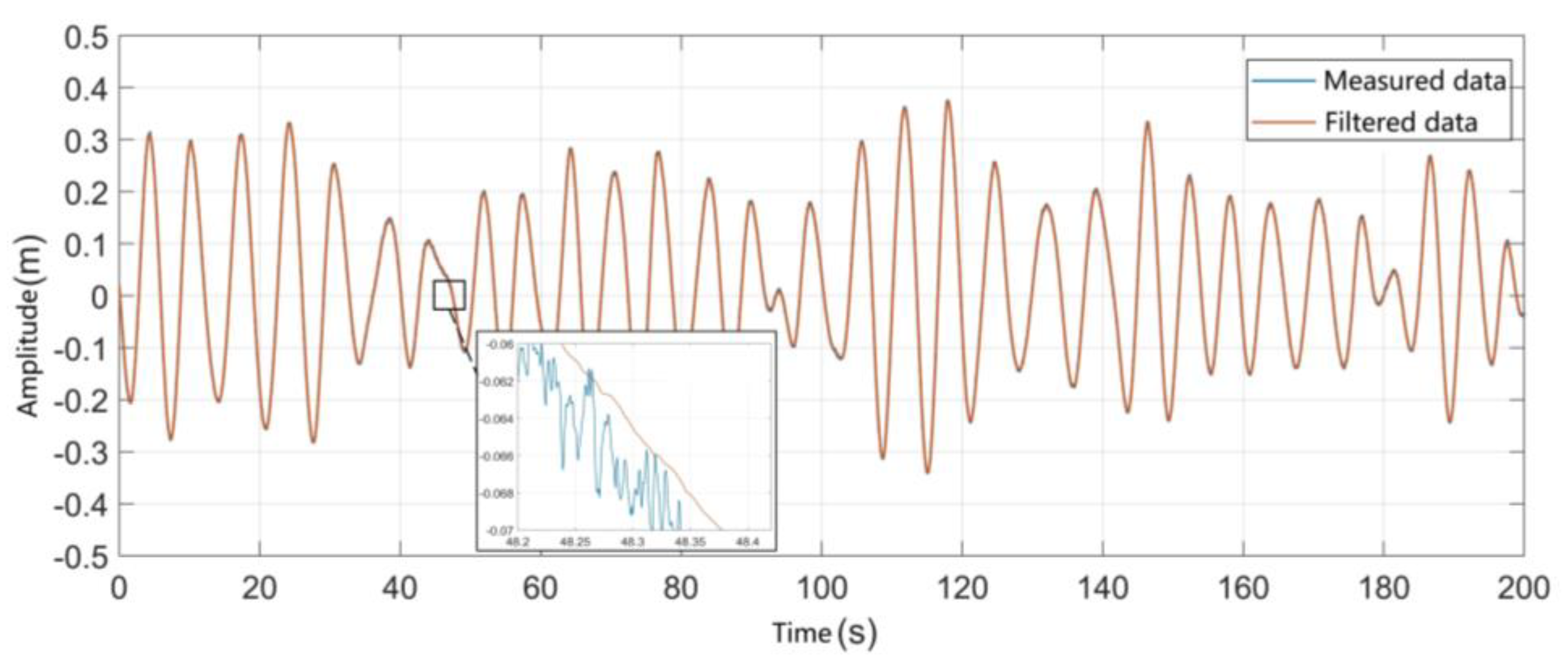
4.3. A Certain Sea Area in China Ship Heave Motion Disturbance Response Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Acronyms | Definition |
|---|---|
| ADRC | Active disturbance rejection control |
| PID | Proportional integral derivative |
| AMESim | Software name |
| A4VSO, A4VSG | Rexroth product model |
| HNC | Rexroth controller |
| AHC | Active heave compensation system |
| SMC | Sliding mode control |
| MPC | Model predictive control |
| IDA-PBC | Interconnection and damping assignment productivity based control |
| ABFTSMC | Adaptive barrier fast terminal sliding mode control |
| UAVs | Unmanned aerial vehicles |
| FTSMC | Fast terminal sliding mode control |
| NMPC | Nonlinear model predictive control |
| TD | Tracking differentiator |
| ESO | Extended state observer |
| NLSEF | Nonlinear states error feedback |
| MRU | Motion reference unit |
| Symbol | Definition | Symbol | Definition |
|---|---|---|---|
| Qsf | Output flow | θer | Main shaft rotation angle of the secondary component |
| I | Coil input current | Ber | Viscous damping coefficient |
| Kv | Flow gain | ML | External load torque |
| s | Laplace operator | xl | Displacement of the load |
| ωn | Natural frequency | xl0 | Initial position of the load |
| ξn | Damping ratio | xh | Displacement due to the heave of the ship |
| q | Flow entering the high-pressure chamber | ijt | Reduction ratio of the gearbox |
| Ag | Effective piston area inside | R | Radius of the winch drum |
| xg | Piston displacement | Δl | Elongation of the cable |
| Ct | Total leakage coefficient | Δld | Dynamic elongation of the cable |
| p | Pressure difference | Δls | Static elongation of the cable |
| Vt | Total volume | meq | Equivalent mass of the load and cable |
| βe | Volumetric modulus of oil | kl | Cable’s elastic coefficient |
| Ci | Internal leakage coefficient | Cl | Cable’s damping coefficient |
| Ce | External leakage coefficient | r | Velocity factor |
| mg | Total mass of the moving components | h0 | Filtering factor |
| Bg | Viscous damping coefficient | h | Integration step size |
| kg | Spring stiffness | fhan | Maximum speed control function |
| Ffg | Resistance force acting | β01, β02, β03 | Observer gain parameters |
| Der | Secondary component displacement | b0 | Compensation factor |
| Dermax | Secondary component maximum displacement | ζ | Heave compensation root-mean-square error compensation rate |
| xgmax | Maximum displacement of the piston | Δ | Load position error in heave compensation |
| ps | Constant pressure of the oil supply | T | Statistical duration |
| Jer | Rotational inertia converted to the output shaft | x | Amplitude of the disturbance |
References
- Woodacre, J.K.; Bauer, R.J.; Irani, R.A. A Review of Vertical Motion Heave Compensation Systems. Ocean Eng. 2015, 104, 140–154. [Google Scholar] [CrossRef]
- Petillot, Y.R.; Antonelli, G.; Casalino, G.; Ferreira, F. Underwater Robots: From Remotely Operated Vehicles to Intervention-Autonomous Underwater Vehicles. IEEE Robot. Autom. Mag. 2019, 26, 94–101. [Google Scholar] [CrossRef]
- Yu, H.; Chen, Y.; Shi, W.; Xiong, Y.; Wei, J. State Constrained Variable Structure Control for Active Heave Compensators. IEEE Access 2019, 7, 54770–54779. [Google Scholar] [CrossRef]
- Woo, N.-S.; Kim, H.-J.; Han, S.-M.; Ha, J.-H.; Huh, S.-C.; Kim, Y.-J. Evaluation of the Structural Stability of a Heave Compensator for an Offshore Plant and the Optimization of Its Shape. J. Nanosci. Nanotechnol. 2020, 20, 263–269. [Google Scholar] [CrossRef] [PubMed]
- Xie, T.; Zou, D.; Huang, L.; Liu, D. Modelling and Simulation Analysis of Active Heave Compensation Control System for Marine Winch. In Proceedings of the 2021 IEEE 4th International Electrical and Energy Conference (CIEEC), Wuhan, China, 28 May 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Jakubowski, A.; Milecki, A. The Investigations of Hydraulic Heave Compensation System. In Automation 2018; Szewczyk, R., Zieliński, C., Kaliczyńska, M., Eds.; Advances in Intelligent Systems and Computing; Springer International Publishing: Cham, Switzerland, 2018; Volume 743, pp. 380–391. ISBN 978-3-319-77178-6. [Google Scholar] [CrossRef]
- Dabing, Z.; Jianzhong, W.; Xin, L. Ship-Mounted Crane’s Heave Compensation System Based on Hydrostatic Secondary Control. In Proceedings of the 2011 International Conference on Mechatronic Science, Electric Engineering and Computer (MEC), Jilin, China, 19–22 August 2011; pp. 1626–1628. [Google Scholar] [CrossRef]
- Busquets, E.; Ivantysynova, M. Adaptive Robust Motion Control of an Excavator Hydraulic Hybrid Swing Drive. SAE Int. J. Commer. Veh. 2015, 8, 568–582. [Google Scholar] [CrossRef]
- Liu, T.; Iturrino, G.; Goldberg, D.; Meissner, E.; Swain, K.; Furman, C.; Fitzgerald, P.; Frisbee, N.; Chlimoun, J.; Van Hyfte, J.; et al. Performance Evaluation of Active Wireline Heave Compensation Systems in Marine Well Logging Environments. Geo-Mar. Lett. 2013, 33, 83–93. [Google Scholar] [CrossRef]
- Moslått, G.-A.; Rygaard Hansen, M.; Padovani, D. Performance Improvement of a Hydraulic Active/Passive Heave Compensation Winch Using Semi Secondary Motor Control: Experimental and Numerical Verification. Energies 2020, 13, 2671. [Google Scholar] [CrossRef]
- Zinage, S.; Somayajula, A. Deep Reinforcement Learning Based Controller for Active Heave Compensation. IFAC-PapersOnLine 2021, 54, 161–167. [Google Scholar] [CrossRef]
- Sun, Y.G.; Qiang, H.Y.; Sheng, X.M. Genetic Algorithm-Based Parameters Optimization for the PID Controller Applied in Heave Compensation System. Appl. Mech. Mater. 2014, 556–562, 2462–2465. [Google Scholar] [CrossRef]
- Feng, Y.; Yu, X.; Han, F. On Nonsingular Terminal Sliding-Mode Control of Nonlinear Systems. Automatica 2013, 49, 1715–1722. [Google Scholar] [CrossRef]
- Mayne, D.Q. Model Predictive Control: Recent Developments and Future Promise. Automatica 2014, 50, 2967–2986. [Google Scholar] [CrossRef]
- Tianxiang, M.; Yi, Y.; Jianbo, C.; Guihong, Z.; Yuanpei, Y.; Jianshan, W.; Haiqin, G.; Hui, Y. Design of Heave Compensation Control System Based on Variable Parameter PID Algorithm. In Proceedings of the 2018 Chinese Control and Decision Conference (CCDC), Shenyang, China, 9–11 June 2018; pp. 825–829. [Google Scholar] [CrossRef]
- Do, K.D.; Pan, J. Nonlinear Control of an Active Heave Compensation System. Ocean Eng. 2008, 35, 558–571. [Google Scholar] [CrossRef]
- Kuchler, S.; Sawodny, O. Nonlinear Control of an Active Heave Compensation System with Time-Delay. In Proceedings of the 2010 IEEE International Conference on Control Applications, Yokohama, Japan, 8–10 September 2010; pp. 1313–1318. [Google Scholar] [CrossRef]
- Zhou, H.; Cao, J.; Yao, B.; Lian, L. Hierarchical NMPC–ISMC of Active Heave Motion Compensation System for TMS–ROV Recovery. Ocean Eng. 2021, 239, 109834. [Google Scholar] [CrossRef]
- Zhang, Q.; Tan, B.; Hu, X. Ship Heave Compensation Based on PID-DDPG Hybrid Control. In Proceedings of the 2023 42nd Chinese Control Conference (CCC), Tianjin, China, 24 July 2023; pp. 8576–8581. [Google Scholar]
- Guerrero-Sanchez, M.-E.; Hernandez-Gonzalez, O.; Valencia-Palomo, G.; Lopez-Estrada, F.-R.; Rodriguez-Mata, A.-E.; Garrido, J. Filtered Observer-Based IDA-PBC Control for Trajectory Tracking of a Quadrotor. IEEE Access 2021, 9, 114821–114835. [Google Scholar] [CrossRef]
- Najafi, A.; Vu, M.T.; Mobayen, S.; Asad, J.H.; Fekih, A. Adaptive Barrier Fast Terminal Sliding Mode Actuator Fault Tolerant Control Approach for Quadrotor UAVs. Mathematics 2022, 10, 3009. [Google Scholar] [CrossRef]
- Zhou, R.; Neusypin, K.A. ADRC-Based UAV Control Scheme for Automatic Carrier Landing. In Proceedings of the 15th International Conference “Intelligent Systems” (INTELS’22), Moscow, Russia, 14–16 December 2022; p. 66. [Google Scholar] [CrossRef]
- Deng, B.; Xu, J. Trajectory Tracking Based on Active Disturbance Rejection Control for Compound Unmanned Aircraft. Aerospace 2022, 9, 313. [Google Scholar] [CrossRef]
- Li, Z.; Ma, X.; Li, Y.; Meng, Q.; Li, J. ADRC-ESMPC Active Heave Compensation Control Strategy for Offshore Cranes. Ships Offshore Struct. 2020, 15, 1098–1106. [Google Scholar] [CrossRef]
- Shuguang, L.; Wuyang, C.; Kecheng, W.; Jia, J. An ADRC-Based Active Heave Compensation for Offshore Rig. In Proceedings of the 2020 Chinese Control and Decision Conference (CCDC), Hefei, China, 22–24 August 2020; pp. 2979–2984. [Google Scholar] [CrossRef]
- Messineo, S.; Serrani, A. Offshore Crane Control Based on Adaptive External Models. Automatica 2009, 45, 2546–2556. [Google Scholar] [CrossRef]
- Li, M.; Gao, P.; Zhang, J.; Gu, J.; Zhang, Y. Study on the System Design and Control Method of a Semi-Active Heave Compensation System. Ships Offshore Struct. 2018, 13, 43–55. [Google Scholar] [CrossRef]
- Röper, R. ölhydraulik und Pneumatik. In Dubbel; Beitz, W., Küttner, K.-H., Eds.; Springer: Berlin/Heidelberg, Germany, 1987; pp. 597–616. ISBN 978-3-662-06779-6. [Google Scholar] [CrossRef]
- Han, J. From PID to Active Disturbance Rejection Control. IEEE Trans. Ind. Electron. 2009, 56, 900–906. [Google Scholar] [CrossRef]
- Gao, Z.; Huang, Y.; Han, J. An Alternative Paradigm for Control System Design. In Proceedings of the 40th IEEE Conference on Decision and Control (Cat. No.01CH37228), Orlando, FL, USA, 4–7 December 2001; Volume 5, pp. 4578–4585. [Google Scholar] [CrossRef]
- Guo, B.-Z.; Zhao, Z. On the Convergence of an Extended State Observer for Nonlinear Systems with Uncertainty. Syst. Control Lett. 2011, 60, 420–430. [Google Scholar] [CrossRef]
- Guo, B.-Z.; Zhao, Z.-L. On Convergence of the Nonlinear Active Disturbance Rejection Control for MIMO Systems. SIAM J. Control Optim. 2013, 51, 1727–1757. [Google Scholar] [CrossRef]
- Guo, B.-Z.; Wu, Z.-H. Output Tracking for a Class of Nonlinear Systems with Mismatched Uncertainties by Active Disturbance Rejection Control. Syst. Control Lett. 2017, 100, 21–31. [Google Scholar] [CrossRef]
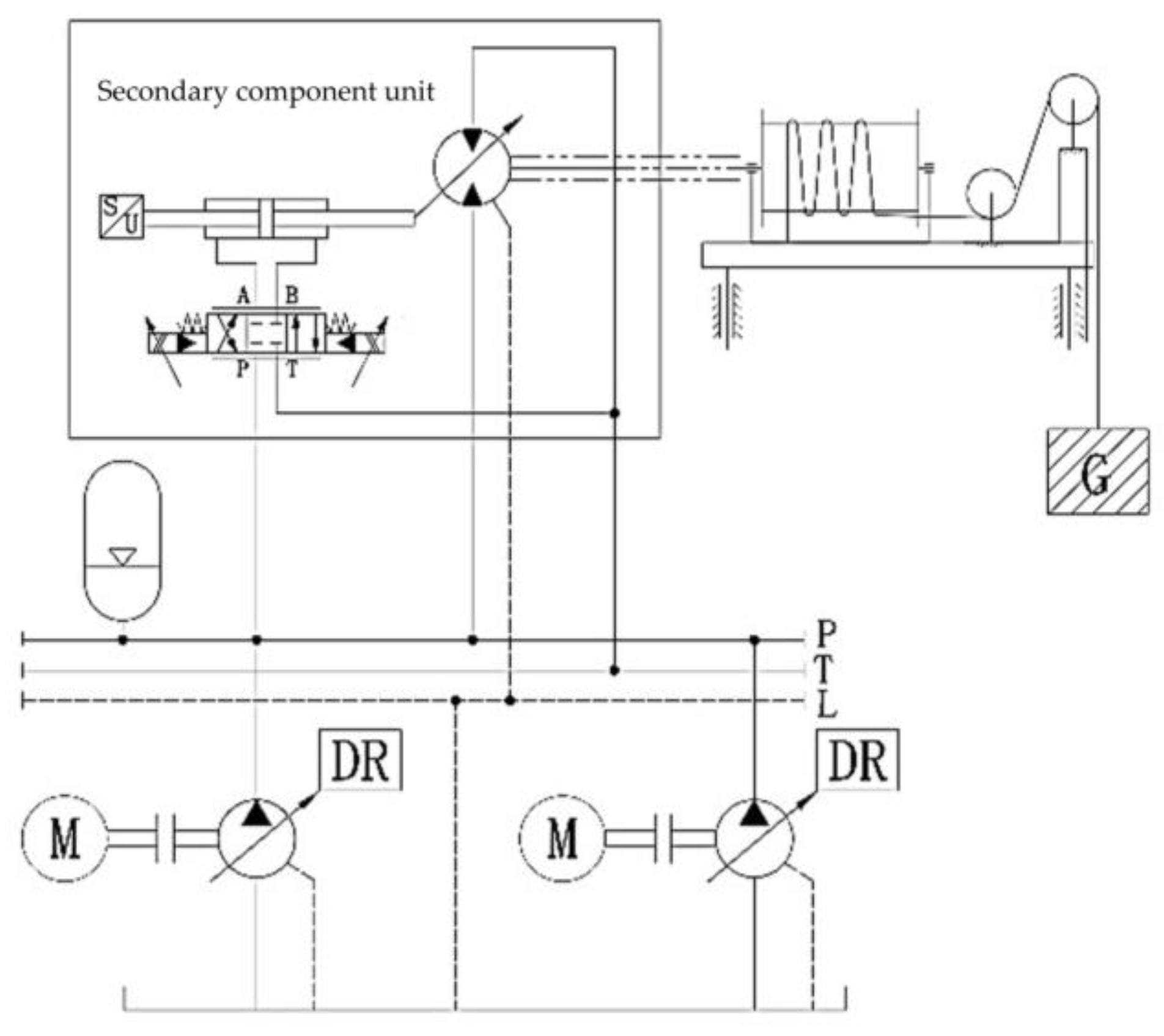




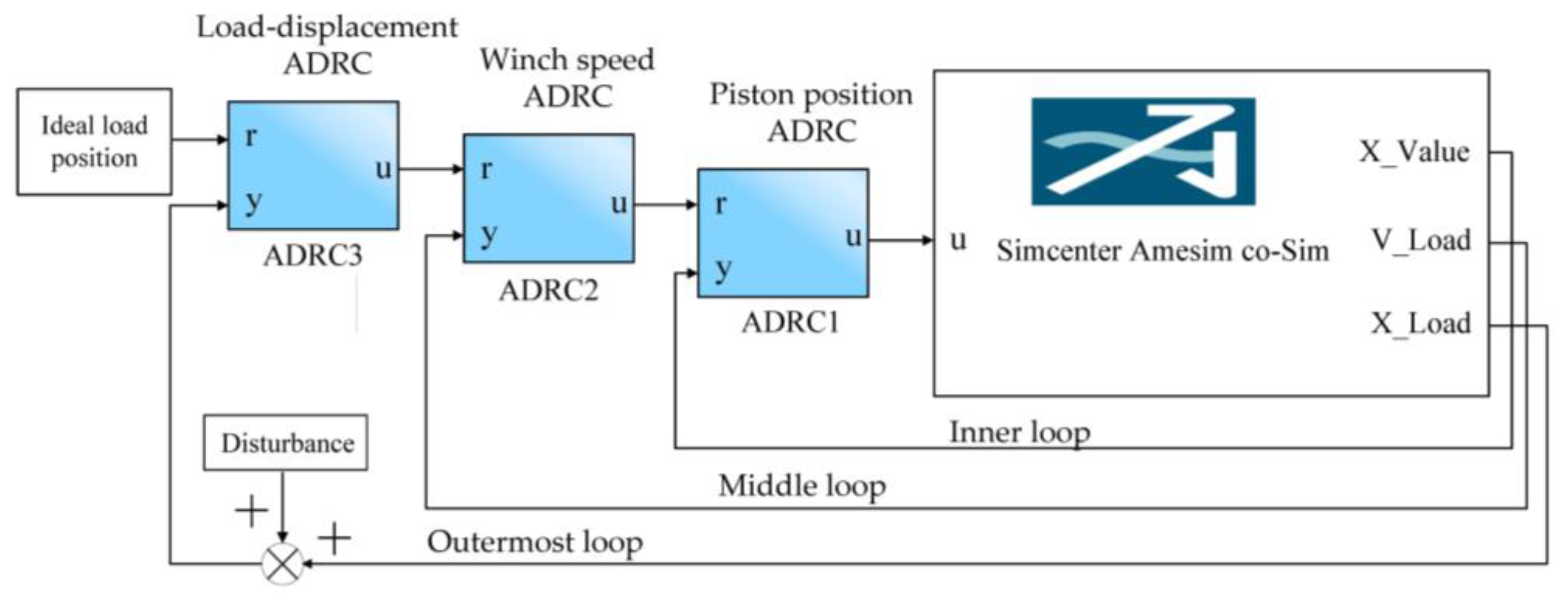


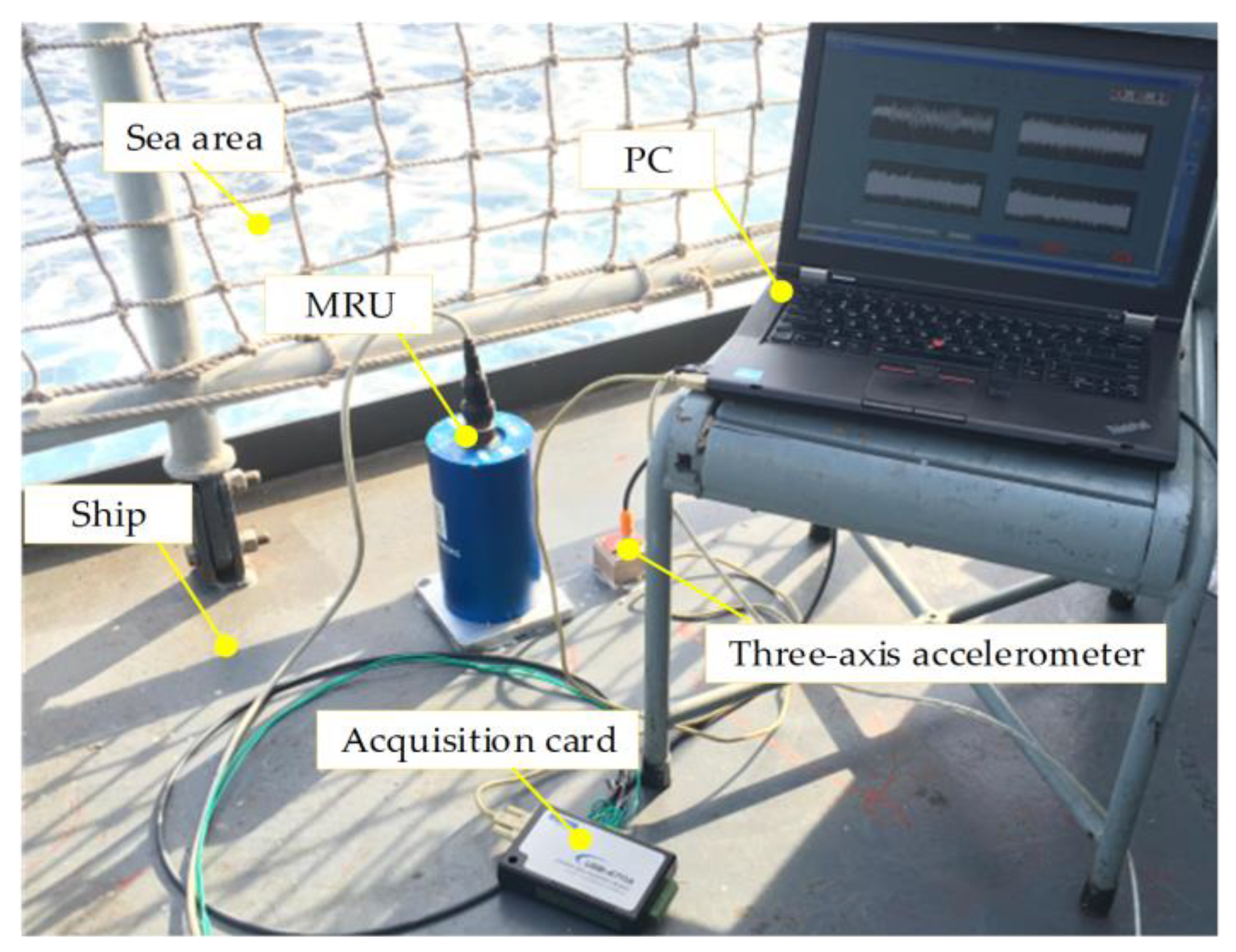


| Main Components | Sub-Model | Functional Description |
|---|---|---|
| Motor | PM000 | Standard electric motor |
| Pump | PP01 | Constant-pressure variable pump |
| Servo valve | SV00 | Three-position four-way directional valve |
| Relief valve | RV012 | Safety valve |
| Accumulator | HA000 | Diaphragm-type accumulator |
| Variable cylinder spring chamber | BAP016 | Variable cylinder reset function chamber |
| Variable cylinder piston chamber | BAF01 | Variable cylinder control function chamber |
| Mass block | MECMAS21/MAS001 | Variable cylinder mass property simulation |
| Hydraulic motor | HYDVPM01 | Bidirectional variable hydraulic motor |
| Winch | WINCH01 | Ideal winch |
| Cable or wire rope | MECROPE0/REND001 | Rigid rope |
| Parameter Name | Value | Unit |
|---|---|---|
| Hydraulic motor displacement Der | 40 | mL/r |
| Maximum motor speed nmdmax | 664 | r/min |
| Gearbox reduction ratio ijt | 26.4 | — |
| Winch drum radius R | 190 | mm |
| System pressure ps | 18 | MPa |
| Accumulator volume V | 20 | L |
| Parameters | h | rTD | rNLSEF | β01 | β02 | β03 | b0 |
|---|---|---|---|---|---|---|---|
| Inner loop ADRC | 0.001 | 10000 | |||||
| Middle loop ADRC | 0.001 | 900 | 10000 | 780 | |||
| Outermost loop ADRC | 0.001 | 900 | 10000 | 7500 |
| Parameters | Rise Time (s) | Peak Time (s) | Maximum Overshoot | Settling Time (s) |
|---|---|---|---|---|
| No-overshoot PID | 1.3445 | 2.3400 | 0 | 1.7077 |
| Overshoot PID | 1.3347 | 1.8900 | 1.18% | 1.6563 |
| ADRC | 1.0257 | 1.5700 | 0 | 1.3532 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, S.; Wu, Q.; Liu, Y.; Qiao, L.; Guo, Z.; Yan, F. Research on Three-Closed-Loop ADRC Position Compensation Strategy Based on Winch-Type Heave Compensation System with a Secondary Component. J. Mar. Sci. Eng. 2024, 12, 346. https://doi.org/10.3390/jmse12020346
Li S, Wu Q, Liu Y, Qiao L, Guo Z, Yan F. Research on Three-Closed-Loop ADRC Position Compensation Strategy Based on Winch-Type Heave Compensation System with a Secondary Component. Journal of Marine Science and Engineering. 2024; 12(2):346. https://doi.org/10.3390/jmse12020346
Chicago/Turabian StyleLi, Shizhen, Qinfeng Wu, Yufeng Liu, Longfei Qiao, Zimeng Guo, and Fei Yan. 2024. "Research on Three-Closed-Loop ADRC Position Compensation Strategy Based on Winch-Type Heave Compensation System with a Secondary Component" Journal of Marine Science and Engineering 12, no. 2: 346. https://doi.org/10.3390/jmse12020346
APA StyleLi, S., Wu, Q., Liu, Y., Qiao, L., Guo, Z., & Yan, F. (2024). Research on Three-Closed-Loop ADRC Position Compensation Strategy Based on Winch-Type Heave Compensation System with a Secondary Component. Journal of Marine Science and Engineering, 12(2), 346. https://doi.org/10.3390/jmse12020346







