Practical Fixed-Time Robust Containment Control of Multi-ASVs with Collision Avoidance

Abstract

A practical fixed-time robust containment control method for multiple autonomous surface vehicles (multi-ASVs) is proposed in this study. This method addresses the containment control problem of multi-ASVs, considering both collision risks and external disturbances. This control scheme improves the cooperative performance of the formation and guarantees safe collision avoidance behavior. First, to enable the online estimation of unknown time-varying disturbances from the external environment, a fixed-time disturbance observer (FNDO) is designed based on fixed-time control theory. Second, the distributed kinematic controller is modified to include the partial derivatives of the artificial potential energy function (APEF), thereby preventing collisions among multi-ASVs. Third, by applying fixed-time theory, graph theory, and fixed-time dynamic surface control techniques, a practical fixed-time robust containment controller for multi-ASVs is proposed. Additionally, the entire closed-loop control system is guaranteed to be practical and fixed-time stable through stability analysis. Finally, the proposed control strategy has been validated by simulation results.

1. Introduction

The complexity and difficulty of offshore operations have greatly increased, making the disadvantages of the traditional single-ship operation mode increasingly apparent, such as limited operational scope and low fault tolerance [1]. Compared to single-ship operations, formations offer better performance in offshore operations due to their wider operation range, improved fault tolerance, and greater execution efficiency [2,3,4,5,6]. In recent years, autonomous surface vehicles (ASVs) equipped with autonomous planning and navigation systems have attracted widespread attention as a type of unmanned surface vehicle [7,8,9]. Therefore, research on multi-ASVs is significant due to their advantages, such as high flexibility, low cost, and good safety.

In the study of multi-ASV formation control, various formation control structures have been proposed, including leader–follower [10], virtual [11], behavior-based [12,13,14], graph-based [15,16], and combination structure [17]. In recent years, the graph theory-based leader–follower formation control structure has become a significant trend in the formation control field [18,19,20], representing a distributed formation control structure where the interaction of formation layout information between individuals is captured using graphs. This approach is particularly significant in solving the containment control problem.

Facing the complex marine environment, especially for some more complex tasks, such as remote underwater exploration with safety zones, multi-target convoy escorting, etc. It is necessary to introduce multiple leaders for guidance. As the most common collaborative formation method for multi-leader guidance, containment control has gained widespread attention in recent years [21]. The control objective of containment control is to design controllers that enable the followers to be led into the convex hull formed by the multiple leaders. Zhu designed a robust containment controller based on graph theory to address the uncertainty of hydrodynamic parameters and unknown time-varying disturbances [22]. To address the issue of communication resource wastage, Jiang et al. proposed a distributed event-triggered adaptive containment controller [23]. Yoo et al. proposed a prescribed performance containment controller for multi-unmanned surface vehicles, which is applicable to heterogeneous ships [24]. Xu et al. proposed a distributed robust control protocol based on model predictive control to solve the problem of multi-ASV cooperative formation [25].

It is worthwhile noting that while previous research on containment control has achieved remarkable results, it also has certain limitations. Specifically, there has been insufficient attention given to the collision avoidance challenges vehicles may encounter during formation navigation, including both inter-vehicle and obstacle-related collisions. For simplicity, the problem of collision avoidance is used hereafter to refer to these issues collectively. Existing approaches to collision avoidance commonly include reinforcement learning [26], prescribed performance [27], behavior-based methods [28], and the artificial potential field (APF) approach [29,30]. The APF method, widely used in multi-agent systems, is particularly effective for solving collision avoidance problems in multi-ASVs due to its simplicity and ease of computation. A collision-free formation model predictive control based on APF for aerial formations was previously proposed by Menegatti et al. [29]. To address the problem of collision avoidance, Li et al. improved the traditional APF method by considering communication resource wastage, proposing a nonlinear model predictive control strategy combining event-triggering with an enhanced APF [30]. However, these works are limited by their focus on either global-time convergence or finite-time convergence, which does not fully address the convergence characteristics of tracking error signals.

The convergence time is a key performance metric in assessing control systems. The upper bound of the convergence time is influenced by the initial value of the control system state, which is a drawback even if the finite-time control research in the past has made systems finite-time stable. Consequently, researchers have explored fixed-time stability in the literature [31,32]. Compared to global asymptotic stability and finite-time stability in existing research, the control performance of the fixed-time control system has been further improved [33,34,35]. In fact, the system’s fixed-time stability does not imply that its convergence time is constant; rather, it means that there is a maximum upper bound independent of the system’s initial state. Currently, related research in other fields based on fixed-time control theory has achieved significant results, including spacecraft [36], mobile robots [37], and multi-agents [38], offering valuable insights for controlling multi-ASVs.

In practical applications, multi-ASVs are inevitably exposed to the effects of unknown time-varying disturbances caused by complex marine environments, which necessitates that the control system overcome the impact of these disturbances to maintain the formation layout. Currently, ship motion control aimed at mitigating external disturbances has yielded certain results [39,40,41]. It is important to note that all of the above results [39,40,41] focused on single-ship rather than formation. Zhu et al. combined a nonlinear disturbance observer with dynamic surface technology to propose a robust containment controller that addresses the problem of unknown time-varying disturbances affecting multiple autonomous surface vehicles [42]. Li et al. designed a prescribed-time disturbance observer and then proposed a novel multi-ASVs’ prescribed-time controller to tackle the prescribed-time control problem [43].

A practical fixed-time robust containment control strategy for multi-ASVs is proposed, utilizing the artificial potential energy function (APEF) and fixed-time nonlinear disturbance observer (FNDO), with considerations for collision avoidance, external disturbances, and fixed-time convergence. First, the unknown time-varying disturbances are estimated using the FNDO, which is independent of the initial state. Second, a distributed kinematic controller incorporating the APEF is designed to address the issue of collision avoidance. Third, with the aid of the backstepping method, fixed-time theory, and dynamic surface control technology, a practical fixed-time robust containment controller based on FNDO is designed. The main contributions are as follows:

• Distinct from previous work that does not consider collision avoidance [24,25], the partial derivatives of the artificial potential energy function (APEF) are introduced into the distributed kinematic controller. The APEF is activated when ASVs are at risk of colliding with other vehicles or obstacles, thus achieving containment control of multi-ASVs with collision avoidance.
• In contrast to containment controllers focused on global asymptotic stability or finite-time stability [29,30], a novel practical fixed-time containment controller is designed based on fixed-time control theory, driving all followers into the convex hull formed by the multiple leaders within a fixed time.
• Compared to the related work in the literature [42], the unknown time-varying disturbances are estimated using a fixed-time nonlinear disturbance observer (FNDO), which has fixed-time convergence. Then, using further developed techniques, a novel, practical, fixed-time robust containment controller based on the FNDO is proposed.

The characteristics of the paper are as follows: The issue formulation and associated lemma are presented in Section 2. The controller design is mostly introduced in Section 3. The stability of the entire closed-loop control system is examined in Section 4. Simulation tests are used in Section 5 to validate the designed controller. The article’s summary and generalization are included in Section 6.

2. Preliminaries and Problem Formulation

2.1. Notation

In the paper, the following notations are used. Let $R^n$ denote a n-dimensional Euclidean space, $R^{n\times m}$ denotes a set of Euclidean $n\times m$ matrices, respectively, $‖•‖$ denotes the Euclidean norm of a vector, $\left|•\right|$ denotes the absolute value of a scalar, ${\lambda }_{\max }\left(\mathit{A}\right)$ denotes the maximum eigenvalue of a square matrix $A$, ${\lambda }_{\min }\left(\mathit{A}\right)$ denotes the minimum eigenvalue, ${\mathit{I}}_n$ denotes an n-dimensional identity matrix, $diag\left\{\left(•\right)\right\}$ denotes the diagonal matrix, $\otimes$ denotes Kronecker product, $si{g}^{\alpha }\left(x\right)=\mathit{sgn}\left(x\right){\left|x\right|}^{\alpha },a\in \left(0,1\right),x\in R,$ where $\mathit{sgn}\left(x\right)$ is the sign function, and it satisfies

$$sgn(x)=\left\{\begin{array}{cc}1,& x>0\\ 0,& x=0\\ -1,& x<0\end{array}\right.$$

(1)

2.2. Graph Theory

To describe the topological relationships between vehicles, graph theory is introduced. The multi-ASV containment control system studied in this paper uses a directed graph to describe the topological relationship between vehicles. Assume that $\mathcal{G}=\left\{\mathit{\upsilon },\mathit{\phi }\right\}$ represents a directed graph, where $\mathit{\upsilon }$ denotes a set of nodes, representing all vehicles in the formation system, as well as $\mathit{\phi }=\left\{\left(i,j\right)\in \mathit{\upsilon }\times \mathit{\upsilon }\right\}$ represents a set of edges. Let $\left(i,j\right)$ represent a set of node pairs, implying that node j can transmit information to node i, and the information flow in the directed graph is unidirectional. Let $\mathcal{A}=\left[a_{ij}\right]$ denote the adjacency matrix, which is used to describe whether there is information transmission between ASVs. If $\left(i,j\right)\in \mathit{\phi }$, then $a_{ij}=1$, otherwise, $a_{ij}=0$. It is worthwhile noting that we assume $a_{ii}$ = 0 for all nodes. To describe the number of communication paths, let $\mathcal{D}$ represent a diagonal matrix called the degree matrix, which describes the number of communication paths for each node, and $d_i={\displaystyle {\sum }_{j\in N_i}{a}_{ij}}$ denotes the diagonal element. In addition, let $\mathcal{L}=\mathcal{D}-\mathcal{A}$ represent the Laplacian matrix.

2.3. Definitions and Lemmas

For the purpose of research, the definition and relevant lemmas are introduced in this section.

Definition 1

([44]). A general nonlinear system is given as:

$$\dot{x}=f\left(x\left(t\right)\right),x\left(0\right)=x_0,f\left(0\right)=0$$

(2)

where $x\in R^n$ denotes the system state variable, $f\left(x\right):R^n\to R^n$ for a nonlinear function that may be discontinuous, and t represents time. The fixed-time stability of the nonlinear system is introduced as follows.

Lemma 1

([44]). Assume that there exists a Lyapunov function $V\left(x\right)$ for system (2), and the derivative of $V\left(x\right)$ following the inequality holds:

$$\dot{V}\left(x\right)\le -\alpha V^{\chi }\left(x\right)-\beta V^{\delta }\left(x\right)$$

(3)

where $\alpha >0$ , $\beta >0$ , $0<\chi <1$ , $\delta >1$ , then the origin of system (2) is said to be uniformly global fixed-time stable, and the convergence time of system (2) satisfies

$$T\le T_{\mathit{max}}={\displaystyle \frac{1}{\alpha \left(1-\chi \right)}}+{\displaystyle \frac{1}{\beta \left(\delta -1\right)}}$$

(4)

Lemma 2

([45]). Assume that there exists a Lyapunov function $V\left(x\right)$ for system (2), and the derivative of $V\left(x\right)$ following the inequality holds:

$$\dot{V}\left(x\right)\le -\alpha V^{\chi }\left(x\right)-\beta V^{\delta }\left(x\right)+\epsilon$$

(5)

where $\alpha >0$, $\beta >0$ , $0<\chi <1$, $\delta >1$, $\epsilon >0$, then the origin of system (2) is said to be practical fixed-time stable, and the convergence time of system (2) satisfies

$$T\le T_{\mathit{max}}={\displaystyle \frac{1}{\alpha \kappa \left(1-\chi \right)}}+{\displaystyle \frac{1}{\beta \kappa \left(\delta -1\right)}}$$

(6)

where $0<\kappa <1$, T_max accounts for the upper bound of convergence time. The residual set of the system is given as

$$\left\{\underset{t\to T}{\lim }x|V\left(x\right)\le \min \left\{{\alpha }^{-\frac{1}{\chi }}{\left(\frac{\epsilon }{1-\kappa }\right)}^{\frac{1}{\chi }},{\beta }^{-\frac{1}{\delta }}{\left(\frac{\epsilon }{1-\kappa }\right)}^{\frac{1}{\delta }}\right\}\right\}$$

(7)

where, if $\epsilon$ is smaller, the convergence effect is better, as reflected in (7). Suppose T_max is connected to the residual set of the system by $\kappa$. When $\epsilon$ is constant, if $\kappa$ is larger, the residual set of the system is larger, T_max is smaller.

Lemma 3.

([46]). For ${\chi }_i\in R$ , $i=1,\dots ,n$ , $0<\gamma \le 1$ , the following inequality holds:

$${\left({\displaystyle \sum _{i=1}^n\left|{\chi }_i\right|}\right)}^{\gamma }\le {\displaystyle \sum _{i=1}^n\left|{\chi }_i\right|}\le n^{1-\gamma }{\left({\displaystyle \sum _{i=1}^n\left|{\chi }_i\right|}\right)}^{\gamma }$$

(8)

Lemma 4.

([47]). For ${\chi }_i\in R,i=1,\dots ,n$ , $\gamma >1$, the following inequality holds:

$${\left({\displaystyle \sum _{i=1}^n\left|{\chi }_i\right|}\right)}^{\gamma }\le {\displaystyle \sum _{i=1}^n\left|{\chi }_i\right|}\le n^{\gamma -1}{\left({\displaystyle \sum _{i=1}^n\left|{\chi }_i\right|}\right)}^{\gamma }$$

(9)

Lemma 5.

(([48]). For $\chi$ , $\delta \in R$ and any real numbers, the following inequality holds:

$$\chi \delta \le {\displaystyle \frac{{\varphi }^{\alpha }}{\alpha }}{\left|\chi \right|}^{\alpha }+{\displaystyle \frac{1}{\beta {\varphi }^{\beta }}}{\left|\delta \right|}^{\beta }$$

(10)

where $\varphi >0$ , $\alpha >1$ , $\beta >1$ , and $\left(\alpha -1\right)\left(\beta -1\right)=1$.

Definition 2.

Let $C$ represent a subset of the real vector space. For $\forall x,y\in C$, $C$ is said to be convex if $\left(1-\lambda \right)x+\lambda y\in C$ for any $\lambda \in \left[0,1\right]$. The convex hull of a set of points in a plane is the smallest convex polygon that encloses all of the points, as illustrated in Figure 1. For a set of points denoted by $\mathit{X}=\left\{x_1,\dots x_n\right\}$ in $C$, the convex hull is the smallest convex set defined as $\mathit{Co}\left(\mathit{X}\right)$ its mathematical form is expressed as follows

$$\mathit{Co}\left(\mathit{X}\right)=\left\{{\displaystyle \sum _{i=1}^n{\Pi }_i{x}_i|x_i\in \mathit{X},{\Pi }_i\ge 0,}{\displaystyle \sum _{i=1}^n{\Pi }_i=1}\right\}$$

(11)

Figure 1 intuitively illustrates the concept of a convex hull, defined as the smallest convex boundary enclosing a set of points. The red vertices represent the virtual leaders, while the black lines denote the edges of the convex hull. The blue points, representing the followers, are entirely contained within the convex hull.

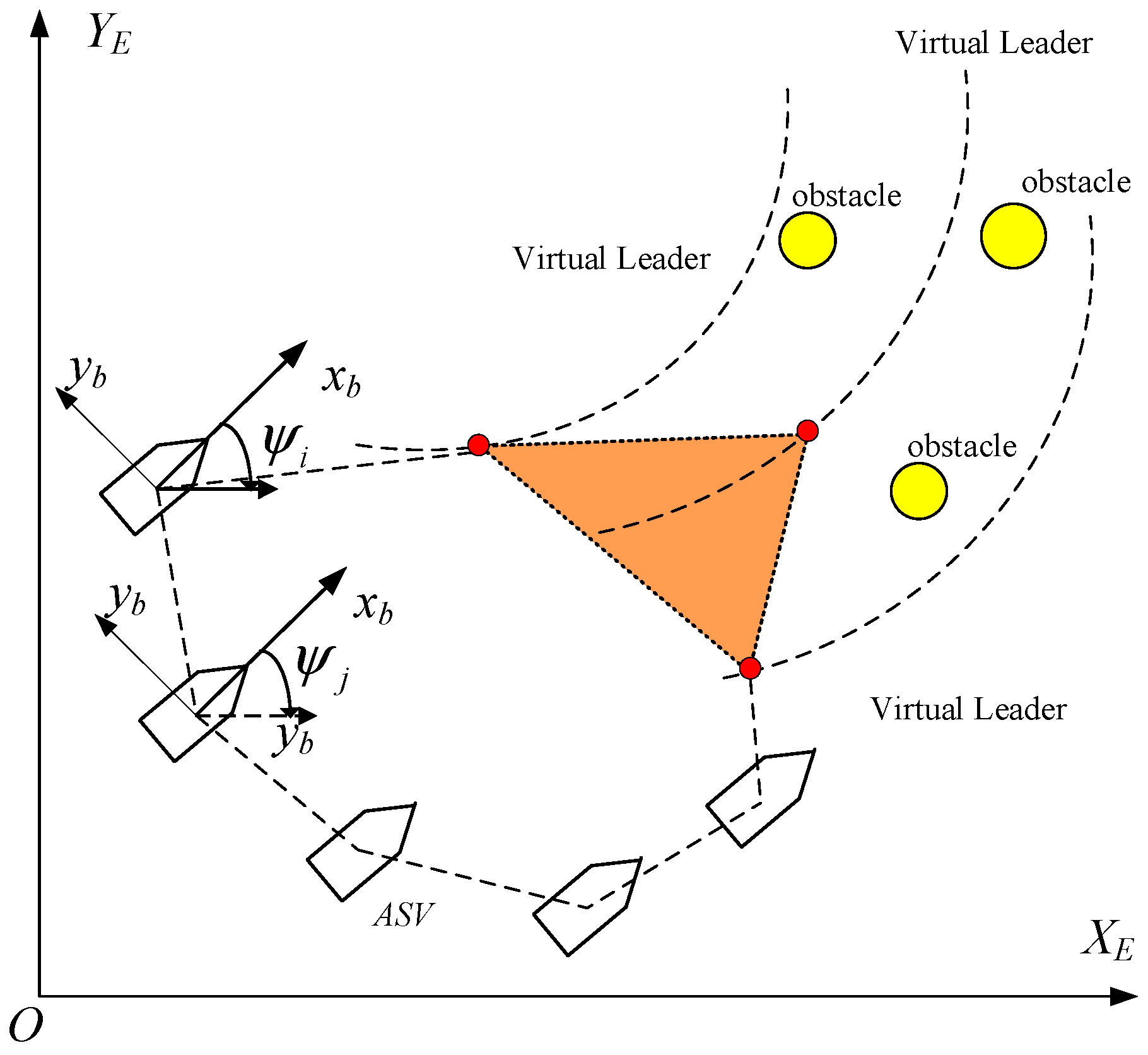
2.4. Problem Formulation

Considering a multi-ASV system composed of N vehicles, including M followers and N − M virtual leaders, the mathematical model of the ith (i = 1,…, M) ASV can be described as follows [49]:

$$\left\{\begin{array}{l}{\dot{\mathit{\eta }}}_i={\mathit{J}}_i(\psi ){\mathit{\upsilon }}_i\hfill \\ {\mathit{M}}_i{\dot{\mathit{\upsilon }}}_i+{\mathit{C}}_i{\mathit{\upsilon }}_i+{\mathit{D}}_i{\mathit{\upsilon }}_i={\mathit{\tau }}_i+{\mathit{\tau }}_{i,w}\hfill \end{array}\right.$$

(12)

where ${\mathit{\eta }}_i={\left(x_i,y_i,{\mathit{\psi }}_i\right)}^{\mathrm{T}}\in R^3$ denotes the vehicle’s position and heading in the earth-fixed frame. ${\mathit{J}}_i({\mathit{\psi }}_i)\in R^{3\times 3}$ is the rotation matrix. ${\mathit{\upsilon }}_i={\left(u_i,v_i,r_i\right)}^{\mathrm{T}}\in R^3$ denotes the velocity vector in the body-fixed frame, where $u_i$, $v_i$, $r_i$ denote surge velocity, roll velocity, and yaw angular velocity, respectively. ${\mathit{M}}_i\in R^{3\times 3}$ accounts for the inertia matrix of the i-th ASV. ${\mathit{C}}_i\in R^{3\times 3}$ represents the Coriolis force matrix. ${\mathit{D}}_i\in R^{3\times 3}$ is the damping coefficient matrix. ${\mathit{\tau }}_i={\left({\mathit{\tau }}_{i,u},{\mathit{\tau }}_{i,v},{\mathit{\tau }}_{i,r}\right)}^{\mathrm{T}}\in R^3$ denotes the control input vector. ${\mathit{\tau }}_{i,w}\in R^3$ denotes the environment disturbances, which are unknown and time-varying. Moreover, ${\mathit{M}}_i$, ${\mathit{C}}_i$, ${\mathit{D}}_i$, and ${\mathit{J}}_i({\mathit{\psi }}_i)$ are given as

$${\mathit{M}}_i=\left[\begin{array}{ccc}{m}_{i,11}& 0& 0\\ 0& m_{i,22}& m_{i,23}\\ 0& m_{i,32}& m_{i,33}\end{array}\right]\hspace{1em}{\mathit{C}}_i=\left[\begin{array}{ccc}0& 0& c_{i,13}\\ 0& 0& c_{i,23}\\ -c_{i,31}& -c_{i,32}& 0\end{array}\right],\hspace{1em}{D}_i=\left[\begin{array}{ccc}{d}_{i,11}& 0& 0\\ 0& d_{i,22}& d_{i,23}\\ 0& d_{i,32}& d_{i,33}\end{array}\right],\hspace{1em}{\mathit{J}}_i({\psi }_i)=\left[\begin{array}{ccc}\cos {\psi }_i& -\sin {\psi }_i& 0\\ \sin {\psi }_i& \cos {\psi }_i& 0\\ 0& 0& 1\end{array}\right]$$

Considering the controller design, the mathematical model is transformed into the following forms

$$\left\{\begin{array}{l}{\dot{\mathit{p}}}_i=\overline{\mathit{J}}\left({\mathit{\psi }}_i\right)\left[\begin{array}{c}{u}_i\\ v_i\end{array}\right]\\ \dot{\mathit{\psi }}=r_i\end{array}\right.$$

(13)

$$\left\{\begin{array}{l}{\dot{u}}_i=(f_{i,1}+{\tau }_{i,u}+{\tau }_{i,wu})/m_{i,11}\\ {\dot{v}}_i=f_{i,2}+{\tau }_{i,u}+{\tau }_{i,wv}/m_{i,22}\\ {\dot{r}}_i=(f_{i,3}+{\tau }_{i,r}+{\tau }_{i,wr})/m_{i,33}\end{array}\right.$$

(14)

where ${\mathit{p}}_i={\left[x_i,y_i\right]}^{\mathrm{T}}$ accounts for the position of the ith ASV, $f_{i,1}=m_{i,22}{v}_i{r}_i-d_{i,11}{u}_i$, $f_{i,2}=-m_{i,11}{u}_i{r}_i-d_{i,22}{v}_i$, and $f_{i,3}=(m_{i,11}-m_{i,22})u_i{v}_i-d_{i,33}{r}_i$. $\overline{\mathit{J}}\left({\psi }_i\right)$ is given as:

$$\overline{\mathit{J}}\left({\psi }_i\right)=\left[\begin{array}{cc}\cos {\psi }_i& -\sin {\psi }_i\\ \sin {\psi }_i& \cos {\psi }_i\end{array}\right]$$

(15)

Let $\mathit{\varpi }={\left[{{\mathit{\varpi }}_{M+1}}^T,\dots ,{{\mathit{\varpi }}_N}^T\right]}^T$ denote the position of virtual leaders, where ${\mathit{\varpi }}_j$$(j=M+1,\dots ,N)$ is the position of the j-th virtual leader. Suppose there is no information flow between virtual leaders, and followers are unable to transmit information to the virtual leaders. Hence, the communication topology between N – M virtual leaders and M followers is given in (16), whose specific form is as follows

$$\mathcal{L}=\left[\begin{array}{cc}{\mathcal{L}}_1& {\mathcal{L}}_2\\ {\mathbf{0}}_{\left(N-M\right)\times M}& {\mathbf{0}}_{\left(N-M\right)\times \left(N-M\right)}\end{array}\right]$$

(16)

where ${\mathcal{L}}_1\in R^{M\times M}$ denotes the Laplacian matrix between M followers, ${\mathcal{L}}_2\in R^{M\times \left(N-M\right)}$ denotes the Laplacian matrix between N − M virtual leaders and M followers, ${\mathbf{0}}_{\left(N-M\right)\times \left(N-M\right)}\in R^{\left(N-M\right)\times \left(N-M\right)}$ denotes the Laplacian matrix between N – M virtual leaders, ${\mathbf{0}}_{\left(N-M\right)\times M}\in R^{\left(N-M\right)\times M}$ denotes the Laplacian matrix between M followers and N − M virtual leaders.

To facilitate the system design, the following assumptions are made.

Assumption 1.

The environment disturbances affecting surface vehicles are bounded, satisfying $\left|{\tau }_{i,w}\right|<{\tau }_{i\max }$, where ${\tau }_{i\max }$ accounts for the upper limit of environmental disturbances.

Remark 1.

Assumption 1 is reasonable because the energy of the external environment is finite and constantly changing, so the unknown time-varying disturbances affecting the vehicles have an upper bound.

Assumption 2.

The speed of the surface vehicles can be measured.

Assumption 3.

For each follower in multi-ASVs, there exists at least one virtual leader, and a communication path exists between them.

Lemma 6

([50]). Under Assumption 3, all eigenvalues of ${\left({\mathcal{L}}_1\right)}^{-1}{\mathcal{L}}_2$ have positive real parts. Additionally, all elements of ${\left({\mathcal{L}}_1\right)}^{-1}{\mathcal{L}}_2$ are non-negative, and the sum of the elements in each row is equal to 1.

Based on Assumptions 1–3, the practical fixed-time robust containment control for multi-ASVs with collision avoidance aims to achieve the following objectives:

Control Objective 1: In order to guide all followers into the convex hull spanned by the multiple leaders, the control system’s primary goal is to design a novel containment controller for each follower in the multi-ASV formation system.

$$\underset{t\to T_i}{\lim }‖{\mathit{\eta }}_i-{\displaystyle \sum _{j=\mathit{M}+1}^{\mathrm{N}}{\prod }_j{\mathit{\varpi }}_j}‖\le {\epsilon }_1$$

(17)

where $T_i$ denotes the convergency time, ${\mathit{\eta }}_i={\left(x_i,y_i,{\mathit{\psi }}_i\right)}^{\mathrm{T}}\in R^3$ denotes the vehicle’s position and heading, ${\mathit{\varpi }}_j\in R^3$ denotes the location information of the j-th virtual leader, ${\epsilon }_1$ is a positive constant. ${\Pi }_j\left(j=M+1,M+2,\dots ,N\right)$ is a positive constant, and ${\displaystyle \sum _{j=M+1}^N{\Pi }_j}=1$.

Control Objective 2: Let the distance between vehicles and the distance between vehicles and obstacles satisfy the following:

$$\left\{\begin{array}{l}‖{\mathit{p}}_i-{\mathit{p}}_j‖>R_c,i=1,\dots M,j\in N_i^F\\ ‖{\mathit{p}}_i-{\mathit{p}}_o‖>R_o,o=1,\dots ,N_k\end{array}\right.$$

(18)

where ${\mathit{p}}_i={\left[x_i,y_i\right]}^{\mathrm{T}}$, ${\mathit{p}}_j={\left[x_j,y_j\right]}^{\mathrm{T}}$, $‖{\mathit{p}}_i-{\mathit{p}}_j‖=\sqrt{{\left(x_i-x_j\right)}^2+{\left(y_i-y_j\right)}^2}$. $R_c\in R^{+}$ denotes the minimum safe collision avoidance radius, ${\mathit{p}}_o={\left[x_o,y_o\right]}^{\mathrm{T}}$ denotes the position of o-th obstacle, $‖{\mathit{p}}_i-{\mathit{p}}_o‖=\sqrt{{\left(x_i-x_o\right)}^2+{\left(y_i-y_o\right)}^2}$. $R_o\in R^{+}$ denotes the minimum safe collision avoidance radius with respect to obstacles.

Figure 2 depicts the designed containment control system for multiple autonomous surface vehicles, considering collision avoidance.

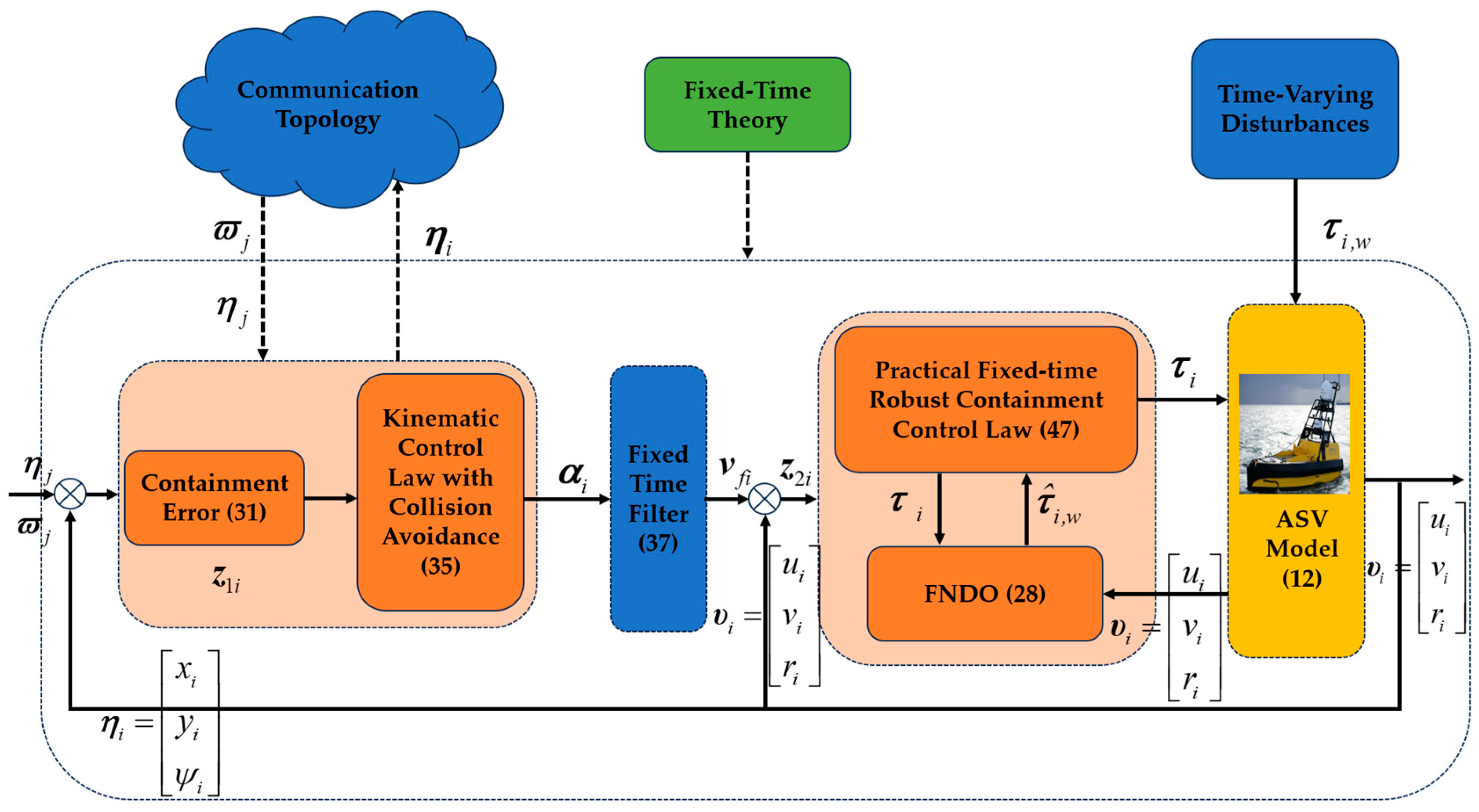
3. Main Result

This section presents the design of a practical fixed-time containment controller for multi-ASVs with collision avoidance. First, a fixed-time disturbance observer (FNDO) is constructed for each ASV to estimate unknown disturbances. Second, to address the issue of collision avoidance, an artificial potential energy function (APEF) is introduced into the design of distributed kinematic controllers, enabling ASVs to achieve both containment control and collision avoidance. Finally, a practical fixed-time robust containment controller for multi-ASVs is designed based on FNDO and dynamic surface control technology. The block diagram of the proposed control method is shown in Figure 3.

3.1. Collision Avoidance Scheme

Collision Avoidance Function: To achieve safe collision avoidance between ASVs, the collision avoidance function is defined as follows

$$V_{ij}^a\left({\mathit{p}}_i,{\mathit{p}}_j\right)=\left\{\begin{array}{cc}{\left({\displaystyle \frac{{\overline{R}}_a^2-{‖{\mathit{p}}_{ij}‖}^2}{{‖{\mathit{p}}_{ij}‖}^2-{\underset{\_}{R}}_a^2}}\right)}^2,& {\underset{\_}{R}}_a\le ‖{\mathit{p}}_{ij}‖\le {\overline{R}}_a\\ 0,& ‖{\mathit{p}}_{ij}‖>{\overline{R}}_a\mathrm{or}‖{\mathit{p}}_{ij}‖<{\underset{\_}{R}}_a\end{array}\right.$$

(19)

By taking the partial derivative of (19) with respect to ${\mathit{p}}_i$, we obtain

$${\displaystyle \frac{\partial V_{ij}^a}{\partial {\mathit{p}}_i}}=\left\{\begin{array}{cc}{\displaystyle \frac{4\left({\overline{R}}_a^2-{\underset{\_}{R}}_a^2\right)\left({‖{\mathit{p}}_{ij}‖}^2-{\overline{R}}_a^2\right)}{{\left({‖p_{ij}‖}^2-{\underset{\_}{R}}_a^2\right)}^3}}{p}_{ij}& {\underset{\_}{R}}_a\le ‖p_{ij}‖\le {\overline{R}}_a\\ 0_2& ‖p_{ij}‖>{\overline{R}}_a\mathrm{or}‖p_{ij}‖<{\underset{\_}{R}}_a\end{array}\right.$$

(20)

where $‖{\mathit{p}}_{ij}‖=‖{\mathit{p}}_i-{\mathit{p}}_j‖=\sqrt{{\left(x_i-x_j\right)}^2+{\left(y_i-y_j\right)}^2}$, ${\underset{\_}{R}}_a$ denotes the minimum safe collision avoidance radius, ${\overline{R}}_a$ denotes the collision avoidance detection radius. If the distance between ASVs is less than ${\overline{R}}_a$, and then the collision avoidance function is activated in the control inputs, which increases as the distance between ASVs decreases. $V_{ij}^a\left({\mathit{p}}_i,{\mathit{p}}_j\right)$ will be large enough to ensure safe collision avoidance when $‖{\mathit{p}}_{ij}‖$ decreases to the minimum safe collision avoidance distance.

Collision Avoidance Function with respect to Obstacle: To achieve safe collision avoidance between ASVs, the collision avoidance function with respect to the obstacle is defined as follows

$$V_{io}^a\left({\mathit{p}}_i,{\mathit{p}}_o\right)=\left\{\begin{array}{cc}{\left({\displaystyle \frac{{\overline{R}}_o^2-{‖{\mathit{p}}_{io}‖}^2}{{‖{\mathit{p}}_{io}‖}^2-{\underset{\_}{R}}_o^2}}\right)}^2,& {\underset{\_}{R}}_o\le ‖{\mathit{p}}_{io}‖\le {\overline{R}}_o\\ 0_2,& ‖{\mathit{p}}_{io}‖>{\overline{R}}_o\mathrm{or}‖{\mathit{p}}_{io}‖<{\underset{\_}{R}}_o\end{array}\right.$$

(21)

By taking the partial derivative of (21) with respect to ${\mathit{p}}_i$, we obtain

$${\displaystyle \frac{\partial V_{io}^a}{\partial {\mathit{p}}_i}}=\left\{\begin{array}{cc}{\displaystyle \frac{4\left({\overline{R}}_o^2-{\underset{\_}{R}}_o^2\right)\left({‖{\mathit{p}}_{io}‖}^2-{\overline{R}}_o^2\right)}{{\left({‖{\mathit{p}}_{io}‖}^2-{\underset{\_}{R}}_o^2\right)}^3}}{p}_{ij}& {\underset{\_}{R}}_o\le ‖{\mathit{p}}_{io}‖\le {\overline{R}}_o\\ 0_2& ‖{\mathit{p}}_{io}‖>{\overline{R}}_o\mathrm{or}‖{\mathit{p}}_{io}‖<{\underset{\_}{R}}_o\end{array}\right.$$

(22)

where $‖{\mathit{p}}_{io}‖=‖{\mathit{p}}_i-{\mathit{p}}_o‖=\sqrt{{\left(x_i-x_o\right)}^2+{\left(y_i-y_o\right)}^2}$. ${\underset{\_}{R}}_o$ denotes the minimum safe collision avoidance radius with respect to the obstacle, and ${\overline{R}}_o$ denotes the collision avoidance detection radius with respect to the obstacle. If the distance between the ASV and obstacle is less than ${\overline{R}}_o$, and $V_{io}^a\left({\mathit{p}}_i,{\mathit{p}}_o\right)$ is activated in the control inputs, which increases when the distance between the ASV and obstacle decreases. $V_{io}^a\left({\mathit{p}}_i,{\mathit{p}}_o\right)$ will increase to be large enough to avoid obstacles when $‖{\mathit{p}}_{io}‖$ decreases to the minimum safe collision avoidance radius with respect to obstacles.

3.2. FNDO Design

This section proposes a novel fixed-time nonlinear disturbance observer based on the status information of the surface vehicle and fixed-time control theory. A new variable denoted by ${\mathit{L}}_i$ and its estimation denoted by ${\hat{\mathit{L}}}_i$ are introduced to design the disturbance observer.

$$\left\{\begin{array}{l}{\mathit{L}}_i={\mathit{M}}_i{\mathit{\upsilon }}_i\in R^3\\ {\hat{\mathit{L}}}_i\in R^3\end{array}\right.$$

(23)

The estimation error of ${\mathit{L}}_i$ can be obtained

$${\tilde{\mathit{L}}}_i={\hat{\mathit{L}}}_i-{\mathit{L}}_i$$

(24)

A suitable Lyapunov function is selected as follows

$$V_r={\displaystyle \frac{1}{2}}{{\tilde{\mathit{L}}}_i}^T{\tilde{\mathit{L}}}_i$$

(25)

Taking the time derivative of Equation (25), it follows that

$$\begin{array}{cc}{\dot{V}}_{di}& ={{\tilde{\mathit{L}}}_i}^T{\dot{\tilde{\mathit{L}}}}_i\hfill \\ & ={{\tilde{\mathit{L}}}_i}^T\left({\dot{\hat{\mathit{L}}}}_i-{\dot{\mathit{L}}}_i\right)\hfill \\ & ={{\tilde{\mathit{L}}}_i}^T\left({\dot{\hat{\mathit{L}}}}_i+{\mathit{C}}_i{\mathit{\upsilon }}_i+{\mathit{D}}_i{\mathit{\upsilon }}_i-{\mathit{\tau }}_i-{\mathit{\tau }}_{i,w}\right)\hfill \end{array}$$

(26)

$\dot{\hat{\mathit{L}}}$ can be designed as follows

$${\dot{\hat{\mathit{L}}}}_i=-{\mathit{C}}_i{\mathit{\upsilon }}_i-{\mathit{D}}_i{\mathit{\upsilon }}_i+{\mathit{\tau }}_i-{\mathit{K}}_{di1}{\tilde{\mathit{L}}}_i-{\mathit{K}}_{di2}si{g}^{p_d}\left({\tilde{\mathit{L}}}_i\right)-{\mathit{K}}_{di3}si{g}^{q_d}\left({\tilde{\mathit{L}}}_i\right)$$

(27)

where ${\mathit{K}}_{di1},{\mathit{K}}_{di2},{\mathit{K}}_{di3}\in R^{3\times 3}$ are diagonal matrices, $0<p_d<1$, $q_d>1$.

The disturbance estimation from the FNDO is given as

$$\begin{array}{cc}{\widehat{\mathit{\tau }}}_{i,w}& ={\widehat{\mathit{L}}}_i+{\mathit{C}}_i{\mathit{\upsilon }}_i+{\mathit{D}}_i{\mathit{\upsilon }}_i-{\mathit{\tau }}_i\hfill \\ & =-{\mathit{K}}_{di1}{\tilde{\mathit{L}}}_i-{\mathit{K}}_{di2}si{g}^{p_d}\left({\tilde{\mathit{L}}}_i\right)-{\mathit{K}}_{di3}si{g}^{q_d}\left({\tilde{\mathit{L}}}_i\right)\hfill \end{array}$$

(28)

where ${\widehat{\mathit{\tau }}}_{i,w}$ denotes the estimation of ${\mathit{\tau }}_{i,w}$.

Remark 2.

According to Assumption 2, we assume that velocity information is measurable. Therefore, in the FNDO design, we did not use position data but instead estimated the disturbances in Equation (12) using only velocity information. It is important to note that when velocity information is not measurable, an extended state observer using position data is typically required to estimate the system’s compound disturbances.

Substituting (27) into (26), we obtain that

$$\begin{array}{cc}{\dot{V}}_{di}& ={{\tilde{\mathit{L}}}_i}^T{\dot{\tilde{\mathit{L}}}}_i\hfill \\ & ={{\tilde{\mathit{L}}}_i}^T\left(-{\mathit{K}}_{di1}{\tilde{\mathit{L}}}_i-{\mathit{K}}_{di2}si{g}^{p_d}\left({\tilde{\mathit{L}}}_i\right)-{\mathit{K}}_{di3}si{g}^{q_d}\left({\tilde{\mathit{L}}}_i\right)-{\mathit{\tau }}_{i,w}\right)\hfill \\ & \le -{\mathit{K}}_{di1}{‖{\tilde{\mathit{L}}}_i‖}^2-{{\tilde{\mathit{L}}}_i}^T{\mathit{K}}_{di2}si{g}^{p_d+1}\left({\tilde{\mathit{L}}}_i\right)-{{\tilde{\mathit{L}}}_i}^T{\mathit{K}}_{di3}si{g}^{q_d+1}\left({\tilde{\mathit{L}}}_i\right)-{{\tilde{\mathit{L}}}_i}^T{\mathit{\tau }}_{i.w}\hfill \\ & \le -2^{\frac{p_d+1}{2}}{\lambda }_{\min }\left({\mathit{K}}_{di2}\right){V_{di}}^{\frac{p_d+1}{2}}-2^{\frac{q_d+1}{2}}{\lambda }_{\min }\left({\mathit{K}}_{di3}\right){V_{di}}^{\frac{q_d+1}{2}}\hfill \\ & \le -{\kappa }_{di2}{V}_{di}^{m_1}-{\kappa }_{di3}{V}_{di}^{m_2}\hfill \end{array}$$

(29)

where ${\kappa }_{di2}=2^{\frac{p_d+1}{2}}{\mathit{\lambda }}_{\min }\left({\mathit{K}}_{di1}\right),{\kappa }_{di3}=2^{\frac{q_d+1}{2}}{\mathit{\lambda }}_{\min }\left({\mathit{K}}_{di2}\right),m_1=\frac{p_d+1}{2},m_2=\frac{q_d+1}{2}$.

According to Lemma 1, the estimated error of the proposed FNDO can converge into an arbitrary tiny neighborhood around zero within a fixed time $T_{di}$, and $T_{di}$ satisfies

$$T_{di}\le {\displaystyle \frac{1}{{\kappa }_{di2}\left(1-m_1\right)}}+{\displaystyle \frac{1}{{\kappa }_{di3}\left(1-m_2\right)}}$$

(30)

3.3. Practical Fixed-Time Containment Controller Design

This section proposes a novel practical fixed-time robust containment controller for multiple autonomous surface vehicles, considering collision avoidance. It achieves this by employing artificial potential energy function (APEF), graph theory, fixed-time control theory, backstepping method, and dynamic surface control technology.

3.3.1. Kinematic Controller Design

First, the containment error of the i-th ASV is defined as follows

$${\mathit{z}}_{1i}={\mathit{J}}^T({\mathit{\psi }}_i)\left[{\displaystyle \sum _{j=1}^M{a}_{ij}({\mathit{\eta }}_i-{\mathit{\eta }}_j)+{\displaystyle \sum _{j=M+1}^N{a}_{ij}({\mathit{\eta }}_j-{\mathit{\varpi }}_j)}}\right]$$

(31)

where ${\mathit{z}}_{1i}$ represents the containment error of the i-th ASV, which consists of two parts. ${\mathit{J}}^T\left({\psi }_i\right){\displaystyle \sum _{j=1}^M{a}_{ij}({\mathit{\eta }}_i-{\mathit{\eta }}_j)}$ denotes the containment error between the i-th ASV and its neighboring ASV. ${\mathit{J}}^T\left({\psi }_i\right){\displaystyle \sum _{j=M+1}^N{a}_{ij}({\mathit{\eta }}_j-{\mathit{\varpi }}_j)}$ denotes the containment error between the i-th ASV and its neighboring virtual leader.

Substituting Equation (12) into Equation (31) and taking the time derivative of Equation (31), it follows that

$$\begin{array}{cc}{\dot{\mathit{z}}}_{1i}& ={\dot{\mathit{J}}}^T\left({\mathit{\psi }}_i\right)\left[{\displaystyle \sum _{j=1}^M{a}_{ij}({\mathit{\eta }}_i-{\mathit{\eta }}_j)+{\displaystyle \sum _{j=M+1}^N{a}_{ij}({\mathit{\eta }}_j-{\mathit{\varpi }}_j)}}\right]+{\mathit{J}}^T\left({\mathit{\psi }}_i\right)\left[{\displaystyle \sum _{j=1}^M{a}_{ij}({\dot{\mathit{\eta }}}_i-{\dot{\mathit{\eta }}}_j)+{\displaystyle \sum _{j=M+1}^N{a}_{ij}({\dot{\mathit{\eta }}}_j-{\dot{\mathit{\varpi }}}_j)}}\right]\hfill \\ & =-r_i\mathit{Q}{\mathit{z}}_{1i}+{\mathit{J}}^T\left({\mathit{\psi }}_i\right)\left[{\displaystyle \sum _{j=1}^N{a}_{ij}{\dot{\mathit{\eta }}}_i-{\displaystyle \sum _{j=M+1}^N{a}_{ij}}{\dot{\mathit{\eta }}}_j-{\displaystyle \sum _{j=M+1}^N{a}_{ij}{\dot{\mathit{\varpi }}}_j}}\right]\hfill \\ & =-r_i\mathit{Q}{\mathit{z}}_{1i}+d_i{\mathit{\upsilon }}_i-{\displaystyle \sum _{j=1}^M{a}_{ij}{\mathit{J}}^T\left({\mathit{\psi }}_i\right)}\mathit{J}\left({\mathit{\psi }}_j\right){\mathit{\upsilon }}_j-{\displaystyle \sum _{j=M+1}^N{a}_{ij}{\mathit{J}}^T\left({\mathit{\psi }}_i\right){\dot{\mathit{\varpi }}}_j}\hfill \end{array}$$

(32)

where $\mathit{Q}=\left[\begin{array}{ccc}0& -1& 0\\ 1& 0& 0\\ 0& 0& 0\end{array}\right]$, $d_i={\displaystyle \sum _{j=1}^N{a}_{ij}}$.

A suitable Lyapunov function is selected as follows,

$$V_{1i}={\displaystyle \frac{1}{2}}{\mathit{z}}_{1i}^T{\mathit{z}}_{1i}$$

(33)

Taking the time derivative of Equation (33), it follows that

$$\begin{array}{cc}{\dot{V}}_{1i}& ={\mathit{z}}_{1i}^T{\dot{\mathit{z}}}_{1i}\hfill \\ & ={\mathit{z}}_{1i}^T(-r_i\mathit{Q}{\mathit{z}}_{1i}+d_i{\mathit{\upsilon }}_i-{\displaystyle \sum _{j=M+1}^N{a}_{ij}{\mathit{J}}^T\left({\mathit{\psi }}_i\right){\dot{\mathit{\varpi }}}_j}-{\displaystyle \sum _{j=1}^M{a}_{ij}{\mathit{J}}^T\left({\mathit{\psi }}_i\right)}\mathit{J}\left({\mathit{\psi }}_j\right){\mathit{\upsilon }}_j)\hfill \\ & ={\mathit{z}}_{1i}^T(d_i{v}_i-{\displaystyle \sum _{j=M+1}^N{a}_{ij}{\mathit{J}}^T\left({\mathit{\psi }}_i\right){\dot{\mathit{\varpi }}}_j}-{\displaystyle \sum _{j=1}^M{a}_{ij}{\mathit{J}}^T\left({\mathit{\psi }}_i\right)}\mathit{J}\left({\mathit{\psi }}_j\right){\mathit{\upsilon }}_j)\hfill \end{array}$$

(34)

To stabilize ${\mathit{z}}_{1i}$, a kinematic virtual control law is proposed as follows:

$${\alpha }_i={\displaystyle \frac{1}{d_i}}\left(-{\mathit{K}}_{i1}{\mathit{z}}_{3i}-{\mathit{K}}_{i2}\mathit{s}\mathit{i}{\mathit{g}}^{\chi }\left({\mathit{z}}_{3i}\right)-{\mathit{K}}_{i3}\mathit{s}\mathit{i}{\mathit{g}}^{\delta }\left({\mathit{z}}_{3i}\right)+Q_1\right)$$

(35)

where ${\mathit{K}}_{i1},{\mathit{K}}_{i2},{\mathit{K}}_{i3}\in R^{3\times 3}$ are diagonal matrices, $0<\chi <1$, $\delta >1$, Q₁ is given as

$$Q_1={\displaystyle \sum _{j=1}^M{a}_{ij}{\mathit{J}}^T\left({\mathit{\psi }}_i\right)}\mathit{J}\left({\mathit{\psi }}_j\right){\mathit{\upsilon }}_j+{\displaystyle \sum _{j=M+1}^N{a}_{ij}{\mathit{J}}^T\left({\mathit{\psi }}_i\right){\dot{\mathit{\varpi }}}_j}$$

(36)

Remark 3.

In Equation (35), ${\mathit{z}}_{3i}={\mathit{z}}_{1i}+{\mathit{J}}^T\left({\mathit{\psi }}_i\right){\mathit{z}}_{vi}$, where ${\mathit{z}}_{vi}={\displaystyle \sum _{j=M+1}^N\frac{\partial V_{ij}^a}{\partial {\mathit{p}}_i}}+{\displaystyle \sum _{o=1}^{N_o}\frac{\partial V_{io}^a}{\partial {\mathit{p}}_i}}$, according to the above introduction, ${\mathit{z}}_{vi}$ is the collision avoidance item, while the remaining items are used to achieve formation layout for containment control. When a collision risk arises, the artificial potential function is activated to generate repulsive forces to avoid the collision; however, this negatively impacts the formation layout. The likelihood of collision increases when the formation layout has a positive influence. Consequently, a compromise solution must be found when both formation layout and collision avoidance are considered simultaneously.

In earlier research, the computational complexity resulting from the development of the virtual control rule was typically addressed using traditional dynamic surface technology. Although this approach streamlines the computation, it overlooks the convergence properties of the filtered error signal. With the aid of dynamic surface technology and fixed-time control theory, a novel fixed-time first-order low-pass filter is designed in this study. The filtered signal and its derivative are obtained by passing the virtual control rule through the fixed-time filter.

The fixed-time first-order nonlinear filter is designed as follows

$$\left\{\begin{array}{l}{\displaystyle \frac{{\dot{\mathit{v}}}_{fi}}{T_{fi}}}=-{\mathit{e}}_{fi}-si{g}^{\chi }\left({\mathit{e}}_{fi}\right)-si{g}^{\delta }\left({\mathit{e}}_{fi}\right)\\ {\mathit{v}}_{fi}\left(0\right)={\alpha }_i\left(0\right)\end{array}\right.$$

(37)

where ${\mathit{v}}_{fi}\in R^3$ denotes the filtered signal of the virtual control law, ${\dot{\mathit{v}}}_{fi}\in R^3$ denotes the derivative of ${\mathit{v}}_{fi}$, $0<\chi <1$, $\delta >1$, $T_{fi}>0$.

Define the following filter error

$${\mathit{e}}_{fi}={\mathit{v}}_{fi}-{\mathit{\alpha }}_i$$

(38)

Considering a suitable Lyapunov function, we define it as

$$V_{fi}={\displaystyle \frac{1}{2}}{\mathit{e}}_{fi}^T{\mathit{e}}_{fi}$$

(39)

Equation (39) can be differentiated with respect to time; it follows that

$$\begin{array}{cc}{\dot{V}}_{fi}& ={\mathit{e}}_{fi}^T{\dot{\mathit{e}}}_{fj}\hfill \\ & ={\mathit{e}}_{fi}^{\mathrm{T}}\left(-T_{fi}{\mathit{e}}_{fi}-T_{fi}si{g}^{\chi }\left({\mathit{e}}_{fi}\right)-T_{fi}si{g}^{\delta }\left({\mathit{e}}_{fi}\right)-{\dot{\mathit{a}}}_i\right)\hfill \end{array}$$

(40)

According to Lemma 5, the following is obtained

$$-{\mathit{e}}_{fi}^{\mathrm{T}}{\dot{\mathit{\alpha }}}_i\le {\mu }_1{\mathit{e}}_{fi}^{\mathrm{T}}{\mathit{e}}_{fi}+{\displaystyle \frac{1}{4{\mu }_1}}{‖{\mathit{\alpha }}_i‖}^2$$

(41)

where ${\mu }_1$ > 0. By selecting the appropriate parameters $T_{fi}$, ${\mu }_1$, the following is obtained

$$\begin{array}{cc}{\dot{V}}_{fi}& \le -2T_{fi}{V}_{fi}-2^{\frac{\chi +1}{2}}{T}_{fi}{V_{fi}}^{\frac{\chi +1}{2}}-2^{\frac{\delta +1}{2}}{T}_{fi}{V_{fi}}^{\frac{\delta +1}{2}}\hfill \\ & +2{\mu }_1{V}_{fi}+{\displaystyle \frac{1}{4{\mu }_1}}{‖{\alpha }_i‖}^2\hfill \\ & \le -2^{\frac{\chi +1}{2}}{T}_{fi}{V_{fi}}^{\frac{\chi +1}{2}}-2^{\frac{\delta +1}{2}}{T}_{fi}{V_{fi}}^{\frac{\delta +1}{2}}+{\displaystyle \frac{1}{4{\mu }_1}}{‖{\alpha }_i‖}^2\hfill \\ & \le -{\kappa }_{fi1}{V}_{fi}^{m_3}-{\kappa }_{fi2}{V}_{fi}^{m_4}+{\xi }_f\hfill \end{array}$$

(42)

where ${\kappa }_{fi1}=2^{\frac{\chi +1}{2}}{T}_{fi}, {\kappa }_{fi2}=2^{\frac{\delta +1}{2}}{T}_{fi}, {\xi }_f={‖{\alpha }_i‖}^2/4{\mu }_1, m_3=2^{\frac{\chi +1}{2}}, m_4=2^{\frac{\delta +1}{2}}$.

According to Lemma 2, the proposed nonlinear first-order filter is practical and fixed-time stable.

3.3.2. Fixed-Time Containment Controller Design

The velocity trajectory error of the i-th ASV can be defined as

$${\mathit{z}}_{2i}={\mathit{\upsilon }}_i-{\mathit{v}}_{fi}$$

(43)

Equation (12) is substituted for the time derivative of Equation (41), yielding

$${\dot{\mathit{z}}}_{2i}={\mathit{M}}_i^{-1}\left(-{\mathit{C}}_i{\mathit{\upsilon }}_i-{\mathit{D}}_i{\mathit{\upsilon }}_i+{\mathit{\tau }}_i+{\mathit{\tau }}_{i.w}\right)-{\dot{\mathit{v}}}_{fi}$$

(44)

A suitable Lyapunov function $V_{2i}$ is selected as follows,

$$V_{2i}={\displaystyle \frac{1}{2}}{\mathit{z}}_{2i}^T{\mathit{z}}_{2i}$$

(45)

Equation (45) can be differentiated with respect to time; it follows that

$$\begin{array}{cc}{\dot{V}}_{2i}& ={\mathit{z}}_{2i}^T{\dot{\mathit{z}}}_{2i}\hfill \\ & ={\mathit{z}}_{2i}^T\left({\mathit{M}}_i^{-1}\left(-{\mathit{C}}_i{\mathit{\upsilon }}_i-{\mathit{D}}_i{\mathit{\upsilon }}_i+{\mathit{\tau }}_i+{\mathit{\tau }}_{i.w}\right)-{\dot{\mathit{v}}}_{fi}\right)\hfill \end{array}$$

(46)

In order to stabilize ${\mathit{z}}_{2i}$, a practical fixed-time robust containment control law is designed as follows

$${\mathit{\tau }}_i={\mathit{M}}_i\left(-{\mathit{K}}_{i4}{\mathit{z}}_{2i}-{\mathit{K}}_{i5}si{g}^{\chi }\left({\mathit{z}}_{2i}\right)-{\mathit{K}}_{i6}si{g}^{\delta }\left({\mathit{z}}_{2i}\right)-d_i{\mathit{z}}_{3i}+{\dot{\mathit{v}}}_{fi}\right)+{\mathit{C}}_i{\mathit{\upsilon }}_i+{\mathit{D}}_i{\mathit{\upsilon }}_i-{\widehat{\mathit{\tau }}}_{i,w}$$

(47)

where ${\mathit{K}}_{i4}, {\mathit{K}}_{i5}, {\mathit{K}}_{i6}\in R^{3\times 3}$ are diagonal matrices.

4. Stability Analysis

The stability analysis of the designed containment control system is presented in this section as follows

Theorem 1:

Based on Assumptions 1–3, by designing fixed-time disturbance observer (27), kinematic control law (35), nonlinear filter (37), containment control law (47), all errors in the designed closed-loop control system converge to a tiny range in a fixed time so as to realize the control objectives.

Proof: 

Considering the following Lyapunov function:

$$V_i={\displaystyle \frac{1}{2}}{\displaystyle \sum _{i=1}^M\left\{{\mathit{z}}_{1i}^T{\mathit{z}}_{1i}+{\mathit{z}}_{2i}^T{\mathit{z}}_{2i}+{\mathit{e}}_{fi}^T{\mathit{e}}_{fi}+d_i{\displaystyle \sum _{j=1}^M{V}_{ij}^a+d_i{\displaystyle \sum _{j=1}^{N_o}{V}_{io}^a}}\right\}}$$

(48)

Taking the time derivative of $V_i$ and using (34), (35), (40), (44), (47), it follows that:

$$\begin{array}{ll}\dot{V}& ={\displaystyle \sum _{i=1}^M\left\{\begin{array}{l}\left({\mathit{z}}_{3i}^T-{\mathit{z}}_{iv}^T\mathit{J}\left({\psi }_i\right)\right)\left(-{\mathit{K}}_{i1}{\mathit{z}}_{3i}-{\mathit{K}}_{i2}\mathit{s}\mathit{i}{\mathit{g}}^{\chi }\left({\mathit{z}}_{3i}\right)-{\mathit{K}}_{i3}\mathit{s}\mathit{i}{\mathit{g}}^{\delta }\left({\mathit{z}}_{3i}\right)+d_i\left({\mathit{\upsilon }}_i-{\alpha }_i\right)\right)\\ +{\mathit{z}}_{2i}^T\left(-{\mathit{K}}_{i4}{\mathit{z}}_{2i}-{\mathit{K}}_{i5}\mathit{s}\mathit{i}{\mathit{g}}^{\chi }\left({\mathit{z}}_{2i}\right)-{\mathit{K}}_{i6}\mathit{s}\mathit{i}{\mathit{g}}^{\delta }\left({\mathit{z}}_{2i}\right)-d_i{\mathit{z}}_{3i}+{\tilde{\mathit{\tau }}}_{i,w}\right)\\ +{\mathit{e}}_{fi}^T\left(-T_{fi}{\mathit{e}}_{fi}-T_{fi}\mathit{s}\mathit{i}{\mathit{g}}^{\chi }\left({\mathit{e}}_{fi}\right)-T_{fi}\mathit{s}\mathit{i}{\mathit{g}}^{\delta }\left({\mathit{e}}_{fi}\right)-{\dot{\alpha }}_i\right)+{\mathit{z}}_{vi}^T{d}_i\mathit{J}\left({\psi }_i\right)\left[\begin{array}{c}{u}_i\\ v_i\end{array}\right]\end{array}\right\}}\\ & \le {\displaystyle \sum _{i=1}^M\left\{\begin{array}{c}-2^{\frac{\chi +1}{2}}{\lambda }_{\min }\left({\mathit{K}}_{i2}\right){V_{1i}}^{\frac{\chi +1}{2}}-2^{\frac{\delta +1}{2}}{\lambda }_{\min }\left({\mathit{K}}_{i3}\right){V_{1i}}^{\frac{\delta +1}{2}}+\frac{1}{4{\mu }_1}{‖{\mathit{e}}_{fi}‖}^2\hfill \\ -2^{\frac{\chi +1}{2}}{\lambda }_{\min }\left({\mathit{K}}_{i5}\right){V_{2i}}^{\frac{\chi +1}{2}}-2^{\frac{\delta +1}{2}}{\lambda }_{\min }\left({\mathit{K}}_{i6}\right){V_{2i}}^{\frac{\delta +1}{2}}+\frac{1}{4{\mu }_2}{‖{\tilde{\mathit{\tau }}}_{i,w}‖}^2\hfill \\ -2^{\frac{\chi +1}{2}}{T}_{fi}{V_{fi}}^{\frac{\chi +1}{2}}-2^{\frac{\delta +1}{2}}{T}_{fi}{V_{fi}}^{\frac{\delta +1}{2}}+\frac{1}{4{\mu }_3}{‖{\alpha }_i‖}^2\hfill \\ +{\mathit{z}}_{vi}^T\left({\displaystyle \sum _{j=1}^M{a}_{ij}}\mathit{J}\left({\psi }_i\right){\mathit{\upsilon }}_j+{\displaystyle \sum _{j=M+1}^N{a}_{ij}{\dot{\mathit{\varpi }}}_j}\right)\hfill \end{array}\right\}}\hfill \end{array}$$

(49)

The stability analysis of the control system is divided into two steps.

Step 1: When the i-th follower is outside the collision avoidance range, which implies that ${\mathit{z}}_{3i}={\mathit{z}}_{1i}$, Equation (49) can be expressed as follows:

$$\dot{V}={\displaystyle \sum _{i=1}^M\left\{\begin{array}{l}-{\mathit{z}}_{1i}^T{\mathit{K}}_{i1}{\mathit{z}}_{1i}-{\mathit{z}}_{1i}^T{\mathit{K}}_{i2}\mathit{s}\mathit{i}{g}^{\chi }\left({\mathit{z}}_{1i}\right)-{\mathit{z}}_{1i}^T{\mathit{K}}_{i3}\mathit{s}\mathit{i}{g}^{\delta }\left(z_{1i}\right)+{\mathit{z}}_{1i}^T{\mathit{e}}_{fi}\\ -{\mathit{z}}_{2i}^T{\mathit{K}}_{i4}{\mathit{z}}_{2i}-{\mathit{K}}_{i5}\mathit{s}\mathit{i}{\mathit{g}}^{\chi }\left({\mathit{z}}_{2i}\right)-{\mathit{K}}_{i6}\mathit{s}\mathit{i}{\mathit{g}}^{\delta }\left({\mathit{z}}_{2i}\right)+{\mathit{z}}_{2i}^T{\tilde{\mathit{\tau }}}_{i,w}\\ -{\mathit{e}}_{fi}^T{T}_{fi}{\mathit{e}}_{fi}-T_{fi}\mathit{s}\mathit{i}{g}^{\chi }\left({\mathit{e}}_{fi}\right)-T_{fi}\mathit{s}\mathit{i}{\mathit{g}}^{\delta }\left({\mathit{e}}_{fi}\right)-{\mathit{e}}_{fi}^T{\dot{\alpha }}_i\end{array}\right\}}$$

(50)

According to Lemma 5, the following is obtained:

$$\left\{\begin{array}{l}{\mathit{z}}_{1i}^T{\mathit{e}}_{fi}\le {\mu }_1{\mathit{z}}_{1i}^T{\mathit{z}}_{1i}+{\displaystyle \frac{1}{4{\mu }_1}}{‖{\mathit{e}}_{fi}‖}^2\\ {\mathit{z}}_{2i}^T{\tilde{\mathit{\tau }}}_{i,w}\le {\mu }_2{\mathit{z}}_{2i}^T{\mathit{z}}_{2i}+{\displaystyle \frac{1}{4{\mu }_2}}{‖{\tilde{\mathit{\tau }}}_{i,w}‖}^2\\ -{\mathit{e}}_{fi}^T{\dot{\alpha }}_i\le {\mu }_3{e}_{fi}^T{e}_{fi}+{\displaystyle \frac{1}{4{\mu }_3}}{‖{\alpha }_i‖}^2\end{array}\right.$$

(51)

Equations (50) and (51) can be combined to obtain:

$$\dot{V}\le {\displaystyle \sum _{i=1}^M\left\{\begin{array}{l}-{\mathit{z}}_{1i}^T{\mathit{K}}_{i1}{\mathit{z}}_{1i}-{\mathit{z}}_{1i}^T{\mathit{K}}_{i2}\mathit{s}\mathit{i}{\mathit{g}}^{\chi }\left({\mathit{z}}_{1i}\right)-{\mathit{z}}_{1i}^T{\mathit{K}}_{i3}\mathit{s}\mathit{i}{\mathit{g}}^{\delta }\left({\mathit{z}}_{1i}\right)+{\mu }_1{\mathit{z}}_{1i}^T{\mathit{z}}_{1i}+\frac{1}{4{\mu }_1}{‖{\mathit{e}}_{fi}‖}^2\\ -{\mathit{z}}_{2i}^T{\mathit{K}}_{i4}{\mathit{z}}_{2i}-{\mathit{z}}_{2i}^T{\mathit{K}}_{i5}\mathit{s}\mathit{i}{\mathit{g}}^{\chi }\left({\mathit{z}}_{2i}\right)-{\mathit{z}}_{2i}^T{\mathit{K}}_{i6}\mathit{s}\mathit{i}{\mathit{g}}^{\delta }\left({\mathit{z}}_{2i}\right)+{\mu }_2{\mathit{z}}_{2i}^T{\mathit{z}}_{2i}+\frac{1}{4{\mu }_2}{‖{\tilde{\mathit{\tau }}}_{i,w}‖}^2\\ -{\mathit{e}}_{fi}^T{T}_{fi}{\mathit{e}}_{fi}-{\mathit{e}}_{fi}^T{T}_{fi}\mathit{s}\mathit{i}{\mathit{g}}^{\chi }\left({\mathit{e}}_{fi}\right)-{\mathit{e}}_{fi}^T{T}_{fi}\mathit{s}\mathit{i}{\mathit{g}}^{\delta }\left({\mathit{e}}_{fi}\right)+{\mu }_3{e}_{fi}^T{e}_{fi}+\frac{1}{4{\mu }_3}{‖{\mathit{\alpha }}_i‖}^2\end{array}\right\}}$$

(52)

By selecting reasonable parameters ${\mu }_1,{\mu }_2,{\mu }_3$, Equation (52) can be expressed as follows:

$$\begin{array}{cc}\dot{V}& \le {\displaystyle \sum _{i=1}^M\left\{\begin{array}{l}-{\mathit{z}}_{1i}^T{\mathit{K}}_{i2}s\mathit{i}{\mathit{g}}^{\chi }\left({\mathit{z}}_{1i}\right)-{\mathit{z}}_{1i}^T{\mathit{K}}_{i3}\mathit{s}\mathit{i}{\mathit{g}}^{\delta }\left({\mathit{z}}_{1i}\right)+\frac{1}{4{\mu }_1}{‖{\mathit{e}}_{fi}‖}^2-{\mathit{z}}_{2i}^T{\mathit{K}}_{i5}\mathit{s}\mathit{i}{\mathit{g}}^{\chi }\left({\mathit{z}}_{2i}\right)\\ -{\mathit{z}}_{2i}^T{\mathit{K}}_{i6}\mathit{s}\mathit{i}{\mathit{g}}^{\delta }\left({\mathit{z}}_{2i}\right)+\frac{1}{4{\mu }_2}{‖{\tilde{\mathit{\tau }}}_{i,w}‖}^2-{\mathit{e}}_{fi}^T{T}_{fi}\mathit{s}\mathit{i}{\mathit{g}}^{\chi }\left({\mathit{e}}_{fi}\right)-{\mathit{e}}_{fi}^T{T}_{fi}\mathit{s}\mathit{i}{\mathit{g}}^{\delta }\left({\mathit{e}}_{fi}\right)+\frac{1}{4{\mu }_3}{‖{\alpha }_i‖}^2\end{array}\right\}}\hfill \\ & \le {\displaystyle \sum _{i=1}^M\left\{\begin{array}{l}-2^{\frac{\chi +1}{2}}{\lambda }_{\min }\left({\mathit{K}}_{i2}\right){V_{1i}}^{\frac{\chi +1}{2}}-2^{\frac{\delta +1}{2}}{\lambda }_{\min }\left({\mathit{K}}_{i3}\right){V_{1i}}^{\frac{\delta +1}{2}}+\frac{1}{4{\mu }_1}{‖{\mathit{e}}_{fi}‖}^2\\ -2^{\frac{\chi +1}{2}}{\lambda }_{\min }\left({\mathit{K}}_{i5}\right){V_{2i}}^{\frac{\chi +1}{2}}-2^{\frac{\delta +1}{2}}{\lambda }_{\min }\left({\mathit{K}}_{i6}\right){V_{2i}}^{\frac{\delta +1}{2}}+\frac{1}{4{\mu }_2}{‖{\tilde{\mathit{\tau }}}_{i,w}‖}^2\\ -2^{\frac{\chi +1}{2}}{T}_{fi}{V_{fi}}^{\frac{\chi +1}{2}}-2^{\frac{\delta +1}{2}}{T}_{fi}{V_{fi}}^{\frac{\delta +1}{2}}+\frac{1}{4{\mu }_3}{‖{\mathit{\alpha }}_i‖}^2\end{array}\right\}}\hfill \\ & \le {\displaystyle \sum _{i=1}^M\left\{-{\kappa }_{1i}{V_i}^{m_3}-{\kappa }_{2i}{V_i}^{m_4}+{\xi }_i\right\}}\hfill \end{array}$$

(53)

where ${\kappa }_{1i}=\min \left\{2^{\frac{\chi +1}{2}}{\lambda }_{\min }\left({\mathit{K}}_{i2}\right),2^{\frac{\chi +1}{2}}{\lambda }_{\min }\left({\mathit{K}}_{i3}\right),2^{\frac{\chi +1}{2}}{T}_{fi}\right\}$, ${\kappa }_{2i}=\min \left\{2^{\frac{\delta +1}{2}}{\lambda }_{\min }\left({\mathit{K}}_{i5}\right),2^{\frac{\delta +1}{2}}{\lambda }_{\min }\left({\mathit{K}}_{i6}\right),2^{\frac{\delta +1}{2}}{T}_{fi}\right\}$, ${\xi }_i={\displaystyle \frac{1}{4{\mu }_1}}{‖{\mathit{e}}_{fi}‖}^2+{\displaystyle \frac{1}{4{\mu }_2}}{‖{ \mathit{\tau } ˜}_{i,w}‖}^2+{\displaystyle \frac{1}{4{\mu }_3}}{‖{\mathit{\alpha }}_i‖}^2$.

According to Lemma 2, this closed-loop control system is practical fixed-time stable, and the upper bound of convergency time satisfies

$$T_i\le {\displaystyle \frac{1}{k_{1i}\rho \left(1-m_3\right)}}+{\displaystyle \frac{1}{k_{2i}\rho \left(m_4-1\right)}}$$

(54)

where $0<\rho <1$.

According to (29) and (30), estimation errors of the FNDO can converge around zero within a fixed time. Thus, all error signals of the closed-loop control system can converge around zero within a fixed time.

Remark 4.

A detailed explanation will be provided on the reason why Control Objective 1 can be achieved.

Let ${\mathit{z}}_1={\left[{\mathit{z}}_{11}^T,\dots ,{\mathit{z}}_{1M}^T\right]}^T$,  $\mathit{\eta }={\left[{\mathit{\eta }}_1^T,\dots ,{\mathit{\eta }}_M^T\right]}^T$, $\mathit{\varpi }={\left[{\mathit{\varpi }}_{M+1}^T,\dots ,{\mathit{\varpi }}_N^T\right]}^T$, ${\mathit{J}}^T=\left[{\mathit{J}}^T\left({\psi }_1\right),\dots ,{\mathit{J}}^T\left({\psi }_M\right)\right]$, according to the containment error defined in (31), ${\mathit{z}}_{1i}$ can converge around zero within a fixed time; when time exceeds $T_i$, it follows that

$${\mathit{z}}_1={\mathit{J}}^T\left(\left({\mathcal{L}}_1\otimes I_3\right)\mathit{\eta }+\left({\mathcal{L}}_2\otimes I_3\right)\mathit{\varpi }\right)={\mathbf{0}}_{3M\times 1}$$

(55)

According to Assumption 3, (55) can be rewritten as follows

$${\mathit{z}}_1={\mathit{J}}^T\left(\left({\mathcal{L}}_1\otimes I_3\right)\left(\mathit{\eta }+\left({\left({\mathcal{L}}_1\right)}^{-1}{\mathcal{L}}_2\otimes I_3\right)\mathit{\varpi }\right)\right)={\mathbf{0}}_{3M\times 1}$$

(56)

Thus, when time exceeds $T_i$, $\mathit{\eta }$ can converge into $-\left({\left({\mathcal{L}}_1\right)}^{-1}{\mathcal{L}}_2\otimes I_3\right)\mathit{\varpi }$, according to Lemma 6, ${\left({\mathcal{L}}_1\right)}^{-1}{\mathcal{L}}_2$ is a non-negative definite matrix, and the sum of the elements in each row of ${\left({\mathcal{L}}_1\right)}^{-1}{\mathcal{L}}_2$ is 1; according to the definition of a convex hull, we can obtain ${\displaystyle \sum _{j=M+1}^N{\Pi }_j}=1$, it follows that

$$\underset{t\to T_i}{\lim }‖{\mathit{\eta }}_i-{\displaystyle \sum _{j=\mathit{M}+1}^{\mathrm{N}}{\prod }_j{\mathit{\varpi }}_j}‖\le {\epsilon }_1$$

(57)

Therefore, Control Objective 1 can be achieved.

Step 2: When the i-th follower is within the collision avoidance range. According to (49), it follows that

$$\begin{array}{cc}\dot{V}& ={\displaystyle \sum _{i=1}^M\left\{\begin{array}{l}-{\mathit{z}}_{3i}^T{\mathit{K}}_{i1}{\mathit{z}}_{3i}-{\mathit{z}}_{3i}^T{\mathit{K}}_{i2}\mathit{s}\mathit{i}{\mathit{g}}^{\chi }\left({\mathit{z}}_{3i}\right)-{\mathit{z}}_{3i}^T{\mathit{K}}_{i3}\mathit{s}\mathit{i}{\mathit{g}}^{\delta }\left({\mathit{z}}_{3i}\right)+{\mathit{z}}_{3i}^T{\mathit{e}}_{fi}-{\mathit{z}}_{2i}^T{\mathit{K}}_{i4}{\mathit{z}}_{2i}\\ -{\mathit{K}}_{i5}\mathit{s}\mathit{i}{\mathit{g}}^{\chi }\left({\mathit{z}}_{2i}\right)-{\mathit{K}}_{i6}\mathit{s}\mathit{i}{\mathit{g}}^{\delta }\left({\mathit{z}}_{2i}\right)+{\mathit{z}}_{2i}^T{\tilde{\mathit{\tau }}}_{i,w}-{\mathit{e}}_{fi}^T{T}_{fi}{\mathit{e}}_{fi}-T_{fi}\mathit{s}\mathit{i}{\mathit{g}}^{\chi }\left({\mathit{e}}_{fi}\right)\\ -T_{fi}\mathit{s}\mathit{i}{\mathit{g}}^{\delta }\left({\mathit{e}}_{fi}\right)-{\mathit{e}}_{fi}^T{\dot{\alpha }}_i+{\mathit{z}}_{iv}^T\left({\displaystyle \sum _{j=1}^M{a}_{ij}}\mathit{J}\left({\mathit{\psi }}_j\right)v_j+{\displaystyle \sum _{j=M+1}^N{a}_{ij}{\dot{\varpi }}_j}\right)\end{array}\right\}}\hfill \\ & \le {\displaystyle \sum _{i=1}^M\left\{\begin{array}{l}-2^{\frac{\chi +1}{2}}{\lambda }_{\min }\left({\mathit{K}}_{i2}\right){\left(\frac{1}{2}{\mathit{z}}_{3i}^T{\mathit{z}}_{3i}\right)}^{\frac{\chi +1}{2}}-2^{\frac{\delta +1}{2}}{\lambda }_{\min }\left({\mathit{K}}_{i3}\right){\left(\frac{1}{2}{\mathit{z}}_{3i}^T{\mathit{z}}_{3i}\right)}^{\frac{\delta +1}{2}}+\frac{1}{4{\mu }_1}{‖e_{fi}‖}^2\\ -2^{\frac{\chi +1}{2}}{\lambda }_{\min }\left({\mathit{K}}_{i5}\right){V_{2i}}^{\frac{\chi +1}{2}}-2^{\frac{\delta +1}{2}}{\lambda }_{\min }\left({\mathit{K}}_{i6}\right){V_{2i}}^{\frac{\delta +1}{2}}+\frac{1}{4{\mu }_2}{‖{\tilde{\mathit{\tau }}}_{i,w}‖}^2\\ -2^{\frac{\chi +1}{2}}{T}_{fi}{V_{fi}}^{\frac{\chi +1}{2}}-2^{\frac{\delta +1}{2}}{T}_{fi}{V_{fi}}^{\frac{\delta +1}{2}}+\frac{1}{4{\mu }_3}{‖{\alpha }_i‖}^2\\ +‖{\mathit{z}}_{iv}‖‖{\mathit{\xi }}_i‖\end{array}\right\}}\hfill \end{array}$$

(58)

When the initial position of a follower is outside the collision avoidance range, implying that both the follower and neighboring followers or obstacles are within each other’s collision avoidance zones, the collision avoidance mode is activated, generating a repulsive force to prevent collision. The artificial potential energy function increases as the vehicles enter the collision avoidance area and decreases to zero when they leave the zone. Therefore, no collisions will occur between the followers or between the followers and obstacles. □

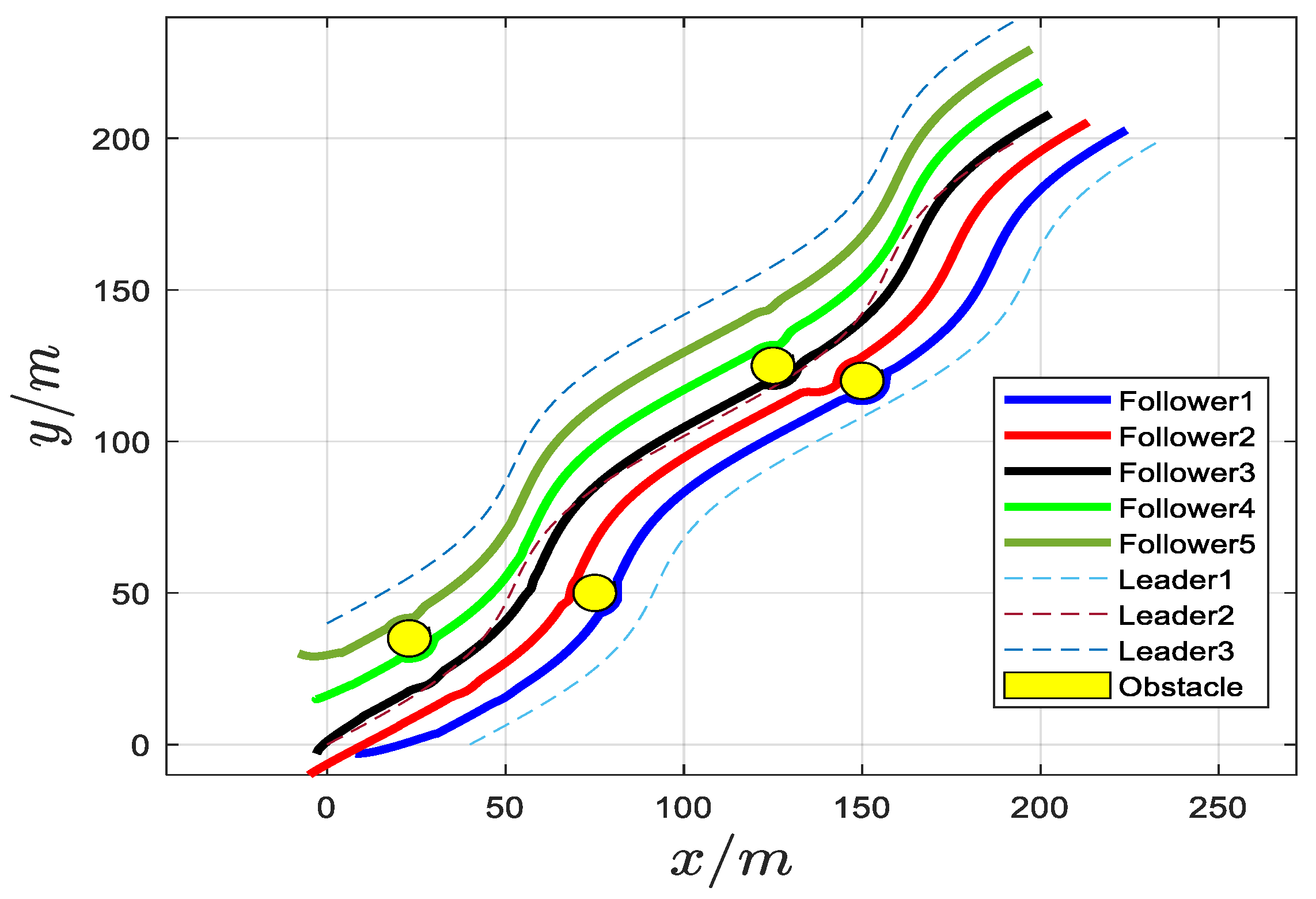
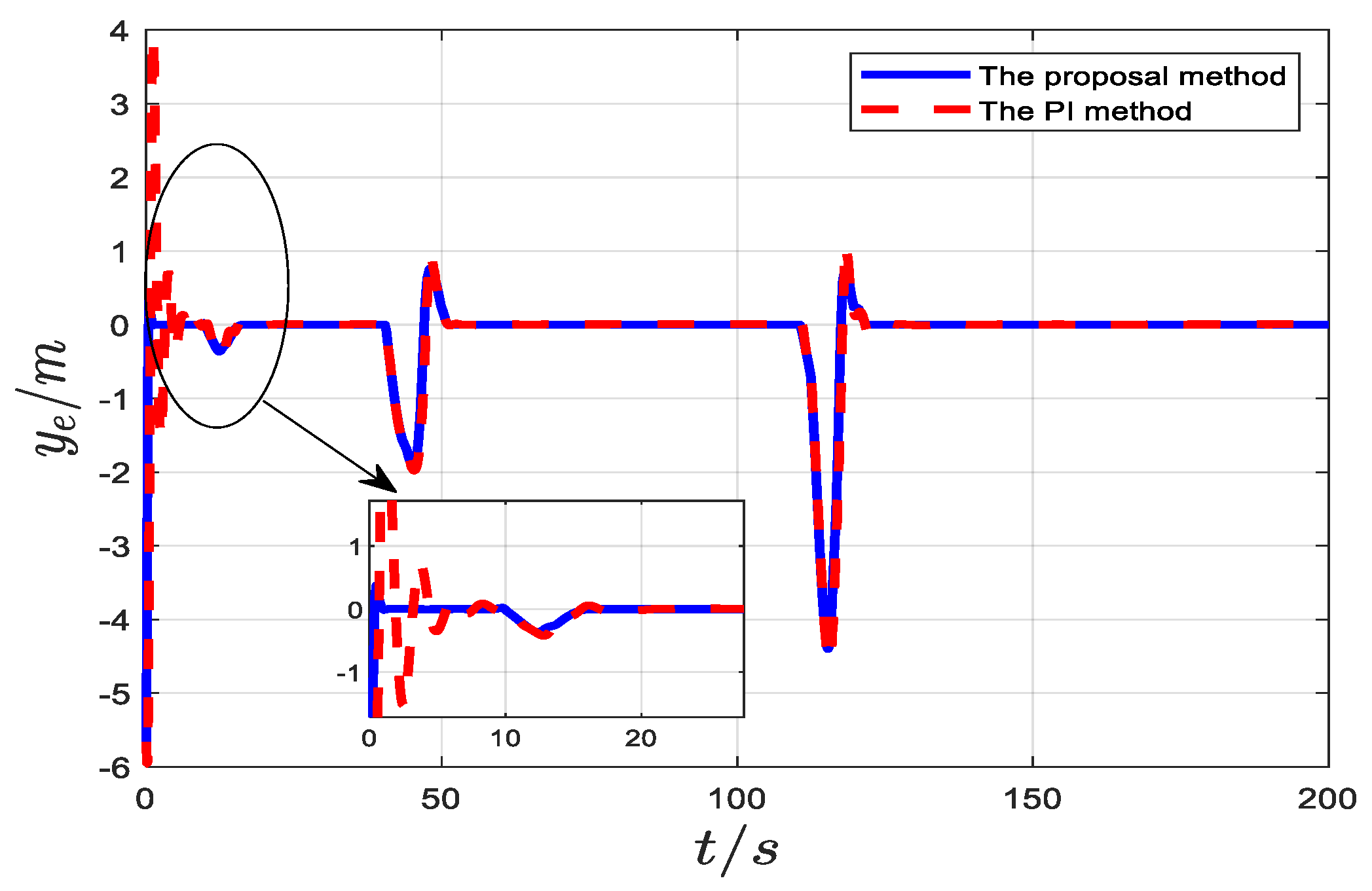
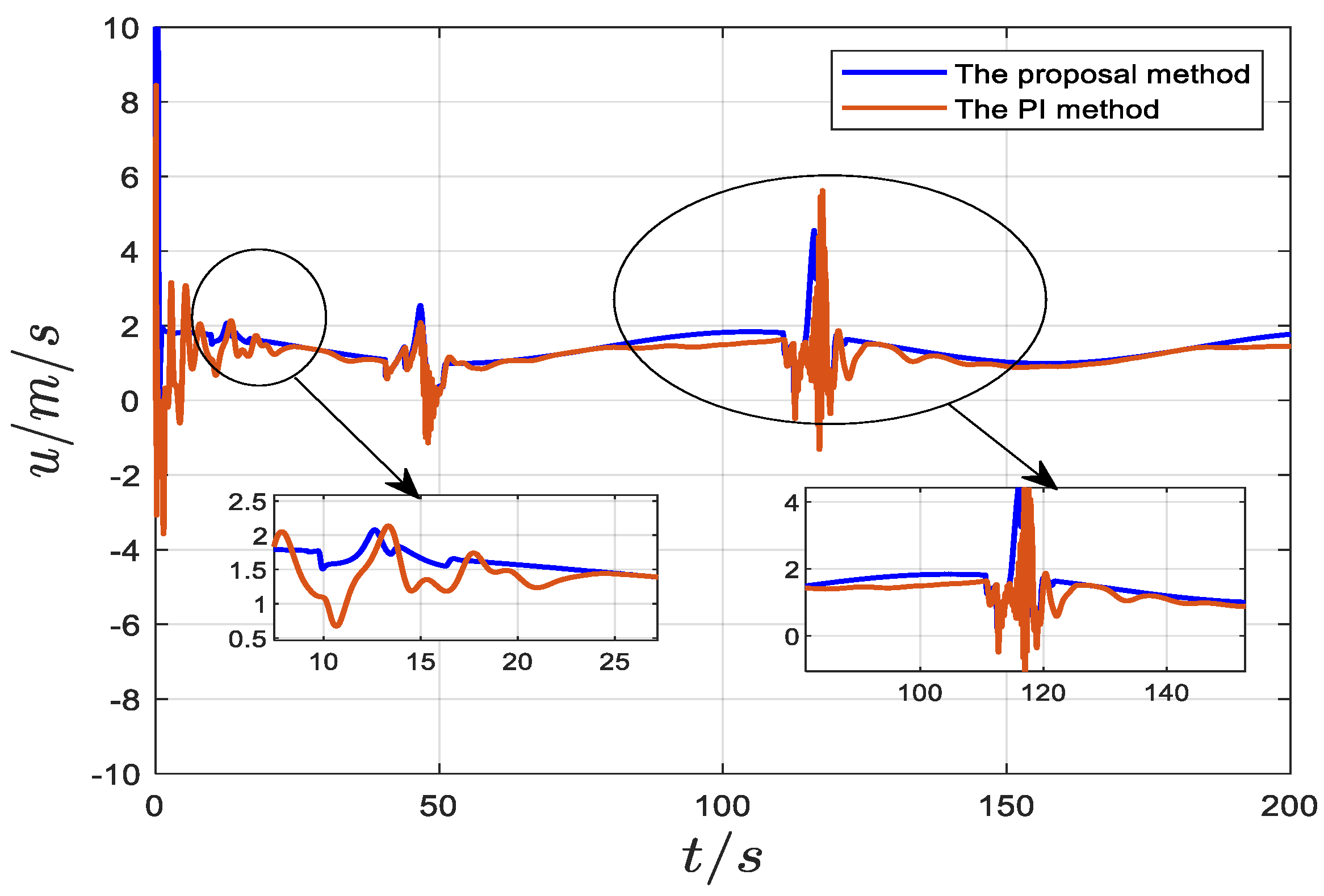
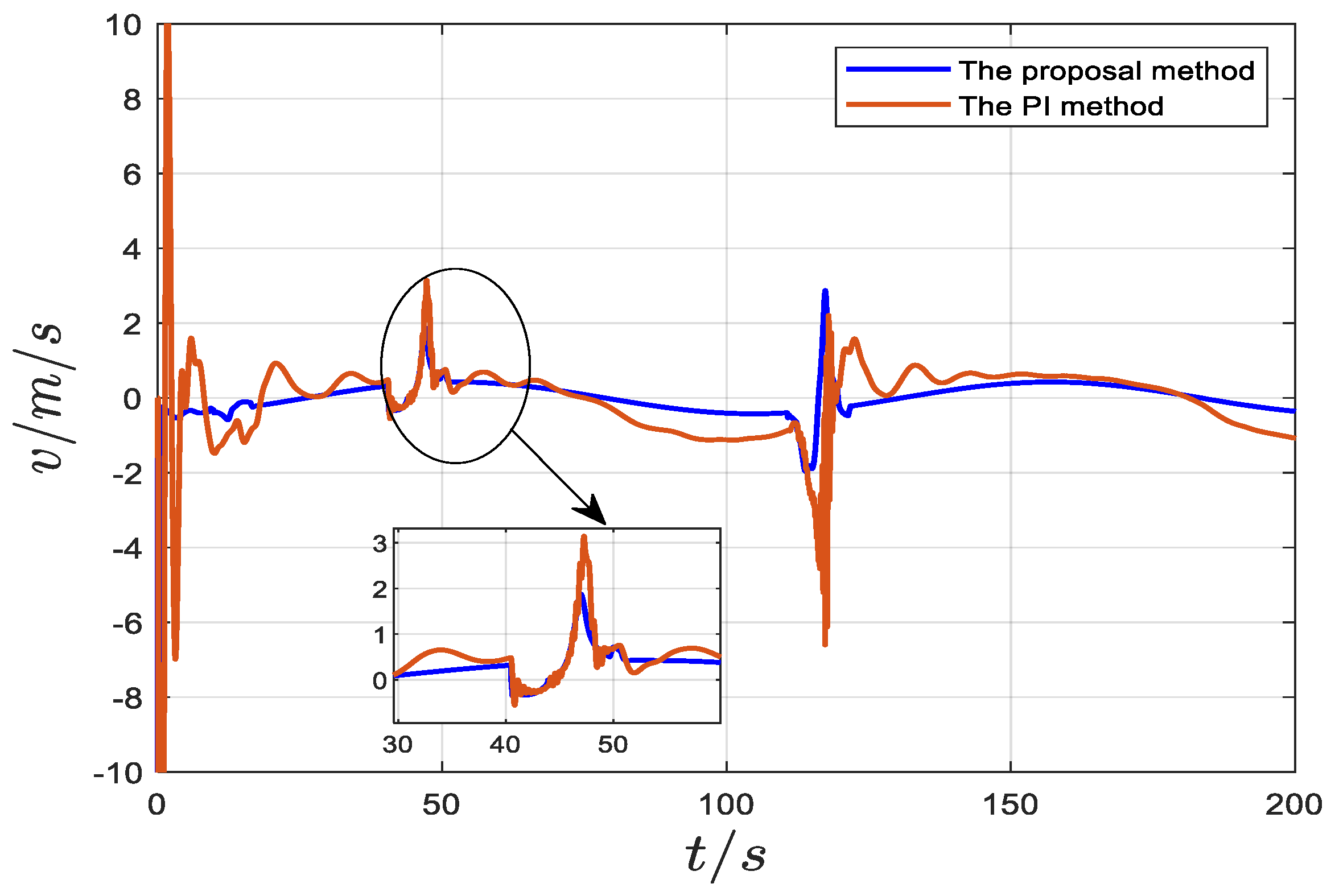
5. Numerical Simulations

This section evaluates the practical fixed-time robust containment controller based on a fixed-time nonlinear disturbance observer (FNDO) through simulated experiments. This study considers a multi-ASV system with three virtual leaders and five followers, where the follower indices are F = 1, 2, 3, 4, 5, and the leader indices are L = 6, 7, and 8. Figure 4 illustrates the formation system’s topology, and the communication topology diagram satisfies Assumption 3. The research objective used in the simulations is the Cybership II surface vehicle model, which weighs 23.8 kg, has a length of 1.255 m, and a width of 0.29 m. Its model parameters are detailed in the literature [49].

Table 1. Setup of obstacles.

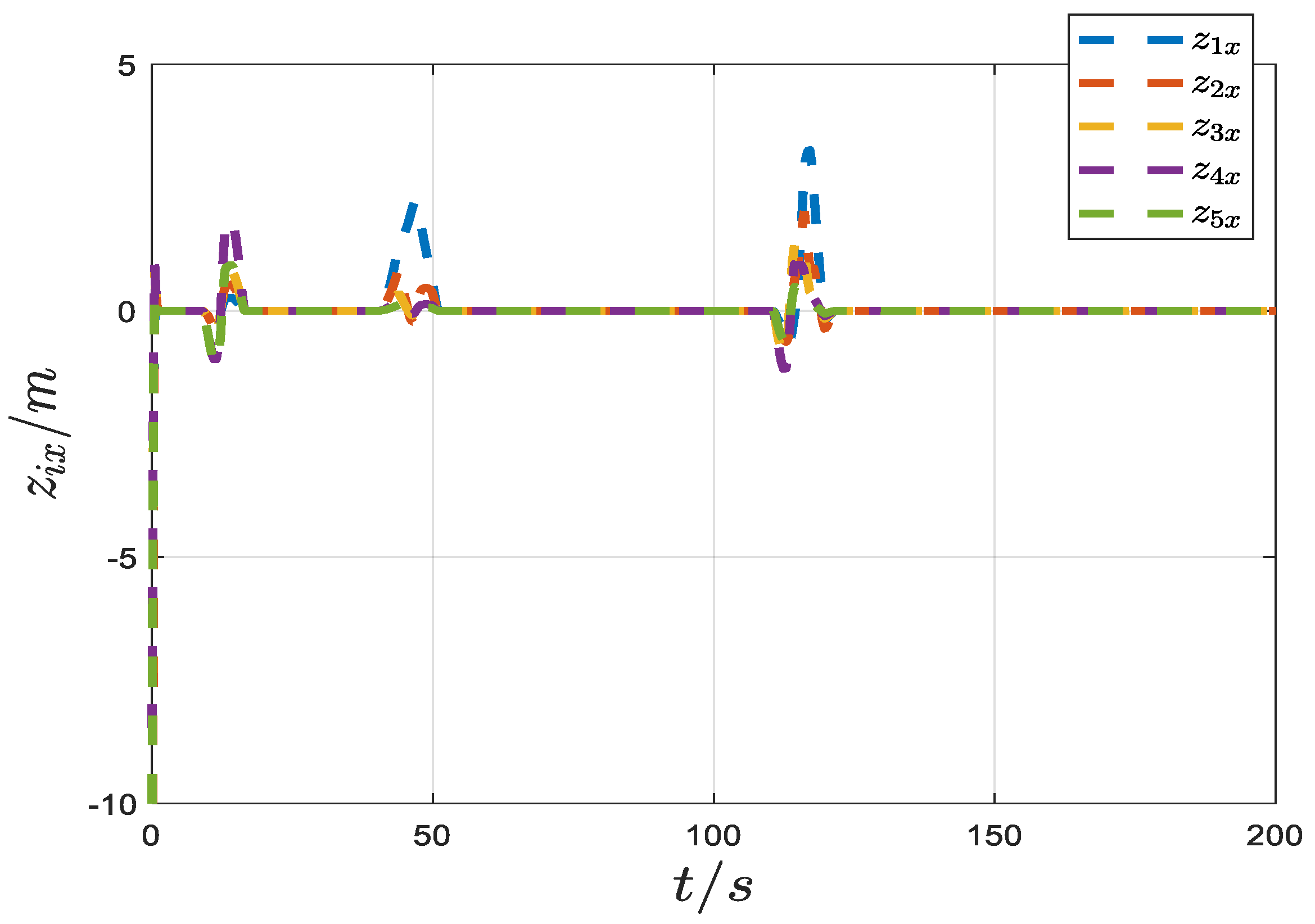
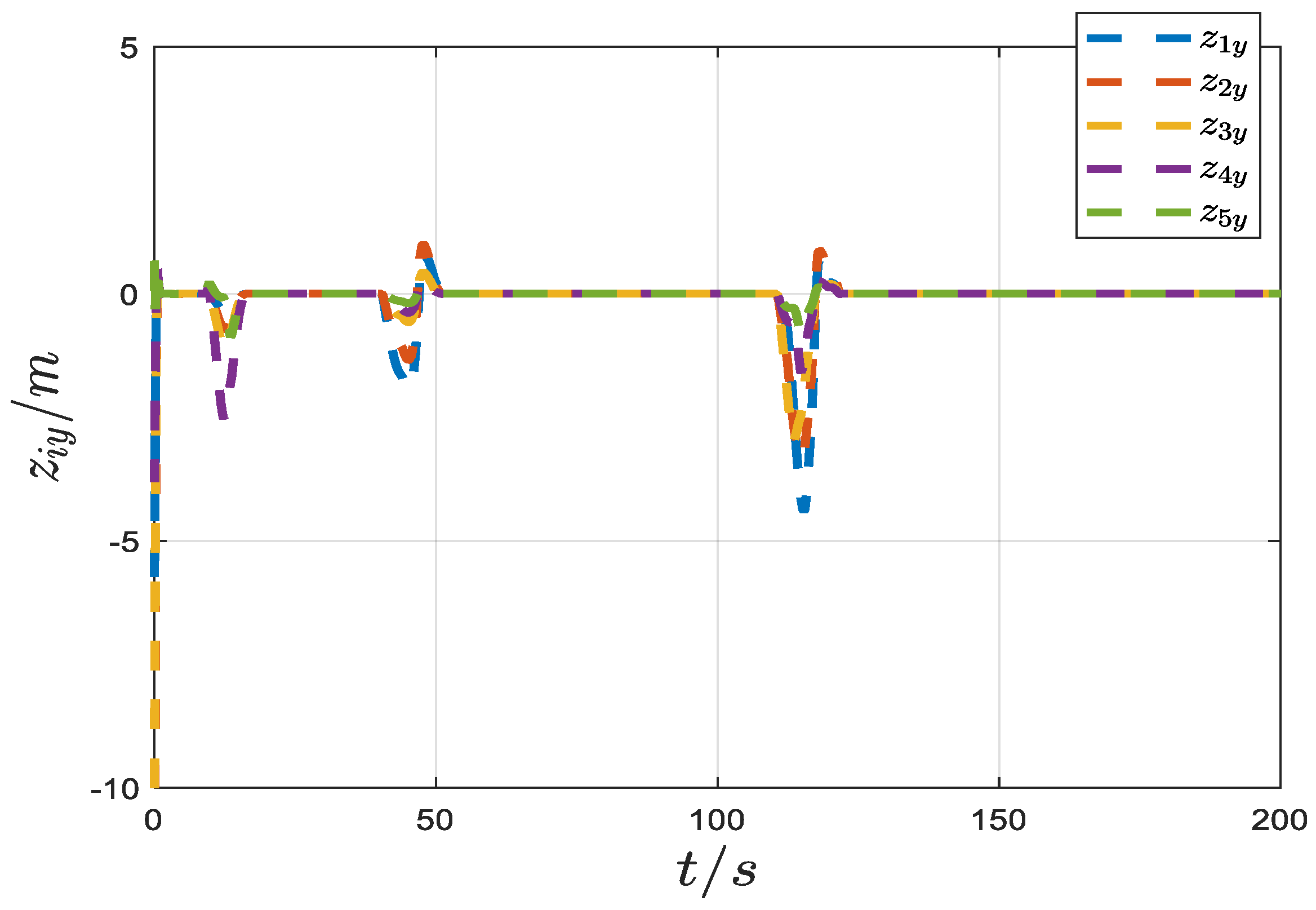
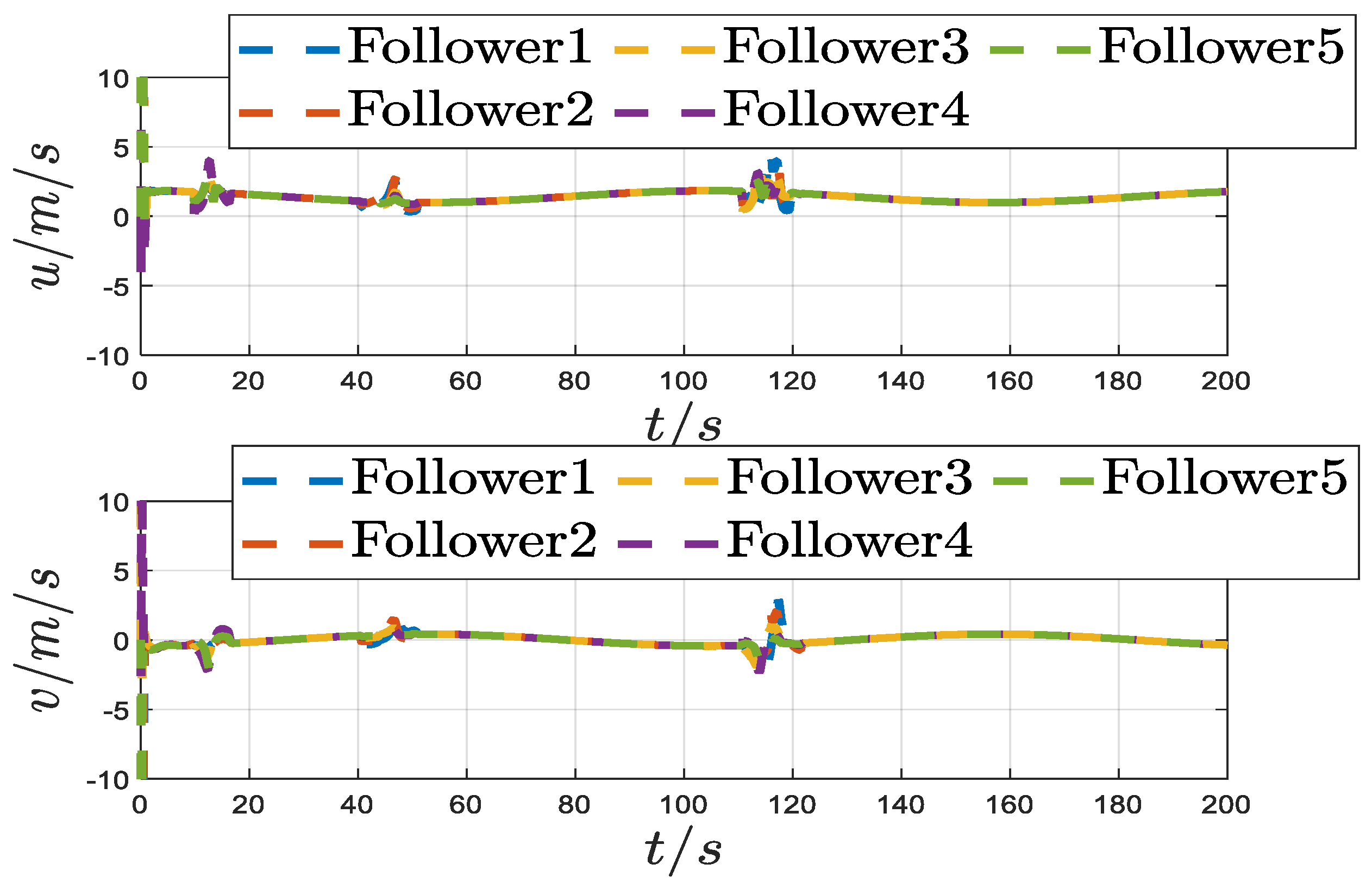
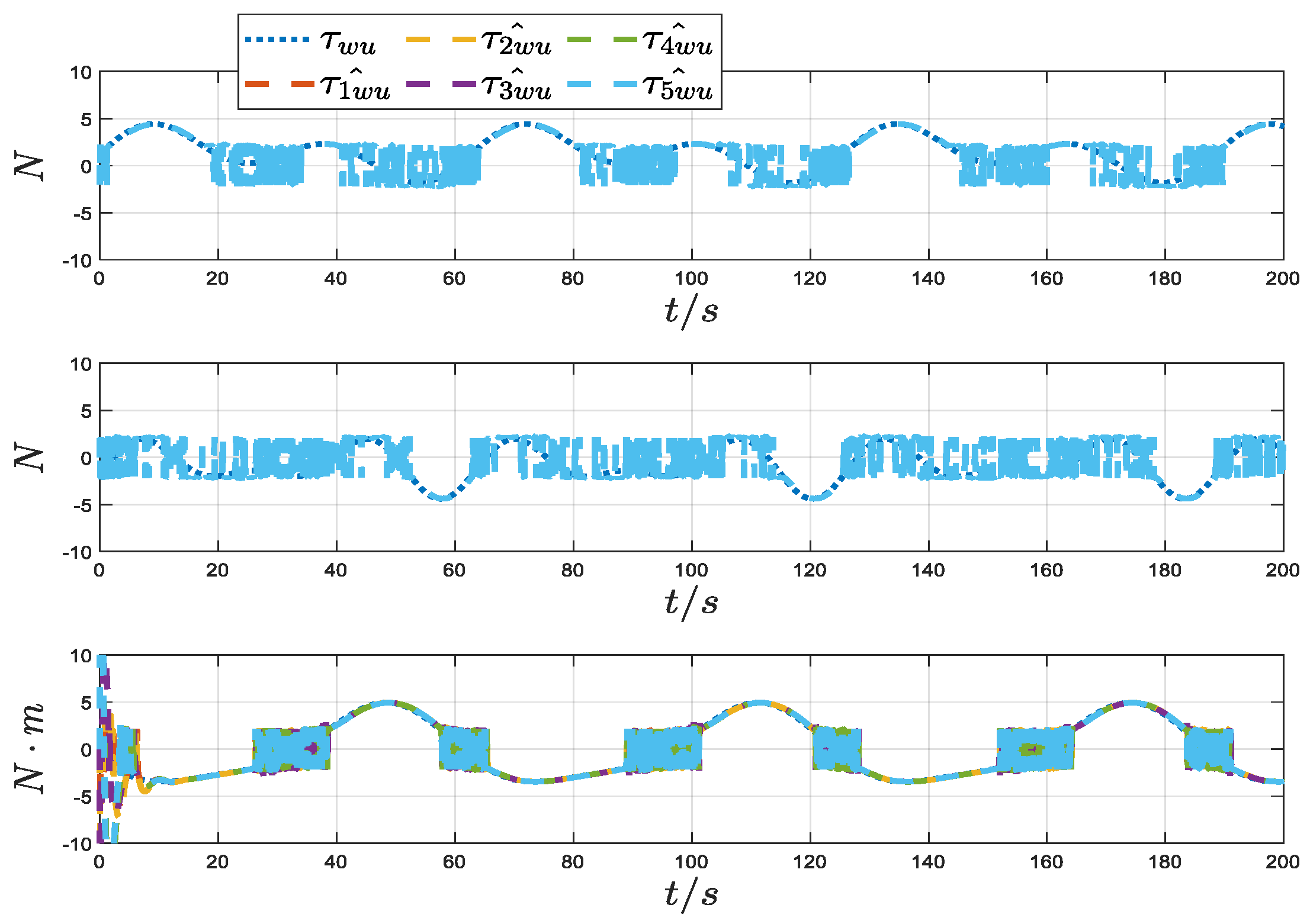
$\mathit{o}=1,2,3,4$	Obstacle 1	Obstacle 2	Obstacle 3	Obstacle 4
$p_o$	${\left[23,35\right]}^{\mathrm{T}}$	${\left[150,120\right]}^{\mathrm{T}}$	${\left[75,50\right]}^{\mathrm{T}}$	${\left[125,125\right]}^{\mathrm{T}}$

presents the location information of four obstacles.

Table 2. Initial of followers.

$\mathit{i}=1,2,3,4,5$	Follower 1	Follower 2	Follower 3	Follower 4	Follower 5
$p_i$	${\left(8,-3\right)}^{\mathrm{T}}$	${\left(-5,-10\right)}^{\mathrm{T}}$	${\left(-3,-3\right)}^{\mathrm{T}}$	${\left(-3,15\right)}^{\mathrm{T}}$	${\left(-8,30\right)}^{\mathrm{T}}$
${\mathit{\psi }}_i$	$pi/4$	$pi/4$	$pi/4$	0	0
${\mathbf{\nu }}_i$	${\left(0,0,0\right)}^{\mathrm{T}}$	${\left(0,0,0\right)}^{\mathrm{T}}$	${\left(0,0,0\right)}^{\mathrm{T}}$	${\left(0,0,0\right)}^{\mathrm{T}}$	${\left(0,0,0\right)}^{\mathrm{T}}$

presents the initial status information of the five followers.

The virtual leader’s reference trajectory is set to:

$$\left\{\begin{array}{l}{\mathit{\eta }}_{6r}={\left[10\sin \left(0.06t\right)+t+40,t,pi/4\right]}^{\mathrm{T}}\\ {\mathit{\eta }}_{7r}={\left[10\sin \left(0.06t\right)+t,t,pi/4\right]}^{\mathrm{T}}\\ {\mathit{\eta }}_{8r}={\left[10\sin \left(0.06t\right)+t,t+40,pi/4\right]}^{\mathrm{T}}\end{array}\right.$$

(59)

The unknown time-varying disturbances are set to:

$$\left\{\begin{array}{l}{\tau }_{wu}=1.8\sin (0.1t)+2.5\sin (0.2t)+1.5\\ {\tau }_{wv}=1.5\sin (0.2t-pi/3)+2.6\sin (0.3t)-1.1\\ {\tau }_{wr}=3\sin (0.1t)-0.5\sin (0.2t+pi/6)+0.5\end{array}\right.$$

(60)

The detailed parameters of fixed-time disturbance observer (27), kinematic controller (35), nonlinear filter (37), and containment controller (47) are introduced in

Table 3. Parameters of the proposed containment controller.

Control Module	Parameters
FNDO	$K_{di1}=diag\left\{\left(2.5,2.5,2.5\right)\right\}$
	$K_{di2}=diag\left\{\left(1.5,1.5,1.5\right)\right\}$
	$K_{di3}=diag\left\{\left(1.2,1.2,1.2\right)\right\}$
	$p_d=0.7$
	$q_d=1.1$
Kinematic Control Law	$K_{i1}=diag\left\{\left(6,6,6\right)\right\}$
	$K_{i2}=diag\left\{\left(0.02,0.02,0.02\right)\right\}$
	$K_{i3}=diag\left\{\left(0.02,0.02,0.02\right)\right\}$
	$\chi =0.7$
	$\delta =1.1$
Nonlinear Filter	$T_{fi}=0.02$
	$\chi =0.7$
	$\delta =1.1$
Control Law	$K_{i4}=diag\left\{\left(8,8,8\right)\right\}$
	$K_{i5}=diag\left\{\left(1.6,1.6,1.6\right)\right\}$
	$K_{i6}=diag\left\{\left(1.6,1.6,1.6\right)\right\}$
	$\chi =0.7$
	$\delta =1.1$

.

The simulation results for the practical fixed-time control scheme are presented in Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10 and Figure 11. Figure 5 shows that the proposed controller enables all followers in the multi-AUV system to converge to the desired position in a relatively short time while sailing it in a prescribed formation layout. When a collision risk occurs, collision avoidance between vehicles and obstacles is successfully achieved. It is worth noting that vehicles prioritize collision avoidance over maintaining the prescribed formation layout when a collision risk is present, which negatively impacts the position consistency of the formation. This effect is reflected in the subsequent simulation results. Figure 6 and Figure 7 show the position tracking errors of the five followers, demonstrating that each follower can track the target trajectory in a short period of time. During t = 9 s~17 s, t = 40 s~51 s, t = 110 s~121 s, the position tracking error of the followers changes significantly, indicating that the vehicles attempt to avoid obstacles, resulting in large position tracking errors. Figure 8 shows the followers’ velocities, including surge and sway velocities. During t = 9 s~17 s, t = 40 s~51 s, t = 110 s~121 s, the velocities of the vehicles change significantly, indicating that the followers are attempting to avoid obstacles. Figure 9 illustrates the distance between the followers, along with the detection and collision avoidance distances. It shows that when the collision avoidance detection distance exceeds the distance between vehicles, the control system’s collision avoidance mechanism is triggered, thus ensuring collision avoidance between the vehicles. Figure 10 shows the control inputs for all followers. Figure 11 shows the estimated value of the external environment and the unknown time-varying disturbance. The estimated value quickly approaches the external disturbance, demonstrating the excellent estimation performance of the constructed fixed-time disturbance observer.

Comparison Simulation: To further illustrate the effectiveness of the designed controller, a comparative analysis is conducted between the proposed controller and the proportional–integral (PI) controller proposed in the literature [51]. The PI controller is given as follows,

$${\mathit{\tau }}_{i\_PI}=-{\mathit{M}}_i{\mathit{K}}_{i4}\left({\mathit{\upsilon }}_i-{\mathit{v}}_{ri}\right)-{\mathit{K}}_{i7}{\displaystyle {\int }_0^t\left({\mathit{\upsilon }}_i-{\mathit{v}}_{ri}\right)dt}$$

(61)

where ${\mathit{K}}_{i7}=diag\left(\left[0.4,0.4,0.4\right]\right)$.

For the purpose of analysis, Follower1 is chosen as the subject for the comparative simulation. To ensure the validity of the results, the initial conditions for both controllers are kept consistent, including the relevant parameters in the controllers. The simulation results are presented in Figure 12, Figure 13, Figure 14, Figure 15 and Figure 16, while the performance evaluation metrics for both controllers are summarized in

Table 4. Controller performance comparison of along-track error.

Comparative Control Methods	MSE	RMSE	MAE
The proposed controller	2.0534	1.4330	0.1108
The PI controller	108.7973	10.4306	5.2420

and

Table 5. Controller performance comparison of cross-track error.

Comparative Control Methods	MSE	RMSE	MAE
The proposed controller	0.1831	0.4279	0.0440
The PI controller	8.0354	2.8347	1.5029

. As shown in Figure 12, the proposed controller ensures that all followers converge within the convex hull formed by the virtual leaders while also achieving safe collision avoidance. This demonstrates that control objectives 1–2 are successfully met. Figure 13 and Figure 14 illustrate the position tracking errors of Follower1 in the lateral and longitudinal directions, respectively. It is evident that the proposed controller leads to a faster and smoother convergence of the position tracking errors. Figure 15 and Figure 16 show the velocity variations of Follower1 in the lateral and longitudinal directions. Notably, when the vessel is required to perform collision avoidance maneuvers, the controller exhibits significant oscillations, indicating that the proposed method offers superior steady-state performance.

This section presents a quantitative analysis to further illustrate the superiority of the proposed controller, comparing its performance with that of the alternative controller. Table 4 and Table 5 provide a comparative analysis of position tracking errors in both lateral and longitudinal directions. The evaluation metrics include MSE (mean squared error), RMSE (root mean squared error), and MAE (mean absolute error). As shown in Table 4 and Table 5, the proposed controller exhibits superior tracking performance.

6. Conclusions

This paper presents a practical fixed-time robust containment controller for multi-ASVs, considering the risk of collision avoidance. To estimate external disturbances, a fixed-time nonlinear disturbance observer is developed, which is straightforward to implement in engineering applications. Meanwhile, a fixed-time distributed robust containment controller is developed by integrating dynamic surface control technology (DSC) with the fixed-time nonlinear disturbance observer (FNDO). To address the collision problem, the controller design incorporates an artificial potential field function. Finally, simulation results demonstrate that the proposed controller can achieve containment control and collision avoidance. Future research will consider constraints such as dynamic obstacle avoidance and switching topologies.