Hydrodynamic Performance and Mooring Safety Assessment of an Offshore Floating Movable Fish Cage
Abstract
1. Introduction
2. Mathematical Formulation
3. Numerical Model and Environmental Condition
4. Results
4.1. Motion Response Amplitude Operators of the Freely Floating Fish Cage
4.2. Dynamics of a Moored Fish Cage
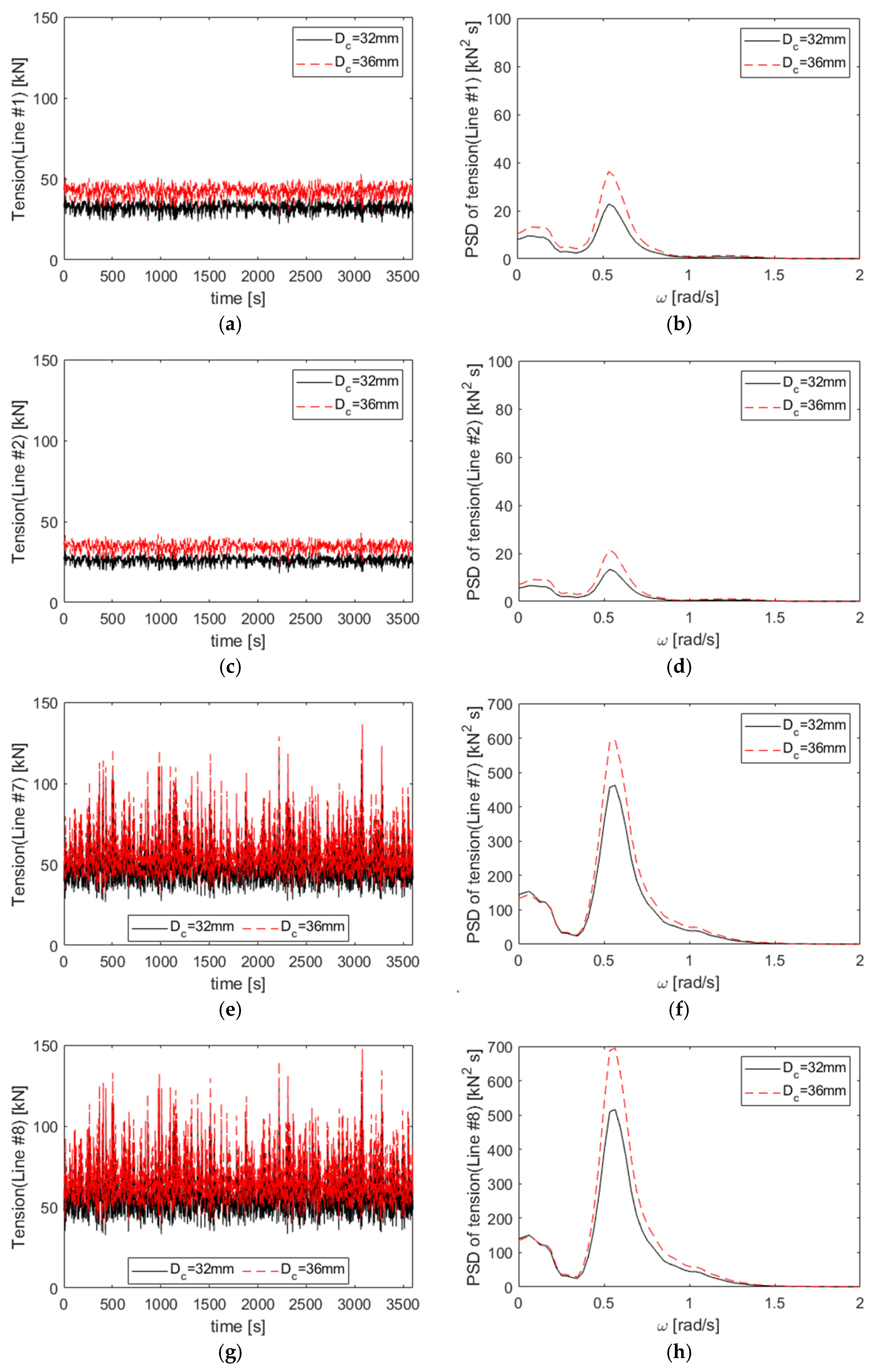
4.3. Effect of Mooring Line Length
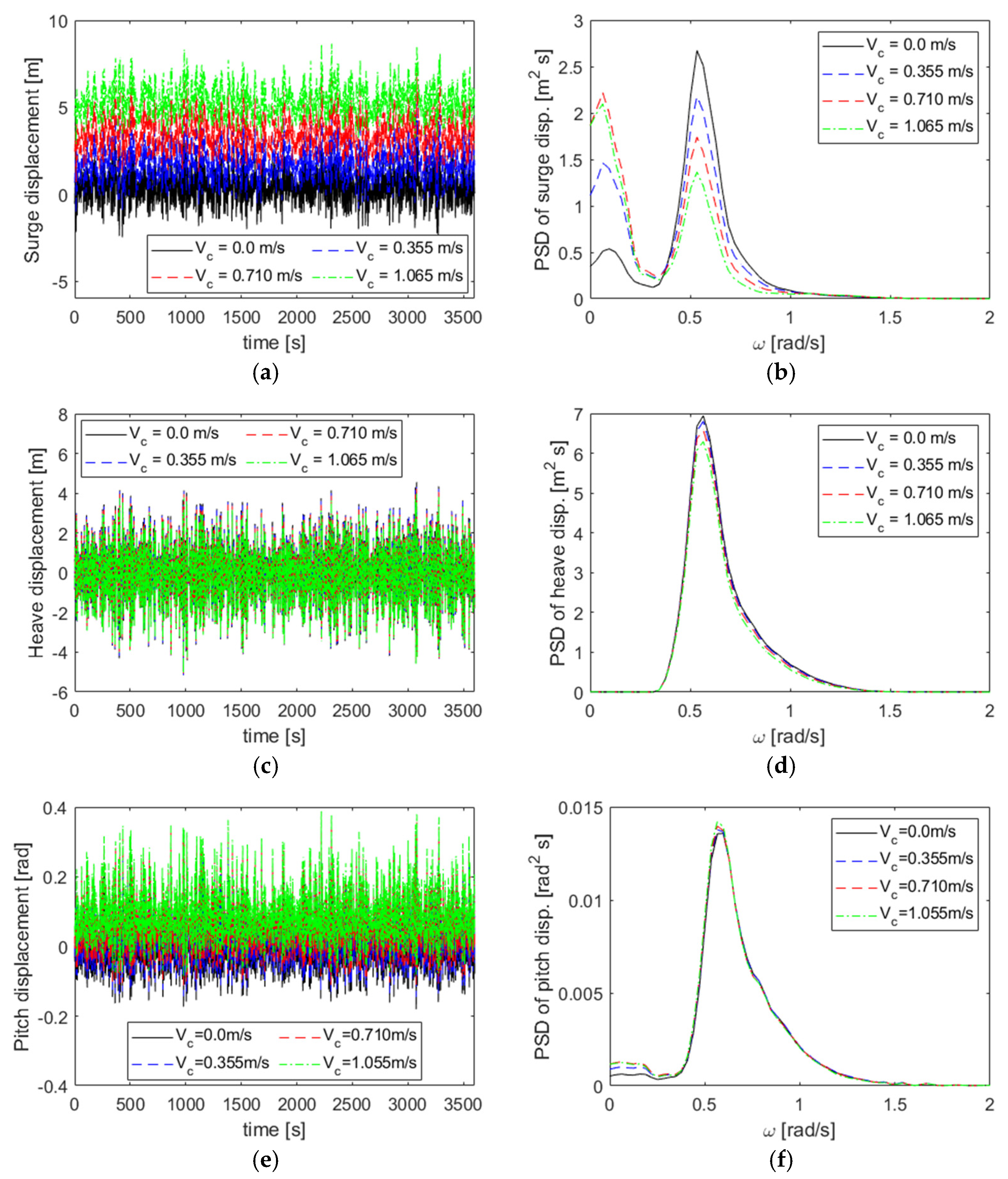
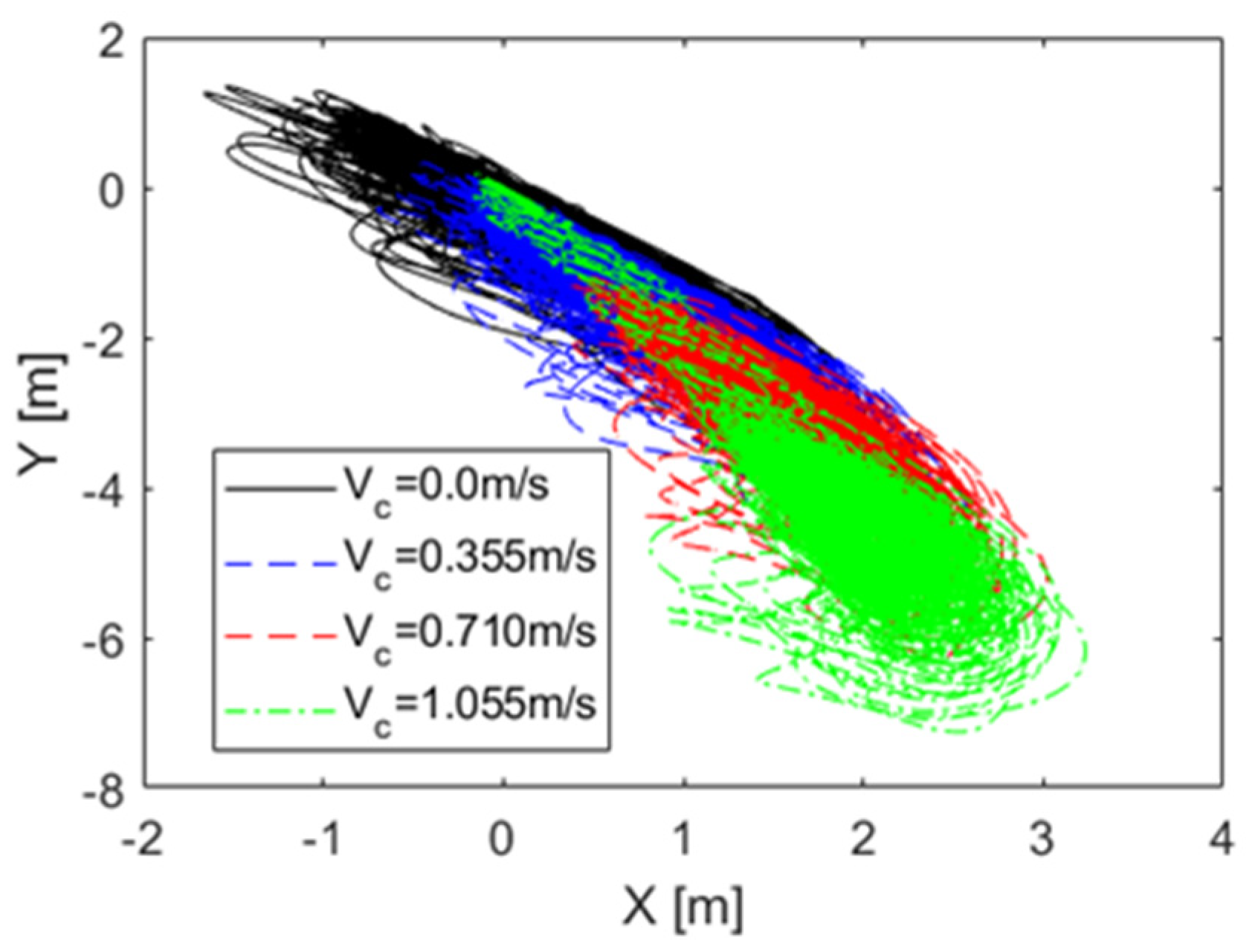
4.4. Effect of Surface Current Speed
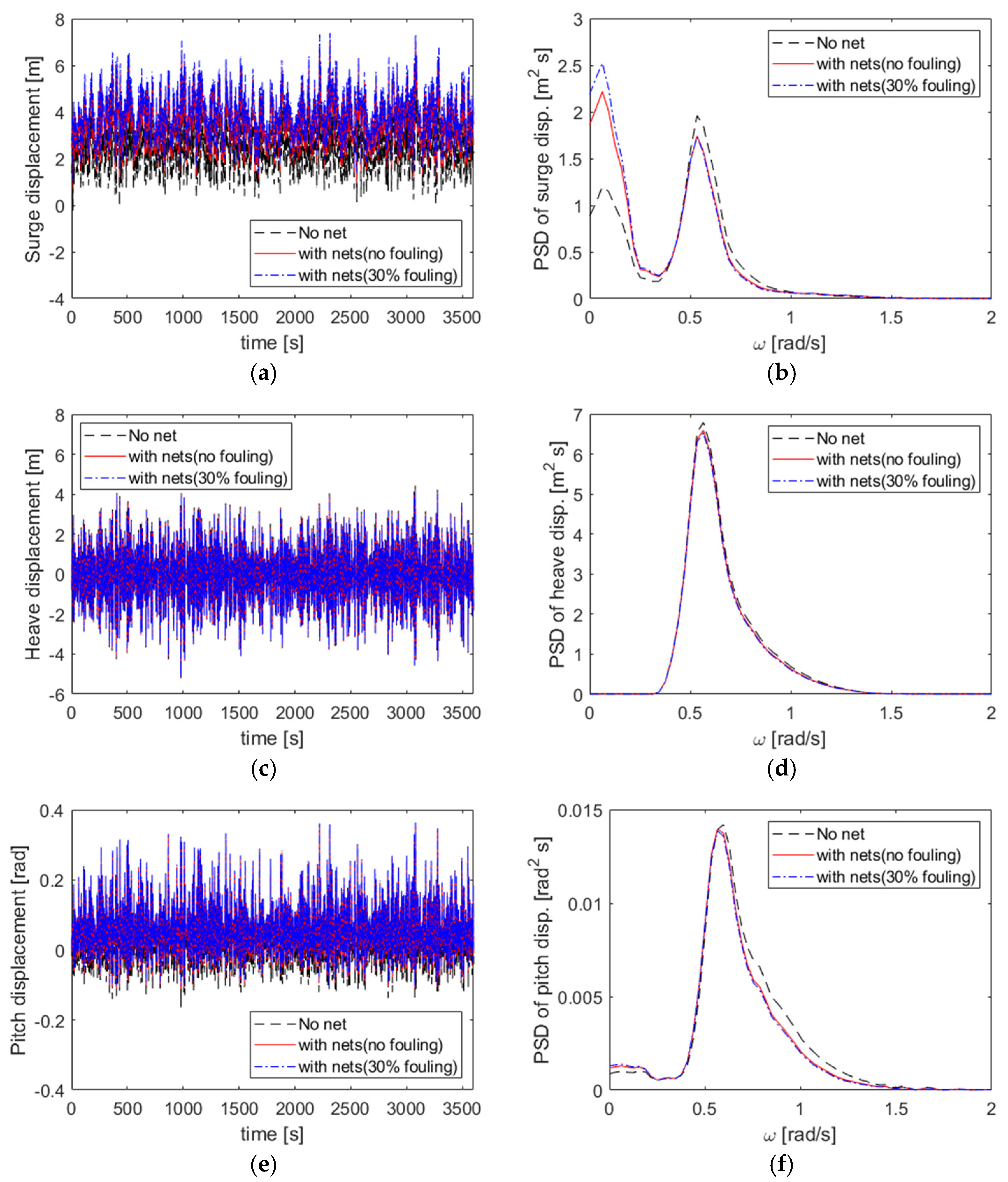
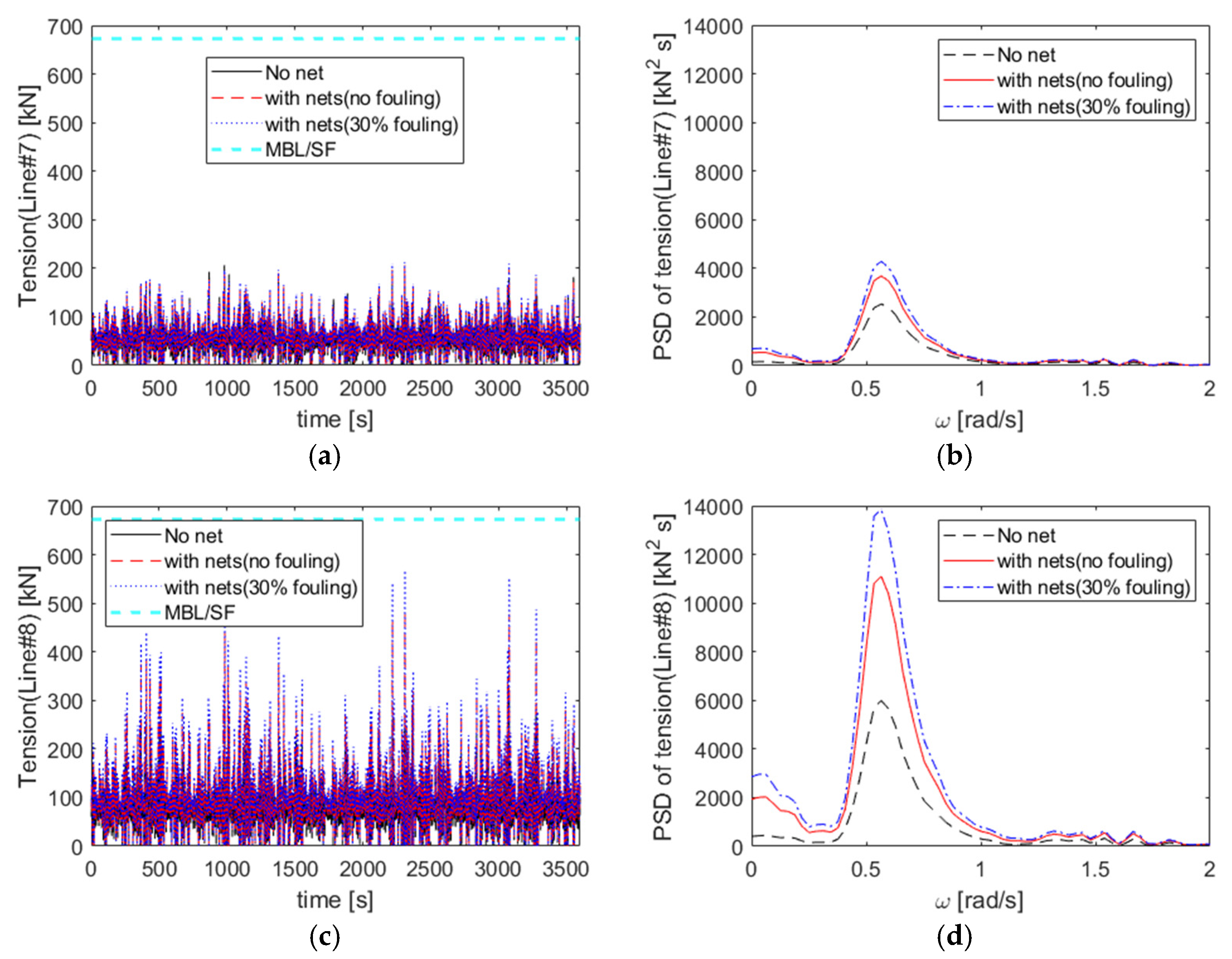
4.5. Effect of the Netting System
4.6. Mooring Line Failure Condition
5. Conclusions
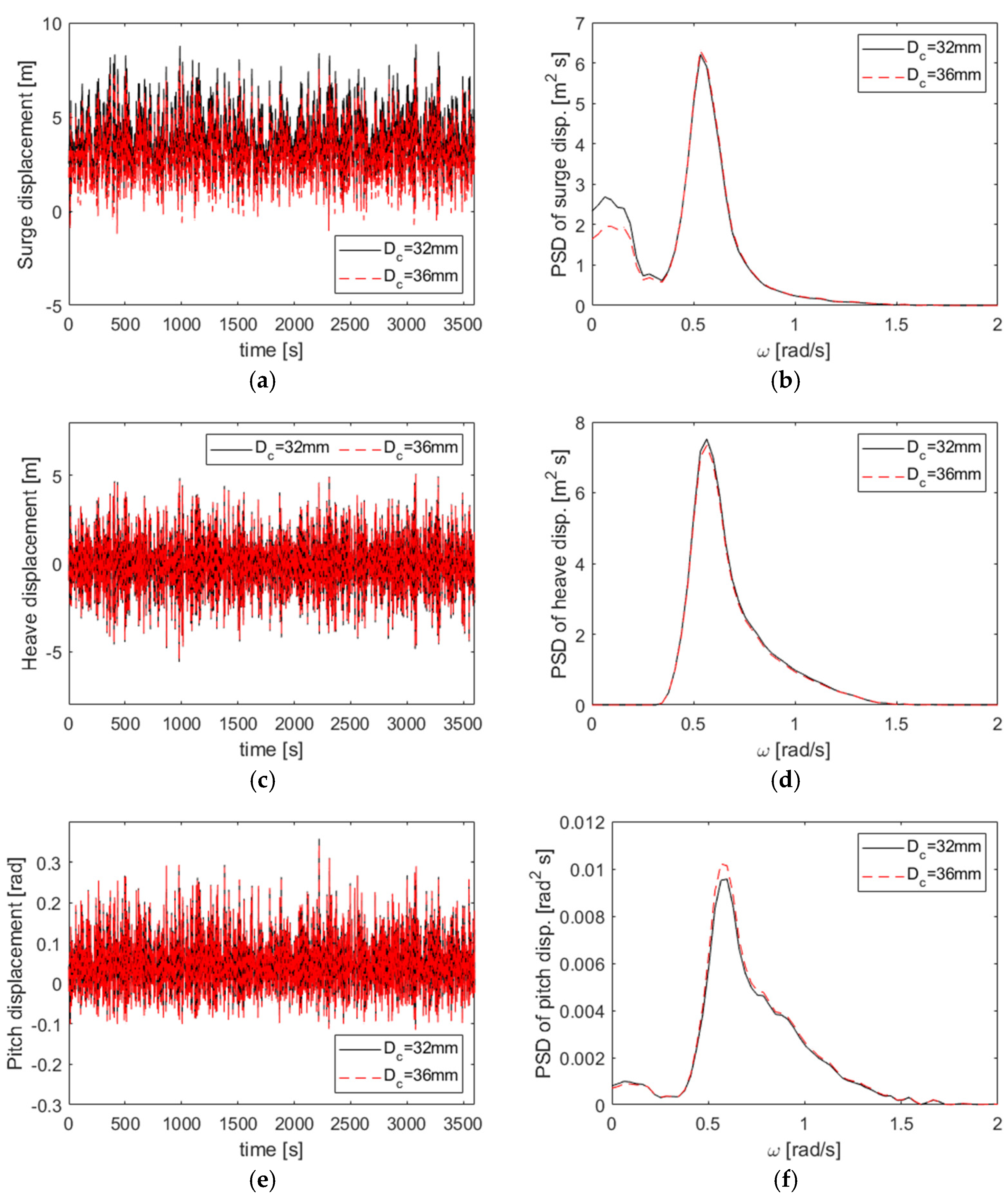
- A parametric study showed that longer mooring lines increased excursions but reduced the pitch motion and tension variability. Heavier chains (36 mm diameter) decreased excursions by up to 33%, improving station-keeping, but increased the maximum line tension by 17% compared with lighter chains. A 290 m line with a 36 mm chain diameter optimized excursions and mooring system safety.
- Higher current speeds significantly affected the surge motion, causing greater drift and stretching mooring lines, while minimally impacting the heave and pitch motions. Increased current speeds stiffened the mooring system, reducing motion responses near the wave peak frequency but increasing mooring line tension. At a 1.055 m/s current speed, mooring line tension exceeded safe limits, emphasizing the importance of considering current speed in mooring system design for stability and structural safety.
- Biofouling substantially altered the fish cage hydrodynamics by changing drag properties, leading to an increased low-frequency surge motion and a 6% rise in the maximum excursion, with minimal effects on the heave and pitch motions. Under the maximum tension conditions, biofouling induced the increased line tension at the wave peak frequency by 17%; however, the line tension remained within allowable limits.
- Two worst-case scenarios involving individual mooring line failures were investigated to evaluate system safety and resilience. Both scenarios led to increased drift and higher line tension levels compared to the intact condition. Nevertheless, the mooring system kept the line tension within the allowable safety threshold.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chu, Y.I.; Wang, C.M.; Park, J.C.; Lader, P.F. Review of cage and containment tank designs for offshore fish farming. Aquaculture 2020, 519, 734928. [Google Scholar] [CrossRef]
- Chu, Y.-I.; Wang, C.-M.; Zhang, H.; Abdussamie, N.; Karampour, H.; Jeng, D.-S.; Baumeister, J.; Aland, P.A. Offshore fish farms: A review of standards and guidelines for design and analysis. J. Mar. Sci. Eng. 2023, 11, 762. [Google Scholar] [CrossRef]
- Kim, M.H.; Koo, B.; Mercier, R.M.; Ward, E.G. Vessel/mooring/riser coupled dynamic analysis of a turret-moored FPSO compared with OTRC experiment. Ocean Eng. 2005, 32, 1780–1802. [Google Scholar] [CrossRef]
- Cifuentes, C.; Kim, M.H. Hydrodynamic response of a cage system under waves and currents using a Morison-force model. Ocean Eng. 2017, 141, 283–294. [Google Scholar] [CrossRef]
- Jin, C.; Kang, H.; Kim, M.H.; Bakti, F.P. Performance evaluation of surface riding wave energy converter with linear electric generator. Ocean Eng. 2020, 218, 108141. [Google Scholar] [CrossRef]
- Kim, S.-J.; Koo, W.; Kim, M.H. The effects of geometrical buoy shape with nonlinear Froude-Krylov force on a heaving buoy point absorber. Int. J. Nav. Archit. Ocean Eng. 2021, 13, 86–101. [Google Scholar] [CrossRef]
- Kim, S.-J.; Koo, W. Numerical study on a multibuoy-type wave energy converter with hydraulic PTO system under real sea conditions. IEEE J. Ocean. Eng. 2021, 46, 573–582. [Google Scholar] [CrossRef]
- Yu, S.; Qin, H.; Li, P.; Xu, Z. Nonlinear vertical accelerations and mooring loads of a semi-submersible offshore fish farm under extreme conditions. Aquac. Eng. 2021, 95, 102193. [Google Scholar] [CrossRef]
- Miao, Y.-J.; Ding, J.; Tian, C.; Chen, X.-J.; Fan, Y.-L. Experimental and numerical study of a semi-submersible offshore fish farm under waves. Ocean Eng. 2021, 225, 108794. [Google Scholar] [CrossRef]
- Ma, C.; Zhao, Y.-P.; Bi, C.-W. Numerical study on hydrodynamic responses of a single-point moored vessel-shaped floating aquaculture platform in waves. Aquac. Eng. 2022, 96, 102216. [Google Scholar] [CrossRef]
- Yue, W.; Wang, W.; Sheng, S.; Ye, Y.; Hong, T. Analysis of the wave load and dynamic response of a new semi-submersible wave-energy-powered aquaculture platform. Ocean Eng. 2022, 248, 110346. [Google Scholar] [CrossRef]
- Ding, W.-W.; Jiang, J.-Q.; Yue, W.-Z.; Li, Y.-Z.; Wang, W.-S.; Sheng, S.-W.; Chen, M. Numerical study on hydrodynamic performance of a new semi-submersible aquaculture platform. Appl. Sci. 2023, 13, 12652. [Google Scholar] [CrossRef]
- Pang, G.; Zhang, S.; Liu, H.; Zhu, S.; Yuan, T.; Li, G.; Han, X.; Huang, X. Hydrodynamic response analysis for a new semi-submersible vessel-shaped fish farm platform based on numerical simulation. Front. Mar. Sci. 2023, 10, 1135757. [Google Scholar] [CrossRef]
- Kim, S.-J.; Jin, C.; Kim, M. Time-dependent responses and mooring tensions of a moored floating structure in tsunami waves. Mar. Struct. 2024, 93, 103538. [Google Scholar] [CrossRef]
- Chen, M.; Huang, L.; Cheng, H.; Wu, Q. Numerical investigation on mooring line configurations of a semisubmersible fish farm for global performance. J. Mar. Sci. Eng. 2024, 12, 880. [Google Scholar] [CrossRef]
- Zhang, L.; Zhen, X.; Duan, Q.; Huang, Y.; Chen, C.; Li, Y. Hydrodynamic characteristics analysis and mooring system optimization of an innovative deep-sea aquaculture platform. J. Mar. Sci. Eng. 2024, 12, 972. [Google Scholar] [CrossRef]
- Lee, C.-W.; Kim, Y.-B.; Lee, G.-H.; Choe, M.-Y.; Lee, M.-K.; Koo, K.-Y. Dynamic simulation of a fish cage system subjected to currents and waves. Ocean Eng. 2008, 35, 1521–1532. [Google Scholar] [CrossRef]
- Mohapatra, S.C.; Guedes Soares, C. A semi-analytical model of an array of moored floating flexible offshore net cages under current loads. Ocean Eng. 2024, 291, 116309. [Google Scholar] [CrossRef]
- Mohapatra, S.C.; Guedes Soares, C. A review of the hydroelastic theoretical models of floating porous nets and floaters for offshore aquaculture. J. Mar. Sci. Eng. 2024, 12, 1699. [Google Scholar] [CrossRef]
- Reyes, R.; del Norte-Campos, A.; Añasco, N.C.; Santander-de Leon, S.M.S. Biofouling development in marine fish farm influenced by net colour, immersion period and environmental conditions. Aquac. Res. 2020, 51, 3129–3138. [Google Scholar] [CrossRef]
- Cornejo, P.; Guerrero, N.M.; Montes, R.M.; Quiñones, R.A.; Sepúlveda, H.H. Hydrodynamic effect of biofouling in fish cage aquaculture netting. Aquaculture 2020, 526, 735367. [Google Scholar] [CrossRef]
- Chen, Q.-P.; Bi, C.-W.; Zhang, Z.-X.; Zhao, Y.-P. Hydrodynamic effect of different biofouling types on aquaculture netting. Ocean Eng. 2023, 279, 114430. [Google Scholar] [CrossRef]
- Tang, H.-J.; Yeh, P.-H.; Huang, C.-C.; Yang, R.-Y. Numerical study of the mooring system failure of aquaculture net cages under irregular waves and current. Ocean Eng. 2020, 216, 108110. [Google Scholar] [CrossRef]
- Cheng, H.; Li, L.; Ong, M.C.; Aarsæther, K.G.; Sim, J. Effects of mooring line breakage on dynamic responses of grid moored fish farms under pure current conditions. Ocean Eng. 2021, 237, 109638. [Google Scholar] [CrossRef]
- Hou, H.-M.; Liu, Y.; Dong, G.-H.; Xu, T.-J. Reliability assessment of mooring system for fish cage considering one damaged mooring line. Ocean Eng. 2022, 257, 111626. [Google Scholar] [CrossRef]
- ABS. Rules for Building and Classing Floating Production Installations; American Bureau of Shipping: Houston, TX, USA, 2014. [Google Scholar]
- ABS. Guide for Building and Classing Aquaculture Installations; American Bureau of Shipping: Spring, TX, USA, 2020. [Google Scholar]
- IMO. Standards for Ship Maneuverability; MSC 76/23/Add. 1; International Maritime Organization: London, UK, 2002. [Google Scholar]
- IMO. Explanatory Notes to the Standards for Ship Maneuverability, MSC/Circ.1053; International Maritime Organization: London, UK, 2002. [Google Scholar]
- Kim, H.-J.; Jeong, S.-J. Resistance and stability evaluation of mobile fish-cage. J. Korean Soc. Fish. Ocean Technol. 2016, 52, 79–87. [Google Scholar] [CrossRef]
- Kristiansen, T.; Faltinsen, O.M. Modeling of current loads on aquaculture net cages. J. Fluids Struct 2012, 34, 218–235. [Google Scholar] [CrossRef]
- Cummins, W. The impulse response function and ship motion. Schiffstechnik 1962, 47, 101–109. [Google Scholar]
- Chung, W.C.; Jin, C.; Kim, M.; Kim, S. Parametric study on mooring system design of submerged floating tunnel under extreme wave and seismic excitation. J. Mar. Sci. Eng. 2023, 11, 2357. [Google Scholar] [CrossRef]
- Depalo, F.; Wang, S.; Xu, S.; Guedes Soares, C. Design and analysis of a mooring system for a wave energy converter. J. Mar. Sci. Eng. 2021, 9, 782. [Google Scholar] [CrossRef]
- Niño, Y.; Vidal, K.; Tamburrino, A.; Zamorano, L.; Beltrán, J.F.; Estay, G.; Muñoz, A. Normal and tangential drag forces of nylon nets, clean and with fouling, in fish farming: An experimental study. Water 2020, 12, 2238. [Google Scholar] [CrossRef]
- Hong, S.N.; Yun, U.H.; Kim, K.W.; Choi, C.Y.; Hwang, B.G.; Lee, S.C. Development of Eco-Friendly Brass Fishing Nets and Cage Aquaculture Facilities; Ministry of Oceans and Fisheries: Sejong-si, Republic of Korea, 2020.
- DNVGL. Environmental Conditions and Environmental Loads; Det Norske Veritas: Oslo, Norway, 2000. [Google Scholar]
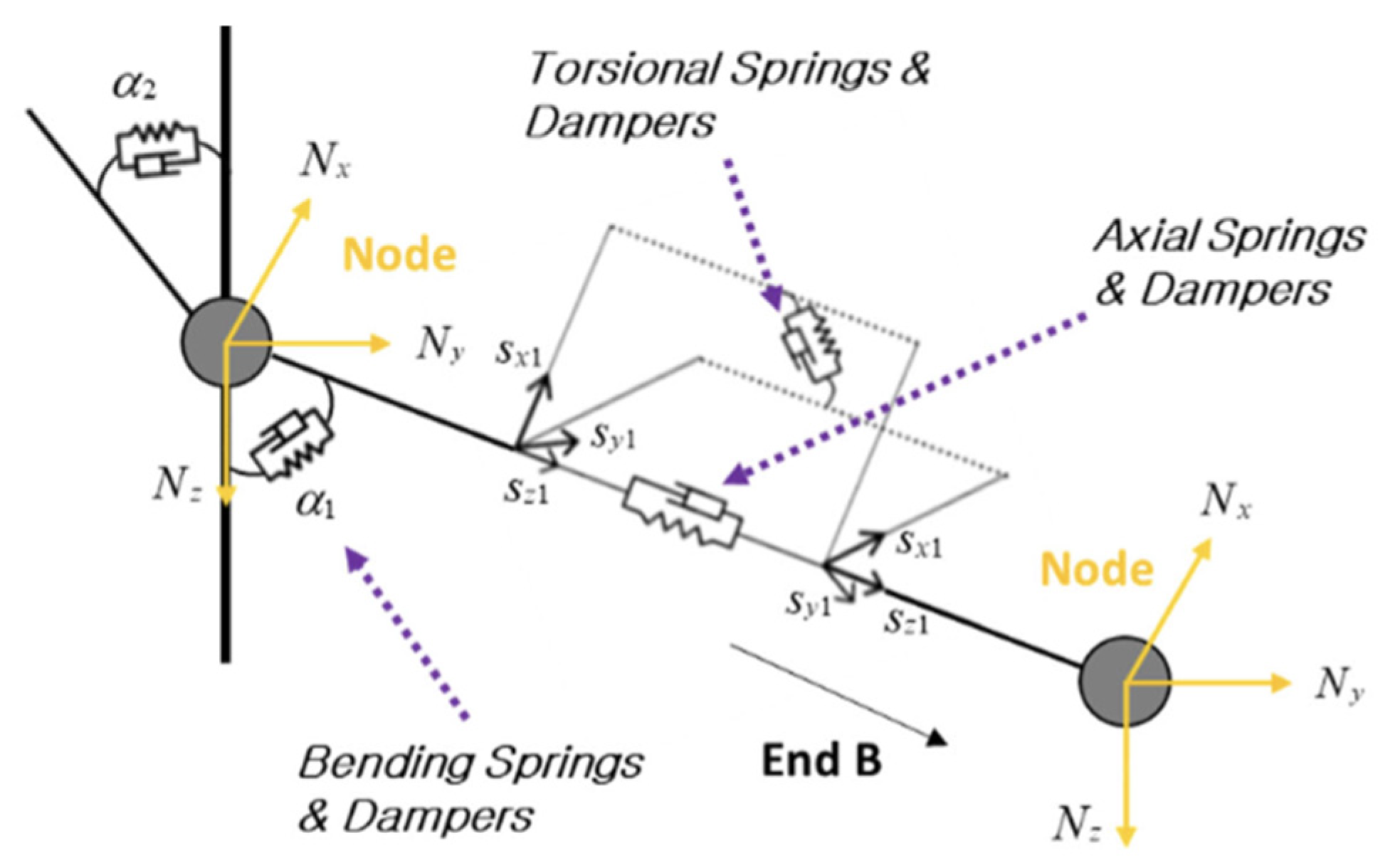
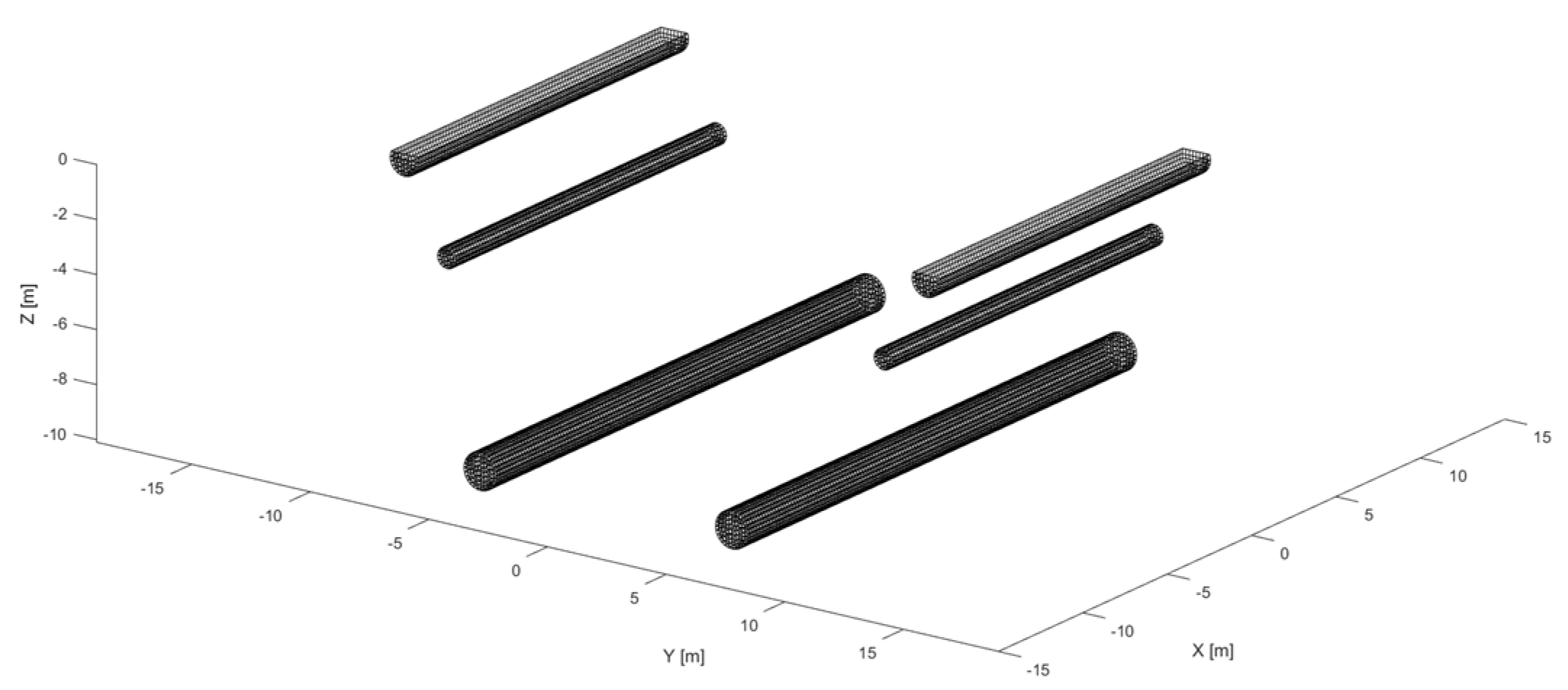
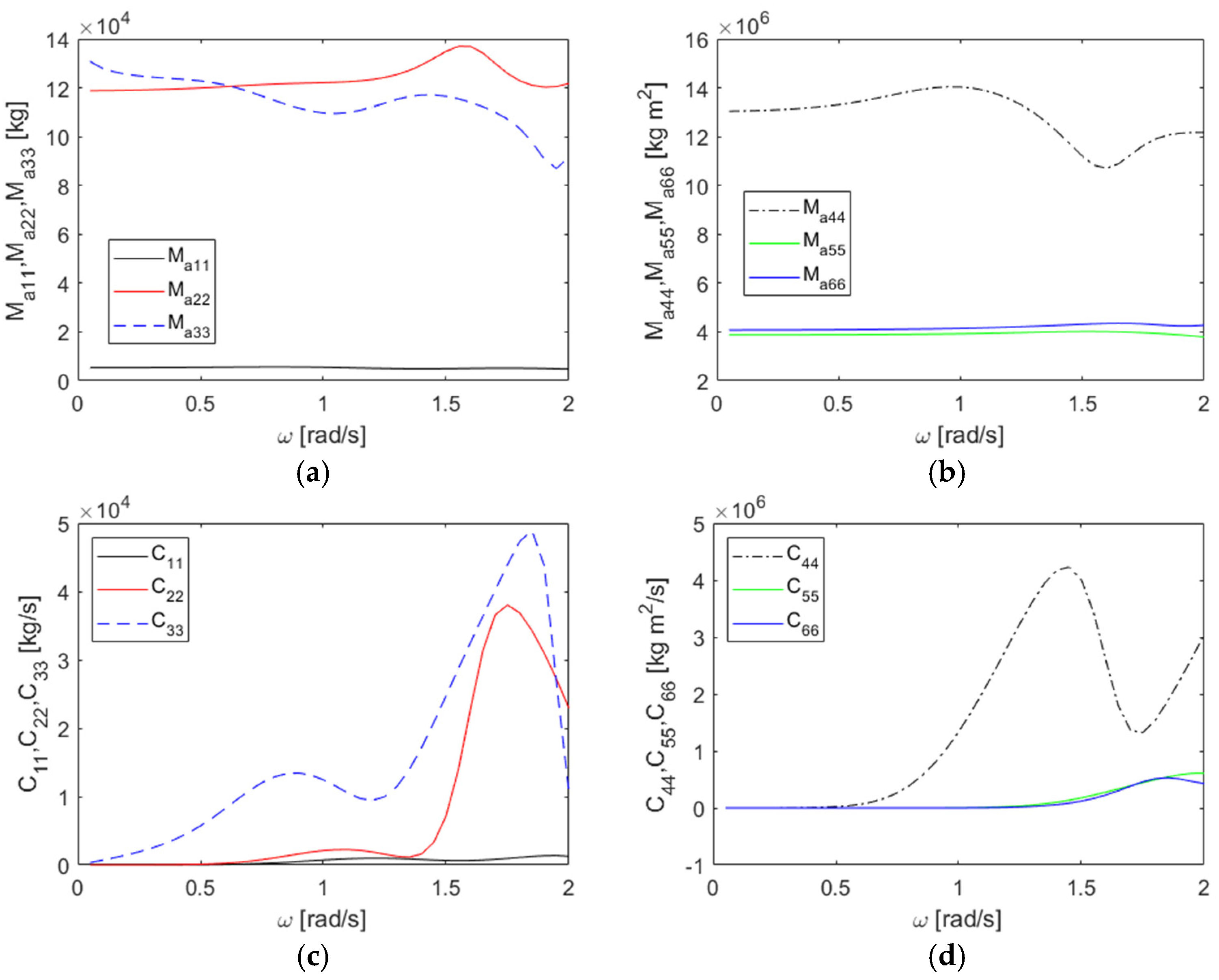

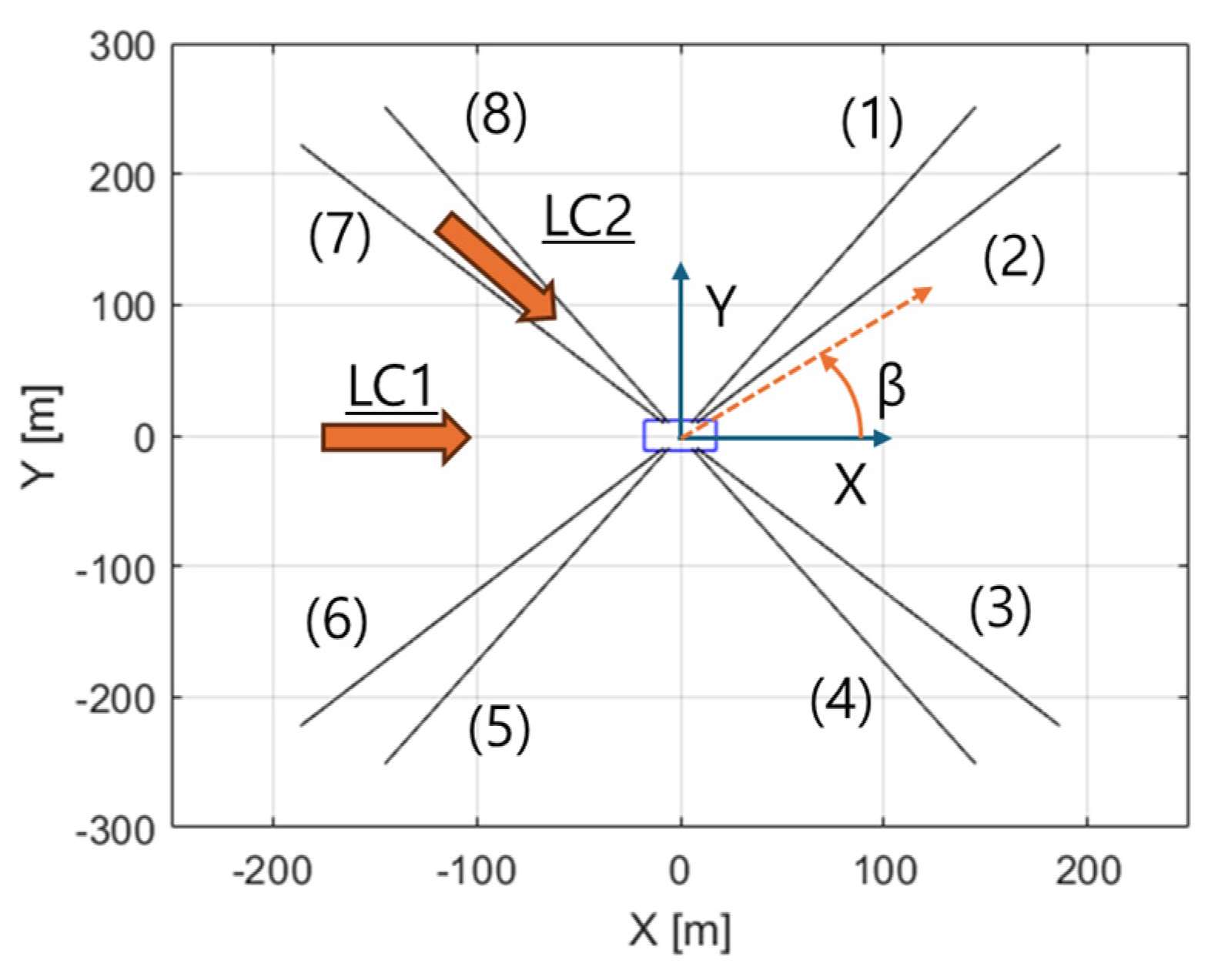
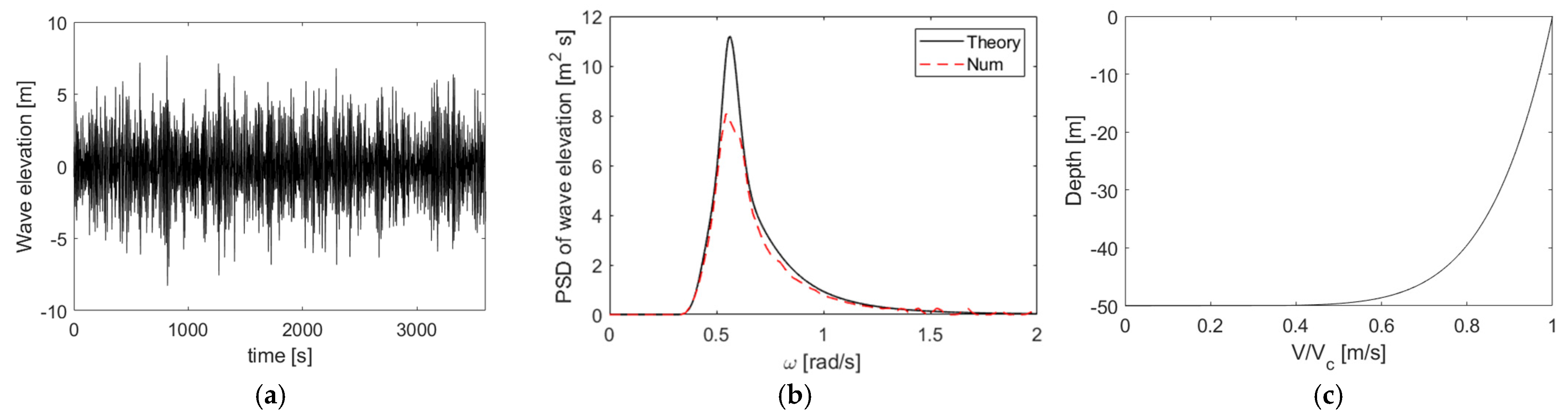

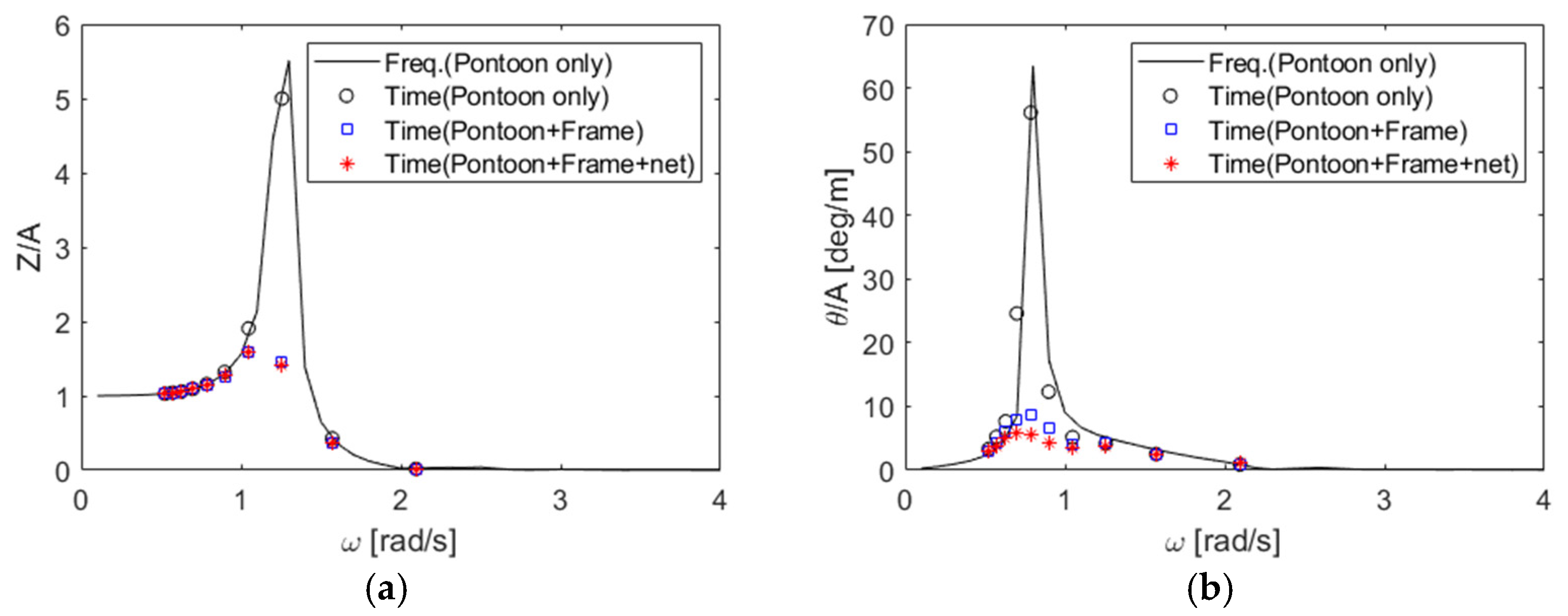






| Item | Unit | Dimension |
|---|---|---|
| Length (L) | m | 35.0 |
| Breadth (B) | m | 23.0 |
| Depth (D) | m | 14.0 |
| Draft (T) | m | 8.5 |
| Volume (V) | m3 | 5500 |
| Center of gravity above Base (KG) | m | 5.2 |
| Pontoon (Material: SS510) | ||
| Upper pontoon diameter (Dup) | m | 1.2 |
| Upper pontoon length (Lup) | m | 16.0 |
| Middle pontoon diameter (Dmd) | m | 0.8 |
| Middle pontoon length (Lmd) | m | 16.0 |
| Lower pontoon diameter (Dlw) | m | 1.4 |
| Lower pontoon length (Llw) | m | 23 |
| Steel frame (Material: STPG) | ||
| Outer diameter | mm | 216.3 |
| Wall thickness | mm | 8.2 |
| Item | Unit | Dimension |
|---|---|---|
| Total mass (M) | ton | 114.03 |
| Roll radius of gyration at CG (Rxx) | m | 4.92 |
| Pitch radius of gyration at CG (Ryy) | m | 5.00 |
| Yaw radius of gyration at CG (Rzz) | m | 5.68 |
| Heave restoring coefficient (K33) | kN/m | 364.1 |
| Roll restoring coefficient (K44) | kN m/rad | 4199.7 |
| Pitch restoring coefficient (K55) | kN m/rad | 40,529.2 |
| # of Nodes | RMSE (Heave–Heave Added Mass) | RMSE (Pitch–Pitch Added Moment of Inertia) | RMSE (Heave–Heave Radiation Damping) | RMSE (Pitch–Pitch Radiation Damping) |
|---|---|---|---|---|
| 5184 | 12.08 | 595.7 | 10.95 | 172.4 |
| 7800 | 7.44 | 413.7 | 6.59 | 90.5 |
| 12,664 | 0.46 | 72.0 | 1.02 | 12.2 |
| Chain Diameter [mm] | Wet Weight [N/m] | Axial Stiffness [MN] | Minimum Breaking Load (MBL) [kN] |
|---|---|---|---|
| 32 | 192 | 92.16 | 895 |
| 36 | 243 | 116.64 | 1125 |
| Condition | Solidity Ratio | an | bn | Drag Coefficient (Re = 2000) | Drag Coefficient (Re = 4000) |
|---|---|---|---|---|---|
| No biofouling | 0.22 | −1.12 × 10−5 | 0.20 | 0.1776 | 0.1552 |
| With biofouling | 0.31 | −1.75 × 10−5 | 0.27 | 0.2350 | 0.2000 |
| Significant Wave Height [m] | Peak Period [s] | Enhancement Factor | Surface Current Speed [m/s] |
|---|---|---|---|
| 6.55 | 11.19 | 2.06 | 0.71 |
| Item | Chain Diameter = 32 mm | Chain Diameter = 36 mm | ||
|---|---|---|---|---|
| Mean | STD | Mean | STD | |
| Surge | 1.095 | 0.923 | 0.980 | 0.922 |
| Sway | −3.537 | 1.091 | −2.954 | 1.061 |
| Heave | −0.045 | 1.349 | −0.041 | 1.332 |
| Roll | 0.015 | 0.063 | 0.015 | 0.062 |
| Pitch | 0.016 | 0.035 | 0.016 | 0.036 |
| Yaw | −0.004 | 0.025 | −0.003 | 0.024 |
| Chain Diameter [mm] | Line Length [m] | Max. Excursion [m] | STD of Heave [m] | STD of Pitch [deg] |
|---|---|---|---|---|
| 32 | 285 | 4.340 | 1.467 | 4.279 |
| 290 | 8.863 | 1.534 | 3.733 | |
| 295 | 15.192 | 1.554 | 3.623 | |
| 300 | 22.305 | 1.563 | 3.633 | |
| 36 | 285 | 3.835 | 1.429 | 4.122 |
| 290 | 8.030 | 1.513 | 3.819 | |
| 295 | 13.754 | 1.539 | 3.639 | |
| 300 | 20.606 | 1.551 | 3.638 |
| Chain Diameter [mm] | Length [m] | Max. Excursion [m] | Line Tension (#7) [kN] | Line Tension (#8) [kN] | ||||
|---|---|---|---|---|---|---|---|---|
| Static | Max | STD | Static | Max | STD | |||
| 32 | 285 | 3.651 | 87.17 | 349.60 | 37.07 | 128.75 | 835.03 | 94.90 |
| 290 | 8.371 | 87.17 | 244.27 | 22.83 | 128.75 | 654.70 | 46.95 | |
| 295 | 13.432 | 87.17 | 188.26 | 17.87 | 128.75 | 550.12 | 39.15 | |
| 300 | 18.755 | 87.17 | 165.37 | 15.71 | 128.75 | 542.36 | 39.04 | |
| 36 | 285 | 3.317 | 107.89 | 357.49 | 39.39 | 158.30 | 908.96 | 95.36 |
| 290 | 7.834 | 107.89 | 250.95 | 24.33 | 158.30 | 623.83 | 45.18 | |
| 295 | 12.685 | 107.89 | 200.18 | 18.15 | 158.30 | 484.93 | 35.10 | |
| 300 | 17.925 | 107.89 | 173.03 | 15.87 | 158.30 | 451.37 | 34.18 | |
| Current Speed [m/s] | Max. Excursion [m] | Line Tension (#7) [kN] | Line Tension (#8) [kN] | ||||
|---|---|---|---|---|---|---|---|
| Static | Max | STD | Static | Max | STD | ||
| 0.0 | 4.275 | 42.01 | 205.08 | 19.97 | 57.32 | 237.20 | 28.84 |
| 0.355 | 5.547 | 42.02 | 210.08 | 25.14 | 74.37 | 331.76 | 39.64 |
| 0.71 | 6.720 | 42.03 | 284.18 | 33.44 | 104.34 | 483.68 | 57.91 |
| 1.065 | 7.693 | 42.03 | 374.84 | 46.30 | 150.06 | 699.74 | 86.38 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, S.-J.; Jeong, S.-J.; Park, S.-J. Hydrodynamic Performance and Mooring Safety Assessment of an Offshore Floating Movable Fish Cage. J. Mar. Sci. Eng. 2024, 12, 2351. https://doi.org/10.3390/jmse12122351
Kim S-J, Jeong S-J, Park S-J. Hydrodynamic Performance and Mooring Safety Assessment of an Offshore Floating Movable Fish Cage. Journal of Marine Science and Engineering. 2024; 12(12):2351. https://doi.org/10.3390/jmse12122351
Chicago/Turabian StyleKim, Sung-Jae, Seong-Jae Jeong, and Sung-Ju Park. 2024. "Hydrodynamic Performance and Mooring Safety Assessment of an Offshore Floating Movable Fish Cage" Journal of Marine Science and Engineering 12, no. 12: 2351. https://doi.org/10.3390/jmse12122351
APA StyleKim, S.-J., Jeong, S.-J., & Park, S.-J. (2024). Hydrodynamic Performance and Mooring Safety Assessment of an Offshore Floating Movable Fish Cage. Journal of Marine Science and Engineering, 12(12), 2351. https://doi.org/10.3390/jmse12122351






