Optimization-Based Energy Management Algorithm for 2-Stroke Hybrid Ship with Controllable Pitch Propeller
Abstract
:1. Introduction
2. Methodology
2.1. Examined Topologies
2.2. Gensets Operation Rule for the Conventional Configuration
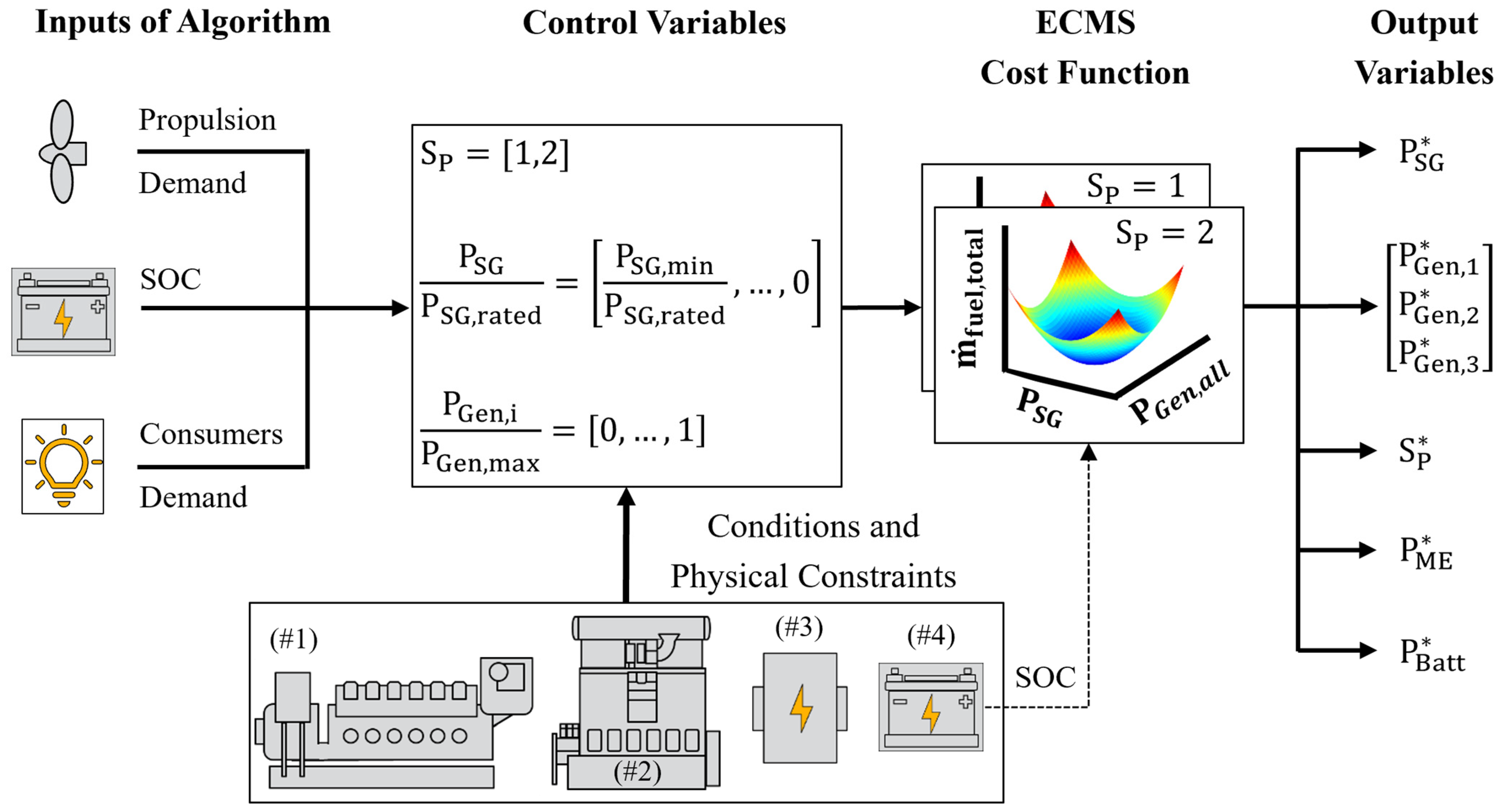
2.3. ECMS Implementation for the Hybrid Configuration
2.4. Examined Operation Phases
2.5. FOC Corrections
3. Results
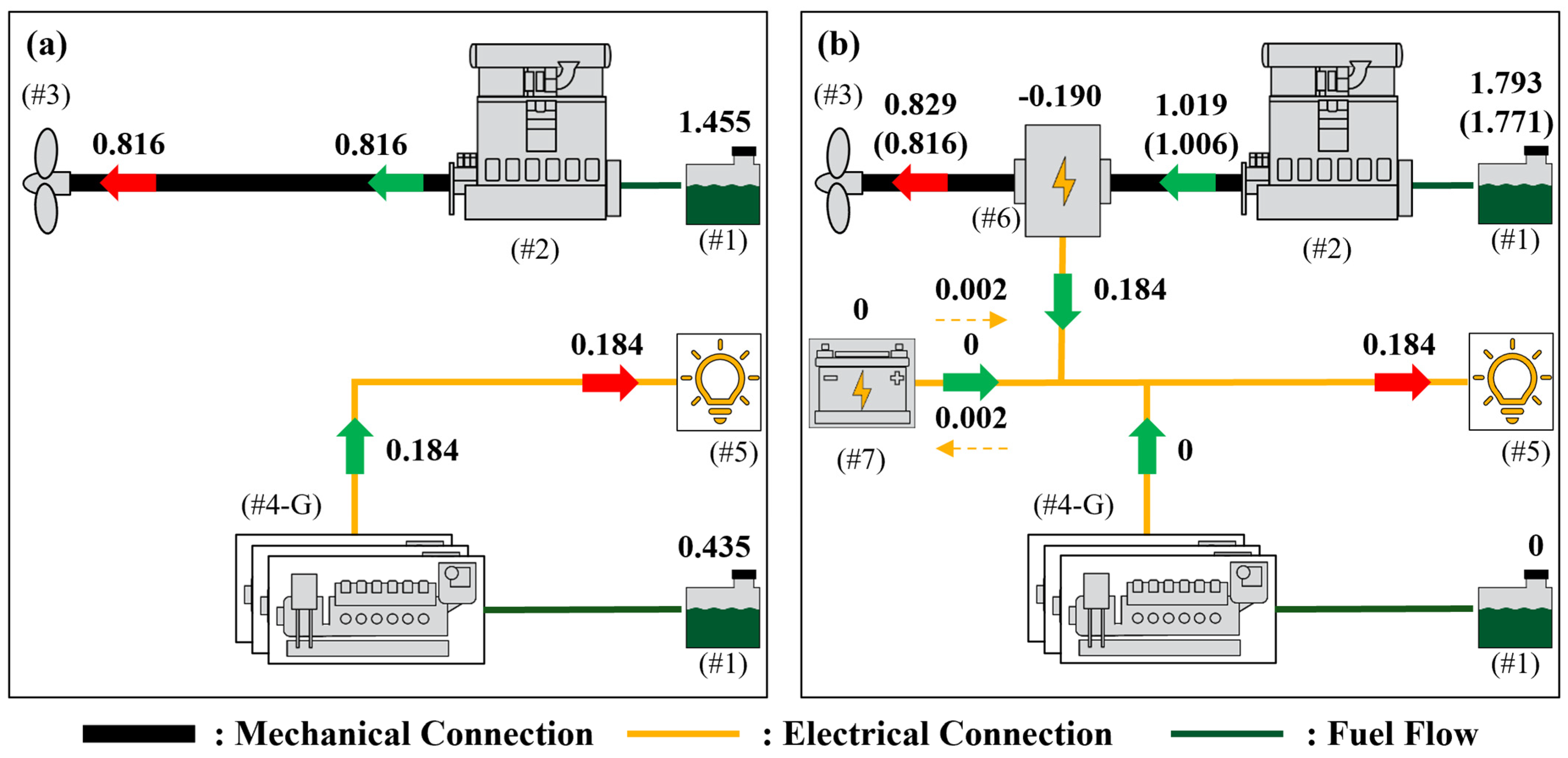
3.1. Port Stay Phase
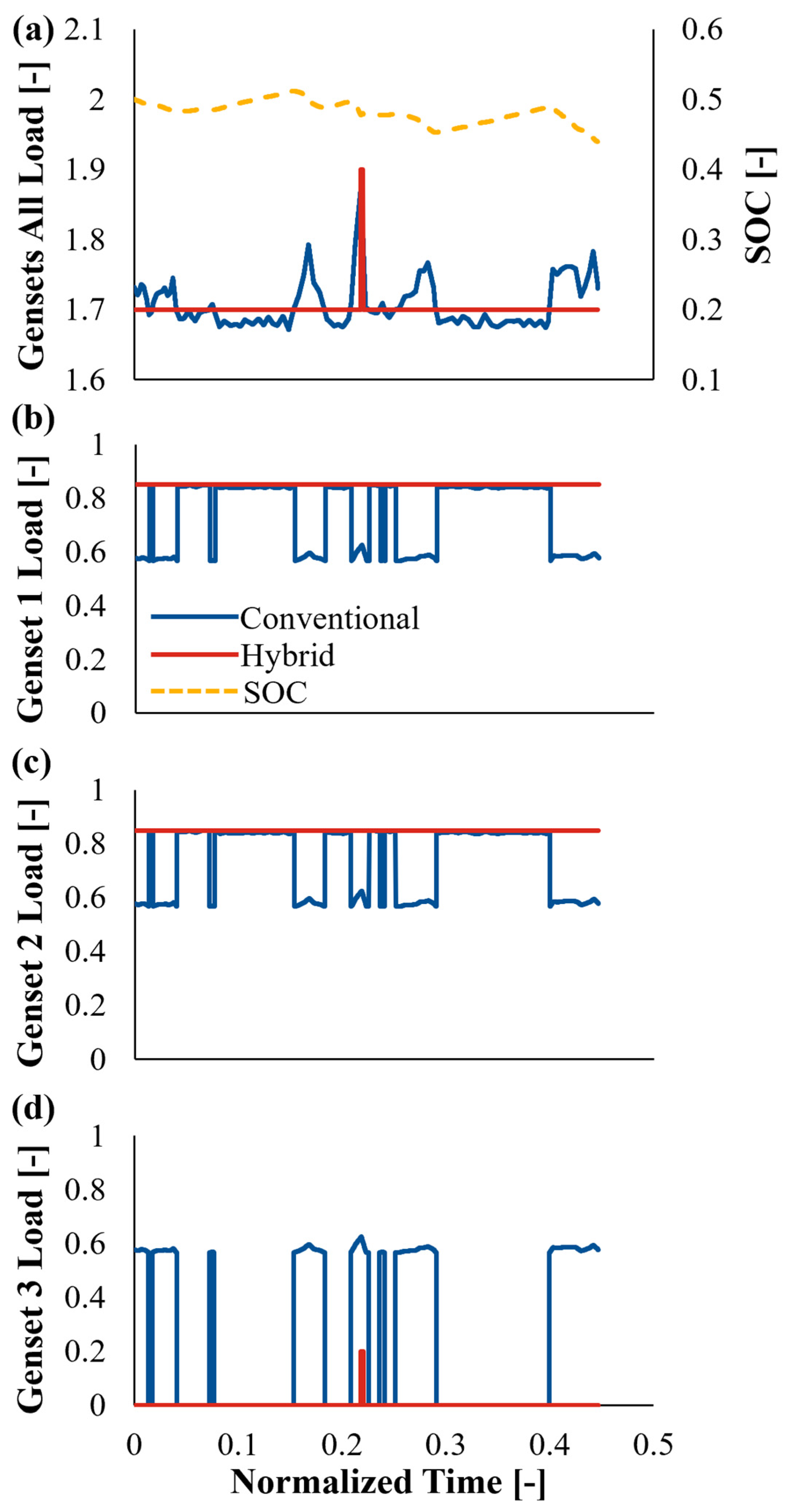
3.2. Open Sea Sailing Phase
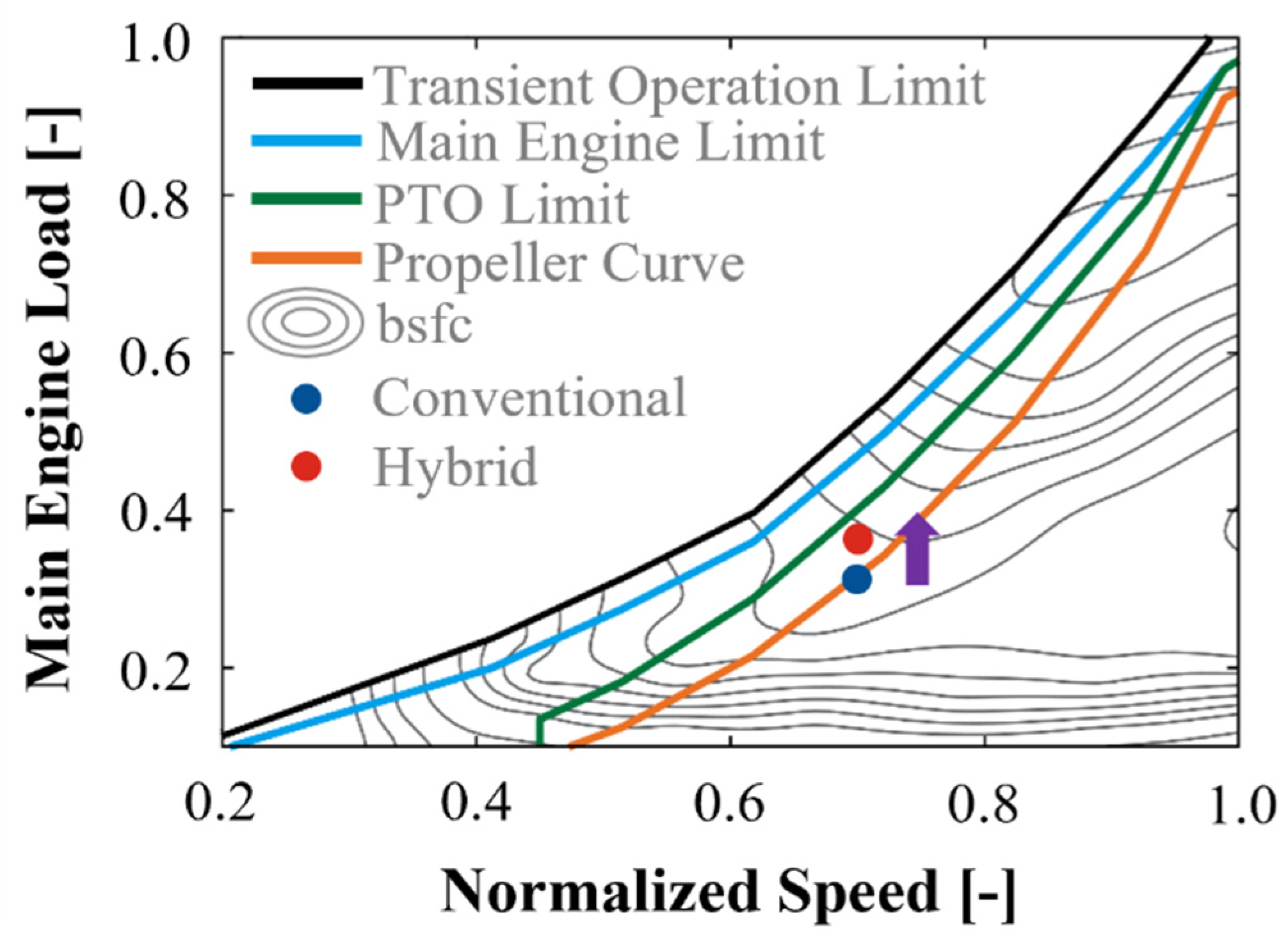
3.3. Port Entering and Leaving Modes
3.4. Parametric Analysis of Battery and SG Sizes on FOCR
4. Discussion
5. Conclusions
- The hybridization of the engine room leads to benefits of up to 6% compared to a conventional configuration, depending on operating conditions.
- The benefits are maximized during open sea sailing, where PTO is enabled more frequently, leading to more efficient electricity generation by the SG compared to gensets in the conventional configuration.
- Integrating CPP usage into the ECMS algorithm can increase FC benefits by up to 2.0 percentage points compared to an FPP hybrid configuration, particularly during port approach and maneuvering operations. The reason is that a CPP allows PTO mode to be enabled more frequently than an FPP.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| BSFOC | brake-specific fuel oil consumption |
| CII | carbon intensity indicator |
| CO2 | carbon dioxide |
| CPP | controllable pitch propeller |
| DP | dynamic programming |
| ECMS | equivalent minimization consumption strategy |
| EEDI | energy efficiency design index |
| EEXI | energy efficiency existing ship index |
| EMS | energy management system |
| FOC | fuel oil consumption |
| FOCR | FOC reduction |
| FPP | fixed pitch propeller |
| IMO | international maritime organization |
| ME | main engine |
| MPC | model predictive control |
| SG | shaft generator |
| Sp | propeller position |
| tPTO | PTO mode activation time share |
| average ME efficiency | |
| average gensets efficiency | |
| average SG efficiency |
Appendix A
| Parameter | Value |
|---|---|
| 3.6 | |
| 1.1 | |
| a | 1 |
| 0.5 | |
| 0.8 | |
| 0.2 |
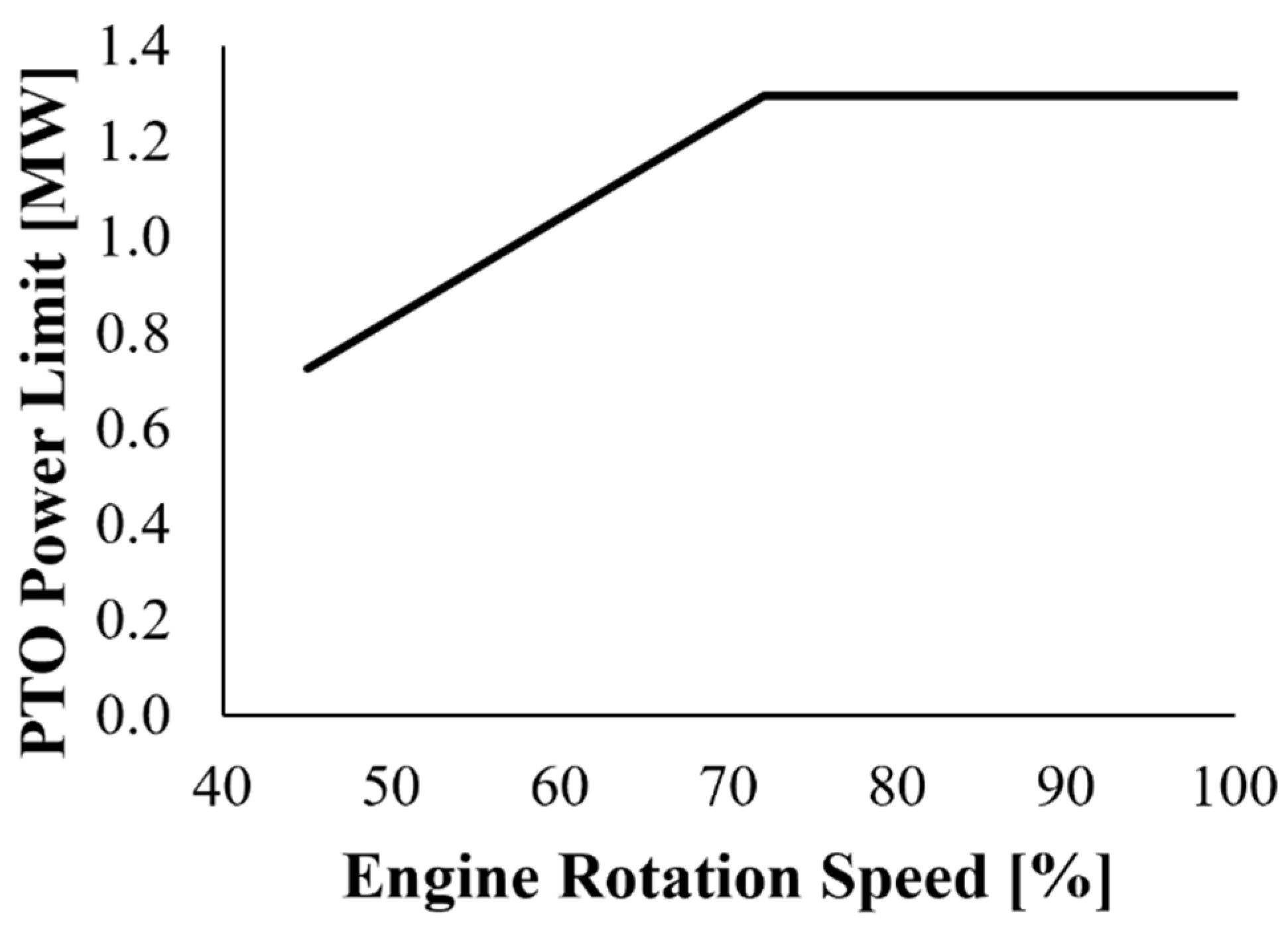
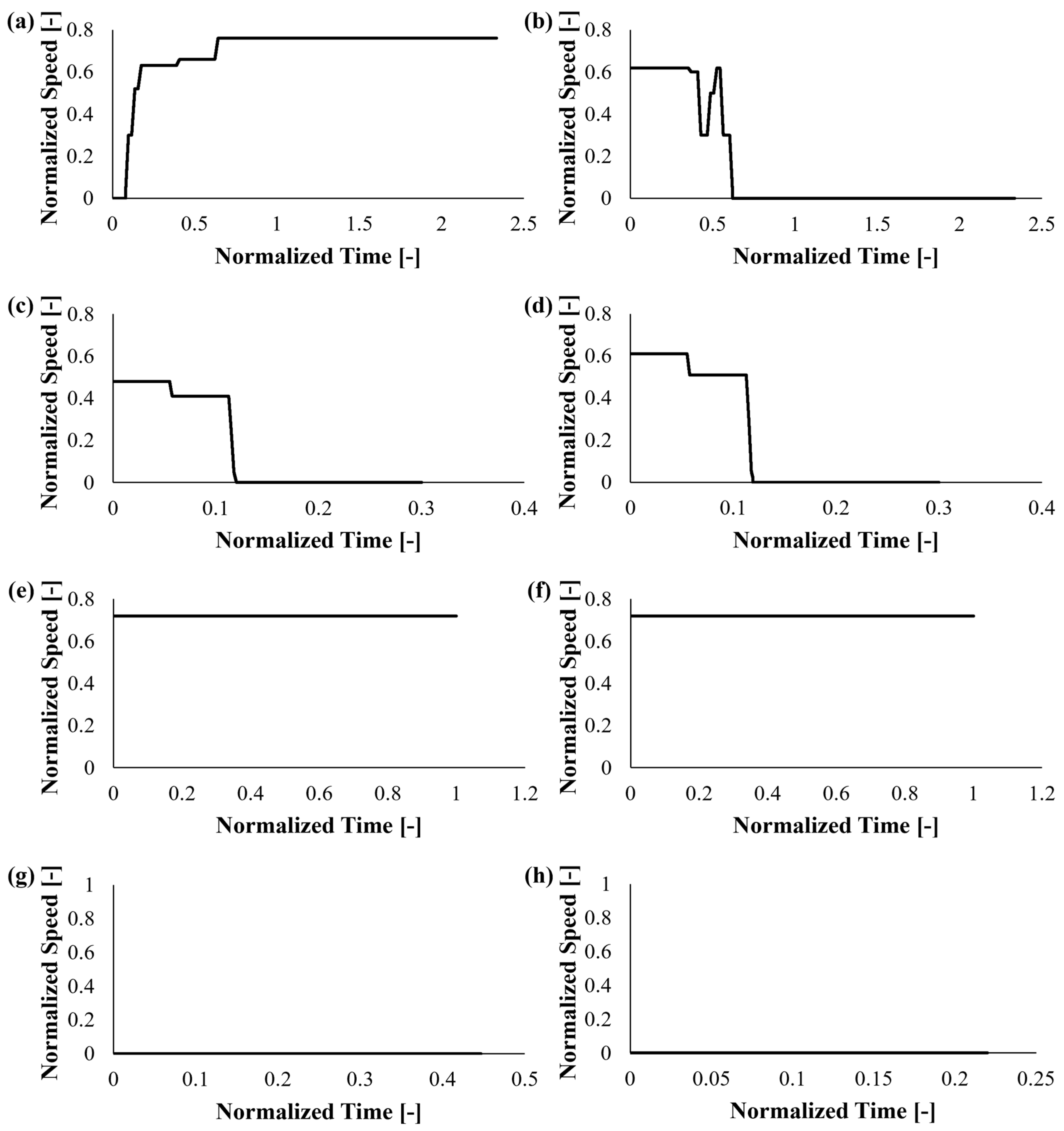
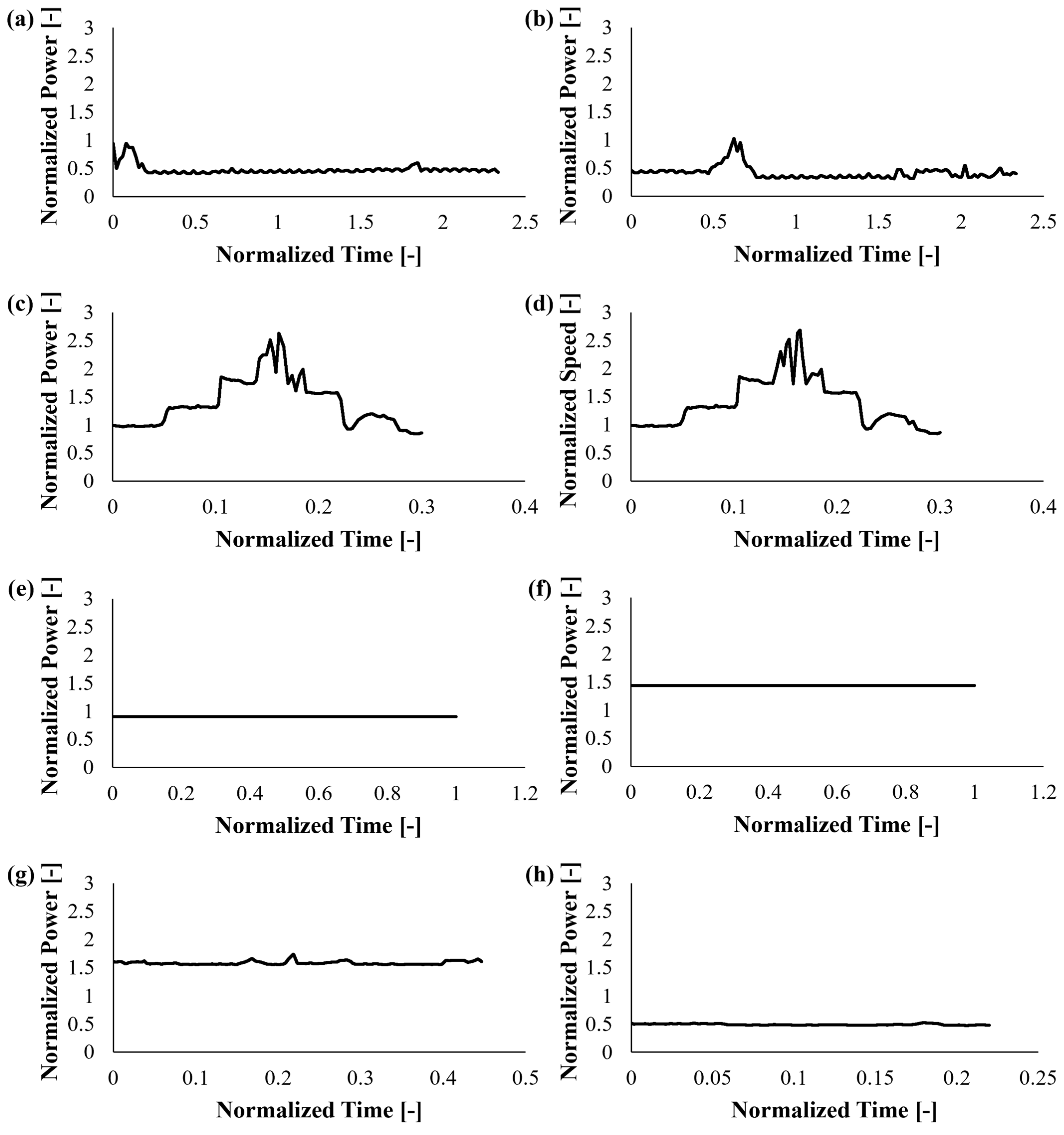

| Point | Operation Phase | |||||||
|---|---|---|---|---|---|---|---|---|
| Port Stay Cargo On | Port Stay Cargo Off | Open Sea Sailing Ventilation On | Open Sea Sailing Ventilation Off | 6 kn Approach | 12 kn Approach | From Port Maneuvering to Sailing | From Sailing to Port Maneuvering | |
| A | 0.000 | 0.000 | 1.313 | 1.455 | 0.490 | 0.694 | 1.586 | 1.071 |
| B | 0.000 | 0.000 | 0.736 | 0.816 | 0.210 | 0.347 | 0.895 | 0.558 |
| C | 0.000 | 0.000 | 0.736 | 0.816 | 0.210 | 0.347 | 0.895 | 0.558 |
| D | 2.222 | 2.332 | 0.574 | 0.435 | 1.780 | 1.472 | 0.248 | 1.086 |
| E | 0.955 | 2.332 | 0.287 | 0.2175 | 0.767 | 0.634 | 0.241 | 1.047 |
| F | 0.955 | 0.000 | 0.287 | 0.2175 | 0.767 | 0.634 | 0.007 | 0.039 |
| G | 0.311 | 0.000 | 0.000 | 0.000 | 0.246 | 0.204 | 0.000 | 0.000 |
| H | 0.434 | 1.000 | 0.132 | 0.092 | 0.340 | 0.281 | 0.102 | 0.424 |
| I | 0.434 | 0.000 | 0.132 | 0.092 | 0.340 | 0.281 | 0.003 | 0.018 |
| J | 0.132 | 0.000 | 0.000 | 0.000 | 0.110 | 0.091 | 0.000 | 0.000 |
| K | 1.000 | 1.000 | 0.264 | 0.184 | 0.790 | 0.653 | 0.105 | 0.442 |
| L | 1.000 | 1.000 | 0.264 | 0.184 | 0.790 | 0.653 | 0.105 | 0.442 |
| M | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| N | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| O | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| P | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| Q | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| R | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| Point | Operation Phase | |||||||
|---|---|---|---|---|---|---|---|---|
| Port Stay Cargo On | Port Stay Cargo Off | Open Sea Sailing Ventilation On | Open Sea Sailing Ventilation Off | 6 kn Approach | 12 kn Approach | From Port Maneuvering to Sailing | From Sailing to Port Maneuvering | |
| A | 0.000 | 0.000 | 1.529 | 1.771 | 0.538 | 0.877 | 1.747 | 1.236 |
| B | 0.000 | 0.000 | 0.865 | 1.006 | 0.236 | 0.463 | 0.994 | 0.666 |
| C | 0.000 | 0.000 | 0.736 | 0.816 | 0.210 | 0.347 | 0.895 | 0.558 |
| D | 2.152 | 2.313 | 0.298 | 0.000 | 1.688 | 1.201 | 0.019 | 0.859 |
| E | 1.076 | 2.313 | 0.298 | 0.000 | 0.967 | 0.711 | 0.019 | 0.855 |
| F | 1.076 | 0.000 | 0.000 | 0.000 | 0.588 | 0.387 | 0.000 | 0.004 |
| G | 0.000 | 0.000 | 0.000 | 0.000 | 0.133 | 0.103 | 0.000 | 0.000 |
| H | 0.500 | 1.000 | 0.139 | 0.000 | 0.439 | 0.321 | 0.009 | 0.336 |
| I | 0.500 | 0.000 | 0.000 | 0.000 | 0.267 | 0.174 | 0.000 | 0.002 |
| J | 0.000 | 0.000 | 0.000 | 0.000 | 0.060 | 0.047 | 0.000 | 0.000 |
| K | 1.000 | 1.000 | 0.139 | 0.000 | 0.766 | 0.542 | 0.009 | 0.338 |
| L | 1.000 | 1.000 | 0.264 | 0.184 | 0.790 | 0.653 | 0.105 | 0.442 |
| M | 0.000 | 0.000 | −0.129 | −0.190 | −0.026 | −0.116 | −0.099 | −0.108 |
| N | 0.000 | 0.000 | 0.125 | 0.184 | 0.024 | 0.111 | 0.096 | 0.104 |
| O | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| P | 0.009 | 0.110 | 0.013 | 0.002 | 0.016 | 0.012 | 0.002 | 0.021 |
| Q | 0.009 | 0.110 | 0.013 | 0.002 | 0.016 | 0.012 | 0.002 | 0.021 |
| R | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| Point | Operation Phase | |||||||
|---|---|---|---|---|---|---|---|---|
| Port Stay Cargo On | Port Stay Cargo Off | Open Sea Sailing Ventilation On | Open Sea Sailing Ventilation Off | 6 kn Approach | 12 kn Approach | From Port Maneuvering to Sailing | From Sailing to Port Maneuvering | |
| A | 0.000 | 0.000 | 1.549 | 1.793 | 0.757 | 0.887 | 1.771 | 1.318 |
| B | 0.000 | 0.000 | 0.877 | 1.019 | 0.355 | 0.467 | 1.008 | 0.711 |
| C | 0.000 | 0.000 | 0.748 | 0.829 | 0.212 | 0.351 | 0.909 | 0.571 |
| D | 2.152 | 2.313 | 0.298 | 0.000 | 1.424 | 1.201 | 0.019 | 0.762 |
| E | 1.076 | 2.313 | 0.298 | 0.000 | 0.890 | 0.711 | 0.019 | 0.760 |
| F | 1.076 | 0.000 | 0.000 | 0.000 | 0.430 | 0.387 | 0.000 | 0.002 |
| G | 0.000 | 0.000 | 0.000 | 0.000 | 0.104 | 0.103 | 0.000 | 0.000 |
| H | 0.500 | 1.000 | 0.139 | 0.000 | 0.408 | 0.321 | 0.009 | 0.306 |
| I | 0.500 | 0.000 | 0.000 | 0.000 | 0.197 | 0.174 | 0.000 | 0.001 |
| J | 0.000 | 0.000 | 0.000 | 0.000 | 0.048 | 0.047 | 0.000 | 0.000 |
| K | 1.000 | 1.000 | 0.139 | 0.000 | 0.653 | 0.542 | 0.009 | 0.307 |
| L | 1.000 | 1.000 | 0.264 | 0.184 | 0.790 | 0.653 | 0.105 | 0.442 |
| M | 0.000 | 0.000 | −0.129 | −0.190 | −0.143 | −0.116 | −0.099 | −0.140 |
| N | 0.000 | 0.000 | 0.125 | 0.184 | 0.137 | 0.111 | 0.096 | 0.135 |
| O | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| P | 0.009 | 0.110 | 0.013 | 0.002 | 0.023 | 0.012 | 0.002 | 0.030 |
| Q | 0.009 | 0.110 | 0.013 | 0.002 | 0.023 | 0.012 | 0.002 | 0.030 |
| R | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| SG Sizing | ||||||||
|---|---|---|---|---|---|---|---|---|
| Port Stay Cargo On | Port Stay Cargo Off | Open Sea Sailing Ventilation On | Open Sea Sailing Ventilation Off | 6 kn Approach | 12 kn Approach | From Port Maneuvering to Sailing | From Sailing to Port Maneuvering | |
| 90% | 0.0 | 0.0 | 0.1 | −0.4 | 0.3 | 0.5 | 0 | 0.4 |
| 80% | 0.0 | 0.0 | 0.1 | 0.7 | 0.4 | 0.5 | 0 | 0.4 |
| 70% | 0.0 | 0.0 | 0.1 | 3.5 | 0.9 | 0.8 | 0 | 0.3 |
| 60% | 0.0 | 0.0 | 0.4 | 3.5 | 0.9 | 1.2 | 0 | 0.4 |
| 50% | 0.0 | 0.0 | 2.2 | 3.5 | 1.4 | 1.6 | 0.1 | 0.4 |
References
- Hansen, J.E.; Sato, M.; Simons, L.; Nazarenko, L.S.; Sangha, I.; Kharecha, P.; Zachos, J.C.; von Schuckmann, K.; Loeb, N.G.; Osman, M.B.; et al. Global warming in the pipeline. Oxf. Open Clim. Chang. 2023, 3, kgad008. [Google Scholar] [CrossRef]
- IEA. CO2 Emissions in 2022. Available online: https://www.iea.org/reports/co2-emissions-in-2022 (accessed on 9 December 2024).
- Cars, Planes, Trains: Where Do CO2 Emissions from Transport Come From? Available online: https://ourworldindata.org/co2-emissions-from-transport (accessed on 9 December 2024).
- IMO. 2023 IMO Strategy on Reduction of GHG Emissions from Ships. Available online: https://www.imo.org/en/OurWork/Environment/Pages/2023-IMO-Strategy-on-Reduction-of-GHG-Emissions-from-Ships.aspx (accessed on 9 December 2024).
- IMO. IMO’s Work to Cut GHG Emissions from Ships. Available online: https://www.imo.org/en/MediaCentre/HotTopics/Pages/Cutting-GHG-emissions.aspx (accessed on 9 December 2024).
- DNV. CII—Carbon Intensity Indicator. Available online: https://www.dnv.com/maritime/insights/topics/CII-carbon-intensity-indicator/answers-to-frequent-questions.html (accessed on 9 December 2024).
- IMO. Improving the Energy Efficiency of Ships. Available online: https://www.imo.org/en/OurWork/Environment/Pages/Improving%20the%20energy%20efficiency%20of%20ships.aspx (accessed on 9 December 2024).
- Inal, O.B.; Charpentier, J.-F.; Deniz, C. Hybrid Power and Propulsion Systems for Ships: Current Status and Future Challenges. Renew. Sustain. Energy Rev. 2022, 156, 111965. [Google Scholar] [CrossRef]
- Geertsma, R.D.; Negenborn, R.R.; Visser, K.; Hopman, J.J. Design and control of hybrid power and propulsion systems for smart ships: A review of developments. Appl. Energy 2017, 194, 30–54. [Google Scholar] [CrossRef]
- Fan, A.; Li, Y.; Liu, H.; Yang, L.; Tian, Z.; Li, Y.; Vladimir, N. Development trend and hotspot analysis of ship energy management. J. Clean. Prod. 2023, 389, 135899. [Google Scholar] [CrossRef]
- Roslan, S.B.; Konovessis, D.; Tay, Z.Y. Sustainable Hybrid Marine Power Systems for Power Management Optimisation: A Review. Energies 2022, 15, 9622. [Google Scholar] [CrossRef]
- Zhang, Y.; Xue, Q.; Gao, D.; Shi, W.; Yu, W. Two-level model predictive control energy management strategy for hybrid power ships with hybrid energy storage system. J. Energy Storage 2022, 52, 104763. [Google Scholar] [CrossRef]
- Planakis, N.; Papalambrou, G.; Kyrtatos, N. Ship energy management system development and experimental evaluation utilizing marine loading cycles based on machine learning techniques. Appl. Energy 2022, 307, 118085. [Google Scholar] [CrossRef]
- Antonopoulos, S.; Visser, K.; Kalikatzarakis, M.; Reppa, V. MPC Framework for the Energy Management of Hybrid Ships with an Energy Storage System. J. Mar. Sci. Eng. 2021, 9, 993. [Google Scholar] [CrossRef]
- Yuan, L.C.W.; Tjahjowidodo, T.; Lee, G.S.G.; Chan, R. Optimizing fuel savings and power system reliability for all-electric hybrid vessels using Model Predictive Control. In Proceedings of the 2017 IEEE International Conference on Advanced Intelligent Mechatronics (AIM), Munich, Germany, 3–7 July 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 1532–1537, ISBN 978-1-5090-5998-0. [Google Scholar] [CrossRef]
- Xie, P.; Guerrero, J.M.; Tan, S.; Bazmohammadi, N.; Vasquez, J.C.; Mehrzadi, M.; Al-Turki, Y. Optimization-Based Power and Energy Management System in Shipboard Microgrid: A Review. IEEE Syst. J. 2022, 16, 578–590. [Google Scholar] [CrossRef]
- Chua, L.W.Y.; Tjahjowidodo, T.; Seet, G.G.L.; Chan, R. Implementation of Optimization-Based Power Management for All-Electric Hybrid Vessels. IEEE Access 2018, 6, 74339–74354. [Google Scholar] [CrossRef]
- Yuan, L.C.W.; Tjahjowidodo, T.; Lee, G.S.G.; Chan, R.; Ådnanes, A.K. Equivalent consumption minimization strategy for hybrid all-electric tugboats to optimize fuel savings. In Proceedings of the 2016 American Control Conference (ACC), Boston, MA, USA, 6–8 July 2016; IEEE: Piscataway, NJ, USA, 2017; pp. 6803–6808, ISBN 978-1-4673-8682-1. [Google Scholar] [CrossRef]
- Zhu, J.; Chen, L.; Wang, X.; Yu, L. Bi-level optimal sizing and energy management of hybrid electric propulsion systems. Appl. Energy 2020, 260, 114134. [Google Scholar] [CrossRef]
- Kalikatzarakis, M.; Geertsma, R.D.; Boonen, E.J.; Visser, K.; Negenborn, R.R. Ship energy management for hybrid propulsion and power supply with shore charging. Control. Eng. Pr. 2018, 76, 133–154. [Google Scholar] [CrossRef]
- Chua, L.W.Y. A Strategy for Power Management of Electric Hybrid Marine Power Systems; Nanyang Technological University: Singapore, 2019. [Google Scholar] [CrossRef]
- Dedes, E.K.; Hudson, D.A.; Turnock, S.R. Investigation of Diesel Hybrid systems for fuel oil reduction in slow speed ocean going ships. Energy 2016, 114, 444–456. [Google Scholar] [CrossRef]
- Sui, C.; Stapersma, D.; Visser, K.; de Vos, P.; Ding, Y. Energy effectiveness of ocean-going cargo ship under various operating conditions. Ocean Eng. 2019, 190, 106473. [Google Scholar] [CrossRef]
- Nguyen, H.P.; Hoang, A.T.; Nizetic, S.; Nguyen, X.P.; Le, A.T.; Luong, C.N.; Chu, V.D.; Pham, V.V. The electric propulsion system as a green solution for management strategy of CO2 emission in ocean shipping: A comprehensive review. Int. Trans. Electr. Energy Syst. 2021, 31, e12580. [Google Scholar] [CrossRef]
- Bacciaglia, A.; Ceruti, A.; Liverani, A. Controllable pitch propeller optimization through meta-heuristic algorithm. Eng. Comput. 2021, 37, 2257–2271. [Google Scholar] [CrossRef]
- Wärtsilä. Controllable Pitch Propeller Systems. Available online: https://www.wartsila.com/marine/products/propulsors-and-gears/propellers/wartsila-controllable-pitch-propeller-systems (accessed on 9 December 2024).
- Jaurola, M.; Hedin, A.; Tikkanen, S.; Huhtala, K. TOpti: A flexible framework for optimising energy management for various ship machinery topologies. J. Mar. Sci. Technol. 2019, 24, 1183–1196. [Google Scholar] [CrossRef]
- Jaurola, M.; Hedin, A.; Tikkanen, S.; Huhtala, K. A TOpti simulation for finding fuel saving by optimising propulsion control and power management. J. Mar. Sci. Technol. 2020, 25, 411–425. [Google Scholar] [CrossRef]
- MathWorks. Simulink. Available online: https://www.mathworks.com/products/simulink.html (accessed on 9 December 2024).
- MathWorks. Powertrain Blockset. Available online: https://www.mathworks.com/products/powertrain.html (accessed on 9 December 2024).
- WinGD. X-EL–Energy Management. Available online: https://www.wingd.com/en/technology-innovation/hybrid-energy-systems/ (accessed on 9 December 2024).
- WinGD. X62DF-2.1. Available online: https://www.wingd.com/en/engines/engine-types/x-df-dual-fuel/x62df-2-1/ (accessed on 9 December 2024).
- Leclanché. Available online: https://www.leclanche.com/ (accessed on 9 December 2024).
- Altosole, M.; Borlenghi, M.; Capasso, M.; Figari, M. Computer-based design tool for a fuel efficient-low emissions marine propulsion plant. In Proceedings of the 2nd International Conference on Marine Research and Transportation, ICMRT’07, Ischia, Napels, Italy, 28–30 June 2007. [Google Scholar]
- HD Hyundai Heavy Industries. Hi-Touch Marine & Stationary ENgine. Available online: https://www.hyundai-engine.com/en/aboutus/Himsen (accessed on 9 December 2024).
- Aletras, N.; Doulgeris, S.; Samaras, Z.; Ntziachristos, L. Comparative Assessment of Supervisory Control Algorithms for a Plug-In Hybrid Electric Vehicle. Energies 2023, 16, 1497. [Google Scholar] [CrossRef]
- Aletras, N.; Broekaert, S.; Bitsanis, E.; Fontaras, G.; Samaras, Z.; Ntziachristos, L. Energy management algorithm based on average power demand prediction for plug-in hybrid electric trucks. Energy Convers. Manag. 2024, 299, 117785. [Google Scholar] [CrossRef]
- Onori, S.; Serrao, L.; Rizzoni, G. Hybrid Electric Vehicles; Springer: London, UK, 2016; ISBN 978-1-4471-6779-2. [Google Scholar] [CrossRef]
- Chan, R.R.; Chua, L.; Tjahjowidodo, T. Enabling technologies for sustainable all—Electric hybrid vessels (Invited paper). In Proceedings of the 2016 IEEE International Conference on Sustainable Energy Technologies (ICSET), Hanoi, Vietnam, 4–16 November 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 401–406, ISBN 978-1-5090-5200-4. [Google Scholar] [CrossRef]
- MAN. Basic Principles of Ship Propulsion. Available online: https://www.man-es.com/docs/default-source/document-sync-archive/basic-principles-of-ship-propulsion-eng.pdf?sfvrsn=48fc05b5_7 (accessed on 9 December 2024).
- Kim, S.; Jeon, H.; Park, C.; Kim, J. Lifecycle Environmental Benefits with a Hybrid Electric Propulsion System Using a Control Algorithm for Fishing Boats in Korea. J. Mar. Sci. Eng. 2022, 10, 1202. [Google Scholar] [CrossRef]
- Diniz, G.H.S.; dos Santos Miranda, V.; Carmo, B.S. Dynamic modelling, simulation, and control of hybrid power systems for escort tugs and shuttle tankers. J. Energy Storage 2023, 72, 108091. [Google Scholar] [CrossRef]
- Al-Falahi, M.D.; Nimma, K.S.; Jayasinghe, S.D.; Enshaei, H.; Guerrero, J.M. Power management optimization of hybrid power systems in electric ferries. Energy Convers. Manag. 2018, 172, 50–66. [Google Scholar] [CrossRef]
- Planakis, N.; Papalambrou, G.; Kyrtatos, N. Predictive power-split system of hybrid ship propulsion for energy management and emissions reduction. Control. Eng. Pr. 2021, 111, 104795. [Google Scholar] [CrossRef]
- Kim, H.; Kim, J. Research on Improving Energy Efficiency Through Optimal Load Control Between a Ship’s Shaft Generator and Diesel Generator. IEEE Access 2024, 12, 156745–156764. [Google Scholar] [CrossRef]
- Tian, W.; Lang, X.; Zhang, C.; Yan, S.; Li, B.; Zang, S. Optimization of Controllable-Pitch Propeller Operations for Yangtze River Sailing Ships. J. Mar. Sci. Eng. 2024, 12, 1579. [Google Scholar] [CrossRef]
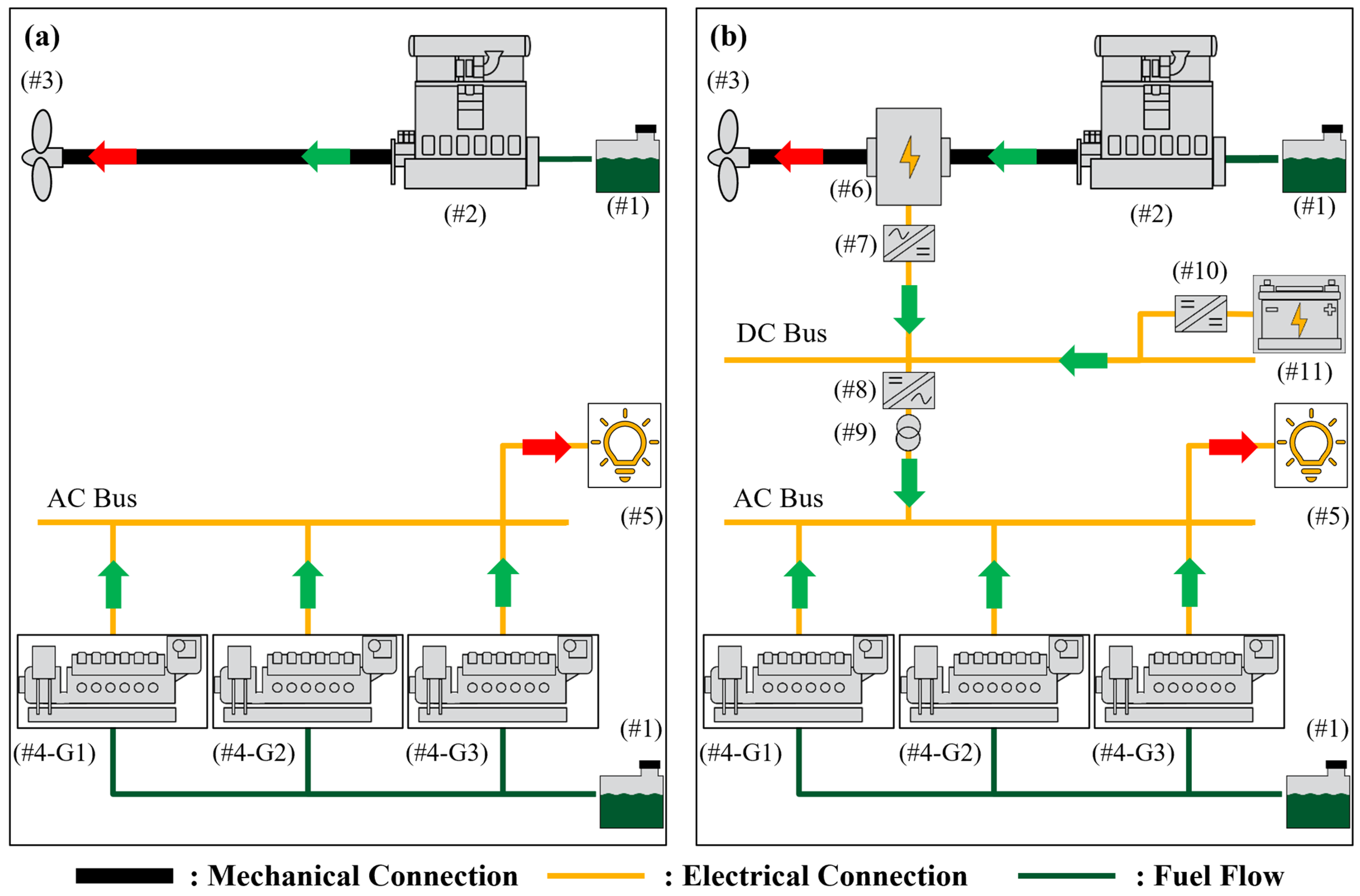



| Component | Engine Room Configuration | |
|---|---|---|
| Conventional | Hybrid | |
| Main engine (ME) | 14.78 MW | |
| Gensets | 3 × 1.22 MW | |
| Shaft generator (SG) | - | 1.30 MW |
| Battery | - | 565 kWh |
| Propeller type | Fixed pitch propeller (FPP) | FPP|CPP |
| Phase | Electrical Consumer Mode | Normalized Duration [-] | Average Normalized Speed [-] | Average Normalized Electrical Consumer Demand [-] |
|---|---|---|---|---|
| Port Stay | Cargo On | 0.45 | 0 | 1.58 |
| Cargo Off | 0.22 | 0 | 0.49 | |
| Open Sea Sailing | Ventilation On | 1 | 0.72 | 1.44 |
| Ventilation Off | 1 | 0.72 | 0.91 | |
| From Port Maneuvering to Sailing | Normal | 2.33 | 0.70 | 0.48 |
| From Sailing to Port Maneuvering | 2.33 | 0.14 | 0.42 | |
| 6 kn Port Approach | 0.3 | 0.17 | 1.39 | |
| 12 kn Port Approach | 0.3 | 0.22 | 1.39 |
| Phase | Configuration | Magnitude | |
|---|---|---|---|
| [%] | FOCR [%] | ||
| Port Stay Cargo On | Conventional | 45.0 | -- |
| Hybrid | 46.5 | 3.15 | |
| Port Stay Cargo Off | Conventional | 42.9 | -- |
| Hybrid | 43.2 | 0.81 | |
| Configuration | Operating Load [-] per Genset | |||
|---|---|---|---|---|
| ALL Gensets | Genset 1 | Genset 2 | Genset 3 | |
| Conventional | 0.90 | 0.45 | 0.45 | 0.00 |
| Hybrid | 0.00 | 0.00 | 0.00 | 0.00 |
| Ventilation | Configuration | Magnitude | ||||
|---|---|---|---|---|---|---|
| [%] | [%] | [%] | FOCR [%] | [%] | ||
| Off | Conventional | 56.1 | − | 42.3 | − | 56.1 |
| Hybrid | 56.8 | 96.8 | − | −5.13 (−6.30) | 56.8 | |
| On | Conventional | 56.1 | − | 46.0 | − | 56.1 |
| Hybrid | 56.6 | 96.9 | 46.6 | −2.23 (−3.18) | 56.6 | |
| Configuration | Magnitude | |||
|---|---|---|---|---|
| [%] | [%] | [%] | FOCR [%] | |
| Conventional | 42.9 | -- | 44.4 | -- |
| FPP Hybrid | 43.9 | 92.3 | 45.4 | −1.94 |
| CPP Hybrid | 46.9 | 95.8 | 45.9 | −3.92 |
| Phase | Magnitude | |||
|---|---|---|---|---|
| FOCR from Hybrid CPP over Conventional [%] | Extra FOCR Benefit from CPP Hybrid over FPP Hybrid [Percentage Units] | ) w/o CPP [%] | with CPP [%] | |
| From port maneuvering to sailing | 2.40 | 0.00 | 94.4 | 96.2 |
| From sailing to port maneuvering | 3.57 | 0.70 | 21.1 | 26.2 |
| 6 kn approach | 3.96 | 1.98 | 18.7 | 38.6 |
| 12 kn approach | 3.60 | 0.00 | 37.7 | 38.7 |
| Phase/Variation | |||
|---|---|---|---|
| +50% Battery Size | −50% Battery Size | −50% SG Size | |
| Port Stay Cargo On | 0.0 | 0.0 | 0.0 |
| Port Stay Cargo Off | −0.1 | 0.1 | 0.0 |
| Open Sea Sailing Ventilation On | 0.1 | −0.1 | 2.2 |
| Open Sea Sailing Ventilation Off | 0.3 | −0.2 | 3.5 |
| From Port Maneuvering to Sailing | 0.0 | 0.0 | 0.1 |
| From Sailing to Port Maneuvering | 0.3 | 0.0 | 0.4 |
| 6 kn Approach | −0.2 | 0.1 | 1.4 |
| 12 kn Approach | 0.0 | 0.0 | 1.6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aletras, N.; Karvountzis-Kontakiotis, A.; Kefalas, N.; Grigoriadis, A.; Samaras, Z.; Ntziachristos, L. Optimization-Based Energy Management Algorithm for 2-Stroke Hybrid Ship with Controllable Pitch Propeller. J. Mar. Sci. Eng. 2024, 12, 2331. https://doi.org/10.3390/jmse12122331
Aletras N, Karvountzis-Kontakiotis A, Kefalas N, Grigoriadis A, Samaras Z, Ntziachristos L. Optimization-Based Energy Management Algorithm for 2-Stroke Hybrid Ship with Controllable Pitch Propeller. Journal of Marine Science and Engineering. 2024; 12(12):2331. https://doi.org/10.3390/jmse12122331
Chicago/Turabian StyleAletras, Nikolaos, Apostolos Karvountzis-Kontakiotis, Nikolaos Kefalas, Achilleas Grigoriadis, Zissis Samaras, and Leonidas Ntziachristos. 2024. "Optimization-Based Energy Management Algorithm for 2-Stroke Hybrid Ship with Controllable Pitch Propeller" Journal of Marine Science and Engineering 12, no. 12: 2331. https://doi.org/10.3390/jmse12122331
APA StyleAletras, N., Karvountzis-Kontakiotis, A., Kefalas, N., Grigoriadis, A., Samaras, Z., & Ntziachristos, L. (2024). Optimization-Based Energy Management Algorithm for 2-Stroke Hybrid Ship with Controllable Pitch Propeller. Journal of Marine Science and Engineering, 12(12), 2331. https://doi.org/10.3390/jmse12122331







