A New Grid-Slat Fusion Device to Improve the Take-Off and Landing Performance of Amphibious Seaplanes
Abstract
1. Introduction
2. Design Considerations and Methods
2.1. Design Requirements for Lift Devices for Amphibious Seaplanes
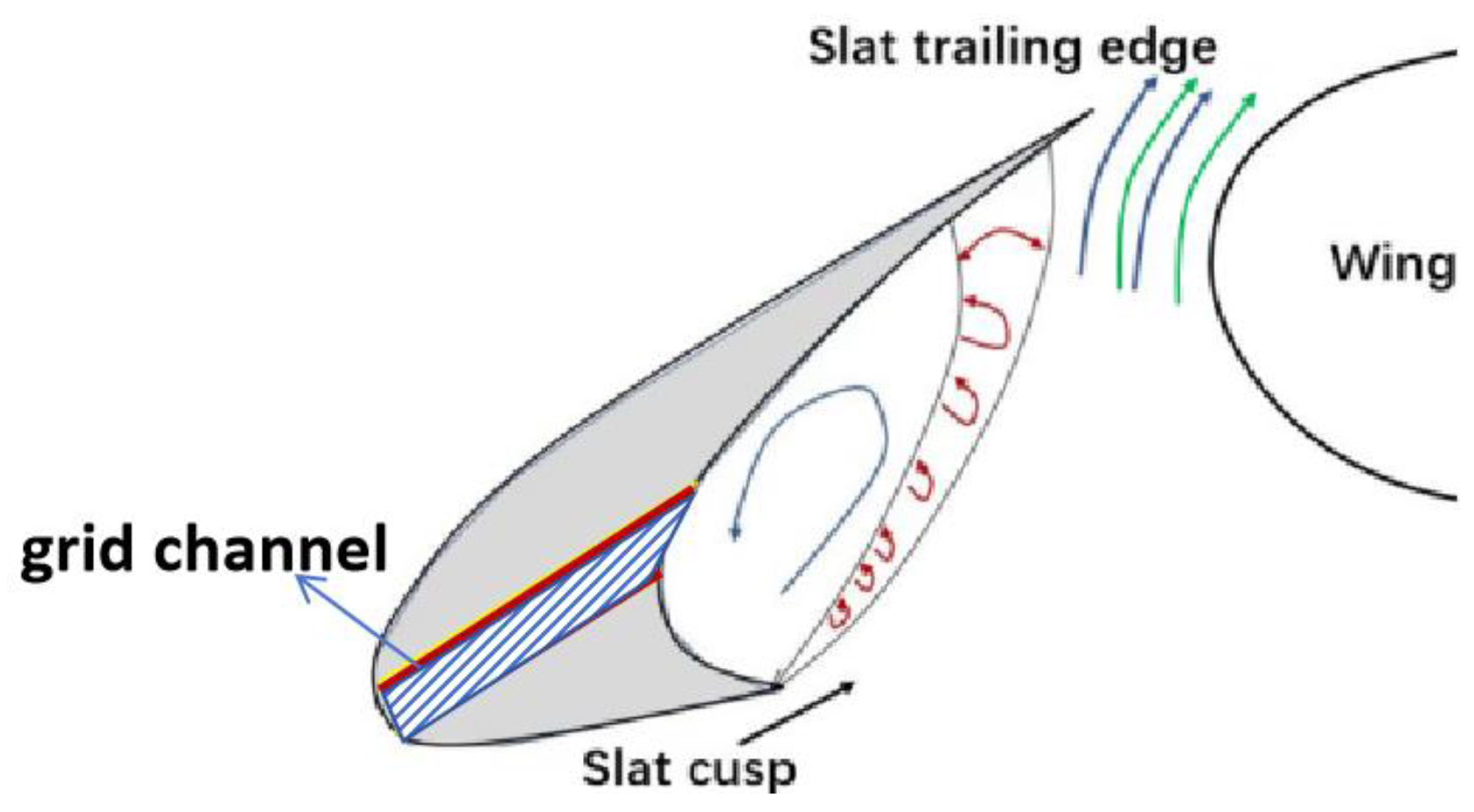
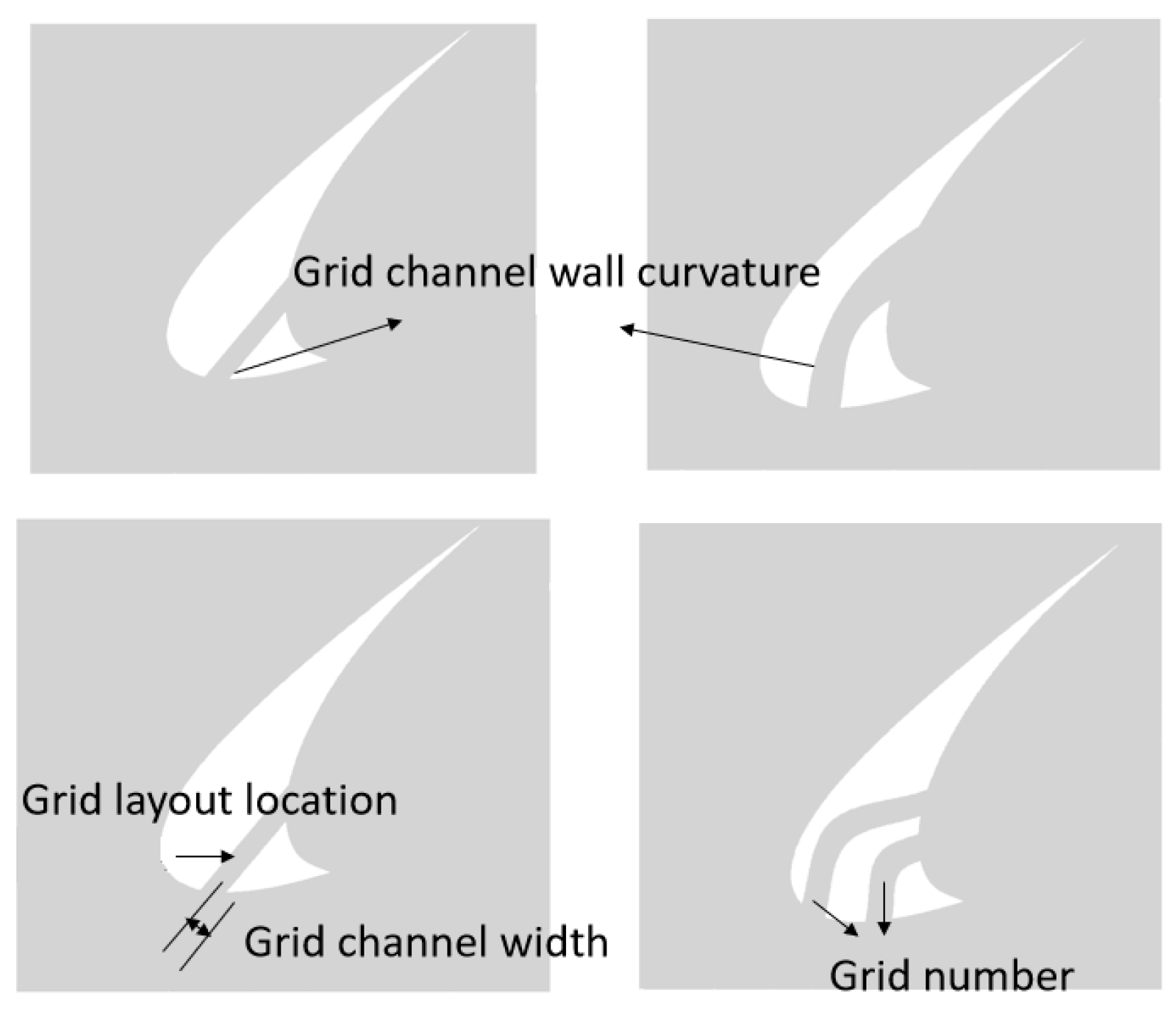
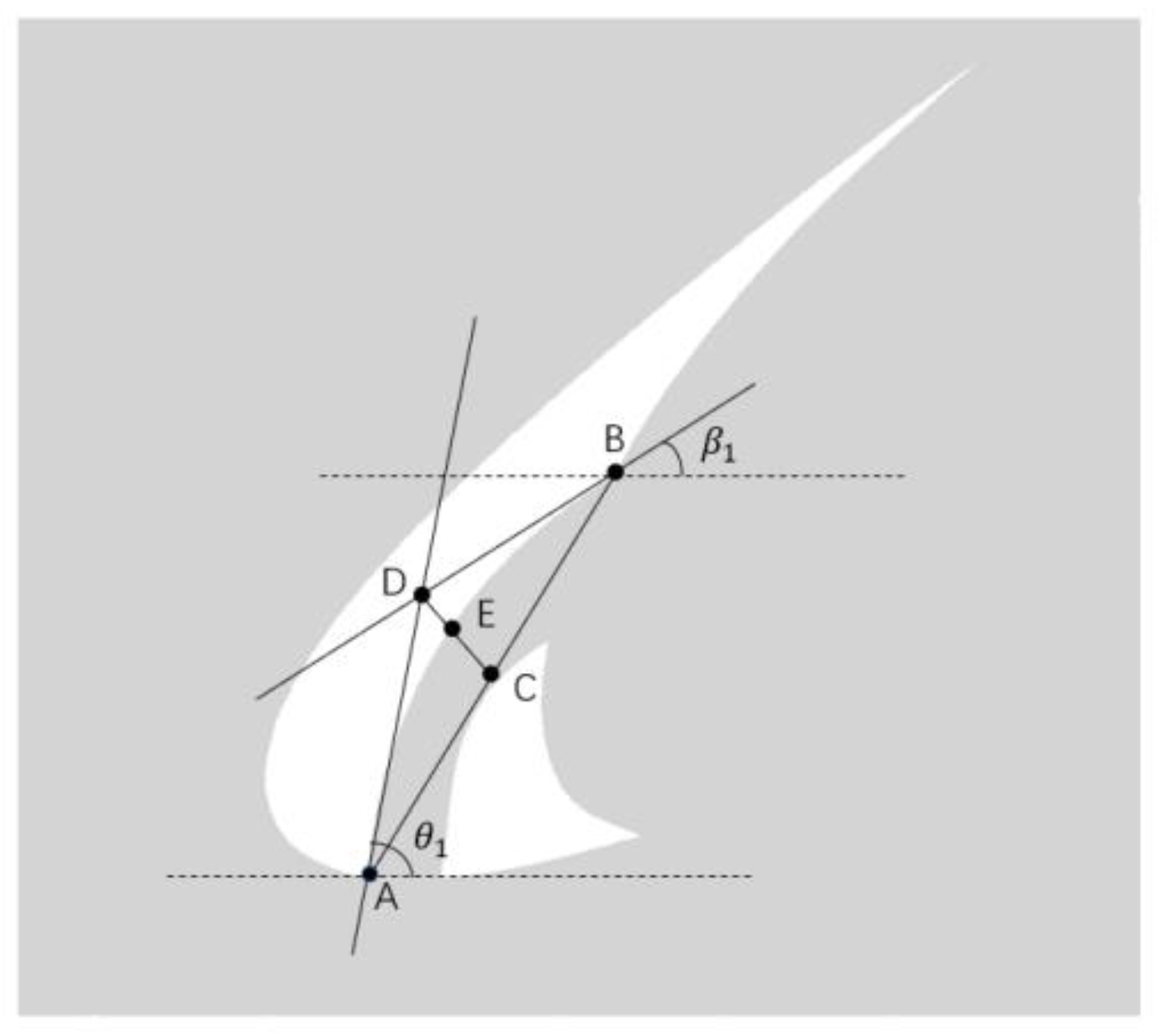
2.2. Design and Parametrization of a Grid-Slat Fusion Device
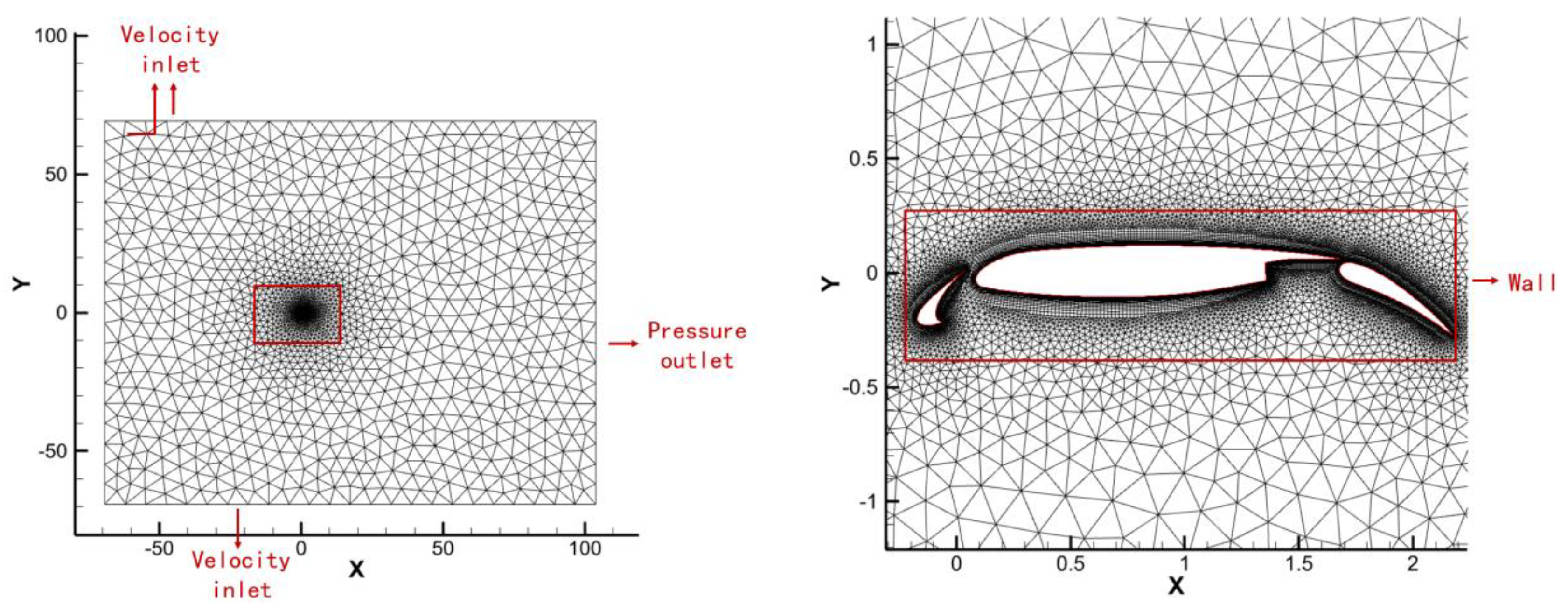
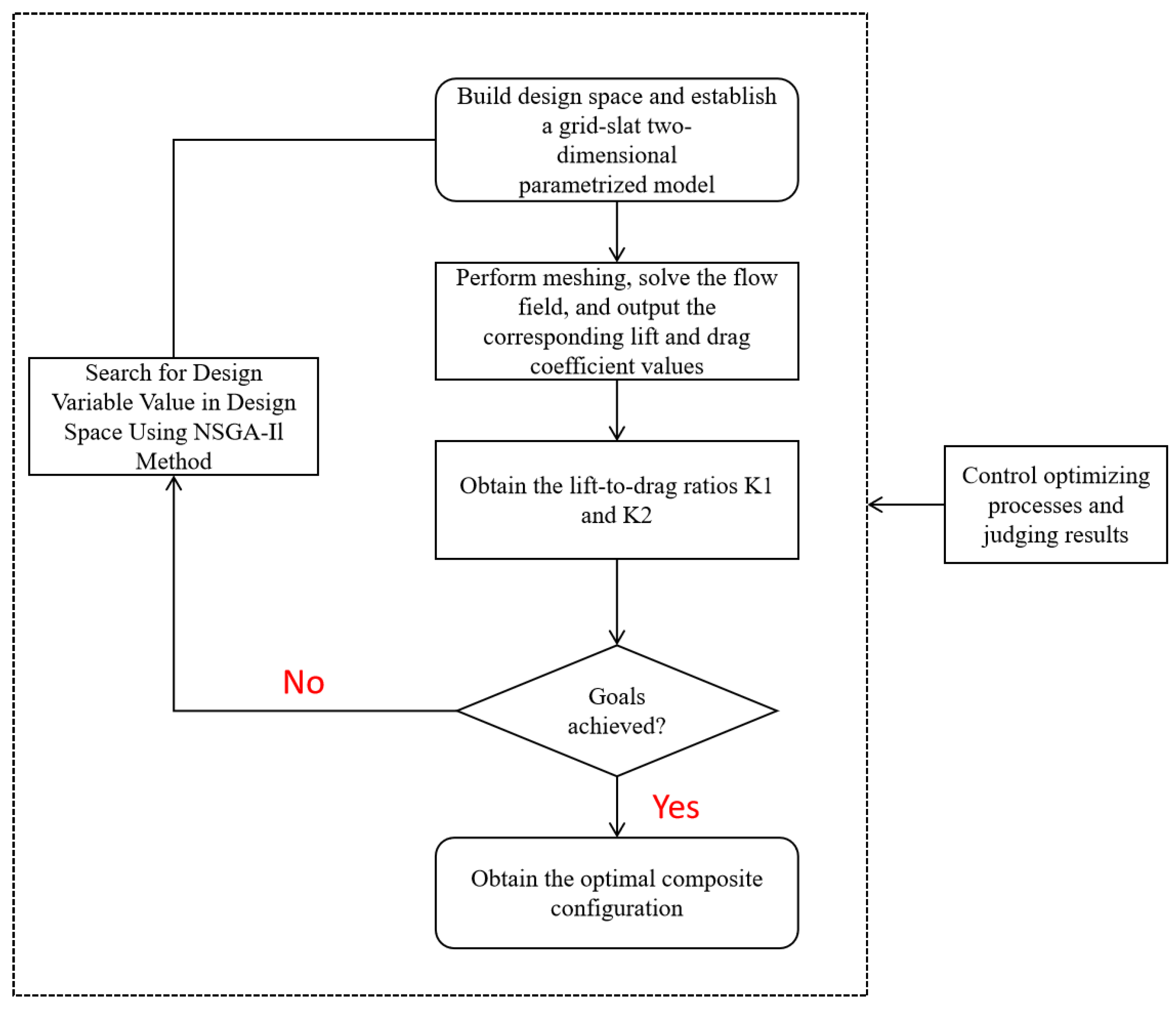
2.3. Optimal Design Methods
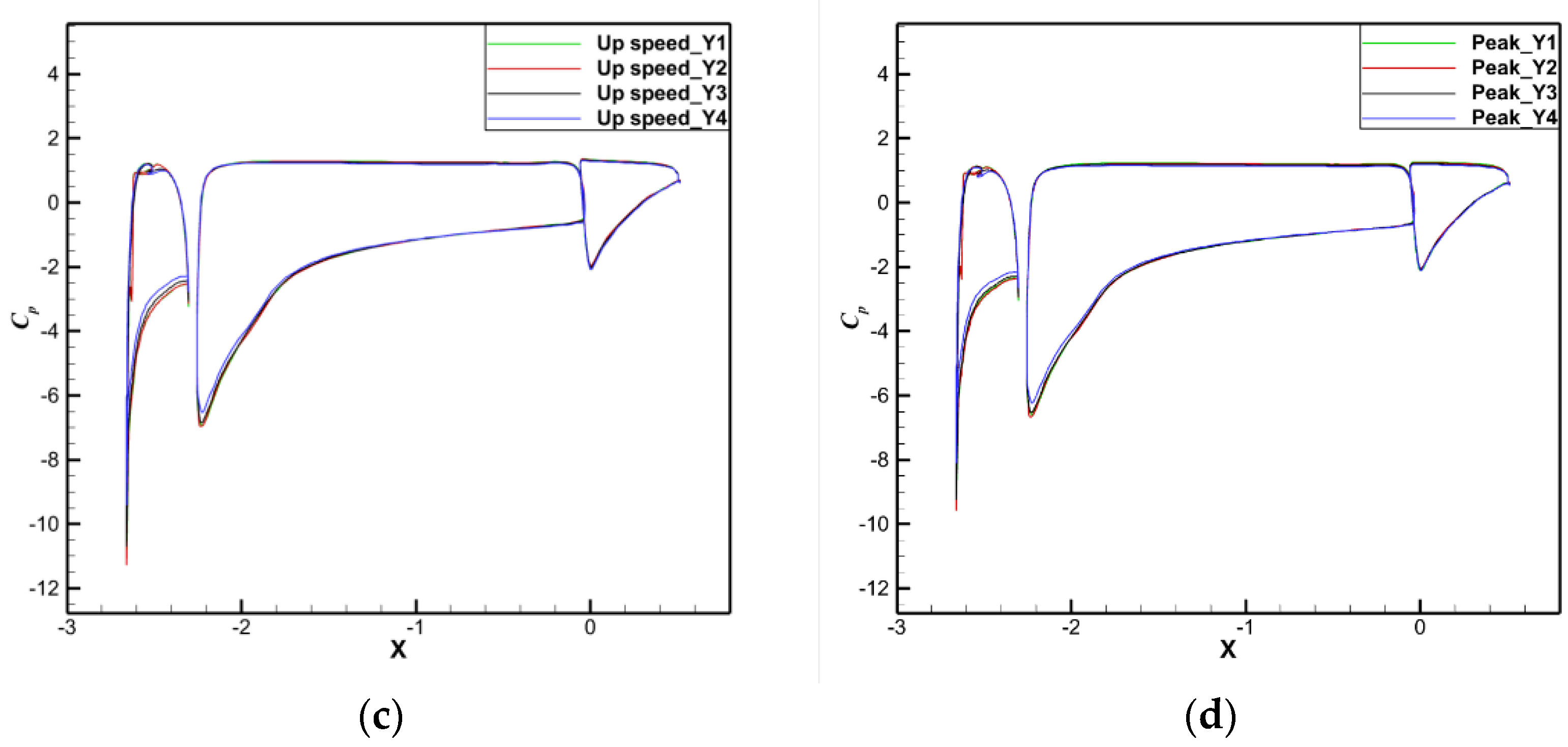
3. Results
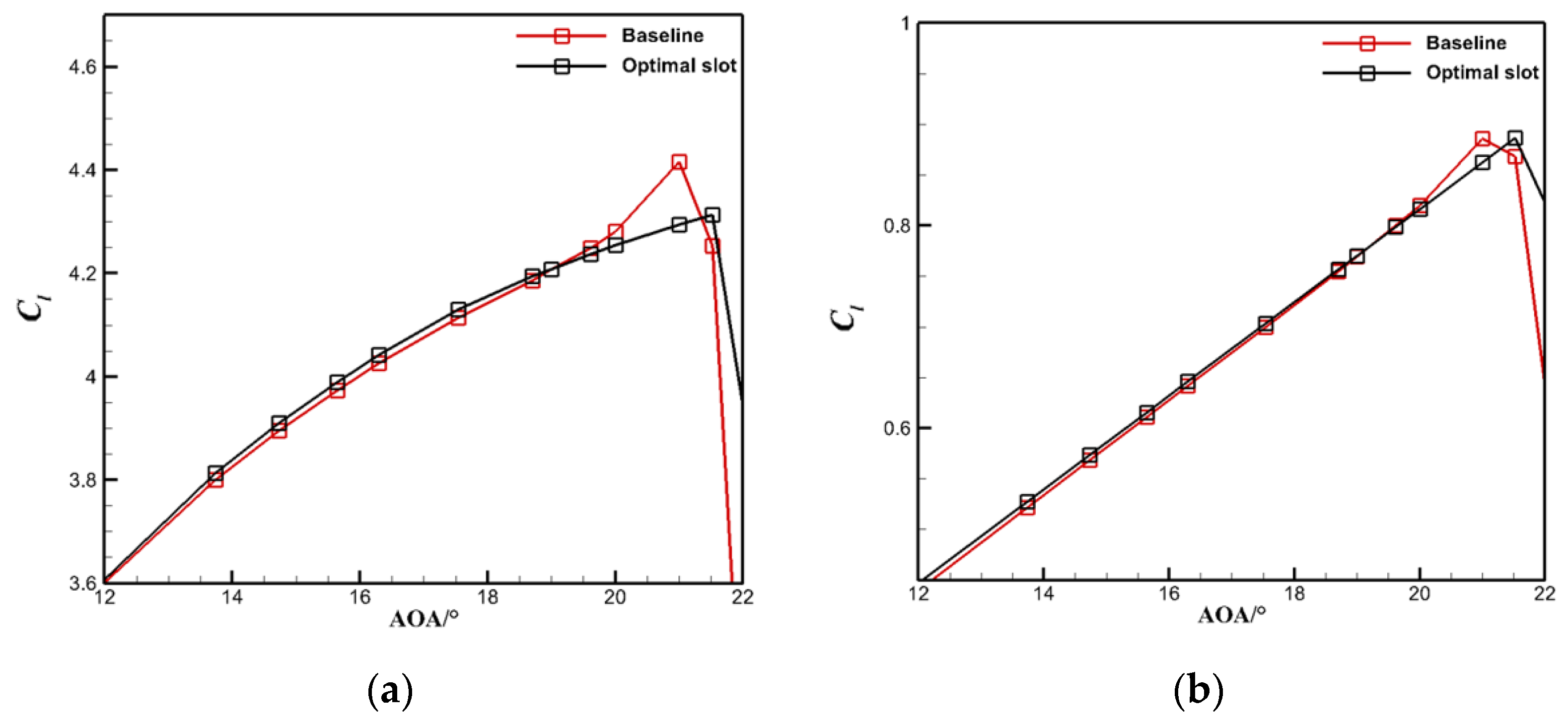
3.1. Analysis of the Increased Lift Efficiency of the Grid-Slat Fusion Configuration
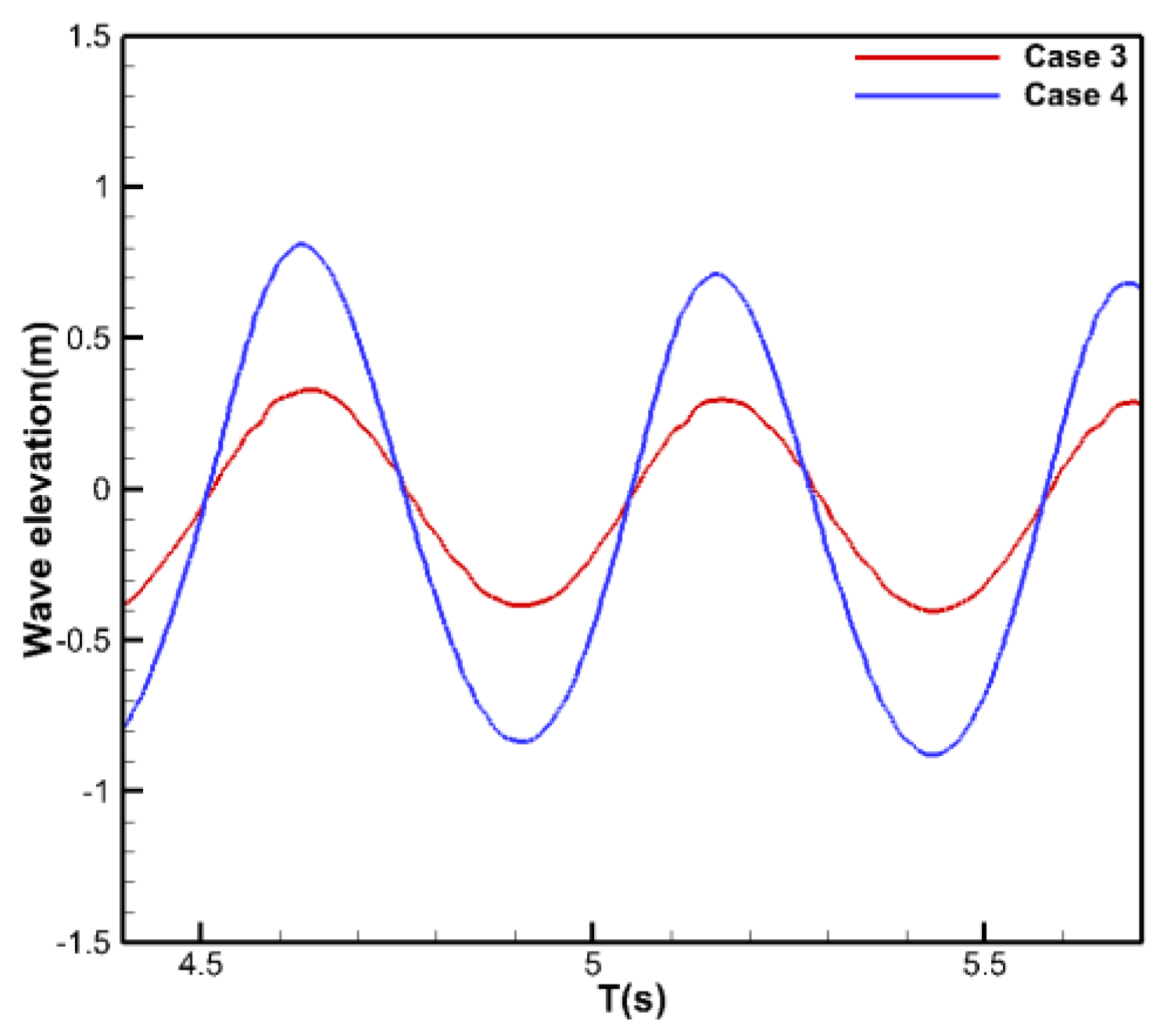
3.2. Applied Research on the Grid-Fusion Device in a Wavy Environment
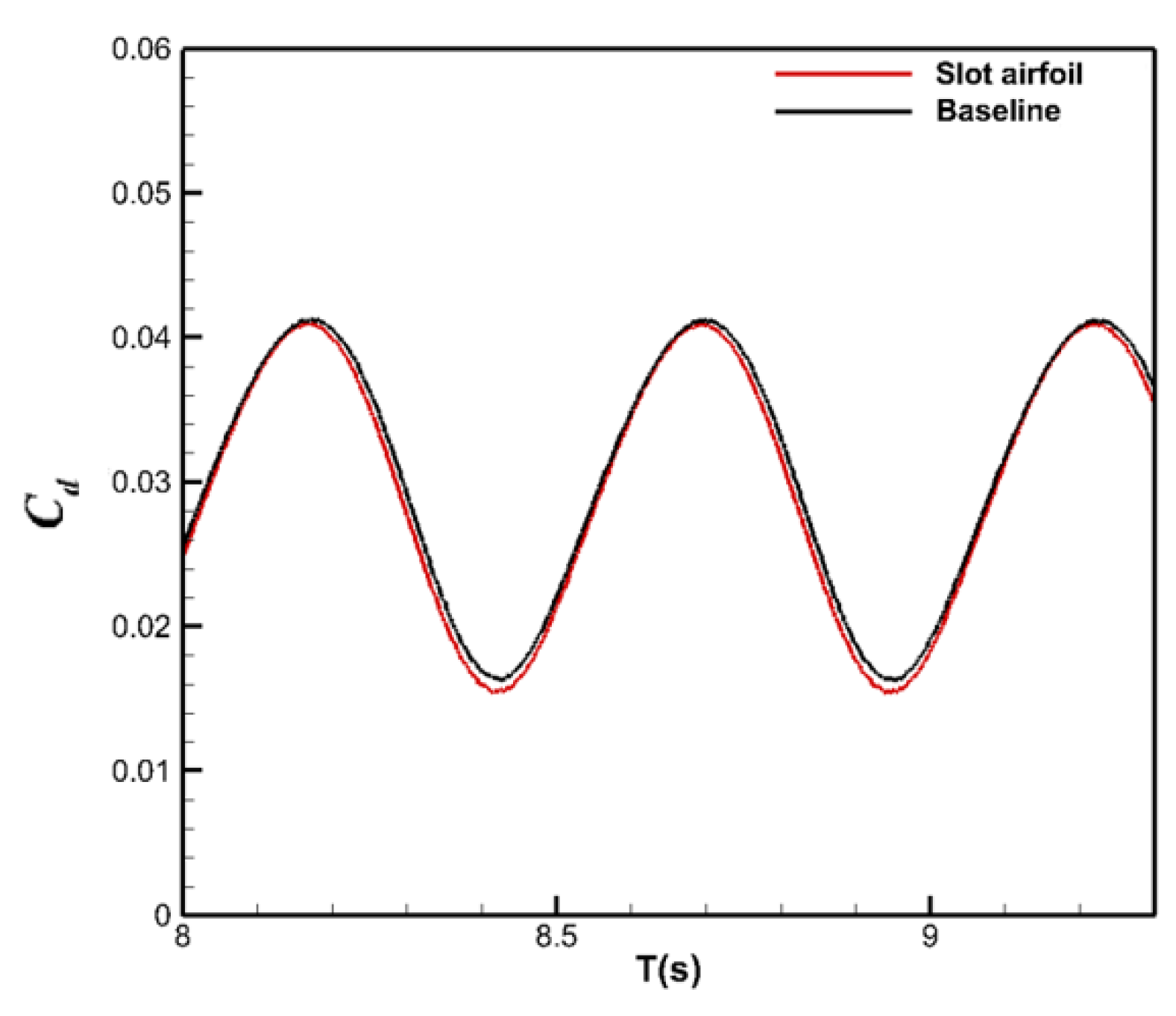
3.2.1. Verification of the Overwater Lift Augmentation of the Two-Dimensional Configuration
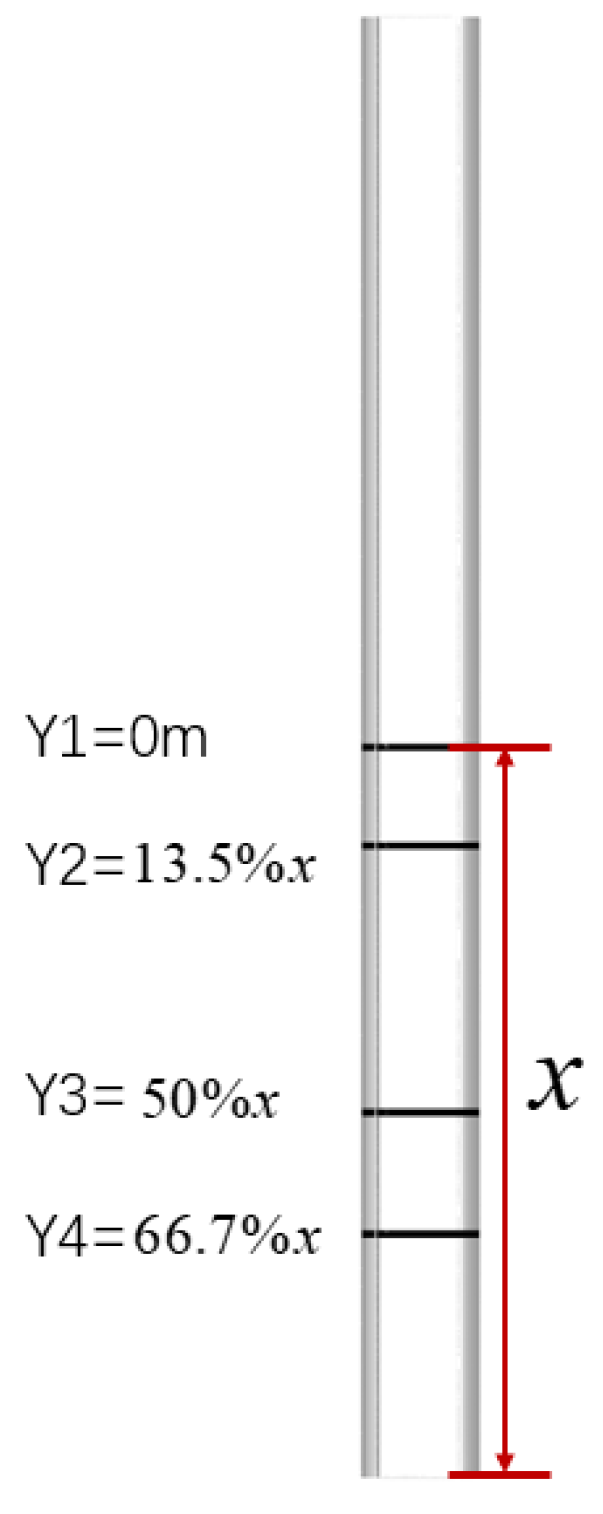
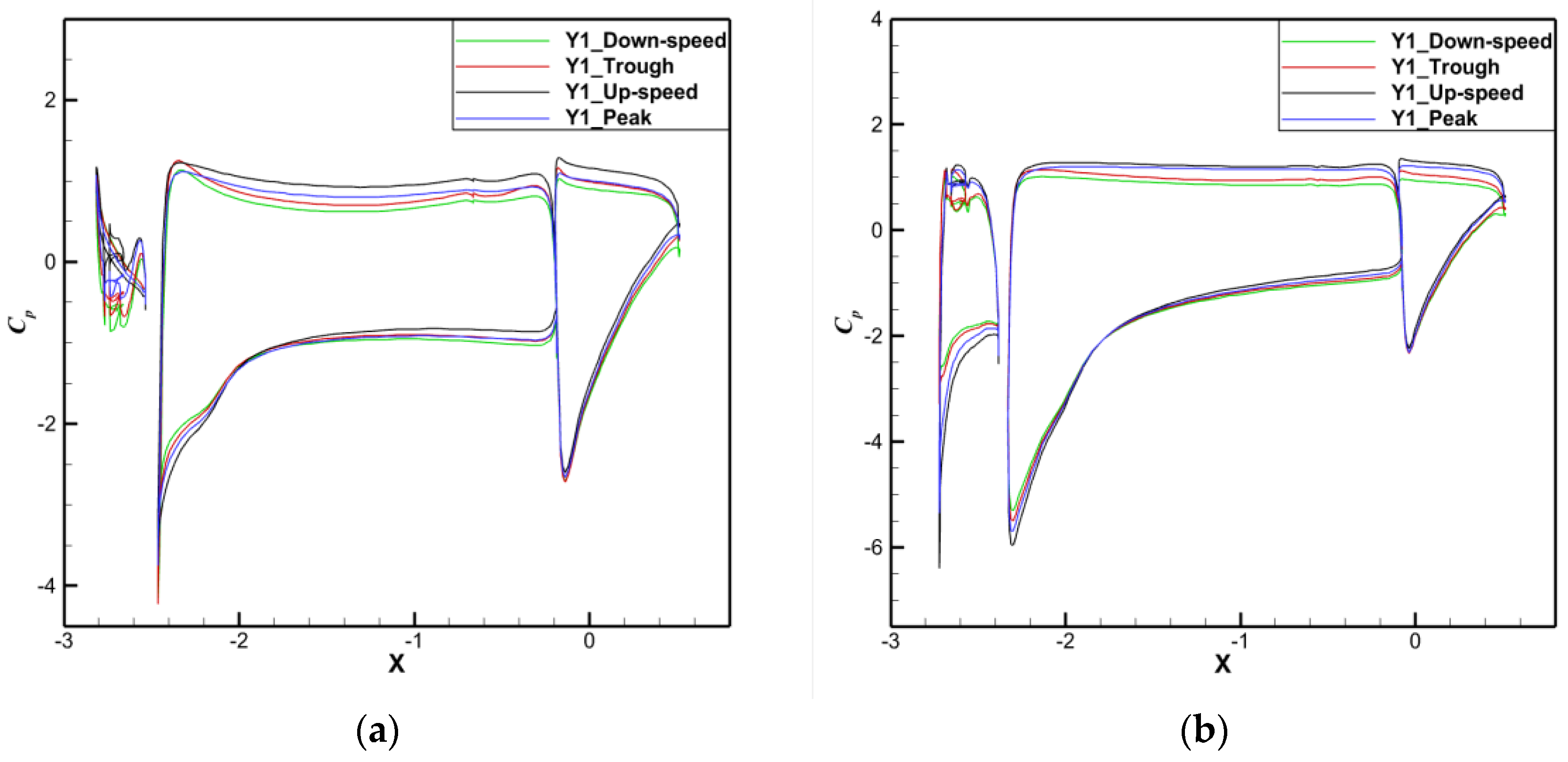
3.2.2. Verification of the Overwater Lift Augmentation of the Three-Dimensional Configuration
- Calculation of different wave heights in a three-dimensional composite two-phase flow.
- 2.
- Analysis of the effect of the angle of attack and position of a wave on the aerodynamic characteristics for a given wave height in a three-dimensional composite configuration.
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chu, L.; Ye, S. Collection of Seaplane Essays; Aviation Industry Press: Beijing, China, 2011; pp. 489–490. [Google Scholar]
- Huang, L.C.; Yong, M.P. Key technologies and industrial application prospects of amphibian aircraft. Acta Aeronaut. Et Astronaut. Sin. 2019, 40, 522708. [Google Scholar]
- Stout, E.G. Development of high-speed water-based aircraft. J. Aeronaut. Sci. 1950, 17, 457–480. [Google Scholar] [CrossRef]
- Leyva, C.; Leonel, A. Seaplane Conceptual Design and Sizing; University of Glasgow: Scotland, UK, 2012. [Google Scholar]
- Anderson, S.B. An Examination of Handling Qualities Criteria for V/STOL Aircraft; NASA: Washington, DC, USA, 1960. [Google Scholar]
- Hickey, D.H.; Aoyagi, K. Large-Scale Wind-Tunnel Tests of an Airplane Model with a 45 Degree Sweptback Wing of Aspect Ratio 2.8 Employing High-Velocity Blowing over the Leading- and Trailing-Edge Flaps; University of Oxford: Oxford, UK, 1958. [Google Scholar]
- Owens, D.; Perkins, J. Improved performance on highly swept wings by suction boundary-layer control. In Proceedings of the 34th Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 15–18 January 1996; p. 431. [Google Scholar]
- Smith, D.; Dickey, E.; vonKlein, T. The ADVINT program. In Proceedings of the 3rd AIAA Flow Control Conference, San Francisco, CA, USA, 5–8 June 2006; pp. 2006–2854. [Google Scholar]
- AEROFILES. Martin, Martin-Willard. Available online: http://www.aerofiles.com/_martin.html (accessed on 20 April 2009).
- Fischer, B. US-1A amphibian retired. AirInt. 2018, 94, 17. [Google Scholar]
- Holzhauser, C.A.; Innis, R.C.; Vomaske, R.F. A Flight and Simulator Study of the Handling Qualities of a Deflected Slipstream Stol Sea-Plane Having Four Propellers and Boundary-Layer Control; TN D-2964; NASA: Washington, DC, USA, 1965. [Google Scholar]
- Abbasov, I.B.; V’iacheslav, V.O. Computational modeling of multipurpose amphibious aircraft Be-200. Adv. Eng. Softw. 2014, 69, 12–17. [Google Scholar] [CrossRef]
- Qu, D.C. Russia’s Be-200 multi-pulfi-purpose amphibious seaplane. Aeronaut. Sci. Technol. 2005, 1, 28–30. [Google Scholar]
- Taylor, J.W.R. Jane’s all the world’s aircraft. In Jane’s Yearbooks; Sampson Low, Marston and Co.: London, UK, 1976. [Google Scholar]
- Hammond, A.D. High-Lift Aerodynamics. In Proceedings of the Vethicle Technology for Civil Aviation the Seventies and Beond, Hampton, VA, USA, 2-4 November 1971. [Google Scholar]
- Ramzi, M.; Abede, G. Passive control via slotted blading in a compressor cascade at stall condition. J. Appl. Fluid Mech. 2013, 571, 3–9. [Google Scholar]
- Ni, Z.; Dhanak, M.; Su, T. Improved performance of a slotted blade using a novel slot design. J. Wind. Eng. Ind. 2019, 34, 2–9. [Google Scholar] [CrossRef]
- Peng, K.; Hu, F.; Zhang, W.H.; Zhou, Z. Review of aerodynamic characteristics and application of grid fin. J. Solid Rocket. Technol. 2015, 38, 8. [Google Scholar]
- Shi, Y.C. New Quadratic Curve Method-A New Method of Designing and Processing Curves and Surface. J. Harbin Inst. Nav. Eng. 1992, 1, 80–93. [Google Scholar]
- Liming, R.A. Practical Analytic Geometric with Application to Aircraft; Macmillan: London, UK, 1944. [Google Scholar]
- Wang, Y.T.; Wang, G.X.; Zhang, Y.L. Numerical study of complex flow over 30P-30N multi-element. Acta Aerodyn. Sin. 2010, 28, 99–103. [Google Scholar]
- Qin, X.; Liu, P.; Qu, Q.; Peng, G. Influence of gap parameters on aerodynamics of multi-element airfoil. J. Beijing Univ. Aeronaut. Astronaut. 2011, 37, 4. [Google Scholar]
- Anderson, J.D. Foundations and Applications of Computational Fluid Mechanics; Machine Press: Beijing, China, 2007. [Google Scholar]
- Lai, Y.Y. Isight arameter Optimization Theory and Case Explanation; Beijing Aerospace Publishing House: Beijing, China, 2012. [Google Scholar]
- Zhu, Y.R. Wave Mechanics in Marine Engineering; Tianjin University Press: Tianjin, China, 2013. [Google Scholar]
- Hirt, C.W.; Nichols, B.D. Volume of fluid (VOF) method for the dynamics of free boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Qin, X.G.; Liu, P.Q.; Qu, Q.L.; Xu, J. Numerical Simulation of Ground Effects on Three dimensional Multisegment Wings. Acta. Aeronaut. Sin. 2011, 32, 257–264. [Google Scholar]







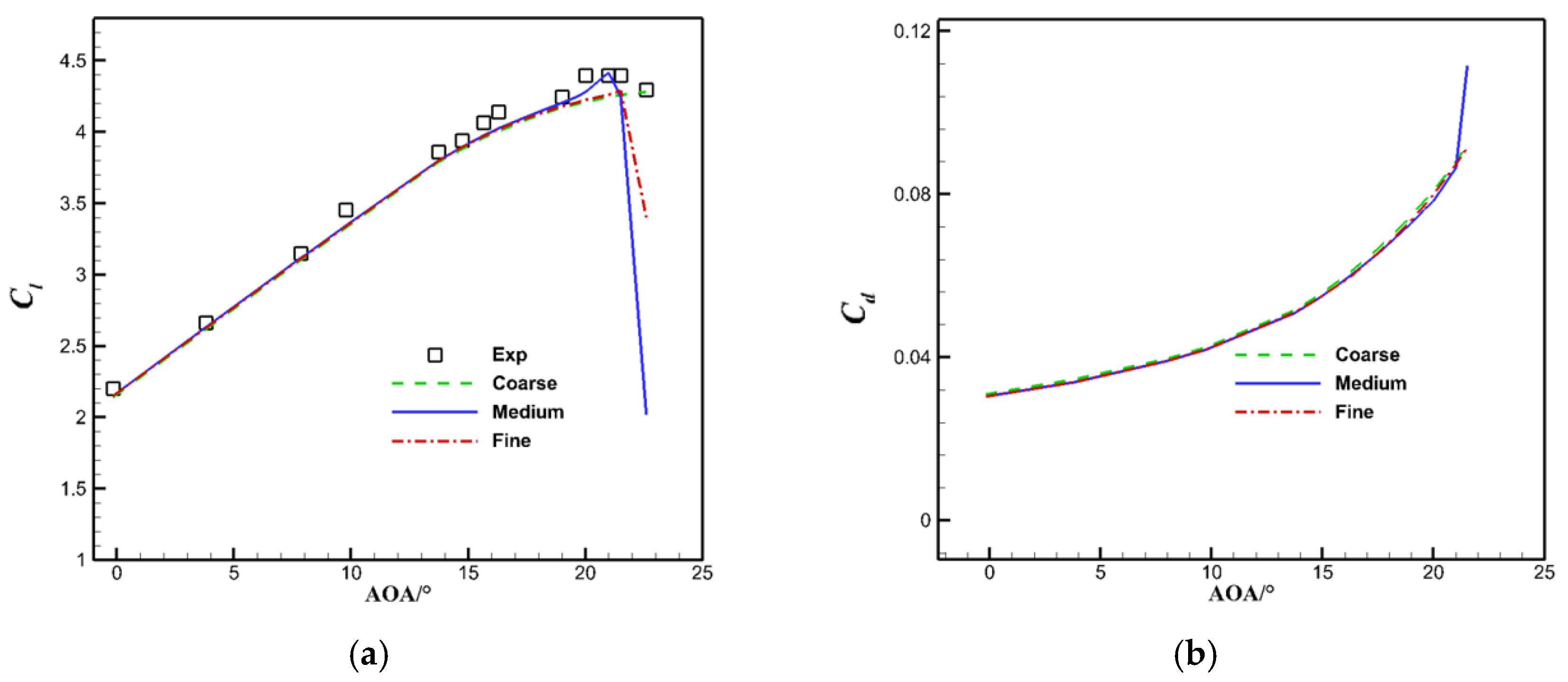



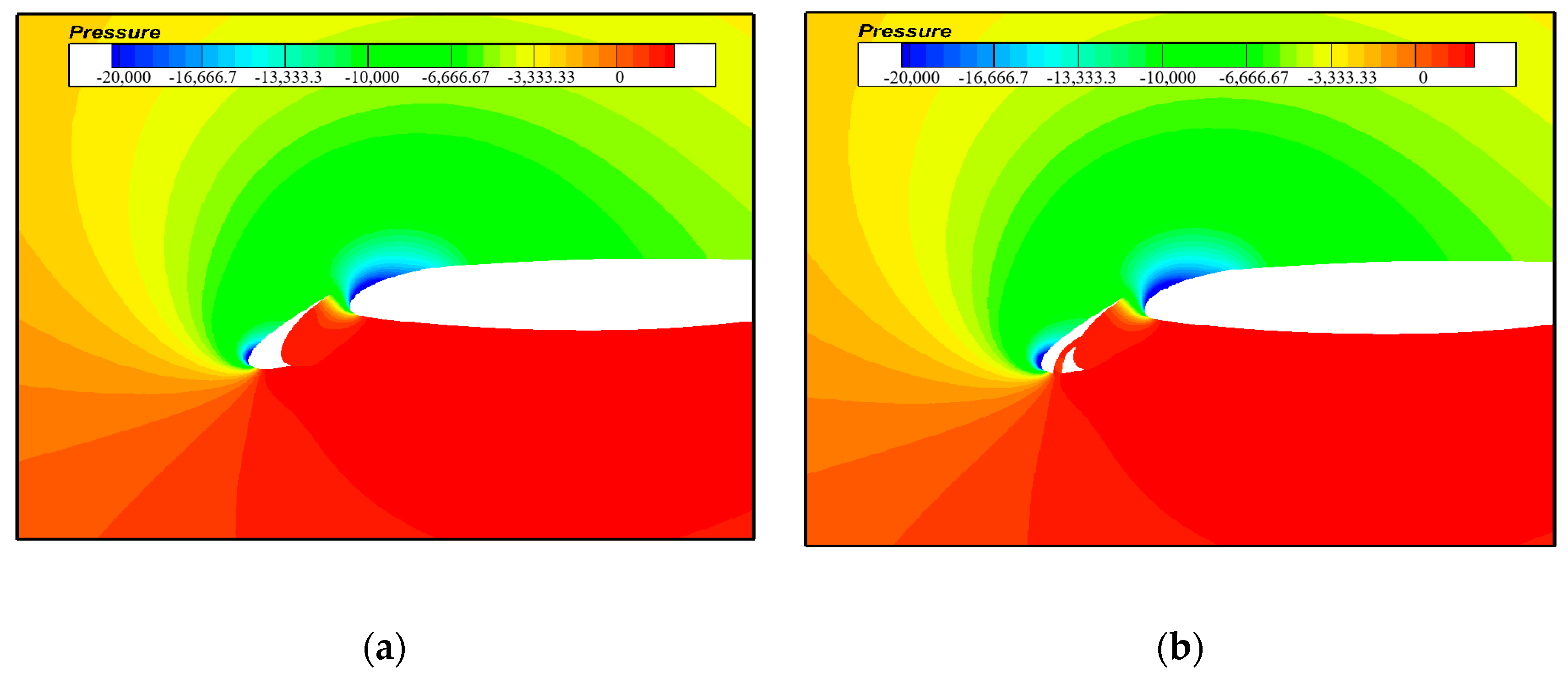
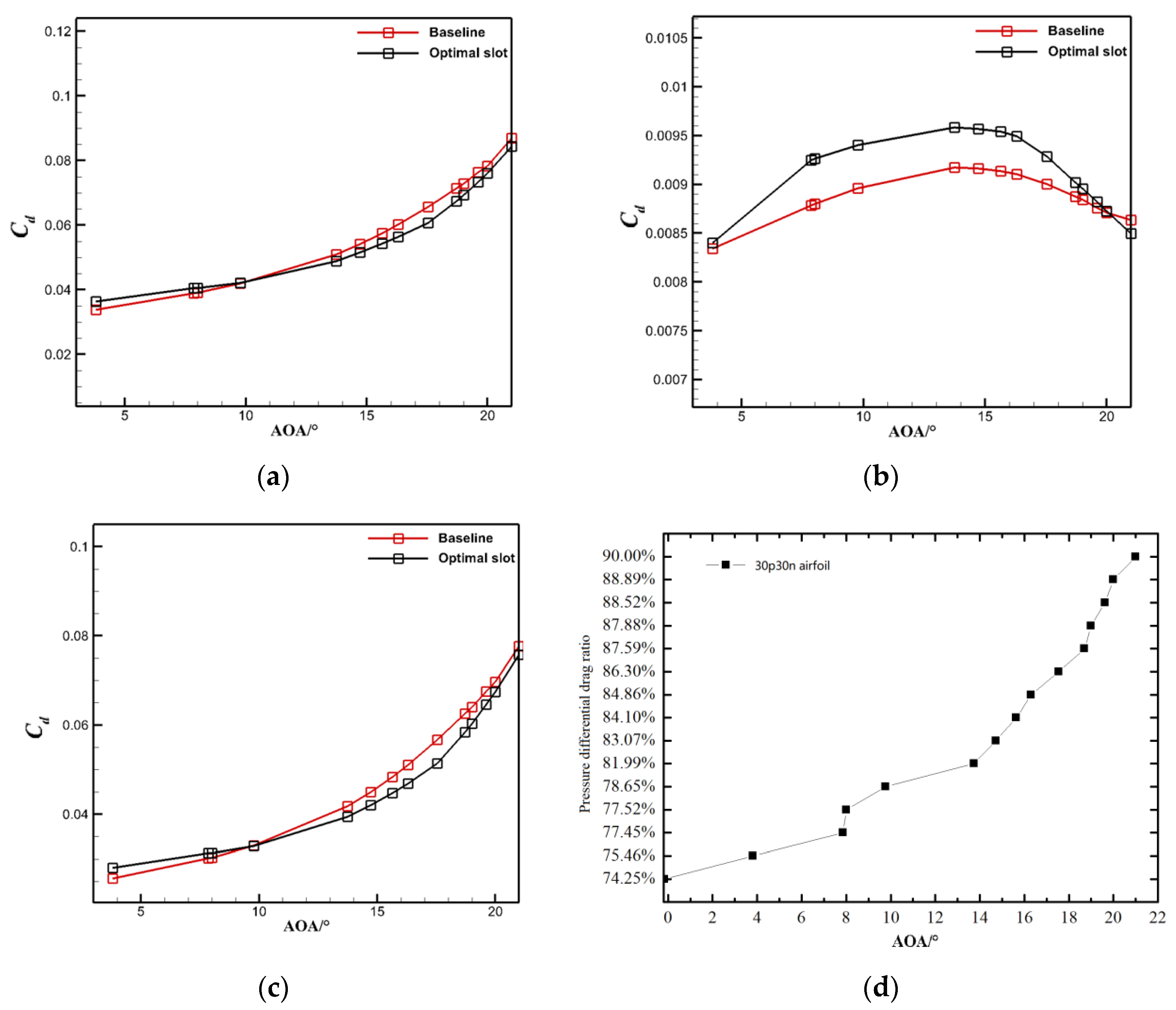
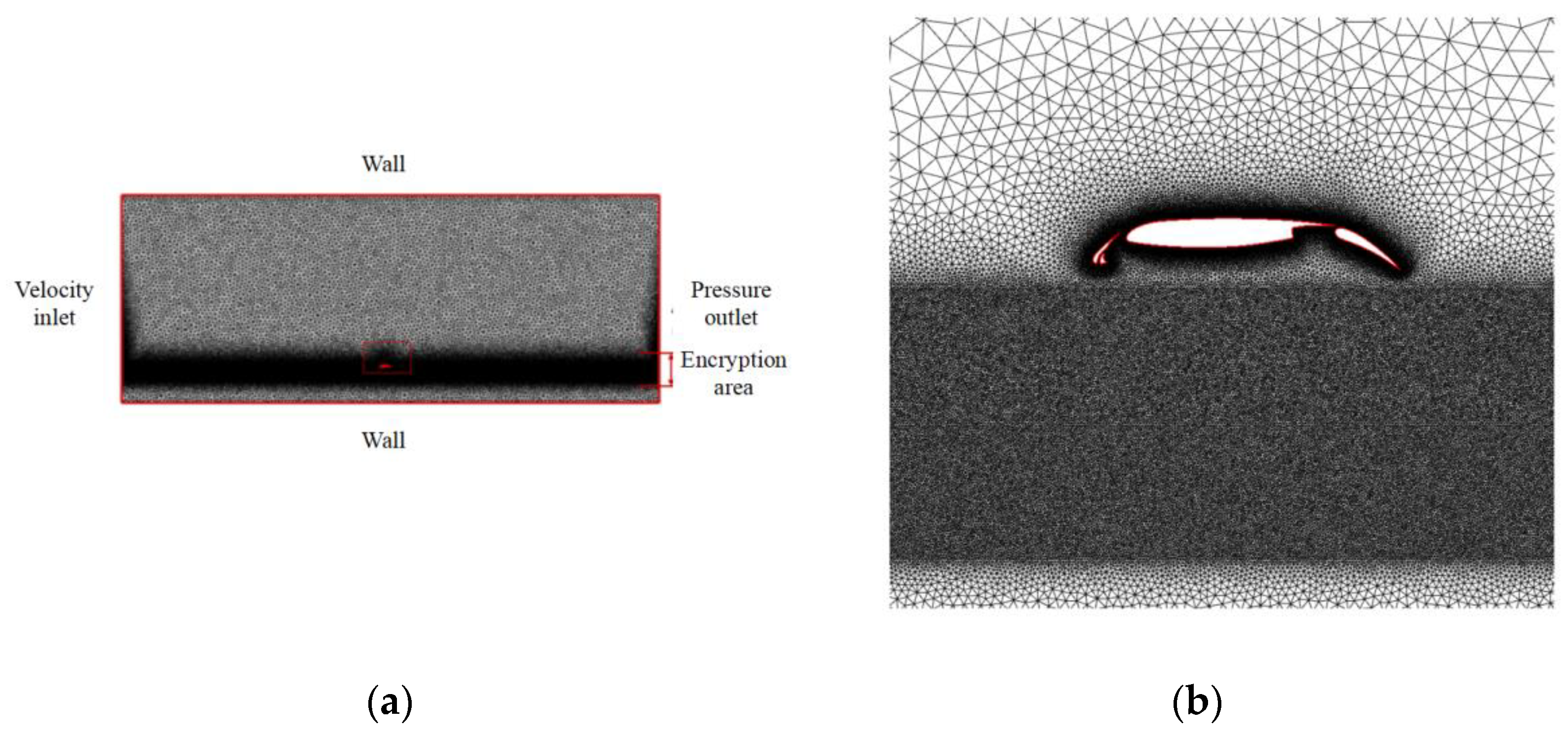
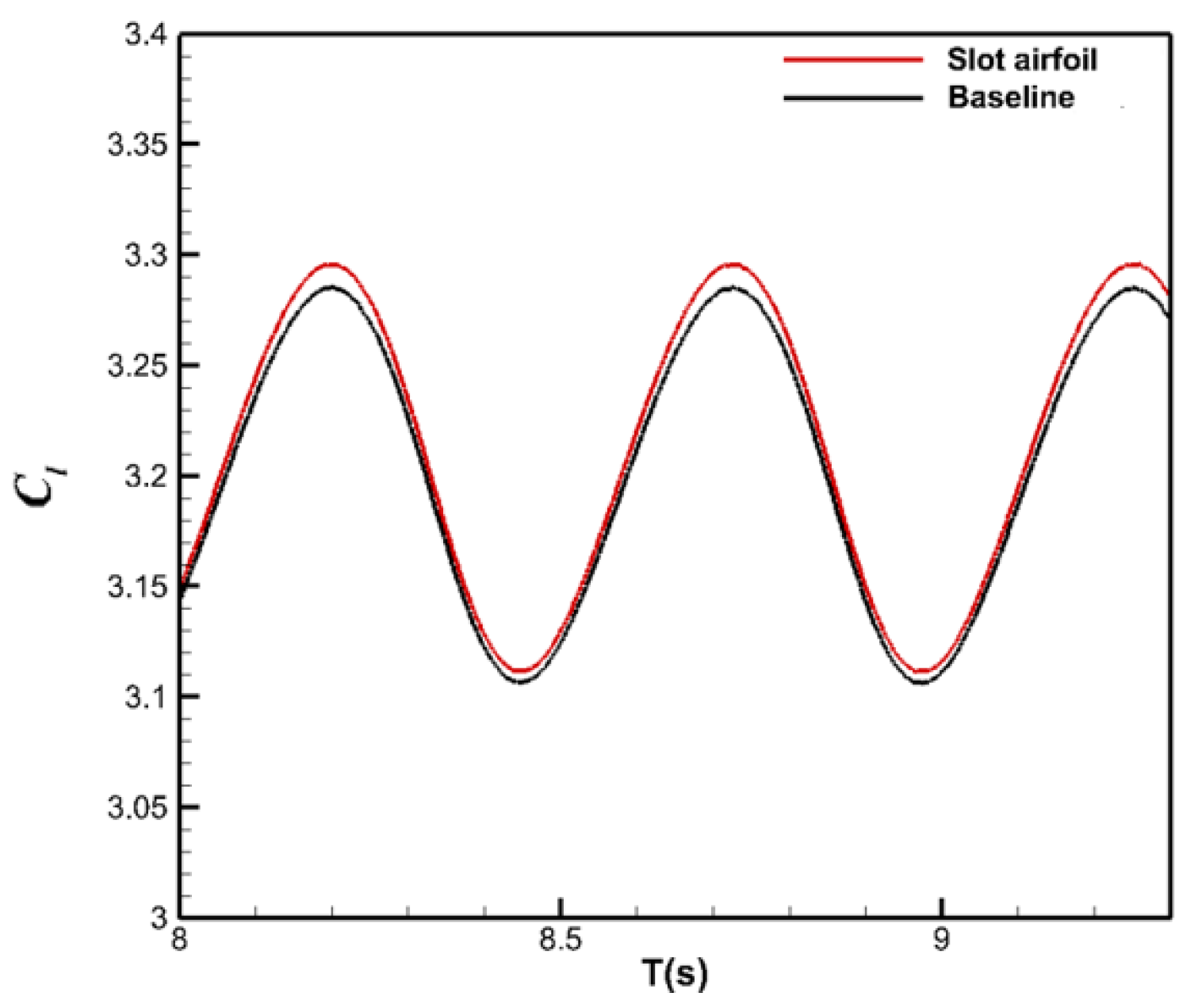






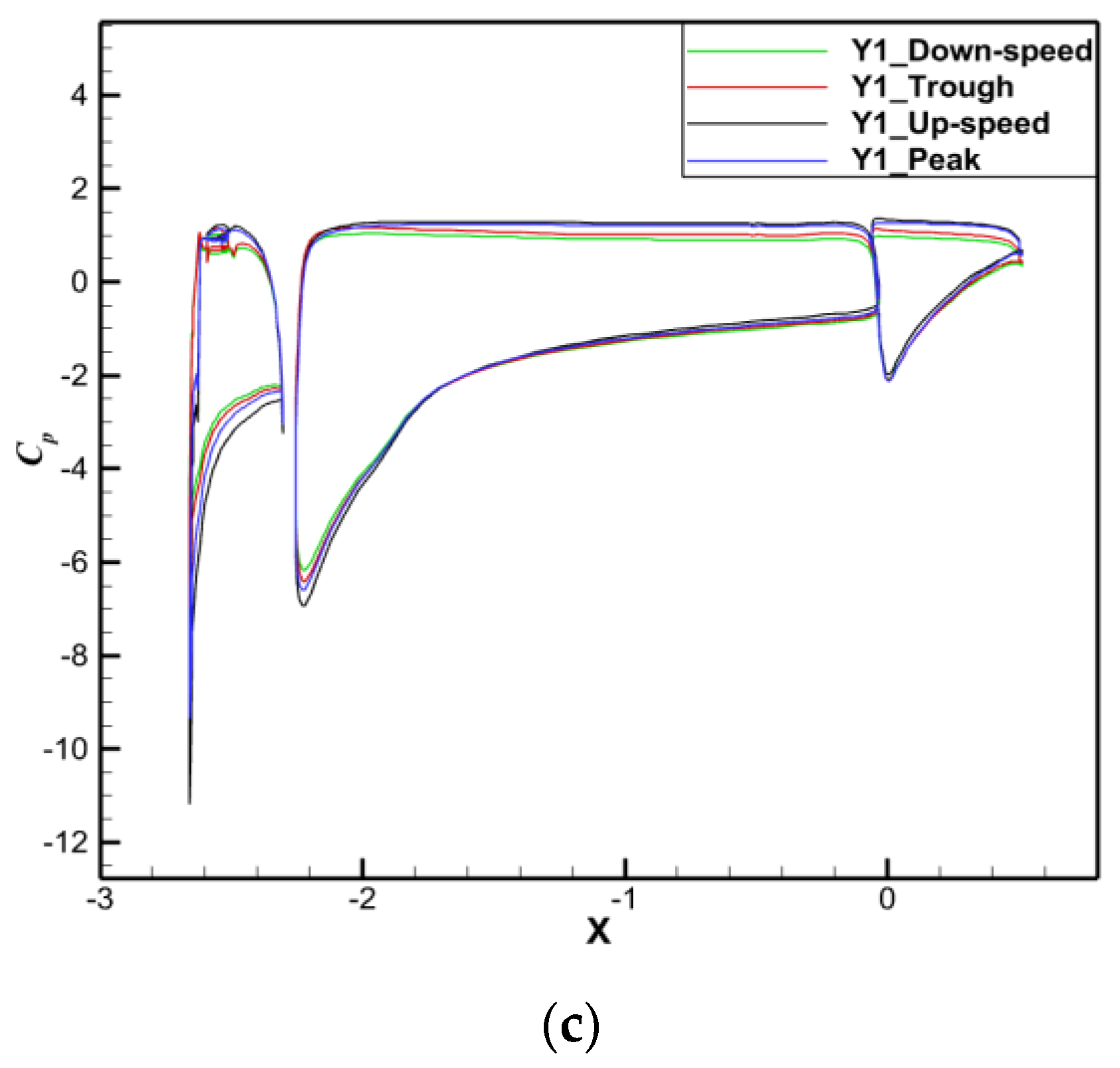
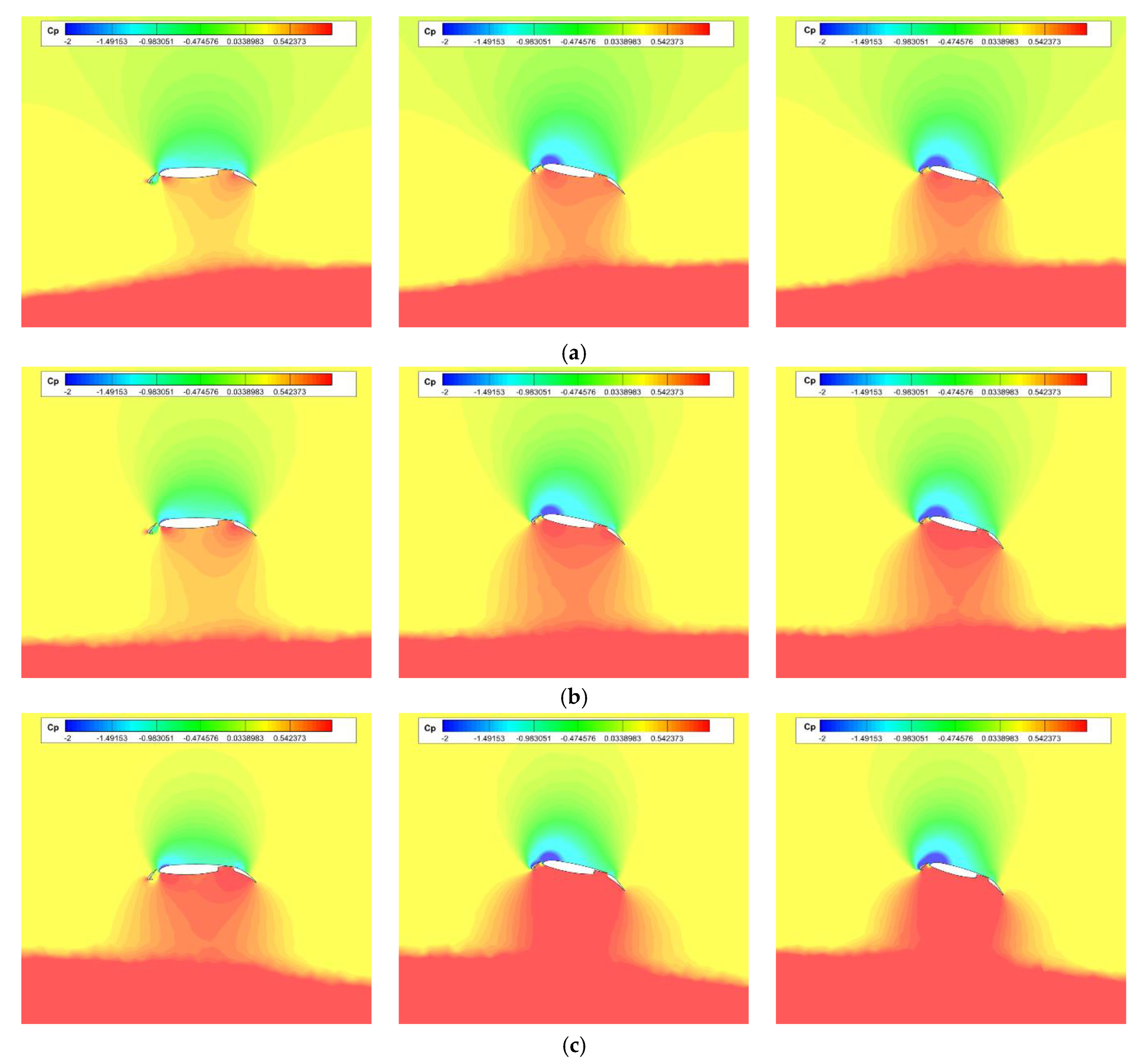
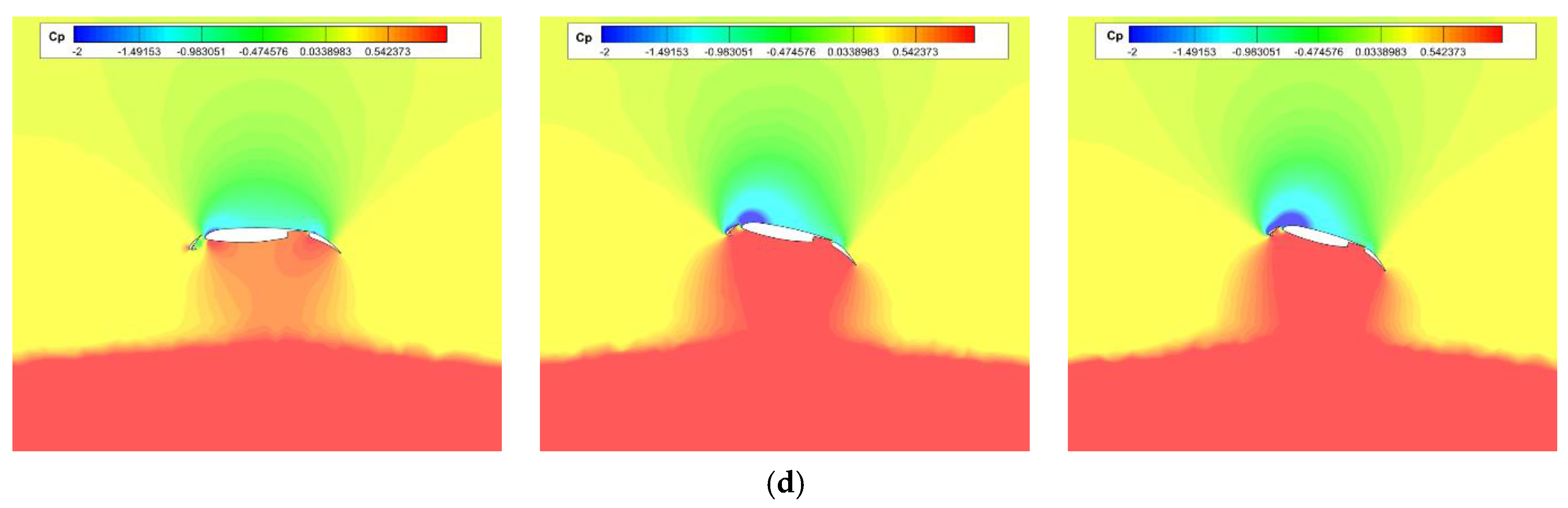
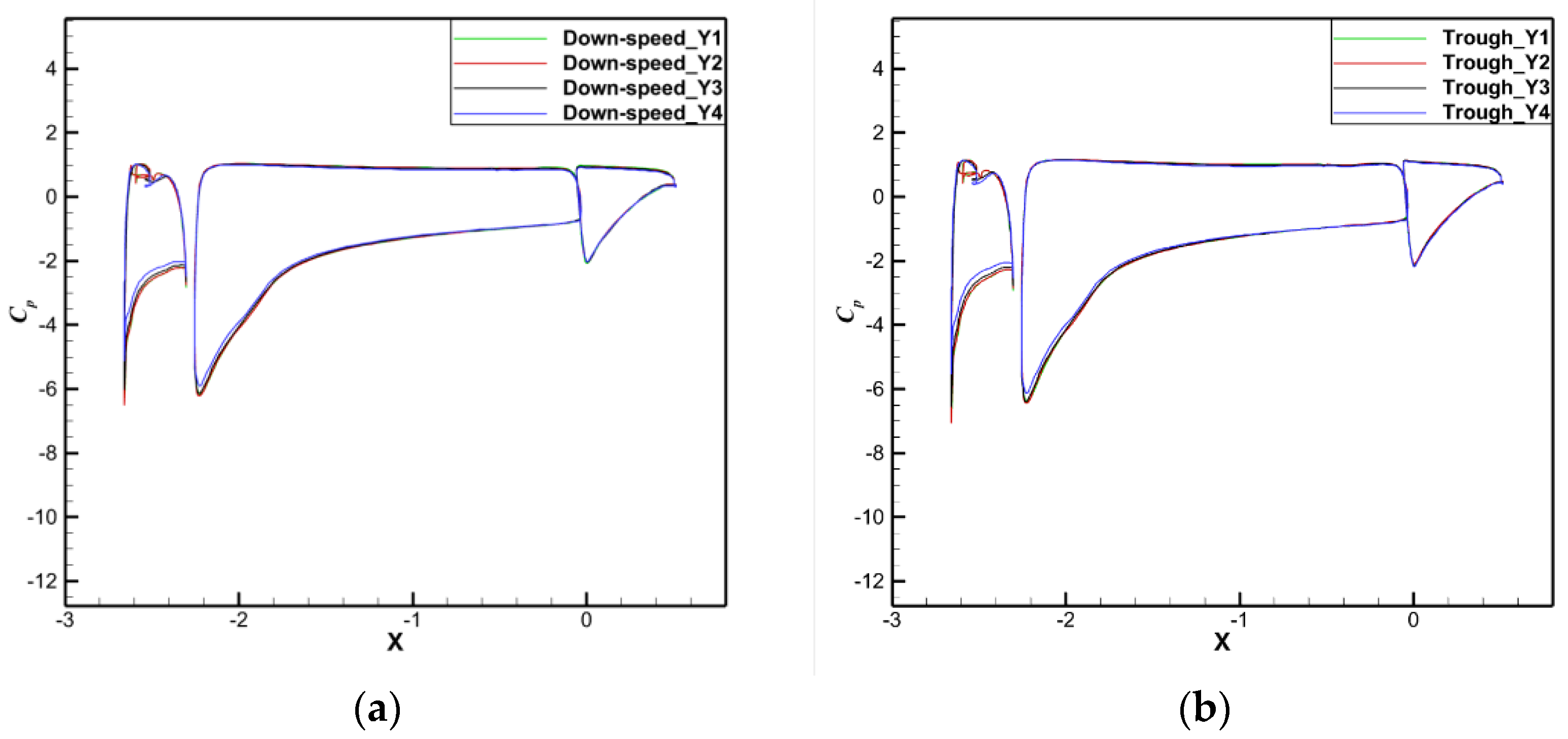
| Case | Grid Number | Lift Coefficient |
|---|---|---|
| Coarse grid | 74,289 | 3.88324 |
| Medium grid | 162,402 | 3.8952 |
| Fine grid | 288,069 | 3.8993 |
| ratio A | ratio B | ratio E | ||
| 0.75–0.85 | 0.55–0.65 | 0–1 | ||
| ratio H | ratio I | ratio P | ||
| 0.8–0.9 | 0.65–0.75 | 0–1 |
| ratio A | ratio B | ratio E | ||
| 0.81 | 0.57 | 0.5 | 85 | 31 |
| ratio H | ratio I | ratio P | ||
| 0.86 | 0.7 | 0.27 | 80 | 30 |
| Computational Model | Velocity m/s | Water Surface Condition | |
|---|---|---|---|
| Case 3 | 0.8c | 68 | wave height: 0.75 m wave length: 40 m |
| Case 4 | 0.8c | 68 | wave height: 1.55 m wave length: 40 m |
| Computational Model | Velocity m/s | Water Surface Condition | |
|---|---|---|---|
| Case 4 | 0.8c | 68 | wave height: 1.55 m wave length: 40 m |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mi, B.; Yu, J. A New Grid-Slat Fusion Device to Improve the Take-Off and Landing Performance of Amphibious Seaplanes. J. Mar. Sci. Eng. 2024, 12, 2303. https://doi.org/10.3390/jmse12122303
Mi B, Yu J. A New Grid-Slat Fusion Device to Improve the Take-Off and Landing Performance of Amphibious Seaplanes. Journal of Marine Science and Engineering. 2024; 12(12):2303. https://doi.org/10.3390/jmse12122303
Chicago/Turabian StyleMi, Baigang, and Jingyi Yu. 2024. "A New Grid-Slat Fusion Device to Improve the Take-Off and Landing Performance of Amphibious Seaplanes" Journal of Marine Science and Engineering 12, no. 12: 2303. https://doi.org/10.3390/jmse12122303
APA StyleMi, B., & Yu, J. (2024). A New Grid-Slat Fusion Device to Improve the Take-Off and Landing Performance of Amphibious Seaplanes. Journal of Marine Science and Engineering, 12(12), 2303. https://doi.org/10.3390/jmse12122303






