Numerical Study on the Hydrodynamics of Fish Swimming with Different Morphologies in Oblique Flow
Abstract
1. Introduction
2. Problem Description and Numerical Model
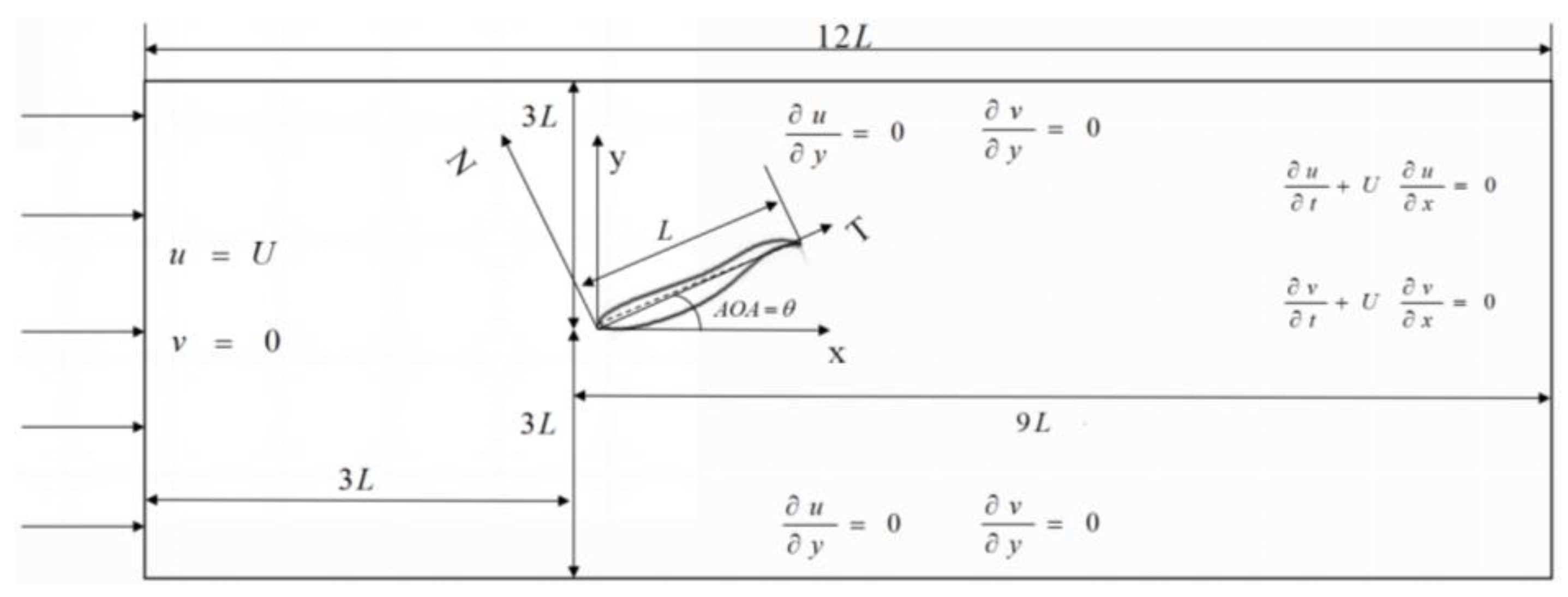
2.1. Description of the Physical Problem
2.2. Numerical Model
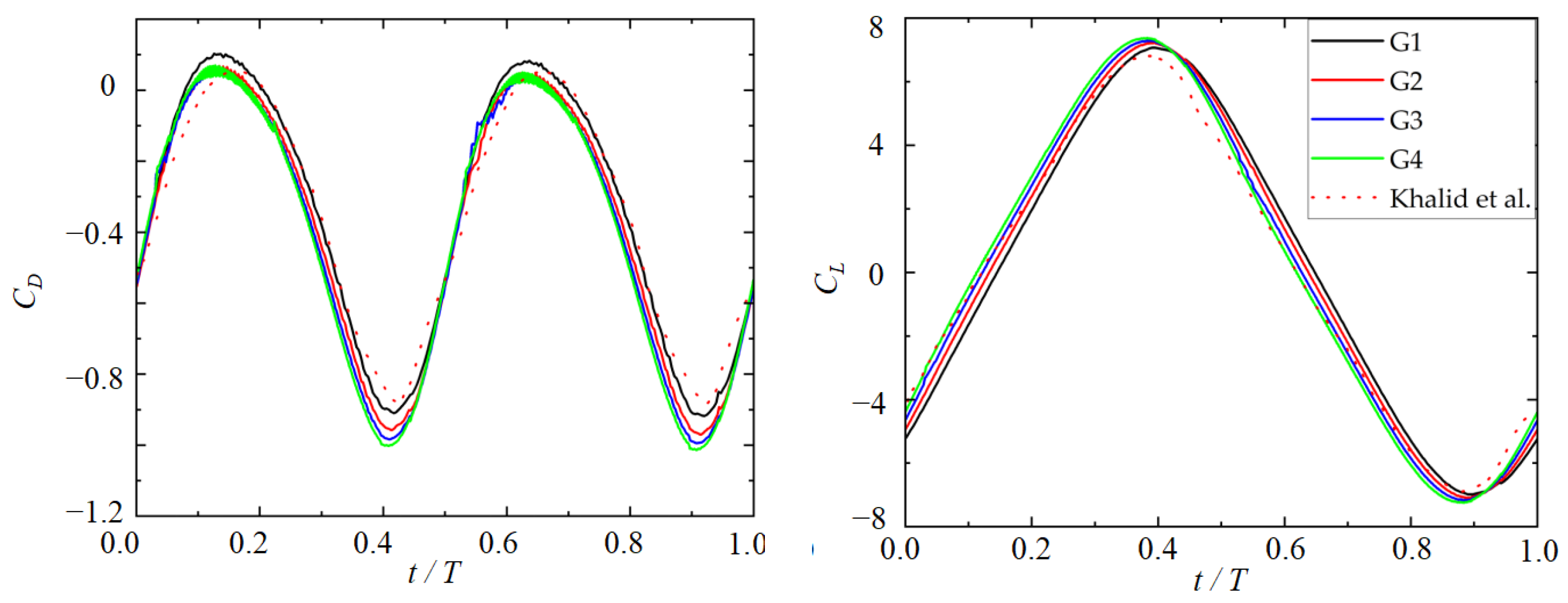
2.3. Numerical Validation
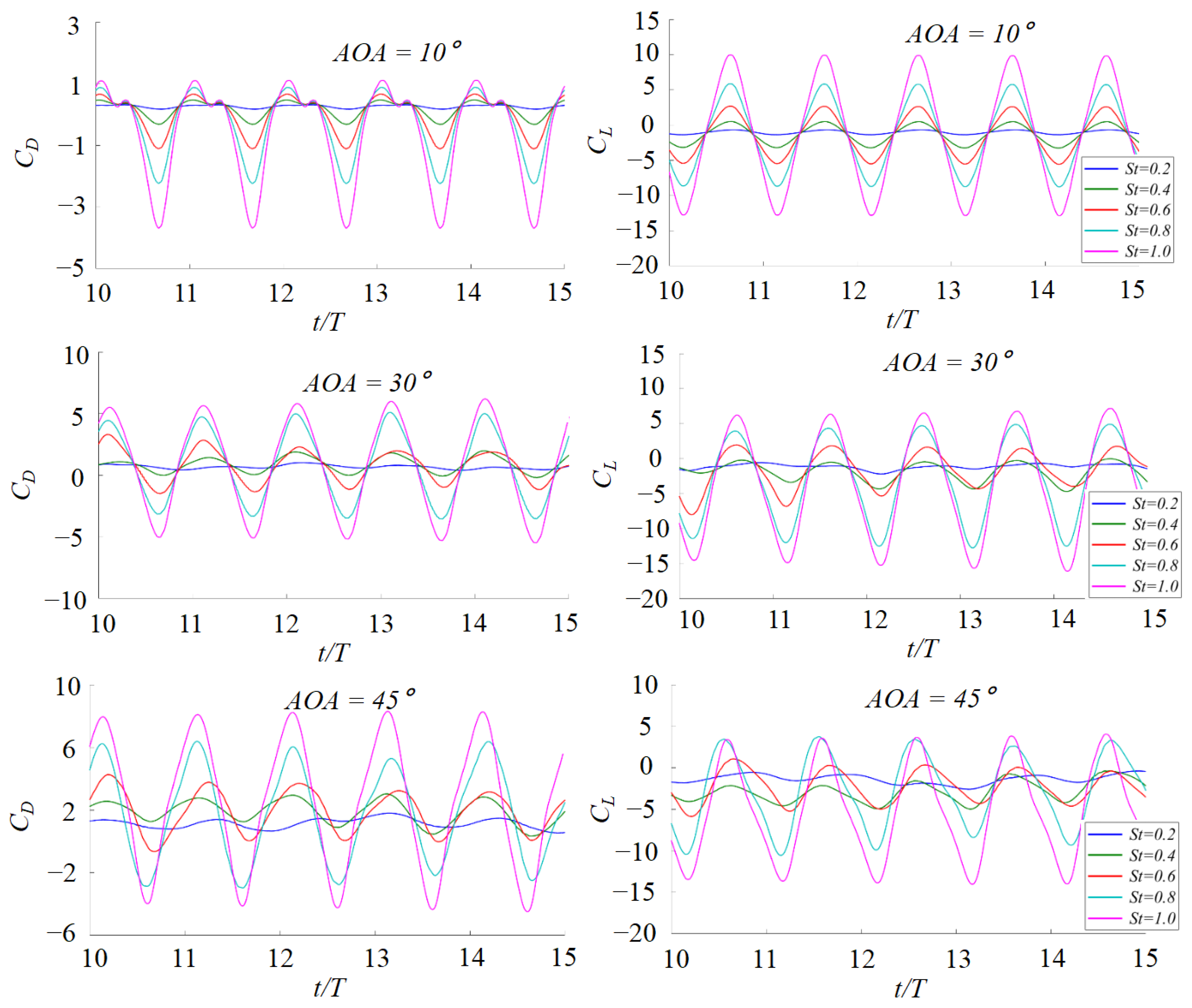
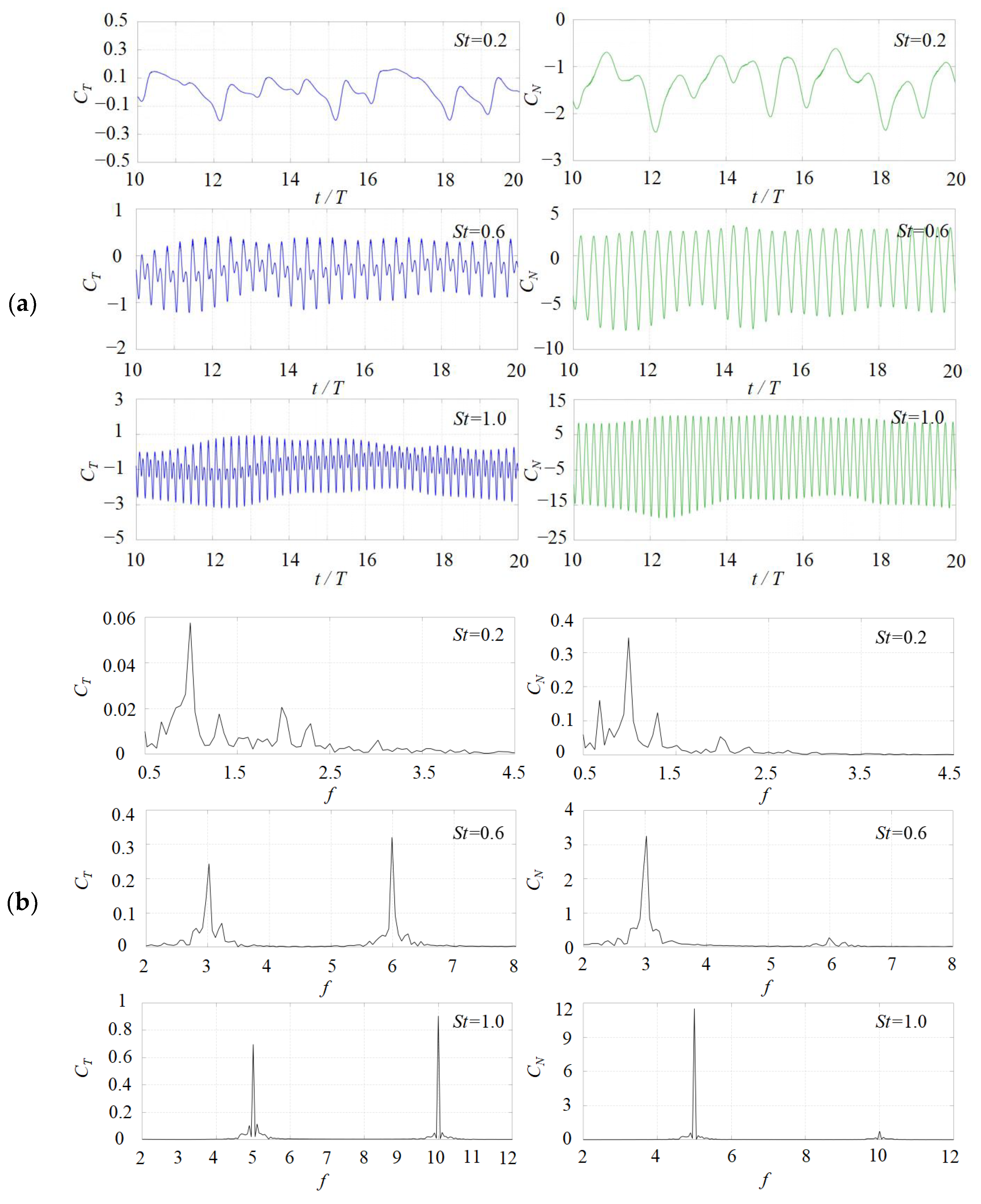
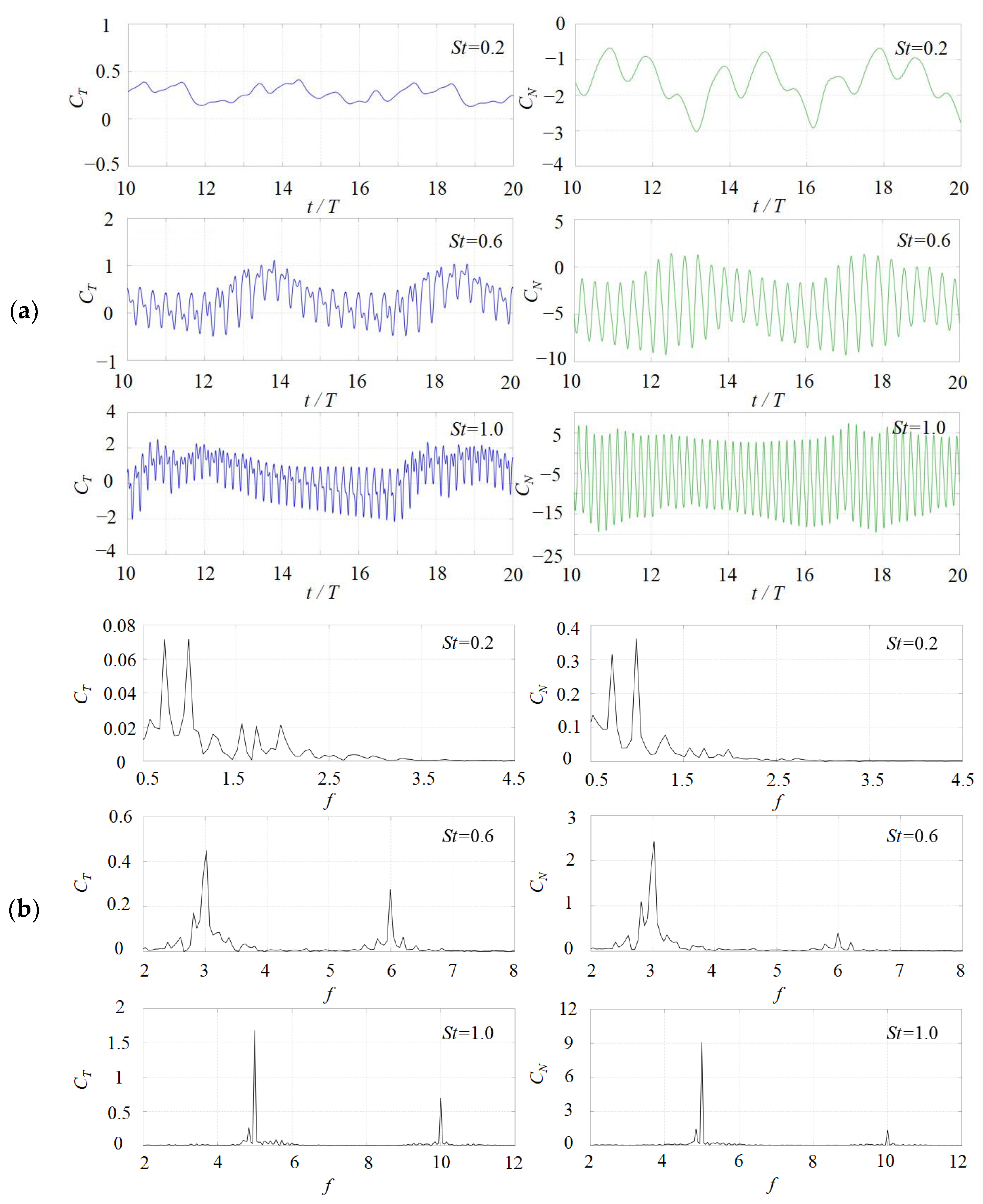
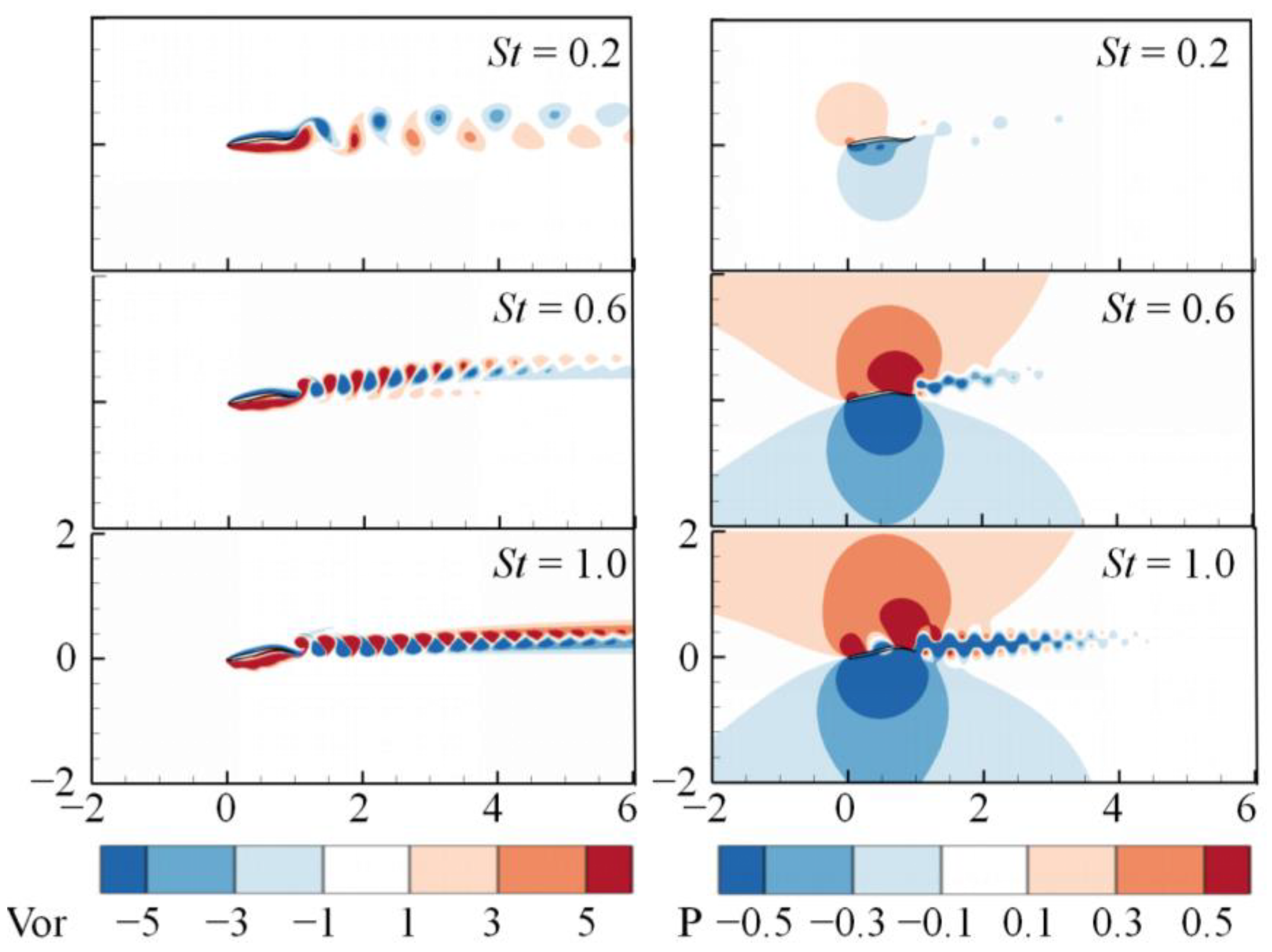
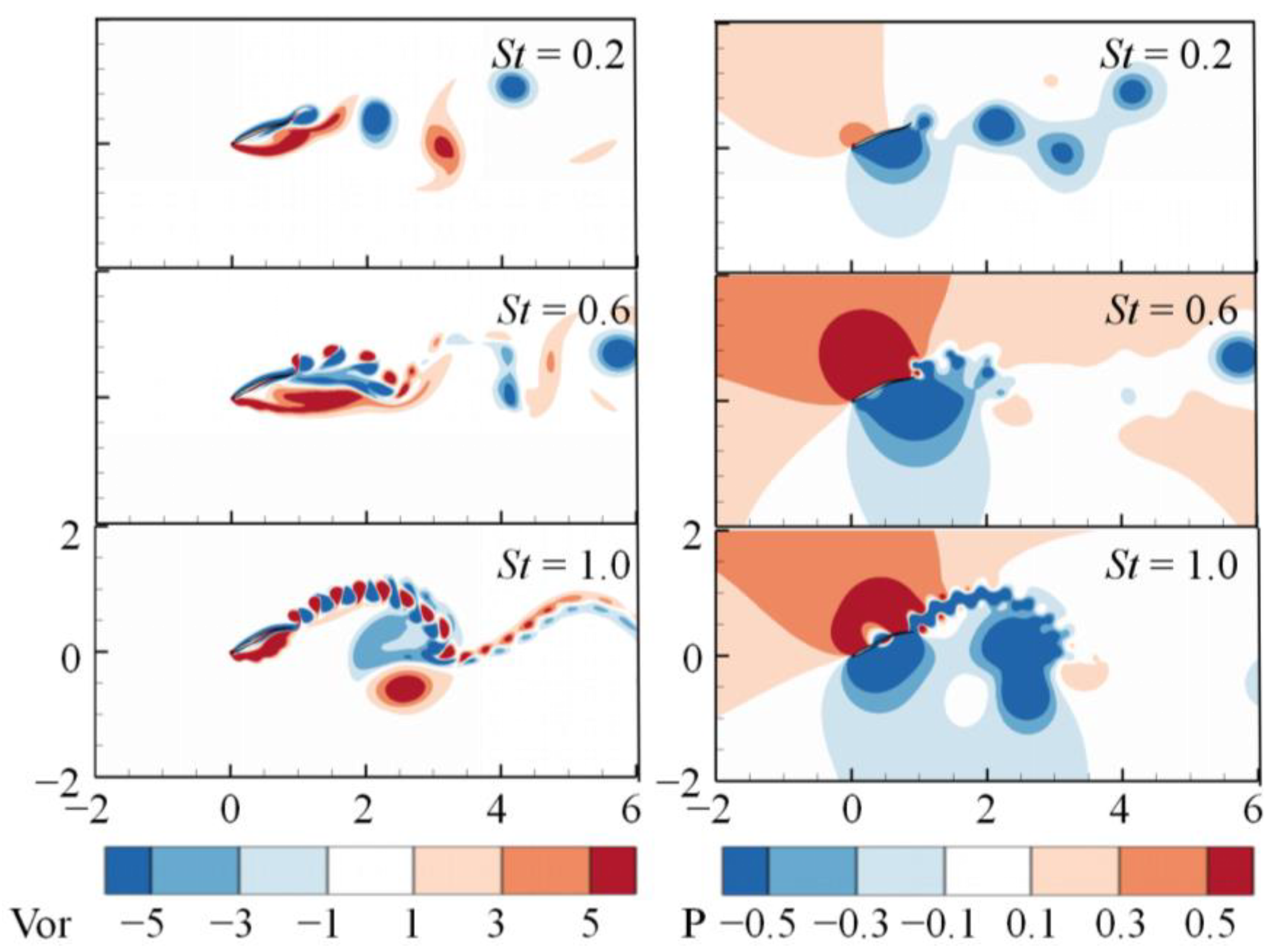
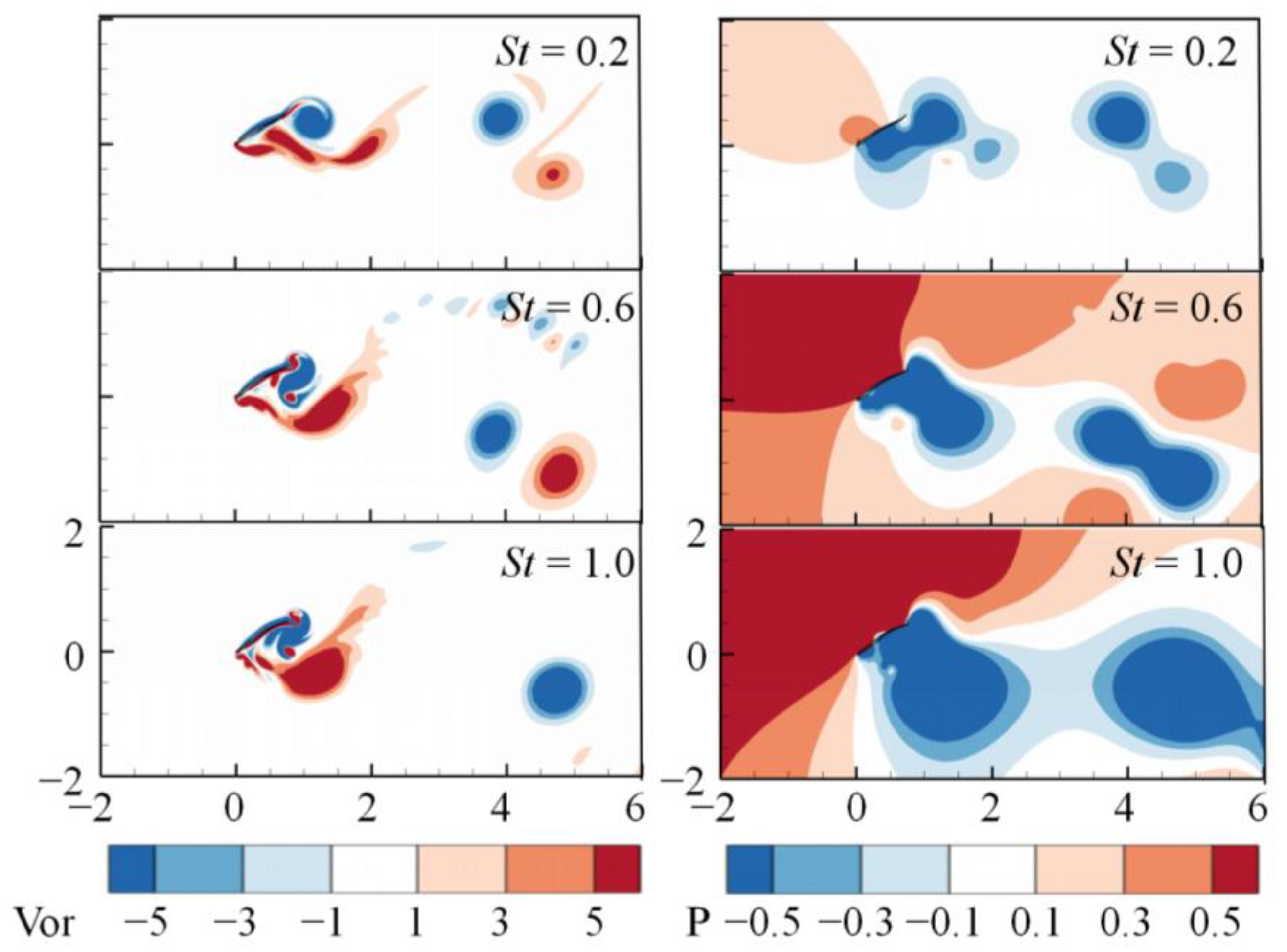
3. Numerical Results and Discussion
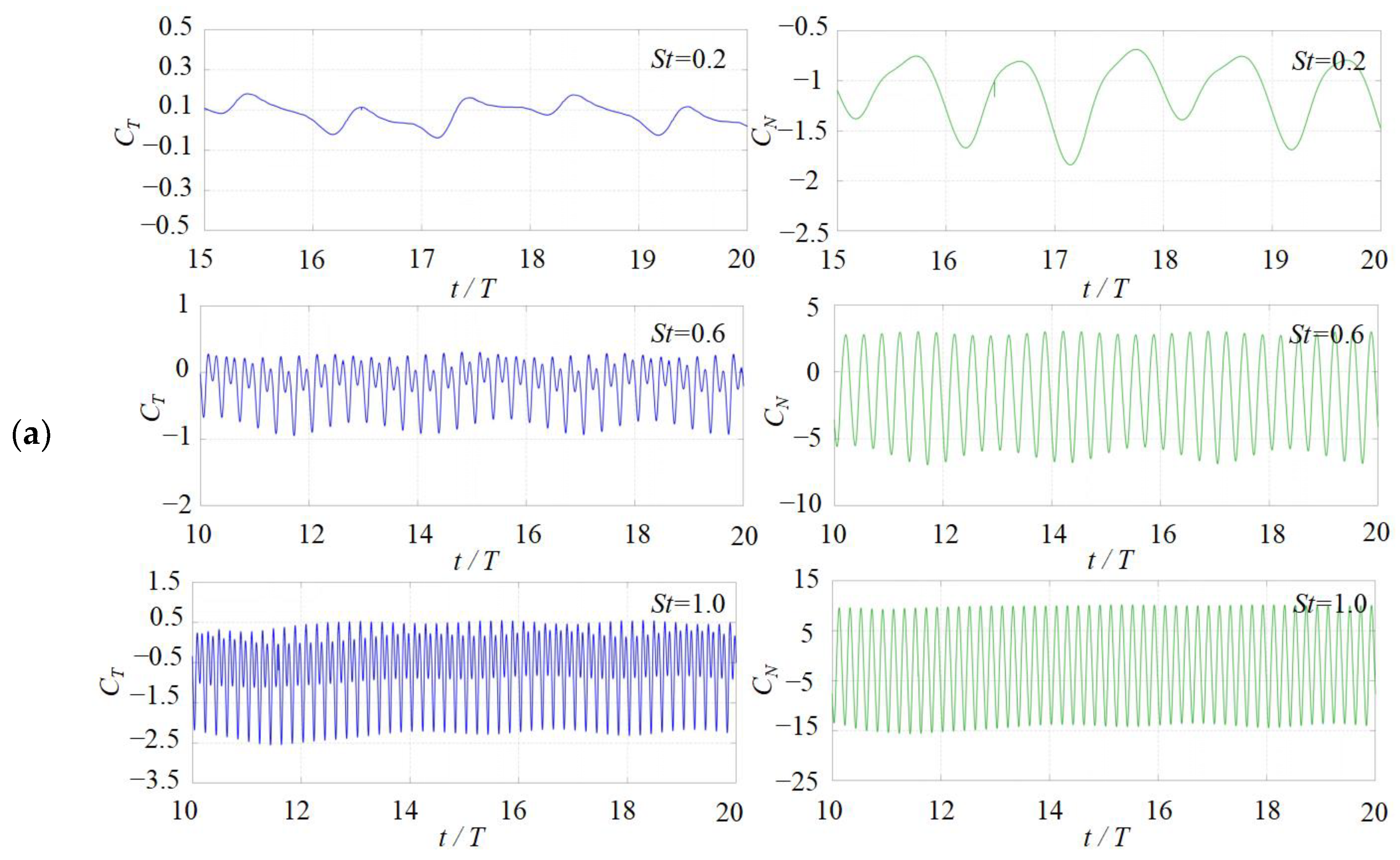
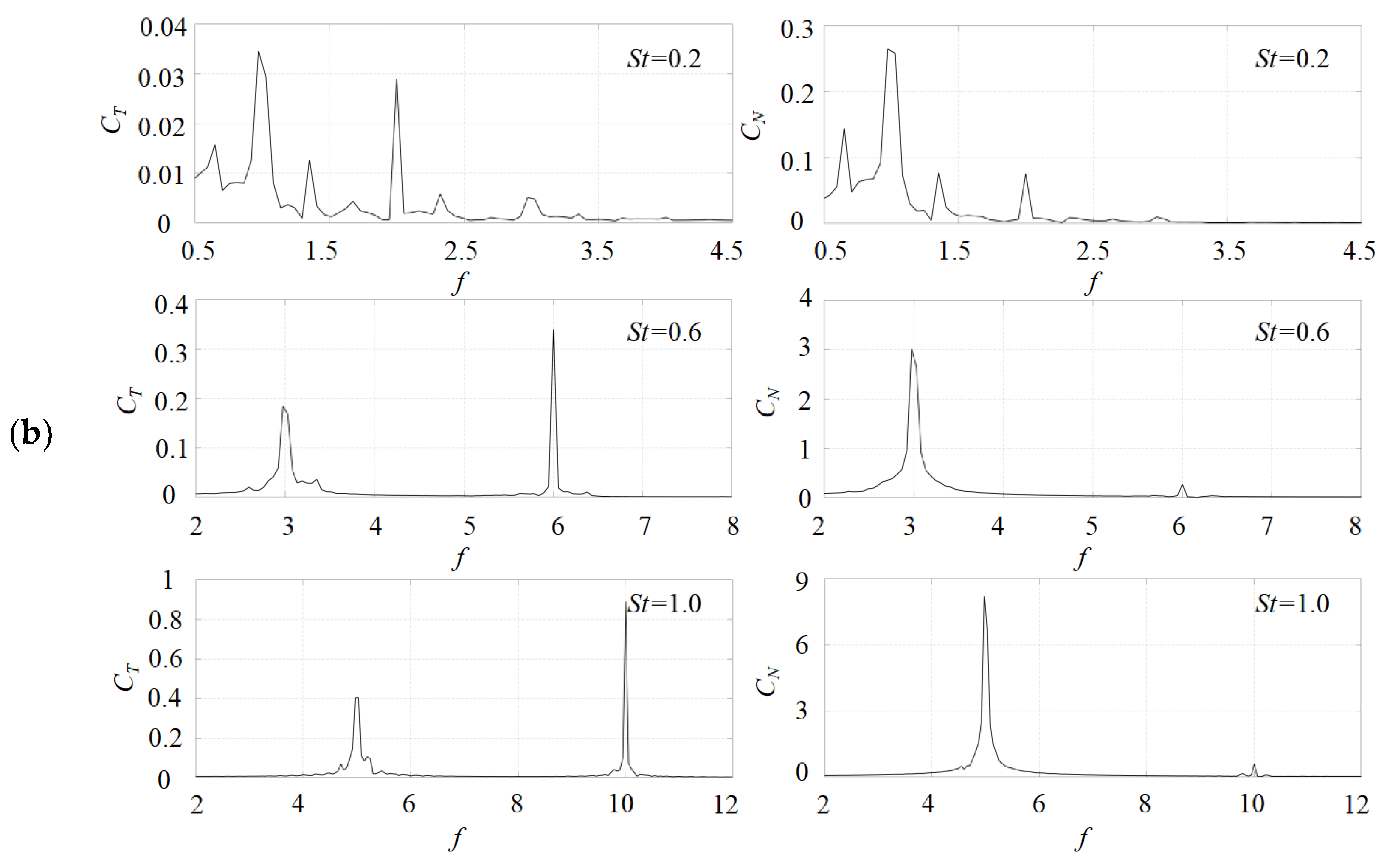
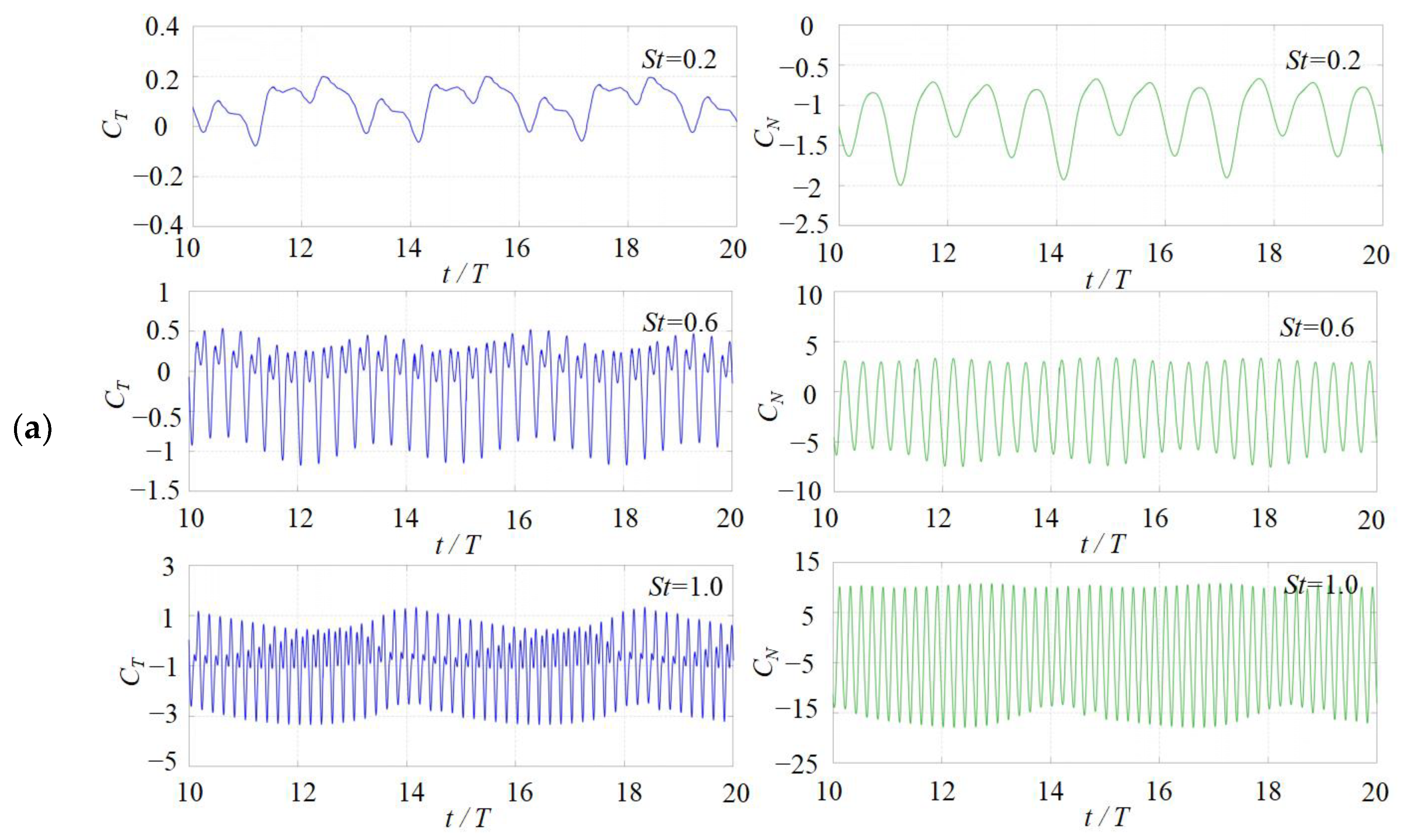
3.1. Effects of the Attack Angle
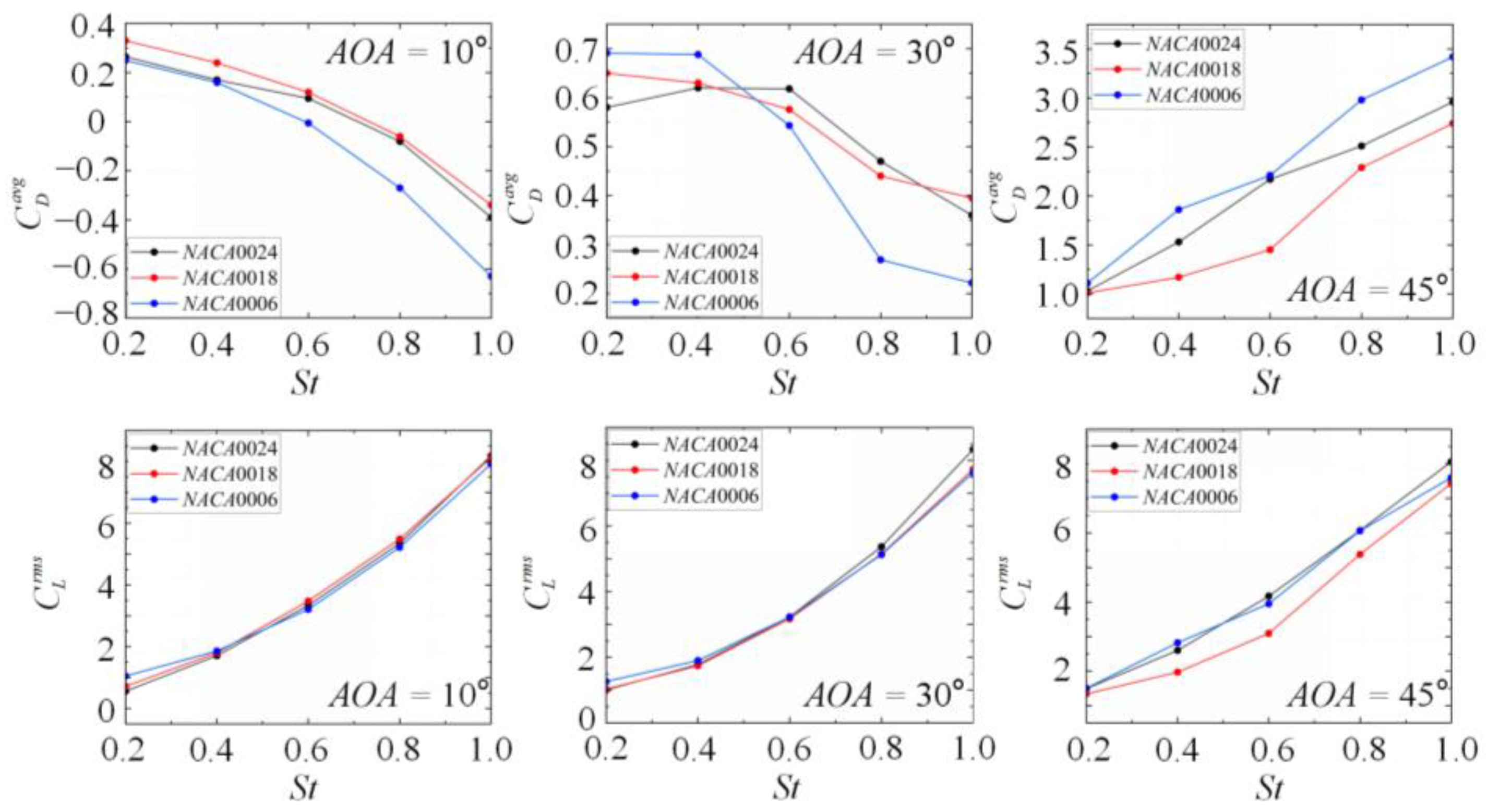
3.2. Effects of the Wing Shape
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| L (m) | Fish body length | U (m/s) | Free-stream velocity |
| t (s) | Time | AOA (°) | Angle of attack |
| η | Swimming efficiency | λ (m) | Wavelength |
| Ρ (Kg/m3) | Density | St | Strouhal numbers |
| T (s) | Swimming cycle | f (Hz) | Vortex shedding frequency |
| Re | Reynolds number | FL, FD (N) | Lift and drag forces on the fish |
| μ (Pa·s) | Kinematic viscosity | FT, FN (N) | Tangential and normal forces on the fish |
| K (m−1) | Wave number | PT (w) | Total power |
| C (m/s) | Phase velocity | Average drag coefficient | |
| CD | Drag coefficient | Root mean square lift coefficient | |
| CL | Lift coefficient | Zuida lift coefficient | |
| CT | Tangential coefficient | Average tangential coefficient | |
| CN | Normal coefficient | Root mean square normal coefficient |
References
- Liao, C. A review of fish swimming mechanics and behaviour in altered flows. Philos. Trans. R. Soc. B Biol. Sci. 2007, 362, 1973–1993. [Google Scholar] [CrossRef] [PubMed]
- Jia, L.; Chen, X. Undulation locomotion analysis of fish in cruising swimming. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2018, 232, 2494–2499. [Google Scholar] [CrossRef]
- Wang, Y.; Tan, J.; Zhao, D. Design and experiment on a biomimetic robotic fish inspired by freshwater stingray. J. Bionic Eng. 2015, 12, 204–216. [Google Scholar] [CrossRef]
- Xue, G.; Bai, F.; Li, Z.; Liu, Y. Experiment for Effect of Attack Angle and Environmental Condition on Hydrodynamics of Near-Surface Swimming Fish-Like Robot. Appl. Bionics Biomech. 2023, 2023, 4377779. [Google Scholar] [CrossRef]
- Wang, M.; Dong, H.; Li, X.; Zhang, Y.; Yu, J. Control and optimization of a bionic robotic fish through a combination of CPG model and PSO. Neurocomputing 2019, 337, 144–152. [Google Scholar] [CrossRef]
- Wei, C.; Hu, Q.; Liu, Y.; Yin, S.; Chen, Z.; Ji, X. Performance evaluation and optimization for two-dimensional fish-like propulsion. Ocean. Eng. 2021, 233, 109191. [Google Scholar] [CrossRef]
- Wei, C.; Hu, Q.; Zhang, T.; Zeng, Y. Passive hydrodynamic interactions in minimal fish schools. Ocean. Eng. 2022, 247, 110574. [Google Scholar] [CrossRef]
- Shua, C.; Liua, N.; Chewa, Y.; Lub, Z. Numerical simulation of fish motion by using lattice Boltzmann-Immersed Boundary Velocity Correction Method. J. Mech. Sci. Technol. 2007, 21, 1352–1358. [Google Scholar] [CrossRef]
- Zhang, J.; Lv, Z.; Hua, H.; Zhang, C.; Yu, H.; Jiao, Y. Numerical Study of the Fish-like Robot Swimming in Fluid with High Reynolds Number: Immersed Boundary Method. Actuators 2022, 11, 158. [Google Scholar] [CrossRef]
- Macias, M.M.; Souza, I.F.; Junior, A.C.B.; Oliveira, T.F. Three-dimensional viscous wake flow in fish swimming-A CFD study. Mech. Res. Commun. 2020, 107, 103547. [Google Scholar] [CrossRef]
- Liu, G.; Ren, Y.; Dong, H.; Akanyeti, O.; Liao, J.C.; Lauder, G.V. Computational analysis of vortex dynamics and performance enhancement due to body–fin and fin–fin interactions in fish-like locomotion. J. Fluid Mech. 2017, 829, 65–88. [Google Scholar] [CrossRef]
- Xia, D.; Chen, W.; Liu, J.; Wu, Z. Effect of head swing motion on hydrodynamic performance of fishlike robot propulsion. J. Hydrodyn. Ser. B. 2016, 28, 637–647. [Google Scholar] [CrossRef]
- Xia, D.; Chen, W.-S.; Liu, J.-K.; Luo, X. Using spanwise flexibility of caudal fin to improve swimming performance for small fishlike robots. J. Hydrodyn. 2018, 30, 859–871. [Google Scholar] [CrossRef]
- Kopman, V.; Laut, J.; Acquaviva, F.; Porfiri, M. Dynamic modeling of a robotic fish propelled by a compliant tail. Ocean. Eng. 2014, 40, 209–221. [Google Scholar] [CrossRef]
- Liu, P.; Wang, S.; Liu, R.; Shang, Z. Effects of St and Re on propulsive performance of bionic oscillating caudal fin. Ocean. Eng. 2020, 217, 107933. [Google Scholar] [CrossRef]
- Ghommem, M.; Bourantas, G.; Wittek, A.; Miller, K.; Hajj, M.R. Hydrodynamic modeling and performance analysis of bio-inspired swimming. Ocean. Eng. 2020, 197, 106897. [Google Scholar] [CrossRef]
- Zhao, Z.; Dou, L. Effects of the structural relationships between the fish body and caudal fin on the propulsive performance of fish. Ocean. Eng. 2019, 186, 106117. [Google Scholar] [CrossRef]
- Liu, G.; Liu, S.; Xie, Y.; Leng, D.; Li, G. The analysis of biomimetic caudal fin propulsion mechanism with CFD. Appl. Bionics Biomech. 2020, 2020, 7839049. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Z.J. Research on Modeling and Performance Analysis of Underwater Bionic Propulsion Based on Numerical Simulation. Ph.D. Thesis, Nanjing University of Science and Technology, Nanjing, China, 2021. [Google Scholar]
- Han, P.; Lauder, G.V.; Dong, H. Hydrodynamics of median-fin interactions in fish-like locomotion: Effects of fin shape and movement. Phys. Fluids 2020, 32, 011902. [Google Scholar] [CrossRef]
- Luo, Y.; Xiao, Q.; Shi, G.; Wen, L.; Chen, D.; Pan, G. A fluid–structure interaction solver for the study on a passively deformed fish fin with non-uniformly distributed stiffness. J. Fluids Struct. 2020, 92, 102778. [Google Scholar] [CrossRef]
- Maertens, A.P.; Gao, A.; Triantafyllou, M.S. Optimal undulatory swimming for a single fish-like body and for a pair of interacting swimmers. J. Fluid Mech. 2017, 813, 301–345. [Google Scholar] [CrossRef]
- Deng, J.; Shao, X.; Ren, A. Numerical study on propulsive performance of fish-like swimming foils. J. Hydrodyn. 2006, 18, 681–687. [Google Scholar] [CrossRef]
- Lin, Z.; Bhalla, A.P.S.; Griffith, B.E.; Sheng, Z.; Li, H.; Liang, D.; Zhang, Y. How swimming style and schooling affect the hydrodynamics of two accelerating wavy hydrofoils. Ocean. Eng. 2023, 268, 113314. [Google Scholar] [CrossRef]
- Gao, A.; Triantafyllou, M.S. Independent caudal fin actuation enables high energy extraction and control in two-dimensional fish-like group swimming. J. Fluid Mech. 2018, 850, 304–335. [Google Scholar] [CrossRef]
- Li, L.; Nagy, M.; Graving, J.M.; Bak-Coleman, J.; Xie, G.; Couzin, I.D. Vortex phase matching as a strategy for schooling in robots and in fish. Nat. Commun. 2020, 11, 5408. [Google Scholar] [CrossRef] [PubMed]
- Berchiche, N.; Krasilnikov, V.I.; Koushan, K. Numerical analysis of azimuth propulsor performance in seaways: Influence of oblique inflow and free surface. J. Mar. Sci. Eng. 2018, 6, 37. [Google Scholar] [CrossRef]
- Han, L.H. Theoretical Analysis and Simulation Study on Passive Propulsion of Robotic Fish. Master’s Thesis, Harbin Institute of Technology, Harbin, China, 2009. [Google Scholar]
- Li, R.; Xiao, Q.; Liu, Y.; Li, L.; Liu, H. Computational investigation on a self-propelled pufferfish driven by multiple fins. Ocean. Eng. 2020, 197, 106908. [Google Scholar] [CrossRef]
- Yan, L.; Chang, X.; Tian, R.; Wang, N.; Zhang, L.; Liu, W. A numerical simulation method for bionic fish self-propelled swimming under control based on deep reinforcement learning. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2020, 234, 3397–3415. [Google Scholar] [CrossRef]
- Nouroozi, H.; Zeraatgar, H. Propeller hydrodynamic characteristics in oblique flow by unsteady RANSE solver. Pol. Marit. Res. 2020, 27, 6–17. [Google Scholar] [CrossRef]
- Yu, J.; Wang, T.; Wu, Z.; Tan, M. Design of a miniature underwater angle-of-attack sensor and its application to a self-propelled robotic fish. Ocean. Eng. 2019, 45, 1295–1307. [Google Scholar] [CrossRef]
- Kang, D.; Xiong, T.; Fang, Z.L.; Chen, Y. Large Eddy Simulation of Flow Field Cleaning Robot under Oblique Flow. Ship Eng. 2023, 45, 21–26+158. [Google Scholar]
- Shao, Y.; Li, T.Q. Fish-like swimming in oblique flows: A numerical investigation. Ocean. Eng. 2021, 230, 109005. [Google Scholar] [CrossRef]
- Xia, D.; Chen, W.; Liu, J.; Wu, Z.; Cao, Y. The three-dimensional hydrodynamics of thunniform swimming under self-propulsion. Ocean Eng. 2015, 110, 1–14. [Google Scholar] [CrossRef]
- Matthews, D.J.; Zhu, R.J.; Wang, S.; Dong, H.B.; Bart-Smith, H.; Lauder, G. Role of the caudal peduncle in a fish-inspired robotic model: How changing stiffness and angle of attack affects swimming performance. Bioinspir. Biomim. 2022, 17, 066017. [Google Scholar] [CrossRef] [PubMed]
- Yu, M.; Wang, Z.J.; Hu, H. High fidelity numerical simulation of airfoil thickness and kinematics effects on flapping airfoil propulsion. J. Fluids Struct. 2013, 42, 166–186. [Google Scholar] [CrossRef]
- Sankarasubramanian, R.; Sridhar, A.; Prashanth, M.; Mohammad, A.; Velamati, R.K.; Laxman, V. Influence of thickness on performance characteristics of non-sinusoidal plunging motion of symmetric airfoil. Aerosp. Sci. Technol. 2018, 81, 333–347. [Google Scholar] [CrossRef]
- Tanvir Ahmed, S.; Hasan Shanto, M. Effects of Trailing Edge Thickness on NACA 4412 Airfoil Performance at Low Reynolds Numbers: A CFD Analysis. arXiv 2024, arXiv:2409.13922. [Google Scholar]
- Wang, P.; Wang, L.; Kong, X.; Wu, D.; Huang, B. Influence of relative thickness on static and dynamic stall characteristics and prediction of airfoils. Ocean. Eng. 2023, 271, 113690. [Google Scholar] [CrossRef]
- Li, Y.; Li, Y.; Pan, Z. Self-propulsion characteristics of fish-like undulating foil–a numerical investigation. Ships Offshore Struct. 2023, 19, 1504–1515. [Google Scholar] [CrossRef]
- Khalid, M.S.U.; Akhtar, I.; Dong, H. Hydrodynamics of a tandem fish school with asynchronous undulation of individuals. J. Fluids Struct. 2016, 66, 19–35. [Google Scholar] [CrossRef]
- Shi, F.; Xin, J.; Yin, P.; Dong, Y. A GPU accelerated three-dimensional ghost cell method with an improved implicit surface representation for complex rigid or flexible boundary flows. Comput. Phys. Commun. 2024, 298, 109098. [Google Scholar] [CrossRef]
- Shi, F.; Xin, J.; Liu, X.; Shu, L.; Chang, X.; Cheng, Y. Symmetrical and asymmetrical water entry of a three-dimensional bow-flared section by a Cartesian grid multiphase flow model with multiple DOF motion. Ocean. Eng. 2024, 304, 117824. [Google Scholar] [CrossRef]
- Xin, J.; Shi, F.; Jin, Q.; Lin, C. A radial basis function based ghost cell method with improved mass conservation for complex moving boundary flows. Comput. Fluids 2018, 176, 210–225. [Google Scholar] [CrossRef]
- Abbott, I.H.; Von Doenhoff, A.E. Theory of Wing Sections: Including a Summary of Airfoil Data; Courier Corporation: San Francisco, CA, USA, 2012. [Google Scholar]
- Majumdar, D.; Bose, C.; Sarkar, S. Capturing the dynamical transitions in the flow-field of a flapping foil using immersed boundary method. J. Fluids Struct. 2020, 95, 102999. [Google Scholar] [CrossRef]
- Yin, P.; Xin, J.; Shi, F.; Gui, Q.; Yang, Y. 2-DOF vortex-induced vibration of two rigidly-connected cylinders in parallel and tandem arrangements by a Cartesian grid method. Ocean. Eng. 2024, 291, 116479. [Google Scholar] [CrossRef]





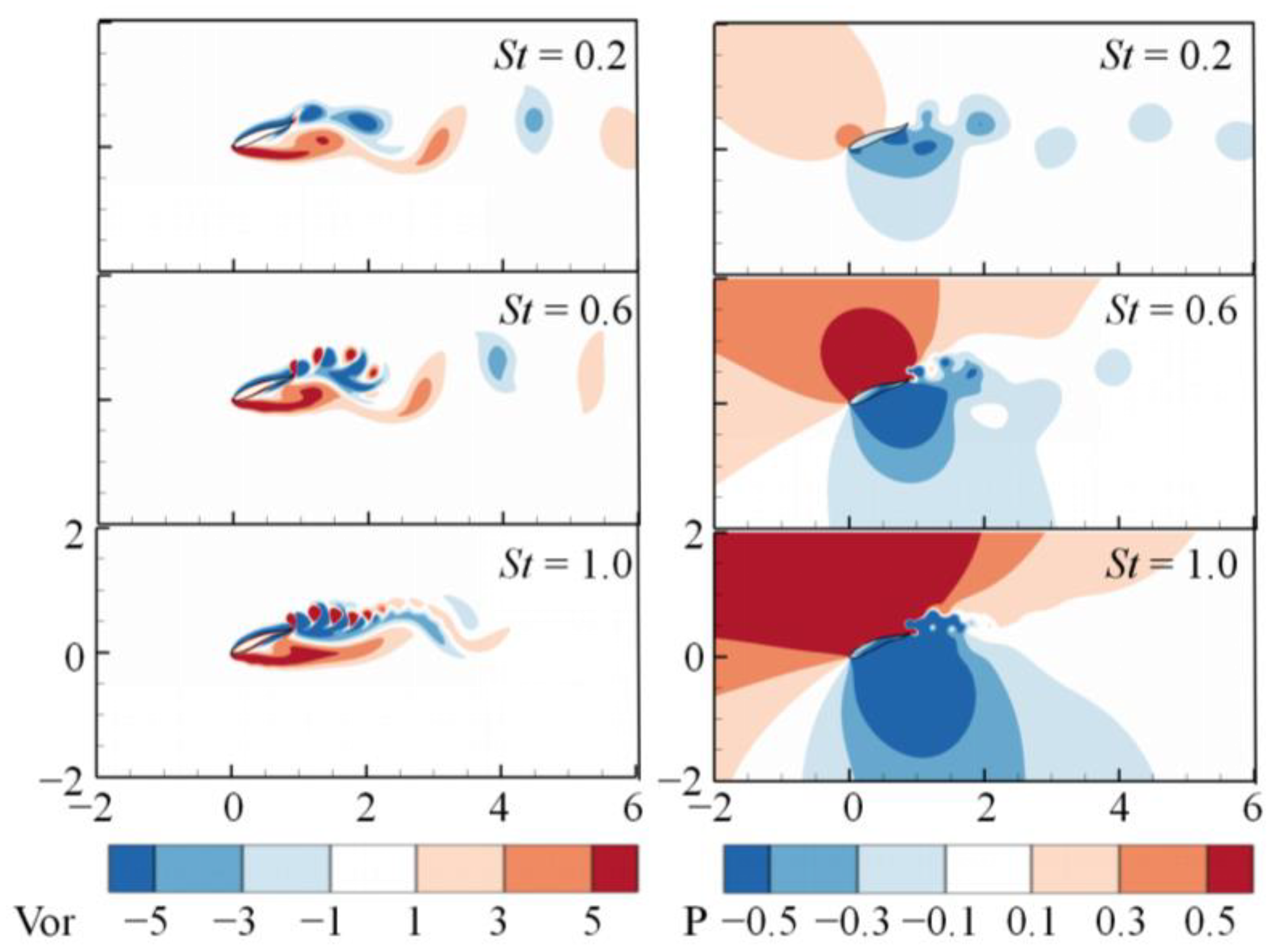
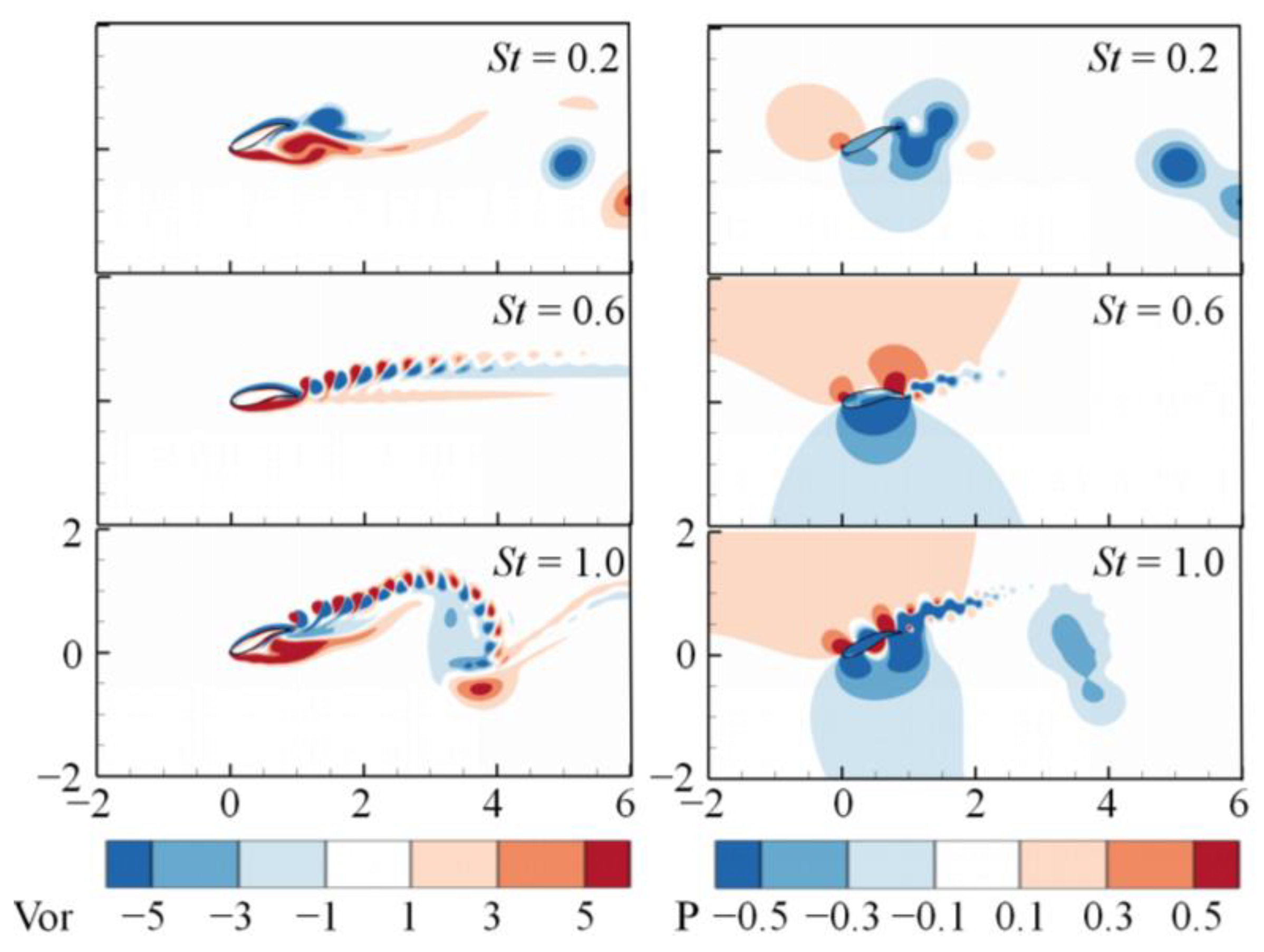
| Test Condition | Wing Shape | Angle of Attack | Strouhal Number |
|---|---|---|---|
| Case#1 | NACA0006 | 10°, 30°, 45° | 0.2, 0.4, 0.6, 0.8, 1.0 |
| Case#2 | NACA0018 | 10°, 30°, 45° | 0.2, 0.4, 0.6, 0.8, 1.0 |
| Case#3 | NACA0024 | 10°, 30°, 45° | 0.2, 0.4, 0.6, 0.8, 1.0 |
| Grid Notion | Grid Size | |||
|---|---|---|---|---|
| G1 | 200 × 80 | 0.0065, 0.005 | 7.10 | −0.35 |
| G2 | 260 × 120 | 0.0065, 0.005 | 7.23 | −0.39 |
| G3 | 350 × 180 | 0.0037, 0.0022 | 7.29 | −0.40 |
| G4 | 440 × 260 | 0.0031, 0.0015 | 7.37 | −0.41 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, F.; Tian, Y.; Xin, J.; Ou, C.; Li, Z.; Rao, M. Numerical Study on the Hydrodynamics of Fish Swimming with Different Morphologies in Oblique Flow. J. Mar. Sci. Eng. 2024, 12, 2302. https://doi.org/10.3390/jmse12122302
Shi F, Tian Y, Xin J, Ou C, Li Z, Rao M. Numerical Study on the Hydrodynamics of Fish Swimming with Different Morphologies in Oblique Flow. Journal of Marine Science and Engineering. 2024; 12(12):2302. https://doi.org/10.3390/jmse12122302
Chicago/Turabian StyleShi, Fulong, Yu Tian, Jianjian Xin, Chuanzhong Ou, Zhiwei Li, and Minjia Rao. 2024. "Numerical Study on the Hydrodynamics of Fish Swimming with Different Morphologies in Oblique Flow" Journal of Marine Science and Engineering 12, no. 12: 2302. https://doi.org/10.3390/jmse12122302
APA StyleShi, F., Tian, Y., Xin, J., Ou, C., Li, Z., & Rao, M. (2024). Numerical Study on the Hydrodynamics of Fish Swimming with Different Morphologies in Oblique Flow. Journal of Marine Science and Engineering, 12(12), 2302. https://doi.org/10.3390/jmse12122302







