A Comparative Analysis of Buckling Pressure Prediction in Composite Cylindrical Shells Under External Loads Using Machine Learning
Abstract
1. Introduction
2. Buckling Pressure Calculation
2.1. Analytical Approaches
2.2. Numerical Approach
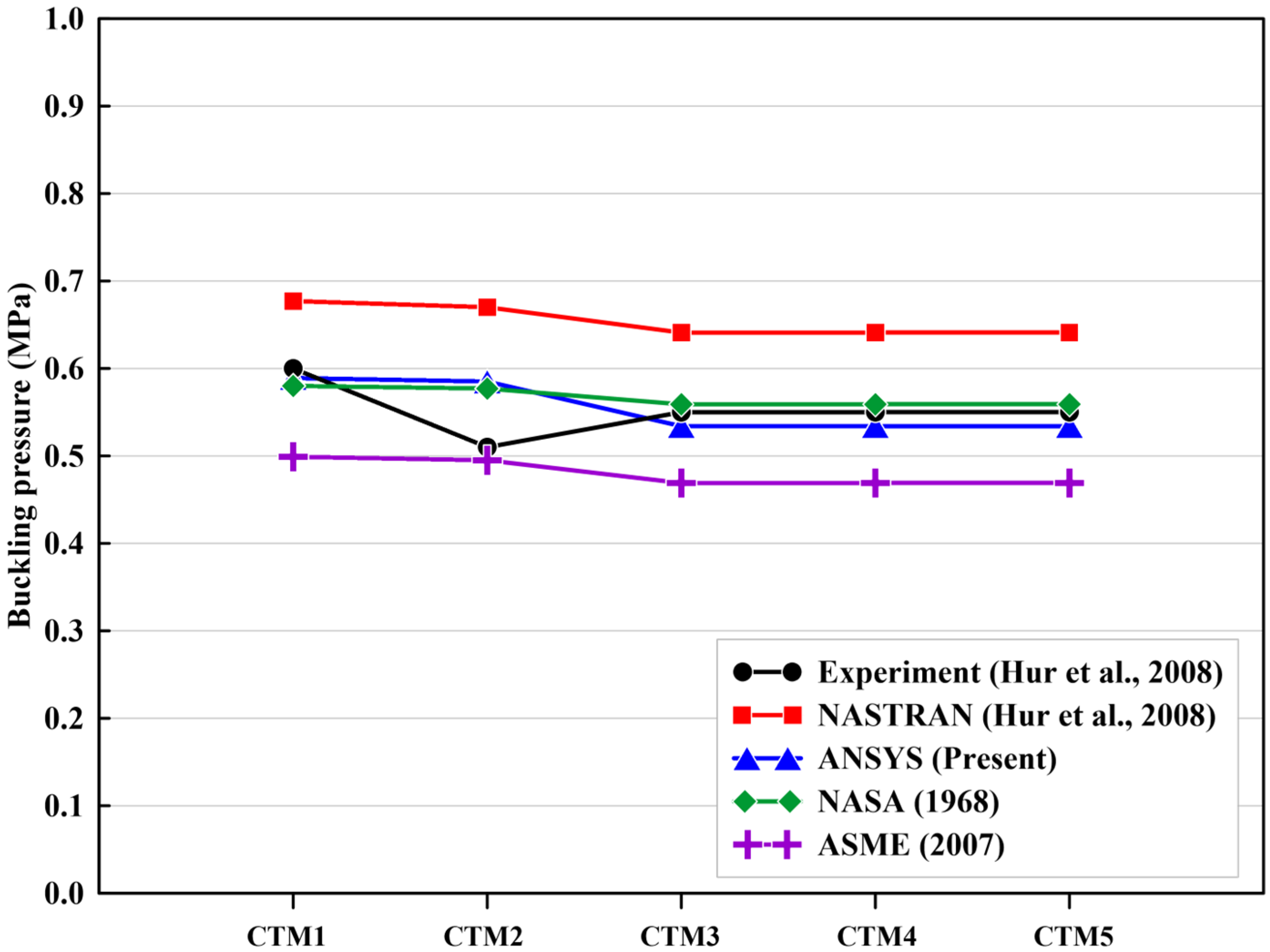
2.3. Validation with Experiment Data
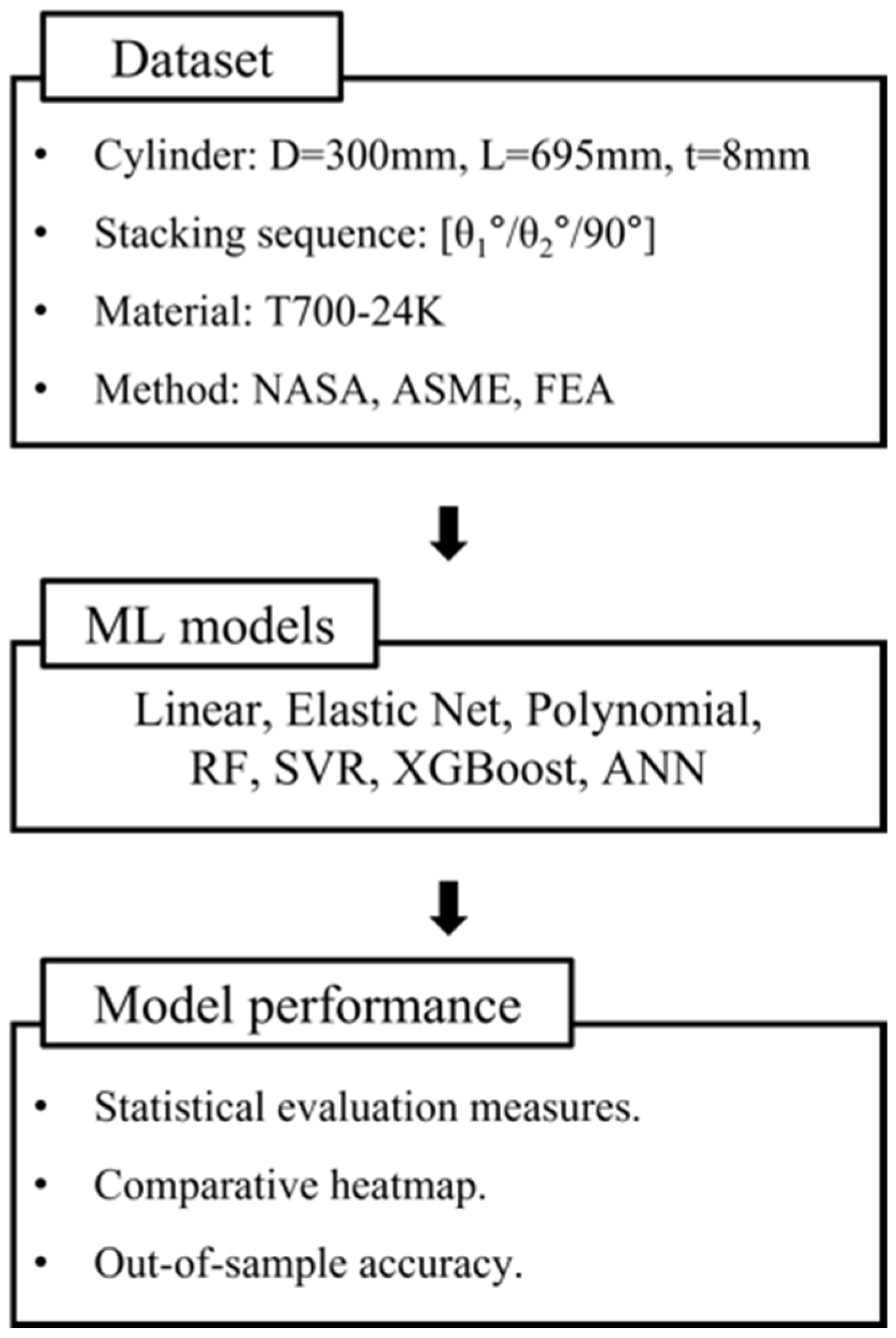
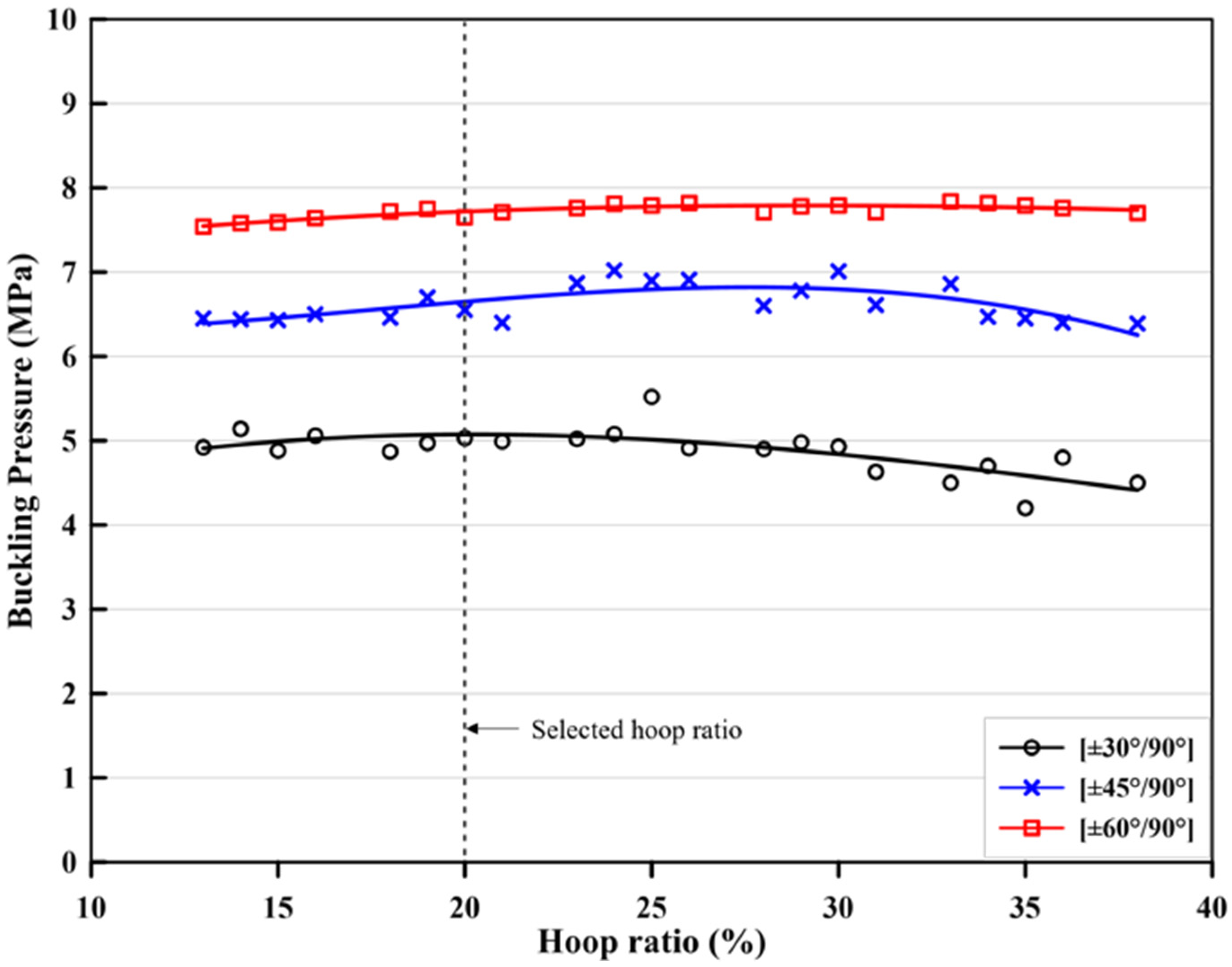
3. Data Collection and Suitability Analysis
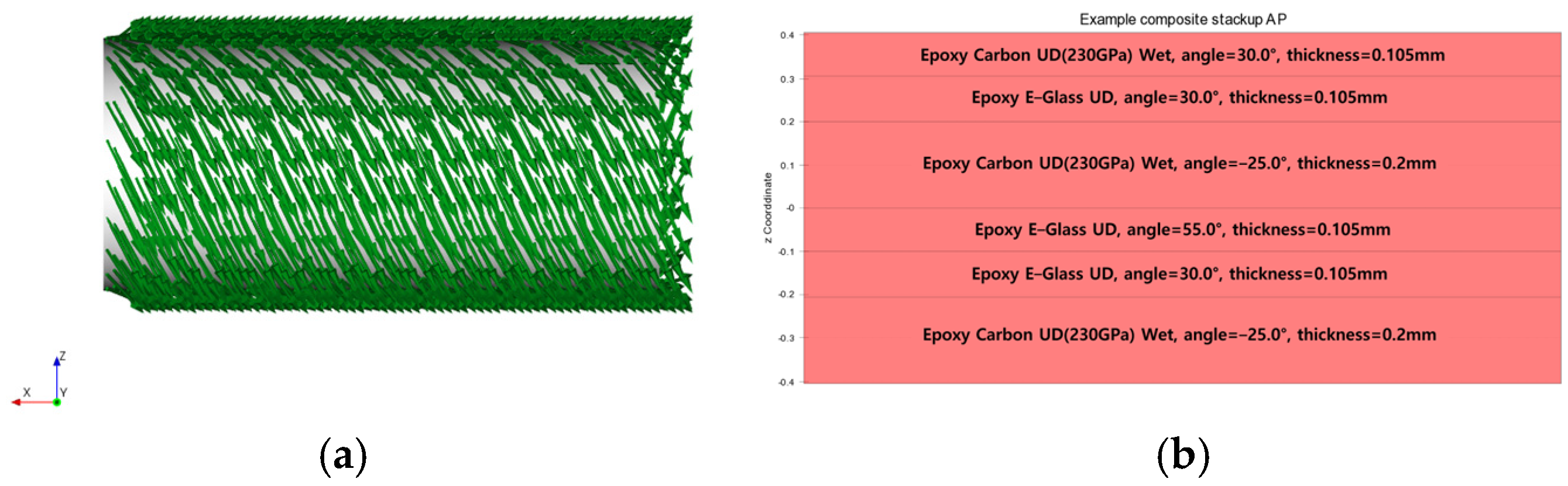
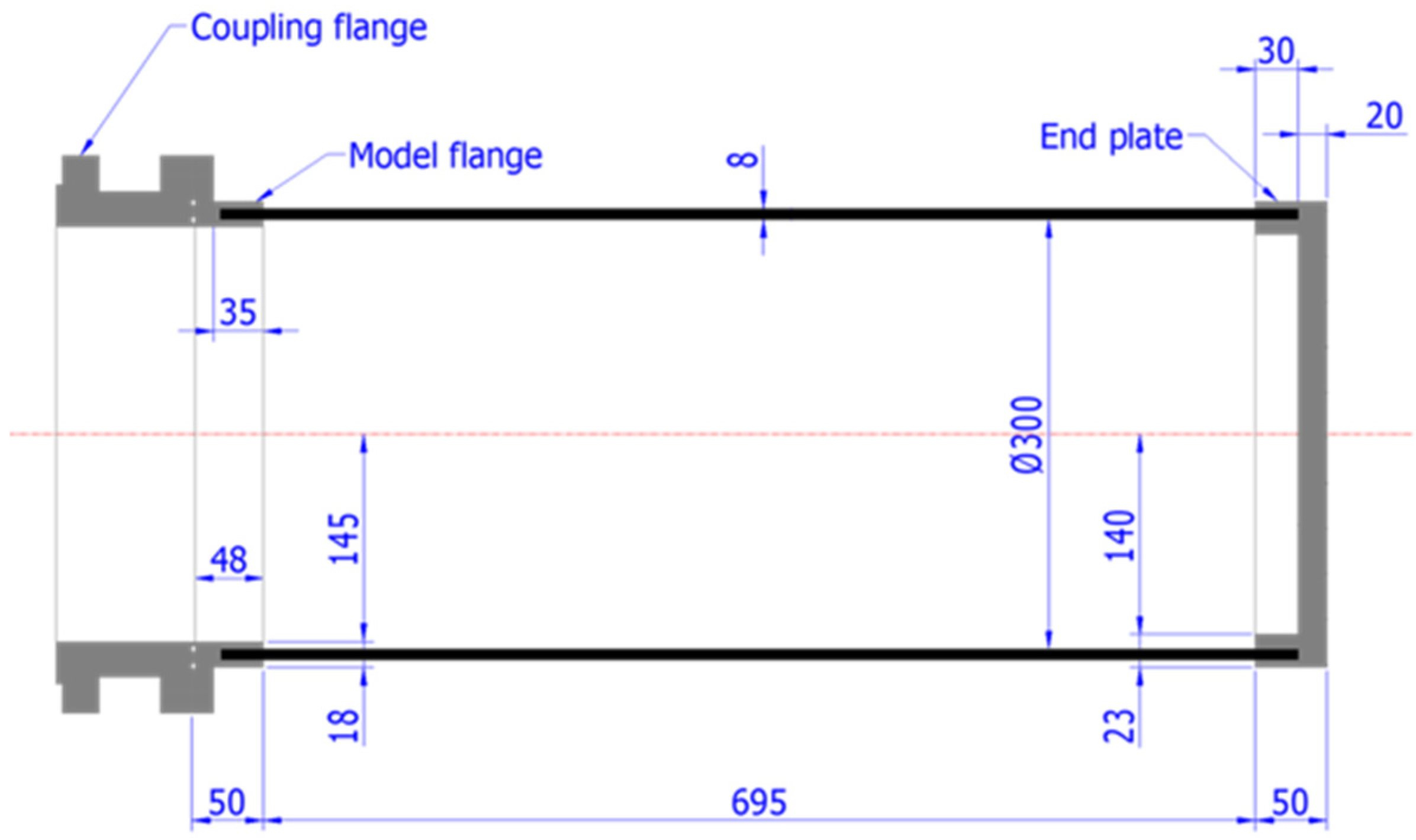
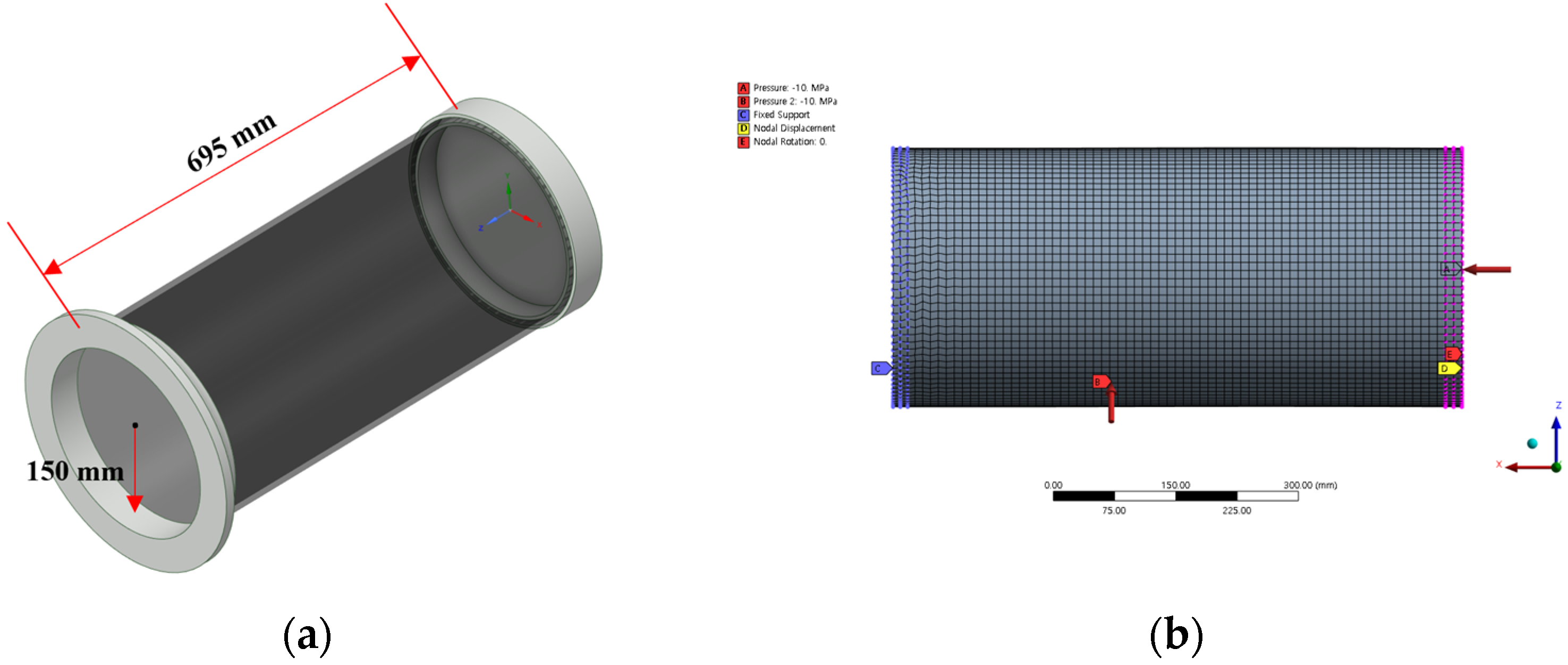
3.1. Composite Cylinder Model
3.2. Data Collection
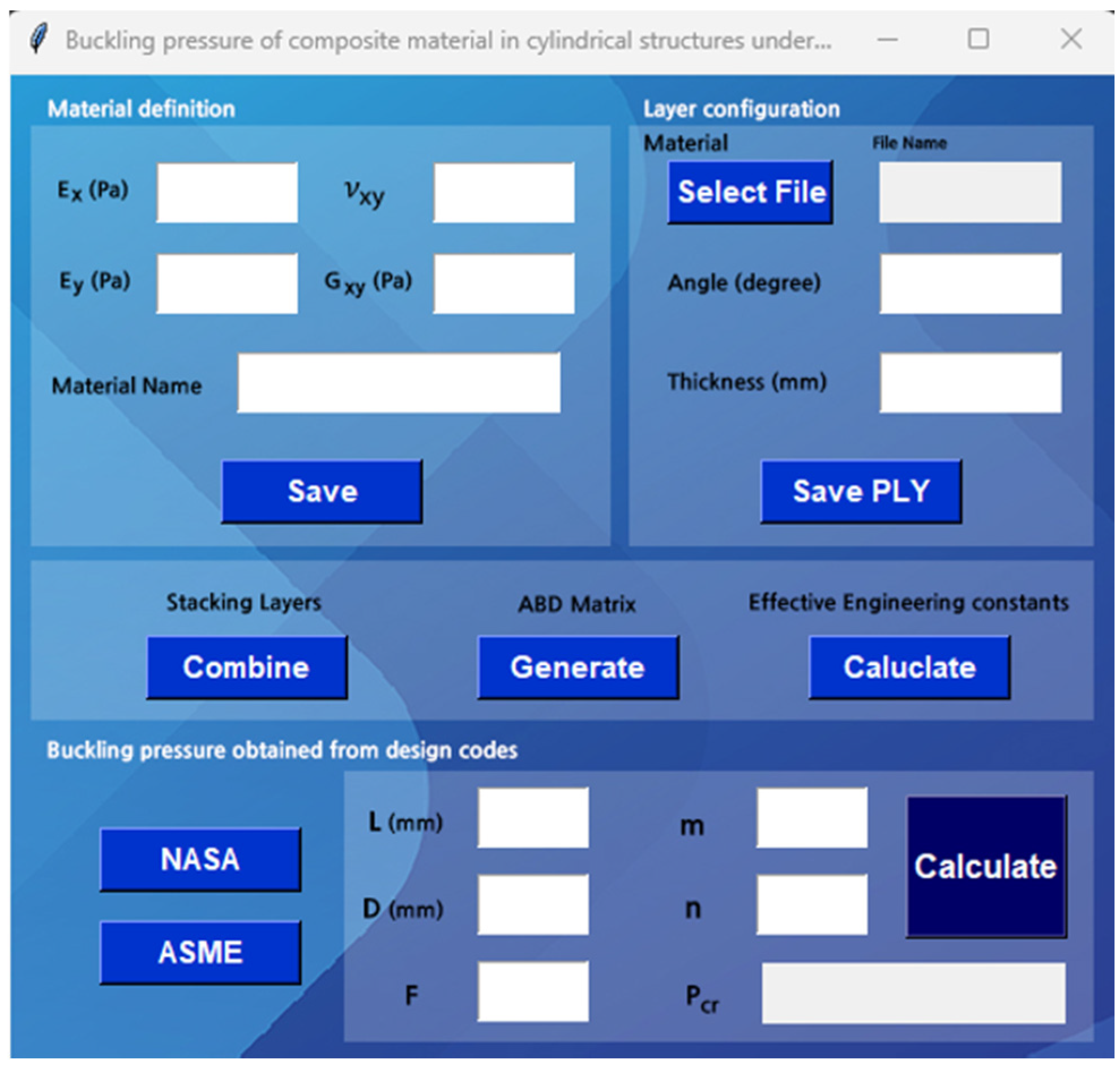
3.2.1. Analytical Approaches
- Composite material properties such as elastic modulus, shear modulus, and Poisson’s ratio are defined;
- A layer is composed by inputting the material, stacking angle, and thickness;
- It assembles the laminate, computes the ABD matrix, and calculates engineering constant;
- Buckling pressure was calculated based on two analytical approaches.
3.2.2. Numerical Approach
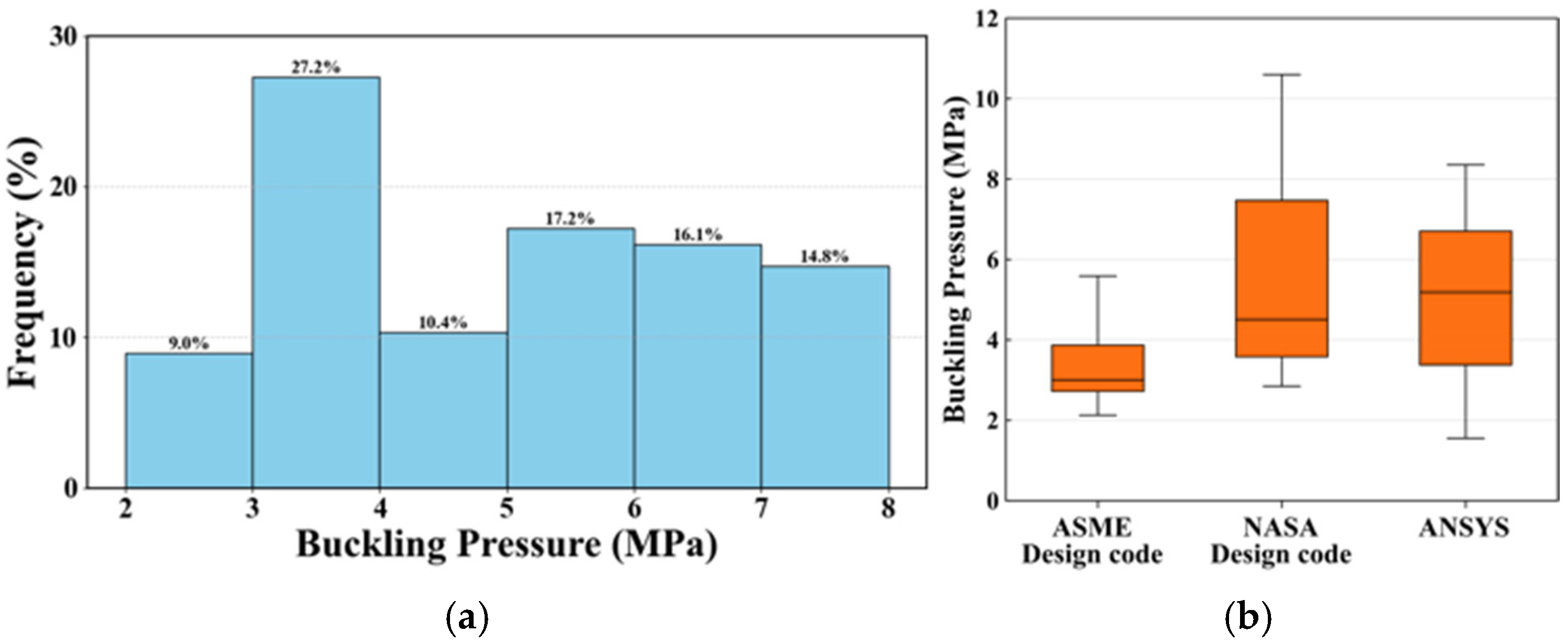
3.3. Data Suitability Analysis
- The ASME box plot showed the lowest median and a narrow range, indicating consistently lower buckling pressures;
- The NASA box plot featured the highest median with a wide range and significant spread above the 75th percentile, reflecting greater variability in the buckling pressure estimates;
- The ANSYS box plot presented an intermediate median with a balanced range and a more even distribution around the central values, along with fewer extreme outliers compared to the other methods.
4. Application of Machine Learning for Predicting Buckling Pressure
4.1. Machine Learning Models
- Linear regression: A basic model that assumes a linear relationship between input and output;
- Elastic net: A regularization method that combines Lasso and Ridge to improve model performance and prevent overfitting, especially with correlated features;
- Polynomial regression: Extends linear regression by fitting a polynomial curve to capture more complex relationships;
- Random forest (RF) regression: An ensemble method that combines multiple decision trees to improve prediction accuracy;
- Support vector regression (SVR): A model that finds the best fit within a margin of tolerance, effectively handling non-linear relationships;
- XGBoost regression: An advanced boosting method that optimizes predictive accuracy by combining multiple weak learners in an iterative manner;
- Artificial neural network (ANN): A neural network designed to learn patterns and relationships in data through interconnected layers of neurons, commonly used for a variety of tasks including classification and regression.
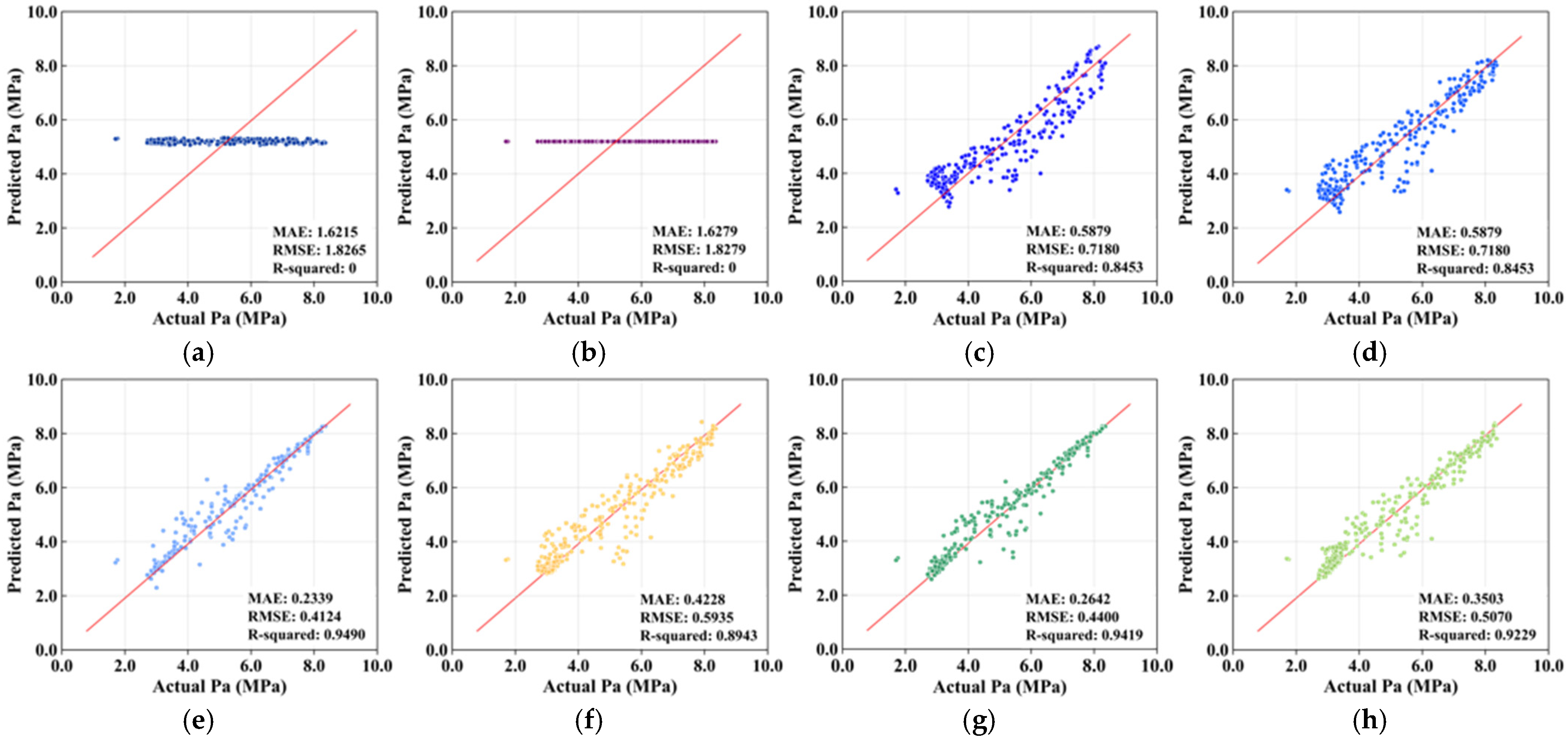
4.2. Model Performance
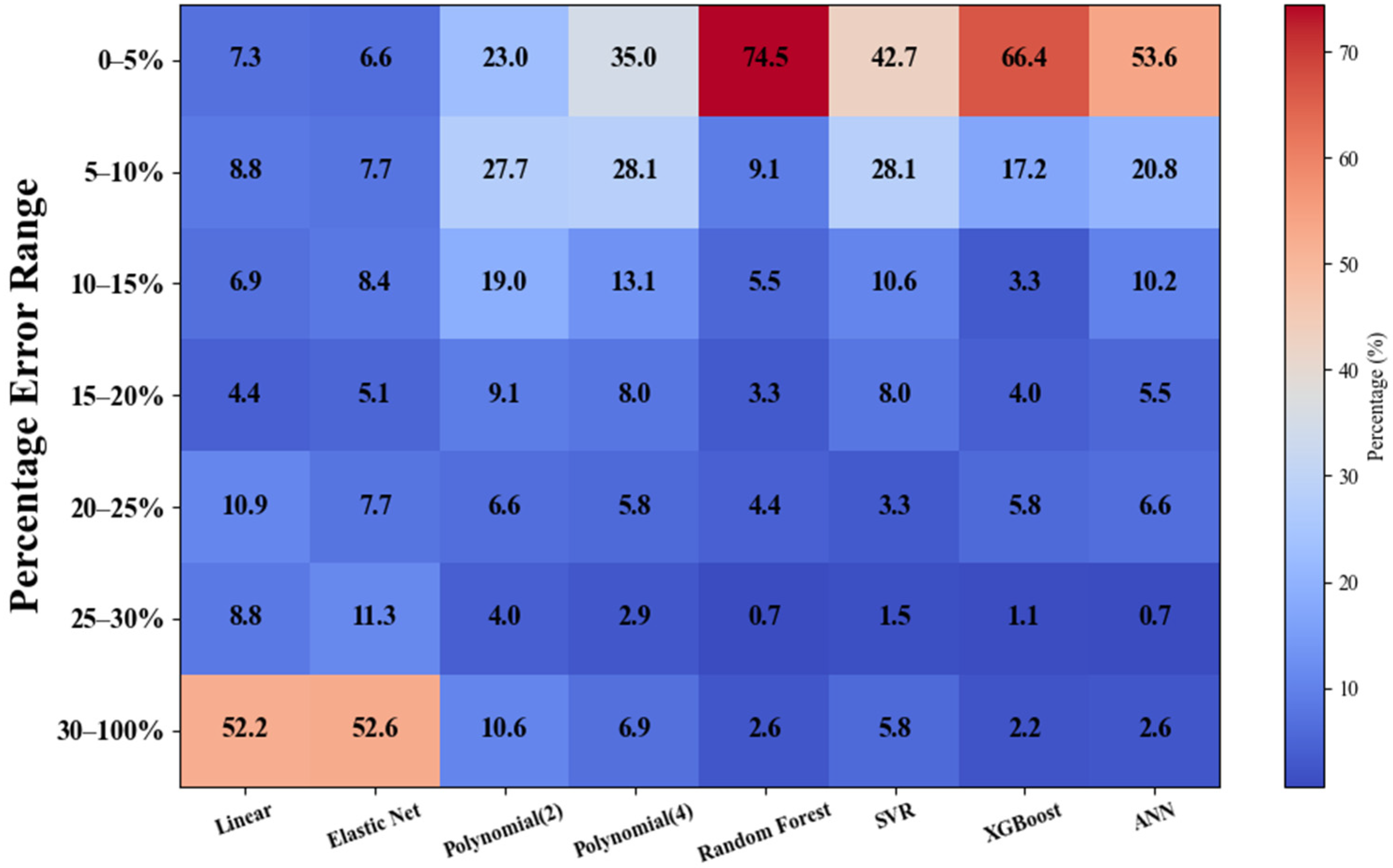
4.3. Comparative Analysis
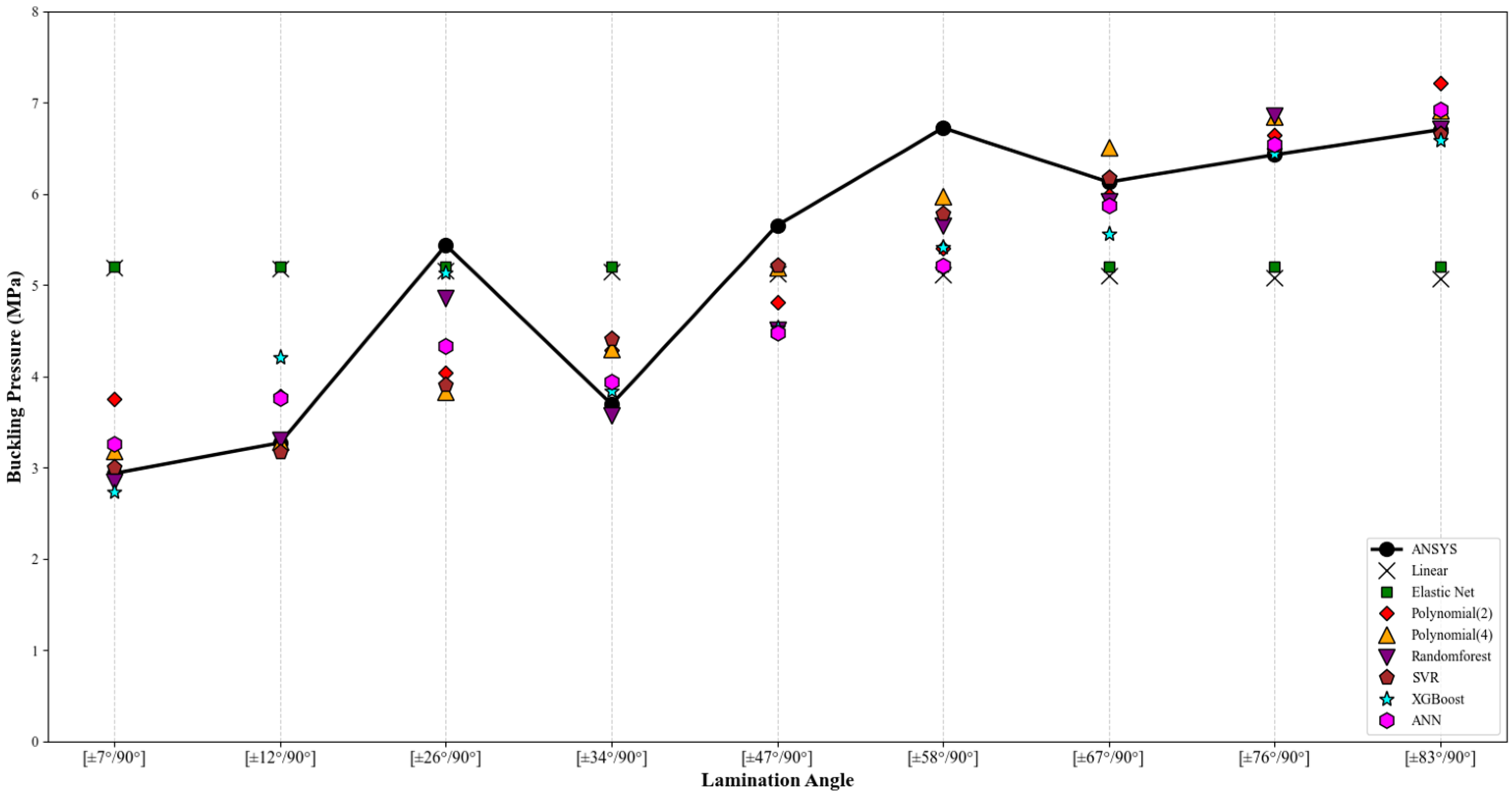
4.4. Out-of-Sample Accuracy Comparison
5. Conclusions
- The accuracy of the ASME, NASA, and ANSYS methods was evaluated through comparisons with the experimental data and analyzed using box plots, with ANSYS exhibiting the highest accuracy among the methods evaluated.
- A total of eight machine learning algorithms were employed to predict the buckling pressure, with their performance systematically evaluated and compared.
- Eight machine learning algorithms were employed to predict the buckling pressure, with random forest and XGBoost emerging as the most accurate and reliable models. ANN and SVR showed reasonable performance but with more variability, while linear regression and elastic net had high error rates and struggled to capture complex relationships. Polynomial regression (4th-order) showed an improvement over linear methods, but lacked the consistency of the top ensemble models.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Davies, P.; Choqueuse, D.; Bigourdan, B.; Chauchot, P. Composite Cylinders for Deep Sea Applications: An Overview. J. Press. Vess. Technol. 2016, 138, 060907. [Google Scholar] [CrossRef]
- Shen, K.C.; Pan, G.; Lu, J. Buckling and Layer Failure of Composite Laminated Cylinders Subjected to Hydrostatic Pressure. Sci. Eng. Compos. Mater. 2017, 24, 415–422. [Google Scholar] [CrossRef]
- Vasiliev, V.V. Mechanics of Composite Structures, 1st ed.; CRC Press: Boca Raton, FL, USA, 1993. [Google Scholar]
- Sun, G.; Mao, R. Optimization of Stiffened Laminated-Composite Circular-Cylindrical Shells for Buckling. Compos. Struct. 1993, 23, 53–60. [Google Scholar] [CrossRef]
- Nikbakt, S.; Kamarian, S.; Shakeri, M. A Review on Optimization of Composite Structures Part I: Laminated Composites. Compos. Struct. 2018, 195, 158–185. [Google Scholar] [CrossRef]
- Talebitooti, R.; Gohari, H.D.; Zarastvand, M.R. Multi-Objective Optimization of Sound Transmission Across Laminated Composite Cylindrical Shell Lined with Porous Core Investigating Non-Dominated Sorting Genetic Algorithm. Aerosp. Sci. Technol. 2017, 69, 269–280. [Google Scholar] [CrossRef]
- Rouhi, M.; Ghayoor, H.; Hoa, S.; Hojjati, M. Computational Efficiency and Accuracy of Multi-Step Design Optimization Method for Variable Stiffness Composite Structures. Thin-Walled Struct. 2017, 113, 136–143. [Google Scholar] [CrossRef]
- Cho, Y.S.; Oh, D.H.; Paik, J.K. An empirical formula for predicting the collapse strength of composite cylindrical-shell structures under external pressure loads. Ocean. Eng. 2019, 172, 191–198. [Google Scholar] [CrossRef]
- Imran, M.; Shi, D.; Tong, L.; Elahi, A.; Uddin, M. On the elastic buckling of cross-ply composite closed cylindrical shell under hydrostatic pressure. Ocean. Eng. 2011, 227, 108633. [Google Scholar] [CrossRef]
- Ehsani, A.; Rezaeepazhand, J. Stacking sequence optimization of laminated composite grid plates for maximum buckling load using genetic algorithm. Int. J. Mech. Sci. 2016, 119, 97–106. [Google Scholar] [CrossRef]
- Cho, Y.S.; Paik, J.K. Optimal Lamination Design of Composite Cylinders using an Empirical Ultimate Pressure Load Formula. J. Soc. Nav. Archit. Korea 2019, 56, 316–326. [Google Scholar] [CrossRef]
- Hur, S.H.; Son, H.J.; Kweon, J.H.; Choi, J.-H. Postbuckling of composite cylinders under external hydrostatic pressure. Compos. Struct. 2008, 86, 114–124. [Google Scholar] [CrossRef]
- Amaechi, C.V.; Gillett, N.; Odijie, A.C.; Hou, X.; Ye, J. Composite risers for deep waters using a numerical modelling approach. Compos. Struct. 2019, 210, 486–499. [Google Scholar] [CrossRef]
- Malinowski, M.; Belica, T.; Magnucki, K. Buckling and post-buckling behaviour of elastic seven-layered cylindrical shells—FEM study. Thin-Walled Struct. 2015, 94, 478–484. [Google Scholar] [CrossRef]
- Tsouvalis, N.; Zafeiratou, A.; Papazoglou, V. The effect of geometric imperfections on the buckling behaviour of composite laminated cylinders under external hydrostatic pressure. Compos. Part B Eng. 2003, 34, 217–226. [Google Scholar] [CrossRef]
- Shen, K.C.; Pan, G. Buckling and strain response of filament winding composite cylindrical shell subjected to hydrostatic pressure: Numerical solution and experiment. Compos. Struct. 2021, 276, 114534. [Google Scholar] [CrossRef]
- Moon, C.J.; Kim, I.H.; Choi, B.H.; Kweon, J.H.; Choi, J.H. Buckling of filament-wound composite cylinders subjected to hydrostatic pressure for underwater vehicle applications. Compos. Struct. 2010, 92, 2241–2251. [Google Scholar] [CrossRef]
- Joung, T.H.; Lee, C.H.; Hong, S.W.; Kim, J.B.; An, C.W. A study on the results of the pressure vessel design, structural analysis, and pressure test of the semi-autonomous underwater vehicle (SAUV). J. Ocean. Eng. Technol. 2004, 18, 52–58. [Google Scholar]
- Pathan, M.V.; Ponnusami, S.A.; Pathan, J.; Pitisongsawat, R.; Erice, B.; Petrinic, N.; Tagarielli, V.L. Predictions of the mechanical properties of unidirectional fib composites by supervised machine learning. Sci. Rep. 2019, 9, 13964. [Google Scholar] [CrossRef]
- Wagner, H.N.R.; Köke, H.; Dähne, S.; Niemann, S.; Hühne, C.; Khakimova, R. Decision tree-based machine learning to optimize the laminate stacking of composite cylinders for maximum buckling load and minimum imperfection sensitivity. Compos. Struct. 2019, 220, 45–63. [Google Scholar] [CrossRef]
- Zhang, Z.; Shi, J.; Yu, T.; Santomauro, A.; Gordon, A.; Gou, J.; Wu, D. Predicting flexural strength of additively manufactured continuous carbon fiber-reinforced polymer composites using machine learning. J. Comput. Inf. Sci. Eng. 2020, 20, 061015. [Google Scholar] [CrossRef]
- Zhang, C.; Li, Y.; Jiang, B.; Wang, R.; Liu, Y.; Jia, L. Mechanical properties prediction of composite laminate with FEA and machine learning coupled method. Compos. Struct. 2022, 299, 116086. [Google Scholar] [CrossRef]
- Cui, R.; Yang, H.; Li, J.; Xiao, Y.; Yao, G.; Yu, Y. Machine learning-based prediction of compressive strength in circular FRP-confined concrete columns. Front. Mater. 2024, 11, 1408670. [Google Scholar] [CrossRef]
- Nettles, A.T. Basic Mechanics of Laminated Composite Plates; No. NASA-RP-1351; NASA: Washington, DC, USA, 1994. [Google Scholar]
- Raju, I.S.; Wang, J.T. Classical laminate theory models for woven fabric composites. Compos. Technol. Res. 1994, 16, 289–303. [Google Scholar] [CrossRef]
- Weingarten, V.I.; Seide, P.; Peterson, J.P. Buckling of Thin-Walled Circular Cylinders; No. NASA-SP-8007; NASA: Washington, DC, USA, 1968. [Google Scholar]
- ASME. ASME Boiler and Pressure Vessel Code, Section X: Fiber-Reinforced Plastic Pressure Vessel; ASME: New York, NY, USA, 2007. [Google Scholar]
- ANSYS. Available online: https://www.ansys.com/products/ansys-workbench (accessed on 7 November 2024).
- Shipman, J.W. Tkinter 8.5 reference: A GUI for Python. N. Mex. Tech. Comput. Cent. 2013, 54, 356–359. [Google Scholar]
- Fushiki, T. Estimation of prediction error by using K-fold cross-validation. Stat. Comput. 2011, 21, 137–146. [Google Scholar] [CrossRef]
- Weir, B.S.; Hill, W.G. Estimating F-statistics. Annu. Rev. Genet. 2002, 36, 721–750. [Google Scholar] [CrossRef] [PubMed]
| Objective | Structure Type | ML Model | Input | Output | Reference |
|---|---|---|---|---|---|
| Evaluate failure strength under different loading conditions | CFRP with different laminate stacking | Artificial neural network (ANN) | Fiber orientation load conditions | Failure strength | [19] |
| Optimize stacking for max. buckling load, min. imperfection | Composite cylindrical Shells | Decision tree | Stacking sequence imperfection | Buckling load imperfection | [20] |
| Predict mechanical properties and assess design parameter’s impact | CFRP composite laminate | Neural networks Random forest | Laminate lay-up material properties | Mechanical properties | [21] |
| Predict flexural strength of additively manufactured CCFRP | CCFRP composites by FDM | Ensemble learning | Fiber layers, fiber rings, infill patterns | Flexural strength | [22] |
| Predict buckling pressure and failure behavior | Composite pressure vessels | Random forest | Material properties geometrical features | Buckling pressure | [23] |
| Elastic Modulus (GPa) | Poisson’s Ratio (−) | Shear Strength (GPa) | Tensile Strength (MPa) | Shear Strength (MPa) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 121 | 8.6 | 8.6 | 0.253 | 0.253 | 0.421 | 3.35 | 3.35 | 2.68 | 2060 | 32 | 32 | 45 | 45 | 64 |
| No. | t1 (mm) | θ1 (Degree) | t2 (mm) | θ2 (Degree) | Pcr_ASME (MPa) | Pcr_NASA (MPa) | Pcr_ANSYS (MPa) |
|---|---|---|---|---|---|---|---|
| 1 | 3.2 | −90 | 3.2 | −90 | 5.732 | 13.703 | 6.621 |
| 2 | 3.2 | −90 | 3.2 | −85 | 5.694 | 13.679 | 6.859 |
| 3 | 3.2 | −90 | 3.2 | −80 | 5.606 | 13.604 | 7.068 |
| ⁝ | ⁝ | ⁝ | ⁝ | ⁝ | ⁝ | ⁝ | ⁝ |
| 1368 | 3.2 | 90 | 3.2 | 85 | 5.694 | 13.679 | 6.584 |
| 1369 | 3.2 | 90 | 3.2 | 90 | 5.732 | 13.703 | 6.515 |
| Model | R2 | MAE | RMSE | K-Fold Cross-Validation RMSE | F-Statistic |
|---|---|---|---|---|---|
| Linear regression | 0 | 1.621 | 1.826 | 1.759 | 0.981 |
| Elastic net | 0 | 1.628 | 1.828 | 1.756 | −0.141 |
| Polynomial regression (2) | 0.845 | 0.588 | 0.718 | 0.725 | 49.784 |
| Polynomial regression (4) | 0.879 | 0.480 | 0.634 | 0.636 | 2.229 |
| RF | 0.949 | 0.234 | 0.412 | 0.383 | 996.875 |
| SVR | 0.894 | 0.423 | 0.593 | 0.591 | 453.527 |
| XGBoost | 0.942 | 0.264 | 0.440 | 0.403 | 869.074 |
| ANN | 0.923 | 0.351 | 0.507 | 0.506 | 641.166 |
| Stacking Angle | ANSYS | Linear (Error %) | Elastic Net (Error %) | Polynomial (2) (Error %) | Polynomial (4) (Error %) | RF (Error %) | SVR (Error %) | XGBoost (Error %) | ANN (Error %) |
|---|---|---|---|---|---|---|---|---|---|
| [±7°/90°] | 2.93 | 5.18 (77%) | 5.19 (77%) | 3.74 (28%) | 3.18 (8%) | 2.84 (3%) | 3.00 (2%) | 2.72 (7%) | 3.26 (11%) |
| [±12°/90°] | 3.27 | 5.18 (58%) | 5.19 (59%) | 3.78 (16%) | 3.27 (0%) | 3.29 (1%) | 3.16 (3%) | 4.20 (29%) | 3.75 (15%) |
| [±26°/90°] | 5.43 | 5.15 (5%) | 5.19 (4%) | 4.04 (26%) | 3.82 (30%) | 4.85 (11%) | 3.90 (28%) | 5.13 (6%) | 4.33 (20%) |
| [±34°/90°] | 3.69 | 5.14 (39%) | 5.19 (41%) | 4.28 (16%) | 4.29 (16%) | 3.57 (3%) | 4.41 (20%) | 3.83 (4%) | 3.94 (7%) |
| [±47°/90°] | 5.65 | 5.12 (9%) | 5.19 (8%) | 4.81 (15%) | 5.19 (8%) | 4.51 (20%) | 5.21 (8%) | 4.52 (20%) | 4.48 (21%) |
| [±58°/90°] | 6.72 | 5.11 (24%) | 5.19 (23%) | 5.40 (20%) | 5.96 (11%) | 5.64 (16%) | 5.78 (14%) | 5.41 (19%) | 5.21 (22%) |
| [±67°/90°] | 6.12 | 5.09 (17%) | 5.19 (15%) | 5.97 (2%) | 6.50 (6%) | 5.92 (3%) | 6.17 (1%) | 5.56 (9%) | 5.86 (4%) |
| [±76°/90°] | 6.42 | 5.08 (21%) | 5.19 (19%) | 6.63 (3%) | 6.84 (7%) | 6.85 (7%) | 6.47 (1%) | 6.44 (1%) | 6.54 (2%) |
| [±83°/90°] | 6.70 | 5.07 (24%) | 5.19 (22%) | 7.21 (8%) | 6.90 (3%) | 6.70 (0%) | 6.65 (1%) | 6.59 (2%) | 6.92 (3%) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, H.G.; Sohn, J.M. A Comparative Analysis of Buckling Pressure Prediction in Composite Cylindrical Shells Under External Loads Using Machine Learning. J. Mar. Sci. Eng. 2024, 12, 2301. https://doi.org/10.3390/jmse12122301
Lee HG, Sohn JM. A Comparative Analysis of Buckling Pressure Prediction in Composite Cylindrical Shells Under External Loads Using Machine Learning. Journal of Marine Science and Engineering. 2024; 12(12):2301. https://doi.org/10.3390/jmse12122301
Chicago/Turabian StyleLee, Hyung Gi, and Jung Min Sohn. 2024. "A Comparative Analysis of Buckling Pressure Prediction in Composite Cylindrical Shells Under External Loads Using Machine Learning" Journal of Marine Science and Engineering 12, no. 12: 2301. https://doi.org/10.3390/jmse12122301
APA StyleLee, H. G., & Sohn, J. M. (2024). A Comparative Analysis of Buckling Pressure Prediction in Composite Cylindrical Shells Under External Loads Using Machine Learning. Journal of Marine Science and Engineering, 12(12), 2301. https://doi.org/10.3390/jmse12122301