Bearing-Only Multi-Target Localization Incorporating Waveguide Characteristics for Low Detection Rate Scenarios in Shallow Water
Abstract
:1. Introduction
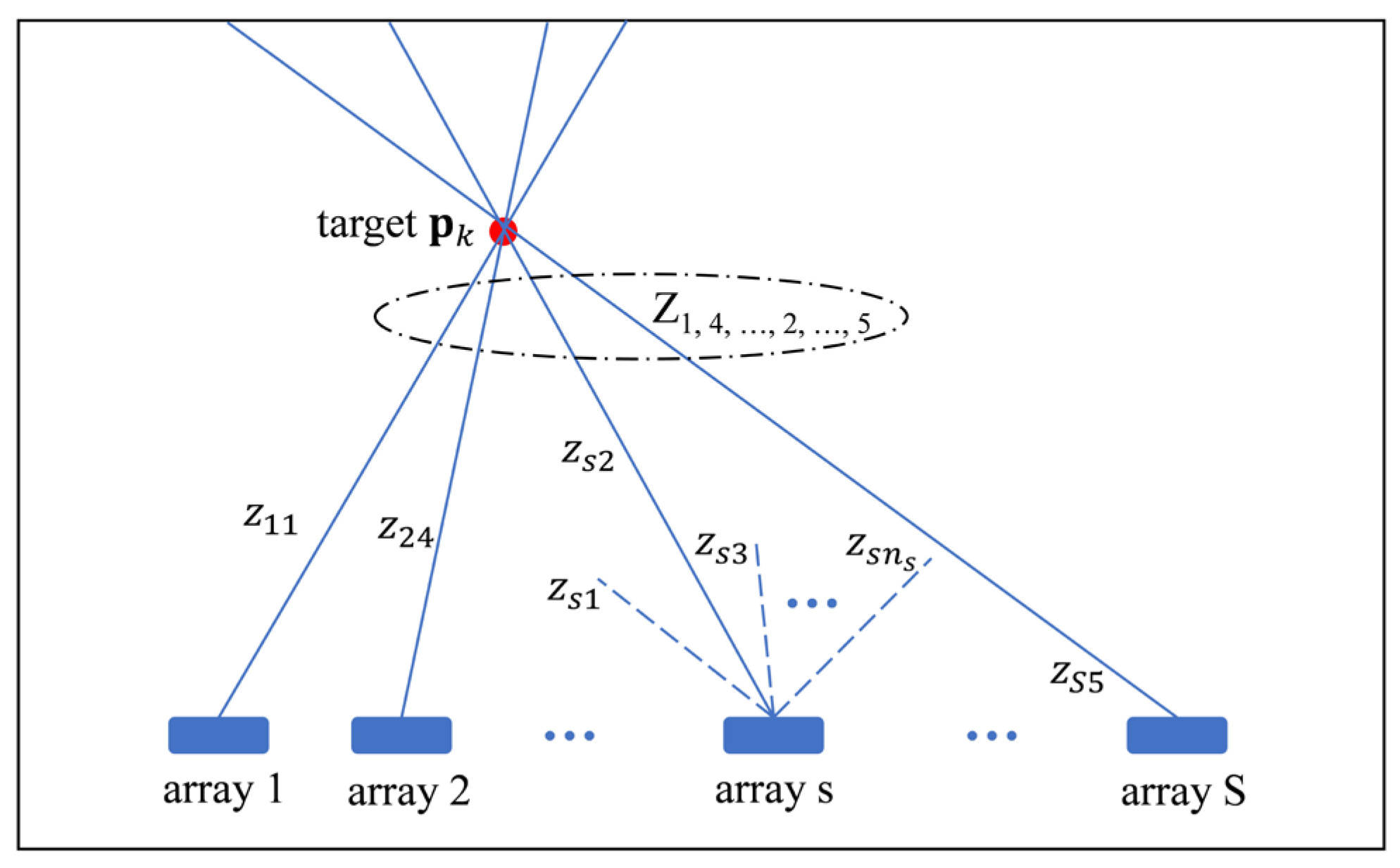
2. Theoretical Development
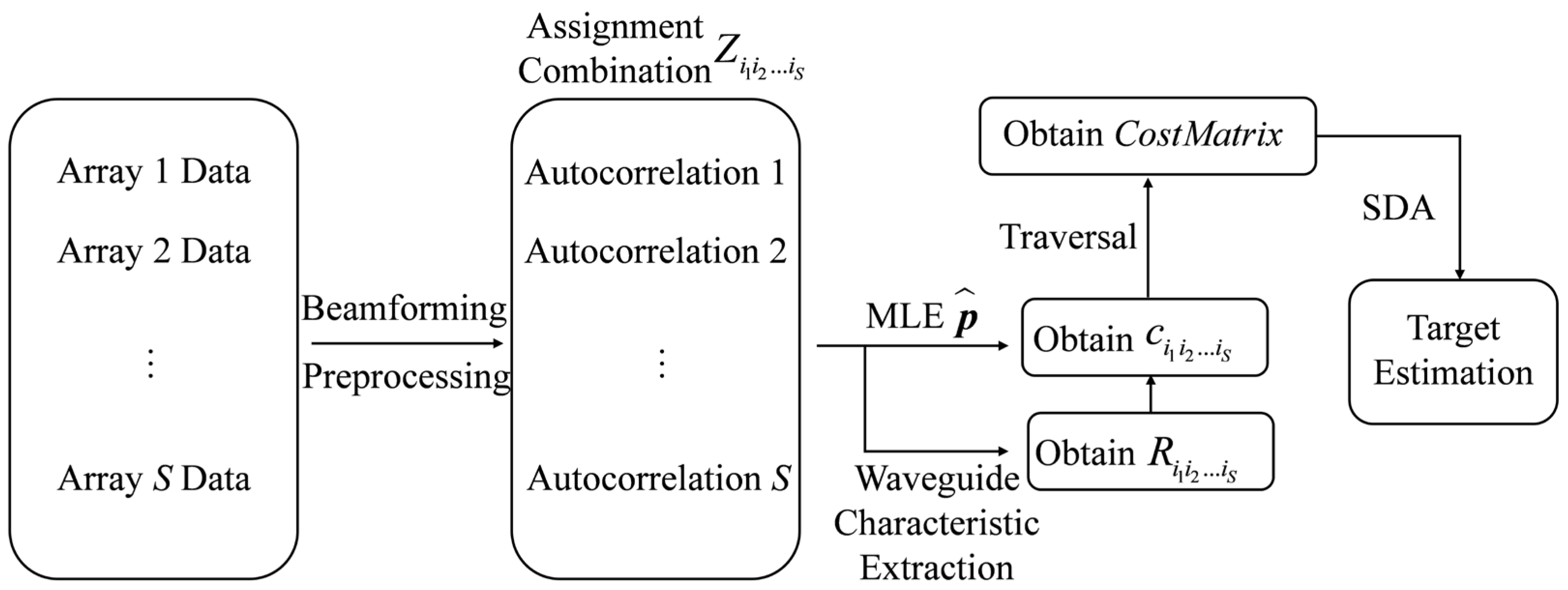
2.1. Extraction of the Characteristic Spectrum from Beamforming Output Signals
2.2. Localization Incorporating Waveguide Characteristics
- When the measurement is originated from target , the measurement can be represented as , where is white Gaussian noise;
- When the measurement originated from a spurious source, the measurement is uniformly distributed within the array’s surveillance area;
- Each target satisfies the observability condition [26], and the positional change of the target during a single measurement interval is negligible.
- Set the values near the maximum of the autocorrelation function to zero, and shift it to the right by and to obtain and , where is the reference sound speed;
- Apply the warping operator and to resample and . Subsequently, perform a Fourier transform to obtain the characteristics spectra and . The correlation coefficient is given by:where and represent the selected frequency ranges of the characteristic spectra. The confidence coefficient is expressed as:
- The likelihood function is expressed as follows:where is given by:
3. Numerical Simulations and Experimental Validation
3.1. Analysis of the Characteristic Spectrum
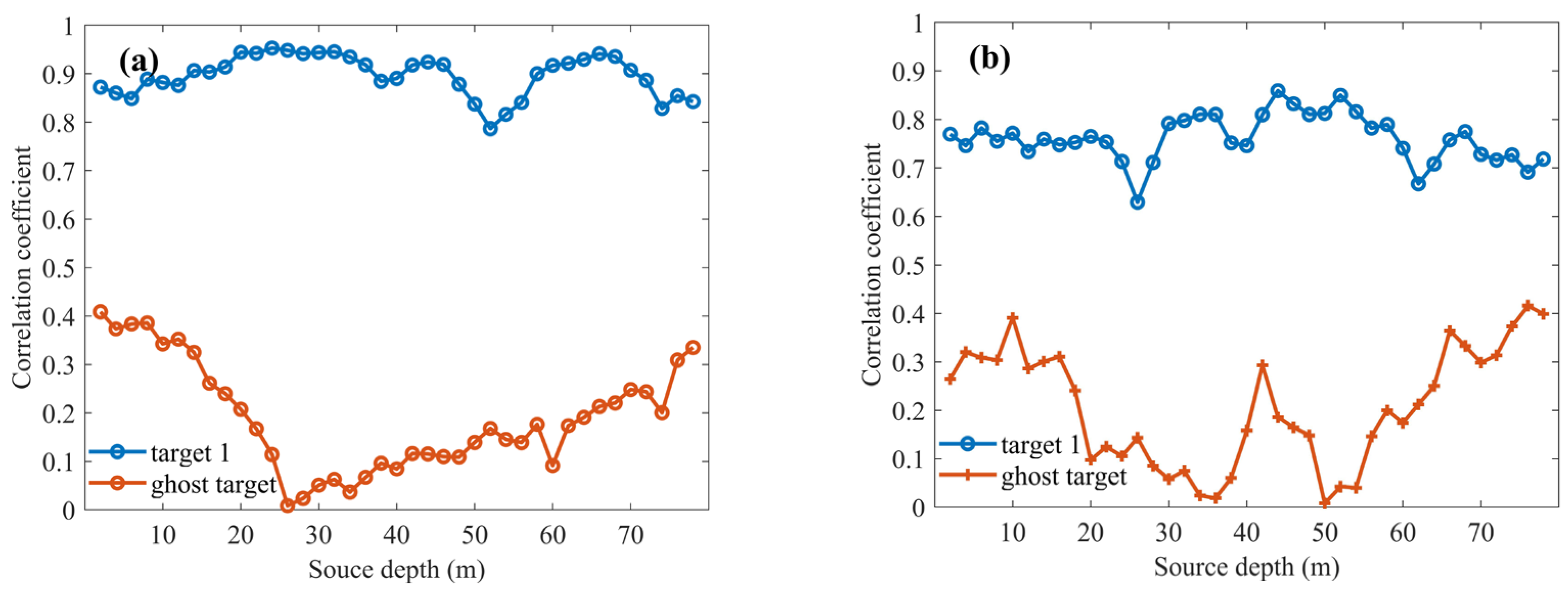
3.1.1. Properties of the Correlation Coefficient
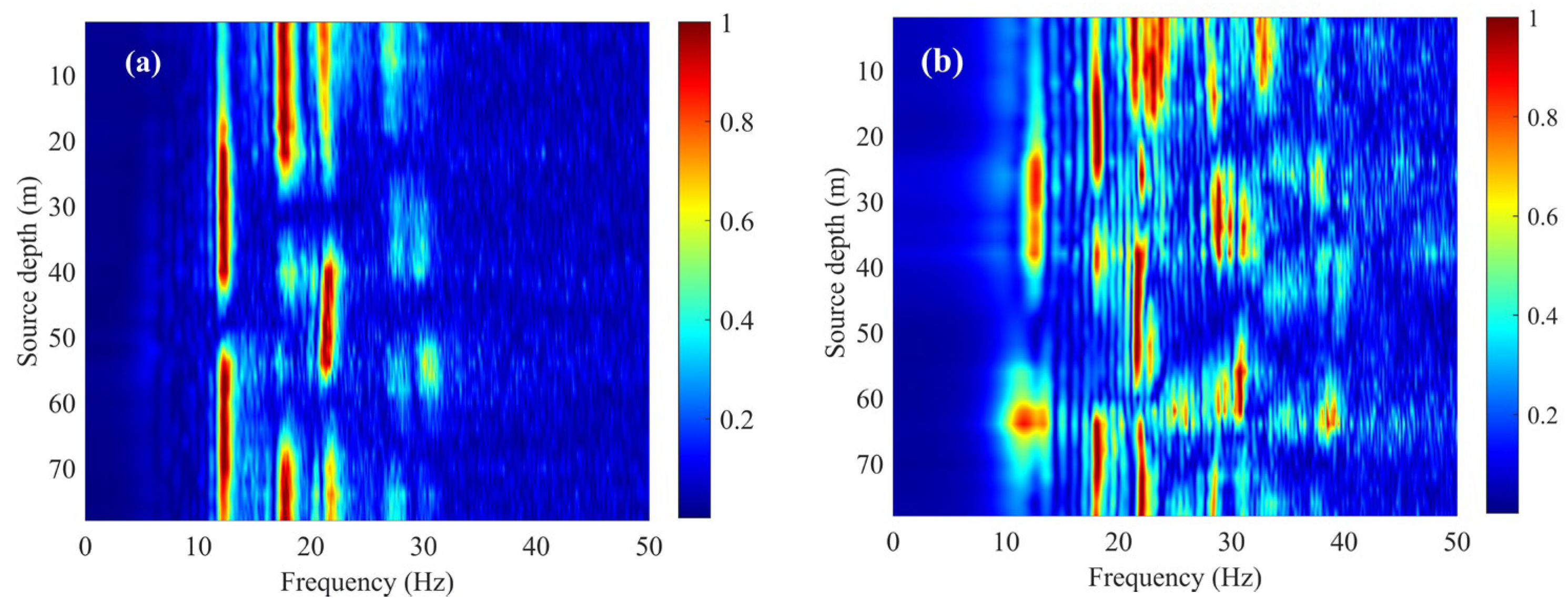
3.1.2. Effect of Source Frequency and Depth
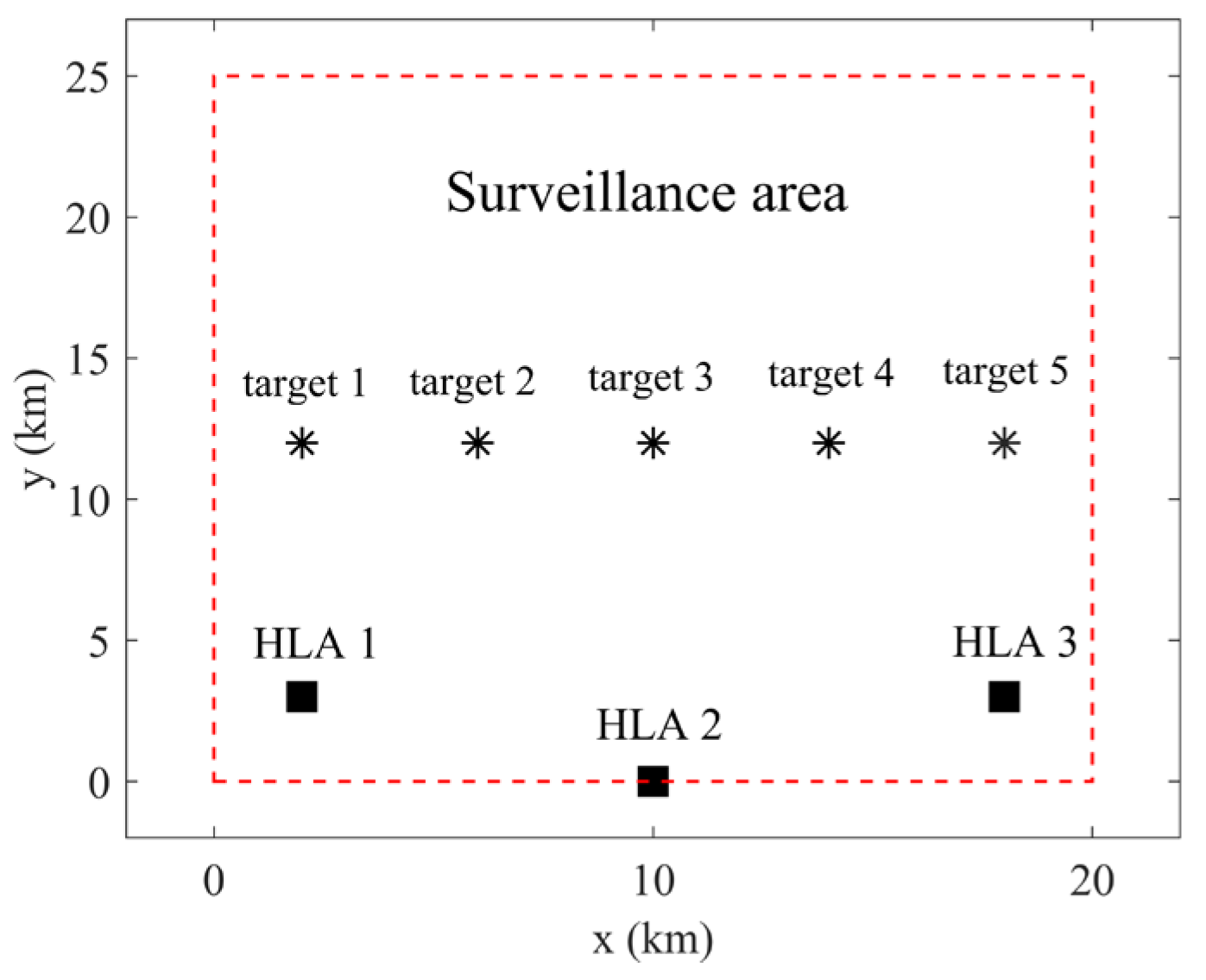
3.2. Localization Performance
3.2.1. Localization Performance at Different Detection Rates
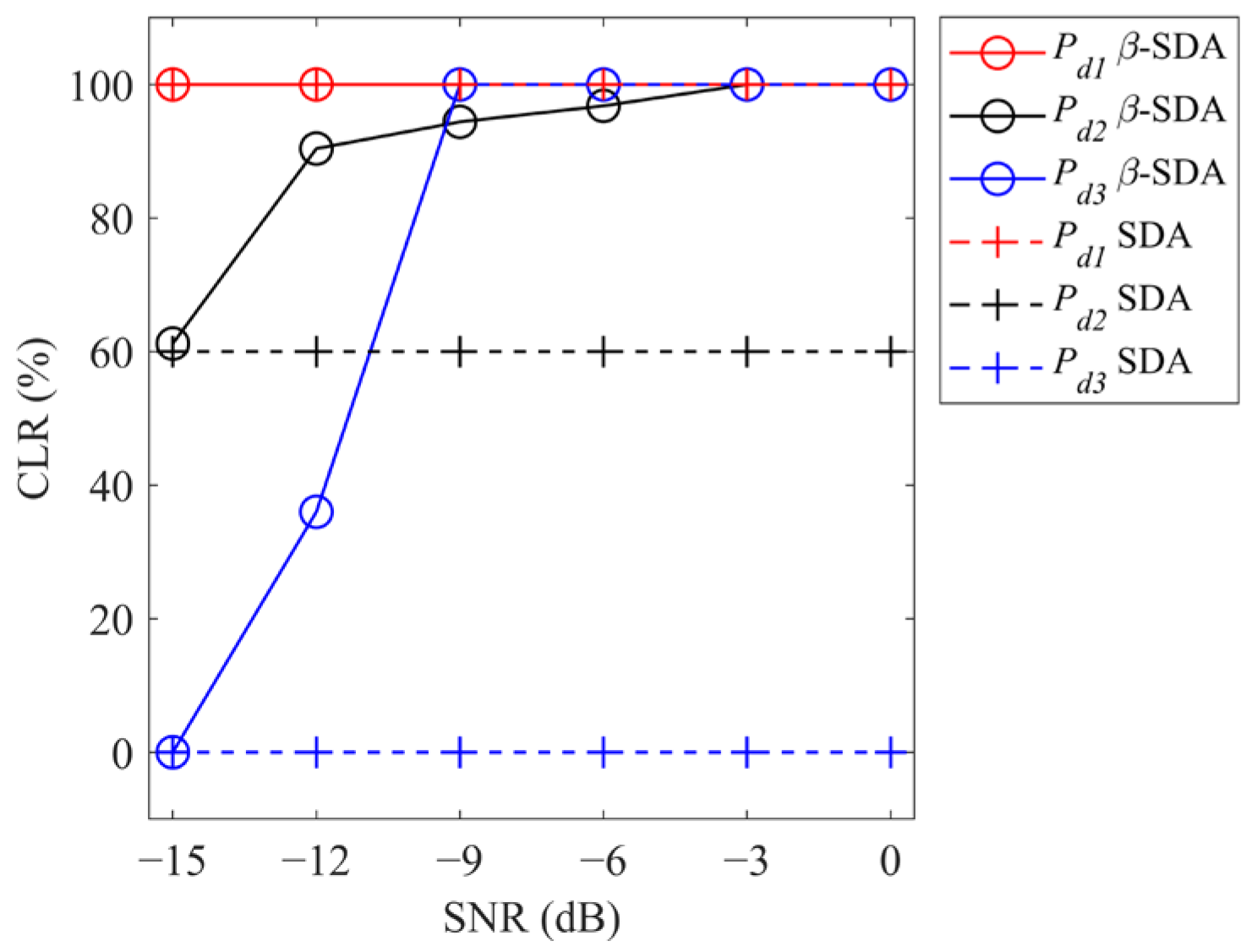
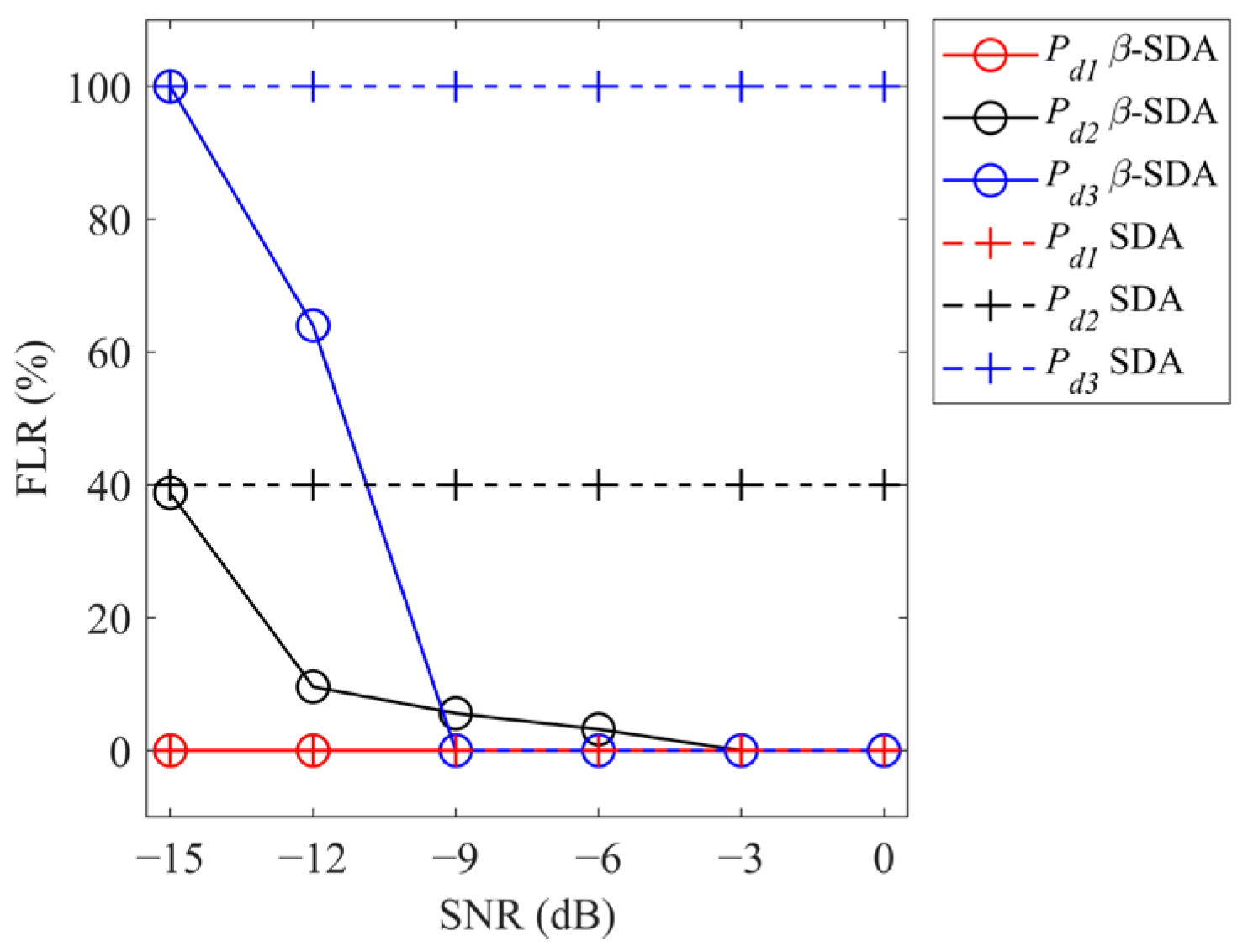
3.2.2. Localization Performance at Different SNR Levels
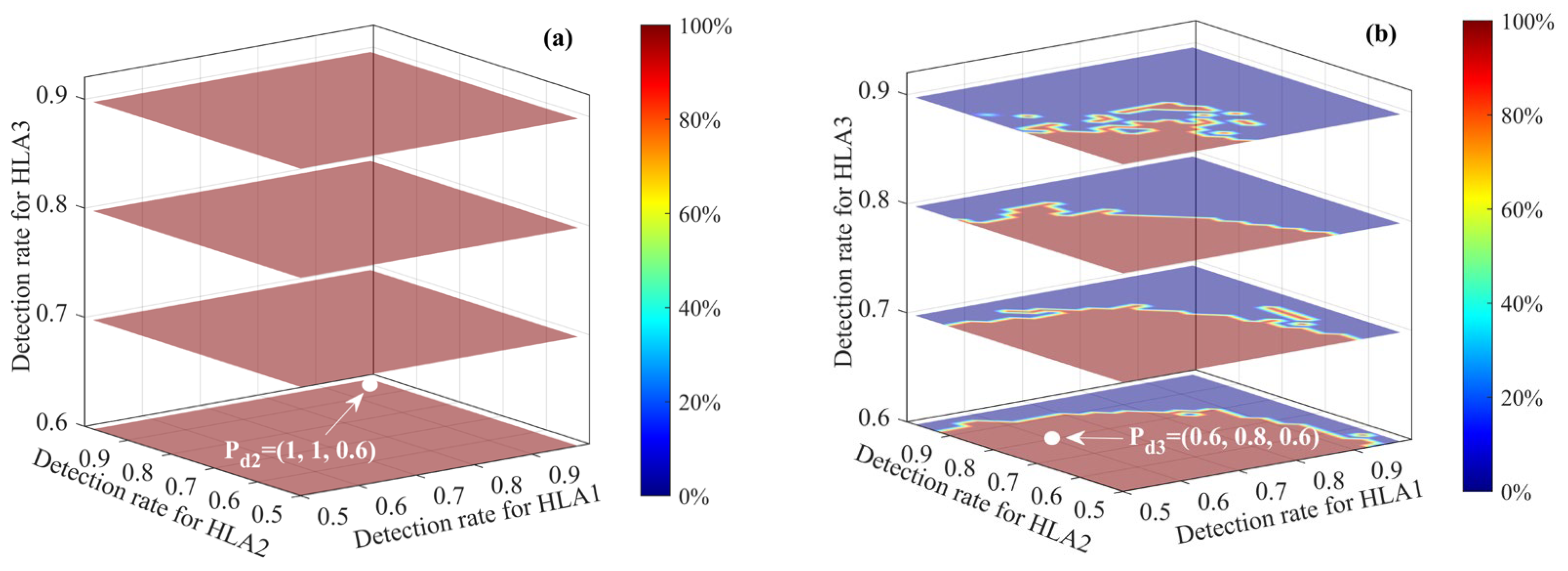
3.2.3. Effect of Preset Parameters on the β-SDA Method
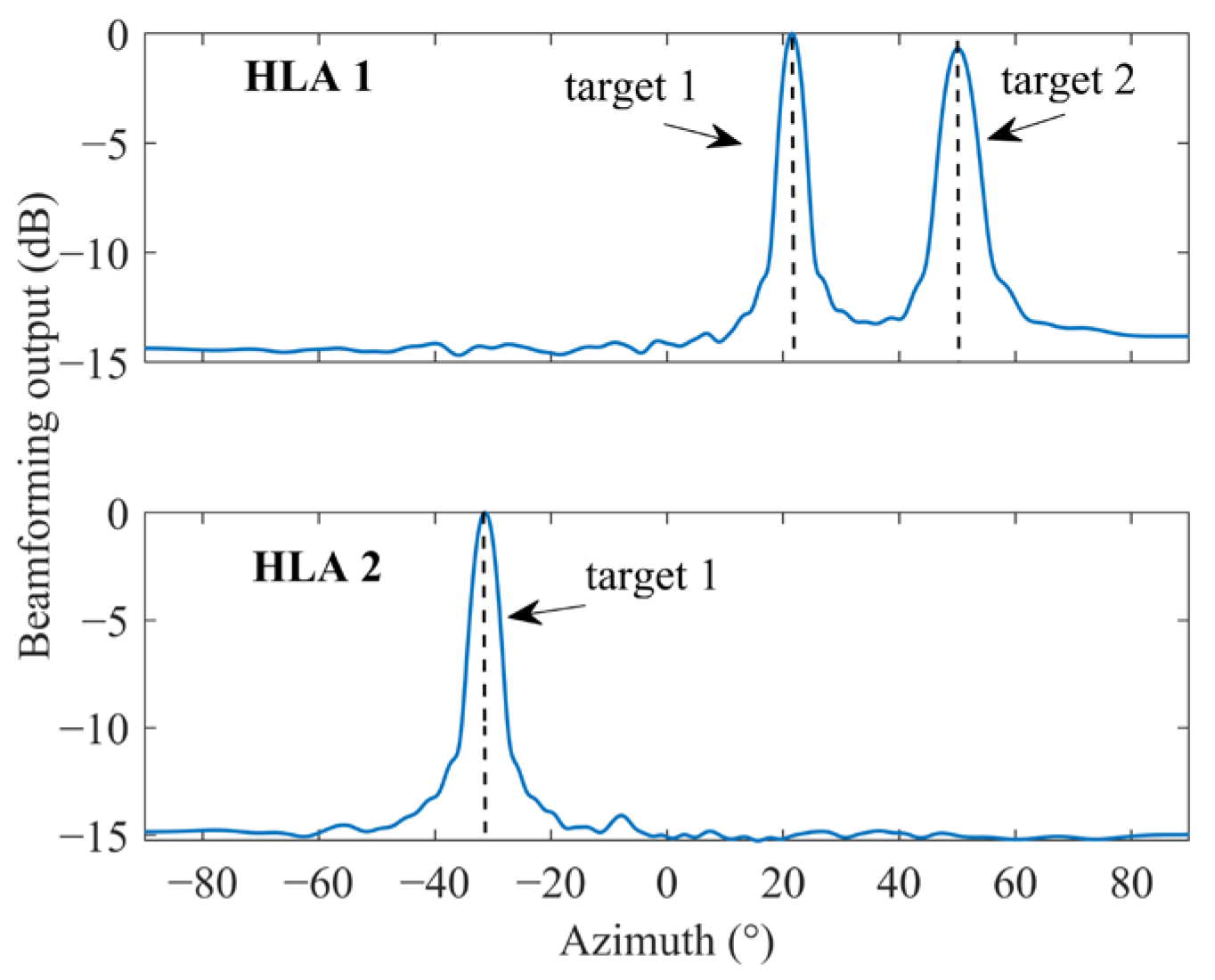
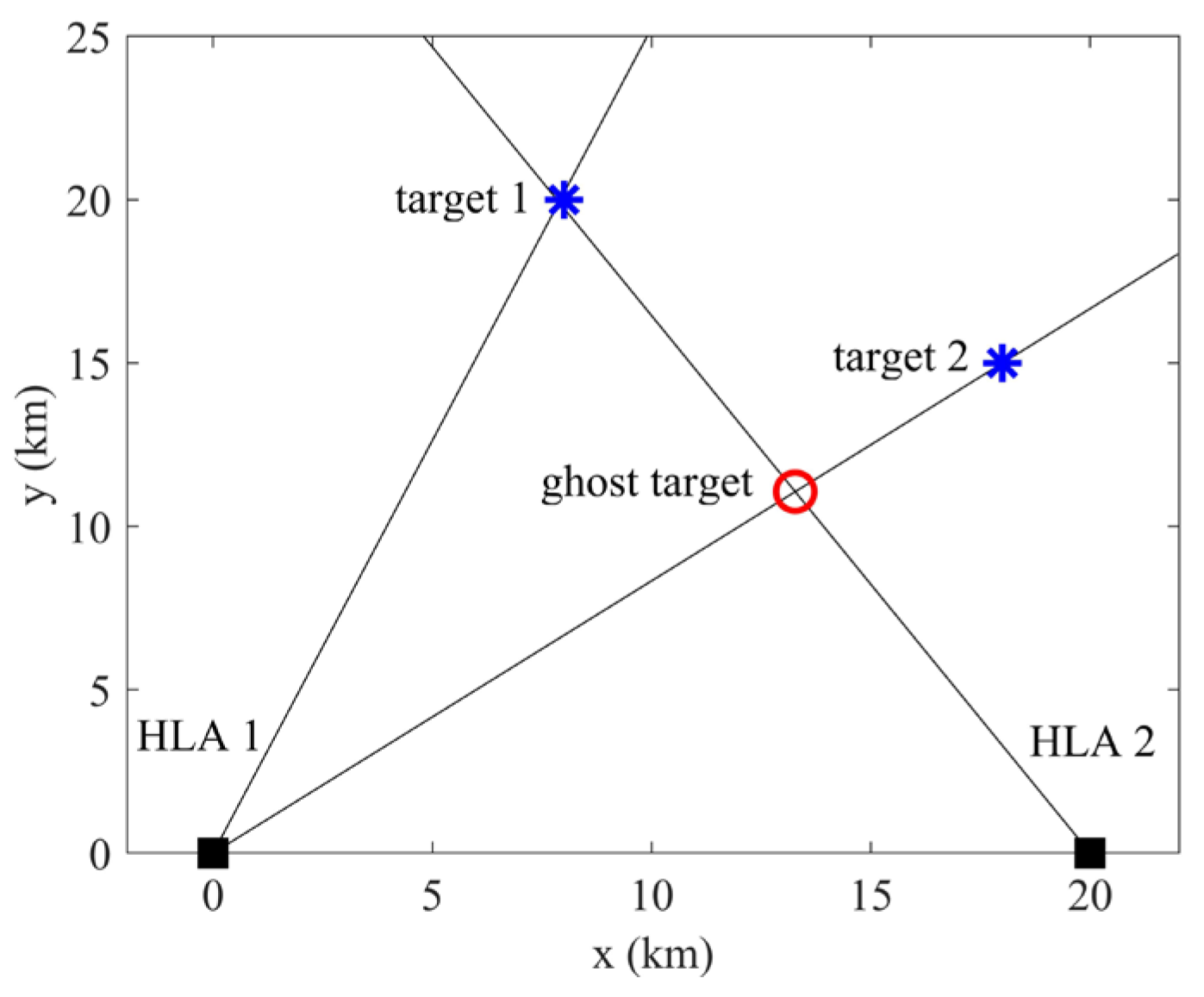
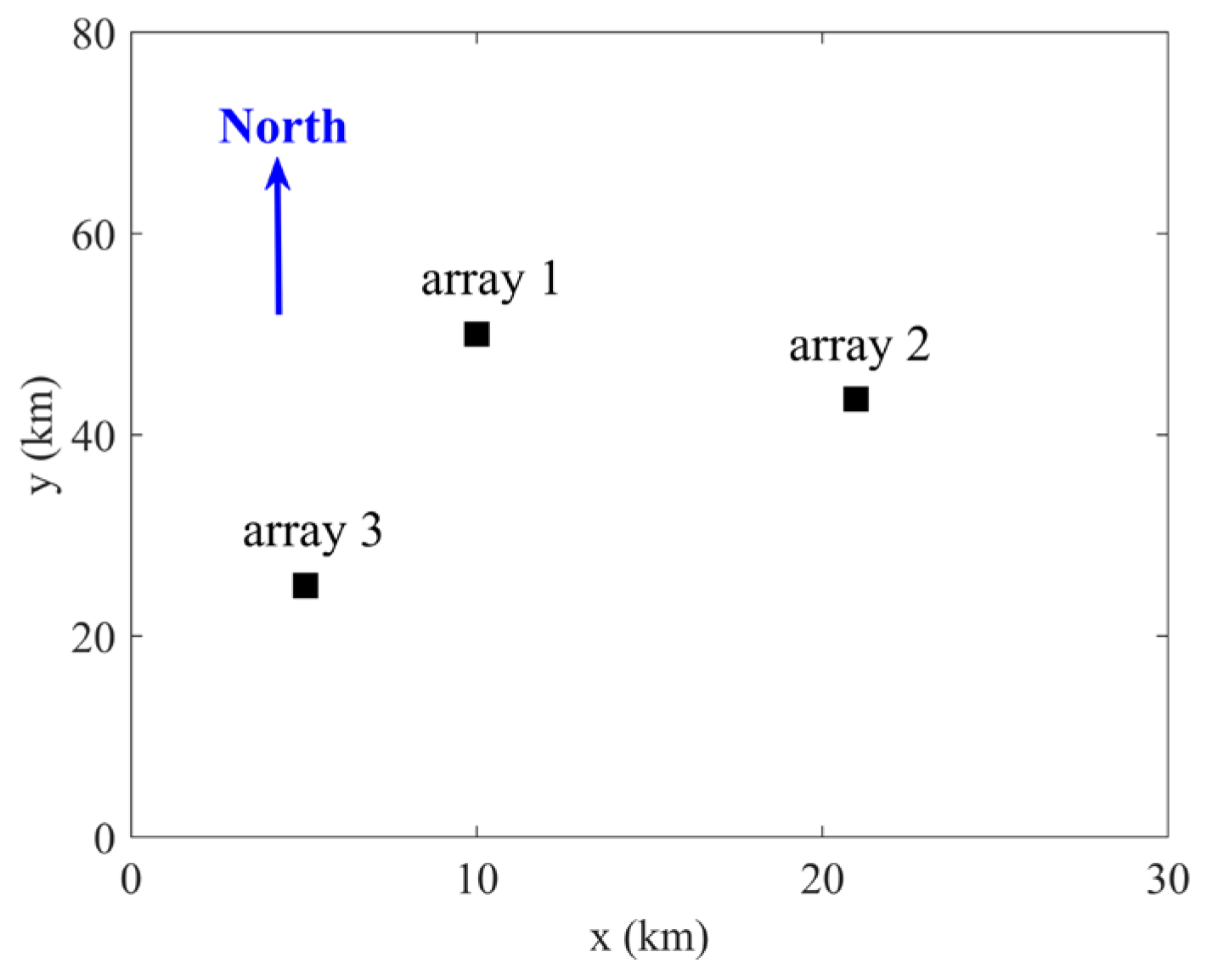
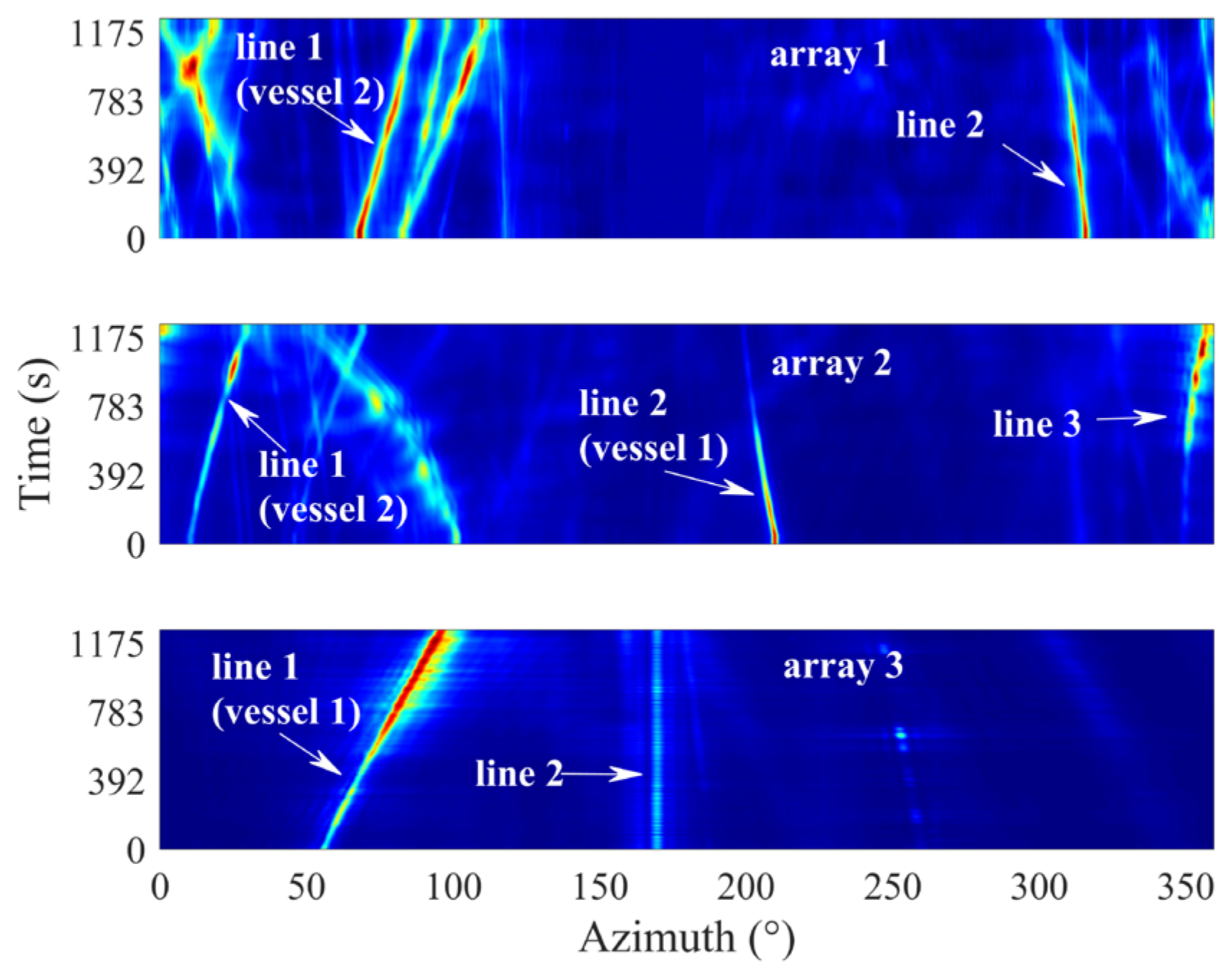
3.3. Sea Trial Data
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Cong, L.; Zhuang, W.H. Hybrid TDOA/AOA mobile user location for wideband CDMA-cellular systems. IEEE Trans. Wirel. Commun. 2002, 1, 439–447. [Google Scholar] [CrossRef]
- Zhang, Y.M.D.; Amin, M.G.; Himed, B. Joint DOD/DOA estimation in MIMO radar exploiting time-frequency signal representations. Eurasip J. Adv. Signal Process. 2012, 2012, 102. [Google Scholar] [CrossRef]
- Xiong, K.; Cui, G.; Yi, W.; Wang, S.; Kong, L. Distributed localization of target for MIMO radar with widely separated directional transmitters and omnidirectional receivers. IEEE Trans. Aerosp. Electron. Syst. 2022, 59, 3171–3187. [Google Scholar] [CrossRef]
- Kim, J. Locating an Underwater Target Using Angle-Only Measurements of Heterogeneous Sonobuoys Sensors with Low Accuracy. Sensors 2022, 22, 3914. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Yang, Y.; Liu, X. A distributed subband valley fusion (DSVF) method for low frequency broadband target localization. Acoust. Soc. Am. J. 2018, 143, 2269–2278. [Google Scholar] [CrossRef]
- Deb, S.; Pattipati, K.R.; Bar-Shalom, Y.; Washburn, R.B. Assignment Algorithms for the Passive Sensor Data Association Problem. Proc. SPIE Int. Soc. Opt. Eng. 1989, 1096, 231–243. [Google Scholar]
- Bar-Shalom, Y.; Willett, P.K.; Tian, X. Tracking and Data Fusion; YBS Publishing: Storrs, CT, USA, 2011; Volume 11. [Google Scholar]
- Su, Z.; Ji, H.; Zhang, Y. Loopy belief propagation based data association for extended target tracking. Chin. J. Aeronaut. 2020, 33, 2212–2223. [Google Scholar] [CrossRef]
- Gavish, M.; Weiss, A.J. Performance analysis of bearing-only target location algorithms. IEEE Trans. Aerosp. Electron. Syst. 1992, 28, 817–828. [Google Scholar] [CrossRef]
- Dogançay, K. Bearings-only target localization using total least squares. Signal Process. 2005, 85, 1695–1710. [Google Scholar] [CrossRef]
- Abatzoglou, T.J.; Mendel, J.M. The constrained total least squares technique and its applications to harmonic superresolution. Signal Process. IEEE Trans. 1991, 39, 1070–1087. [Google Scholar] [CrossRef]
- Bishop, A.N.; Pathirana, P.N. Localization of emitters via the intersection of bearing lines: A ghost elimination approach. IEEE Trans. Veh. Technol. 2007, 56, 3106–3110. [Google Scholar] [CrossRef]
- Oshman, Y.; Davidson, P. Optimization of observer trajectories for bearings-only target localization. IEEE Trans. Aerosp. Electron. Syst. 1999, 35, 892–902. [Google Scholar] [CrossRef]
- Bar-Shalom, Y.; Jaffer, A.G. Adaptive nonlinear filtering for tracking with measurements of uncertain origin. In Proceedings of the 1972 IEEE Conference on Decision and Control and 11th Symposium on Adaptive Processes, New Orleans, NY, USA, 13–15 December 1972; pp. 243–247. [Google Scholar]
- Reed, J.D.; da Silva, C.R.; Buehrer, R.M. Multiple-source localization using line-of-bearing measurements: Approaches to the data association problem. In Proceedings of the MILCOM 2008–2008 IEEE Military Communications Conference, San Diego, CA, USA, 16–19 November 2008; pp. 1–7. [Google Scholar]
- Gardner, W.; Brown, W.; Chih-Kang, C. Spectral Correlation of Modulated Signals: Part II—Digital Modulation. IEEE Trans. Commun. 1987, 35, 595–601. [Google Scholar] [CrossRef]
- Xu, L.; Yang, Y. Parameter estimation of underwater moving sources by using matched Wigner transform. Appl. Acoust. 2016, 101, 5–14. [Google Scholar] [CrossRef]
- Avitzour, D. A maximum likelihood approach to data association. IEEE Trans. Aerosp. Electron. Syst. 1992, 28, 560–566. [Google Scholar] [CrossRef]
- Poore, A.P.; Rijavec, N. A Lagrangian relaxation algorithm for multidimensional assignment problems arising from multitarget tracking. SIAM J. Optim. 1993, 3, 544–563. [Google Scholar] [CrossRef]
- Deb, S.; Yeddanapudi, M.; Pattipati, K.; BarShalom, Y. A generalized S-D assignment algorithm for multisensor-multitarget state estimation. IEEE Trans. Aerosp. Electron. Syst. 1997, 33, 523–538. [Google Scholar] [CrossRef]
- Popp, R.L.; Pattipati, K.R.; Bar-Shalom, Y. m-best S-D assignment algorithm with application to multitarget tracking. Aerosp. Electron. Syst. IEEE Trans. 1998, 37, 22–39. [Google Scholar] [CrossRef]
- Bonnel, J.; Nicolas, B.; Mars, J.I.; Walker, S.C. Estimation of modal group velocities with a single receiver for geoacoustic inversion in shallow water. J. Acoust. Soc. Am. 2010, 128, 719–727. [Google Scholar] [CrossRef] [PubMed]
- Yu-Bo, Q.; Shi-Hong, Z.; Ren-He, Z.; Yun, R. A passive source ranging method using the waveguide-invariant-warping operator. Acta Phys. Sin. 2015, 64, 074301. [Google Scholar] [CrossRef]
- Yang, T.C. Beam intensity striations and applications. J. Acoust. Soc. Am. 2003, 113, 1342–1352. [Google Scholar] [CrossRef] [PubMed]
- Arnol’d, V.I. Remarks on the stationary phase method and Coxeter numbers. Russ. Math. Surv. 1973, 28, 19–48. [Google Scholar] [CrossRef]
- Nardone, S.C.; Aidala, V.J. Observability criteria for bearings-only target motion analysis. IEEE Trans. Aerosp. Electron. Syst. 1981, AES-17, 162–166. [Google Scholar] [CrossRef]
- Porter, M.B.; Reiss, E.L. A numerical method for bottom interacting ocean acoustic normal modes. J. Acoust. Soc. Am. 1985, 77, 1760–1767. [Google Scholar] [CrossRef]
- Bonnel, J.; Chapman, N.R. Geoacoustic inversion in a dispersive waveguide using warping operators. J. Acoust. Soc. Am. 2011, 130, EL101–EL107. [Google Scholar] [CrossRef]
- Yang, X.; Li, F.; Zhang, B.; Luo, W. Seasonally-invariant head wave speed extracted from ocean noise cross-correlation. J. Acoust. Soc. Am. 2020, 147, EL241–EL245. [Google Scholar] [CrossRef] [PubMed]
- Wen-Hua, S.; Ning, W.; Da-Zhi, G.; Hao-Zhong, W.; Ke, Q. Concept of waveguide invariant spectrum and algorithm for its extraction. Acta Phys. Sin. 2017, 66, 114301. [Google Scholar] [CrossRef]
- Niu, H.; Zhang, R.; Li, Z. Theoretical analysis of warping operators for non-ideal shallow water waveguides. J. Acoust. Soc. Am. 2014, 136, 53–65. [Google Scholar] [CrossRef]






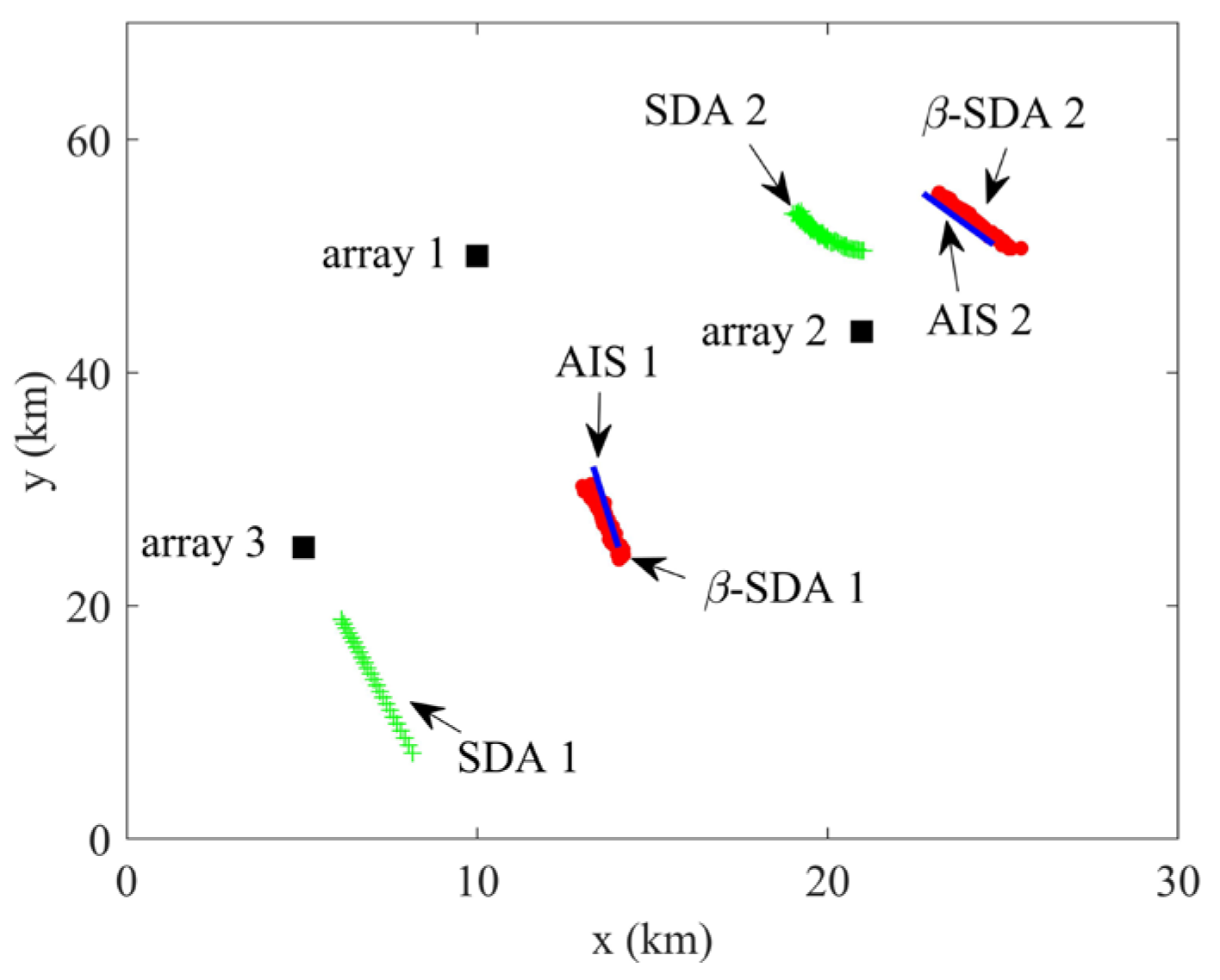
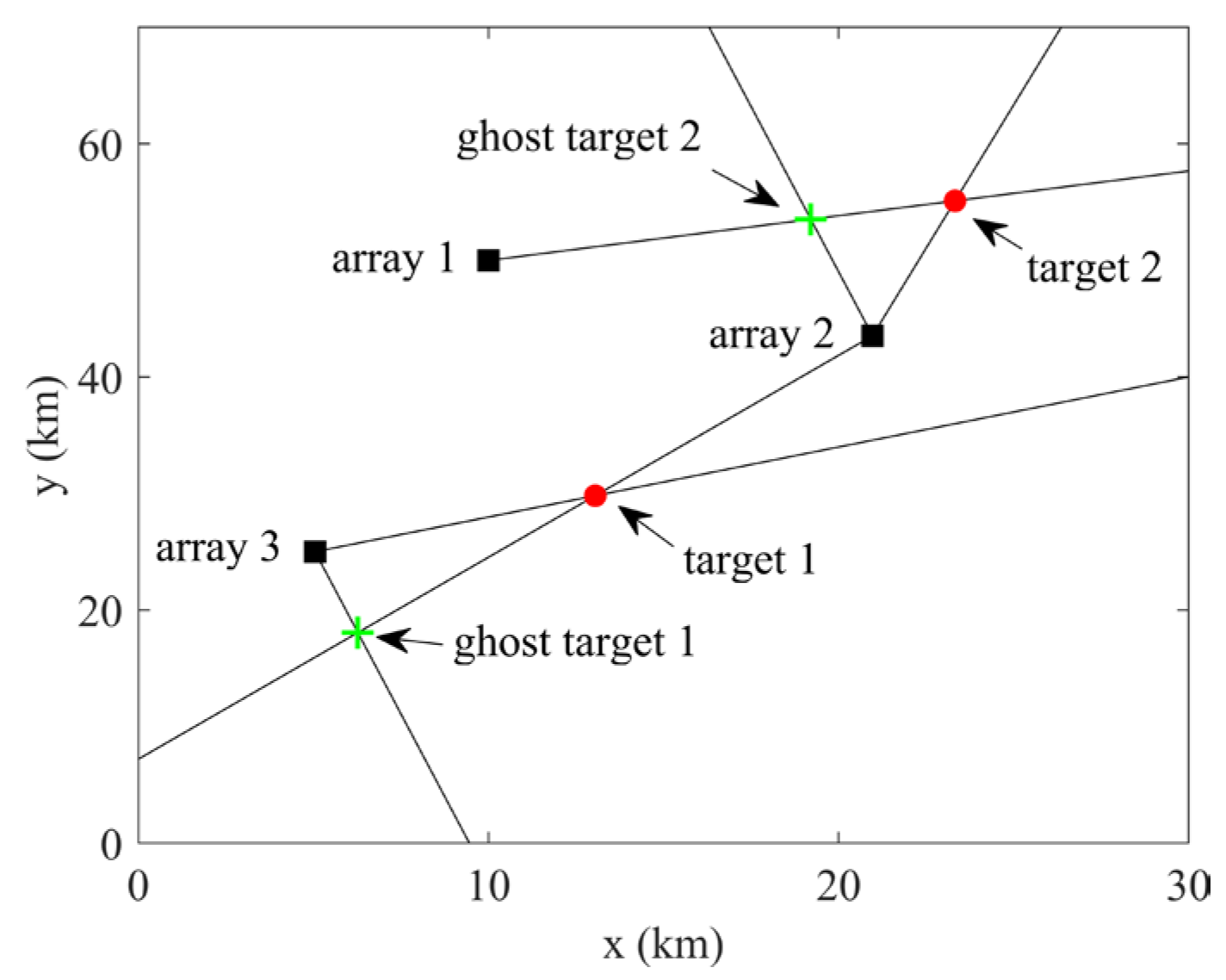
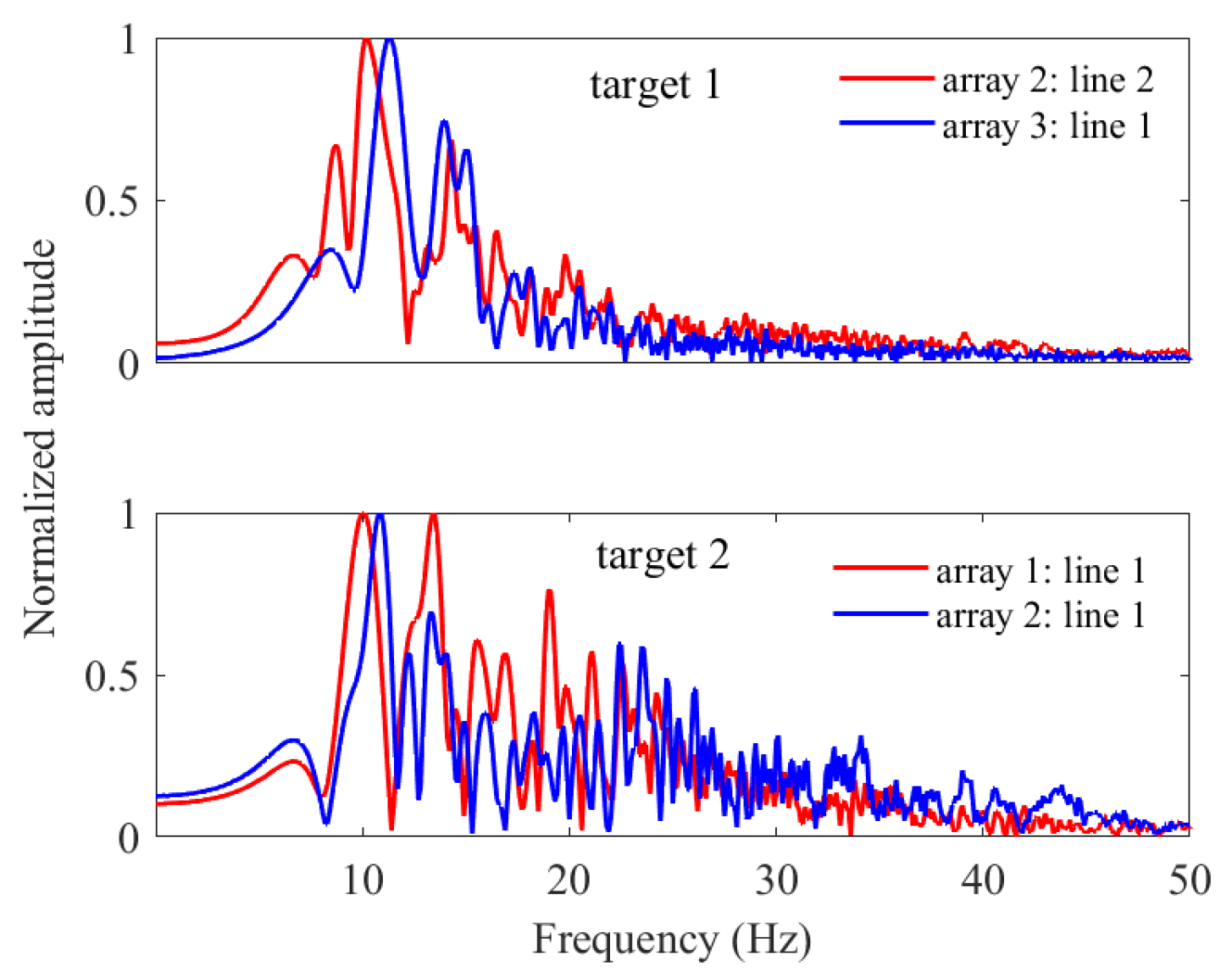
| Number of valid intersection points | |
| , | Measurements from arrays and |
| , | Azimuths of and |
| , | Frequency domain outputs of beamformers |
| , | Time domain autocorrelation functions |
| , | Distances from the intersection point to arrays |
| Detection rate of the array s | |
| Indicator function | |
| Field of view of array s | |
| Confidence coefficient for combination | |
| Likelihood function for combination | |
| Association cost for combination |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mei, X.; Zhang, B.; Zhai, D.; Peng, Z. Bearing-Only Multi-Target Localization Incorporating Waveguide Characteristics for Low Detection Rate Scenarios in Shallow Water. J. Mar. Sci. Eng. 2024, 12, 2300. https://doi.org/10.3390/jmse12122300
Mei X, Zhang B, Zhai D, Peng Z. Bearing-Only Multi-Target Localization Incorporating Waveguide Characteristics for Low Detection Rate Scenarios in Shallow Water. Journal of Marine Science and Engineering. 2024; 12(12):2300. https://doi.org/10.3390/jmse12122300
Chicago/Turabian StyleMei, Xiaohan, Bo Zhang, Duo Zhai, and Zhaohui Peng. 2024. "Bearing-Only Multi-Target Localization Incorporating Waveguide Characteristics for Low Detection Rate Scenarios in Shallow Water" Journal of Marine Science and Engineering 12, no. 12: 2300. https://doi.org/10.3390/jmse12122300
APA StyleMei, X., Zhang, B., Zhai, D., & Peng, Z. (2024). Bearing-Only Multi-Target Localization Incorporating Waveguide Characteristics for Low Detection Rate Scenarios in Shallow Water. Journal of Marine Science and Engineering, 12(12), 2300. https://doi.org/10.3390/jmse12122300





