Neural Network Identification-Based Model Predictive Heading Control for Wave Gliders
Abstract
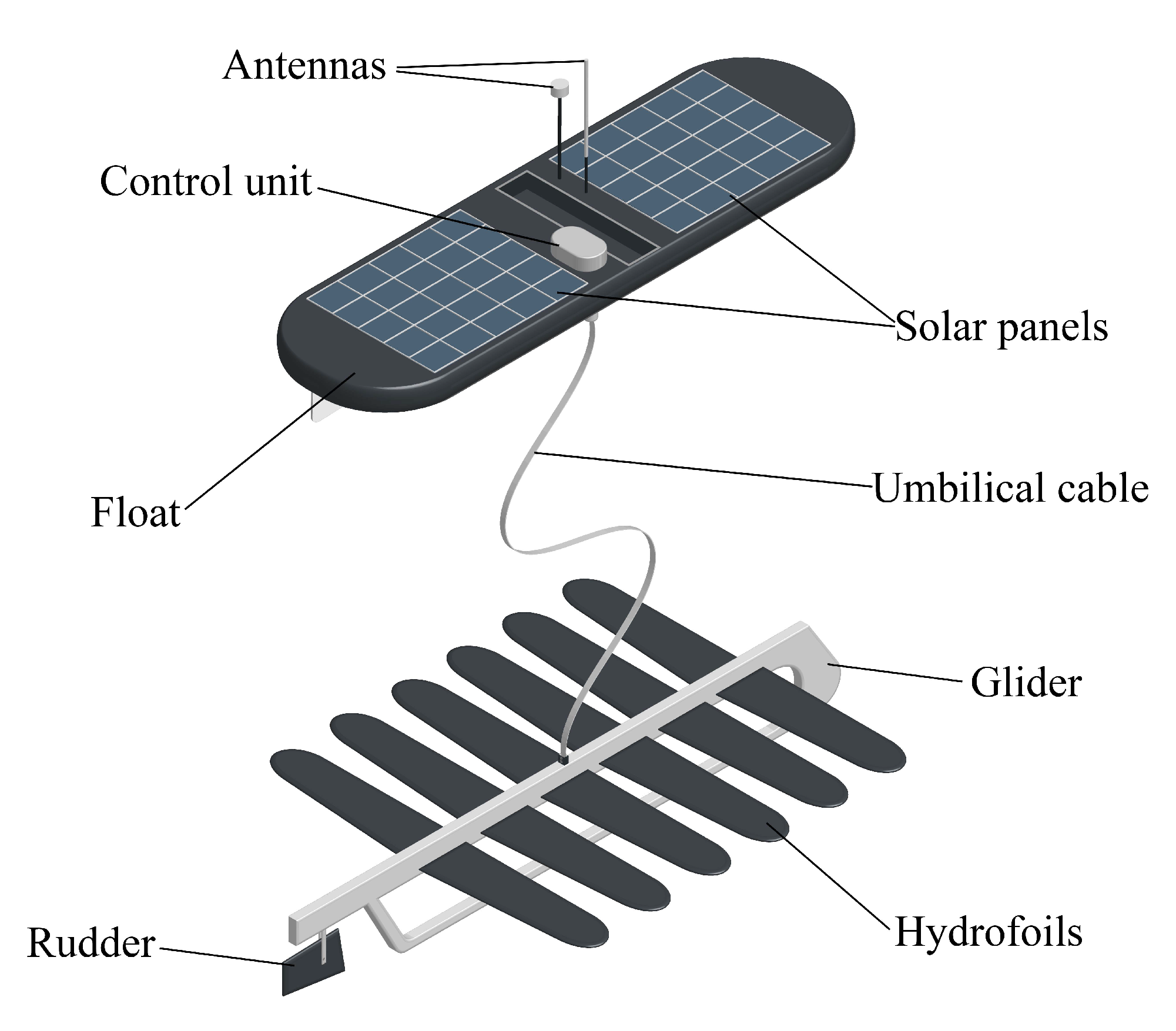
1. Introduction
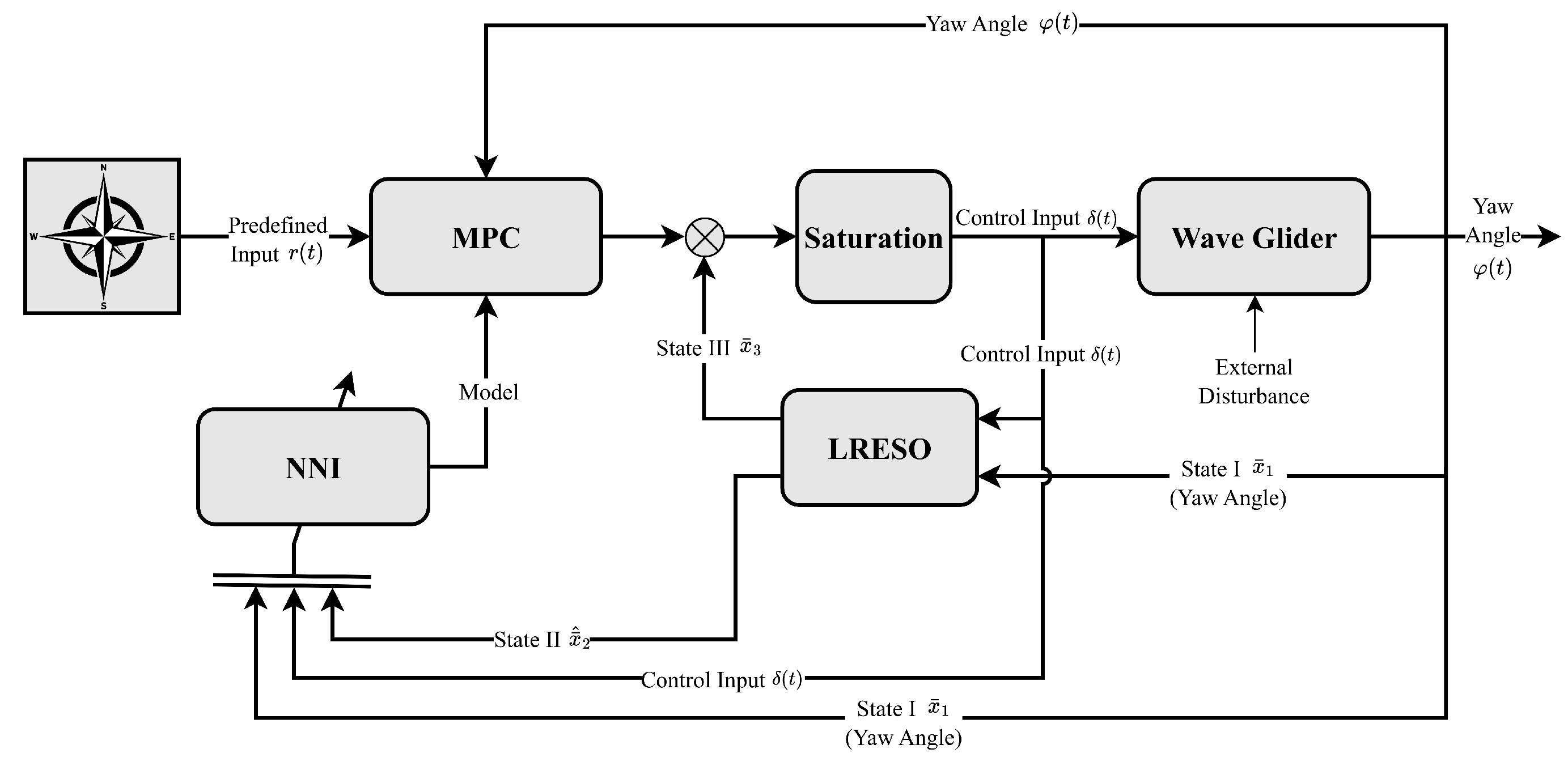
- An NNI-based model predictive heading controller (NNI-MPHC) is developed for wave gliders, where only the system order of a glider is required, the system parameters can be identified online, and a reduced-order extended state observer is designed to estimate the unmodeled dynamics and unknown disturbance.
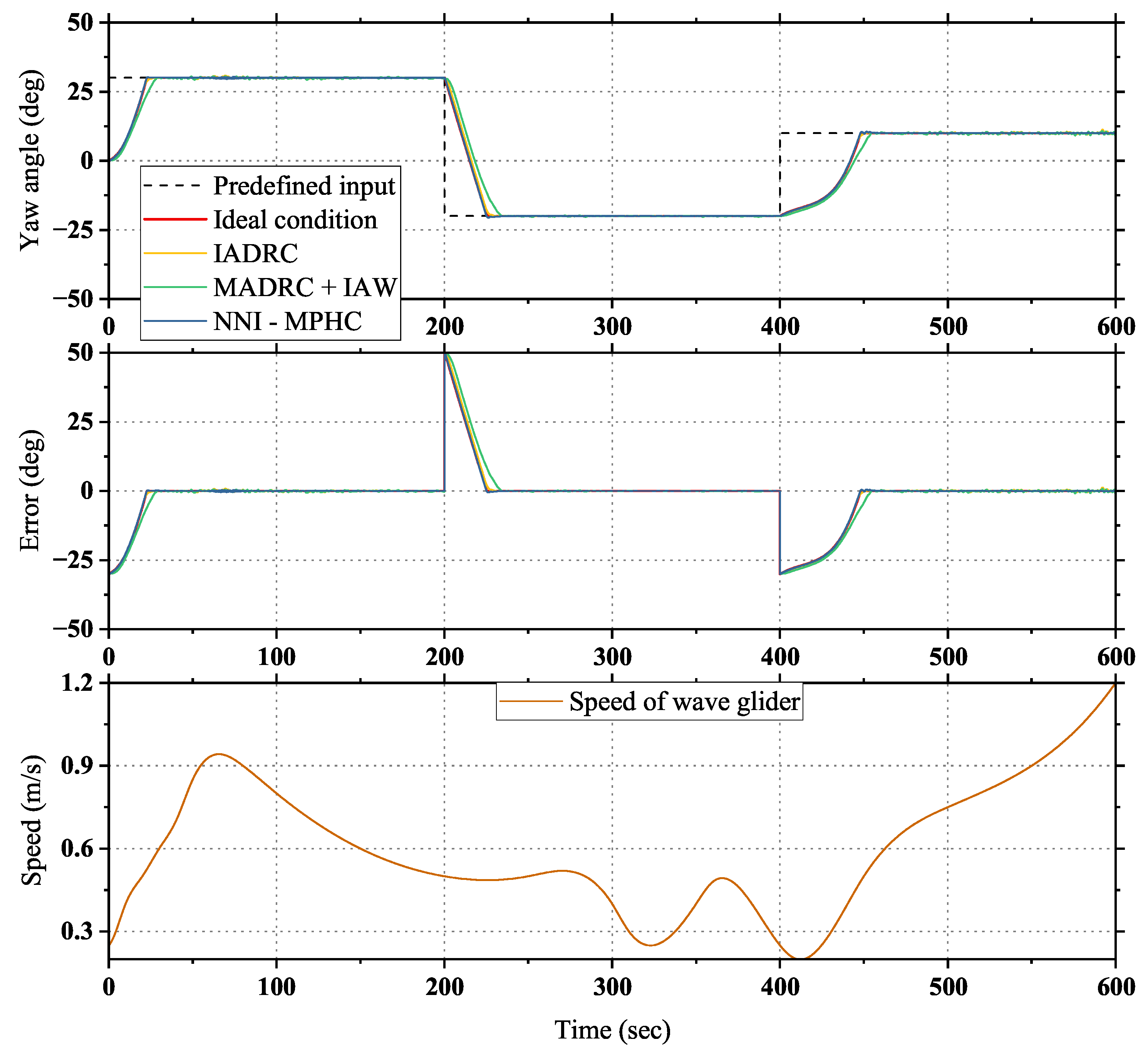
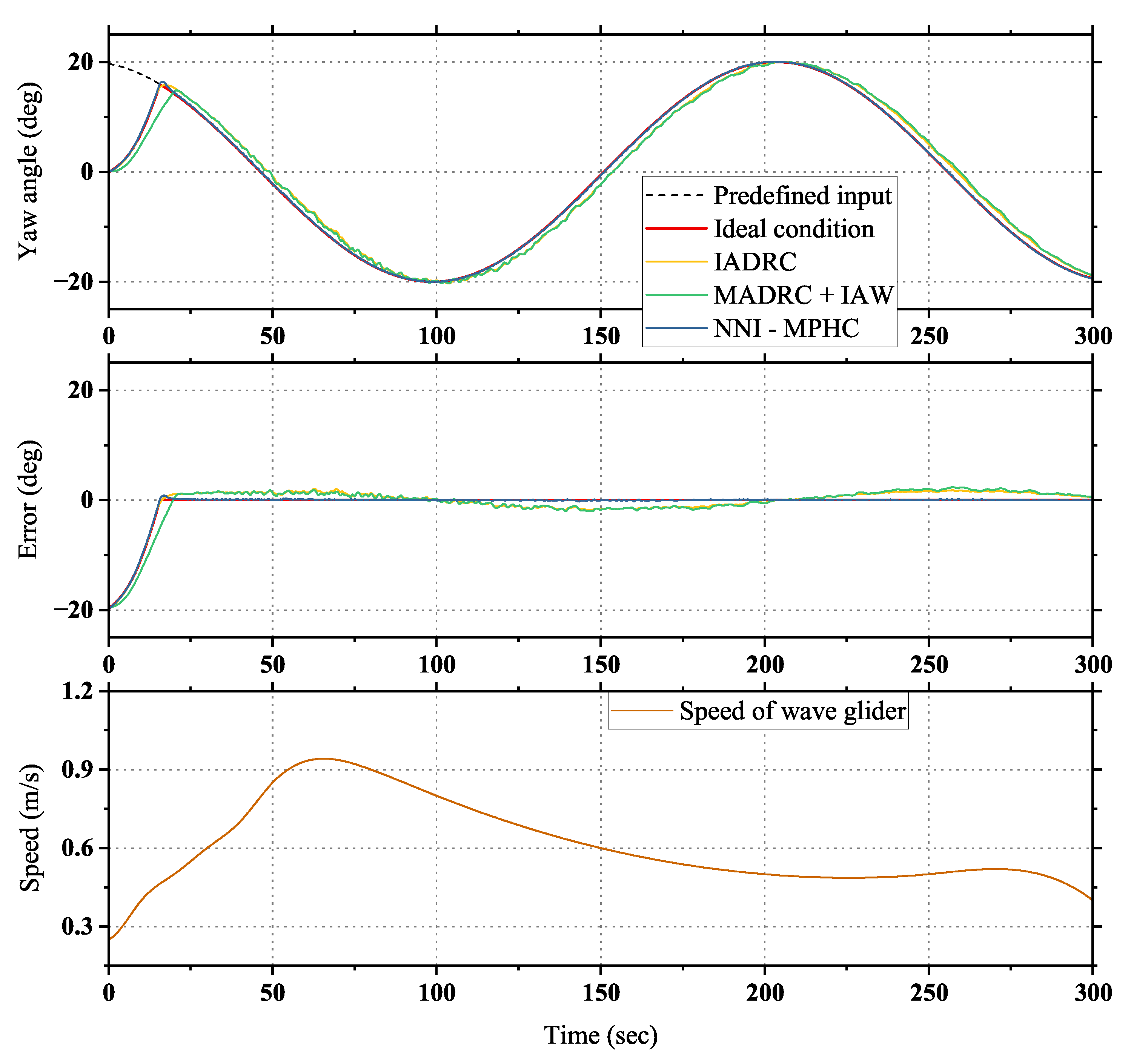
- Simulation results show that the designed NNI-MPHC is effective at tracking the predefined input of the wave glider. In addition, the NNI-MPHC outperforms the existing heading controllers of wave gliders with respect to the accuracy and rapidity of tracking and the robustness to the model uncertainty and/or external disturbances.
2. Problem Formulation

3. Heading Controller Design of Wave Glider
3.1. Design of the LRESO
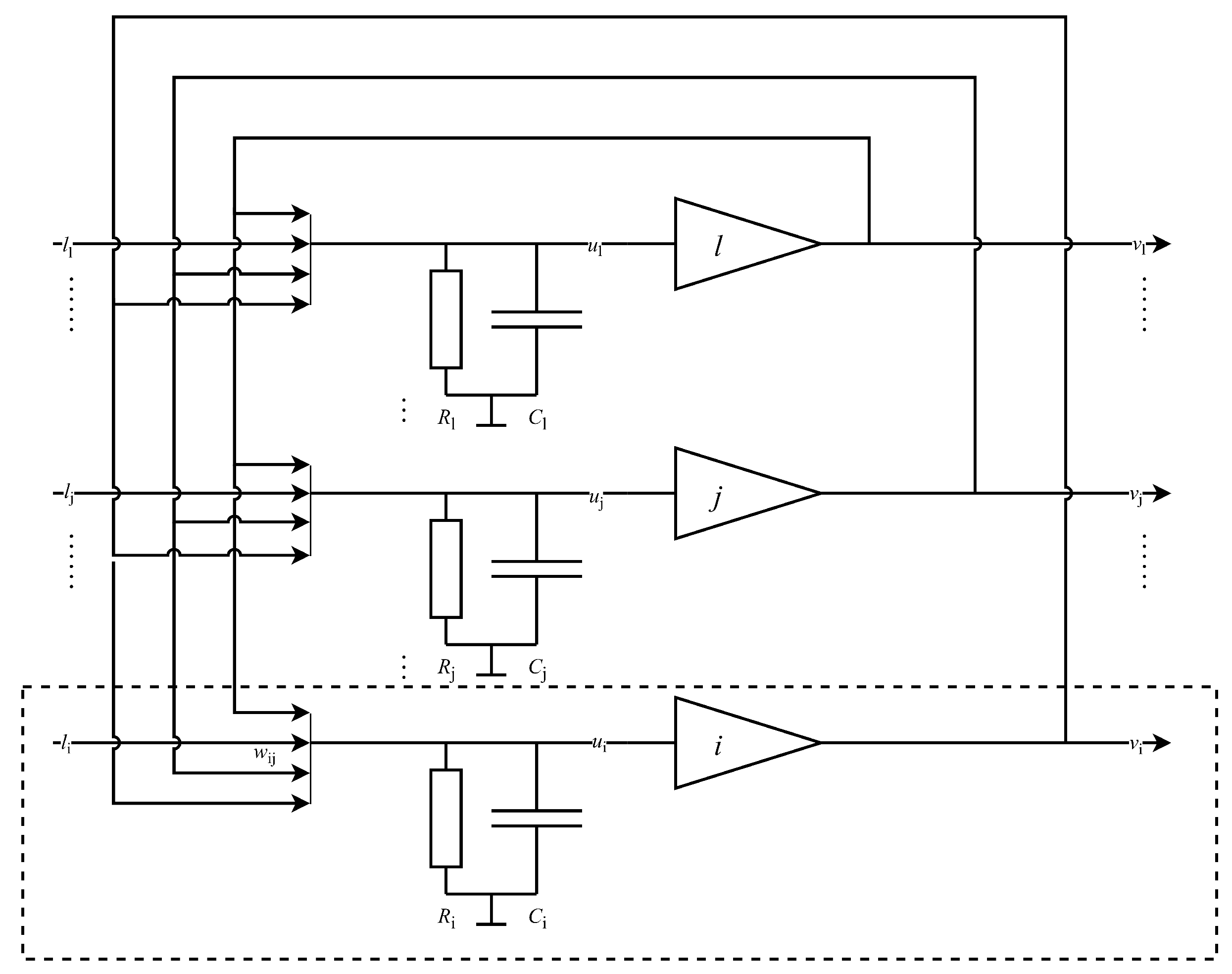
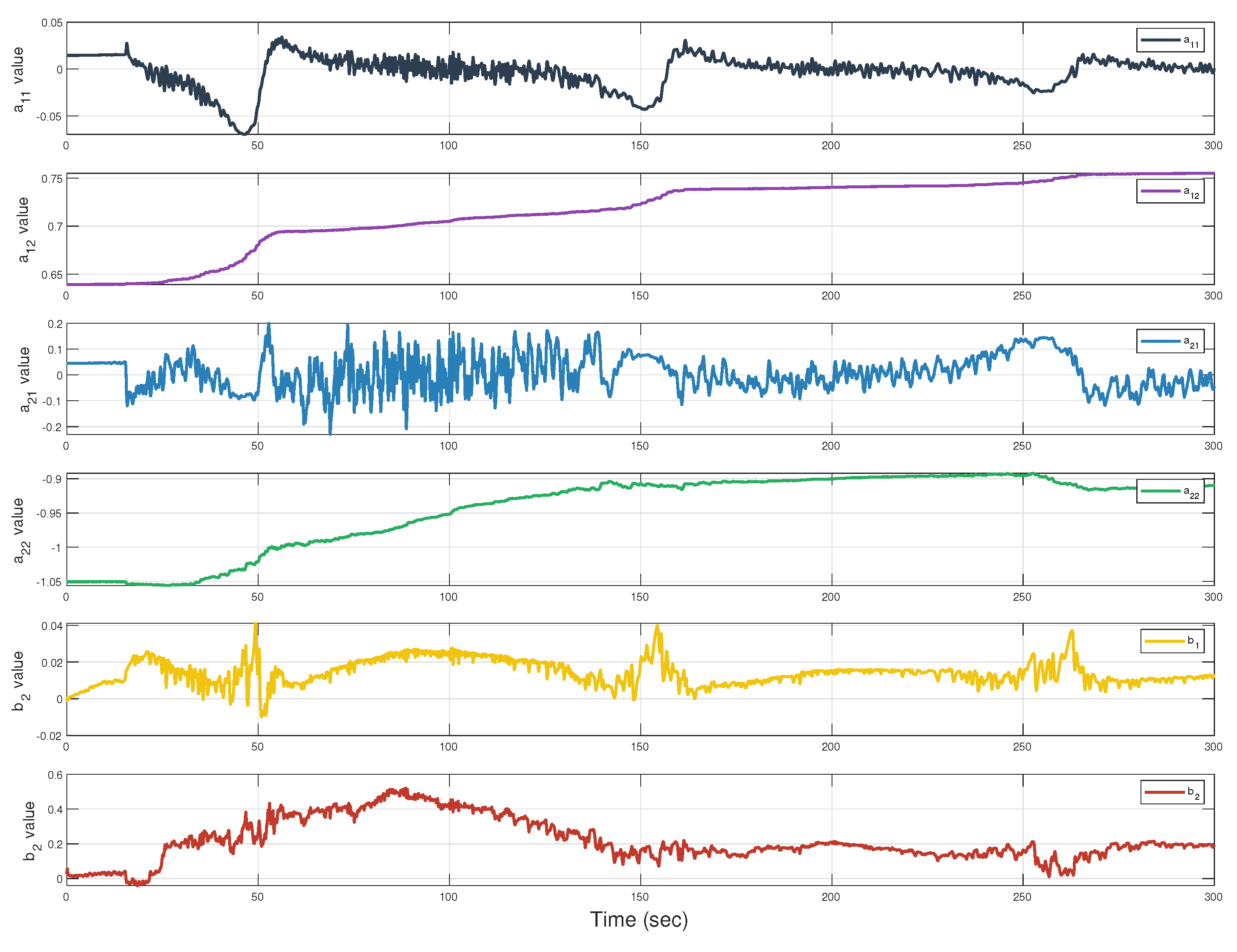
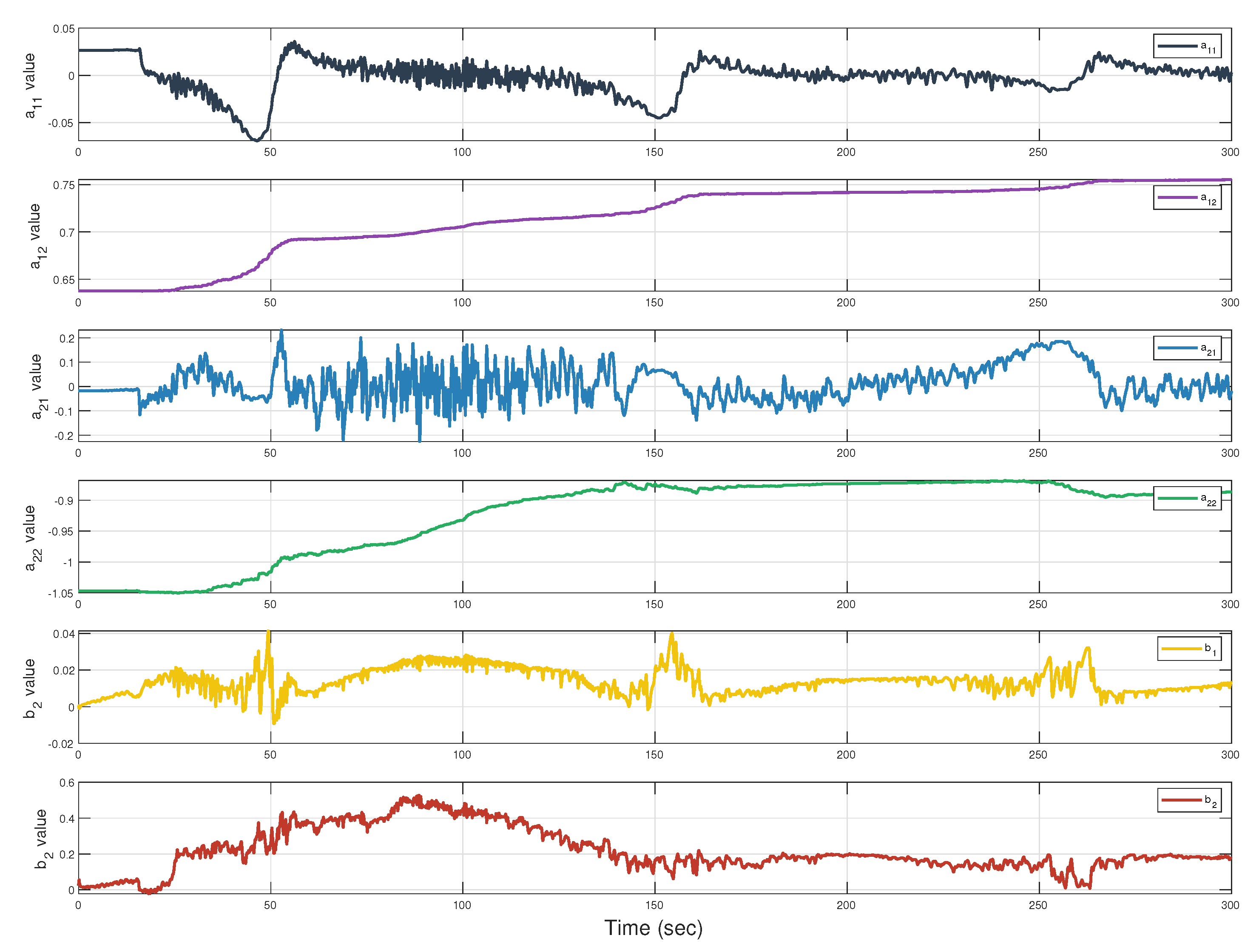
3.2. Design of NNI
3.3. Design of MPC
| Algorithm 1 An algorithm of NNI-MPHC |
|
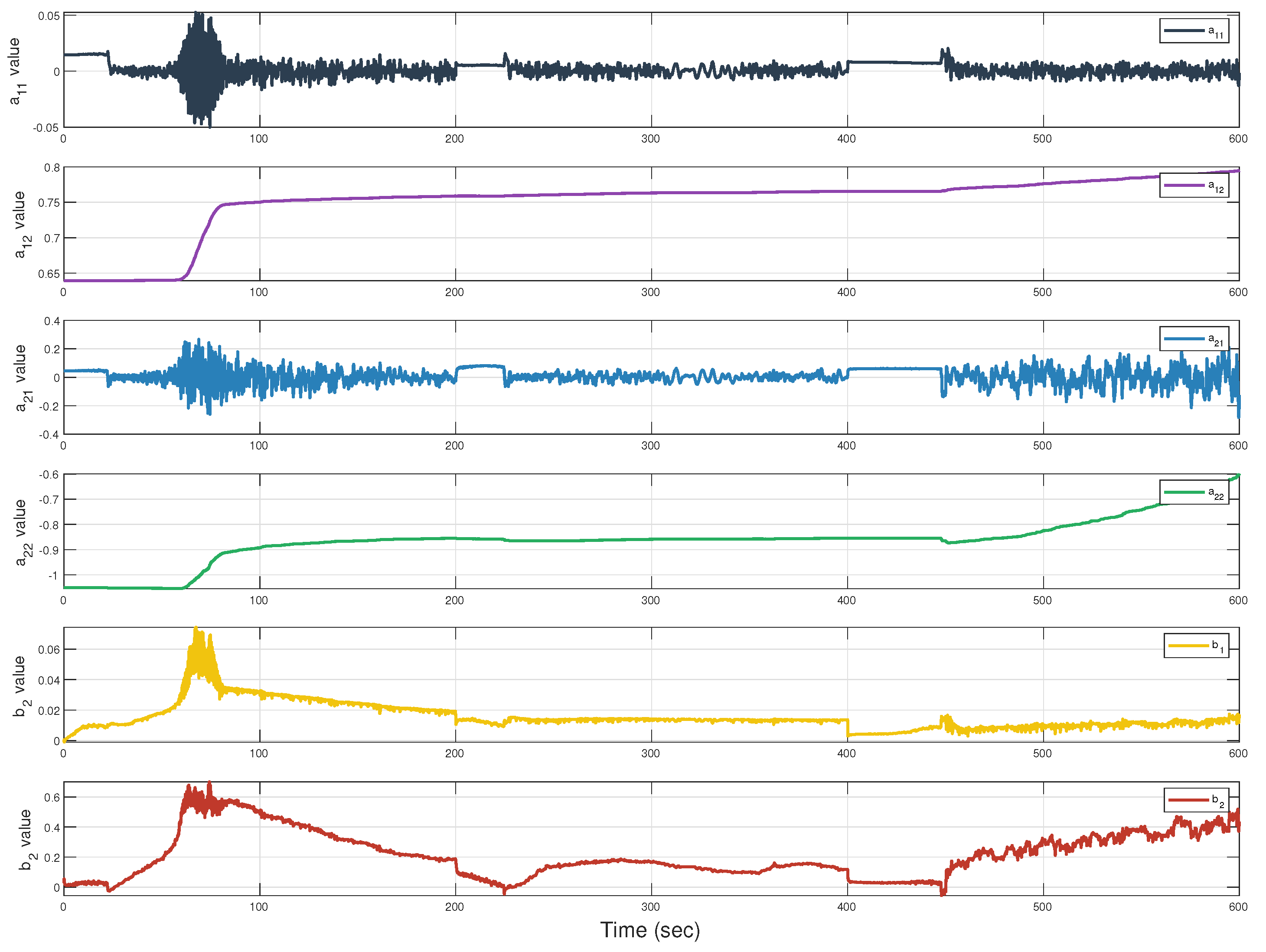
4. Simulation Results
4.1. Parameters of the Wave Glider
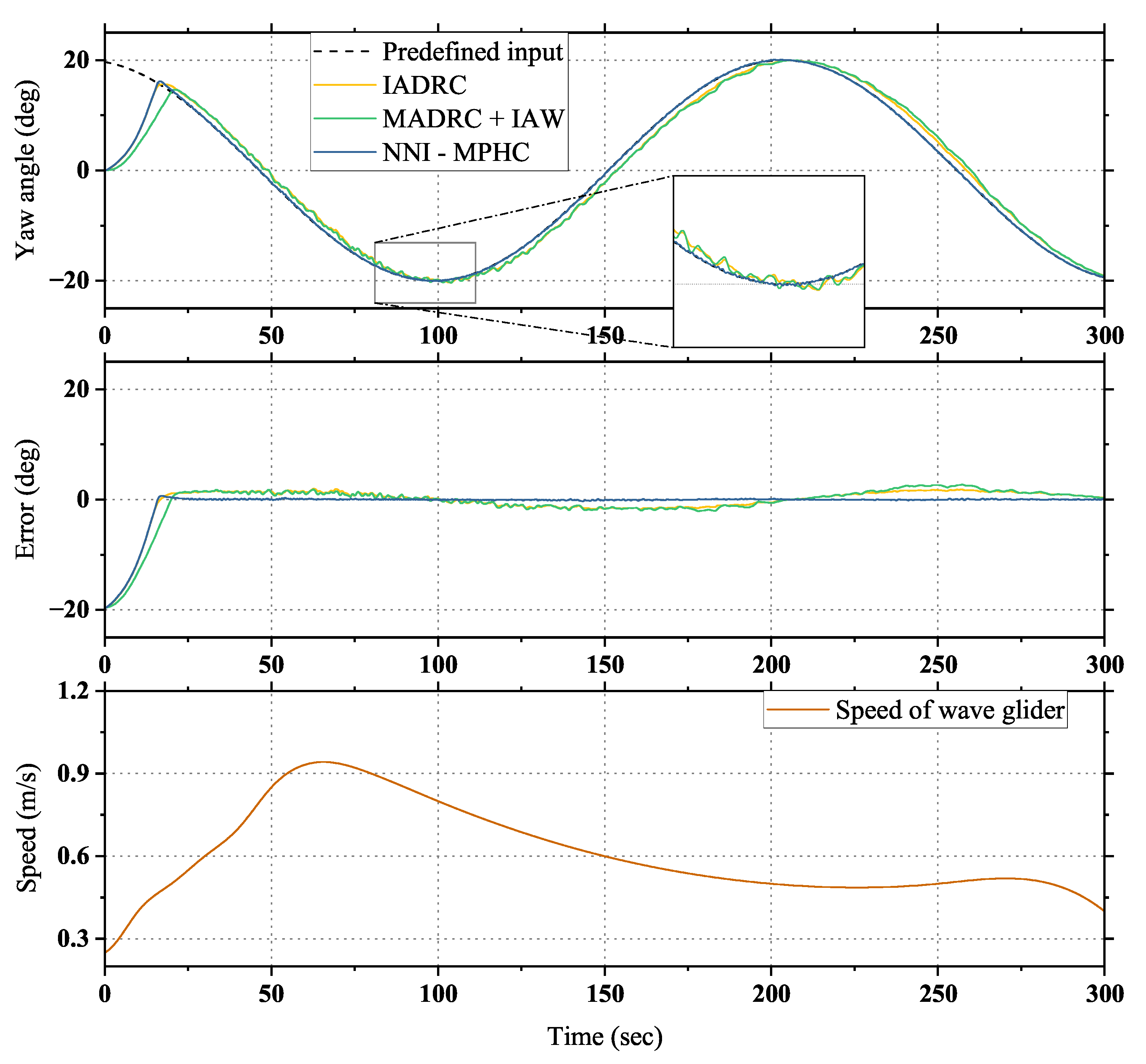
4.2. Performance of Glider with Different Heading Controllers
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sun, X.; Zhou, Y.; Sang, H.; Yu, P.; Zhang, S. Adaptive path following control for Wave gliders in time-varying environment. Ocean Eng. 2020, 218, 108165. [Google Scholar] [CrossRef]
- Yazdani, A.; MahmoudZadeh, S.; Yakimenko, O.; Wang, H. Perception-aware online trajectory generation for a prescribed manoeuvre of unmanned surface vehicle in cluttered unstructured environment. Robot. Auton. Syst. 2023, 169, 104508. [Google Scholar] [CrossRef]
- Liu, F.; Liu, Y.; Sun, X.; Sang, H. A new multi-sensor hierarchical data fusion algorithm based on unscented Kalman filter for the attitude observation of the wave glider. Appl. Ocean Res. 2021, 109, 102562. [Google Scholar] [CrossRef]
- Yazdani, A.; Sammut, K.; Yakimenko, O.; Lammas, A. A survey of underwater docking guidance systems. Robot. Auton. Syst. 2020, 124, 103382. [Google Scholar] [CrossRef]
- Yazdani, A.; Sammut, K.; Yakimenko, O.; Lammas, A.; Tang, Y.; Mahmoud Zadeh, S. IDVD-based trajectory generator for autonomous underwater docking operations. Robot. Auton. Syst. 2017, 92, 12–29. [Google Scholar] [CrossRef]
- Abbasi, A.; MahmoudZadeh, S.; Yazdani, A. A Cooperative Dynamic Task Assignment Framework for COTSBot AUVs. IEEE Trans. Autom. Sci. Eng. 2022, 19, 1163–1179. [Google Scholar] [CrossRef]
- Wang, L.; Li, Y.; Liao, Y.; Pan, K.; Zhang, W. Course control of unmanned wave glider with heading information fusion. IEEE Trans. Ind. Electron. 2019, 66, 7997–8007. [Google Scholar] [CrossRef]
- Yiming, L.; Ye, L.; Shuo, P. Variable-structure filtering method for an unmanned wave glider. Appl. Ocean Res. 2021, 107, 102450. [Google Scholar] [CrossRef]
- Yiming, L.; Ye, L.; Shuo, P. Double-body coupled heading manoeuvrability response model considering umbilical lag of unmanned wave glider. Appl. Ocean Res. 2021, 113, 102640. [Google Scholar] [CrossRef]
- Li, Y.; Pan, K.; Liao, Y.; Zhang, W.; Wang, L. Improved active disturbance rejection heading control for unmanned wave glider. Appl. Ocean Res. 2021, 106, 102438. [Google Scholar] [CrossRef]
- Zhou, Y.; Sun, X.; Sang, H.; Yu, P. Robust dynamic heading tracking control for wave gliders. Ocean Eng. 2022, 256, 111510. [Google Scholar] [CrossRef]
- Hu, Y.; Wang, H.; Yazdani, A.; Man, Z. Adaptive full order sliding mode control for electronic throttle valve system with fixed time convergence using extreme learning machine. Neural Comput. Appl. 2022, 34, 5241–5253. [Google Scholar] [CrossRef]
- Chen, L.; Liu, J.; Wang, H.; Hu, Y.; Zheng, X.; Ye, M.; Zhang, J. Robust control of reaction wheel bicycle robot via adaptive integral terminal sliding mode. Nonlinear Dyn. 2021, 104, 2291–2302. [Google Scholar] [CrossRef]
- Chen, L.; Zhang, H.; Wang, H.; Shao, K.; Wang, G.; Yazdani, A. Continuous adaptive fast terminal sliding mode-based speed regulation control of PMSM drive via improved super-twisting observer. IEEE Trans. Ind. Electron. 2023, 71, 5105–5115. [Google Scholar] [CrossRef]
- Wen, H.; Li, X.; Liang, Z.; Yao, B.; Lian, L. Orientation control of the Wave Glider with uncertain environment disturbances and unknown variable hydrodynamics coefficients: Theory and simulation. Ocean Eng. 2023, 275, 114110. [Google Scholar] [CrossRef]
- Wang, P.; Zhang, X.; Wang, D.; Guo, X.; Lu, W.; Tian, X. A restricted circle based position keeping strategy for the wave glider. Appl. Ocean Res. 2020, 97, 102081. [Google Scholar] [CrossRef]
- Yu, P.; Sun, X.; Zhou, Y.; Sang, H.; Zhang, S. Adaptive station-keeping strategy for wave gliders considering uncertain environmental disturbances. Ocean Eng. 2023, 277, 114326. [Google Scholar] [CrossRef]
- Zhang, S.; Sang, H.; Sun, X.; Liu, F.; Zhou, Y.; Yu, P. Research on the maneuverability and path following control of the wave glider with a propeller-rudder system. Ocean Eng. 2023, 278, 114346. [Google Scholar] [CrossRef]
- Zhang, S.; Sang, H.; Sun, X.; Liu, F.; Zhou, Y.; Yu, P. A multi-objective path planning method for the wave glider in the complex marine environment. Ocean Eng. 2022, 264, 112481. [Google Scholar] [CrossRef]
- Valencia-Palomo, G.; Rossiter, J.; López-Estrada, F. Improving the feed-forward compensator in predictive control for setpoint tracking. ISA Trans. 2014, 53, 755–766. [Google Scholar] [CrossRef]
- Valencia-Palomo, G.; Rossiter, J. Novel programmable logic controller implementation of a predictive controller based on Laguerre functions and multiparametric solutions. IET Control. Theory Appl. 2012, 6, 1003–1014. [Google Scholar] [CrossRef]
- Cui, D.; Zou, W.; Guo, J.; Xiang, Z. Neural network-based adaptive finite-time tracking control of switched nonlinear systems with time-varying delay. Appl. Math. Comput. 2022, 428, 127216. [Google Scholar] [CrossRef]
- Atencia, M.; Joya, G.; Sandoval, F. Hopfield Neural Networks for Parametric Identification of Dynamical Systems. Neural Process. Lett. 2005, 21, 143–152. [Google Scholar] [CrossRef]
- Yu, J.B.; Wu, Y.Q. Global robust tracking control for a class of cascaded nonlinear systems using a reduced-order extended state observer. Nonlinear Dyn. 2018, 94, 1277–1289. [Google Scholar] [CrossRef]
- Kraus, N.D. Wave Glider Dynamic Modeling, Parameter Identification and Simulation. Master’s Thesis, University of Hawaii at Manoa, Honolulu, HI, USA, 2012. [Google Scholar]
- Wang, L.; Li, Y.; Liao, Y.; Pan, K.; Zhang, W. Dynamics modeling of an unmanned wave glider with flexible umbilical. Ocean Eng. 2019, 180, 267–278. [Google Scholar] [CrossRef]
- Wang, P.; Tian, X.; Lu, W.; Hu, Z.; Luo, Y. Dynamic modeling and simulations of the wave glider. Appl. Math. Model. 2019, 66, 77–96. [Google Scholar] [CrossRef]
- Wen, H.; Zhou, H.; Fu, J.; Zhang, X.; Yao, B.; Lian, L. Multi-body coupled dynamic modelling of the Wave Glider. Ocean Eng. 2022, 257, 111499. [Google Scholar] [CrossRef]
- Fossen, T.I. Handbook of Marine Craft Hydrodynamics and Motion Control; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2011; Chapter 7; pp. 133–186. [Google Scholar] [CrossRef]
- Tsingtao Hydrotech Co., Ltd. Black Pearl Wave Glider. 2022. Available online: https://image.brandpano.com/app/cimee/2021pro/glider/index.html#/ (accessed on 6 December 2024).
- Gu, N.; Wang, D.; Peng, Z.; Wang, J.; Han, Q.L. Disturbance observers and extended state observers for marine vehicles: A survey. Control Eng. Pract. 2022, 123, 105158. [Google Scholar] [CrossRef]
- Habibi, H.; Yazdani, A.; Darouach, M.; Wang, H.; Fernando, T.; Howard, I. Observer-based sensor fault tolerant control with prescribed tracking performance for a class of nonlinear systems. IEEE Trans. Autom. Control 2023, 68, 8259–8266. [Google Scholar] [CrossRef]
- Han, J. From PID to active disturbance rejection control. IEEE Trans. Ind. Electron. 2009, 56, 900–906. [Google Scholar] [CrossRef]
- Cui, D.; Ahn, C.K.; Xiang, Z. Fault-Tolerant Fuzzy Observer-Based Fixed-Time Tracking Control for Nonlinear Switched Systems. IEEE Trans. Fuzzy Syst. 2023, 31, 4410–4420. [Google Scholar] [CrossRef]
- Hopfield, J.J. Neurons with graded response have collective computational properties like those of two-state neurons. Proc. Natl. Acad. Sci. USA 1984, 81, 3088–3092. [Google Scholar] [CrossRef] [PubMed]
- Maciejowski, J. Predictive Control with Constraints; Wiley Online Library: Hoboken, NJ, USA, 2003. [Google Scholar]
- Li, Z.X. Research on Adaptive Heading Control of Wave Glider. Master’s Thesis, Qingdao University of Science and Technology, Qingdao, China, 2022. [Google Scholar]
- Schultz, W.C.; Rideout, V.C. Control system performance measures: Past, present, and future. IRE Trans. Autom. Control 1961, AC-6, 22–35. [Google Scholar] [CrossRef]

| Parameter | Value | Parameter | Value |
|---|---|---|---|
| 0.02 | 0.15 | ||
| 1.5 | 10 | ||
| 1 |
| NNI-MPHC | ||
|---|---|---|
| Component | Parameter | Value |
| MPC | Q | 40 |
| R | 0.27 | |
| n | 10 | |
| m | 3 | |
| T | 0.1 | |
| NNI | 1.2 | |
| 0.06 | ||
| LRESO | 26 | |
| 0.2 | ||
| 0.1 | ||
| IADRC [10] | MADRC+IAW [11] | ||||
|---|---|---|---|---|---|
| Component | Parameter | Value | Component | Parameter | Value |
| TD | r | 1.2 | TD | r | 1.2 |
| h | 1.0 | h | 1.0 | ||
| S-surface | 6.0 | NLSEF | 0.25 | ||
| controller | 4.5 | controller | 0.5 | ||
| 40 | 1.5 | ||||
| ILESO | 6.0 | 8.0 | |||
| 12 | 0.5 | ||||
| 8.0 | RESO | 0.5 | |||
| 0.2 | 0.1 | ||||
| 0.7 | 0.01 | ||||
| 1.5 | 20 | ||||
| 0.768 | 0.5 | ||||
| 0.25 | |||||
| IAW | 0.02 | ||||
| 0.2 | |||||
| 1 | |||||
| Controller | (s) | IAE (deg) |
|---|---|---|
| Ideal condition | 600 | 2087.5 |
| IADRC [10] | 600 | 2203 |
| MADRC+IAW [11] | 600 | 2479 |
| NNI-MPHC | 600 | 2104.9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jin, P.; Zhang, B.; Zhang, Y. Neural Network Identification-Based Model Predictive Heading Control for Wave Gliders. J. Mar. Sci. Eng. 2024, 12, 2279. https://doi.org/10.3390/jmse12122279
Jin P, Zhang B, Zhang Y. Neural Network Identification-Based Model Predictive Heading Control for Wave Gliders. Journal of Marine Science and Engineering. 2024; 12(12):2279. https://doi.org/10.3390/jmse12122279
Chicago/Turabian StyleJin, Peng, Baolin Zhang, and Yun Zhang. 2024. "Neural Network Identification-Based Model Predictive Heading Control for Wave Gliders" Journal of Marine Science and Engineering 12, no. 12: 2279. https://doi.org/10.3390/jmse12122279
APA StyleJin, P., Zhang, B., & Zhang, Y. (2024). Neural Network Identification-Based Model Predictive Heading Control for Wave Gliders. Journal of Marine Science and Engineering, 12(12), 2279. https://doi.org/10.3390/jmse12122279






