The Prediction and Dynamic Correction of Drifting Trajectory for Unmanned Maritime Equipment Based on Fully Connected Neural Network (FCNN) Embedding Model
Abstract
:1. Introduction
- We propose a prediction and dynamic correction model of drifting trajectory based on an FCNN. It can dynamically correct the original trajectory predicted by the traditional method using the SAR target’s feedback of its own position information. This method can significantly improve the prediction accuracy of drifting trajectory.
- We propose a methodological framework for the prediction and dynamic correction of drifting trajectory under the condition of unmanned maritime equipment with position information returned. The position information of equipment can be fully used to dynamically improve the accuracy of prediction, and the effectiveness was successfully validated using unmanned maritime equipment drifting experiment data.
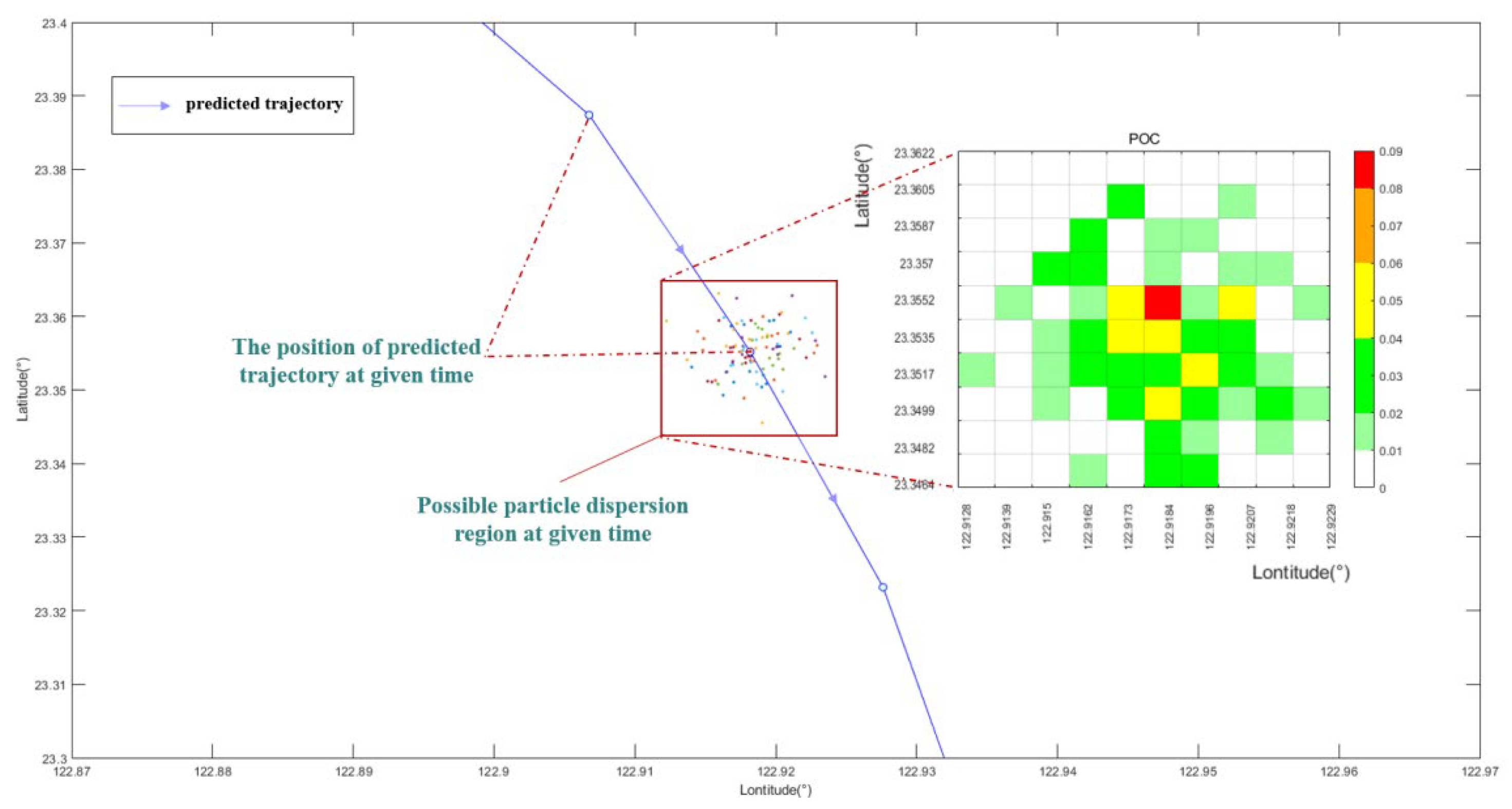
- Based on the proposed FCNN embedding drifting trajectory prediction and correction model for unmanned maritime equipment, the obtained POC for the unmanned maritime equipment SAR region show a significant improvement in accuracy compared to the traditional methods.
2. Methodology
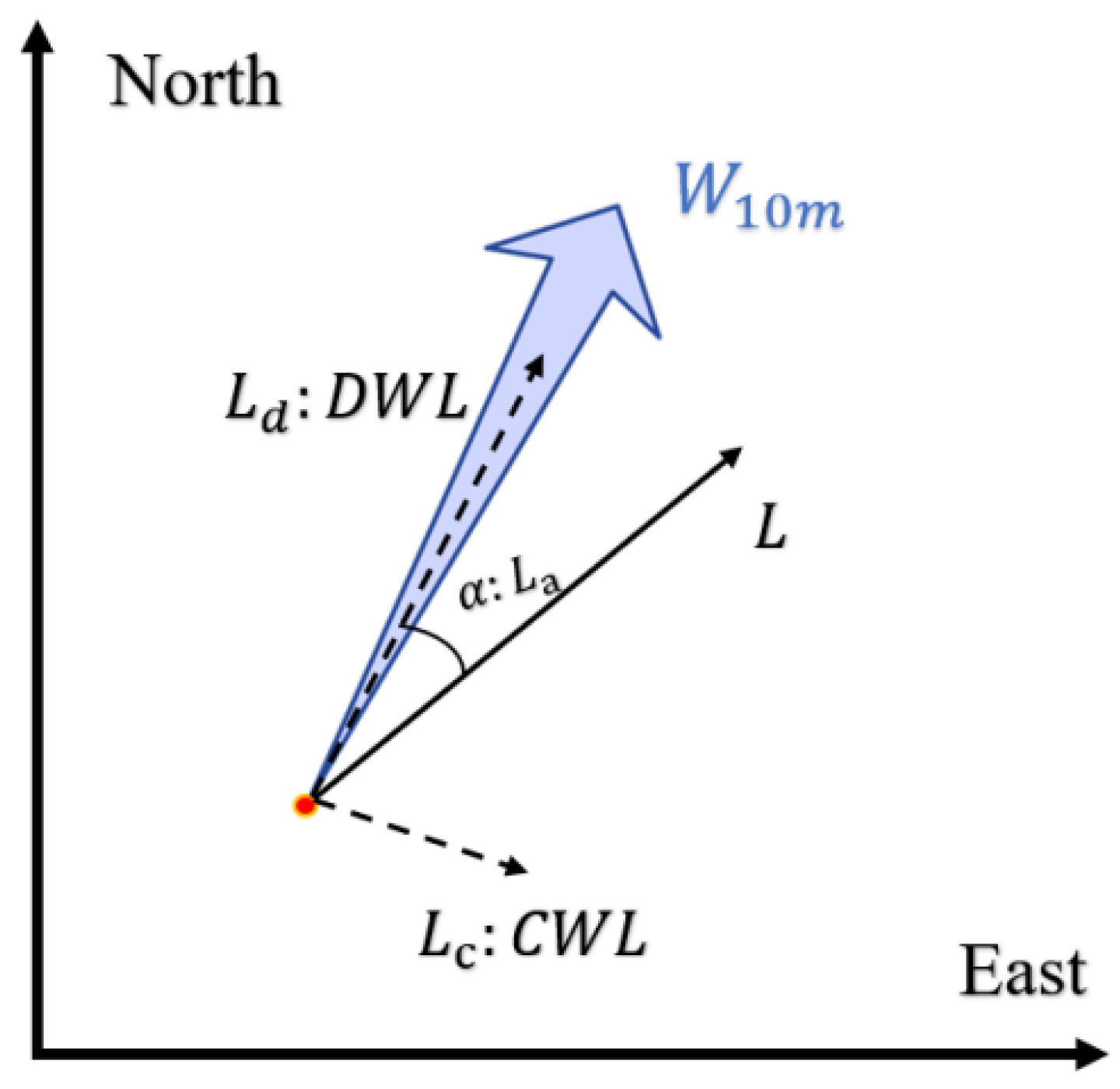
2.1. Unmanned Maritime Equipment Drifting Model
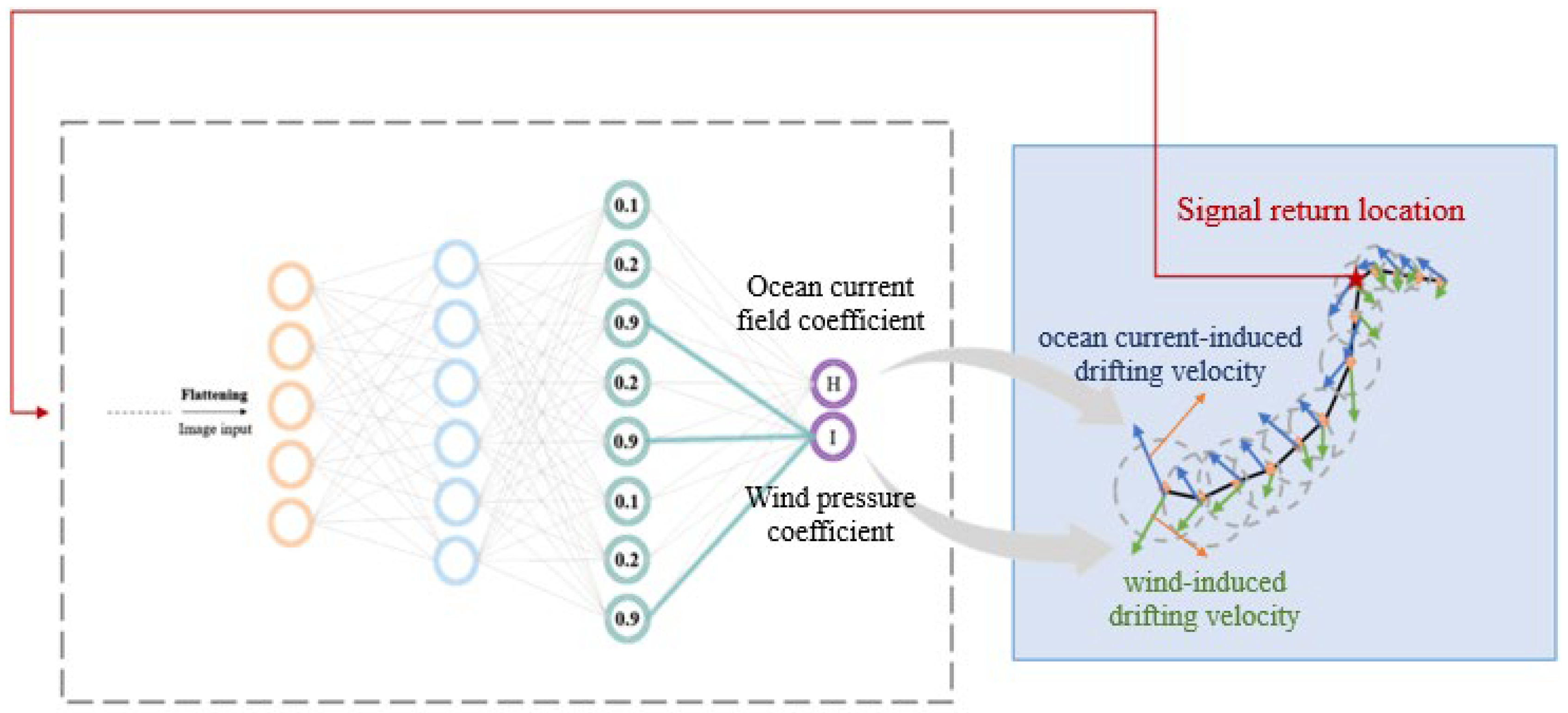
2.2. Trajectory Dynamic Correction Algorithm Based on FCNN
2.3. Monte Carlo Simulation-Based Quantification of the POC in SAR Region
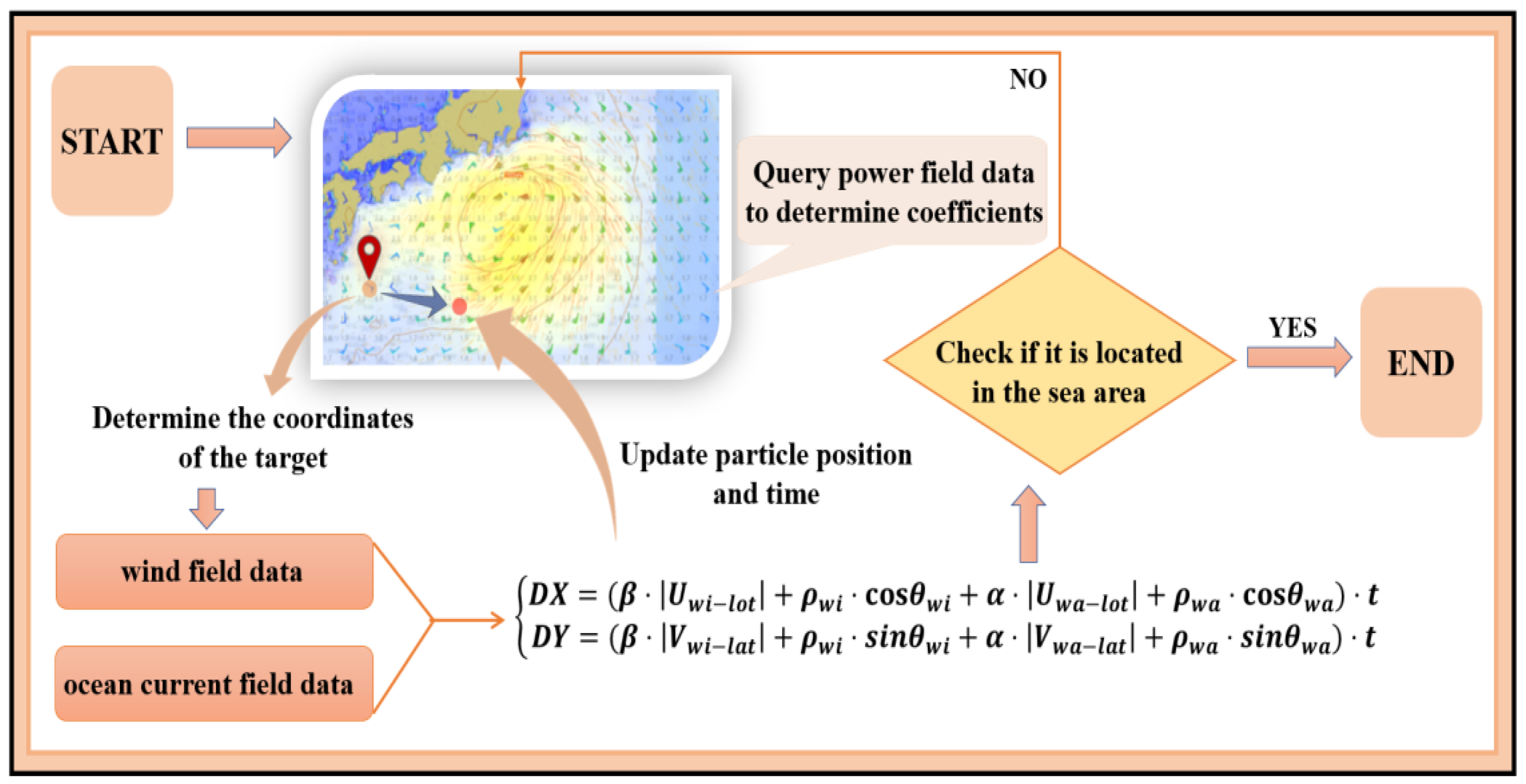
2.4. Steps for Predicting Target Drift Trajectory
3. Experiments
3.1. Data Preparation
3.2. Model Parameter Setting and Initialization
3.3. Model Training
3.4. Evaluation Criteria
4. Results and Discussions
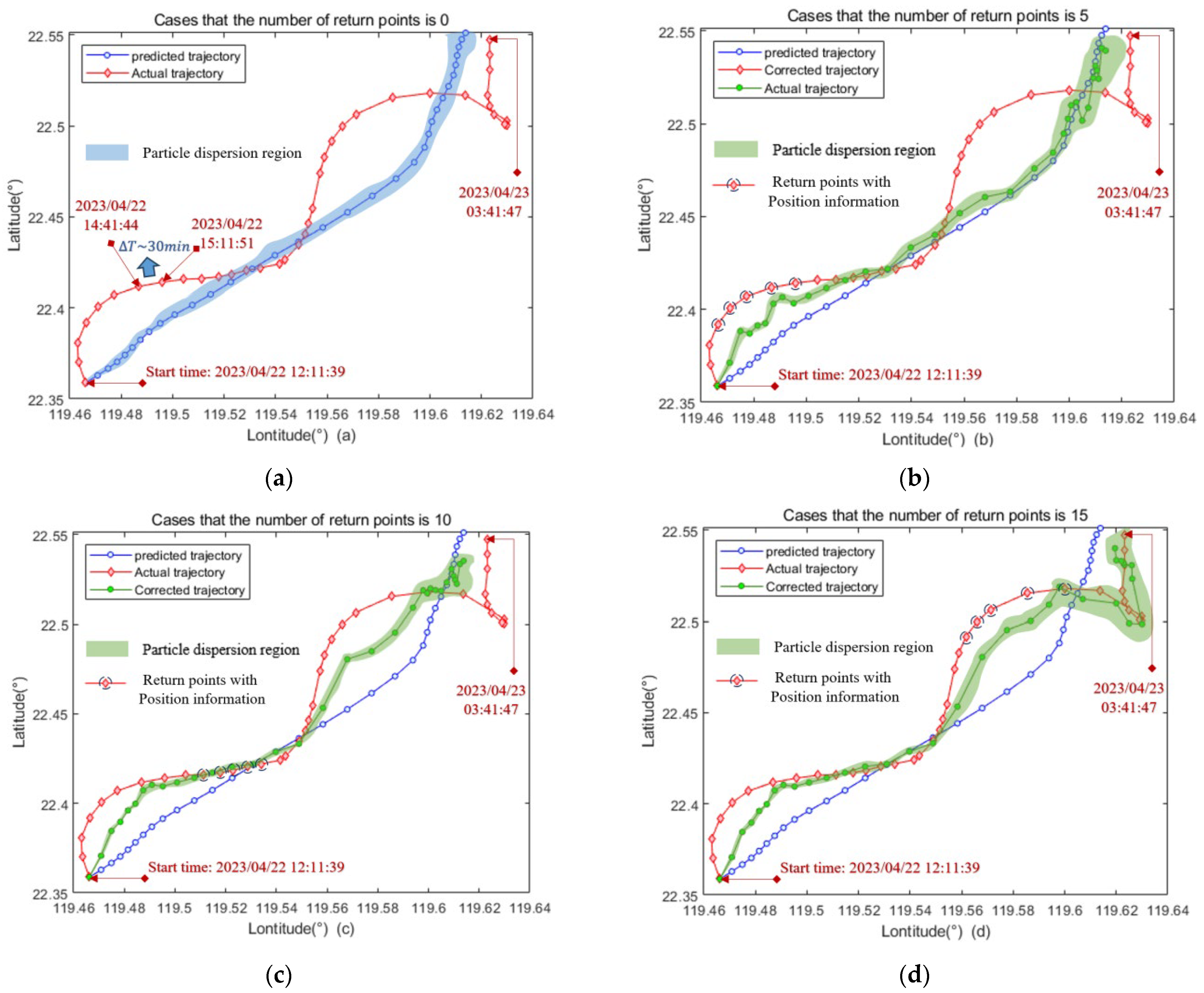
4.1. Trajectory Correction Based on Single-Point Position Information Returns and Discussion
4.2. Trajectory Correction Based on Multi-Point Position Information Returns and Discussion
4.3. Quantification of the POC in the SAR Region Based on Corrected Trajectories
5. Conclusions
5.1. Limitations
5.2. Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Anderson, E.; Odulo, A.; Spaulding, M. Modeling of Leeway Drift; U.S. Coast Guard Research and Development Center: Washington, DC, USA, 1998.
- Hodgins, D.O.; Hodgins, S.L.M. Phase II Leeway Dynamics Program: Development and Verification of a Mathematical Drift for Liferafts and Small Boats; Canadian Coast Guard: Ottawa, ON, Canada, 1998.
- Allen, A.; Plourde, J.V. Review of Leeway: Field Experiments and Implementation; U.S. Coast Guard Research and Development Center: Groton, MA, USA, 1999.
- Allen, A. Leeway Divergence. Leeway Divergence; U.S. Coast Guard Research and Development Center: Washington, DC, USA, 2005.
- Röhrs, J.; Christensen, K.H.; Hole, L.R.; Broström, G.; Drivdal, M.; Sundby, S. Observation-based evaluation of surface wave effects on currents and trajectory forecasts. Ocean Dyn. 2012, 62, 1519–1533. [Google Scholar] [CrossRef]
- Xu, J.; Gao, S.; Ge, Y.; Li, R.; Wu, L.-J.; Liu, G. Analysis of Wave Effect on Drifting Trajectory of Float at Sea. J. Inst. Disaster Prev. 2017, 19, 75–79. [Google Scholar]
- Spaulding, M.L.; Howlett, E. Application of SARMAP to estimate probable search area for objects lost at sea. Mar. Technol. Soc. J. 1996, 30, 17–25. [Google Scholar]
- Zhu, G.; Mou, L.; Wang, D. Advance in maritime search and rescue decision support techniques. J. Appl. Oceanogr. 2019, 38, 440–449. [Google Scholar]
- Jiang, H.L.; Sun, Z.C.; Li, L.L.; Liu, B.; Wu, J.P. A Monte Carlo-based model for maritime search area determination. Waterw. Ports 2011, 32, 6. [Google Scholar]
- International Maritime Organization/International Civil Aviation Organization. International Aviation and Maritime Search and Rescue Manual. Maritime Safety Administration of the People’s Republic of China, Translation; Science Press: Beijing, China, 2005. [Google Scholar]
- Huang, J.; Xu, J.; Gao, S.; Guo, J. Factors analysis on sea surface drift trajectory forecasting based on field experiment. Mar. Forecast. 2014, 31, 8. [Google Scholar]
- Zhou, S.; Yang, Y.; Feng, W. Experimental study of sea drift of simulated human and unpowered fishing vessels in Guangdong waters. J. Trop. Oceanogr. 2013, 32, 87–94. [Google Scholar]
- Wu, W. Neural Network Computing; Higher Education Press: Beijing, China, 2003. [Google Scholar]
- Zhang, Q. Introduction to Artificial Neural Networks; China Water Resources and Hydropower Press: Beijing, China, 2004. [Google Scholar]
- Jia, K. Improvement of a Backpropagation Algorithm for Feedforward Neural Networks. Ph.D. Thesis, Dalian University of Technology, Dalian, China, 2011. [Google Scholar]
- Xiao, F. Research on Key Technologies of Maritime Search and Rescue Decision Support System. Ph.D. Thesis, Dalian Maritime University, Dalian, China, 2011. [Google Scholar]
- Xiao, F.; Yin, Y.; Jin, Y. Determination of Maritime Search Area Based on Stochastic Particle Simulation. Navig. China 2011, 34, 34–39. [Google Scholar]
- Jiang, H.-L. Study on Determining Search Area Model for SAR at Sea. Master’s Thesis, Dalian University of Technology, Dalian, China, 2011. [Google Scholar]
- FIO Coupled Ocean Model. Available online: http://fiocom.fio.org.cn/introduction.html (accessed on 22 April 2023).
- Li, Y.; Qi, L.; Liang, G. A Ship Trajectory Clustering Method Considering the Spatiotemporal Characteristics of Traffic Flow. J. Wuhan Univ. Technol. 2024, 46, 107–115. [Google Scholar]






| Lon_1 | Lat_1 | t_1 | Lon_2 | Lat_2 | t_2 | … | Lon_n | Lat_n | t_n | Wind_c | Water_c |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 119.38° E | 22.97° N | … | 119.40° E | 22.95° N | … | … | 119.68° E | 22.66° N | … | 0.0405 | 1.0431 |
| 122.47° E | 21.61° N | … | 122.49° E | 21.58° N | … | … | 124.17° E | 19.67° N | … | 0.0485 | 1.4819 |
| … | … | … | … | … | … | … | … | … | … | … | … |
| 124.91° E | 22.08° N | … | 124.92° E | 22.07° N | … | … | 125.20° E | 22.04° N | … | 0.0370 | 1.1100 |
| Data Date | Starting Moment | Prediction Interval (min) | Projected Length (h) | Latitude and Longitude of the Starting Point |
|---|---|---|---|---|
| 22 April 2023 | 12:00:00 | 5 | 24 | (122.5° E, 23.7° N) |
| Equipment Drifting Parameters | Data |
|---|---|
| Wind pressure coefficient (×10−2) | 4.00 |
| Wind pressure perturbation coefficient | 0.16 |
| Ocean current field coefficient | 1.20 |
| Ocean current perturbation coefficient | 0.25 |
| Equipment Type | Data Date | Predicting the Starting Moment | Projected Length (h) | Latitude and Longitude of the Starting Point |
|---|---|---|---|---|
| PO1 | 22 April 2023 | 12:11:39 | 24 | (119.4662° E, 22.3588° N) |
| Equipment Drifting Parameters | Predicted Parameters | Corrected Parameters |
|---|---|---|
| Wind pressure coefficient (×10−2) | 4.00 | 3.85 |
| Ocean current field coefficient | 1.20 | 1.1575 |
| Number of Return Points | Feedback Time for Position Information | Distance of Average Offset (km) |
|---|---|---|
| 0 | \ | 5.75 |
| 1 | 22 April 2023 13:41:45 | 5.17 |
| 2 | 22 April 2023 14:11:38 | 4.92 |
| 3 | 22 April 2023 14:41:44 | 4.69 |
| 4 | 22 April 2023 15:11:51 | 4.34 |
| 5 | 22 April 2023 15:41:45 | 3.94 |
| Number of Return Points | Predicted Value (Wind Pressure Coefficient (×10−2), Ocean Current Field Coefficient) | Corrected Value (Wind Pressure Coefficient (×10−2), Ocean Current Field Coefficient) | Distance of Average Offset (km) |
|---|---|---|---|
| 0 | (4.00, 1.2000) | \ | 5.75 |
| 5 | (4.00, 1.2000) | (3.87, 1.2595) | 3.94 |
| 10 | (4.00, 1.2000) | (3.53, 1.2351) | 1.11 |
| 15 | (4.00, 1.2000) | (4.35, 1.2384) | 4.11 × 10−1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, Y.; Wang, D.; Xiong, X.; Cheng, X.; Huang, L.; Zhang, Y. The Prediction and Dynamic Correction of Drifting Trajectory for Unmanned Maritime Equipment Based on Fully Connected Neural Network (FCNN) Embedding Model. J. Mar. Sci. Eng. 2024, 12, 2262. https://doi.org/10.3390/jmse12122262
Song Y, Wang D, Xiong X, Cheng X, Huang L, Zhang Y. The Prediction and Dynamic Correction of Drifting Trajectory for Unmanned Maritime Equipment Based on Fully Connected Neural Network (FCNN) Embedding Model. Journal of Marine Science and Engineering. 2024; 12(12):2262. https://doi.org/10.3390/jmse12122262
Chicago/Turabian StyleSong, Yuxuan, Dezhi Wang, Xiaodan Xiong, Xinghua Cheng, Lingzhi Huang, and Yichao Zhang. 2024. "The Prediction and Dynamic Correction of Drifting Trajectory for Unmanned Maritime Equipment Based on Fully Connected Neural Network (FCNN) Embedding Model" Journal of Marine Science and Engineering 12, no. 12: 2262. https://doi.org/10.3390/jmse12122262
APA StyleSong, Y., Wang, D., Xiong, X., Cheng, X., Huang, L., & Zhang, Y. (2024). The Prediction and Dynamic Correction of Drifting Trajectory for Unmanned Maritime Equipment Based on Fully Connected Neural Network (FCNN) Embedding Model. Journal of Marine Science and Engineering, 12(12), 2262. https://doi.org/10.3390/jmse12122262





