Influence of Free Surface on the Hydrodynamic and Acoustic Characteristics of a Highly Skewed Propeller
Abstract
1. Introduction
2. Mathematical and Numerical Model
2.1. Numerical Methods and Flow Solver
2.2. FW-H Method
3. Geometry and Simulation Conditions
3.1. Geometric Model
3.2. Boundary Conditions and Mesh Details
3.3. Numerical Validation
3.3.1. Hydrodynamic Performance Validation
3.3.2. Noise Validation
4. Results and Analysis
4.1. Global Parameters of Performance
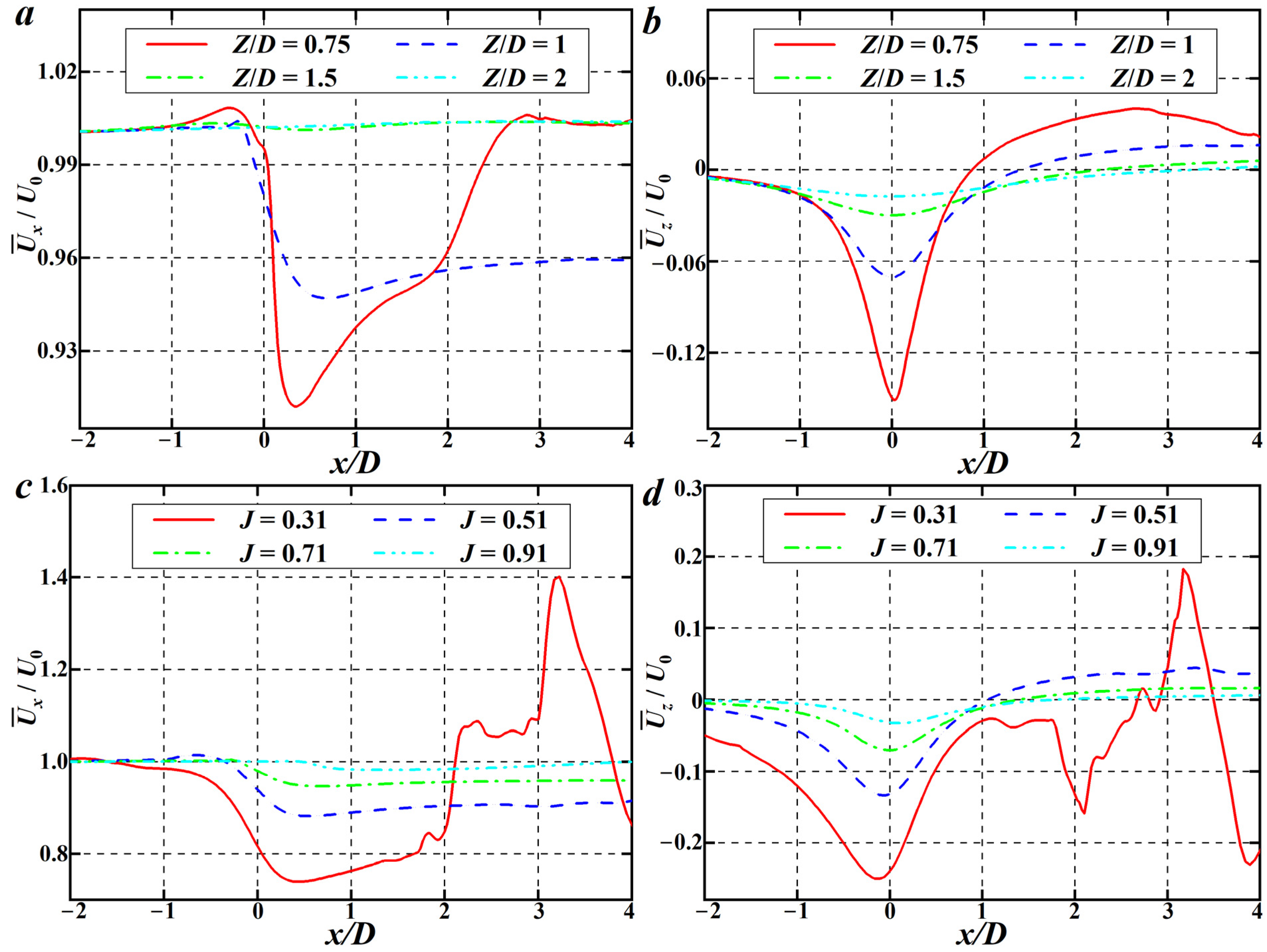
4.2. Flow Field Details
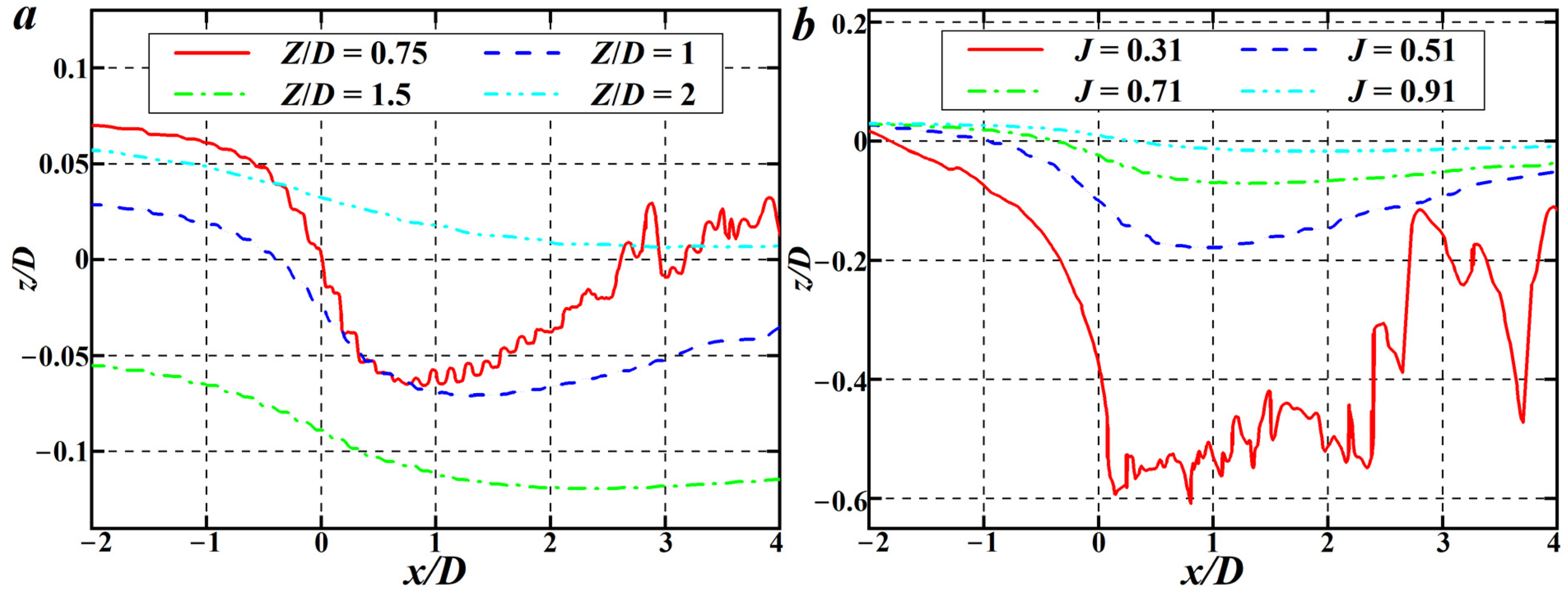
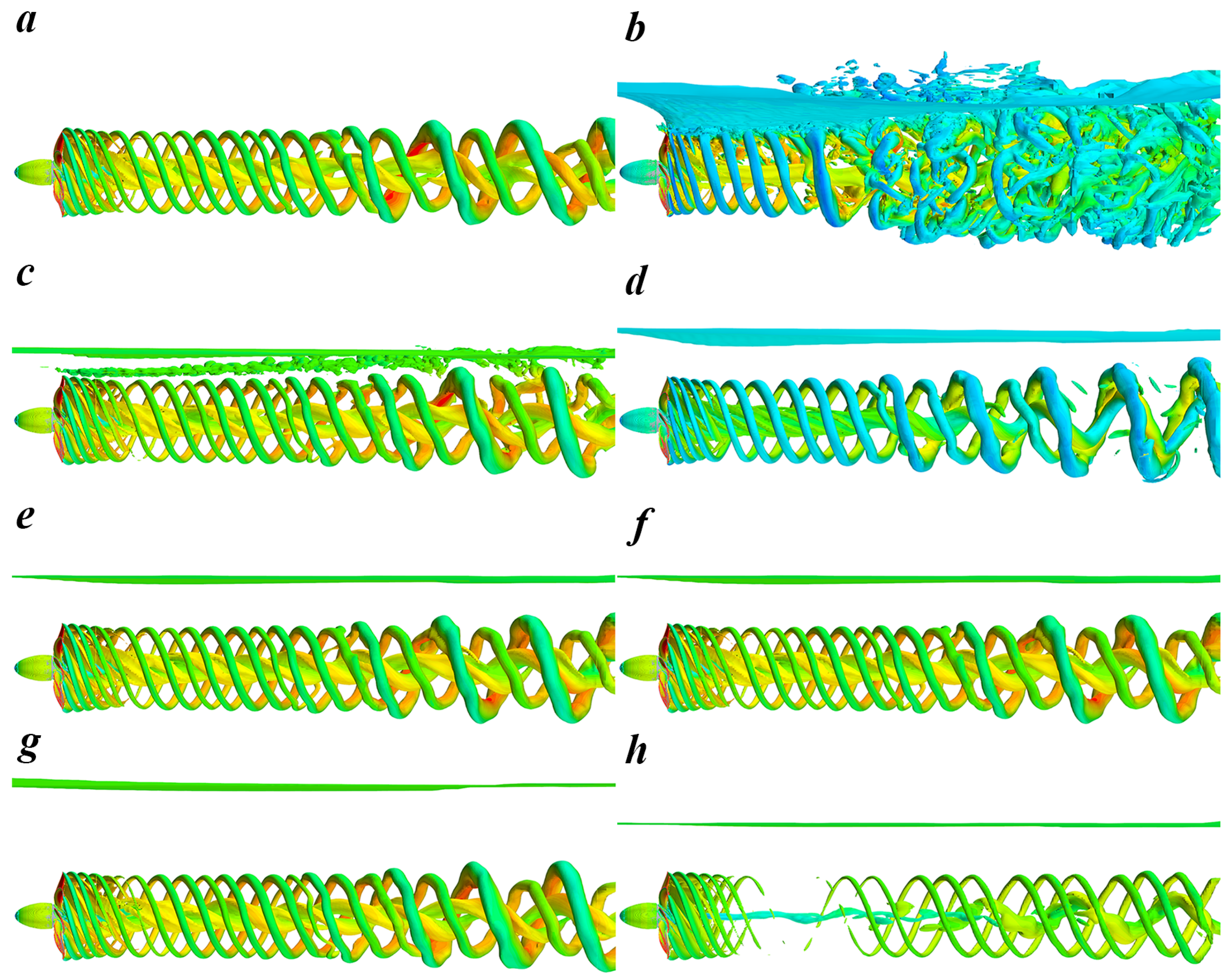
4.3. Vortex Structures
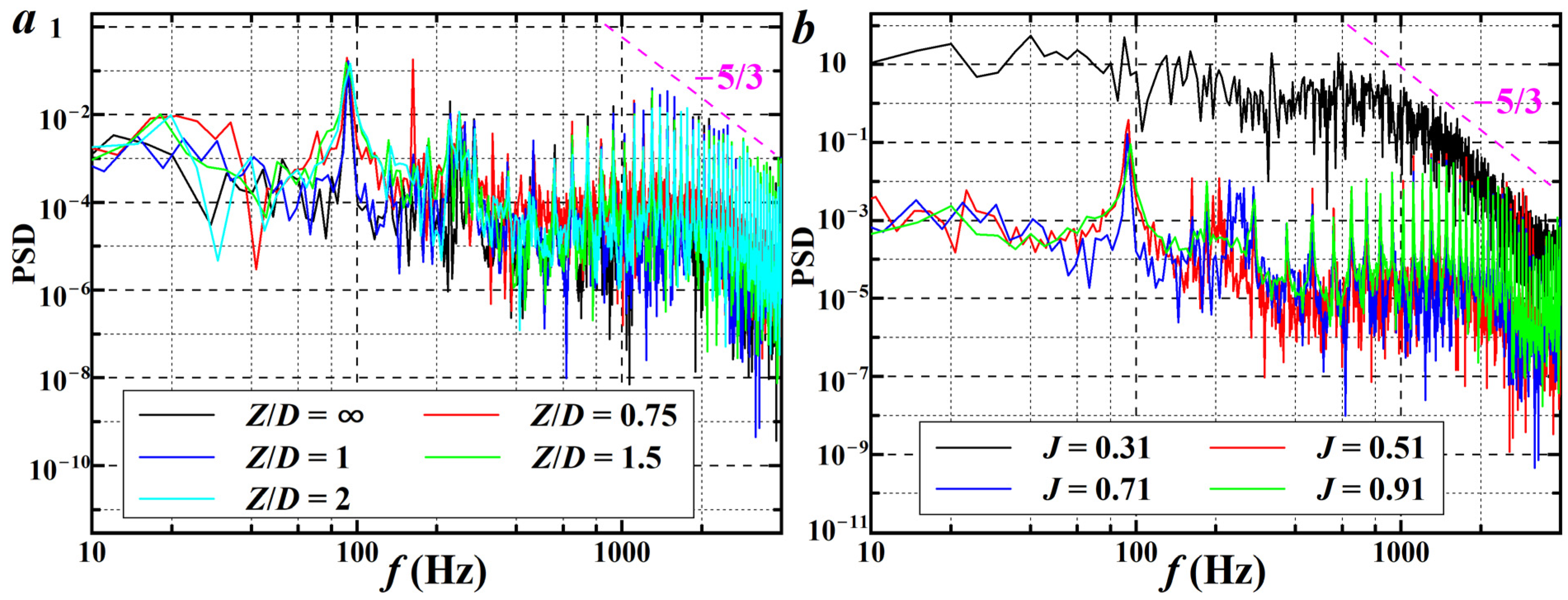
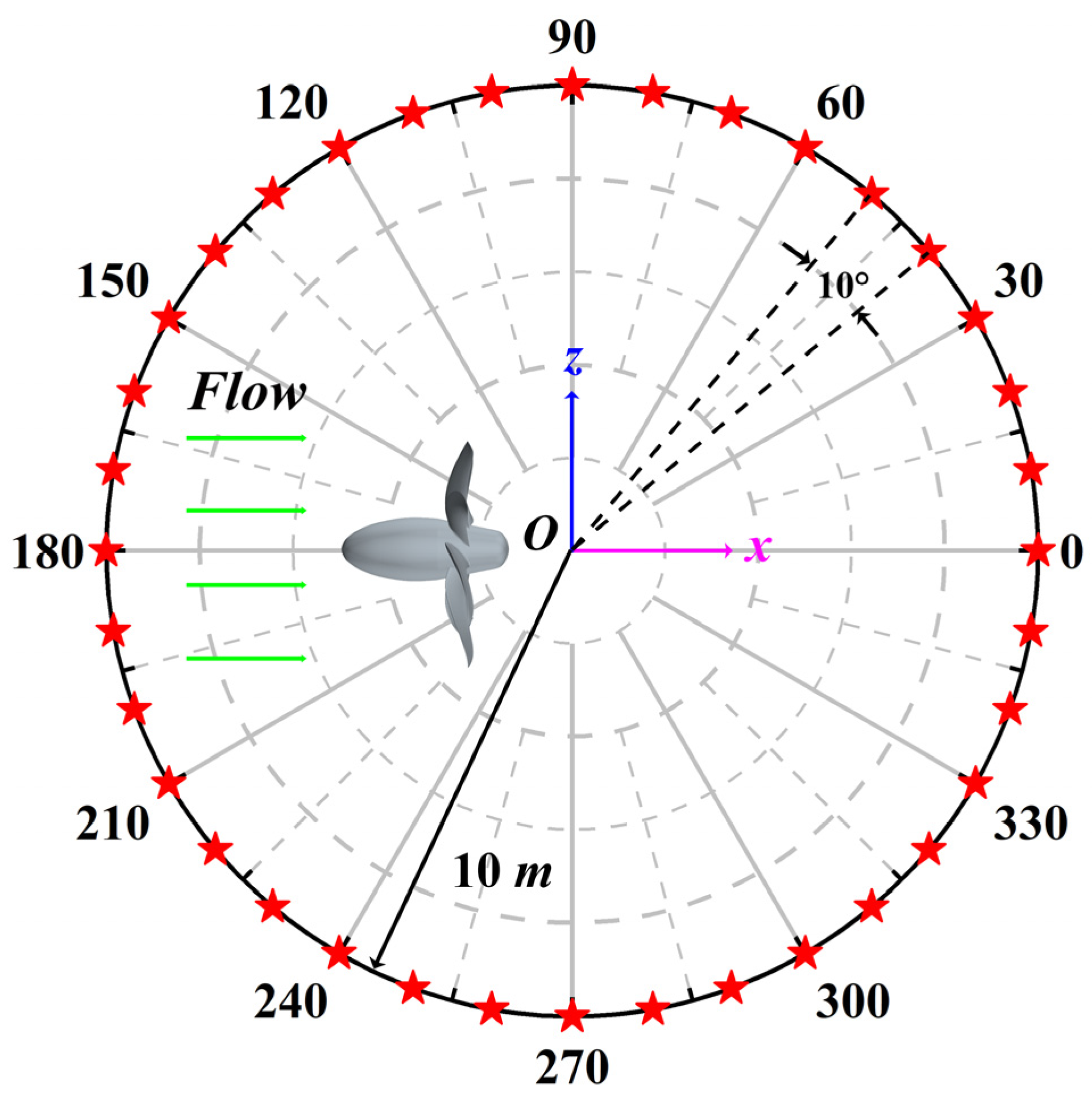
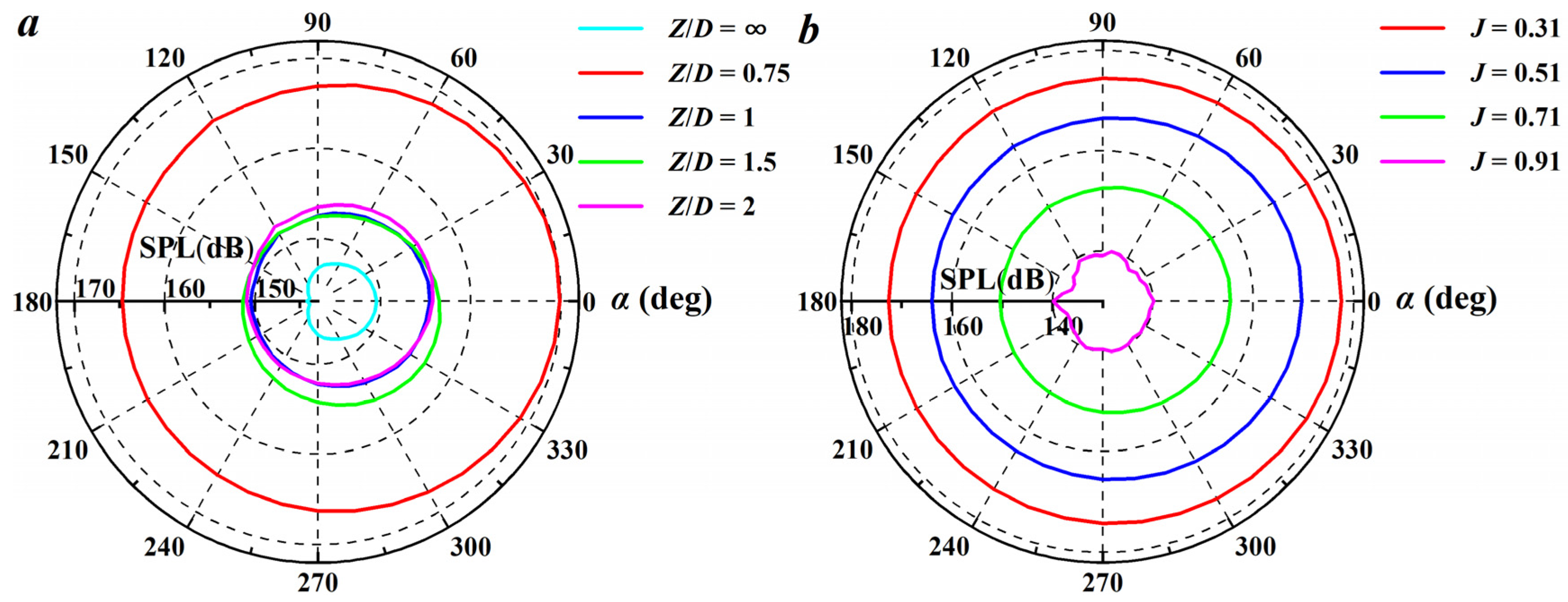
4.4. Radiated Noise
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Re | Reynolds number |
| z | Number of blades |
| Z | Immersion depth of the propeller |
| D | Propeller diameter |
| CP | Dimensionless pressure coefficient |
| R | Propeller radius |
| k | Turbulence kinetic energy |
| Dhub/D | Propeller/Hub diameter ratio |
| f | Frequency |
| P0.7R | Pitch at r = 0.7R |
| DES | Detached eddy simulation |
| c0.75R | Chord at 0.75R |
| URANS | Unsteady Reynolds-averaged Navier–Stokes |
| rG | Refinement ratio |
| LES | Large eddy simulation |
| KT | Thrust coefficient of the propeller |
| FW-H | Ffowcs-Williams and Hawkings |
| KQ | Torque coefficient of the propeller |
| IDDES | Improved delayed detached eddy simulation |
| η | Efficiency of the propeller |
| CFD | Computational fluid dynamics |
| T | Thrust of the propeller |
| N-S | Navier–Stokes |
| Q | Torque of the propeller |
| FVM | Finite volume method |
| J | Advance coefficient of the propeller |
| CNR-INSEAN | Institute of Marine Engineering-National Research Council Rome |
| n | Propeller rotational speed |
| EFD | Experimental fluid dynamics |
| U0 | Inflow velocity |
| SPL | Sound pressure level |
| L | Length of the submarine model |
| PSD | Power spectral density |
References
- Wang, L.Z.; Guo, C.Y.; Wan, L.; Su, Y.M. Numerical analysis of propeller during heave motion near a free surface. Mar. Technol. Soc. J. 2017, 51, 40–51. [Google Scholar]
- Mascio, D.A.; Dubbioso, G.; Muscari, R. Vortex structures in the wake of a marine propeller operating close to a free surface. J. Fluid Mech. 2022, 949, A33. [Google Scholar] [CrossRef]
- Orihara, H.; Miyata, H. Evaluation of added resistance in regular incident waves by computational fluid dynamics motion simulation using an overlapping grid system. J. Mar. Sci. Technol. 2003, 8, 47–60. [Google Scholar] [CrossRef]
- Arribas, F.P. Some methods to obtain the added resistance of a ship advancing in waves. Ocean Eng. 2007, 34, 946–955. [Google Scholar] [CrossRef]
- Sadat-Hosseini, H.; Wu, P.C.; Carrica, P.M.; Kim, H.; Toda, Y.; Stern, F. CFD verification and validation of added resistance and motions of KVLCC2 with fixed and free surge in short and long head waves. Ocean Eng. 2013, 59, 240–273. [Google Scholar] [CrossRef]
- Chuang, Z.; Steen, S. Prediction of speed loss of a ship in waves. In Proceedings of the Second International Symposium on Marine Propulsors smp, Hamburg, Germany, 15–17 June 2011; Volume 11, pp. 24–32. [Google Scholar]
- Ueno, M.; Tsukada, Y.; Tanizawa, K. Estimation and prediction of effective inflow velocity to propeller in waves. J. Mar. Sci. Technol. 2013, 18, 339–348. [Google Scholar] [CrossRef]
- Yu, D.; Wang, L.; Liu, H.; Cui, M. Influence of Load Conditions on the Propeller Wake Evolution. J. Mar. Sci. Eng. 2023, 11, 1674. [Google Scholar] [CrossRef]
- Sun, P.; Pan, L.; Liu, W.; Zhou, J.; Zhao, T. Wake characteristic analysis of a marine propeller under different loading conditions in coastal environments. J. Coast. Res. 2022, 38, 613–623. [Google Scholar] [CrossRef]
- Zhou, J.; Sun, P.; Pan, L. Modal analysis of the wake instabilities of a propeller operating in coastal environments. J. Coast. Res. 2022, 38, 1163–1171. [Google Scholar] [CrossRef]
- Gong, J.; Guo, C.Y.; Zhao, D.G.; Wu, T.C.; Song, K.W. A comparative DES study of wake vortex evolution for ducted and non-ducted propellers. Ocean Eng. 2018, 160, 78–93. [Google Scholar] [CrossRef]
- Chase, N. Simulations of the DARPA Suboff Submarine Including Self-Propulsion with the E1619 Propeller. Master’s Thesis, University of Iowa, Iowa City, IA, USA, 2012. [Google Scholar]
- Wang, L.; Liu, X.; Guo, J.; Li, M.; Liao, J. The dynamic characteristics in the wake systems of a propeller operating under different loading conditions. Ocean Eng. 2023, 286, 115518. [Google Scholar] [CrossRef]
- Baek, D.G.; Yoon, H.S.; Jung, J.H.; Kim, K.S.; Paik, B.G. Effects of the advance ratio on the evolution of a propeller wake. Comput. Fluids 2015, 118, 32–43. [Google Scholar] [CrossRef]
- Kozlowska, A.M.; Steen, S.; Koushan, K. Classification of different type of propeller ventilation and ventilation inception mechanism. In Proceedings of the First International Symposium on Marine Propulsors, Trondheim, Norway, 22–24 June 2009; pp. 22–24. [Google Scholar]
- Kozlowska, A.M.; Wöckner, K.; Steen, S.; Rung, T.; Koushan, K.; Spence, S. Numerical and experimental study of propeller ventilation. In Proceedings of the Second International Symposium on Marine Propulors, Hamburg, Germany, 15–17 June 2011. [Google Scholar]
- Paik, K.J. Numerical study on the hydrodynamic characteristics of a propeller operating beneath a free surface. Int. J. Nav. Archit. Ocean Eng. 2017, 9, 655–667. [Google Scholar] [CrossRef]
- Califano, A.; Steen, S. Numerical simulations of a fully submerged propeller subject to ventilation. Ocean Eng. 2011, 38, 1582–1599. [Google Scholar] [CrossRef]
- Paik, B.G.; Lee, J.Y.; Lee, S.J. Effect of propeller immersion depth on the flow around a marine propeller. J. Ship Res. 2008, 52, 102–113. [Google Scholar]
- Wang, L.; Martin, J.E.; Felli, M.; Carrica, P.M. Experiments and CFD for the propeller wake of a generic submarine operating near the surface. Ocean Eng. 2020, 206, 107304. [Google Scholar] [CrossRef]
- Lungu, A. A DES-based study of the flow around the self-propelled DARPA Suboff working in deep immersion and beneath the free-surface. Ocean Eng. 2022, 244, 110358. [Google Scholar] [CrossRef]
- Yu, M.S.; Wu, Y.S.; Pang, Y.Z. A review of progress for hydrodynamic noise of ships. J. Ship Mech. 2007, 11, 152–158. [Google Scholar]
- Leaper, R.; Renilson, M.; Ryan, C. Reducing underwater noise from large commercial ships: Current status and future directions. J. Ocean Technol. 2014, 9, 51. [Google Scholar]
- Carlton, J. Marine Propellers and Propulsion; Butterworth-Heinemann: Oxford, UK, 2018. [Google Scholar]
- Sezen, S.; Atlar, M. Marine propeller underwater radiated noise prediction with the FWH acoustic analogy part 3: Assessment of full-scale propeller hydroacoustic performance versus sea trial data. Ocean Eng. 2022, 266, 112712. [Google Scholar] [CrossRef]
- Özden, M.C.; Gürkan, A.Y.; Özden, Y.A.; Canyurt, T.G.; Korkut, E. Underwater radiated noise prediction for a submarine propeller in different flow conditions. Ocean Eng. 2016, 126, 488–500. [Google Scholar] [CrossRef]
- Chen, Y.W.; Pan, C.C.; Lin, Y.H.; Shih, C.F.; Shen, J.H.; Chang, C.M. Acoustic Field Radiation Prediction and Verification of Underwater Vehicles under a Free Surface. J. Mar. Sci. Eng. 2023, 11, 1940. [Google Scholar] [CrossRef]
- Ross, D.; Kuperman, W. Mechanics of Underwater Noise; Acoustical Society of America: Melville, NY, USA, 1989. [Google Scholar]
- Burella, G.; Moro, L.; Colbourne, B. Noise sources and hazardous noise levels on fishing vessels: The case of newfoundland and Labrador’s fleet. Ocean Eng. 2019, 173, 116–130. [Google Scholar] [CrossRef]
- Farkas, A.; Degiuli, N.; Martić, I.; Dejhalla, R. Numerical and experimental assessment of nominal wake for a bulk carrier. J. Mar. Sci. Technol. 2019, 24, 1092–1104. [Google Scholar] [CrossRef]
- Wilcox, D.C. Turbulence Modeling for CFD; DCW Industries, Incorporated: La Canada, CA, USA, 1994; Volume 2, pp. 103–217. [Google Scholar]
- Spalart, P.R. Comments on the Feasibility of LES for Wings and on the Hybrid RANS/LES Approach. In Proceedings of the First AFOSR International Conference on DNS/LES Ruston, LA, USA, 4–8 August 1997; pp. 137–147. [Google Scholar]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Guo, H.; Guo, C.; Hu, J.; Zhang, W. Wake-structure interaction of flow over a freely rotating hydrofoil in the wake of a cylinder. J. Fluids Struct. 2023, 119, 103891. [Google Scholar] [CrossRef]
- Zhang, J.; Gidado, F.; Adamu, A.; He, K.; Krajnović, S.; Gao, G. Assessment of URANS, SAS, and IDDES on the bi-stable wake flow of a generic ship. Ocean Eng. 2023, 286, 115625. [Google Scholar] [CrossRef]
- Guo, H.; Li, G.; Zou, Z. Numerical simulation of the flow around NACA0018 airfoil at high incidences by using RANS and DES methods. J. Mar. Sci. Eng. 2022, 10, 847. [Google Scholar] [CrossRef]
- Posa, A.; Broglia, R.; Shi, W.; Mario, F. Large eddy simulation of a marine propeller with leading edge tubercles. Phys. Fluids 2024, 36, 115148. [Google Scholar] [CrossRef]
- He, K.; Su, X.; Gao, G.; Krajnović, S. Evaluation of LES, IDDES and URANS for prediction of flow around a streamlined high-speed train. J. Wind Eng. Ind. Aerodyn. 2022, 223, 104952. [Google Scholar] [CrossRef]
- Lighthill, M.J. On sound generated aerodynamically I. General theory. Proc. R. Soc. Lond. A 1952, 211, 564–587. [Google Scholar]
- Zhou, B.Y.; Albring, T.A.; Gauger, N.R.; Economon, T.D.; Palacios, F.; Alonso, J.J. A discrete adjoint framework for unsteady aerodynamic and aeroacoustic optimization. In Proceedings of the 16th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference, Dallas, TX, USA, 22–26 June 2015; p. 3355. [Google Scholar]
- Zhou, B.Y.; Albring, T.; Gauger, N.R.; Ilario da Silva, C.R.; Economon, T.D.; Alonso, J.J. A discrete adjoint approach for jet-flap interaction noise reduction. In Proceedings of the 58th AIAA/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Grapevine, TX, USA, 9–13 January 2017; p. 0130. [Google Scholar]
- Choi, W.S.; Choi, Y.; Hong, S.Y.; Song, J.H.; Kwon, H.W.; Jung, C.M. Turbulence-induced noise of a submerged cylinder using a permeable FW–H method. Int. J. Nav. Archit. Ocean Eng. 2016, 8, 235–242. [Google Scholar] [CrossRef]
- Farassat, F.; Brentner, K.S. Supersonic quadrupole noise theory for high-speed helicopter rotors. J. Sound Vib. 1998, 218, 481–500. [Google Scholar] [CrossRef]
- Wang, L.; Wu, T.; Gong, J.; Yang, Y. Numerical analysis of the wake dynamics of a propeller. Phys. Fluids 2021, 33, 095120. [Google Scholar] [CrossRef]
- Guo, H.; Guo, C.; Hu, J.; Lin, J.; Zhong, X. Influence of jet flow on the hydrodynamic and noise performance of propeller. Phys. Fluids 2021, 33, 065123. [Google Scholar] [CrossRef]
- Felice, D.F.; Felli, M.; Liefvendahl, M.; Svennberg, U. Numerical and experimental analysis of the wake behavior of a generic submarine propeller. Prism 2009, 1, 158. [Google Scholar]
- Chase, N.; Carrica, P.M. Submarine propeller computations and application to self-propulsion of DARPA Suboff. Ocean Eng. 2013, 60, 68–80. [Google Scholar] [CrossRef]
- Rodriguez, S. Applied Computational Fluid Dynamics and Turbulence Modeling. In Practical Tools, Tips and Techniques; Springer Nature: Berlin, Germany, 2019. [Google Scholar]
- Felli, M.; Camussi, R.; Felice, D.F. Mechanisms of evolution of the propeller wake in the transition and far fields. J. Fluid Mech. 2011, 682, 5–53. [Google Scholar] [CrossRef]
- Lu, Y.; Zhang, H.; Pan, X. Comparison between the simulations of flow-noise of a submarine-like body with four different turbulent models. Chin. J. Hydrodyn. 2008, 23, 348–355. [Google Scholar]
- Jiang, W.C.; Zhang, H.X.; Meng, K.Y. Research on the flow noise of underwater submarine based on boundary element method. Chin. J. Hydrodyn. 2013, 28, 453–459. [Google Scholar]
- Heydari, M.; Sadat-Hosseini, H. Analysis of propeller wake field and vortical structures using k − ω SST Method. Ocean Eng. 2020, 204, 107247. [Google Scholar] [CrossRef]
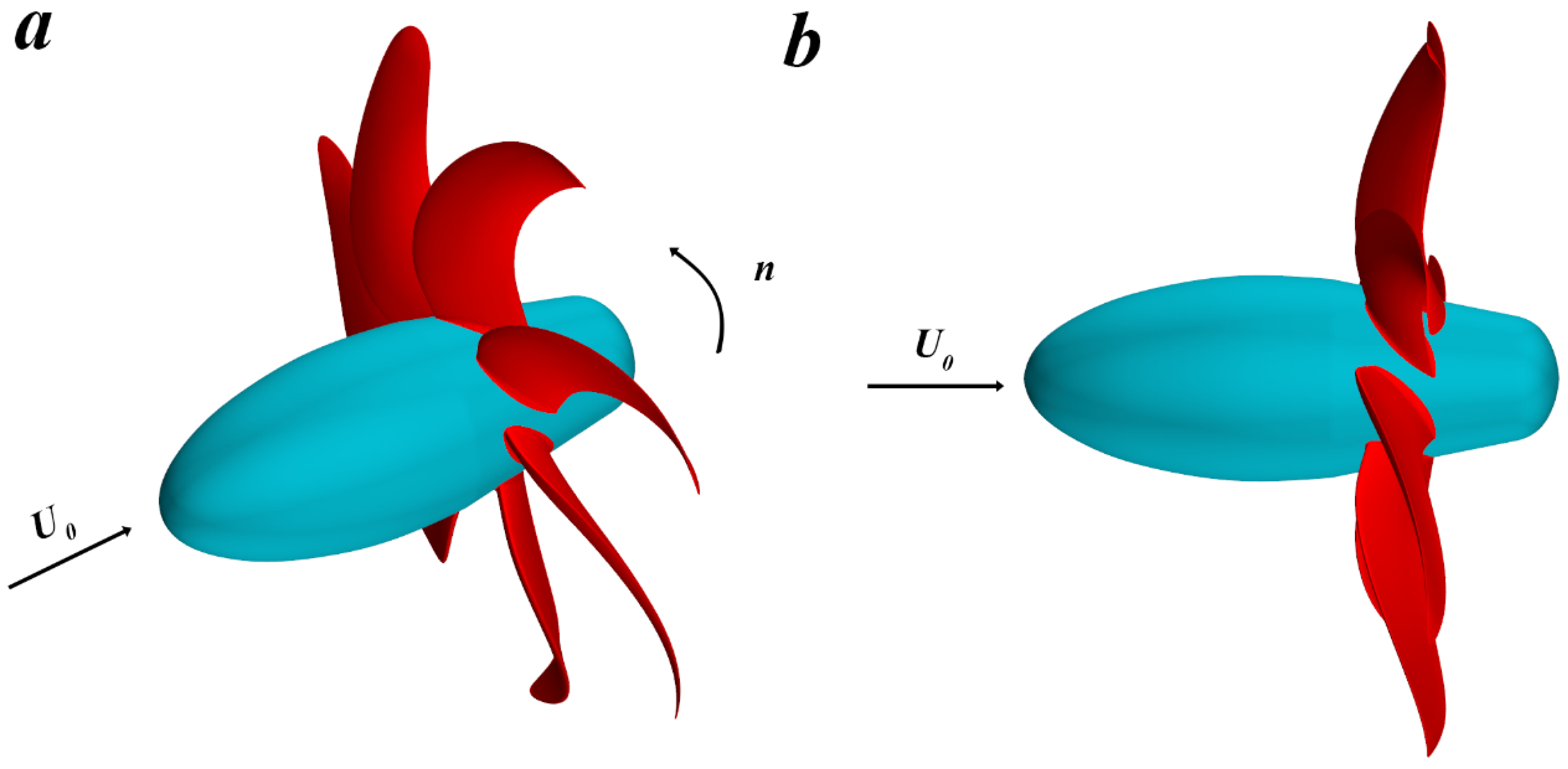
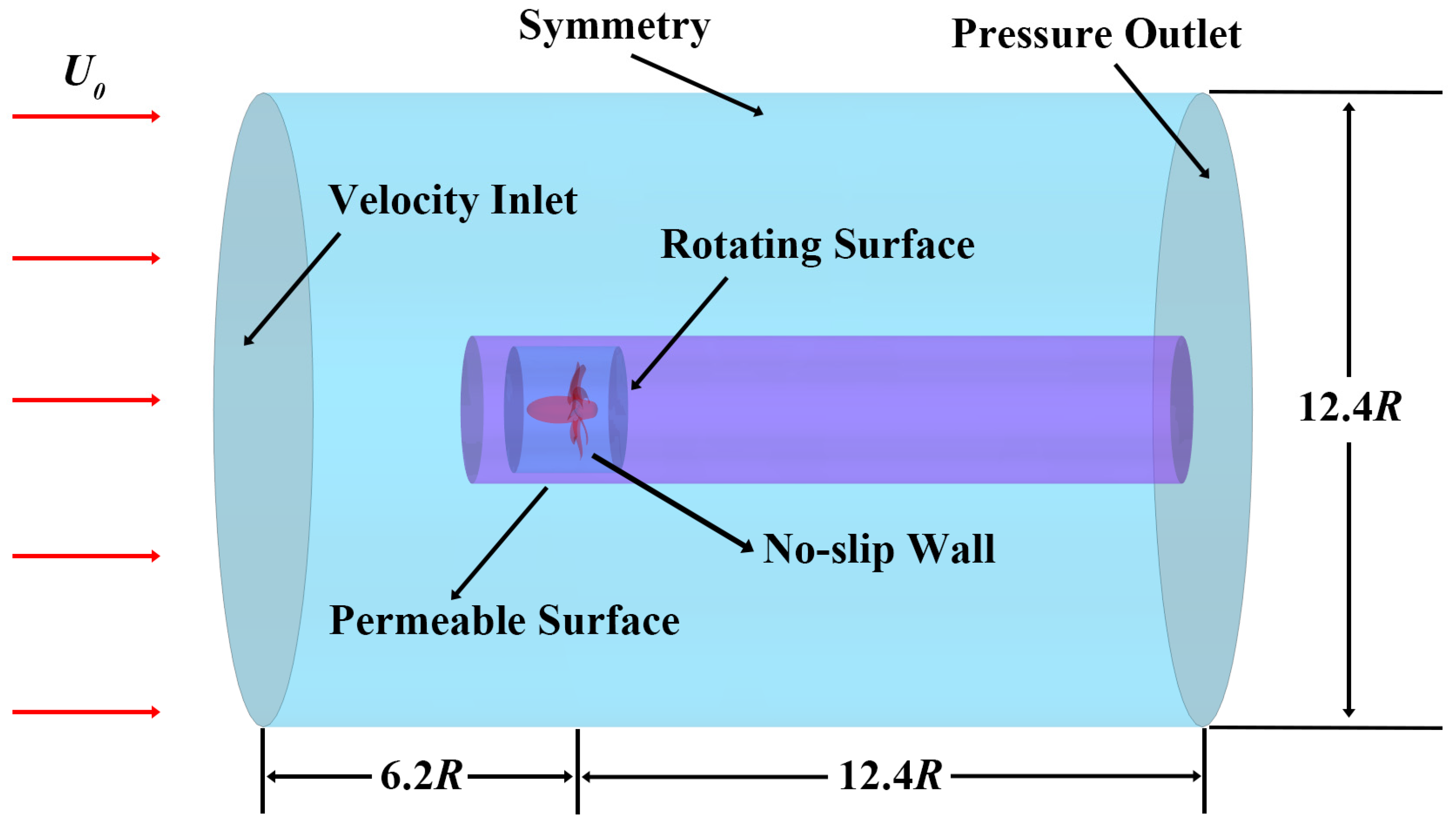
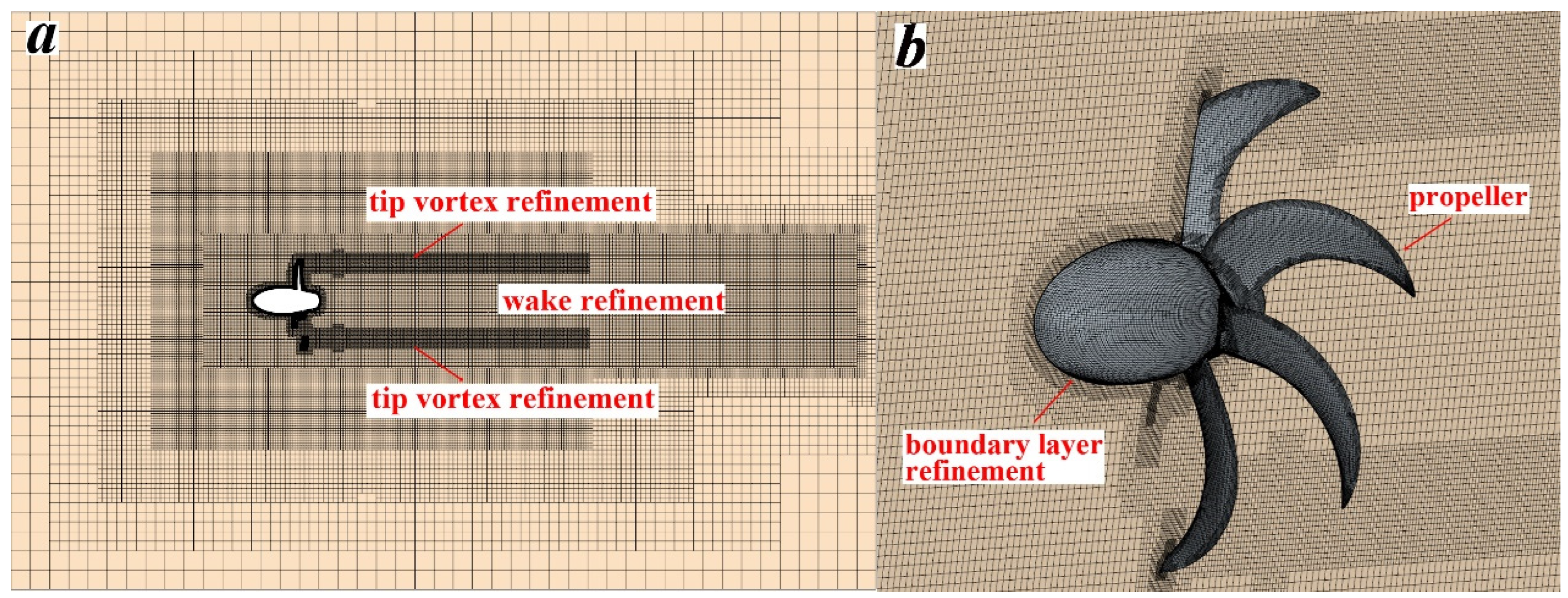
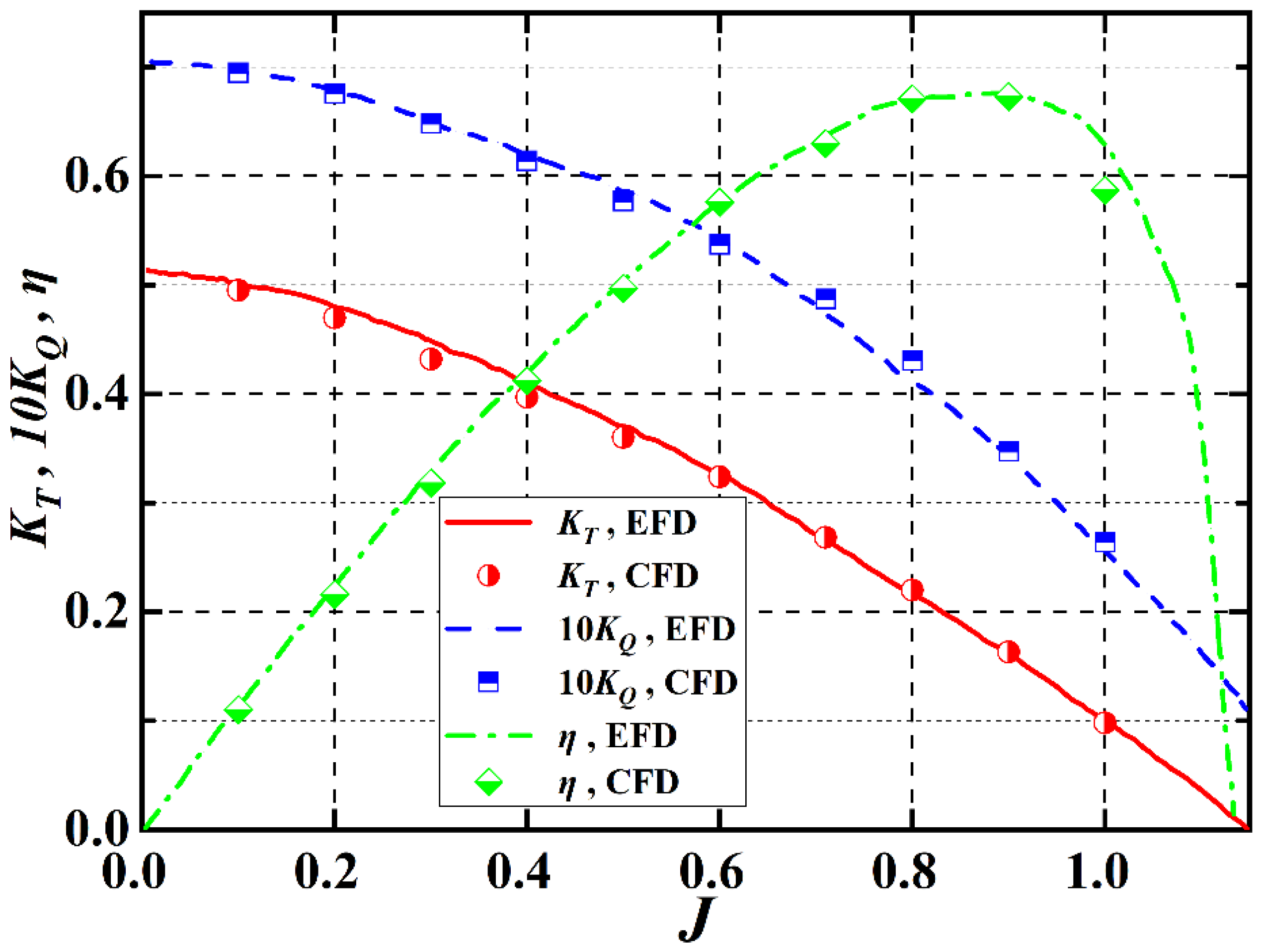
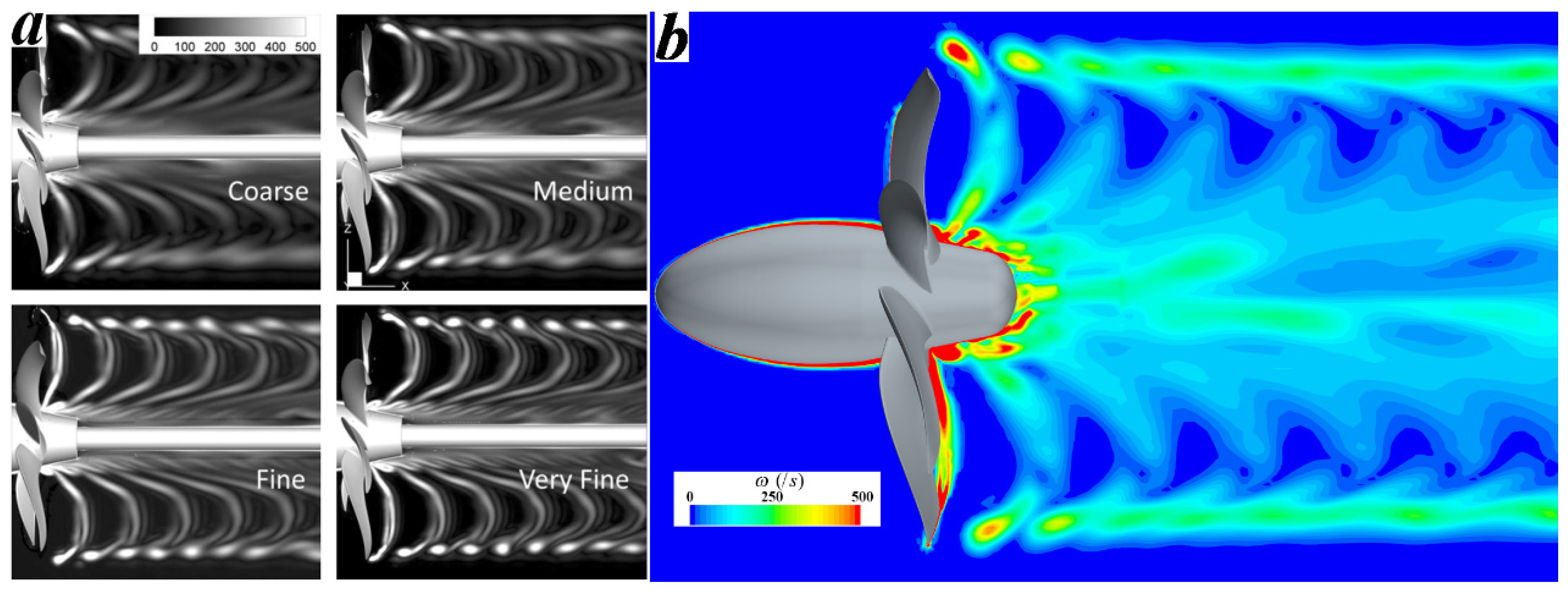

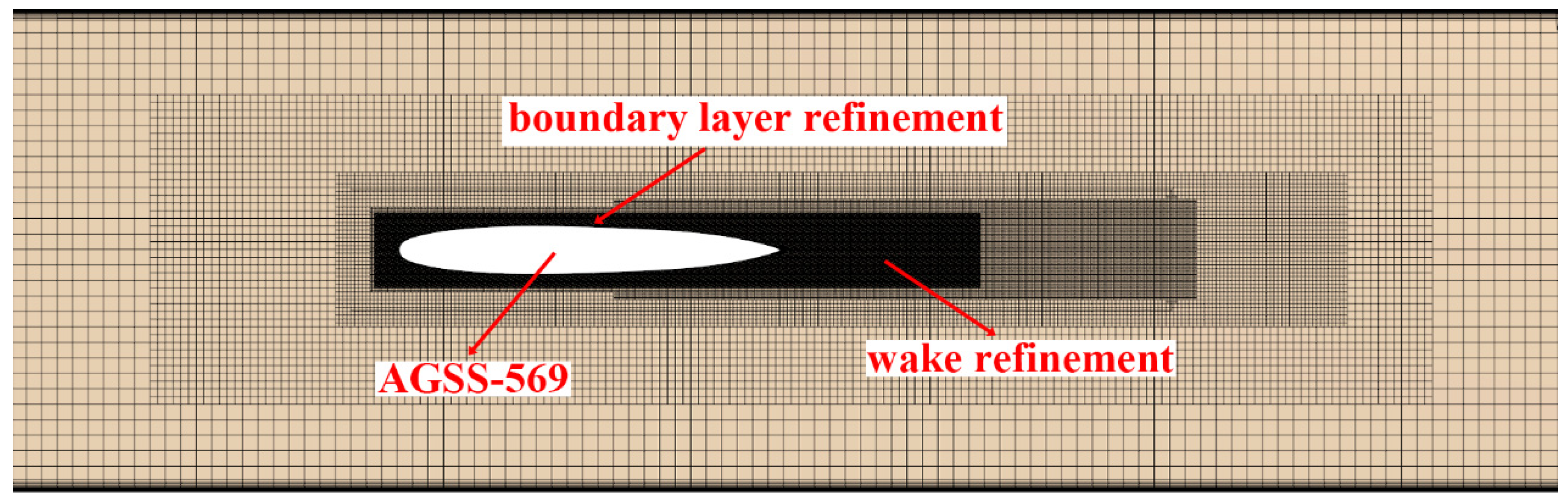
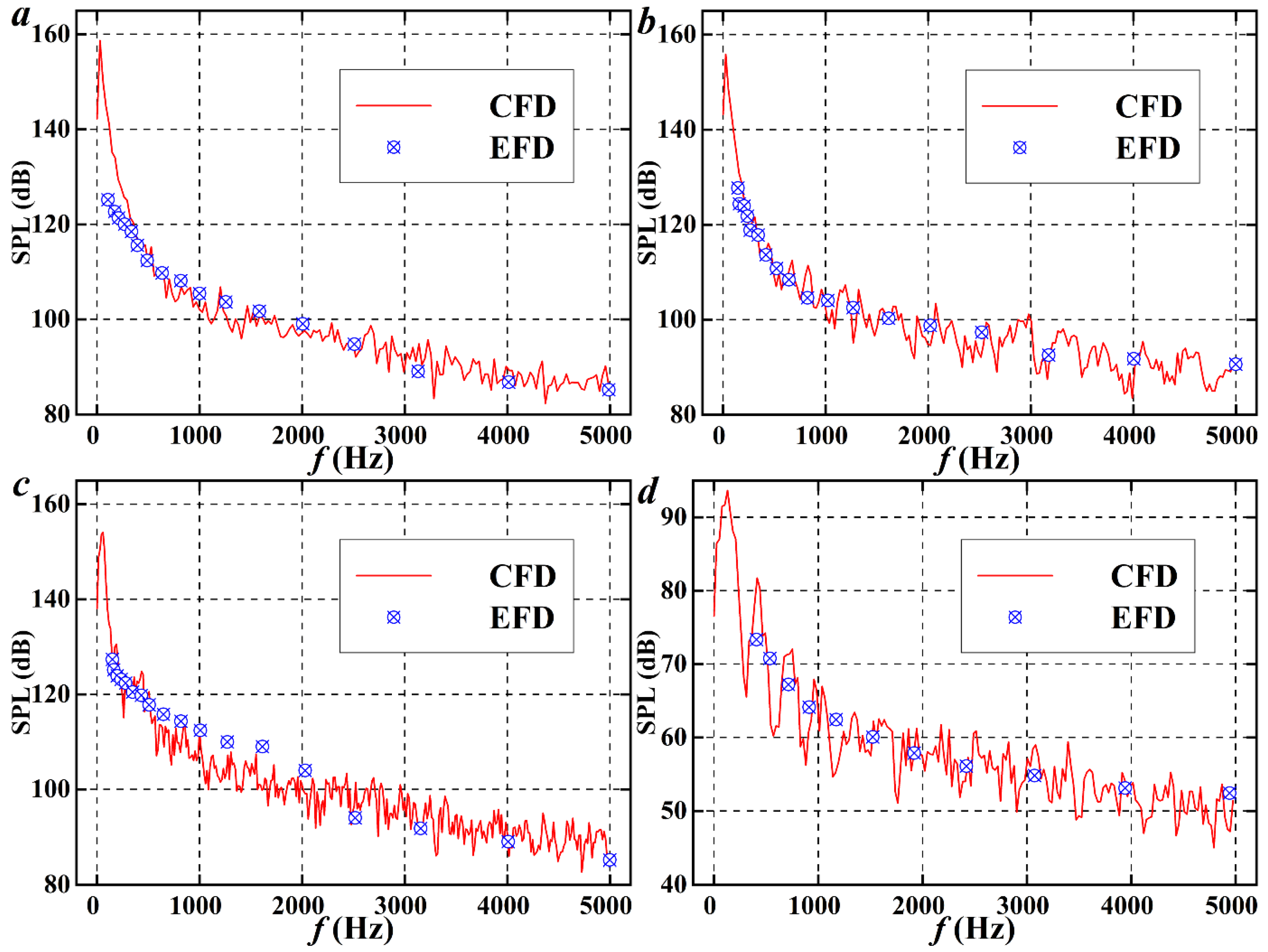
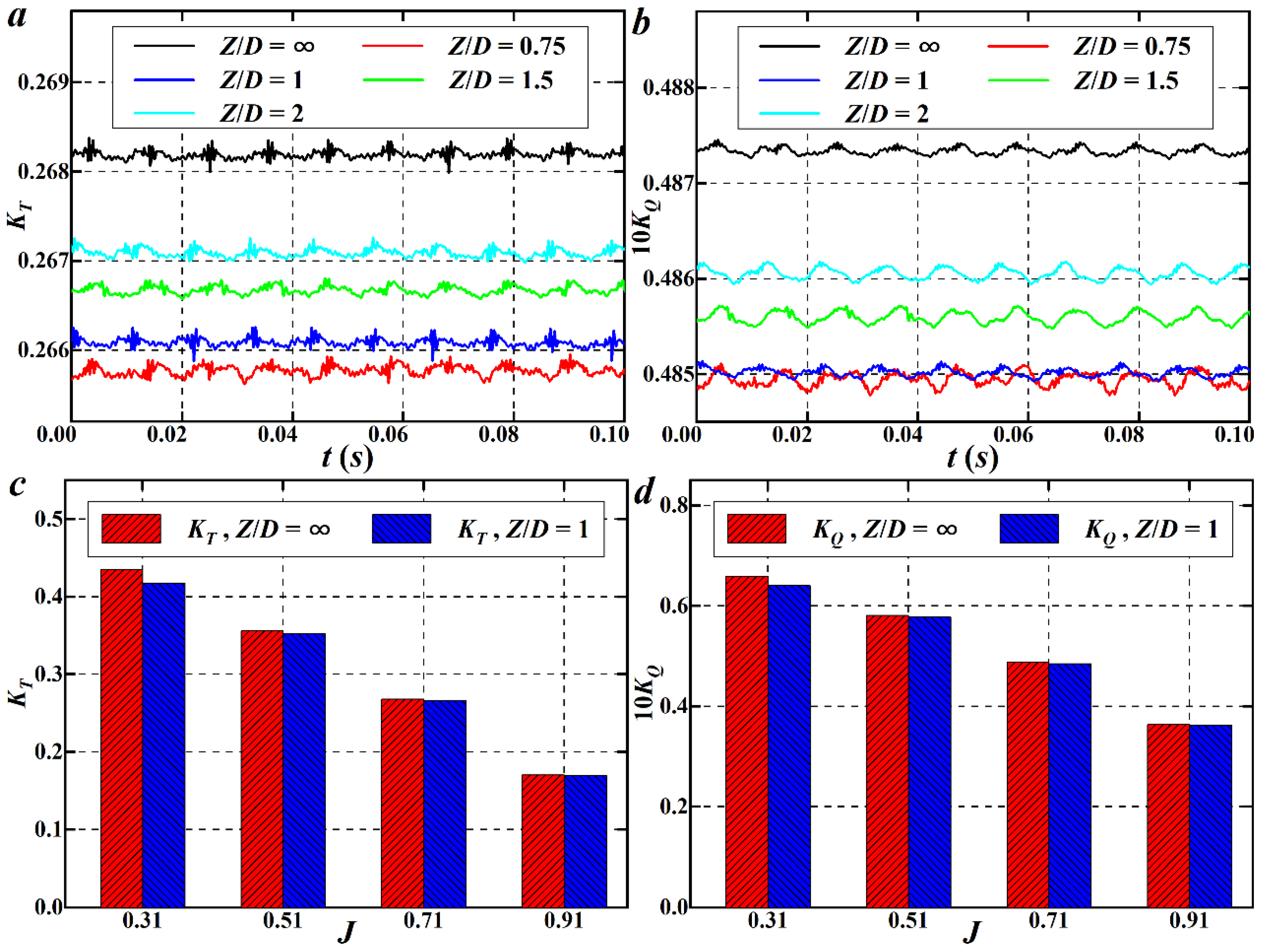



| Quantity | Symbol | Unit | Value |
|---|---|---|---|
| Number of blades | B | - | 7 |
| Propeller diameter | D | mm | 485 |
| Propeller radius | R | mm | 242.5 |
| Propeller/Hub diameter ratio | Dhub/D | - | 0.226 |
| Pitch at r = 0.7R | P0.7R | - | 1.15 |
| Chord at r = 0.75R | c0.75R | mm | 6.8 |
| J = 0.71 | KT | 10KQ | η | |
|---|---|---|---|---|
| Experiment [46] | 0.2657 | 0.4719 | 0.6389 | |
| Simulation | coarse grid | 0.2703 | 0.4947 | 0.6175 |
| medium grid | 0.2682 | 0.4873 | 0.6219 | |
| fine grid | 0.2676 | 0.4856 | 0.6227 | |
| Error (%) | coarse grid | 1.74 | 4.82 | 3.35 |
| medium grid | 0.95 | 3.27 | 2.66 | |
| fine grid | 0.72 | 2.90 | 2.53 | |
| Hydrophone | H1 | H2 | H3 | H4 |
|---|---|---|---|---|
| Coordinate | (0.4L, 180°) | (0.5L, 180°) | (0.65L, 180°) | (1.6 m, 0, −1.339 m) |
| J = 0.71 | KT | 10KQ | η |
|---|---|---|---|
| Z/D = ∞ | 0.2682 | 0.4873 | 0.6219 |
| Z/D = 0.75 | 0.2658 | 0.4849 | 0.6194 |
| Z/D = 1 | 0.2661 | 0.4850 | 0.6200 |
| Z/D = 1.5 | 0.2667 | 0.4856 | 0.6206 |
| Z/D = 2 | 0.2671 | 0.4861 | 0.6209 |
| Z/D = 1 | KT/KT0 | KQ/KQ0 | η/η0 |
|---|---|---|---|
| J = 0.31 | 0.9607 | 0.9727 | 0.9876 |
| J = 0.51 | 0.9895 | 0.9940 | 0.9955 |
| J = 0.71 | 0.9922 | 0.9953 | 0.9969 |
| J = 0.91 | 0.9940 | 0.9964 | 0.9976 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, D.; Yu, Y.; Yang, S. Influence of Free Surface on the Hydrodynamic and Acoustic Characteristics of a Highly Skewed Propeller. J. Mar. Sci. Eng. 2024, 12, 2208. https://doi.org/10.3390/jmse12122208
Yu D, Yu Y, Yang S. Influence of Free Surface on the Hydrodynamic and Acoustic Characteristics of a Highly Skewed Propeller. Journal of Marine Science and Engineering. 2024; 12(12):2208. https://doi.org/10.3390/jmse12122208
Chicago/Turabian StyleYu, Duo, Youbin Yu, and Suoxian Yang. 2024. "Influence of Free Surface on the Hydrodynamic and Acoustic Characteristics of a Highly Skewed Propeller" Journal of Marine Science and Engineering 12, no. 12: 2208. https://doi.org/10.3390/jmse12122208
APA StyleYu, D., Yu, Y., & Yang, S. (2024). Influence of Free Surface on the Hydrodynamic and Acoustic Characteristics of a Highly Skewed Propeller. Journal of Marine Science and Engineering, 12(12), 2208. https://doi.org/10.3390/jmse12122208






