The Dynamic Characteristics of the Water Entry of a Lifeboat

Abstract

The International Convention for the Safety of Life at Sea (SOLAS) stipulates that all ships must be equipped with lifesaving devices. The freefall lifeboat has the advantages of simple operation, fast release speed, and good safety performance, so it is widely used. The interaction between the hull and the water body of the freefall lifeboat during the water entry process is a complex fluid–structure interaction process that has great influence on the motion characteristics and structural force of the lifeboat. In order to improve the safety of lifeboats used in the lifesaving process, this paper establishes a 3D, full-scale model of a lifeboat and the fluid area, uses the ALE method to deal with the fluid–structure interaction problem, and numerically simulates the water entry of a lifeboat. Key information such as the hull motion trajectory, motion speed, and impact load are obtained, and three typical modes of lifeboat movement are summarized. At the same time, the influence of different skid angles, skid heights, and skid lengths on the lifeboat launch process is explored. The results show that increasing the angle, height, and length of the skid to a certain extent is conducive to the rapid escape of the lifeboat from a danger zone. The research results of this paper can provide a reference for the design of lifesaving systems for offshore floating facilities such as ships, which is of great significance for ensuring the safety of marine personnel.

1. Introduction

Floating facilities at sea, such as ships, often face harsh conditions and safety incidents like collisions, necessitating effective lifesaving measures to ensure onboard safety [1]. Currently, lifeboats are the primary equipment used, including both sliding and hanging types. The sliding lifeboat launches from the ship via a fixed inclined skid and falls freely into the water [2]. During this fall, it accumulates significant kinetic energy and experiences considerable hydrodynamic load upon hitting the water. This interaction between the hull and water results in dramatic changes in hull movement and presents significant challenges to the hull’s structural integrity [3]. Thus, examining the motion and force conditions of the water entry of a lifeboat is crucial for improving design safety.

Structural water entry is the process by which a structure or moving body enters a water medium through a free liquid surface from an air medium. It is an instantaneous nonlinear cross-medium multiphase flow problem involving the coupling of three solid–liquid–gas phases. Scholars have conducted much research on structural water entry under different conditions. In terms of theoretical research, Von Karman [4] first proposed using asymptotic line theory to deal with the problem of 2D, wedge-shaped bodies entering water. On this basis, Wagner [5] used the improved asymptotic line theory to obtain the velocity change and pressure distribution of the water body under the assumption that the water body is irrotational. Subsequently, Zhao and Faltinsen [6] introduced the potential flow theory to study the water entry of 2D objects of arbitrary cross-section. For the lifeboat water entry problem, the influence of different falling parameters on the motion of the lifeboat was studied a using mathematical model [7]. Boef et al. [8] proposed an added mass concept to impact problems of long cylinders with various cross-sectional shapes, and extending the analysis concept to the water entry of free-fall lifeboats provides a practical means of analysis for this problem [9]. By solving the lifeboat motion equation, Khondoker et al. [10] explored the influence of different falling parameters on lifeboat motion posture. Arai et al. [11] presented a mathematical model where impact was evaluated for a realistic lifeboat hull, based on the concept of momentum theory. Most of the early studies were 2D models, ignoring the lateral effect of the water body during the water entry of the lifeboat, and the results had certain limitations. Raman-Nair and White [12] used the Kane method to establish the motion equation of a free-fall lifeboat. A 2D model was used in the sliding stage, and a 3D model was proposed for the entry stage. The entry behavior characteristics of the lifeboat were obtained by solving an equation. Ringsberg et al. [13] used linear elastic and nonlinear beam models and nonlinear transient dynamic finite element analysis theory to solve the problem of slamming loads of water entry on a lifeboat. In terms of experimental research, Wei et al. [14] used a high-speed digital camera to conduct a series of experiments on the water entry of low Froude number cylinders, focusing on the lift and drag characteristics of the cylinders at different entry angles. Considering that most vehicles can be simplified as wedge-shaped structures, many scholars designed experiments to study the water entry of wedge-shaped bodies. Zeraatgar et al. [15] studied the effect of sampling rate on impact pressure in a wedge entry experiment. For wedges with different ramp angles, appropriate sampling frequencies were selected to improve the accuracy of peak pressure on value and position. Barjasteh et al. [16] conducted experimental research on the entry of asymmetric wedges into water at different ramp angles, inclinations, and velocities and compared them with symmetric wedges. They found that the initial ramp angle and inclination had a greater impact on the slamming of asymmetric wedges entering water. In addition to kinematic characteristics, many experimental studies focused on the evolution of cavities and jets after structures enter the water [17,18,19,20]. Based on the study of regular geometric bodies, Ré et al. [21] conducted free-fall tests on lifeboats under different weather conditions to evaluate whether the performance of the launch and entry process met design requirements. In addition, the lifeboat launch test can directly obtain the maximum slamming load, which is convenient for improving the safety of the lifeboat by adopting a design method to strengthen vulnerable areas [22]. To some extent, theoretical analysis and experimental research can obtain the motion response and force characteristics of the structure during the entry process, but most theoretical analyses are based on linear assumptions and cannot effectively solve the nonlinear problems that occur during the lifeboat entering the water. The process is also complicated. Also, the cost of experimental research is generally high, and the results obtained are highly dependent on high-speed cameras or sensors pre-arranged on the structure. They have certain limitations, and it is difficult to guarantee the accuracy of the results.

With the development of computer technology and computational-fluid-dynamics-related theories, numerical simulation can achieve high-precision water entry characteristics of structures in a short time. The research methods are mainly divided into two branches. One is the mesh-free method, which is mainly based on smoothed-particle hydrodynamics (SPH). Chen et al. [23] proposed an improved boundary algorithm and studied the dynamic characteristics of water entry of a lifeboat based on SPH. Lyu et al. [24] used a 3D, multi-resolution SPH model to explore the motion characteristics and cavity evolution of lifeboats at different entry angles. In order to improve computational efficiency, Li et al. [25] introduced the rigid-body 6-DOF motion equation and GPU acceleration technology to simulate the entry of lifeboats and analyzed the influence of different entry angles, horizontal speeds, and vertical speeds on motion attitude and slamming forces. When using SPH to calculate a 3D model, it is necessary to track a large number of particles, which is computationally expensive, and particle generation is complex. When dealing with solid boundaries, non-physical boundary effects are prone to occur, which affects calculation accuracy. By contrast, the numerical simulation method with mesh is more suitable for the study of complex structures entering water. Many scholars have used overlapping mesh technology to explore the characteristics of structures entering water [26,27,28,29,30], but the overlapping mesh method requires frequent data exchange in the overlapping area, which increases computational memory and may cause numerical instability. The ALE (arbitrary Lagrange Euler) method uses Lagrange to handle structure boundaries and Euler to construct meshes, which is suitable for situations involving large spatial displacements. In a study by Derakhshanian et al. [31], design experiments and numerical simulations were conducted to compare the finite volume Euler method, the finite difference Euler method, and the ALE. The results showed that the ALE method can obtain the slamming load more accurately at extreme entry angles and entry speeds. Shi et al. [32] used the ALE algorithm to establish a simulation model of a high-speed underwater vehicle; they analyzed the cavitation characteristics and the change in the slamming load under different head shapes and different entry parameters, and the simulation results were in good agreement with the experimental data. Peng et al. [33] studied the load characteristics of different opening methods at typical entry angles of a cross-medium vehicle based on the ALE method and completed a load reduction design based on the simulation results to effectively improve the structural strength of the vehicle. In addition, the ALE method can accurately simulate the large deformation problem of fluid–structure interaction under the condition of a small number of grids [34], which is suitable for the simulation of lifeboat launching into the water [35,36].

As for the dynamic characteristics of lifeboat water entry, many scholars have conducted several investigations. Specific analyses are shown in

Table 1. Discrepancy between this present study and other investigations regarding the comparison of dynamic characteristics.

Study	Model Type and Computational Method	Key Parameters	Dynamic Characteristic Outcome
Present study	3D and ALE	Skid angle, skid height, skid length	CG displacement, pitch angle, acceleration of stem and stern points, transversal and vertical velocity, slamming force
Raman-Nair and White [12]	2D in sliding stagr, 3D in entry stage and Kane method	CG position	Pitch angle, CG displacement
Boef et al. [8]	2D and mass concept theory	Still water, wave	Acceleration of the boat. CDRRs for seat positions at stern and bow
Ré et al. [21]	3D and experiment	Wave height, wind speed	Lifeboat trajectory, acceleration
Qiu et al. [37]	2D and mathematical theory	Wave height, entry position	Acceleration and velocity of pitch; acceleration of the bow, midship, and stern; trajectory pitch angle
Chen et al. [23]	3D and SPH	Entry angle	Vertical and transversal velocity, vertical and transversal displacement, rotation
Li et al. [25]	3D and SPH	Entry angle, entry transversal velocity, entry vertical velocity	CG displacement, pitch angle, transversal and vertical velocity
Huang et al. [27]	3D and CFD	Dropping angle, dropping height	Transversal and vertical velocity

. The key parameters used in previous studies were not comprehensive enough, and the dynamic characteristics results obtained had certain limitations.

In summary, through theoretical analysis, experimental research, and numerical simulation, significant progress has been made in the study of lifeboat launches. However, most research focuses on scaled or 2D lifeboat models, which inherently have certain limitations. Although a small portion of studies employs 3D, full-scale models, these methods are often complex, requiring significant computational resources and memory, along with high time costs. Additionally, some studies fail to account for fluid–structure interaction, leading to issues with accuracy. In addition, most scholars only focus on the entry stage of lifeboats and ignore the influence of the sliding stage, which is inconsistent with the actual application scenario. ALE more effectively allocates computing resources when dealing with large deformation problems. This paper takes advantage of this and establishes a 3D, real-scale model of lifeboats and fluids, considers the influence of fluid–structure interaction to simulate the entire process of sliding down and entering the water, and obtains comprehensive motion characteristics and load of the hull. Combined with the actual application scenario, the skid angle, height, and length are adjusted to explore the influence of different skid parameters on the entry process. This study can provide guidance and reference for the design of lifesaving systems for ships and marine floating structures and has very important practical engineering value.

This manuscript has been organized as follows: Section 2 mainly introduces the basic theory of the ALE method, penalty Function Algorithm, and lifeboat motion equations. Section 3 presents an overall introduction to the simulation model and verifies the numerical method; Section 4 contains the results and discussion of lifeboats entering water; and Section 5 offers some conclusions.

2. Numerical Methods

2.1. ALE Method Governing Equations

The ALE method combines the advantages of Lagrange and Euler. It uses a method similar to Lagrange to effectively track the structural boundaries. Compared with the traditional Euler method, ALE can adjust the position of the grid at any time during the numerical calculation process according to a specific situation to avoid excessive deformation of the grid [38].

In the ALE method, a third arbitrary reference coordinate is introduced in addition to Lagrange and Euler coordinates. The material differential quotient with respect to the reference coordinate is expressed as follows [38]:

$${\displaystyle \frac{\partial f\left(X_i,t\right)}{\partial t}}={\displaystyle \frac{\partial f\left(x_i,t\right)}{\partial t}}+w_i{\displaystyle \frac{\partial f\left(x_i,t\right)}{\partial x_i}}$$

(1)

where $X_i$ is the Lagrangian coordinate, $x_i$ is the Eulerian coordinate, and $w_i$ is the relative velocity, assuming $\nu$ represents material velocity, and u represents grid velocity; relative velocity is introduced as $w$ = $\nu$ − $u$.

The governing equations for ALE are derived from the time derivative of the material and the time derivative of the reference geometry configuration and are expressed as the following conservation equations for mass, momentum, and energy:

$${\displaystyle \frac{\partial \rho }{\partial t}}=-\rho {\displaystyle \frac{\partial {\nu }_i}{\partial x_i}}-w_i{\displaystyle \frac{\partial \rho }{\partial x_i}}$$

(2)

$$\upsilon {\displaystyle \frac{\partial {\nu }_i}{\partial t}}={\sigma }_{ij,j}+\rho b_i-\rho w_i{\displaystyle \frac{\partial {\nu }_i}{\partial x_j}}$$

(3)

$$\rho {\displaystyle \frac{\partial E}{\partial t}}={\sigma }_{ij}{\nu }_{i,j}+\rho b_i{\nu }_i-\rho w_j{\displaystyle \frac{\partial E}{\partial x_j}}$$

(4)

where $\rho$ is the density, and ${\sigma }_{ij}$ is the stress tensor, which can be expressed as follows:

$${\sigma }_{ij}=-p{\delta }_{ij}+\mu \left({\nu }_{i,j}+{\nu }_{j,i}\right)$$

(5)

This equation can be solved by combining the following boundary conditions and initial conditions:

$$\begin{array}{c}{\nu }_i=U_i^0\mathrm{on}{\mathsf{\Gamma }}_{1}domain\\ {\sigma }_{ij}{n}_j=0on{\mathsf{\Gamma }}_2\mathrm{d}\mathrm{o}\mathrm{m}\mathrm{a}\mathrm{i}\mathrm{n}\end{array}$$

where ${\mathsf{\Gamma }}_1\bigcup {\mathsf{\Gamma }}_2=\mathsf{\Gamma },{\mathsf{\Gamma }}_1\bigcap {\mathsf{\Gamma }}_2=0$. $\mathsf{\Gamma }$ represents the whole boundary of the computational domain, ${\mathsf{\Gamma }}_1$ represents the structure surface, and ${\mathsf{\Gamma }}_2$ represents the fluid surface. The subscript indicates that the parameter is an initial value, $n_j$ represents the unit vector of the outer normal of the boundary, and ${\sigma }_{ij}$ represents the Kronecker δ function.

In fluid mechanics, the Eulerian viewpoint can be implemented using two approaches, and, similarly, there are two methods for solving the ALE equation. The first method involves solving fully coupled equations through computational fluid dynamics (CFD), which allows for the control of only a single material within a single element. The second method is the operator-split approach, where the calculation for each time step is divided into two stages. The first stage of the calculation is a Lagrangian process, in which the grid moves with the material. At this time, the calculation speed is the change in internal energy caused by internal and external forces. When calculating the Lagrangian process, no material flows through the element boundary, and the mass is automatically conserved at this stage. The second stage of the calculation is the convection phase, which calculates the mass transport, internal energy, and momentum across the element boundary. This stage can be regarded as remapping the displacement grid of the first stage to its original position or an arbitrary position. The solution is calculated step by step according to the increment of time, and the central difference method with second-order time accuracy is used. For each node, the velocity and displacement are updated according to the following equations:

$$u^{n+{\displaystyle \frac{1}{2}}}=u^{n-{\displaystyle \frac{1}{2}}}+\mathsf{\Delta }t{M}^{-1}\left(F_{ext}^n+F_{int}^n\right)$$

(6)

$$x^{n+1}=x^{n-1}+\mathsf{\Delta }t{u}^{n+1/2}$$

(7)

where $F_{int}^n$ represents the internal force vector, $F_{ext}^n$ represents the external force vector, and $M$ represents the mass diagonal matrix.

2.2. Fluid–Structure Interaction Penalty Function Algorithm

Fluid–Structure Interaction problems are about the various behaviors of deformed solids under the action of flow fields and the influence of solid deformation on the flow field. They can be defined by a set of coupling equations that include both fluid and solid domains. The coupling effect is realized in different ways, depending on whether the domains overlap and penetrate each other. When there is no overlap and penetration between the domains, the coupling effect is realized through interface forces; when there are overlap and penetration, the coupling effect is realized by establishing differential equations such as constitutive equations, which are different from those of single-phase media.

In the ALE method, the penalty function algorithm is used to deal with Fluid–Structure Interaction problems. The solid structure uses Lagrange units, and the fluid domain uses ALE units. The basic principle of the penalty function algorithm is that node penetration is checked at each time step, and different treatments are made according to different penetration situations. If no penetration is detected, no response is made; if penetration occurs, an interface coupling force ($F_s)$ needs to be introduced between the node and the penetration main surface, which is proportional to the penetration ($\delta$) and main surface stiffness ($k$). The coupling force is described as follows:

$$F_s=-k\delta$$

(8)

The physical meaning of the above formula is equivalent to placing a normal spring between the slave node that is about to penetrate and the master surface. The force of this spring will limit the penetration of the slave node into the master surface. $k$ is the stiffness of the spring, and its value is as follows:

$$k=p_f{\displaystyle \frac{K{A}^2}{V}}$$

(9)

where $K$ is the bulk modulus of the fluid unit involved in the coupling, $V$ is the volume of the fluid unit including the master fluid node, and $A$ is the average area of the solid units connected to the slave nodes. $p_f$ is a scaling factor introduced to avoid the instability of the numerical simulation and is taken as 0.1 in this paper [39].

2.3. 6-DOF Equations of Motion for a Lifeboat

During the lifeboat launch, a motion coordinate system is established on the hull, with the X-axis pointing forward toward the bow, the Y-axis pointing to the left side of the hull, and the Z-axis pointing vertically upward. If the center of gravity of the hull does not coincide with the origin O of the moving coordinate system, the center of gravity is regarded as a point on a rigid body in general motion ($S_i\left(x,y,z\right)$). According to theoretical mechanics, the velocity vector ($V_i)$ of this point relative to the earth can be written as follows:

$$V_i=\left(u+qz-ry\right)i+\left(v+rx-pz\right)j\times \left(w+py-qx\right)k$$

(10)

where $u$, $v$, and $w$ are the velocity components of point O along the O_x, O_y, O_z axes, respectively; $p$, $q$, and $r$ are the angular velocity components of point $S_i$ along the O_x, O_y, and O_z axes; and $i$, $j$, and $k$ are the unit vectors of the moving system along the O_x, O_y, and O_z axes.

When the hull rotates at an angular velocity Ω, the derivative of the motion with respect to time is obtained according to the vector derivative law, as follows:

$$\begin{array}{c}{\displaystyle \frac{d{V}_i}{dt}}=[(u-vr+wq)-x(q^2+r^2)+y(pq-r)+z(pr+q)]i\\ +\left[(\nu -wp+ur)-y(r^2+p^2)+z(qr-p)+x(qp+r)\right]j\\ +\left[\right(w-uq+vp)-z(p^2+q^2)+x(rp-q)+y(rq+p\left)\right]k\end{array}$$

(11)

From this, we can know that the external force acting on the hull is

$$F=m{\displaystyle \frac{d{V}_i}{dt}}$$

(12)

Decompose F into its components $X$, $Y$, and $Z$ along the O_x, O_y, and O_z axes as follows:

$$X=m\left(\left(u-vr+wq\right)-x\left(q^2+r^2\right)+y\left(pq-r\right)+z\left(pr+q\right)\right)$$

(13)

$$Y=m\left(\left(\nu -wp+ur\right)-y\left(r^2+p^2\right)+z\left(qr-p\right)+x\left(qp+r\right)\right)$$

(14)

$$Z=m\left(\left(w-uq+vp\right)-z\left(p^2+q^2\right)+x\left(rp-q\right)+y\left(rq+p\right)\right)$$

(15)

$K$, $M$, and $N$ are the moments acting on the hull around the direction of axes O_x, O_y, and O_z.

$$K=I_{xx}p+\left(I_{zz}-I_{yy}\right)qr+m\left(y\left(w+pv-qu\right)-z\left(v+ru-pw\right)\right)$$

(16)

$$M=I_{\mathrm{yy}}q+\left(I_{xx}-I_{zz}\right)rp+m\left(z\left(u+qw-rv\right)-x\left(w+pv-qu\right)\right)$$

(17)

$$N=I_{zz}r+\left(I_{yy}-I_{xx}\right)pq+m\left(x\left(\nu +ru-pw\right)-y\left(u+qw-rv\right)\right)$$

(18)

Equations (13)–(18) are the 6-DOF motion equations of the lifeboat. In 3D motion, the kinematic response of the lifeboat can be obtained by coupling and solving the 6-DOF motion equations.

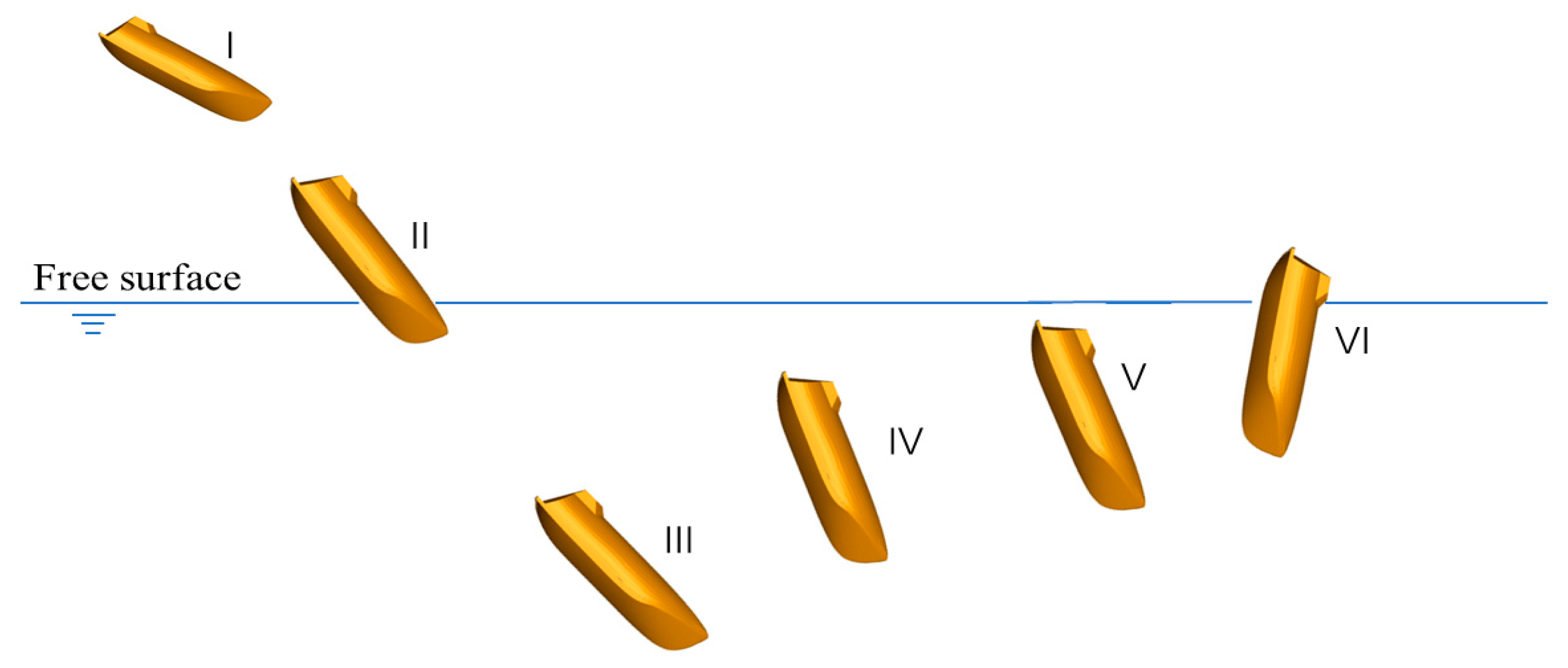
3. Numerical Model and Validation

3.1. Numerical Model

The model used for simulation in this paper is shown in Figure 1. The lifeboat hull type length is 14.8 m, the type width is 3.75 m, and the type depth is 4.22 m. The total mass is 38,098 kg. The fluid domain consists of air at the top and water at the bottom. The depths of the air domain and the water domain are 8 m and 20 m, respectively, the lengths are both 80 m, and the widths are both 20 m. The X-axis is defined as the forward movement direction of the lifeboat, the Y-axis is defined as the lateral movement direction, and the Z-axis is defined as the vertical movement direction. The angle between the base plane of the lifeboat and the free surface is the pitch angle of the hull (the initial angle is the same as the skid angle of the skid). The gravity acceleration is 9.8 m/s². At the start, the lifeboat launches down the skid without initial velocity. The dynamic friction coefficient between the skid and the hull is 0.2; this is a measured result from a previous experiment [21]. After leaving the skid, the lifeboat falls into the water freely under the effect of gravity.

In order to better simulate the lifeboat falling and water entering process, the lifeboat shell is set as a rigid body in LS-DYNA software (Ansys LS-DYNA 2022 R1 &LS-DYNA R12.0), and the lagrange_shell unit is used for modeling. The water and air domains are modeled using Euler_solid units. Since this study is not concerned with tracking the propagation of energy and pressure in water and air, water and air are regarded as compressible fluids, and their properties are defined by linear polynomial state equations [40]. The properties of the EOS linear polynomial of water are shown in

Table 2. Properties of EOS linear polynomial of water.

C0	C1	C2	C3	C4	C5	C6
1.013 × 105	2.250 × 109	0	0	0	0	0

. The bottom boundary is set as a non-moving wall to simulate the seabed, and the four vertical boundaries are defined as non-reflecting boundaries to prevent limitations on fluid behavior due to the confined water area.

3.2. Numerical Validation

This paper uses the sphere model in [41] to assess the effectiveness of the algorithm. The simulation model is shown in Figure 2. The radius of the sphere is 109 mm, and the mass is 3.76 kg. The length, width, and height of the water area are 560 mm, 560 mm, and 260 mm, respectively. The initial velocity of the sphere is 11.8 m/s, and the direction is vertically downward. At the beginning of the simulation, there is no gap between the sphere and the water surface.

The acceleration of the sphere is investigated to validate the effectiveness of the simulation algorithm, due to the presence of high-frequency signals seen in the numerical acceleration time histories. The data are filtered by the Savitzky–Golay filter. The results are shown in Figure 3. It can be seen from Figure 3 that the two curves are in good agreement, indicating that the simulation results are basically similar to the test results. The first peak value observed in the experiment is 64.4 g, while the corresponding peak value obtained using the ALE method is 68.29 g, representing a 6.04% increase compared to the experimental result. For the second acceleration peak, the simulation error is 1.2%, which falls within a reasonable and acceptable range. In the simulation, the small ball is regarded as completely rigid, and the initial kinetic energy is completely transferred to the fluid and acts on the sphere, but, in reality, the sphere has elastic deformation, and part of the initial kinetic energy is converted into deformation energy and dissipated due to the plastic characteristics of the material, so when the acceleration of the ball is stable, the calculation result is slightly higher than the test value. In summary, the ALE calculation method used in this paper has small discrepancy, showing that it is accurate and reliable and can be used for subsequent lifeboat entry simulation.

3.3. Mesh Convergence Validation

In this section, mesh convergence is verified for the water entry of the freefall lifeboat. Three sets of meshes are considered, i.e., coarse ($\mathsf{\Delta }x=1\mathrm{m}$), medium ($\mathsf{\Delta }x=0.5\mathrm{m}$), and fine ($\mathsf{\Delta }x=0.25\mathrm{m}$). The mesh convergence analysis in this paper measures vertical displacement during the overall process of the lifeboat falling down (Figure 4). Note that the results obtained using the coarse mesh do not agree with those obtained using medium and fine meshes. However, the results from the medium and fine mesh agreed well with each other. This suggests that the simulation results are reliable. As the mesh size decreases, the calculation time increases gradually. The specific differences are shown in

Table 3. Comparison of calculation times of different mesh sizes.

Mesh Size	Number of Processes	Computation Time
1 m	16	0.4 days
0.5 m	16	3 days
0.25 m	16	7 days

. In order to accurately capture the flow field characteristics around the lifeboat and save simulation time, the medium mesh was chosen for subsequent simulations.

4. Results and Discussion

4.1. Influence of Different Skid Angles

The lifeboat slides freely from skid with different inclined angles and enters the water at different angles and speeds. Its movement and slamming load are somewhat different. Selecting an optimal skid angle can effectively improve safety and comfort during the launching process. At present, the skid angle used by ships is generally 30–40° (the angle between the slide and the ship’s baseline), but in extreme sea conditions, the angle between the lifeboat and the free liquid surface will change to a certain extent as the ship moves. In order to investigate the influence of the skid angle on the lifeboat’s freefall launch, six skids with different inclined angles of 20°, 30°, 40°, 50°, 60°, and 70° were selected for research. The height of the end of the skid from the water surface is 35 m, and the center of gravity of the lifeboat is 13.2 m away from the end of the skid. At t = 0 s, the lifeboat begins to slide down along the skid due to gravity.

When the skid angles are 20–50°, the velocity cloud of the flow field during the lifeboat water entry process changes, as shown in Figure 5. The angle of the lifeboat changes during the leaving-skid phase, but this article focuses on the characteristics of the lifeboat after entering the water, so the motion image of the lifeboat in the air phase is not shown. In Figure 5, the moment when the lifeboat is about to contact the water surface is defined as the initial moment, that is, T = 0 s. As can be seen from Figure 5, at T = 0.3–0.6 s, the bow of the lifeboat enters the water, and the water around the hull is squeezed to form a jet that spreads around and forms a huge cavity. At moment T = 0.9 s, under the impact of the water, the bow of the lifeboat begins to rise, the jet and cavity at the rear of the hull are further broken, the tail falls rapidly, and the hull rotates counterclockwise. At T = 1.2–1.5 s, as the hull floats up, the rear cavitation begins to collapse, the surrounding liquid converges to the bottom of the cavitation, and droplets around the cavity splash. At T = 1.8–2.7 s, when the bow of the boat quickly crosses the water surface, a low-pressure cavity is formed at the tail, and the cavity crushing causes impact on the hull and forms a jet. At T = 3.0–3.3 s, under the effect of gravity, the hull and splashing water droplets gradually fall into the water.

Figure 6 shows the velocity cloud of the flow field during the lifeboat entering the water when the skid angles are 60° and 70°. When the skid angle is 60° (Figure 6a), the lifeboat enters the water at a similar angle to that at smaller angles (Figure 5), reaching its deepest position at T = 1.2 s. At this point, the hull is inclined downward. At T = 2.1 s, the hull surges out of the water at great speed, and a large low-pressure cavity is quickly formed at the tail, which interferes with the previously formed cavity jet and causes a huge impact on the hull, affecting the lifting movement of the hull. As shown in Figure 6b, when the skid angle is 70°, the lifeboat enters the water at a nearly vertical angle and reaches the deepest position at T = 2.1 s. At this moment, it still has a large downward inclined angle, and a cavity is generated inside the fluid. At T = 2.4–3.0 s, the cavity develops further, causing the hull angle to gradually increase. At T = 3.0–3.3 s, the hull undergoes clockwise rotation and begins to rise under the influence of buoyancy.

To more clearly illustrate the differences in the motion of the lifeboat after sliding down skids with varying angles, this paper collected the curve of the center of gravity (CG) of the lifeboat (Figure 7). The abscissa represents the displacement of the CG on the X-axis, and the ordinate represents the displacement of CG on the Z-axis. From Figure 7, it is evident that as the skid angle increases, the depth of water entry also increases. When the skid angle is less than 30°, the lifeboat does not become fully submerged, encountering minimal resistance from the water. Consequently, it travels further forward as the skid angle increases. However, when the skid angle exceeds 30°, the lifeboat becomes completely submerged, significantly reducing its horizontal advancement due to increased hydrodynamic resistance. Notably, at a skid angle of 60°, the lifeboat exhibits a tendency to sink again and reverse direction during the lifting stage. This effect becomes even more pronounced at a skid angle of 70°, where the reverse motion of the hull is highly significant, posing considerable risks.

During the sliding stage, the pitch angle of the lifeboat is consistent with the skid. Then, the lifeboat rotates clockwise around the CG, and the pitch angle increases. After entering the water, the bow of the boat is lifted up by the impact of the water body. Under the effect of buoyancy, it moves through the water surface at a certain rate. Under the effect of gravity, the pitch angle gradually decreases until it stabilizes. When the skid angle is below 60°, a smaller angle results in a reduced entry angle between the lifeboat and the water surface while increasing the exit angle as the lifeboat is lifted out of the water. In general, a smaller skid angle leads to less variation in the lifeboat’s longitudinal tilt, enhancing passengers’ comfort. As can be seen from Figure 8, when the skid angle is greater than 60°, the pitch angle of the lifeboat after entering the water is significantly different from that of the smaller skid angles. When the skid angle is 60°, the pitch angle of the lifeboat changes repeatedly during the lifting stage; when the skid angle is 70°, the bow of the lifeboat is not lifted to a horizontal position after entering the water, and the pitch angle continues to increase. In both cases, it is difficult for the lifeboat to return to a horizontal forward state.

Figure 9 shows the curve of vertical acceleration of the stem point and stern point changing with time, which reflects the intensity of the lifeboat’s pitch movement. As the skid angle increases, the bow movement becomes more intense, and the maximum acceleration of the tail occurs when the skid angle is 40°. This may be because at this angle, the lifeboat is subject to less water resistance at the moment of leaving the water, and the tail of the lifeboat has greater vertical acceleration under the crushing propulsion of the cavity. For passengers in the boat, the smaller the bow and stern acceleration, the more comfortable it can be. Considering this, a larger skid angle should not be adopted.

Figure 10 shows the time-varying curves of the velocity of the lifeboat along the X-axis corresponding to different skid angles. As shown in Figure 10a, the transversal velocity of the lifeboat when entering the water increases first and then decreases with the skid angle becoming bigger. During the water entry process, the impact of the water and the boat body causes the first velocity escalation. The first peak of transversal velocity is caused by the break of the cavity at the tail of the lifeboat, and the second peak takes place at the moment when the lifeboat crosses the water surface. A larger transversal velocity can allow the lifeboat to quickly move away from the mother ship to avoid collision. Figure 11 shows the time-varying curves of the speed of the lifeboat along the Z-axis, corresponding to different skid angles. As shown in Figure 11a, larger skid angles result in higher vertical speeds upon water entry but lower speeds during the lifting stage as the lifeboat exits the water. Additionally, Figure 10b and Figure 11b demonstrate that when the skid angle exceeds 60°, the lifeboat’s transversal and vertical velocity changes after water entry become highly complex and lack clear patterns. This irregularity poses significant risks and may lead to strong discomfort for passengers onboard.

Figure 12 illustrates the variation in slamming force on the lifeboat over time after water entry when the skid angle is 30°. In Figure 12, T = 0 is the moment when the lifeboat contacts the free surface. Combined with Figure 10 and Figure 11, it is evident that the hull experiences a significant impact force upon entering the water, leading to a rapid reduction in vertical velocity. At the same time, due to the squeezing effect of the water on the bottom of the boat, the transversal velocity of the lifeboat increases slightly. Since the lateral pressure of the water is relatively small, its influence on the lateral movement of the lifeboat is not discussed in this paper. As the cavity at the tail of the lifeboat is broken, vertical and transversal thrusts are generated to cause the hull to rotate counterclockwise around the Y axis and gain a certain amount of kinetic energy to jump out of the water. When the bow moves through the free surface, a low-pressure cavity is generated at the tail, which is quickly broken to produce a huge impact force, especially in the X direction (Figure 12) which significantly increases the vertical and transversal velocity of the hull, makes the lifeboat quickly float up, and leaves the water. Under the effect of gravity, the lifeboat falls back to the water surface and produces a second slamming effect with the water. During this second impact, the lifeboat has a smaller pitch angle, and the slamming force is notably reduced compared to that of initial water entry.

The impact on the lifeboat falling at different angles was analyzed. Figure 13 shows the transversal and vertical slamming forces after entering the water after sliding down the skid with different angles. The impact on the lifeboat is relatively large when entering and leaving the water. As shown in Figure 13, the vertical impact force decreases as the skid angle increases, while the transversal impact force remains nearly constant. This may be because a smaller entry angle increases the vertical contact area between the lifeboat and the water surface. When leaving the water, the greater the angle of the skid, the more severe the impact, especially when the angle is greater than 60°, as the transversal and vertical impact forces are significantly greater than those at a smaller angle.

Scholars have adjusted the skid parameters, explored the motion models of lifeboats, and summarized them into four types [41]. However, as ships become larger, lifeboat designs also gradually become larger, and early research on the movement posture of lifeboats is not enough to meet the design requirements of large lifeboats. In this study, the freefall movement modes of the lifeboat in the skid range of 20–70° can be summarized into three types: safe mode, acceptable mode, and dangerous mode (as shown in Figure 14, Figure 15 and Figure 16). The movement of the lifeboat is mainly divided into six processes. Taking the safe mode (Figure 14) as an example, the blue dotted line represents the free fluid surface. The six processes are as follows: Ⅰ—free fall; Ⅱ—bow entering the water; Ⅲ—underwater sliding; IV—lifting out of the water; Ⅴ—leaving the water body; and Ⅵ—stable floating. The safe mode is the most recommended by DNV [42]. This mode means that when the lifeboat engine is not working, it can still float to the surface at a certain forward speed. Even under the influence of wind and waves, the lifeboat can better avoid being dragged into the vicinity of the mother ship and collisions and other dangers. When the lifeboat movement state is in acceptable mode, starting the engine during the bow lifting stage can minimize the impact of the jet, which can basically ensure that the lifeboat can escape from danger safely. When the lifeboat is in danger mode, it is difficult to move away from the mother ship, with the bow lifting up even if the engine is started. This situation should be avoided.

In summary, for the lifeboat model used in this paper, the critical skid angle is 50°. At this angle, the lifeboat movement belongs to safe mode I, the peak transversal force is 25,160 kN, and the vertical peak slamming force is 218,602 kN. The skid angle has a great influence on the movement of the freefall lifeboat. A larger skid angle reduces the vertical slamming force on the hull. However, it also causes the lifeboat to submerge deeper, resulting in greater kinetic energy loss and delaying its departure from the mother ship. When the skid angle is too large, the lifeboat may flip in the opposite direction, causing great danger. In addition, as the skid angle of the skid increases, the change in the longitudinal tilt of the hull during the launch process increases, which may cause discomfort to the people in the boat.

4.2. Influence of Different Skid Heights

The freefall lifeboat and its skid are usually placed on the deck of the mother ship. The decks of different ship types have different heights from the water surface, resulting in different entry angles and speeds for the lifeboat after sliding down. Small and medium-sized lifeboats are usually installed on small and medium-sized ships. Their optimal drop height is generally 15–30 m [43]. As ships become larger, the installation position of lifeboats is gradually raised, reaching 30–40 m [44]. This section studies the influence of the skid height on the motion posture of the lifeboat. Considering that the lifeboat model used in this paper is 14.8 m long, the heights of the end of the skid from the water surface are selected to be 15 m, 25 m, 35 m, 45 m, and 55 m, respectively, for simulation. In the simulation, the CG of the lifeboat is 13.2 m away from the end of the skid, and the skid angle is 30°.

Figure 17 and Figure 18 show the trajectory of the CG of the lifeboat and the temporal variation in the pitch angle when falling from different heights. As shown in Figure 17, the depth of the lifeboat entering the water increases with the skid height becoming higher, and the forward distance is generally greater. It is worth noting that when the skid height is 25 m, the forward distance is significantly greater than that of the other conditions when the lifeboat enters the water at a small depth. This may be because, in this case, the hull has a certain transversal velocity when entering the water, and the entire hull is not completely immersed in the water. The water resistance is small during the lifting stage, and the kinetic energy loss is small. As shown in Figure 18, the smaller the skid height is, the more conducive it is to slow down the longitudinal shaking of the hull. It can be seen from Figure 19 that as the height of the skid increases, the vertical acceleration of the stem and stern of the lifeboat first increases and then decreases. The maximum value occurs when the skid height is 45 m, at which time the passengers in the boat feel more uncomfortable.

The evolution of the flow field velocity and free surface of the water entry of a lifeboat are shown in Figure 20. It is used to analyze falling velocity. Figure 21 shows the transversal and vertical velocity of the lifeboat changing with time after it slides freely from the skid at different heights. When entering the water, a higher drop height results in greater transversal and vertical peak velocities. However, in the underwater sliding and jumping stages, the drop height has no significant effect on the velocity. As shown in Figure 21a, at T = 4.6 s, the transversal velocity of the lifeboat sliding down from 25 m has a significant increase. The reason for this phenomenon may be that the hull of the lifeboat is not completely submerged in the water after entering the water and is less affected by water resistance. During the lifting process of the lifeboat, the tail cavitation jet impacts the hull and causes it to suddenly rush forward. Combined with the slamming force on the lifeboat, transversal and vertical slamming forces are exerted on the lifeboat, as shown in Figure 22. Upon water entry, both transversal and vertical impacts on the hull increase as the skid height rises. However, during the jumping phase, skid height has minimal influence on the hull forces. Due to the complex flow field, the hull force also has multiple peaks, but the maximum peak of the jumping impact is larger when the drop height is the smallest. In order to ensure the safety of the hull structure, large local stress should be avoided during the falling process, so a smaller drop height should not be selected.

In summary, the height of the skid mainly affects the vertical movement of the lifeboat. For the lifeboat studied in this paper, the optimal skid height is 45 m. If the skid height is low, the hull will not be fully submerged after entering the water. In this case, the kinetic energy loss is minimal, allowing the lifeboat to quickly move away from the mother ship area. However, the hull is significantly affected by the impact of the tail cavity jet, which can potentially damage the tail structure. At the same time, increasing the height of the skid will cause the hull to be hit harder when entering the water, which increases the risk of causing danger and discomfort to passengers. Reasonable selection of the skid height is critical to the stability of the lifeboat’s falling movement and structural safety.

4.3. Influence of Different Skid Length

The skid length is related to the size of the lifeboat. Generally, the sliding length is 0.5 the boat’s length [45]. This section studies the effect of the skid length on lifeboat water entry, with the goal of selecting a reasonable skid length to make the lifeboat safer, while minimizing discomfort to the people in the boat. To achieve this goal, three skids of different lengths, 20 m, 22 m, and 24 m, were selected for simulation. In the simulation, the height of the skid end from the water surface was 35 m, and the skid angle was 30°.

Figure 23 and Figure 24 show the trajectory of the CG and the temporal variation in the pitch angle of a lifeboat falling from skids of different lengths. As shown in Figure 23, the length of the skid has a certain influence on the vertical and transversal displacement of the lifeboat. As the skid length increases, both the entry depth and forward distance of the lifeboat initially increase and then decrease. The entry depth changes slightly, whereas the forward distance varies more obviously. The reason for this phenomenon may be that the increase in the length of the skid allows the lifeboat to have a longer air time, and the entry point is farther from the mother ship. However, the entry angle will also change, resulting in different water impacts, which affect the forward distance and entry depth. As shown in Figure 24, the pitch angle caused by the impact of the water on the bow decreases with the increase in skid length. In order to improve comfort for passengers in the lifeboat, the skid length can be appropriately increased. From the vertical acceleration curves at the stem and stern (Figure 25), it is evident that when the skid length is 20 m, passengers experience a higher level of comfort. As the skid length increases, the acceleration changes more dramatically, which is not conducive to improving the lifeboat experience.

The evolution of the flow field velocity and free surface of the water entry of a lifeboat is shown in Figure 26. They are used to analyze falling velocity, and Figure 27 shows the transversal and vertical velocity of the lifeboat changing with time. The transversal velocity of the lifeboat shows two positive peaks, and the vertical speed shows a negative peak and a positive peak. The two peaks correspond to the two processes of entering and leaving the water. The transversal and vertical speeds in the air stage increase with the increase in the skid length, but it has little effect on the speed of the lifeboat in a short period of time after entering the water. After jumping out of the water, the shorter the skid length, the greater the transversal forward speed and vertical lifting speed of the lifeboat. When the skid length is 20 m, the transversal forward speed when jumping out of the water is 17.76 m/s. When the skid length is 24 m, the transversal velocity is only 7.77 m/s. A higher transversal velocity is more beneficial for the lifeboat to quickly exit the danger zone. However, the faster the speed, the more likely it is to cause discomfort to the passengers in the boat.

The length of the skid has a certain influence on the slamming force after the lifeboat enters the water. Figure 28 shows the transversal and vertical slamming forces on the lifeboat over time after entering the water domain.

As shown in Figure 28, when entering the water for the first time, the magnitudes of the transversal and vertical slamming forces on the lifeboat are not greatly affected by the length of the skid, but when jumping out of the water, the force of the low-pressure cavitation at the tail of the lifeboat on the hull decreases with the increase in the skid length. Combined with speed analysis (Figure 27), this phenomenon may be because the lifeboat sliding down the longer skid has a smaller speed, the volume of the low-pressure cavity generated at the tail when leaving the water is smaller, and the impact force generated by the breakage is relatively small. When the skid length is 24 m, the slamming force on the lifeboat is much smaller than in the other two cases, and the structural safety is higher.

In summary, the length of the skid has an influence on the entry position and transversal velocity of the lifeboat. For the lifeboat used in this simulation, the optimal skid length is 24 m. Properly increasing the length of the skid can make the lifeboat have a greater forward speed and reduce the impact of the water body during the jumping stage. At the same time, it can slow down the pitch change in the hull and improve the comfort of the passengers in the boat. However, when designing the lifeboat skid for ships and marine structures, it is crucial to consider the deck space it occupies. If the skid is too long, it may interfere with other deck structures.

4.4. Simultaneous Effect of Skid Angle and Skid Length

The simultaneous effect of skid parameters during the water entry of a lifeboat influences the dynamics motion, flow field velocity, and the overall hydrodynamic forces experienced by the lifeboat. The skid parameters studied in this paper are angle, height, and length. The most sensitive parameters are the skid angle and skid length. The skid angle mainly affects the speed and angle of the lifeboat when entering the water, and the skid length mainly affects the position and transversal speed. The simultaneous effect of the two is analyzed as follows:

• Large Skid Angle with Short Skid Length:
  This configuration leads to an abrupt, steep impact upon contact with the water. The lifeboat experiences rapid deceleration and a short transversal distance. The combination of steep entry and concentrated water contact results in higher forces, potentially causing structural damage
• Large Skid Angle with Long Skid Length:
  Although the lifeboat enters the water steeply, the extended skid length helps distribute the forces over a larger surface area, providing more gradual deceleration. The transversal distance is still relatively short, but the entry is smoother than with a short skid length.
• Small Skid Angle with Short Skid Length:
  With shallow entry and short skid length, the lifeboat contacts the water at a lower angle, resulting in a moderate deceleration and a relatively longer transversal glide distance compared to a steep angle. The slamming force is lower than in scenarios with steep angles, but the distribution of forces is less favorable than with a longer skid length.
• Small Skid Angle with Long Skid Length:
  To some extent, this combination provides the smoothest and most controlled water entry. The shallow angle minimizes the vertical velocity, and the long length provides relatively large transversal velocity. The lifeboat experiences a long glide, with stable motion across the water. The slamming force is the lowest in this configuration, as the forces are distributed over a large area and the entry is more gradual. This scenario is ideal for minimizing the impact forces and ensuring safe water entry for a lifeboat and its occupants.

5. Conclusions

Based on the ALE method, this paper establishes a 3D, full-scale fluid–structure interaction model to simulate the water entry of a freefall lifeboat. It investigates the effects of varying skid angles, heights, and lengths on the dynamic characteristics of the water entry of a lifeboat. The key findings are summarized as follows:

• There are three main motion modes for the freefall lifeboat, namely, safe mode, acceptable mode, and dangerous mode. Safe mode: At maximum water depth, the hull has no downward angle. Without starting the engine, the lifeboat can achieve forward motion and safely move away from the mother ship. Acceptable mode: the hull has a slight downward angle at maximum water depth. The engine can be used to provide power to quickly leave the danger zone. Dangerous mode: The hull has a large angle at maximum water depth. The engine cannot help to lift the bow. And the lifeboat will move toward the mother ship and is likely to collide, which is very dangerous.
• The skid angle of the skid has a great influence on the movement of the lifeboat. Increasing the skid angle of the skid to a certain extent can allow the lifeboat to have enough speed to move away from the mother ship and reduce the impact of the water body. However, an excessively large skid angle can lead to substantial kinetic energy loss, a reduction in the transversal velocity peak, and excessive movement amplitude. These factors may result in dangerous situations such as capsizing or reverse collision with the mother ship.
• The height of the skid mainly affects the vertical movement of the lifeboat. A lower skid results in shallower water entry, leading to less kinetic energy loss. However, this also makes the lifeboat more vulnerable to the impact of the tail jet. Properly increasing the height of the skid can help the lifeboat stay away from the mother ship and improve the safety of the falling process.
• The length of the skid mainly affects the entry position and transversal movement of the lifeboat. Properly increasing the skid length can give the lifeboat enough transversal velocity to move away from the mother ship, while slowing down the change in the pitch angle of the hull and improving the comfort of the people in the boat. Increasing the length of the skid without conflicting with the mother ship structure is an effective measure to improve the safety of the lifeboat’s descent.

In this work, the lifeboat is considered rigid. However, the material should be deformable in an actual marine engineer situation. Therefore, in the future, studies considering deformable structure can be investigated. In practical applications, the number and position of people in the lifeboat have a certain influence on the movement and load of the hull. Subsequent research can consider changing the CG and weight of the lifeboat according to load conditions to more accurately simulate lifeboat water entry.